Automatic Detection and Unsupervised Clustering-Based Classification of Cetacean Vocal Signals †
Abstract
1. Introduction
1.1. Data Collection
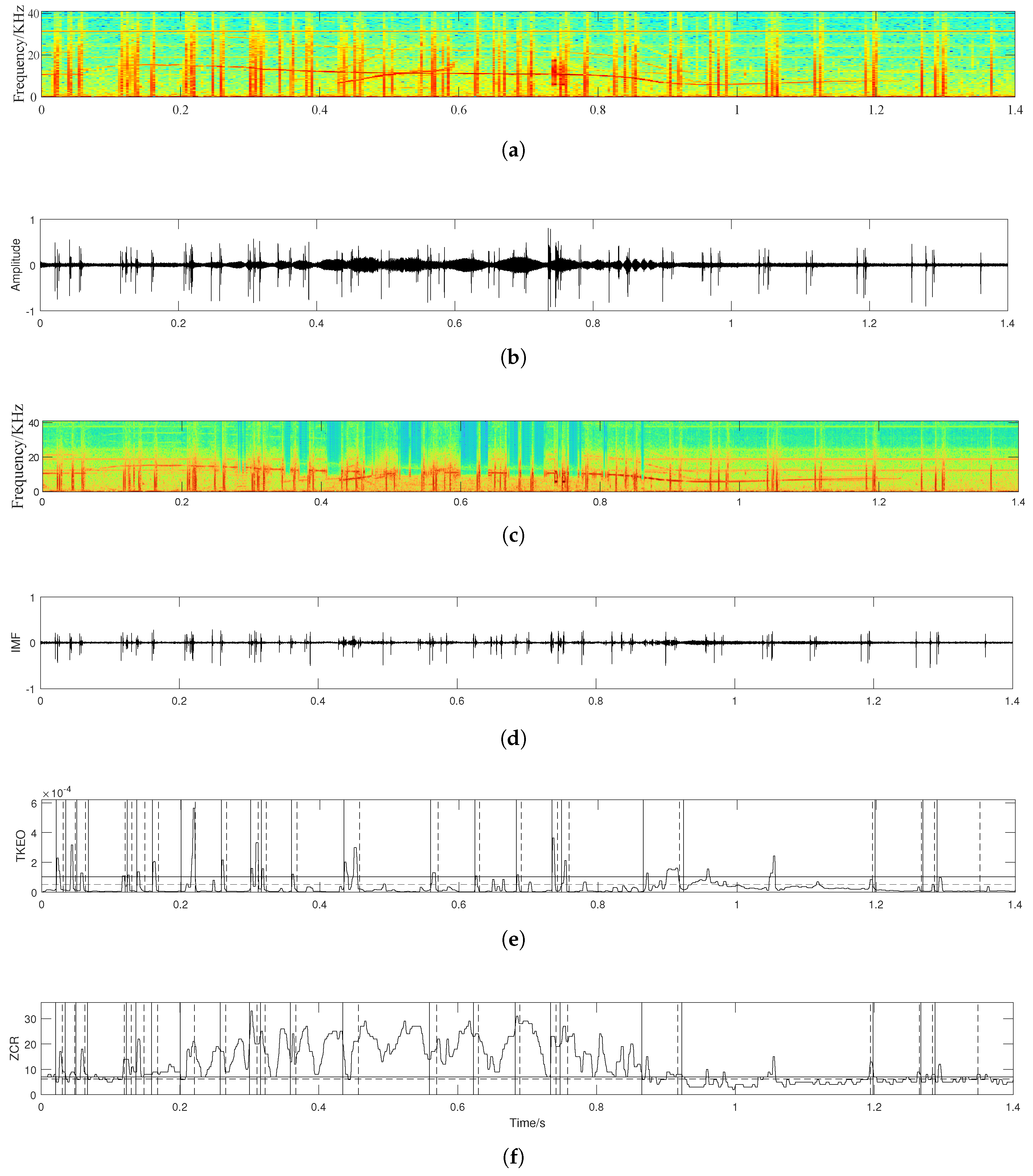
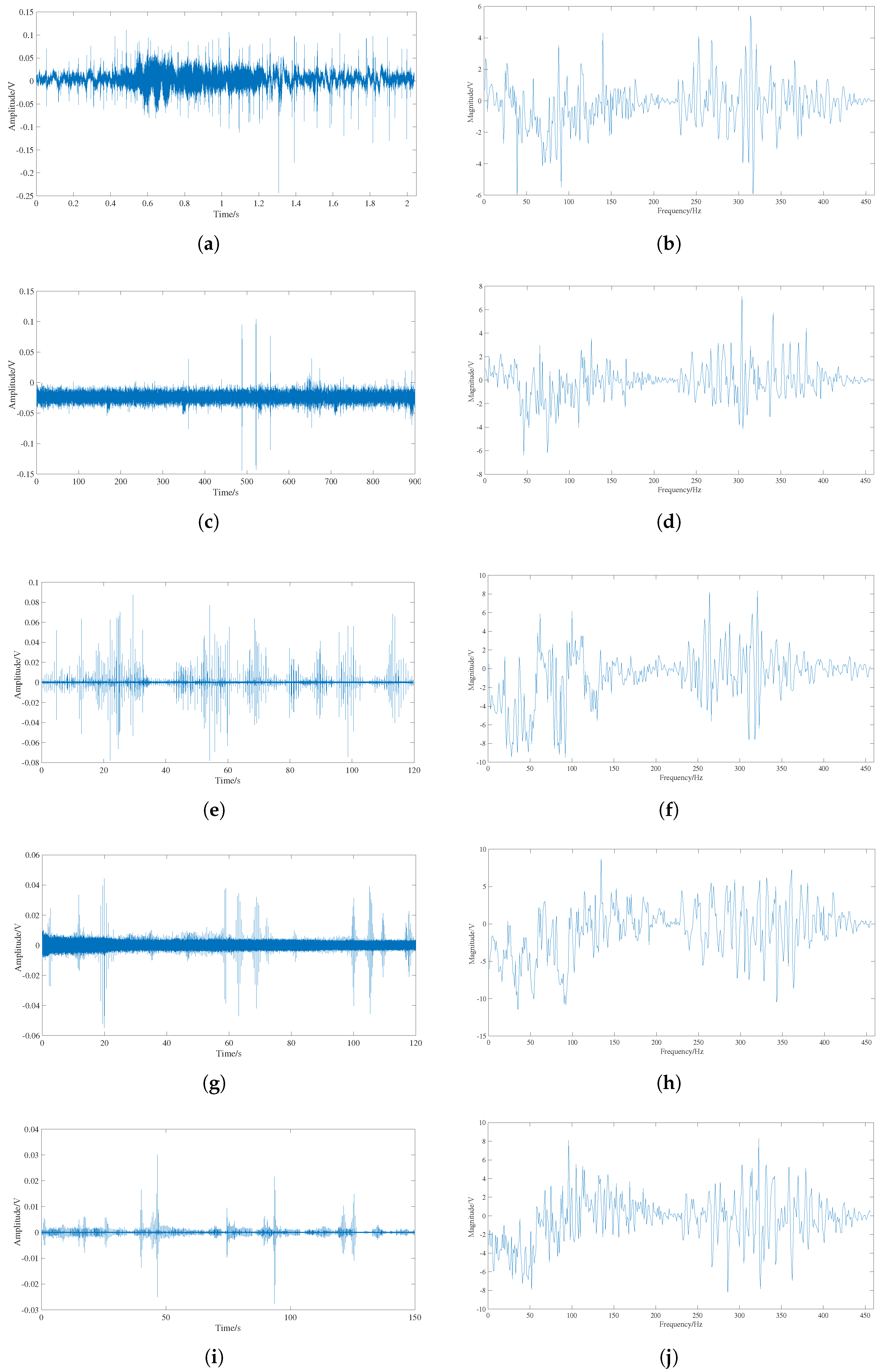
1.2. Automatic Detection
1.3. Feature Extraction
1.4. Unsupervised Classification
1.5. Evaluation Metrics
2. Experiments and Results
2.1. Detection
2.2. Clustering
3. Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Braulik, G.T.; Taylor, B.L.; Minton, G.; Notarbartolo di Sciara, G.; Collins, T.; Rojas-Bracho, L.; Crespo, E.A.; Ponnampalam, L.S.; Double, M.C.; Reeves, R.R. Red-list status and extinction risk of the world’s whales, dolphins, and porpoises. Conserv. Biol. 2023, 37, e14090. [Google Scholar]
- Mellinger, D.K.; Stafford, K.M.; Moore, S.E.; Dziak, R.P.; Matsumoto, H. An Overview of Fixed Passive Acoustic Observation Methods for Cetaceans. Oceanography 2007, 20, 36–45. [Google Scholar]
- Zimmer, W.M. Passive Acoustic Monitoring of Cetaceans; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Rankin, S.; Archer, F.; Keating, J.L.; Oswald, J.N.; Oswald, M.; Curtis, A.; Barlow, J. Acoustic classification of dolphins in the California Current using whistles, echolocation clicks, and burst pulses. Mar. Mammal Sci. 2017, 33, 520–540. [Google Scholar]
- Griffiths, E.T.; Archer, F.; Rankin, S.; Keating, J.L.; Keen, E.; Barlow, J.; Moore, J.E. Detection and classification of narrow-band high frequency echolocation clicks from drifting recorders. J. Acoust. Soc. Am. 2020, 147, 3511–3522. [Google Scholar]
- Staaterman, E. Passive Acoustic Monitoring in Benthic Marine Crustaceans: A New Research Frontier. In Listening in the Ocean; Au, W.W.L., Lammers, M.O., Eds.; Springer: New York, NY, USA, 2016; pp. 325–333. [Google Scholar]
- Wiggins, S.M.; Hildebrand, J.A. High-frequency Acoustic Recording Package (HARP) for broad-band, long-term marine mammal monitoring. In Proceedings of the 2007 Symposium on Underwater Technology and Workshop on Scientific Use of Submarine Cables and Related Technologies, Tokyo, Japan, 17–20 April 2007; pp. 551–557. [Google Scholar]
- Gillespie, D. An acoustic survey for sperm whales in the Southern Ocean Sanctuary conducted from the RSV Aurora Australis. Rep. Int. Whal. Comm. 1997, 47, 897–907. [Google Scholar]
- Kandia, V.; Stylianou, Y. Detection of sperm whale clicks based on the Teager–Kaiser energy operator. Appl. Acoust. 2006, 67, 1144–1163. [Google Scholar]
- Houser, D.S.; Helweg, D.A.; Moore, P.W. Classification of dolphin echolocation clicks by energy and frequency distributions. J. Acoust. Soc. Am. 1999, 106, 1579–1585. [Google Scholar]
- Klinck, H.; Mellinger, D. The energy ratio mapping algorithm: A tool to improve the energy-based detection of odontocete echolocation clicks. J. Acoust. Soc. Am. 2011, 129, 1807–1812. [Google Scholar]
- Gong, W.; Tian, J.; Liu, J.; Li, B. Underwater Object Classification in SAS Images Based on a Deformable Residual Network and Transfer Learning. Appl. Sci. 2023, 13, 899. [Google Scholar] [CrossRef]
- Ji, F.; Li, G.; Lu, S.; Ni, J. Research on a Feature Enhancement Extraction Method for Underwater Targets Based on Deep Autoencoder Networks. Appl. Sci. 2024, 14, 1341. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet classification with deep convolutional neural networks. Commun. ACM 2017, 60, 84–90. [Google Scholar]
- Luo, W.; Yang, W.; Zhang, Y. Convolutional neural network for detecting odontocete echolocation clicks. J. Acoust. Soc. Am. 2019, 145, EL7–EL12. [Google Scholar] [PubMed]
- Yang, W.; Luo, W.; Zhang, Y. Classification of odontocete echolocation clicks using convolutional neural network. J. Acoust. Soc. Am. 2020, 147, 49–55. [Google Scholar] [PubMed]
- Rasmussen, J.H.; Širović, A. Automatic detection and classification of baleen whale social calls using convolutional neural networks. J. Acoust. Soc. Am. 2021, 149, 3635–3644. [Google Scholar]
- Roch, M.A.; Soldevilla, M.S.; Burtenshaw, J.C.; Henderson, E.E.; Hildebrand, J.A. Gaussian mixture model classification of odontocetes in the Southern California Bight and the Gulf of California. J. Acoust. Soc. Am. 2007, 121, 1737–1748. [Google Scholar]
- Roch, M.; Soldevilla, M.; Hoenigman, R.; Wiggins, S.; Hildebrand, J. Comparison of Machine Learning Techniques for the Classification of Echolocation Clicks from Three Species of Odontocetes. Can. Acoust. 2008, 36, 41–47. [Google Scholar]
- Luo, W.; Yang, W.; Song, Z.; Zhang, Y. Automatic species recognition using echolocation clicks from odontocetes. In Proceedings of the 2017 IEEE International Conference on Signal Processing, Communications and Computing (ICSPCC), Xiamen, China, 22–25 October 2017; pp. 1–5. [Google Scholar]
- Roch, M.A.; Lindeneau, S.; Aurora, G.S.; Frasier, K.E.; Hildebrand, J.A.; Glotin, H.; Baumann-Pickering, S. Using context to train time-domain echolocation click detectors. J. Acoust. Soc. Am. 2021, 149, 3301–3310. [Google Scholar]
- Jiang, J.J.; Bu, L.R.; Wang, X.Q.; Li, C.Y.; Sun, Z.B.; Yan, H.; Hua, B.; Duan, F.J.; Yang, J. Clicks classification of sperm whale and long-finned pilot whale based on continuous wavelet transform and artificial neural network. Appl. Acoust. 2018, 141, 26–34. [Google Scholar]
- Trinh, Y.; Lindeneau, S.; Ackerman, M.; Baumann-Pickering, S.; Roch, M. Unsupervised clustering of toothed whale species from echolocation clicks. J. Acoust. Soc. Am. 2016, 140, 3302. [Google Scholar]
- Frasier, K.E.; Elizabeth Henderson, E.; Bassett, H.R.; Roch, M.A. Automated identification and clustering of subunits within delphinid vocalizations. Mar. Mammal Sci. 2016, 32, 911–930. [Google Scholar]
- Reyes Reyes, M.V.; Iñíguez, M.A.; Hevia, M.; Hildebrand, J.A.; Melcón, M.L. Description and clustering of echolocation signals of Commerson’s dolphins (Cephalorhynchus commersonii) in Bahía San Julián, Argentina. J. Acoust. Soc. Am. 2015, 138, 2046–2053. [Google Scholar]
- Li, K.; Sidorovskaia, N.A.; Tiemann, C.O. Model-based unsupervised clustering for distinguishing Cuvier’s and Gervais’ beaked whales in acoustic data. Ecol. Inform. 2020, 58, 101094. [Google Scholar]
- LeBien, J.G.; Ioup, J.W. Species-level classification of beaked whale echolocation signals detected in the northern Gulf of Mexico. J. Acoust. Soc. Am. 2018, 144, 387–396. [Google Scholar] [PubMed]
- Frasier, K.E.; Roch, M.A.; Soldevilla, M.S.; Wiggins, S.M.; Garrison, L.P.; Hildebrand, J.A. Automated classification of dolphin echolocation click types from the Gulf of Mexico. PLoS Comput. Biol. 2017, 13, e1005823. [Google Scholar]
- Ozanich, E.; Thode, A.; Gerstoft, P.; Freeman, L.A.; Freeman, S. Deep embedded clustering of coral reef bioacoustics. J. Acoust. Soc. Am. 2021, 149, 2587–2601. [Google Scholar]
- Mellinger, D.K.; Clark, C.W. MobySound: A reference archive for studying automatic recognition of marine mammal sounds. Appl. Acoust. 2006, 67, 1226–1242. [Google Scholar]
- Watkins, W.A.; Fristrup, K.; Daher, M.A.; Howald, T.J. Sound Database of Marine Animal Vocalizations Structure and Operations; Woods Hole Oceanographic Institution: Falmouth, MA, USA, 1992. [Google Scholar]
- Li, M.M.; Yang, H.W.; Hong, N.; Yang, S. Endpoint detection based on EMD in noisy environment. In Proceedings of the 2011 6th International Conference on Computer Sciences and Convergence Information Technology (ICCIT), Seogwipo, Republic of Korea, 29 November–1 December 2011; pp. 783–787. [Google Scholar]
- Liang, Y.; Chen, F.; Yu, H.; Chen, Y.; Ji, F. An EMD Based Automatic Endpoint Detection Method for Cetacean Vocal Signals. In Proceedings of the 2023 IEEE International Conference on Electrical, Automation and Computer Engineering (ICEACE), Changchun, China, 26–28 December 2023. [Google Scholar]
- Rabiner, L.; Schafer, R. Theory and Applications of Digital Speech Processing; Prentice Hall Press: Saddle River, NJ, USA, 2010; pp. 1–1056. [Google Scholar]
- Arthur, D.; Vassilvitskii, S. k-Means++: The Advantages of Careful Seeding; Technical Report 2006-13; Stanford InfoLab: San Francisco, CA, USA, 2006. [Google Scholar]
- Yang, J.; Zhang, D.; Frangi, A.F.; Yang, J.Y. Two-dimensional PCA: A new approach to appearance-based face representation and recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2004, 26, 131–137. [Google Scholar]
- Elhamifar, E.; Vidal, R. Sparse subspace clustering: Algorithm, theory, and applications. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 2765–2781. [Google Scholar]
- Liu, J.; Cai, D.; He, X. Gaussian mixture model with local consistency. In Proceedings of the AAAI Conference on Artificial Intelligence, Atlanta, GA, USA, 11–15 July 2010; Volume 24, pp. 512–517. [Google Scholar]
- Ali, M.; Alqahtani, A.; Jones, M.W.; Xie, X. Clustering and classification for time series data in visual analytics: A survey. IEEE Access 2019, 7, 181314–181338. [Google Scholar]
- Yang, K.; Shahabi, C. A PCA-based similarity measure for multivariate time series. In Proceedings of the 2nd ACM International Workshop on Multimedia Databases, Washington, DC, USA, 13 November 2004; pp. 65–74. [Google Scholar]
- Lin, T.H.; Tsao, Y.; Akamatsu, T. Comparison of passive acoustic soniferous fish monitoring with supervised and unsupervised approaches. J. Acoust. Soc. Am. 2018, 143, EL278–EL284. [Google Scholar]
- Brown, J.C.; Smaragdis, P. Hidden Markov and Gaussian mixture models for automatic call classification. J. Acoust. Soc. Am. 2009, 125, EL221–EL224. [Google Scholar] [CrossRef] [PubMed]
- Peso Parada, P.; Cardenal-López, A. Using Gaussian mixture models to detect and classify dolphin whistles and pulses. J. Acoust. Soc. Am. 2014, 135, 3371–3380. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Wright, J.; Huang, T.S.; Ma, Y. Image super-resolution via sparse representation. IEEE Trans. Image Process. 2010, 19, 2861–2873. [Google Scholar] [PubMed]
- Wu, C.; Zhao, J. Joint learning framework of superpixel generation and fuzzy sparse subspace clustering for color image segmentation. Signal Process. 2024, 222, 109515. [Google Scholar] [CrossRef]
- Song, S.; Ren, D.; Jia, Z.; Shi, F. Adaptive Gaussian Regularization Constrained Sparse Subspace Clustering for Image Segmentation. In Proceedings of the ICASSP 2024—2024 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Seoul, Republic of Korea, 14–19 April 2024; IEEE: New York, NY, USA, 2024; pp. 4400–4404. [Google Scholar]
- Razik, J.; Glotin, H.; Hoeberechts, M.; Doh, Y.; Paris, S. Sparse coding for efficient bioacoustic data mining: Preliminary application to analysis of whale songs. In Proceedings of the 2015 IEEE International Conference on Data Mining Workshop (ICDMW), Atlantic City, NJ, USA, 14–17 November 2015; IEEE: New York, NY, USA, 2015; pp. 780–787. [Google Scholar]
- Wright, J.; Ma, Y.; Mairal, J.; Sapiro, G.; Huang, T.S.; Yan, S. Sparse representation for computer vision and pattern recognition. Proc. IEEE 2010, 98, 1031–1044. [Google Scholar] [CrossRef]
- Sui, Y.; Wang, G.; Zhang, L. Sparse subspace clustering via low-rank structure propagation. Pattern Recognit. 2019, 95, 261–271. [Google Scholar]
- Goel, A.; Majumdar, A. Sparse subspace clustering incorporated deep convolutional transform learning for hyperspectral band selection. Earth Sci. Inform. 2024, 17, 2727–2735. [Google Scholar] [CrossRef]
- Xing, Z.; Peng, J.; He, X.; Tian, M. Semi-supervised sparse subspace clustering with manifold regularization. Appl. Intell. 2024, 54, 6836–6845. [Google Scholar] [CrossRef]
- Sui, J.; Liu, Z.; Liu, L.; Jung, A.; Li, X. Dynamic sparse subspace clustering for evolving high-dimensional data streams. IEEE Trans. Cybern. 2020, 52, 4173–4186. [Google Scholar] [CrossRef]
- Powers, D.; Ailab. Evaluation: From precision, recall and F-measure to ROC, informedness, markedness and correlation. J. Mach. Learn. Technol. 2011, 2, 2229–3981. [Google Scholar]
- Avon, G.; Bucolo, M.; Buscarino, A.; Fortuna, L. Sensing frequency drifts: A lookup table approach. IEEE Access 2022, 10, 96249–96259. [Google Scholar] [CrossRef]
- Buscarino, A.; Famoso, C.; Fortuna, L.; Frasca, M. Multi-jump resonance systems. Int. J. Control 2020, 93, 282–292. [Google Scholar] [CrossRef]
- Mandic, D.P.; ur Rehman, N.; Wu, Z.; Huang, N.E. Empirical mode decomposition-based time-frequency analysis of multivariate signals: The power of adaptive data analysis. IEEE Signal Process. Mag. 2013, 30, 74–86. [Google Scholar] [CrossRef]
- Kaiser, J. On a simple algorithm to calculate the ‘energy’ of a signal. In Proceedings of the International Conference on Acoustics, Speech, and Signal Processing, Albuquerque, NM, USA, 3–6 April 1990; Volume 1, pp. 381–384. [Google Scholar]
- Junqua, J.C.; Reaves, B.; Mak, B. A study of endpoint detection algorithms in adverse conditions: Incidence on a DTW and HMM recognizer. In Proceedings of the Eurospeech, Genova, Italy, 24–26 September 1991; Volume 91, pp. 1371–1374. [Google Scholar]
- Giannakopoulos, T.; Pikrakis, A. Introduction to Audio Analysis Chapter 4—Audio Features; Academic Press: Oxford, UK, 2014; pp. 59–103. [Google Scholar]


| Class Name | Species | Sample Number | Mean Values | Standard Deviation |
|---|---|---|---|---|
| RD | Rissos’ Dolphin | 1799 | ||
| RW | Right Whale | 2257 | ||
| PW | Pilot Whale | 264 | ||
| BW | Beaked Whale | 722 | ||
| CD | Common Dolphin | 184 | ||
| NW | Environmental Sound | 8985 |
| Dataset | Class | Sample | Species | |
|---|---|---|---|---|
| 1 | RDRW | 2 | 3598 | Rissos’ Dolphin, Right Whale |
| 2 | RWNW | 2 | 4514 | Right Whale, NoWhale * |
| 3 | RDNW | 2 | 3598 | Rissos’ Dolphin, NoWhale |
| 4 | RDPWBW | 3 | 792 | Rissos’ Dolphin, Pilot Whale, Beaked Whale |
| 5 | CDRWNW | 3 | 552 | Common Dolphin, Right Whale, NoWhale |
| 6 | RDRWNW | 3 | 5397 | Rissos’ Dolphin, Right Whale, NoWhale |
| 7 | RWRDPWBW | 4 | 1056 | Rissos’ Dolphin, Right Whale, Pilot Whale, Beaked Whale |
| 8 | NWRWRDPWBW | 5 | 1320 | NoWhale, Right Whale, Rissos’ Dolphin, Pilot Whale, Beaked Whale |
| Cetacean Species (Abbreviation) | File Number (n) | Before (MB) | After (MB) | Extraction Rate (%) |
|---|---|---|---|---|
| Common Dolphin (CD) | 61 | 42.3 | 2.61 | 6.17 |
| Right Whale (RW) | 96 | 329 | 33 | 10.03 |
| Risso’s Dolphin (RD) | 13 | 452 | 26 | 5.75 |
| Pilot Whale (PW) | 8 | 263 | 3.74 | 1.42 |
| Beaked Whale (BW) | 16 | 495 | 10.4 | 2.1 |
| Total | 194 | 1581.3 | 75.75 | 25.47 |
| Class Number | Dataset | K-Means | PCA | GMM | SSC |
|---|---|---|---|---|---|
| m = 2 | RDRW | 91.20 ± 0.59 | 92.86 ± 0.11 | 73.84 ± 0.66 | |
| RWNW | 99.69 ± 0.23 | 99.72 ± 0.15 | 98.18 ± 0.1 | ||
| RDNW | 99.86 ± 0.1 | 99.63 ± 0.45 | 97.76 ± 0.65 | ||
| m = 3 | RDPWBW | 74.01 ± 0.51 | 74.47 ± 0.05 | 58.48 ± 0.53 | |
| CDRWNW | 92.46 ± 0.24 | 92.78 ± 0.25 | 87.32 ± 0.88 | ||
| RDRWNW | 95.78 ± 1.56 | 94.51 ± 0.01 | 86.49 ± 0.25 | ||
| m = 4 | RWRDPWBW | 72.51 ± 0.83 | 69.07 ± 1.40 | 40.80 ± 0.29 | |
| m = 5 | NWRWRDPWBW | 78 ± 1.19 | 76.23 ± 0.58 | 54.19 ± 0.64 |
| Class Number | Dataset | K-Means | PCA | GMM | SSC |
|---|---|---|---|---|---|
| m = 2 | RDRW | 84.08 ± 0.95 | 77.92 ± 1.12 | 64.00 ± 0.82 | |
| RWNW | 99.38 ± 0.14 | 99.45 ± 0.29 | 96.42 ± 0.68 | ||
| RDNW | 99.72 ± 0.16 | 99.26 ± 0.90 | 95.59 ± 0.52 | ||
| m = 3 | RDPWBW | 62.58 ± 0.82 | 63.34 ± 0.09 | 44.235 ± 0.41 | |
| CDRWNW | 86.78 ± 0.35 | 87.27 ± 0.38 | 77.76 ± 0.58 | ||
| RDRWNW | 92.06 ± 2.68 | 89.86 ± 0.02 | 77.22 ± 0.23 | ||
| m = 4 | RWRDPWBW | 57.39 ± 0.99 | 52.95 ± 1.94 | 31.25 ± 0.16 | |
| m = 5 | NWRWRDPWBW | 65.58 ± 1.35 | 62.80 ± 0.61 | 44.55 ± 0.15 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, Y.; Wang, Y.; Chen, F.; Yu, H.; Ji, F.; Chen, Y. Automatic Detection and Unsupervised Clustering-Based Classification of Cetacean Vocal Signals. Appl. Sci. 2025, 15, 3585. https://doi.org/10.3390/app15073585
Liang Y, Wang Y, Chen F, Yu H, Ji F, Chen Y. Automatic Detection and Unsupervised Clustering-Based Classification of Cetacean Vocal Signals. Applied Sciences. 2025; 15(7):3585. https://doi.org/10.3390/app15073585
Chicago/Turabian StyleLiang, Yinian, Yan Wang, Fangjiong Chen, Hua Yu, Fei Ji, and Yankun Chen. 2025. "Automatic Detection and Unsupervised Clustering-Based Classification of Cetacean Vocal Signals" Applied Sciences 15, no. 7: 3585. https://doi.org/10.3390/app15073585
APA StyleLiang, Y., Wang, Y., Chen, F., Yu, H., Ji, F., & Chen, Y. (2025). Automatic Detection and Unsupervised Clustering-Based Classification of Cetacean Vocal Signals. Applied Sciences, 15(7), 3585. https://doi.org/10.3390/app15073585









