Recall Mechanism and Multi-Head Attention for Numerical Reasoning
Abstract
1. Introduction
- We propose a recall mechanism for numerical reasoning, which refocuses on the embedding information of questions and passages before generating operators and operands. This mechanism prevents the loss of critical information as the model deepens, ensuring that the initial input embeddings are retained throughout the network.
- We propose multi-head attention for numerical reasoning, which enhances the model’s ability to handle complex, multi-step reasoning tasks. By efficiently extracting multiple relevant information fragments, this mechanism optimizes the solution process for multi-step problems.
- We evaluate our proposed model, RMMANR (recall mechanism and multi-head attention for numerical reasoning), on the FINQA dataset [2]. Experiment results show that RMMANR outperforms several baseline models, achieving superior accuracy and robustness.
2. Related Works
2.1. Datasets
2.2. Question and Document Representation
2.3. Reasoning Module
3. Methods
3.1. Task Definition
3.2. Proposed RMMANR
3.3. Encoder
3.4. Decoder
3.4.1. Decoding Vocabulary and Token Embedding
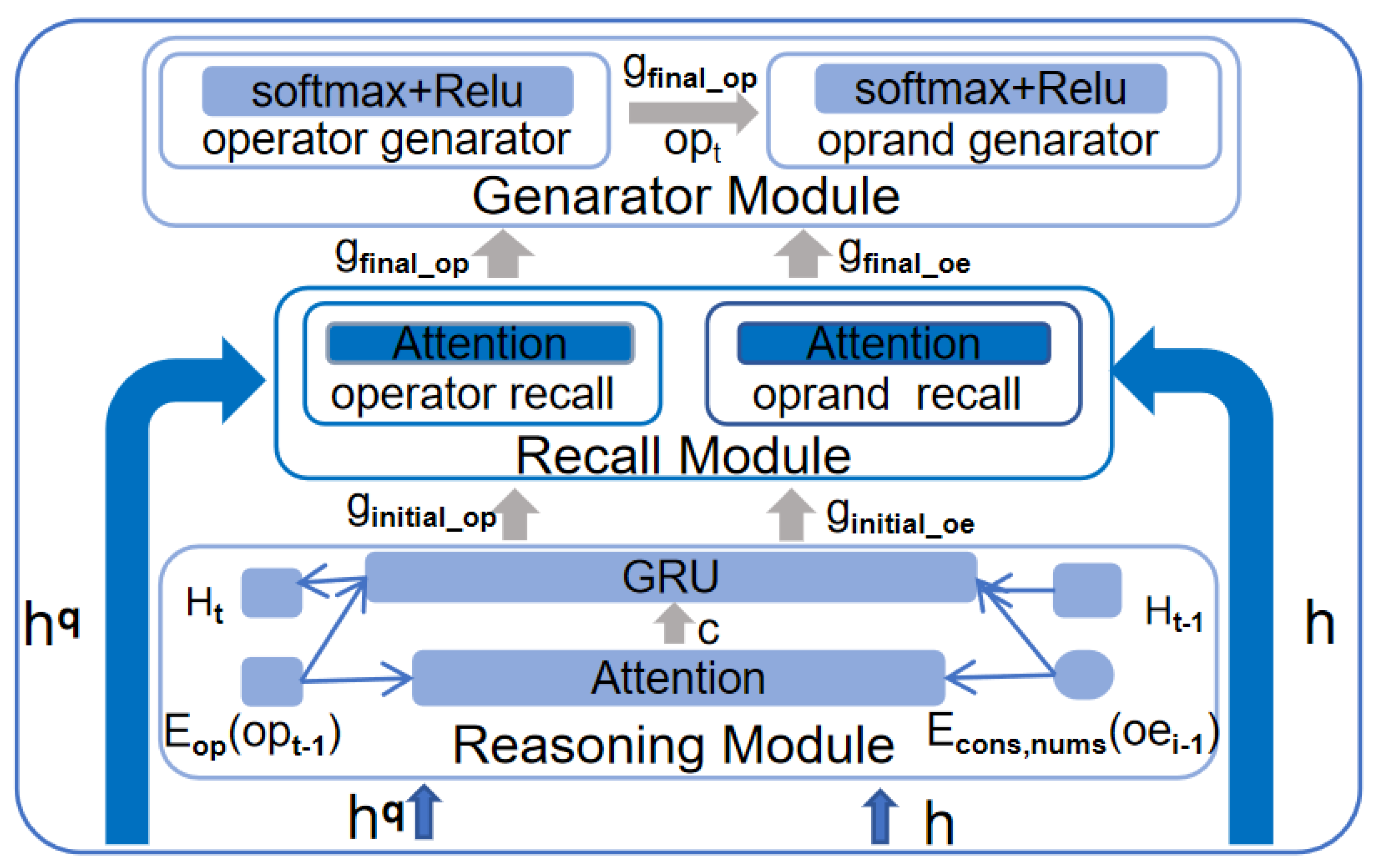
3.4.2. RM Module
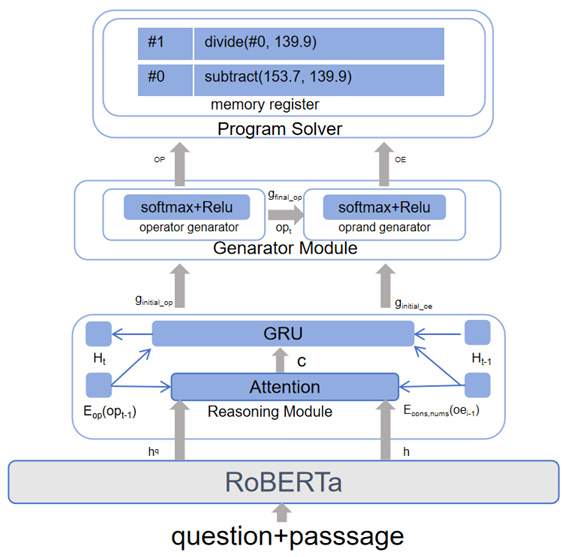
3.4.3. MA Module
- Calculate the attention weights for each attention head: For the kth attention head, calculate the attention weight from the previously generated symbol and the context vector h:where the scoring function for the kth attention head is:Here, and are trainable parameters of the kth attention head, where .
- Calculate the context vector for each attention head: Different heads provide diverse attention perspectives, enabling the model to focus on multiple levels of information simultaneously, thereby enhancing its modeling capability. Sum the weighted vectors of attention heads to obtain the context vector for the kth attention head:
- Merge the context vectors of multiple attention heads: Combine the context vectors from all attention heads and obtain the final context vector c through a linear transformation:where is the linear transformation matrix after merging, andis the number of attention heads.
3.4.4. Selector
3.4.5. Program Solve
3.5. RMNR and MANR
4. Experiments
4.1. Dataset
4.2. Evaluation Metrics
- Execution Accuracy measures the correctness of the final answer produced by executing the model-predicted program against the gold-standard executable result.
- Program Accuracy evaluates the precision of the predicted program by comparing the operands and operators in the model-generated program with those in the gold-standard program.
4.3. Baselines
- GPT-3.5-turbo: GPT-3.5-turbo is a large language model with 175 billion parameters [32].
- GPT-4: GPT-4 is a large multimodal model that is able to process both text and image inputs and generate text outputs [33].
- Program-of-Thought: Program-of-Thought first generates programming and text statements, and then produces an answer [28].
- FINQANet: FINQANet employs a typical encoder–decoder architecture, where pre-trained LMs are used as the encoder, and LSTM serves as the decoder [2].
- NeRd: NeRd generates symbolic nested programs using BERT and a model based on pointer generators [21].
- NumNet: NumNet models arithmetic information through GNN networks [34].
- ELASTIC: ELASTIC separately generates mathematical operators and operands, reducing the occurrence of cascading errors [6]. (The preprocessed FINQA dataset and code are available at https://github.com/NeuraSearch/NeurIPS-2022-Submission-3358 (accessed on 15 July 2022).)
- DyRRen: DyRRen is an extended retriever-reranker-generator framework [35].We also compared the reasoning results of non-experts and experts from the original FINQA paper [2].
4.4. Implementation Details
5. Experiment Results and Analysis
5.1. Overall Results
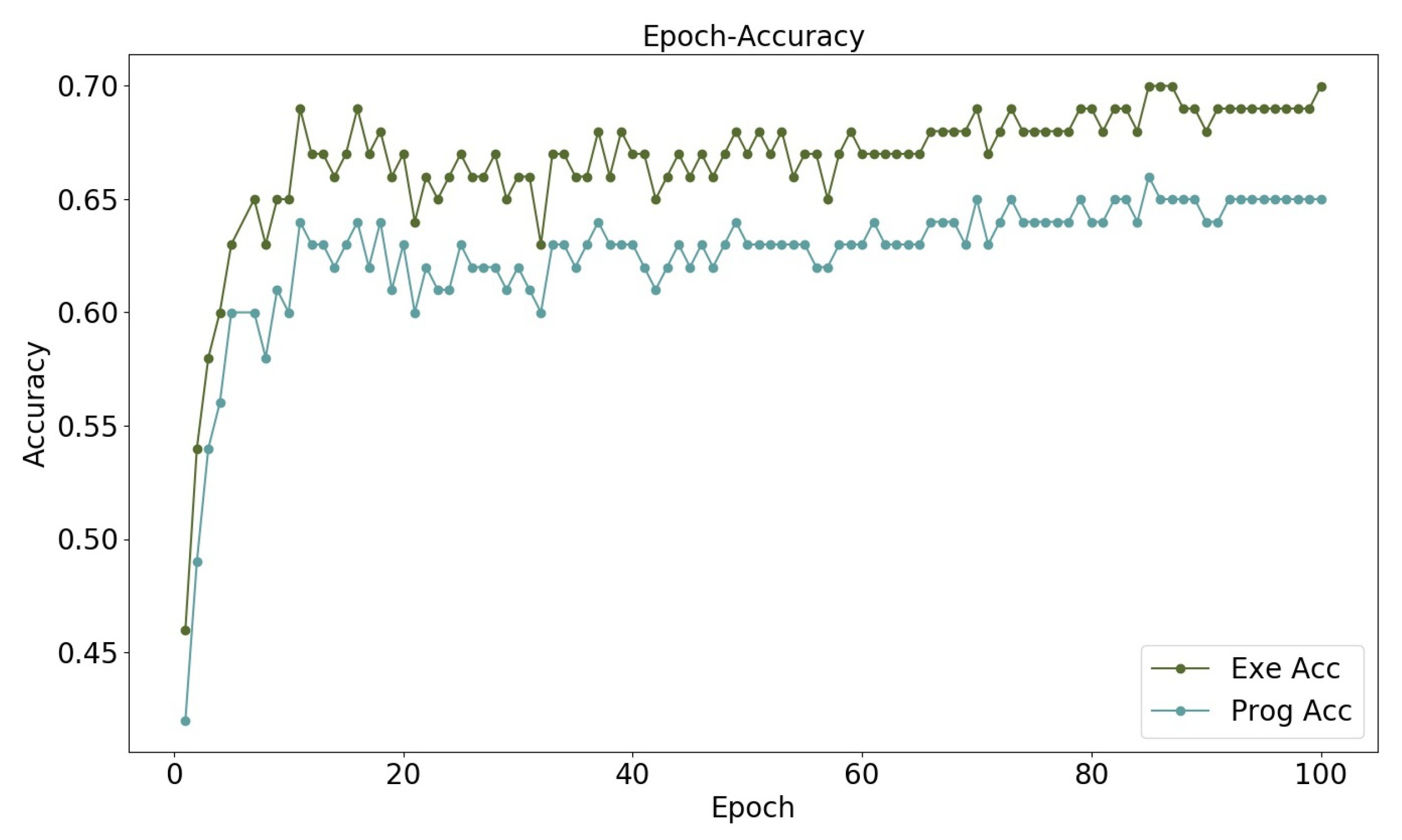
5.2. The Convergence Process
5.3. Performance on Different Program Steps
5.4. Error Analysis
- Enhancing the model’s ability to understand mathematical relationships by refining operation selection mechanisms.
- Improving number extraction accuracy through better numerical alignment techniques.
- Strengthening multi-step reasoning to ensure all steps are correctly executed.
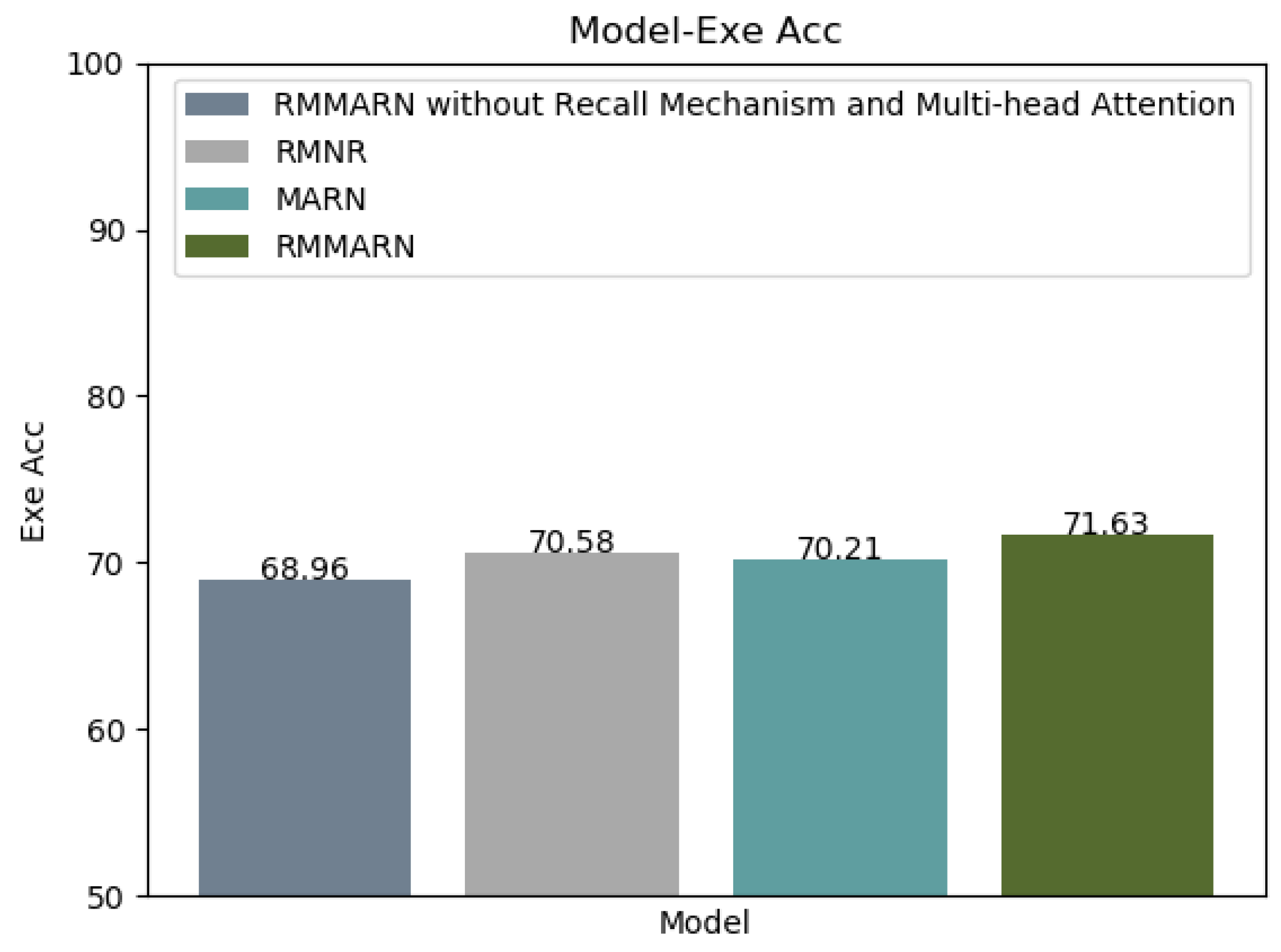
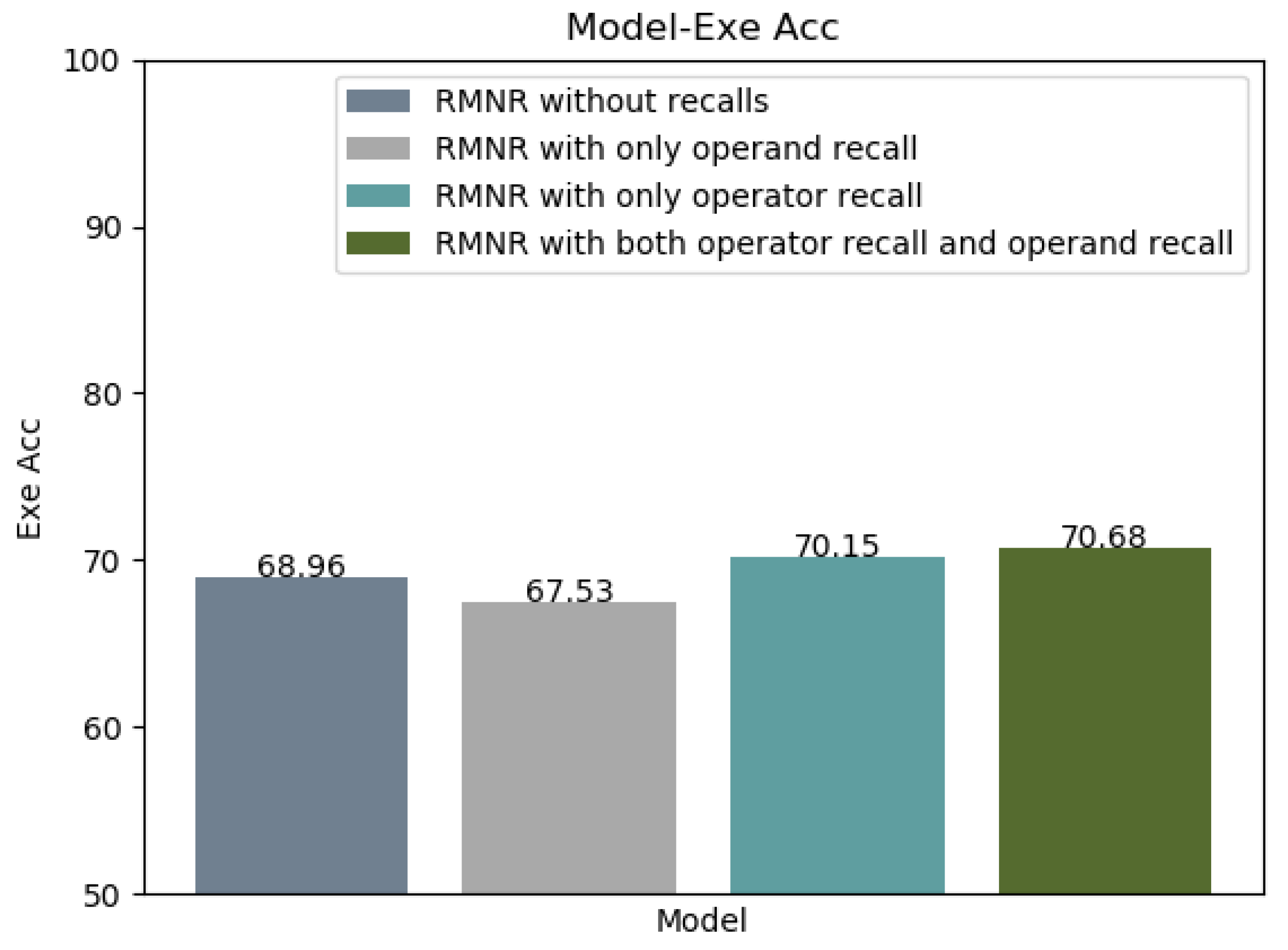
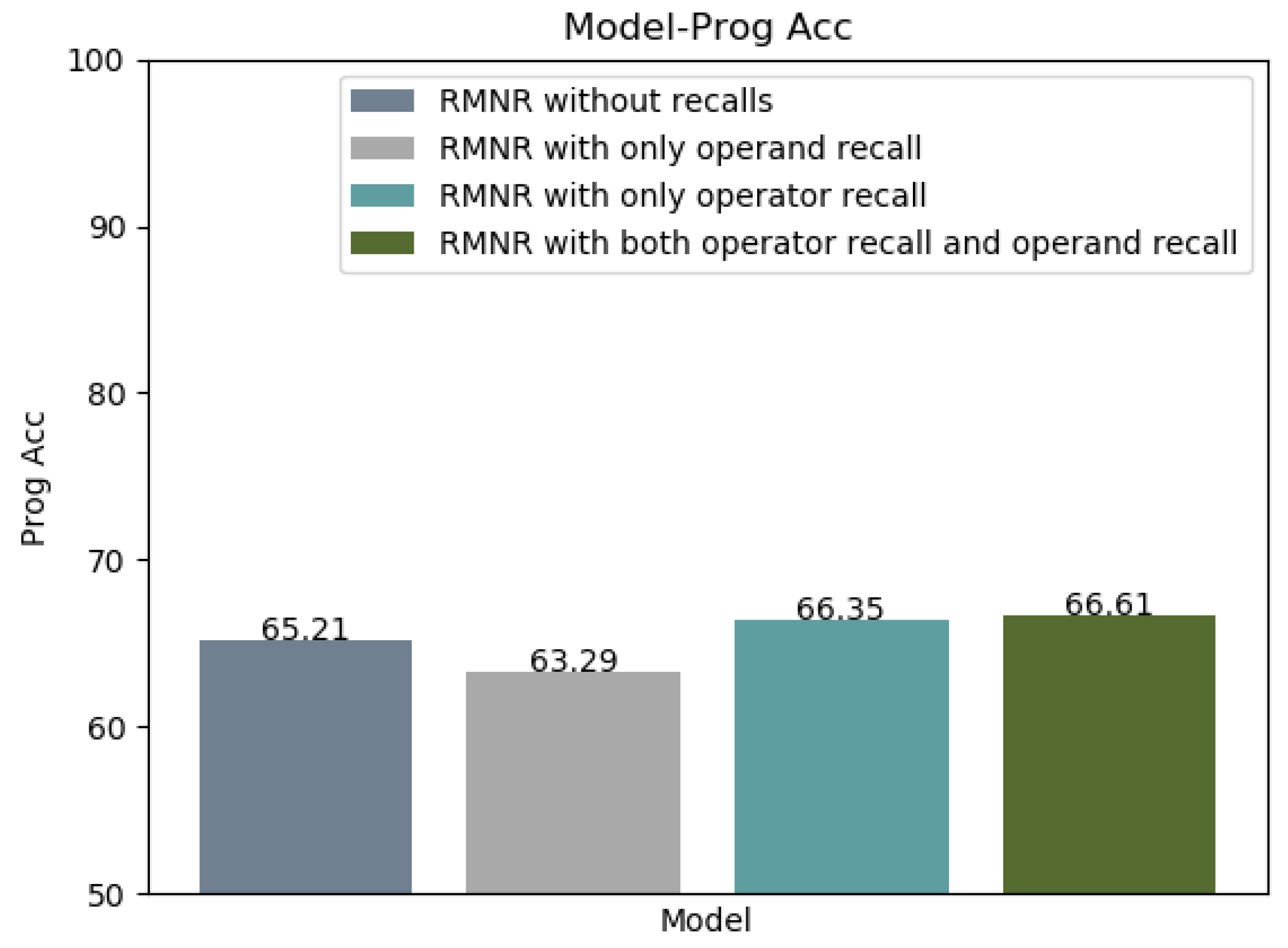
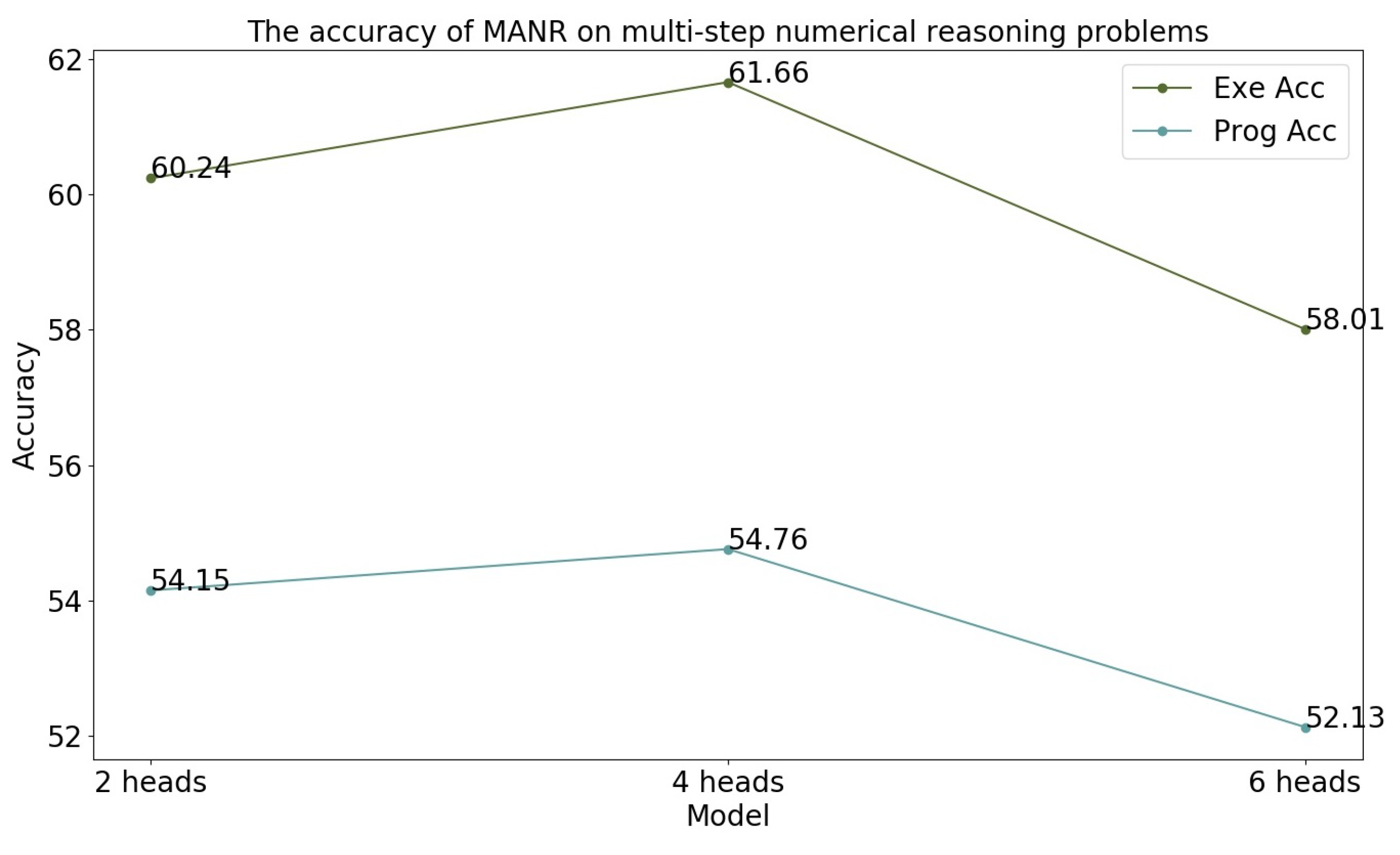
5.5. Ablation Studies
6. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| RMMANR | Recall Mechanism and Multi-head Attention for Numerical Reasoning |
| RMNR | Recall Mechanism for Numerical Reasoning |
| MANR | Multi-head Attention for Numerical Reasoning |
Appendix A. An Example of Financial Question–Answering Problems Using Notations Defined in Table 2
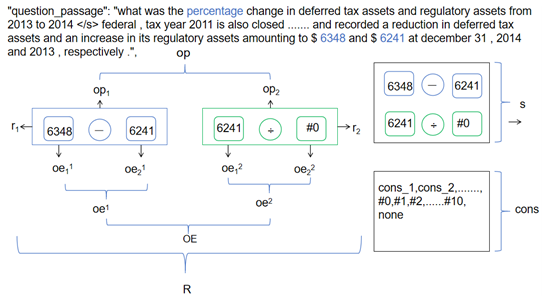
Appendix B. Recall Mechanism for Numerical Reasoning (RMNR)
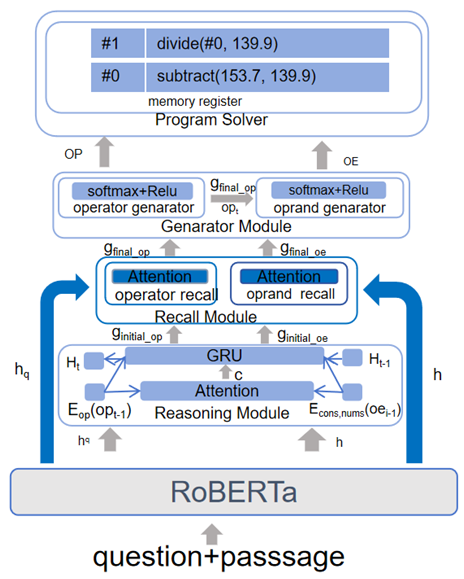
Appendix C. Multi-Head Attention for Numerical Reasoning (MANR)

Appendix D. RMMANR Without Recall Mechanism and Multi-Head Attention
References
- Hosseini, M.J.; Hajishirzi, H.; Etzioni, O.; Kushman, N. Learning to solve arithmetic word problems with verb categorization. In Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing (EMNLP), Doha, Qatar, 25–29 October 2014; pp. 523–533. [Google Scholar]
- Chen, Z.; Chen, W.; Smiley, C.; Shah, S.; Borova, I.; Langdon, D.; Moussa, R.; Beane, M.; Huang, T.H.; Routledge, B. Finqa: A dataset of numerical reasoning over financial data. arXiv 2021, arXiv:2109.00122. [Google Scholar]
- Cheng, W.K.; Bea, K.T.; Leow, S.M.H.; Chan, J.Y.L.; Hong, Z.W.; Chen, Y.L. A review of sentiment, semantic and event-extraction-based approaches in stock forecasting. Mathematics 2022, 10, 2437. [Google Scholar] [CrossRef]
- Ooi, B.Y.; Lee, W.K.; Shubert, M.J.; Ooi, Y.W.; Chin, C.Y.; Woo, W.H. A flexible and reliable internet-of-things solution for real-time production tracking with high performance and secure communication. IEEE Trans. Ind. Appl. 2023, 59, 3121–3132. [Google Scholar]
- Callanan, E.; Mbakwe, A.; Papadimitriou, A.; Pei, Y.; Sibue, M.; Zhu, X.; Ma, Z.; Liu, X.; Shah, S. Can GPT models be Financial Analysts? In An Evaluation of ChatGPT and GPT-4 on mock CFA Exams. In Proceedings of the Eighth Financial Technology and Natural Language Processing and the 1st Agent AI for Scenario Planning, Jeju, Republic of Korea, 3 August 2024; pp. 23–32. [Google Scholar]
- Zhang, J.; Moshfeghi, Y. ELASTIC: Numerical reasoning with adaptive symbolic compiler. Adv. Neural Inf. Process. Syst. 2022, 35, 12647–12661. [Google Scholar]
- Zhu, F.; Li, M.; Xiao, J.; Feng, F.; Wang, C.; Chua, T.S. SoarGraph: Numerical Reasoning over Financial Table-Text Data via Semantic-Oriented Hierarchical Graphs. In Proceedings of the Companion Proceedings of the ACM Web Conference 2023, Austin, TX, USA, 30 April–4 May 2023; pp. 1236–1244. [Google Scholar]
- Wang, L.; Wang, Y.; Cai, D.; Zhang, D.; Liu, X. Translating a math word problem to an expression tree. arXiv 2018, arXiv:1811.05632. [Google Scholar]
- Xie, Z.; Sun, S. A Goal-Driven Tree-Structured Neural Model for Math Word Problems. In Proceedings of the IJCAI, Macao, China, 10–16 August 2019; pp. 5299–5305. [Google Scholar]
- Wang, Y.; Liu, X.; Shi, S. Deep neural solver for math word problems. In Proceedings of the 2017 Conference on Empirical Methods in Natural Language Processing, Copenhagen, Denmark, 9–11 September 2017; pp. 845–854. [Google Scholar]
- Dua, D.; Wang, Y.; Dasigi, P.; Stanovsky, G.; Singh, S.; Gardner, M. DROP: A reading comprehension benchmark requiring discrete reasoning over paragraphs. arXiv 2019, arXiv:1903.00161. [Google Scholar]
- Zhu, F.; Lei, W.; Huang, Y.; Wang, C.; Zhang, S.; Lv, J.; Feng, F.; Chua, T.S. TAT-QA: A question answering benchmark on a hybrid of tabular and textual content in finance. arXiv 2021, arXiv:2105.07624. [Google Scholar]
- Chen, Q.; Gao, X.; Guo, X.; Wang, S. Multi-head attention based candidate segment selection in QA over hybrid data. Intell. Data Anal. 2023, 27, 1839–1852. [Google Scholar]
- Liang, C.C.; Hsu, K.Y.; Huang, C.T.; Li, C.M.; Miao, S.Y.; Su, K.Y. A tag-based English math word problem solver with understanding, reasoning and explanation. In Proceedings of the 2016 Conference of the North American Chapter of the Association for Computational Linguistics, Demonstrations, San Diego, CA, USA, 12–17 June 2016; pp. 67–71. [Google Scholar]
- Chen, D.; Manning, C.D. A fast and accurate dependency parser using neural networks. In Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing (EMNLP), Doha, Qatar, 25–29 October 2014; pp. 740–750. [Google Scholar]
- Mikolov, T.; Chen, K.; Corrado, G.; Dean, J. Efficient estimation of word representations in vector space. arXiv 2013, arXiv:1301.3781. [Google Scholar]
- Pennington, J.; Socher, R.; Manning, C.D. Glove: Global vectors for word representation. In Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing (EMNLP), Doha, Qatar, 25–29 October 2014; pp. 1532–1543. [Google Scholar]
- Lazaridou, A.; Pham, N.T.; Baroni, M. Combining language and vision with a multimodal skip-gram model. arXiv 2015, arXiv:1501.02598. [Google Scholar]
- Alammary, A.S.J.A.S. BERT models for Arabic text classification: A systematic review. Appl. Sci. 2022, 12, 5720. [Google Scholar] [CrossRef]
- Touvron, H.; Lavril, T.; Izacard, G.; Martinet, X.; Lachaux, M.A.; Lacroix, T.; Rozière, B.; Goyal, N.; Hambro, E.; Azhar, F.; et al. Llama: Open and efficient foundation language models. arXiv 2023, arXiv:2302.13971. [Google Scholar]
- Chen, X.; Liang, C.; Yu, A.W.; Zhou, D.; Song, D.; Le, Q.V. Neural symbolic reader: Scalable integration of distributed and symbolic representations for reading comprehension. In Proceedings of the International Conference on Learning Representations, New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Chen, K.; Xu, W.; Cheng, X.; Xiaochuan, Z.; Zhang, Y.; Song, L.; Wang, T.; Qi, Y.; Chu, W. Question directed graph attention network for numerical reasoning over text. arXiv 2020, arXiv:2009.07448. [Google Scholar]
- Zhu, F.; Lei, W.; Feng, F.; Wang, C.; Zhang, H.; Chua, T.S. Towards complex document understanding by discrete reasoning. In Proceedings of the 30th ACM International Conference on Multimedia, Lisboa, Portugal, 10–14 October 2022; pp. 4857–4866. [Google Scholar]
- Xu, Y.; Xu, Y.; Lv, T.; Cui, L.; Wei, F.; Wang, G.; Lu, Y.; Florencio, D.; Zhang, C.; Che, W.; et al. Layoutlmv2: Multi-modal pre-training for visually-rich document understanding. arXiv 2020, arXiv:2012.14740. [Google Scholar]
- Li, B.; Chen, W.; Tang, X.; Bian, S.; Liu, Y.; Guo, J.; Zhang, D.; Huang, F. Squeeze and Excitation Convolution with Shortcut for Complex Plasma Image Recognition. Comput. Mater. Contin. 2024, 80, 2221–2236. [Google Scholar] [CrossRef]
- Li, C.; Ye, W.; Zhao, Y. Finmath: Injecting a tree-structured solver for question answering over financial reports. In Proceedings of the Thirteenth Language Resources and Evaluation Conference, Marseille, France, 11–16 May 2020; pp. 6147–6152. [Google Scholar]
- Wang, L.; Zhang, D.; Zhang, J.; Xu, X.; Gao, L.; Dai, B.T.; Shen, H.T. Template-based math word problem solvers with recursive neural networks. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; Volume 33, pp. 7144–7151. [Google Scholar]
- Chen, W.; Ma, X.; Wang, X.; Cohen, W.W. Program of thoughts prompting: Disentangling computation from reasoning for numerical reasoning tasks. arXiv 2022, arXiv:2211.12588. [Google Scholar]
- Wang, X.; Wei, J.; Schuurmans, D.; Le, Q.; Chi, E.; Narang, S.; Chowdhery, A.; Zhou, D. Self-consistency improves chain of thought reasoning in language models. arXiv 2022, arXiv:2203.11171. [Google Scholar]
- Schick, T.; Dwivedi-Yu, J.; Dessì, R.; Raileanu, R.; Lomeli, M.; Hambro, E.; Zettlemoyer, L.; Cancedda, N.; Scialom, T. Toolformer: Language models can teach themselves to use tools. Adv. Neural Inf. Process. Syst. 2023, 36, 68539–68551. [Google Scholar]
- Chung, J.; Gulcehre, C.; Cho, K.; Bengio, Y. Empirical evaluation of gated recurrent neural networks on sequence modeling. arXiv 2014, arXiv:1412.3555. [Google Scholar]
- Ouyang, L.; Wu, J.; Jiang, X.; Almeida, D.; Wainwright, C.; Mishkin, P.; Zhang, C.; Agarwal, S.; Slama, K.; Ray, A.; et al. Training language models to follow instructions with human feedback. Adv. Neural Inf. Process. Syst. 2022, 35, 27730–27744. [Google Scholar]
- Li, X.; Chan, S.; Zhu, X.; Pei, Y.; Ma, Z.; Liu, X.; Shah, S. Are ChatGPT and GPT-4 general-purpose solvers for financial text analytics? A study on several typical tasks. arXiv 2023, arXiv:2305.05862. [Google Scholar]
- Ran, Q.; Lin, Y.; Li, P.; Zhou, J.; Liu, Z. NumNet: Machine reading comprehension with numerical reasoning. arXiv 2019, arXiv:1910.06701. [Google Scholar]
- Li, X.; Zhu, Y.; Liu, S.; Ju, J.; Qu, Y.; Cheng, G. Dyrren: A dynamic retriever-reranker-generator model for numerical reasoning over tabular and textual data. In Proceedings of the AAAI Conference on Artificial Intelligence, Vancouver, BC, Canada, 20–27 February 2023; Volume 37, pp. 13139–13147. [Google Scholar]
- Wolf, T.; Debut, L.; Sanh, V.; Chaumond, J.; Delangue, C.; Moi, A.; Cistac, P.; Rault, T.; Louf, R.; Funtowicz, M.; et al. Transformers: State-of-the-art natural language processing. In Proceedings of the 2020 Conference on Empirical Methods in Natural Language Processing: System Demonstrations, Online, 16–20 November 2020; pp. 38–45. [Google Scholar]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. Pytorch: An imperative style, high-performance deep learning library. arXiv 2019, arXiv:1912.01703. [Google Scholar]
- Kingma, D.P. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Sun, J.; Zhang, H.; Lin, C.; Su, X.; Gong, Y.; Guo, J. Apollo: An optimized training approach for long-form numerical reasoning. arXiv 2022, arXiv:2212.07249. [Google Scholar]
- Lake, B.; Baroni, M. Generalization without systematicity: On the compositional skills of sequence-to-sequence recurrent networks. In Proceedings of the International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; pp. 2873–2882. [Google Scholar]








| Category | Model | Math23K | DROP | FINQA | TAT QA | |||
|---|---|---|---|---|---|---|---|---|
| Prog Acc | Exu Acc | F1 | Exu Acc | Prog Acc | Exu Acc | F1 | ||
| Human Expert [2] | - | - | - | 91.16 | 87.49 | - | - | |
| FF | MHST [23] | - | - | - | - | - | 63.6 | 72.7 |
| FinMath [26] | - | - | - | - | - | 58.3 | 68.2 | |
| RNN | DNS [10] | 64.7 | - | - | - | - | - | - |
| NeRd [21] | 78.55 | 81.85 | 52.48 | 49.9 | - | - | - | |
| ELASTIC [6] | - | - | - | 68.96 | 65.21 | - | - | |
| Transformer | Ensemble [27] | 66.7 | - | - | - | - | - | - |
| Graph | ODGAT [22] | - | 64.56 | 67.97 | 13.1 | - | 39.1 | 49.7 |
| SoarGraph [7] | - | - | - | 67.2 | - | 65.4 | 75.3 | |
| Notation | Description |
|---|---|
| P, Q, R | The text of the passage, the text of the question, the program of numerical reasoning. |
| The numbers that appear in Q and P. | |
| Constants described in domain-specific language (DSL). | |
| All mathematical operators. | |
| The i-th mathematical operator in R. | |
| All operands. | |
| All operands associated with . | |
| The j-th operand of . | |
| An array of mathematical operators generated by RM Module. | |
| An array of mathematical operators generated by MA Module. | |
| An array of mathematical operands generated by RM Module. | |
| An array of mathematical operands generated by MA Module. | |
| s | Selected from either or , R consists of s. |
| , the i-th subprogram of R. | |
| Symbol s’s embedding from the decoding vocabulary. | |
| The embedding retrieval function of . | |
| The embedding retrieval function of . | |
| The embedding retrieval function of . |
| Category | Models | FINQA Results | |
|---|---|---|---|
| Exe Acc (%) | Prog Acc (%) | ||
| Prompting-Model | GPT-3.5-turbo [32] ! | 48.56 | - |
| GPT-4 [33] ! | 68.79 | - | |
| Program-of-Thought [28] ! | 68.10 | - | |
| Fine-Tuning-Model | NumNet [34] * | 2.32 | - |
| NumNet+ [34] * | 10.29 | - | |
| NeRd [21] ‡ | 52.48 | 49.90 | |
| FINQANet (RoBERTa-base) [2] † | 60.10 | 58.38 | |
| FINQANet (RoBERTa-large) [2] † | 65.05 | 63.52 | |
| ELASTIC (RoBERTa-base) [6] † | 62.66 | 59.28 | |
| ELASTIC (RoBERTa-large) [6] † | 68.96 | 65.21 | |
| DyRRen [35] ! | 63.30 | 61.29 | |
| RMNR (RoBERTa-base) | 65.33 | 61.20 | |
| RMNR (RoBERTa-large) | 70.58 | 66.61 | |
| MANR (RoBERTa-base) | 64.98 | 61.12 | |
| MANR (RoBERTa-large) | 70.21 | 65.74 | |
| RMMANR (RoBERTa-large) | 71.63 | 67.31 | |
| Human Performance | Human Expert † | 91.16 | 87.49 |
| Human Non-Expert † | 50.68 | 48.17 | |
| Model | The Entire Dataset | =1(3717) | =2(3013) | ≥3(512) | ||||
|---|---|---|---|---|---|---|---|---|
| Eex Acc | Prog Acc | Eex Acc | Prog Acc | Eex Acc | Prog Acc | Eex Acc | Prog Acc | |
| FINQANet † | 65.05 | 63.52 | 73.70 | 71.25 | 62.34 | 59.65 | 28.57 | 23.80 |
| ELASTIC † | 68.96 | 65.21 | 76.30 | 75.66 | 66.01 | 66.01 | 31.78 | 31.10 |
| RMNR | 70.58 | 66.61 | 78.96 | 76.61 | 65.04 | 58.68 | 32.14 | 27.38 |
| MANR | 70.21 | 65.74 | 76.49 | 74.01 | 68.22 | 60.88 | 30.95 | 25.00 |
| RMMANR | 71.63 | 67.31 | 80.34 | 77.68 | 66.01 | 59.41 | 30.95 | 25.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lai, L.; Tan, T.-P.; Zeng, B. Recall Mechanism and Multi-Head Attention for Numerical Reasoning. Appl. Sci. 2025, 15, 3528. https://doi.org/10.3390/app15073528
Lai L, Tan T-P, Zeng B. Recall Mechanism and Multi-Head Attention for Numerical Reasoning. Applied Sciences. 2025; 15(7):3528. https://doi.org/10.3390/app15073528
Chicago/Turabian StyleLai, Linjia, Tien-Ping Tan, and Bocan Zeng. 2025. "Recall Mechanism and Multi-Head Attention for Numerical Reasoning" Applied Sciences 15, no. 7: 3528. https://doi.org/10.3390/app15073528
APA StyleLai, L., Tan, T.-P., & Zeng, B. (2025). Recall Mechanism and Multi-Head Attention for Numerical Reasoning. Applied Sciences, 15(7), 3528. https://doi.org/10.3390/app15073528






