A 328 nW, 0.45 V Current Differencing Transconductance Amplifier and Its Application in a Current-Mode Universal Filter
Abstract
1. Introduction
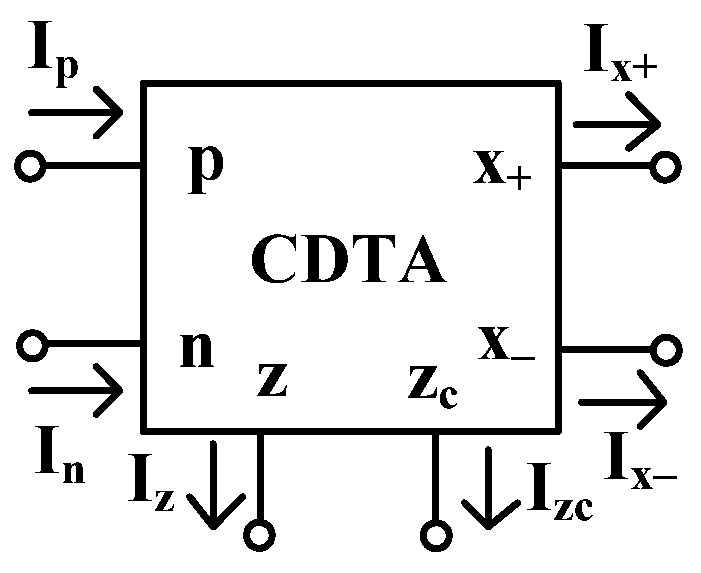
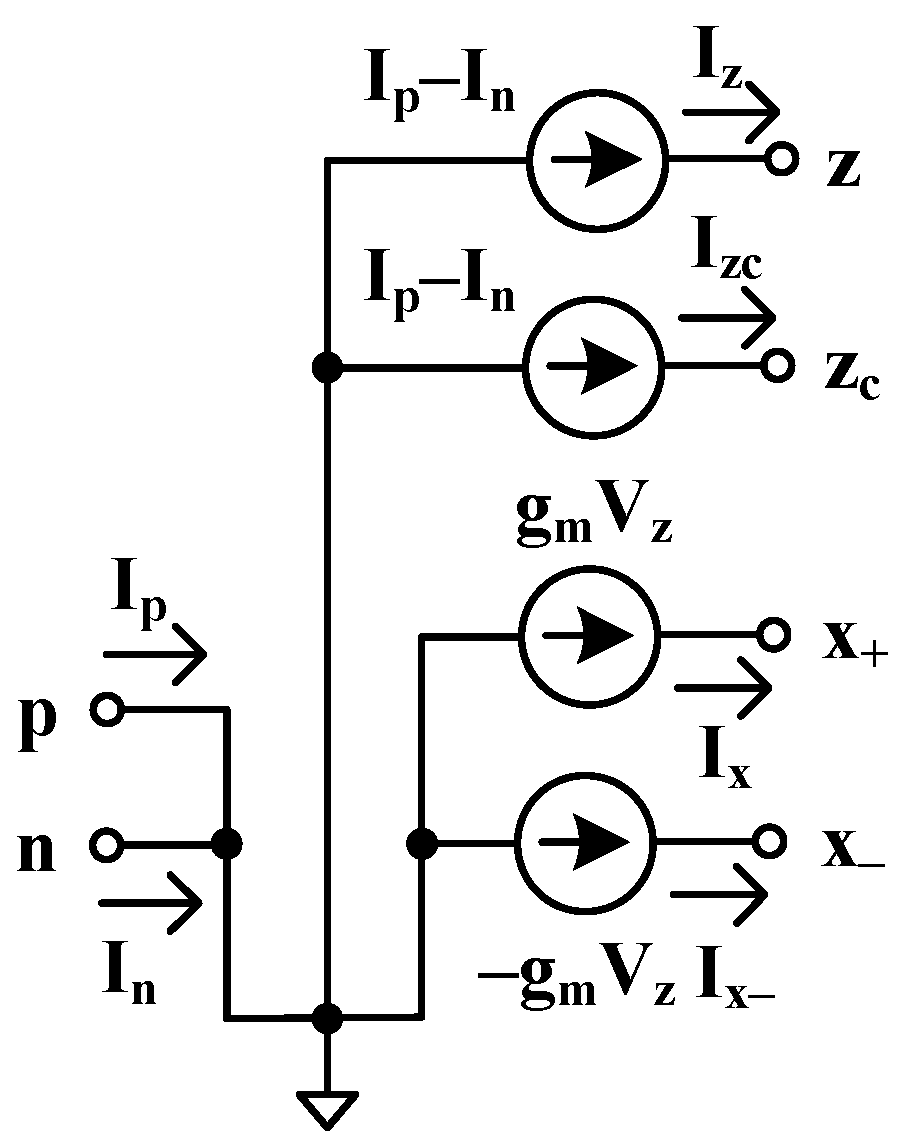
2. Circuit Description
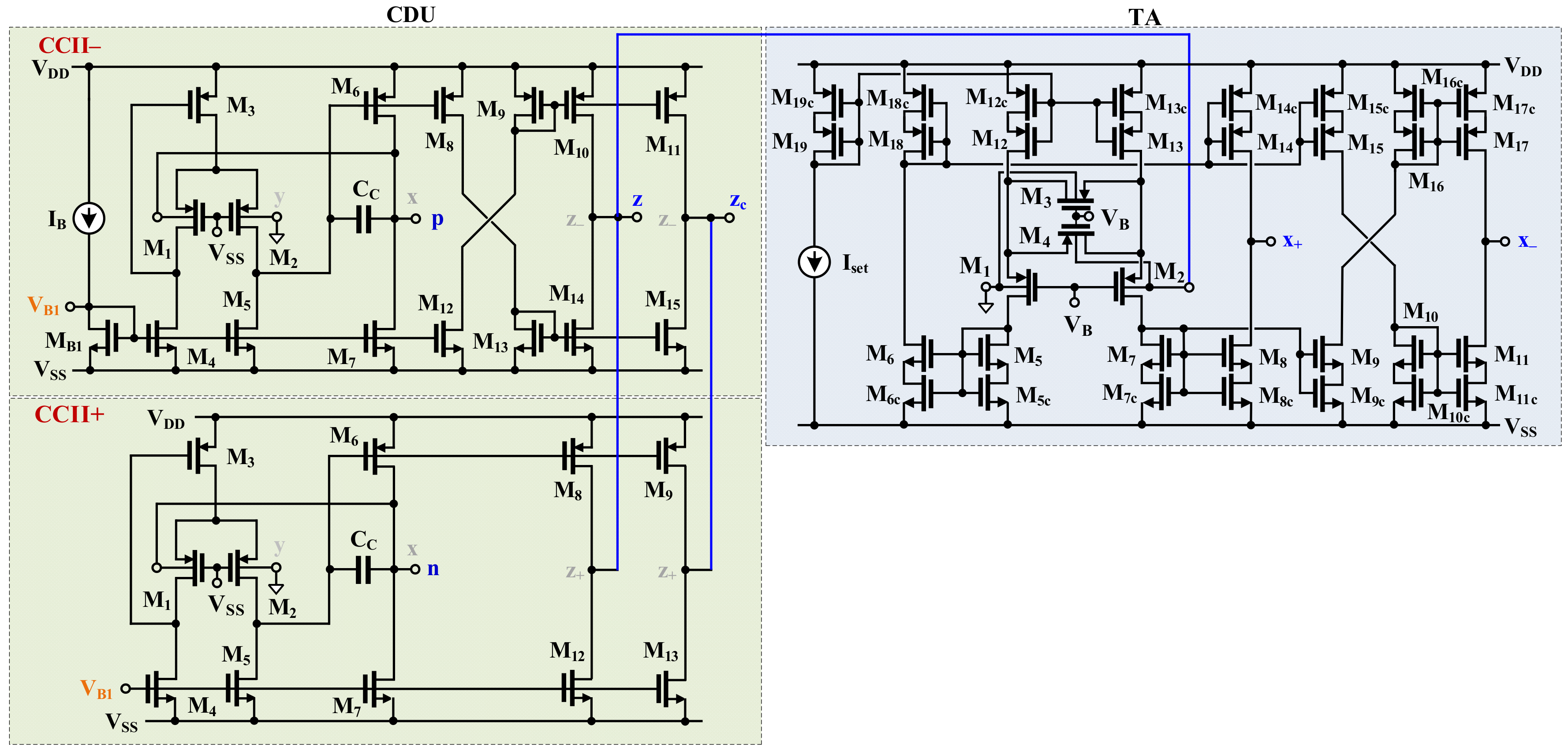
2.1. Proposed 0.45 V CDTA
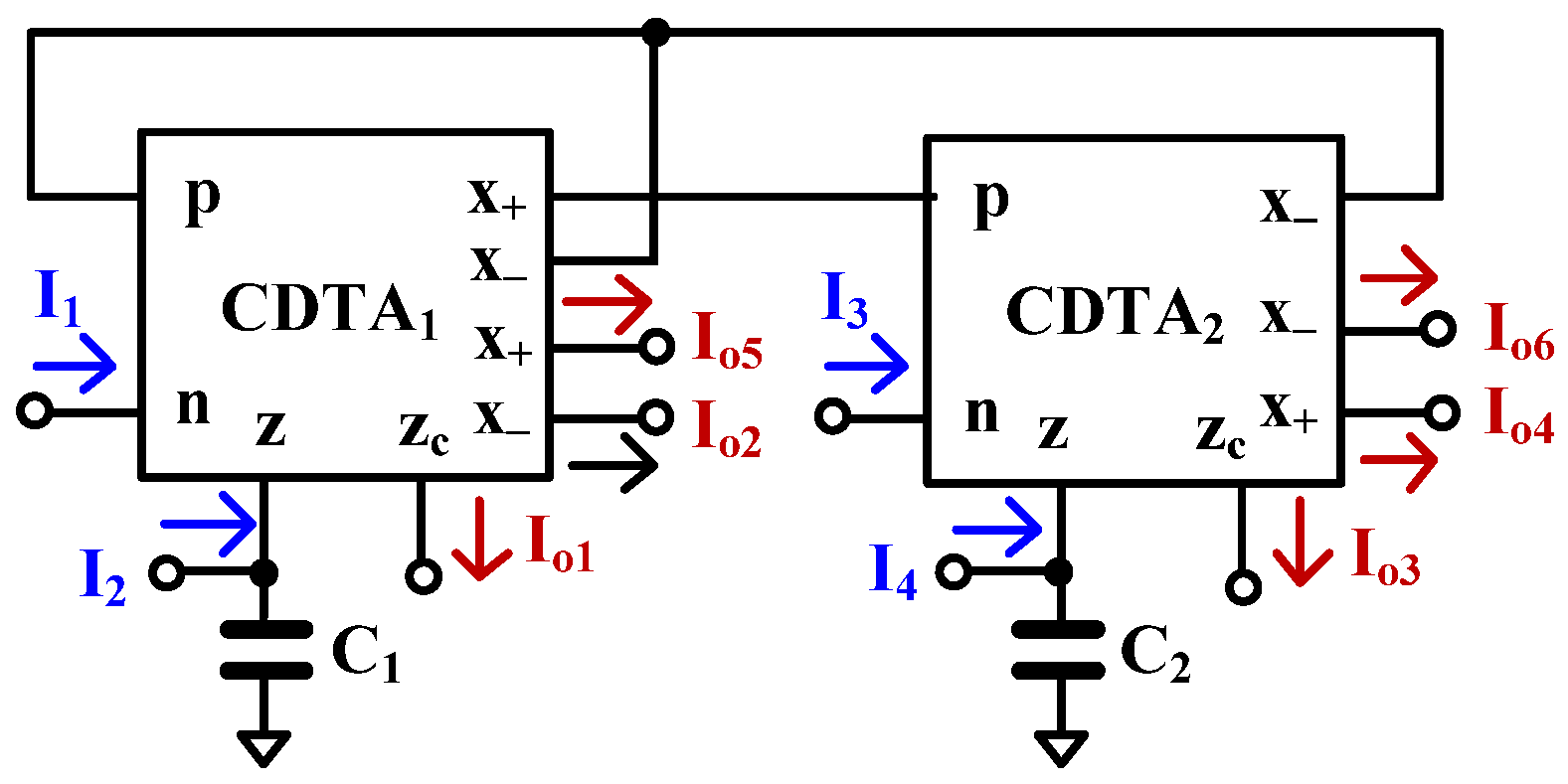
2.2. Proposed Current-Mode Analog Filter
2.3. Non-Ideal Analysis
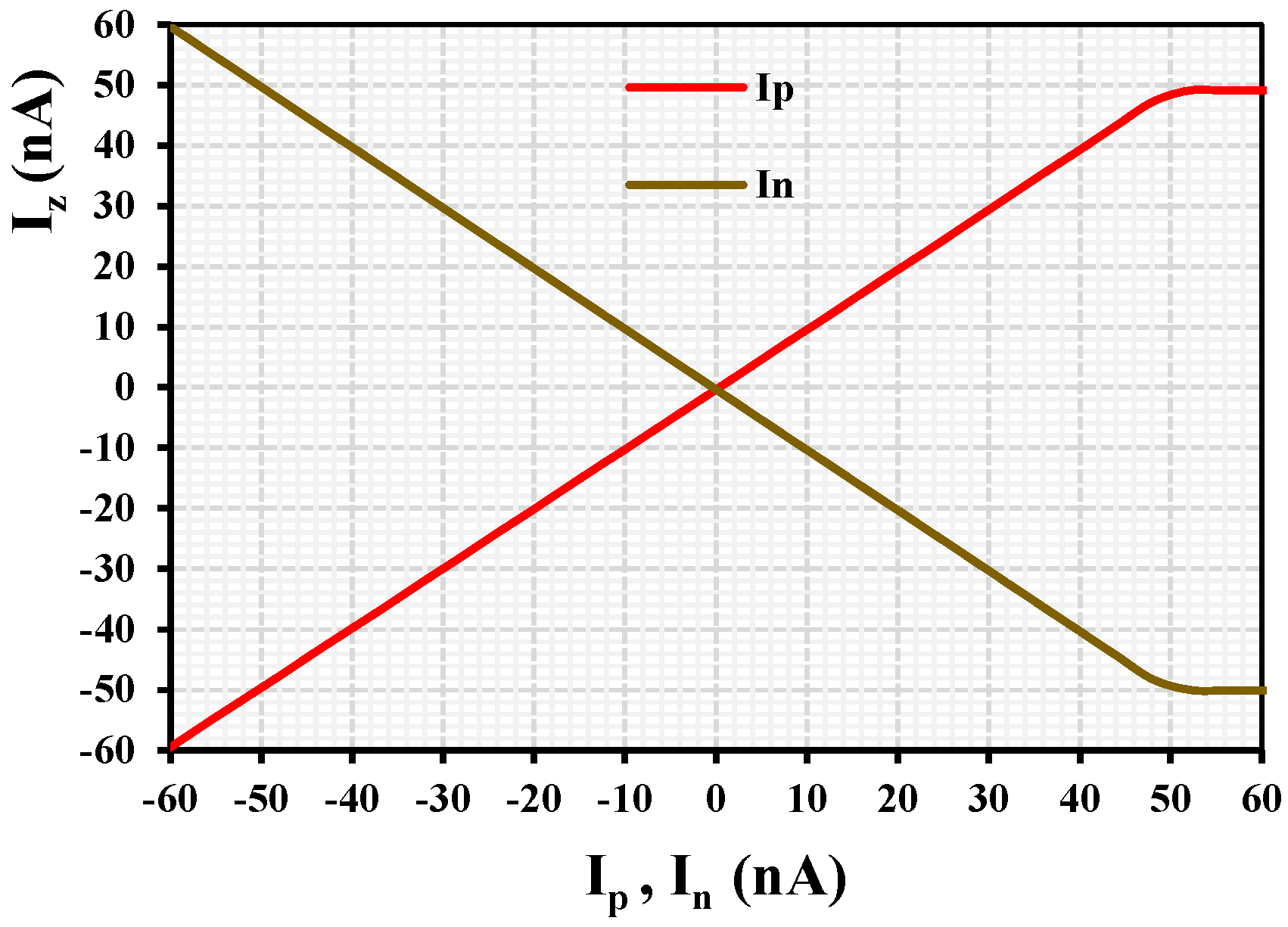
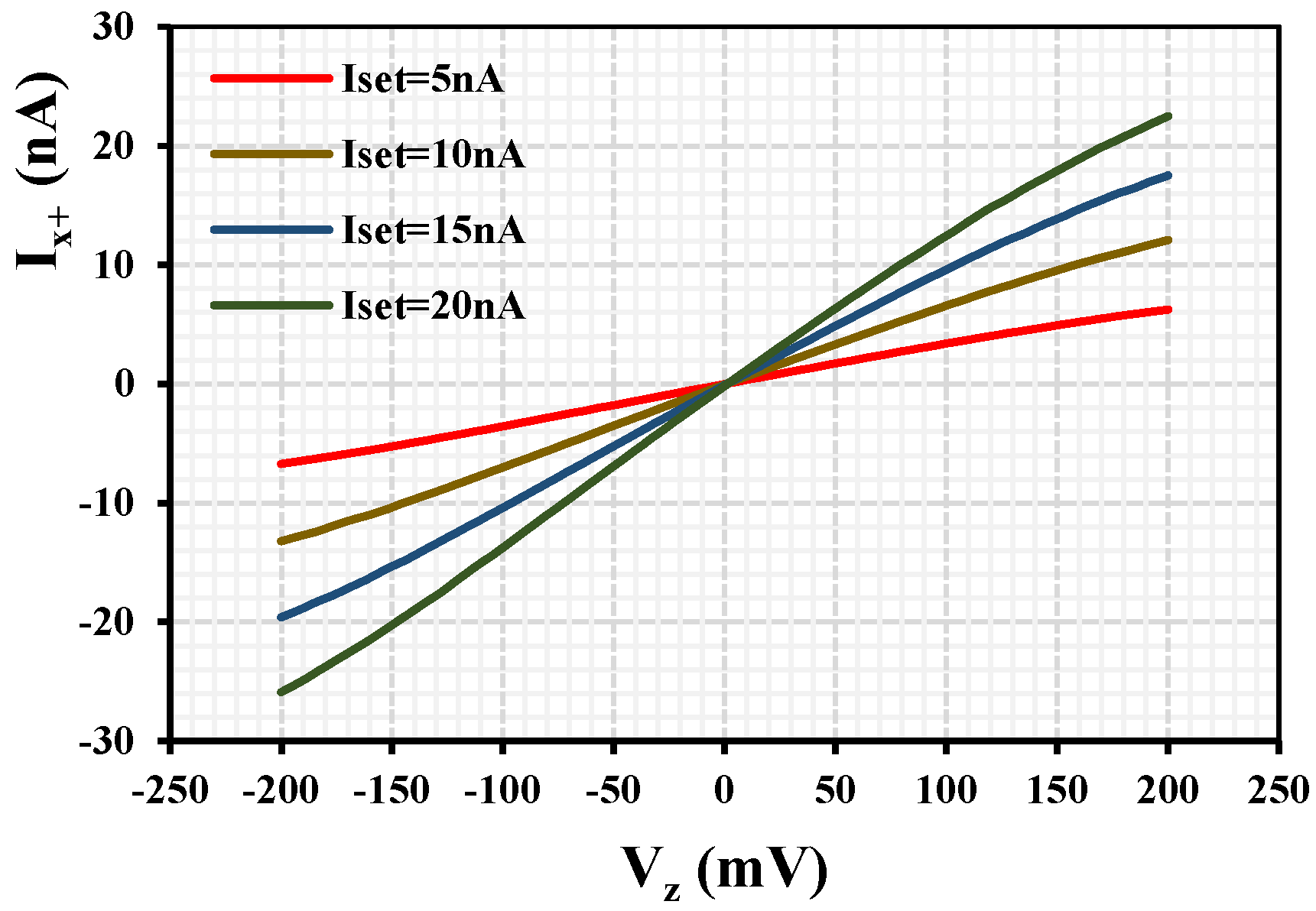
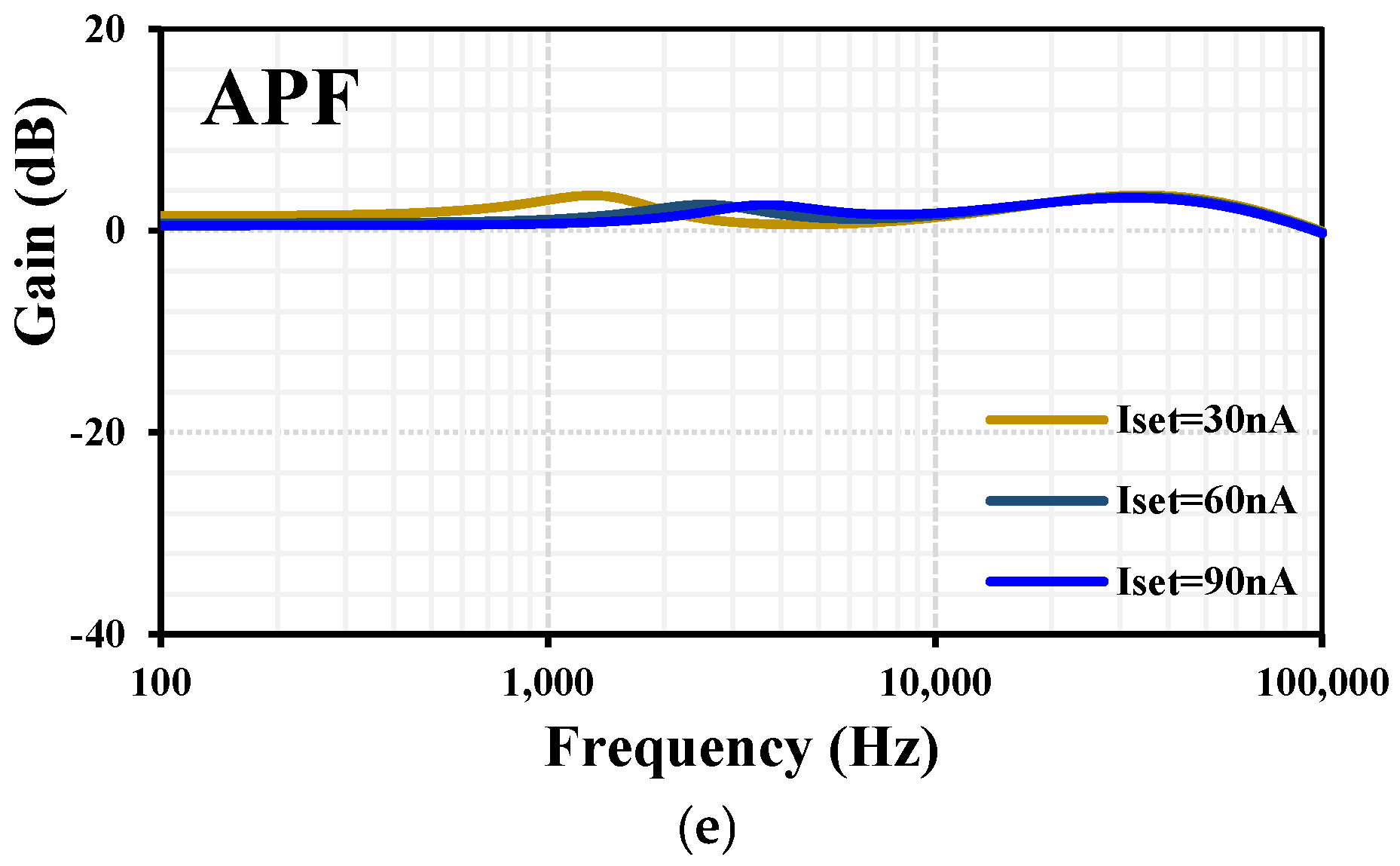
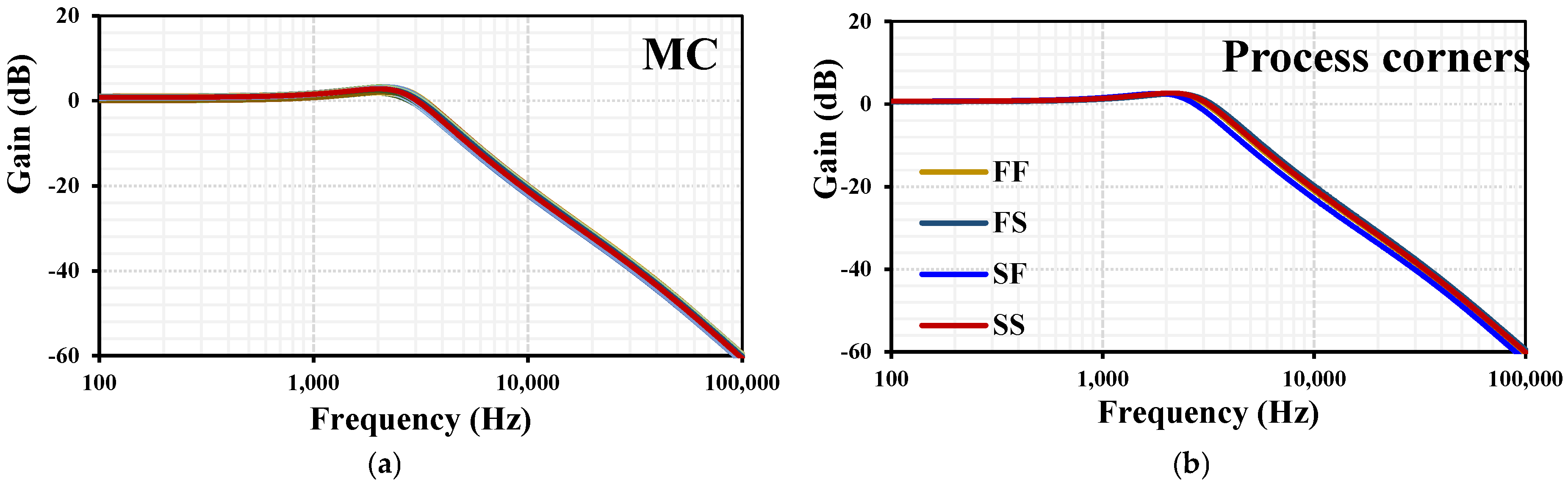
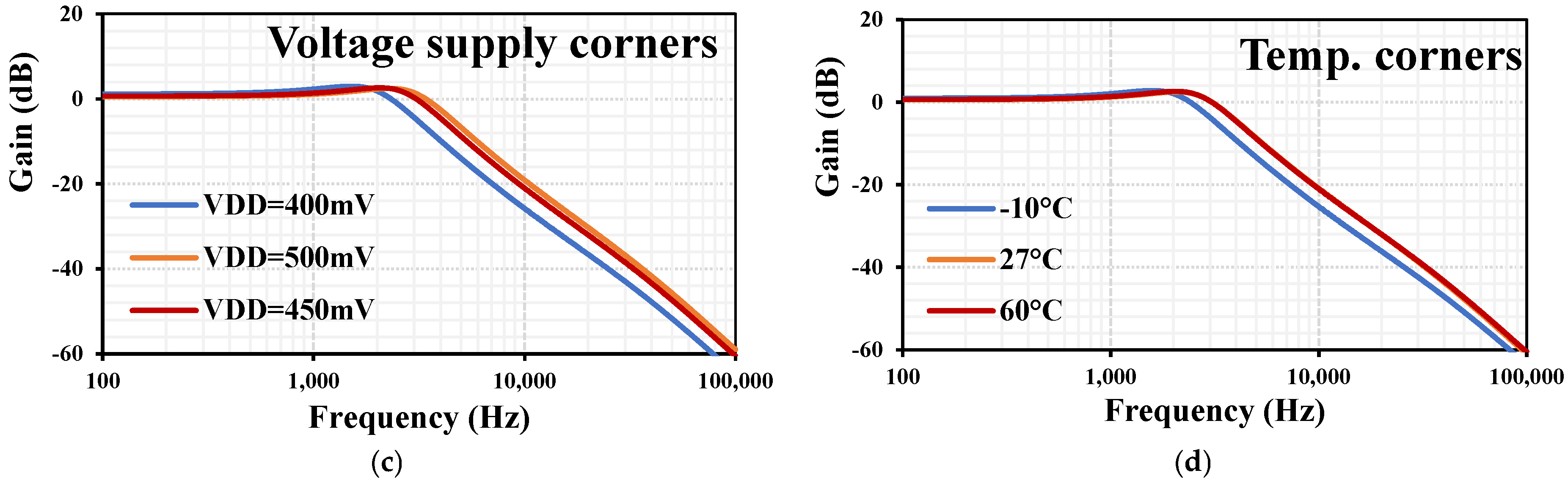
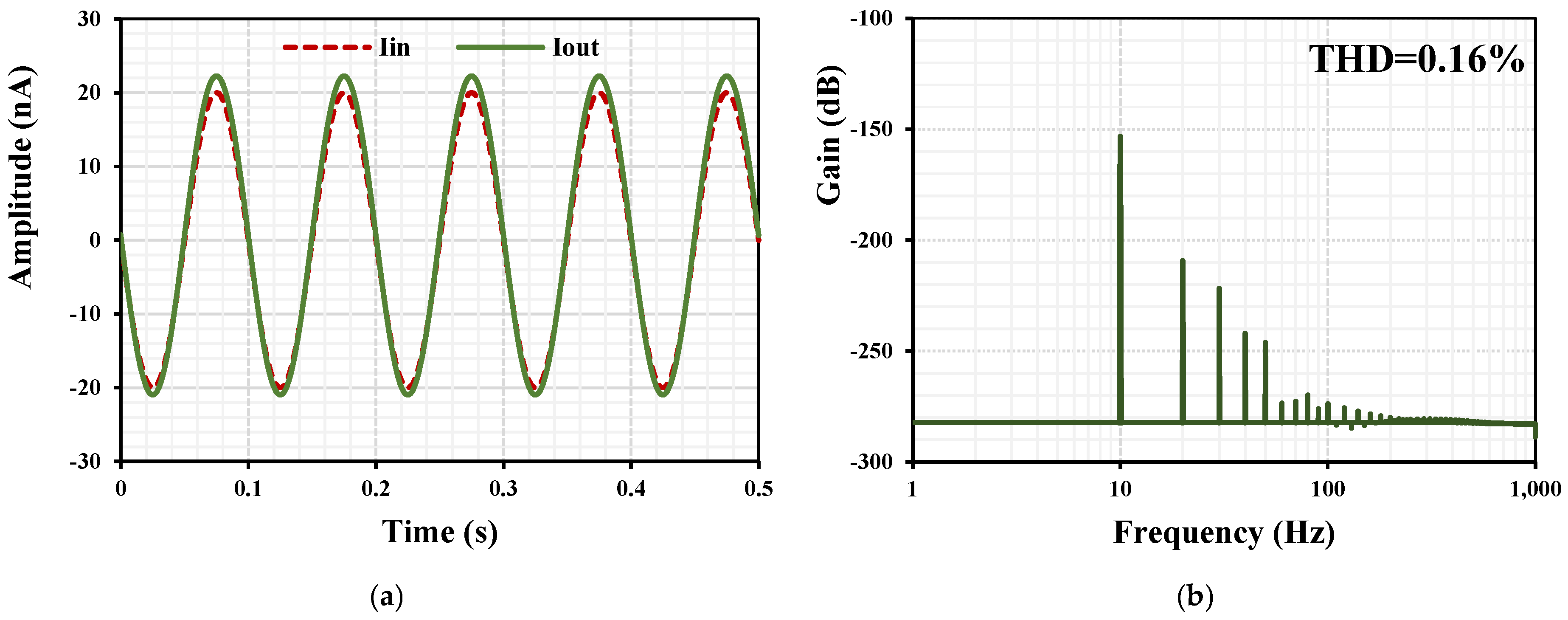
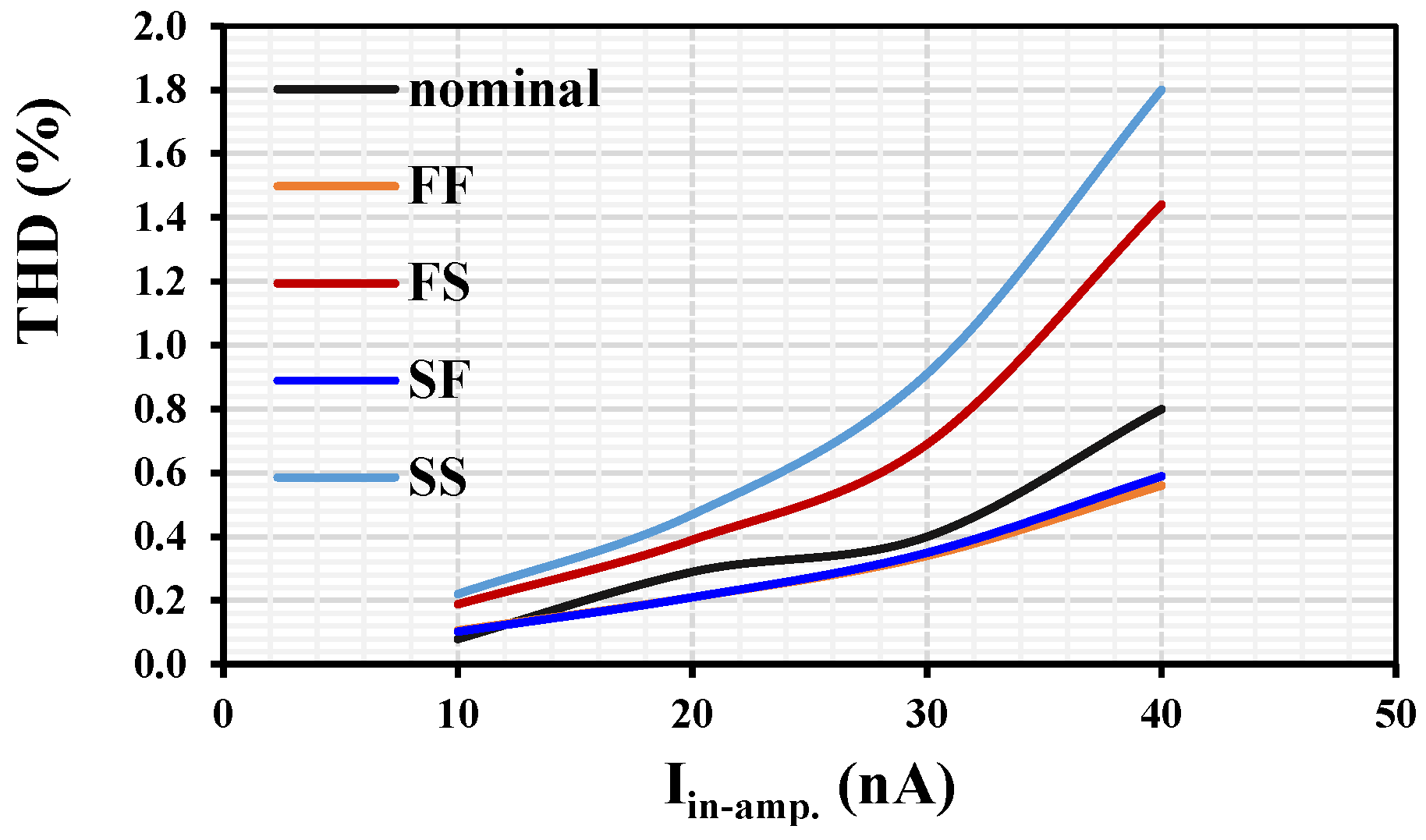
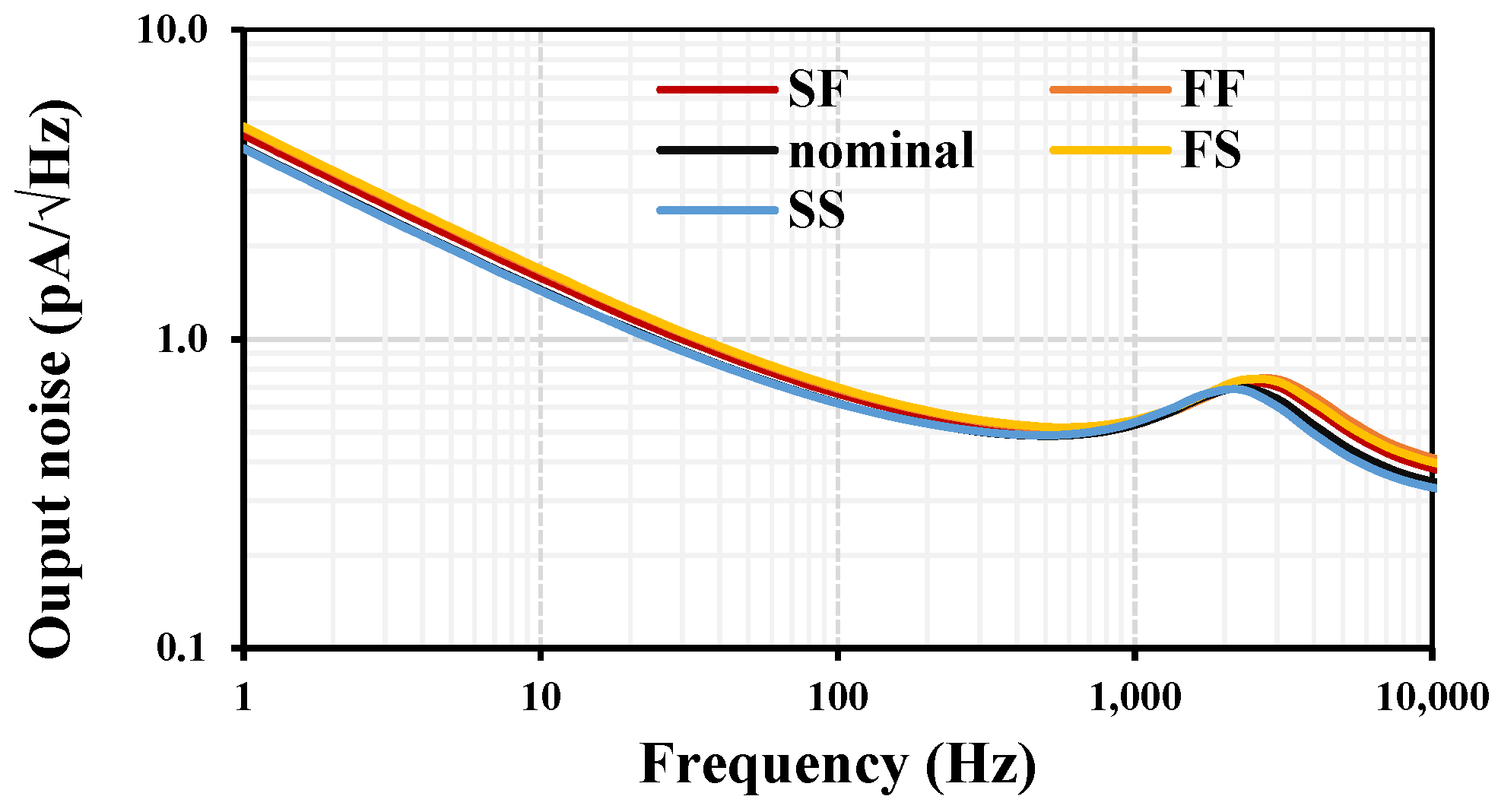
3. Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Biolek, D. CDTA-Building Block for Current-Mode Analog Signal Processing. In Proceedings of the European Conference on Circuit Theory and Design, Krakow, Poland, 1–4 September 2003; pp. 397–400. [Google Scholar]
- Keskin, A.U.; Biolek, D.; Hancioglu, E.; Biolkova, V. Current-mode KHN filter employing current differencing transconductance amplifiers. AEU-Int. J. Electron. Commun. 2006, 60, 443–446. [Google Scholar] [CrossRef]
- Tangsrirat, W.; Dumawipata, T.; Surakampontorn, W. Multiple- input single-output current-mode multifunction filter using current differencing transconductance amplifiers. AEU-Int. J. Electron. Commun. 2007, 61, 209–214. [Google Scholar] [CrossRef]
- Xu, J.; Wang, C.; Jin, J.; Xia, Z. Low-Voltage High-Linearity Wideband Current Differencing Transconductance Amplifier and Its Application on Current-Mode Active Filter. Radioengineering 2014, 23, 512–522. [Google Scholar]
- Kumngern, M.; Dejhan, K. Current-mode multifunction biquad filter with three inputs five outputs using ZC-CDTAs. In Proceedings of the 2012 Second International Conference on Digital Information and Communication Technology and It’s Applications (DICTAP), Bangkok, Thailand, 16–18 May 2012; pp. 309–313. [Google Scholar] [CrossRef]
- Thakur, R.; Singh, S. Voltage tunable current MODE KHN filter based on current differencing transconductance amplifier (CDTA). Int. J. Mod. Phys. B 2021, 35, 2150181. [Google Scholar] [CrossRef]
- Chien, H.-C. CDTA and CCCDTA-Based Mixed-Mode Single-Resistance-Controlled Sinusoidal Oscillators. Appl. Sci. Eng. 2014, 17, 437–446. [Google Scholar] [CrossRef]
- Summart, S.; Thongsopa, C.; Jaikla, W. Dual-Output Current Differencing Transconductance Amplifiers-Based Current-Mode Sinusoidal Quadrature Oscillators. J. Circuits Syst. Comput. 2014, 23, 1450084. [Google Scholar] [CrossRef]
- Rai, S.K.; Gupta, M. Current differencing transconductance amplifier (CDTA) with high transconductance and its application in filter and oscillator. Optik 2016, 127, 3388–3396. [Google Scholar] [CrossRef]
- Biolek, D.; Vavra, J.; Keskin, A.U. CDTA-Based Capacitance Multipliers. Circuits Syst. Signal Process. 2019, 38, 1466–1481. [Google Scholar] [CrossRef]
- Ozenli, D.; Alaybeyoglu, E. An electronically tunable CMOS implementation of capacitance multiplier employing CCCDTA. AEU-Int. J. Electron. Commun. 2022, 155, 154359. [Google Scholar] [CrossRef]
- Koton, J.; Herencsar, N.; Vrba, K.; Minaei, S. Precision full-wave current-mode rectifier using current differencing transconductance amplifier. In Proceedings of the 2011 IEEE 3rd International Conference on Communication Software and Networks, Xi’an, China, 27–29 May 2011; pp. 460–463. [Google Scholar] [CrossRef]
- Kacar, F.; Basak, E. A new mixed mode full-wave rectifier realization with current differencing transconductance amplifier. J. Circuits Syst. Comput. 2014, 23, 1450101. [Google Scholar] [CrossRef]
- Sharma, V.K.; Parveen, T.; Ansari, M.S. Four quadrant analog multiplier based memristor emulator using single active element. AEU-Int. J. Electron. Commun. 2021, 130, 153575. [Google Scholar] [CrossRef]
- Singh, A.; Rai, S.K. OTA and CDTA-based new memristor-less meminductor emulators and their applications. J. Comput. Electron. 2022, 21, 1026–1037. [Google Scholar] [CrossRef]
- Ozenli, D. A Compact Fully Electronically Tunable Memristive Circuit Based on CCCDTA with Experimental Results. Micromachines 2023, 14, 1484. [Google Scholar] [CrossRef] [PubMed]
- Lin, Y.; Gong, J.; Yu, F.; Huang, Y. Current mode multi scroll chaotic oscillator based on CDTA. Front. Phys. 2023, 11, 1202398. [Google Scholar] [CrossRef]
- Alimisis, V.; Papathanasiou, A.; Georgakilas, E.; Eleftheriou, N.P.; Sotiriadis, P.P. An ultra-low power adjustable current-mode analog integrated general purpose artificial neural network classifier. AEU-Int. J. Electron. Commun. 2024, 186, 155467. [Google Scholar] [CrossRef]
- Saberi, M.; Yaghoobzadeh Shadmehri, H.; Tavakkoli Ghouchani, M.; Schmid, A. A High-Precision and High-Dynamic-Range Current-Mode WTA Circuit for Low-Supply-Voltage Applications. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2024, 32, 1955–1958. [Google Scholar] [CrossRef]
- Malmir, R.; Ghaznavi-Ghoushchi, M.B. Design and Analysis of an Ultralow-Voltage Complementary Fold-Interleaved Multiple-Tail Current Mode Logic. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2023, 31, 1675–1685. [Google Scholar] [CrossRef]
- Khateb, F.; Biolek, D. Bulk-Driven Current Differencing Transconductance Amplifier. Circuits Syst. Signal Process. 2011, 30, 1071–1089. [Google Scholar] [CrossRef]
- Rana, C.; Prasad, D.; Afzal, N. Low voltage floating gate MOSFET based current differencing transconductance amplifier and its applications. J. Semicond. 2018, 39, 094002. [Google Scholar] [CrossRef]
- Gangal, A.; Bhanoo, V.; Pandey, N. Low Transconductance M-CDTA Block and its Application in Biomedical Signal Processing. In Proceedings of the 2020 International Conference on Electronics and Sustainable Communication Systems (ICESC), Coimbatore, India, 2–4 July 2020; pp. 1101–1107. [Google Scholar] [CrossRef]
- Arora, Y.; Aggarwal, B.; Kaur, J. Low Voltage High Performance Floating Gate and Quasi Floating Gate CDTA. J. Eng. Res. 2022, 10, 144–152. [Google Scholar] [CrossRef]
- Kumngern, M.; Khateb, F.; Kulej, T. 0.5 V, Low-Power Bulk-Driven Current Differencing Transconductance Amplifier. Sensors 2024, 24, 6852. [Google Scholar] [CrossRef] [PubMed]
- Hayt, W.H.; Kemmerly, J.E.; Durbin, S.M. Engineering Circuit Analysis; McGraw-Hill: New York, NY, USA, 2002. [Google Scholar]
- Ibrahim, M.A.; Minaei, S.; Kuntman, H. A 22.5 MHz current-mode KHN-biquad using differential voltage current conveyor and grounded passive elements. AEU-Int. J. Electron. Commun. 2005, 59, 311–318. [Google Scholar] [CrossRef]
- Sarpeshkar, R. Ultra Low Power Bioelectronics: Fundamentals, Biomedical Applications, and Bio-Inspired Systems; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Zanjani, S.M.A.; Dousti, M.; Dolatshahi, M. A new low-power, universal, multi-mode Gm-C filter in CNTFET technology. Microelectron. J. 2019, 90, 342–352. [Google Scholar] [CrossRef]
- Namdari, A.; Dolatshahi, M. A new ultra low-power, universal OTA-C filter in subthreshold region using bulk-drive technique. AEU-Int. J. Electron. Commun. 2017, 82, 458–466. [Google Scholar] [CrossRef]
- Namdari, A.; Dolatshahi, M. Design of a low-voltage and low-power, reconfigurable universal OTA-C filter. Analog. Integr. Circuits Signal Process. 2022, 111, 169–188. [Google Scholar] [CrossRef]
- Safari, L.; Barile, G.; Ferri, G.; Stornelli, V. A New Low-Voltage Low-Power Dual-Mode VCII-Based SIMO Universal Filter. Electronics 2019, 8, 765. [Google Scholar] [CrossRef]
- Kumngern, M.; Khateb, F.; Kulej, T. 0.5 V Current-Mode Low-Pass Filter Based on Voltage Second Generation Current Conveyor for Bio-Sensor Applications. IEEE Access 2022, 10, 12201–12207. [Google Scholar] [CrossRef]
- Della Sala, R.; Centurelli, F.; Scotti, G.; Trifiletti, A. A 0.3 V OTA with Enhanced CMRR and High Robustness to PVT Variations. J. Low Power Electron. Appl. 2024, 14, 21. [Google Scholar] [CrossRef]
- Shah, M.O.; Caruso, M.; Pennisi, S. 0.35 V Subthreshold Bulk-Driven CMOS Second-Generation Current Conveyor. J. Low Power Electron. Appl. 2024, 14, 36. [Google Scholar] [CrossRef]
- Catania, A.; Gagliardi, F.; Piotto, M.; Bruschi, P.; Dei, M. Ultralow-Power Inverter-Based Delta-Sigma Modulator for Wearable Applications. IEEE Access 2024, 12, 80009–80019. [Google Scholar] [CrossRef]
- Namdari, A.; Aiello, O.; Caviglia, D.D. 0.5 V 32 nW Inverter-Based Gm-C Filter for Bio-Signal Processing. In Proceedings of the 2024 IEEE International Symposium on Circuits and Systems (ISCAS), Singapore, 19–22 May 2024; pp. 1–5. [Google Scholar] [CrossRef]
- Khateb, F.; Kulej, T.; Akbari, M.; Tang, K.-T. A 0.5-V multiple-input bulk-driven OTA in 0.18-μm CMOS. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2022, 30, 1739–1747. [Google Scholar] [CrossRef]
- Pevarez-Lozano, H.; Sanchez-Sinencio, E. Minimum parasitic effects biquadratic OTA-C filter architectures. Analog. Integr. Circuits Signal Process. 1991, 1, 297–319. [Google Scholar] [CrossRef]

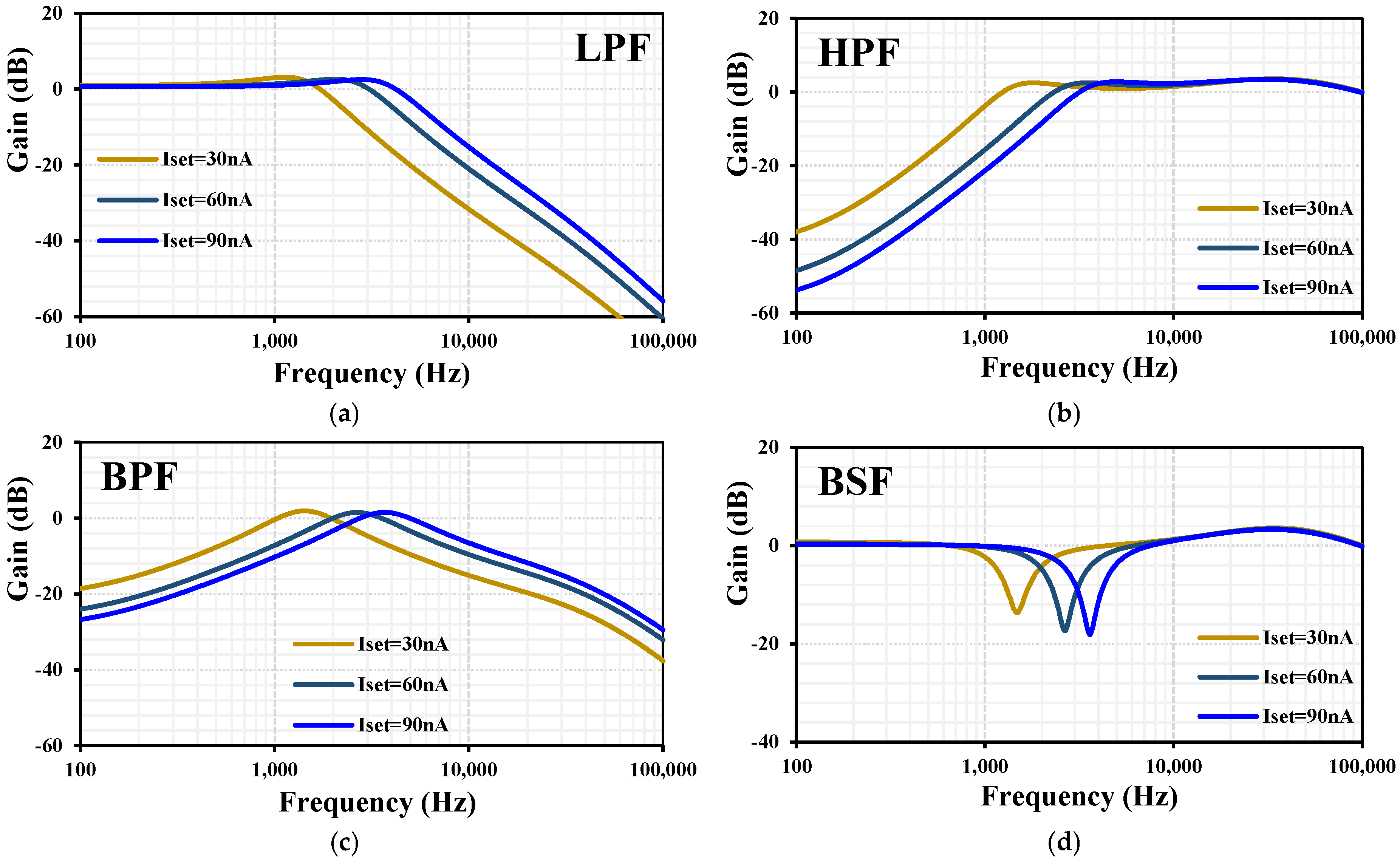
| Filtering Function | Output | Input | Transfer Functions | |
|---|---|---|---|---|
| LPF | Non-inverting | |||
| Inverting | ||||
| HPF | Non-inverting | |||
| BPF | Non-inverting | |||
| Inverting | ||||
| BSF | Non-inverting | |||
| APF | Non-inverting | |||
| CCII | W/L (µm/µm) | TA | W/L (µm/µm) |
|---|---|---|---|
| M1, M2 | 40/3 | M1, M2 | 2 × 15/1 |
| M3, M6, M8, M9–M11 | 50/3 | M5–M11 | 2 × 10/1 |
| MB, M4, M5, M7, M12–M15 | 30/3 | M3, M4 | 15/1 |
| M5c–M11c | 10/1 | ||
| M12–M19 | 2 × 15/1 | ||
| M12c–M19c | 15/1 | ||
| Capacitor: CC = 5 pF | |||
| Parameters | Value |
|---|---|
| Supply voltage | 0.45 V |
| Bias current IB | 50 nA |
| Technology | 0.18 μm |
| DC current swings: | ±50 nA |
| Current gains: | 0.988, 0.999 |
| Offset current = 0) | 0.3 nA |
| −3 dB bandwidth: | [135, 124] kHz |
| −3 dB bandwidth of = 10 nA) | 76 kHz |
| 19 kΩ | |
| 62.27 MΩ | |
| [861, 792] MΩ | |
| = [5, 10, 15, 20] nA) | [34.5, 67.5, 99.5, 130.6] nS |
| Power dissipation = 10 nA) | 328 nW |
| Factor | Proposed 2025 | [25] 2024 | [29] 2019 | [31] 2022 | [32] 2019 |
|---|---|---|---|---|---|
| Number of active devices | 2-CDTA | 4-CDTA | 8-INV | 8-OTA | 3-VCII, 1-ICB |
| Realization | 0.18 µm CMOS | 0.18 µm CMOS | 32 nm CNTFET | 0.18 µm CMOS | 0.18 µm CMOS |
| Number of passive devices | 2-C | 2-C, 2-R | 2-C | 2-C | 2-C, 3-R |
| Filter mode | CM (MIMO) | CM (MISO) | CM (MISO) | MM (MIMO) | TIM (SIMO) |
| Total number of filter responses | 19 | 12 | 5 (CM) | 5 (CM) | 5 |
| Yes | Yes | Yes | Yes | No | |
| All passive devices grounded | Yes | Yes | Yes | Yes | No |
| Without inverted/double input conditions/input-matching condition | Yes | No | No | No | Yes |
| High-output impedance | Yes | Yes | Yes | Yes | - |
| Power supply (V) | 0.45 | 0.5 | ±0.2 | ±0.3 | ±0.9 |
| Power dissipation (μW) | 1.098 | 3.39 | 447 × 10−3 | 5.77 | 1.47 × 103 |
| Natural frequency (Hz) | 2.66 × 103 | 104.7 | 1.1 × 106 | 5 × 103 | 1.5 × 106 |
| Integrated noise (pA) | 42.35 | 38.32 | - | - | - |
| THD (%) | 0.8@40 nA | 0.936@150 nA | >1.16 | 0.8@100 nA | 3.6@5 μA |
| Dynamic range (dB) | 61 | 68.86 | - | 53.2 | - |
| Verification of result | Sim. | Sim. | Sim. | Sim. | Sim. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khateb, F.; Kumngern, M.; Kulej, T.; Vavra, J. A 328 nW, 0.45 V Current Differencing Transconductance Amplifier and Its Application in a Current-Mode Universal Filter. Appl. Sci. 2025, 15, 3471. https://doi.org/10.3390/app15073471
Khateb F, Kumngern M, Kulej T, Vavra J. A 328 nW, 0.45 V Current Differencing Transconductance Amplifier and Its Application in a Current-Mode Universal Filter. Applied Sciences. 2025; 15(7):3471. https://doi.org/10.3390/app15073471
Chicago/Turabian StyleKhateb, Fabian, Montree Kumngern, Tomasz Kulej, and Jiri Vavra. 2025. "A 328 nW, 0.45 V Current Differencing Transconductance Amplifier and Its Application in a Current-Mode Universal Filter" Applied Sciences 15, no. 7: 3471. https://doi.org/10.3390/app15073471
APA StyleKhateb, F., Kumngern, M., Kulej, T., & Vavra, J. (2025). A 328 nW, 0.45 V Current Differencing Transconductance Amplifier and Its Application in a Current-Mode Universal Filter. Applied Sciences, 15(7), 3471. https://doi.org/10.3390/app15073471









