Analytical Investigation of Electromechanical Hierarchical Metamaterials for Vibration Attenuation and Energy Harvesting

Abstract

This work presents a theoretical study of outward and inward hierarchical metamaterials. Hierarchically configured multiple electromechanical resonators with shunt circuits are implemented, maintaining the same overall mass as that of a comparable single resonator metamaterial. The governing equations of motion for the outward and inward hierarchical configurations are derived. Dispersion relations are determined for each configuration with varying system parameters to identify key design parameters and assess their impact on the system’s dynamic behavior. Furthermore, outer mass displacement transmissibility and normalized total power output of finite chain hierarchical metamaterials are compared to observe vibration attenuation and energy harvesting capacity. The results reveal that the band structure of the hierarchical electromechanical metamaterials depends on the configuration type, the resonator masses, the electromechanical coupling coefficient, and the resistance of the shunt circuit. The first-order hierarchy offers a greater total band gap width, increased bandwidth, and greater flexibility in tuning the band structure. Finite chain transmissibility analysis demonstrates that, compared to the baseline performance of the zero-order hierarchy, the first-order hierarchy exhibits superior abilities in vibration attenuation and energy harvesting for the same total mass. The ideal design requires careful consideration of the resonator masses and their configuration, electromechanical coupling coefficient, and resistance of the shunt circuits. This theoretical work provides a foundation for designing lightweight hierarchical metamaterials for simultaneous vibration attenuation and energy harvesting.

1. Introduction

Periodic metastructures are well-known for their wave-filtering properties within a specific frequency range, called the band gap. In phononic crystals and structural materials, Bragg scattering and local resonance are two primary mechanisms of band gap formation [1]. However, achieving low-frequency band gaps through Bragg scattering presents challenges, prompting Liu et al. [2] to propose locally resonant metamaterials as an alternative. Metamaterials are periodic [3] or non-periodic [4] structures composed of unit cells, where the unit cell size is typically smaller than the wavelength of the waves they interact with. These metamaterials can be acoustic [5,6], elastic [7] or electromagnetic [8,9] depending on the type of waves they are designed to manipulate. Acoustic metamaterials manipulate sound waves, elastic metamaterials control elastic or mechanical waves, and electromagnetic metamaterials interact with electromagnetic waves. Each class is engineered to exhibit unique properties, such as negative refraction, negative density, or negative stiffness for a tunable response.

The integration of local resonators has become a pivotal development in controlling the propagation of waves. Locally resonant metamaterials manipulate wave behavior by tuning the system frequency to match that of the local resonators, thereby enabling selective wave transmission or attenuation [10]. Those metamaterials find applications in vibration control [11], energy harvesting [12], sound manipulation [13], electromagnetic waves control [14] and in the development of tunable devices [15]. Moreover, locally resonant metamaterials are attracting attention in civil engineering due to their unique properties for stress wave isolation, which are useful for structural protection [16].

The dispersion relations in locally resonant metamaterials have been studied for more than a decade [17,18]. The dispersion of locally resonant metamaterials with a single local resonator is characterized by a narrow fixed band gap, which limits wave control to a small frequency range, making it unsuitable for applications requiring broadband attenuation. The wave propagation properties are dictated by the configuration and physical properties of the respective unit cells of the metamaterials. To address the challenge of narrow and fixed band gaps, numerous approaches have been proposed. The most prominent approaches include the integration of multiple local resonators [19], gradient geometry [20], grading [21,22], and electromechanical coupling [23,24].

A locally resonant metamaterial that integrates multiple local resonators at different scales is called a hierarchical metamaterial [25], and is well-established in the literature. The dispersion profiles of a multi-resonator metamaterial were investigated, and band structure tuning was demonstrated by changing the stiffness constants and masses of the resonators [26,27]. Zhao et al. [28] studied coupled multi-resonator metamaterials to broaden an elastic band gap, and Gorshkov et al. [29] introduced a multi-resonator concept to 3D acoustic metamaterials. Hierarchical metamaterials provide a flexible band structure and dynamically stable periodic configurations. Hierarchically configured resonators have been shown to achieve multiple broad local resonance band gaps in beams [30] and mass-in-mass chains [31]. These multiple band gaps emerge as a result of the presence of various tuning frequencies within the hierarchy. Some researchers proposed nonlinear metamaterials with hierarchical unit cells for amplitude-dependent broadband wave filtering [32,33]. Moreover, hierarchical metamaterials exhibit nonreciprocal vibrational energy transfer in nonlinear systems. The nonreciprocal nature of wave propagation in hierarchical metamaterials makes them suitable for the design of mechanical diodes [34]. A comprehensive understanding of the dispersion dynamics in different hierarchical configurations is essential for effective energy flow control [35,36].

In general, for the locally resonant metamaterials, stiffness [30] and inertial properties [37] are the two significant mechanical parameters governing band gap formation. However, recently it has been observed that the band structure of locally resonant metamaterials can be tuned by electromechanical tuning parameters [38]. An electromechanical local resonator is a resonator that incorporates a piezoelectric transducer, with its piezoelectric layer typically connected to electrical circuits. In strong electromechanical coupling, the resonant frequency of the metamaterial changes due to the effect of the electromechanical coupling coefficient and the resistance of the shunt circuit [39]. Electromechanical coupling refers to the interaction between electrical and mechanical elements, where energy is exchanged between the two domains. Piezoelectric patches and shunt circuits embedded in metamaterials are used to modify the band structure of strongly coupled electromechanical metamaterials [40]. Passive electromechanical resonators [41] and active piezoelectric elements have been used for vibration control [42]. In this vibration control method, the charge and current flow associated with piezoelectric shunts are used to control vibrations. Moreover, periodic shunts are used to attenuate and localize the propagation of waves [43,44]. They effectively dampen multimode vibrations in the beam and dissipate energy all without requiring external mechanical dampers. This indicates that piezoelectric layers, in conjunction with shunt circuits, can be used to vary the stiffness of the local resonators. Beyond that, piezoelectric-embedded locally resonant metamaterials have applications in biomedical devices [45], noise reduction, structural health monitoring, and the development of tunable acoustic devices [46].

Recent studies have investigated the impact of electromechanical resonators and shunt circuits on single-resonator mass-in-mass metamaterials for simultaneous energy harvesting and vibration reduction [47,48]. These studies found that weakly coupled electromechanical resonators with shunted circuits minimally affect dispersion, enabling simultaneous energy harvesting with negligible impact on vibration control. However, strong electromechanical coupling can deform band structures, potentially merging acoustic and optical modes. Malla et al. explored electromechanical metamaterials with resistor and inductor shunts [49]. In strongly coupled systems featuring a single resonator shunted to a resistor and inductor, triple passbands were observed.

Despite the fact that several works have focused on the use of metamaterials for vibration attenuation and energy harvesting with electromechanical elements [50,51], no research has investigated hierarchical mass-in-mass metamaterials incorporating electromechanical resonators and shunt circuits. Tang, L. and Yang, Y. [52] studied the optimal energy harvesting performance of a multidegree-of-freedom configuration using a single unit cell. While this design includes multiple hierarchically configured local resonators, only a single piezoelectric layer and shunt circuit were associated with the main chain. Their results showed that a multiple degree-of-freedom energy harvester increases the power output density with an increase of overall mass compared to a single degree-of-freedom system. This work differs from the study of Tang, L. and Yang, Y. [52] by adopting a hierarchical configuration of multiple electromechanical resonators and shunt circuits, without changing the overall mass equivalent to that of a comparable single resonator metamaterial. The hierarchy is designed in two types: the outward and inward configurations. The shunt circuits are integrated into the electromechanical resonator chain rather than the main chain. The key motivation for this research is to investigate the effect of combining hierarchically configured resonators with electrical parameters on band gap formation and band structure tunability, without introducing additional mass, an aspect that has not been addressed previously. Considering the vibration attenuation and energy harvesting applications, this work seeks to further explore the advantages of outward and inward hierarchical configurations under weak and strong electromechanical coupling conditions.

This paper explores the influence of hierarchical configurations, electromechanical coupling conditions, shunt circuit resistances, and electromechanical resonator masses on the band structure. From the governing equations of motion, the dispersion relationships are determined for zero-order and first-order hierarchies at different system parameters. Moreover, the displacement transmissibility and the normalized total power output of finite chain hierarchical metamaterials have been thoroughly examined.

2. Mathematical Modeling

The schematic diagram in Figure 1 illustrates two types of hierarchical configurations, namely the outward and inward configurations. The outward configuration Figure 1a arranges the electromechanical resonators in parallel; however, the inward configuration Figure 1b arranges them in a nested manner such that the $n^{\mathrm{t}\mathrm{h}}$ electromechanical resonator is connected to the $(n-1)$ and ${(n+1)}^{\mathrm{t}\mathrm{h}}$ electromechanical resonators [25]. In this setup, a unit cell consists of N electromechanical local resonators with masses $m_1,m_2,\cdots ,m_n,\cdots ,m_N$, arranged within an outer mass $m_0$. Adjacent unit cells are linked by a spring with a stiffness constant, $k_0$, creating a continuous metamaterial chain. The stiffness of the resonator connectors is denoted as $k_1$, $k_2$, ⋯, $k_N$. A resistor-loaded shunt circuit is integrated into each piezoelectric patch. The parameters ${\theta }_n^{\left(j\right)}$, $C_n^{\left(j\right)}$, and $R_n^{\left(j\right)}$ are the electromechanical coupling coefficient, the capacitance of the piezoelectric materials, and the resistance of the shunt circuit, respectively. The maximum number of local resonators, N, is determined by the hierarchy order, which is defined as $N-1$. In this work, in this work, the zero-order and first-order configurations, with $N=1$ and $N=2$, respectively, will be studied.

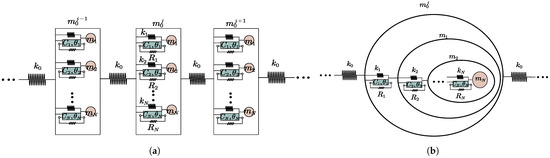
Figure 1. Schematic diagrams of the hierarchy: (a) outward and (b) inward configurations of electromechanical resonators shunted with resistor loaded circuits.

Accordingly, the equations of motion for the $j^{\mathrm{t}\mathrm{h}}$ unit cell in the outward configuration can be expressed as:

$$m_0{\ddot{u}}_0^{\left(j\right)}-k_0{u}_0^{(j-1)}+2k_0{u}_0^{\left(j\right)}-k_0{u}_0^{(j+1)}+\sum _{n=1}^N{m}_n{\ddot{u}}_n^{\left(j\right)}=0$$

(1)

$$m_n{\ddot{u}}_n^{\left(j\right)}-k_n{u}_0^{\left(j\right)}+k_n{u}_n^{\left(j\right)}+{\theta }_n{v}_n^{\left(j\right)}=0$$

(2)

$$R_n{C}_n{\dot{v}}_n^{\left(j\right)}+v_n^{\left(j\right)}+R_n{\theta }_n{\dot{u}}_0^{\left(j\right)}-R_n{\theta }_n{\dot{u}}_n^{\left(j\right)}=0$$

(3)

Further, the governing equations of motion for the inward configuration’s unit cell are

$$m_0{\ddot{u}}_0^{\left(j\right)}-k_0{u}_0^{(j-1)}+(2k_0+k_1)u_0^{\left(j\right)}-k_0{u}_0^{(j+1)}-k_1{u}_1^{\left(j\right)}-{\theta }_1{v}_1^{\left(j\right)}=0$$

(4)

$$m_n{\ddot{u}}_n^{\left(j\right)}-k_n{u}_{n-1}^{\left(j\right)}+(k_n+k_{n+1})u_n^{\left(j\right)}-k_{n+1}{u}_{n+1}^{\left(j\right)}+{\theta }_n{v}_n^{\left(j\right)}-{\theta }_{n+1}{v}_{n+1}^{\left(j\right)}=0$$

(5)

$$m_N{\ddot{u}}_N^{\left(j\right)}-k_N{u}_{N-1}^{\left(j\right)}+k_N{u}_N^{\left(j\right)}+{\theta }_N{v}_N^{\left(j\right)}=0$$

(6)

$$R_n{C}_n{\dot{v}}_n^{\left(j\right)}+v_n^{\left(j\right)}+R_n{\theta }_n{\dot{u}}_{n-1}^{\left(j\right)}-R_n{\theta }_n{\dot{u}}_n^{\left(j\right)}=0$$

(7)

Here, $u_0^{\left(j\right)}$ and $u_n^{\left(j\right)}$ are the displacements of the outer mass and $n^{\mathrm{t}\mathrm{h}}$ resonator, respectively, and $v_n^{\left(j\right)}$ is the induced voltage across the $n^{\mathrm{t}\mathrm{h}}$ shunt circuit, all of which are within the $j^{th}$ unit cell. A general harmonic solution of the form

$$\begin{array}{cc}\hfill u_0^{\left(j\right)}& =A_0{e}^{i(j\kappa -\omega t)},\hfill \\ \hfill u_n^{\left(j\right)}& =A_n{e}^{i(j\kappa -\omega t)},\mathrm{and}\hfill \\ \hfill v_n^{\left(j\right)}& =B_n{e}^{i(j\kappa -\omega t)}.\hfill \end{array}$$

is assumed to establish the frequency-wavenumber relations for the infinite lattice [53,54]. In this solution, t is time, $\omega$ is excitation frequency of the system, and $\kappa$ is the normalized wavenumber. Substituting the presumed solution into Equations (1)–(7) provides $2N+1$ simultaneous equations for each configurations. By substituting the assumed solution form into Equations (1)–(3), we obtain the following results:

$$\left(2k_0\left(1-cos(\kappa )\right)-m_0{\omega }^2\right)A_0-\sum _{n=1}^N{A}_n{m}_n{\omega }^2=0$$

(8)

$$-k_n{A}_0+\left(k_n-m_n{\omega }^2\right)A_n+{\theta }_n{B}_n=0$$

(9)

$$-i\omega R_n{\theta }_n{A}_0+i\omega R_n{\theta }_n{A}_n+\left(1-i\omega R_n{C}_n\right)B_n=0$$

(10)

Upon substituting the assumed solution into the equations of motion for the inward configuration, presented in Equations (4)–(7), the system simplifies to Equations (11)–(14).

$$\left(2k_0(1-cos(\kappa ))-m_0{\omega }^2+k_1\right)A_0-k_1{A}_1-{\theta }_1{B}_1=0$$

(11)

$$-k_n{A}_{n-1}+\left(k_n+k_{n+1}-m_n{\omega }^2\right)A_n-k_{n+1}{A}_{n+1}+{\theta }_n{B}_n-{\theta }_{n+1}{B}_{n+1}=0$$

(12)

$$-k_N{A}_{N-1}+(k_N-{\omega }^2{m}_N)A_N+{\theta }_N{B}_N=0$$

(13)

$$-i\omega R_n{\theta }_n{A}_{n-1}+i\omega R_n{\theta }_n{A}_n+\left(1+i\omega R_n{C}_n\right)B_n=0$$

(14)

The determinants given in Equations (A1) and (A2) were expanded using Mathematica to obtain the dispersion equations used in the simulations presented in this study. Then, the roots of the dispersion relation, along with the finite chain transmissibility and power output, solved in MATLAB R2024a.

A local resonance band gap is created as a result of mode separation caused by the local resonance effect. In an undamped single degree-of-freedom resonator, the natural frequency of the resonator marks the center of the local resonance band gap and is called the tuning frequency [10]. In this context, an undamped resonator refers to a local resonator without piezoelectric patch, shunt circuit, or mechanical damping element. A local resonance band gap tuning frequency equation can be derived by assuming the outer mass as a fixed boundary [53]. In the outward configuration, motion of the resonators are not coupled; therefore, the undamped tuning frequency, ${\omega }_n$, of the $n^{\mathrm{th}}$ local resonator can be treated as a single degree-of-freedom system and expressed as

$${\omega }_n=\sqrt{{\displaystyle \frac{k_n}{m_n}}}$$

(15)

However, the coupled motion of the resonators in the inward configuration yields a multiple degree-of-freedom system. The multiple degree-of-freedom local resonator undamped tuning frequencies in the inward configuration are the eigenvalues of Equation (16), which is the characteristic polynomial determined from the coefficient matrix of Equations (12) and (13).

$$\left|\begin{array}{ccccc}-{\omega }_n^2{m}_1+k_1+k_2& -k_2& 0& \cdots & 0\\ -k_2& \ddots & \ddots & ⋮& ⋮\\ ⋮& \ddots & \ddots & -k_{N-1}& ⋮\\ & 0& -k_{N-1}& -{\omega }_n^2{m}_{N-1}+k_{N-1}+k_N& -k_N\\ 0& \cdots & \cdots & -k_N& -{\omega }_n^2{m}_N+k_N\end{array}\right|=0$$

(16)

The tuning frequency of the $n^{\mathrm{th}}$ electromechanical resonator, ${\omega }_{em}$, shunted with an electrical circuit in the outward configuration is derived from Equations (9) and (10). Equations (17) and (18) are used to characterize the tuning frequency of the electromechanical resonator in the zero-order hierarchy, as discussed in the next section.

$$\left(k_n-m_n{\omega }_{em}^2\right)A_n+{\theta }_n{B}_n=0$$

(17)

$$i{\omega }_{em}{R}_n{\theta }_n{A}_n+\left(1-i{\omega }_{em}{R}_n{C}_n\right)B_n=0$$

(18)

For the analysis, the parameter values listed in Table 1 are utilized [49]. In addition, the dimensionless ratio of the total mass of the electromechanical resonator to the outer mass is defined as $\eta ={\displaystyle \frac{m_r}{m_0}}$, where $m_r$ represents the total mass of the electromechanical resonators within the unit cell. The ratio of the $n^{\mathrm{t}\mathrm{h}}$ electromechanical resonator mass to the resonators total mass is defined as ${\beta }_n={\displaystyle \frac{m_n}{m_r}}$. Based on this generic definition, for the first-order hierarchy, $\eta ={\displaystyle \frac{m_1+m_2}{m_0}}$ and ${\beta }_1={\displaystyle \frac{m_1}{m_1+m_2}}$. For the zero-order configuration ${\beta }_1$ is 1. The normalized frequency, $\mathrm{\Omega }$, is the ratio of $\omega$ to ${\omega }_0$, $\mathrm{\Omega }={\displaystyle \frac{\omega }{{\omega }_0}}$, where ${\omega }_0=\sqrt{{\displaystyle \frac{k_0}{m_0}}}$. The stiffness of the local resonator connecting spring is $k_1=k_2=\eta k_0$. The electromechanical coupling coefficients and the shunt circuit resistances of the first-order hierarchy are ${\theta }_1={\theta }_2$, and $R_1=R_2$, respectively.

Table 1. Material parameters used in the analysis.

Properties	${\mathit{m}}_0$	${\mathit{\omega }}_0$	${\mathit{C}}_1$, ${\mathit{C}}_2$
Value	$0.125$ kg	$2\times {10}^5$ rad/s	$1.13\times {10}^{-10}$ F

3. Band Structure of Hierarchical Metamaterials

In this section, the effect of electromechanical coupling coefficients and shunt circuit resistances on the band structure of the zero-order and first-order hierarchies is first observed. Then, the effect of resonator mass ratios on the band structure will be determined to explore the effectiveness of hierarchical metamaterials under optimized conditions.

3.1. Effect of Electromechanical Coupling Coefficients and Shunt Circuit Resistances

The effect of the strong and weak electromechanical coupling coefficients is shown in Figure 2, generated at a shunt circuit resistance of ${10}^4$ ohms. According to Bukhari et al. [50], strong electromechanical coupling is for an electromechanical coupling coefficient that is greater than ${10}^{-3}$ N/V, while the electromechanical coupling coefficient between ${10}^{-10}$ N/V and ${10}^{-3}$ N/V is considered as weak electromechanical coupling. In this study, a transverse electromechanical coupling system was selected [55]. In transverse coupling, the mechanical and electrical domains are coupled such that the electric field polarization aligns with the thickness direction of the piezoelectric material, and strain is applied along the axial direction. To quantify the effects of hierarchy, electromechanical coupling, and shunt circuits, attention will be given to changes to the band gaps and bandwidths in the dispersion relations. A band gap is the frequency range between the upper and lower limits of consecutive passbands. On the other hand, the bandwidth of the passbands is the range of frequencies within which wave propagation is allowed. The dispersion of the zero-order hierarchy has two passbands and a single local resonance bandgap. In contrast, the dispersion of the first-order hierarchy, which is distinct for the outward and inward configurations, generates three passbands and two local resonance bandgaps. A dispersion relation at a given wavenumber corresponds to the natural frequencies of the masses. This explains why the number of passbands and local resonance bandgaps increases with higher-order hierarchies. This relationship is affected by the electromechanical couplings and the resistances of the shunt circuit.

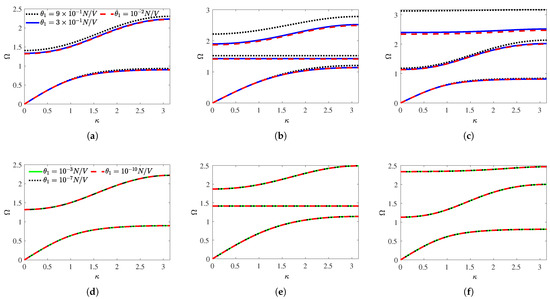
Figure 2. The effect of strong electromechanical coupling coefficients on the band structure of (a) zero-order, (b) outward, and (c) inward configurations. The effect of weak electromechanical coupling coefficients on the band structure of (d) zero-order, (e) outward, and (f) inward configurations at $\eta =0.75$ and ${\beta }_1=0.5$.

The parameters used to generate Figure 2a–c are selected based on the order of magnitude of the strong electromechanical coupling coefficient, ranging from ${10}^{-2}$ N/V to ${10}^{-1}$ N/V, as ${10}^{-3}$ N/V represents the lower boundary. For lower electromechanical coupling coefficients, such as 10⁻² N/V and 3 × 10⁻¹ N/V, the influence on the band structure and band gap width is minimal, resulting in only subtle shifts on the curves. This highlights that at the lower end of the strong coupling regime, the system’s dynamic response is not highly sensitive to variations in the electromechanical coupling coefficient. However, as the electromechanical coupling coefficient approaches higher values, 9 × 10⁻¹ N/V, a more noticeable widening of the band gap occurs. Strong electromechanical coupling coefficients shift the location of the local resonance band gaps upward. Increasing the strong electromechanical coupling coefficients, as shown in Figure 2a–c, increases the width of the local resonance band gaps and the bandwidths. The band gap width and bandwidth changes are greater in the first-order hierarchy compared to the zero-order hierarchy, with the inward configuration showing the most significant increment. Due to strong electromechanical coupling, the band gap width increases by $11.52\%$ for the zero-order configuration, and by $13.49\%$ and $7.51\%$ in the first band gap for the outward and inward configurations, respectively. A more significant increase is observed in the second band gap width for the first-order configuration, reaching $51.87\%$ and $193.80\%$ for the outward and inward configurations, respectively. The strong electromechanical coupling appears to have a stronger effect at higher frequencies. In contrast to the strong electromechanical coupling, weak electromechanical coupling does not produce variation in the band structure, as illustrated in Figure 2d,e for both the zero-order and first-order hierarchies. Furthermore, the dispersion relationship of the zero-order configuration agrees well with the dispersion of the electromechanical metamaterial with a single resonator studied by Bukhari et al. [47].

Figure 3 shows the dispersion curves of hierarchical metamaterials for strongly and weakly coupled systems, evaluated at different resistance values of the shunt circuit. The resistances of the shunt circuit show a noticeable impact on the band structure of strongly coupled hierarchical metamaterials, as evidenced in Figure 3a–c. However, it exhibits minimal effect on the band structures for the weakly coupled system, as shown in Figure 3d–f. This highlights how the coupling strength dictates the sensitivity of the system’s band structure to changes made to the shunt circuit resistance values.

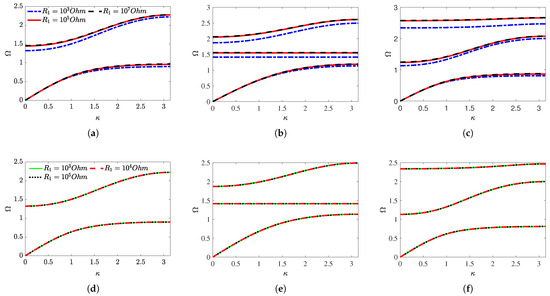
Figure 3. The effect of shunt circuit resistances on the band structure of strongly coupled systems at ${\theta }_1=0.3$ N/V: (a) zero-order, (b) outward, and (c) inward configurations. The effect of shunt circuit resistances on the band structure of weakly coupled systems at ${\theta }_1={10}^{-10}$ N/V: (d) zero-order, (e) outward, and (f) inward configurations at $\eta =0.75$ and ${\beta }_1=0.5$.

For a relatively strong electromechanical coupling, such as ${10}^{-1}$ N/V, the second and third passbands of the first-order configurations are affected by the resistances of the shunt circuit. Although the effect on the first passband at lower frequencies is almost negligible, an influence is observed at higher frequencies. Under strong electromechanical coupling, with a shunt circuit resistance of ${10}^5$ ohms, the band gap width increases by $15.74\%$ for the zero-order configuration, and by $30.55\%$ and $11.51\%$ in the first band gap for the outward and inward configurations, respectively. Additionally, the second band gap width increases for the first-order configurations, reaching $10.11\%$ and $47.50\%$ for the outward and inward configurations, respectively. The band structure is significantly affected when the resistance of the shunt circuits is between ${10}^3$ and ${10}^5$ ohms. Within this range, increasing the shunt circuit resistance leads to a band gap width expansion. The impact of the shunt circuit resistances on the band structure primarily depends on the electromechanical coupling coefficients. The band structure of strongly coupled hierarchical metamaterials with lower resistance values is similar to that observed in weakly coupled scenarios.

To obtain a detailed understanding of the band structure and the attenuation level of hierarchical metamaterials, it is crucial to study the real and imaginary wavenumber components. However, before analyzing the wavenumber components, let us first examine how the tuning frequencies of the electromechanical resonators behave as a function of the electromechanical coupling coefficient and the shunt circuit resistance. For simplicity, this analysis focuses on the zero-order hierarchy. The tuning frequency of the electromechanical resonator, ${\omega }_{em}$, for the zero-order configuration ($n=1$), is obtained by solving the determinant of Equations (17) and (18). By equating the determinant to zero and applying mathematical manipulations, Equation (19) is obtained.

$${\omega }_1^2-{\omega }_{em}^2-i{R}_1{C}_1\left(\left(1+{\displaystyle \frac{{\theta }_1^2}{C_1{k}_1}}\right){\omega }_1^2{\omega }_{em}-{\omega }_{em}^3\right)=0$$

(19)

Here, ${\omega }_1=\sqrt{{\displaystyle \frac{k_1}{m_1}}}$, and ${\omega }_{em}$ is the electromechanical resonator tuning frequency.

In Equation (19), the term ${\displaystyle \frac{{\theta }_1^2}{C_1}}$ represents the additional stiffness introduced by the electromechanical coupling coefficient, and $R_1{C}_1$ is the decay rate induced by the shunt circuit. The electromechanical coupling coefficient and shunt circuit resistance lead to three possible cases on the solution of ${\omega }_{em}$. These cases include the short circuit (when $R_1=0$), weak coupling, and strong coupling scenarios. When $R_1=0$, the electromechanical resonator tuning frequency becomes identical to that of the undamped resonator tuning frequency, i.e., ${\omega }_{em}={\omega }_1$. In this case, the resonator is purely mechanical. When the system is weakly coupled, the dimensionless stiffness, ${\displaystyle \frac{{\theta }_1^2}{C_1{k}_1}}$, becomes negligible. As a result, Equation (19) provides three roots: ${\omega }_{em}=\pm {\omega }_1$ and ${\omega }_{em}=-i{\displaystyle \frac{1}{R_1{C}_1}}$. Originally, the undamped resonator did not have an imaginary component. For the weakly coupled resonator, the tuning frequency includes both real and imaginary components. The real part remains the same, so the resonator resonates at the same frequency. However, the added imaginary part introduces attenuation around the tuning frequency. In the third case, the strong coupling of the electrical and mechanical systems alters the stiffness of the resonators, leading to a substantial change in the tuning frequency. For a strongly coupled electromechanical resonator, solving Equation (19) for ${\omega }_{em}$ yields three roots. Two of these roots are complex, consisting of both real and imaginary components, while the third root is purely imaginary.

The roots of Equation (19) are shown graphically in Figure 4, providing a visual representation of their behavior under varying electromechanical coupling coefficients and the resistance of the shunt circuits for the zero-order hierarchy. The red dotted horizontal lines represents the undamped tuning frequency, ${\omega }_1$, of the resonator. The real part of the electromechanical resonator tuning frequency increases with both the electromechanical coupling coefficient and the resistance of the shunt circuit. Relative to ${\omega }_1$, it increases by $3.28\%$ as the coupling coefficient increases, as shown in Figure 4a, and by $8.87\%$ as $R_1$ increases, as shown in Figure 4c. At lower values of the electromechanical coupling coefficients and shunt circuit resistances, the real part of ${\omega }_{em}$ aligns with ${\omega }_1$. The first two imaginary parts are equal and increase as the electromechanical coupling coefficient increases, while the third imaginary part decreases, as shown in Figure 4b. At low shunt circuit resistance, the imaginary component of the third root increases rapidly, which is important for strong vibration attenuation at the tuning frequency. Roots 1 and 3, as depicted in Figure 4c,d, swap positions without affecting the magnitude of the tuning frequency. The tuning frequency analysis of the electromechanical resonator reveals that the weakly coupled electromechanical resonator, shunted with a resistor-loaded circuit, adds only an imaginary component. However, strong electromechanical coupling increases the real part’s magnitude and introduces an imaginary part as the coupling coefficient and shunt resistance increase. The imaginary part contributes to the increase in peak attenuation, while the real part shifts the tuning frequency upward and widens the band gap.

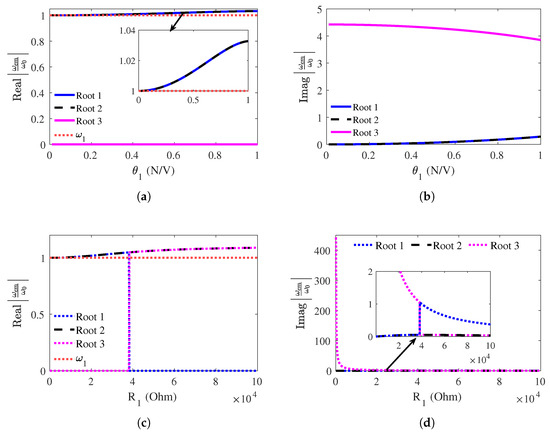
Figure 4. The effect of the electromechanical coupling coefficient and shunt circuit resistance on the tuning frequency of a strongly coupled electromechanical resonator in the zero-order hierarchy, with $\eta =0.75$, $R_1={10}^4$ ohms and ${\theta }_1$ = 3 × 10⁻¹ N/V: (a) effect of ${\theta }_1$ on the real part, (b) imaginary part as a function of ${\theta }_1$, (c) effect of $R_1$ on the real part and (d) imaginary part as a function of $R_1$.

Now, let us proceed with the wavenumber analysis of hierarchical electromechanical metamaterials. The real part of the wavenumber provides information about the nature of the passband branches. The imaginary part is related to the attenuation constant, offering insight into the damping properties and energy dissipation in the stopband regions. From this point onward, the curve corresponding to the imaginary component of the wavenumber is referred to as the attenuation curve. The red dotted horizontal lines in Figure 5 and Figure 6 are the undamped tuning frequencies of the resonators. The wavenumber components of the strongly coupled first-order configurations are generated at ${\beta }_1=0.5$. Figure 5a–c show the wavenumber components of the zero-order and first-order hierarchies under the strong electromechanical coupling conditions, as determined by the inversion method [53]. The local resonance band gaps are characterized by extended peaks, while the Bragg scattering band gap is characterized by the semi-elliptical band gap above the local resonance band gaps. At ${\theta }_1={10}^{-2}$ N/V, as illustrated by the blue curves, there are distinct and clearly separated passband branches for all configurations. The characteristics of the wavenumber components of the zero-order hierarchy at this electromechanical coupling coefficient are similar to those of the undamped dispersion of the locally resonant metamaterial with a single resonator reported by Hussein et al. [10]. The authors established that metamaterials with undamped local resonators generate passbands distinguished by well separated mode branches. The wavenumber components of strongly coupled hierarchical metamaterials at low electromechanical coupling coefficients reveal that energy dissipation, or damping, is too small to affect the passbands.

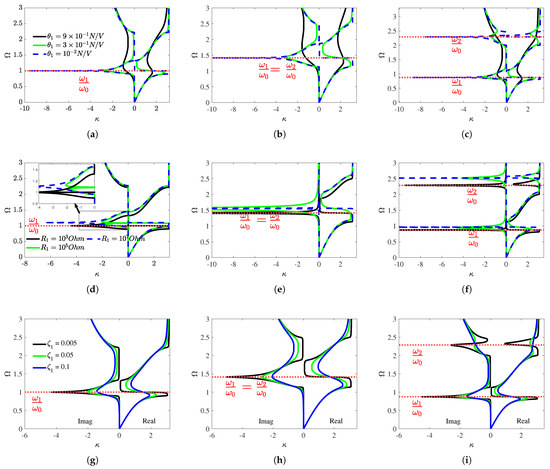
Figure 5. Real and imaginary wavenumber components of strongly coupled hierarchical metamaterials: The effect of the electromechanical coupling coefficients at ${\beta }_1=0.5$ and $R_1={10}^4$ ohms: (a) zero-order, (b) outward, and (c) inward. The effect of shunt circuit resistances, ${\theta }_1$ = 0.3 N/V: (d) zero-order, (e) outward, and (f) inward. The effect of mechanical damper: (g) zero-order, (h) outward, and (i) inward.

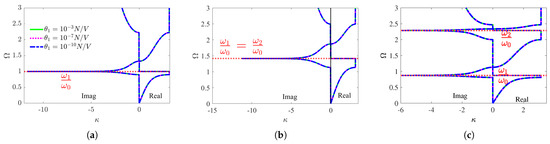
Figure 6. Real and imaginary wavenumber components of weakly coupled hierarchical metamaterials; the effect of electromechanical coupling coefficients, ${\beta }_1=0.5$ and $R_1=R_2={10}^4$ ohms: (a) zero-order, (b) outward, and (c) inward.

The strong electromechanical coupling coefficients introduce energy dissipation in hierarchical metamaterials due to their effect on the tuning frequency. Energy dissipation effectively reduces the resonance peaks and moderately broadens the bandwidth of the passbands. At higher electromechanical coupling coefficients, the horizontal lines (resonance branches) seen on the real wavenumber component transform into descending curves. This effect results from energy dissipation as a result of the strong electromechanical coupling. Previously, the horizontal lines were aligned with the local resonance peak attenuation at a lower electromechanical coupling coefficient. Further increasing the electromechanical coupling coefficient in a strong electromechanical coupling scenario eventually merges the separated passband branches into a single curve, and the distinct behaviors of these modes blend. The black curve in Figure 5 illustrates that the merged passband exhibits a wider bandwidth compared to the separated branches. The local resonance peaks decrease as the electromechanical coupling coefficient increases further for each case. This phenomenon shows that as the electromechanical coupling coefficient increases, the energy dissipation becomes more pronounced in hierarchical metamaterials. Higher energy dissipation causes the peak attenuation constant at the center of the local resonance band gap to be reduced, while the bandwidth increases. Moreover, strong electromechanical coupling alters the resonator’s tuning frequency, causing shifts in the local resonance band gap location. From this, it is inferred that strong electromechanical coupling merges the passband branches, broadens the bandwidth, and reduces the local resonance peak attenuation in hierarchical metamaterials.

The wavenumber components of the strongly coupled hierarchical metamaterial at different resistances of the shunt circuits are detailed in Figure 5d–f. In some cases, the zero-order hierarchy attenuation curve splits into two regions within a single band gap for certain shunt circuit resistance values, as depicted in Figure 5d. At a shunt circuit resistance of ${10}^3$ ohms, the horizontal black line divides the attenuation curve. With this shunt circuit resistance, the attenuation curve shows an overlapping peak. The separation of the attenuation curve at a shunt circuit resistance of ${10}^5$ ohms becomes more evident, revealing distinct peaks. However, increasing the resistance value of the shunt circuit reduces the peak attenuation constant. When the resistance of the shunt circuit is ${10}^7$ ohms, as shown by the blue curve in Figure 5d, the split in the attenuation curve disappears, and the peak attenuation increases once again. In the strongly coupled zero-order hierarchy, along with these effects, increasing the shunt circuit resistance pushes the local resonance band gap boundaries upward. Although an attenuation curve split is observed in the zero-order hierarchy, the real part of the wavenumber indicates the presence of a single local resonance band gap. The width of the local resonance band gap also exhibits a slight increase. The effect of the shunt circuit resistance on the wavenumber components of the first-order hierarchy is demonstrated in Figure 5e,f. The split of the attenuation curves is not observed in the first-order hierarchy; however, the passband branches merge as the resistance of the shunt circuits increases. The higher peak attenuation in the first-order hierarchy indicates stronger damping compared to the zero-order hierarchy. The strongly coupled first-order hierarchy for some shunt circuit resistance values exhibits a higher degree of energy dissipation and resistive damping around the tuning frequencies. The local resonance band gaps and the peak attenuation shift upward as the shunt circuit resistance increases. The results of the wavenumber analysis for the strongly coupled hierarchical system indicate that the resistance of the shunt circuit plays a key role in tuning the band structure in various ways. Furthermore, it is important to note that adjusting the resistance values modifies the electromechanical resonator’s tuning frequency, leading to the band gap peak shifting away from the undamped mechanical tuning frequency.

To further understand the effect of electromechanical coupling in this system, the response will also be compared to that of a purely mechanical damped system, shown in Figure 5g–i. The simulation of the hierarchical metamaterial with mechanically damped local resonators is carried out by first removing the piezoelectric patches and shunt circuits, followed by the introduction of a mechanical damping force into the governing equations. The equations of motion for mechanically damped resonators are given in Appendix B. The damping ratios of the mechanical dampers are designated as ${\zeta }_1={\zeta }_2$. The dispersion curves illustrate that the strongly coupled electromechanical resonators and mechanically damped resonators exhibit a similar band structure pattern in hierarchical metamaterials. Like strongly coupled electromechanical hierarchical metamaterials, the peak attenuation decreases as the value of ${\zeta }_1$ increases in the mechanically damped hierarchical metamaterials. Although mechanical damping decreases the peak attenuation, it is perfectly aligned with the undamped resonator tuning frequency. In the electromechanical system, as the electromechanical coupling coefficient and the resistance of the shunt circuit increase, the local resonance band gaps shift upward. In contrast, the mechanically damped system does not affect the location of the band gap, with changes more closely related to the reduction in peak attenuation. In both electromechanically and mechanically damped hierarchical resonators, the attenuation curve widens, and the peak attenuation decreases as the electromechanical coupling coefficient and the mechanical damping ratio increase. Electromechanical resonators create an attenuation curve with extended peaks compared to mechanically damped resonators.

As discussed previously, the electromechanical coupling coefficient and resistance of the shunt circuits do not affect the band structure of the weakly coupled hierarchical metamaterial. Additionally, the wavenumber analysis indicates that the attenuation constants and passbands of hierarchical metamaterials remain unaffected by the electromechanical coupling coefficient and the shunt circuit resistances in a weakly coupled system, as seen in Figure 6. The undamped tuning frequencies of the local resonators, ${\omega }_1$ and ${\omega }_2$, are perfectly aligned with the peak attenuation for weakly coupled hierarchical metamaterials. Based on wavenumber analysis, the local resonance band gap in hierarchical electromechanical metamaterials can be adjusted using hierarchy, electromechanical coupling coefficient, and shunt circuit resistance. This enables control over band gap properties, including location, width, peak attenuation, and resonance reduction, which are challenging to achieve with mass and stiffness changes alone.

3.2. Effect of Resonator Mass Ratios

Next, the effect of electromechanical resonator masses is analyzed through ${\beta }_1$ and $\eta$. Analyzing the effect of the resonator masses on the band structure of hierarchical metamaterials is fundamental because it directly influences the system’s dynamic properties. The masses of the resonators, along with stiffness determine the tuning frequency of the local resonance band gap. For the design of hierarchical metamaterials, understanding the distribution of resonator mass helps predict and optimize the emergence of multiple band gaps. In this analysis, the electromechanical local resonator mass for the zero-order configuration is $m_1=\eta m_0$. To maintain a constant local resonator mass between hierarchies, the electromechanical resonator masses for the first-order configurations are $m_1=\eta {\beta }_1{m}_0$, and $m_2=\eta (1-{\beta }_1)m_0$. To isolate individual effects, $\eta$ is kept constant at $\eta =0.75$ when ${\beta }_1$ is varied, and ${\beta }_1$ is kept constant at ${\beta }_1=0.85$ when $\eta$ is varied.

The effect of $\eta$ follows a similar trend for strongly coupled and weakly coupled systems, except that stronger electromechanical coupling leads to a greater increase in the band structure. The effect of $\eta$ was exclusively investigated for the weakly coupled system to highlight its characteristics. The graphs in Figure 7 illustrate the influence of the total electromechanical resonator mass ratio, $\eta$, on the band structure. Increasing the value of $\eta$ lowers the upper limit of the first passband in both hierarchies. A higher value of $\eta$ increases the width of the first local resonance band gap for both zero-order and first-order hierarchies. The second band gap shifts upward, with the width increasing for the outward configuration and decreasing for the inward configuration. As $\eta$ increases, the lower limit of the second passband and the third passband of the outward configuration shift upward, as shown in Figure 7b. The third passband of the inward configuration remains nearly flat for any ${\beta }_1$ and is minimally affected by $\eta$, as seen in Figure 7c. In the first-order hierarchy, $\eta$ allows tuning the boundaries of all three passbands in the outward configuration. However, in the inward configuration, only the first and second passbands can be tuned, while the third remains unaffected. A significant drawback of increasing $\eta$ is the associated increase in the total mass of the metamaterial. Therefore, the effect of ${\beta }_1$ becomes particularly interesting and important, as it does not alter the total mass, making it a key focus.

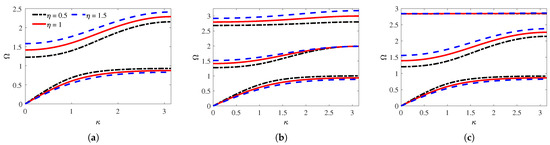
Figure 7. The effect of $\eta$ at ${\beta }_1=0.85$, on band structure of the weakly coupled configurations: (a) zero-order, (b) outward, and (c) inward configurations.

The effect of ${\beta }_1$ on the dispersion of the weakly and strongly coupled first-order hierarchy is shown in Figure 8. The band structure of the outward configuration, as demonstrated in Figure 8a,b, is symmetric with respect to ${\beta }_1$ = 0.5. In the outward configuration, the distinction between $m_1$ and $m_2$ is arbitrary, and the physical system mirrors itself at values above and below ${\beta }_1=0.5$. As such, the dynamic response of the system is identical for ${\beta }_1$ values equally far from $0.5$. For example, in Figure 8a, the same dispersion curves are obtained at ${\beta }_1=0.15$ and ${\beta }_1=0.85$. The symmetrical nature seen in the outward configuration can offer the opportunity to tailor the band structure on one side of ${\beta }_1=0.5$. As the value of ${\beta }_1$ diverges from $0.5$, the upper limit of the first passband decreases, leading to an increase in the width of the first band gap. This helps to push the boundary of the first local resonance band gap to the lower frequency, which is desirable. At ${\beta }_1=0.5$, the two resonators are identical, and the second passband becomes flat. This flat passband corresponds to a resonance mode branch and perfectly aligns with the undamped tuning frequency of the local resonators, as shown in Figure 8a,b. A flat passband has less extended boundaries toward the adjacent band gaps, which will help to increase the band gap width.

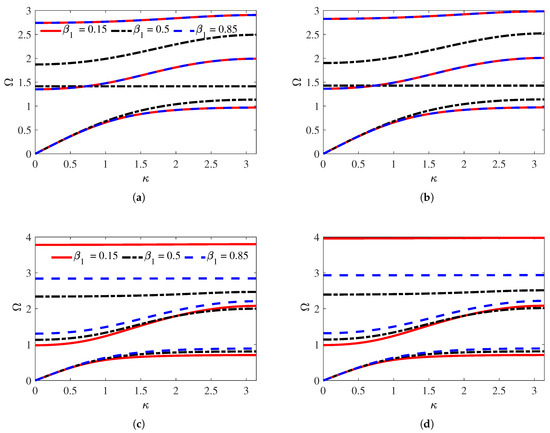
Figure 8. The effect of ${\beta }_1$ at $\eta =0.75$, on the band structure of first-order configurations: (a) weakly coupled outward, (b) strongly coupled outward, (c) weakly coupled inward, and (d) strongly coupled inward.

Unlike the outward configuration, there is no symmetry in the first-order inward configuration with respect to ${\beta }_1$. As ${\beta }_1$ advances toward and exceeds 0.5, the upper limit of the first passband increases, while for ${\beta }_1<0.5$, the first band gap shifts to lower frequencies, as shown in Figure 8c,d. The third passband appears to be a nearly flat band for the inward configuration; however, its location is strongly affected by the variation of ${\beta }_1$. This can effectively widen the second local resonance band gap. When the value of ${\beta }_1$ is much lower than 0.5, the inward configuration generates an ultrawide second band gap and a lower frequency first band gap. The effect of ${\beta }_1$ on the strongly coupled electromechanical band structure is similar to that of the weakly coupled electromechanical band structure. Decreasing or increasing the value of ${\beta }_1$ from $0.5$ increases the bandwidth and the width of the band gap. The outward configuration has a broad bandwidth for each passband relative to the inward configuration at any value of ${\beta }_1$. On the other hand, the inward configuration can create a lower frequency initial local resonance band gap and a broad local resonance second band gap with a nearly flat third passband.

The primary mechanical tuning parameter that affects the wavenumber components of the weakly coupled first-order hierarchy is ${\beta }_1$. Figure 9 illustrates the wavenumber components of the weakly coupled first-order hierarchical metamaterial to examine how ${\beta }_1$ contributes to the formation of the band gap. It also helps to see whether ${\beta }_1$ affects the attenuation peak in the weak electromechanical coupling. The blue shaded regions are the attenuation zones and the black curves are the passband branches. The values ${\beta }_1=0.1$ and ${\beta }_1=0.9$ were chosen to highlight the pseudo-merging of the local resonance and Bragg scattering attenuation zones, a characteristic that is especially evident in the inward configuration. The near coupling effect of the local resonance and Bragg scattering band gaps, as illustrated in Figure 9d,f, is referred to as pseudo-merging, owing to the presence of a nearly flat passband between. The wavenumber components for the outward configuration are the same in ${\beta }_1=0.1$ and ${\beta }_1=0.9$. The motion of the resonators in the outward configurations is decoupled from each other so that the resonator mass that contributes to the formation of the local resonance band gap can be readily identified. The undamped tuning frequency of the second local resonator is aligned with the first local resonance band gap peak attenuation as seen in Figure 9a. This suggests that the first local resonance band gap originates from the second electromechanical resonator. The second local resonance band gap is formed by the first electromechanical resonator, shown in Figure 9c. This occurs because the peak vibration attenuation of the second local resonance band gap aligns with the undamped tuning frequency of the first local resonator.

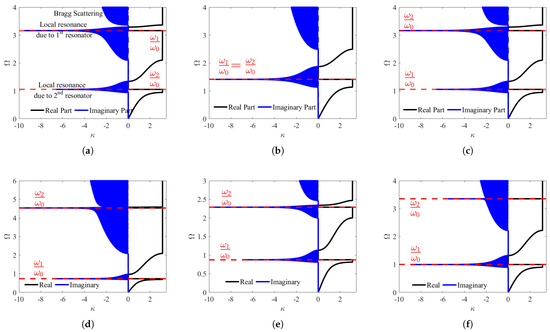
Figure 9. Real and imaginary wavenumber components of weakly coupled systems. (a) outward at ${\beta }_1=0.1$, (b) outward ${\beta }_1=0.5$, (c) outward at ${\beta }_1=0.9$, (d) inward ${\beta }_1=0.1$, (e) inward ${\beta }_1=0.5$, (f) inward ${\beta }_1=0.9$.

The interaction between coupled local resonators in the inward configuration is responsible for the formation of two distinct local resonance band gaps for all values of ${\beta }_1$. The undamped tuning frequencies of the first-order inward configuration’s local resonators are the eigenvalues of the characteristic equation given in Equation (16). The undamped eigenvalues of the resonators align with the peak attenuation of the weakly coupled local resonance band gap for the inward configuration, as depicted in Figure 9d–f. The effect of ${\beta }_1$ on the peak attenuation is negligible, but it significantly alters the boundaries of the passbands. The coupled motion of local resonators offers different tuning frequencies, causing the inward configuration to produce two local resonance band gaps at any ${\beta }_1$. This is clearly demonstrated in Figure 9e. When ${\beta }_1=0.5$, both resonators are identical, but there are still two distinct band gaps, unlike in the outward case in Figure 9b.

The band structure enhancement of the weakly coupled first-order hierarchical metamaterial due to ${\beta }_1$ is summarized in Figure 10. To compare the band gap width of the first-order configurations with the zero-order hierarchy, the total width of these gaps must be the sum of all individual band gap widths. The first-order hierarchy opens two local resonance band gaps, with the total width of the local resonance band gap being the sum of the first and second band gaps. The total band gap width ratio is defined as the ratio of the total band gap width to the upper limit frequency of the last passband. Due to the absence of clearly separated band gaps in strongly coupled systems, the total band gap width ratio is not performed for strongly coupled systems.

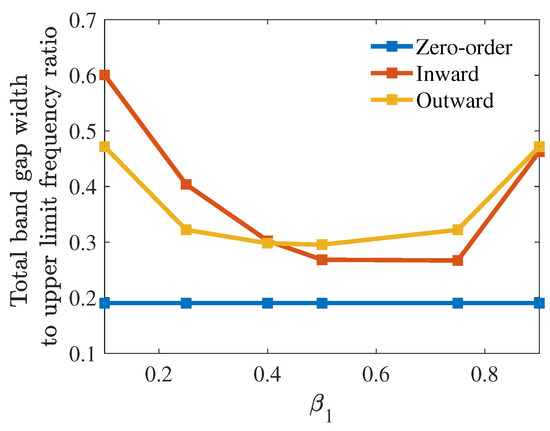
Figure 10. Comparison of the total band gap width to last passband upper limit frequency ratio for the weakly coupled hierarchical metamaterials.

In the zero-order hierarchy, the total band gap width ratio is defined as the ratio of the band gap width to the upper limit frequency of the second passband. This ratio remains constant regardless of the variation of ${\beta }_1$. In the first-order hierarchy, the total band gap width ratio is the ratio of the total band gap width to the upper limit frequency of the third passband. The inward configuration’s total band gap width ratio is lower than the outward configuration’s total band gap width ratio when ${\beta }_1$ is greater than 0.4. For ${\beta }_1<0.4$, the total band gap width ratio of the inward configuration exceeds the outward configuration’s total band gap width ratio. The inward configuration enhances the zero-order configuration’s band structure by a minimum of $40.95\%$, while the outward configuration achieves at least $55.17\%$ enhancement, as illustrated in Figure 10. Moreover, the total band gap width ratios of the first-order configurations are larger than the zero-order hierarchy. This implies that, relative to the zero-order hierarchy, the first-order hierarchy produces a larger total band gap width and increased bandwidth.

4. Transmissibility

In this section, the transfer function linking the outer mass displacement of the last unit cell with the input excitation force is derived for the finite-chain hierarchical metamaterial comprising k unit cells. Applying this transfer function, the outer mass displacement transmissibility and the normalized total power output of the last unit cell are evaluated. The evaluation of displacement transmissibility and normalized total power output serves two main purposes. First, it validates the band structure identified in the infinite chain. Second, it facilitates the optimization of vibration control and energy harvesting in electromechanical hierarchical metamaterials. The finite chain transfer function is derived using fixed-free boundary conditions. An input excitation force in the form of $A_0^{\left(0\right)}{e}^{i\omega t}$ is applied to the fixed wall attached to the first unit cell. After performing the necessary mathematical rearrangements on Equations (1)–(7), applying the boundary conditions and taking the Laplace transform ($s=i\omega$), the resulting finite chain equations for the outward and inward configurations of the first-order hierarchy are provided in Equation (20) and Equation (21), respectively.

$$\left\{\begin{array}{l}\left(s^2{m}_0+2k_0+k_1+k_2\right)A_0^{\left(j\right)}-k_0{A}_0^{(j-1)}-k_0{A}_0^{(j+1)}\hfill \\ -k_1{A}_1^{\left(j\right)}-k_2{A}_2^{\left(j\right)}-{\theta }_1{B}_1^{\left(j\right)}-{\theta }_2{B}_2^{\left(j\right)}=0,\\ \left(s^2{m}_0+k_0+k_1+k_2\right)A_0^{\left(k\right)}-k_0{A}_0^{(k-1)}-k_1{A}_1^{\left(k\right)}\hfill \\ -k_2{A}_2^{\left(k\right)}-{\theta }_1{B}_1^{\left(k\right)}-{\theta }_2{B}_2^{\left(k\right)}=0,\hfill \\ \left(s^2{m}_1+k_1\right)A_1^{\left(j\right)}-k_1{A}_0^{\left(j\right)}+{\theta }_1{B}_1^{\left(j\right)}=0,\hfill \\ \left(s^2{m}_2+k_2\right)A_2^{\left(j\right)}-k_2{A}_0^{\left(j\right)}+{\theta }_2{B}_2^{\left(j\right)}=0,\hfill \\ \left(s{R}_1{C}_1+1\right)B_1^{\left(j\right)}+s{R}_1{\theta }_1{A}_0^{\left(j\right)}-s{R}_1{\theta }_1{A}_1^{\left(j\right)}=0,\hfill \\ \left(s{R}_2{C}_2+1\right)B_2^{\left(j\right)}+s{R}_2{\theta }_2{A}_0^{\left(j\right)}-s{R}_2{\theta }_2{A}_1^{\left(j\right)}=0.\hfill \end{array}\right.$$

(20)

$$\left\{\begin{array}{c}\left(s^2{m}_0+2k_0+k_1\right)A_0^{\left(j\right)}-k_0{A}_0^{(j-1)}-k_0{A}_0^{(j+1)}\hfill \\ -k_1{A}_1^{\left(j\right)}-{\theta }_1{B}_1^{\left(j\right)}=0,\hfill \\ \left(s^2{m}_0+k_0+k_1\right)A_0^{\left(k\right)}-k_0{A}_0^{(k-1)}-k_1{A}_1^{\left(k\right)}-{\theta }_1{B}_1^{\left(k\right)}=0,\hfill \\ \left(s^2{m}_1+k_1+k_2\right)A_1^{\left(j\right)}-k_1{A}_0^{\left(j\right)}-k_2{A}_2^{\left(j\right)}+{\theta }_1{B}_1^{\left(j\right)}-{\theta }_2{B}_2^{\left(j\right)}=0,\hfill \\ \left(s^2{m}_2+k_2\right)A_2^{\left(j\right)}-k_1{A}_1^{\left(j\right)}-{\theta }_2{B}_2^{\left(j\right)}=0,\hfill \\ \left(s{R}_1{C}_1+1\right)B_1^{\left(j\right)}+s{R}_1{\theta }_1{A}_0^{\left(j\right)}-s{R}_1{\theta }_1{A}_1^{\left(j\right)}=0,\hfill \\ \left(s{R}_2{C}_2+1\right)B_2^{\left(j\right)}+s{R}_2{\theta }_2{A}_0^{\left(j\right)}-s{R}_2{\theta }_2{A}_1^{\left(j\right)}=0.\hfill \end{array}\right.$$

(21)

In Equations (20) and (21), the first equation corresponds to the $j^{\mathrm{th}}$ unit cell, while the second equation, identified by the superscript k, pertains to the last unit cell. The remaining equations describe the resonators and shunt circuits. By applying the back substitution method [39], the displacement amplitudes can be expressed as Equation (22)

$$\left\{\begin{array}{c}{A}_0^{\left(j\right)}=T_1\left(A_0^{(j-1)}+A_0^{(j+1)}\right),\hfill \\ A_0^{\left(k\right)}=T_k{A}_0^{(k-1)},\hfill \\ B_n^{\left(k\right)}=b_n{A}_0^{\left(k\right)}.\hfill \end{array}\right.$$

(22)

The coefficients $T_1$ and $T_k$ are transfer functions that connect the $j^{th}$ unit cell to its neighboring unit cells and the last unit cell with the preceding unit cell, respectively, and $b_n$ is a coefficient that connects the voltage output of the $n^{\mathrm{t}\mathrm{h}}$ shunt circuit to the displacement amplitude of the last unit cell. $T_1$ and $T_k$ are distinct for the first and last unit cells and expressed as

$$\left\{\begin{array}{c}{T}_1={\displaystyle \frac{c_1}{d_1}},\hfill \\ T_k={\displaystyle \frac{c_k}{d_k}}.\hfill \end{array}\right.$$

(23)

Refer to Appendix C for the details of the constants $c_1$, $c_k$, $d_1$, $d_k$, and $b_n$.

By substituting the second equation of Equation (22) into the first, the transfer function of the $j^{th}$ unit cell, $Q_j$, can be expressed in terms of the transfer function of the last unit cell, $Q_k$, as

$$\left\{\begin{array}{c}{Q}_k={\displaystyle \frac{A_0^{\left(k\right)}}{A_0^{(k-1)}}}=T_k,\hfill \\ ⋮\hfill \\ Q_j={\displaystyle \frac{A_0^{\left(j\right)}}{A_0^{(j-1)}}}={\displaystyle \frac{T_1}{1-T_1{Q}_j}},\hfill \\ ⋮\hfill \\ Q_1={\displaystyle \frac{A_0^{\left(1\right)}}{A_0^{\left(0\right)}}}={\displaystyle \frac{T_1}{1-T_1{Q}_2}}.\hfill \end{array}\right.$$

(24)

The outer mass displacement transmissibility of the last unit cell relative to the input excitation is [56]

$$T={\displaystyle \frac{A_0^{\left(k\right)}}{A_0^{\left(0\right)}}}=\prod _{j=1}^k{Q}_j$$

(25)

where T is the transfer function that links the last unit cell outer mass displacement to the input excitation amplitude, $A_0^{\left(0\right)}$. The power output, $P_n^{\left(k\right)}$, of the $n^{\mathrm{t}\mathrm{h}}$ shunt circuit in the last unit cell is given by Equation (26).

$$P_n^{\left(k\right)}={\displaystyle \frac{{\left(B_n^{\left(k\right)}\right)}^2}{R_n^{\left(k\right)}}}$$

(26)

The power output from each shunt circuit can be expressed in a non-dimensional form by normalizing it with respect to the resonators input power, ${\displaystyle \frac{m_n{\left({\omega }^2{A}_0^{\left(0\right)}\right)}^2}{{\omega }_n^2}}$ [39]. The normalized total power output of the last unit cell is obtained by summing the dimensionless power harvested from all the shunt circuits within the unit cell. This is expressed in Equation (27).

$$|P_{norm}|=\sum _{n=1}^N\left|{\displaystyle \frac{P_n^{\left(k\right)}}{\frac{m_n{\left({\omega }^2{A}_0^{\left(0\right)}\right)}^2}{{\omega }_n^2}}}\right|$$

(27)

The outer mass displacement transmissibility and the normalized total power output of the last unit cell relative to the input excitation for the finite chain consisting of 100 unit cells are examined for the zero-order and first-order hierarchies. Figure 11 demonstrates the outer mass displacement transmissibility of the last unit cell for weakly and strongly coupled hierarchical metamaterials at different ${\beta }_1$ values, respectively. The band structure identified in the dispersion is in good agreement with the transmissibility results, which confirms the consistency of the results. The outer mass displacement transmissibility of the weakly coupled first-order hierarchy shows that the vibration attenuation frequency range depends on the value of β₁, as illustrated in Figure 11a–c. In contrast, the outer mass displacement transmissibility of the zero-order hierarchy exhibits a fixed frequency range. The weakly coupled zero-order hierarchy exhibits higher local displacement transmissibility peaks compared to the first-order hierarchy, particularly at lower frequencies. The vibration attenuation depth in the first local resonance band gap region is similar in both hierarchies.

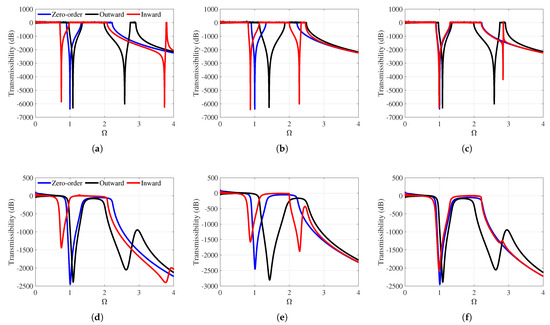
Figure 11. The displacement transmissibilities of hierarchical metamaterial at different system parameters. Weakly coupled electromechanical resonator (a) ${\beta }_1=0.15$, (b) ${\beta }_1=0.5$, and (c) ${\beta }_1=0.85$. Strongly coupled electromechanical resonator (d) ${\beta }_1=0.15$, (e) ${\beta }_1=0.5$, and (f) ${\beta }_1=0.85$.

For the inward configuration, the first attenuation region shifts to the left when ${\beta }_1$ is less than $0.5$, indicating its ability to attenuate vibrations at lower frequencies. The zero-order and first-order hierarchies show equivalent sizes of the first attenuation regions when ${\beta }_1$ is greater than $0.5$. The first-order hierarchy produces a first attenuation zone of similar size to the zero-order hierarchy at certain ${\beta }_1$ such as ${\beta }_1$ = 0.85. This is one of the benefits of the first-order hierarchy, as it retains the same effective frequency attenuation, while also introducing the potential for additional attenuation through the second attenuation region. The second local resonance vibration attenuation zone in the first-order configurations is located within the Bragg scattering attenuation zone of the zero-order hierarchy. Local resonance attenuation is stronger than Bragg attenuation, which is crucial for effective vibration attenuation. The local resonance attenuation regions can be tuned through ${\beta }_1$ to target specific frequencies and broaden the band of attenuated frequencies compared to the fixed band gap of the zero-order hierarchy. The first-order hierarchy transmits the high-frequency third passband, which is not possible in the zero-order hierarchy, with a narrower bandwidth in the inward configuration compared to the outward configuration. In addition to the effect of ${\beta }_1$, the outer mass displacement transmissibility of strongly coupled hierarchical metamaterials is affected by electromechanical parameters. Strongly coupled hierarchical metamaterials effectively suppress higher frequency resonance peaks, as demonstrated in Figure 11d–f. The strongly coupled system significantly reduces the local resonance peaks of the third passband in first-order configurations. However, the second passband exhibits higher transmissibility, and the first local resonance band gap shows weaker attenuation in the strongly coupled inward configuration. The decrease in peak displacement transmissibility with increasing frequency in strongly coupled electromechanical systems indicates that strong electromechanical coupling is more effective at damping higher frequency vibrations. The outward configuration shows relatively minimal peaks and deep valleys.

The curves seen in Figure 12 illustrate the normalized total power output of the shunt circuits in the last unit cell at a shunt circuit resistance of ${10}^4$ ohms. The zero-order hierarchy harvests energy at low frequencies, and in this case, it is limited to a normalized frequency of $2.5$. The first-order hierarchy harvests energy at frequencies higher than those of the zero-order hierarchy. The normalized power output increases as the electromechanical coupling coefficient transitions from weak to strong coupling. In the strongly coupled scenario, the maximum peaks are observed at lower frequencies and gradually flatten as the normalized frequency increases. For harvesting energy from lower frequency vibrations, the inward configuration is more effective, whereas the outward configuration excels across a wider frequency range. Their ability to capture energy across a wide range of frequencies makes them preferable for broadband energy harvesting.

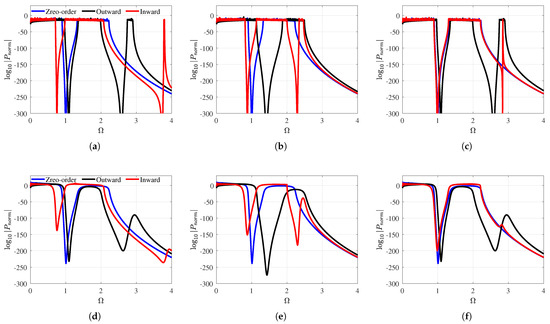
Figure 12. The normalized total power output of hierarchical metamaterial at different system parameters. Weakly coupled electromechanical resonator (a) ${\beta }_1=0.15$, (b) ${\beta }_1=0.5$, and (c) ${\beta }_1=0.85$. Strongly coupled electromechanical resonator (d) ${\beta }_1=0.15$, (e) ${\beta }_1=0.5$, and (f) ${\beta }_1=0.85$.

When designing a vibration attenuator and energy harvester, optimizing performance across different system parameters is essential [57]. The vibration attenuation and energy harvesting performance of each configuration are optimized for shunt circuit resistance in the strong coupling case. Optimizing shunt circuit resistance in strongly coupled metamaterials is necessary for vibration attenuation and energy harvesting. This is because shunt circuit resistances in strong coupling significantly dampen the local resonance peak attenuation and directly impact power estimation. Based on the results illustrated in Figure 13, the effect of shunt circuit resistance can be categorized into three groups. The first group corresponds to a shunt circuit resistance less than ${10}^3$ ohms characterized by narrow bandwidths and deep, narrow local resonance attenuation regions.

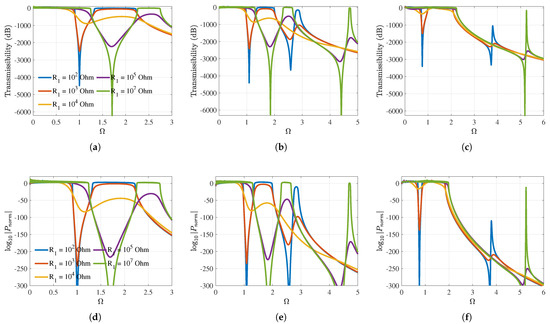
Figure 13. Optimizing the shunt circuit resistance of strongly coupled hierarchical metamaterial at ${\beta }_1=0.15$ and ${\theta }_1=0.9$ N/V. Optimum displacement transmissibility (a) zero-order, (b) outward, and (c) inward. Optimum normalized total power output (d) zero-order, (e) outward, and (f) inward configurations.

The second group includes resistance between ${10}^3$ and ${10}^5$ ohms where the damping effect becomes more pronounced. A shallow first local resonance attenuation valley is followed by a strongly damped high frequency resonance peak. Although these resistance values reduce the peak resonance, they also decrease the depth of vibration attenuation within the local resonance attenuation zone. Moreover, the maximum power output is predominantly confined to the lower frequency domain for both hierarchies, while the higher frequency peak vibration transmission is significantly suppressed. The zero-order hierarchy follows a trend similar to that of the outward configuration. The transmissibility of the outward and inward configurations showcase some differences as the resistance of the shunt circuit varies. Considering the inward configuration, when the resistance of the shunt circuit is ${10}^5$ ohms, as shown in Figure 13c, an ultrabroad first local resonance attenuation zone is observed. This is beneficial for both lower frequency vibration attenuation and energy harvesting. Since the inward configuration shows a unique displacement transmissibility feature in the strong coupling case and its band structure is not symmetric with respect to ${\beta }_1$, the displacement transmissibility at ${\beta }_1=0.85$ is depicted in Figure 14. Figure 14a shows that the first local resonance vibration attenuation zone is very broad but shallow with a resistance of ${10}^4$ ohms.

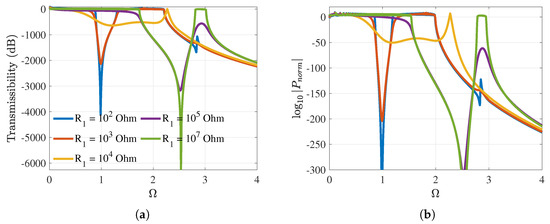
Figure 14. (a) Outer mass displacement transmissibility and (b) Normalized total power output of strongly coupled inward configuration at ${\beta }_1=0.85$ and ${\theta }_1=0.9$ N/V.

The third category is observed when the resistance exceeds ${10}^5$ ohms, which is characterized by the shift of the local resonance attenuation zones to higher frequencies. In the strongly coupled first-order outward configuration, designed with a combination of ${\beta }_1=0.15$ and a shunt circuit resistance of ${10}^7$ ohms, two attenuation zones are observed at high frequencies. In contrast, for the inward configuration at ${\beta }_1=0.15$ and ${10}^7$ ohms, the first local resonance attenuation region disappears due to mode merging. In this configuration, increasing ${\beta }_1$ to $0.85$ reduces the bandwidth to a normalized frequency of 4.

The optimal power output of the strongly coupled system depends on both the configuration type and the shunt circuit resistance values. Due to the narrow first band gap in the inward configuration at low shunt circuit resistances, it enables a broad frequency range for energy harvesting. Additionally, the disappearance of the first local resonance band gap in the inward configuration at high shunt circuit resistances enhances the lower frequency bandwidth, thereby maximizing power output. Table 2 summarizes the effects of different parameters on the vibration attenuation and energy harvesting performance of hierarchical metamaterials.

Table 2. Summary of the effects of electromechanical resonators and shunt circuits on the simultaneous vibration attenuation and energy harvesting of hierarchical metamaterials.

Parameter	Effect on Vibration Attenuation	Effect on Energy Harvesting	Remarks
Strong Electromechanical Coupling
${\theta }_1$ and ${\theta }_2$	Increase in band gap width, mode merging, and reduction in resonance peaks.	Power output increases with ${\theta }_1$ and ${\theta }_2$.	This is critical for optimizing dual functionality.
$R_1$ and $R_2$	For lower frequency attenuation, smaller $R_1$ and $R_2$ values are preferred, for higher frequency and stronger attenuation, higher $R_1$ and $R_2$ values.	Between ${10}^3$ and ${10}^5$ ohms results in power output with minimal drop.	Higher frequency passbands are predominantly impacted.
${\beta }_1$	Smaller or higher ${\beta }_1$ creates broad band gap, which is desirable for vibration attenuation.	Power output in the third passband decreases as ${\beta }_1$ deviates farther from $0.5$.	It affects performance based on configuration type.
Weak Electromechanical Coupling
${\theta }_1$ and ${\theta }_2$	Minimal effect.	Increasing ${\theta }_1$ and ${\theta }_2$ raises the local power output peaks.	Less effective for attenuating vibrations.
$R_1$ and $R_2$	Minimal effect.	Increases the local peaks of the power output.	Resistance mainly influences energy harvesting.
${\beta }_1$	As ${\beta }_1$ moves farther from 0.5, the vibration attenuation spectrum increases. The inward configuration suppresses lower frequency vibrations.	Power can be harvested across a broad frequency range by varying ${\beta }_1$.	It offers tunability for specific applications depending on configuration type.

5. Conclusions

This study explored the band structure of hierarchical metamaterials containing electromechanical resonators shunted to resistor-loaded circuits for vibration attenuation and energy harvesting applications. The outward and inward hierarchical metamaterials were designed by configuring multiple electromechanical resonators hierarchically and integrating shunt circuits. The influence of the electromechanical coupling coefficients, resistances of the shunt circuit, and resonator mass ratios on the band structure of the zero-order and first-order hierarchies was examined. The dispersion of hierarchical metamaterials designed with strongly coupled electromechanical resonators shunted to an electric circuit was compared to that of hierarchical metamaterials with a resonator connected by springs and pure mechanical dampers. Finally, the displacement transmissibility and normalized total power output for finite-chain hierarchical configurations are analyzed.

The study reveals that the local resonance band gaps of hierarchical electromechanical metamaterials are a function of configuration type, mechanical and electrical tuning parameters. The effects of electrical parameters are dependent on the coupling conditions. The first-order hierarchical configurations offer a broad total band gap width and a broad bandwidth compared to the zero-order hierarchy for the same total mass. The role of ${\beta }_1$ in tuning the band structure of the first-order hierarchical metamaterials is paramount. The strongly and weakly coupled outward configuration generates a symmetric band structure about ${\beta }_1=0.5$, allowing the band structure to be tuned on only one side of ${\beta }_1$. In contrast, the strongly and weakly coupled inward configuration produces a lower frequency first band gap and a broad second band gap when ${\beta }_1$ is much less than $0.5$. In addition to the mechanical tuning parameter ${\beta }_1$, the band structure of a strongly coupled hierarchical metamaterial is affected by the electromechanical coupling coefficients and resistance of the shunt circuits. As the coupling coefficient increases, the bandwidth of strongly coupled hierarchical metamaterials increases, and the passbands merge into a single curve. The width and location of the band gaps are substantially influenced by the resistance of the shunt circuit. The finite chain transmissibility showed that resistance of the shunt circuit significantly affects boundaries of high-frequency passbands. In weakly coupled hierarchical metamaterials, the band structure is unaffected by the electromechanical coupling coefficient and shunt circuit resistance, enabling energy harvesting without altering the band structure. Electromechanical damping showed strong peak attenuation and a shift of the band gap location compared to pure mechanical damping.

The outer mass displacement transmissibility identified that the vibration attenuation performance of first-order hierarchical metamaterials is larger than the zero-order hierarchy. The inward configuration is effective for attenuating relatively lower and higher frequency waves, whereas the outward configuration is more suitable for achieving wave control where the inward configuration does not. The normalized total power output demonstrates that energy harvesting is strongly influenced by the configuration type and electromechanical tuning parameters, requiring careful selection of both to optimize the performance. From this, it is concluded that hierarchical electromechanical metamaterials provide a broader total band gap width, increased bandwidth, and a highly tunable band structure for vibration attenuation and energy harvesting applications, outperforming single-resonator metamaterials with the same total mass.