Permeability of Broken Coal Around CBM Drainage Boreholes with the Compound Disaster of the Rockburst and Outburst

Abstract

Coal seam gas drainage serves as an effective engineering measure to mitigate compound disasters of the rockburst and outburst in deep mining, and its efficacy is fundamentally governed by the permeability of coal around the gas drainage borehole. To systematically study the permeability law of broken coal body around borehole under different stress states and particle size distribution, the coal particle samples were prepared for the triaxial permeability tests by the gradation theory whose Talbot power exponents n are 0.1 to 1.0. Several valuable findings have been obtained through meticulous research and analysis, according to Darcy’s law and the Forchheimer equation. The seepage velocity is affected by the Talbot power exponent, pressure gradient, confining pressure, and axial pressure, among which the pressure gradient has the most prominent influence. The larger the Talbot power exponent of the sample composition and the larger of the pressure gradient inside the sample, the larger is the seepage velocity obtained by the sample. The axial pressure has a notable influence on permeability by modifying the pore structure of broken coal. As the axial pressure increases, the permeability decays exponentially until it reaches a stable state at a specific limit. The permeability decreases exponentially with the increase of effective stress, while the power exponent (a) decreases gradually with the increase of Talbot power exponent, and the coefficient (b) increases gradually with the increase of Talbot power exponent (index), in the effective stress-permeability equation, which implies that the inhibition and amplitude effects of effective stress on permeability become more intense. The permeability shows three stages of growth, namely the slow growth stage, the linear growth stage, and the exponential growth stage, which are influenced by small-sized coal particles, particle-size ratio, and large-sized coal particles respectively, when the Talbot power exponent (n) of the broken coal increases from 0.1 to 1.0. These findings advance understanding of the permeability of broken coal around boreholes, providing theoretical foundations for optimizing gas drainage parameters and preventing the compound disaster of the rockburst and outburst.

1. Introduction

Coal mining constitutes a foundational component of China’s energy infrastructure [1]. With progressive depletion of shallow coal reserves, an increasing number of mining operations have advanced into deep geological structures [2]. Deep coal seams are subjected to high geostress and intensive mining induced disturbances, resulting in escalated occurrences of coal rock dynamic disasters such as the compound disaster of the rockburst and outburst, which pose a substantial threat to safe mining [3]. In response to these challenges, coal seam gas drainage has been established as a critical engineering intervention for prevention and control of coal rock dynamic disasters [4]. However, the effectiveness of such operations is frequently constrained by the inherently low permeability of deep coal seams. The permeability of coal seams is regulated by a multifactorial [5], including porosity [6], pore structure [7], coal quality [8], stress state [9], temperature [10], pressure [11], and pore fluid properties [12]. The stress state emerges as the predominant determinant of permeability [13], by inducing pore compression and structure deformation [14].

The permeability around the gas drainage borehole is principally governed by the stress state [15] and the degree broken coal [16]. The stress state plays a key role in controlling the efficiency of coalbed methane drainage. The redistribution of stress arises from spatial variations in stress fields, which are intrinsically linked to the geometric configuration of working face, roadway, and borehole [17]. The stress state within this field impacts the permeability of broken coal mainly by two ways that the stress [13,18] and the rate of stress loading [19]. As the pressure (including axial pressure and confining pressure) gradually increasing, the coal particles are compacted [20] and the reducing of pore volume inside of the broken coal [21,22] and the closing of pores [23,24] lead to narrowing of the seepage channel and an exponential decrease in the permeability [25,26]. The rapid loading rate and unloading rate result in a sharp reduction in permeability [27] and a relatively low degree of permeability recovery [28], respectively. In addition, the slow loading rate and unloading rate show the opposite effects [29,30]. In understanding the seepage law of coalbed methane, particle-size distribution plays an important role. The degree of coal broken is generally described using gradation theory [31]. The gradation theory pertains to the distribution law of particles of different sizes within the broken coal body, which is typically quantified by the Talbot power exponent [32]. As the Talbot power exponent increases from 0.1 to 1.0, the proportion of large particles [33] and the number of pores increase [34], and the connectivity of pore are enhanced [35], which promotes the growth of permeability [36,37].

Collectively, these studies highlight the critical role of particle size, stress state, and gradation in elucidating the complex permeability behaviors of broken coal and gas drainage boreholes. The key parameters of broken coal under multiple permeability conditions were quantified, and the impact of gradation theory on permeability was evaluated. However, intricate mechanisms exist among the stress state, coal seepage, and the degree of coal broken. The spatially heterogeneous stress fields around the boreholes induce progressive broken gradients of coal. Consequently, understanding the permeability law of the continuously broken coal around the borehole remains of paramount importance. As a crucial indicator of the seepage–pressure coupling effect, the influence of effective stress on permeability requires further clarification.

In this study, controlled broken coal specimens were made in accordance with gradation theory, followed by a triaxial permeability test under simulated in situ stress conditions to explain the permeability of broken coal around gas drainage boreholes. The quantitative relationship between the effective stress and the permeability in broken coal under triaxial stress conditions was established. The variation in relevant parameters reflects the impact of effective stress on permeability. The research findings provide a reference for assessing the gas permeability of broken coal surrounding gas drainage boreholes and contribute to strategies for preventing and mitigating rockburst and outburst disasters.

2. Materials and Methods

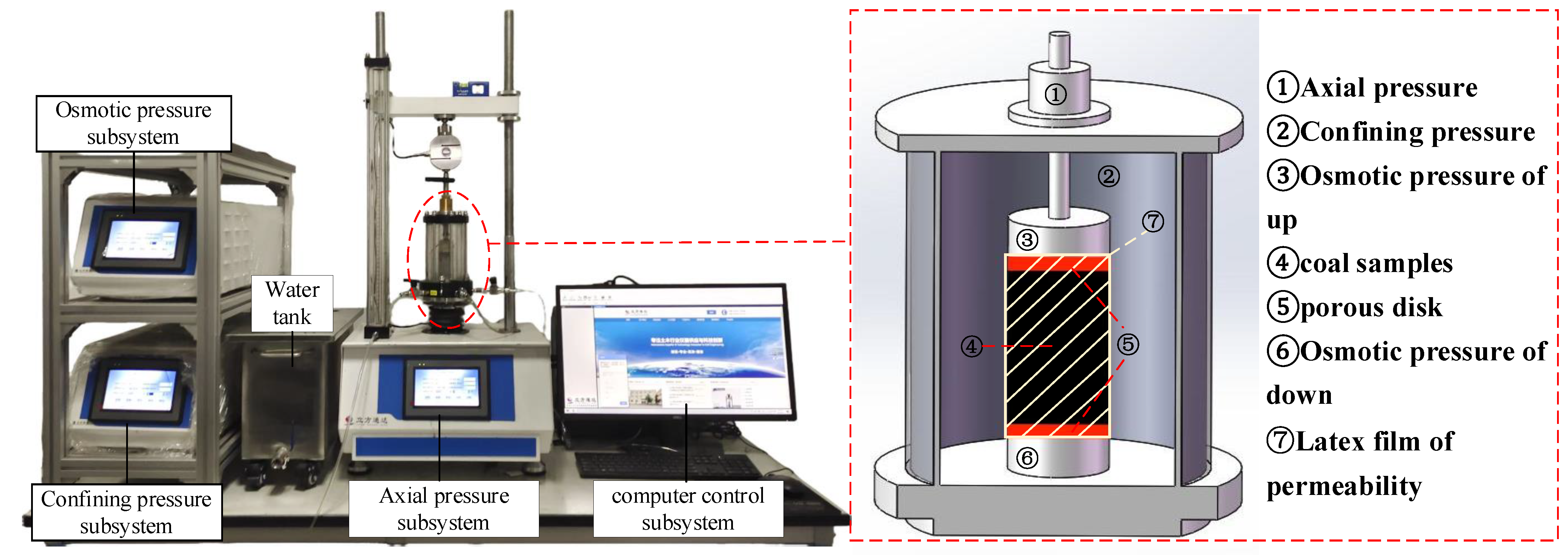
2.1. Instruments

The experimental investigation employed an LFTD1812-3 automatic triaxial permeameter (Lifetime China Co., Ltd. Tianjin, China) configured with triaxial servo-controlled stress loading capabilities. The system incorporates four core modules: an axial stress servo-actuator, a confining pressure hydraulic generator, a pore pressure regulation unit, and a digital control interface with real-time feedback. Axial pressure is generated through the vertical movement of the chassis beneath the pressure chamber and confining and osmotic pressures are supplied by independent pressure pumps. These pressures are displayed in real-time on the screen and recorded by the computer. The entire testing process is automatically controlled by the triaxial permeability test software (Lifetime China Co., Ltd. Tianjin, China), according to preset parameters. A schematic diagram of the triaxial permeability test system is shown in Figure 1.

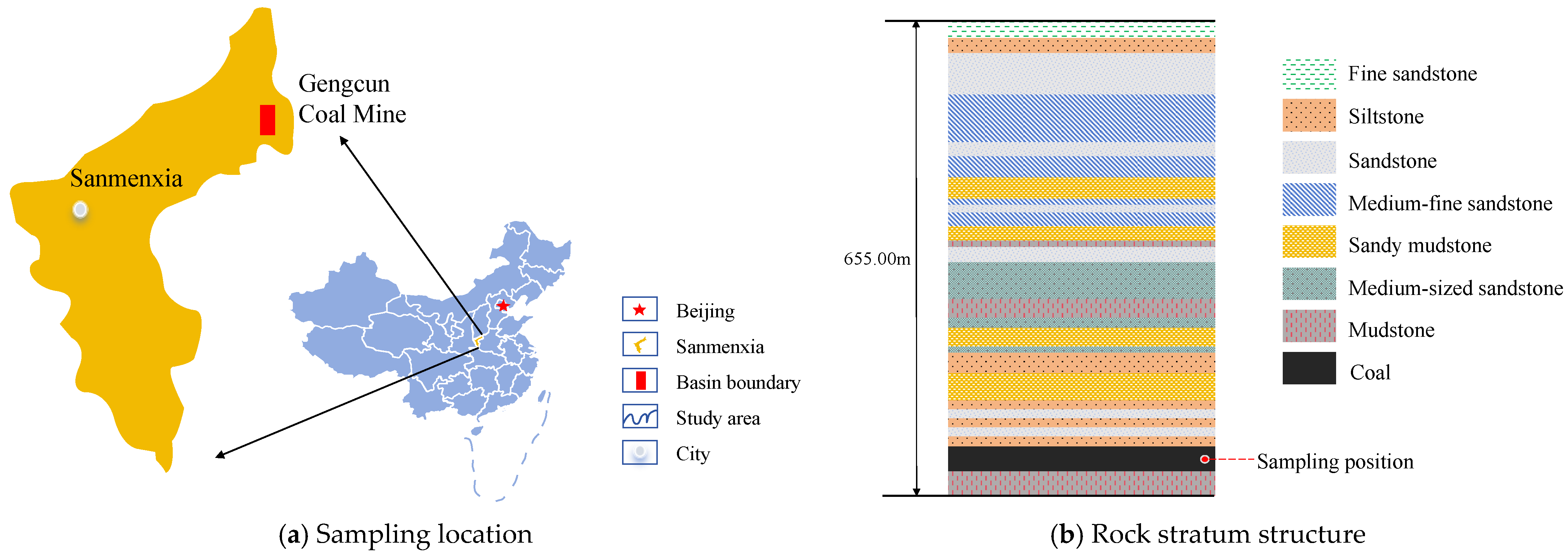
2.2. Specimen Preparation

The coal sample was collected from the 11,240 working face of Gengcun coal mine (Sanmenxia, China), and the sampling position is shown in Figure 2.

The sample preparation process was as follows. Initially, the raw coal extracted from Gengcun mine was crushed using a coal crusher and then sieved into six distinct particle size ranges. In accordance with the sample preparation conditions for broken rock mass [31,38], and to ensure the validity of both field and experimental results, the diameter of the coal sample was required to be at least five times the maximum particle size. This ensures the structural stability of the coal sample and the reliability of the antireflection effect. The Talbot power exponent, defined by the gradation of the raw coal mixture, was determined by the A.N. Talbot gradation design method [34].

$$P_i={\left({\displaystyle \frac{\mathrm{d}}{D}}\right)}^n\times 100\%$$

(1)

where d is the pore diameter of the sieve (mm); D is the maximum particle size (4 mm); n is the Talbot power exponent; P_i is the proportion of broken coal samples passing through d.

By substituting different values of n and the sieve diameters (0.2 mm, 0.4 mm, 0.8 mm, 1.25 mm, 2 mm, and 4 mm) into Equation (1), the proportion P_i for each particle-size interval was calculated as shown in Figure 3.

According to the mass fraction of each particle-size interval in Figure 3, the mass of each particle-size interval was determined and the briquette samples were prepared by mixing. After screening the coal particles and preparing the graded dry material, each gradation was individually mixed with water and thoroughly stirred until it achieved a consistency that could be easily grasped by hand and the sample could be prepared. Subsequently, the mixture was incrementally added to a cylindrical mold, and coal samples measuring 100 mm in height and 50 mm in diameter were formed through repeated compaction using a drop hammer.

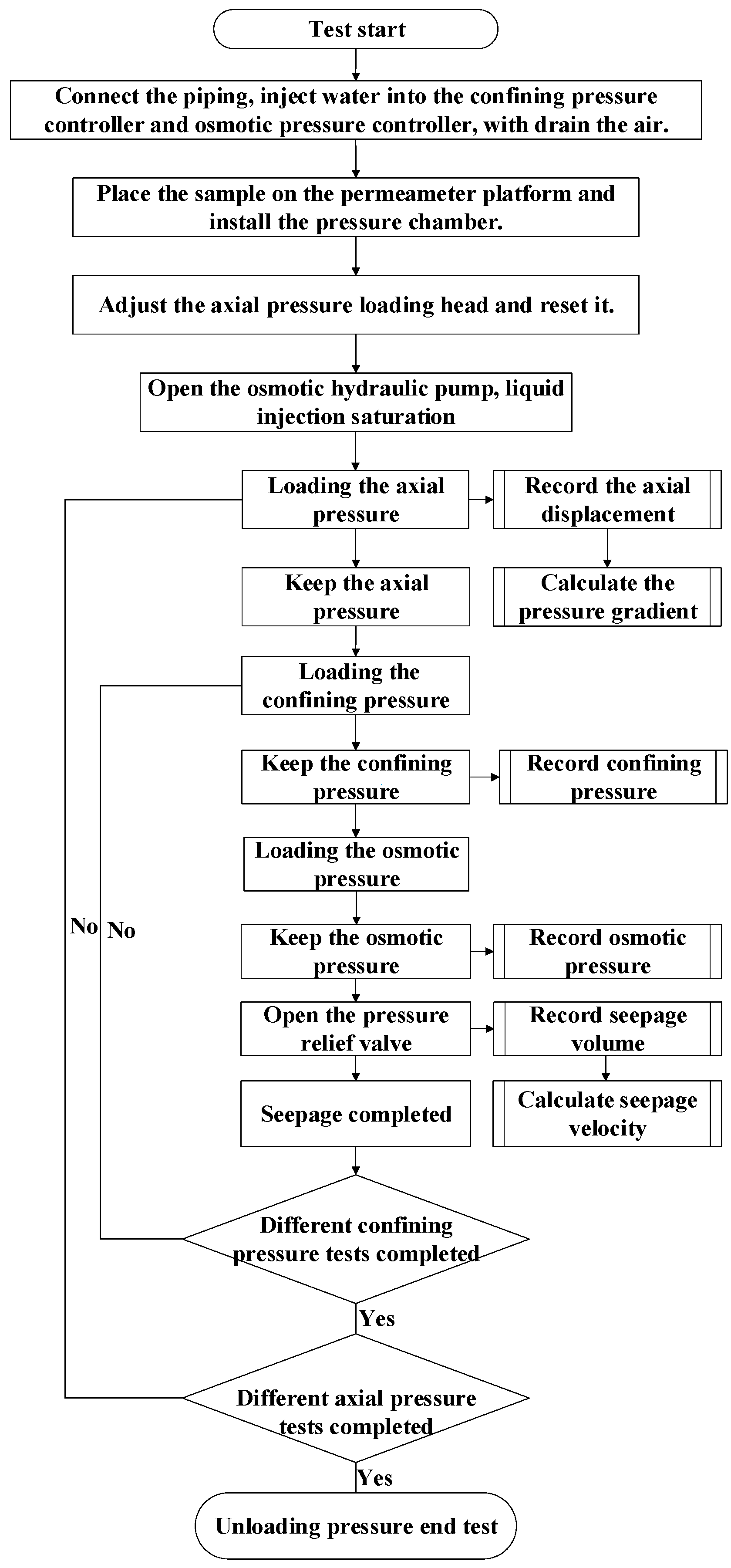
2.3. Test Procedure

In line with the distribution law of gas pressure in the underground coal seam of a high-gas mine and considering the influence of the particle-size ratio of broken coal samples on permeability, the steady-state permeability method was used to conduct the test. Ten types of coal sample gradation groups were prepared, and the Talbot power exponent of each group was measured five times. According to the stratigraphic structure of the Gengcun coal mine shown in Figure 2b, the axial pressures of 500 N, 600 N, and 700 N were applied to each Talbot power exponent group, which were converted to equivalent vertical stresses of 0.25–0.35 MPa (calculated according to the cross-sectional area of φ 50× 100 mm coal samples). This stress range was determined by considering both the relationship between in situ stress and burial depth in Chinese coal mines [39] and the proportional reduction in the compressive strength threshold of the coal samples tested. The experimental configuration maintained confining pressures between 0.2–0.3 MPa through a triaxial permeability system. This confinement range was optimized to maintain linear permeability behavior while avoiding stress mismatch artifacts, thus ensuring experimental controllability under controlled pressure conditions. A closed-loop pressure control system maintained constant osmotic pressure of 0.03 MPa, enabling steady-state permeability monitoring of the seepage process. The specific steps of the test are shown in Figure 4.

3. Results

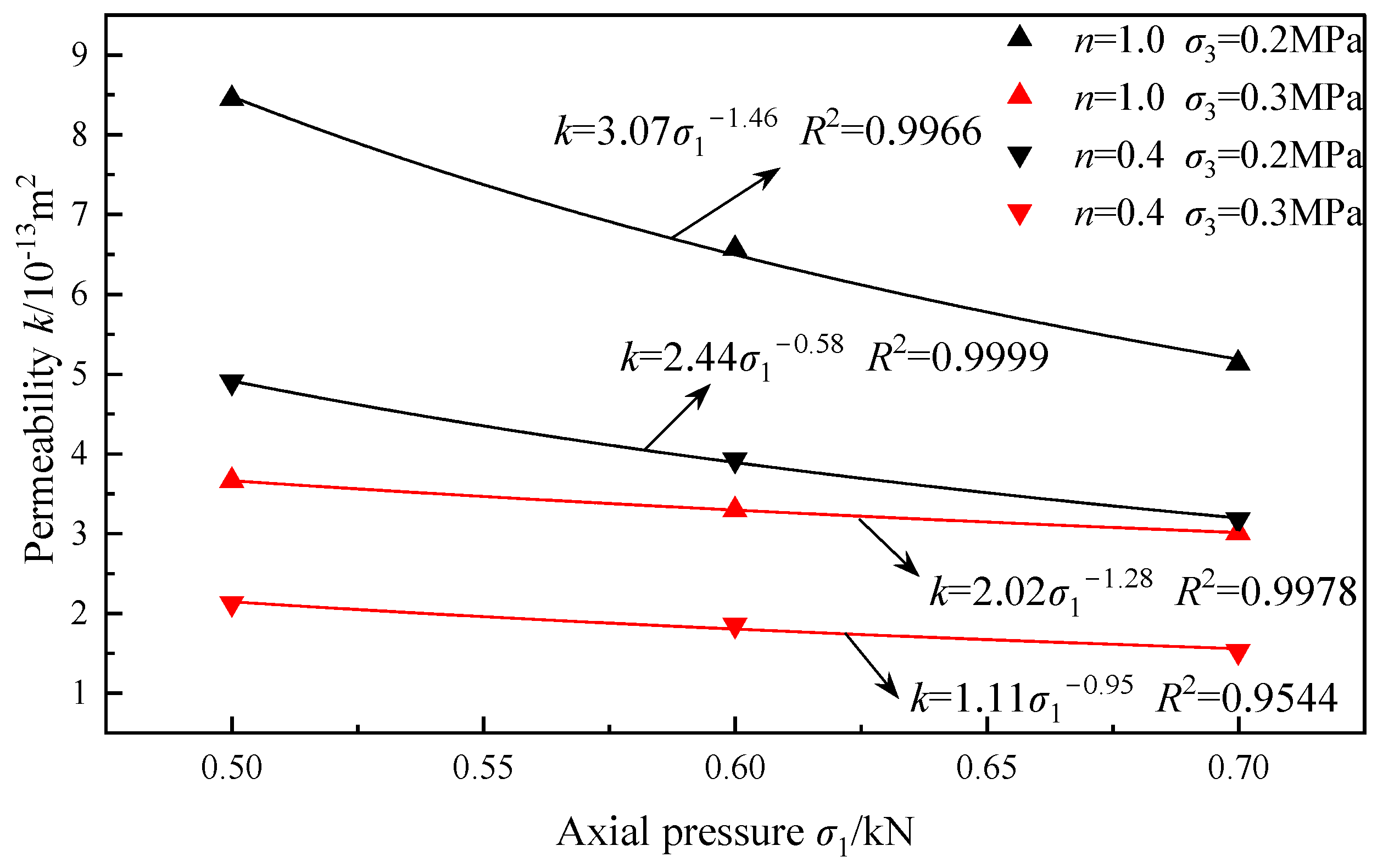
3.1. Effect of Axial Pressure on Permeability

Variations in axial pressure induce modifications to the internal porosity of coal specimens, thereby directly governing of permeability. Thus, elucidating the interdependence between the axial stress and permeability in broken coal is a research priority. According to Darcy’s law, the permeability in the test is calculated as follows [16]:

$$-{\displaystyle \frac{d{p}_k}{dx}}={\displaystyle \frac{\mu }{k}}v$$

(2)

where p_k is the pore pressure, MPa; μ is the hydrodynamic viscosity, Pa·s; k is the permeability of coal sample, m²; v is the fluid seepage velocity m/s.

The relationship between the axial pressure and permeability k is shown in Figure 5. The results show a gradual decrease in permeability k of the broken coal samples with increasing the axial pressure. Under constant confining pressure, the rate of permeability reduction decreases progressively with the axial pressure escalation, suggesting attenuated stress-induced permeability suppression. In comparison, samples with n = 1.0 show a 40% decrease in permeability under the axial loading, while those with n = 0.4 show a 25% decrease followed by stabilization. Under these conditions, the coal samples attain structural stability and incompressibility [31], while the permeability decreases slowly, tending to a stable state.

A stable value emerges as permeability asymptotically approaches a steady state. This behavior is primarily determined by the progressive stabilization of the pore structure of the coal samples induced by the axial pressure. These observations are consistent with the compaction-dependent permeability reported by Pang et al. [37]. This implies the existence of a critical permeability threshold during triaxial loading cycles. The threshold value is contingent upon three interdependent factors: internal structural stability of the coal samples, progressive closure of interparticle flow pathways, and intrinsic permeability of constituent particles.

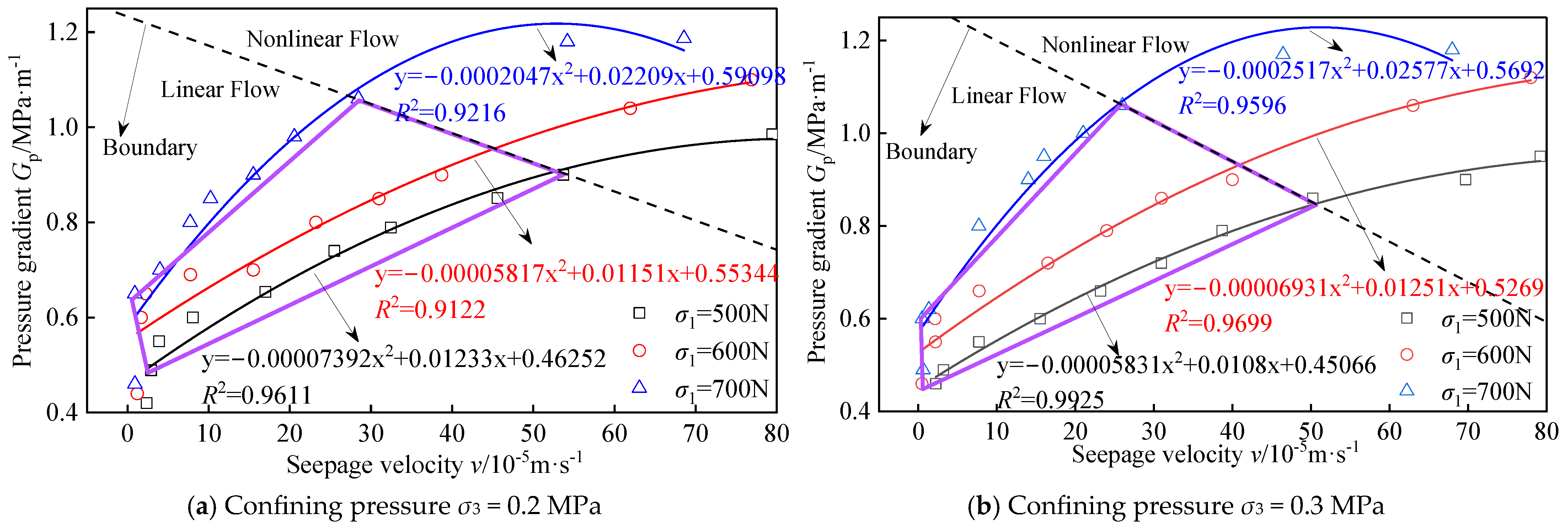
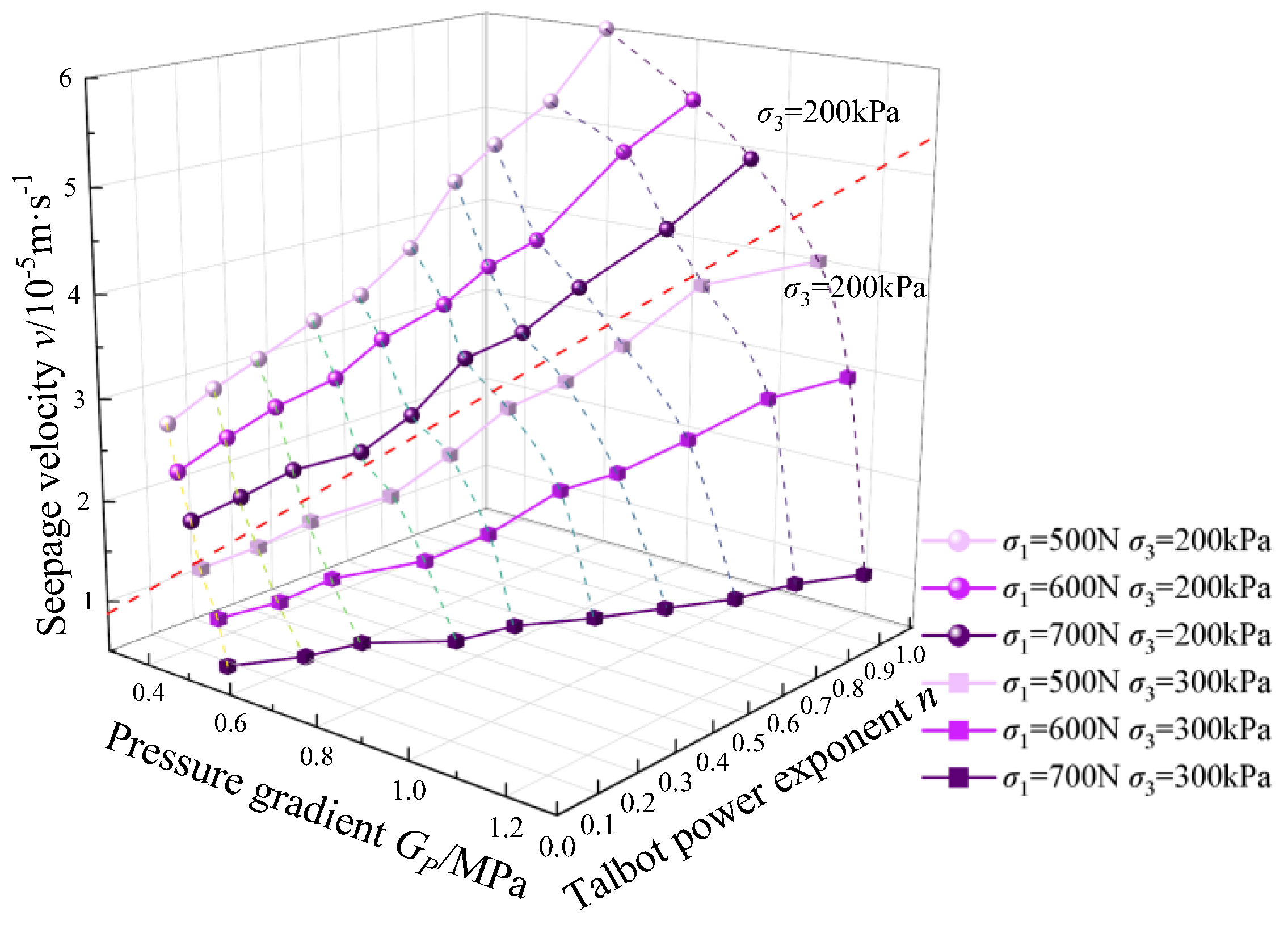
3.2. Effect of Axial Pressure on Seepage Velocity

Different seepage velocity and pressure gradients were generated by changing the axial pressure step by step. The seepage discharge (Q) under various loads and confining pressures was recorded, and the seepage velocity (v) of the broken coal sample was calculated according to Equation (3) [32]:

$$v={\displaystyle \frac{Q}{A}}$$

(3)

where Q is the seepage discharge under standard conditions (Room temperature: 20 °C, atmospheric pressure: 101 kPa), m³/s; A is the cross-sectional area of the specimen, m²;

The pressure gradient is calculated according to the osmotic pressure difference between both ends of the coal sample [36]:

$$G_P=-{\displaystyle \frac{P_1-P_2}{H}}$$

(4)

where P₁ is the pore pressure when the fluid flows into the coal sample, MPa; P₂ is the pore pressure when the fluid flows out of the coal sample, and the outlet of the permeability is connected with the air. H is the height of the coal sample, m.

The Forchheimer-type permeability equation was employed to characterize the permeability law of broken coal. Equation (5) accurately describes the nonlinear permeability state [31]:

$$-{\displaystyle \frac{dp}{dx}}={\displaystyle \frac{\mu }{k}}v+\beta \rho v^2$$

(5)

where k denotes permeability, m²; β is a non-Darcy factor; ρ is fluid density, kg/m³.

The permeability curve of a typical coal sample with n = 1.0 was obtained, as shown in Figure 6.

The relationship between the seepage velocity and the pressure gradient of the coal sample during the axial pressure loading is shown in Figure 6. As shown by the curve, linear flow occurs below the boundary line, resembling a quadrilateral region. Within this quadrilateral region, the flow retains linear characteristics, while beyond these boundaries the flow exhibits non-linear behavior. Reduced axial pressure promotes linear flow behavior, whereas increased confinement pressure not only shifts the boundary downward but also amplifies non-linear flow characteristics.

Under constant confining pressure, the non-linear flow characteristics show a progressive increase as the axial load increases from 500 N to 700 N. This evolution is primarily due to the increase in confining stress, which induces particle rearrangement and densification of broken coal. The resulting compaction leads to a reduction in both the porosity and the number of interconnected permeability channels within the coal sample. Consequently, the permeability process intensifies, amplifying the deviation from the linear region.

Comparison of Figure 6a,b shows that the extent of the linear region increases as the confining pressure increases. The reason for this may be that the increase in confining pressure increases the strength of the coal sample. As a result, the osmotic pressure has greater difficulty in altering the internal structure of the coal sample, thereby weakening the effect of the pressure gradient at both ends. Consequently, permeability has a wider linear range.

Based on the linear region shown in Figure 6, the corresponding linear regions for different Talbot power exponents are shown in Figure 7. As the Talbot power exponent increases, C1 and C2 increase progressively and their difference increases, indicating an upward shift and expansion of the linear region. Similarly, D1 and D2 also increase progressively and their difference increases, indicating a rightward shift and expansion of the linear region.

This phenomenon suggests that the Talbot power exponent improves linear permeability as shown in Figure 7. The upward and rightward shift of the linear region indicates that the seepage velocity of the coal sample increases under identical stress conditions, indicating improved permeability capacity and efficiency. The extension of the linear zone implies a linear relationship between seepage velocity and pressure gradient over a wider stress range, allowing improved prediction and control of the permeability of the coal sample. This can be attributed to the fact that coal samples with larger Talbot power exponents have wider permeability channels. Consequently, under the same pressure gradient, the seepage velocity of coal samples is relatively lower. According to the Forchheimer equation, the permeability characteristics are influenced by the quadratic term of the seepage velocity. The non-linear effect caused by the low seepage velocity is negligible and shows a distinct linear characteristic, as shown by the extension of the linear region in the figure.

Comparison of Figure 7a,b shows that as the confining pressure increases, the permeability linear zone shifts to the right and its range expands. This suggests that the confining pressure facilitates the expansion of the linear zone. A plausible explanation for this phenomenon is that the increase in confining pressure makes the coal sample denser. Consequently, for the same pressure gradient, the permeability channel becomes narrower, leading to a higher seepage velocity. At the same time, the effect of the pressure gradient at both ends of the coal sample is reduced.

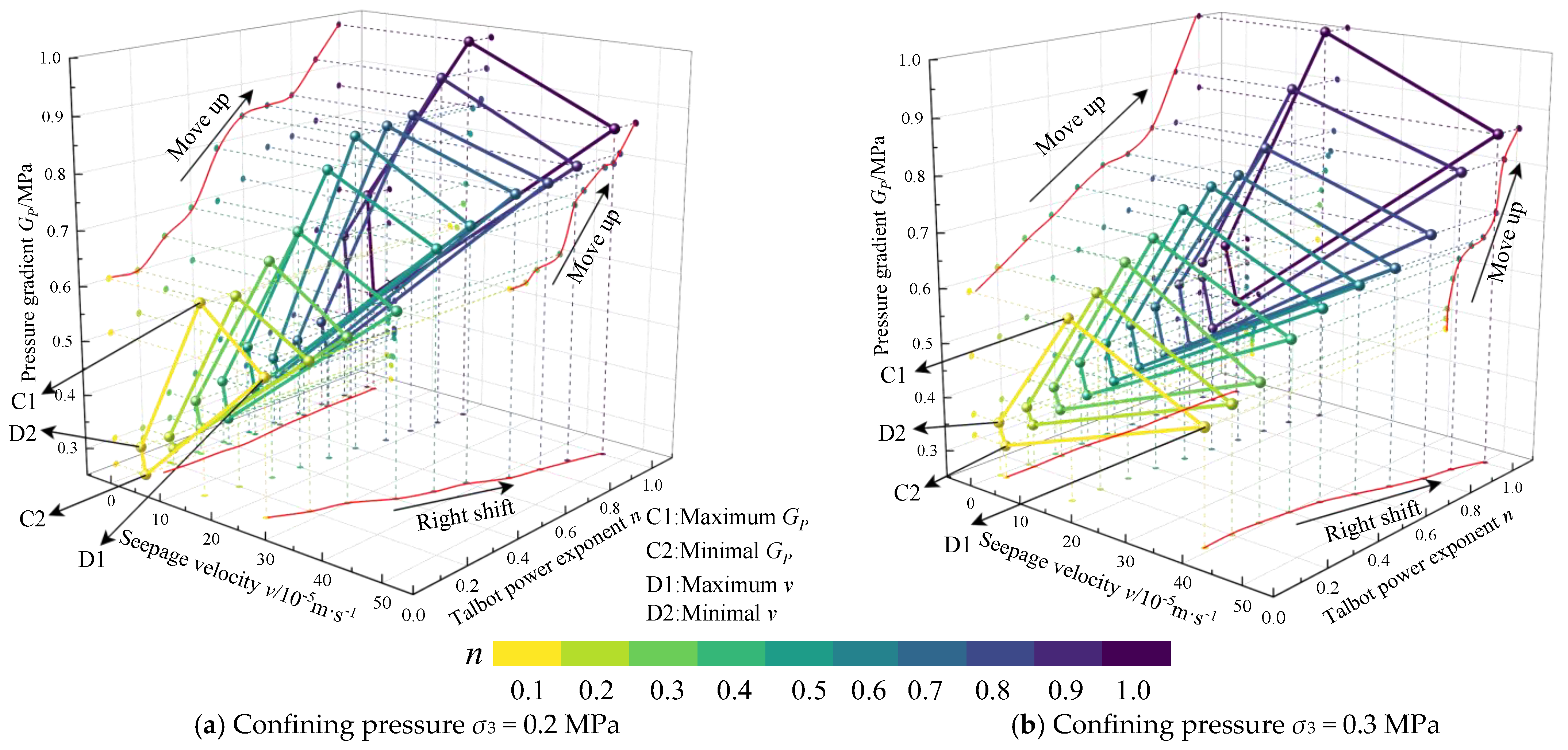
3.3. The Influence of Talbot Power Exponent on Seepage Velocity

The relationship between seepage velocity, pressure gradient, and Talbot power exponent under ten-stage Talbot power exponent and six-stage different stress levels was shown in Figure 8.

The seepage velocity is influenced by the Talbot power exponent, pressure gradient, confining pressure, and axial pressure, with the pressure gradient having the most significant effect, as shown in Figure 8. It can be observed that a higher Talbot power exponent and pressure gradient, combined with lower confining and axial pressures, result in a higher seepage velocity. Increasing the Talbot power exponent increases the seepage velocity, while increasing the axial and confining pressures inhibits the ability of the Talbot power exponent to increase the seepage velocity. Specifically, the pressure gradient amplifies the enhancing effect of the Talbot power exponent on seepage velocity, while the axial and confining pressures counteract this effect. Additionally, the Talbol power exponent enhances axial stress and peripheral pressure suppression effects on seepage velocity.

Among these factors, the enhancement of the promoting effect of the Talbot power exponent on the seepage velocity by the pressure gradient differs slightly from the experimental observations of Lei et al. [16]. This difference is due to subtle variations in experimental principles. In steady-state permeability experiments, the osmotic pressure at both ends of the sample remains constant, ensuring a stable pressure gradient. In contrast, during transient permeability experiments, the osmotic pressure difference between the ends of the sample gradually decreases during the infiltration process.

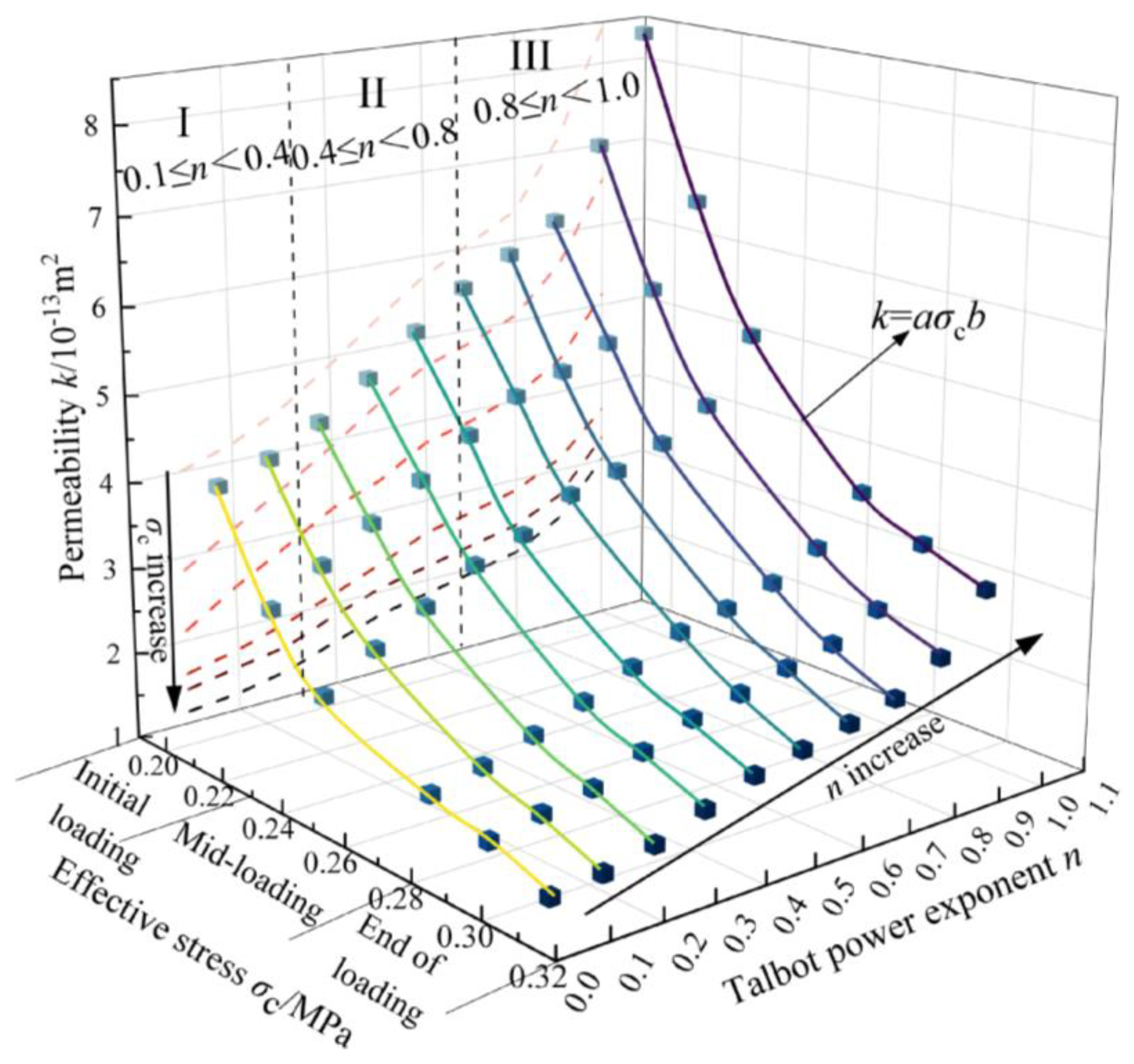
3.4. The Influence of Talbot Power Exponent on Permeability

The effective stress calculated according to Equation (6), the relationship between the effective stress, the permeability k and the broken coal with different Talbot power exponents was plotted as shown in Figure 9.

As n increases from 0.1 to 1.0, the permeability k of the broken coal samples generally follows a power exponential distribution with three stages, which are shown in the YZ projection surface of Figure 9. In the first stage, the permeability k increases slowly. This is due to the dominance of smaller coal particles within the coal sample during this stage. As a result, the total voids within the sample remain relatively small, resulting in minimal changes in permeability. In the second stage, the permeability k generally shows a linear increase. This is due to an increased proportion of larger particle sizes, which increases the voids within the coal sample. Consequently, the internal penetration rate increases, resulting in significant variations in flow rate and rapid changes in permeability k. In the third stage, permeability shows exponential growth. This is due to the compression of smaller coal particles to less than 10%. Consequently, larger coal particles dominate within the coal sample. The gaps between the larger particles widen and interconnect to form an extensive network of seepage. This leads to an increase in overall porosity, resulting in a second sharp increase in permeability.

Figure 9 shows that the permeability of coal samples increases with the increases in the Talbot power exponent. This observation is consistent with the permeability model for broken rock masses proposed by Li et al. [30]. Under conditions of maximum gradation particle size, the permeability k of the coal sample reaches its peak value. This phenomenon may be attributed to the initial state of gap development and larger particle sizes, where a coal sample with a higher Talbot power exponent forms a highly loose skeleton. The strong pore connectivity in this state increases the permeability of the coal sample.

3.5. Permeability in the Coordination of the Effective Stress

The study of Section 3.3 has clarified inhibitory effects of the axial pressure and confining pressure on seepage velocity. To further clarify this effect, the concept of effective stress was introduced to represent the actual stress state of broken coal particles under triaxial stress. According to Terzaghi’s effective stress principle, the mean effective stress of coal samples under triaxial stress conditions is calculated as follows [15].

$${\sigma }_c={\displaystyle \frac{1}{3}}\left(2{\sigma }_3+{\sigma }_1\right)-{\displaystyle \frac{1}{2}}\left(P_1+P_2\right)$$

(6)

where σ_c represents the mean effective stress, MPa; σ₃ is the test confining pressure, MPa; σ₁ is the axial pressure, N.

The effective stress during the permeability process of broken coal is calculated according to Equation (6), and the relationship between the effective stress and the permeability with different Talbot power exponents is shown in Figure 9.

Effective stress effectively characterizes the inhibiting effects of the axial and confining pressures on the seepage velocity, as shown in Figure 9. With increasing effective stress, permeability decreases significantly, and the enhancing effect of the Talbot power exponent on permeability decreases. Simultaneously, the inhibiting effect of effective stress on permeability increases as the increases of the Talbot power exponent. This indicates that at constant effective stress, an increase in the Talbot power exponent tends to increase coal permeability. This trend is consistent across different effective stress conditions. As the stress continues to increase, the influence of the Talbot power exponent on coal permeability gradually decreases and stabilizes.

The underlying mechanism for this phenomenon may be explained as follows. During the initial stress loading stage, the coal sample has a relatively large void volume. As the axial and confining pressures increase, effective stress correspondingly rises. Due to the relatively large void volume, the permeability remains at a high level. At the intermediate loading stage, the increased effective stress induces greater compaction in the coal sample, resulting in shrinkage deformation. Under pressure, the gaps within the coal body close, reducing the diameter of the permeability channels and thereby reducing permeability. In the final loading stage, the effective stress further compresses the pore volume of the coal body. However, the compressive effect on the effective pores and permeability channels gradually diminishes. The permeability channels stabilize and the changes in permeability of the coal sample gradually reach a steady state.

3.6. Considering the Permeability Law of Gradation and Effective Stress

To describe the relationship between effective stress and permeability under different Talbot power exponents, the power function is introduced based on Figure 9, and the relationship between Talbot power exponents and parameters a and b is given, as shown in Figure 10.

As can be seen from Figure 9, there is an obvious exponential relationship that exists between the permeability and effective stress for different Talbot power exponents n:

$$k=b{\sigma }_c^a$$

(7)

where k represents permeability, m²; σ_c represents the effective stress, MPa; a and b are parameters.

The power exponent a determines the shape of the permeability curve. When a is negative, it reflects the degree of the decrease in coal permeability as the effective stress increases, embodying the inhibitory effect of the Talbot power exponent on permeability. The coefficient b generally determines the overall longitudinal position and magnitude of the function. When b is positive, it represents the amplitude effect of the effective stress on permeability.

Figure 10 shows that as the Talbot power exponent increases, the parameters change to varying degrees of change. Similar to the permeability-Talbot power exponent curve, three distinct stages can be identified: the first stage (I): n < 0.4; the second stage (II): 0.4 ≤ n < 0.8 and the third stage (III): 0.8 ≤ n < 1.0. The power exponent a generally shows a decreasing trend. As the absolute value of a increases, the function becomes steeper, and permeability shows greater sensitivity to effective stress, indicating that the inhibitory effect of the Talbot power exponent on permeability is enhanced. The coefficient b increases with the Talbot power exponent, and the curve height of the curve gradually increases, indicating a continuous increase in the amplitude effect of effective stress on permeability. It is observed that the changes in the parameters a and b occur in three stages, which is consistent with the permeability change in Figure 9. In the first stage (n < 0.4), a decreases gradually, while b increases slowly. In the second stage (0.4 ≤ n < 0.8), a decreases linearly, and b increases linearly. In the third stage (0.8 ≤ n < 1.0), a decreases exponentially, and b increases exponentially.

4. Conclusions

The efficiency of CBM drainage systems is fundamentally controlled by the permeability of broken coal around drainage boreholes, with in the stress state acting as the primary determinant of permeability. Significantly, the effective stress serves as a holistic parameter to characterize the anisotropic stress distributions around drainage boreholes. Through systematic triaxial permeability testing on broken coal samples, the stage variation characteristics of permeability are revealed, and the quantitative relationship between the effective stress and permeability of broken coal is established. The following conclusions are drawn:

(1)

A specific correlation exists between the permeability of broken coal and axial pressure. Axial pressure affects permeability by altering the pore structure of broken coal samples. During the loading process, as the axial pressure increases, the permeability of broken coal decreases exponentially. This decrease is accompanied by the compression of the pore structure, the gradual closure of permeability channels, and a consequent decrease in permeability.

(2)

A specific correlation also exists between the permeability of broken coal and the Talbot power exponent. As the Talbot power exponent (n) of the broken coal samples increases from 0.1 to 1.0, the permeability (k) shows a three-stage growth pattern. In the initial stage, the permeability increases slowly due to the predominance of smaller particle sizes. In the second stage, as the proportion of larger particles increases, the permeability increases linearly. In the third stage, with the dominance of larger particle sizes, the permeability exhibits exponential growth.

(3)

The seepage velocity may be influenced by the combined effect of the Talbot power exponent, pressure gradient, confining pressure, and axial pressure. Of these factors, the pressure gradient may have the most significant effect. The Talbot power exponent enhances the seepage velocity, while the axial and confining pressures inhibit it.

(4)

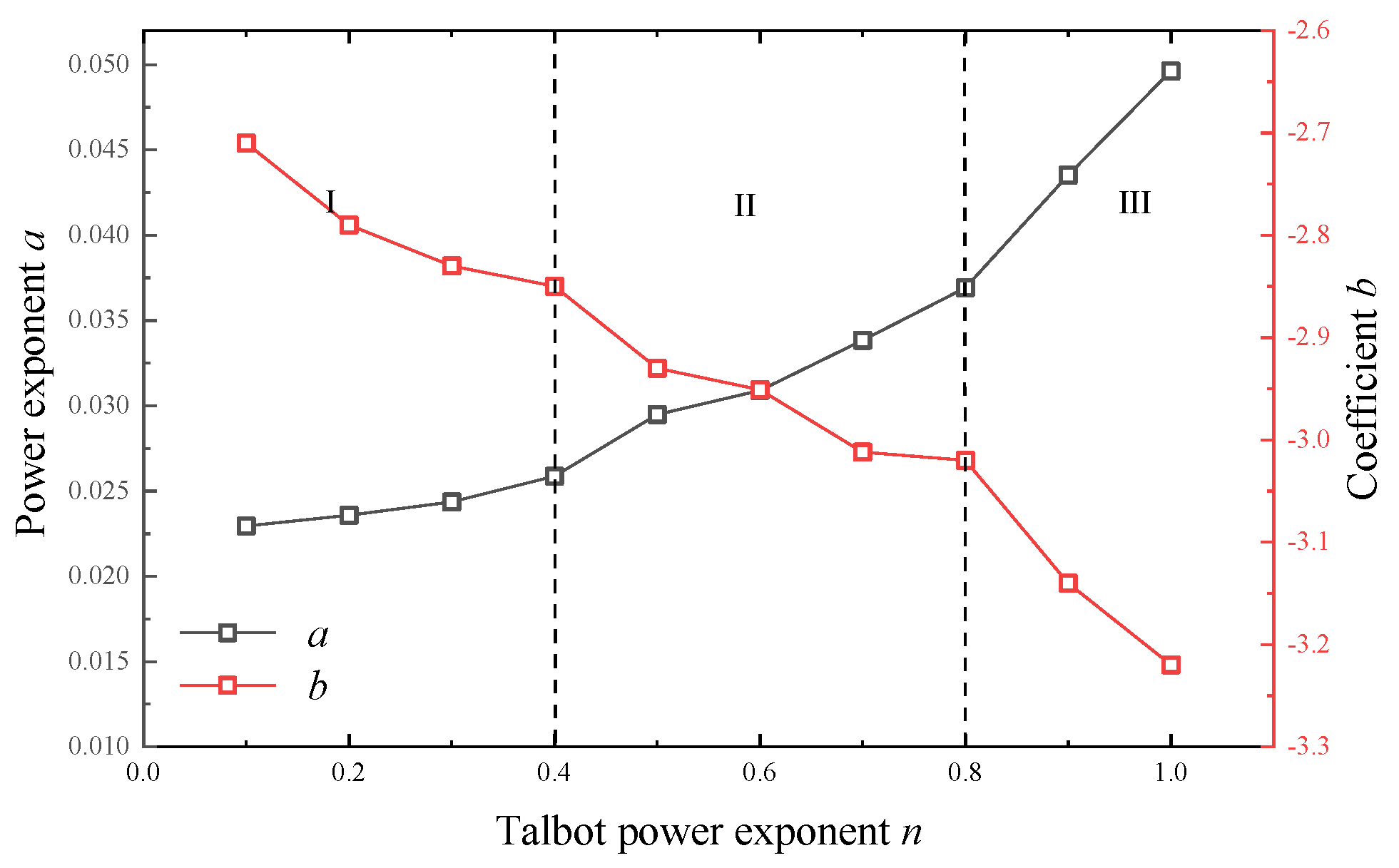
The permeability of broken coal with different Talbot power exponents typically exhibits an exponential decay as the effective stress increases. Both the parameters and the permeability-Talbot power exponent curve display three stages. As the Talbot power exponent increases, the power exponent (a) gradually decreases, while the coefficient (b) increases. This indicates that broken particles increase both the inhibitory effect of the effective stress and the amplitude effect.

The stresses and broken state of the coal around the gas drainage borehole are complex and varied, resulting in the coexistence of multiple gas seepage channels. The permeability of each channel is interrelated, which greatly affects the gas migration path and drainage efficiency. In fact, we explored the serial seepage problem of the broken coal body around the drainage borehole, and due to the existence of different gas flow channels, the follow-up should focus on the parallel seepage modeling of coals with different degrees of brokenness and evaluate the comprehensive effects of parallel seepage mechanisms on coalbed methane drainage under different mining stages and stress environments.