Quality Risk Evaluation of the Whole Process of Assembly Building Based on Game Theory-Combinatorial Empowerment and Three-Dimensional Cloud Modeling
Abstract
1. Introduction
2. Materials and Methods
2.1. Construction of Quality Risk Evaluation Indicator System for Assembled Building
2.1.1. Identification of Quality Risk Factors for Assembled Building
- (1)
- Literature search and preliminary screening
- (2)
- Accident case studies
- (3)
- Classification and optimization of indicators
- (4)
- Expert consultation (Delphi method)
- (5)
- Construction of the final indicator system
2.1.2. Determination of Weights of Indicators for Quality Risk Evaluation of Assembled Building
- (1)
- Ordinal priority approach method
- (2)
- Anti-entropy weighting method
- 1)
- Determine the original risk judgment matrix. There are m experts to evaluate n risk evaluation indicators and so the evaluation results formed the original risk judgment matrix , as in Formula (3):
- 2)
- Normalization processing of the original risk judgment matrix. In order to ensure that each indicator has the same importance in the evaluation process and to avoid the bias caused by the difference in the scale and the difference in the range of values, the raw data are normalized and converted into the [0, 1] interval as shown in Equation (4):
- 3)
- Calculate the anti-entropy value of the indicators. Using the normalized data, calculate the anti-entropy value for each indicator, as Equation (6):
- 4)
- Calculate the objective weights of the indicators. The anti-entropy value is normalized to ensure that the sum of the weights of the indicators is 1. Equation (7) is as follows:
- (3)
- Combinatorial Empowerment Based on Game Theory
- (1)
- Linear combination model construction. The subjective weight vector W(1) determined by the OPA method and the objective weight vector W(2) determined by the inverse entropy weight method are linearly combined, and the linear combination coefficients α1 and α2 are introduced as in Equation (9):
- (2)
- Optimizing objective function construction. In order to find the optimal weight vector W′ in the set of possible weight vectors, the optimization objective function is constructed. In this paper, the principle of departure minimization is adopted, and the goal is to minimize the deviation between W′, and W(1) and W(2) at the same time, that is, the weight vectors are subjected to deviation minimization as shown in Equation (10):
- (3)
- Optimal solution solving. The first-order derivative condition of the optimal solution is obtained according to the matrix differentiation property, and the form of the corresponding system of linear equations is shown in Equation (11), and the optimal linear combination coefficients α1 and α2 can be obtained by solving the system of linear equations:
- (4)
- Normalization. The calculated optimal combination coefficients α1, α2 are normalized to obtain the final composite weight vector W′, Equation (12) as follows:
- (5)
- Conflict resolution validation. The validation analysis of the examples below reveals significant deviations between subjective and objective weights for some indicators (e.g., U23 and U32). Through optimization, the final distribution of comprehensive weights is more balanced, and subjective preferences and data laws are fully reflected, which verifies the effectiveness of game theoretic combinatorial assignment in resolving weight conflicts.
2.2. Constructing a Game Theory-Combinatorial Empowerment Three-Dimensional Cloud Evaluation Model
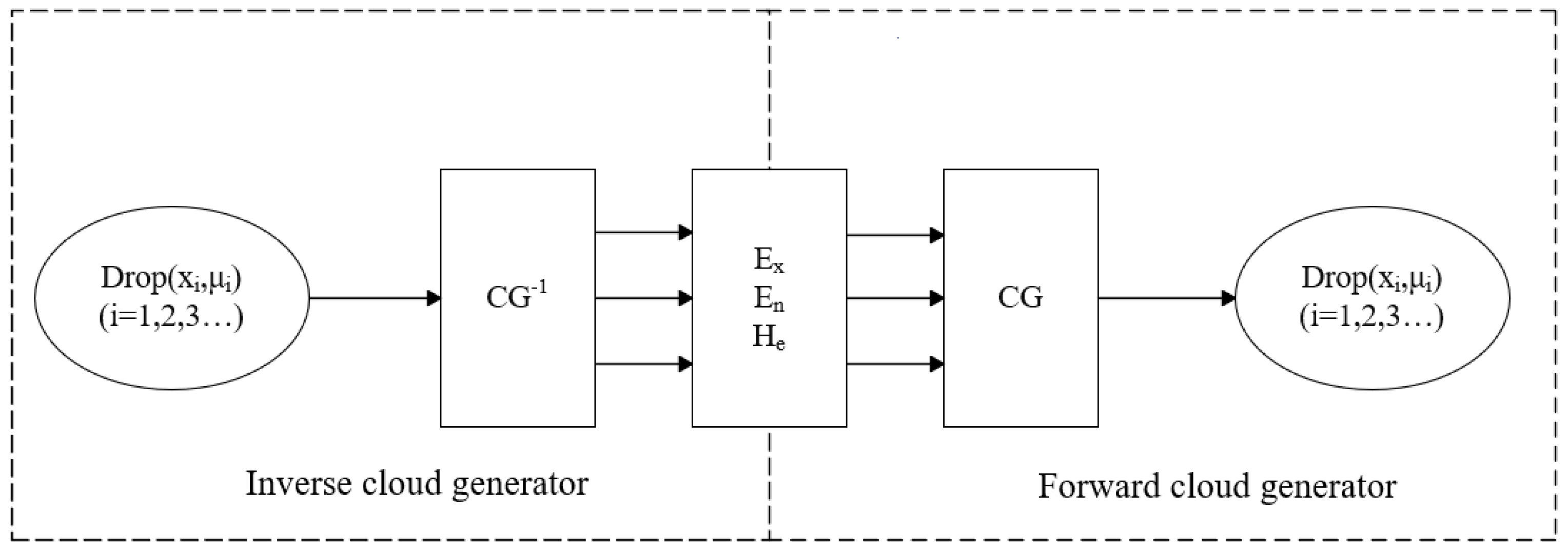
2.2.1. Basic Theory of the Cloud Model
2.2.2. Construction of Three-Dimensional Cloud Evaluation Model
- (1)
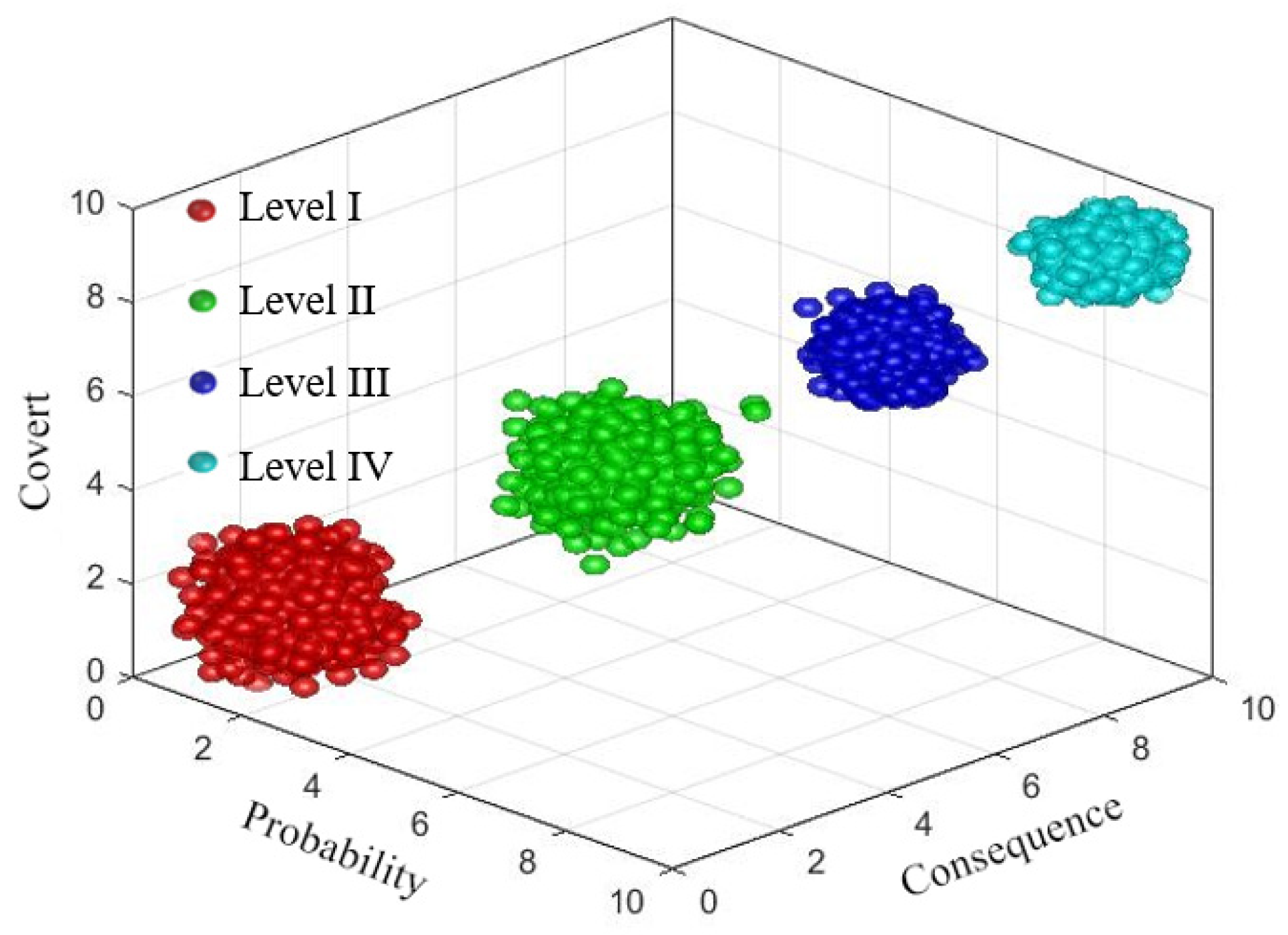
- Determine the three-dimensional cloud droplet clusters for risk level criteria clouds
- (2)
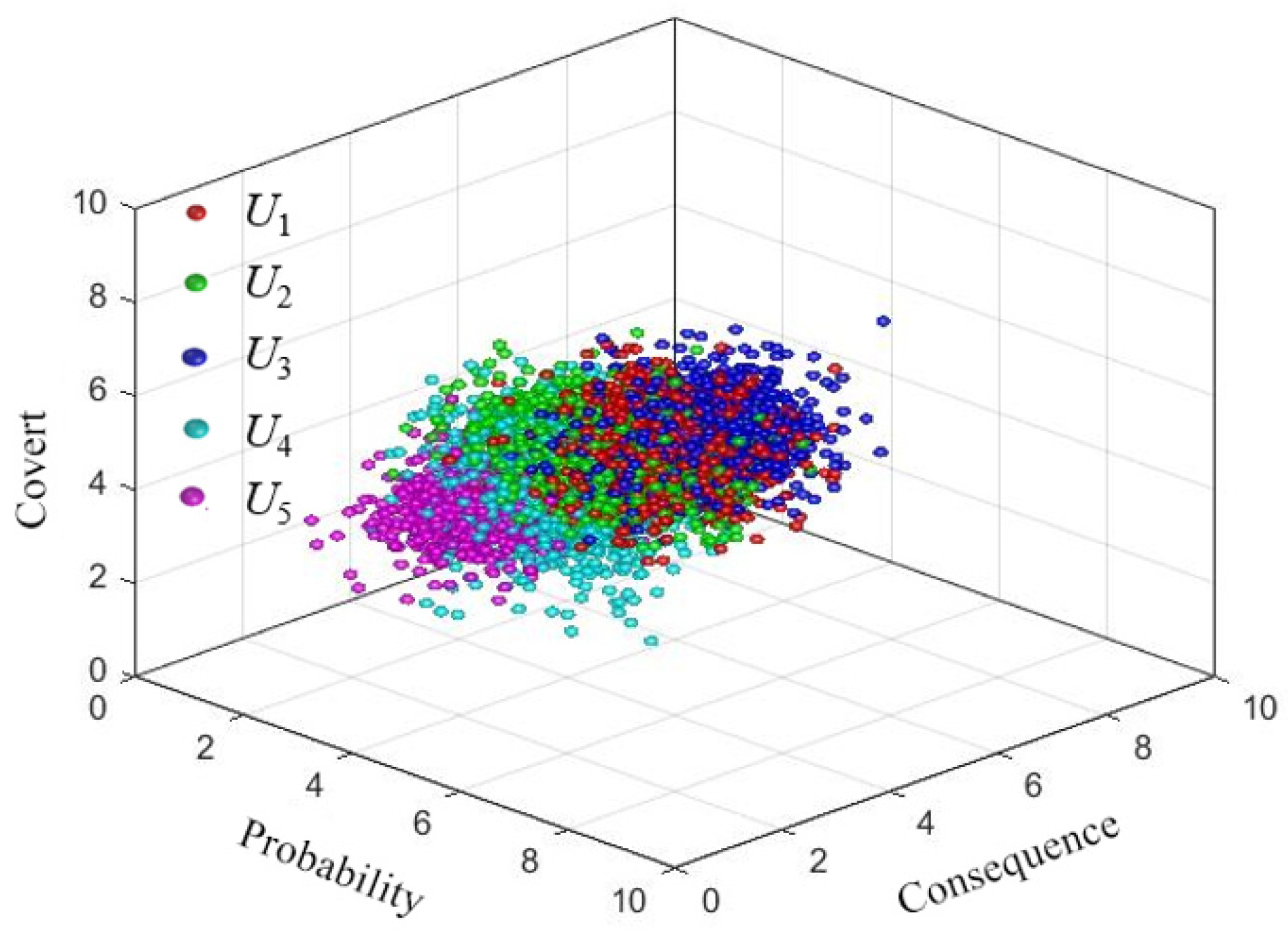
- Determine the three-dimensional cloud droplet clusters for risk indicator evaluation clouds
- (3)
- Determine the three-dimensional cloud droplet clusters for integrated evaluation clouds
- (4)
- Determine the level of risk
3. Instance Validation
3.1. Overview of the Project
3.2. Weighting Calculation
3.3. Cloud Modeling
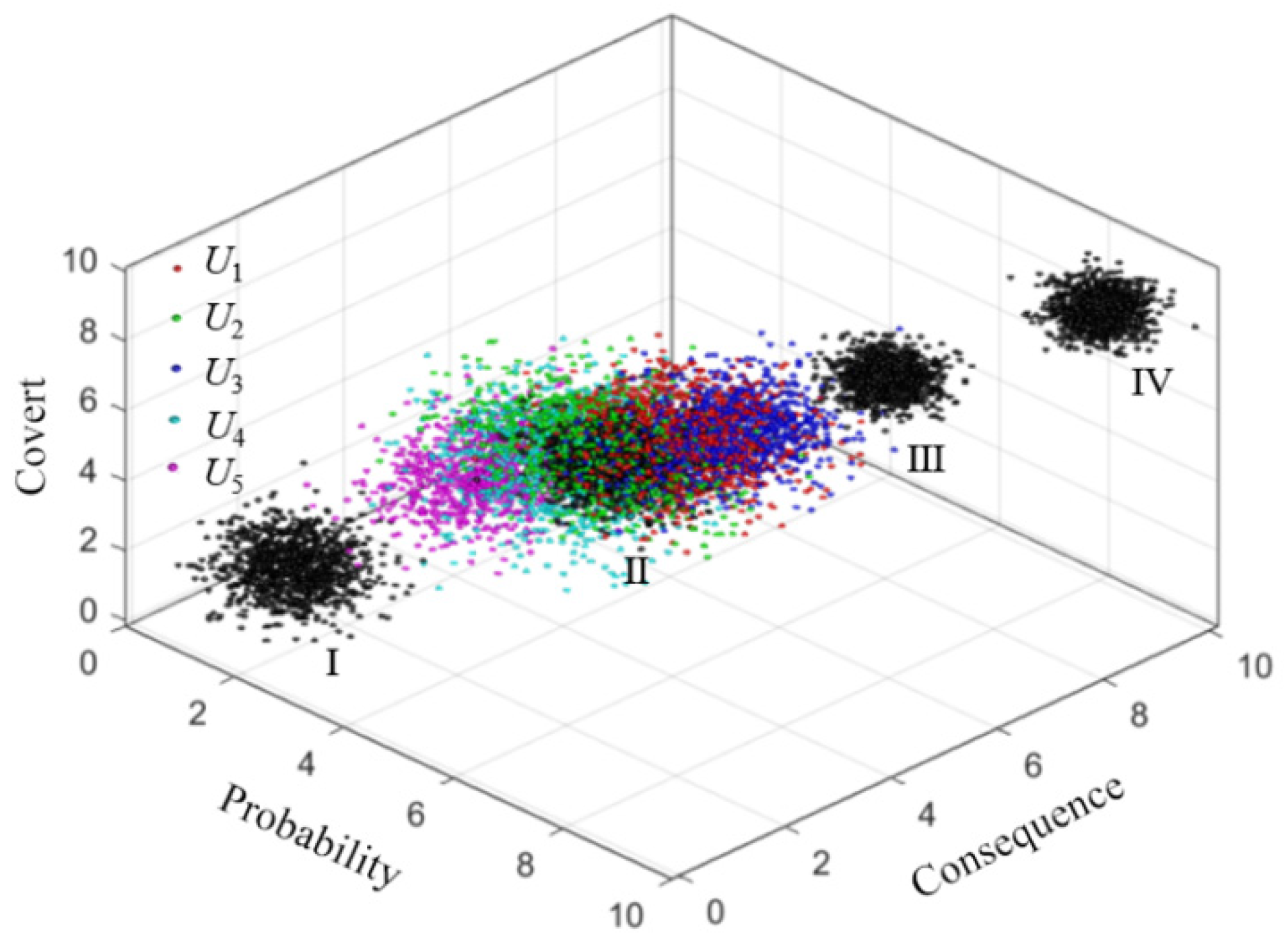
3.4. Analysis of Results
4. Model Comparison and Validation
5. Conclusions and Prospects
5.1. Conclusions
- (1)
- This paper systematically analyzes the potential quality risk factors in the whole process of assembled buildings from the five stages of decision-making and design, bidding and procurement, production and transportation, on-site assembly and construction, and operation and maintenance, identifies the key risk points, and puts forward targeted coping strategies. On this basis, a quality risk evaluation index system for the whole process of assembled buildings, containing 20 secondary indicators, is established, which provides a theoretical framework for the quantitative assessment of quality risk.
- (2)
- Applying the game theory-combinatorial method for quality risk evaluation and introducing the OPA (Ordinal Priority Approach) to calculate the subjective weights and the anti-entropy weight method to calculate the objective weights, through expert scoring and weight optimization, the weights of the risk factors are determined objectively and impartially, which improves the scientific nature and accuracy of the risk assessment. The game theory-combinatorial method effectively integrates the subjective judgment of experts and the objective analysis of data, which enhances the credibility and practicality of the model.
- (3)
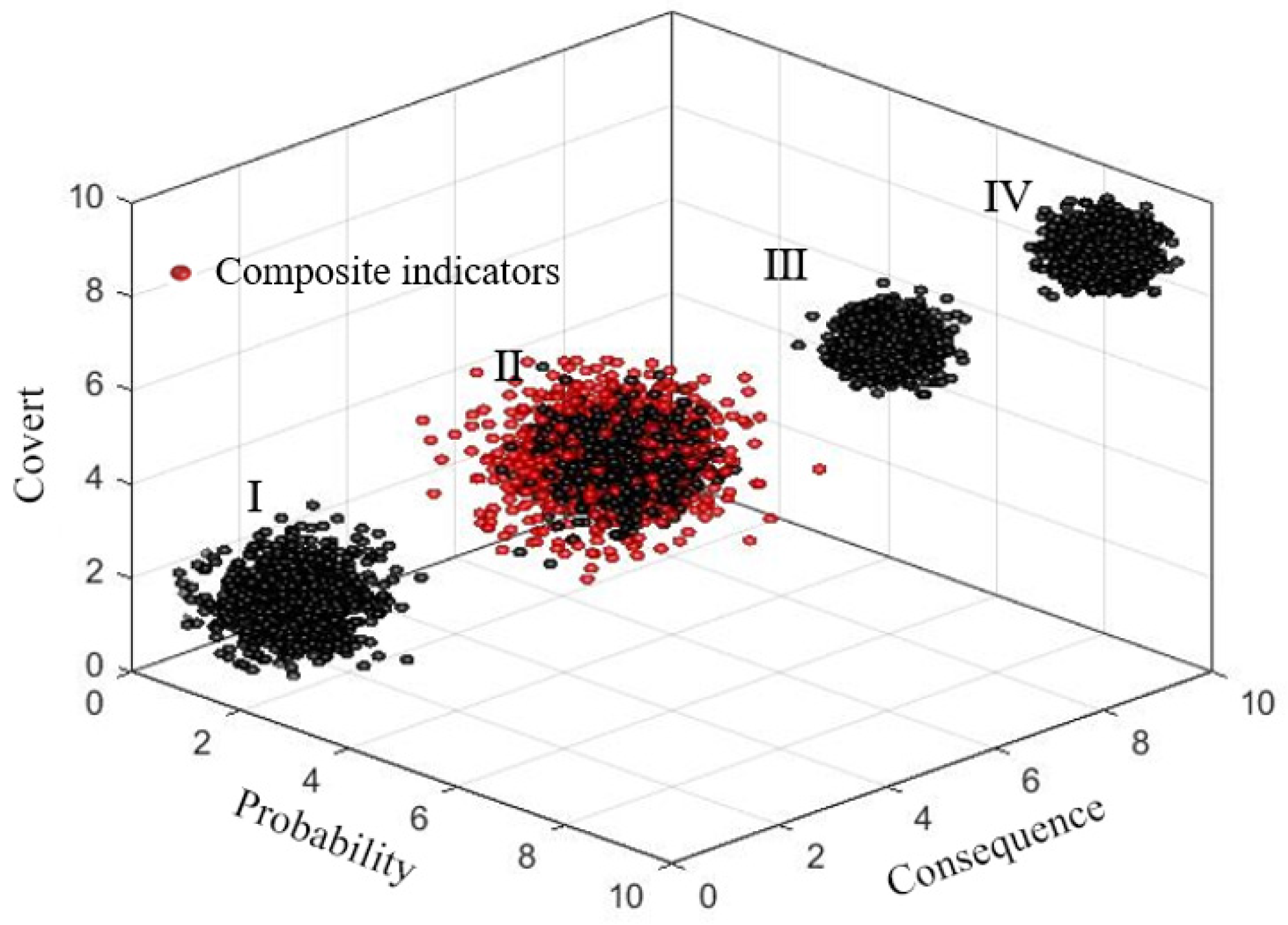
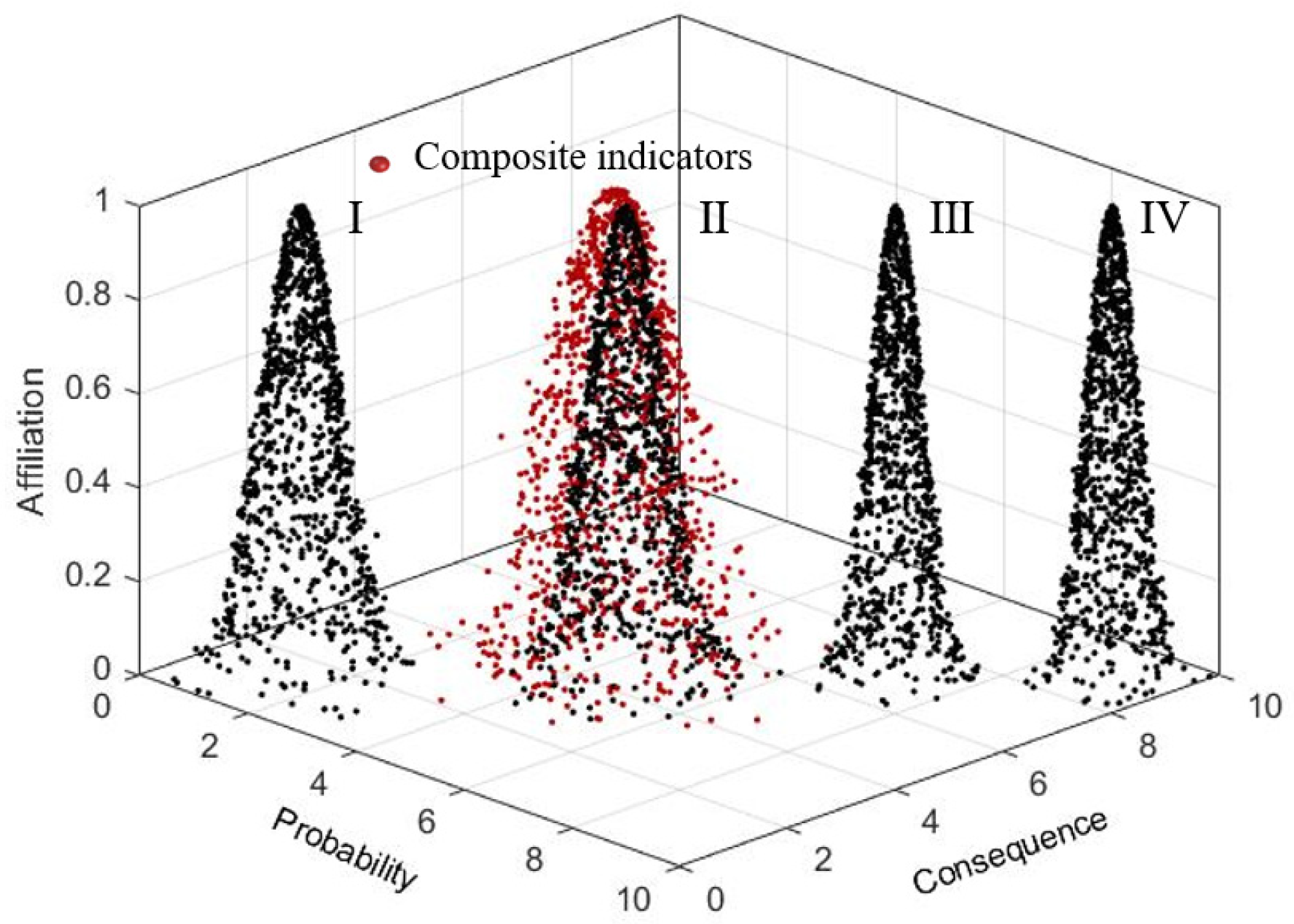
- A three-dimensional cloud model is used to evaluate the quality risk of the whole process of assembly building, combining the three dimensions of risk probability, risk consequence, and risk concealment to quantitatively analyze the risk characteristics of each index. Example validation shows that the overall risk level is II, which is highly consistent with the actual situation of the project, and the risk level of key risk indicators U13 and U32 are both III, while the rest of the risk indicators are all II, reflecting the significant impact of frequent design adjustments and the quality of raw materials themselves on the quality risk. Comparison results with the traditional two-dimensional cloud model show that the three-dimensional cloud model can more accurately identify high hidden risks, especially in the risk evaluation of U37 and U51, and that the assessment results of the three-dimensional cloud model are closer to the actual project situation than the two-dimensional cloud model.
5.2. Prospects
- (1)
- Applicable scenario expansion can be expended in the future. The three-dimensional cloud model can be applied to more complex assembly building types, such as ultra-high-rise buildings, modular buildings, or intelligent buildings, so as to validate the model’s versatility and applicability in diversified scenarios.
- (2)
- Enriching the dimensions of risk evaluation. Although this paper introduces a three-dimensional cloud model (probability, consequence, and hiddenness), future research can explore more dimensions affecting risk to improve its scientific and comprehensive nature. For example, economy, as the direct or indirect impact of risk occurrence on cost. The time factor, as the dynamic monitoring of risk trends over time. Socio-environmental impacts, such as assessing the long-term impacts and social satisfaction of assembly building quality risks on the community and the environment.
- (3)
- Optimization of indicator selection. The selection of indicators in the current study mainly relies on the literature research, accident case analysis, and expert opinions, which is somewhat subjective. In the future, data-driven indicator mining can be combined to mine high-frequency risk points in the whole life cycle of the building through the introduction of big data analysis technology, which can automatically screen key markers and reduce the impact of human intervention on the indicator system, as well as dynamically updating the indicator system according to the characteristics of different types of projects (e.g., building scale, regional conditions, construction environment, etc.) to make it more adaptable.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ma, R. Development status and future tr-end of assembly building. Constr. Technol. 2021, 50, 64–68, (In Chinese and English). [Google Scholar]
- Wang, L.; Ji, Y.; Li, D. Research on Material Quality Risk Management Based on Machine Learning for Prefabricated Civil Buildings. For. Chem. Rev. 2022, 1858–1871. [Google Scholar]
- Qu, F.; Chen, C.; Yan, W. Quality risk evaluation of prefabricated components for assembled buildings based on ANP-FUZZY. J. Civ. Eng. Manag. 2019, 36, 92–98. [Google Scholar]
- Zhang, B.; Liu, F.; Cha, X. Quality risk evaluation of assembled buildings—based on ISM-ANP gray clustering model. Constr. Econ. 2023, 44, 101–107. [Google Scholar]
- Deng, H.; Liu, J. Research on PC Component Quality Risk Evaluation Based on Intuitionistic Fuzzy Analytic Hierarchy Process. IOP Conf. Ser. Earth Environ. Sci. 2020, 525, 012043. [Google Scholar] [CrossRef]
- Li, X.J. Research on investment risk influence factors of prefabricated building projects. J. Civ. Eng. Manag. 2020, 26, 599–613. [Google Scholar] [CrossRef]
- Yi, Z.; Lai, S.; Li, X.; Dai, E.; Sun, H. Quality and safety risk assessment of assembled buildings based on multilevel topology. J. Wuhan Eng. Univ. 2020, 42, 669–673+705. [Google Scholar]
- Dai, Y.; An, Q.; Li, D.; Pei, F.; Zhou, J.; Jiao, B.; Lin, N. Risk evaluation of potential defects in basement waterproofing project quality based on game theory-cloud model. J. Civ. Eng. Manag. 2024, 41, 82–88. [Google Scholar]
- Tang, Y.; Huang, B.; Li, W.; Guan, M. Neural network-based risk evaluation of drain breakage-induced subsidence. People’s Yangtze River 2024, 55, 133–138. [Google Scholar]
- Ma, T.; Lin, Y.; Zhou, X.; Zhang, M. Grading evaluation of goaf stability based on entropy and normal cloud model. Adv. Civ. Eng. 2022, 2022, 9600909. [Google Scholar] [CrossRef]
- Guo, J.; Gu, C.; He, J. Risk evaluation of embankment project based on combined empowerment two-dimensional cloud model. Adv. Water Conserv. Hydropower Sci. Technol. 2022, 42, 117–122. [Google Scholar]
- Xie, B.; Liu, Y.; Cui, L. Early warning of construction risk of high-altitude railroad tunnel based on improved game theory-two-dimensional cloud model. Railw. Stand. Des. 2025, 1–10. [Google Scholar]
- Cheng, L.; Xu, Y.; Jing, G. Risk analysis of deep coal mine roof accidents based on combined-assigned three-dimensional cloud assessment technology. J. Saf. Environ. 2024, 24, 413–422. [Google Scholar]
- Sun, Y.; Yang, H.; Gao, X.; Yang, Y.; Sun, W. Research on quality influencing factors in the whole process of assembled building. Constr. Econ. 2023, 44, 21–29. [Google Scholar]
- Sun, Y.; Wu, X.; He, M.; Cong, X. Research on the whole process quality management of assembly building based on BIM+IoT technology. Constr. Econ. 2021, 42, 58–61. [Google Scholar]
- Shi, Z.; Liu, D.; Ji, F.; Feng, C. Construction risk assessment of super-large sinkhole foundation. J. Southwest Jiaotong Univ. 2021, 56, 1241–1249. [Google Scholar]
- Ataei, Y.; Mahmoudi, A.; Feylizadeh, M.R.; Li, D.F. Ordinal Priority Approach (OPA) in Multiple Attribute Decision-Making. Appl. Soft Comput. J. 2020, 86, 105893. [Google Scholar] [CrossRef]
- Xiang, S.; Cai, Z.; Liu, P.; Li, L. Fuzzy comprehensive evaluation of low-carbon operation of distribution networks based on AHP-inverse entropy weight method. J. Electr. Power Sci. Technol. 2019, 34, 69–76. [Google Scholar]
- Huang, Y.; Xu, S.; Jiang, M.; Li, W. A game-theoretic combinatorial empowerment-based navigation safety evaluation of waterways. J. Saf. Environ. 2021, 21, 2430–2437. [Google Scholar]
- Yang, Y.; Zhao, Y. Safety risk evaluation of assembly building component lifting construction based on combined empowerment two-dimensional cloud model. J. Nat. Hazards 2022, 31, 167–174. [Google Scholar]




| Target Layer | Guideline Layer (Level 1 Indicators) | Indicator Layer (Level 2 Indicators) | Meaning of the Indicator |
|---|---|---|---|
| Quality Risks throughout the Assembly Building Process | Decision-making design phase U1 | Deviation rates for key design parameters U11 | Excessive discrepancies between prefabricated component design parameters and actual requirements |
| Number of design team experience on relevant projects U12 | Insufficient experience gained by the design team in similar projects in the field of assembled buildings | ||
| Number of design changes in prefabricated components U13 | Frequent changes and adjustments to the precast program | ||
| Construction rework rate after meetings and handovers U14 | Inadequate review and communication of drawings and technical requirements | ||
| Bidding and procurement phase U2 | Number of enterprises participating in the tender U21 | Insufficient number of firms participating in the bidding, which may result in insufficient competition for bids | |
| Scoring of suppliers’ and contractors’ qualifications U22 | Poor qualifications and credibility of suppliers and contractors do not guarantee the quality of projects | ||
| Acceptance rate of purchased materials U23 | Procurement and acceptance not in accordance with specifications | ||
| Production and transportation phase U3 | Immature technical specifications for component production U31 | Inadequate production technical specifications and reduced production efficiency | |
| Raw material quality and supply chain stability U32 | Delayed delivery of materials or components in the supply chain chain | ||
| Production equipment failure rate and utilization rate U33 | Frequent malfunctions in the use of production equipment | ||
| Average years of experience of production staff U34 | Insufficient relevant skills and experience of production personnel, affecting the accuracy of operations | ||
| Number of production meetings and time for communication and feedback U35 | Poor communication in the production chain, problems occur without timely feedback and resolution | ||
| Transportation damage rate U36 | Inadequate transportation planning resulting in damage to components during transportation | ||
| Compliance rate of stacking protection and handling measures U37 | Inadequate protection of components during stacking and handling, resulting in damage prior to assembly | ||
| On-site assembly construction phase U4 | Construction personnel training pass rate U41 | Low level of skills and training of construction personnel | |
| Assembly construction technology implementation compliance rate U42 | Non-compliance with technical specifications during construction, or imperfect technical standards | ||
| Unreasonable site plan U43 | Lack of scientific and systematic organization and planning of the construction site | ||
| Acceptance pass rate U44 | Unstandardized construction quality inspection and acceptance | ||
| Operation and maintenance phase U5 | Frequency of monitoring of facilities and maintenance of equipment U51 | Inadequate routine monitoring and periodic overhaul of project follow-up | |
| Troubleshooting capabilities of maintenance staff U52 | Inadequate ability of maintenance staff to resolve equipment or facility malfunctions |
| Rating | Grade Description | Probability Level Description | Consequence Level Description | Concealment Level Description | Score Range | Standard Cloud Digital Features |
|---|---|---|---|---|---|---|
| I | Risks are negligible | Hardly ever | Minor hazards | Easily recognized | [0, 3) | (1.5, 0.5, 0.05) |
| II | Risks are acceptable | Less likely | Lesser hazards | Easier recognized | [3, 6) | (4.5, 0.5, 0.05) |
| III | Acceptable after risk repair | Greater probability of occurrence | Greater hazards | Harder to recognize | [6, 8) | (7, 0.33, 0.033) |
| IV | Risks are unacceptable and must be rectified | High probability occurrence | Dreadful hazards | Extremely difficult to recognize | [8, 10] | (9, 0.33, 0.033) |
| Level 1 Indicators | Subjective Weighting | Objective Weighting | Combined Weighting | Level 2 Indicators | Subjective Weighting | Objective Weighting | Combined Weighting |
|---|---|---|---|---|---|---|---|
| U1 | 0.203 | 0.201 | 0.203 | U11 | 0.282 | 0.251 | 0.279 |
| U12 | 0.220 | 0.240 | 0.222 | ||||
| U13 | 0.244 | 0.263 | 0.246 | ||||
| U14 | 0.254 | 0.246 | 0.253 | ||||
| U2 | 0.208 | 0.191 | 0.204 | U21 | 0.301 | 0.307 | 0.302 |
| U22 | 0.326 | 0.349 | 0.328 | ||||
| U23 | 0.373 | 0.344 | 0.370 | ||||
| U3 | 0.210 | 0.225 | 0.213 | U31 | 0.179 | 0.131 | 0.174 |
| U32 | 0.207 | 0.153 | 0.202 | ||||
| U33 | 0.081 | 0.134 | 0.086 | ||||
| U34 | 0.093 | 0.160 | 0.100 | ||||
| U35 | 0.167 | 0.150 | 0.164 | ||||
| U36 | 0.136 | 0.119 | 0.134 | ||||
| U37 | 0.138 | 0.155 | 0.140 | ||||
| U4 | 0.215 | 0.196 | 0.211 | U41 | 0.252 | 0.239 | 0.251 |
| U42 | 0.244 | 0.236 | 0.243 | ||||
| U43 | 0.221 | 0.247 | 0.224 | ||||
| U44 | 0.283 | 0.278 | 0.282 | ||||
| U5 | 0.164 | 0.187 | 0.169 | U51 | 0.504 | 0.486 | 0.502 |
| U52 | 0.496 | 0.514 | 0.498 |
| Industry Expert | x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x9 | x10 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Risk Indicators | |||||||||||
| U11 | 5.5/5.4/3.4 | 4.3/5.5/4.0 | 4.3/5.4/3.4 | 5.8/5.8/4.1 | 4.7/5.5/3.3 | 4.8/4.9/3.5 | 5.6/5.2/3.4 | 5.9/5.7/3.0 | 5.0/5.0/4.4 | 4.1/6.0/4.5 | |
| U12 | 3.4/4.5/4.9 | 4.2/4.5/4.2 | 2.9/2.9/4.0 | 4.4/4.6/5.0 | 2.3/3.5/3.7 | 2.6/3.4/3.9 | 3.2/4.3/5.7 | 4.0/2.9/3.8 | 4.0/4.0/5.8 | 2.3/3.3/5.7 | |
| U13 | 6.8/7.5/7.0 | 5.8/7.1/6.2 | 6.1/5.8/6.6 | 7.1/5.2/7.0 | 6.0/7.5/6.7 | 5.9/6.0/5.3 | 5.8/5.6/6.3 | 7.2/5.5/5.5 | 6.5/7.5/6.3 | 7.3/7.3/8.2 | |
| U14 | 4.9/3.3/4.5 | 4.2/5.0/4.0 | 5.0/4.5/5.0 | 3.0/3.2/4.3 | 3.0/3.8/3.6 | 3.8/3.8/3.8 | 3.0/3.0/4.3 | 3.4/5.4/3.8 | 5.1/4.9/5.5 | 4.0/4.0/4.0 | |
| U21 | 4.0/5.0/4.8 | 5.1/4.5/3.9 | 5.1/5.2/4.5 | 3.4/4.8/4.6 | 3.3/4.8/4.6 | 3.3/5.0/4.0 | 4.3/5.1/4.2 | 5.0/5.2/4.4 | 4.5/5.0/4.2 | 4.0/5.5/4.0 | |
| U22 | 5.4/5.5/6.5 | 3.9/6.5/6.7 | 3.4/3.5/6.0 | 3.9/3.9/7.1 | 3.6/3.6/6.5 | 3.3/3.8/6.3 | 3.3/3.9/7.6 | 5.2/5.0/6.0 | 5.1/4.8/6.0 | 5.2/4.4/5.5 | |
| U23 | 4.9/5.5/4.0 | 3.3/5.0/2.3 | 4.9/4.0/3.4 | 2.9/4.5/2.7 | 3.2/3.9/4.3 | 3.3/3.7/2.8 | 3.0/3.9/3.0 | 4.8/5.2/4.2 | 5.0/5.2/4.1 | 3.4/4.5/2.5 | |
| U31 | 5.8/6.4/4.8 | 6.0/6.3/3.2 | 5.3/4.5/5.3 | 4.0/4.8/3.5 | 4.2/4.4/3.8 | 4.9/4.7/4.5 | 4.0/5.6/4.4 | 5.0/5.2/3.5 | 5.5/5.5/5.0 | 6.0/4.7/4.1 | |
| U32 | 7.4/8.0/7.6 | 7.2/7.5/8.0 | 7.0/6.7/7.0 | 6.7/6.8/6.9 | 6.5/6.5/6.9 | 7.6/7.0/7.5 | 7.3/6.5/7.8 | 6.9/8.6/7.2 | 7.0/7.5/7.4 | 8.0/7.8/7.5 | |
| U33 | 4.5/5.0/6.5 | 2.9/5.3/6.3 | 3.6/3.9/6.9 | 2.9/4.0/6.5 | 3.0/4.5/5.8 | 3.2/3.7/6.7 | 3.0/3.5/6.8 | 4.0/5.5/6.4 | 3.5/5.8/6.8 | 4.0/5.4/7.0 | |
| U34 | 4.0/5.1/4.6 | 4.4/5.5/4.3 | 2.5/4.1/3.9 | 3.5/3.3/4.4 | 3.5/4.4/3.5 | 3.1/3.4/4.5 | 3.3/4.7/4.3 | 3.8/5.4/4.5 | 4.2/6.0/5.0 | 4.4/6.2/4.0 | |
| U35 | 4.8/4.5/6.5 | 3.3/2.9/6.5 | 4.5/5.7/4.5 | 3.0/3.4/5.0 | 3.5/3.3/6.0 | 3.3/4.0/6.0 | 3.2/4.1/6.4 | 4.5/5.6/6.4 | 5.5/5.0/5.4 | 5.3/3.8/5.1 | |
| U36 | 3.5/5.4/3.1 | 3.8/5.2/3.8 | 4.2/4.3/4.0 | 3.2/3.8/2.7 | 2.9/4.0/2.2 | 2.2/3.9/1.7 | 2.9/3.1/2.5 | 2.5/4/2.2 | 3.7/5.0/3.5 | 3.0/6.0/2.5 | |
| U37 | 6.4/7.1/3.9 | 6.5/6.4/2.7 | 6.5/5.5/3.6 | 7.0/6.4/2.6 | 6.7/6.1/2.4 | 7.6/7.5/2.2 | 6.9/5.7/2.2 | 6.5/6.8/3.0 | 6.5/7.0/4.4 | 6.2/7.0/3.6 | |
| U41 | 2.8/6.0/4.5 | 4.4/5.1/2.7 | 2.1/4.5/2.5 | 2.2/5.0/2.5 | 2.2/4.8/2.8 | 2.8/4.3/3.2 | 2.9/4.2/3.9 | 3.8/5.0/4.1 | 4.4/5.5/4.5 | 3.5/4.0/4.5 | |
| U42 | 3.7/4.5/3.5 | 4.1/4.6/3.5 | 2.1/5.6/3.3 | 2.8/3.9/3.1 | 2.5/3.9/3.5 | 2.4/3.8/3.2 | 1.9/3.4/3.0 | 4.5/6.0/4.4 | 3.8/6.0/4.5 | 4.0/5.3/5.0 | |
| U43 | 4.7/4.5/4.6 | 4.5/5.0/3.1 | 3.2/4.8/3.3 | 4.1/4.2/3.5 | 3.1/4.2/4.0 | 3.8/3.5/3.6 | 3.1/4.2/3.1 | 4.0/4.8/4.0 | 4.5/5.0/4.0 | 5.3/3.2/4.3 | |
| U44 | 3.6/5.8/4.7 | 2.5/4.9/2.3 | 4.2/4.0/3.5 | 2.7/3.5/1.5 | 3.2/4.0/2.5 | 3.0/4.0/2.6 | 2.5/5.3/4.5 | 3.0/5.2/4.2 | 3.5/5.0/5.0 | 3.5/4.8/3.0 | |
| U51 | 2.3/5.2/4.0 | 2.5/3.8/3.7 | 2.7/3.7/3.1 | 1.8/3.0/2.9 | 2.0/3.5/3.3 | 2.5/2.8/2.7 | 2.1/5.4/3.2 | 3.0/4.5/4.0 | 2.7/4.4/3.8 | 2.0/4.6/2.8 | |
| U52 | 3.5/4.4/2.9 | 2.2/3.5/2.8 | 2.2/3.8/2.1 | 2.6/3.9/2.0 | 2.4/3.5/3.4 | 2.2/3.5/2.5 | 2.0/5.5/3.0 | 4.0/5.8/3.0 | 3.5/4.4/3.8 | 3.4/5.5/3.5 | |
| Composite Indicators | Probability | Result | Covert | Level 1 Indicators | Probability | Result | Covert | Level 2 Indicators | Probability | Result | Covert |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Quality risks throughout the assembly building process U | (4.00, 0.76, 0.26) | (4.83, 0.78, 0.22) | (4.25, 0.67, 0.24) | U1 | (4.72, 0.77, 0.25) | (4.99, 0.74, 0.30) | (4.75, 0.68, 0.29) | U11 | (5.00, 0.70, 0.22) | (5.44, 0.33, 0.11) | (3.7, 0.55, 0.21) |
| U12 | (3.33, 0.84, 0.28) | (3.79, 0.74, 0.31) | (4.67, 0.94, 0.40) | ||||||||
| U13 | (6.45, 0.66, 0.27) | (6.50, 1.10, 0.55) | (6.51, 0.74, 0.35) | ||||||||
| U14 | (3.94, 0.88.0.24) | (4.09, 0.86, 0.25) | (4.28, 0.55, 0.21) | ||||||||
| U2 | (4.09, 0.94, 0.40) | (4.67, 0.64, 0.14) | (4.64, 0.60, 0.23) | U21 | (4.20, 0.75, 0.21) | (5.01, 0.24, 0.13) | (4.32, 0.33, 0.12) | ||||
| U22 | (4.23, 1.00, 0.46) | (4.49, 0.96, 0.06) | (6.42, 0.58, 0.20) | ||||||||
| U23 | (3.87, 1.03, 0.51) | (4.54, 0.69, 0.22) | (3.33, 0.84, 0.34) | ||||||||
| U3 | (5.03, 0.64, 0.18) | (5.47, 0.84, 0.22) | (4.97, 0.62, 0.19) | U31 | (5.07, 0.81, 0.21) | (5.21, 0.74, 0.17) | (4.21, 0.74, 0.22) | ||||
| U32 | (7.16, 0.43, 0.11) | (7.29, 0.74, 0.22) | (7.38, 0.38, 0.06) | ||||||||
| U33 | (3.46, 0.58, 0.14) | (4.66, 0.93, 0.39) | (6.57, 0.34, 0.10) | ||||||||
| U34 | (3.67, 0.61, 0.06) | (4.81, 1.04, 0.24) | (4.30, 0.38, 0.18) | ||||||||
| U35 | (4.09, 1.04, 0.46) | (4.23, 0.97, 0.16) | (5.78, 0.78, 0.29) | ||||||||
| U36 | (3.19, 0.61, 0.04) | (4.47, 0.93, 0.28) | (2.82, 0.78, 0.20) | ||||||||
| U37 | (6.68, 0.37, 0.15) | (6.55, 0.66, 0.16) | (3.06, 0.82, 0.27) | ||||||||
| U4 | (3.35, 0.80, 0.22 | (4.64, 0.75, 0.22) | (3.58, 0.89, 0.31) | U41 | (3.11, 0.92, 0.28) | (4.84, 0.60, 0.12) | (3.52, 0.98, 0.46) | ||||
| U42 | (3.18, 1.05, 0.48) | (4.70, 1.03, 0.35) | (3.70, 0.70, 0.16) | ||||||||
| U43 | (4.03, 0.74, 0.08) | (4.34, 0.60, 0.12) | (3.75, 0.54, 0.17) | ||||||||
| U44 | (3.17, 0.54, 0.05) | (4.65, 0.78, 0.26) | (3.38, 1.25, 0.42) | ||||||||
| U5 | (2.58, 0.60, 0.23) | (4.23, 0.92, 0.23) | (3.13, 0.54, 0.19) | U51 | (2.36, 0.40, 0.12) | (4.09, 0.91, 0.26) | (3.35, 0.53, 0.19) | ||||
| U52 | (2.80, 0.80, 0.35) | (4.38, 0.93, 0.19) | (2.90, 0.55, 0.19) |
| Risk Class | I | II | III | IV | Level of Affiliation | |
|---|---|---|---|---|---|---|
| Evaluation Indicators | ||||||
| U | 0.200 | 1.559 | 0.217 | 0.124 | II | |
| U1 | 0.174 | 1.679 | 0.265 | 0.138 | II | |
| U2 | 0.194 | 2.143 | 0.227 | 0.127 | II | |
| U3 | 0.158 | 0.833 | 0.311 | 0.150 | II | |
| U4 | 0.238 | 0.675 | 0.181 | 0.112 | II | |
| U5 | 0.298 | 0.421 | 0.154 | 0.101 | II | |
| U11 | 0.175 | 0.751 | 0.240 | 0.133 | II | |
| U12 | 0.232 | 0.725 | 0.185 | 0.113 | II | |
| U13 | 0.116 | 0.291 | 1.123 | 0.230 | III | |
| U14 | 0.221 | 1.373 | 0.199 | 0.118 | II | |
| U21 | 0.190 | 1.617 | 0.230 | 0.128 | II | |
| U22 | 0.157 | 0.516 | 0.264 | 0.142 | II | |
| U23 | 0.234 | 0.752 | 0.185 | 0.113 | II | |
| U31 | 0.172 | 1.047 | 0.261 | 0.138 | II | |
| U32 | 0.100 | 0.208 | 1.984 | 0.335 | III | |
| U33 | 0.159 | 0.431 | 0.234 | 0.134 | II | |
| U34 | 0.206 | 1.101 | 0.208 | 0.121 | II | |
| U35 | 0.175 | 0.729 | 0.238 | 0.132 | II | |
| U36 | 0.273 | 0.469 | 0.161 | 0.104 | II | |
| U37 | 0.135 | 0.301 | 0.251 | 0.146 | II | |
| U41 | 0.237 | 0.577 | 0.177 | 0.110 | II | |
| U42 | 0.236 | 0.643 | 0.180 | 0.111 | II | |
| U43 | 0.226 | 1.112 | 0.194 | 0.116 | II | |
| U44 | 0.248 | 0.573 | 0.173 | 0.109 | II | |
| U51 | 0.303 | 0.406 | 0.152 | 0.100 | II | |
| U52 | 0.289 | 0.428 | 0.156 | 0.102 | II | |
| Risk Class | I | II | III | IV | Level of Affiliation | |
|---|---|---|---|---|---|---|
| Evaluation Indicators | ||||||
| U | 0.240 | 1.688 | 0.270 | 0.154 | II | |
| U1 | 0.211 | 1.856 | 0.329 | 0.171 | II | |
| U2 | 0.245 | 2.251 | 0.268 | 0.153 | II | |
| U3 | 0.188 | 0.906 | 0.401 | 0.188 | II | |
| U4 | 0.274 | 0.863 | 0.230 | 0.140 | II | |
| U5 | 0.340 | 0.516 | 0.192 | 0.125 | II | |
| U11 | 0.190 | 0.939 | 0.394 | 0.187 | II | |
| U12 | 0.341 | 0.731 | 0.205 | 0.130 | II | |
| U13 | 0.142 | 0.358 | 1.345 | 0.280 | III | |
| U14 | 0.281 | 1.441 | 0.237 | 0.142 | II | |
| U21 | 0.226 | 1.690 | 0.291 | 0.160 | II | |
| U22 | 0.247 | 3.701 | 0.268 | 0.152 | II | |
| U23 | 0.259 | 1.584 | 0.251 | 0.147 | II | |
| U31 | 0.194 | 1.098 | 0.380 | 0.183 | II | |
| U32 | 0.124 | 0.259 | 3.019 | 0.398 | III | |
| U33 | 0.269 | 0.950 | 0.236 | 0.142 | II | |
| U34 | 0.253 | 1.129 | 0.251 | 0.147 | II | |
| U35 | 0.266 | 2.037 | 0.249 | 0.146 | II | |
| U36 | 0.293 | 0.763 | 0.219 | 0.136 | II | |
| U37 | 0.138 | 0.334 | 1.811 | 0.296 | III | |
| U41 | 0.270 | 0.699 | 0.225 | 0.139 | II | |
| U42 | 0.277 | 0.749 | 0.224 | 0.138 | II | |
| U43 | 0.263 | 2.014 | 0.251 | 0.147 | II | |
| U44 | 0.280 | 0.747 | 0.223 | 0.137 | II | |
| U51 | 0.459 | 0.366 | 0.183 | 0.121 | I | |
| U52 | 0.316 | 0.587 | 0.202 | 0.129 | II | |
| Evaluation Methodology | U | Decision-Making Design Phase U1 | Bidding and Procurement Phase U2 | Production and Transportation Phase U3 | On-Site Assembly Construction Phase U4 | Operation and Maintenance Phase U5 | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2D cloud model | II | II | II | II | II | II | ||||||||||||||
| 3D cloud model | II | II | II | II | II | II | ||||||||||||||
| U11 | U12 | U13 | U14 | U21 | U22 | U23 | U31 | U32 | U33 | U34 | U35 | U36 | U37 | U41 | U42 | U43 | U44 | U51 | U52 | |
| 2D cloud model | II | II | III | II | II | II | II | II | III | II | II | II | II | III | II | II | II | II | I | II |
| 3D cloud model | II | II | III | II | II | II | II | II | III | II | II | II | II | II | II | II | II | II | II | II |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Q.; Ye, Z.; Wei, X.; Wang, Z.; Li, D. Quality Risk Evaluation of the Whole Process of Assembly Building Based on Game Theory-Combinatorial Empowerment and Three-Dimensional Cloud Modeling. Appl. Sci. 2025, 15, 3417. https://doi.org/10.3390/app15073417
Sun Q, Ye Z, Wei X, Wang Z, Li D. Quality Risk Evaluation of the Whole Process of Assembly Building Based on Game Theory-Combinatorial Empowerment and Three-Dimensional Cloud Modeling. Applied Sciences. 2025; 15(7):3417. https://doi.org/10.3390/app15073417
Chicago/Turabian StyleSun, Qiao, Ziyang Ye, Xin Wei, Zecheng Wang, and Dongwei Li. 2025. "Quality Risk Evaluation of the Whole Process of Assembly Building Based on Game Theory-Combinatorial Empowerment and Three-Dimensional Cloud Modeling" Applied Sciences 15, no. 7: 3417. https://doi.org/10.3390/app15073417
APA StyleSun, Q., Ye, Z., Wei, X., Wang, Z., & Li, D. (2025). Quality Risk Evaluation of the Whole Process of Assembly Building Based on Game Theory-Combinatorial Empowerment and Three-Dimensional Cloud Modeling. Applied Sciences, 15(7), 3417. https://doi.org/10.3390/app15073417






