A Comparative Analysis of Hyper-Parameter Optimization Methods for Predicting Heart Failure Outcomes
Abstract
1. Introduction
- The Support Vector Machine, Random Forest, and eXtreme Gradient Boosting algorithms were used to evaluate and compare the effectiveness of the Grid, Random, and Bayesian search methods in determining the ideal configuration for optimizing the performance of a model.
- The robustness of the proposed models was examined through comprehensive 10-fold cross-validation.
2. Materials and Methods
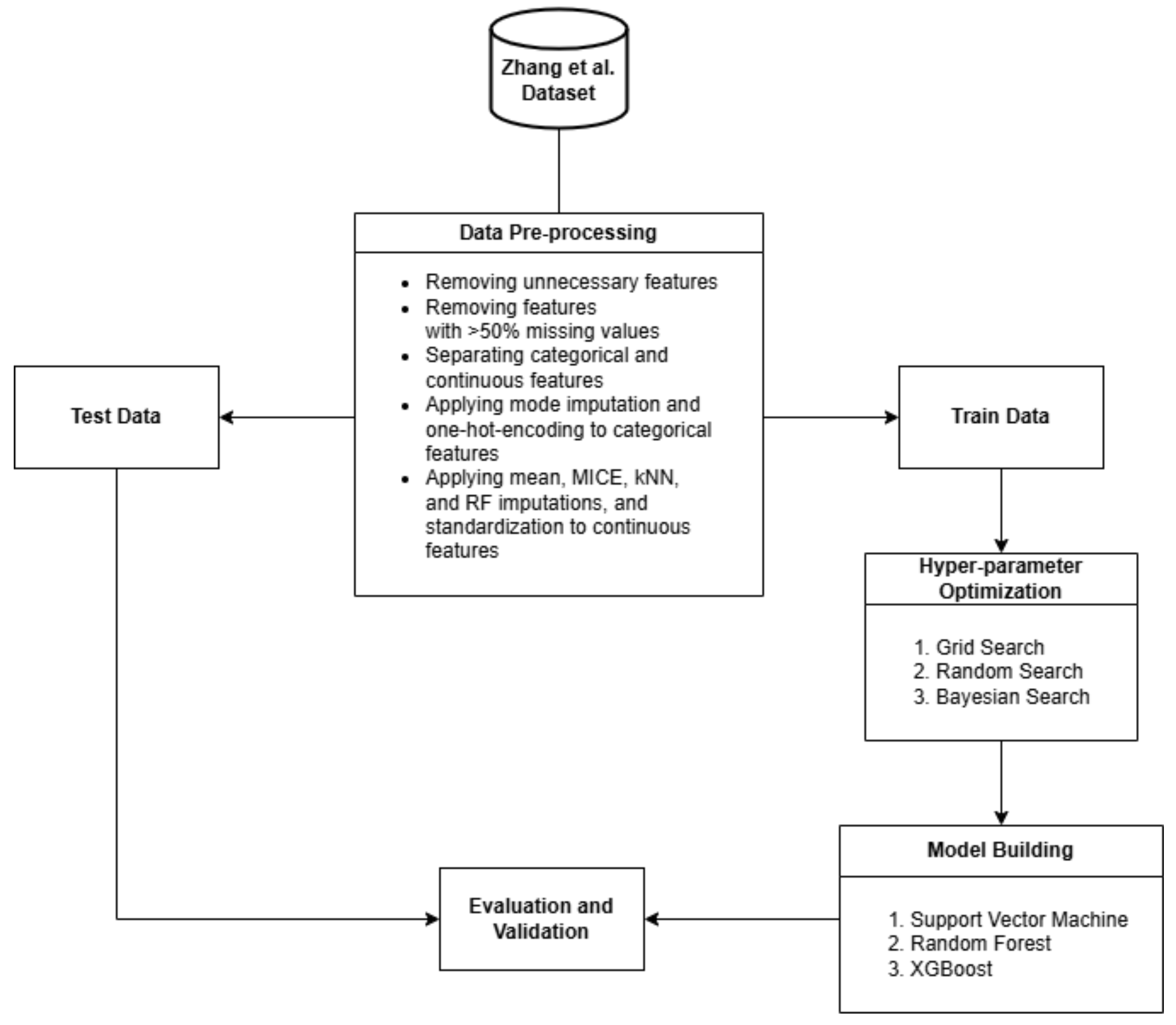
2.1. Dataset
2.2. Preprocessing
2.3. Hyper-Parameter Optimization
2.3.1. Grid Search and Randomized Search
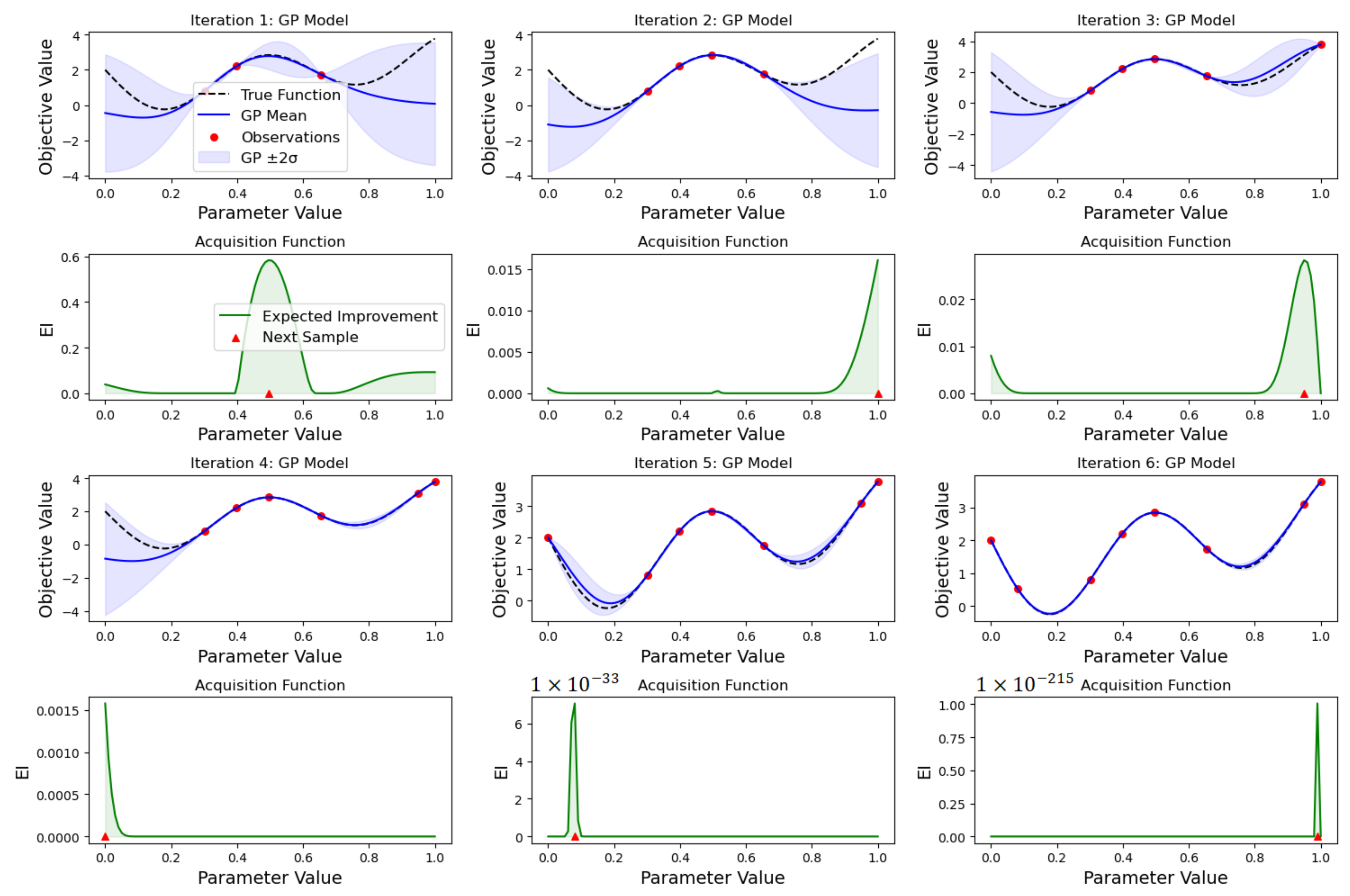
2.3.2. Bayesian Search
- Sampling the objective function at a few initial points.
- Using the initial samples to build a surrogate model of the objective function.
- Defining an acquisition function that uses the surrogate model to determine the next point to evaluate.
- Evaluating the objective function at the point suggested by the acquisition function.
- Updating the surrogate model with the new data point.
- Repeating steps 3–5 until a stopping criterion is met.
2.4. Model Building
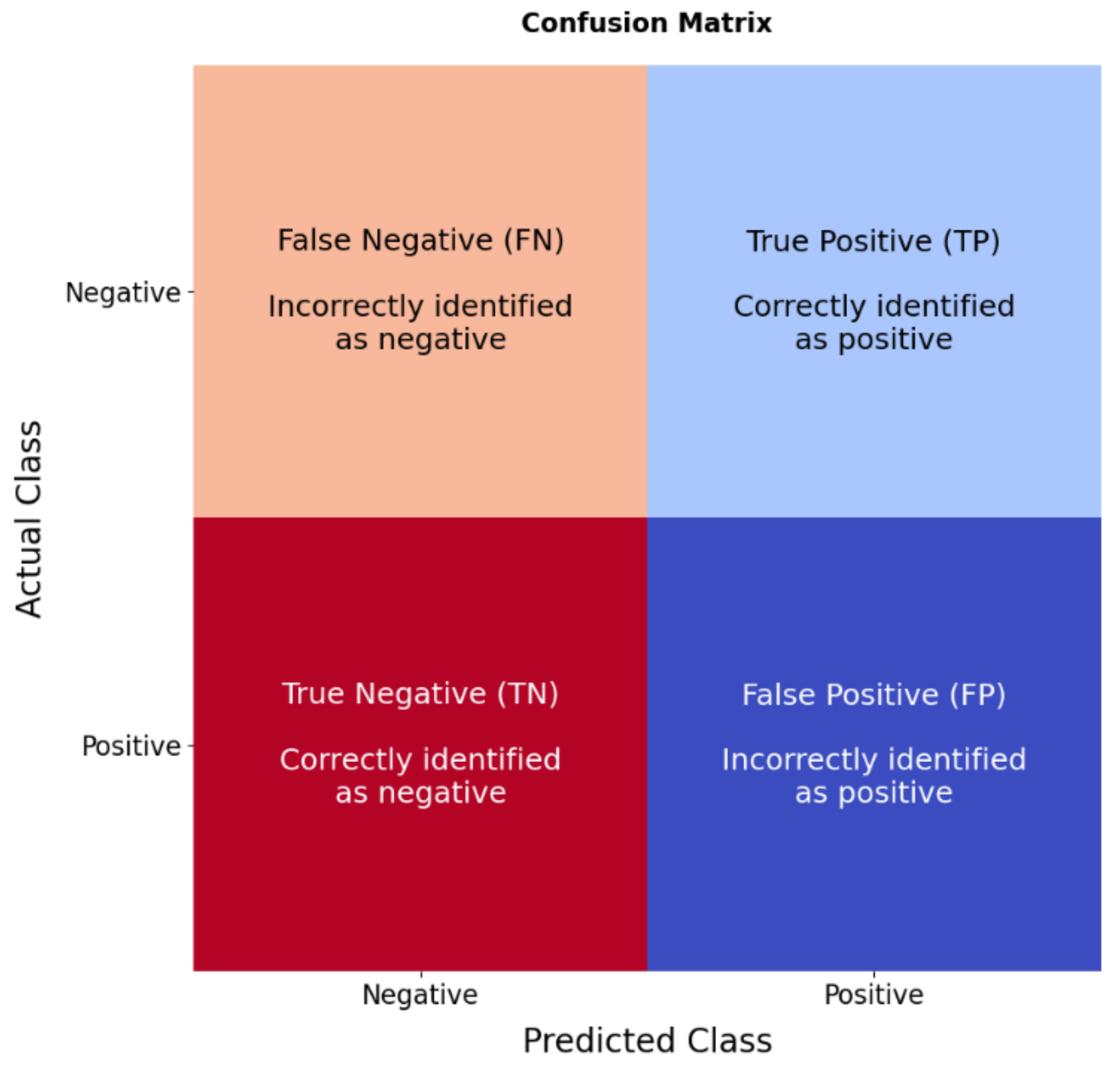
2.5. Model Evaluation
3. Results
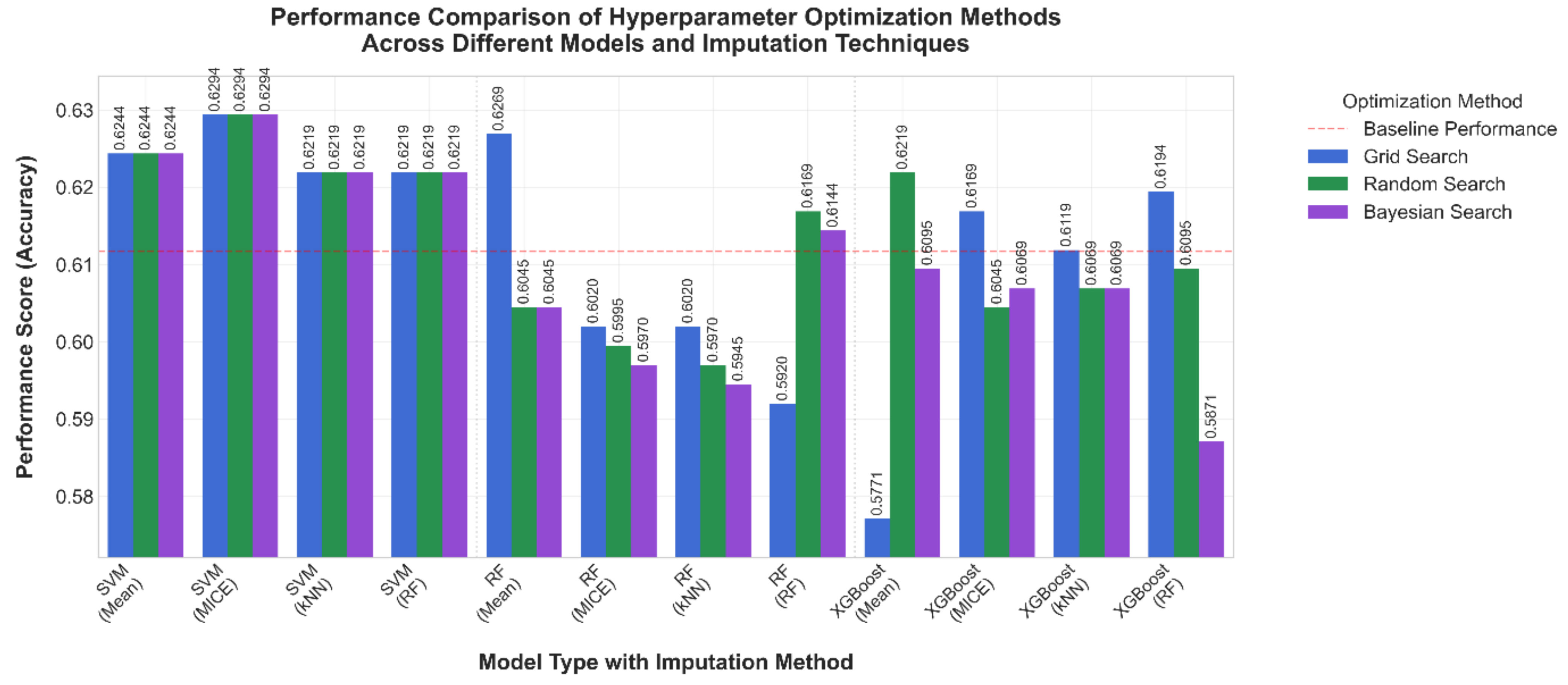
3.1. Comparative Results
3.2. Comparison After 10-Fold Cross Validation
3.3. Optimized Hyper-Parameter
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Khan, M.S.; Shahid, I.; Bennis, A.; Rakisheva, A.; Metra, M.; Butler, J. Global Epidemiology of Heart Failure. Nat. Rev. Cardiol. 2024, 21, 717–734. [Google Scholar] [CrossRef] [PubMed]
- Zhao, H.; Liu, Z.; Li, M.; Liang, L. Optimal Monitoring Policies for Chronic Diseases under Healthcare Warranty. Socio-Econ. Plan. Sci. 2022, 84, 101384. [Google Scholar] [CrossRef]
- Badawy, M.; Ramadan, N.; Hefny, H.A. Healthcare Predictive Analytics Using Machine Learning and Deep Learning Techniques: A Survey. J. Electr. Syst. Inf. Technol. 2023, 10, 40. [Google Scholar] [CrossRef]
- Landicho, J.A.; Esichaikul, V.; Sasil, R.M. Comparison of Predictive Models for Hospital Readmission of Heart Failure Patients with Cost-Sensitive Approach. Int. J. Healthc. Manag. 2021, 14, 1536–1541. [Google Scholar] [CrossRef]
- Plati, D.K.; Tripoliti, E.E.; Bechlioulis, A.; Rammos, A.; Dimou, I.; Lakkas, L.; Watson, C.; McDonald, K.; Ledwidge, M.; Pharithi, R.; et al. A Machine Learning Approach for Chronic Heart Failure Diagnosis. Diagnostics 2021, 11, 1863. [Google Scholar] [CrossRef]
- Li, F.; Xin, H.; Zhang, J.; Fu, M.; Zhou, J.; Lian, Z. Prediction Model of In-hospital Mortality in Intensive Care Unit Patients with Heart Failure: Machine Learning-Based, Retrospective Analysis of the MIMIC-III Database. BMJ Open 2021, 11, e044779. [Google Scholar] [CrossRef]
- Bischl, B.; Binder, M.; Lang, M.; Pielok, T.; Richter, J.; Coors, S.; Thomas, J.; Ullmann, T.; Becker, M.; Boulesteix, A.; et al. Hyperparameter Optimization: Foundations, Algorithms, Best Practices, and Open Challenges. WIREs Data Min. Knowl. 2023, 13, e1484. [Google Scholar] [CrossRef]
- Fernando, T.; Gammulle, H.; Denman, S.; Sridharan, S.; Fookes, C. Deep Learning for Medical Anomaly Detection—A Survey. ACM Comput. Surv. 2022, 54, 3464423. [Google Scholar] [CrossRef]
- Patil, S.; Bhosale, S. Hyperparameter Tuning Based Performance Analysis of Machine Learning Approaches for Prediction of Cardiac Complications. In Proceedings of the 12th International Conference on Soft Computing and Pattern Recognition (SoCPaR 2020), Virtual, 15–18 December 2020; Advances in Intelligent Systems and Computing. Abraham, A., Ohsawa, Y., Gandhi, N., Jabbar, M.A., Haqiq, A., McLoone, S., Issac, B., Eds.; Springer International Publishing: Cham, Switzerland, 2021; Volume 1383, pp. 605–617, ISBN 978-3-030-73688-0. [Google Scholar]
- Firdaus, F.F.; Nugroho, H.A.; Soesanti, I. Deep Neural Network with Hyperparameter Tuning for Detection of Heart Disease. In Proceedings of the 2021 IEEE Asia Pacific Conference on Wireless and Mobile (APWiMob), Bandung, Indonesia, 8 April 2021; pp. 59–65. [Google Scholar]
- Belete, D.M.; Huchaiah, M.D. Grid Search in Hyperparameter Optimization of Machine Learning Models for Prediction of HIV/AIDS Test Results. Int. J. Comput. Appl. 2022, 44, 875–886. [Google Scholar] [CrossRef]
- Asif, D.; Bibi, M.; Arif, M.S.; Mukheimer, A. Enhancing Heart Disease Prediction through Ensemble Learning Techniques with Hyperparameter Optimization. Algorithms 2023, 16, 308. [Google Scholar] [CrossRef]
- Valarmathi, R.; Sheela, T. Heart Disease Prediction Using Hyper Parameter Optimization (HPO) Tuning. Biomed. Signal Process. Control 2021, 70, 103033. [Google Scholar] [CrossRef]
- Sharma, N.; Malviya, L.; Jadhav, A.; Lalwani, P. A Hybrid Deep Neural Net Learning Model for Predicting Coronary Heart Disease Using Randomized Search Cross-Validation Optimization. Decis. Anal. J. 2023, 9, 100331. [Google Scholar] [CrossRef]
- Gao, L.; Ding, Y. Disease Prediction via Bayesian Hyperparameter Optimization and Ensemble Learning. BMC Res. Notes 2020, 13, 205. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Wu, Y.; Wu, H. Machine Learning Enabled 3D Body Measurement Estimation Using Hybrid Feature Selection and Bayesian Search. Appl. Sci. 2022, 12, 7253. [Google Scholar] [CrossRef]
- Zhang, Z.; Cao, L.; Chen, R.; Zhao, Y.; Lv, L.; Xu, Z.; Xu, P. Electronic Healthcare Records and External Outcome Data for Hospitalized Patients with Heart Failure. Sci. Data 2021, 8, 46. [Google Scholar] [CrossRef]
- Zhang, Z.; Cao, L.; Zhao, Y.; Xu, Z.; Chen, R.; Lv, L.; Xu, P. Hospitalized Patients with Heart Failure: Integrating Electronic Healthcare Records and External Outcome Data. PhysioNet 2020, 101, e215–e220. [Google Scholar] [CrossRef]
- Hidayaturrohman, Q.A.; Hanada, E. Impact of Data Pre-Processing Techniques on XGBoost Model Performance for Predicting All-Cause Readmission and Mortality Among Patients with Heart Failure. BioMedInformatics 2024, 4, 2201–2212. [Google Scholar] [CrossRef]
- Psychogyios, K.; Ilias, L.; Ntanos, C.; Askounis, D. Missing Value Imputation Methods for Electronic Health Records. IEEE Access 2023, 11, 21562–21574. [Google Scholar] [CrossRef]
- Dahouda, M.K.; Joe, I. A Deep-Learned Embedding Technique for Categorical Features Encoding. IEEE Access 2021, 9, 114381–114391. [Google Scholar] [CrossRef]
- Sinsomboonthong, S. Performance Comparison of New Adjusted Min-Max with Decimal Scaling and Statistical Column Normalization Methods for Artificial Neural Network Classification. Int. J. Math. Math. Sci. 2022, 2022, 3584406. [Google Scholar] [CrossRef]
- Pei, X.; Zhao, Y.H.; Chen, L.; Guo, Q.; Duan, Z.; Pan, Y.; Hou, H. Robustness of Machine Learning to Color, Size Change, Normalization, and Image Enhancement on Micrograph Datasets with Large Sample Differences. Mater. Des. 2023, 232, 112086. [Google Scholar] [CrossRef]
- Pfob, A.; Lu, S.-C.; Sidey-Gibbons, C. Machine Learning in Medicine: A Practical Introduction to Techniques for Data Pre-Processing, Hyperparameter Tuning, and Model Comparison. BMC Med. Res. Methodol. 2022, 22, 282. [Google Scholar] [CrossRef] [PubMed]
- Priyadarshini, I.; Cotton, C. A Novel LSTM–CNN–Grid Search-Based Deep Neural Network for Sentiment Analysis. J Supercomput. 2021, 77, 13911–13932. [Google Scholar] [CrossRef] [PubMed]
- Bergstra, J.; Bengio, Y. Random Search for Hyper-Parameter Optimization. J. Mach. Learn. Res. 2012, 13, 281–305. [Google Scholar]
- Ali, Y.; Awwad, E.; Al-Razgan, M.; Maarouf, A. Hyperparameter Search for Machine Learning Algorithms for Optimizing the Computational Complexity. Processes 2023, 11, 349. [Google Scholar] [CrossRef]
- Tunçel, M.; Duran, A. Effectiveness of Grid and Random Approaches for a Model Parameter Vector Optimization. J. Comput. Sci. 2023, 67, 101960. [Google Scholar] [CrossRef]
- Bahan Pal, J.; Mj, D. Improving Multi-Scale Attention Networks: Bayesian Optimization for Segmenting Medical Images. Imaging Sci. J. 2023, 71, 33–49. [Google Scholar] [CrossRef]
- Hidayaturrohman, Q.A.; Hanada, E. Predictive Analytics in Heart Failure Risk, Readmission, and Mortality Prediction: A Review. Cureus 2024, 16, e73876. [Google Scholar] [CrossRef]
- Hearst, M.A.; Dumais, S.T.; Osuna, E.; Platt, J.; Scholkopf, B. Support Vector Machines. IEEE Intell. Syst. Their Appl. 1998, 13, 18–28. [Google Scholar] [CrossRef]
- Chen, Y.; Mao, Q.; Wang, B.; Duan, P.; Zhang, B.; Hong, Z. Privacy-Preserving Multi-Class Support Vector Machine Model on Medical Diagnosis. IEEE J. Biomed. Health Inform. 2022, 26, 3342–3353. [Google Scholar] [CrossRef]
- Manzali, Y.; Elfar, M. Random Forest Pruning Techniques: A Recent Review. Oper. Res. Forum 2023, 4, 43. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-Learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13 August 2016; pp. 785–794.
- Vujovic, Ž.Ð. Classification Model Evaluation Metrics. Int. J. Adv. Comput. Sci. Appl. 2021, 12, 599–606. [Google Scholar] [CrossRef]
- Ali, M.M.; Paul, B.K.; Ahmed, K.; Bui, F.M.; Quinn, J.M.W.; Moni, M.A. Heart Disease Prediction Using Supervised Machine Learning Algorithms: Performance Analysis and Comparison. Comput. Biol. Med. 2021, 136, 104672. [Google Scholar] [CrossRef]
- Zhang, Y.; Gao, Z.; Wittrup, E.; Gryak, J.; Najarian, K. Increasing Efficiency of SVMp+ for Handling Missing Values in Healthcare Prediction. PLoS Digit. Health 2023, 2, e0000281. [Google Scholar] [CrossRef]
- Chen, S.; Hu, W.; Yang, Y.; Cai, J.; Luo, Y.; Gong, L.; Li, Y.; Si, A.; Zhang, Y.; Liu, S.; et al. Predicting Six-Month Re-Admission Risk in Heart Failure Patients Using Multiple Machine Learning Methods: A Study Based on the Chinese Heart Failure Population Database. J. Clin. Med. 2023, 12, 870. [Google Scholar] [CrossRef]
- Bates, S.; Hastie, T.; Tibshirani, R. Cross-Validation: What Does It Estimate and How Well Does It Do It? J. Am. Stat. Assoc. 2024, 119, 1434–1445. [Google Scholar] [CrossRef]
- Lasfar, R.; Tóth, G. The Difference of Model Robustness Assessment Using Cross-validation and Bootstrap Methods. J. Chemom. 2024, 38, e3530. [Google Scholar] [CrossRef]


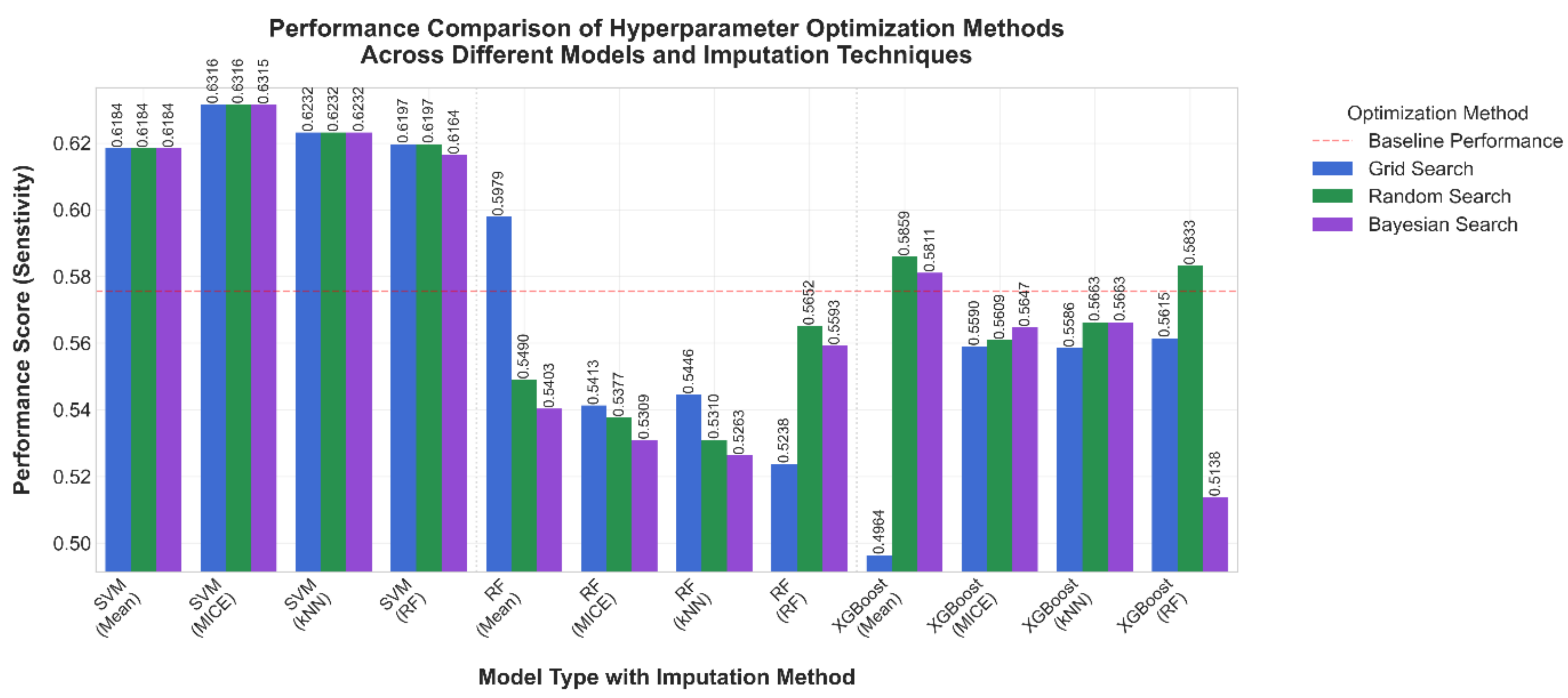
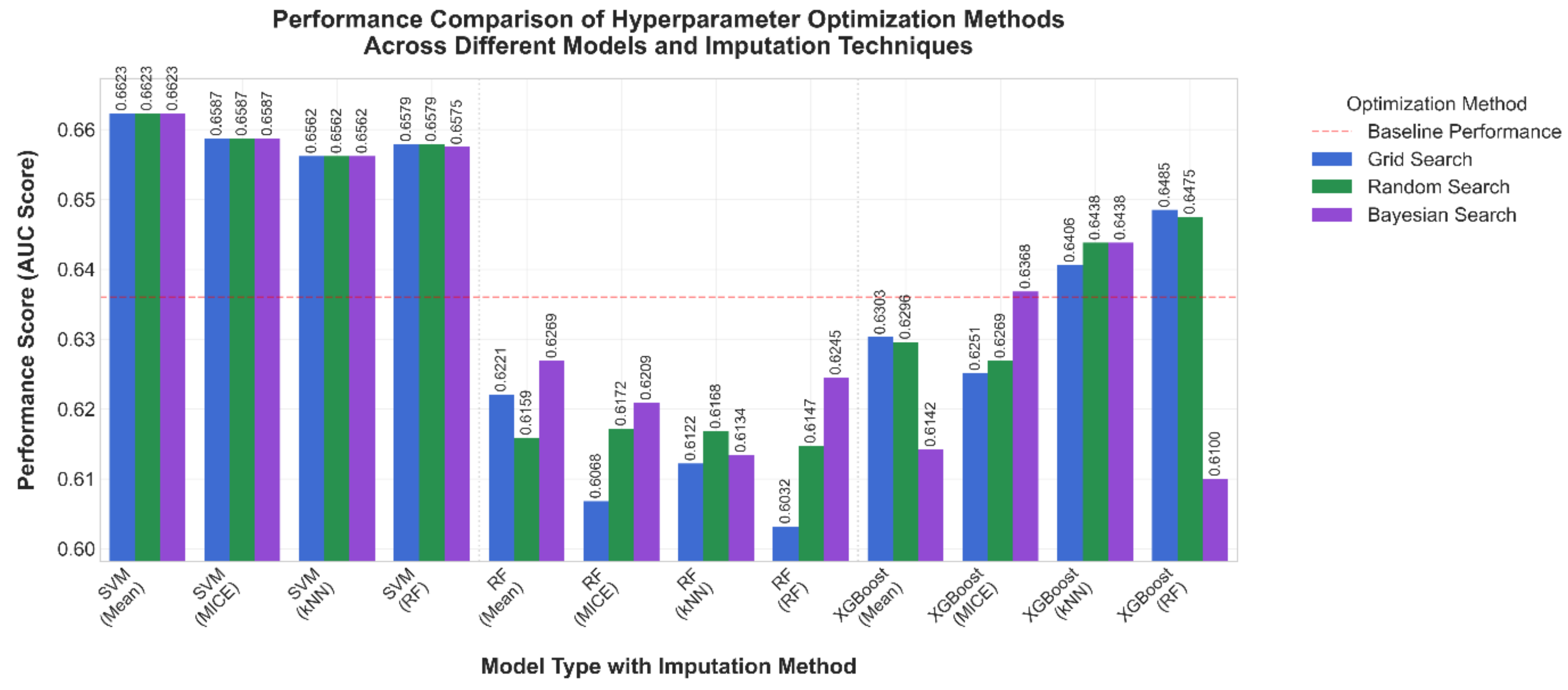
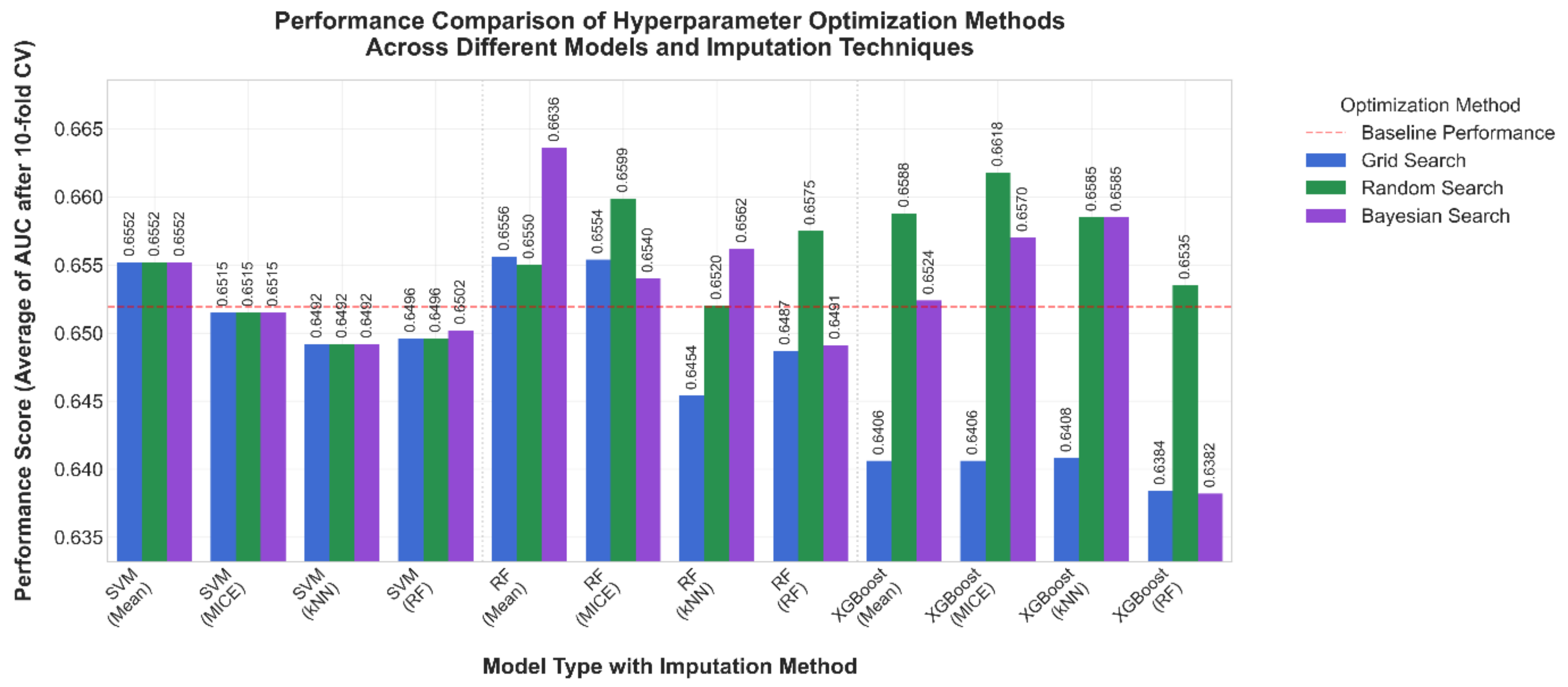
| Algorithm | Hyper-Parameter | Values |
|---|---|---|
| Support Vector Machine | C | 0.1, 1.0, 10, 100, 1000 |
| Gamma | 1, 0.1, 0.01, 0.001, 0.0001, auto, scale | |
| Kernel | Linear, RBF, Sigmoid | |
| Random Forest | Bootstrap | True, False |
| Max depth | 10, 20, 30, None | |
| Max feature | 2, 3 | |
| Min samples leaf | 3, 4, 5 | |
| Min sample split | 2, 5, 10 | |
| N-estimators | 100, 200, 300, 500 | |
| XGBoost | Max depth | 3, 5, 7, 10 |
| Learning rate | 0.2, 0.15, 0.1, 0.01, 0.001 | |
| Subsample | 0.5, 0.7, 1.0 | |
| N-estimators | 50, 100, 150, 200, 300 | |
| Colsample bytree | 0.5, 0.7, 1.0 |
| Model | Optimized Parameters | |||
|---|---|---|---|---|
| Algorithm | Imputation | Grid Search | Random Search | Bayesian Search |
| SVM | Mean | C = 1; gamma = 0.01; kernel = RBF | C = 1; gamma = 0.01; kernel = RBF | C = 1; gamma = 0.01; kernel = RBF |
| MICE | C = 1; gamma = 0.01; kernel = RBF | C = 1; gamma = 0.01; kernel = RBF | C = 1; gamma = 0.01; kernel = RBF | |
| kNN | C = 1; gamma = auto; kernel = RBF | C = 1; gamma = auto; kernel = RBF | C = 1; gamma = auto; kernel = RBF | |
| RF | C = 1; gamma = 0.01; kernel = RBF | C = 1; gamma = 0.01; kernel = RBF | C = 1; gamma = 0.01; kernel = RBF | |
| RF | Mean | bootstrap = True; max depth = 20; max feature = 3; min samples leaf = 3; min samples split = 5; n_estimators = 300 | bootstrap = False; max depth = 20; max features = 3; min samples leaf = 3; min samples split = 5; n_estimators = 200 | bootstrap = False; max depth = 20; max features = 3; min samples leaf = 4; min samples split = 5; n_estimators = 300 |
| MICE | bootstrap = True; max depth = 20; max feature = 3; min samples leaf = 4; min samples split = 10; n_estimators = 300 | bootstrap = True; max depth = None; max features = 3; min samples leaf = 3; min samples split = 10; n_estimators = 300 | bootstrap = False; max depth = 20; max features = 3; min samples leaf = 3; min samples split = 2; n_estimators = 200 | |
| kNN | bootstrap = True; max depth = 20; max feature = 2; min samples leaf = 3; min samples split = 10; n_estimators = 300 | bootstrap = False; max depth = 20; max features = 3; min samples leaf = 4; min samples split = 10; n_estimators = 500 | bootstrap = False; max depth = 20; max features = 3; min samples leaf = 4; min samples split = 2; n_estimators = 300 | |
| RF | bootstrap = True; max depth = 20; max feature = 2; min samples leaf = 3; min samples split = 5; n_estimators = 300 | bootstrap = False; max depth = None; max feature = 2; min samples leaf = 3; min samples split = 5; n_estimators = 200 | bootstrap = False; max depth = 30; max feature = 3; min samples leaf = 5; min samples split = 10; n_estimators = 300 | |
| XGBoost | Mean | learning rate = 0.2; max depth = 7; subsample = 1; colsample_bytree = 1; n_estimators = 100 | learning rate = 0.01; max depth = 10; subsample = 0.7; colsample_bytree = 0.7; n_estimators = 300 | learning rate = 0.01; max depth = 7; subsample = 0.7; colsample_bytree = 0.5; n_estimators = 150 |
| MICE | learning rate = 0.15; max depth = 7; subsample = 0.5; colsample_bytree = 1; n_estimators = 100 | learning rate = 0.01; max depth = 10; subsample = 0.7; colsample_bytree = 1; n_estimators = 300 | learning rate = 0.01; max depth = 10; subsample = 0.7; colsample_bytree = 0.5; n_estimators = 300 | |
| kNN | learning rate = 0.1; max depth = 7; subsample = 0.5; colsample_bytree = 1; n_estimators = 100 | learning rate = 0.01; max depth = 10; subsample = 0.5; colsample_bytree = 1; n_estimators = 300 | learning rate = 0.01; max depth = 10; subsample = 0.5; colsample_bytree = 1; n_estimators = 300 | |
| RF | learning rate = 0.1; max depth = 5; subsample = 1; colsample_bytree = 1; n_estimators = 100 | learning rate = 0.01; max depth = 7; subsample = 0.5; colsample_bytree = 0.7; n_estimators = 200 | learning rate = 0.1; max depth = 5; subsample = 0.7; colsample_bytree = 0.7; n_estimators = 50 | |
| Optimization Method | Algorithm | Average Processing Time per Model (Min) |
|---|---|---|
| Grid Search | SVM | 12 |
| RF | 7 | |
| XGBoost | 6 | |
| Random Search | SVM | 10 |
| RF | 6.5 | |
| XGBoost | 6 | |
| Bayesian Search | SVM | 7 |
| RF | 5.3 | |
| XGBoost | 4.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hidayaturrohman, Q.A.; Hanada, E. A Comparative Analysis of Hyper-Parameter Optimization Methods for Predicting Heart Failure Outcomes. Appl. Sci. 2025, 15, 3393. https://doi.org/10.3390/app15063393
Hidayaturrohman QA, Hanada E. A Comparative Analysis of Hyper-Parameter Optimization Methods for Predicting Heart Failure Outcomes. Applied Sciences. 2025; 15(6):3393. https://doi.org/10.3390/app15063393
Chicago/Turabian StyleHidayaturrohman, Qisthi Alhazmi, and Eisuke Hanada. 2025. "A Comparative Analysis of Hyper-Parameter Optimization Methods for Predicting Heart Failure Outcomes" Applied Sciences 15, no. 6: 3393. https://doi.org/10.3390/app15063393
APA StyleHidayaturrohman, Q. A., & Hanada, E. (2025). A Comparative Analysis of Hyper-Parameter Optimization Methods for Predicting Heart Failure Outcomes. Applied Sciences, 15(6), 3393. https://doi.org/10.3390/app15063393






