Solar Irradiance Mitigation in LEO Optical Inter-Satellite Links via Inter-Shell Based Path Optimization
Abstract
1. Introduction
2. System Modeling
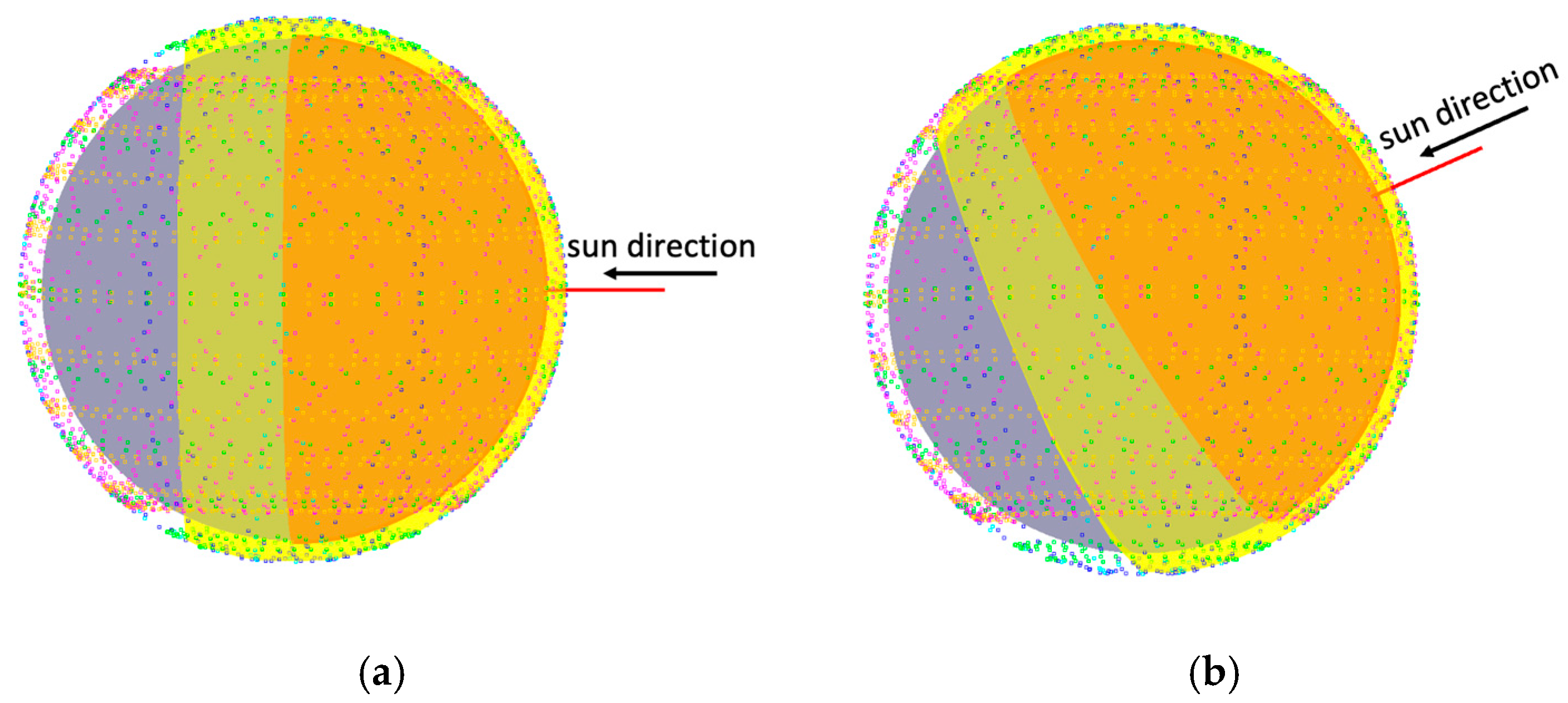
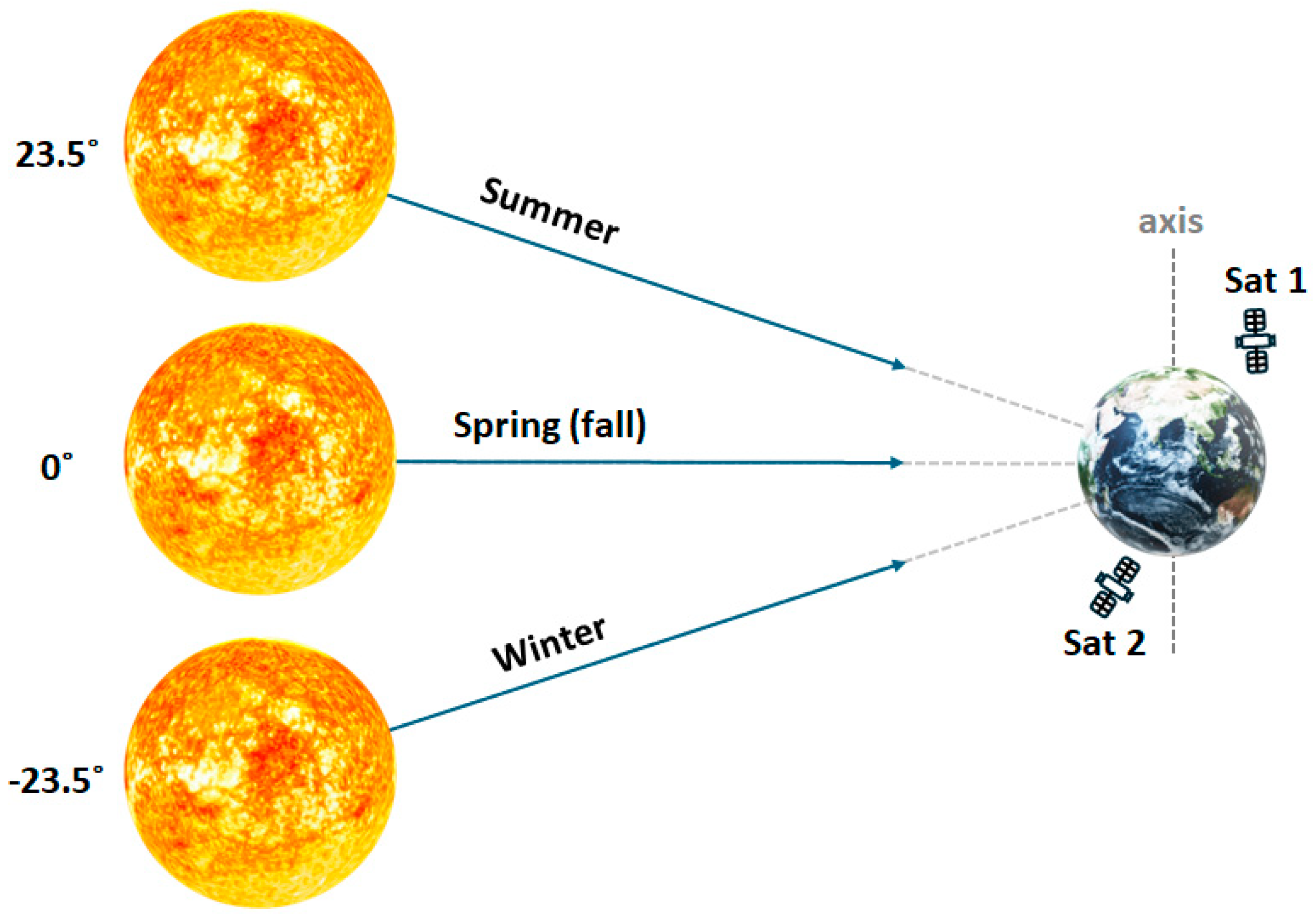
2.1. Solar Irradiance: Theoretical Approach
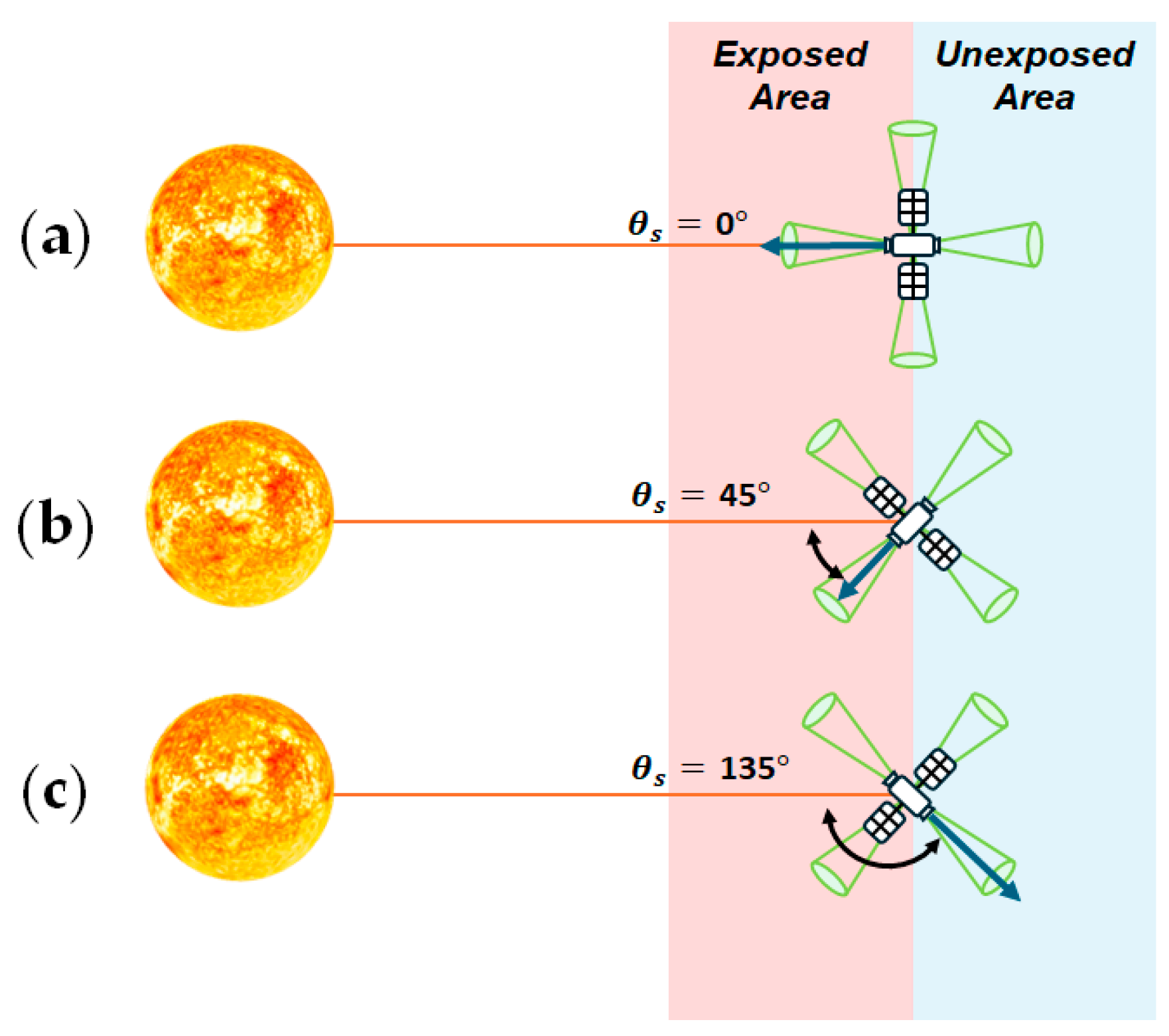
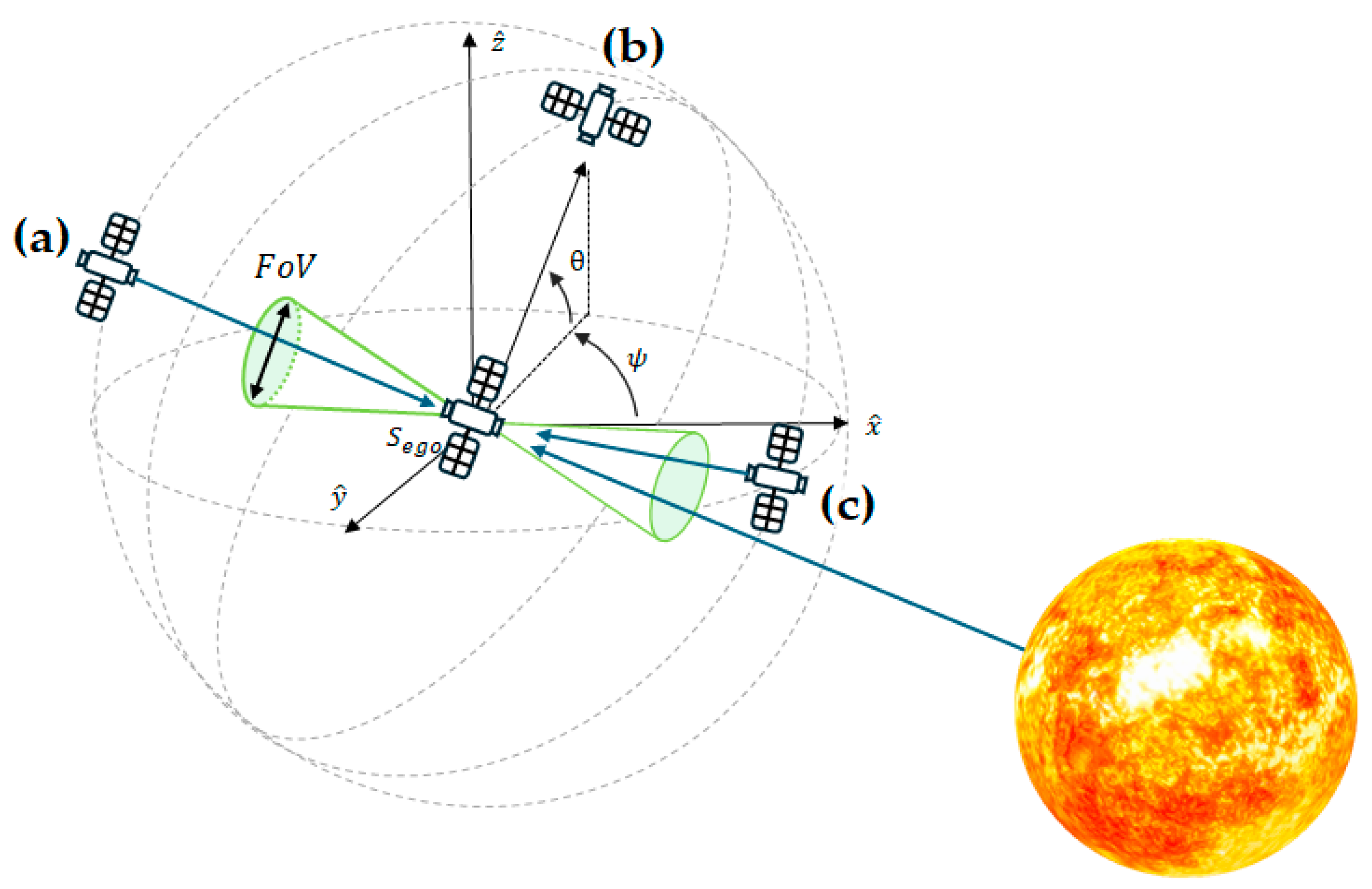
2.2. Individual-Satellite-Oriented Multi-Directional FoV
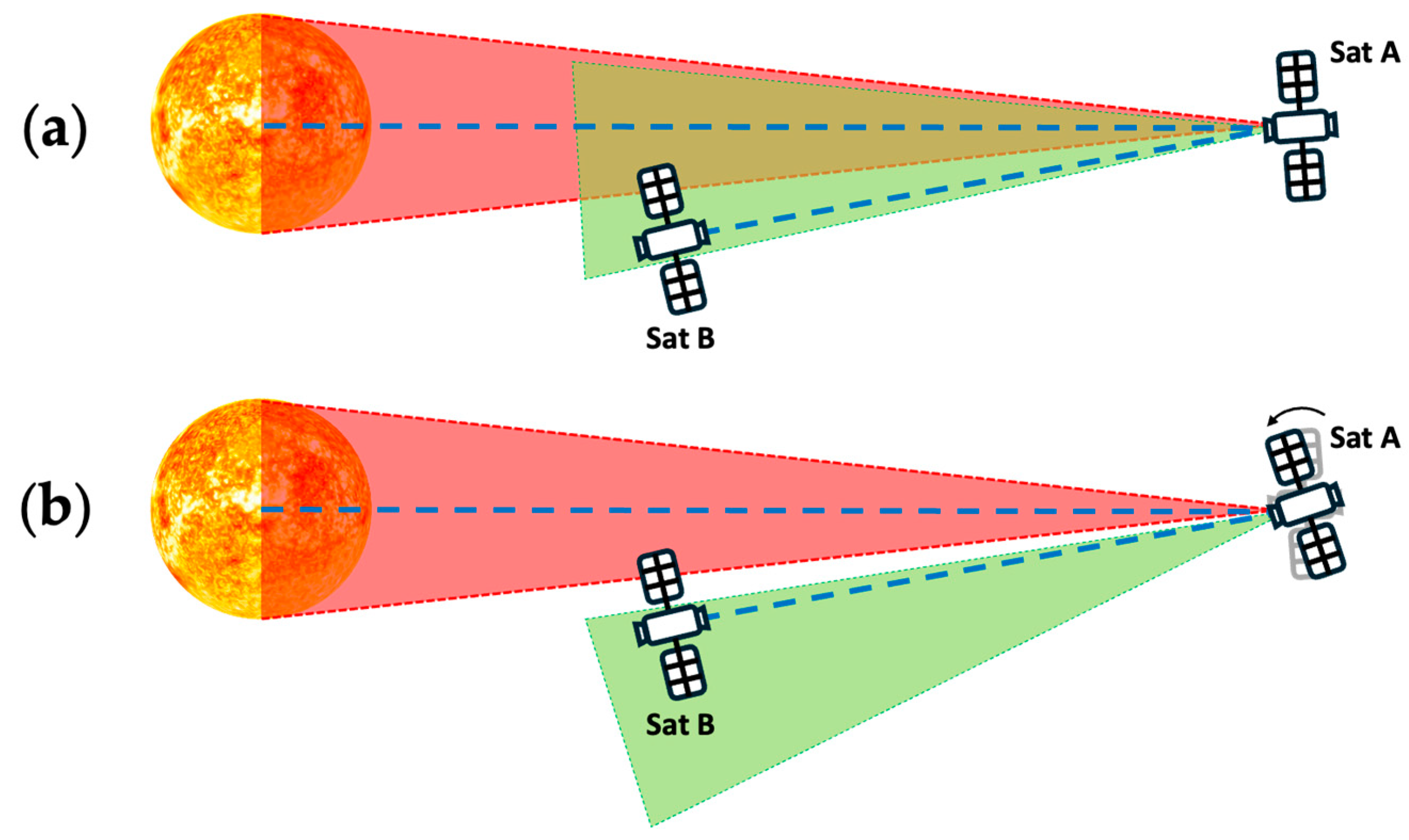
2.3. Inter-Plane and Inter-Shell Configurations
3. Results
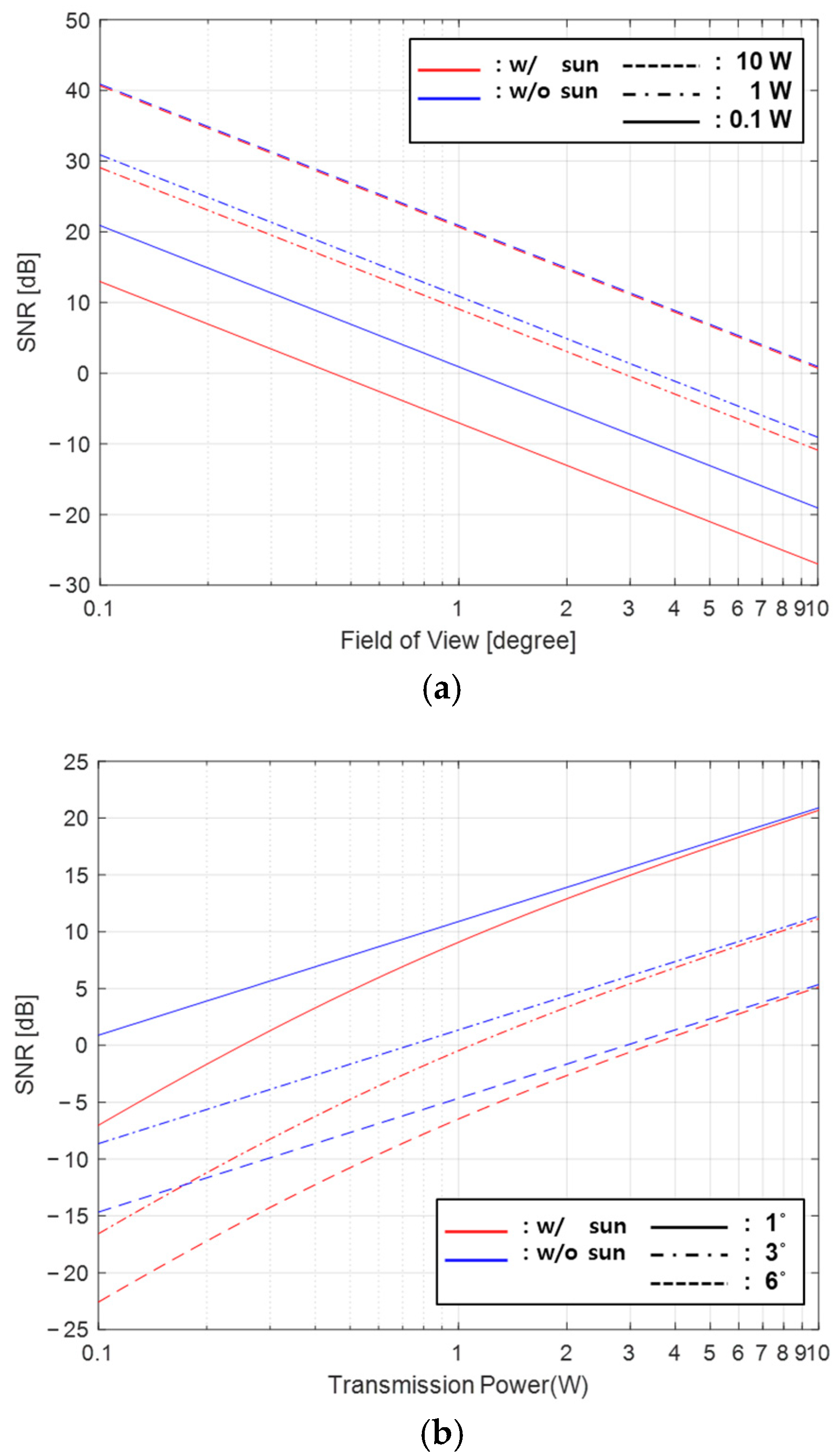
3.1. Solar Irradiation Simulation Results
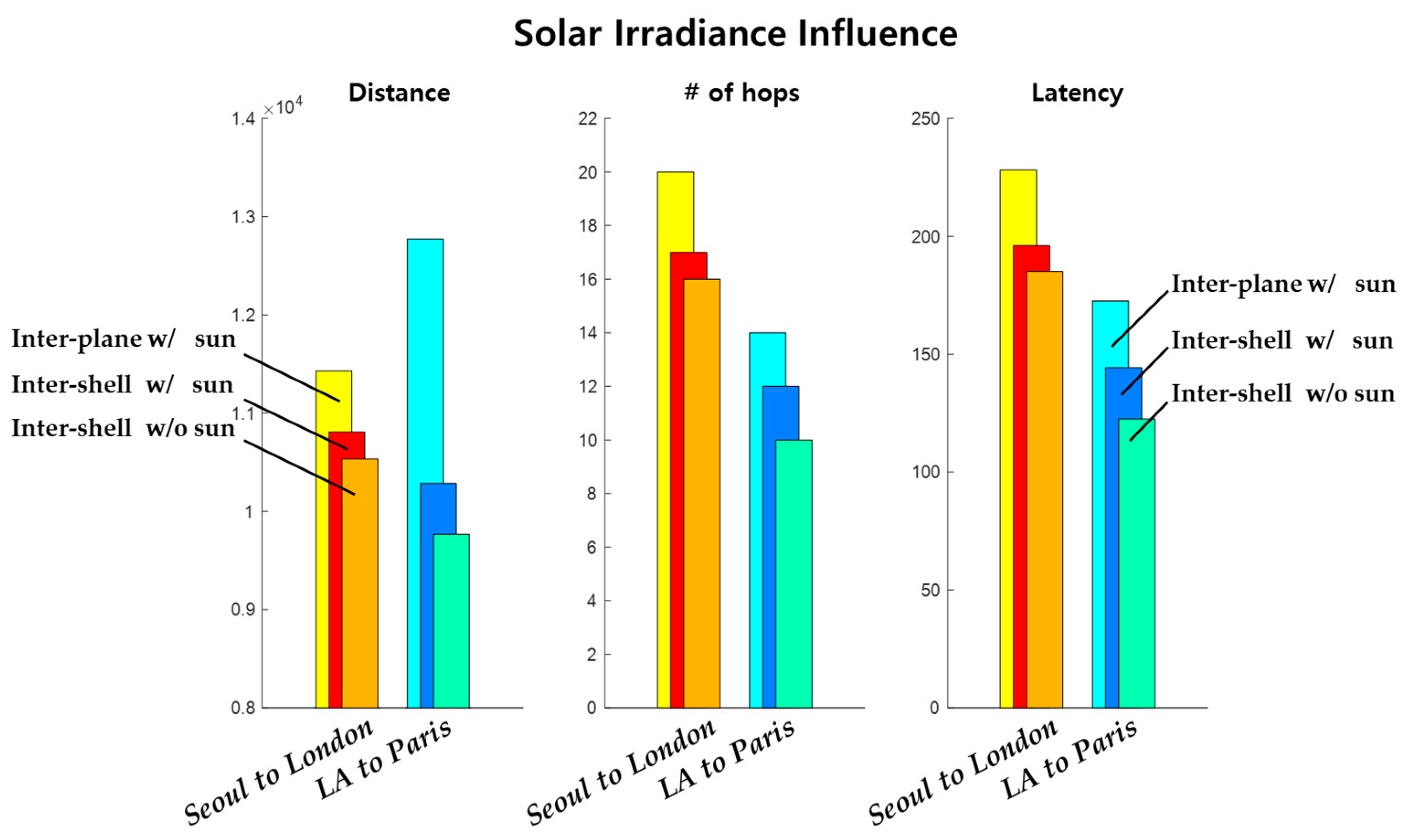
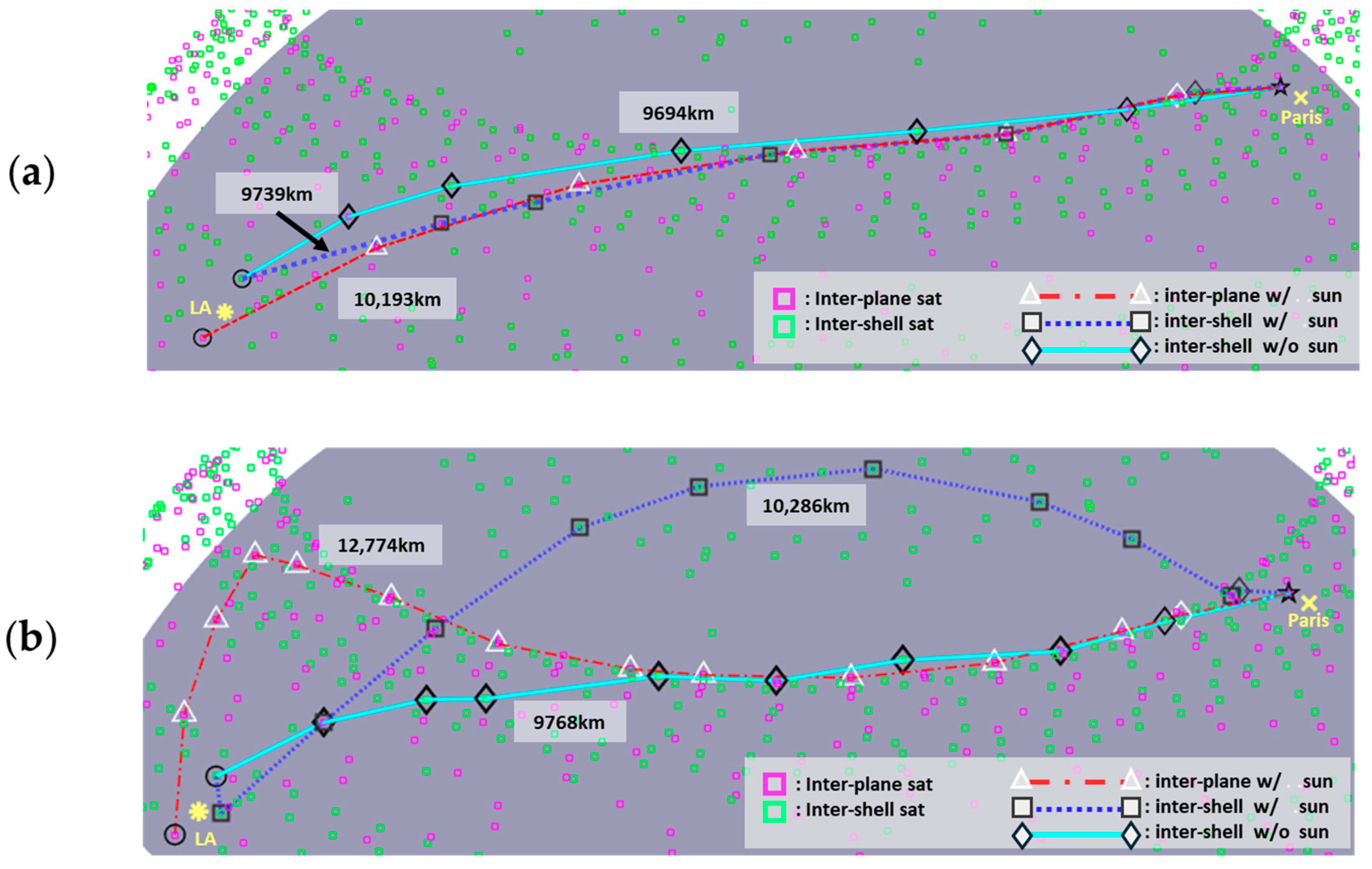
3.2. Path Optimization Strategies via Inter-Plane and Inter-Shell Configurations
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Xiao, Z.; Fan, P.; Gao, Y.; You, X.; Dai, L. LEO Satellite Access Network (LEO-SAN) Toward 6G: Challenges and Approaches. IEEE Wirel. Commun. 2024, 31, 89–96. [Google Scholar] [CrossRef]
- Bhattacharjee, D.; Bhandari, N.; Tiwari, A.; Singh, K.; Sridhar, S.; Ravichandran, R.; Panda, G. On-Demand Routing in LEO Mega-Constellations With Dynamic Laser Inter-Satellite Links. IEEE Trans. Aerosp. Electron. Syst. 2024, 60, 7089–7105. [Google Scholar] [CrossRef]
- Lin, X.; Cioni, S.; Charbit, G.; Chuberre, N.; Hellsten, S.; Boutillon, J.-F. On the Path to 6G: Embracing the Next Wave of Low Earth Orbit Satellite Access. IEEE Commun. Mag. 2021, 59, 36–42. [Google Scholar] [CrossRef]
- Kurnaz, S.; Abdulwahid, M.M. The Channel WDM System Incorporates Optical Wireless Communication (OWC) Hybrid MDM-PDM for Higher Capacity (LEO-GEO) Inter-Satellite Link. Optik 2022, 273, 170449. [Google Scholar] [CrossRef]
- Singh, K.; Chebaane, S.; Ben Khalifa, S.; Benabdallah, F.; Ren, X.; Khemakhem, H.; Grover, A.; Singh, M. Investigations on Mode-Division Multiplexed Free-Space Optical Transmission for Inter-Satellite Communication Link. Wirel. Netw. 2022, 28, 1003–1016. [Google Scholar] [CrossRef]
- Kurnaz, S.; Turkben, A.; Hayal, M.R.; Elsayed, E.; Juraev, D. Inter-Satellite Optical Wireless Communication (Is-OWC) Trends: A Review, Challenges, and Opportunities. IOP Conf. Ser. Mater. Sci. Eng. 2024, 3, 1–15. [Google Scholar]
- Chaudhry, A.U.; Yanikomeroglu, H. Laser Intersatellite Links in a Starlink Constellation: A Classification and Analysis. IEEE Veh. Technol. Mag. 2021, 16, 48–56. [Google Scholar] [CrossRef]
- Hwang, J.S.; Lee, J.-Y.; Chun, H. Ego-Satellite Perspective Multi-PAT Configurations for Optical Inter-Satellite Links. IEEE Access 2024, 12, 144412–144419. [Google Scholar] [CrossRef]
- Excelitas Technologies. C30733EH-1 InGaAs Datasheet. Available online: https://www.excelitas.com/file-download/download/public/104302?filename=C30733EH-1_InGaAs_APD_Datasheet.pdf (accessed on 19 January 2025).
- Thorlabs. DFB15TK-Turkey Low-Noise DFB System. Available online: https://www.thorlabs.com/thorproduct.cfm?partnumber=DFB15TK (accessed on 19 January 2025).
- Islim, M.S.; Videv, S.; Haas, H. The Impact of Solar Irradiance on Visible Light Communications. J. Lightwave Technol. 2018, 36, 2376–2386. [Google Scholar] [CrossRef]
- Yong, J.; Wen, F.; Hu, Z.; Fan, F.; Qiu, K. High-Dynamic Transmission Modeling for Laser Inter-Satellite Links (LISLs). In Proceedings of the 2022 Asia Communications and Photonics Conference (ACP), Shenzhen, China, 5–8 November 2022; pp. 590–594. [Google Scholar] [CrossRef]
- Cornwell, D. Space-Based Laser Communications Break Threshold. Opt. Photonics News 2016, 27, 24–31. [Google Scholar] [CrossRef]
- NASA. Laser Communications Relay Demonstration (LCRD) Overview. Available online: https://www.nasa.gov/mission_pages/tdm/lcrd/index.html (accessed on 19 January 2025).
- TELESAT. Telesat Lightspeed LEO Network. Available online: https://www.telesat.com/leo-satellites/ (accessed on 19 January 2025).
- Jin, J.; Shang, L.; Yang, Z.; Wang, H.; Li, G. A Local Pre-Rerouting Algorithm to Combat Sun Outage for Inter-Satellite Links in Low Earth Orbit Satellite Networks. Appl. Sci. 2024, 14, 1625. [Google Scholar] [CrossRef]
- Pachler, N.; del Portillo, I.; Crawley, E.F.; Cameron, B.G. An Updated Comparison of Four Low Earth Orbit Satellite Constellation Systems to Provide Global Broadband. In Proceedings of the 2021 IEEE International Conference on Communications Workshops (ICC Workshops), Montreal, QC, Canada, 14–23 June 2021; pp. 1–7. [Google Scholar] [CrossRef]
- Thorlabs. FSM75-P01 Fast Steering Mirror (SpecSheet). Available online: https://www.thorlabs.de/thorproduct.cfm?partnumber=FSM75-P01 (accessed on 19 January 2025).


| Feature | Ref. [12] | Ref. [16] | Our Work |
|---|---|---|---|
| Dedicated solar irradiance modeling | O | O | O |
| Distinguishment of unaffected solar exposure | Δ | X | O |
| Analysis of seasonal influence | X | X | O |
| Fully adaptive multi-directional FoV | X | Δ | O |
| Robustness against varying orbital inclinations | Δ | Δ | O |
| Large-scale multi-shell scenarios | X | X | O |
| Notation | Definition | Value(s) |
|---|---|---|
| Altitude of the satellite | 540 km, 550 km, 560 km, and 570 km | |
| Radius of the Earth | 6371 km | |
| Distance between Earth and the sun | 1 AU (149,597,870 km) | |
| APD’s area | ||
| Angle of the field of view | 1°, 3°, and 6° | |
| The maximum transmission power | 0.1 W, 1 W, and 10 W | |
| M | Beam divergence used for m | 65 μrad |
| Excess noise factor | 5.5 | |
| APD’s bandwidth | 3 GHz | |
| Load’s resistance | 50 Ω |
| Number of Planes | Number of Satellites Per Plane | Altitude (km) | Inclination |
|---|---|---|---|
| 72 | 22 | 540 | 53.2° |
| 72 | 22 | 550 | 53° |
| 6 | 58 | 560 | 97.6° |
| 4 | 43 | 560 | 97.6° |
| 36 | 20 | 570 | 70° |
| Link Constraint | Link Loss | Distribution | |
|---|---|---|---|
| (a) Inter-plane | |||
| 1000 km | 5.54% | 7232/7656 | |
| 3000 km | 6.57% | 50,236/53,768 | |
| 1000 km | 11.60% | 6768/7656 | |
| 3000 km | 11.59% | 47,538/53,768 | |
| (b) Inter-shell | |||
| 1000 km | 10.82% | 34,580/38,776 | |
| 3000 km | 8.85% | 293,780/322,292 | |
| 1000 km | 12.47% | 33,942/38,776 | |
| 3000 km | 12.14% | 283,154/322,292 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hwang, J.S.; Lee, J.-Y.; Chun, H. Solar Irradiance Mitigation in LEO Optical Inter-Satellite Links via Inter-Shell Based Path Optimization. Appl. Sci. 2025, 15, 3364. https://doi.org/10.3390/app15063364
Hwang JS, Lee J-Y, Chun H. Solar Irradiance Mitigation in LEO Optical Inter-Satellite Links via Inter-Shell Based Path Optimization. Applied Sciences. 2025; 15(6):3364. https://doi.org/10.3390/app15063364
Chicago/Turabian StyleHwang, Jae Seong, Ji-Yung Lee, and Hyunchae Chun. 2025. "Solar Irradiance Mitigation in LEO Optical Inter-Satellite Links via Inter-Shell Based Path Optimization" Applied Sciences 15, no. 6: 3364. https://doi.org/10.3390/app15063364
APA StyleHwang, J. S., Lee, J.-Y., & Chun, H. (2025). Solar Irradiance Mitigation in LEO Optical Inter-Satellite Links via Inter-Shell Based Path Optimization. Applied Sciences, 15(6), 3364. https://doi.org/10.3390/app15063364






