Abstract
To enhance the balance between lateral stability and energy efficiency, we propose an adaptive compound controller based on phase plane analysis for four-wheel independent drive electric vehicles (4WID-EVs). The adaptive stability and energy-saving controller (SEC) is designed with a three-layer structure. The upper-layer controller employs model predictive control (MPC) to compute the external yaw moment based on the desired yaw rate and side slip angle derived from a reference model. The adaptive-layer controller utilizes a phase plane diagram to evaluate vehicle stability and reduces unnecessary external yaw moment consumption by accounting for the vehicle’s steering state and battery’s state-of-charge (SOC) level. The lower-layer controller implements an optimal torque distribution algorithm to minimize an objective function that considers tire workload, energy consumption, and smooth motor control. Numerical simulations are performed in MATLAB/Simulink using three distinct steering angles to evaluate the performance of the proposed control strategy. At each steering angle, the SEC’s stability and energy efficiency are compared to those of the energy-saving controller (EC) and stability controller (SC) under varying battery charge levels. The results indicate that, at small steering angles, the vehicle operates in a highly stable state, enabling a reduction in the external yaw moment to achieve substantial energy savings. As the steering angle increases, the vehicle approaches a critical stability state, where the external yaw moment is applied to maintain lateral stability. Furthermore, as the SOC decreases, the SEC strategy will increasingly prioritize energy savings. Simulation results verify that the SEC strategy effectively balances lateral stability and energy savings while maintaining consistent performance across a range of operating conditions.
1. Introduction
As an environment-friendly alternative to internal combustion engine vehicles, electric vehicles (EVs) have gained significant attention due to the high efficiency of electric motors and their minimal greenhouse gas emissions [1,2]. Safety and sustainability are the primary objectives in the development of electric vehicles. Stability control aims to keep the vehicle’s driving state within a controllable range, minimizing the risk of accidents due to insufficient driver control. However, accurately estimating a vehicle’s stability remains a challenging task [3,4,5], which is a main focus of the present study. Improving vehicle range primarily depends on either increasing battery capacity or reducing energy consumption. Given the limitations of battery capacity, optimizing both vehicle stability and energy efficiency through strategic motor torque distribution offers an effective approach to reducing energy consumption.
In EVs, hierarchical control is commonly employed to study lateral stability, where the upper-layer controller computes the required external yaw moment, and the lower-layer controller allocates the torque accordingly. The complex dynamic control capabilities of the four-wheel independent drive electric vehicle (4WID-EV) offer significant advantages over other powertrain layouts in EVs, particularly in terms of lateral stability control and energy efficiency [6,7,8]. Lateral stability is a crucial component of vehicle stability control. By independently distributing torque to each of the four motors, the vehicle’s stability is improved through the generation of external yaw moment [9]. Additionally, implementing appropriate torque distribution can reduce energy consumption. The 4WID-EV uses a hierarchical control structure [10] to enhance lateral stability control by simplifying the optimization process. The upper-layer controller employs direct yaw moment control (DYC) to generate external yaw moment, thereby achieving the desired state through control methods such as the sliding mode control (SMC) [11,12], linear quadratic regulator (LQR) [13,14,15], proportional-integral-derivative (PID) [16], and model predictive control (MPC) methods [17]. Zhang et al. [18] proposed a switching strategy based on a stability criterion that involved real-time observation of side slip angle. They also implemented a steering support system for the operation of the active steering system. To minimize actuator usage, the DYC method based on control theory was employed for lateral stability control. Guo et al. [19] introduced an adaptive sliding mode control method for vehicle stability, where switching surfaces were designed using linear matrix inequalities, and fuzzy logic was applied to dynamically adjust the uncertain term and the switching control gain. Chen et al. [20] utilized a dynamic sliding mode control to compute the external yaw moment and proposed an adaptive energy-efficient control allocation method based on the Karush–Kuhn–Tucker conditions for optimal torque distribution. Liu et al. [21] introduced a hierarchical control concept to balance energy efficiency and vehicle motion, with a concise and modular framework that enabled superior dynamic trade-offs.
The lower-layer controller typically applies the optimal torque distribution algorithm [22] to provide precise control and achieve the desired steering performance, including dynamic load distribution [23] and average distribution [24]. According to refs. [25,26], the use of an appropriate torque control allocation method can help reduce energy consumption. In ref. [27], a torque control allocation method based on experimentally measured efficiency maps of motors was proposed to enhance motor efficiency. Additionally, Wang et al. [28] considered torque distribution under tire–road friction conditions. Zhai et al. [29] used tire workload usage as the objective function for torque distribution and compared it with dynamic load distribution and average load distribution algorithms. Zheng et al. [30] identified several optimization objectives in torque distribution, such as vehicle stability, energy savings, and tire wear energy consumption, with the weight coefficient adapted to different working conditions using fuzzy logic theory. Ma et al. [31] also developed a torque distribution strategy to reduce tire slip energy.
Minimizing energy usage during turns, in addition to lateral stability, is also a key research focus. This is primarily accomplished by operating the motors in efficient ranges or reducing motor losses. Liu et al. [32] used the power of four motors as the cost function and employed an exhaustive search method to obtain the front-to-rear torque distribution ratio. Lin et al. [33] introduced a slip energy factor into the objective function to minimize unnecessary tire slip and reduce tire slip energy. Jing et al. [34] combined DYC with active front steering and incorporated a minimum driving energy objective function in the lower-layer controller, enabling dual-layer energy-saving control. Han et al. [35] designed a yaw stability controller to minimize external yaw torque, achieving energy savings without the application of economic optimization algorithms. Zhai et al. [36] developed a continuous steering stability controller based on an energy-saving torque distribution algorithm, achieving a balance between lateral stability and energy savings.
Since the 4WID-EV is a typical over-actuated system [37], multiple possible torque distribution schemes are possible among the four wheels during steering. These systems require sufficient torque for both driving and generating external yaw moment. This paper proposes an adaptive compound controller based on a hierarchical control structure. The objective of this work is to integrate the battery’s state of charge and vehicle stability to dynamically modify the external yaw moment, thereby balancing lateral stability and energy efficiency. The proposed approach provides a novel solution for enhancing energy efficiency in 4WID-EVs.
The rest of this paper is structured as follows: Section 2 presents the seven-degree-of-freedom (7-DOF) nonlinear dynamic model and driver model of the 4WID-EV. Section 3 introduces the adaptive stability and energy-saving control method. Section 4 discusses the main simulation results. Conclusions are summarized in Section 5.
2. System Overview and Vehicle Model
2.1. System Overview
Figure 1 depicts a control system that integrates a vehicle model, a motor model, a battery model, and an adaptive compound controller. The controller improves lateral stability and energy efficiency by dynamically modifying the external yaw moment. The modified yaw moment is determined through a hierarchical structure consisting of a reference model, an upper-layer controller, an adaptive-layer controller, and a lower-layer controller. The upper-layer controller uses MPC to generate the external yaw moment based on the reference model. The adaptive-layer controller evaluates vehicle stability using phase plane diagrams and modifies the external yaw moment accordingly. Finally, the lower-layer controller optimizes tire workload and minimizes total power loss across the four motors using nonlinear torque distribution methods.
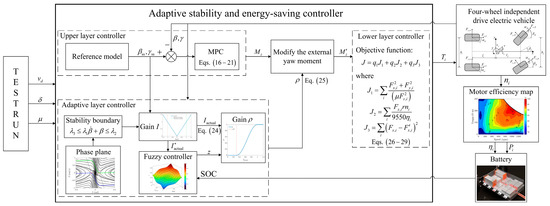
Figure 1.
Adaptive stability and energy-saving control system for the 4WID-EV.
2.2. Vehicle Model
The nomenclature used in this paper is presented in Table 1. In this section, we present a 7-DOF dynamic model of an electric vehicle for the design of the adaptive-layer controller to enhance both the lateral stability and battery energy savings, as shown in Figure 2. The longitudinal, lateral, and yaw motions of the vehicle body are considered with the pitch, roll, and vertical motions being ignored. The rotational motion of the front left, front right, rear left, and rear right wheels are indexed by fl, fr, rl, and rr, respectively. Let denote the origins of the vehicle body frame. Note that the origin is tied to the center of gravity (CG) of the vehicle body. In the vehicle body frame, and represent the distances from the origin to the front and rear axles, resulting in a wheelbase . Let and represent the front and rear track width, and and represent the steering angles and the steering ratio, respectively.

Table 1.
Nomenclature.
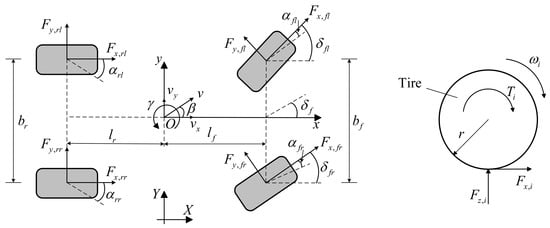
Figure 2.
Schematic of the vehicle dynamics model and the tire longitudinal dynamics model.
The Ackermann steering characteristics are employed to model the kinematics of the vehicle, which means that all wheels possess an instantaneous center of rotation. Based on geometric correlations, the following relation holds:
The longitudinal, lateral, and yaw motions of the vehicle can be represented by the following differential Equations (4)–(6):
where , , and denote the longitudinal velocity, lateral velocity, and the yaw rate, and denote the vehicle mass and yaw moment of inertia, and and denote the longitudinal and lateral forces exerted on tire (), respectively.
The kinematic equation for the rotational motion of the wheel is as follows:
where denotes the wheel moment of inertia, and denote motor torque and vertical force exerted on the ith wheel, and and denote the rolling friction coefficient and wheel dynamic rolling radius. The slip angle of each wheel is denoted by
The lateral tire force can be calculated using the Magic Formula tire model [38] through curve fitting:
where represents the peak factor, is the road surface friction coefficient, and , , and represent the stiffness factor, the shape factor, and the curvature factor, respectively.
In this study, the 4WID-EV is driven by four independently operating permanent magnet synchronous motors, as shown in Figure 3. The input power of the motor is determined by the output power and the power losses , which are mainly caused by the copper loss, iron loss, and mechanical loss. Based on the motor’s torque, speed, and efficiency characteristics, and can be calculated as follows:
where is the efficiency, based on the torque and speed of the motor.
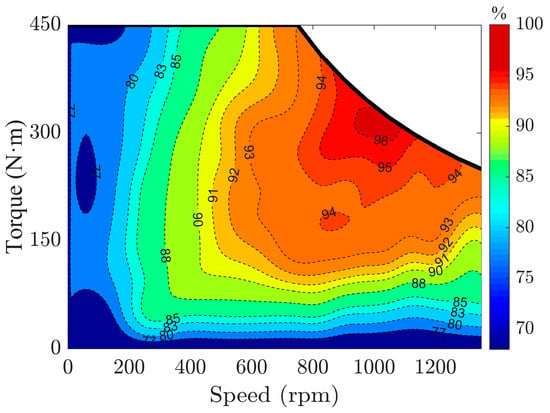
Figure 3.
Efficiency map of the permanent magnet synchronous motor.
As shown in Figure 4, a speed tracking driver model is developed using a proportional-integral (PI) controller. The difference between the desired velocity and the current velocity serves as the input for the controller, which determines the total required torque.
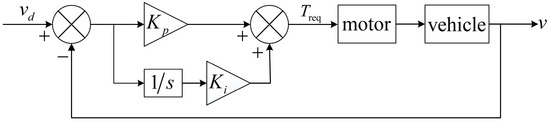
Figure 4.
Design of the vehicle speed tracking controller.
In this study, we design an adaptive compound controller to balance lateral stability and energy efficiency. The controller consists of high-precision sensors, actuators, and a control unit to facilitate its implementation. A high-precision gyroscope, radar speed sensor, inertial measurement unit, and optical encoder measure the yaw rate, longitudinal velocity, lateral velocity, and steering wheel angle, respectively.
3. Design of an Adaptive Compound Controller for Reference Model
3.1. Dynamics of the Reference Vehicle Model
A 2-DOF single-track vehicle model is developed in Equations (14) and (15), which includes both the lateral and yaw motions, as shown in Figure 5. The steering angles of the front left and front right wheels are assumed identical and denoted by . This model provides the desired yaw rate and the side slip angle for the predictive model. Under the assumption of a small side slip angle at the CG, we have . Therefore, the equations governing the vehicle dynamics can be written as
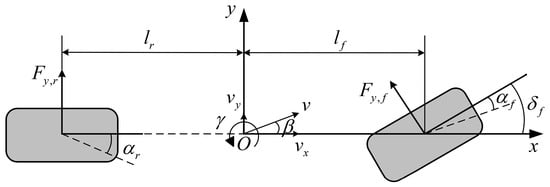
Figure 5.
2-DOF vehicle dynamics model.
Assuming that the front wheel steering angle is small, we have . The lateral forces acting on tires and tire side slip angles for the front and rear axles can be expressed as follows:
where and denote the cornering stiffness of the front and rear tires, represents the total cornering stiffness of the vehicle, and and represent the tire slip angles for the front and rear axles, respectively.
Given that the maximum lateral acceleration is constrained by road friction conditions, the yaw rate should satisfy the condition [39]. Note that high-friction road surfaces lead to a larger effective region for maintaining vehicle lateral stability. When the vehicle reaches a steady state, both the accelerations and are equal to zero. The reference yaw rate and side slip angle can be computed as follows:
where represents the understeer gradient.
3.2. Upper-Layer Controller
In this section, the MPC is used to determine the required yaw moment for steering. The predictive model is a critical component of MPC, as it accurately captures the dynamic characteristics of the controlled system and enables real-time problem-solving. The predictive model in this section is a nonlinear 2-DOF model that accounts for the external yaw moment. As presented in Equation (22), the external yaw moment is incorporated into Equation (15) as follows:
Based on the linear relationship between the tire slip angle and the lateral force, the system’s nonlinear state-space representation can be linearized as follows:
where
The predictive model is discretized with an equal step size of , retaining only the first-order terms. At each discrete step, the steering angle is treated as a constant value, . Taking into accounting that , the incremental state-space representation is thus obtained as follows:
where
The predictive equation, with a prediction horizon of steps and a control horizon of steps, is defined as follows:
where
The desired yaw rate and side slip angle are used as reference inputs. Let ; then, the reference sequence can be defined as follows:
To ensure that the system follows the desired yaw rate and side slip angle , the optimization objective function is formally defined as follows:
where and represent the weighted weight coefficients, and the external yaw moment sequence is .
If we define , then substituting Equations (28) and (33) into Equation (34) results in the following optimization problem:
which is subjected to the following constraint:
3.3. Adaptive-Layer Controller
The optimization of vehicle steering angles aims to achieve a balance between stability and energy savings. The adaptive-layer controller is employed to reduce the excessive yaw moment addition in the upper-layer controller, which works in conjunction with the lower-layer controller to achieve energy savings. The vehicle stability is evaluated through a phase plane diagram. In the present analysis, we focus on the vehicle stability evaluation index , which ranges from 0 to 1. The external yaw moment obtained from the upper-layer controller is adjusted based on the evaluation index to produce the modified external yaw moment . We use the side slip angle and its rate of change for phase plane analysis, i.e., , which effectively addresses accuracy issues on low-adhesion road surfaces or with large side slip angles [40,41]. The fitted boundary of the stability region can be represented as follows:
where , , and represent the stability region boundary coefficients. Figure 6 illustrates the saddle point positions and boundary curves in the phase plane diagram. Two grey dashed lines represent right and left boundaries, and a blue solid line and a green solid line represent the minimum and maximum yaw rates. The region enclosed by these lines is the stability region. The phase trajectories within the stability region will converge to the equilibrium point. The coefficients of , , and are calculated as follows:
where and are the side slip angles for the right and left saddle points. The negative values in Table 2 are obtained by numerically fitting the stability boundaries and saddle points through a two-lines method [35,42].
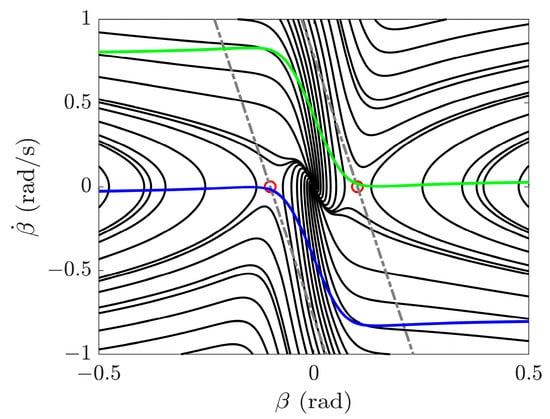
Figure 6.
Phase plane analysis with the simulation parameters , , and . The red circle represents the saddle point, the two grey dashed lines represent the left and right stability boundaries, and a blue solid line and a green solid line represent minimum and maximum yaw rates, respectively.

Table 2.
Parameters of the self-stable boundary.
The above method defines the boundary of the stability region; however, vehicle stability differs near the node and saddle boundaries. Therefore, an evaluation index is introduced to quantitatively describe the vehicle’s current stability state [42]:
where , , , and ; is the adaptive coefficient; is used to describe the level of the side slip angle; is used to describe the level of the yaw rate; and and are indices ranging from 0 to 1, determined by the shortest distance from the vehicle’s current state to the upper and lower boundaries of the stability region. If we define , then and are unified to obtain the evaluation index in Equation (43).
By analyzing the phase plane diagram, the vehicle’s stability level can be determined. The evaluation index is closely correlated with the adaptive coefficient . By properly adjusting the adaptive coefficient , the external yaw moment in the upper-layer controller can be regulated. The parameter tuning method is summarized as follows.
The phase plane diagram is divided into three regions based on the value of the evaluation index : Type I , representing the energy-saving region; Type II , representing the transition region; and Type III , representing the critical stability region. These three regions correspond to three distinct control methods, designated as Type = 0, 1, and 2, respectively. In the energy-saving region, the vehicle reaches a highly stable state and does not require an external yaw moment. In the critical stability region, the vehicle’s steering maneuverability is insufficient, so the actual external yaw moment is exactly equal to the external yaw moment obtained from the upper-layer controller. In the transition region, the evaluation index is scaled between 0.25 and 0.75, with less external yaw moment being added, i.e., . When performing phase plane analysis, it is also necessary to determine the adaptive coefficient . The adaptive coefficient influences both energy consumption and vehicle stability. For a fixed SOC, with an increase in , the energy-saving region expands, and the difference between and increases, leading to a reduction in the external yaw moment. Conversely, as decreases, the energy-saving region narrows, and the difference between and decreases, resulting in an increase in the external yaw moment.
In this section, a fuzzy controller is used with and as inputs and as the output. The value of is derived by substituting and into Equations (41) and (42). The values of and are classified into three levels: L (Low), M (Medium), and H (High), while the value of is classified into five levels: VL (Very Low), L (Low), M (Medium), H (High), and VH (Very High). The fuzzy rules are presented in Table 3 and Figure 7, where the adaptive coefficient is determined as a function of the stability evaluation index and the SOC. The surface reflects the controller’s ability to dynamically balance lateral stability and energy savings.

Table 3.
Rule base of the fuzzy logic controller.
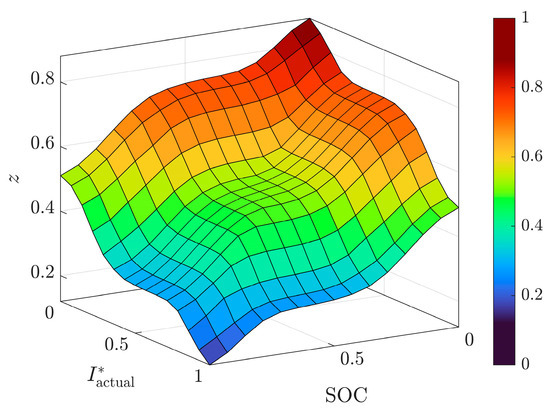
Figure 7.
Control surface output of the fuzzy logic controller.
3.4. Lower-Layer Controller
The lower-layer controller optimally distributes torque to the four motors based on the required torque and the external yaw moment. The primary goal of the torque distribution algorithm is to reduce the tire workload, that is, the required lateral and longitudinal forces based on the normal load, thereby minimizing energy loss due to the side slip. Assuming that the road surface friction coefficients are equal for each tire, the objective function for minimizing the workload of all four tires is calculated as follows:
Additionally, a primary objective of the lower-layer controller is to minimize the energy consumed during steering. This objective function is presented in Equation (13). Based on the relationship between and , the motor energy consumption can be converted into the objective function as follows:
To ensure smooth motor control and minimize control increments, the sum of the squared differences between and for each motor is used as the objective function. Therefore, the objective function is defined as follows:
where represents the force provided by each motor in the previous time step.
By combining the three objective functions with the weighting coefficients , , and , the final objective function is formulated. The following constraints are considered when distributing torque to the tires:
4. Numerical Simulations
A simulation platform is developed based on Figure 1 to verify the efficacy of the proposed adaptive compound controller in regulating lateral stability and energy savings. The platform comprises a 7-DOF vehicle dynamics model, motor model, battery model, driver model, and adaptive compound controller, all implemented in MATLAB/Simulink 2023b. Outputs from the vehicle dynamics model, such as the vehicle speed, side slip angle, yaw rate, and from the battery model, are provided as feedback to the adaptive compound controller. The torque distribution results from the adaptive compound controller are then used as inputs to the vehicle dynamics model, forming a closed-loop control system.
This section evaluates the performance of the adaptive stability and energy-saving controller (SEC) in comparison to two limiting cases: the energy-saving controller (EC) and the stability controller (SC). In the EC, no external yaw moment control is applied, which corresponds to (Type I) in the SEC, whereas in the SC, no external yaw moment modification is added, which corresponds to (Type III) in the SEC.
The vehicle performs a lane-changing maneuver on a flat road surface () at a constant speed of 72 km/h, with the remaining vehicle parameters shown in Table 4. Various steering angles (0.5 rad, 1.0 rad, and 1.5 rad) and initial levels (0.2 and 0.8) are considered, with the vehicle speed maintained at 72 km/h while following the desired path under PI control. A larger steering angle generally indicates a higher likelihood of vehicle instability. Note that represents a typical low battery charge, while represents a high battery charge. The steering angle varies sinusoidally with an amplitude of 0.5 rad and a frequency of , ranging between 1 s and 5 s, as illustrated in Figure 8.

Table 4.
Parameters of vehicle dynamics.
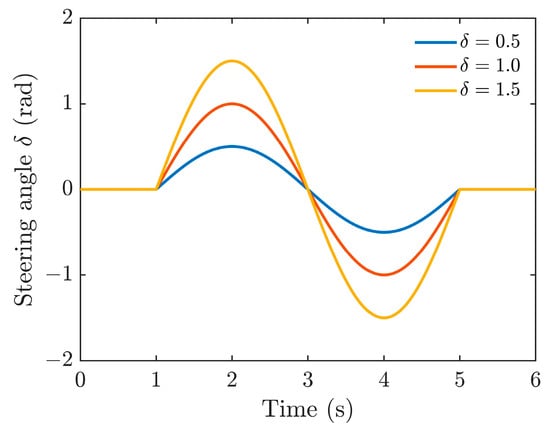
Figure 8.
Temporal variation in the vehicle’s steering angles.
4.1. Case 1:
The simulation results for a steering angle of 0.5 rad are presented in Figure 9, Figure 10 and Figure 11. Figure 9a–c depict the variations in the coefficient , , and within the adaptive-layer controller under the SEC strategy, while Figure 9d shows the time history of the modified external yaw moment .
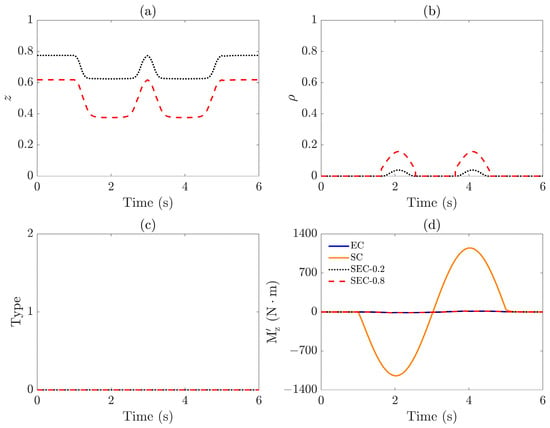
Figure 9.
Responses of stability and energy-saving controller under : (a) adaptive coefficient , (b) evaluation index , (c) control method in the SEC, and (d) external yaw moment .
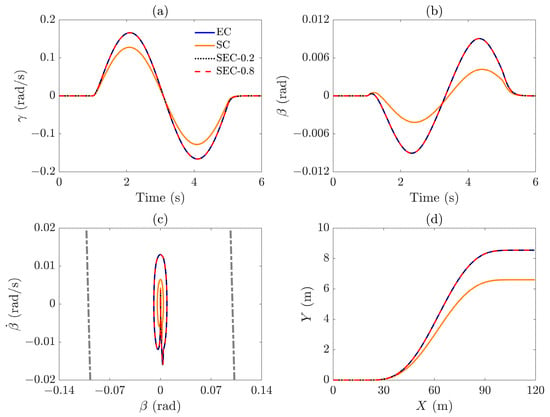
Figure 10.
Vehicle stability responses under : (a) yaw rate , (b) side slip angle , (c) phase plane diagram , and (d) vehicle trajectory in the X–Y plane.
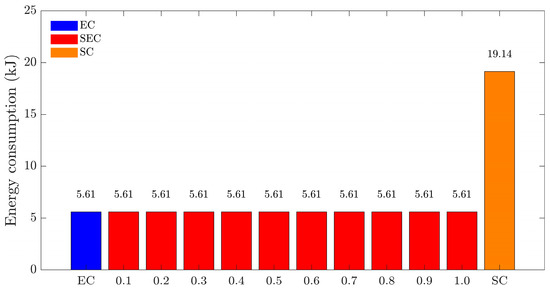
Figure 11.
Vehicle energy consumption at different levels for a fixed .
Figure 9a,b indicate that, under the SEC strategy, the initialization of introduces variations in the adaptive coefficient , leading to differences in the evaluation index when (SEC-0.2) and (SEC-0.8), respectively. In these two cases, the evaluation index remains within the range , corresponding to the energy-saving region described in Section 3.3. And the value of remains constant at 0, as shown in Figure 9c. Consequently, no external yaw moment is applied in this region.
Figure 10a–d show the yaw rate , side slip angle , phase plane diagram , and vehicle trajectory in the X-Y plane, respectively. It is worth noting that under the scenario of , SEC-0.2 and SEC-0.8 yield equivalent external yaw moments, leading to nearly identical vehicle trajectories, as shown in Figure 10d. The maximum yaw rates for both the EC and SEC strategies are identical when , with a corresponding side slip angle of . In contrast, the SC strategy generates a reduced maximum yaw rate at and a side slip angle at , which indicates enhanced stability at the cost of reduced maneuverability (lateral displacement), as demonstrated in Figure 10a–d. The phase plane diagram in Figure 10c further confirms that the phase trajectories of the EC, SEC, and SC are significantly distant from the stability boundary, indicating a highly stable state.
The overall vehicle energy consumption is summarized in Figure 11, where the EC and SEC achieve energy consumptions of 5.61 kJ and 19.14 kJ, respectively, indicating significant energy savings compared to the SC.
4.2. Case 2:
From the analysis of Case 1, it is clear that, when the steering angle is 0.5 rad, the vehicle exhibits high lateral stability, with the SEC strategy prioritizing energy savings. As the steering angle increases from to , the evaluation index ranges from 0.25 to 0.75, and the value of increases to 1, as shown in Figure 12d, which demonstrates the system’s adaptive response to the higher steering angle. In this case, the energy-saving strategy remains the primary focus.
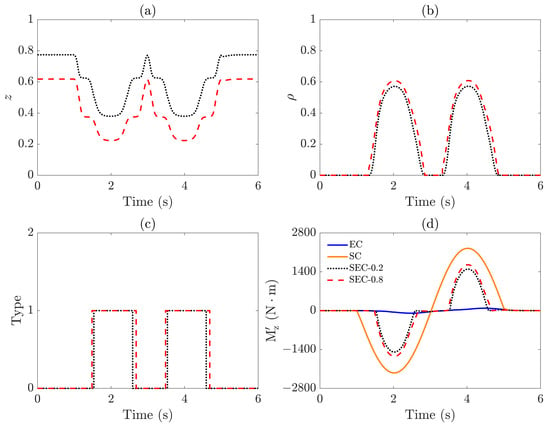
Figure 12.
Responses of stability and energy-saving controller under : (a) adaptive coefficient , (b) evaluation index , (c) control method in the SEC, and (d) external yaw moment .
Figure 12a shows that the adaptive coefficient for the SEC-0.2 is larger than that of the SEC-0.8. Figure 12b reveals that the SEC-0.8 achieves a higher value and faster dynamic response compared to the SEC-0.2. In Figure 12d, the absolute value of for the SEC lies between those of the EC and SC, and the SEC-0.2 exhibits a lower value of than the SEC-0.8. These observations highlight that the SEC-0.8 strategy maintains better stability under these conditions.
Figure 13a,b compare the maximum yaw rates and side slip angles for different control strategies. The maximum yaw rates for the EC, SEC-0.2, SEC-0.8, and SC are 0.3218 rad/s, 0.2638 rad/s, 0.2576 rad/s, and 0.2358 rad/s, respectively. Similarly, the side slip angle gradually decreases from 0.0236 rad (EC) to 0.0085 rad (SC). Figure 13c demonstrates that the stability of the EC, SEC-0.2, SEC-0.8, and SC improves sequentially, as shown in Figure 13d. Regarding stability, the boundary of the yaw rate is constrained by , which can reach a maximum value of 0.4165 rad/s, while the boundary of the side slip angle is approximately 0.1 rad. Since the yaw rate becomes closer to the boundary in the control process, it is considered a more critical factor influencing stability.
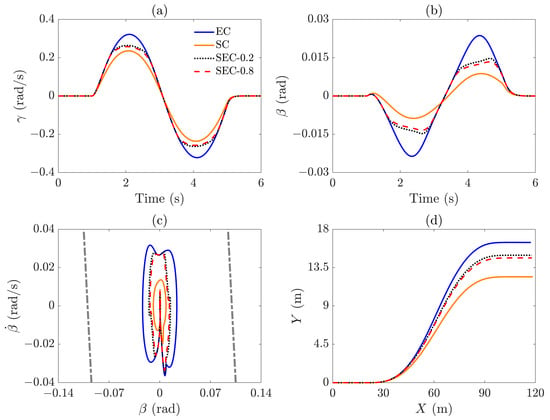
Figure 13.
Vehicle stability responses under : (a) yaw rate , (b) side slip angle , (c) phase plane diagram , and (d) vehicle trajectory in the X–Y plane.
In Figure 13 and Figure 14, the lateral stability and energy consumption of the EC, SEC-0.8, and SC are compared. The SEC-0.8 can increase vehicle stability by 19.95% over the EC at the cost of a 21.79% increase in energy consumption, with these values computed as and , respectively. Compared to the SC, the SEC-0.8 reduces vehicle stability by 9.25% but achieves 30.51% energy savings. Under identical conditions, the SEC-0.2 reduces stability by 2.41% while improving energy savings by 4.34% compared to the SEC-0.8. Notably, the SEC with an SOC of 0.1 achieves approximately 8.44% greater energy savings than the SEC with an SOC of 1.0.
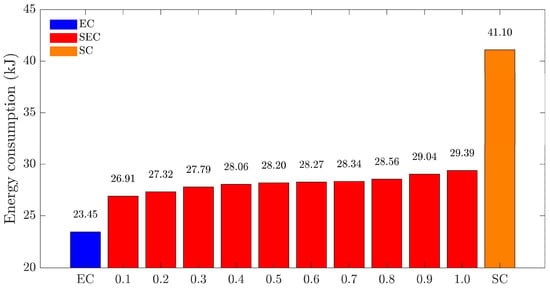
Figure 14.
Vehicle energy consumption at different levels for a fixed .
4.3. Case 3:
Similar trends are observed for the control parameters shown in Figure 15, with the underlying physics consistent with those described for Case 2. However, a key distinction lies in the fact that the evaluation index extends into the range , indicating the critical stability region. Additionally, this scenario introduces a value of , as demonstrated in Figure 15c,d. For , no modification of the external yaw moment is required, i.e., , while for a value of , the external yaw moment should be modified as . Moreover, no external yaw moment is required when .
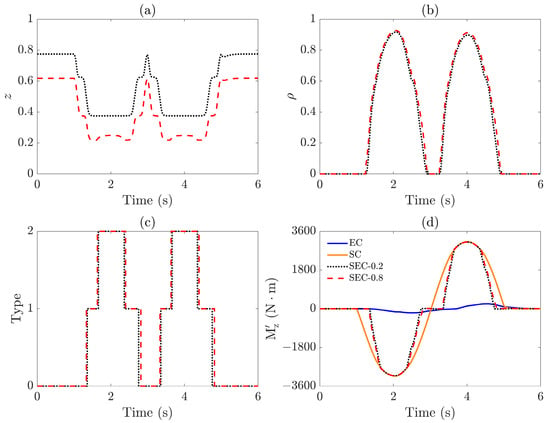
Figure 15.
Responses of stability and energy-saving controller under : (a) adaptive coefficient , (b) evaluation index , (c) control method in the SEC, and (d) external yaw moment .
Due to the modification of the external yaw moment, the yaw rate and the side slip angle under SEC control consistently fall between those of the EC and SC, as shown in Figure 16a,b. The maximum yaw rate closely matches that of the SC, thereby ensuring stability. Figure 16c indicates that the phase trajectories of SEC-controlled vehicles are closer to those of the SC, while EC-controlled vehicles show a significant deviation from the phase trajectories of both the SC and SEC. In terms of maneuverability, an SEC-controlled vehicle yields a balanced performance between the EC and SC. However, the SEC-0.2 strategy exhibits slightly reduced lateral displacement compared to the SEC-0.8, as illustrated in Figure 16d. As shown in Figure 17, the energy consumption of the SEC ranges from 59.21 kJ to 61.24 kJ, depending on the initial level, which represents a reduction of at least 9.11% compared to the SC. These results suggest that, in scenarios approaching the maximum cornering threshold, an SEC-controlled vehicle can maintain stability and maneuverability similar to the SC, while achieving significant energy savings.
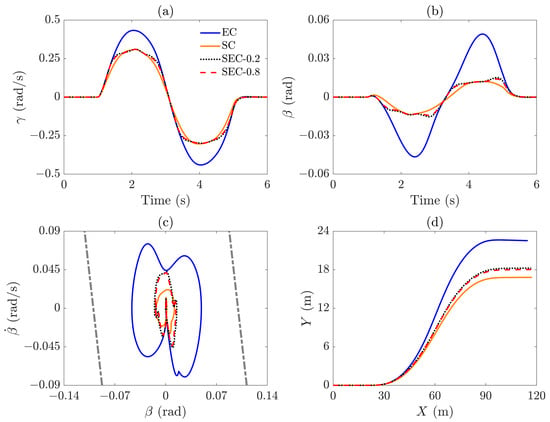
Figure 16.
Vehicle stability responses under : (a) yaw rate , (b) side slip angle , (c) phase plane diagram , and (d) vehicle trajectory in the X–Y plane.
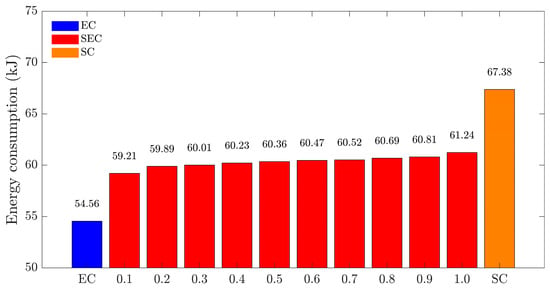
Figure 17.
Vehicle energy consumption at different levels for a fixed .
5. Conclusions
During steering maneuvers, real-time monitoring of the vehicle’s side slip angle and yaw rate is essential. To maintain lateral stability, an external yaw moment must be applied, which increases energy consumption. Therefore, balancing lateral stability with energy consumption becomes a critical challenge.
This paper presents a novel adaptive compound controller based on phase plane analysis to effectively balance vehicle stability and energy savings during the steering process. By quantifying the overall stability of the vehicle, the control framework can continuously switch between the pure energy-saving controller, the adaptive stability and energy-saving controller, and the stability controller in real time, with the obtained results summarized as follows:
- A compound control strategy, which integrates an adaptive-layer controller, is employed to preserve the advantages of hierarchical control and simultaneously improve energy efficiency.
- The proposed SEC strategy dynamically adjusts the adaptive coefficient based on the vehicle’s battery state and divides the phase plane diagram into three regions according to the evaluation index, which effectively balances lateral stability and energy savings.
- Simulation results demonstrate that the SEC strategy prioritizes energy savings as the battery’s state of charge decreases.
- These findings verify the effectiveness of the proposed adaptive compound controller in achieving a robust balance between lateral stability and energy savings.
Author Contributions
Conceptualization, X.H. and X.C.; Methodology, K.X. and X.C.; Software, K.X.; Validation, K.X.; Formal analysis, K.X. and X.C.; Resources, X.H.; Writing—original draft, K.X.; Writing—review & editing, X.H., X.C. and X.N.; Supervision, X.H. and X.C.; Project administration, X.H. and X.N.; Funding acquisition, X.H., K.X. and X.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the National Natural Science Foundation of China through Grant No. 52005443, the Natural Science Foundation of Zhejiang Province through Grant No. LQ21E050016, the China Scholarship Council through Grant No. 202407280003, and the Key Laboratory of Acoustics and Vibration Applied Measuring Technology, State Administration for Market Regulation through Grant No. AVL202303.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Acknowledgments
The authors are grateful to Jun Cao for his valuable discussions during the preparation of the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Spanoudakis, P.; Tsourveloudis, N.C.; Doitsidis, L.; Karapidakis, E.S. Experimental Research of Transmissions on Electric Vehicles’ Energy Consumption. Energies 2019, 12, 388. [Google Scholar] [CrossRef]
- Zhang, L.; Ding, H.; Shi, J.; Huang, Y.; Chen, H.; Guo, K.; Li, Q. An Adaptive Backstepping Sliding Mode Controller to Improve Vehicle Maneuverability and Stability via Torque Vectoring Control. IEEE Trans. Veh. Technol. 2020, 69, 2598–2612. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, P.; Lin, J.; Chen, H.; Hong, J.; Zhang, L. Real-time nonlinear predictive controller design for drive-by-wire vehicle lateral stability with dynamic boundary conditions. Fundam. Res. 2022, 2, 131–143. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Z.; Tang, X.; Qin, Y.; Huang, Y.; Hashemi, E. A survey of lateral stability criterion and control application for autonomous vehicles. IEEE Trans. Intell. Transp. Syst. 2023, 24, 10382–10399. [Google Scholar] [CrossRef]
- Liang, J.; Feng, J.; Fang, Z.; Lu, Y.; Yin, G.; Mao, X.; Wu, J.; Wang, F. An energy-oriented torque-vector control framework for distributed drive electric vehicles. IEEE Trans. Transp. Electrif. 2023, 9, 4014–4031. [Google Scholar] [CrossRef]
- Yin, G.; Jin, X.; Qing, Z.; Bian, C. Lateral Stability Region Conservativeness Estimation and Torque Distribution for FWIA Electric Vehicle Steering. Sci. China Technol. Sci. 2015, 58, 669–676. [Google Scholar] [CrossRef]
- Qiu, L.; Qian, L.; Zomorodi, H.; Pisu, P. Design and Optimization of Equivalent Consumption Minimization Strategy for 4WD Hybrid Electric Vehicles Incorporating Vehicle Connectivity. Sci. China Technol. Sci. 2018, 61, 147–157. [Google Scholar] [CrossRef]
- Zhuang, W.; Zhang, X.; Yin, G.; Peng, H.; Wang, L. Mode Shift Schedule and Control Strategy Design of Multimode Hybrid Powertrain. IEEE Trans. Control Syst. Technol. 2020, 28, 804–815. [Google Scholar] [CrossRef]
- Shi, K.; Yuan, X.; Huang, G.; Liu, Z.L. Compensation-Based Robust Decoupling Control System for the Lateral and Longitudinal Stability of Distributed Drive Electric Vehicle. IEEE ASME Trans. Mechatron. 2019, 24, 2768–2778. [Google Scholar] [CrossRef]
- Zhang, H.; Zhao, W. Decoupling Control of Steering and Driving System for In-Wheel-Motor-Drive Electric Vehicle. Mech. Syst. Signal Proc. 2018, 101, 389–404. [Google Scholar] [CrossRef]
- Shtessel, Y.; Edwards, C.; Fridman, L.; Levant, A. Sliding Mode Control and Observation; Springer: New York, NY, USA, 2014; ISBN 978-0-8176-4892-3. [Google Scholar]
- Ding, S.; Liu, L.; Zheng, W.X. Sliding Mode Direct Yaw-Moment Control Design for in-Wheel Electric Vehicles. IEEE Trans. Ind. Electron. 2017, 64, 6752–6762. [Google Scholar] [CrossRef]
- Zhao, B.; Xu, N.; Chen, H.; Guo, K.; Huang, Y. Stability Control of Electric Vehicles with In-Wheel Motors by Considering Tire Slip Energy. Mech. Syst. Signal Proc. 2019, 118, 340–359. [Google Scholar] [CrossRef]
- Jiang, Z.; Xiao, B. LQR Optimal Control Research for Four-Wheel Steering Forklift Based-on State Feedback. J. Mech. Sci. Technol. 2018, 32, 2789–2801. [Google Scholar] [CrossRef]
- Wang, Z.; Montanaro, U.; Fallah, S.; Sorniotti, A.; Lenzo, B. A Gain Scheduled Robust Linear Quadratic Regulator for Vehicle Direct Yaw Moment Control. Mechatronics 2018, 51, 31–45. [Google Scholar] [CrossRef]
- Zhao, Y.; Deng, H.; Li, Y.; Xu, H. Coordinated Control of Stability and Economy Based on Torque Distribution of Distributed Drive Electric Vehicle. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2020, 234, 1792–1806. [Google Scholar] [CrossRef]
- Ren, B.; Chen, H.; Zhao, H.; Yuan, L. MPC-Based Yaw Stability Control in in-Wheel-Motored EV via Active Front Steering and Motor Torque Distribution. Mechatronics 2016, 38, 103–114. [Google Scholar] [CrossRef]
- Zhang, J.; Sun, W.; Feng, Z. Vehicle Yaw Stability Control via H∞ Gain Scheduling. Mech. Syst. Signal Proc. 2018, 106, 62–75. [Google Scholar] [CrossRef]
- Guo, J.; Luo, Y.; Li, K. An Adaptive Hierarchical Trajectory Following Control Approach of Autonomous Four-Wheel Independent Drive Electric Vehicles. IEEE Trans. Intell. Transp. Syst. 2018, 19, 2482–2492. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, J. Adaptive Energy-Efficient Control Allocation for Planar Motion Control of over-Actuated Electric Ground Vehicles. IEEE Trans. Control Syst. Technol. 2014, 22, 1362–1373. [Google Scholar] [CrossRef]
- Liu, W.; Khajepour, A.; He, H.; Wang, H.; Huang, Y. Integrated Torque Vectoring Control for a Three-Axle Electric Bus Based on Holistic Cornering Control Method. IEEE Trans. Veh. Technol. 2018, 67, 2921–2933. [Google Scholar] [CrossRef]
- De Novellis, L.; Sorniotti, A.; Gruber, P.; Orus, J.; Fortun, J.M.R.; Theunissen, J.; De Smet, J. Direct Yaw Moment Control Actuated through Electric Drivetrains and Friction Brakes: Theoretical Design and Experimental Assessment. Mechatronics 2015, 26, 1–15. [Google Scholar] [CrossRef]
- Kang, J.; Yoo, J.; Yi, K. Driving Control Algorithm for Maneuverability, Lateral Stability, and Rollover Prevention of 4WD Electric Vehicles with Independently Driven Front and Rear Wheels. IEEE Trans. Veh. Technol. 2011, 60, 2987–3001. [Google Scholar] [CrossRef]
- Nam, K.; Fujimoto, H.; Hori, Y. Lateral Stability Control of In-Wheel-Motor-Driven Electric Vehicles Based on Sideslip Angle Estimation Using Lateral Tire Force Sensors. IEEE Trans. Veh. Technol. 2012, 61, 1972–1985. [Google Scholar] [CrossRef]
- De Novellis, L.; Sorniotti, A.; Gruber, P. Wheel Torque Distribution Criteria for Electric Vehicles with Torque-Vectoring Differentials. IEEE Trans. Veh. Technol. 2014, 63, 1593–1602. [Google Scholar] [CrossRef]
- Fujimoto, H.; Harada, S. Model-Based Range Extension Control System for Electric Vehicles with Front and Rear Driving–Braking Force Distributions. IEEE Trans. Ind. Electron. 2015, 62, 3245–3254. [Google Scholar] [CrossRef]
- Chen, J.; Yu, J.; Zhang, K.; Ma, Y. Control of Regenerative Braking Systems for Four-Wheel-Independently-Actuated Electric Vehicles. Mechatronics 2018, 50, 394–401. [Google Scholar] [CrossRef]
- Wang, R.; Hu, C.; Wang, Z.; Yan, F.; Chen, N. Integrated Optimal Dynamics Control of 4WD4WS Electric Ground Vehicle with Tire-Road Frictional Coefficient Estimation. Mech. Syst. Signal Proc. 2015, 60–61, 727–741. [Google Scholar] [CrossRef]
- Zhai, L.; Sun, T.; Wang, J. Electronic Stability Control Based on Motor Driving and Braking Torque Distribution for a Four In-Wheel Motor Drive Electric Vehicle. IEEE Trans. Veh. Technol. 2016, 65, 4726–4739. [Google Scholar] [CrossRef]
- Zheng, H.; Yang, S. A Trajectory Tracking Control Strategy of 4WIS/4WID Electric Vehicle with Adaptation of Driving Conditions. Appl. Sci. 2019, 9, 168. [Google Scholar] [CrossRef]
- Ma, Y.; Chen, J.; Zhu, X.; Xu, Y. Lateral Stability Integrated with Energy Efficiency Control for Electric Vehicles. Mech. Syst. Signal Proc. 2019, 127, 1–15. [Google Scholar] [CrossRef]
- Liu, J.; Zhong, H.; Wang, L.; Chen, H. A Novel Torque Distribution Strategy for Distributed-Drive Electric Vehicle Considering Energy Saving and Brake Stability; SAE Technical Paper 2019-01-0334; SAE International: Warrendale, PA, USA, 2019. [Google Scholar]
- Lin, F.; Qian, C.; Cai, Y.; Zhao, Y.; Wang, S.; Zang, L. Integrated Tire Slip Energy Dissipation and Lateral Stability Control of Distributed Drive Electric Vehicle with Mechanical Elastic Wheel. J. Frankl. Inst. Eng. Appl. Math. 2022, 359, 4776–4803. [Google Scholar] [CrossRef]
- Jing, C.; Shu, H.; Song, Y.; Guo, C. Hierarchical Control of Yaw Stability and Energy Efficiency for Distributed Drive Electric Vehicles. Int. J. Automot. Technol. 2021, 22, 1169–1188. [Google Scholar] [CrossRef]
- Han, Z.; Xu, N.; Chen, H.; Huang, Y.; Zhao, B. Energy-Efficient Control of Electric Vehicles Based on Linear Quadratic Regulator and Phase Plane Analysis. Appl. Energy 2018, 213, 639–657. [Google Scholar] [CrossRef]
- Zhai, L.; Hou, R.; Sun, T.; Kavuma, S. Continuous Steering Stability Control Based on an Energy-Saving Torque Distribution Algorithm for a Four in-Wheel-Motor Independent-Drive Electric Vehicle. Energies 2018, 11, 350. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, J. Design and Experimental Evaluations on Energy Efficient Control Allocation Methods for Overactuated Electric Vehicles: Longitudinal Motion Case. IEEE ASME Trans. Mechatron. 2014, 19, 538–548. [Google Scholar] [CrossRef]
- Pacejka, H.B.; Besselink, I. Tire and Vehicle Dynamics; Butterworth-Heinemann Elsevier: Waltham, MA, USA, 2012; ISBN 978-0-08-097016-5. [Google Scholar]
- Liu, J.; Zhuang, W.; Zhong, H.; Wang, L.; Chen, H.; Tan, C.A. Integrated Energy-Oriented Lateral Stability Control of a Four-Wheel-Independent-Drive Electric Vehicle. Sci. China Technol. Sci. 2019, 62, 2170–2183. [Google Scholar] [CrossRef]
- Inagaki, S.; Kshiro, I.; Yamamoto, M. Analysis on vehicle stability in critical cornering using phase-plane method. In Proceedings of the International Symposium on Advanced Vehicle Control, Tsukuba, Japan, 24–28 October 1994; pp. 287–292. [Google Scholar]
- Shen, S.; Wang, J.; Shi, P.; Premier, G. Nonlinear Dynamics and Stability Analysis of Vehicle Plane Motions. Veh. Syst. Dyn. 2007, 45, 15–35. [Google Scholar] [CrossRef]
- Guo, N.; Zhang, X.; Zou, Y.; Lenzo, B.; Du, G.; Zhang, T. A Supervisory Control Strategy of Distributed Drive Electric Vehicles for Coordinating Handling, Lateral Stability, and Energy Efficiency. IEEE Trans. Transp. Electrif. 2021, 7, 2488–2504. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).