The Design, Analysis, and Verification of an Axial Flux Permanent Magnet Motor with High Torque Density
Abstract
1. Introduction
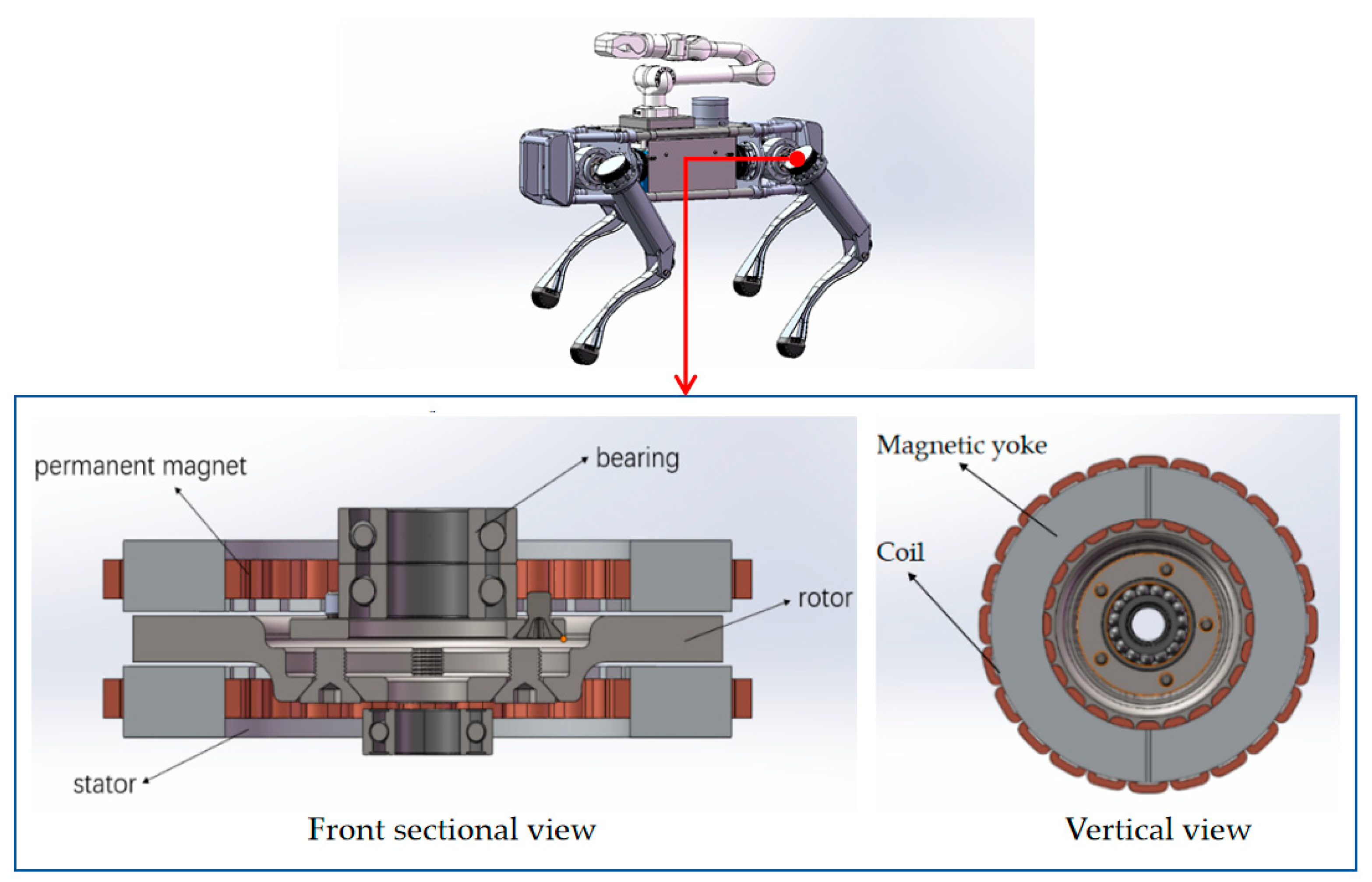
2. Structure and Working Principle
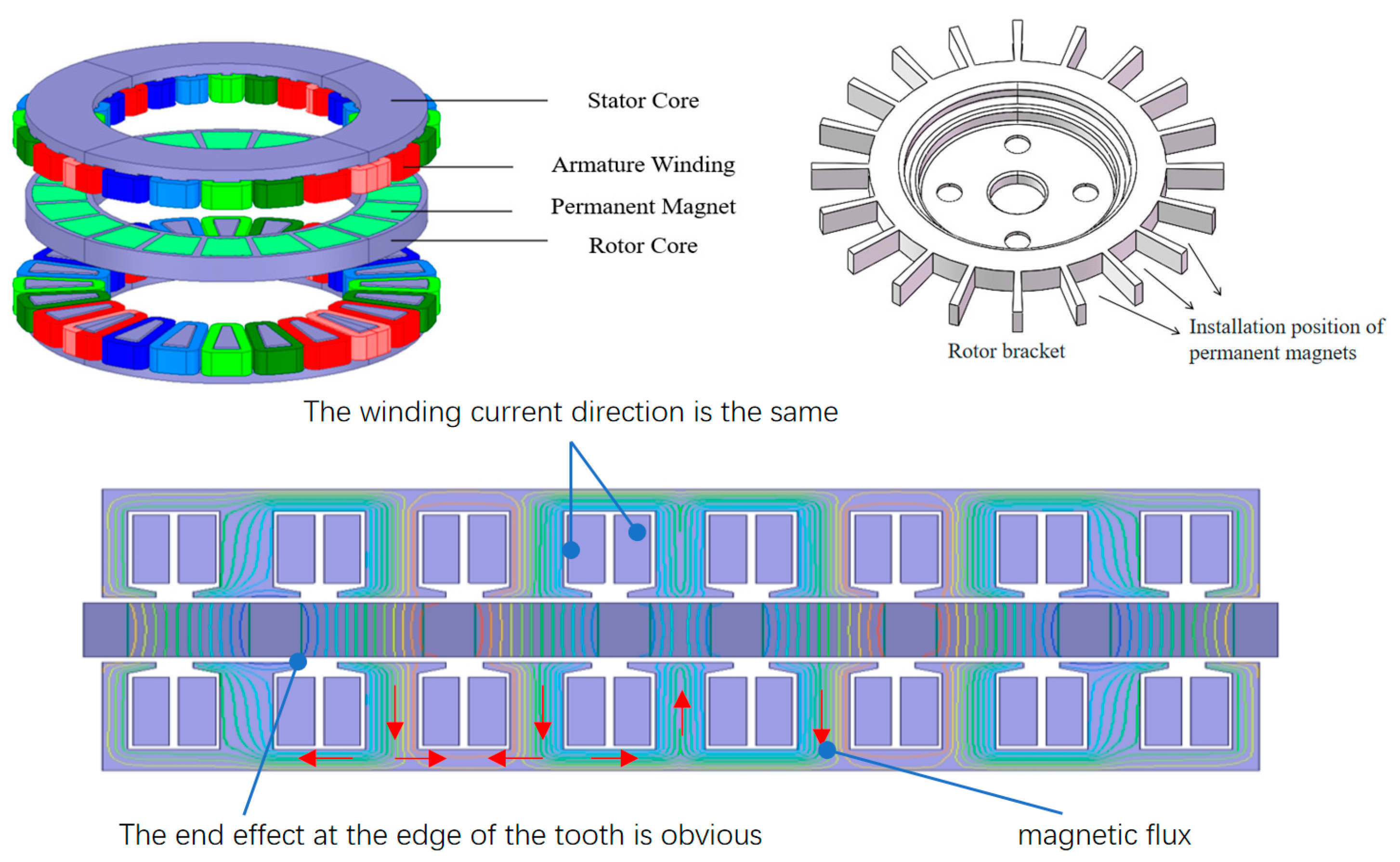
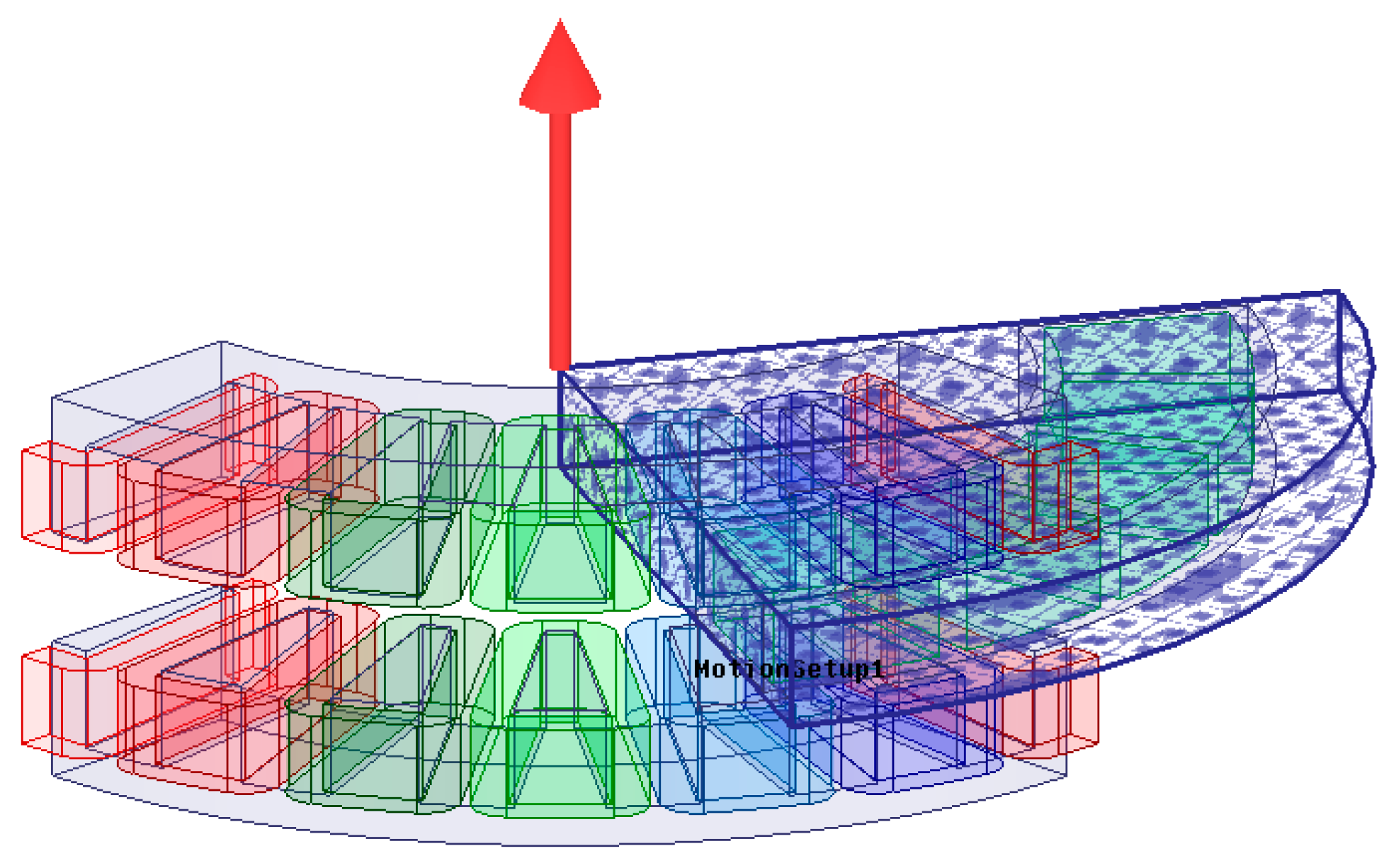
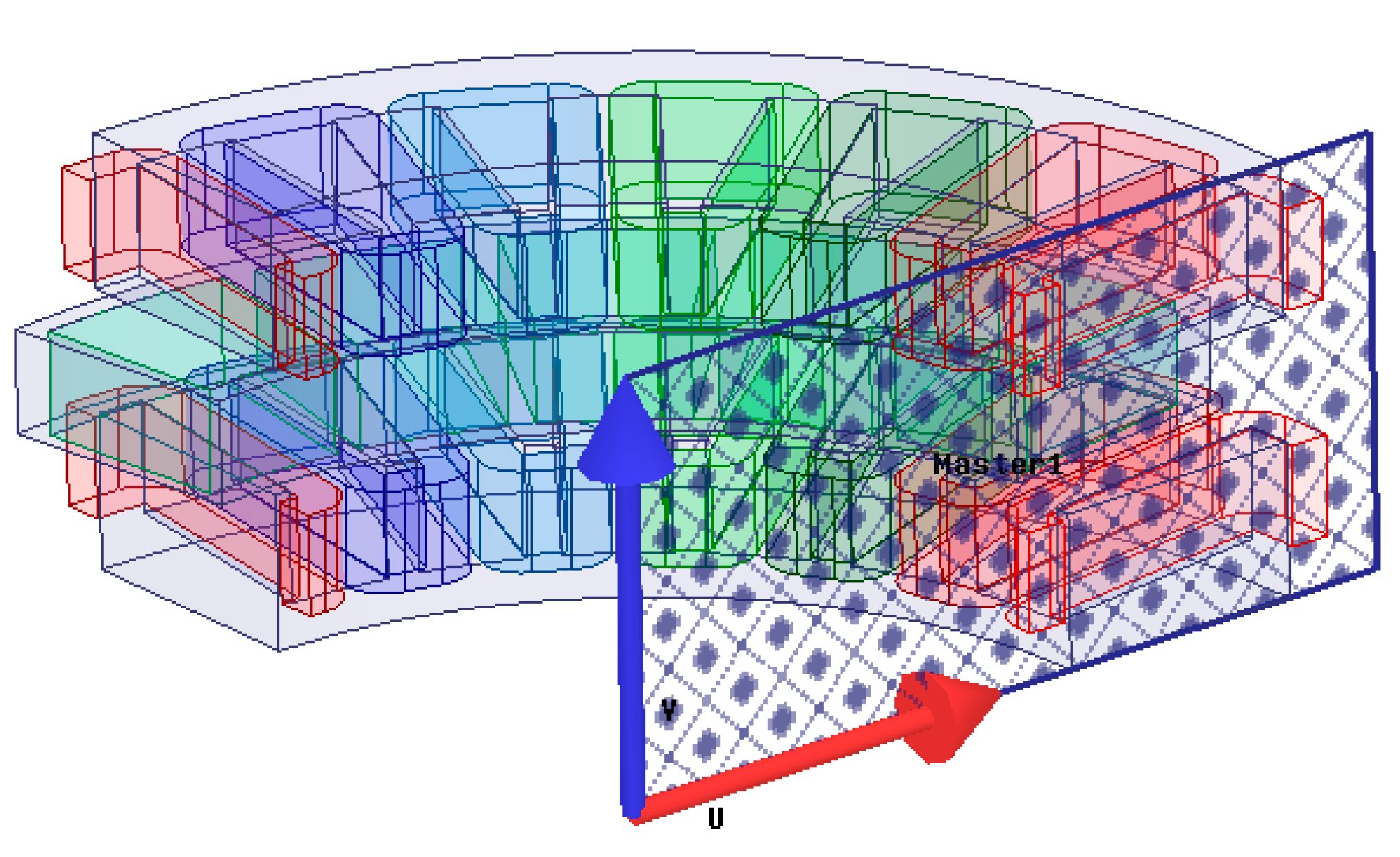
2.1. Structure and Composition of Axial Flux Permanent Magnet Synchronous Motor
2.2. Working Principle
3. Electromagnetic Characteristic Analysis
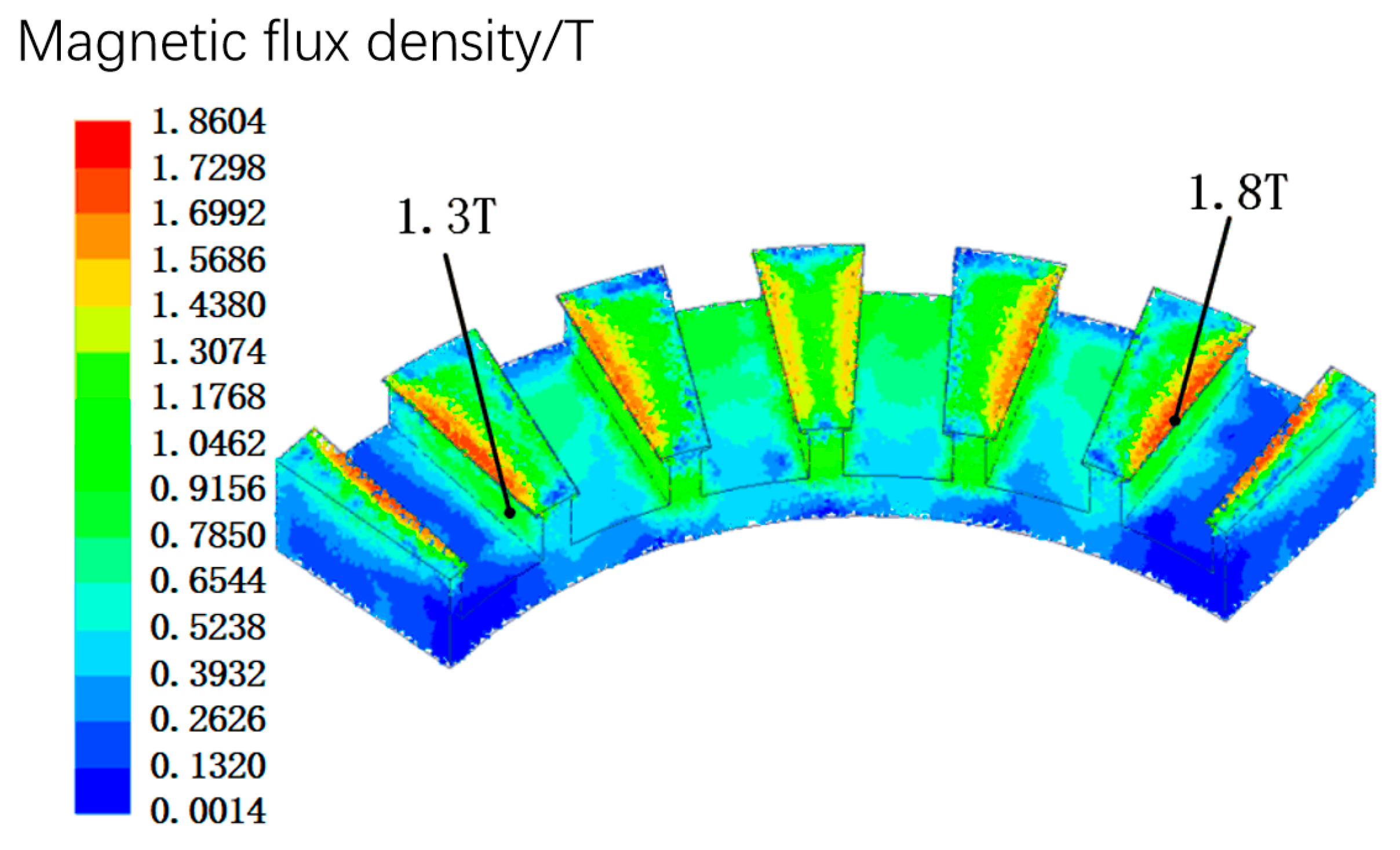
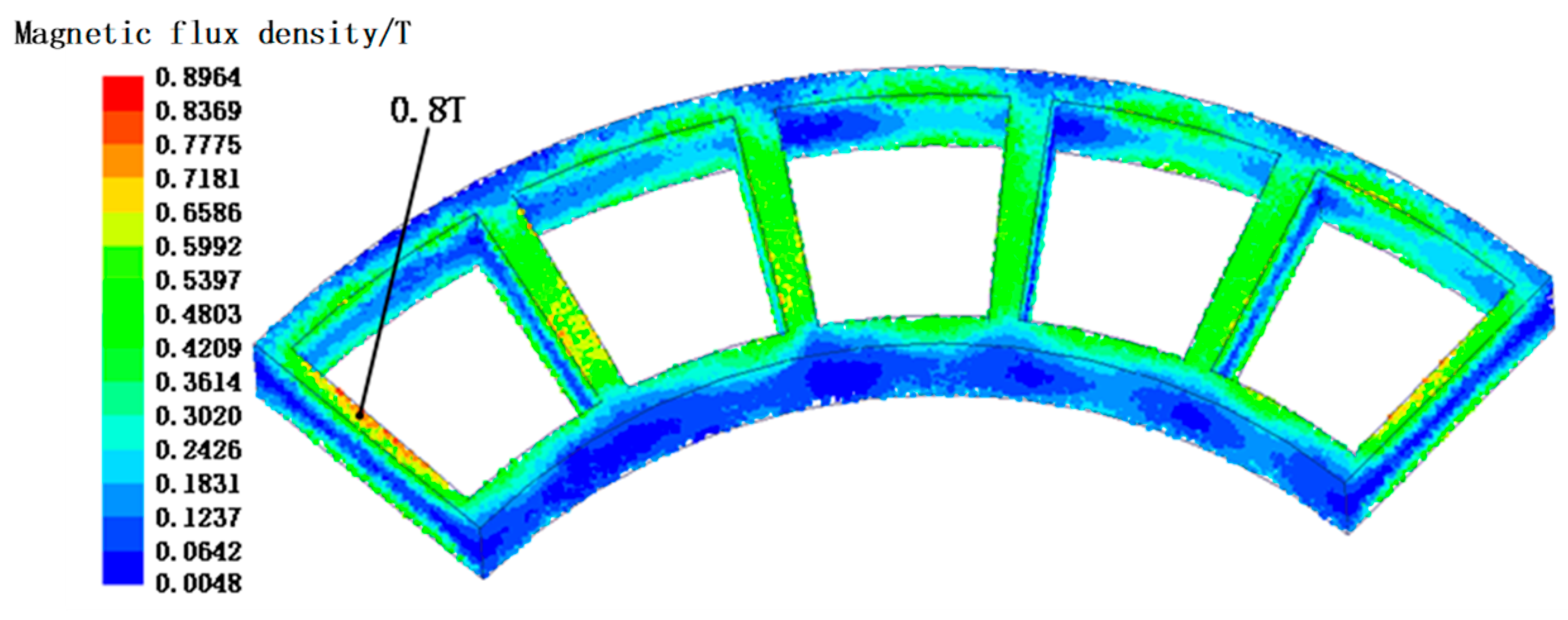
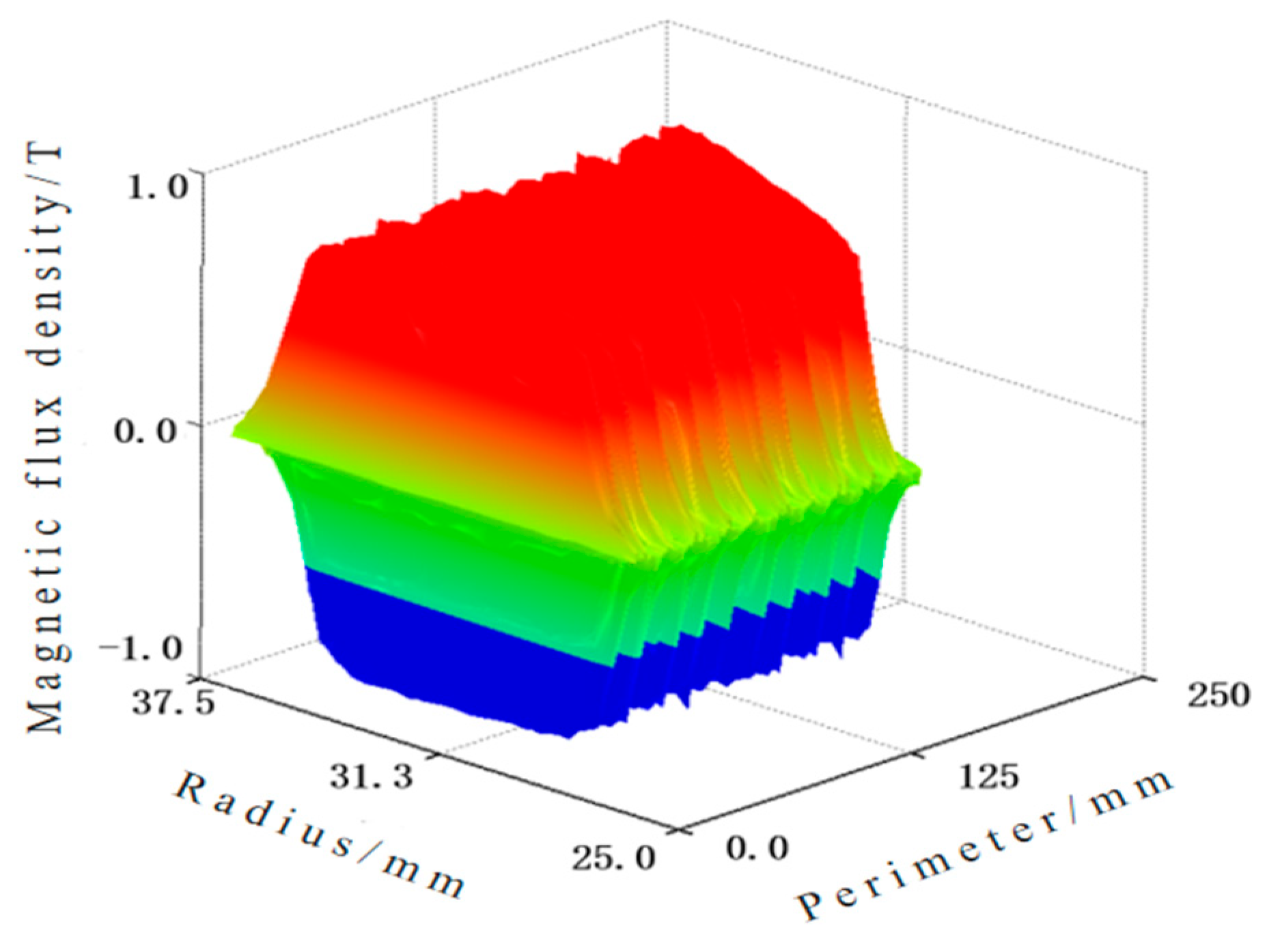
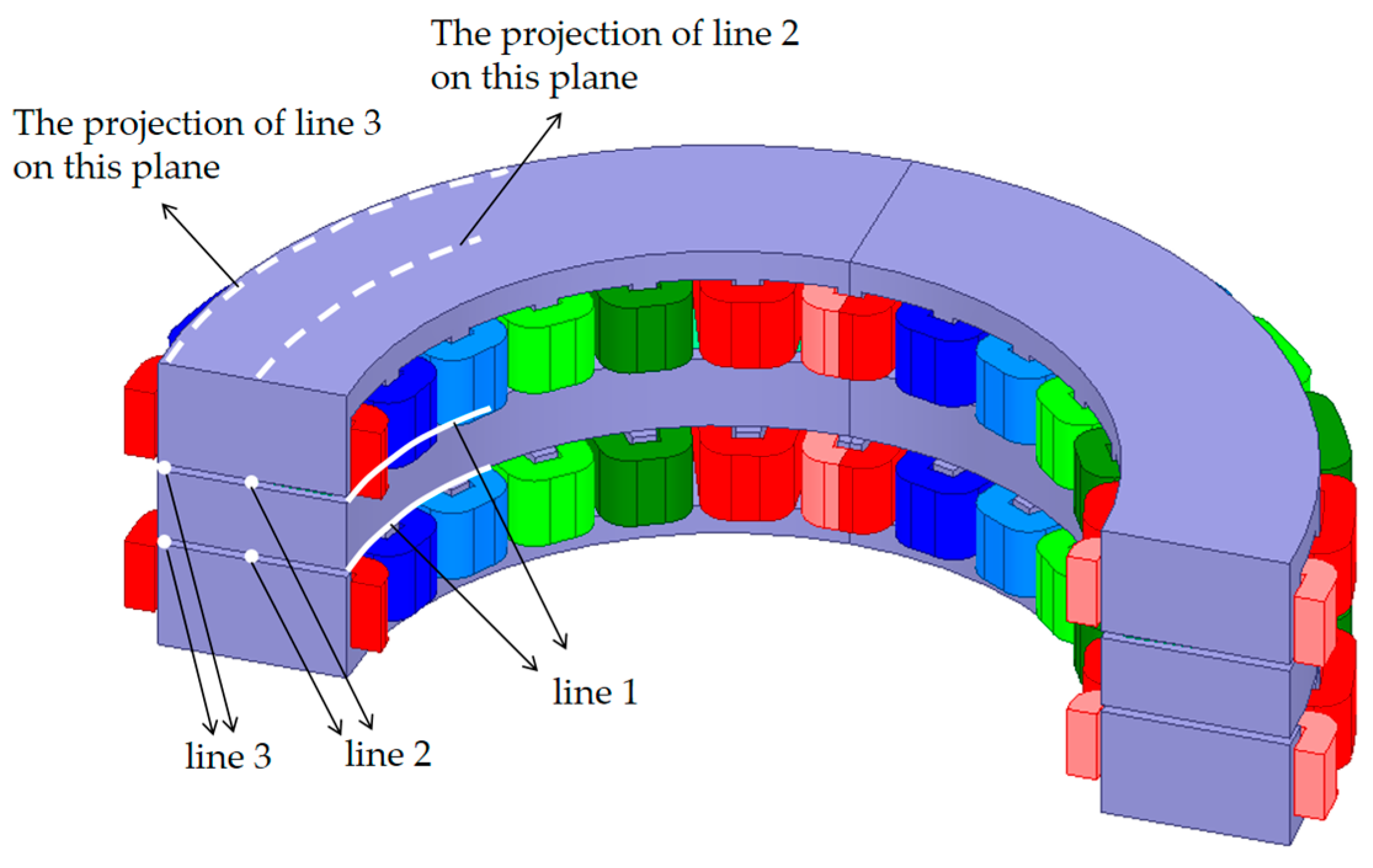
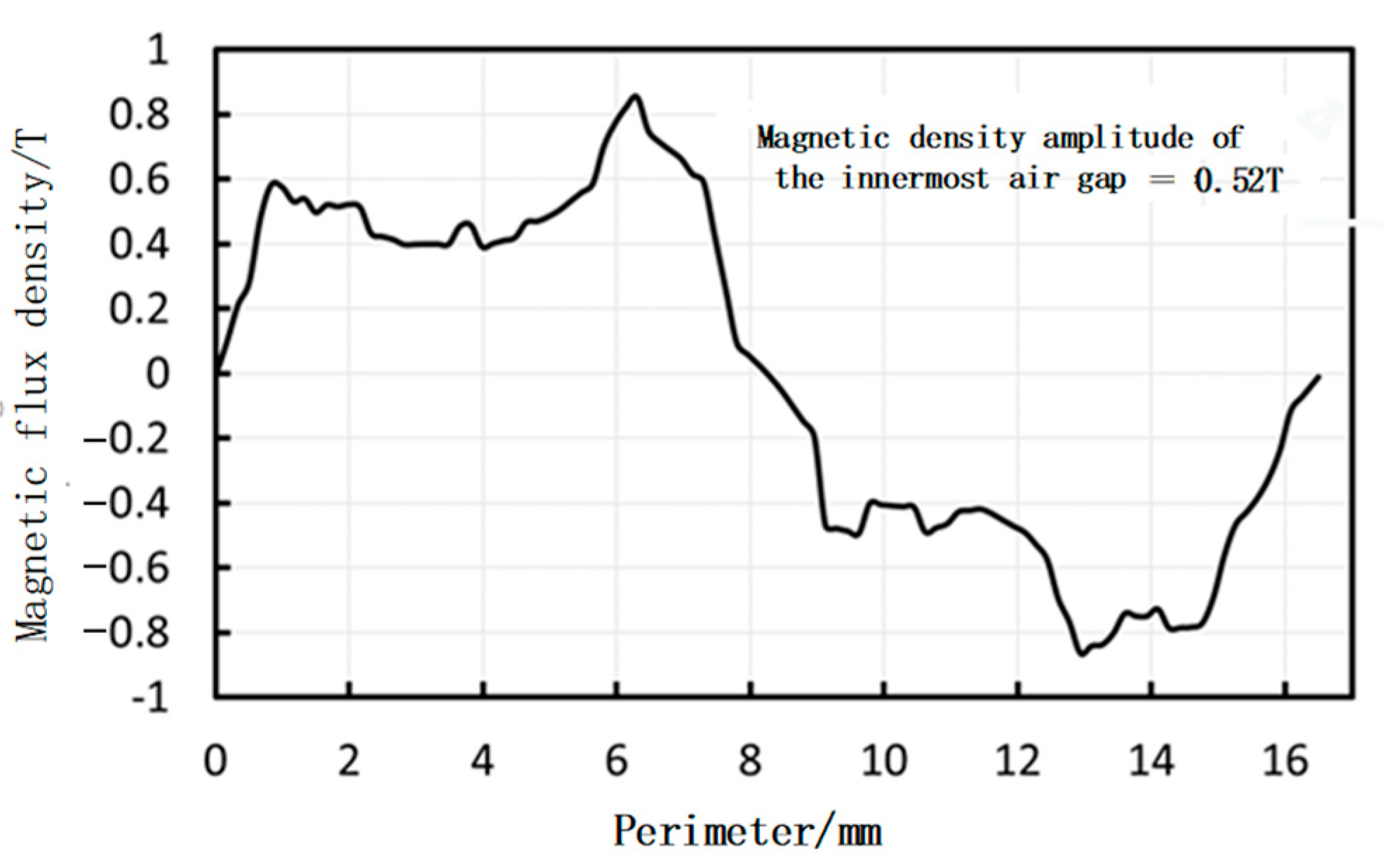
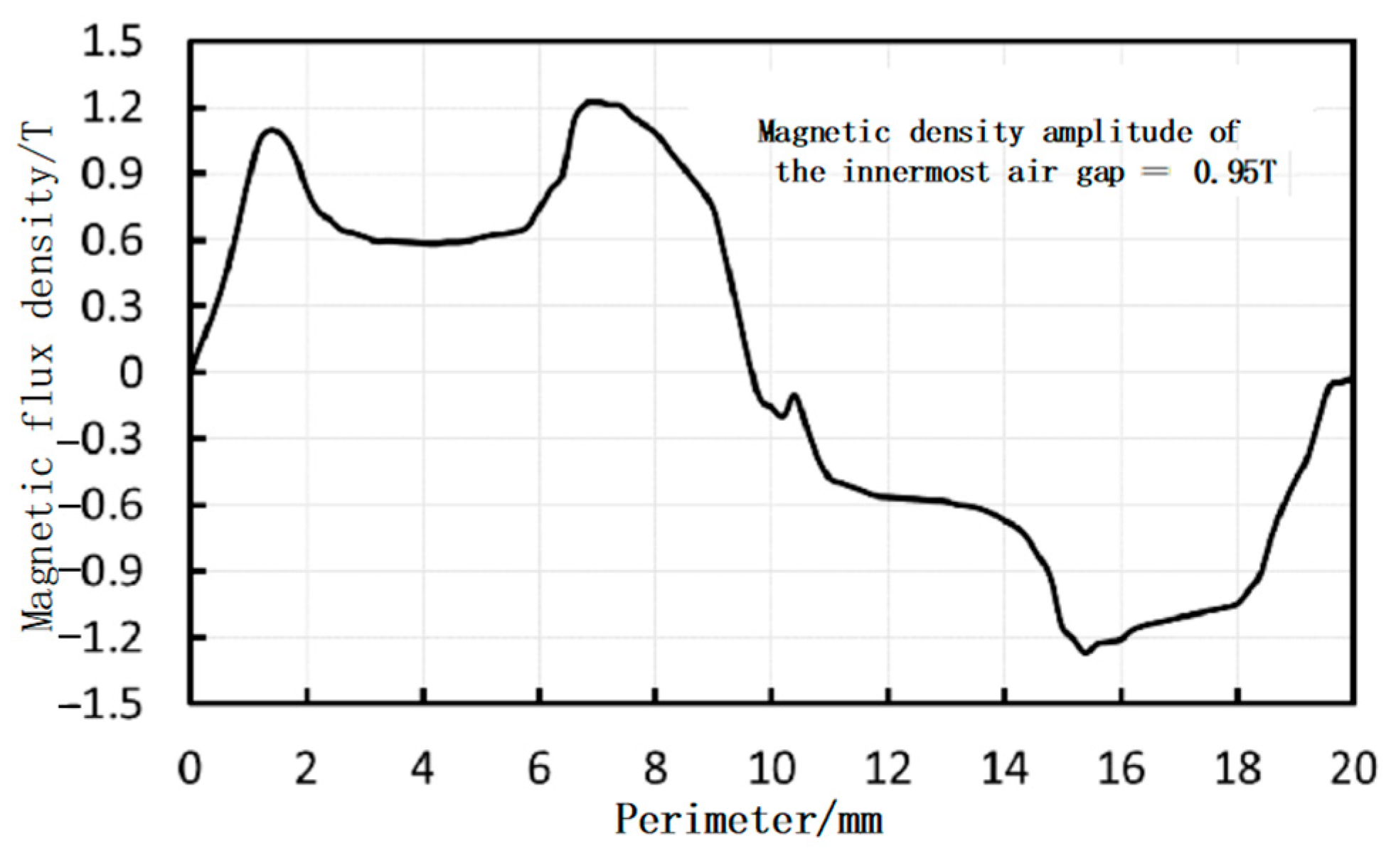
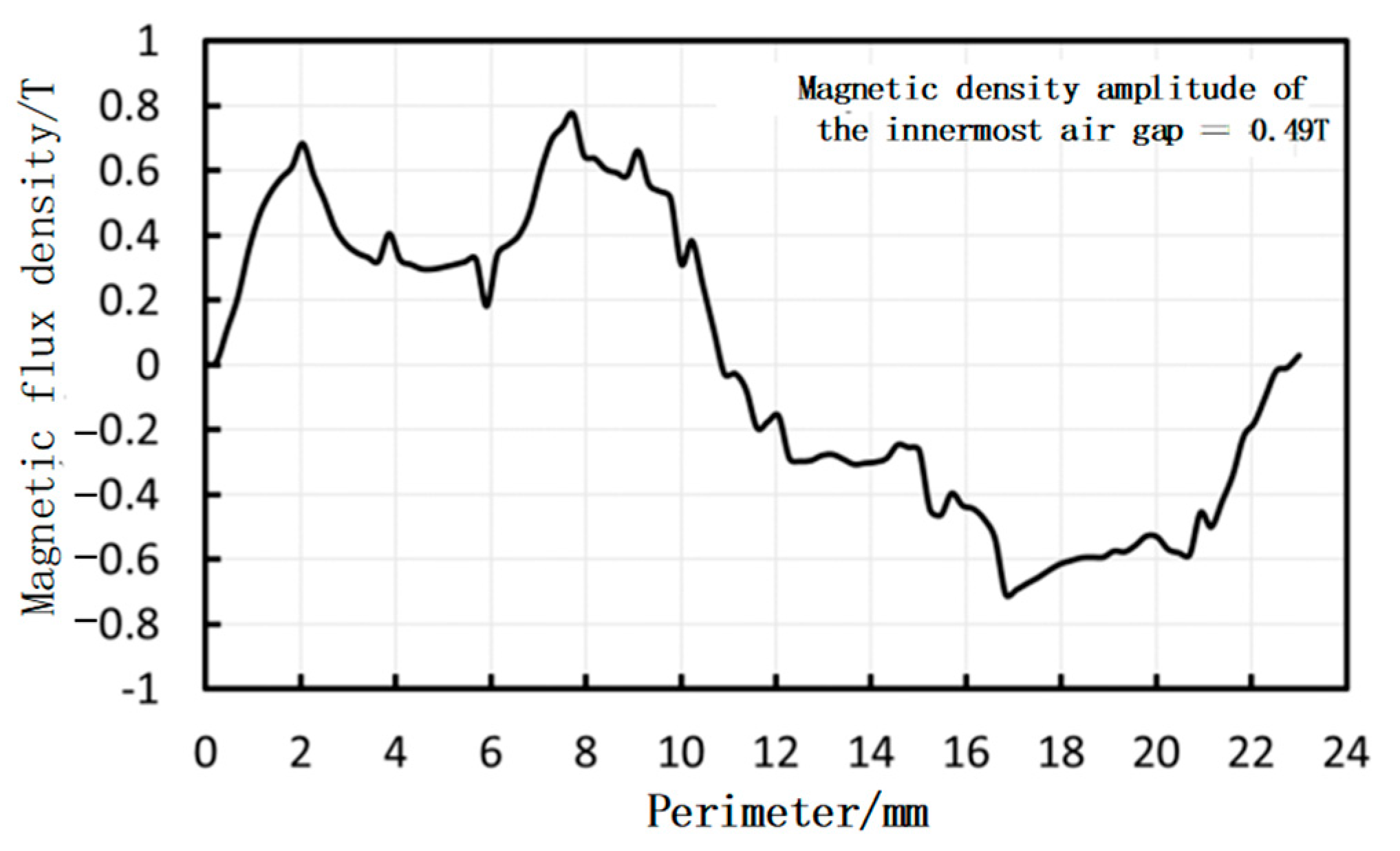
3.1. Static Magnetic Field Analysis
3.2. Transient Analysis
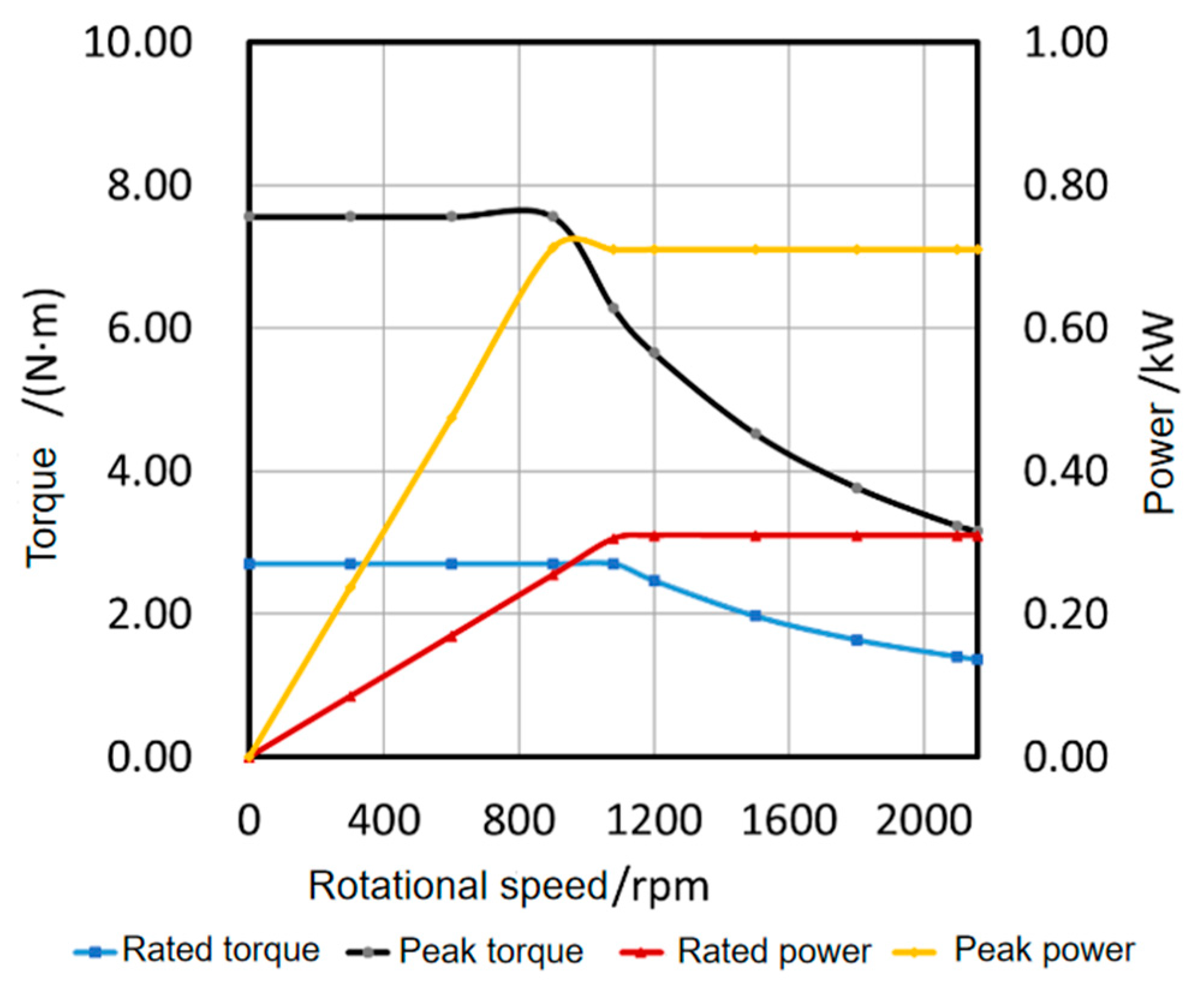
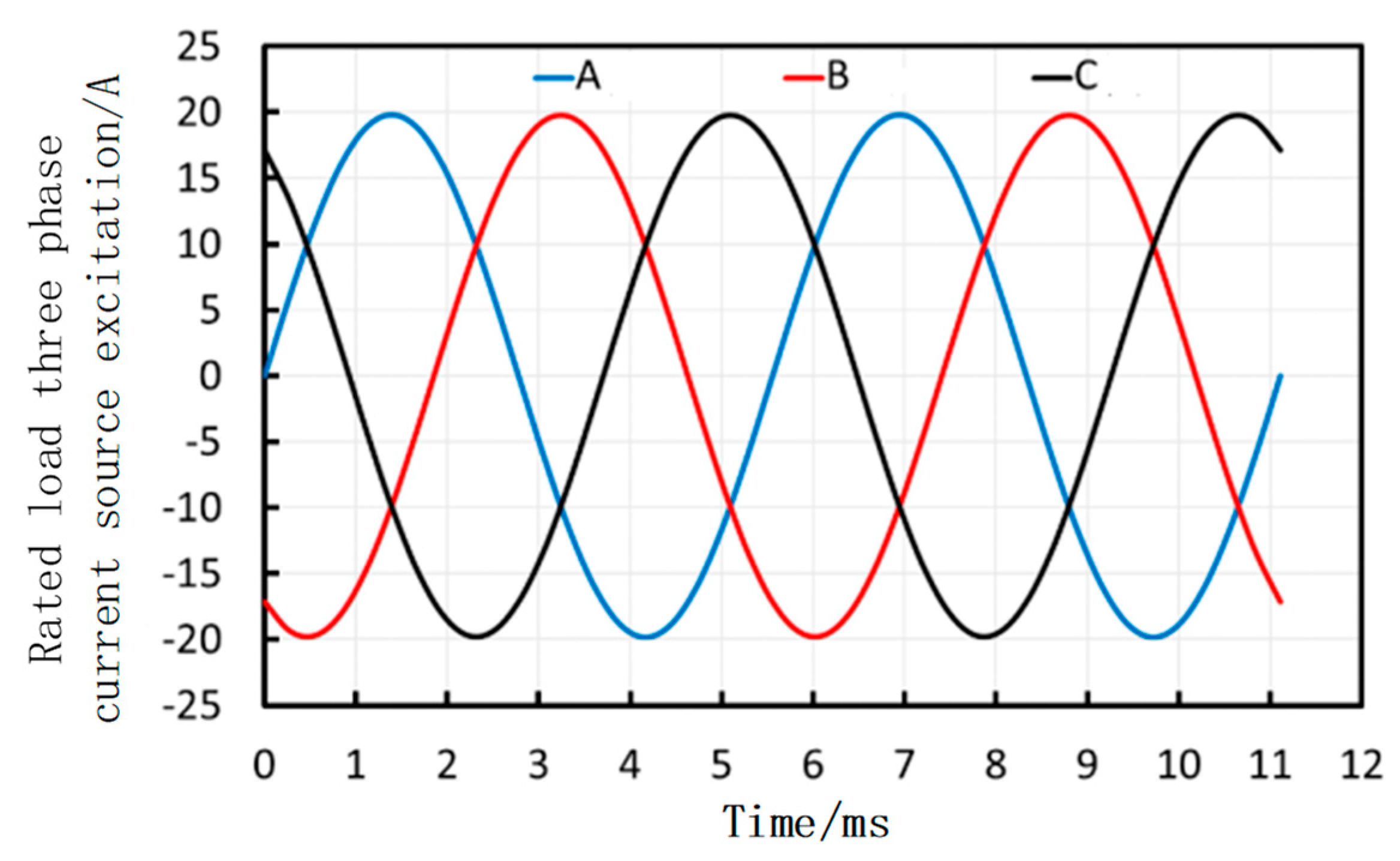
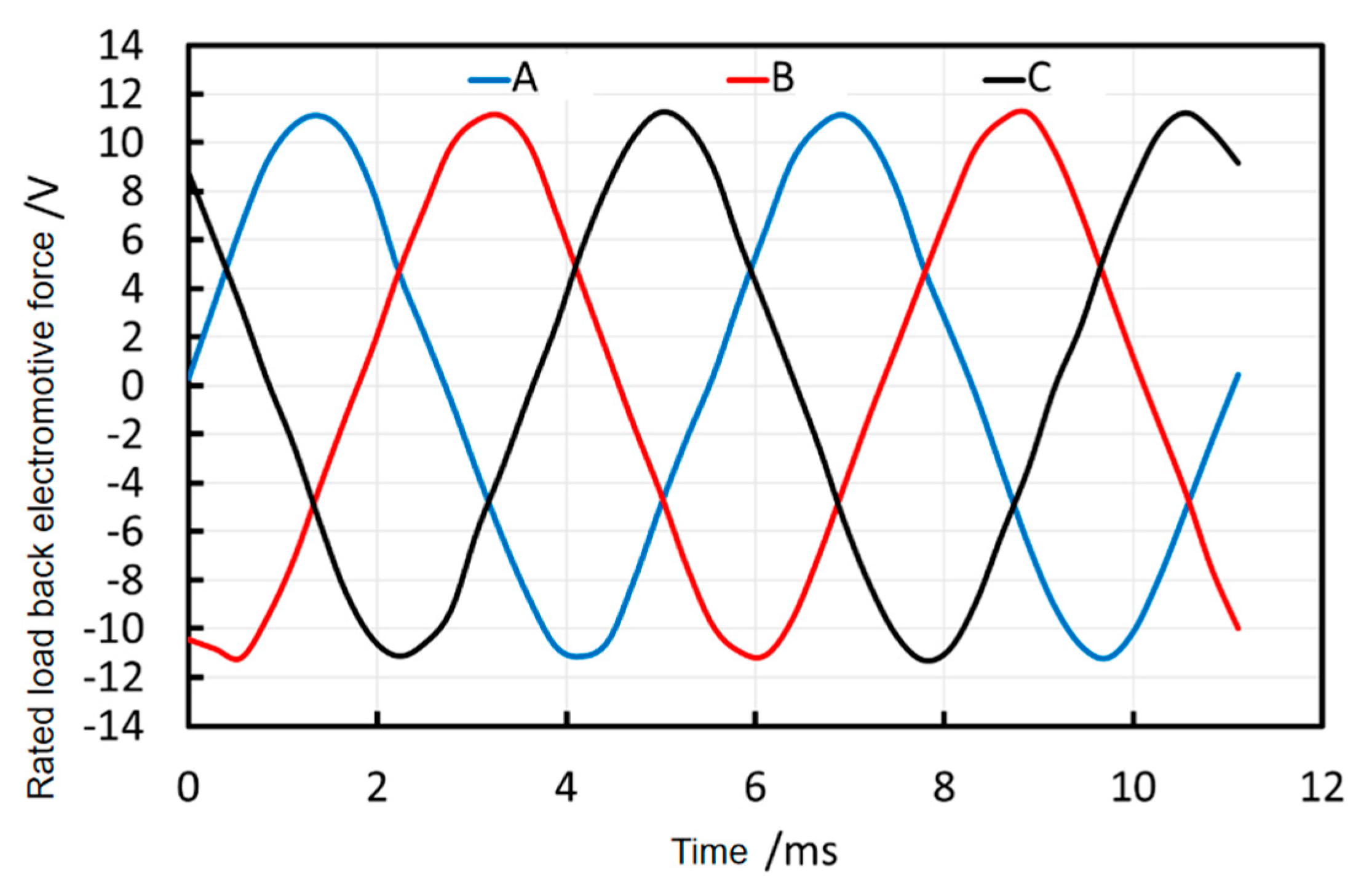
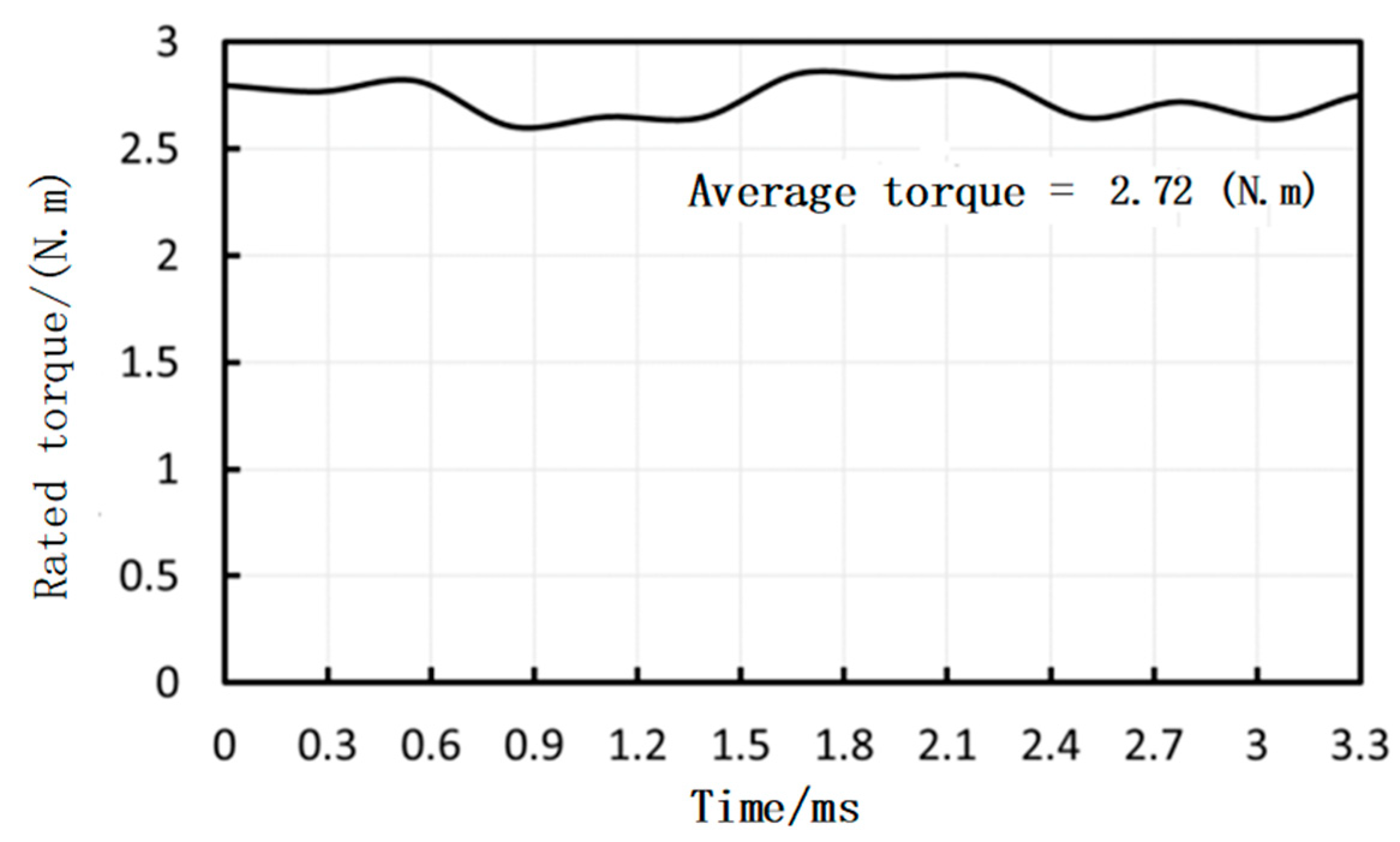
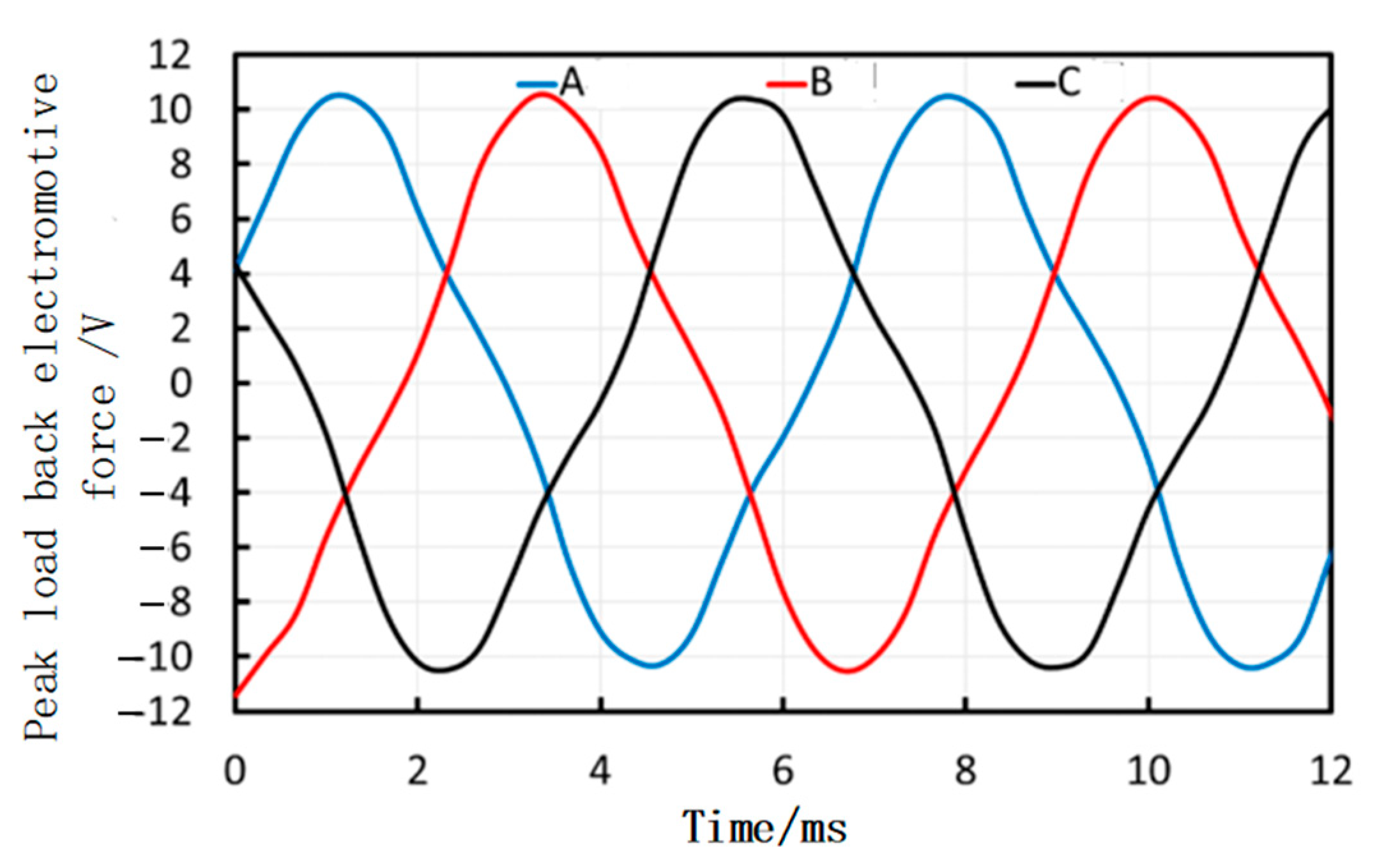
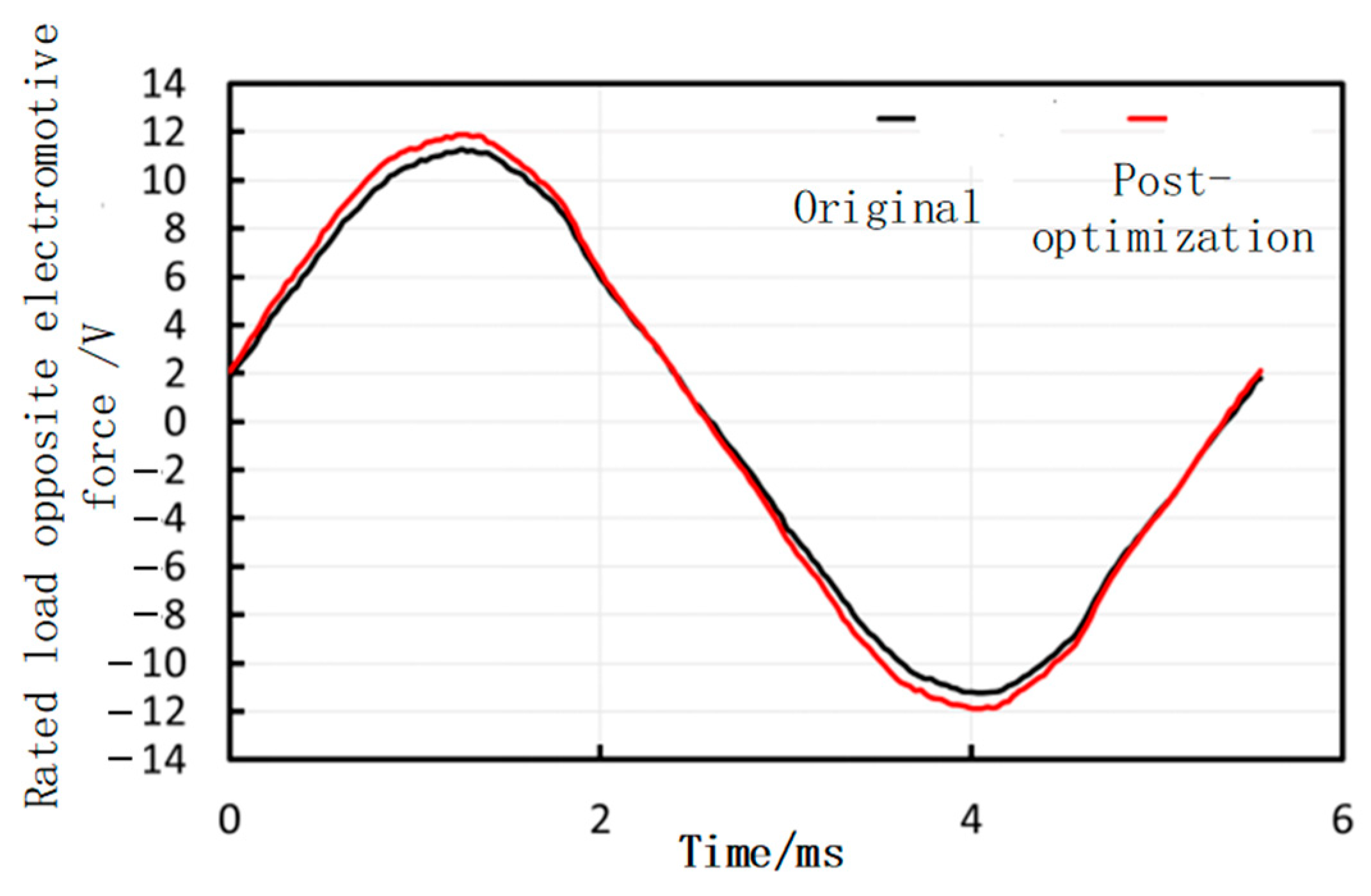
3.2.1. Rated Load Characteristics
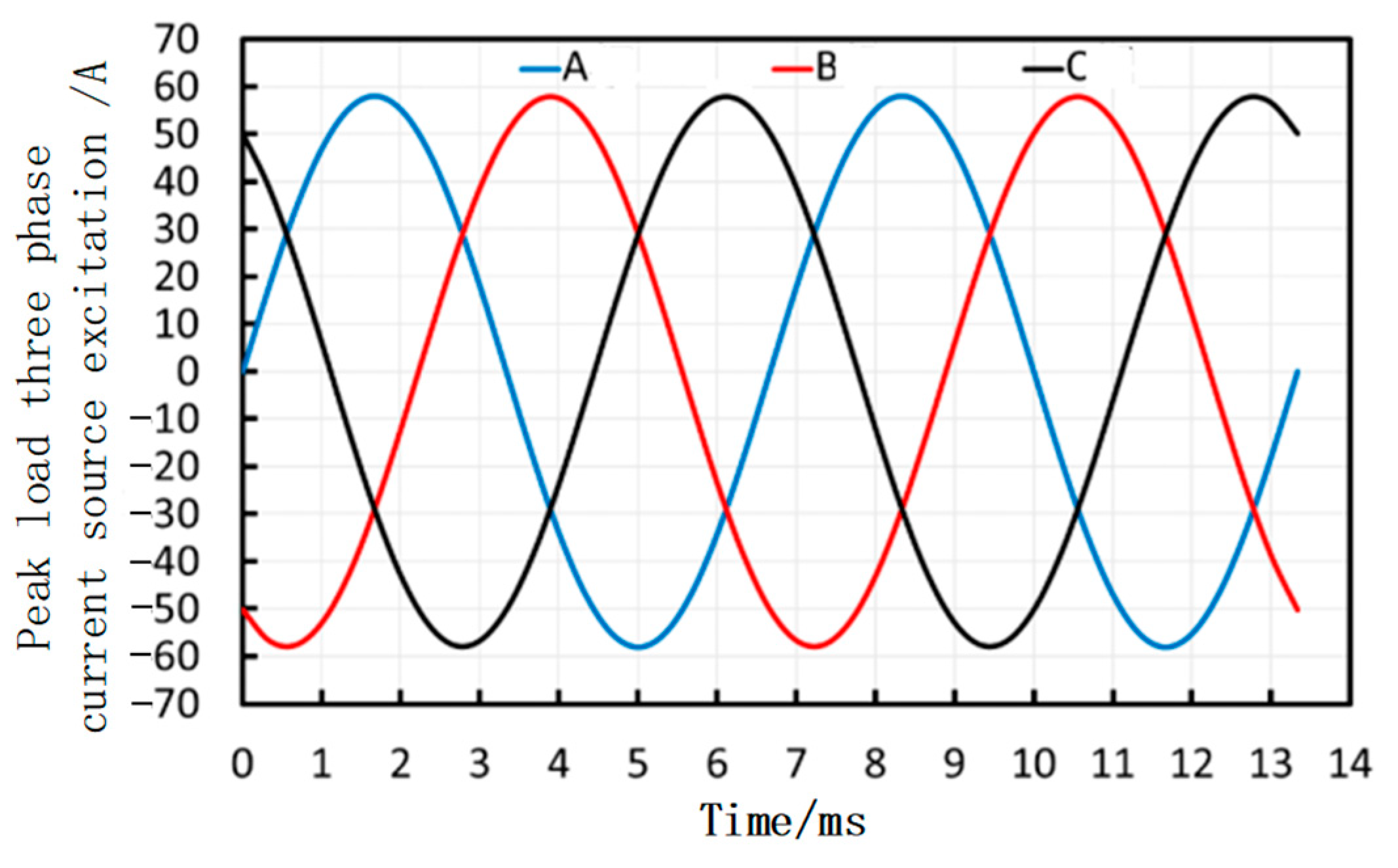
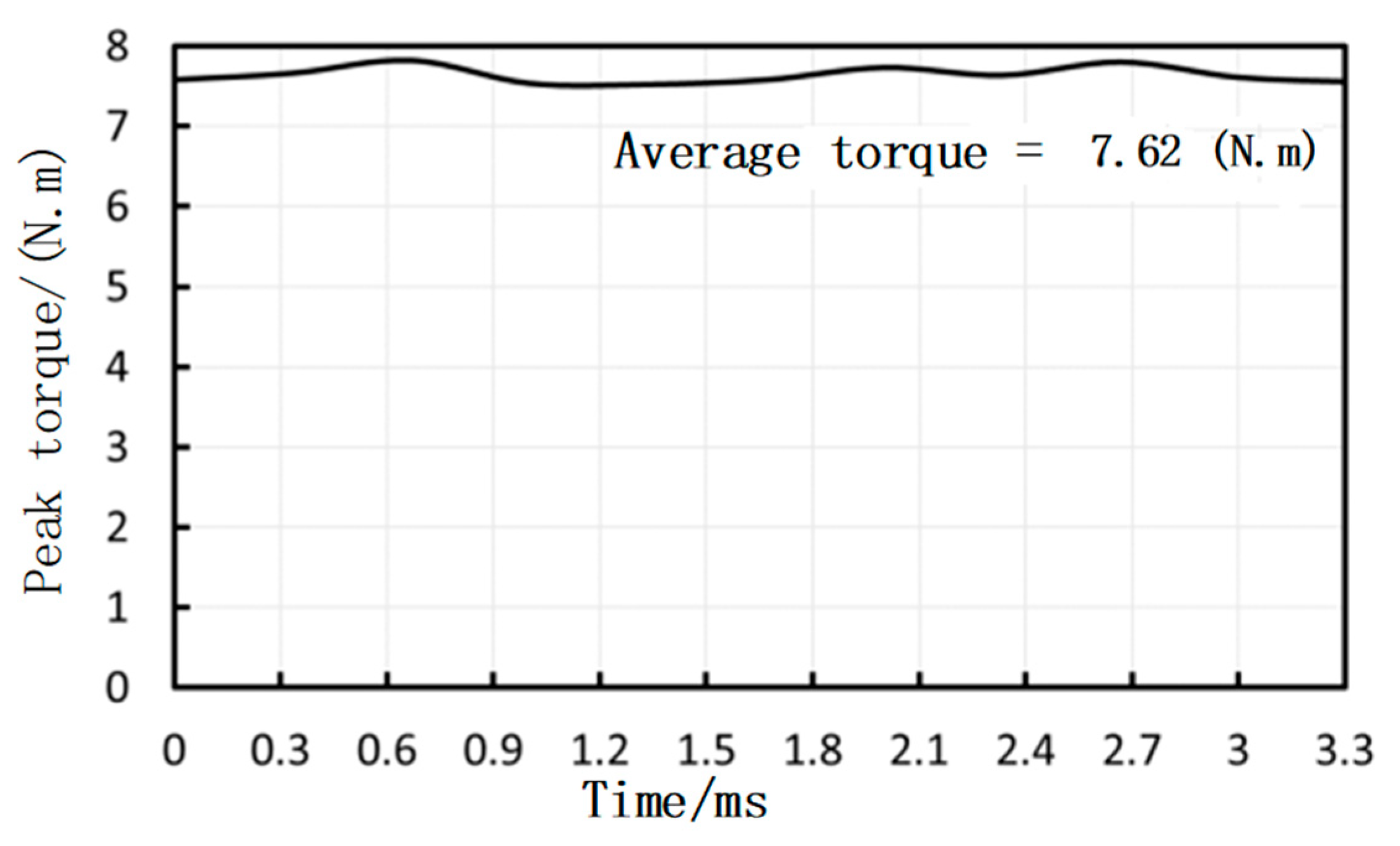
3.2.2. Peak Load Characteristics
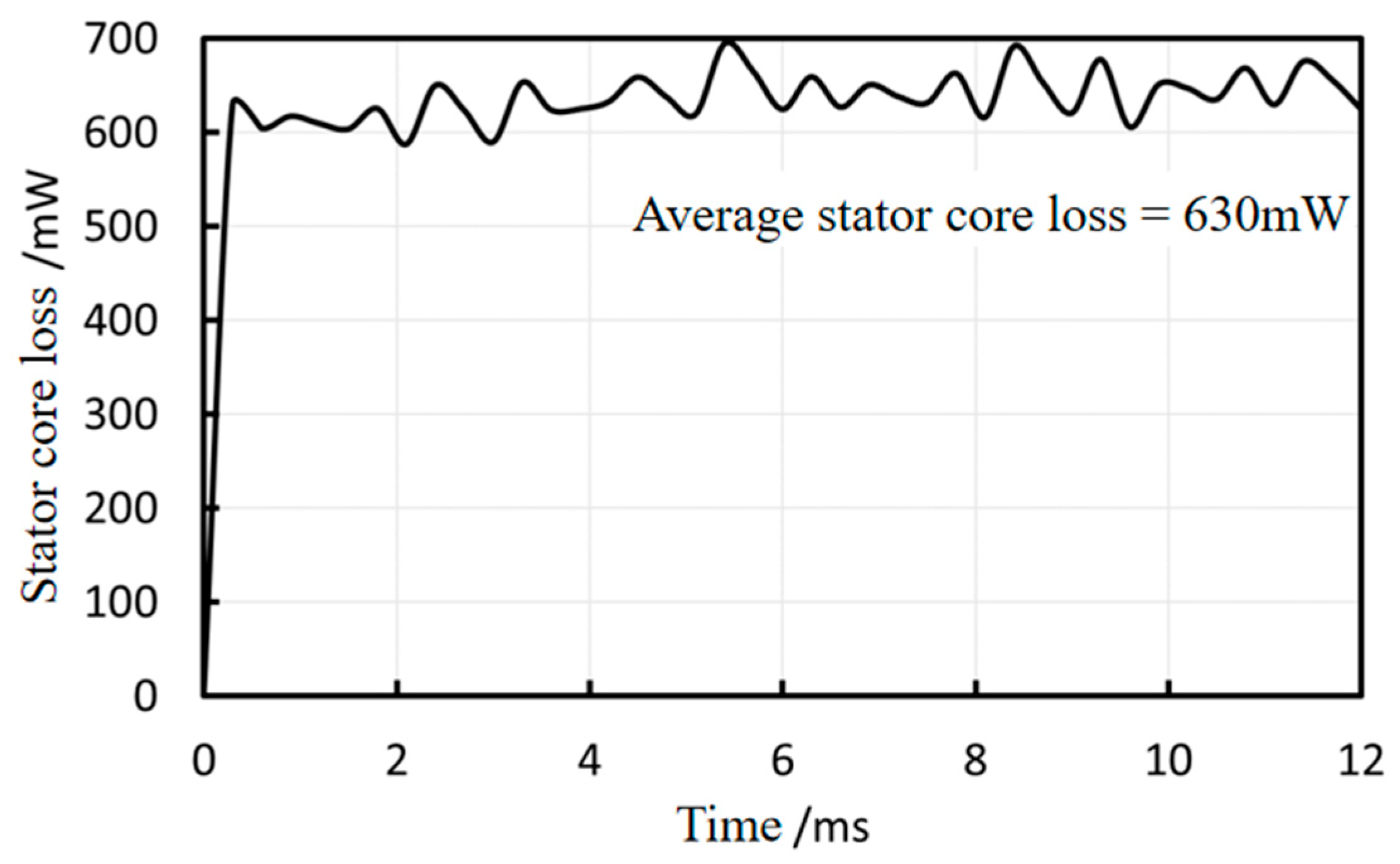
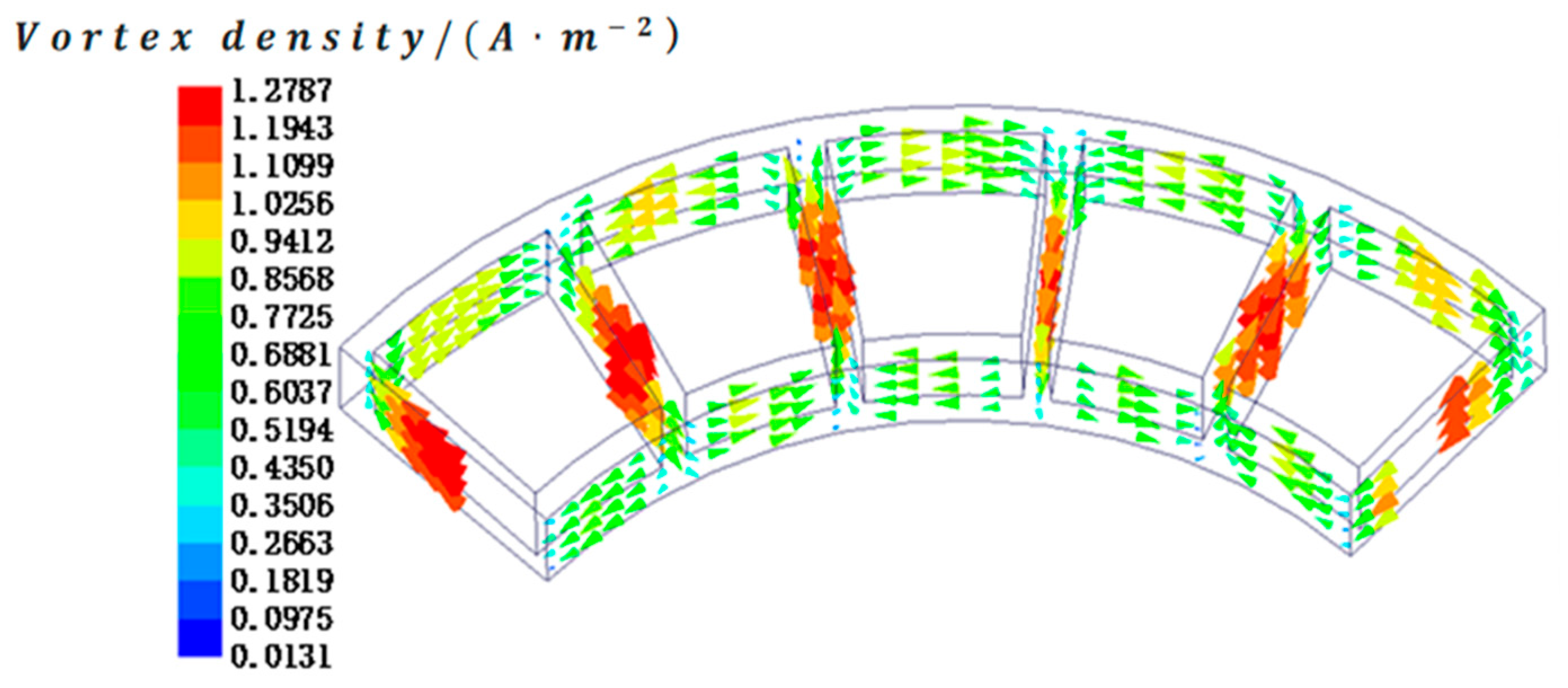
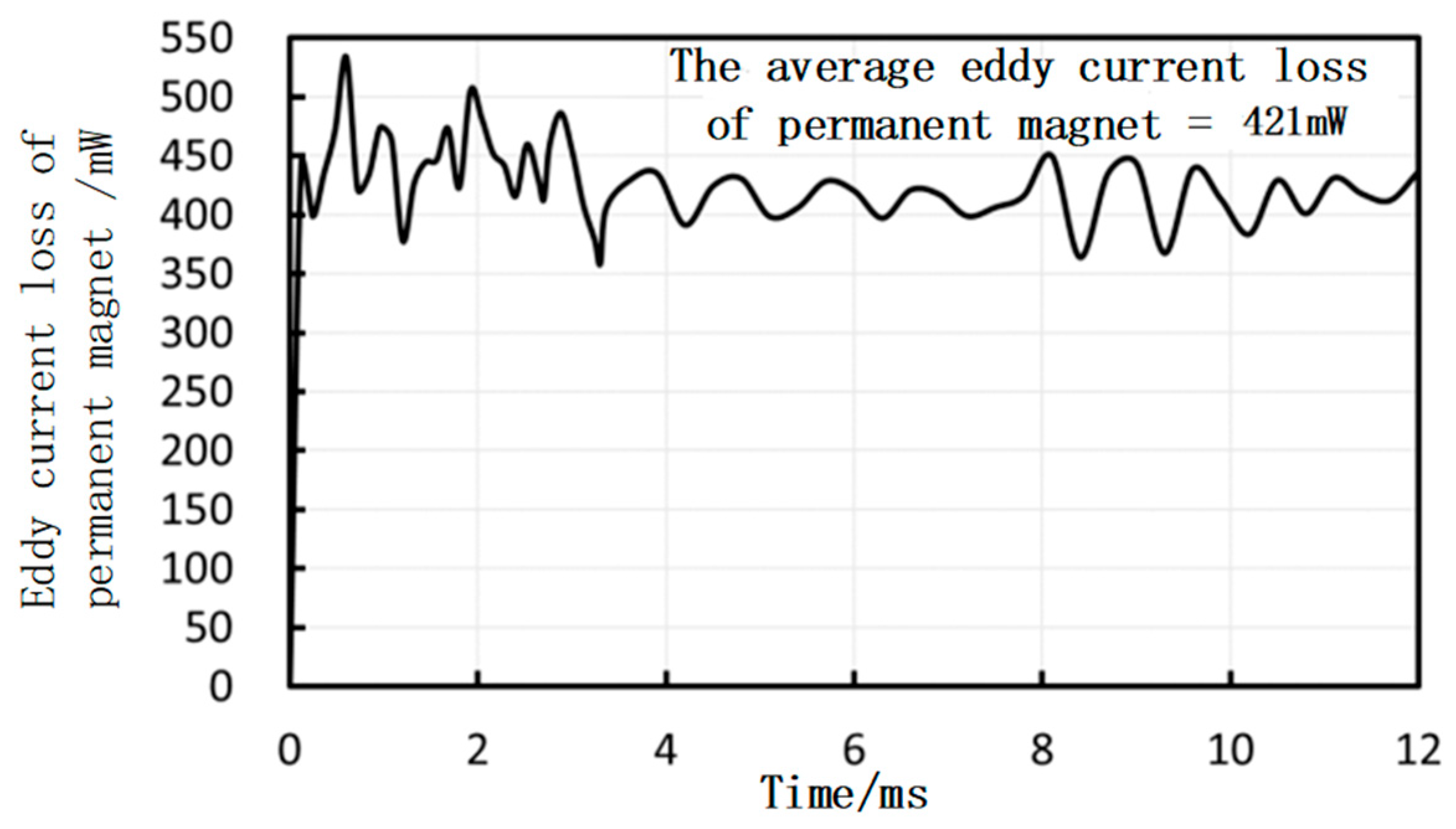
3.3. Loss Analysis
4. Electromagnetic Torque Modeling and Torque Density Optimization
4.1. Electromagnetic Torque Model
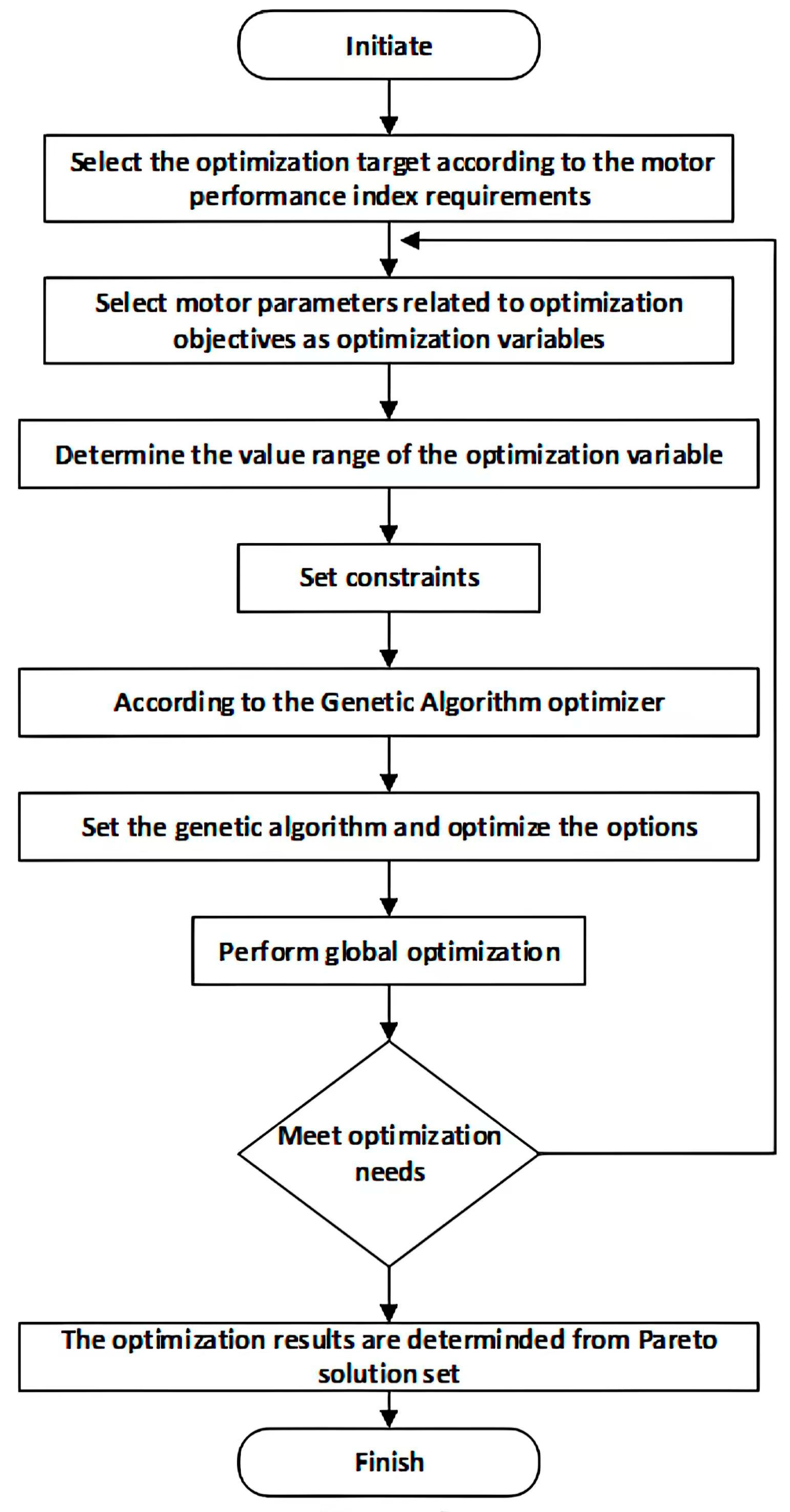
4.2. Torque Density Optimization
5. Performance Testing
5.1. Principle Prototype Development
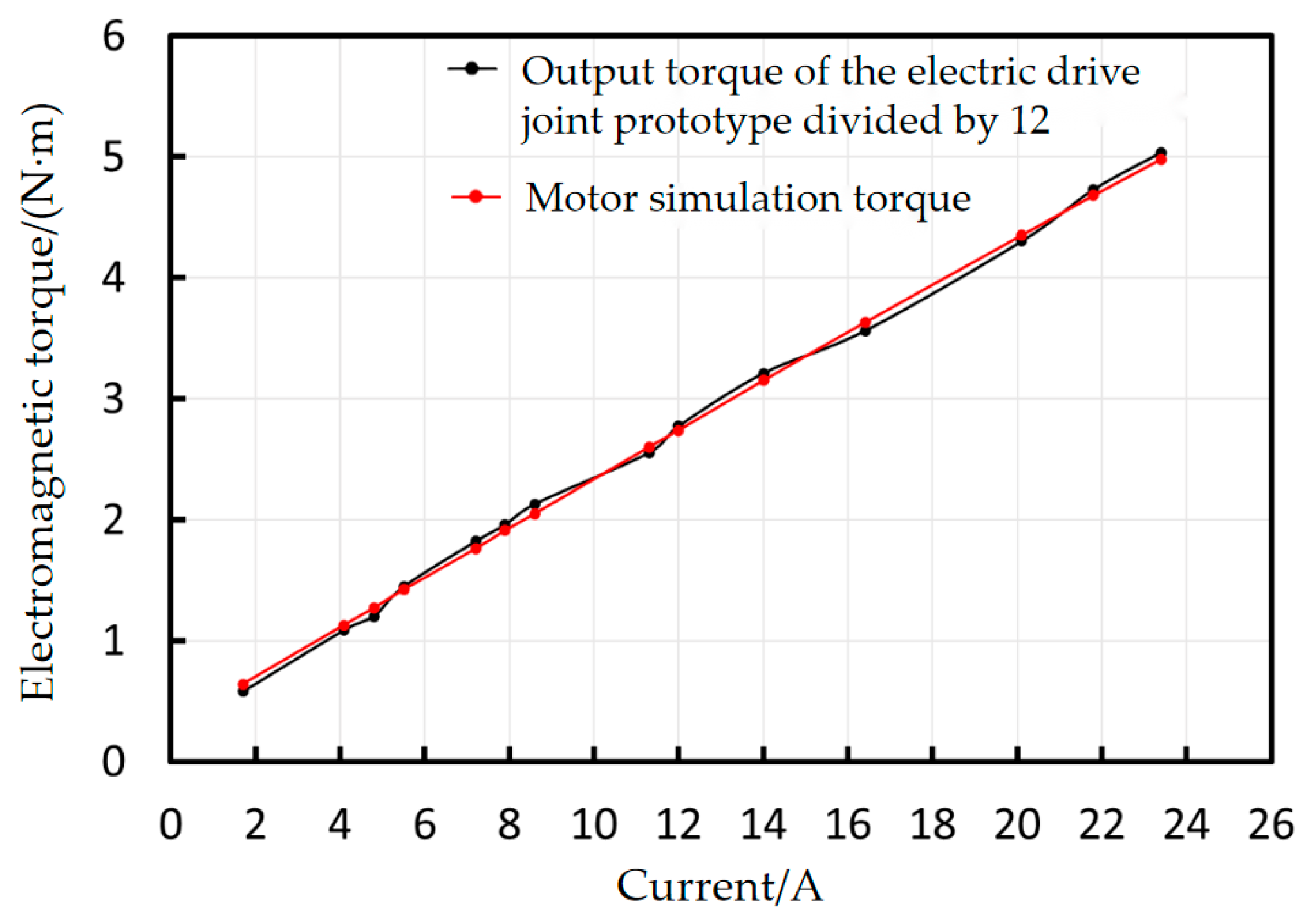
5.2. Torque Test
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kaliyev, V.; Helwig, A.; Ahfock, T. Axial flux PM coreless stator machine development for low sp eed wind generator. In Proceedings of the 2017 Australasian Universities Power Engineering Conference (AUPEC), Melbourne, Australia, 19–22 November 2017; pp. 1–6. [Google Scholar]
- Eser, E.; Üstkoyuncu, N. Design and Analysis of a Novel Axial Flux Permanent Magnet Assisted Synchronous Reluctance Motor. J. Electr. Eng. Technol. 2024, 1–10, prepublish. [Google Scholar] [CrossRef]
- Kahourzade SMahmoudi, A.; Ping, H.W. A Comprehensive Review of Axial-Flux Permanent-Magnet Machines. Can. J. Electr. Comput. Eng. 2014, 37, 19–33. [Google Scholar] [CrossRef]
- Park, W.S.; Moon, H.J.; Kang, W.D.; Su, K.H. A Study on Enhancing Axial Flux Motor Efficiency Using Cladding Core Technology. Mathematics 2024, 12, 2981. [Google Scholar] [CrossRef]
- Augusto, A.; Caetano, E.R. Design of a Yokeless double disc axial flux motor for light electric vehicles. Frankl. Open 2024, 8, 100166. [Google Scholar] [CrossRef]
- Parada, G.A.; Valle, D.M.F.; Tous, B.R. Design and Construction of a Multipole Electric Motor Using an Axial Flux Configuration. World Electr. Veh. J. 2024, 15, 256. [Google Scholar] [CrossRef]
- Yim, W.; Yoon, J.; Cha, J.; Bong, U.; Hahn, S. A design study on 20 kW class axial flux motor with HTS field winding for 100 MPa liquid hydrogen pump. Cryogenics 2024, 139, 103829. [Google Scholar] [CrossRef]
- Jiujian, C.; Kaijie, Y.; Yuhao, D.; Lu, X. Design and Optimization of a Novel External-Rotor Axial Flux Motor for In-Wheel Application. J. Electr. Eng. Technol. 2024, 19, 2473–2479. [Google Scholar]
- Jiujian, C.; Chen, W. Electromagnetic thermal coupling analysis for a novel cooling system of an axial flux hub motor. IET Electr. Power Appl. 2021, 16, 421–433. [Google Scholar]
- Chelarem, B.D.; Bilal, A.; Elhadj, A.; Felseghi, R.A.; Filote, C.; Dumitrescu, C.; Raboaca, M.S. Design Development and Analysis of a Partially Superconducting Axial Flux Motor Using YBCO Bulks. Materials 2021, 14, 4295. [Google Scholar]
- Laitram, L.L.C. Patent Issued for Axial Flux Motor For A Conveyor (USPTO 10,723,562). J. Eng. 2020, 6472. [Google Scholar]
- Gieras, J.F.; Gieras, I.A. Performance analysis of a coreless permanent magnet brushless motor. In Proceedings of the 2002 IEEE Industry Applications Conference. 37th IAS Annual Meeting (Cat. No.02CH37344), Pittsburgh, PA, USA, 13–18 October 2002; pp. 2477–2482. [Google Scholar]
- Gieras, J.F.; Wang, R.J.; Kamper, M. Axial Flux Permanent Magnet Brushless Machines; Springer: New York, NY, USA, 2008; pp. 29–34. [Google Scholar]
- Ahmed, D.; Ahmad, A. An optimal design of coreless direct-drive axial flux permanent magnet generator for wind turb ine. In Proceedings of the 6th Vacuum and Surface Sciences Conference of Asia and Australia (VASSCAA-6), Islamabad, Pakistan, 9–13 October 2012. J. Phys. Conf. Ser. 2013, 439, 012039. [Google Scholar] [CrossRef]
- Credo, A.; Tursini, M.; Villani, M.; Di Lodovico, C.; Orlando, M.; Frattari, F. Axial Flux PM In-Wheel Motor for Electric Vehicles: 3D Multiphysics Analysis. Energies 2021, 14, 2107. [Google Scholar] [CrossRef]
- Hong, K.M.; Pyo, J.H.; Song, W.S.; Jung, D.H.; Kim, W.H. A Study on the Improvement of Power Density of Axial Flux Motors for Collaborative Robot Joints through Same-Direction Skew. Machines 2023, 11, 591. [Google Scholar] [CrossRef]
- Tiegna, H.; Amara, Y.; Barakat, G. Study of Cogging Torque in Axial Flux Permanent Magnet Machines Using an Analytical Model. IEEE Trans. Magn. 2014, 50, 845–848. [Google Scholar] [CrossRef]
- Polikarpova, M.; Lindh, P.; Gerada, C.; Rilla, M.; Naumanen, V.; Pyrhönen, J. Thermal effects of stator potting in an axial-flux permanent magnet synchronous generator. Appl. Therm. Eng. 2015, 75, 421–429. [Google Scholar] [CrossRef]
- Yang, Y.P.; Shih, G.Y. Optimal Design of an Axial-Flux Permanent-Magnet Motor for an Electric Vehicle Based on Driving Scenarios. Energies 2016, 9, 285. [Google Scholar] [CrossRef]
- Darabi, A.; Baghayip, M.; Mirzahosseini, R. An Extended Analytical Algorithm for Optimal Designing of a TORUS-type Non-slotted Axial-Flux Permanent Magnet Motor. J. Control Autom. Electr. Syst. 2017, 28, 748–761. [Google Scholar] [CrossRef]
- Zhao, J.; Hua, M.; Liu, T. Research on a Sliding Mode Vector Control System Based on Collaborative Optimization of an Axial Flux Permanent Magnet Synchronous Motor for an Electric Vehicle. Energies 2018, 11, 3116. [Google Scholar] [CrossRef]
- Kutt, F.; Blecharz, K.; Karkosiński, D. Axial-Flux Permanent-Magnet Dual-Rotor Generator for a Counter-Rotating Wind Turb ine. Energies 2020, 13, 2833. [Google Scholar] [CrossRef]
- Wang, H.; Zeng, X.; Eastham, F.J.; Pei, X. Axial Flux Permanent Magnet Motor Topologies Magnetic Performance Comparison. Energies 2024, 17, 401. [Google Scholar] [CrossRef]
- Ge, W.; Xiao, Y.; Cui, F.; Wu, X.; Liu, W. Optimization Comparison of Torque Performance of Axial-Flux Permanent-Magnet Motor Using Differential Evolution and Cuckoo Search. Actuators 2024, 13, 255. [Google Scholar] [CrossRef]













| Motor Component | Material Name |
|---|---|
| Permanent magnet | N45SH |
| Rotor core | Stainless steel 304 |
| Stator core | 1J22 |
| Stator winding | Copper |
| Loss Name | Parameter Value | Unit |
|---|---|---|
| Stator core loss | 0.63 | W |
| Stator winding loss | 33.31 | W |
| Eddy current loss of rotor core | 0.11 | W |
| Eddy current loss of permanent magnet | 0.42 | W |
| Mechanical loss | 7.5 | W |
| Parameter Name | Parameter Range | Unit |
|---|---|---|
| 4.5~5.5 | mm | |
| Stator groove depth | 4.9~5.9 | mm |
| Thickness of stator yoke | 1.6~2.6 | mm |
| 4.5~5.5 | mm | |
| Motor air gap length | 0.3~0.7 | mm |
| Name | Quantity | Pre-Optimized Weight | Optimized Weight | Unit |
|---|---|---|---|---|
| Stator core | 2 | 0.288 | 0.284 | kg |
| Winding | 48 | 0.254 | 0.254 | kg |
| Permanent magnet | 20 | 0.064 | 0.061 | kg |
| Gross weight | 1 | 0.606 | 0.599 | kg |
| Parameter Name | Before Optimization | Post-Optimization | Unit |
|---|---|---|---|
| Width of stator notch | 5 | 4.8 | mm |
| Stator groove depth | 5.4 | 5.2 | mm |
| Thickness of stator yoke | 2.1 | 2 | mm |
| Thickness of permanent magnet | 5 | 4.8 | mm |
| Air gap length | 0.5 | 0.4 | mm |
| Slot filling rate | 0.68 | 0.74 | / |
| Opposite maximum electromotive force | 11.3 | 11.9 | V |
| 1.4 | 1.42 | T | |
| 1.8 | 1.83 | T | |
| Average electromagnetic torque | 2.7 | 3.2 | N.m |
| Effective mass | 0.606 | 0.599 | kg |
| Torque density | 4.45 | 5.34 | N.m/kg |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Quan, D.; He, C.; Li, C.; Zhao, Z.; Yang, X.; Ma, L.; Li, M.; Zhao, Y.; Wu, H. The Design, Analysis, and Verification of an Axial Flux Permanent Magnet Motor with High Torque Density. Appl. Sci. 2025, 15, 3327. https://doi.org/10.3390/app15063327
Quan D, He C, Li C, Zhao Z, Yang X, Ma L, Li M, Zhao Y, Wu H. The Design, Analysis, and Verification of an Axial Flux Permanent Magnet Motor with High Torque Density. Applied Sciences. 2025; 15(6):3327. https://doi.org/10.3390/app15063327
Chicago/Turabian StyleQuan, Dapeng, Caiting He, Chenyuan Li, Zeming Zhao, Xiaoze Yang, Limei Ma, Mingyang Li, Yong Zhao, and Hongtao Wu. 2025. "The Design, Analysis, and Verification of an Axial Flux Permanent Magnet Motor with High Torque Density" Applied Sciences 15, no. 6: 3327. https://doi.org/10.3390/app15063327
APA StyleQuan, D., He, C., Li, C., Zhao, Z., Yang, X., Ma, L., Li, M., Zhao, Y., & Wu, H. (2025). The Design, Analysis, and Verification of an Axial Flux Permanent Magnet Motor with High Torque Density. Applied Sciences, 15(6), 3327. https://doi.org/10.3390/app15063327






