Voronoi-GRU-Based Multi-Robot Collaborative Exploration in Unknown Environments

Abstract

In modern society, the autonomous exploration of unknown environments has attracted extensive attention due to its broad applications, such as in search and rescue operations, planetary exploration, and environmental monitoring. This paper proposes a novel collaborative exploration strategy for multiple mobile robots, aiming to quickly realize the exploration of entire unknown environments. Specifically, we investigate a hierarchical control architecture, comprising an upper decision-making layer and a lower planning and mapping layer. In the upper layer, the next frontier point for each robot is determined using Voronoi partitioning and the Multi-Agent Twin Delayed Deep Deterministic policy gradient (MATD3) deep reinforcement learning algorithm in a centralized training and decentralized execution framework. In the lower layer, navigation planning is achieved using A* and Timed Elastic Band (TEB) algorithms, while an improved Cartographer algorithm is used to construct a joint map for the multi-robot system. In addition, the improved Robot Operating System (ROS) and Gazebo simulation environments speed up simulation times, further alleviating the slow training of high-precision simulation engines. Finally, the simulation results demonstrate the superiority of the proposed strategy, which achieves over 90% exploration coverage in unknown environments with a significantly reduced exploration time. Compared to MATD3, Multi-Agent Proximal Policy Optimization (MAPPO), Rapidly-Exploring Random Tree (RRT), and Cost-based methods, our strategy reduces time consumption by 41.1%, 47.0%, 63.9%, and 74.9%, respectively.

1. Introduction

With the advent of critical applications such as Mars exploration and cave rescue missions, research on multi-robot collaborative exploration in unknown environments [1,2,3] has garnered significant attention. Multi-robot systems significantly enhance task efficiency and robustness over single-robot exploration by sharing information and operating in parallel through a centralized decision-distributed execution paradigm [4,5]. However, challenges such as exploration redundancy—where multiple robots inadvertently cover the same area—impede effective collaboration. This not only wastes valuable resources but also prevents multi-robot systems from achieving optimal exploration efficiency [6,7]. Therefore, addressing these challenges is necessary to fully leverage the potential of multi-robot systems in critical applications, ensuring that missions are completed more effectively.

To address these challenges, researchers have proposed various methods for multi-robot collaborative exploration. Environment partitioning techniques, such as Voronoi partitioning [1,8], have shown promise in minimizing redundancy by dividing the exploration area into non-overlapping regions [9]. Numerical optimization approaches have been employed to optimize robot trajectories and coverage [10], while heuristic methods have been developed to guide exploration strategies [11,12]. Distributed control algorithms have also been introduced to enhance scalability and reduce communication overhead [13,14]. Voronoi partitioning has emerged as particularly effective for its ability to minimize redundant exploration [1]. This approach reduces redundancy and enables scalable, efficient exploration by allowing robots to make independent decisions within their designated areas, thereby reducing communication overhead.

Alongside these approaches, model-based methods [15,16], such as RACER (Rapid Collaborative Exploration with a Decentralized Multi-UAV System) [16], have demonstrated strong performance in multi-robot exploration. RACER employs a decentralized approach, where each UAV makes decisions based on local information and limited communication with neighbors, enabling efficient and scalable exploration. Model-based methods often leverage explicit representations of the environment and robot dynamics to achieve optimal or near-optimal exploration strategies.

Deep Reinforcement Learning (DRL) [17] and Multi-Agent Reinforcement Learning (MARL) approaches [18,19] have also been widely applied to multi-robot collaborative exploration due to their ability to learn complex policies from raw sensory inputs [20]. The corresponding algorithms enable robots to adapt to dynamic environments and unforeseen challenges without explicit programming, thereby enhancing their decision-making capabilities [21]. Therefore, the multi-robot collaborative exploration problem can be effectively modeled as a Decentralized Partially Observable Markov Decision Process (Dec-POMDP) [22], where each robot acts as an agent.

Despite these advancements, existing methods face several challenges. Voronoi partitioning lacks adaptability in highly dynamic or unpredictable environments, as static partitioning may not reflect current environmental states or robot positions [1]. Conversely, MARL approaches, while powerful in learning collaborative behaviors, often suffer from slow convergence rates, scalability issues, and high communication overhead, especially when applied to large-scale or complex real-world scenarios [23,24]. Furthermore, many existing MARL methods are validated in simplified two-dimensional grid environments, limiting their applicability to practical exploration tasks that involve continuous and high-dimensional spaces [25].

To address these challenges, we propose a hierarchical exploration framework based on Voronoi partitioning and an enhanced MATD3, termed V-R-MATD3. This framework first utilizes Voronoi diagrams to partition the environment, autonomously assigning exploration areas to each robot to minimize redundant exploration and facilitate scalability [26]. Our choice of a learning-based approach, specifically V-R-MATD3, is motivated by its inherent adaptability [27,28]. Research [17] has demonstrated that model-free reinforcement learning provides greater flexibility in robotics applications and is particularly suitable for addressing complex problems. Unlike model-based methods, V-R-MATD3, which is based on the TD3 algorithm [29], learns directly from experience, allowing it to handle complex, high-dimensional state spaces, unmodeled dynamics, and sensor noise more effectively [30,31]. The integration of a Gated Recurrent Unit (GRU) layer further amplifies this adaptability by allowing robots to capture temporal dependencies within their observational data streams, thereby enhancing the coordination and informed decision-making capabilities of exploration strategies [32]. Additionally, we optimize the navigation and mapping performance by utilizing advanced SLAM techniques, providing high-quality experimental data and accelerating the training process.

The main contributions of this paper are as follows:

1.

An Innovative Decision-Making Framework: We propose V-R-MATD3, a hierarchical framework that, for the first time, combines Voronoi-driven spatial decomposition with GRU-augmented MATD3 for multi-robot exploration. The Voronoi partitioning allocates non-overlapping regions to eliminate redundant coverage, while the enhanced MATD3 algorithm leverages Voronoi-constrained action spaces and dual critic networks to optimize collaborative policies. The GRU layers model sequential state transitions, ensuring temporally coherent decision-making.

2.

Development of a Multi-Robot RL Toolkit: We develop an open-source toolkit compatible with the ROS and Gazebo platforms for multi-robot reinforcement learning. By adjusting the Cartographer framework, we achieve high-precision joint map construction, ensuring data quality during accelerated training.

3.

Design of a Prior-Guided Adaptive Hybrid Reward (PGAHR) Function: We propose a hybrid reward function, termed PGAHR, which combines dynamically adjusted intrinsic rewards with fixed extrinsic rewards. This function incorporates prior knowledge to maximize overall rewards and enhance learning efficiency. Specifically, we simplify the state space by subsampling the LiDAR measurements, and we reduce the robot’s action space using a spatial segmentation technique, which helps avoid excessive proximity between robots and contributes to maximizing the reward.

2. Background

2.1. Preliminaries

Voronoi partitioning: Numerous studies have introduced this spatial partitioning method [26,33,34]. Consider n robots collaboratively exploring a region Q. Let ${\mathit{p}}_i$ denote the position vector of robot i, and let ${\mathcal{N}}_i$ represent its neighbor set, where $i=1,\cdots ,n$. The Voronoi cell $V\left(i\right)$ is defined in Equation (1):

$$V\left(i\right)=\left\{\mathit{q}\in Q\mid \parallel \mathit{q}-{\mathit{p}}_i\parallel \le \parallel \mathit{q}-{\mathit{p}}_j\parallel ,\forall j\in {\mathcal{N}}_i\right\},$$

(1)

ensuring that any point $\mathit{q}$ within $V\left(i\right)$ is always closer to robot i than to any other neighboring robot j. This geometrically intuitive decomposition enables efficient spatial task allocation by minimizing coverage overlaps between adjacent robots.

Reinforcement learning: In reinforcement learning (RL), the reward is a scalar feedback signal that indicates how well an agent is performing in an environment. It is used to guide the learning process by providing immediate feedback after each action the agent takes. The objective of the reinforcement learning technique is to find an optimal shared policy ${\pi }^{*}$ [35,36] that maximizes the expected cumulative reward:

$${\pi }^{*}=arg\underset{\pi }{max}{\mathbb{E}}_{\pi }\left[R\right],$$

(2)

where $\pi$ represents the shared policy, and ${\mathbb{E}}_{\pi }\left[R\right]$ denotes the expected cumulative reward. By learning this policy, the robots can effectively coordinate their actions to explore the region Q more efficiently through iterative environment interactions, balancing the exploration of unknown areas and the exploitation of gathered knowledge.

Robot motion planning: Robot motion planning serves as the core technology for robotic autonomous navigation and task execution, aiming to generate safe and efficient motion trajectories for robots operating in complex environments. The key terminology employed in this paper is outlined as follows:

• LiDAR: A laser-based sensor used to measure distances, used in this work for mapping and obstacle detection.
• Global Plan: The optimal path from the start to the goal computed using algorithms like A* [37], considering static obstacles and map constraints, as well as serving as a reference trajectory for navigation systems.
• A*: A heuristic search algorithm that efficiently finds minimum-cost paths by combining the actual traversal cost ($g\left(n\right)$) and the estimated remaining cost ($h\left(n\right)$) [38], being widely used in robotics for global path planning.
• Local Plan: Short-term path planning that handles immediate obstacles and dynamics, optimizing robot movement.
• TEB [39]: Timed Elastic Band, a local planner that optimizes robot trajectories as elastic bands, balancing path smoothness, obstacle clearance, and kinematic constraints, as well as supporting dynamic obstacle avoidance through receding-horizon optimization.
• Cartographer [40]: A graph-based SLAM system that uses submaps and loop closure detection for consistent 2D/3D mapping, supporting multi-sensor fusion (LiDAR and IMU) for robust localization.
• Multi-Robot Map Merge: The process of combining maps from multiple robots to create a unified map, essential for cooperative navigation.
• Optional Goal Set: A set of possible goals that robots can choose from, used in task allocation and planning.
• Relative Position: The position of one robot relative to another, based on coordinate systems, critical for coordination.
• Target Point: A specific point that a robot needs to reach, used in path planning and navigation.

2.2. Problem Statement

In this paper, we investigate the problem of multi-robot cooperative exploration in unknown environments, aiming to achieve maximal coverage rapidly. We consider a system of N agents in a two-dimensional, bounded, and unknown environment $\mathcal{E}\subset {\mathbb{R}}^2$. The state of each agent i is denoted as ${\mathcal{S}}_i=({\mathit{r}}_i,{\mathit{p}}_i,{\alpha }_i)$, where ${\mathit{r}}_i$ indicates agent i’s LiDAR scan information, ${\mathit{p}}_i={\left\{(d_{ij},{\beta }_{ij})\right\}}_{j\ne i}$ represents the relative distance $d_{ij}$ and relative angle ${\beta }_{ij}$ to agent j, and ${\alpha }_i\in [-\pi ,\pi )$ is agent i’s own heading angle. Therefore, the system state can be defined as the Cartesian product of all agents’ states: $\mathcal{S}={\mathcal{S}}_1\times {\mathcal{S}}_2\times \dots \times {\mathcal{S}}_N$. Likewise, the action space of agent i is denoted as ${\mathcal{A}}_i=(\mathsf{\Delta }{\alpha }_i,\mathsf{\Delta }{d}_i)$, where $\mathsf{\Delta }{\alpha }_i\in [-{\alpha }_{max},{\alpha }_{max}]$ represents the deviation angle relative to the current heading, and $\mathsf{\Delta }{d}_i\in [0,d_{\max }]$ denotes the travel distance along that direction with the radar detection range d. Therefore, the joint action space of the system is $\mathcal{A}={\mathcal{A}}_1\times {\mathcal{A}}_2\times \dots \times {\mathcal{A}}_N$. In addition, the central server is aware of the positions of all agents, and the terms ‘robot’ and ‘agent’ are used interchangeably in this context.

In order to make a reasonable assessment, we define three key metrics:

1.

Exploration Time Steps (T): The total number of navigation operations (each considered a step), thus indicating the efficiency of the reinforcement learning strategies.

2.

Coverage Rate ($\mathcal{C}\left(t\right)$): The proportion of environment $\mathcal{E}$ explored at time step t, calculated as

$$\mathcal{C}\left(t\right)={\displaystyle \frac{\left|{\bigcup }_{i=1}^N{\mathcal{A}}_i(1:t)\right|}{\left|\mathcal{E}\right|}},$$

(3)

where ${\mathcal{A}}_i(1:t)$ represents the cumulative area explored by agent i from $A_1$ to $A_t$. An unknown area is considered fully explored when it is entirely enclosed by detected obstacles.

3.

Exploration Time ($\tau$): The total time spent completing the exploration task, distinct from the number of time steps (T), thus reflecting the overall efficiency of the process.

3. Methodology

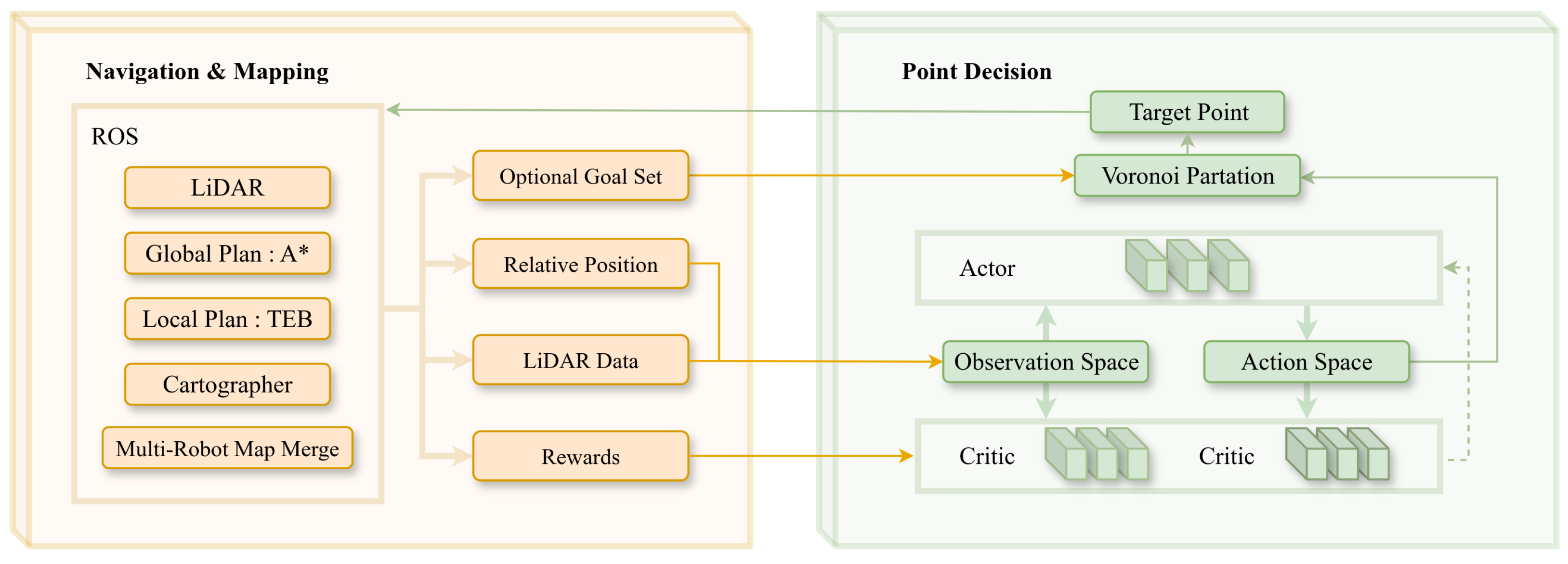
3.1. Framework

To address redundant exploration and low efficiency in unknown environments, we propose a two-layer control architecture, as shown in Figure 1, with the fundamental concepts established in Section 2.1. This architecture enhances multi-robot collaborative exploration efficiency through coordinated centralized task decision-making and distributed navigation and mapping.

The upper layer employs V-R-MATD3, a novel goal decision-making method combining Voronoi partitioning, Recurrent Neural Networks (specifically the GRU), MATD3, and curiosity-driven intrinsic rewards to efficiently select target points for each robot. Voronoi partitioning is incorporated to divide the exploration space among robots, enhancing multi-robot cooperative exploration efficiency. The GRU is introduced to effectively handle the sequential, time-dependent data of robot states and actions, capturing temporal correlations and improving performance. The lower layer utilizes a customized RL simulation environment [1] based on ROS [41] and Gazebo [42] for high-precision navigation and mapping. We enhance Cartographer-based multi-robot joint mapping and implement environment randomization tools. Robots navigate and map according to upper-layer decisions while collecting global exploration rates and robot states as training data.

3.2. V-R-MATD3 Strategy

This subsection introduces V-R-MATD3, an upper-layer point decision strategy that guides the multi-robot system to select appropriate action outputs as target points for collaborative exploration. Figure 2 illustrates the data flow and control architecture of the V-R-MATD3 strategy. As shown in the lower left quadrant of the diagram, the environmental state information acquired by the robots (visualized through Rviz) is systematically fed into the actor–critic neural networks of the MATD3 framework located in the right panel. These networks undergo policy training to generate optimal action outputs. Subsequently, the neural network-derived actions establish geometric correspondence with the Voronoi partitions depicted in the upper left quadrant, thereby determining target waypoints for robotic navigation. Detailed settings are provided below.

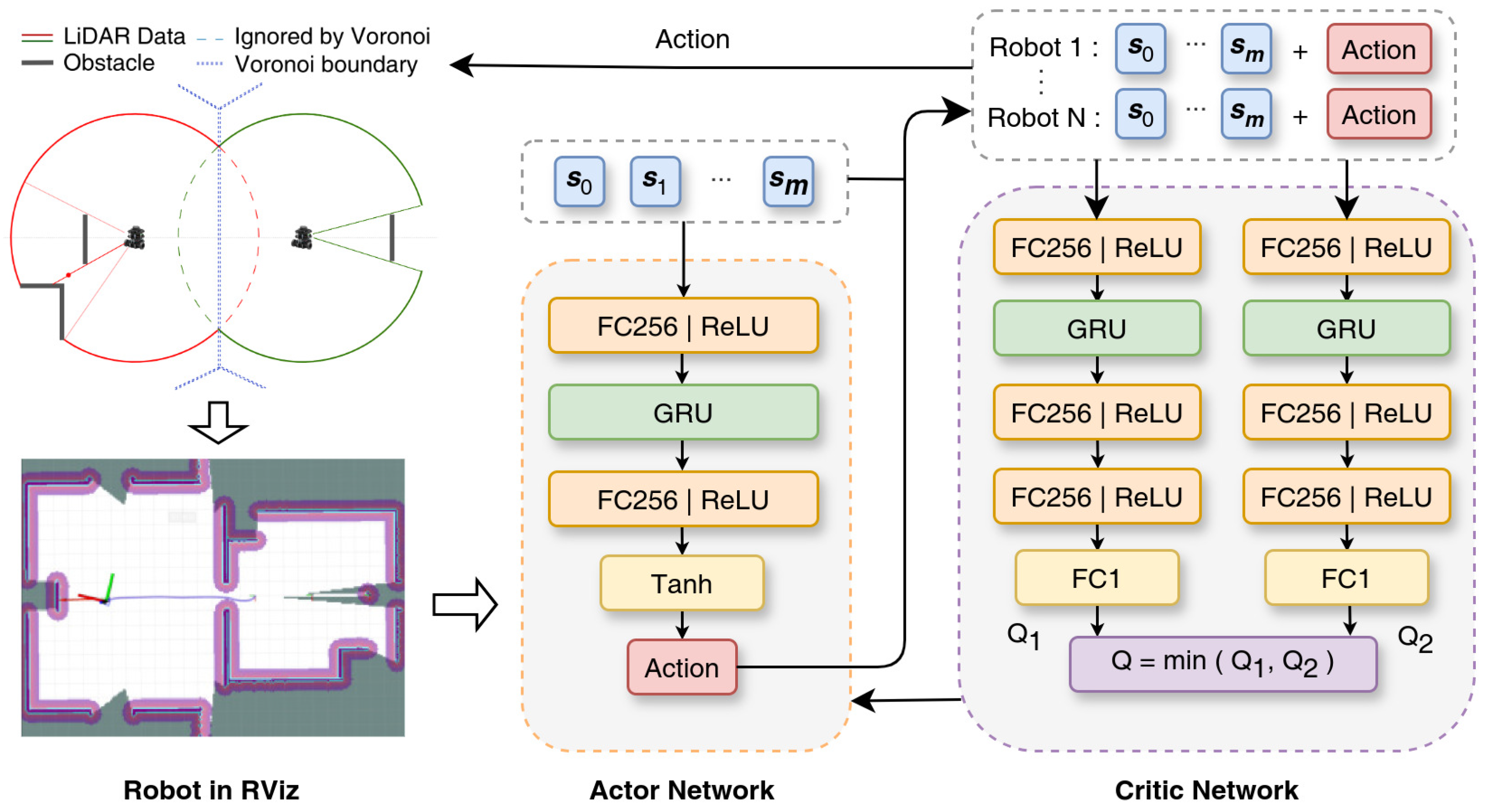
3.2.1. Observation and Action Spaces

In our setup, the observation state ${\mathit{o}}_i$ of each robot i at each time step consists of three components: the range measurements ${\mathit{r}}_i$ sampled by the robot’s onboard LiDAR, the relative positions ${\mathit{p}}_i={\left\{(d_{ij},{\beta }_{ij})\right\}}_{j\ne i}$ to other robots, and the current robot’s orientation ${\alpha }_i\in [-\pi ,\pi )$. Specifically, ${\mathit{r}}_i$ is a subsampled array of 120 elements, uniformly extracted from the original 720 LiDAR range measurements. This subsampling approach reduces the neural network’s input complexity while maintaining sufficient accuracy for lower-layer navigation and mapping tasks. ${\mathit{p}}_i={\left\{(d_{ij},{\beta }_{ij})\right\}}_{j\ne i}$ represents the relative distance and relative angle to agent j. It deserves to be mentioned that we use relative positions instead of absolute coordinates to reduce the dependency of the state data on the global map, and each robot only shares its own location and not its own LiDAR information.

The action space ${\mathit{A}}_i$ is a two-element array with continuous values in $(-1,1)$, mapping to selectable target points around the robot. Specifically, ${\mathit{A}}_i\left[0\right]$ corresponds to an angle in $[-\pi ,\pi ]$ relative to the robot’s forward direction, and ${\mathit{A}}_i\left[1\right]\in [d_{min},d_{max}]$ represents the Euclidean distance that the robot advances in this step. Figure 2 illustrates the refined action spaces for multiple robots—shown as solid red and green arcs—after applying the Voronoi partitioning method, the principle of which is given in Equation (1).

3.2.2. Network Architecture

The detailed network architecture design is shown in Figure 2. We propose a parameter-shared centralized actor architecture with decentralized critics. While each robot i nominally corresponds to an actor network ${\pi }_i(·|\theta )$, all actors share identical parameters (${\theta }_1={\theta }_2=\cdots ={\theta }_N=\theta$) and receive global observations to enable coordinated control. This design reduces training complexity while achieving full collaboration. The actor–critic neural network consists of an actor network ${\pi }_i\left(o_i\right|{\theta }_i)$, with weight ${\theta }_i$, and two critic networks $Q_i^{\pi }(o_{1:N},a_{1:N}|{\varphi }_1)$ and $Q_i^{\pi }(o_{1:N},a_{1:N}|{\varphi }_2)$, with weights ${\varphi }_1$ and ${\varphi }_2$, respectively. Corresponding target networks ${\pi }_i^{\prime }$ and $Q_i^{\prime \pi }$ are also maintained.

The actor network receives an input tensor of shape $(t,n,input\_dim)$, representing the state information of n collaborating robots over t time steps, where $input\_dim$ is the state dimension per robot per time step. This input passes through a 256-unit ReLU-activated fully connected layer, a GRU layer, and another 256-unit ReLU-activated fully connected layer. A final tanh-activated output layer produces the action vector $\mathit{A}$ for all robots. The critic networks share a similar architecture but output a scalar Q value via linear activation to estimate the expected cumulative reward; the smaller Q value is chosen to prevent overestimation [29]. Incorporating the GRU allows the model to capture time-series dynamics, enhancing learning stability and efficiency.

3.2.3. MATD3 Algorithm

The MATD3 algorithm is developed from the Twin Delayed Deep Deterministic Policy Gradient (TD3), where Equations (4)–(6) define the core components of the algorithm [17,29,43]. In the j-th trajectory from the replay buffer, the target Q-value of agent i is defined as

$$y_i^j=r_i^j+\gamma \underset{c=1,2}{min}{Q}_{i,{\varphi }_c^{\prime }}^{{\pi }^{\prime }}\left(s^{\prime j},a_{1:N}^{\prime },h_t^Q\right){|}_{a_k^{\prime }={\pi }_k^{\prime }(o_k^{\prime j},h_t^{\pi })},$$

(4)

where $r_i^j$ is the immediate reward, $\gamma$ is the discount factor, and $Q_{i,{\varphi }_c^{\prime }}^{{\pi }^{\prime }}$ denotes the c-th target critic network with parameters ${\varphi }_c^{\prime }$. The action $a_k^{\prime }$ is generated by the target policy ${\pi }_k^{\prime }$ based on the next time step’s observation $o_k^{\prime j}$ and the policy network’s hidden state $h_t^{\pi }$.

The parameters ${\varphi }_c$ of the critic networks are updated by minimizing the mean squared error loss function $L\left({\varphi }_{i,c}\right)$:

$$L\left({\varphi }_{i,c}\right)={\displaystyle \frac{1}{B}}\sum _j{\left(y_i^j-Q_{i,{\varphi }_c}^{\pi }(s^j,a_{1:N},h_t^Q)\right)}^2,$$

(5)

where B is the batch size. The actor networks update their parameters ${\theta }_i$ to maximize the expected cumulative reward J by using delayed policy updates based on the critic networks’ estimated Q-values [29]. The policy gradient is

$${\nabla }_{{\theta }_i}J\approx {\displaystyle \frac{1}{B}}\sum _j{\nabla }_{{\theta }_i}{\pi }_i(o_i^j,h_t^{\pi }){\nabla }_{a_i}{Q}_{i,{\varphi }_1}^{\pi }(s^j,a_{1:N},h_t^Q){|}_{a_i={\pi }_i(o_i^j,h_t^{\pi })},$$

(6)

where ${\nabla }_{{\theta }_i}{\pi }_i(o_i^j,h_t^{\pi })$ is the gradient of the policy network with respect to its parameters ${\theta }_i$, and ${\nabla }_{a_i}{Q}_{i,{\varphi }_1}^{\pi }$ is the gradient of the Q-function with respect to the action $a_i$.

The parameters are updated in each iteration until the exploration is complete or the maximum number of time steps is reached.

The V-R-MATD3 algorithm is defined in Algorithm 1.

3.2.4. Reward Shaping

We propose a hybrid reward function, named Prior-Guided Adaptive Hybrid Reward (PGAHR), which consists of two parts: an intrinsic reward and an extrinsic reward. The intrinsic reward is curiosity-driven, including rewards for newly explored map areas, as well as penalties for robots becoming too close to each other and their own historical trajectories. The extrinsic reward includes an ongoing negative reward based on time steps, as well as a final reward upon the completion of the task. This function leverages prior knowledge to optimize overall rewards and improve learning efficiency. Specifically, we simplify the state space by subsampling the LiDAR data and reduce the robot’s action space by using a Voronoi-based spatial segmentation method. This approach helps prevent excessive closeness between robots, ultimately accelerating the convergence of rewards.

Algorithm 1 Multi-robot Exploration based on V-R-MATD3

1: Input: ${\pi }_{\theta }$, $Q_{\varphi }$, $\mathit{s}$, $\mathit{o}$; $h_{1,0}^{\pi },\dots ,h_{n,0}^{\pi },h_{1,0}^Q,\dots ,h_{n,0}^Q$ 2: Output: the updated ${\pi }_{\theta }$, $Q_{\varphi }$, $\mathcal{A}$, $\mathcal{C}\left(t\right)$ 3: Initialize ${\pi }_{\theta }$, $Q_{\varphi }$, ${\theta }^{\prime }\leftarrow \theta$, ${\varphi }^{\prime }\leftarrow \varphi$, replay buffer $\mathcal{D}$ 4: for $episode=1$ to M do 5:    Initialize environment $\mathcal{E}$, Gaussian noise $\mu$ 6:    Get initial states: $\mathit{s}$, $\mathit{o}$, $h_{1,0}^{\pi },\dots ,h_{n,0}^{\pi }$, $h_{1,0}^Q,\dots ,h_{n,0}^Q$ 7:    repeat 8:      for each robot i do 9:         $a_{i,t},h_{i,t}^{\pi }\sim {\pi }_{{\theta }_i}(o_{i,t},h_{i,t-1}^{\pi })+{\mu }_t$; Calculate Vor $\left(i\right)$ 10:         Map $\mathit{a}$ to $\mathit{g}$; Plan path P to goal $g_i$ 11:         Obtain ${\mathit{o}}^{\prime }$, $\mathit{r}$, ${\mathit{s}}^{\prime }$, $done$ 12:         Store transition ($\mathit{o}$, $\mathit{s}$, $\mathit{a}$, $\mathit{r}$, ${\mathit{o}}^{\prime }$, ${\mathit{s}}^{\prime }$, $done$) in $\mathcal{D}$ 13:         Update $\mathit{o}\leftarrow {\mathit{o}}^{\prime }$ 14:      end for 15:      for each robot i do 16:         Sample batch $({\mathit{o}}^j,{\mathit{s}}^j,{\mathit{a}}^j,{\mathit{r}}^j,{\mathit{o}}^{\prime j},{\mathit{s}}^{\prime j},d^j)$ from $\mathcal{D}$ 17:         Compute $y_i^j$ in Equation (4); Update $Q_{{\varphi }_i}$ in Equation (5) 18:         if $episode$ % policy_delay = 0 then 19:           Update ${\pi }_{{\theta }_i}$ using Equation (6) 20:           ${\theta }_i^{\prime }\leftarrow \tau {\theta }_i+(1-\tau ){\theta }_i^{\prime }$ 21:           ${\varphi }_{i,c}^{\prime }\leftarrow \tau {\varphi }_{i,c}+(1-\tau ){\varphi }_{i,c}^{\prime }$, $c=1,2$ 22:         end if 23:      end for 24:    until $\mathcal{C}\left(t\right)$ = 90% or $t=T$ 25: end for

The general total reward R is defined as

$$R=\sum _{t=1}^T{R}^t=\sum _{t=1}^T(R_m^t+R_p^t+R_c^t+R_{ts}^t),$$

(7)

where $R^t$ represents the reward obtained by the robot system at time step t, which is slightly different from $r_i^j$ for the j-th trajectory as defined in Equation (1). $R_m^t$ is the newly explored map reward, $R_p^t$ is the proximity penalty, $R_c^t$ is the task completion reward, and $R_{ts}^t$ is a time step penalty.

$R_m^t$ is calculated as

$$R_m^t=k·(\mathcal{C}\left(t\right)-\mathcal{C}(t-1))-C_0,$$

(8)

where the weight k is dynamically adjusted to maintain an effective exploration strategy and avoid local optima. When $C\left(t\right)<50\%$, $k=k_0-\mathsf{\Delta }{k}_0$; when $C\left(t\right)>50\%$, $k=k_0+\mathsf{\Delta }{k}_0$. The hyperparameters $k_0$ and $\mathsf{\Delta }{k}_0$ are adjusted based on map size and task complexity. $\mathcal{C}\left(t\right)$ is the global map exploration rate at time t, and $C_0$ is a bias term. $R_p^t$ consists of two parts:

$$R_p^t=n_1·{R_p^t}^{\prime }+n_2·{R_p^t}^{\prime \prime },$$

(9)

where $n_1$ represents the counts of distances between the robot’s next target point and historical target points below threshold $d_1$, and $n_2$ represents the number of distances to other robots’ next target points below threshold $d_2$. ${R_p^t}^{\prime }$ and ${R_p^t}^{\prime \prime }$ are the negative reward values, respectively.

$R_c^t$ is designed as

$$R_c^t=\left\{\begin{array}{cc}{R_c^t}^{\prime }·{\displaystyle \frac{\mathcal{C}\left(t\right)}{{\mathrm{C}}_{\mathrm{target}}}}\hfill & \mathrm{if}\mathcal{C}\left(t\right)\ge C_{\mathrm{target}},\hfill \\ 0\hfill & \mathrm{otherwise},\hfill \end{array}\right.$$

(10)

where $C_{\mathrm{target}}$ is the target coverage rate, and ${R_c^t}^{\prime }$ is the base reward value for reaching the target coverage rate.

$R_{ts}^t$ is defined as a constant negative value:

$$R_{ts}^t=-R_0,R_0>0.$$

(11)

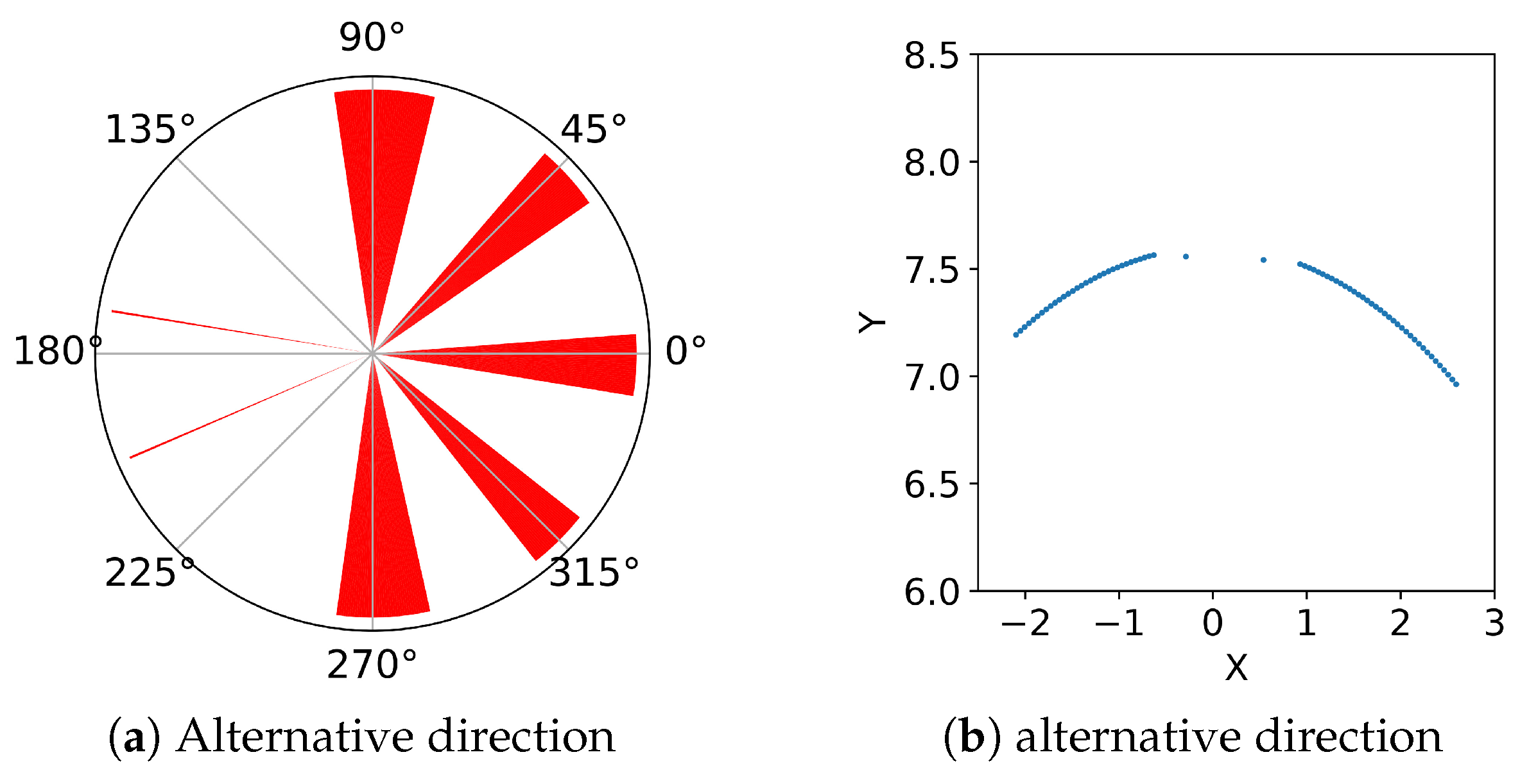
3.3. Action Space Transformation

This section introduces the transformation process of converting action vectors from the continuous space into actual target point coordinates, linking the upper and lower layers of the decision-making architecture.

Figure 3a plots the radar coverage, with red regions indicating measurements exceeding the effective range or exhibiting discontinuities. These positions represent feasible directions for the robot’s next move. Figure 3b shows the resulting optional target point coordinates. The generation of these target points follows the transformation relationship

$$\alpha =\left(i-{\displaystyle \frac{M}{2}}\right)·\mathsf{\Delta }\alpha +\psi ,$$

(12)

$$\left\{\begin{array}{c}{x}_{\mathrm{target}}=x_{\mathrm{pos}}+d·cos\left(\alpha \right),\hfill \\ y_{\mathrm{target}}=y_{\mathrm{pos}}+d·sin\left(\alpha \right),\hfill \end{array}\right.$$

(13)

where $\alpha$ denotes the target direction angle, i is the laser beam index, M represents the total number of sampling beams, $\mathsf{\Delta }\alpha$ represents the angular difference between adjacent laser beams, and $\psi$ is the robot’s real-time rotation angle (obtained by subscribing to the pose topic). $x_{\mathrm{pos}}$ and $y_{\mathrm{pos}}$ are the robot’s current position coordinates, and d is the dynamically adjusted distance between the target point and the robot.

4. Experiments and Discussion

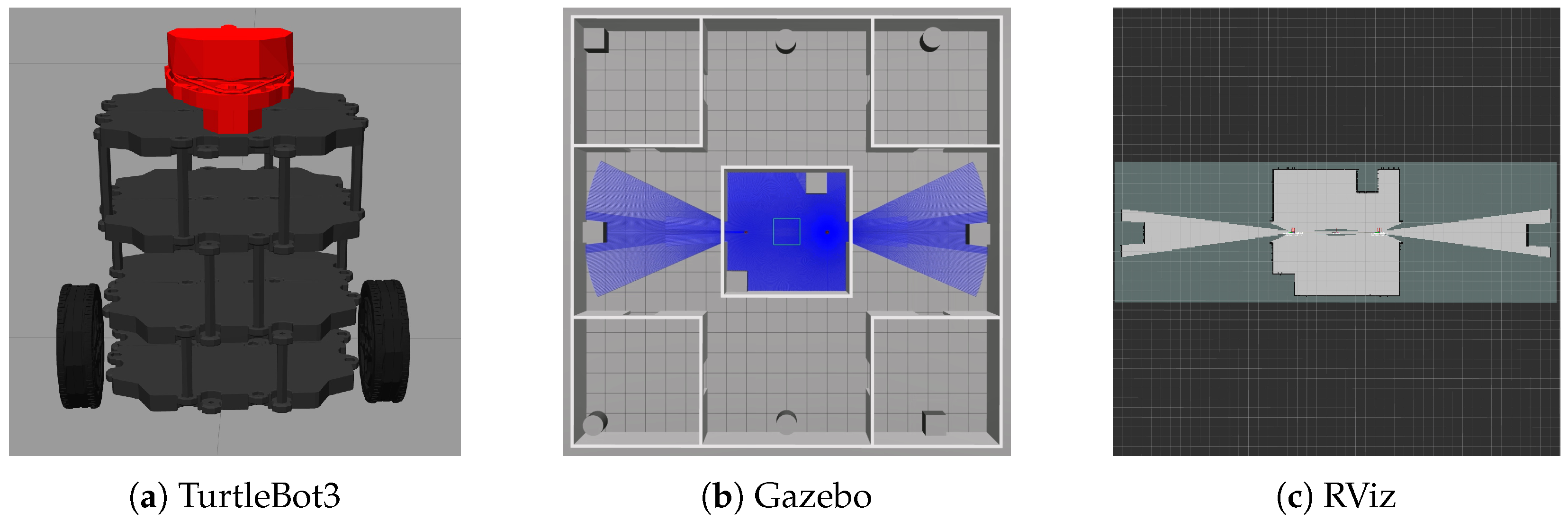
4.1. Experimental Setup

The proposed method was evaluated using simulations based on ROS and Gazebo, executed on a server equipped with an Intel i9-13900k CPU and an NVIDIA RTX 4080 GPU, utilizing Docker containers running ROS Melodic. Figure 4 illustrates our simulation environment: Figure 4a represents the Turtlebot3 robot; Figure 4b shows the Gazebo simulator with two Turtlebot3 robots in the custom map, with the blue fan-shaped lines indicating the scanning range of the LiDAR; and Figure 4c shows the visualization tool Rviz, with the white areas representing the regions already explored by the LiDAR.

Our paper focuses on strategies for multiple robots to collaboratively explore unknown environments, with the experimental background being set in disaster rescue scenarios, such as post-fire buildings or chemical plant leaks. We use three simulation maps: World1 (20 m × 20 m corridor) corresponds to a real-world scenario of building hallways, which require the exploration of narrow spaces; World2 (40 m × 40 m hall) corresponds to real-world scenarios like warehouses or conference halls, requiring large-scale coverage; and World3 (12 m × 17 m office interior) corresponds to individual rooms or offices with complex layouts. These maps are shown in Figure 5.

Each TurtleBot3 robot is equipped with a ${360}^{\circ }$ single-line LiDAR sensor (with an effective range of $5\mathrm{m}$ and a sampling frequency of $720\mathrm{Hz}$). The robot parameters are configured with a maximum speed of $1.0\mathrm{m}/\mathrm{s}$, an acceleration of $0.3\mathrm{m}/{\mathrm{s}}^2$, a friction coefficient of $0.5\mathrm{N}·\mathrm{s}/\mathrm{m}$, and an inertia coefficient of $50\mathrm{kg}$. These settings ensure accurate environmental perception, smooth motion, and high-quality simulation data while minimizing potential inconsistencies from the Gazebo physics engine.

Training episodes terminate upon goal achievement or reaching the maximum time steps. The key training parameters are summarized in

Table 1. Hyperparameter settings for RL training.

Parameter	Parameter	Value
Learning rate	$\eta$	2.5 × ${10}^{-4}$
Batch size	B	64
Discount rate	$\gamma$	0.9
Hidden layer size	H	256
Max episode length	$\eta$	2.5 × ${10}^{-4}$
Replay buffer size	$T_{\max }$	20
Exploration noise std	$\sigma$	0.3
Use shared policy	${\rho }_t$	true

. Data from each episode—including observations, shared observations, rewards, actions, and termination flags—are stored in an experience replay buffer. Neural networks are trained by sampling batches from this buffer.

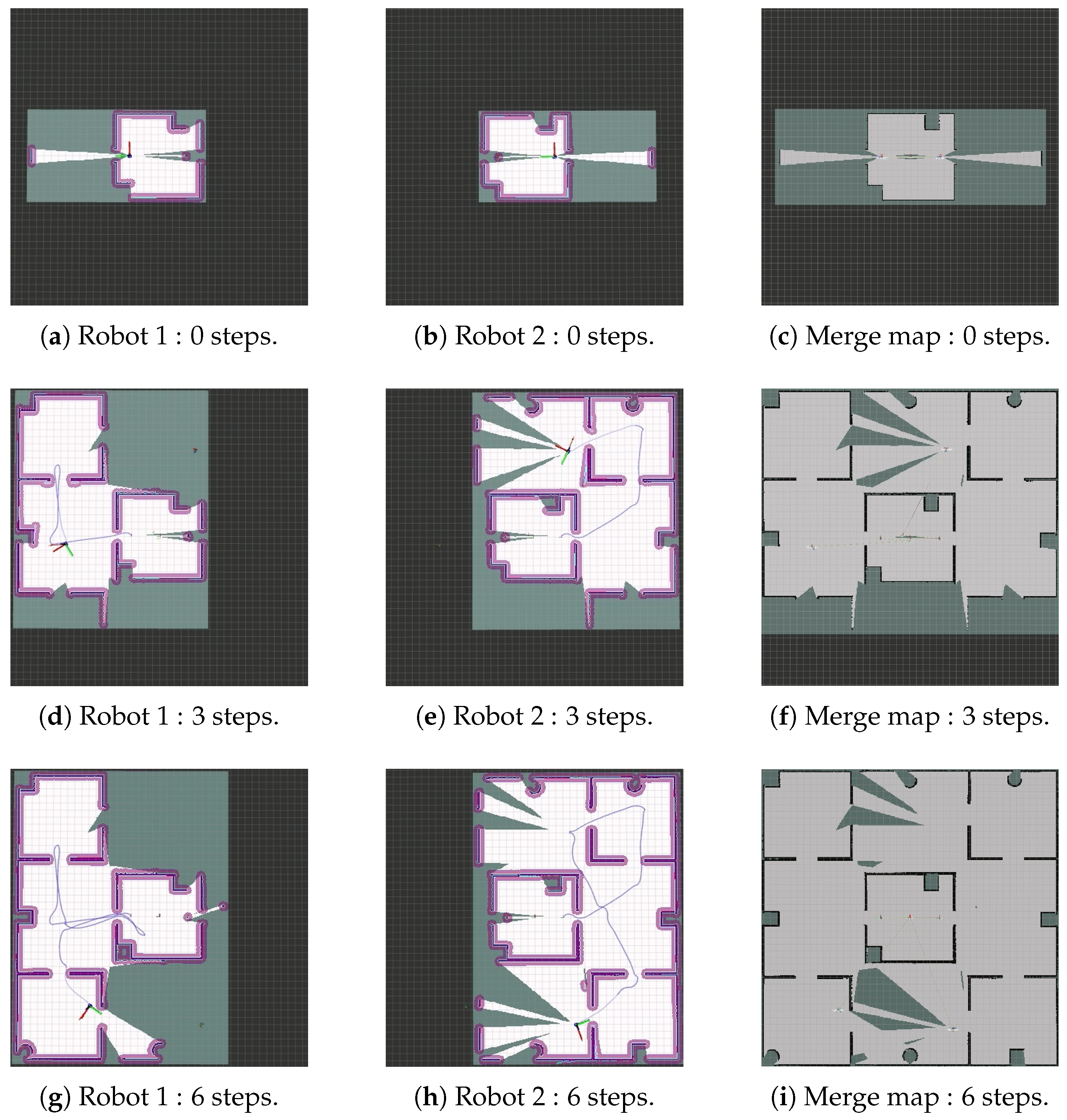
4.2. Development of Motion Planning and Map Merging

We improved an ROS and Gazebo-based simulation platform for RL training, featuring customized motion planning, multi-robot map merging, and environment reset modules. The motion planning module uses the TEB for local planning and obstacle avoidance. The multi-robot map merging module employs the Cartographer algorithm and a modified multirobot_map_merge toolkit for real-time map merging.

Specifically, we deployed four Docker containers on a server to maximize computational resource utilization for parallel training experiments. Within each container, we adjusted the Gazebo simulator’s physical engine parameters, specifically max_step_size and real_time_update_rate, which, together, determine the speed ratio of the simulation time to the real-world time. We set max_step_size to 0.001 (adjustable based on CPU usage, allowing for a minor trade-off in simulation precision while maintaining data quality) and real_time_update_rate to 5000. Extensive experiments revealed that the maximum achievable acceleration was constrained by the hardware, Gazebo, and Cartographer settings. To ensure reliable simulations, we upgraded Gazebo 9 to the latest version using the official Ubuntu Personal Package Archives. Additionally, we modified the map_by_time.h file in the Cartographer source code, changing CHECK_GT to CHECK_GE to relax the timestamp consistency check during map fusion. These modifications, coupled with rigorous testing, enabled us to achieve a Gazebo training speed approximately 4 times faster than real time per Docker container while ensuring proper map merging and preventing training interruptions. Our hardware supports at least four concurrent Docker simulations, resulting in an overall acceleration of approximately 16 times compared to the original setup.

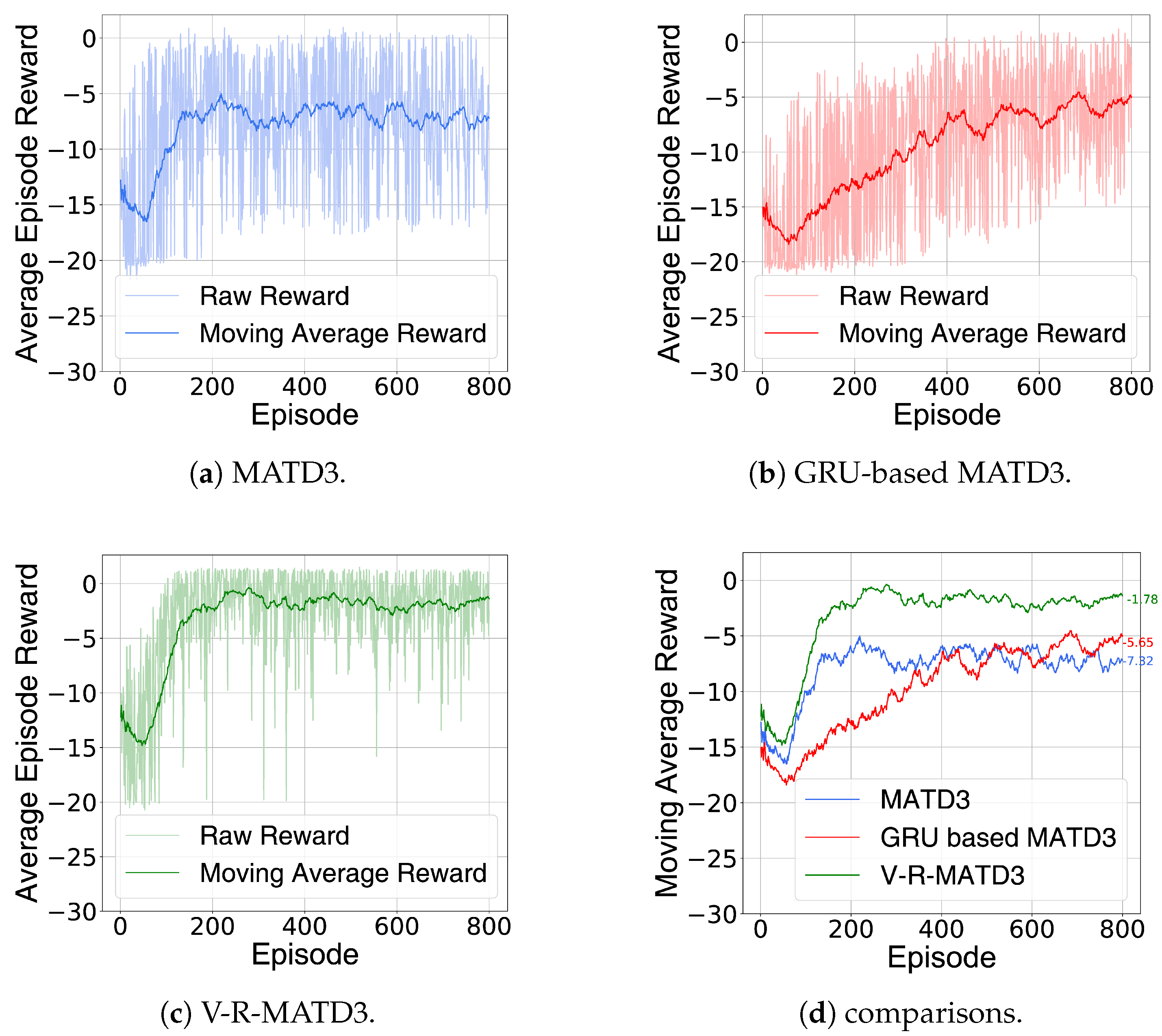
4.3. Ablation Study

4.3.1. Training Process

Figure 6 illustrates the progression of the moving average reward over episodes during the training of the MATD3, GRU-based MATD3, and V-R-MATD3 strategies on the World II map. Each subfigure displays the number of episodes on the x-axis and the average cumulative reward per episode on the y-axis. The maximum episode length $T_{\max }$ is set to 20, allowing for up to 20 motion steps per episode.

We trained each strategy for 800 episodes. The moving average rewards after convergence for the three strategies are −7.32, −5.65, and −1.78, respectively. The V-R-MATD3 strategy outperforms the other two in terms of average reward after convergence. Furthermore, our strategy begins to converge around episode 200, which is faster than MATD3 (around episode 260) and GRU-based MATD3 (around episode 530). A comparison of Figure 6a,b reveals that, while GRU-based MATD3 exhibits slower convergence due to its GRU network layer, it ultimately achieves higher average rewards than MATD3, indicating enhanced long-term strategy performance. Our proposed V-R-MATD3 strategy demonstrates superior performance, maintaining higher average rewards and faster convergence. It reduces the average time consumption by 45.8% and 51.4% compared to the GRU-based MATD3 and MATD3 strategies, respectively.

4.3.2. Testing Process

Ultimately, in order to validate the average performance across repeated experiments, we applied these three methods to three different maps. In our evaluation protocol, the single task terminated when either the motion steps exceeded 20 or the map coverage rate surpassed 90%.

Figure 7 presents the simulation process at different step stages under the V-R-MATD3 strategy, including the state information of robot1 and robot2, as well as their merged map. More details are provided in the caption of Figure 7. For instance, Figure 7e illustrates the local map and trajectory information of robot2 in the third step. In the Rviz visualization, the red and green right-angle arrows indicate the robot’s poses, the black lines represent the detected obstacles, and the purple bar-shaped regions surrounding them denote the inflation radii within which the robot moves more slowly. The purple curve depicts the robot’s trajectory, the white area on the right shows the explored region, the black areas on the left and bottom represent completely unknown regions, and the bluish-green area indicates regions that are reachable but not yet explored.

Figure 7 clearly demonstrates each robot’s exploration process, showing that the areas explored by the two robots are relatively separated, with the exploration task completed in a total of six steps. In Figure 8a–c, the exploration process under the MATD3 strategy is shown, with the task completed in nine steps, while Figure 8d–f display the exploration under the R-MATD3 strategy, which completes the task in eight steps. Our V-R-MATD3 strategy not only requires fewer steps to complete the task but also results in less repetitive exploration trajectories.

In our study, we adopted both the mean absolute error (MAE) of the exploration rate and the number of exploration time steps to provide a comprehensive analysis of exploration efficiency. The MAE describes the difference between the measured exploration coverage of each iteration by the robot and the expected coverage. Therefore, using the absolute error better reflects the extent to which the task achieves its intended goal. However, we also noticed an issue. On the World II map, both V-R-MATD3 and R-MATD3 achieved an average map coverage exceeding 90%, with V-R-MATD3 exhibiting a larger absolute error relative to the expected 90%. However, in our exploration task, the robot may not always perfectly explore 90%. By observing the robot’s movement process, we found that, under the R-MATD3 strategy, the robot exhibited a significant amount of redundant exploration, resulting in slower overall exploration rate growth and a longer exploration time, though the final exploration rate was closer to 90%. In contrast, with the Voronoi-based V-R-MATD3 strategy, the overall exploration rate grew faster. There may be instances where the exploration rate of the previous step is below 90% but that of the next step exceeds 90% by a large margin, and the exploration time is shorter. Clearly, this represents a more efficient exploration strategy.

As shown in

Table 2. Results of V-R-MATD3, R-MATD3, and MATD3.

	World I		World II		World III
	Steps	MAE 1	Steps	MAE	Steps	MAE
V-R-MATD3	3.67	−1.0%	7.69	4.2%	5.42	−2.3%
R-MAPPO	5.11	−4.1%	9.04	3.8%	7.31	−0.8%
MATD3	6.80	−11.8%	11.58	−4.7%	14.10	16.8%

¹ MAE: mean absolute error of map coverage rate relative to the expected 90%.

, V-R-MATD3 has the lowest number of time steps on all maps and achieves superior mapping completion rates of 90.3% on average across all environments, outperforming both R-MATD3 (88.9%) and MATD3 (78.9%). While V-R-MATD3 demonstrates particular advantages on World I and World II, its slightly inferior performance on World III (compared to that of R-MATD3) may be attributed to the map’s unique topological features, with certain peripheral areas remaining persistently unexplored due to limitations in our Voronoi-based partitioning approach. This phenomenon suggests that the current implementation might benefit from the incorporation of enhanced stochastic exploration mechanisms during later mission phases to address residual uncovered regions. The consistent performance gap across scenarios (V-R-MATD3 > R-MATD3 > MATD3) confirms the effectiveness of our hierarchical decision-making architecture in improving both multi-robot collaborative exploration performance and algorithm convergence speed.

4.4. Comparison with Existing Methods

We conducted comparative experiments to evaluate our V-R-MATD3 strategy against baseline MAPPO [44], MATD3 [19], and classical methods such as Rapidly-Exploring Random Trees (RRTs) [45] and Cost-based [46] approaches across three distinct map environments. Figure 9 illustrates the experimental process conducted on a simple test map. Figure 9a–c show the state information of V-R-MATD3 while it completes the exploration task. Notably, robot1 and robot2 finish the task in just two steps, with trajectories closely resembling the ideal, intuitive path envisioned by humans. In contrast, the trajectories generated by the other three methods are more complex, and, even on this simple map, the RRT and Cost methods exhibit redundant coverage of the exploration area.

To further investigate the general case, each experiment was repeated 50 times, and the average results are presented in

Table 3. Results of the MATD3, MAPPO, RRT, and Cost-based methods and our strategy.

	World I			World II			World III
	Steps	Time (s)	Overlap (%)	Steps	Time (s)	Overlap (%)	Steps	Time (s)	Overlap (%)
Ours	3.65	22.41	0.02	7.72	97.04	0.24	5.42	36.87	0.13
MATD3	7.14	38.03	0.10	12.40	106.35	0.31	8.73	50.03	0.17
MAPPO	9.92	42.29	0.14	18.05	114.24	0.33	11.26	44.54	0.19
RRT	24.86	89.13	0.47	55.53	153.86	0.42	43.08	85.74	0.21
Cost	56.81	62.09	0.44	148.14	151.40	0.46	95.68	98.82	0.20

Testing map World II refers to [1], with modifications.

.

We used motion time steps as an efficiency metric during training to mitigate early-stage irregular movements and to accelerate learning. As robot motion stabilizes, steps correlates with time, ensuring optimal exploration in minimal time. Table 3 shows that our strategy consumes the lowest average time on World I, reducing the time consumption by 41.1%, 47.0%, 63.9%, and 74.9% compared to the MATD3, MAPPO, RRT, and Cost-based methods, respectively. Similar results are observed on the other two maps. Our V-R-MATD3 strategy consistently outperforms the other methods across all metrics on all three maps, particularly in terms of the steps metric.

5. Conclusions

This paper presents a novel collaborative exploration strategy (V-R-MATD3) for multiple mobile robots in unknown environments, employing a hierarchical control architecture. The proposed framework specifically contains a hybrid reward function that synergistically combines coverage completeness, time efficiency, and inter-robot coverage overlap penalties, trained through a multi-robot reinforcement learning toolkit. The high-level decision layer determines the next frontier point for each robot through Voronoi-based task allocation and our enhanced MATD3 algorithm with GRU-enhanced coordination, while the low-level execution layer generates collision-free motion trajectories. Extensive simulation experiments demonstrate significant improvement in exploration efficiency compared to conventional frontier-based methods and other learning-based approaches. Comprehensive ablation studies quantitatively validate the necessity of both Voronoi partitioning and GRU components—their removal induces redundant inter-robot spatial coverage due to task allocation imbalances and severely disrupts cooperative decision-making mechanisms while simultaneously slowing policy convergence during training. These results demonstrate the superiority of our tightly coupled hierarchical framework in addressing the cooperative exploration challenges of multi-robot systems in unknown environments.

Nevertheless, there is still room for improvement in our work. Below are the disadvantages of the proposed method, along with potential solutions:

• Centralized computation limits flexibility in the robotic system: Our approach utilizes a centralized decision-making and distributed execution architecture, which is widely adopted due to its global optimality. However, it faces scalability issues as the number of robots increases and encounters communication bottlenecks. A distributed architecture could address these problems [47], but RL inference has high computational complexity and is resource-intensive. If a distributed approach were adopted, each robot would require high performance [48]. Due to hardware limitations in our lab, we initially chose the centralized decision-making model. Future work will explore the efficiency of distributed solutions in multi-robot systems.
• Lack of real-world experiments: Our experiments were conducted in the high-fidelity Gazebo simulation environment [1]. While this environment considers many dynamic factors, it still deviates significantly from the real world. We plan to conduct experiments with real robots in real environments and utilize domain randomization to mitigate the Sim–Real gap [49].
• Insufficient robustness to dynamic obstacles and robot failures: The experiments in this paper were conducted in a static environment, which is ideal and rarely prone to faults. Previous studies have explored the need for the reallocation of coverage areas in the event of system failures [8,50]. Additionally, communication failures are a key research area. Reference [51] discusses multi-robot coordination in communication-limited environments. Our future work will investigate emergency mechanisms for communication failures, considering establishing communication protocols that only activate when necessary in limited communication scenarios.

Our future work will focus on addressing these issues, particularly by exploring the training of the strategy on broader datasets to enhance its generalization capabilities, with a specific emphasis on improving its performance in special terrains within real-world environments.