The Correlation Factors and Mechanisms of Diffusion for P and S in the Cu Single Crystal

Abstract

The full description of the mechanisms for the diffusion of substitutional impurities requires an account of the correlation of the atomic jumps. This study investigated the diffusion of phosphorus (P) and sulfur (S) in the fcc copper (Cu) single crystal using density functional theory (DFT). Vacancy formation energies and impurity–vacancy interactions were calculated, revealing attractive interactions of P and S with the vacancies. The attractive interactions between S and a vacancy were roughly twice as strong as those between P and a vacancy. The 5-frequency—or 5-jump—model was employed to describe the correlation effects during diffusion. The potential energy profiles and activation energies were determined for the different jump paths necessary for the model and to account for all the correlation effects in substitutional impurity diffusion in the single crystal. The results indicated that S diffuses significantly faster than P in Cu, primarily due to lower activation energies for certain jump paths and a more favorable vacancy–impurity interaction. This occurs because when bonding with the crystal, S tends to prefer atomic sites with larger volumes and more asymmetric geometric arrangements when compared to P. This favors the interactions between S and the vacancies, and reduces friction with the matrix during the diffusion of S. The effective diffusion coefficients were calculated and compared with experimental data. The findings provide insights into the diffusion mechanisms of P and S in Cu and how these can be affected by the presence of extended defects such as grain boundaries.

1. Introduction

In the Swedish repository for spent nuclear fuel (KBS-3), the fuel is encapsulated in a cylindrical iron container that, in turn, is protected from the environment with an outer copper cannister [1]. The copper cannister serves thus as the ultimate barrier that separates the iron container from the environment. The copper barrier is expected to keep the iron container and the fuel protected from the environment for at least 100,000 years. Within this time frame the mobility of impurities that can eventually affect the properties of the copper material has to be well understood for proper safety assessment.

A complete description of impurity diffusion in a lattice needs to account for the correlation between the movement of the impurity and the movement of the surrounding lattice atoms [2]. The quantity that accounts for this is the correlation factor and it is defined as the ratio of the mean squared displacement of the impurity to the mean squared displacement of a random walker in the same lattice [3]. Within random walk theory [4], the correlation factor quantifies how much the directions of the successive impurity jumps are random. The correlation factor is affected by the binding energy between the impurity and the surrounding lattice atoms as well as aspects related to the geometry of the bonding that will affect the transition states for the diffusion jumps [2,5,6]. For the case of substitutional impurities, whose diffusion mechanism is via vacancies, the binding energy between the impurity and the vacancy has important implications, both in the diffusion mechanism and in the diffusion rate. The binding energy of the impurity to the vacancy is directly proportional to the diffusion coefficient but it also depends on the correlation factors between matrix atoms and impurities [6,7,8].

Thus, correlation terms for the diffusion of vacancies, for the diffusion of the matrix atoms—self-diffusion—and of the impurities are necessary to account for the complete correlation picture that determines the migration of substitutional impurities, and that affects the directions of the successive atomic jumps and consequently the diffusion coefficient [2]. The diffusion coefficient D for isotropic diffusion is given by

$$D={\displaystyle \frac{1}{6}}{\lambda }^2\nu$$

(1)

where λ is the jump distance and ν is the jump frequency. This expression would be complete if the direction of the diffusive jump did not depend on the directions of the previous jumps. However, because of the correlated mobility, the direction of the jump depends to some degree on the directions of previous jumps [6] and the expression for D has to be modified to account for these correlations, and thus it becomes

$$D={\displaystyle \frac{1}{6}}{\lambda }^2\nu f$$

(2)

where f is the correlation factor that considers the degree of correlation between the successive jumps. A widespread convention used for defining the correlation factor is the one previously proposed by Manning [9]. In this model, correlation factors for a cubic lattice have values in the interval [0, 1] refs. [2,4], proportionally affect the diffusion coefficient and depend on the crystal structure [2,5]. If f is close to 0, it implies that the impurity moves with a high degree of correlation with the previous jumps, while the closer f is to 1, the more randomly the impurity moves. The degree of correlation is determined by the chemical bonding between the matrix and the impurity, and f is also affected by the effects that vacancy mobility has on the atomic jumps of both the matrix and impurity atoms. The correlation factors for self-diffusion in the matrixes of different structural ordering are known and their derivation has been previously detailed [5]. But the correlation factors for interactions between impurities and different matrixes must be determined for each case, considering the possible mechanisms for vacancy jumps [6], because both matrix atoms and impurity diffusion depend on the vacancy jumps. The monovacancy mechanism is able to grasp the vacancy-mediated diffusion at low and medium temperatures [10], while at high temperatures, divacancy mechanisms should be considered. Deviations from Arrhenius behavior at high temperatures have been attributed to the role of extended defects such as dislocations and grain boundaries [11,12]. In a non-defective single crystal without extended defects, the diffusion of P and S follows the Arrhenius correlation between the diffusion coefficient and temperature. In this work, we consider diffusion at room temperature. At this temperature, the contribution of divacancies is negligible [13] and thus, the 5-frequency model [5,6,8,14] for the monovacancy aided diffusion mechanism was employed here.

2. Materials and Methods

2.1. The Effective Diffusion Model—5-Frequency Model

An effective diffusion coefficient for a substitutional impurity must consider the correlations between the different jumps that can affect its mobility. The frequency (w_i) of each of these jumps (i) affects the probability of the impurity jump to a neighboring vacancy. The importance of the collection of w_i and the derivation of their expressions for the fcc lattice have been previously reported [5,6]. The correlation for the diffusion of an impurity in the dilute limit, with no interactions between the impurities, is accounted for with the 5-frequency—or 5-jump—model, shown in Figure 1 for the fcc lattice.

This model considers that these frequencies are the only vacancy jump frequencies in the crystal and it is thus a complete correlation model for the bulk of the fcc single crystal [6]. The nomenclature here used is the same as in the original papers [5,6,8] and of more recent work [10], where for clarity, all jump frequencies are denominated w_i, and the index i = [0, 1, 2, 3, 4] represents the jump as in the original works. In this model, the diffusion coefficient for a substitutional impurity that diffuses via monovacancies in the dilute limit of a solid solution is

$$D_1=D_0 {\displaystyle \frac{f_2}{f_0}}{\displaystyle \frac{w_2}{w_0}}{\displaystyle \frac{w_4}{w_3}}$$

(3)

where D₁ is the diffusion coefficient of the monovacancy and D₀ is the self-diffusion of the matrix atoms, f₀ is the correlation factor for the diffusion of matrix atoms and f₂ is the correlation factor for impurity diffusion. D₀ = 7.161 × 10⁻³⁷ cm²·s⁻¹ at T = 298 K from a linear fit from previously published low temperature data [15]. At low defect and impurity concentrations [16], the correlation factor f₀ for self-diffusion in the fcc lattice is 0.781 [5]. This factor accounts for the correlation effects between the vacancy and the diffusing Cu atom in the atomic jumps of Cu in the fcc lattice. The correlation factor f₂ for the diffusion of a substitutional impurity by a monovacancy-assisted mechanism in a face-centered cubic lattice is given by [6,8,10]

$$f_2={\displaystyle \frac{2w_1+7F{w}_3}{2w_2+2w_1+7F{w}_3}}$$

(4)

where F is the fraction of vacancies that make w₃ jumps (Figure 1) that effectively do not return to the site from which the jump was made. This term is also called the fraction of dissociating vacancies. F has been derived for the fcc lattice [6,17] with a basis in the Bardeen–Herring model [14] and is defined as

$$F=1-{\displaystyle \frac{y}{7}}\left({\displaystyle \frac{11.56+50.10x+40.00x^2}{0.52+4.71x+12.06x^2+8.00x^3}}\right),\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h} y={\displaystyle \frac{w_4}{12w_0}} \mathrm{a}\mathrm{n}\mathrm{d} x={\displaystyle \frac{{(w}_4-w_0)}{12w_0}}$$

(5)

where F depends on the jump frequencies w₄ and w₀ shown in Figure 1. The jump frequencies w_i are given by

$$w_i={\nu }_{i}exp\left({\displaystyle \frac{\Delta S_i^{‡}}{k_B}}\right)exp\left(-{\displaystyle \frac{\Delta H_i^{‡}}{k_{B}T}}\right)$$

(6)

where ν_i is the jump attempt frequency for the jump i as defined in Equation (1); this quantity is a vibrational frequency and its significance within the different transition state (TS) theories has been previously discussed in detail [10,18]. It has been shown that ν_i is very similar for the different jumps of the matrix atoms and the approximation ν₀ ≈ ν₁ ≈ ν₃ ≈ ν₄ is valid without a significant loss of accuracy [6,19]; ${\Delta S}_i^{‡}$ and ${\Delta H}_i^{‡}$ are the activation entropies and enthalpies for the jump i respectively and T is the temperature. The attempt frequencies ν_i can be obtained via two methods: (a) according to the original Wert–Zener work [20] as

$${\nu }_i=\sqrt{\left({\displaystyle \frac{{\Delta H}_i^{‡}}{2m_i{\lambda }^2}}\right)}$$

(7)

where m_i is the mass of the jumping atom and λ is the distance between the lattice sites according to Equation (1); and (b) according to the method by Neumann et al. [19] that considers the relation between normalized jump frequencies. Upon expressing the later equation as a relation between attempt frequencies, for the case of the impurity, which corresponds to the jump frequency w₂, we obtain

$${\displaystyle \frac{{\nu }_2}{{\nu }_0}}=\sqrt{{\displaystyle \frac{m_0{T}_{m2}}{m_2{T}_{m0}}}}$$

(8)

where m₀ and m₂ are the masses of the matrix atom and of the impurity atom, in this case S or P, and T_m0 and T_m2 are the melting temperatures of the matrix and the impurities, respectively. In this case: T_m0 = 1357 K and T_m2 = 317 K and 392 K for P and S, respectively. The activation entropies ${\Delta S}_i^{‡}$ can be determined from the Wert–Zener relation [20]

$${\Delta S}_i^{‡}\approx \beta {\displaystyle \frac{{\Delta H}_i^{‡}}{T_{m0}}}$$

(9)

where β is the temperature dependence of the sheer modulus of the matrix. As previously demonstrated [7], because the value of β is in the order of 0.10 for Cu [21], Equation (9) implies that for room temperature conditions, ${\Delta S}_i^{‡}\approx 0.21{\Delta H}_i^{‡}$ and thus we can disregard the entropy contribution in Equation (6) as previously performed in other works [21], and we have

$$w_i={\nu }_{i}exp\left(-{\displaystyle \frac{\Delta H_i^{‡}}{k_{B}T}}\right)$$

(10)

The ${\Delta H}_i^{‡}$ was computed for the transition state (TS) configuration of the corresponding jump i, as described below.

2.2. Computational Details

Density functional theory (DFT) calculations of the absorption of the P and S impurities in the fcc Cu lattice and of their vacancy-assisted diffusion, including the energy barriers for the jumps, were performed with the Vienna ab initio simulation package (VASP 5.4.4) [22] with the Perdew–Burke–Ernzerhof [23] (PBE) exchange–correlation functional with pseudopotentials of the projector augmented wave [24,25] (PAW) type. The PBE functional has shown good accuracy for describing the physical–chemical properties of the impurities in Cu [26,27,28,29]. For all calculations, a plane wave cutoff at 460 eV was employed. Each supercell employed in this work contained 108 Cu atoms whose internal coordinates were optimized with DFT. The convergence of the obtained energies with the model size has been tested in previous work [28]. The k-point meshes of 4 × 4 × 4 in the Monkhorst–Pack sampling scheme were adjusted to produce minimal errors while keeping good computational efficiency [30]. The absorption energy of a substitutional impurity atom at a lattice site of the perfect fcc crystal is defined as

ΔE_abs = E_{P,S_Cu} − (E_P,S + E_Cu)

(11)

where E_{P,S_Cu} is the energy of a supercell of a single crystal fcc Cu containing one atom of either P or S; E_P,S is the energy of a P or S atom in a vacuum in the same supercell employed to model the Cu crystal; and E_Cu is the energy of the supercell with 108 atoms of pure fcc Cu. A more negative value for ΔE_abs implies stronger bonding with the Cu lattice. A similar procedure was followed for the determination of the vacancy formation energy.

The energy barriers for diffusion (ΔE_a) were computed with the nudged elastic band (NEB) method as implemented in VASP [31,32]. The electronic structure parameters for these computations were the same as for the geometry optimizations and 7 images were employed in the TS search with the NEB routine. The activation energies reported here have been determined as

ΔE_a = E_TS − E_initial

(12)

where E_TS is the electronic energy of the saddle point that corresponds to the TS, and E_initial is the electronic energy of the initial structure from which the diffusion takes place. A more positive value for ΔE_a implies a larger energy barrier for the atomic jump. A similar expression was employed in the determination of the activation enthalpies ${\Delta H}^{‡}$. Vibrational frequencies were calculated by numerical differentiation of the forces using a second-order finite difference with a step size of 0.015 Å. The Hessian matrix was mass-weighted and diagonalized to yield the frequencies and normal modes of the system. The 0 K enthalpies were obtained by adding the zero-point energies (ZPE) to the electronic energies.

3. Results

3.1. Vacancy Formation Energies and Vacancy–Impurity Interactions

The vacancy formation energies (ΔE_vac) and the binding—or absorption—energies (ΔE_P,S) of P and S to the Cu lattice, and the interaction energies between P and S with a vacancy (ΔE_P,S) at the nearest neighbor site are shown in

Table 1. Vacancy formation energies (ΔE_vac) for Cu and interaction energies between P and S with a vacancy at the nearest neighbor site (ΔE_vac__P,S). Values in eV.

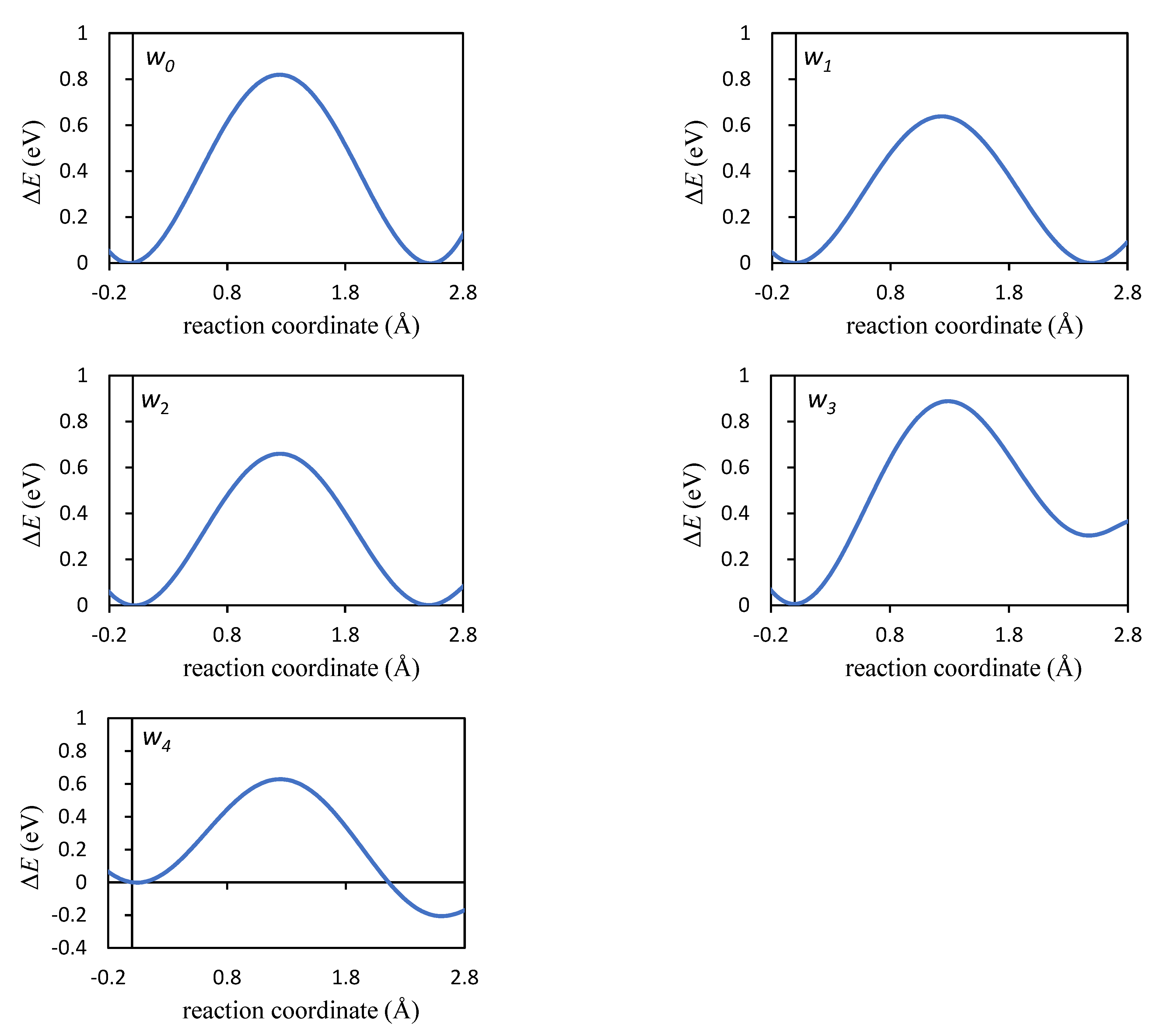
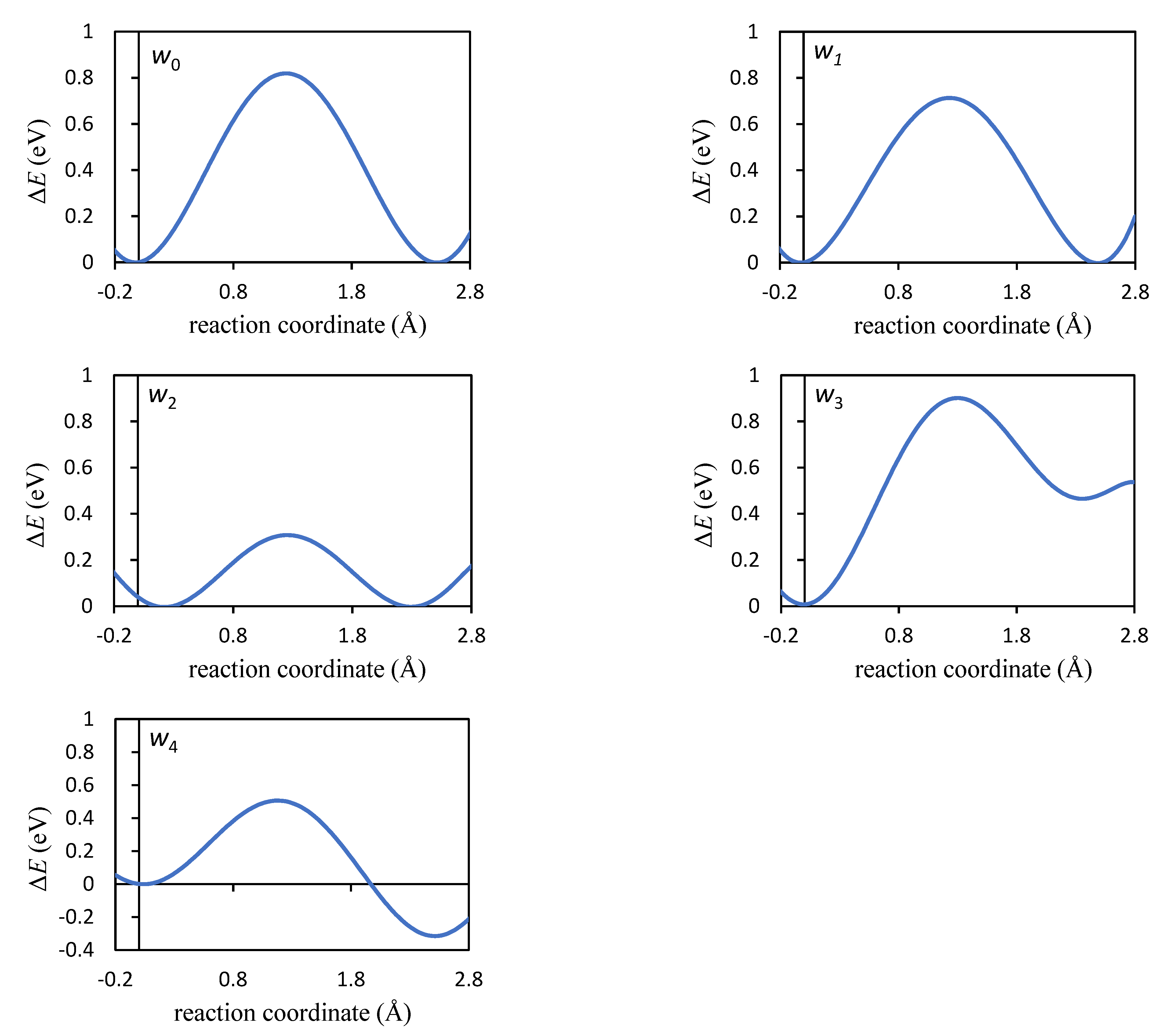
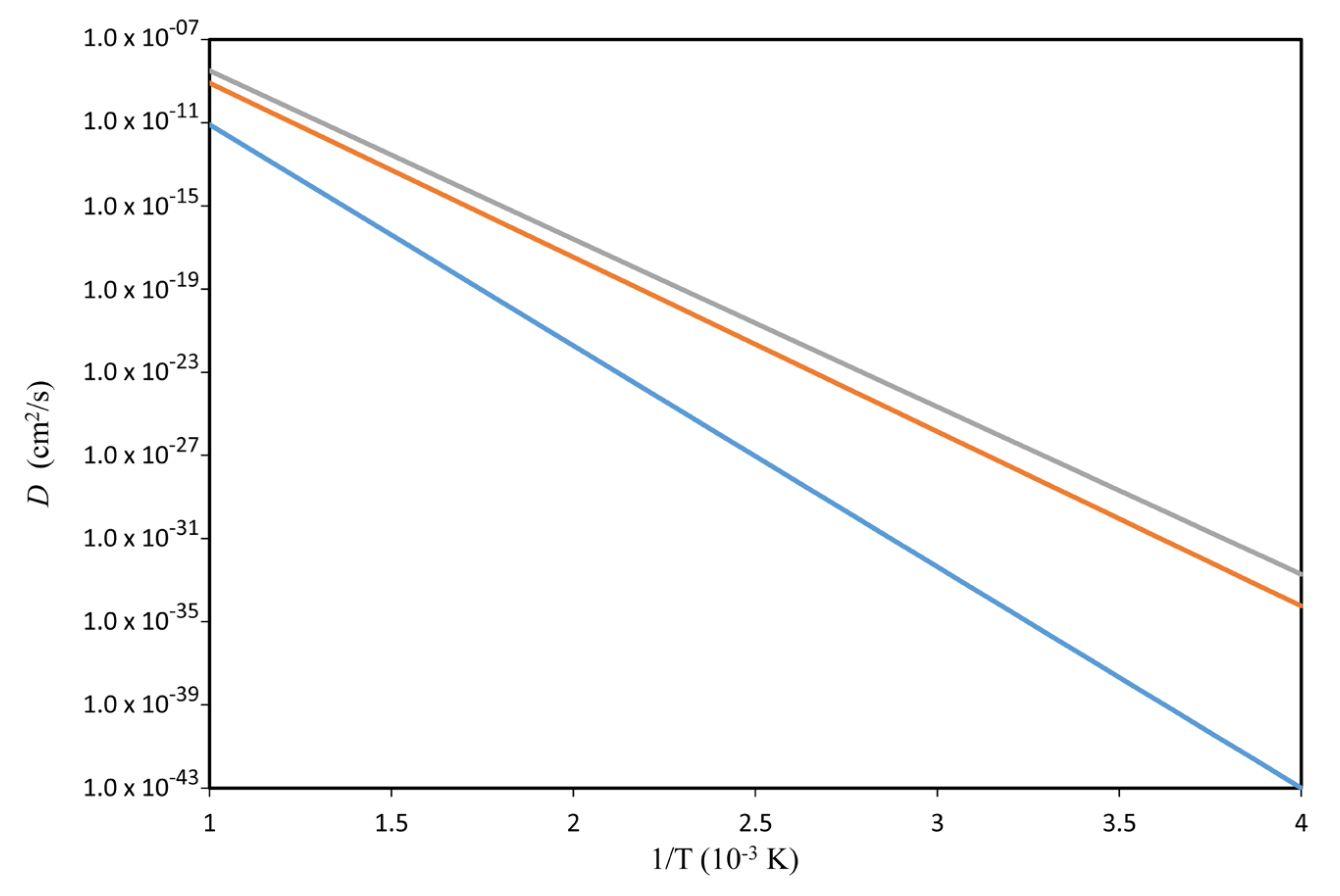
ΔEP	ΔES	ΔEvac	ΔEvac_P	ΔEvac_S
−0.653	−0.511	1.176	−0.229	−0.432

.

The vacancy formation energies of Cu, the absorption energies of P and S and the interaction energies between P, S and the vacancies agreed well with our and other authors’ previously published data [33,34,35,36]. The absorption energies ΔE_P and ΔE_S were presented here for contextualization but we alert the reader to the large uncertainty of these values because of the computation of single S and P atoms in a vacuum, especially because these two elements have different spin states and DFT cannot account fully for these configurations with accuracy [37,38]. Considering the underlying uncertainties, the ΔE_P and ΔE_S of fcc Cu were approximately the same when no vacancies are near. However, when the vacancies were the nearest neighbors to the impurities, this picture changes. Both P and S could stabilize a vacancy as the nearest neighbor, which is the result of an attractive interaction between these elements and the vacancy. This has also reflected in the jumps that involve the impurities whose activation energies follow the Brønsted–Evans–Polanyi (BEP) principle [39], as will be shown later. As expected, ΔE_vac__S was more negative than ΔE_vac__P [40]. This was also observed for the segregation of these two elements at the grain boundaries of Cu where S benefited more from bonding with substitutional sites with a larger volume as compared to P [26,27,29]. When bonding at the GB sites, S also tends to form more asymmetrical geometries when compared to P [26]. This happened both for the single impurity and for impurity pairs. This result was in line with the trends on coordination preferences in complexes that contain transition metal centers and these two p-block elements. The fact that the strength of the bonds between the Cu matrix and S benefited from asymmetry, when compared to P, is the factor responsible for the stronger interactions between S and a vacancy when compared to P and a vacancy, as shown in the data presented in Table 1. This also had effects on the diffusion coefficients for these elements, as will be shown below.

3.2. Correlation Effects: The Effective Diffusion Model or 5-Frequency Model for the Diffusion of P and S in Cu

The 5-frequency (5-jump or 5-hop) model for diffusion, described in the Methods section, is a good approximation to describe the complex correlation effects that occur when substitutional impurities diffuse in the fcc matrix. This model has been employed both at high and low temperatures with success. Because the results of Equations (3) to (8) depend on the accuracy of the energetic and vibrational data employed, we employed methods that have been thoroughly benchmarked and tested and will not present the details of such benchmarking here. Such details are given in the Methods section and in the cited references of our previous works [26,27,36].

The potential energy profiles from which we obtained the ΔE_a for each of the 5-jumps necessary to describe the correlation effects in the diffusion of S and P in Cu are shown in Figure 2 and Figure 3. The corresponding jumps are illustrated in Figure 1. Jump w₀ was independent of the impurities, but it is shown in both figures for comparison; all remaining jumps were impurity specific.

The DFT data used to determine the correlation parameters for the 5-frequency model are given in

Table 2. Distance of the jump (λ), activation energy (ΔE_a), contribution of the zero-point vibrational energy at the transition state (ΔZPE) and activation enthalpy (ΔH_a) values for the corresponding jumps for the Cu atoms and the P and S that are represented in Figure 1.

P
Jump	λ (Å)	ΔEa (eV)	ΔZPE (eV)	ΔHa (eV)
w1	2.518	0.639	0.012	0.650
w2	2.501	0.663	0.005	0.668
w3	2.545	0.884	0.005	0.889
w4	2.521	0.626	−0.014	0.611
w0	2.495	0.819	0.008	0.828
S
Jump	λ (Å)	ΔEa (eV)	ΔZPE (eV)	ΔHa (eV)
w1	2.518	0.714	0.010	0.724
w2	2.501	0.315	0.012	0.327
w3	2.545	0.895	0.009	0.904
w4	2.459	0.505	−0.008	0.496
w0	2.495	0.819	0.008	0.828

.

The jump of S to the vacancy, w₂, had less than half of the ΔE_a of the corresponding jump of P. The jump of the Cu atom away from the impurity, w₄, also had a considerably lower ΔE_a for S than for P. The remaining Cu atom jumps that could be affected by the type of impurity—w₃ and w₁—had similar ΔE_a values for both P and S. Because w₃ and w₁ are similar, the considerably lower ΔE_a for w₂ and w₄ for S when compared to P agreed with the experimental observation that S is a faster diffuser than P in Cu over a wide range of temperatures [41]. It is known that substitutional P is a fast diffuser in Ni via a vacancy-mediated mechanism [42,43]. Its diffusion coefficient is highly dependent on temperature. In Cu, this was also expected as the mechanisms of impurity diffusion and segregation share many commonalities with Ni. The data in Table 2 show additionally that the magnitude of the ZPE correction was at most 0.014 eV. The differences between the corresponding ZPE for the jumps of S and P were at most 0.007 eV. We can thus conclude that the inclusion of the computationally demanding ZPE was not necessary to obtain accurate data on the diffusion of these impurities.

The quantities necessary to obtain the correlation factors that accounted for the effective diffusion coefficients of P and S in Cu, as described in Equations (3) to (10), are given in

Table 3. The values of ν (Equation (8)) and w (Equation (10)) for each of the jumps (w_i) in the 5-frequency model, as shown in Figure 1, for P and S in Cu at 298 K.

Jump Index i	P		S
	ν (Hz)	wi (Hz)	ν (Hz)	wi (Hz)
1	8.982 × 109	0.0905146	9.478 × 109	0.0053790
2	1.313 × 1010	0.0665103	9.031 × 109	26661.4233049
3	1.039 × 1010	9.5 × 10−6	1.048 × 1010	5.3 × 10−6
4	8.701 × 109	0.3974227	8.038 × 109	32.2438087
0	1.023 × 1010	1.020 × 10−4	1.023 × 1010	1.020 × 10−4

.

The fastest diffusion of S when compared to P had most of its origins in the w₂ frequency, which was five orders of magnitude larger for S, as shown in Table 3. There was also a considerable contribution due to the three orders of magnitude differences in w₄. This was related with the lower ΔE_a value that, in turn, depended on the most favorable bonding, due to the larger volume and the asymmetry in the impurity coordination to the vacancy that occurred for S. When the diffusion coefficients were determined from the whole set of data, according to Equations (3) to (6), we obtained the values given in

Table 4. The values of x and y (Equation (5)), F, f₂ and f₀ (Equations (3) and (4)) and the corresponding diffusion coefficients (Equation (3)) for the P and S impurities in fcc Cu at T = 298 K and T = 373 K.

Quantity	Impurity
	P	S
T = 298 K
x	324.53063	26,336.58531
y	324.61396	26,336.66865
F	0.28609	0.28572
f2	0.57637	2.0195 × 10−7
f0 (fcc lattice)	0.781	0.781
D (cm2·s−1)	1.44 × 10−29	2.95 × 10−28
D (cm2·year−1)	4.56 × 10−22	9.30 × 10−21
D (cm2·100,000 year−1)	4.56 × 10−17	9.30 × 10−16
Diffusion length √(Dt) (cm·year−1)	2.13 × 10−11	9.64 × 10−11
Diffusion length √(Dt) (cm·100,000 year−1)	0.674 × 10−8	3.05 × 10−8
T = 373 K
D (cm2·s−1)	6.61× 10−24	8.06 × 10−23
D (cm2·year−1)	2.09 × 10−16	2.54 × 10−15
D (cm2·100,000 year−1)	2.09 × 10−11	2.54 × 10−10
Diffusion length √(Dt) (cm·year−1)	1.44 × 10−08	5.04 × 10−08
Diffusion length √(Dt) (cm·100,000 year−1)	4.57 × 10−06	1.60 × 10−05

. The temperature-dependent diffusion coefficients obtained from our data for S and P in Cu, according to Equation (10), and the experimental data for the self-diffusion coefficient for Cu are shown in Figure 4.

4. Discussion

The value of D obtained for S was in the range of experimental and computational values for the diffusion of S in Ni. At 1000 °C, the value of D for the diffusion of S in Ni is 7.1 × 10⁻⁹ cm²·s⁻¹ [7]; our data in Figure 4 showed that the corresponding value for S in Cu is 3.18 × 10⁻⁹ cm²·s⁻¹. Both of the D values for S and P agreed with those previously published and with the fact that S is a much faster diffuser in Cu single crystals than P [45]. S is also a faster diffuser than P in polycrystalline Cu [41]. A polycrystalline material with a microstructure has extended defects such as GBs, where diffusion can be considerably faster than at the bulk. However, the rate-determining step for overall diffusion is largely determined by the diffusion at the bulk, provided that the impurities are homogeneously distributed in the materials at the start of the experiments. In experimental observations in polycrystals, S diffused 10 times as fast as P [41], while in the pure single crystal, the difference was of 20 times that at room temperature according to our data. The difference was even larger at high temperatures [45]. From the experimental data, it is known that the presence of GBs and other polycrystal defects reduces the differences in D values between S and P. The possible mechanistic origin for this observation can be as follows: the data presented in Table 4 show that the correlation factor for impurity diffusion, f₂, was orders of magnitude smaller for S than for P. This is a limiting case where the stability of the vacancy–impurity complex is much higher for S than for P. The measures of this stability are, for each impurity, the following ratios: w₃/w₀, which corresponds to the dissociation of the vacancy–impurity complex and was 1.79 times larger for P than for S, and w₄/w₃, which corresponds to the probability of reassociation of the vacancy–impurity complex via w₄ in case it was dissociated via w₃, which gives a measure of the stability of the vacancy–impurity complex, and was 145 times larger for S than for P. Hence, the dissociation of the vacancy–impurity pair is much more unlikely to occur for S than for P. This means together with the magnitude of w₃, which was much lower for S than for P, implies that the probability of the S–vacancy pair to diffuse as a single entity via the w₁ and w₂ jumps, forming a pair that is called a “Johnson molecule”, is very high [46]. Additionally, because f₂ is very close to zero for S, this also implies that this impurity diffusion is strongly correlated in the Cu single crystal, while P has a diffusion mechanism that is an almost ideal balance—50/50—between diffusion along a straight line and in random directions. However, the very low energy barrier for an impurity jump in the case of S, w₂, led to a jump frequency which was six orders of magnitude larger than that of P (Table 3). This caused the diffusion of S to be faster than P despite being less efficient due to the correlation factor being close to zero. When extended defects, for example GBs, are present in the material, the diffusion of these impurities is largely constrained by the features of the defects that have well defined diffusion paths, such as channels [26,47]. This implies that at these constrained diffusion pathways, random diffusion is largely constrained and both S and P will adopt similar diffusion mechanisms. This can cause a decrease in the large differences in the diffusion coefficients between S and P, because at the GBs, the differences in the correlation factor for their diffusion, f₂, is smaller than that observed for the bulk single crystal.

The origins of the effects that lead to differences in the D value and the correlation factors can be traced down to both geometric and electronic structure phenomena, as we recently detailed for the bonding of these impurities to Cu [26]. The diffusion of these substitutional impurities requires a vacancy and the symmetry of the matrix-impurity complex is lowest when the vacancy is the nearest neighbor to the impurity. When bonding with transition metals, S is known to prefer lower symmetry arrangements and larger volumes of the atomic sites when compared to P. This leads to an energetic gain that was reflected in the two important parameters that affect both the diffusion mechanism and the corresponding diffusion coefficient: (a) the binding energy between the S–vacancy (−0.432 eV), which was larger when compared to the P–vacancy (−0.229 eV); and (b) in the considerably smaller ΔE_a values for the jumps w₂ and w₄ for S when compared to P. This, in turn, led to attempted frequencies for these jumps which were orders of magnitude larger for S than for P. From a detailed electronic structure analysis of the bonding between S and Cu, and P and Cu [26], we found that S had both more populated bonding states and less populated antibonding states than P. This explains both the stronger bonding with the Cu matrix and the lower ΔE_a value for diffusion because of less friction between S and the matrix when compared to P and the matrix at the transition state. Both the geometric and electronic structural features explain the differences in the diffusion coefficients for these impurities: S diffuses faster than P in the Cu single crystal and it is also known to be a faster diffuser in polycrystals.

5. Conclusions

Based on the DFT calculations and data analysis presented here, we observed that both P and S exhibited attractive interactions with the vacancies in the Cu lattice. This interaction was stronger for S compared to P, leading to a more stable vacancy configuration. The 5-frequency model accurately described the correlation effects during the diffusion of P and S in Cu. The activation energies for the different jump paths were determined, revealing that S has lower activation energies for certain jumps compared to P. The led to the fact that S diffused significantly faster than P in Cu due to the lower activation energies and more favorable vacancy–impurity interaction. The calculated diffusion coefficients were consistent with experimental observations and previous computational studies. The correlation factors for P and S diffusion differed significantly from unity and from each other. S had a much smaller correlation factor, indicating a more correlated diffusion mechanism, while P followed an almost ideal balance between a straight path and random directions. This difference is attributed to the geometric and electronic structural features of the impurity–vacancy complexes.

While this study focused on bulk diffusion, the findings suggest that the mechanisms of S and P diffusion at grain boundaries are considerably more similar than at the bulk due to the constrained diffusion paths in grain boundary regions.