Abstract
Artificial muscles underlie exciting, novel technologies that have many wide-reaching applications: exoskeleton actuation, walker robots, prosthetics and stealthy underwater propulsion. Actuating these muscles via electrostatic forces promises excellent energy efficiency and output force density and a high strength-to-weight ratio. Building these muscles through 3D-printed and conductive microfluidics promises fast mass production at a low cost. A microfluidic double-helix weave as a potential solution for the architectural design of these actuators has previously been reported. However, more recent experimental work showed that a weave architecture was not manufacturable at the necessary scale, given the limitations of current 3D-printing technology. Herein, several alternative architectures are presented. They are more advanced and more compatible with current manufacturing requirements, and offer additional benefits. The presented experimental results confirm their improvements in manufacturability. These advanced architectures represent a significant step towards the experimental proof of principle and the practical implementation of electrostatic microfluidic 3D-printed artificial muscles.
Keywords:
actuator; muscle; muscle fiber; biomimetic; electrostatic; architecture; geometry; microfluidic; microchannel; 3D-printing; microcapacitor; capacitor 1. Introduction
Robotic or similar actuation systems use a multitude of methods, each of which offer distinct advantages and disadvantages [1,2,3,4,5]. Their specific features make each of those methods suitable for various applications. Electromagnetic actuation [6,7,8] is used in sensors, motors or robotics, has a high power-to-weight ratio and is highly versatile [9,10] and reliable [11,12]. However, this form of actuation is not energy-efficient and cannot easily be scaled down to a small form factor. Pneumatic [13,14,15,16,17] or hydraulic [18,19,20] actuation is suitable for tasks that require high force generation, e.g., heavy machinery. For instance, in McKibben artificial muscles and prosthetics [17,21,22], hydraulic actuation provides large forces in macroscale systems [18,23]. Pneumatic and hydraulic actuation also dominate in other fields [20], e.g., construction vehicles, industrial assembly lines or the U.S. Army’s robot mule [24]. One of their disadvantages is the requirement of a fluid reservoir, which is prone to leaks and requires regular maintenance [10,21,25,26,27,28,29,30].
The limitations of electromagnetic, hydraulic and pneumatic actuation have motivated the search for alternative actuators in applications such as exoskeletal locomotion, walking robots, surgical robots, biomimetic underwater propulsion, prosthetics, medical servo-assists and small-scale biomimetic robots [8,13,29,30,31], including artificial muscles [30,31,32,33,34,35,36,37,38]. In most of these applications, high precision and energy efficiency are required.
Piezoelectric actuation [39,40,41,42,43,44,45] is one option. Piezoelectric devices offer high precision and can generate very large forces. However, the length of motion is small, and the devices are expensive and very difficult to upscale. Yet another option is actuators based on thermal expansion, e.g., torsional muscles [41,46] and shape-memory alloys muscles [47,48]. These can generate large forces, but the need to cool to cycle severely limits cycling frequency and responsiveness. This method is also not energy efficient. In comparison, electrostatic actuation is scalable, energy-efficient and low-cost (if combined with 3D printing). A comparison of the different approaches is given in Table 1.

Table 1.
Visual comparison of actuators.
This makes electrostatic actuation an attractive candidate mechanism. Electrostatic actuators have no moving parts that require lubrication and they also require no use of fluid systems. Therefore, actuation using electrostatic motors or capacitor motors requires little maintenance [49]. The force output of electrostatic actuators is limited; however, the force scales as the inverse square of the separation between the charged plates [36], their power consumption is very low and they are highly suited at the micro- and nanoscales. A particularly intriguing conceptual design for artificial muscles is that of dielectric elastomer actuators (DEAs) [7,50,51,52,53,54,55,56,57]. Their actuation is based on the deformation of a polymer (elastomer) slab from the electrostatic force between the charges built on the slab’s surfaces, under applied voltage [33,36].
Finite-element analysis (FEA) simulations of artificial muscles have confirmed this size–force relationship [58]. Hence, downscaling the devices to the microscale would result in a disproportionate gain in the generated force. Creating arrays of such devices in three dimensions would increase both the resultant force output and the resultant strain. When an array is constructed with the individual DEAs arranged to be mechanically in parallel, the total force produced is equal to the sum of the forces produced by each individual unit, but the overall elongation is unchanged by the array. When an array is constructed with the individual DEAs arranged to be mechanically in series, the total elongation is equal to the sum of the elongations produced by each unit, but the overall force is unchanged by the array.
Implementing a 3D array allows both benefits to be obtained simultaneously. Unfortunately, fabricating such arrays when scaled up to macro sizes is impractically expensive if performed using traditional methods [33,59]. We previously reported on an alternative solution to this problem: artificial muscles that combine microfluidics, electrostatic actuation, in-built electrodes and 3D-printing [36].
Briefly, the muscle is fabricated via 3D-printing [60], where microchannels turn into conductive wiring, and the support material acts as the dielectric material [61]. Since the microchannels are initially filled with sacrificial material [59], that material has to be removed by a clearing protocol [59]. The cleared channels can then be filled with conductive fluid to act as both flexible electrical connections and plates of parallel-plate microcapacitors. The 3D-printed resin is used both as the dielectric between the capacitor plates and the “tendon” to transfer force to the outside world [33,36]. In this approach [33], a single pair of channels, forming a stack of capacitors arranged mechanically in series, can be thought of as a single artificial-muscle “fiber”. These fibers can, in turn, be laterally arrayed to form an artificial-muscle-fiber “bundle”. As with biological muscles, small effects on local areas can become large effects at the system level. FEA simulations using COMSOL (v.6.1). Multiphysics [36,58,62], a solver and simulation software package for various physics and engineering applications, have predicted up to 900 kPa saturation force density from such bundles, when the individual microcapacitors are built at the 10 m scale.
An earlier work [63] and recent advancements [59,60,64] in 3D-printed microfluidics [65,66] have made it possible to fabricate such devices and test them experimentally. In particular Hornik et al. [59], experimentally demonstrated the consistent fabrication of microfluidic channels embedded in devices that were 3D-printed. The microchannels, defined as negative features filled with support material, were embedded inside the surrounding flexible resin. Then, a novel protocol was used to remove the support material from the embedded microchannels, thereby opening them for further use [59]. Further characterization experiments have shown [60] that the results of the technique are reproducible.
Hence, it is already possible to engineer 3D-printed microfluidic devices to specifications and with predictable performance. In consequence, the new 3D-printed microfluidics technique has already been successfully applied to produce depositions by self-assembly in heterogeneous systems [64], e.g., for microbial fuel cell applications. Similarly, this 3D-printed microfluidics technique now enables device fabrication and the experimental testing of artificial muscles. Hence, what is now needed is to devise practical geometries and architectures to help implement such devices.
We already proposed a weave architecture for these devices, which is both scalable and practicable in principle [33]. However, the weave architecture was invented before the development of these experimental techniques [59,60,64]. Experimental evidence showed that clearance could reliably be achieved down to perhaps a 400 m wide channel, with partial success down to a width of 200 m. On the other hand, artificial muscles benefit from features that are as small as possible, as identified by previous theoretical calculations and simulations [33,36]. These show that the output force density is proportional to the inverse square of the plate separation. In a nutshell, using the weave architecture at a sufficiently small scale to output significant actuation forces would require making the connecting channels too small to fabricate and clear reliably, at least with current PolyJet printing. Hence, new architectures have become necessary.
Accordingly, herein, we propose new advanced muscle architectures that are compatible with the developed clearance techniques [59], as well as introduce further novel concepts. While the clearing of sacrificial material remains a challenge with double-serpentine structures, significant success has been reported with potato spiral structures. Evidence of actuation has also been described and reported with potato spirals. Further optimizations ought to lead to measurable actuation and an experimental proof of principle. The new architectures have been experimentally confirmed to be manufacturable through the developed 3D-printed microfluidics technique [59,60,64]. The presented solutions are thus a major step towards the practical implementation of this type of artificial muscle.
The fundamental challenges of creating microcapacitor arrays, which are needed for electrostatic artificial muscles, stem from microfluidic, mechanical, electrical and scaling restrictions. These are especially daunting since all must be addressed simultaneously. We previously devised and reported on a joint solution comprising a double-helix “weave” geometry [33,36]. The microfluidic weave successfully addressed the electrical connection scaling problem by using helical microchannels connected in a dendritic binary branching structure [33]. This allowed all the microcapacitors to be connected in parallel electrically while being arranged mechanically in series within the same fiber, whereas the fibers were arranged mechanically in parallel. Additionally, bundles made of many fibers can also be set up to be connected electrically in parallel under this scheme [33].
After the weave was proposed, we developed a clearance method to remove the sacrificial material following 3D-printing [59], as well as a method of predictable fabrication [60]. Our results indicated that 3D-printing and the clearing of smaller channel becomes progressively more difficult and unreliable with the weave design. This indicated that the weave pattern, with its small channels, bottlenecks and dead-end corners, would be very difficult to implement with the newly developed technique. Furthermore, if the microcapacitor plates were designed to be in sufficiently close proximity to each other to produce significant forces, the required connection channels in the weave would likely be too small to fabricate and clear reliably [59,60]. Hence, a major architectural redesign became necessary to address these issues directly.
2. Materials and Methods
Chip Fabrication. All chips were printed on our Stratasys Objet500 Connex 1 3D printer (Stratasys, Rehovot, Israel). The chips were initially designed in the 3D Computer-aided Design software SOLIDWORKS 2022 (SolidWorksCorp., Waltham, MA, USA) and then converted for compatibility with the Objet500 Connex 1. All sets of chips were printed in batches.
Materials. Three different photopolymer materials were used in this study. The core material used for all chip architectures was Agilus30 Clear FLX985 (Stratasys, Eden Prairie, MN, USA), a soft resin. That material was chosen based on its chemical resistance and deformability. SUP706B (Stratasys, Eden Prairie, MN, USA) was used throughout as the sacrificial material to create negative features, i.e., microchannels. In some chips Agilus30 Black FLX985 (Stratasys, Eden Prairie, MN, USA), a black resin, was used because it provides a good optical contrast, for visual demonstration purposes. It was used to visualize microchannels instead of sacrificial material by filling negative spaces normally filled with sacrificial material (e.g., Figure 1D). All chips were printed monolithically in a single process with SUP706B or Agilus30 Black FLX985 and embedded in Agilus30 Clear FLX985 to form the microchannels in each specific architecture.

Figure 1.
The serpentine artificial muscle fiber architecture is formed of two entwining microchannels shown in light and dark gray, respectively. These microchannels have a constant cross-section and thus offer improved manufacturability. (A) Isometric view. (B) Side view. (C) Single-serpentine arrays were super-arrayed inside 3D-printed chips (1–4) and subjected to the support material clearing procedure [59]. The approximate chip size was 41 mm × 53 mm (width × length). See Table 2 for the quantitative results. (D) Double-serpentine chips whose microchannels were printed and filled with black resin to improve optical contrast for visualization.
Visual Assessment of Clearance Magnitude. The microchannels of all printed chips were cleared from the SUP706B sacrificial material as previously described [59]. In some chips, the success and magnitude of the clearance procedure were visually assessed by injecting blue food dye (McCormick Assorted Food Colors, Hunt Valley, MD, USA) into the cleared microchannels, at a concentration of 5 L in 1 mL water.
Analysis of Serpentine Clearance Percentage. Single serpentine-shaped microchannels were printed in flat chips. The dimensions of a chip were 41 mm × 53 mm (width × length). Four chips were printed, where each chip contained sets of four cross-sectional sizes (XL = 700 m; L = 550 m; S = 400 m; XS = 250 m), referred here as a super-array of arrays. The degree of success of the clearance procedure was assessed by measuring the linear length of the cleared fraction. This fraction was expressed as a percentage of the entire length of the channel.
Electrical Tests and Measurements. Electrical resistance measurements to test wired chips were conducted using a Fluke 87V Industrial Multimeter (Everett, WA, USA) and Agilent 34410A Multimeter (Santa Clara, CA, USA). Actuation voltage was provided by Spellman SA60 (Hauppauge, NY, USA).
3. Results
3.1. Serpentine Architecture
One solution that addresses the weave’s problems, as outlined in the Section 1 is the serpentine architecture (Figure 1). It is named “serpentine” due to the snake-like winding of the microchannels. Figure 1A shows an isometric view and Figure 1B shows a side view of the geometry. Each serpentine is a single channel with an essentially constant cross-section along the length of the channel. This avoids the weave’s bottlenecks, which can produce clogging and interfere with the clearance process. Also, there are no dead-end corners as in the weave, which would be difficult to clear due to reduced flow speed. Like the weave, the serpentine can be axially extended as desired by repeating the pattern as many times as needed. Furthermore, as only the individual fiber element of the weave is directly replaced, the overarching connecting structures, such as the dendritic tree structures in the lateral dimensions, remain the same. Hence the serpentine structure addresses several implementation issues compared to the weave structure while still benefiting from the advantages of the microchannel branching introduced with the weave [33].
The serpentine is designed in such a way that the distance between the parts of the channels that make up the microcapacitor plates is at least three times smaller than the distance between the channels in the lateral direction of the fiber. Hence, the force produced in the intended longitudinal contraction [36] is at least 9 times larger compared to an unintended lateral contraction. That lateral contractive force can limit lateral expansion, which hinders the desired longitudinal contraction. The bounded geometric ratio should help minimize this effect and, thus, should improve the overall performance of the muscle. With channel cross-sections in the order of hundreds of micrometers and microcapacitor separation in the order of tens of micrometers, FEA simulations have indicated that hundreds of kPa of force density can be produced [36,58], while experimental characterizations have proven that the 3D-printed microchannels can be appropriately formed and cleared [59,60].
The serpentine architecture was implemented in test chips fabricated in soft resin using the now established 3D-printed microfluidics technique, including embedded channels and a support material clearance procedure [59,60,64]. One purpose of these test chips was to establish the degree of success of the clearance procedure, as a function of the serpentine microchannel width. Single serpentines were chosen for this test to maximize their ability to assess the clearance of channels optically, as the entwining of the channels in a double-serpentine would have complicated the optical measurement unnecessarily.
Four chips were printed and each contained 12 serpentine microchannels, three of each of the four cross-sectional widths studied. The cross-sectional widths were XL = 700 m; L = 550 m; S = 400 m; and XS = 250 m. The chips are shown in Figure 1C. The cleared channels appear white due to scattering at the rough boundary between the channel surface and air. The uncleared channels appear invisible, since the support material refractive index is close to that of the 3D-printed resin, so interfacing boundaries would not scatter the light significantly.
The experimental results showed 100% successful clearance of the XL and L widths, while partial success was noted for the S width, and almost no success for the XS width. The results of the measurements are presented in Table 2.

Table 2.
Clearance of single-serpentine channels by channel size. All values represent the percentage of the channel arclength that was successfully cleared.
These results demonstrate that single serpentines can be cleared, at least for channel widths of ≥400 m. As a result, the fabrication of double-serpentine devices, generally referred to as simply “serpentine”, was undertaken. The individual channels entwining in each pair are difficult to discern, particularly at smaller scales. Figure 1D shows an example of a double-serpentine device. Note that microchannels in these chips are printed with black resin, are non-functional and are for demonstration purposes only (see Section 2).
Functional double-serpentine chips were 3D-printed; however, clearing their microchannels was very challenging. Initially, the usual clearance procedure led to delamination between the soft resin [67], which makes up the body of the chip, and the hard resin, which makes up the ends of the device (Figure 1D). To avoid delamination, the design of the device was updated by extending the soft material nearly all the way to the access ports. As a result, all microchannels were printed entirely from soft material. This design change fixed the material-boundary delamination failure; however, the devices still failed during the clearance procedure.
We attribute this failure to two connected factors. First, PolyJet technology prints devices in layers that are less strongly connected than the material within the same printing layer. Consequently, layer delamination is possible, particularly if a small region of delamination happens. Once layer delamination begins, it triggers positive feedback in wedge-like processes, where the defect creates increased local stress, which creates a larger defect, resulting in more stress. The result of this wedging is that once layer delamination begins, it will likely grow until the device fails. As fluidic pressure is used in the clearance procedure, it is likely that the pressure generated partial delamination and then helped it spread through the wedging effect.
The second factor has to do with the geometry of the serpentine. The serpentine winds back and forth, producing many approximately 90-degree turns. Each turn necessitates a corner, which produces stress concentrations that aid in the initial generation of splits between layers. Rounding off these corners can mitigate this effect at the cost of additional lateral space usage or further plate separation. Since maximal resolution is achieved along the vertical z-axis, the devices are printed “standing”, i.e., the longitudinal axis is lined up with the z-axis. This means that the corners of the turns would likely end up at the boundaries between printing layers. The combined effect of these two factors is a likely explanation for the observed layer delamination during the clearance procedure.
A potential solution to this problem is to switch to stereolithography 3D printers (SLA) [68]. Like with PolyJet, SLA printers produce objects in layers; however, the bonding between layers is much closer in strength to the bonding within the layers. This removes the failure point that the PolyJet technology inherently produces. Additionally, the support material in SLA printing is a liquid monomer and is thus far easier to remove than the solid PolyJet support material. This means that while serpentine architectures have tractable problems with PolyJet printing, they are likely to be far more suitable for the SLA printing of embedded microfluidics.
3.2. Potato Spiral Architectures
To solve the problems experienced by the serpentine design under PolyJet technology, we devised a new architectural solution, which is shown in Figure 2. This architecture is named the “potato spiral” due to its resemblance to the helix produced by a spiral-cut potato. Figure 2A shows one of the helical capacitor “plates” in isolation, while Figure 2B shows both plates together.

Figure 2.
The potato spiral artificial muscle fiber architecture comprises two entwined spiral microchannels, shown in light gray and dark gray (A–E), respectively. (A) An isometric view of a single constituent spiraling microchannel. (B) An isometric view of the potato spiral muscle fiber. (C) An alternative isometric view cut to display the layering. (D) An isometric view of a pair of microchannels with pylons added for improved force transfer and mechanical strength. (E) A side view of the potato spiral fiber without pylons. (F) The 3D-printed potato spiral muscle fiber after clearing [59] with a thin layer of material on the surface peeled off to increase optical transparency by removing layer lines. The central tendon is visible along the central longitudinal axis. (G) The 3D-printed potato spiral muscle fiber cleared of support material. A thin layer of material on the surface was peeled off to increase optical transparency by removing layer lines. One channel is stained with blue dye to help visualization. Both spirals are filled with liquid gallium to produce the needed electrical conductivity.
Like the weave and the serpentine, the potato spiral can be lengthened as desired through pattern repetition. Unlike the weave and the serpentine, the potato spiral can be easily scaled up or down in the lateral direction by altering the radius of the outer dimension until it reaches the desired size, providing greater design freedom and adaptability. The inner radius of the potato spiral (most visible in Figure 2E) can be altered analogously. This would be carried out to find a balanced tradeoff between force production by the potato spiral and force transfer by the central tendon. Additional considerations were made regarding cross-section size. A larger cross-section would result in lower fluidic resistance and, thus, less pressure needed when clearing. Unlike with the serpentine, with the potato spiral architecture, this can be achieved without effecting the critical separation distance or lateral space usage adversely. These parameters also affect the device’s ability to hold the overall structure together mechanically.
The initial prototype of the potato spiral shown in Figure 2F,G had channels with a cross-section of 4000 m × 800 m and a plate separation of 1000 m. These dimensions resulted in a robust device that was able to be reliably fabricated and cleared under PolyJet technology. While smaller separation is highly desirable to boost force output quadratically [36,58], the requirements of clearance and manufacturability prompted this choice of dimensions. Further work on the clearing protocol and related aspects can allow for desirably smaller separations. The devices showed no signs of layer delamination or fluidic short circuits, unless extreme pressures were applied during the clearance procedure. These observations seem to confirm the hypothesis that the potato spiral architecture avoids the delamination problems of the serpentine architecture while still permitting the use of PolyJet technology for fabrication.
A potential disadvantage of the potato spiral has to do with the high aspect ratio of the channel’s cross-section, i.e., the channel width is large while its height is small. Ideally, the channel height should be small, to maximize the output force, while the channel cross-sectional area should be large, to minimize the fluidic resistance and the likelihood of short circuits. These conditions result in a channel that is low and wide. However, a general rule of thumb in elastomer microfluidics is to keep the cross-sectional aspect ratio below 10:1 [59,60,64]. Significant deviations from this rule can cause channel collapse and other problems [59,60,64,69]. Such problems could limit the aspect ratio available to potato spiral devices.
To solve the potential aspect ratio problem, structural supports or “pylons” can be added in the capacitor plates of the potato spiral, as shown in Figure 2D. These pylons decrease the effective aspect ratio and thus help prevent channel collapse while preserving the benefits of the low-and-wide channel. The pylons would also improve force transfer [36]. Alas, this improvement would come at the cost of a small loss in force-generating area and would incur additional axial stiffness. Fortunately, both costs can be offset by decreasing the size of the inner circle and/or increasing the size of the outer circle of the potato spiral, thus returning the axial stiffness and force-generating area to their respective values before the pylons are added. This can be thought of as reorganization of the tendon that was concentrated on the boundaries to a more distributed tendon with the same overall cross-sectional area.
The pyloned potato spiral chips were implemented and showed improved mechanical strength and success in clearing without rupturing. The cleared chips were filled with gallium and tested for short circuits between the two spirals using electrical resistance measurements. The end-to-end resistance of the same spiral was typically a few ohms, whereas the cross-spiral resistance was typically a few megaohms. These devices were then subjected to an external DC voltage, which was gradually raised from 0 V to 3 kV. Most devices experienced dielectric failure between 2 kV and 3 kV. Internal light emission at the short was observed at failure. Also, before failure, gallium was typically observed to squirt out of the open ports of the devices. This observation is evidence of actuation, since the internal contraction would eject part of the gallium through the generated hydraulic pressure. These results are very encouraging and a major step towards measurable actuation force and elongation, and thus, provide experimental proof of principle. As a result, the potato spiral design is the frontrunner in the competition among the tested architectures.
The above advantages establish the high utility of the potato spiral as a new design solution. However, it also comes with some new challenges. First, when actuated, the potato spiral, unlike the serpentine or weave, could produce torque about its longitudinal axis. When a mathematical helix is compressed, the total arclength can shorten to compensate for the change. In contrast, when a physical helix is compressed, the total arclength tries to remain constant, which results in “twisting”, or torsional angular elongation. This twisting could be a small effect, but it is worth noting. If desired parameters can be chosen to increase or decrease this twisting effect, for a device intended for purely linear actuation comprising a single potato spiral fiber, this twisting may not be an issue, as the structure could be allowed to twist without loss of contractive capability. However, in a potato spiral fiber bundle, the twisting can be thwarted or supported by the nearest neighbors as desired by selecting appropriate chiralities. Thereby, this potentially adverse affect can be mitigated, thus allowing each fiber to compress linearity and to maximize its output force.
3.3. Onion Architectures
An alternative solution to the aspect ratio problem of the potato spiral is shown in Figure 3. It is made of concentric helices organized in alternating chirality along the radial direction. Each individual nested helix pair offers a smaller aspect ratio than the potato spirals of Figure 2. This architecture is named the “onion” due to its similarity to the potato spiral, but with the addition of concentric layering when seen from the top down. This is most easily visible in Figure 3B and Figure 4B. This architecture also removes the expected twisting effect of the potato spiral fibers, since each concentric channel pair will twist in opposite directions.

Figure 3.
The onion architecture. Each set of similarly charged microchannels is shown in light gray and dark gray, respectively. This architecture would produce aspect ratios close to 1, would cancel twisting motion and would distribute tendon supports. (A) An isometric view of a single microchannel set (10 channels total) of the same polarity. (B) An isometric view of an onion muscle fiber containing two sets of channels (10 channels each) of opposite polarity (sets shown in light gray and dark gray, respectively). (C) An isometric view of the onion geometry cut to show the layering. (D) An isometric view of a pair of opposite-chirality microchannels, to show the chirality change. (E) A side view of an onion muscle fiber.
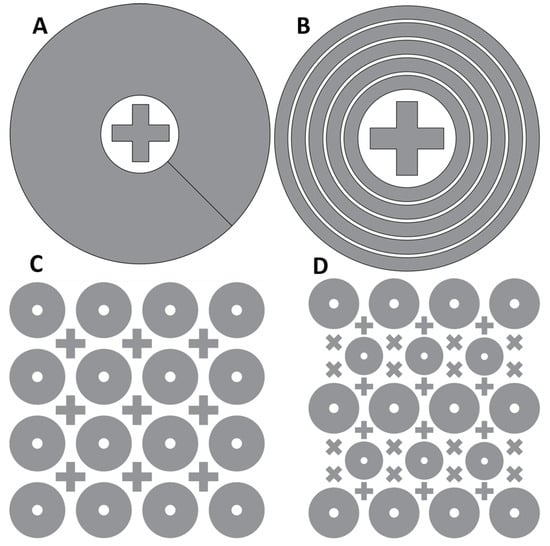
Figure 4.
Bundles of heterogeneous muscle fibers. All panels in this figure show heterogeneous bundles of muscle fibers viewed from the top along the longitudinal axis of a device. The plus-sign-shaped symbols represent the top view of the serpentine. The large donut shape represents the potato spiral. The concentrically layered rings represent the onion. (A) A concentric array containing serpentine and potato spiral architectures. (B) A concentric array containing serpentine and onion architectures. (C) A rectangular array containing serpentine and potato spiral architectures of constant scale and orientation. (D) A rectangular array containing serpentine and potato spiral architectures of variable scale and orientation.
For some applications, the overall torsional elongation may be disadvantageous. While this can be addressed at the array level, it can also be done individually. Thus, we propose incorporating helices of alternating chirality in a single fiber, so that the result is a cancellation of the expected twisting. Although this is present in all parts of Figure 3, Figure 3D illustrates this idea best, where only two strands are shown. Due to the similar nature of the individual channel cross-sections, it is reasonable to apply the same general view of sizing channels between the onion and the serpentine. Additionally, due to the similar outer geometry, it is reasonable to apply the same general view of sizing the overall structure between the onion and potato spiral with pylons.
This alternating chirality would also create lateral repulsive forces that act to increase the overall effectiveness of the fiber. This is the exact opposite of the undesirable lateral attraction in the serpentine fiber. Additionally, the spacing between concentric layers functions as extra tendon area in a similar way to the pylons discussed above. Thus, the onion architecture could be less prone to collapse and internal ruptures. The number of concentric layers can be altered as desired. There are five concentric “layers” shown in Figure 3. This corresponds to a total of twenty interwoven independent helices, as each “layer” produces four channels. Such complexity would produce serious problems during device assembly under conventional manufacturing, but 3D-printing can handle the same complexity with relative ease even at this scale [60].
An alternative option to the use of pylons in a potato spiral fiber is to simultaneously decrease the inner and outer circles defining the boundaries of the potato spiral, so it has a reduced and thus potentially more desirable aspect ratio. However, this may make the design less efficient in terms of output force, as it will decrease the portion of cross-section dedicated to force generation. This can be thought of as an onion fiber but with only a single pair of microchannels (half of a layer), or as a potato spiral fiber appropriately downscaled in the radial direction. This can then be compensated for by increasing the number of potato spiral fibers in a bundle of the same lateral size. In some cases, pylons may be a better solution, but they are not the only solution.
3.4. Heterogeneous-Array Fiber Bundles
The fibers of the weave architecture [33] were homogeneously arrayed and then connected by a binary dendritic structure. The same arrangement makes sense with the serpentines. However, the advent of potato spiral and onion architectures suggests alternative heterogeneous arraying. Figure 4 introduces several categories of possibilities for such arrays. Figure 4A,B each show concentric arrays centered around a single serpentine. In these concentric arrangements, the radius can be increased as needed by ether increasing the outer radius of the potato spiral or adding additional concentric “layers” around the onion. Figure 4C,D show Cartesian arrays with serpentines intermixed with potato spirals. Figure 4C shows that the serpentine nests neatly into the gaps between the potato spirals, thus using the available space more efficiently. Using a heterogeneous array design, in addition to providing nesting and lateral scaling benefits, may allow for the simultaneous exploitation of the unique benefits of multiple individual architectures.
4. Discussion and Conclusions
This article presents multiple innovative designs of 3D-printed microfluidic devices. After clearing and embedding of the microchannels with conductive material [61], the devices can be serially connected such that the microchannels act as microcapacitors. At this point, a device constitutes a novel form of artificial muscle [36,58]. Based on Coulomb’s law, the force density is proportional to the inverse square of the microcapacitor plate distance, a hypothesis confirmed by an FEA analysis of parallel-plate capacitors [36]. This is the reason why in all three presented designs, the double-serpentine, the potato and the onion, performance will be critically affected by the longitudinal scaling and size of the device. Exploiting Coulomb’s law was possible with all three designs; however, a nuanced balance needs to be struck between force density and microchannel size to maintain the important ability to effectively clear devices of sacrificial material.
Scaling can affect the serpentine architecture in significant ways. If the entire structure is uniformly scaled down, the effects from the electrostatic interaction will scale up disproportionately, as verified via simulations [36,58]. This benefit comes at the cost of increased difficulty in fabrication. If scaled such that the axial direction is held constant and the lateral direction is scaled up (making the architecture “wider”), the ratios contributing to lateral contraction mentioned above would improve with the scaling and potentially aid in the functionality of the fiber. An additional tendon structure that aids in force transmission would also be created by this scaling. However, these benefits come at the cost of a larger fiber cross-section that decreases the overall output force density.
If the serpentine were scaled such that the lateral direction is held constant and the axial direction is scaled down (making the architecture “lower”), the same mitigating effect on the lateral force resisting axial deformation would be obtainable. Additionally, this scaling reduces the spacing between plates, thus obtaining the associated disproportionate benefit. However, this scaling would come at the cost of smaller channels that are more difficult to handle and thinner membranes that can decrease overall robustness. Thus, with all of these considerations in mind, appropriate scales must be carefully selected to fit a given application and have a net positive effect. Channel heights around 500 m are already practicable with PolyJet. SLA technology as well as improvements in PolyJet technology are likely to reduce the practicable heights further.
Likewise, scaling can significantly affect the performance of the potato spiral architecture. If the entire architecture is uniformly scaled down, the effects from the electrostatic interaction will scale up disproportionately due to Coulomb’s law. This increase in performance is a tradeoff with other considerations, such as ease of fabrication and how robust the device is to internal fluidic short circuits and other similar failure modes and fabrication constraints discussed above.
If the axial direction is held constant and the lateral direction is scaled up, i.e., the architecture is made “wider”, the aspect ratio of the channels will increase, potentially causing a collapse in the center. If pylons are used in conjunction with this scaling, this single large cross-section fiber could be a viable alternative to a bundle of small fibers. This type of scaling would also reduce the influence of edge effects, which has already been shown to improve overall output force density [58]. Obtaining channel heights of ≈500 m with aspect ratios below 10 (width-to-height), and axial spacing between channels of opposite polarity of tens to hundreds of micrometers, appears feasible with PolyJet technology.
Alternatively, if the lateral direction is held constant while the axial direction is scaled down, i.e., the architecture is made “lower”, the spacing between plates will decrease and the associated disproportionate benefit to output force density can be obtained. However, this would have undesirable effects on the channel’s aspect ratio and the design’s overall robustness in terms of manufacturability and mechanical strength. It is clear then that such tradeoffs will have to be informed by a combination of further FEA simulations and experimental work.
The potato spiral design offers several important advantages compared to the weave and the serpentine. First, the potato spiral addresses the likely causes of internal fluidic short circuits during clearing by possessing a much larger channel width with no sharp turns. This lowers fluidic resistance, thus reducing the required clearing pressure and increasing success in clearing the channels. Critically, the potato spiral achieves this improvement while keeping the channel separation small, thus ensuring high output force density, as predicted by previous work [36,58]. The potato spiral also allows for larger radii of curvature (in the axial direction) compared to the weave and the serpentine, thereby decreasing the likelihood of delamination between the longitudinally stacked layers. So, overall, the potato spiral should be much more resistant to that failure mode.
Second, the potato spiral’s entire arclength is dedicated to the capacitor “plates”, with no real estate given to connections between plates. Thus, this architecture allows for increased utilization of the cross-sectional area towards force generation without sacrificing the cross-sectional area or arclength to wiring connections. Thus, the same output force density can then be achieved with larger separation of the electrodes. Hence, the material would be more robust to rupture, and thus less likely to produce a fluidic short and/or electric breach. This is critical when attempting to optimize the force density output, as suggested by previous simulations [36,58].
Third, the potato spiral fiber would avoid generating the lateral contractive force that the serpentine fiber experiences due to the mutual winding. Thus, the potato spiral fiber could offer less resistance to lateral expansion and thus to longitudinal contraction. This allows for an additional advantage to be obtained from the nonlinearity of the electrostatic force with plate distance.
The twisting motion of the potato spiral could be undesirable at various scales and/or in different applications. One way to reduce this effect if desired could be to arrange an array of potato spiral fibers with parallel primary axes and opposite chirality. Unfortunately, the cancellation of the twisting effect by this method can add to the experienced resistance to longitudinal contraction, because the neighboring fibers will act partly against each other’s natural motions. This establishes another design tradeoff between limiting twisting and limiting the overall longitudinally assessed force density. Alternatively, the two fibers could be based on helices that possess matching chirality. This would reinforce the twisting on the outer boundary of the two fiber bundles.
Another way to reduce the twisting effect expected from the potato spiral architecture is to decrease the angle of the helix, thus making the capacitor “plates” closer to orthogonal to the longitudinal axis. This would effectively redirect a fraction of the generated force acting towards torsional elongation to now act towards linear compression. This method does not have the same drawback associated with canceling the effect with arrays, since the force is not canceled out but instead repurposed. Twisting can also be decreased by laterally scaling down, as this type of scaling would reduce the moment arm that produces the torque. Again with this method, there is no cancellation of the forces, and thus, it avoids the associated tradeoff inherent to the array method discussed above. These various strategies intended to reduce the twisting effect can be implemented together for a combined result.
The onion architecture promises to have the ability to be enlarged in the radial direction with no predicted ill effects related to increasing the aspect ratio. This introduces the possibility of a concentric array containing a single onion fiber with many layers added. This concentric array could then be centered around a through hole fitted around a stiff member. This member would not contract with the fiber, instead remaining fixed in relation to the contractive motion. In this arrangement, the stiff member would add robustness to the overall muscle as well as provide a bone-like supporting structure to affix external loads or mechanical joints. One potentially important benefit of this scheme would be a different weighting of parameters for the tradeoff between force generation and force-transferring areas (capacitor plates and tendons) such that less tendon would be required. This can be thought of as similar in application to a pneumatic/hydraulic piston due to the constraint of movement along the axial direction.
As with the other architectures, scaling significantly affects the onion design. If the onion is uniformly scaled down, the electrostatic force will disproportionately scale up in much the same way as with the potato spiral and serpentine architectures [36,58]. In the same manner as the designs described earlier, there is a balance between the desired plate proximity for electrostatic reasons and the desired distance needed to prevent internal ruptures when pressure is applied. This distance is especially important with the onion due to the higher number of adjacent channels. If the axial direction is held constant and the lateral direction is scaled up (making the architecture “wider”), the result would be a structure somewhere between that of the potato spiral and onion. It may even be possible to obtain a hybrid formation that boasts the upsides of both. Channel sizes like those discussed for the serpentine architecture above would be feasible.
The arraying techniques shown in Figure 4 are still subject to the tradeoff between the channels (shown in gray in Figure 4) needed to generate force for actuation and the tendon material (shown as whitespace in Figure 4) needed to transfer the generated force to the outside world. Hence, the utilization of heterogeneous arrays would require optimization through extensive parameter sweeps in FEA simulations. The complexity added through heterogeneity will have to be justified by concomitant, sizeable gains in output force density. One potential solution to find the best balance is to take an optimally nested array (an array with a minimized tendon area) and then enlarge the array uniformly while holding the fiber sizes constant. This should act to distribute the tendon more evenly throughout the array. Figure 4D illustrates that arrays can also be made of various sizes or orientations with the same architecture.
In conclusion, recent advances in 3D-printed microfluidics have enabled the fabrication of artificial muscles based on the electrostatic actuation of large 3D arrays of microcapacitors, built from conductive microfluidic channels and the surrounding dielectric 3D-printed resin. This has necessitated the advent of respective microfluidic architectures that possess the necessary electrical and mechanical features. Herein, several such advanced architectures have been proposed, described, discussed and compared (see Table 3). Furthermore, the design choices have been checked against and backed with experimental results. The most important conclusion of this work is that its developments pave the way for the imminent implementation of practical and effective 3D-printed microfluidic, electrostatic artificial muscles. Experimental proof of principle through pyloned potato spirals appears to be only one or two tweaks away in terms of the scaling choices and clearing protocol, as demonstrated by the described devices. Such muscles have a wide range of practical applications, such as robotic actuators, exoskeletal locomotion, prosthetics and stealthy undersea propulsion. With these advances, the reality of the practical fabrication and implementation of such devices is now closer than ever before.

Table 3.
Visual comparison of presented architectures.
Author Contributions
Conceptualization, T.H., J.K.C. and E.P.K.; methodology, T.H., M.K., J.L.-A., J.K.C. and E.P.K.; software, T.H. and J.K.C.; validation, T.H., A.R., M.K. and J.L.-A.; formal analysis, T.H., A.R. and M.K.; investigation, T.H., A.R., M.K., J.L.-A., J.K.C. and E.P.K.; resources E.P.K.; writing—original draft preparation, T.H.; writing—review and editing, T.H., M.K., J.K.C. and E.P.K.; visualization, T.H., J.K.C. and E.P.K.; supervision, T.H. and E.P.K.; project administration, E.P.K.; funding acquisition, E.P.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Office of Naval Research through grant number N0001423WX01092.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to privacy.
Acknowledgments
The authors thank the Office of Naval Research for their financial support.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Hunter, I.W.; Hollerbach, J.M.; Ballantyne, J. A comparative analysis of actuator technologies for robotics. Robot. Rev. 1991, 2, 299–342. [Google Scholar]
- Hannan, M.W.; Walker, I.D. Kinematics and the Implementation of an Elephant’s Trunk Manipulator and Other Continuum Style Robots. J. Robot. Syst. 2003, 20, 45–63. [Google Scholar] [CrossRef]
- Yasa, O.; Toshimitsu, Y.; Michelis, M.Y.; Jones, L.S.; Filippi, M.; Buchner, T.; Katzschmann, R.K. An Overview of Soft Robotics. Annu. Rev. Control. Robot. Auton. Syst. 2023, 6, 1–29. [Google Scholar] [CrossRef]
- Luo, M.; Tao, W.; Chen, F.; Khuu, T.K.; Ozel, S.; Onal, C.D. Design improvements and dynamic characterization on fluidic elastomer actuators for a soft robotic snake. In Proceedings of the IEEE International Conference on Technologies for Practical Robot Applications (TePRA), Woburn, MA, USA, 14–15 April 2014; pp. 1–6. [Google Scholar] [CrossRef]
- Xavier, M.S.; Fleming, A.J.; Yong, Y.K. Image-Guided Locomotion of a Pneumatic-Driven Peristaltic Soft Robot. In Proceedings of the IEEE International Conference on Robotics and Biomimetics (ROBIO), Dali, China, 6–8 December 2019; pp. 2269–2274. [Google Scholar] [CrossRef]
- Liptak, B.G.; Piovoso, M.J.; Shinskey, F.G.; Eren, H.; Totherow, G.K.; Jamison, J.E.; Morgan, D.; Hertanu, H.I.; Marszal, E.M.; Berge, J.; et al. Instrument Engineers’ Handbook, Volume Two: Process Control and Optimization; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Qiu, Y.; Zhang, E.; Plamthottam, R.; Pei, Q. Dielectric elastomer artificial muscle: Materials innovations and device explorations. Acc. Chem. Res. 2019, 52, 316–325. [Google Scholar] [CrossRef] [PubMed]
- El-Atab, N.; Mishra, R.B.; Al-Modaf, F.; Joharji, L.; Alsharif, A.A.; Alamoudi, H.; Diaz, M.; Qaiser, N.; Hussain, M.M. Soft actuators for soft robotic applications: A review. Adv. Intell. Syst. 2020, 2, 2000128. [Google Scholar] [CrossRef]
- Liu, D.K.C.; Friend, J.; Yeo, L. A brief review of actuation at the micro-scale using electrostatics, electromagnetics and piezoelectric ultrasonics. Acoustic. Sci. Technol. 2010, 31, 115–123. [Google Scholar] [CrossRef]
- Pustavrh, J.; Hočevar, M.; Podržaj, P.; Trajkovski, A.; Majdič, F. Comparison of hydraulic, pneumatic and electric linear actuation systems. Sci. Rep. 2023, 13, 20938. [Google Scholar] [CrossRef] [PubMed]
- Song, Y.; Wang, B. Survey on reliability of power electronic systems. IEEE Trans. Power Electron. 2012, 28, 591–604. [Google Scholar] [CrossRef]
- Falck, J.; Felgemacher, C.; Rojko, A.; Liserre, M.; Zacharias, P. Reliability of power electronic systems: An industry perspective. IEEE Ind. Electron. Mag. 2018, 12, 24–35. [Google Scholar] [CrossRef]
- De Volder, M.; Reynaerts, D. Pneumatic and hydraulic microactuators: A review. J. Micromech. Microeng. 2010, 20, 043001. [Google Scholar] [CrossRef]
- Pham Huy Anh, H.; Ahn, K.K. Hybrid control of a pneumatic artificial muscle (PAM) robot arm using an inverse NARX fuzzy model. Eng. Appl. AI 2011, 24, 697–716. [Google Scholar] [CrossRef]
- Hesselroth, T.; Sarkar, K.; van der Smagt, P.; Schulten, K. Neural network control of a pneumatic robot arm. IEEE Trans. Syst. Man Cybern. 1994, 24, 28–38. [Google Scholar] [CrossRef]
- Daerden, F.; Lefeber, D. The Concept and Design of Pleated Pneumatic Artificial Muscles. Int. J. Fluid Power 2001, 2, 41–50. [Google Scholar] [CrossRef]
- Gariya, N.; Kumar, S.; Shaikh, A.; Prasad, B.; Nautiyal, H. A review on soft pneumatic actuators with integrated or embedded soft sensors. Sens. Actuators A Phys. 2024, 372, 115364. [Google Scholar] [CrossRef]
- Hunt, T.; Vaughan, N. The Hydraulic Handbook; Elsevier Science Ltd.: Amsterdam, The Netherlands, 1996. [Google Scholar]
- Xia, J.; Durfee, W.K. Analysis of small-scale hydraulic actuation systems. J. Mech. Des. 2013, 135, 091001. [Google Scholar] [CrossRef]
- Lindell, J.E.; Moore, W.P.; King, H.W. Handbook of Hydraulics; McGraw-Hill Education: New York, NY, USA, 2018; Available online: https://www.accessengineeringlibrary.com/content/book/9781259859687 (accessed on 25 February 2025).
- Chou, C.P.; Hannaford, B. Measurement and modeling of McKibben pneumatic artificial muscles. IEEE Trans. Robot. 1996, 12, 90–102. [Google Scholar] [CrossRef]
- Zhang, Z.; Philen, M. Pressurized artificial muscles. J. Intell. Mater. Syst. Struct. 2012, 23, 255–268. [Google Scholar] [CrossRef]
- Tavakoli, M.; Marques, L.; de Almeida, A.T. A comparison study on pneumatic muscles and electrical motors. In Proceedings of the 2008 IEEE International Conference on Robotics and Biomimetics, Bangkok, Thailand, 22–25 February 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 1590–1594. [Google Scholar] [CrossRef]
- LS3 Pack Mule. Available online: https://www.darpa.mil/about-us/timeline/legged-squad-support-system (accessed on 15 November 2024).
- Acome, E.; Mitchell, S.K.; Morrissey, T.; Emmett, M.; Benjamin, C.; King, M.; Radakovitz, M.; Keplinger, C. Hydraulically amplified self-healing electrostatic actuators with muscle-like performance. Science 2018, 359, 61–65. [Google Scholar] [CrossRef]
- Cho, H.S.; Kim, T.H.; Hong, T.H.; Park, Y.L. Ratchet-integrated pneumatic actuator (RIPA): A large-stroke soft linear actuator inspired by sarcomere muscle contraction. Bioinspir. Biomim. 2020, 15, 036011. [Google Scholar] [CrossRef]
- Daerden, F.; Lefeber, D. Pneumatic artificial muscles: Actuators for robotics and automation. Eur. J. Mech. Environ. Eng. 2002, 47, 11–21. [Google Scholar] [CrossRef]
- Naclerio, N.D.; Hawkes, E.W. Simple, low-hysteresis, foldable, fabric pneumatic artificial muscle. IEEE Robot. Autom. Lett. 2020, 5, 3406–3413. [Google Scholar] [CrossRef]
- Xavier, M.S.; Tawk, C.D.; Zolfagharian, A.; Pinskier, J.; Howard, D.; Young, T.; Lai, J.; Harrison, S.M.; Yong, Y.K.; Bodaghi, M.; et al. Soft pneumatic actuators: A review of design, fabrication, modeling, sensing, control and applications. IEEE Access 2022, 10, 59442–59485. [Google Scholar] [CrossRef]
- Gravert, S.D.; Varini, E.; Kazemipour, A.; Michelis, M.Y.; Buchner, T.; Hinchet, R.; Katzschmann, R.K. Low-voltage electrohydraulic actuators for untethered robotics. Sci. Adv. 2024, 10, eadi9319. [Google Scholar] [CrossRef]
- Wang, H.; York, P.; Chen, Y.; Russo, S.; Ranzani, T.; Walsh, C.; Wood, R.J. Biologically inspired electrostatic artificial muscles for insect-sized robots. Int. J. Robot. Res. 2021, 40, 895–922. [Google Scholar] [CrossRef]
- Madden, J.D.; Vandesteeg, N.A.; Anquetil, P.A.; Madden, P.G.; Takshi, A.; Pytel, R.Z.; Lafontaine, S.R.; Wieringa, P.A.; Hunter, I.W. Artificial muscle technology: Physical principles and naval prospects. IEEE J. Ocean. Eng. 2004, 29, 706–728. [Google Scholar] [CrossRef]
- Coltelli, M.A.; Kartalov, E.P. Scalable microfluidic double-helix weave architecture for wiring of microcapacitor arrays in 3D-printable biomimetic artificial muscles. Sens. Actuators A Phys. 2022, 340, 113543. [Google Scholar] [CrossRef]
- Mirvakili, S.M.; Hunter, I.W. Artificial muscles: Mechanisms, applications, and challenges. Adv. Mater. 2018, 30, 1704407. [Google Scholar] [CrossRef]
- Zhang, J.; Yang, Y.; Zhao, J.; Shi, L.; Xu, Y.; Yu, K.; Guo, C. Investigation of BRAF mutation in a series of papillary thyroid carcinoma and matched-lymph node metastasis with ARMS PCR. Pathol. Res. Pract. 2019, 215, 761–765. [Google Scholar] [CrossRef]
- Coltelli, M.A.; Catterlin, J.; Scherer, A.; Kartalov, E.P. Simulations of 3D-Printable biomimetic artificial muscles based on microfluidic microcapacitors for exoskeletal actuation and stealthy underwater propulsion. Sens. Actuators A Phys. 2021, 325, 112700. [Google Scholar] [CrossRef]
- Shi, M.; Yeatman, E.M. A comparative review of artificial muscles for microsystem applications. Microsys. Nanoeng. 2021, 7, 95. [Google Scholar] [CrossRef]
- De Pascali, C.; Naselli, G.A.; Palagi, S.; Scharff, R.B.; Mazzolai, B. 3D-printed biomimetic artificial muscles using soft actuators that contract and elongate. Sci. Robot. 2022, 7, eabn4155. [Google Scholar] [CrossRef] [PubMed]
- Peng, J.Y.; Chen, X. A Survey of Modeling and Control of Piezoelectric Actuators. Mod. Mech. Eng. 2013, 3, 1–20. [Google Scholar] [CrossRef]
- Chi, Z.; Xu, Q. Recent Advances in the Control of Piezoelectric Actuators. Int. J. Adv. Robot. Syst. 2014, 11, 182. [Google Scholar] [CrossRef]
- Aziz, S.; Spinks, G. Torsional artificial muscles. Mater. Horiz. 2020, 7, 667–693. [Google Scholar] [CrossRef]
- Chang, Q.; Chen, W.; Zhang, S.; Deng, J.; Liu, Y. Review on Multiple-Degree-of-Freedom Cross-Scale Piezoelectric Actuation Technology. Adv. Intell. Syst. 2024, 6, 2300780. [Google Scholar] [CrossRef]
- Ali, M.R.R.; Tigno, S.D.; Caldona, E.B. Piezoelectric approaches to organic polymeric materials. Polym. Int. 2024, 73, 176–190. [Google Scholar] [CrossRef]
- Ajnada, T.; Bernard, Y.; Daniel, L. Snap-through of a bistable beam using piezoelectric actuation. J. Intell. Mater. Syst. Struct. 2024, 35, 1137–1148. [Google Scholar] [CrossRef]
- Jin, H.; Gao, X.; Ren, K.; Liu, J.; Qiao, L.; Liu, M.; Chen, W.; He, Y.; Dong, S.; Xu, Z.; et al. Review on Piezoelectric Actuators Based on High-Performance Piezoelectric Materials. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2022, 69, 3057–3069. [Google Scholar] [CrossRef]
- Song, H.; Hori, Y. Force control of twisted and coiled polymer actuators via active control of electrical heating and forced convective liquid cooling. Adv. Robot. 2018, 32, 736–749. [Google Scholar] [CrossRef]
- Yin, H.; Zhou, J.; Li, J.; Joeseph, V. Fabrication and Properties of Composite Artificial Muscles Based on Nylon and a Shape Memory Alloy. J. Mater. Eng. Perform. 2018, 27, 3581–3589. [Google Scholar] [CrossRef]
- Lee, H.; Kim, M.; Lee, G.; Kim, C.; Ahn, S. Shape Memory Alloy (SMA)-Based Microscale Actuators with 60Deformation Rate and 1.6 kHz Actuation Speed. Small 2018, 14, 1801023. [Google Scholar] [CrossRef]
- Fennimore, A.; Yuzvinsky, T.; Regan, B.; Zettl, A. Electrically driven vaporization of multiwall carbon nanotubes for rotary bearing creation. In Proceedings of the AIP Conference Proceedings American Institute of Physics, Kirchberg, Austria, 6–13 March 2004; Volume 723, pp. 587–590. [Google Scholar] [CrossRef]
- Bahramzadeh, Y.; Shahinpoor, M. A review of ionic polymeric soft actuators and sensors. Soft Robot. 2014, 1, 38–52. [Google Scholar] [CrossRef]
- Imamura, H.; Kadooka, K.; Taya, M. Dielectric elastomer actuator with variable stiffness based on interlaminar electrostatic chucking. In Proceedings of the Electroactive Polymer Actuators and Devices (EAPAD), Portland, OR, USA, 25–29 March 2017; SPIE: Bellingham, WA, USA, 2017; Volume 10163, pp. 116–121. [Google Scholar] [CrossRef]
- Duduta, M.; Hajiesmaili, E.; Zhao, H.; Wood, R.J.; Clarke, D.R. Realizing the potential of dielectric elastomer artificial muscles. Proc. Natl. Acad. Sci. USA 2019, 116, 2476–2481. [Google Scholar] [CrossRef] [PubMed]
- Molberg, M.; Leterrier, Y.; Plummer, C.J.G.; Walder, C.; Löwe, C.; Opris, D.M.; Nüesch, F.A.; Bauer, S.; Månson, J.A.E. Frequency dependent dielectric and mechanical behavior of elastomers for actuator applications. J. Appl. Phys. 2009, 106, 054112. [Google Scholar] [CrossRef]
- Li, J.; Liu, L.; Liu, Y.; Leng, J. Dielectric elastomer bending actuator: Experiment and theoretical analysis. In Electroactive Polymer Actuators and Devices (EAPAD); SPIE Proceedings; SPIE: Bellingham, WA, USA, 2014; Volume 9056. [Google Scholar] [CrossRef]
- Kofod, G.; Paajanen, M.; Bauer, S. New design concept for dielectric elastomer actuators. In Smart Structures and Materials 2006: Electroactive Polymer Actuators and Devices (EAPAD); SPIE: Bellingham, WA, USA, 2006; Volume 6168, pp. 689–697. [Google Scholar] [CrossRef]
- Jia, K.; Lu, T.; Wang, T. Response time and dynamic range for a dielectric elastomer actuator. Sens. Actuators A Phys. 2016, 239, 8–17. [Google Scholar] [CrossRef]
- Ozsecen, M.Y.; Mavroidis, C. Nonlinear force control of dielectric electroactive polymer actuators. In Electroactive Polymer Actuators and Devices (EAPAD); SPIE Proceedings; SPIE: Bellingham, WA, USA, 2010; Volume 7642, pp. 673–680. [Google Scholar] [CrossRef]
- Coltelli, M.A.; Keeven, J.M.; Leckie, J.M.; Catterlin, J.K.; Sadagic, A.; Kartalov, E.P. Output Force Density Saturation in COMSOL Simulations of Biomimetic Artificial Muscles. Appl. Sci. 2023, 13, 9286. [Google Scholar] [CrossRef]
- Hornik, T.; Kempa, J.; Catterlin, J.; Kartalov, E. A Solution to the Clearance Problem of Sacrificial Material in 3D Printing of Microfluidic Devices. Micromachines 2022, 14, 16. [Google Scholar] [CrossRef]
- Krause, M.; Marshall, A.; Catterlin, J.K.; Hornik, T.; Kartalov, E.P. Dimensional Fidelity and Orientation Effects of PolyJet Technology in 3D Printing of Negative Features for Microfluidic Applications. Micromachines 2024, 15, 389. [Google Scholar] [CrossRef]
- Krause, M.; Marshall, A.; Catterlin, J.K.; Kartalov, E. Self-assembled electrically conductive biocompatible CNF wiring enables 3D-printed microfluidics applications. Sens. Actuators A Phys. 2024, 381, 116070. [Google Scholar] [CrossRef]
- Introduction to COMSOL Multiphysics®. Available online: https://cdn.comsol.com/doc/5.5/IntroductionToCOMSOLMultiphysics.pdf (accessed on 15 November 2024).
- Goh, G.L.; Agarwala, S.; Yong, W.Y. 3D printing of microfludic sensor for soft robots: A preliminary study in design and fabrication. In Proceedings of the 2nd International Conference on Progress in Additive Manufacturing (Pro-AM 2016), Singapore, 16–19 May 2016; pp. 177–181. [Google Scholar]
- Hornik, T.; Kempa, J.; Catterlin, J.; Kartalov, E. A Qualitative Experimental Proof of Principle of Self-Assembly in 3D Printed Microchannels towards Embedded Wiring in Biofuel Cells. Micromachines 2023, 14, 807. [Google Scholar] [CrossRef]
- Au, A.K.; Huynh, W.; Horowitz, L.F.; Folch, A. 3D-printed microfluidics. Angew. Chem. Int. Ed. 2016, 55, 3862–3881. [Google Scholar] [CrossRef] [PubMed]
- Nielsen, A.V.; Beauchamp, M.J.; Nordin, G.P.; Woolley, A.T. 3D printed microfluidics. Ann. Rev. Anal. Chem. 2020, 13, 45–65. [Google Scholar] [CrossRef] [PubMed]
- Gibson, I.; Rosen, D.; Stucker, B. Additive Manufacturing Technologies: 3D Printing, Rapid Prototyping, and Direct Digital Manufacturing; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar] [CrossRef]
- Kalpakjian, S.; Schmid, S. Manufacturing Engineering & Technology; Pearson Education: London, UK, 2013. [Google Scholar]
- Nguyen, T.; Arias-Thode, Y.M.; Obraztsova, A.; Sarmiento, A.; Stevens-Bracy, A.; Grbovic, D.; Kartalov, E.P. Proof-of-concept for a novel application for in situ microfluidic benthic microbial fuel cell device (MBMFC). J. Environ. Chem. Eng. 2021, 9, 105659. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).