MVCG-SPS: A Multi-View Contrastive Graph Neural Network for Smart Ponzi Scheme Detection
Abstract
:1. Introduction
- We propose a multi-view GNN framework that decomposes blockchain data into distinct meta-path-based views, enabling rich cross-view anomaly detection.
- We design a meta-path-based view construction module that ensures diverse semantic relationships are well-represented, improving both the interpretability and robustness of the learned embeddings.
- We integrate a reinforcement-learning-driven aggregation mechanism to dynamically adjust view weights, maximizing the model’s fraud detection capabilities.
- We implement a contrastive learning approach to align embeddings across views, enhancing the overall robustness and discriminative power of the model.
2. Related Work
2.1. Multi-View Graph Representation Learning
2.2. Graph Neural Networks for Fraud Detection
3. Preliminary
3.1. Multi-View Heterogeneous Graph Structure
3.2. Meta-Path-Based Views
- 1.
- : Externally Owned Accounts (EOA) to Contract Accounts (CA), representing fund inflows.
- 2.
- : CA to EOA, representing fund outflows or transfers.
3.3. Anomaly Detection in Multi-View Graphs
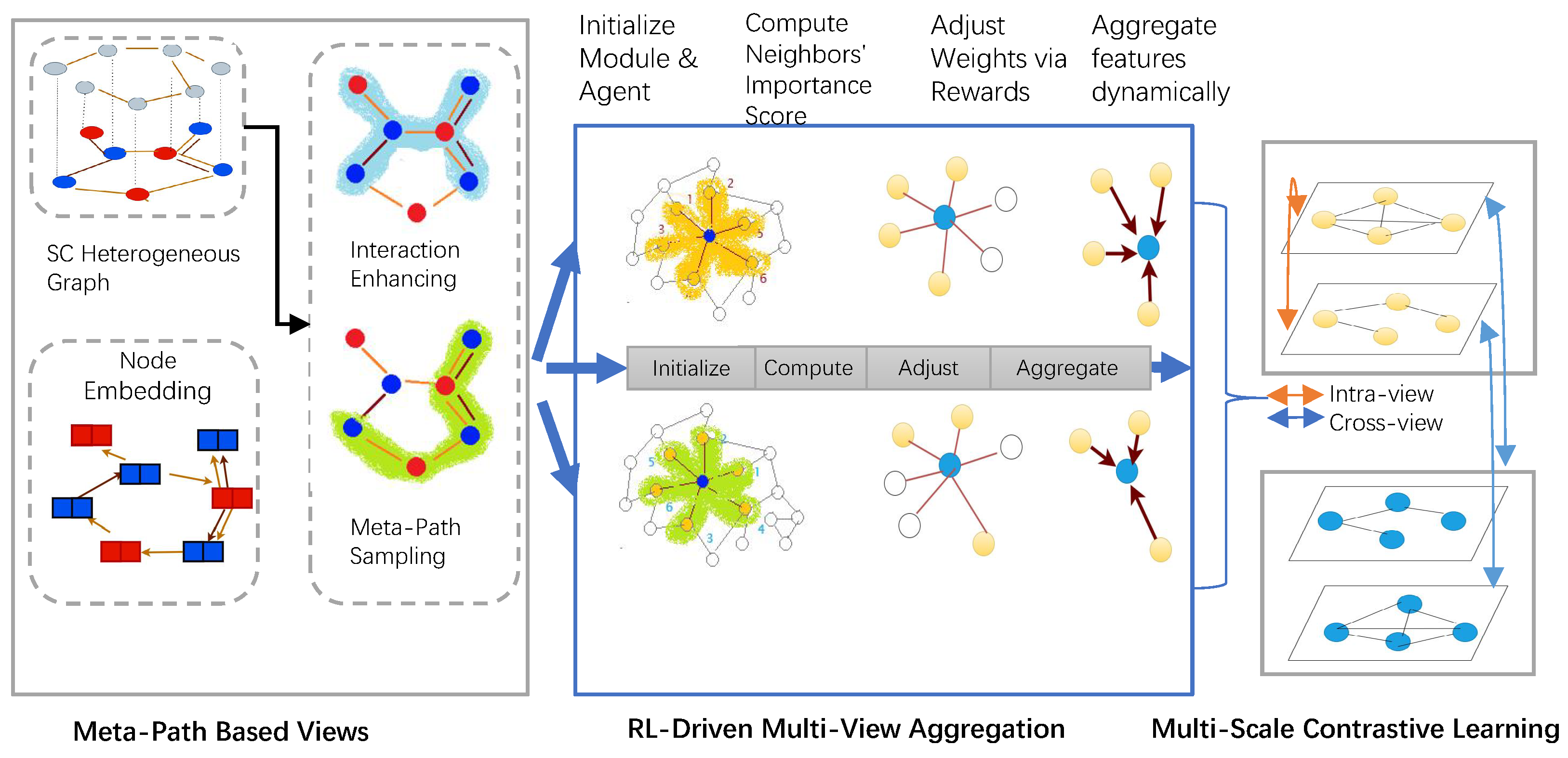
4. MVCG-SPS Method
4.1. Smart Contract Heterogeneous Graph Construction
- : Node set, including EOA and CA.
- : Edge set, capturing interaction relationships between entities, including transaction edges (Pay, Invest Edge) and call edges (Call Edge).
- : Node type set (EOA or CA).
- : Edge type set (Transaction or Call).
4.2. Meta-Path-Based Multi-View Generation
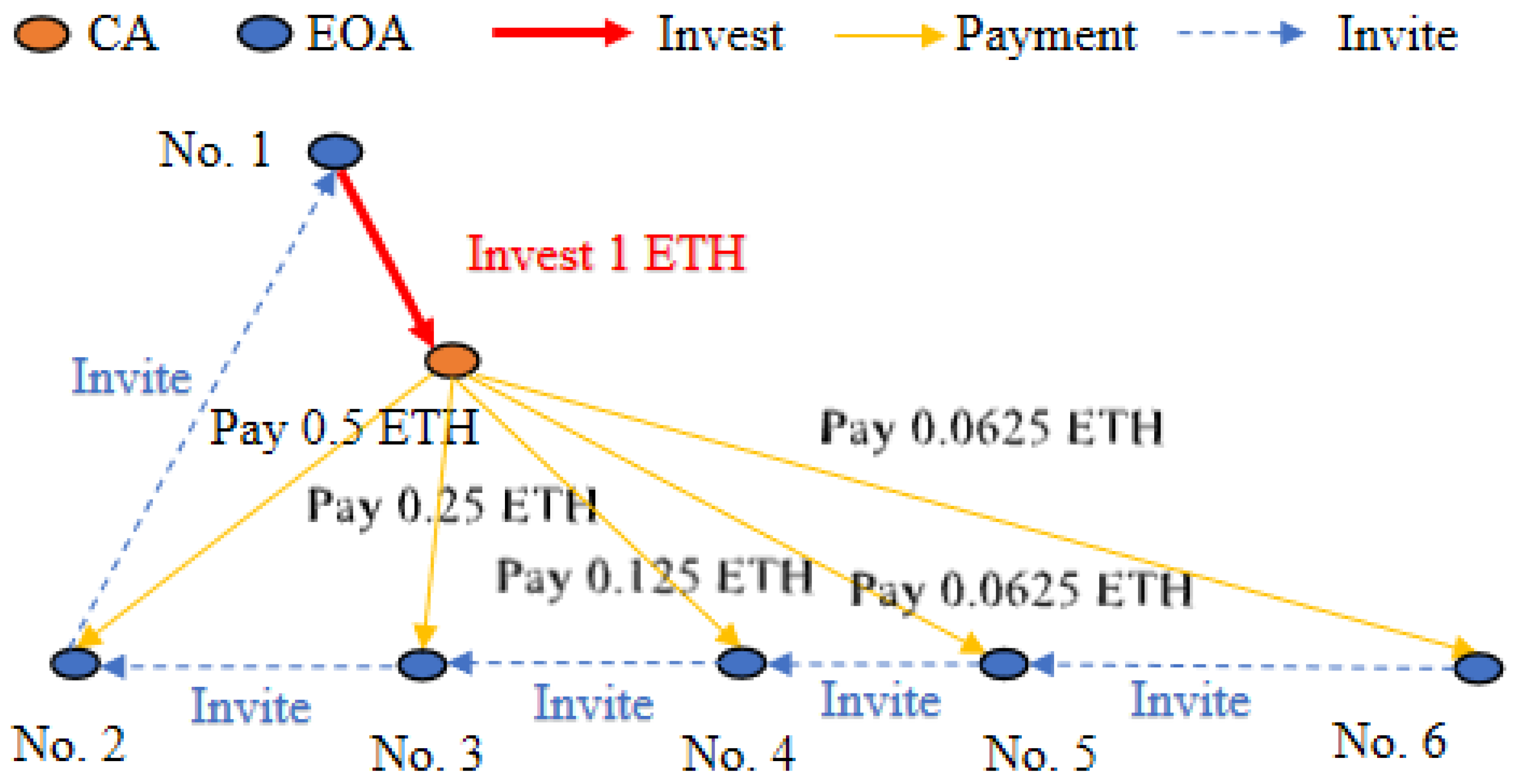
- No.6 → No.5: EOA No.6 invited EOA No.5.
- No.5 → No.4: EOA No.5 invited EOA No.4.
- No.4 → No.3: EOA No.4 invited EOA No.3.
- No.3 → No.2: EOA No.3 invited EOA No.2.
- No.2 → No.1: EOA No.2 invited EOA No.1.
- : Represents the invitation pattern between EOAs.
- : Represents the relationship between smart contracts and external accounts, where external accounts invest in the smart contract and the contract returns the investment to the upstream EOAs, capturing the fund flow.
| Algorithm 1 Interaction-Enhancement-Based View Decomposition Algorithm |
|
- : Represents the fund flow pattern where the Ponzi account interacts with external accounts via contract calls.
- : Describes the behavior pattern where the Ponzi account distributes funds after receiving them, revealing the fund transfer path.
| Algorithm 2 Meta-Path Sampling View Decomposition Algorithm | |
Input: Heterogeneous graph | |
| 2: | Output: Set of subgraphs |
Initialize the set of subgraphs | |
| 4: | for each meta-path in the predefined set of meta-paths do |
| 6: | Compute the node features of |
Add to the set | |
| 8: | end for |
return | |
4.3. Reinforcement-Learning-Driven Multi-View Aggregation
- represents the set of views,
- is the node representation of view v,
- is the weight for view v, dynamically optimized by the RL module.
4.4. Multi-Scale Contrastive Learning
| Algorithm 3 Multi-Scale Contrastive Learning |
|
5. Experiments
5.1. Dataset Preprocessing
5.2. Evaluation Metrics
5.3. Baselines
5.4. Results and Analysis
5.4.1. Performance Evaluation
5.4.2. Ablation Study
5.4.3. Sensitivity Analysis
5.4.4. Explainability Analysis
5.4.5. Complexity and Scalability
- Time: (interaction enhancement) + (encoding) + (contrastive loss)
- Space: (sparse adjacency) + (multi-view features)
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hassan, M.U.; Rehmani, M.H.; Chen, J. Anomaly detection in blockchain networks: A comprehensive survey. IEEE Commun. Surv. Tutorials 2022, 25, 289–318. [Google Scholar] [CrossRef]
- Chen, W.; Zheng, Z.; Cui, J.; Ngai, E.; Zheng, P.; Zhou, Y. Detecting ponzi schemes on ethereum: Towards healthier blockchain technology. In Proceedings of the 2018 World Wide Web Conference, Lyon, France, 23–27 April 2018; pp. 1409–1418. [Google Scholar]
- Fernandes, G.; Rodrigues, J.J.; Carvalho, L.F.; Al-Muhtadi, J.F.; Proença, M.L. A comprehensive survey on network anomaly detection. Telecommun. Syst. 2019, 70, 447–489. [Google Scholar] [CrossRef]
- Quinlan, J.R. Induction of decision trees. Mach. Learn. 1986, 1, 81–106. [Google Scholar] [CrossRef]
- Chandola, V.; Banerjee, A.; Kumar, V. Anomaly detection: A survey. Acm Comput. Surv. (CSUR) 2009, 41, 1–58. [Google Scholar] [CrossRef]
- Callegari, C.; Coluccia, A.; D’Alconzo, A.; Giordano, S. A Methodological Overview on Anomaly Detection. In Data Traffic Monitoring and Analysis; Springer: Berlin/Heidelberg, Germany, 2013; pp. 148–183. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Khan, S.; Yairi, T. A Review of Machine Learning and Deep Learning Techniques for Anomaly Detection. Appl. Sci. 2021, 11, 5320. [Google Scholar] [CrossRef]
- Khan, S.; Madden, M.G. A comprehensive survey of anomaly detection techniques for high dimensional big data. J. Big Data 2014, 2, 1–22. [Google Scholar] [CrossRef]
- Kipf, T.N.; Welling, M. Semi-supervised classification with graph convolutional networks. arXiv 2016, arXiv:1609.02907. [Google Scholar]
- Velickovic, P.; Cucurull, G.; Casanova, A.; Romero, A.; Lio, P.; Bengio, Y. Graph attention networks. Stat 2017, 1050, 10–48550. [Google Scholar]
- Zhang, Z.; Zhang, J.; Xie, R.; Dai, H.; Yuan, B.; Wang, W.; Philip, S.Y. FRAUDRE: Fraud Detection in Ethereum via Learning Representations of Transaction Subgraphs. In Proceedings of the 27th ACM SIGKDD Conference on Knowledge Discovery & Data Mining, Virtually, 14–18 August 2021; pp. 2954–2962. [Google Scholar] [CrossRef]
- Liu, Y.; Zheng, V.W.; Zhao, Z.; Li, K.C.C. HeteroEmbed: Heterogeneous Information Network Embedding for Fraud Detection. In Proceedings of the 43rd International ACM SIGIR Conference on Research and Development in Information Retrieval, Virtually, 25–30 July 2020; pp. 1111–1120. [Google Scholar] [CrossRef]
- Zhang, X.; Yang, H.; Zhang, C.; Chawla, N.V. Graph Neural Networks for Multi-View Learning: A Taxonomic Review. Artif. Intell. Rev. 2024, 57, 341. [Google Scholar]
- Rossi, E.; Chamberlain, B.; Frasca, F.; Eynard, D.; Monti, F.; Bronstein, M. Temporal Graph Networks for Deep Learning on Dynamic Graphs. arXiv 2020, arXiv:2006.10637. [Google Scholar]
- Yang, X.; Li, X.; Yang, J.; Ming, Q.; Wang, W.; Tian, Q.; Yan, J. Beyond the Spectrum: Detecting Deepfakes via Re-Synthesis. arXiv 2021, arXiv:2105.14376. [Google Scholar]
- Zhu, J.; Yan, Y.; Zhao, L.; Heimann, M.; Akoglu, L.; Koutra, D. Beyond Homophily in Graph Neural Networks: Current Limitations and Effective Designs. In Proceedings of the Advances in Neural Information Processing Systems, Virtually, 6–12 December 2020; Curran Associates, Inc.: Red Hook, NY, USA, 2020; Volume 33, pp. 15987–16002. [Google Scholar]
- Federici, M.; Dutta, A.; Forré, P.; Kushman, N.; Akata, Z. Learning robust representations via multi-view information bottleneck. In Proceedings of the International Conference on Learning Representations, Addis Ababa, Ethiopia, 30 April 2020. [Google Scholar]
- You, Y.; Chen, T.; Sui, Y.; Chen, T.; Wang, Z.; Shen, Y. Graph contrastive learning with augmentations. Adv. Neural Inf. Process. Syst. 2020, 33, 5812–5823. [Google Scholar]
- Zhu, Y.; Xu, Y.; Yu, F.; Liu, Q.; Wu, S.; Wang, L. Graph contrastive learning with adaptive augmentation. In Proceedings of the Web Conference 2021, Ljubljana, Slovenia, 19–23 April 2021; pp. 2069–2080. [Google Scholar]
- Liu, Y.; Zheng, Y.; Zhang, D.; Lee, V.C.; Pan, S. Beyond smoothing: Unsupervised graph representation learning with edge heterophily discriminating. In Proceedings of the AAAI conference on artificial intelligence, Montréal, QC, Canada, 8–10 August 2023; Volume 37, pp. 4516–4524. [Google Scholar]
- Golan, I.; El-Yaniv, R. Deep anomaly detection using geometric transformations. In Proceedings of the Advances in Neural Information Processing Systems, Montréal, QC, Canada, 3–8 December 2018; Volume 31. [Google Scholar]
- Cheng, D.; Wang, X.; Zhang, Y.; Zhang, L. Graph neural network for fraud detection via spatial-temporal attention. IEEE Trans. Knowl. Data Eng. 2020, 34, 3800–3813. [Google Scholar] [CrossRef]
- Akoglu, L.; Tong, H.; Koutra, D. Graph based anomaly detection and description: A survey. Data Min. Knowl. Discov. 2015, 29, 626–688. [Google Scholar] [CrossRef]
- Peng, Z.; Luo, M.; Li, J.; Xue, L.; Zheng, Q. A deep multi-view framework for anomaly detection on attributed networks. IEEE Trans. Knowl. Data Eng. 2020, 34, 2539–2552. [Google Scholar] [CrossRef]
- Adaloglou, N.; Vretos, N.; Daras, P. Multi-view adaptive graph convolutions for graph classification. In Proceedings of the Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020; Proceedings, Part XXVI 16. Springer: Berlin/Heidelberg, Germany, 2020; pp. 398–414. [Google Scholar]
- Tan, M.J.; Zheng, Y.; Li, Y.F.; Gong, C.; Zhou, C.; Pan, S. Multi-scale contrastive siamese networks for self-supervised graph representation learning. In Proceedings of the 30th International Joint Conference on Artificial Intelligence (IJCAI). IJCAI, Virtually, 23–29 July 2021; pp. 1588–1594. [Google Scholar] [CrossRef]
- Ma, J.; Chang, B.; Zhang, X.; Mei, Q. Copulagnn: Towards integrating representational and correlational roles of graphs in graph neural networks. arXiv 2020, arXiv:2010.02089. [Google Scholar]
- Schlichtkrull, M.; Kipf, T.N.; Bloem, P.; Van Den Berg, R.; Titov, I.; Welling, M. Modeling relational data with graph convolutional networks. In Proceedings of the The semantic web: 15th international conference, ESWC 2018, Heraklion, Crete, Greece, 3–7 June 2018; proceedings 15. Springer: Berlin/Heidelberg, Germany, 2018; pp. 593–607. [Google Scholar]
- Vimal, S.; Kayathwal, K.; Wadhwa, H.; Dhama, G. Application of Deep Reinforcement Learning to Payment Fraud. arXiv 2021, arXiv:2112.04236. [Google Scholar]
- Kim, H.; Choi, J.; Whang, J.J. Dynamic Relation-Attentive Graph Neural Networks for Fraud Detection. arXiv 2023, arXiv:2310.04171. [Google Scholar]
- Hu, J.; Xiao, B.; Jin, H.; Duan, J.; Wang, S.; Lv, Z.; Wang, S.; Liu, X.; Zhu, E. SAMCL: Subgraph-Aligned Multiview Contrastive Learning for Graph Anomaly Detection. IEEE Trans. Neural Netw. Learn. Syst. 2023, 36, 1664–1676. [Google Scholar] [CrossRef]
- Wu, T.; Ren, J.; Li, P.; Leskovec, J. Graph Information Bottleneck for Subgraph Recognition. arXiv 2020, arXiv:2010.05563. [Google Scholar]
- Jin, C.; Jin, J.; Zhou, J.; Wu, J.; Xuan, Q. Heterogeneous feature augmentation for ponzi detection in ethereum. IEEE Trans. Circuits Syst. II Express Briefs 2022, 69, 3919–3923. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Wu, F.; Souza, A.; Zhang, T.; Fifty, C.; Yu, T.; Weinberger, K. Simplifying graph convolutional networks. In Proceedings of the International conference on machine learning. PMLR, Long Beach, CA, USA, 9–15 June 2019; pp. 6861–6871. [Google Scholar]
- Xu, K.; Hu, W.; Leskovec, J.; Jegelka, S. How powerful are graph neural networks? In Proceedings of the International Conference on Learning Representations, New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Hamilton, W.L.; Ying, Z.; Leskovec, J. Inductive representation learning on large graphs. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 1024–1034. [Google Scholar]
- Busbridge, D.; Sherburn, D.; Cavallo, P.L. Relational graph attention networks. In Proceedings of the Graph Representation Learning Workshop, NeurIPS, Vancouver, BC, Canada, 8–14 December 2019. [Google Scholar]
- Hu, Z.; Dong, Y.; Wang, K.; Sun, Y. Heterogeneous graph transformer. In Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Virtually, 6–10 July 2020; pp. 2704–2713. [Google Scholar]
- Hassani, K.; Khasahmadi, A.H. Contrastive multi-view representation learning on graphs. In Proceedings of the International Conference on Machine Learning. PMLR, Virtually, 13–18 July 2020; pp. 4116–4126. [Google Scholar]

| Description | Number | Detection Relevance |
|---|---|---|
| Nodes | 57,130 | Entities involved in transactions |
| Edges | 156,255 | Transaction network topology |
| CA | 4616 | Smart contracts facilitating interactions |
| EOA | 52,514 | User-controlled accounts |
| Call edges | 69,653 | Execution events triggering scheme |
| Transaction edges | 86,602 | Monetary transfers indicative of fund flows |
| Labeled Ponzi accounts | 191 | Known fraudulent targets (imbalanced ratio 1:299) |
| Model Category | F1 Score | AUPRC | RecK |
|---|---|---|---|
| Machine Learning Methods: | |||
| RF | 0.746 | 0.728 | 0.692 |
| XGBoost | 0.771 | 0.752 | 0.718 |
| Homogeneous Graph Methods: | |||
| GCN | 0.812 | 0.789 | 0.751 |
| SGC | 0.801 | 0.771 | 0.733 |
| GIN | 0.831 | 0.810 | 0.792 |
| GraphSAGE | 0.845 | 0.827 | 0.811 |
| GAT | 0.843 | 0.824 | 0.812 |
| Heterogeneous Graph Methods: | |||
| RGCN | 0.854 | 0.835 | 0.822 |
| RGAT | 0.878 | 0.861 | 0.846 |
| HGT | 0.865 | 0.847 | 0.830 |
| Perturbation-Based Methods: | |||
| MVGRL | 0.876 | 0.860 | 0.841 |
| MERIT | 0.889 | 0.872 | 0.855 |
| Proposed Method: | |||
| MVCG-SPS (Ours) | 0.902 | 0.891 | 0.871 |
| Configuration | F1 Score | AUPRC | RecK |
|---|---|---|---|
| MVCG-SPS (Full Model) | 0.902 | 0.891 | 0.871 |
| MVCG-SPS w/o RL | 0.879(−2.6%) | 0.861(−3.4%) | 0.843(−3.2%) |
| MVCG−SPS w/o MSCL | 0.868(−3.8%) | 0.853(−4.3%) | 0.835(−4.1%) |
| MVCG−SPS w/o MPBV | 0.854(−5.3%) | 0.840(−5.7%) | 0.822(−5.6%) |
| Hyperparameter | Search Range | Final Value |
|---|---|---|
| Learning Rate | {0.001, 0.005, 0.01, 0.05} | 0.01 |
| Hidden Layer Dimension | {64, 128, 256} | 128 |
| RL Learning Rate () | {0.01, 0.05, 0.1} | 0.05 |
| [0.1, 1.0] | 0.7/0.3 | |
| Meta-Path Views (V) | {2, 3, 5, 7} | 5 |
| Reward Discount Factor () | {0.5, 0.7, 0.9, 0.99} | 0.9 |
| Configuration | F1 Score | AUPRC |
|---|---|---|
| Baseline (Full Model) | 0.902 | 0.891 |
| Replace with temporal path | 0.874 (−3.1%) | 0.863 (−3.1%) |
| Add extra sampling meta-path | 0.924 (+2.4%) | 0.912 (+2.4%) |
| Feature | SHAP Value | Domain Significance |
|---|---|---|
| Upstream invitation density | +0.23 | Reflects pyramid recruitment patterns |
| Investment/payment ratio | +0.19 | Indicates unsustainable returns |
| Nodes | Training Time (s/epoch) | GPU Memory (GB) | F1 Score |
|---|---|---|---|
| 10K | 12.3 | 0.2 | 0.901 |
| 100K | 124.7 | 0.3 | 0.895 |
| 500K | 618.4 | 0.4 | 0.887 |
| 1M | 1235.1 | 0.5 | 0.881 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, X.; Tsai, W.-T. MVCG-SPS: A Multi-View Contrastive Graph Neural Network for Smart Ponzi Scheme Detection. Appl. Sci. 2025, 15, 3281. https://doi.org/10.3390/app15063281
Jiang X, Tsai W-T. MVCG-SPS: A Multi-View Contrastive Graph Neural Network for Smart Ponzi Scheme Detection. Applied Sciences. 2025; 15(6):3281. https://doi.org/10.3390/app15063281
Chicago/Turabian StyleJiang, Xiaofang, and Wei-Tek Tsai. 2025. "MVCG-SPS: A Multi-View Contrastive Graph Neural Network for Smart Ponzi Scheme Detection" Applied Sciences 15, no. 6: 3281. https://doi.org/10.3390/app15063281
APA StyleJiang, X., & Tsai, W.-T. (2025). MVCG-SPS: A Multi-View Contrastive Graph Neural Network for Smart Ponzi Scheme Detection. Applied Sciences, 15(6), 3281. https://doi.org/10.3390/app15063281






