Mission: Dexterous Functionality—Redesigning the Palmar Configuration Paradigm of Underactuated Prosthetic Hands
Abstract
Featured Application
Abstract
1. Introduction
1.1. Background and Motivation
- The two-DoF metacarpophalangeal (MCP) joint has been selected for analysis to simplify the prosthetic hand design. A novel palmar configuration has been developed since a two-DoF joint introduces significant complexity in both kinematics and control. The design incorporates a one-DoF MCP joint, allowing only flexion/extension (F/E) motion. The simplified configuration is achieved through the application of performance indices.
- A novel design approach for finger placement based on anatomical and physiological considerations is also proposed, focusing on optimizing size considerations.
- A minimalistic motion transmission mechanism that provides a differential input to the finger for anthropomorphic motion is developed. The novel mechanism aims to allow the fingers to grasp objects of various shapes and sizes with sufficient dexterity and stability.
1.2. Related Literature
2. Materials and Methods
2.1. Kinematic Experiment
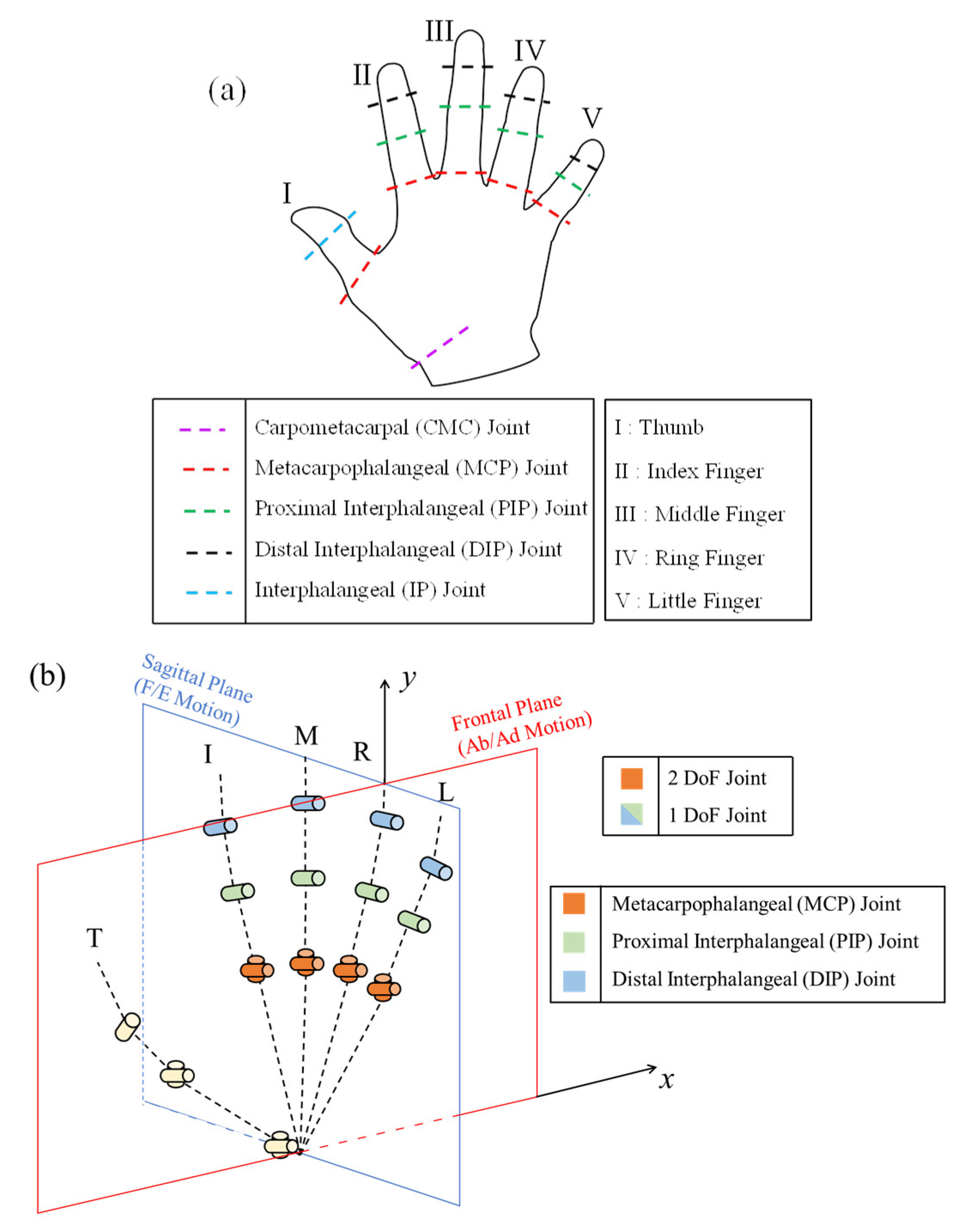
2.1.1. Kinematic Model of the Human Hand
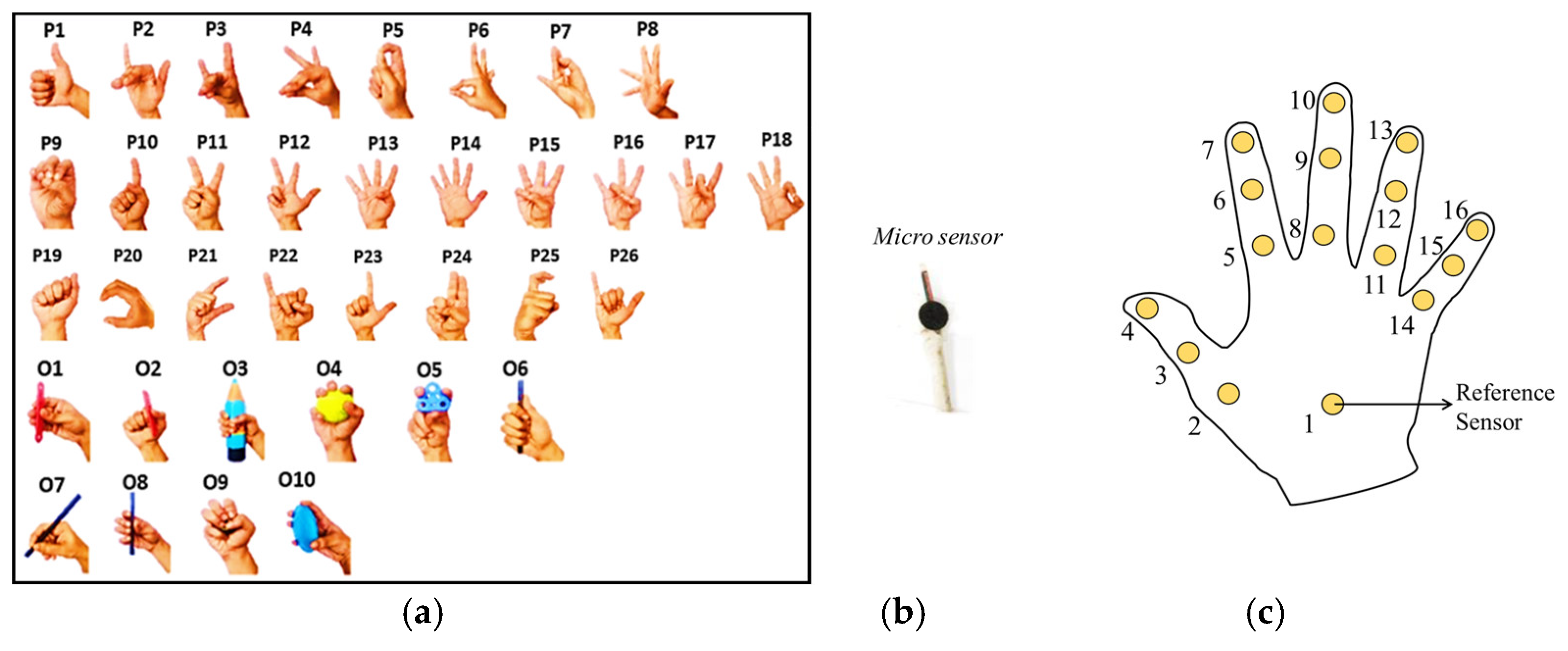
2.1.2. Experiment Design
2.1.3. Data Collection and Processing
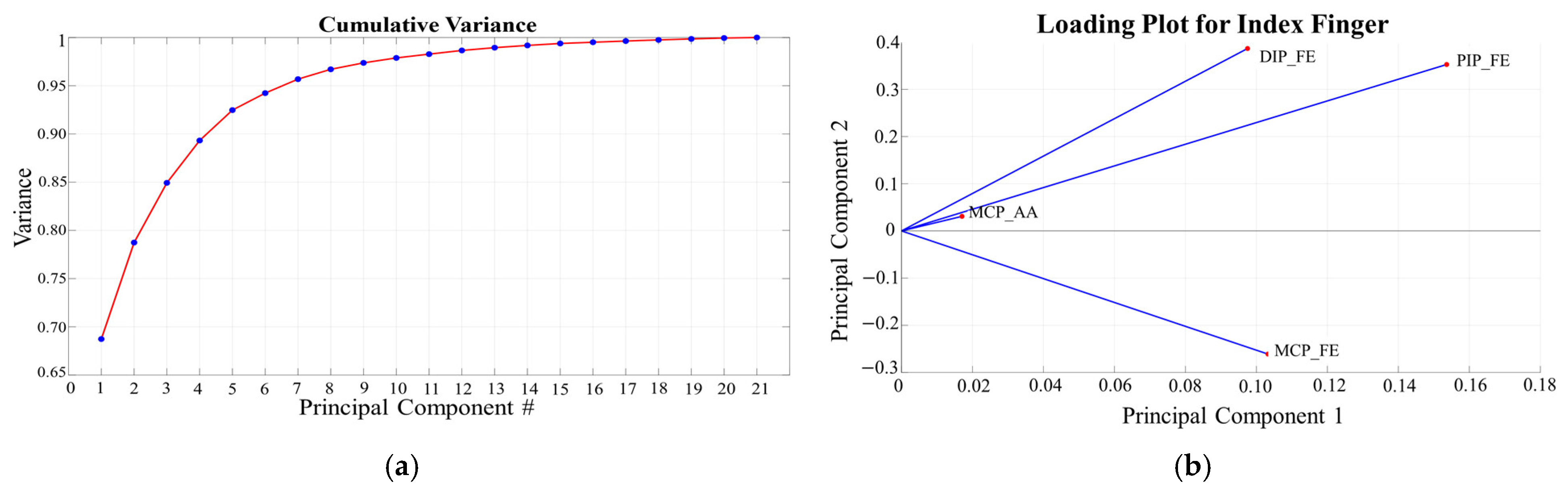
2.1.4. Data Analysis
2.2. Finger Workspace Calculation
MCP Ab/Ad Joint Calculation
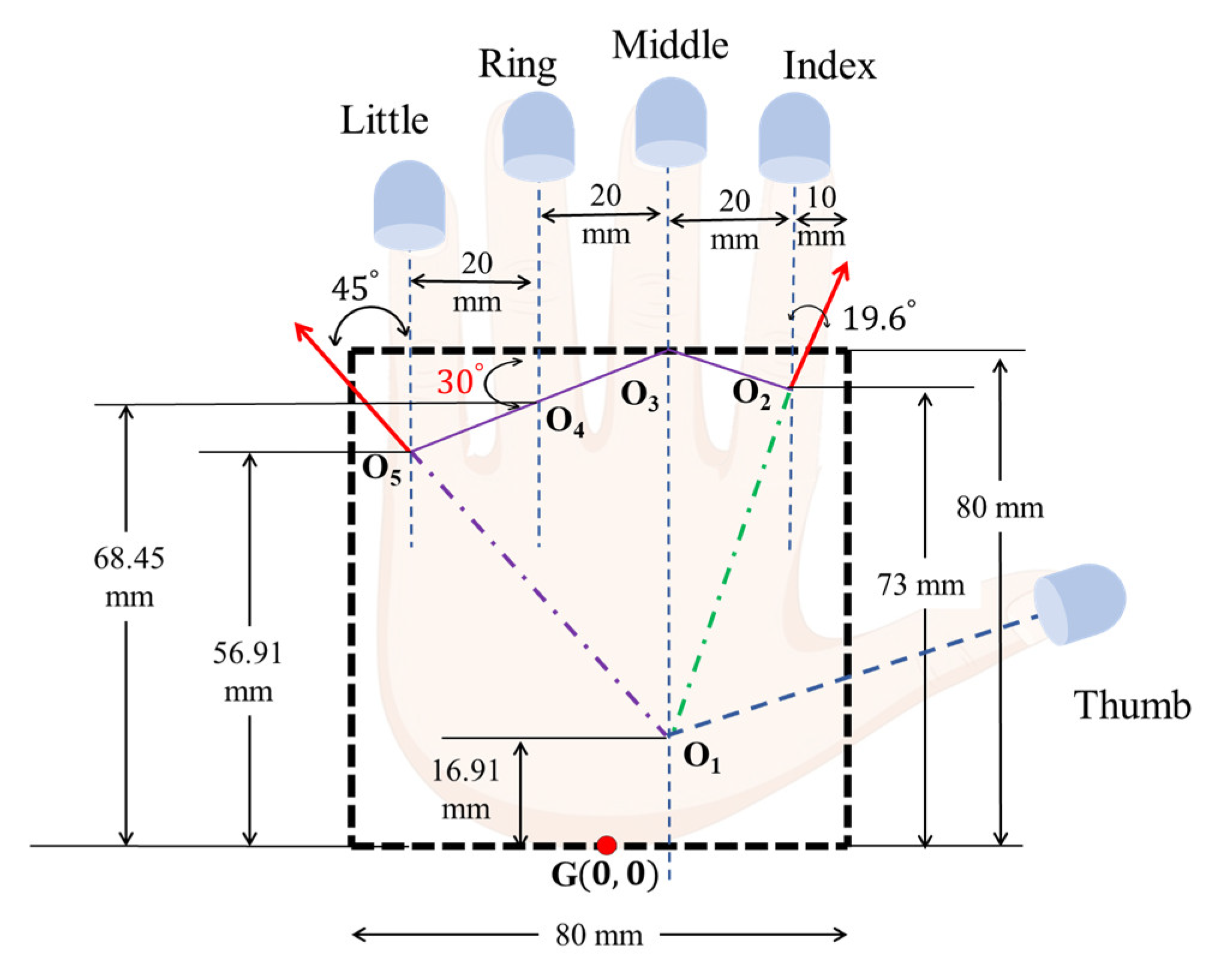
2.3. Location of Finger Bases
2.4. Grasp Simulation
3. Results
3.1. Finger Configuration
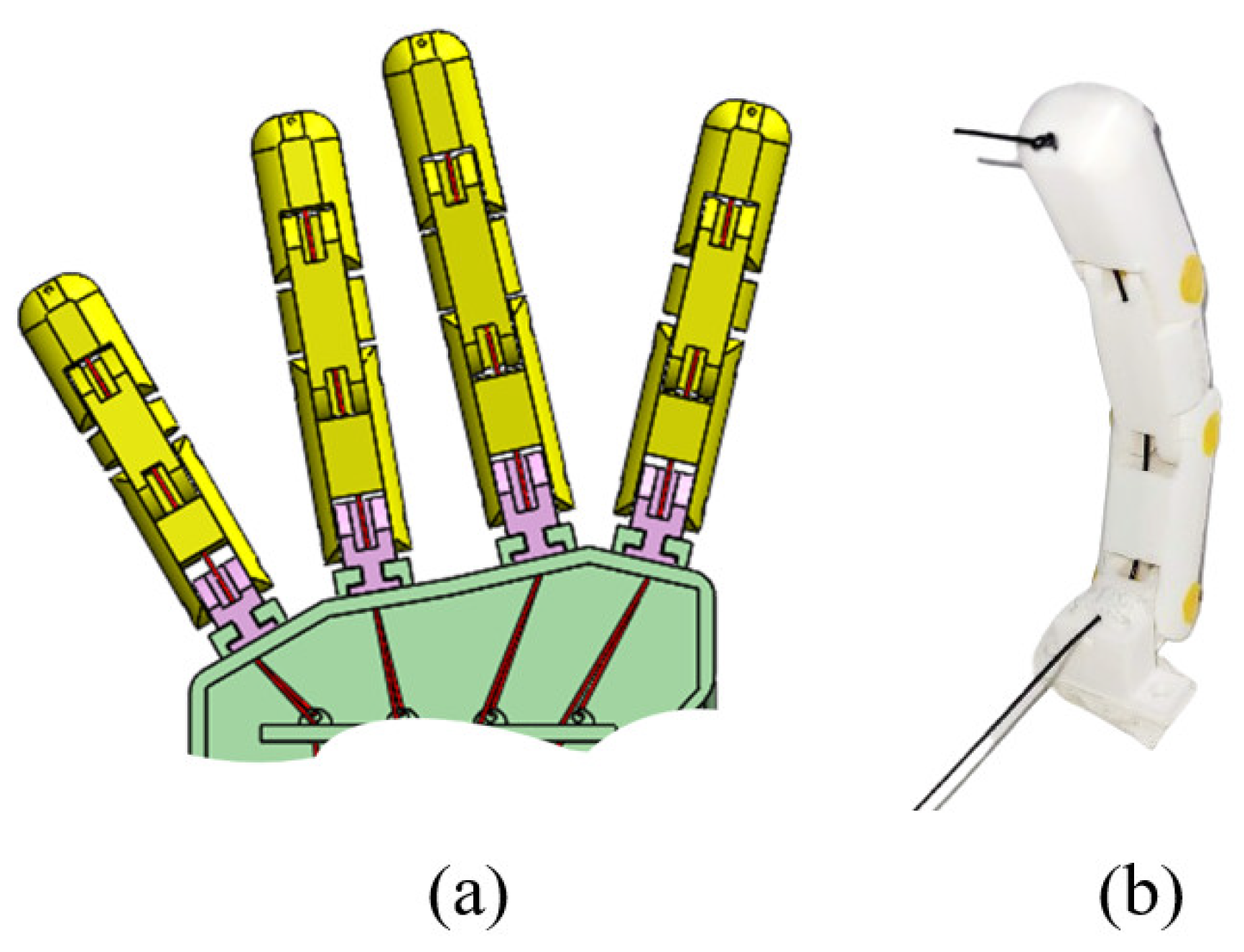
3.2. Prosthetic Hand Design
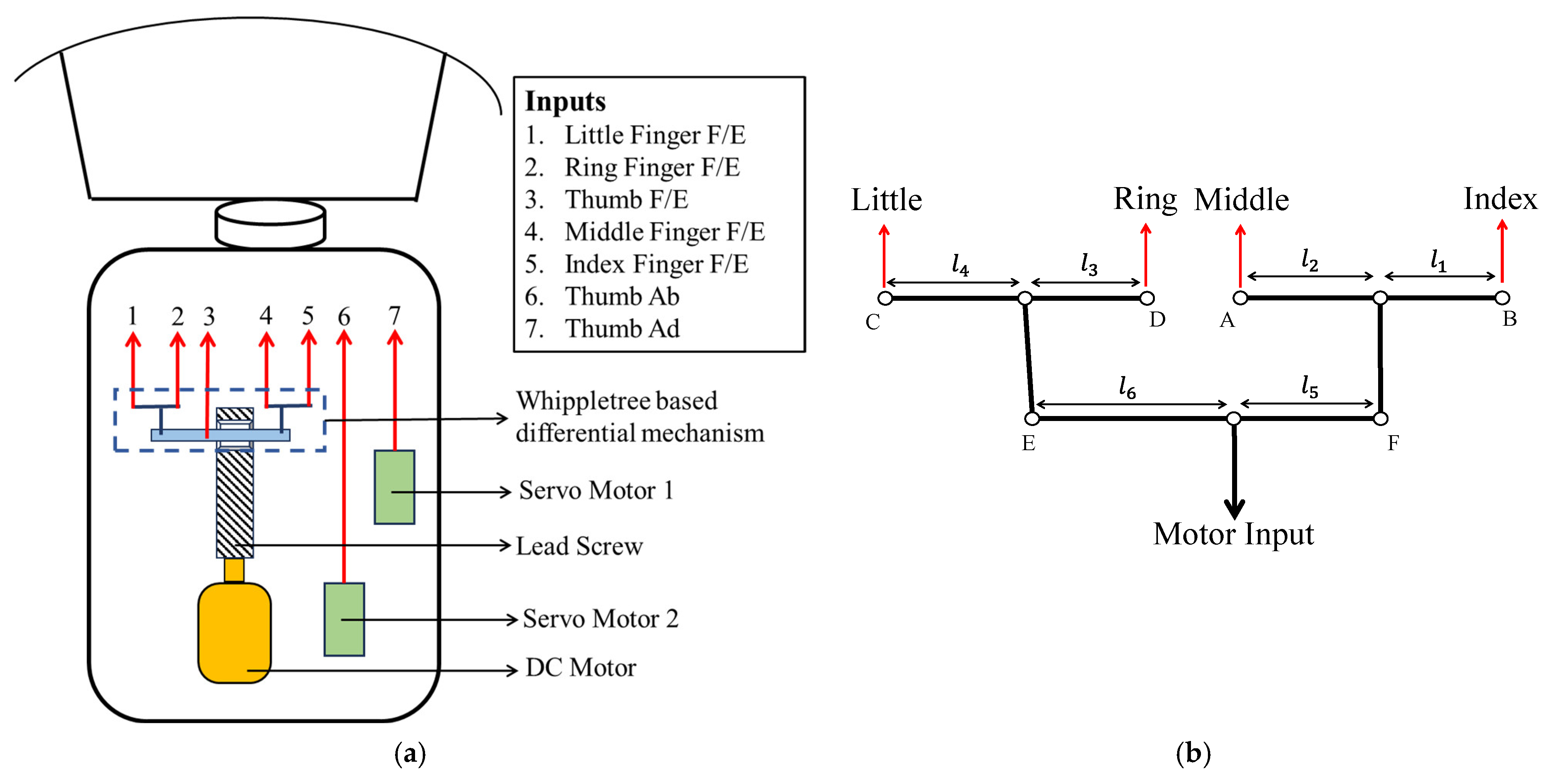
3.2.1. Motion Transmission Mechanism
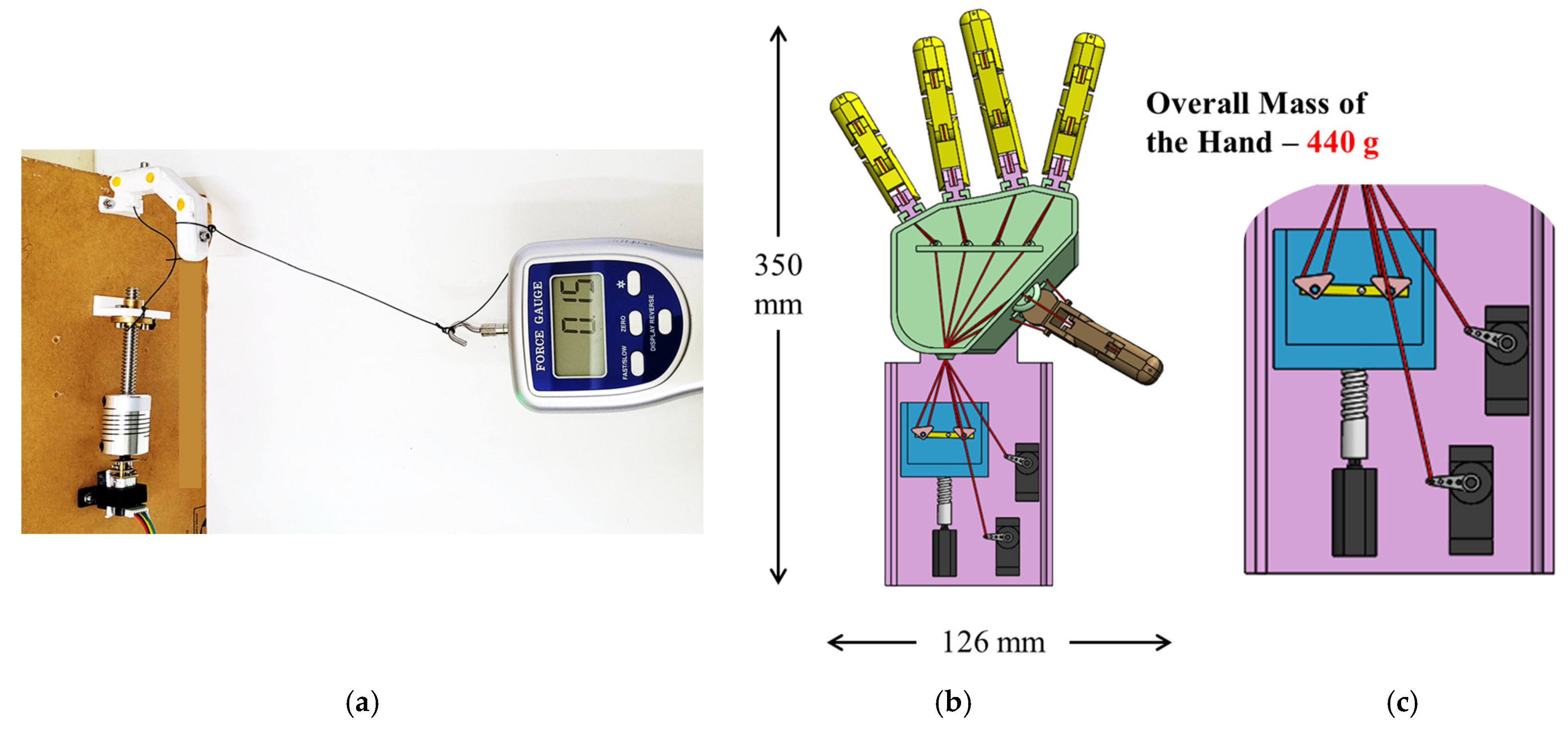
3.2.2. Prototyping and Experiments
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Ab/Ad | Abduction/Adduction |
| ADL | Activities of Daily Living |
| CAD | Computer-Aided Design |
| CMC | Carpometacarpal |
| DH | Denavit–Hartenberg |
| DIP | Distal Interphalangeal |
| DoF | Degree of Freedom |
| EMG | Electromyography |
| F/E | Flexion/Extension |
| MCP | Metacarpophalangeal |
| MTM | Motion Transmission Mechanism |
| PCA | Principal Component Analysis |
| PI | Performance Index |
| PIP | Proximal Interphalangeal |
| PLA | Poly-Lactic Acid |
| ROM | Range of Motion |
| SD | Standard Deviation |
Appendix A
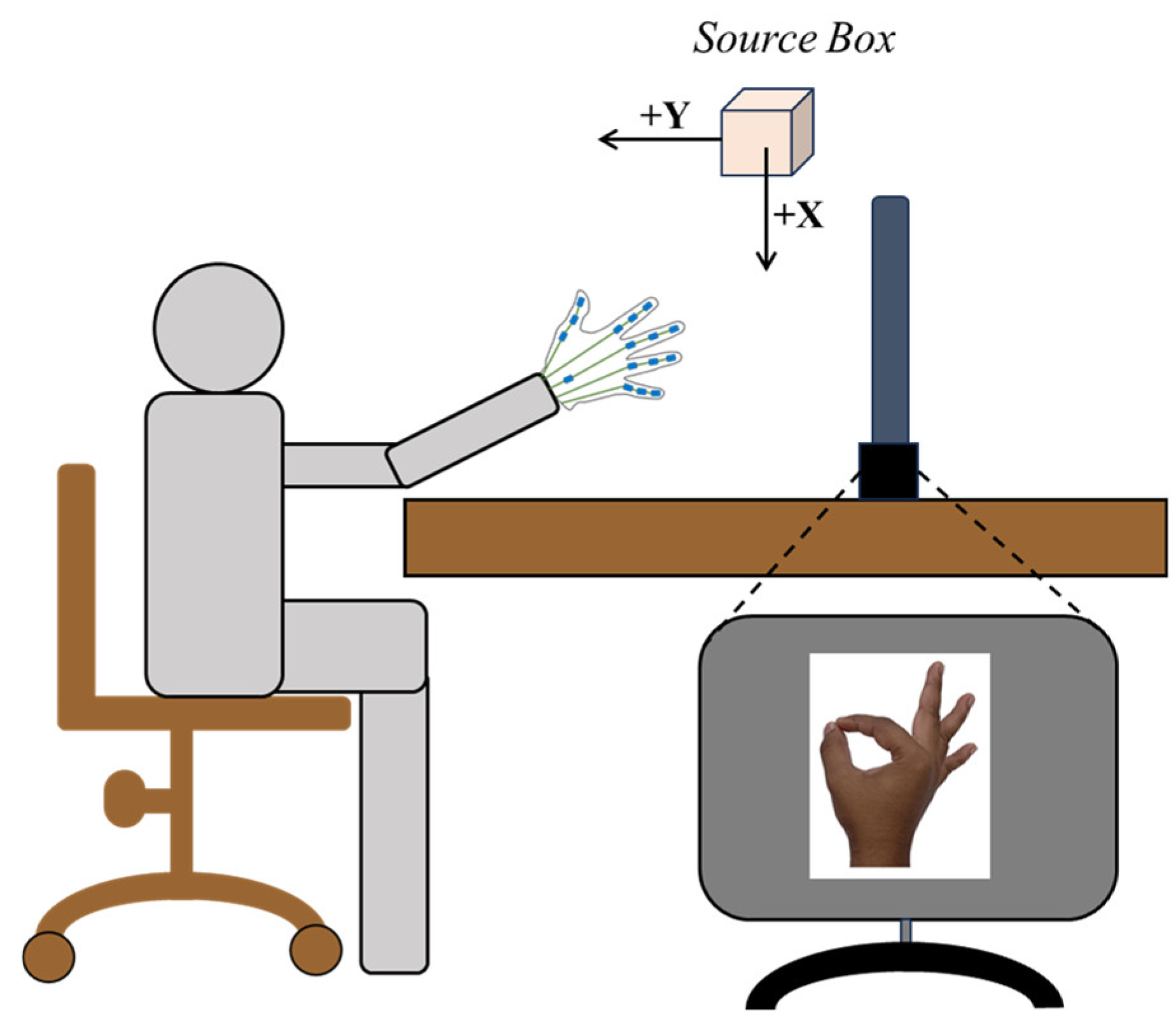
Appendix A.1. Kinematic Data Collection Experiment—Setup
References
- Ingram, J.N.; Körding, K.P.; Howard, I.S.; Wolpert, D.M. The statistics of natural hand movements. Exp. Brain Res. 2008, 188, 223–236. [Google Scholar] [CrossRef] [PubMed]
- Balasubramanian, R.; Santos, V.J. (Eds.) The Human Hand as an Inspiration for Robot Hand Development; Springer Tracts in Advanced Robotics; Springer International Publishing: Cham, Switzerland, 2014; Volume 95. [Google Scholar] [CrossRef]
- Meghdari, A.; Arefi, M.; Mahmoudian, M. Geometric adaptability: A novel mechanical design in the Sharif artificial hand. Int. J. Robot. Autom. 1992, 7, 80–85. [Google Scholar]
- Crowder, R.M. An anthropomorphic robotic end effector. Robot. Auton. Syst. 1991, 7, 253–268. [Google Scholar] [CrossRef]
- Mouri, T.; Kawasaki, H.; Yoshikawa, K.; Takai, J.; Ito, S. Anthropomorphic robot hand: Gifu hand III. In Proceedings of the International Conference (ICCAS 2002), Muju Resort, Republic of Korea, 16–19 October 2002; pp. 1288–1293. [Google Scholar]
- Mendez, V.; Iberite, F.; Shokur, S.; Micera, S. Current Solutions and Future Trends for Robotic Prosthetic Hands. Annu. Rev. Control. Robot. Auton. Syst. 2021, 4, 595–627. [Google Scholar] [CrossRef]
- Cordella, F.; Ciancio, A.L.; Sacchetti, R.; Davalli, A.; Cutti, A.G.; Guglielmelli, E.; Zollo, L. Literature review on needs of upper limb prosthesis users. Front. Neurosci. 2016, 10, 209. [Google Scholar] [CrossRef]
- Jarque-Bou, N.J.; Vergara, M.; Sancho-Bru, J.L.; Gracia-Ibáñez, V.; Roda-Sales, A. Hand kinematics characterization while performing activities of daily living through kinematics reduction. IEEE Trans. Neural Syst. Rehabil. Eng. 2020, 28, 1556–1565. [Google Scholar] [CrossRef]
- Gentile, C.; Cordella, F.; Zollo, L. Hierarchical Human-Inspired Control Strategies for Prosthetic Hands. Sensors 2022, 22, 2521. [Google Scholar] [CrossRef]
- Piazza, C.; Grioli, G.; Catalano, M.G.; Bicchi, A. A Century of Robotic Hands. Annu. Rev. Control Robot. Auton. Syst. 2019, 2, 1–32. [Google Scholar] [CrossRef]
- Kandel, E.R.; Schwartz, J.H.; Jessell, T.M.; Siegelbaum, S.A.; Hudspeth, A.J. Principles of Neural Science, 5th ed.; McGraw Hill Professional: New York, NY, USA, 2013. [Google Scholar]
- Napier, J.R.; Tuttle, R.H. Hands; Princeton University Press: Princeton, NJ, USA, 1993. [Google Scholar]
- van der Hulst, F.P.J.; Schatzle, S.; Preusche, C.; Schiele, A. A functional anatomy based kinematic human hand model with simple size adaptation. In Proceedings of the 2012 IEEE International Conference on Robotics and Automation, St Paul, MN, USA, 14–18 May 2012; pp. 5123–5129. [Google Scholar] [CrossRef]
- MacKenzie, C.L.; Iberall, T. The Grasping Hand; Elsevier: Amsterdam, The Netherlands, 1994. [Google Scholar]
- Cobos, S.; Ferre, M.; Aracil, R. Simplified human hand models based on grasping analysis. In Proceedings of the 2010 IEEE/RSJ International Conference on Intelligent Robots and Systems, Taipei, Taiwan, 1 October 2010; pp. 610–615. [Google Scholar] [CrossRef]
- Demers, L.-A.A.; Gosselin, C. Kinematic design of a planar and spherical mechanism for the abduction of the fingers of an anthropomorphic robotic Hand. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 5350–5356. [Google Scholar] [CrossRef]
- Kontoudis, G.P.; Liarokapis, M.; Vamvoudakis, K.G.; Furukawa, T. An Adaptive Actuation Mechanism for Anthropomorphic Robot Hands. Front. Robot. AI 2019, 6, 47. [Google Scholar] [CrossRef]
- Cerruti, G.; Chablat, D.; Gouaillier, D.; Sakka, S. Design method for an anthropomorphic hand able to gesture and grasp. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 3660–3667. [Google Scholar] [CrossRef]
- Yan, Y.; Chen, X.; Cheng, C.; Wang, Y. Design, kinematic modeling and evaluation of a novel soft prosthetic hand with abduction joints. Med. Nov. Technol. Devices 2022, 15, 100151. [Google Scholar] [CrossRef]
- Halim, A. Human Anatomy: Volume I: Upper Limb and Thorax; I. K. International Pvt Ltd.: New Delhi, India, 2008. [Google Scholar]
- The GRASP Taxonomy of Human Grasp Types | IEEE Journals & Magazine | IEEE Xplore. Available online: https://ieeexplore.ieee.org/abstract/document/7243327 (accessed on 11 March 2024).
- Shenoy, P.; Sompur, V.; Skm, V. Methods for Measurement and Analysis of Full Hand Angular Kinematics Using Electromagnetic Tracking Sensors. IEEE Access 2022, 10, 42673–42689. [Google Scholar] [CrossRef]
- Hamilton, W.R. Elements of Quaternions; Longmans, Green, & Company: London, UK, 1866. [Google Scholar]
- Santello, M.; Flanders, M.; Soechting, J.F. Postural Hand Synergies for Tool Use. J. Neurosci. 1998, 18, 10105–10115. [Google Scholar] [CrossRef] [PubMed]
- Peña-Pitarch, E.; Falguera, N.T.; Yang, J. Virtual human hand: Model and kinematics. Comput. Methods Biomech. Biomed. Eng. 2014, 17, 568–579. [Google Scholar] [CrossRef] [PubMed]
- Yang, W.; Wu, X.; Zhang, H. Workspace Modeling and Analysis for Dexterous Hands. Int. J. Human. Robot. 2015, 12, 1550006. [Google Scholar] [CrossRef]
- Yang, W.; Xuan, J.; Wu, X.; Lian, C.; Pan, Z. A Workspace Modeling Approach for Multi-finger Hands. In Proceedings of the 2016 International Conference on Cyberworlds (CW), Chongqing, China, 28–30 September 2016; pp. 104–110. [Google Scholar] [CrossRef]
- Russo, M. Measuring performance: Metrics for manipulator design, control, and optimization. Robotics 2022, 12, 4. [Google Scholar] [CrossRef]
- Yoshikawa, T. Manipulability of Robotic Mechanisms. Int. J. Robot. Res. 1985, 4, 3–9. [Google Scholar] [CrossRef]
- Llop-Harillo, I.; Pérez-González, A.; Andrés-Esperanza, J. Anthropomorphism Indexes of the Kinematic Chain for Artificial Hands. J. Bionic Eng. 2020, 17, 501–511. [Google Scholar] [CrossRef]
- Kapandji, A. Clinical test of apposition and counter-apposition of the thumb. Ann. Chir. Main 1986, 5, 67–73. [Google Scholar] [CrossRef]
- Biagiotti, L.; Lotti, F.; Melchiorri, C.; Vassura, G. How Far Is the Human Hand. A Review on Anthropomorphic Robotic End-Effectors; University of Bologna: Bologna, Italy, 2004. [Google Scholar]
- Liu, Y.; Yang, D.; Jiang, L.; Liu, H. A synthetic framework for evaluating the anthropomorphic characteristics of prosthetic hands. In Proceedings of the 2015 IEEE International Conference on Advanced Intelligent Mechatronics (AIM), Busan, Republic of Korea, 7–11 July 2015; pp. 877–884. [Google Scholar] [CrossRef]
- Feix, T.; Romero, J.; Ek, C.H.; Schmiedmayer, H.-B.; Kragic, D. A Metric for Comparing the Anthropomorphic Motion Capability of Artificial Hands. IEEE Trans. Robot. 2012, 29, 82–93. [Google Scholar] [CrossRef]
- Liarokapis, M.V.; Artemiadis, P.K.; Kyriakopoulos, K.J. Quantifying anthropomorphism of robot hands. In Proceedings of the 2013 IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 6–10 May 2013; pp. 2041–2046. [Google Scholar] [CrossRef]
- Malvezzi, M.; Gioioso, G.; Salvietti, G.; Prattichizzo, D. Syngrasp: A matlab toolbox for underactuated and compliant hands. IEEE Robot. Autom. Mag. 2015, 22, 52–68. [Google Scholar] [CrossRef]
- Roa, M.A.; Suárez, R. Grasp quality measures: Review and performance. Auton. Robot. 2015, 38, 65–88. [Google Scholar] [CrossRef]
- Banuvathy, R.; Varadhan, S.K.M. Distinct behavior of the little finger during the vertical translation of an unsteady thumb platform while grasping. Sci. Rep. 2021, 11, 21064. [Google Scholar] [CrossRef]
- Birglen, L.; Laliberté, T.; Gosselin, C. Underactuated Robotic Hands; Springer Tracts in Advanced Robotics; Springer: Berlin/Heidelberg, Germany, 2008; Volume 40. [Google Scholar] [CrossRef]
- Fukaya, N.; Toyama, S.; Asfour, T.; Dillmann, R. Design of the TUAT/Karlsruhe humanoid hand. In Proceedings of the 2000 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS 2000) (Cat. No. 00CH37113), Takamatsu, Japan, 31 October–5 November 2000; pp. 1754–1759. [Google Scholar]
- Kumarage, K.P.L.; Wickramarathan, W.H.S.; Madhushan, V.; Mugilgeethan, V.; Neethan, R.; Thanihaichelvan, T. A Novel 3 -D Printed Wrist Powered Upper Limb Prosthesis Using Whippletree Mechanism. 2019. Available online: http://repo.lib.jfn.ac.lk/ujrr/handle/123456789/8647 (accessed on 5 February 2024).
- Yang, H.; Tao, Z.; Yang, J.; Ma, W.; Zhang, H.; Xu, M.; Wu, M.; Sun, S.; Jin, H.; Li, W.; et al. A lightweight prosthetic hand with 19-DOF dexterity and human-level functions. Nat. Commun. 2025, 16, 955. [Google Scholar] [CrossRef] [PubMed]
- You, W.S.; Lee, Y.H.; Oh, H.S.; Kang, G.; Choi, H.R. Design of a 3D-printable, robust anthropomorphic robot hand including intermetacarpal joints. Intell. Serv. Robot. 2019, 12, 1–16. [Google Scholar] [CrossRef]
- Gollob, S.D.; Poss, J.; Memoli, G.; Roche, E.T. A Multi-Material, Anthropomorphic Metacarpophalangeal Joint with Abduction and Adduction Actuated by Soft Artificial Muscles. IEEE Robot. Autom. Lett. 2022, 7, 5882–5887. [Google Scholar] [CrossRef]
- Zhang, T.; Jiang, L.; Liu, H. Design and Functional Evaluation of a Dexterous Myoelectric Hand Prosthesis with Biomimetic Tactile Sensor. IEEE Trans. Neural Syst. Rehabil. Eng. 2018, 26, 1391–1399. [Google Scholar] [CrossRef]
- Controzzi, M.; Clemente, F.; Barone, D.; Ghionzoli, A.; Cipriani, C. The SSSA-MyHand: A Dexterous Lightweight Myoelectric Hand Prosthesis. IEEE Trans. Neural Syst. Rehabil. Eng. 2016, 25, 459–468. [Google Scholar] [CrossRef]
- Jeong, S.H.; Kim, K.-S.; Kim, S. Designing Anthropomorphic Robot Hand with Active Dual-Mode Twisted String Actuation Mechanism and Tiny Tension Sensors. IEEE Robot. Autom. Lett. 2017, 2, 1571–1578. [Google Scholar] [CrossRef]
- Weiner, P.; Starke, J.; Hundhausen, F.; Beil, J.; Asfour, T. The KIT Prosthetic Hand: Design and Control. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 3328–3334. [Google Scholar] [CrossRef]

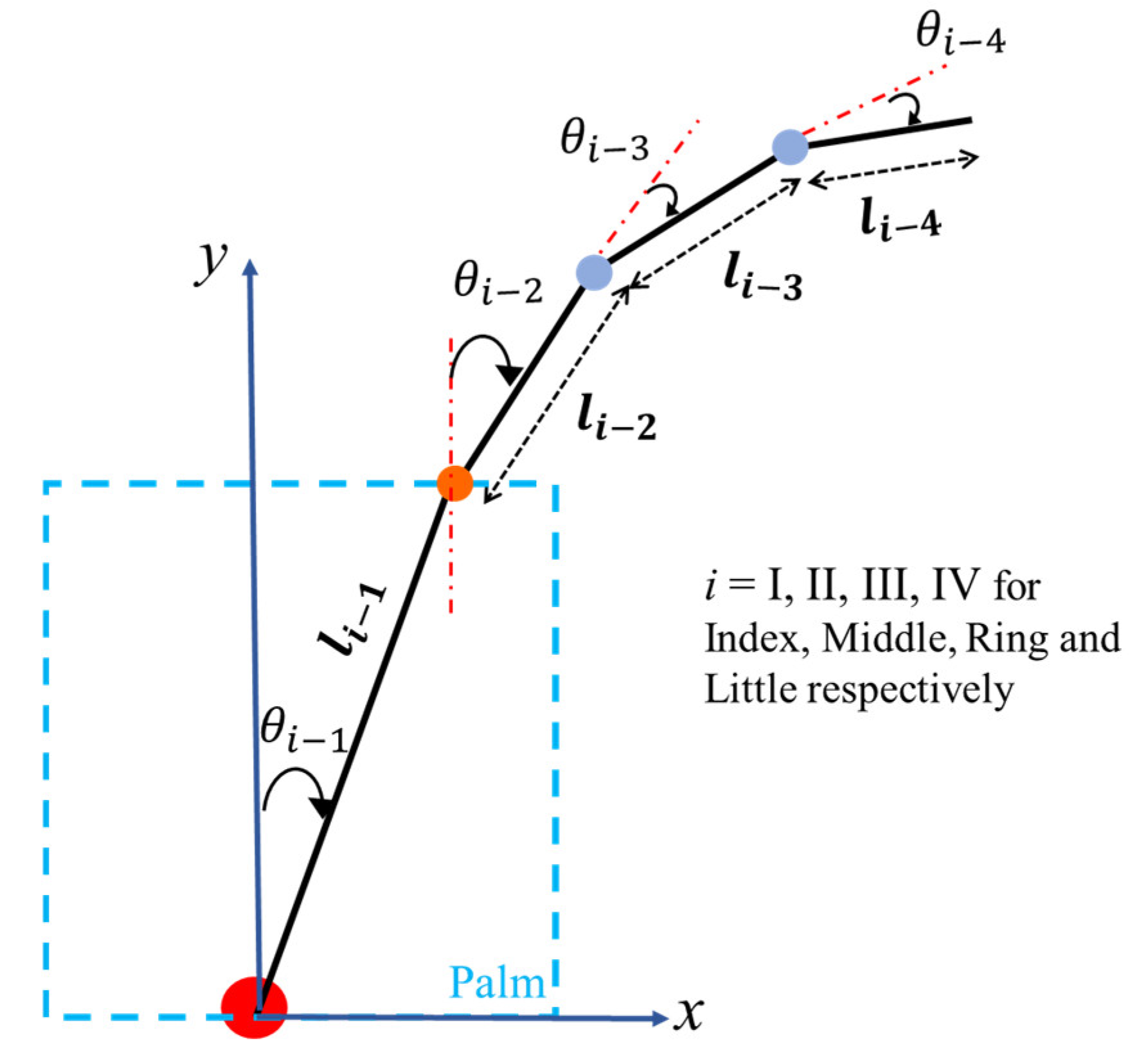
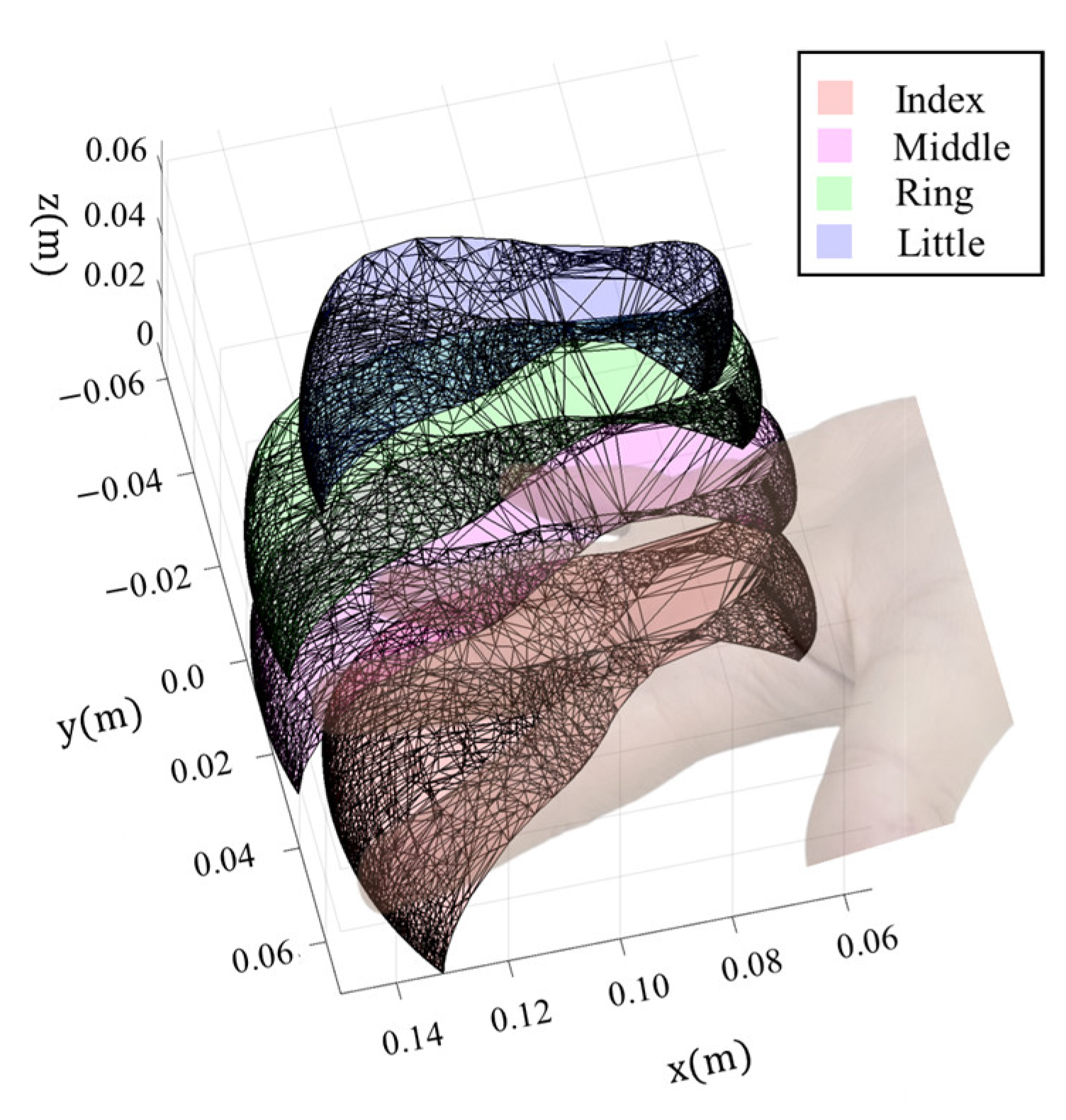
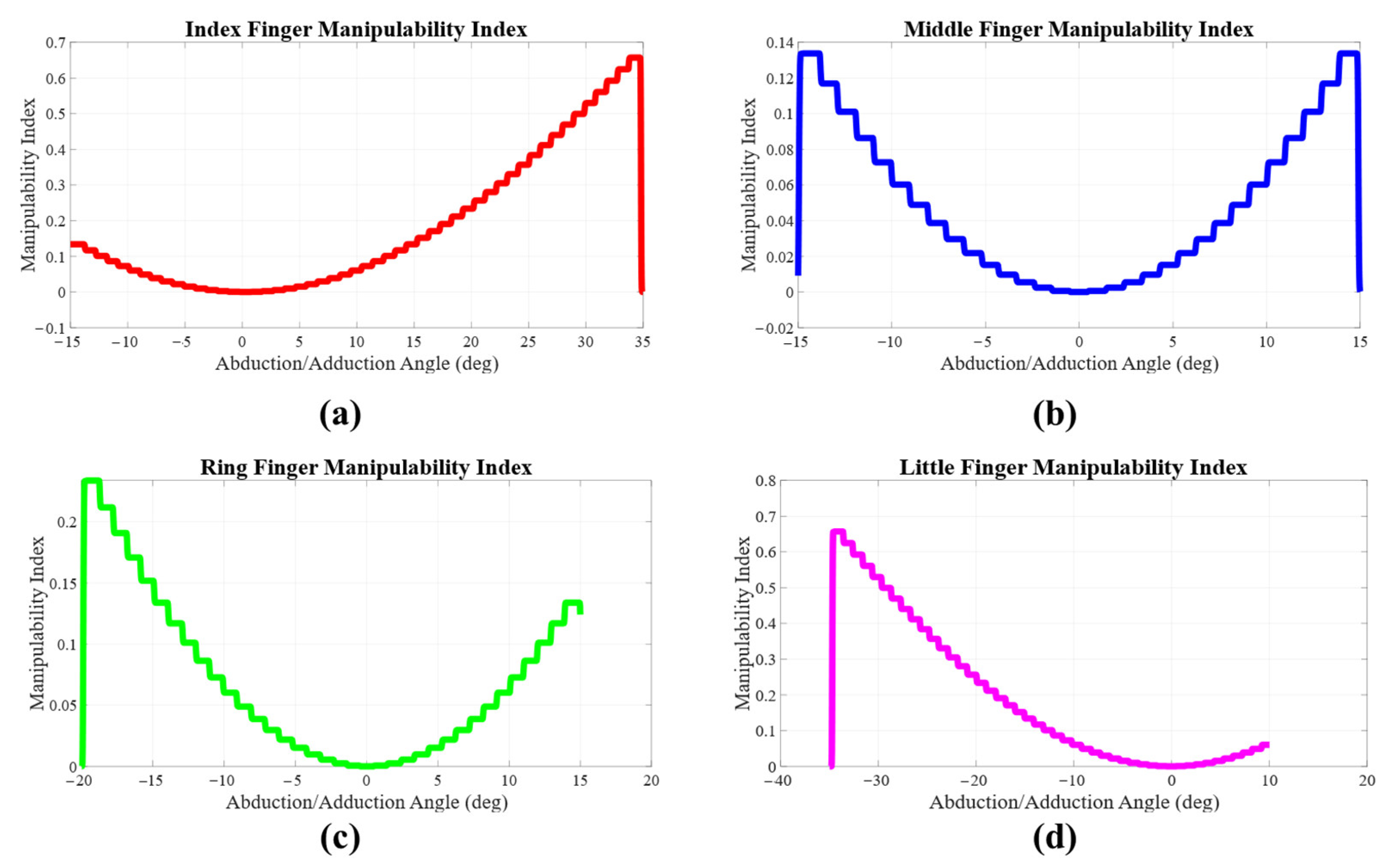

| Joint No. | (rad) | (mm) | (mm) | (rad) |
|---|---|---|---|---|
| 1 | (MCP Ab/Ad) | 0 | 0 | |
| 2 | (MCP F/E) | 0 | 0 | |
| 3 | (PIP F/E) | 0 | 0 | |
| 4 | (DIP F/E) | 0 | 0 |
| MCP Ab/Ad (deg) | MCP F/E (deg) | PIP F/E (deg) | DIP F/E (deg) | |
|---|---|---|---|---|
| Index | 35/−15 | 90/0 | 100/0 | 90/0 |
| Middle | 15/−15 | 90/0 | 100/0 | 90/0 |
| Ring | −20/15 | 90/0 | 100/0 | 90/0 |
| Little | −35/10 | 90/0 | 100/0 | 90/0 |
| Index (mm) | Middle (mm) | Ring (mm) | Little (mm) |
|---|---|---|---|
| = 24 | |||
| Finger | Index | Middle | Ring | Little |
|---|---|---|---|---|
| Ab/Ad Angle | 13° | −13° | −10° | −30° |
| Point | Coordinate (mm) | Point | Coordinate (mm) |
|---|---|---|---|
| G | O3 | ||
| O1 | O4 | ||
| O2 | O5 |
| Objects | Parallel Finger Design | Current Design | |
|---|---|---|---|
| mm Sphere | 109.3 | 51.8 | 66.9 |
| mm Sphere | 2066.9 | 77.7 | 1950.3 |
| mm Sphere | 236.2 | 85.5 | 216.7 |
| mm; mm Cylinder | 10.5 | 5.5 | 6.5 |
| mm; mm Cylinder | 208.2 | 15.5 | 50.1 |
| 30 mm side Cube | 43.9 | 32.3 | 34.1 |
| Human Hand | Parallel Finger Design | Current Design | |
|---|---|---|---|
| IF | 7.7 | 4.7 | 5.9 |
| Link | Length (mm) | Link | Length (mm) | Link | Length (mm) |
|---|---|---|---|---|---|
| 6 | 5 | 12 | |||
| 8 | 8 | 16 |
| Reference | MCP Joint DoF | Active Ab/Ad | Finger Arrangement | Actuation Mechanism | Key Features |
|---|---|---|---|---|---|
| [42] | 2 | Yes | Non-Parallel (Random) | Shape memory alloys with wires | 19-DoF biomimetic hand with 38 shape memory alloys for control. |
| [43] | 2 | Yes | Non-Parallel (Random) | Hybrid—Tendons, ball screw, and movable pulleys | The SKKU hand has 14 DoF across only four fingers. The MCP joint has a decoupled mechanism for separate control of F/E and Ab/Ad motions. |
| [44] | 2 | Yes | Single finger designed | McKibben soft actuators | A single finger‘s biomimetic structure, control, and anthropomorphic motion are achieved through artificial muscles. |
| [17] | 2 | Yes | Parallel (default) | Bilateral tendons | The hand consists of soft fingers capable of simultaneous F/E and Ab/Ad motion through selective actuation of tendons. |
| [45] | 1 | No | Parallel Arrangement | Individual DC motors | 6-DoF myoelectric hand with modular fingers with motors mounted inside the finger body. |
| [46] | 1 | No | Non-Parallel | DC motors with Geneva drive | This 5-fingered hand has index, middle, ring, and little fingers evenly spaced at 10. Index and thumb motions are coupled. |
| [47] | 1 | No | Not Available | Twisted string actuation | 6-DoF hand. 10 motors to provide all the inputs. |
| [48] | 1 | No | Parallel | Tendons | 10-DoF KIT Prosthetic hand has two motors to control and 3 segmented fingers. |
| Current Work | 1 | No | Non-Parallel (Specific) | Tendons | Fingers oriented at specific angles based on performance indices for optimal grasping capabilities. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sompur, V.; SKM, V.; Thondiyath, A. Mission: Dexterous Functionality—Redesigning the Palmar Configuration Paradigm of Underactuated Prosthetic Hands. Appl. Sci. 2025, 15, 3214. https://doi.org/10.3390/app15063214
Sompur V, SKM V, Thondiyath A. Mission: Dexterous Functionality—Redesigning the Palmar Configuration Paradigm of Underactuated Prosthetic Hands. Applied Sciences. 2025; 15(6):3214. https://doi.org/10.3390/app15063214
Chicago/Turabian StyleSompur, Vignesh, Varadhan SKM, and Asokan Thondiyath. 2025. "Mission: Dexterous Functionality—Redesigning the Palmar Configuration Paradigm of Underactuated Prosthetic Hands" Applied Sciences 15, no. 6: 3214. https://doi.org/10.3390/app15063214
APA StyleSompur, V., SKM, V., & Thondiyath, A. (2025). Mission: Dexterous Functionality—Redesigning the Palmar Configuration Paradigm of Underactuated Prosthetic Hands. Applied Sciences, 15(6), 3214. https://doi.org/10.3390/app15063214






