Modeling and Simulation of Standing Wave Configurations for Outflow Improvement and Minimizing Undesired Recirculation
Abstract
1. Introduction
2. Materials and Methods
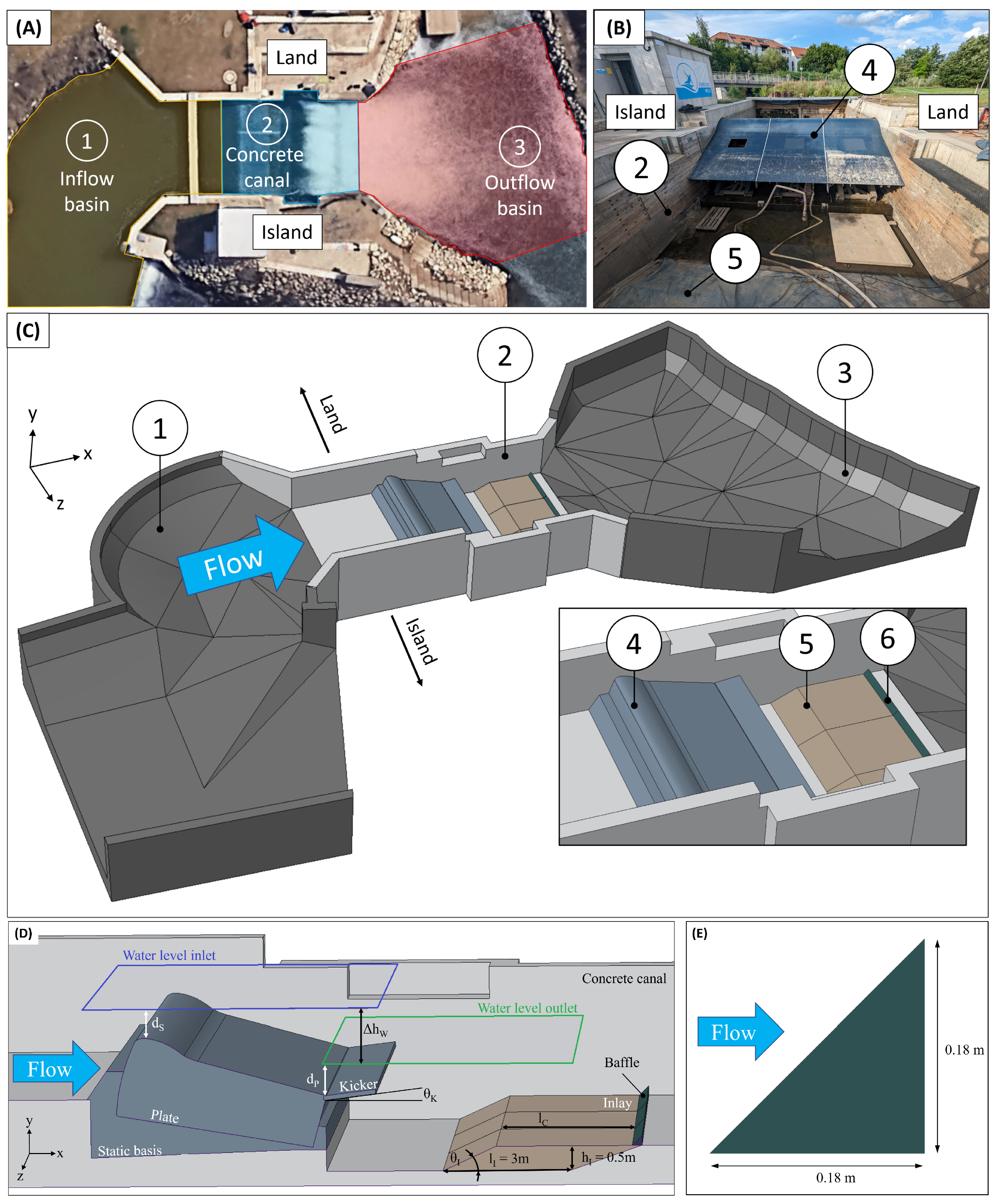
2.1. Geometry
2.2. Boundary Conditions and Setup
2.3. Numerical Methods
2.4. Mesh Generation and Grid Independence Study
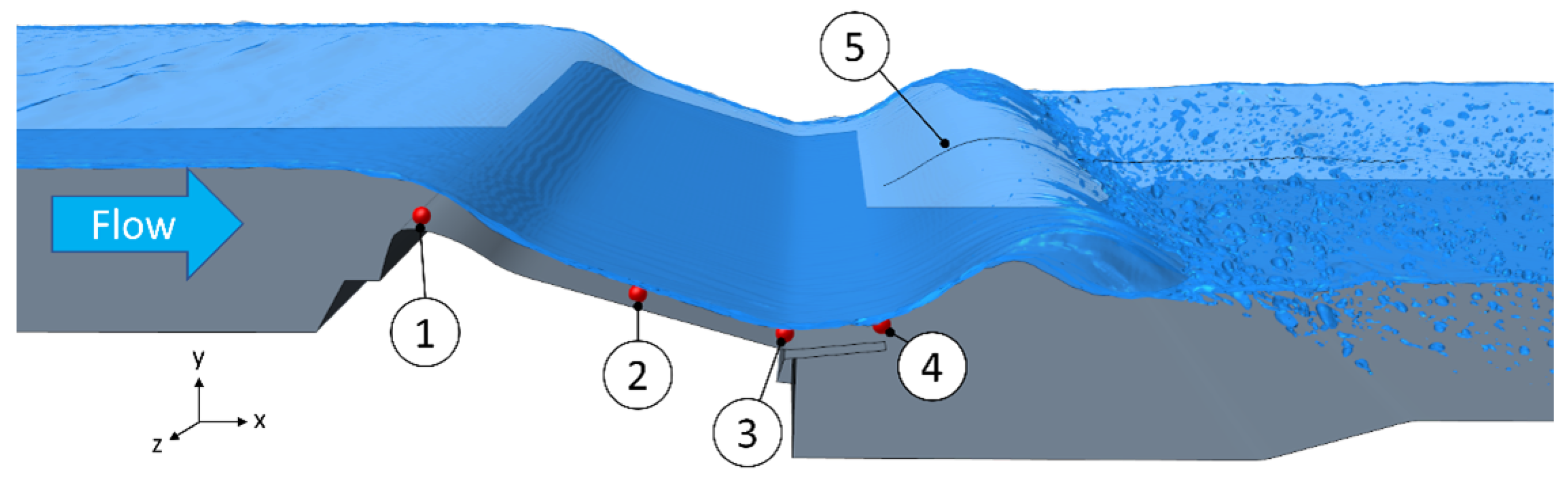
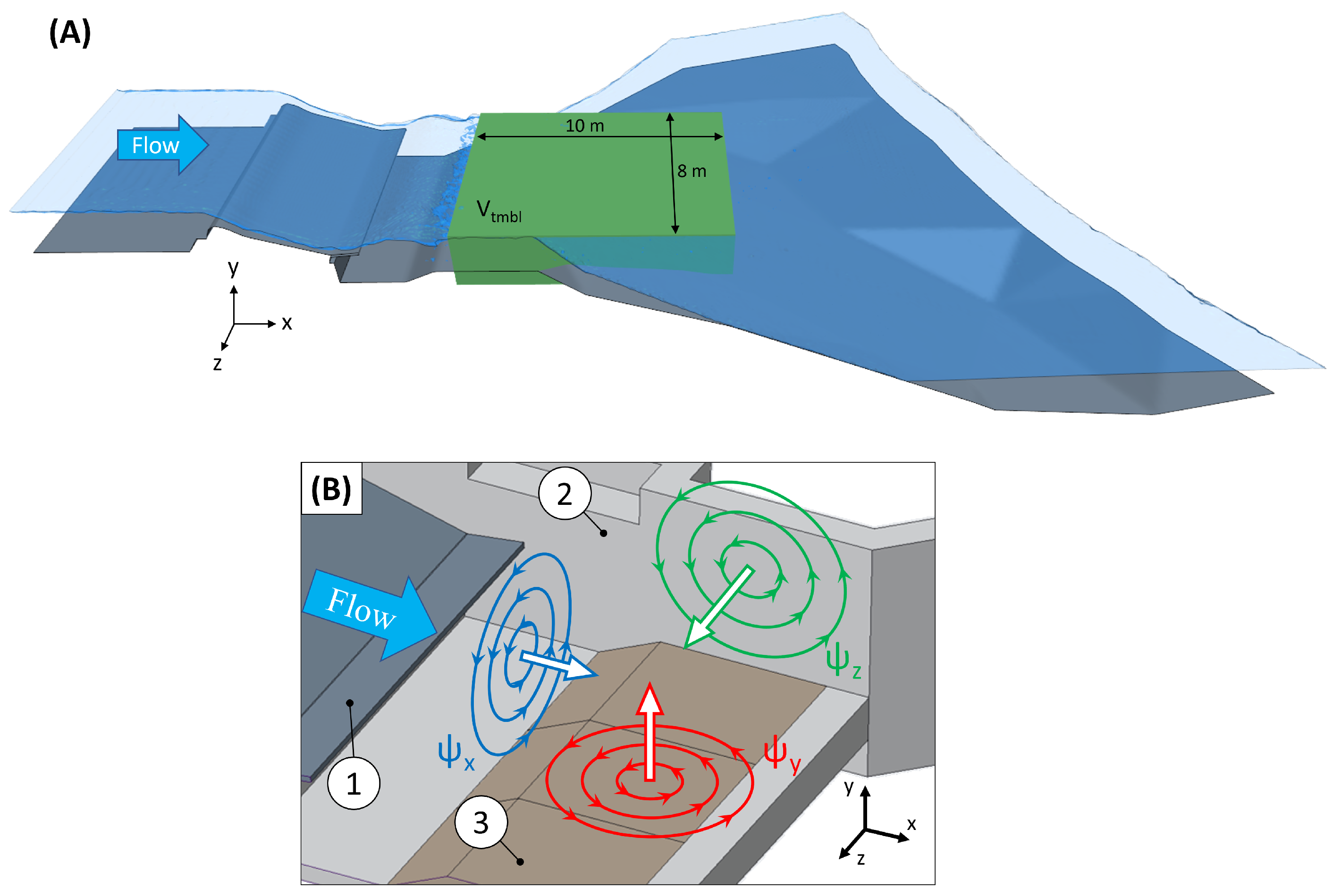
2.5. Evaluation
3. Results and Discussion
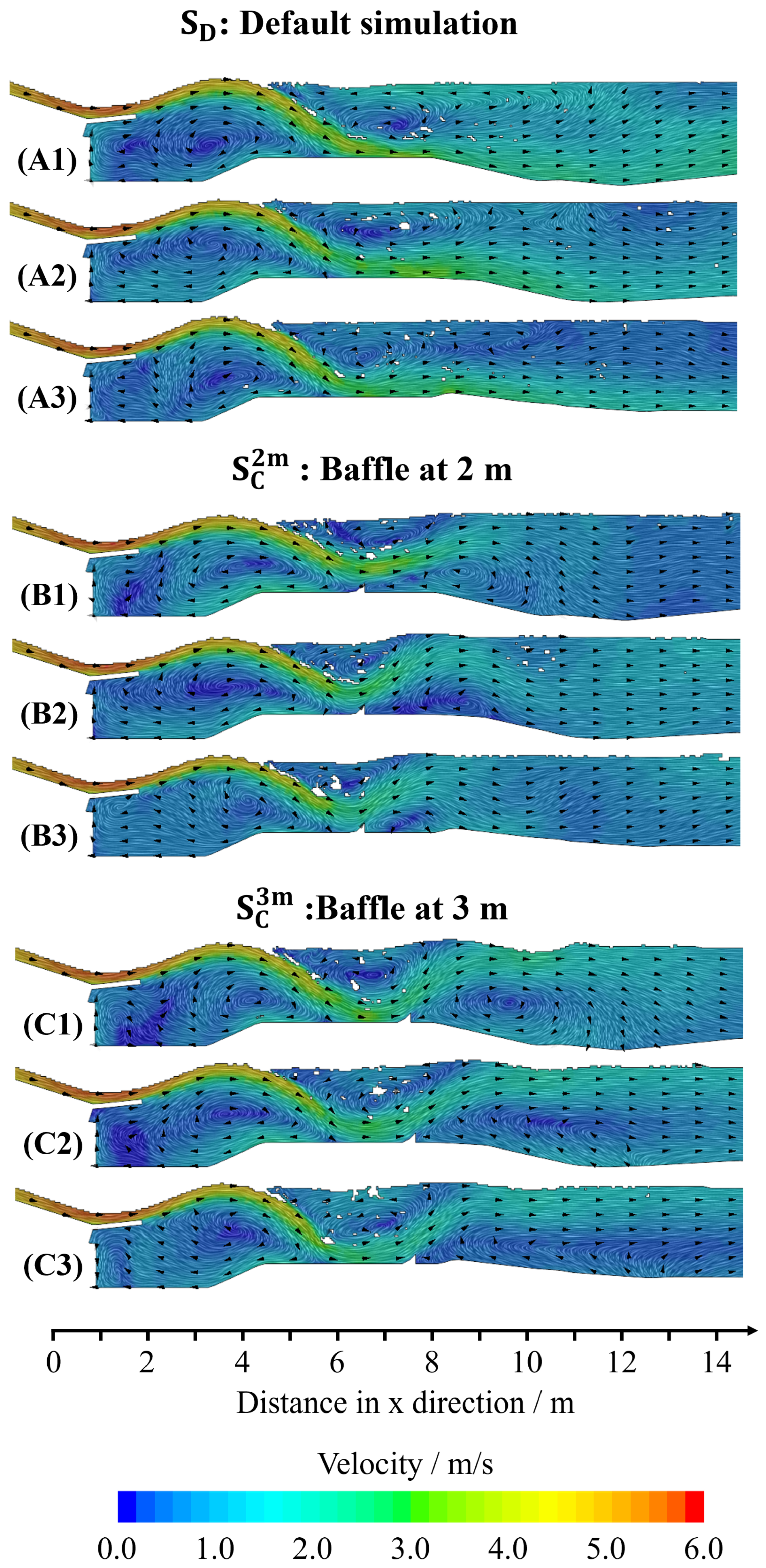
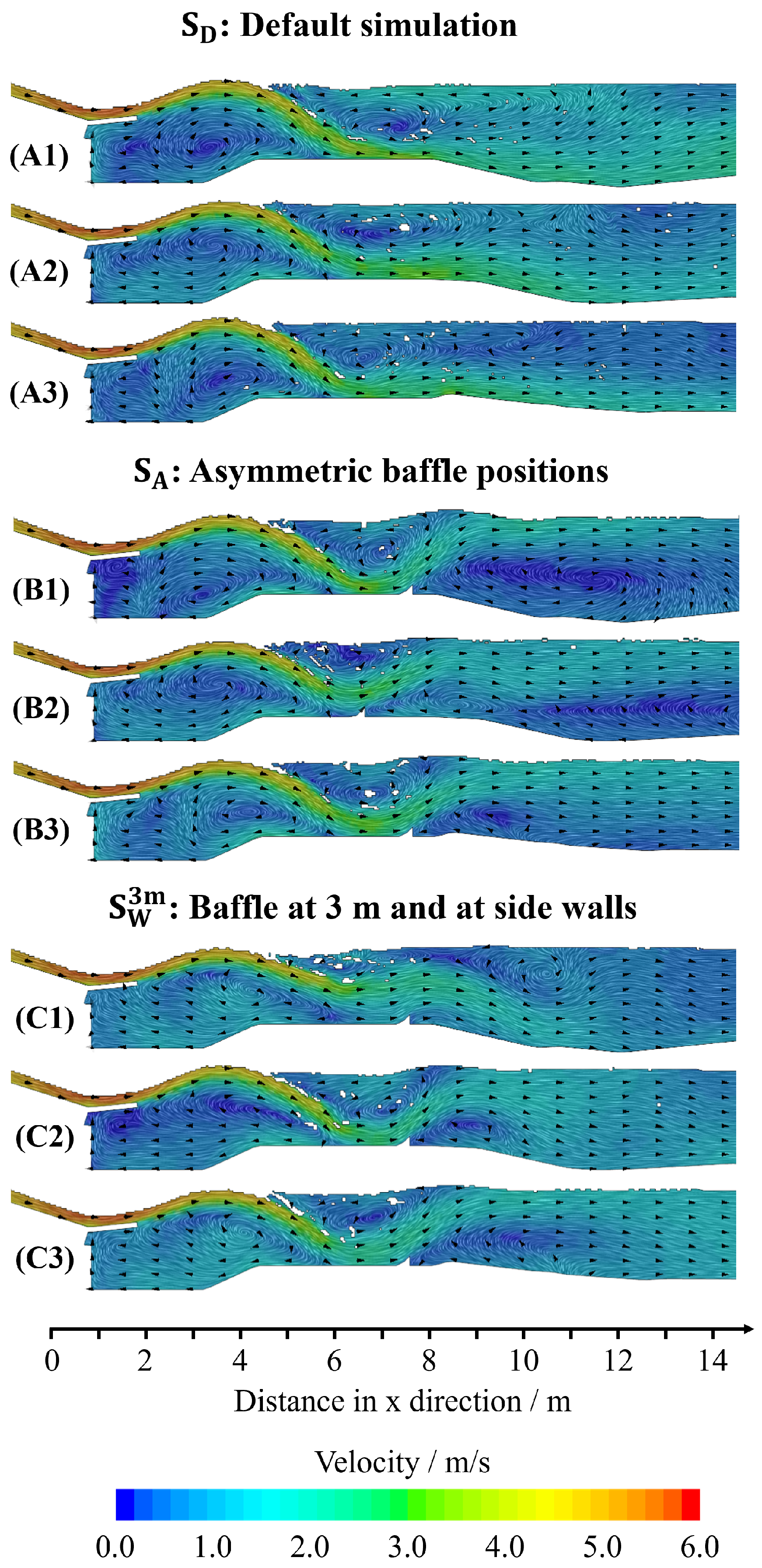
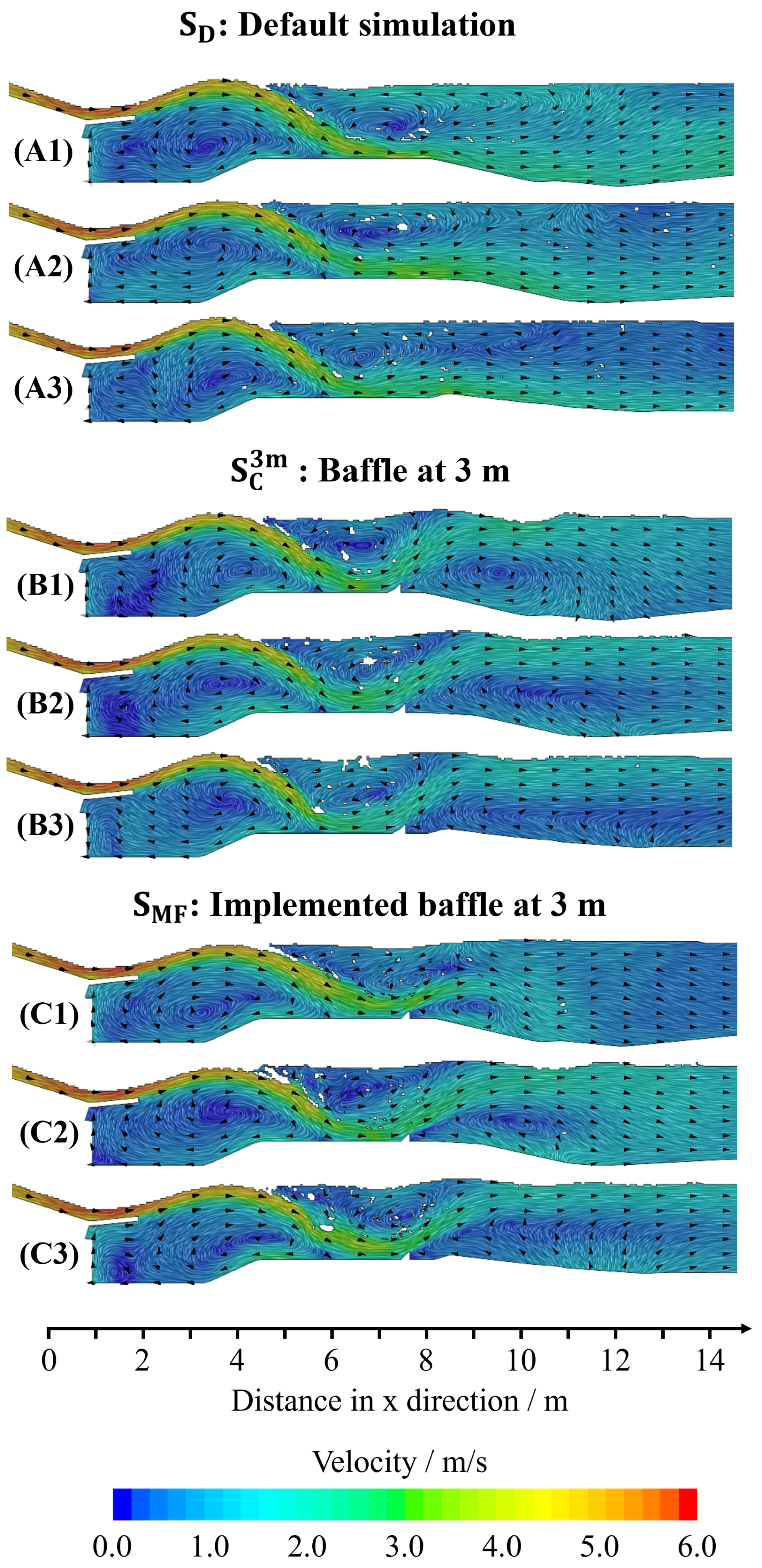
3.1. Flow Behavior
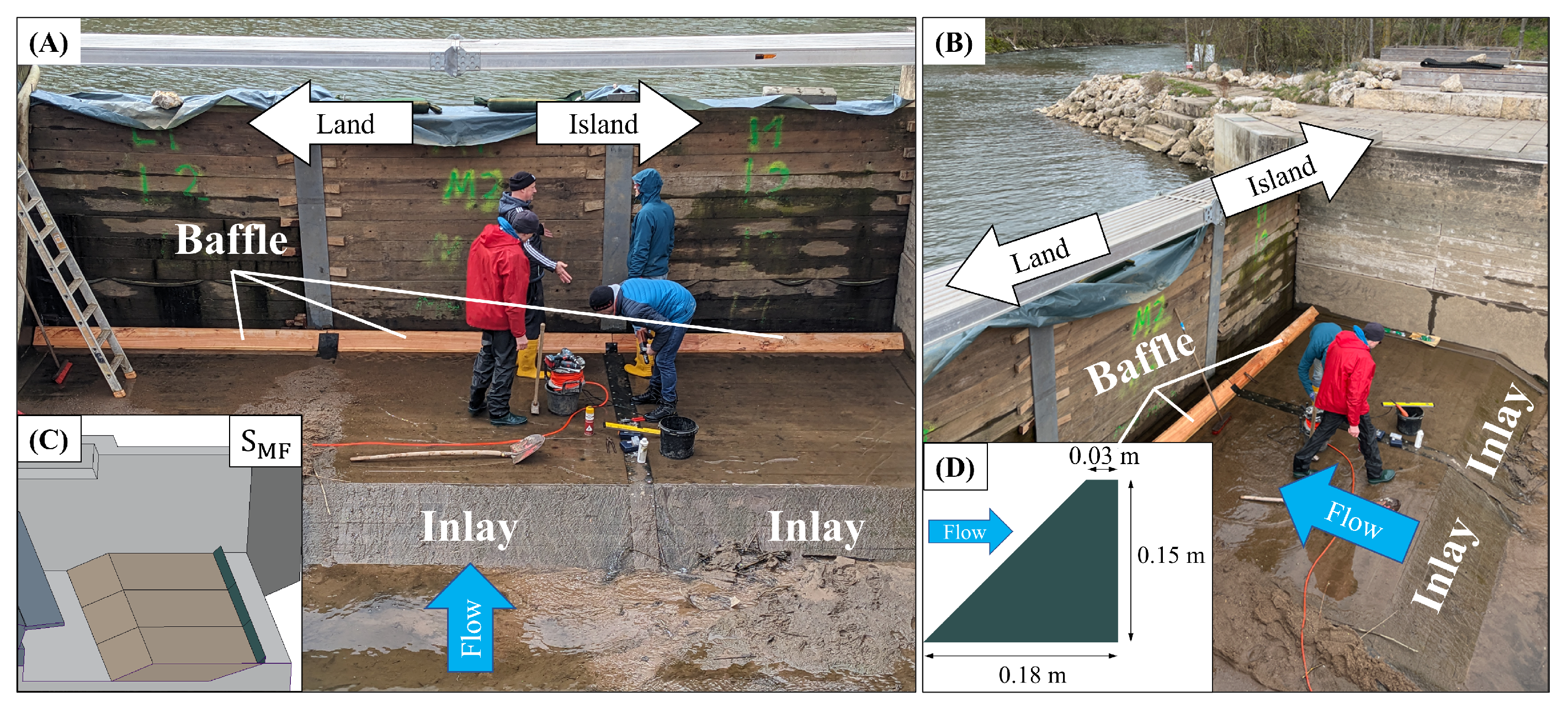
3.2. Real-World Implementation of the Baffle
3.3. Limitations
4. Conclusions
- A realistic 3D-CAD model of the Fuchslochwelle was created. A total of 16 configurations were simulated, including both symmetrical and asymmetrical baffle and inlay configurations. The default configuration, intended to represent the current state of the Fuchslochwelle, exhibited similar recirculation patterns to those reported by surfers.
- In the symmetrical group, the reduction in these recirculation zones was most effectively achieved by placing baffles on the inlay at 2 m. In contrast, in the and groups, recirculation was best minimized by a combination of baffles at the wall and baffles on the inlay at 3 m.
- We simulated a baffle geometry that was subsequently constructed and installed in the Fuchslochwelle. Although this baffle was installed at 3 m rather than the 2 m suggested by the simulations as the optimal placement, it still resulted in a significant reduction in the undesired recirculation zone. This reduction in recirculation was also reported by experienced surfers.
- The results of this study demonstrate that baffles placed on the inlay at 2 m and on the sidewalls can reduce recirculation zones by more than half in terms of vorticity. This approach can be adopted by other wave operators to improve flow conditions in their installations.
- For future work, priority should be given to validation through in situ measurements to further enhance confidence in the presented simulations. Additionally, the impact of geometric simplifications, such as the neglected inflow basin, should be investigated. Lastly, improvements to the numerical setup should be considered to enhance stability, realism, and accuracy.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Leinewelle, e.V. Surfen mitten in Hannover. 2024. Available online: https://www.enercity-leinewelle.de/ (accessed on 12 February 2025).
- Nürnberger Dauerwelle e.V. Die FuchslochWelle-SURFEN IN DER STADT. 2024. Available online: https://www.nuernberger-dauerwelle.de/fuchslochwelle/ (accessed on 12 February 2025).
- Fuchs, H. Effect of adjustable flaps on river surf waves at abrupt drops. In Proceedings of the 37th IAHR World Congress: Learning from the Past for the Future, Kuala Lumpur, Malaysia, 13–18 August 2017; ETH Zurich: Zurich, Switzerland, 2017; p. 7. [Google Scholar] [CrossRef]
- Hornung, H.G.; Killen, P. A stationary oblique breaking wave for laboratory testing of surfboards. J. Fluid Mech. 1976, 78, 459–480. [Google Scholar] [CrossRef]
- D’Ambrosio, D. Hydrodynamic Characterization of Planing Surfboards Using CFD. In Proceedings of the 13th Conference of the International Sports Engineering Association, Tokyo, Japan, 22–25 June 2020; p. 68. [Google Scholar] [CrossRef]
- Oggiano, L. Numerical Comparison between a Modern Surfboard and an Alaia Board using Computational Fluid Dynamics (CFD). In Proceedings of the 5th International Congress on Sport Sciences Research and Technology Support, Funchal, Portugal, 30–31 October 2017; pp. 75–82. [Google Scholar] [CrossRef]
- Oggiano, L.; Pierella, F. CFD for Surfboards: Comparison between Three Different Designs in Static and Maneuvering Conditions. In Proceedings of the the 12th Conference of the International Sports Engineering Association, Brisbane, Australia, 26–29 March 2018; p. 309. [Google Scholar] [CrossRef]
- Forsyth, J.R.; Barnsley, G.; Amirghasemi, M.; Barthelemy, J.; Elshahomi, A.; Kosasih, B.; Perez, P.; Beirne, S.; Steele, J.R.; In Het Panhuis, M. Understanding the relationship between surfing performance and fin design. Sci. Rep. 2024, 14, 8734. [Google Scholar] [CrossRef] [PubMed]
- Falk, S.; Kniesburges, S.; Janka, R.; Grosso, R.; Becker, S.; Semmler, M.; Döllinger, M. Computational hydrodynamics of a typical 3-fin surfboard setup. J. Fluids Struct. 2019, 90, 297–314. [Google Scholar] [CrossRef]
- Falk, S.; Kniesburges, S.; Janka, R.; O’Keefe, T.; Grosso, R.; Döllinger, M. Numerical Investigation of the Hydrodynamics of Changing Fin Positions within a 4-Fin Surfboard Configuration. Appl. Sci. 2020, 10, 816. [Google Scholar] [CrossRef]
- Scarfe, B.E.; Elwany, M.H.S.; Mead, S.T.; Black, K.P. The Science of Surfing Waves and Surfing Breaks—A Review; UC San Diego, Scripps Institution of Oceanography: La Jolla, CA, USA, 2003. [Google Scholar]
- Antunes Do Carmo, J.S.; Neves, M.G.; Ten Voorde, M. Designing a multifunctional artificial reef: Studies on the influence of parameters with most influence in the vertical plane. J. Coast. Conserv. 2011, 15, 99–112. [Google Scholar] [CrossRef]
- Black, K.; Mead, S. Design of Surfing Reefs. Reef J. 2009, 1, 177–191. [Google Scholar]
- Cáceres, I.; Trung, L.H.; Dirk Van Ettinger, H.; Reniers, A.; Uijttewaal, W. Wave and Flow Response to an Artificial Surf Reef: Laboratory Measurements. J. Hydraul. Eng. 2010, 136, 299–310. [Google Scholar] [CrossRef]
- Ten Voorde, M.; Do Carmo, J.S.A.; Neves, M.G. Designing a Preliminary Multifunctional Artificial Reef to Protect the Portuguese Coast. J. Coast. Res. 2009, 251, 69–79. [Google Scholar] [CrossRef]
- Hager, W.H.; Bretz, N.V. Hydraulic jumps at positive and negative steps. J. Hydraul. Res. 1986, 24, 237–253. [Google Scholar] [CrossRef]
- Kawagoshi, N.; Hager, W.H. Wave type flow at abrupt drops: I. Flow geometry. J. Hydraul. Res. 1990, 28, 235–252. [Google Scholar] [CrossRef]
- Moore, W.L.; Morgan, C.W. Hydraulic Jump at An Abrupt Drop. Trans. Am. Soc. Civ. Eng. 1959, 124, 507–516. [Google Scholar] [CrossRef]
- Mossa, M.; Petrillo, A.; Chanson, H. Tailwater level effects on flow conditions at an abrupt drop. J. Hydraul. Res. 2003, 41, 39–51. [Google Scholar] [CrossRef]
- Ohtsu, I.; Yasuda, Y. Transition from supercritical to subcritical flow at an abrupt drop. J. Hydraul. Res. 1991, 29, 309–328. [Google Scholar] [CrossRef]
- Rajaratnam, N.; Ortiz, N.V. Hydraulic Jumps and Waves at Abrupt Drops. J. Hydraul. Div. 1977, 103, 381–394. [Google Scholar] [CrossRef]
- Oertel, M.; Mönkemöller, J.; Schlenkhoff, A. Artificial stationary breaking surf waves in a physical and numerical model. J. Hydraul. Res. 2012, 50, 338–343. [Google Scholar] [CrossRef]
- Borman, D.J.; Sleigh, P.A.; Coughtrie, A.; Horton, L. Hydraulic Free-Surface Modelling with a Novel Validation Approach. In Proceedings of the 9th South African Conference on Computational and Applied Mechanics, Somerset West, South Africa, 14–16 January 2014. [Google Scholar]
- Asiaban, P.; Rennie, C.D.; Egsgard, N. Sensitivity Analysis of Adjustable River Surf Waves in the Absence of Channel Drop. Water 2021, 13, 1287. [Google Scholar] [CrossRef]
- Hirt, C.; Nichols, B. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Wilcox, D.C. Reassessment of the scale-determining equation for advanced turbulence models. AIAA J. 1988, 26, 1299–1310. [Google Scholar] [CrossRef]




| Environment | Wave Module | Inlay | |||||
|---|---|---|---|---|---|---|---|
| Q/m3/s | /m | /m | /m | /m | /m | ||
| 9.3 | 1.14 | 0.717 | 0.91 | 6 | 0.5 | 3 | 24.65 |
| (A) | Name | Inlay Setup | Baffle | Figure 3 | (B) | Name | Inlay Setup | Baffle | Figure 3 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Setup | lc/m | Setup | lc/m | ||||||||
| SCB | 1-1-1 | 0-0-0 | - | A1 | ACB | 1-1-1 | 1-1-1 | 3-2-3 | C1 | ||
| 0-1-0 | 0-0-0 | - | A5 | \-1-/ | \-2-/ | C2 | |||||
| 0-1-0 | 0-1-0 | 1 | A6 | /-1-\ | /-2-\ | C3 | |||||
| 0-1-0 | 0-1-0 | 2 | A7 | SCBW | 1-1-1 | >0-0-0< | - | B1 | |||
| 0-1-0 | 0-1-0 | 3 | A8 | >1-1-1< | 1 | B2 | |||||
| 1-1-1 | 1-1-1 | 1 | A2 | >1-1-1< | 2 | B3 | |||||
| 1-1-1 | 1-1-1 | 2 | A3 | >1-1-1< | 3 | B4 | |||||
| 1-1-1 | 1-1-1 | 3 | A4 | ||||||||
| Setting | Name | Thickness | #Cells | Stretch Factor |
|---|---|---|---|---|
| 1 | Inflow | 70 mm | 8 | |
| 2 | Wave module | 40 mm | 12 | |
| 3 | Edge | 60 mm | 6 | 1.1 |
| 4 | Refinement | 50 mm | 16 | |
| 5 | Global | 50 mm | 12 |
| Grid | #Nodes | Base Size | #Cells | Runtime/h Setup 1 per 100 s | Runtime/h Setup 2 per 100 s | Average Wave Height over the Last X Seconds/m | Average over the Last Second, of Velocity Magnitude at Probes/m/s | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 s | 2 s | 3 s | Probe 1 | Probe 2 | Probe 3 | Probe 4 | ||||||
| 1 | 32 | 2.3 | 06:13 | - | - | - | - | - | - | - | - | |
| 2 | 32 | 1.1 | 06:20 | 16:50 | 0.96 | 0.94 | 0.95 | 2.88 | 5.03 | 5.29 | 5.42 | |
| 3 | 32 | 0.6 | 10:16 | 19:46 | 0.92 | 0.92 | 0.93 | 2.68 | 5.00 | 5.28 | 5.35 | |
| 4 | 32 | 0.5 | 12:39 | 22:03 | 0.98 | 0.98 | 0.98 | 2.96 | 5.01 | 4.96 | 5.27 | |
| 5 | 64 | 0.4 | 16:38 | 28:24 | 0.90 | 0.90 | 0.92 | 2.96 | 5.02 | 4.98 | 5.37 | |
| Sim. | Name | Wave Height (m) | () | () | () |
|---|---|---|---|---|---|
| SCB | 0.64 | 1.27 | 1.05 | 4.28 | |
| 0.75 | 1.53 | 1.01 | 3.37 | ||
| 0.78 | 1.42 | 1.15 | 3.68 | ||
| 0.76 | 1.31 | 1.12 | 3.21 | ||
| 0.74 | 1.43 | 0.91 | 2.63 | ||
| 0.62 | 1.20 | 0.97 | 3.86 | ||
| 0.65 | 1.21 | 0.73 | 2.07 | ||
| 0.71 | 1.55 | 0.75 | 2.16 | ||
| ACB | 0.64 | 1.32 | 0.73 | 2.04 | |
| 0.68 | 1.30 | 1.05 | 2.53 | ||
| 0.65 | 1.48 | 1.01 | 2.81 | ||
| SCBW | 0.70 | 1.25 | 0.87 | 3.78 | |
| 0.69 | 1.14 | 0.86 | 3.66 | ||
| 0.76 | 1.21 | 0.79 | 2.48 | ||
| 0.71 | 1.44 | 0.70 | 1.96 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schwalbe, J.; Tur, B.; Kniesburges, S.; Neuss, N.; Stingl, M.; Keck, T.; Buff, J.; Döllinger, M. Modeling and Simulation of Standing Wave Configurations for Outflow Improvement and Minimizing Undesired Recirculation. Appl. Sci. 2025, 15, 3127. https://doi.org/10.3390/app15063127
Schwalbe J, Tur B, Kniesburges S, Neuss N, Stingl M, Keck T, Buff J, Döllinger M. Modeling and Simulation of Standing Wave Configurations for Outflow Improvement and Minimizing Undesired Recirculation. Applied Sciences. 2025; 15(6):3127. https://doi.org/10.3390/app15063127
Chicago/Turabian StyleSchwalbe, Julien, Bogac Tur, Stefan Kniesburges, Nicolas Neuss, Michael Stingl, Thorsten Keck, Joachim Buff, and Michael Döllinger. 2025. "Modeling and Simulation of Standing Wave Configurations for Outflow Improvement and Minimizing Undesired Recirculation" Applied Sciences 15, no. 6: 3127. https://doi.org/10.3390/app15063127
APA StyleSchwalbe, J., Tur, B., Kniesburges, S., Neuss, N., Stingl, M., Keck, T., Buff, J., & Döllinger, M. (2025). Modeling and Simulation of Standing Wave Configurations for Outflow Improvement and Minimizing Undesired Recirculation. Applied Sciences, 15(6), 3127. https://doi.org/10.3390/app15063127







