Verification of the Scots Pine (Pinus sylvestris L.) Crown Length Model
Abstract
1. Introduction
2. Materials and Methods
2.1. Description of the Study Site
- -
- the dominant species (>95%) on each plot was the Scots pine;
- -
- the stands represented the second age class;
- -
- selected stands occurred on coniferous habitat types characteristic for this species.
2.2. Biometric Measurements
2.3. Allometric Model
- —calculated crown length (m),
- —diameter of the tree at ground height (diameter of the base of the tree):
- —tree height (m),
- —density index (actual number of trees per ha/normative number of trees (taken from Tables of Stands Volume and Increment [48])
2.4. Statistical Analysis
3. Results
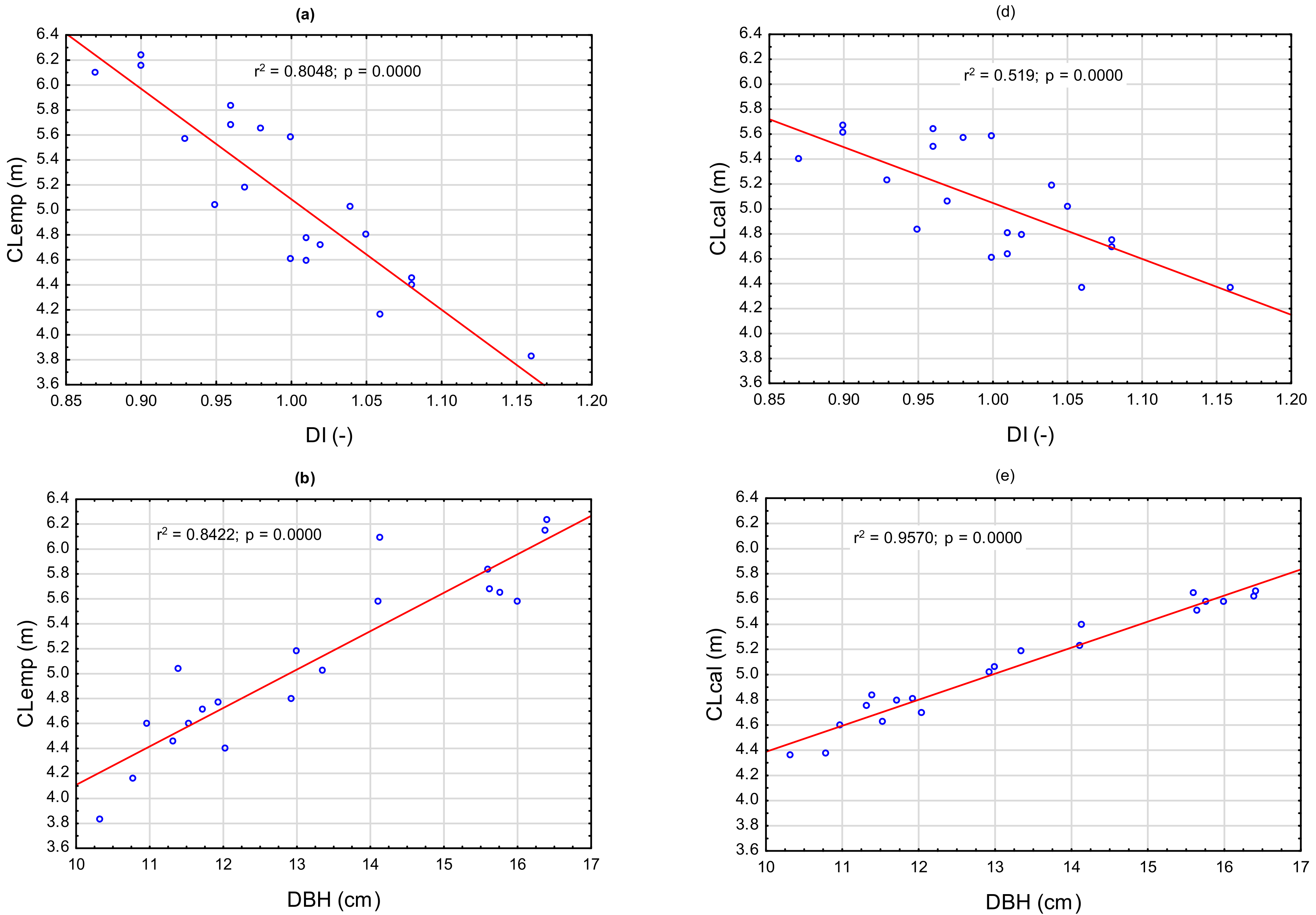
3.1. Model Predictors
3.2. Model Verification on Sample Trees
3.3. Testing the Crowns Length Model on Averaged Samples
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Vacek, S.; Vacek, Z.; Bílek, L.; Simon, J.; Remeš, J.; Hůnová, I.; Král, J.; Putalová, T.; Mikeska, M. Structure, regeneration and growth of Scots pine (Pinus sylvestris L.) stands with respect to changing climate and environmental pollution. Silva Fenn. 2016, 50, 1564. [Google Scholar] [CrossRef]
- Kara, F.; Topaçoğlu, O. Influence of stand density and canopy structure on the germination and growth of Scots pine (Pinus sylvestris L.) seedlings. Environ. Monit. Assess. 2018, 190, 749. [Google Scholar] [CrossRef] [PubMed]
- Burger, H. Wood, number of leaves and growth. V. Spruces and pines of different origins at different sites. Mitt. Schweiz. Anst. Forstl. Versuchsw. 1941, 22, 10–60. (In German) [Google Scholar]
- Socha, J.; Tymińska-Czabańska, L.; Bronisz, K.; Zięba, S.; Hawryło, P. Regional height growth models for Scots pine in Poland. Sci. Rep. 2021, 11, 10330. [Google Scholar] [CrossRef]
- Bose, A.K.; Gessler, A.; Büntgen, U.; Rigling, A. Tamm review: Drought-induced Scots pine mortality–trends, contributing factors and mechanisms. For. Ecol. Manag. 2024, 561, 121873. [Google Scholar] [CrossRef]
- Dudek, A.; Ek, A.R. A bibliography of worldwide literature on individual tree based forest stand growth models. Staff Paper Ser. 1980, 12, 33. [Google Scholar]
- Cieszewski, C.J.; Zasada, M.; Strub, M. Analysis of different base models and methods of site model derivation for Scots Pine. For. Sci. 2006, 52, 187–197. [Google Scholar] [CrossRef]
- Hallingbäck, H.R.; Burton, V.; Vizcaíno-Palomar, N.; Trotter, F.; Liziniewicz, M.; Marchi, M.; Berlin, M.; Ray, D.; Benito-Garzón, M. Managing Uncertainty in Scots Pine Range-Wide Adaptation Under Climate Change. Front. Ecol. Evol. 2021, 9, 724051. [Google Scholar] [CrossRef]
- Tomppo, E.; Gschwantner, T.; Lawrence, M.; McRoberts, R.E. (Eds.) National Forest Inventories. Pathways for Common Reporting; Springer: Berlin/Heidelberg, Germany; Dordrecht, The Netherlands; London, UK; New York, NY, USA, 2010; p. 614. ISBN 978-90-481-3232-4. [Google Scholar] [CrossRef]
- Condes, S.; Sterba, H. Derivation of compatible crown width equations for some important tree species of Spain. For. Ecol. Manag. 2005, 217, 203–218. [Google Scholar] [CrossRef]
- Meng, S.X.; Lieffers, V.J.; Huang, S.M. Modelling crown volume of lodgepole pine based upon the uniform stress theory. For. Ecol. Manag. 2007, 251, 174–181. [Google Scholar] [CrossRef]
- Qiu, S.; Gao, P.; Pan, L.; Zhou, L.; Liang, L.; Sun, Y.; Wang, Y. Developing nonlinear additive tree crown width models based on decomposed competition index and tree variables. J. For. Res. 2023, 34, 1407–1422. [Google Scholar] [CrossRef]
- Rouvinen, S.; Kuuluvainen, T. Structure and asymmetry of tree crowns in relation to local competition in a natural mature Scots pine forest. Can. J. For. Res. 1997, 27, 890–902. [Google Scholar] [CrossRef]
- Sporek, M.; Sporek, K. Allometric Model of Crown Length for Pinus sylvestris L. Stands in South-Western Poland. Forests 2023, 14, 1779. [Google Scholar] [CrossRef]
- Gill, S.J.; Biging, G.S.; Murphy, E.C. Modeling conifer tree crown radius and estimating canopy cover. For. Ecol. Manag. 2000, 126, 405–416. [Google Scholar] [CrossRef]
- Fu, L.; Sharma, R.P.; Hao, K.; Tang, S. A generalized interregional nonlinear mixed-effects crown width model for Prince Rup precht larch in northern China. For. Ecol. Manag. 2017, 389, 364–373. [Google Scholar] [CrossRef]
- Sharma, R.P.; Bílek, L.; Vacek, Z.; Vacek, S. Modelling crown width-diameter relationship for Scots pine in the central Europe. Trees 2017, 31, 1875–1889. [Google Scholar] [CrossRef]
- Qiu, S.; Liang, R.; Wang, Y.; Luo, M.; Sun, Y. Comparative analysis of machine learning algorithms and statistical models for predicting crown width of Larix olgensis. Earth Sci. Inform. 2022, 15, 2415–2429. [Google Scholar] [CrossRef]
- Raptis, D.; Kazana, V.; Kazaklis, A.; Stamatiou, C.A. Crown Width-Diameter Model for Natural Even-Aged Black Pine Forest Management. Forests 2018, 9, 610. [Google Scholar] [CrossRef]
- Di Salvatore, U.; Marchi, M.; Cantiani, P. Single-tree crown shape and crown volume models for Pinus nigra J. F. Arnold in central Italy. Ann. For. Sci. 2021, 78, 76. [Google Scholar] [CrossRef]
- Ebiś, M. Structure of the Biomass of the Scots Pine; PWN: Warszawa, Poland, 2001; p. 158. ISBN 83-01-13380-5. (In Polish) [Google Scholar]
- Pretzsch, H.; Biber, P.; Dursky, J. The single tree-based stand simulator SILVA: Construction, application and evaluation. For. Ecol. Manag. 2002, 162, 3–21. [Google Scholar] [CrossRef]
- Leites, L.P.; Robinson, A.P.; Crookston, N.L. Accuracy and equivalence testing of crown ratio models and assessment of their impact on diameter growth and basal area increment predictions of two variants of the Forest Vegetation Simulator. Can. J. For. Res. 2009, 39, 655–665. [Google Scholar] [CrossRef]
- Jucker, T.; Caspersen, J.; Chave, J.; Antin, C.; Barbier, N.; Bongers, F.; Dalponte, M.; van Ewijk, K.Y.; Forrester, D.I.; Haeni, M.; et al. Allometric equations for integrating remote sensing imagery into forest monitoring programmes. Glob. Change Biol. 2016, 23, 177–190. [Google Scholar] [CrossRef] [PubMed]
- Sporek, M. The Leaf Area of Scots Pine (Pinus sylvestris L.) as a Function of the Population Structure; PWN: Warszawa, Poland, 2018; p. 208. ISBN 978-83-01-20366-5. (In Polish) [Google Scholar]
- Gonzalez-Benecke, C.A.; Gezan, S.A.; Samuelson, L.J.; Cropper, W.P.; Leduc, D.J.; Martin, T.A. Estimating Pinus palustris tree diameter and stem volume from tree height, crown area and stand-level parameters. J. For. Res. 2014, 25, 43–52. [Google Scholar] [CrossRef]
- Monserud, R.A.; Sterba, H. Modeling individual tree mortality for Austrian forest species. For. Ecol. Manag. 1999, 113, 109–123. [Google Scholar] [CrossRef]
- Hasenauer, H.; Monserud, R.A. A crown ratio model for Austrian forests. For. Ecol. Manag. 1996, 84, 49–60. [Google Scholar] [CrossRef]
- Pretzsch, H.; Schutze, G. Crown allometry and growing space efficiency of Norway spruce (Picea abies L. Karst.) and European beech (Fagus sylvatica L.) in pure and mixed stands. Plant. Biol. 2005, 7, 628–639. [Google Scholar] [CrossRef]
- Valentine, H.T.; Ludlow, A.R.; Furnival, G.M. Modeling crown rise in even-aged stands of Sitka spruce or loblolly pine. For. Ecol. Manag. 1994, 69, 189–197. [Google Scholar] [CrossRef]
- Kuprevicius, A.; Auty, D.; Achim, A.; Caspersen, J.P. Quantifying the influence of live crown ratio on the mechanical properties of clear wood. Forestry 2014, 87, 449–458. [Google Scholar] [CrossRef]
- Navratil, S. Wind damage in thinned stands. In Proceedings of the a Commercial Thinning Workshop, Whitecourt, AB, Canada, 17–18 October 1997; pp. 29–36. [Google Scholar]
- Monserud, R.A.; Sterba, H. A basal area increment model for individual trees growing in even- and uneven-aged forest stands in Austria. For. Ecol. Manag. 1996, 80, 57–80. [Google Scholar] [CrossRef]
- Russell, M.; Weiskittel, A. Maximum and Largest Crown Width Equations for 15 Tree Species in Maine. North. J. Appl. For. 2011, 28, 84–91. [Google Scholar] [CrossRef]
- Assmann, E. The Principles of Forest Yield Study; Pergamon Press: Oxford, UK, 1970; p. 506. [Google Scholar]
- Baldocchi, D.; Penuelas, J. The physics and ecology of mining carbon dioxide from the atmosphere by ecosystems. Glob. Change Biol. 2019, 25, 1191–1197. [Google Scholar] [CrossRef]
- Sporek, M.; Sporek, K.; Stebila, J.; Kučerka, M.; Kminiak, R.; Lubis, M.A.R. Assessment of the mass and surface area of the Scots pine (Pinus sylvestris L.) needles. Appl. Sci. 2022, 12, 8204. [Google Scholar] [CrossRef]
- Gardiner, B.A.; Peltola, H.; Kellomaki, S. Comparison of two models for predicting the critical wind speed required to damage coniferous trees. Ecol. Mod. 2000, 129, 1–23. [Google Scholar] [CrossRef]
- Pallardy, S.G. Physiology of Woody Plants, 3rd ed.; Academic Press: Cambridge, MA, USA, 2010; p. 453. [Google Scholar]
- Mátyás, C.; Varga, G. Effect of intra-specific competition on tree architecture and aboveground dry matter allocation in Scots pine. For. Syst. 2000, 9, 111–119. [Google Scholar] [CrossRef]
- Stenberg, P.; Kuuluvainen, T.; Kellomäki, S.; Grace, J.C.; Jokela, E.J.; Gholz, H.L. Crown Structure, Light Interception and Productivity of Pine Trees and Stands. Ecol. Bull. 1994, 43, 20–34. [Google Scholar]
- Starr, M.; Saarsalmi, A.; Hokkanen, T.; Merila, P.; Helmisaari, H.S. Models of litterfall production for scots pine (Pinus sylvestris L.) in Finland using stand, site and climate factors. For. Ecol. Manag. 2005, 205, 215–225. [Google Scholar] [CrossRef]
- Palahí, M.; Pukkala, T.; Trasobares, A. Modelling the diameter distribution of Pinus sylvestris, Pinus nigra and Pinus halepensis forest stands in Catalonia using the truncated Weibull function. Forestry 2006, 79, 553–562. [Google Scholar] [CrossRef]
- Chytrý, M.; Danihelka, J.; Horsák, M.; Kočí, M.; Kubešová, S.; Lososová, Z.; Otýpková, Z.; Tichý, L.; Martynenko, V.; Baisheva, E. Modern analogues from the Southern Urals provide insights into biodiversity change in the early Holocene forests of Central Europe. J. Biogeogr. 2010, 37, 767–780. [Google Scholar] [CrossRef]
- Statistical Yearbook of Forestry; Statistics Poland: Warszawa, Poland, 2022. Available online: https://stat.gov.pl (accessed on 3 August 2024).
- Institute of Meteorology and Water Management, National Research Institute. Index of Meteorological Data. Available online: https://www.google.pl/url?sa=t&rct=j&q=&esrc=s&source=web&cd=&cad=rja&uact=8&ved=2ahUKEwiU_ofV_ISMAxUjBxAIHRVIBQkQFnoECBQQAQ&url=https%3A%2F%2Fdanepubliczne.imgw.pl%2Fdata%2Fdane_pomiarowo_obserwacyjne%2Fdane_meteorologiczne%2Fmiesieczne%2F&usg=AOvVaw0-j79ccaceKNa6kggpa9Qx&opi=89978449 (accessed on 1 July 2024).
- Czarnowski, M.S. Investigation of the potential productive capacity of forest sites as a function of soil, climate and ecological properties of tree species. (A proposal of standardized method for the world-wide gathering action). Acta Univ. Wratisl. Pr. Bot. 1971, 134, 127–151. [Google Scholar]
- Szymkiewicz, B. Volume and Increment Stands Tables; PWRiL: Warszawa, Poland, 1961. (In Polish) [Google Scholar]
- Montgomery, D.C.; Peck, E.A.; Vining, G.G. Introduction to Linear Regression Analysis; Wiley: New York, NY, USA, 2001; p. 641. [Google Scholar]
- Reineke, L.H. Perfecting a stand-density index for even-aged forests. J. Agric. Res. 1933, 46, 627–638. [Google Scholar]
- Yang, Y.; Huang, S. Two-stage ingrowth models for four major tree species in Alberta. Eur. J. For. Res. 2015, 134, 991–1004. [Google Scholar] [CrossRef]
- Pinheiro, J.C.; Bates, D.M. Mixed-Effects Models in S and S-PLUS; Springer: New York, NY, USA, 2000. [Google Scholar]
- Gregoire, T.G.; Schabenberger, O.; Barrett, J.P. Linear modelling of irregularly spaced, unbalanced, longitudinal data from permanent-plot measurements. Can. J. For. Res. 1995, 25, 137–156. [Google Scholar] [CrossRef]
- Fu, L.; Sun, H.; Sharma, R.P.; Lei, Y.; Zhang, H.; Tang, S. Nonlinear mixed-effects crown width models for individual trees of Chinese fir (Cunninghamia lanceolata) in south-central China. For. Ecol. Manag. 2013, 302, 210–220. [Google Scholar] [CrossRef]
- Ojansuu, R.; Maltamo, M. Sapwood and heartwood taper in Scots pine stems. Can. J. For. Res. 1995, 25, 1928–1943. [Google Scholar] [CrossRef]
- Uusitalo, J.; Kivinen, V.P. Constructing bivariate dbh/dead-branch distribution of pines for use in sawing production planning. Scand. J. For. Res. 1998, 3, 509–514. [Google Scholar] [CrossRef]
- Maltamo, M.; Bollandsås, O.M.; Vauhkonen, J.; Breidenbach, J.; Gobakken, T.; Næsset, E. Comparing different methods for prediction of mean crown height in Norway spruce stands using airborne laser scanner data. Forestry 2010, 83, 257–268. [Google Scholar] [CrossRef]
- Pretzsch, H. The Effect of Tree Crown Allometry on Community Dynamics in Mixed-Species Stands versus Monocultures. A Review and Perspectives for Modeling and Silvicultural Regulation. Forests 2019, 10, 810. [Google Scholar] [CrossRef]
- del Río, M.; Bravo-Oviedo, A.; Ruiz-Peinado, R.; Condés, S. Tree allometry variation in response to intra- and inter-specific competitions. Trees 2019, 33, 121–138. [Google Scholar] [CrossRef]
- Zhu, W.; Liu, Z.; Jia, W.; Li, D. Modelling the Tree Height, Crown base height, and effective crown height of Pinus koraiensis plantations based on knot analysis. Forests 2021, 12, 1778. [Google Scholar] [CrossRef]
- Czarnowski, M.S. Outline of Terrestrial Plant Ecology; PWN: Warsaw, Poland, 1989; p. 555. (In Polish) [Google Scholar]
- Sporek, K. Length of Trees-Crown as Function of Structure of Scots Pine Even-Aged Forest Stands; PWN: Warszawa, Poland, 1990; p. 31. ISBN 83-01-10228-4. (In Polish) [Google Scholar]
- Rodríguez de Prado, D.; San Martín, R.; Bravo, F.; Herrero, C. Potential climatic influence on maximum stand carrying capacity for 15 Mediterranean coniferous and broadleaf species. For. Ecol. Manag. 2020, 460, 117824. [Google Scholar] [CrossRef]
- Vázquez-Veloso, A.; Pando, V.; Ordóñez, C.; Bravo, F. Evaluation and validation of forest models: Insight from Mediterranean and Scots pine models in Spain. Ecol. Inform. 2023, 77, 102246. [Google Scholar] [CrossRef]

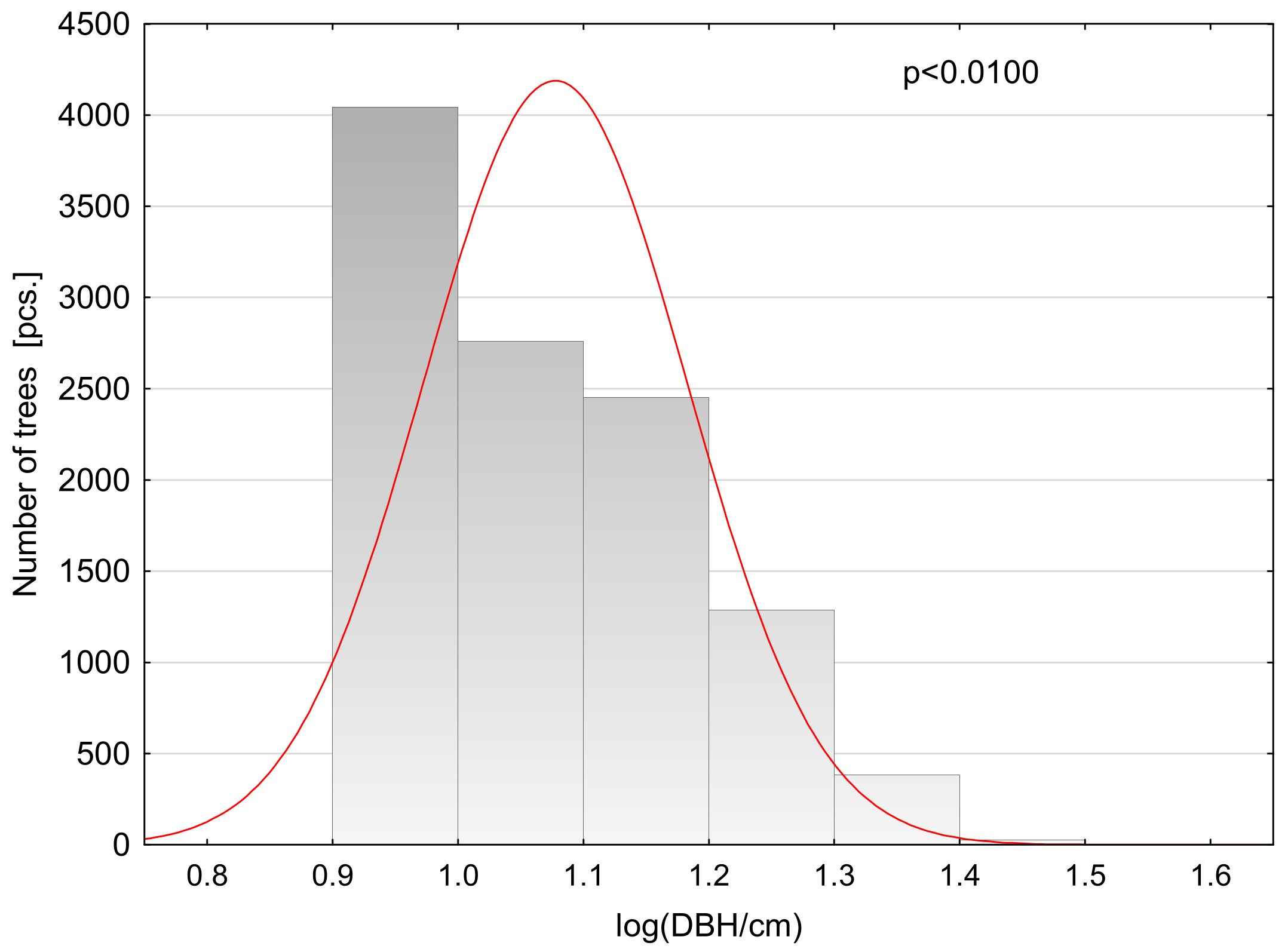
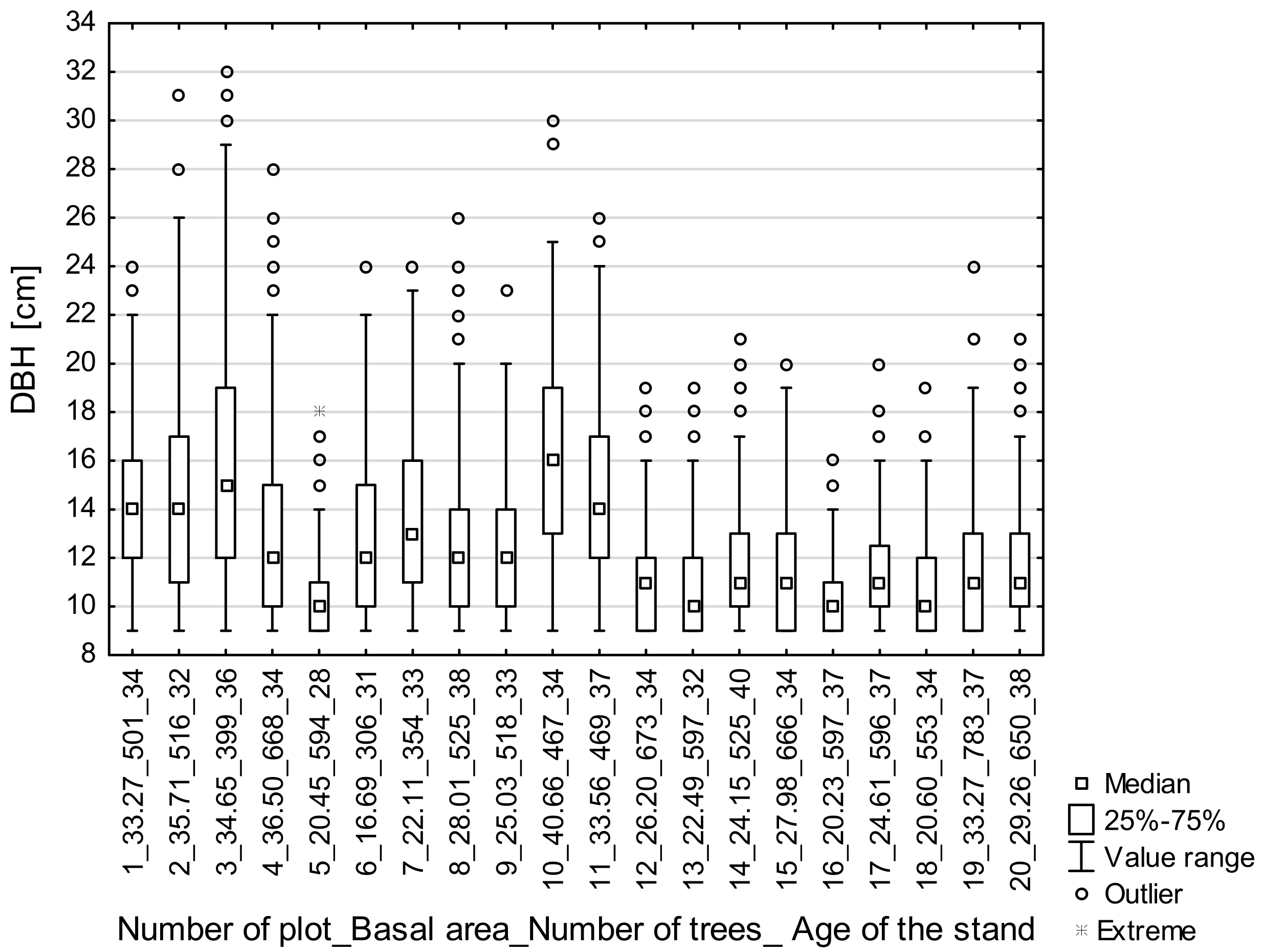
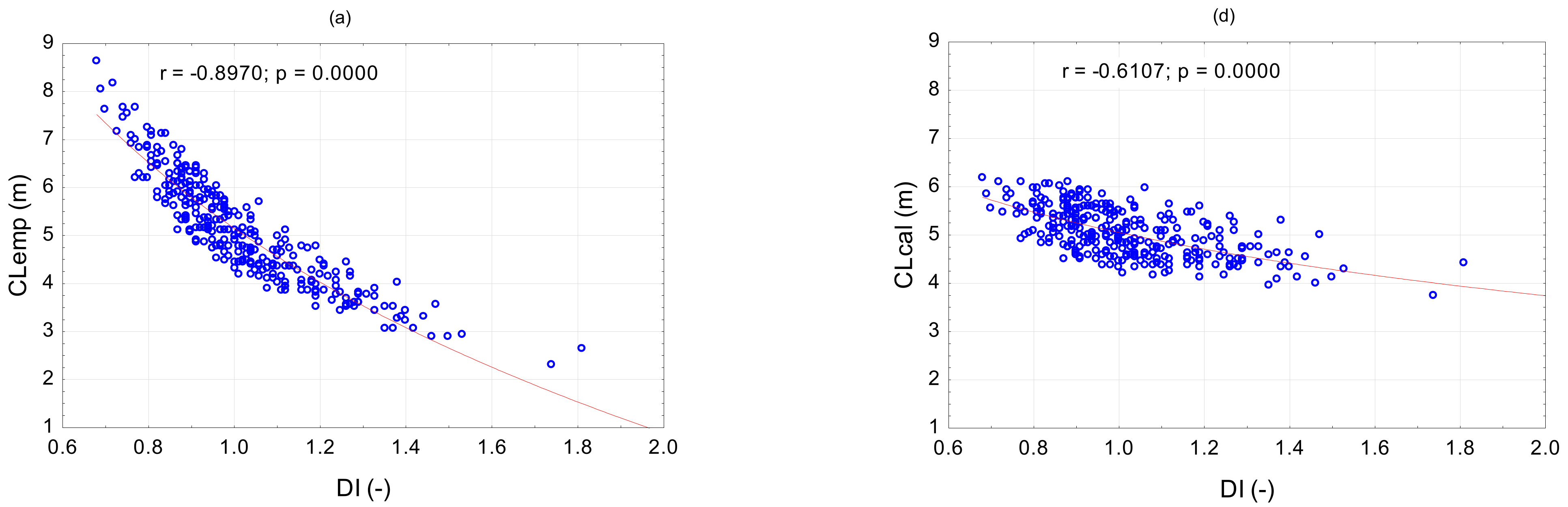
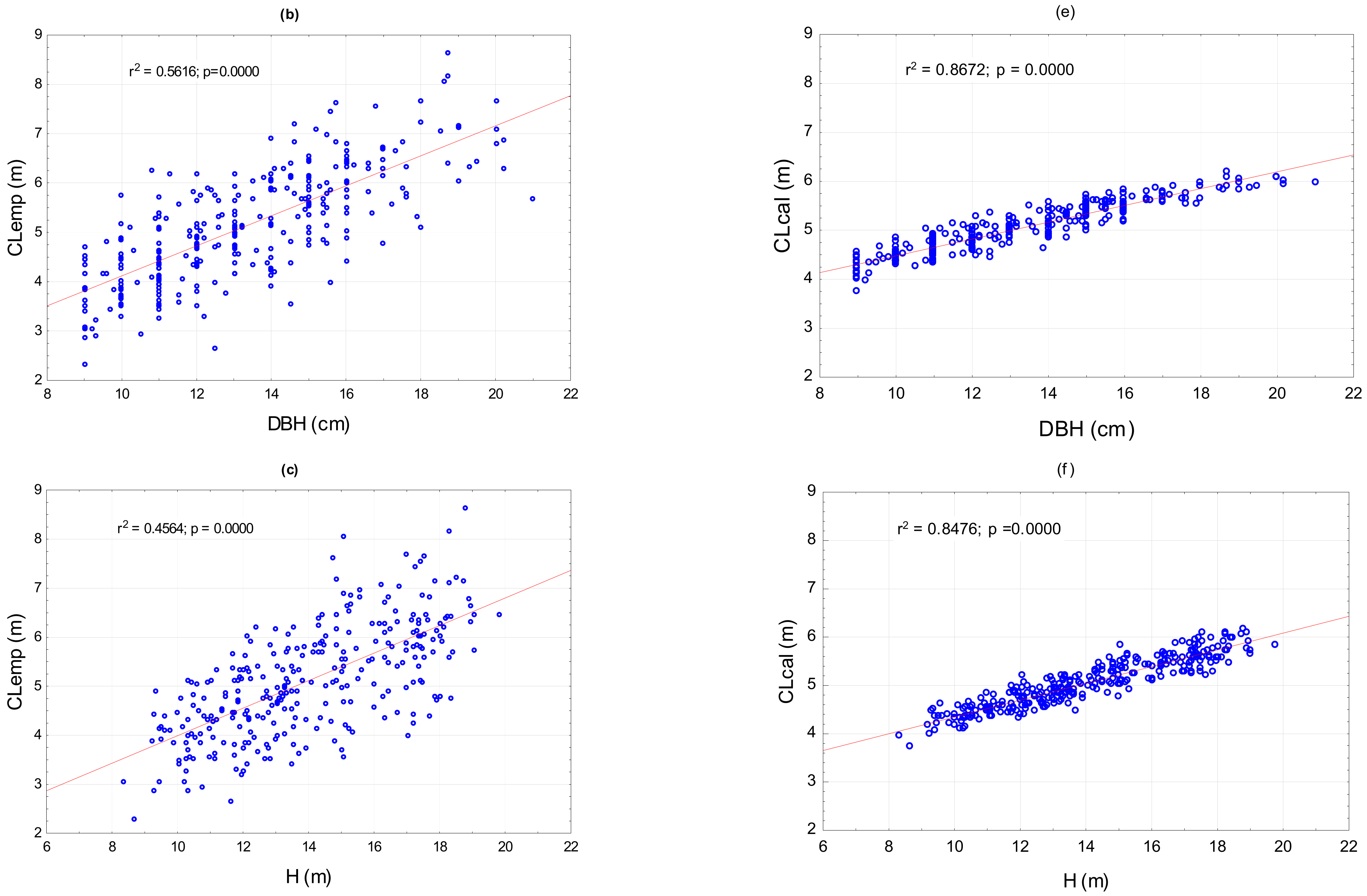


| Variables | Model Validation Data Mean ± SD (Range Min–Max) |
|---|---|
| Stands | |
| Total number of the sample plots | 20 |
| Total number of trees per sample plots | 10 957 |
| Age of stands (years) | 34.65 ± 2.78 (28–40) |
| Number of trees per ha (, ha) | 2191± 452 (1224–3132) |
| Number of trees per sample plot (, 0.25 ha) | 547.85 ± 112.96 (306–783) |
| Stand basal area (, m2 ha−1) | 27.77 ± 6.43 (16.69–40.66) |
| Diameter at breast height , cm) | 12.29 ± 3.24 (9–32) |
| Sample trees | |
| Number of trees cut down (, pcs.) | 300 |
| Height of cut trees (, m) | 13.99 ± 2.67 (8.33–19.79) |
| Diameter at breast height , cm) | 13.27 ± 2.75 (9.0–21.0) |
| Diameter of the trees at ground height (; cm) | 14.97 ± 2.75 (10.7–22.7) |
| Crowns length (, m) | 5.12 ± 1.11 (2.31–8.63) |
| (m) | (m) | (cm) | (m) | (-) | |
|---|---|---|---|---|---|
| (m) | 0.8567 | – | |||
| (cm) | 0.7503 | 0.9352 | – | ||
| (m) | 0.6789 | 0,9227 | 0.7868 | – | |
| (–) | −0.9273 | −0.6129 | −0.4942 | −0.3975 | – |
| Number of Plots | DI | Mean | Mean | RMSE | Divergence | R2 | |||
|---|---|---|---|---|---|---|---|---|---|
| (cm) | (m) | (-) | (m) | (m) | (m) | (%) | (-) | (Trees ha−1) | |
| 1 | 17.47 | 17.41 | 0.98 | 5.65 | 5.57 | 0.01 | 1.42 | 0.81 | 2004 |
| 2 | 17.70 | 17.40 | 1.00 | 5.58 | 5.58 | 0.00 | 0.00 | 0.72 | 2064 |
| 3 | 17.30 | 18.23 | 0,96 | 5.83 | 5.64 | 0.04 | 3.26 | 0.77 | 1596 |
| 4 | 17.34 | 16.46 | 0.96 | 5.68 | 5.50 | 0.03 | 3.17 | 0.79 | 2672 |
| 5 | 12.49 | 9.61 | 1.06 | 4.16 | 4.37 | 0.04 | 5.15 | 0.81 | 2376 |
| 6 | 13.74 | 11.63 | 1.08 | 4.40 | 4.69 | 0.08 | 6.53 | 0.79 | 1224 |
| 7 | 15.82 | 14.48 | 0.93 | 5.57 | 5.23 | 0.12 | 6.10 | 0.66 | 1416 |
| 8 | 15.83 | 15.79 | 0.87 | 6.09 | 5.39 | 0.49 | 11.49 | 0.85 | 2100 |
| 9 | 15.05 | 15.58 | 1.04 | 5.02 | 5.18 | 0.03 | 3.27 | 0.77 | 2072 |
| 10 | 18.09 | 16.57 | 0.90 | 6.15 | 5.61 | 0.29 | 5.53 | 0.64 | 1868 |
| 11 | 18.11 | 17.18 | 0.90 | 6.23 | 5.66 | 0.32 | 11.24 | 0.79 | 1876 |
| 12 | 13.03 | 12.95 | 1.08 | 4.45 | 4.75 | 0.09 | 6.78 | 0.69 | 2692 |
| 13 | 12.67 | 11.23 | 1.00 | 4.60 | 4.60 | 0.00 | 0.00 | 0.72 | 2388 |
| 14 | 13.63 | 12.36 | 1.01 | 4.77 | 4.80 | 0.00 | 0.55 | 0.76 | 2100 |
| 15 | 13.43 | 12.59 | 1.02 | 4.71 | 4.79 | 0.01 | 1.67 | 0.74 | 2664 |
| 16 | 12.03 | 10.30 | 1.16 | 3.83 | 4.36 | 0.28 | 13.76 | 0.81 | 2388 |
| 17 | 13.09 | 12.93 | 0.95 | 5.03 | 4.83 | 0.04 | 3.98 | 0.72 | 2384 |
| 18 | 13.23 | 11.14 | 1.01 | 4.59 | 4.63 | 0.00 | 0.81 | 0.83 | 2212 |
| 19 | 14.63 | 13.94 | 1.05 | 4,80 | 5.01 | 0.04 | 4.30 | 0.71 | 3132 |
| 20 | 14.70 | 14.06 | 0.97 | 5.18 | 5.06 | 0.01 | 2.32 | 0.88 | 2600 |
| Mean | 14.97 | 14.09 | 1.00 | 5.12 | 5.06 | 0.31 | 4.57 | 0.76 | 2191 |
| (m) | (m) | (cm) | (m) | (−) | |
|---|---|---|---|---|---|
| (m) | 0.9549 | – | |||
| (cm) | 0.9038 | 0.9549 | – | ||
| (m) | 0.8947 | 0.9669 | 0.9128 | – | |
| (−) | −0.8874 | −0.7390 | −0.6719 | −0.6350 | – |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sporek, M.; Sporek, K.; Kučerka, M. Verification of the Scots Pine (Pinus sylvestris L.) Crown Length Model. Appl. Sci. 2025, 15, 3124. https://doi.org/10.3390/app15063124
Sporek M, Sporek K, Kučerka M. Verification of the Scots Pine (Pinus sylvestris L.) Crown Length Model. Applied Sciences. 2025; 15(6):3124. https://doi.org/10.3390/app15063124
Chicago/Turabian StyleSporek, Monika, Kazimierz Sporek, and Martin Kučerka. 2025. "Verification of the Scots Pine (Pinus sylvestris L.) Crown Length Model" Applied Sciences 15, no. 6: 3124. https://doi.org/10.3390/app15063124
APA StyleSporek, M., Sporek, K., & Kučerka, M. (2025). Verification of the Scots Pine (Pinus sylvestris L.) Crown Length Model. Applied Sciences, 15(6), 3124. https://doi.org/10.3390/app15063124







