Abstract
Accurate characterization of soil dynamic response is paramount for geotechnical and protective engineering. However, the impact properties of unsaturated cohesive soil have not been well characterized due to lack of sufficient research. For this purpose, impact tests using the Split Hopkinson Pressure Bar (SHPB) were elaborately designed to investigate the dynamic stress–strain response of unsaturated clay with strain rates of 204~590 s−1. As the strain rate increased up to 500 s−1, a lock-up behavior was observed in the plastic flow stage, which can be explained as the breakage and rearrangement of soil gains under a high level of stress. Further, the strain rate dependency of the dynamic strength was quantitatively characterized by the Cowper Symonds (CS) model and the CS coefficients were determined to be the intercept of 55 and slope of 0.8 in the double logarithmic scale of Dynamic Increase Factor (DIF) and strain rate space. Furthermore, the SHPB test was reproduced using a modified Material Particle Method (MPM), which involves an improved dynamic constitutive model for unsaturated soil considering the strain rate effect. The simulated stress–strain curves basically agree with the experimental results, indicating the feasibility of MPM for investigating the dynamic properties of unsaturated soil under SHPB impact loading.
1. Introduction
Soil, a typical carrier for military or civil construction, suffers from not only conventional static load, but also unexpected dynamic load. In the past decades, the mechanical behavior of soil under static and cyclic loading conditions has been examined many times. However, accurate characterization of the soil dynamic response subjected to impact loading is still a big challenge for researchers and needs further study. This will provide better insight into various engineering applications, such as the design of dynamic compaction [1] in geotechnical engineering, the assessment of landmine impact or projectile penetration [2] in military engineering, the investigation of underground structure damage from accidental explosions [3,4] in protection engineering, and the design of aseismic performance and shock absorption for structures [5] in earthquake engineering.
Extensive studies have demonstrated that the strain rate dependency [6,7,8,9] plays an important role in characterizing the mechanical behavior of material. Since the Split Hopkinson Pressure Bar (SHPB) [10,11] technique was developed and applied to investigate the dynamic behavior of material, the recognition of the strain rate effect has been extended from a quasi-static condition (~ s−1) to a medium or high loading rate condition (~ s−1). However, when the conventional SHPB is adopted to study the impact properties of soil with a low wave velocity and high energy attenuation, it is difficult to obtain valid data due to the high-frequency oscillation and dispersion effect [12,13]. Subsequently, many beneficial attempts have been made to overcome these problems, for instance, applying a pulse shaper [14,15] to increase the rise time of the incident wave, embedding a quartz crystal [16,17] to capture the weak transmission signal, placing the soil sample within a confining rigid tube to remedy the lack of structure strength, thereby causing an effective dynamic response [18,19]. Based on the above improved techniques, the SHPB testing system has been successfully used for researching the dynamic properties of various soils under impact loading.
Song et al. [20] performed the SHPB test on dry sand by placing the sample in a cylindrical tube made of three different materials and discussed the influence of the passive confining level. As the confining level increases, the sand can sustain more axial stress, thereby resulting in a stiffer dynamic response. Furthermore, Luo et al. [21] pointed out that the shearing resistance of sand is highly affected by gain crushing at lower confining pressures, but is negligible at high confining pressures. Martin et al. [22] found that water can lubricate the soil particles, resulting in sand in an unsaturated state becoming more compressible and presenting a more obvious strain rate dependency compared to dry sand. Unlike sand, the dynamic response of clay under SHPB impact loading presents a remarkable strain rate effect [23,24,25]. To evaluate the rate dependency properties of compacted clay, Liu et al. [24] adopted the dynamic increase factor (DIF) to carry out an analysis on the dynamic peak stress and maximum strain. The results showed that the DIFs for peak stress and maximum strain exponentially increased with the increase in strain rate, while the fitting parameters were highly affected by the compaction degree and water content. Yang et al. [25] studied the effect of the consolidation state on the mechanical behavior of clay under dynamic uniaxial compressive conditions. The results indicate that the applied preconsolidation pressure contributed to the rate-sensitive characteristic of clay. Up until now, the research object of the soil SHPB test has been mainly concentrated in cohesionless soil and saturated clay; meanwhile, there has been little SHPB experimental research conducted on unsaturated clay, thereby causing an imperfect knowledge of the dynamic properties of unsaturated clay subjected to impact loading.
To overcome the imperfection of SHPB experimental evaluations regarding certain complicated and unstable problems of material dynamic mechanical behavior, various numerical methods have been applied to carry out in-depth analyses. The classical Finite Element Method (FEM) has been used for reproducing the SHPB test and extensively studying the friction and inertial effect [26,27], as well as the optimization of specimen height [28] through the commercial software ABAQUS (https://www.3ds.com/products/simulia/abaqus (accessed on 6 March 2025)) or LS-DYNA (https://lsdyna.ansys.com/ (accessed on 6 March 2025)). However, the above-mentioned Finite Element Methods (FEMs) have been proven to be more applicable for simulating the mechanical behavior of solid material due to the native defect of continuum mechanical theory. Especially for dealing with granular matter, some problems stand out, such as modeling the fracture and examining the particle breakage. Thus, some meshless methods have been put forward. For example, Prabhu et al. [29] and Xu et al. [30] studied the breakage of cohesionless soil particles using the 3D discrete element method. Baranowski et al. [31] simulated the interaction between the copper shaper and SHPB bar using the smoothed particle hydrodynamics method. By combining the benefits of Lagrangian and Eulerian descriptions, the Material Point Method (MPM) was recently employed to solve a problem involving extensive deformation and dynamics. Maassen et al. [32] successfully reported the performance of MPM on the steel SHPB test and verified its efficiency. However, there have been no reports on MPM simulations for the dynamic behavior of unsaturated clay under impact loading due to lack of experimental research and effective dynamic constitutive models.
In this paper, the objective of this paper is to clarify some of the previously outlined controversial issues on unsaturated clay through SHPB experiment and MPM simulation. Firstly, the SHPB test on unsaturated clay is elaborately designed to ensure the validity of testing data. The dynamic stress–strain response of unsaturated clay is systematically examined and the Cowper Symonds (CS) model is adopted to represent the strain rate dependency behavior. Accordingly, a modified elastic–plastic constitutive model combining the Van Genuchten (VG) retention curve and the Drucker–Prager (DP) yield function considering strain rate effect is proposed and employed to interpret the dynamic behavior of unsaturated clay. Lastly, the above SHPB test is reproduced and numerically simulated by MPM, and the simulated and testing results are compared to verify the accuracy of the improved MPM computation program.
2. SHPB Test on Unsaturated Clay
2.1. Specimen Preparation
In this study, the clay samples were collected from Guizhou Province, located in the southwest of China, using a borehole sampling method. After determining the basic physical parameters, the undisturbed soil was dried, crushed, and screened to prepare two sizes of cylindrical remolded specimens with a target water content of 40%. One set of specimens, measuring 39.1 mm in diameter and 80 mm in height, was used for triaxial shear tests to determine the static mechanical parameters. Table 1 presents the obtained physical and mechanical parameters of soil samples. Another set of cylindrical specimens, measuring 50 mm in diameter and 20 mm in thickness, was prepared for the SHPB test, following the method described by Song et al. [20].

Table 1.
Properties of clay sample.
2.2. SHPB Setup and Testing Method
The dynamic impact experiment on unsaturated clay employed the SHPB apparatus, namely ALT1000. Figure 1 shows the photograph and schematic diagram of the SHPB setup. The incident and transmitted bars are made of aluminum, each measuring 2500 mm in length and 50 mm in diameter. The gas pressures (0.05~0.25 MPa) can be adjusted using an air compressor and pneumatic value, thereby controlling the striking velocity of the bullet (400 mm in length) and achieving various loading rate conditions. Moreover, a cylindrical tube made of 4030 steel was used to apply passive confinement on the soil specimen. The inner and outer diameters of the cylindrical tube are 50.1 mm and 55.1 mm, respectively. The modulus and Poisson’s ratio of the steel are 195 GPa and 0.28, respectively. A rubber disk with a thickness of 2.0 mm and a diameter of 45 mm was employed as a pulse shaper to mitigate high-frequency oscillations and dispersion effects. To reduce friction effects, a thin layer of petroleum jelly was applied between the soil specimen and the inner wall of the steel tube.
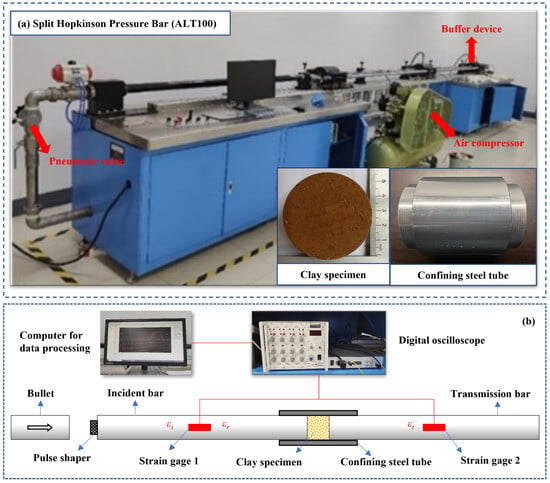
Figure 1.
Split Hopkinson Pressure Bar equipment: (a) photograph and (b) schematic diagram.
As illustrated in Figure 1b, strain gauge 1 was positioned at the center of the incident bar to record dynamic signals, including the incident stress wave propagating from left to right and the reflected stress wave propagating from right to left along the incident bar. Additionally, strain gauge 2 was positioned to record the transmitted stress wave propagating from left to right along the transmission bar. According to the computing theory of a one-dimensional stress wave, the stresses at the front and back ends of the specimen are considered to be equal, as defined in Equation (1). Equation (2) is used for calculating the strain rate, with the corresponding strain obtained through integration.
where denotes the calculated stress of the specimen at the front-end surface (i.e., the contact surface of the incident bar and the soil); denotes the calculated stress of the specimen at the back-end surface (i.e., the contact surface of the transmission bar and the soil); , , and denote the incident, reflected, and transmitted signals, respectively; E denotes the elastic modulus of the bar; A and denote the cross-sectional areas of the bar and specimen, respectively; denotes the specimen thickness; and v denotes the elastic wave velocity of the bar.
2.3. Data Processing and Validity Verification
Figure 2a presents the original waveforms recorded during the SHPB test. By employing the pulse shaping technique, the rise time of the incident wave increased up to approximately 50 μs, while the constant loading time extended to approximately 200 μs. This condition facilitates the achievement of stress equilibrium in the specimen. Table 2 outlines the calculation parameters for data processing. Parameters k and U were used for transforming the voltage signal recorded using a digital oscilloscope (sampling frequency of 1024 kHz) into strain. Subsequently, the “2-wave” and “1-wave” methods were adopted to calculate the front- and back-end stresses of the specimen by substituting E, C, , and into Equation (1), thereby further validating the dynamic stress equilibrium. Figure 2b shows the calculated stress histories at the front and back ends of the specimen. It can be seen that the front-end stress, calculated by superposing the incident and reflected pulses, closely matches the back-end stress calculated with the transmission pulse, indicating the realization of dynamic stress equilibrium.
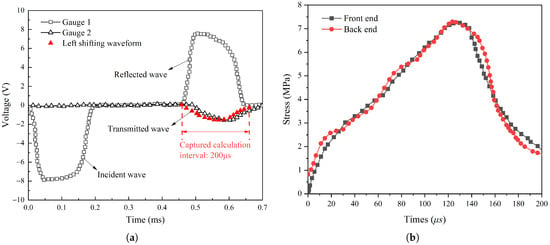
Figure 2.
Data processing: (a) original waveforms and (b) dynamic stress equilibrium.

Table 2.
Calculation parameters used for data processing.
2.4. Results and Discussion
Figure 3 shows the stress–strain curves of unsaturated clay at strain rates ranging from 204 s−1 to 590 s−1. Since soil is a non-homogeneous material and the applied gas pressure cannot be precisely controlled by the air compressor and pneumatic value, impact tests at each gas pressure were repeated at least 3 times for self-calibration. Error bars were added in Figure 3 to indicate the data scatter extent for repeated tests. Although there is some discrepancy for repeated tests, the stress–strain curves obtained at the same gas pressure exhibit good consistency. According to Figure 3, the dynamic stress–strain curve of unsaturated clay under passive confinement demonstrates three distinct stages:
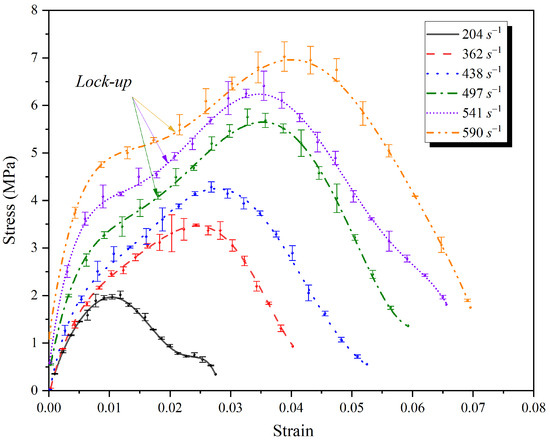
Figure 3.
Dynamic stress–strain curves of unsaturated clay with strain rates from 204 s−1 to 590 s−1.
- Elastic compression: The stress increases linearly with strain in this stage. Under high loading rate conditions, the closure speed of cracks or pores inside the soil becomes rapid. Consequently, unsaturated clay typically reaches its yield limit at a tiny strain.
- Plastic flow: Following elastic compression, a distinct plastic flow stage occurs, during which the breakage and rearrangement of soil gains may take place. Since soil particles move into a dense arrangement, the relative motion between particles becomes increasingly difficult. Due to the rising strain rate and passive confinement, the soil sample experiences a high-stress condition, causing soil particles to break and the soil skeleton to contract more tightly, thereby enhancing compression resistance. Eventually, an even denser state of particles or aggregates forms, shifting the response of the soil sample to a lock-up behavior [20,21]. As can been seen from Figure 3, at a strain rate of approximately 500 s−1, a lock-up behavior can be observed in this stage.
- Failure: A significant downward trend in the stress–strain curve is observed after the stress reaches its peak value. As plastic strain increases, soil fracture or damage occurs, eventually leading to a fully damaged state.
Considering whether a lock-up behavior can be observed during the plastic flow stage, the stress–strain curves of unsaturated soil under high loading rate condition were classified into two types: (a) Type-I, composed of elastic compression, yielding of the soil skeleton, and failure stages; (b) Type-II, composed of elastic compression, yielding of the soil skeleton, lock-up, hardening, and failure stages. As the strain rate increases, the energy of soil particles or aggregates under passive confinement increases with the axial pressure, promoting the breakage and arrangement of particles or aggregates. When the pores inside the soil are fully occupied by finer particles or water, a lock-up behavior emerges, indicating that the soil sample transforms from an unsaturated state to a saturated state. Based on the above analysis, the lock-up behavior depends on the applied and confining pressures, breakage and arrangement of soil particles or aggregates, and closure of pores. Notably, these factors are all related to the strain rate. Therefore, the evolution of the lock-up was observed to be a function of strain rate, as illustrated in Figure 3.
Moreover, Figure 3 shows that the dynamic response parameters, including the slope of the curve in the elastic stage, yield limit, peak stress, and maximum strain, increase with strain rate, indicating a significant strain rate effect for unsaturated clay under SHPB impact loading. The CS model, as shown in Equation (3), was generally used to characterize strain rate dependency behavior of material [33,34]. Because the determination of CS coefficients requires curve fitting, a rearranged form of Equation (3) is expressed as Equation (4).
where and are the static and dynamic strength values, respectively; C and P are the intercept and slope of the fitting curve in a double logarithmic scale of the and the strain rate space, respectively.
Figure 4a shows the calibrated CS coefficients of various geomaterials [25,33,35,36,37]. The results indicate that the CS model is appropriate for representing strain rate dependency behavior of various materials with a large range of strain rate. Figure 4b shows that when the strain rate of unsaturated clay in the SHPB test is in the range of 204~590 s−1, the CS model agrees well with the measured data. In this case, the intercept C of 56 and slope P of 0.8 are determined in the CS formula of dynamic peak stress.
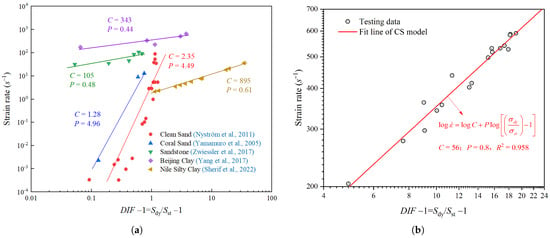
Figure 4.
CS model parameters for (a) geomaterials in the existing literature [25,33,35,36,37], and (b) unsaturated clay in this paper.
3. MPM Simulation on SHPB Test of Unsaturated Clay
MPM has been proved to be an efficient method for solving the dynamic problem for geotechnical materials under extreme loading conditions [38,39,40]. There is no doubt that [41,42] impact problems involved in SHPB tests, where large deformations occur, represent a well-suited application for MPM. Hence, this paper presents a modified MPM implementation for partially saturated granular media.
3.1. MPM Formulation for Unsaturated Soil
To balance computational cost and efficiency, the three-phase-one-point MPM formulation for unsaturated soil proposed by Yerro [43] was employed in this paper. Figure 5 shows the schematic diagram of MPM implementation for unsaturated soil. As shown in Figure 5, the unsaturated media are discretized by a certain number of material points (MPs), and each MP represents the mixture composed of solid, liquid, and gas phases. The detailed numerical procedure of the MPM algorithm at each time increment is summarized in Figure 6.
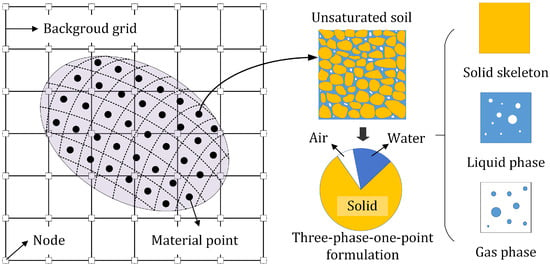
Figure 5.
Schematic diagram of MPM implementation for unsaturated soil.
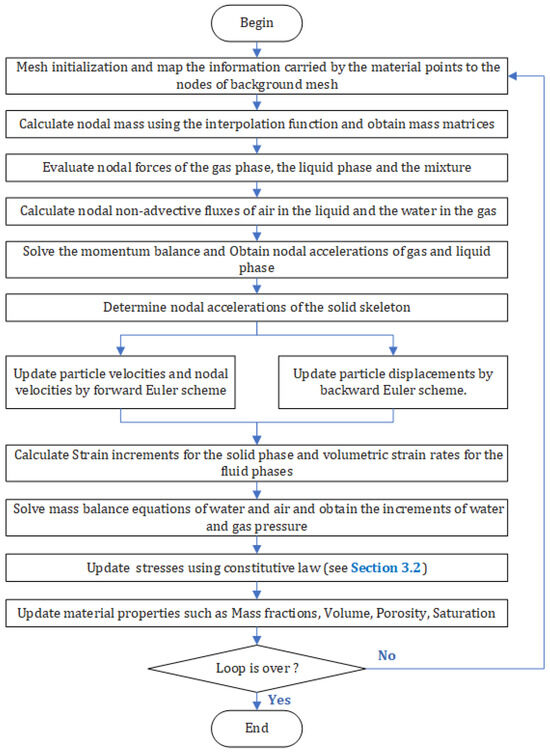
Figure 6.
Detailed numerical procedure at each time increment.
3.2. Constitutive Law for Unsaturated Clay
In this paper, the net stress and suction s are employed in constitutive modeling and interpreting unsaturated clay behavior, as defined in Equation (5). Subsequently, the calculation of stress increment must account for the coupling effect of the soil skeleton strain increment and suction change, as expressed in Equation (6).
where and are the net stress and total stress tensors, respectively; is the Kronecker delta; s is the suction; and are the water pressure and gas pressure; D is the tangent matrix; H is a constitutive vector controlling the influence of suction; is the soil skeleton strain increment vector; and is the suction increment vector.
3.2.1. Soil Water Retention Curve (SWRC)
To represent the hydraulic behavior of unsaturated soil, the well-known VG model [44] is adopted to predict the moisture–suction relationship. The expression of VG model is defined as Equation (7).
where , , , and are fitting parameters for lateritic clay, whose water retention behavior [45] is similar to the clay sample investigated in this paper (as shown in Figure 7).
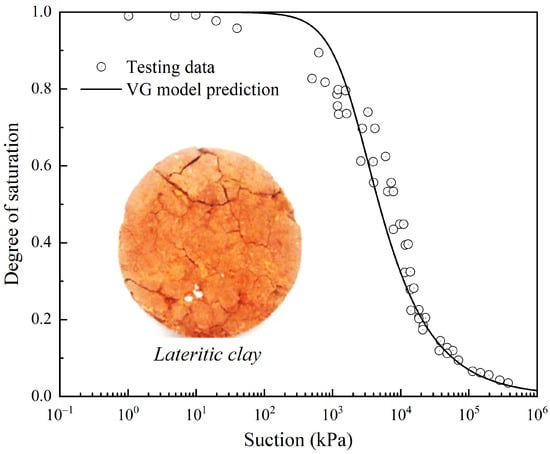
Figure 7.
SWRC of lateritic clay and prediction of VG model.
3.2.2. Mechanical Constitutive Model Considering Strain Rate Effect
On the basis of elastic–plastic theory, two types of strain increment were considered in the establishment of the mechanical constitutive model. The resumable elastic strain and its increment were represented by Hooke’s law. The unresumable plastic strain was described using a modified D-P yield function to define the direction and degree of plastic deformation, in which the strain rate enhancement effect was taken into account. As the yield surface expands or shrinks, its shape and size change accordingly. And this change contributes to the strain rate strengthening effect in the modified DP model. However, the central part for describing the rate-dependent behavior with the DP criterion is determining the appropriate hardening parameter from the view of material constitutive model. The specific expression of the modified DP model is given in Equation (8).
where is the first invariant of the stress tensor; is the second invariant of the stress deviation tensor; is a constant of the D-P function; denotes the hardening parameter; represents the dynamic strength increase factor, whose expression is shown in Equation (9).
where C and P are calibrated CS coefficients based on static shear test and dynamic SHPB test, as given in Figure 4.
Moreover, a damage parameter D, as defined in Equation (10), was introduced to account for the failure or fracture process. When the plastic strain reaches the value of (the strain corresponding to the peak of the stress–strain curve), , indicating that the soil begins to undergo damage. When the plastic strain reaches the value of (the maximum strain of the stress–strain curve), , indicating that the soil becomes fully damaged.
where D is the damage parameter; is the plastic strain; equals the strain corresponding to the peak of the stress–strain curve; equals the maximum strain of the stress–strain curve.
3.3. Numerical Model of SHPB Test
Figure 8 shows the model description of the SHPB test. The incident bar (defined as a rigid body) and the soil specimen (defined as a flexible body) are discretized by finite material points. The spacing distances between MPs for the bar and soil are set as 5 mm and 1mm, respectively. The background mesh size is set as 5 mm × 5 mm × 5 mm. The mass of the incident bar equals its actual mass in the SHPB test. The density, Young’s modulus, and Poisson’s ratio of the SHPB bar are 2750 kg/m3, 75 GPa, and 0.3, respectively. The material parameters for the unsaturated soil used in the MPM simulation are summarized in Table 3.
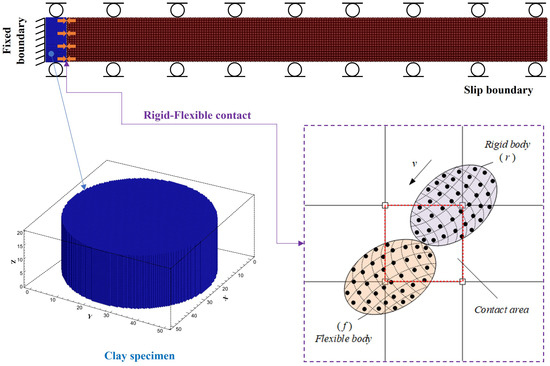
Figure 8.
Model description of SHPB test.

Table 3.
Material parameters of unsaturated clay used in simulation.
To simulate the loading condition in the SHPB test, the incident bar moves with a constant velocity to impact the soil specimen. By implementing the rigid–flexible contact algorithm proposed by Zhang et al. [46], the velocity of the rigid body can be automatically adjusted and the corresponding contact force can be updated, thereby achieving the nonlinear contact process. The initial velocity of the rigid boy was determined through trial calculation until the contact force matched the front force (or stress) of the specimen obtained in the SHPB test.
To replicate the stress state of the sample as accurately as possible, the front surface between the incident bar and the soil sample is set as a free boundary, while the end surface of the soil sample was set as a fixed boundary. Furthermore, a slip boundary is applied to the square background mesh tangent to the cylinder specimen.
3.4. Numerical Simulation Validation
Figure 9 shows the comparison of experimental and simulated stress–strain curves of unsaturated clay at different strain rates. As can be seen, the simulated stress–strain curve has a similar variation trend to the experimental results. Additionally, the testing and simulated dynamic peak stresses are almost the same. However, as the strain rate increases up to 541 and 590 s−1, there are some differences between the testing and simulated curves in the plastic flow and failure stages. For numerical simulation, the update of volumetric strain and stress follows the strict theoretical formula. But for the SHPB tests, the experimental results may be affected by various factors, such as microscopic pore characteristics and saturation conditions. Especially for high loading rate conditions, local saturation or stress concentration is likely to occur as the pore pressure develops rapidly and cannot dissipate in time [22]. These uncertainties may account for the observed differences between the experimental and simulated stress–strain curves. Anyhow, the comparison results demonstrate the potential of the modified MPM to effectively simulate the dynamic properties of unsaturated soil with a reasonable accuracy.
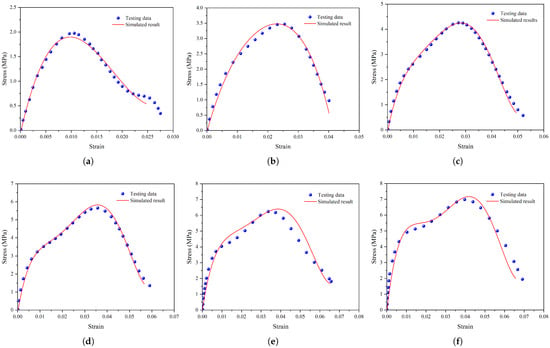
Figure 9.
Comparison of testing and simulated stress–strain curves at different strain rates: (a) 204 s−1, (b) 362 s−1, (c) 438 s−1, (d) 497 s−1, (e) 541 s−1, and (f) 590 s−1.
4. Conclusions
This study examined the dynamic stress–strain response of unsaturated clay with a saturation of 85% using a modified SHPB device. Based on the experimental results, the rate dependency of the dynamic strength of the specimen was evaluated for strain rates ranging from 204 s−1 to 590 s−1. Subsequently, a modified dynamic elastic–plastic model for unsaturated soil was proposed and embedded the MPM program to reproduce the SHPB test. The main conclusions are summarized as follows:
- Under passive confinement, the stress–strain curve of unsaturated clay experienced three typical stages, which are elastic compression, plastic flow and failure. As the strain rate increases up to approximately 500 s−1, much more soil particles or aggregates may break up at high stress state and the pores were occupied by finer gains and water. Eventually, an even denser arrangement of particles formed, leading to a lock-up behavior observed in the plastic flow stage.
- The dynamic response of unsaturated clay exhibited a significant strain rate effect. The strain rate dependency of dynamic strength can be quantitatively characterized using the CS model. When the strain rate was in the range of 204~590 s−1, the appropriate CS parameters were calibrated to be an intercept C of 55 and a slope P of 0.8 in the double logarithmic scale of dynamic increase factor and strain rate space.
- An improved dynamic constitutive model for unsaturated soil was proposed, incorporating a VG model to represent the hydraulic behavior and a modified D-P model considering strain rate effect to characterize the mechanical behavior. Additionally, a modified MPM program was employed to perform numerical simulations of the SHPB test. The simulated stress–strain curves basically agree with the experimental results, indicating the feasibility of the proposed dynamic constitutive model for unsaturated clay under impact loading.
Author Contributions
Conceptualization, Y.Y., F.Z., J.L. (Junjie Li) and J.L. (Jun Liu); Data curation, F.Z., Z.L., R.Z., L.L., Y.Z. and Z.X.; Formal analysis, F.Z., Z.L., Y.W., R.Z., L.L., Y.Z. and Z.X.; Investigation, F.Z., Z.L., Y.W., R.Z., L.L., Y.Z. and Z.X.; Methodology, Y.Y., F.Z., J.L. (Junjie Li) and J.L. (Jun Liu); Resources, Y.Y., F.Z., J.L. (Junjie Li) and J.L. (Jun Liu); Software, F.Z., Z.L. and Y.W.; Validation, F.Z., J.L. (Jun Liu) and Y.W.; Visualization, F.Z.; Writing—original draft, F.Z.; Writing—review and editing, F.Z. All authors have read and agreed to the published version of the manuscript.
Funding
The authors are grateful for the financial support provided by National Natural Science Foundation of China (No. 51874118; No. 52478525), Jiangsu Funding Program for Excellent Postdoctoral Talent (No. 2023ZB583), and State Key Laboratory of Precision Blasting and Hubei Key Laboratory of Blasting Engineering, Jianghan University (No. PBSKL2022A03; No. PBSKL2023B5).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Some or all data, models, or codes that support the findings of this study are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare no potential conflicts of interest concerning the research, authorship, and/or publication of this article.
References
- Gu, Q.; Lee, F.H. Ground response to dynamic compaction of dry sand. Geotechnique 2002, 52, 481–493. [Google Scholar] [CrossRef]
- Taylor, T.; Fragaszy, R.J.; Ho, C.L. Projectile Penetration in Granular Soils. J. Geotech. Eng. 1991, 117, 658–672. [Google Scholar] [CrossRef]
- Wang, Z.Q.; Lu, Y. Numerical analysis on dynamic deformation mechanism of soils under blast loading. Soil Dyn. Earthq. Eng. 2003, 23, 705–714. [Google Scholar] [CrossRef]
- Wang, Z.Q.; Lu, Y.; Hao, H.; Chong, K. A full coupled numerical analysis approach for buried structures subjected to subsurface blast. Comput. Struct. 2005, 83, 339–356. [Google Scholar] [CrossRef]
- Ji, S.Y.; Li, P.F.; Chen, X.D. Experiments on shock-absorbing capacity of granular matter under impact load. Acta Phys. Sin. 2012, 61, 184703. [Google Scholar]
- Shirinbayan, M.; Rizi, H.B.; Abbasnezhad, N.; Tcharkhtchi, A.; Fitoussi, J. Tension, compression, and shear behavior of advanced sheet molding compound (A-SMC): Multi-scale damage analysis and strain rate effect. Compos. Part B Eng. 2021, 225, 109287. [Google Scholar] [CrossRef]
- Lamri, A.; Shirinbayan, M.; Pereira, M.; Truffault, L.; Fitoussi, J.; Lamouri, S.; Bakir, F.; Tcharkhtchi, A. Effects of strain rate and temperature on the mechanical behavior of high-density polyethylene. J. Appl. Polym. Sci. 2020, 137, 48778. [Google Scholar] [CrossRef]
- Shirinbayan, M.; Fitoussi, J.; Kheradmand, F.; Montazeri, A.; Zuo, P.Y.; Tcharkhtchi, A. Coupling effect of strain rate and temperature on tensile damage mechanism of polyphenylene sulfide reinforced by glass fiber (PPS/GF30). J. Thermoplast. Compos. Mater. 2022, 35, 1994–2008. [Google Scholar] [CrossRef]
- Fitoussi, J.; Nikooharf, M.H.; Kallel, A.; Shirinbayan, M. Mechanical Properties and Damage Behavior of Polypropylene Composite (GF50-PP) Plate Fabricated by Thermocompression Process Under High Strain Rate Loading at Room and Cryogenic Temperatures. Appl. Compos. Mater. 2022, 29, 1959–1979. [Google Scholar] [CrossRef]
- Hopkinson, B. A Method of Measuring the Pressure Produced in the Detonation of High Explosives or by the Impact of Bullets. Proc. R. Soc. Lon. Ser. A 1914, 89, 411–413. [Google Scholar]
- Kolsky, H. An investigation of the mechanical properties of materials at very high rates of loading. Proc. Phys. Soc. Sect. B 1949, 62, 676–700. [Google Scholar] [CrossRef]
- Bragov, A.M.; Grushevsky, G.M.; Lomunov, A.K. Use of the Kolsky method for confined tests of soft soils. Exp. Mech. 1996, 36, 237–242. [Google Scholar] [CrossRef]
- Bazhenov, V.G.; Bragov, A.M.; Kotov, V.L.; Zefirov, S.V.; Kochetkov, A.V.; Krylov, S.V.; Lomunov, A.K. Analysis of the applicability of a modified Kol’skii’s method for dynamic tests of soils in a deformable casing. J. Appl. Mech. Tech. Phys. 2000, 41, 519–525. [Google Scholar] [CrossRef]
- Bragov, A.M.; Kotov, V.L.; Lomunov, A.K.; Sergeichev, I.V. Measurement of the Dynamic Characteristics of Soft Soils Using the Kolsky Method. J. Appl. Mech. Tech. Phys. 2004, 45, 580–585. [Google Scholar] [CrossRef]
- Frew, D.J.; Forrestal, M.J.; Chen, W. Pulse shaping techniques for testing elastic-plastic materials with a split Hopkinson pressure bar. Exp. Mech. 2005, 45, 186–195. [Google Scholar] [CrossRef]
- Chen, W.; Lu, F.; Zhou, B. A quartz-crystal-embedded split Hopkinson pressure bar for soft materials. Exp. Mech. 2000, 40, 1–6. [Google Scholar] [CrossRef]
- Chen, W.; Lu, F.; Frew, D.J.; Forrestal, M.J. Dynamic Compression Testing of Soft Materials. J. Appl. Mech. 2002, 69, 214–223. [Google Scholar] [CrossRef]
- Charlie, W.A.; Ross, C.A.; Pierce, S.J. Split-Hopkinson Pressure Bar Testing of Unsaturated Sand. Geotech. Test. J. 1990, 13, 291–300. [Google Scholar] [CrossRef]
- Semblat, J.F.; Luong, M.P.; Gary, G. 3D-Hopkinson bar: New experiments for dynamic testing on soils. Soils Found. 1999, 39, 1–10. [Google Scholar] [CrossRef]
- Song, B.; Chen, W.; Luk, V. Impact compressive response of dry sand. Mech. Mater. 2009, 41, 777–785. [Google Scholar] [CrossRef]
- Luo, H.; Lu, H.; Cooper, W.L.; Komanduri, R. Effect of Mass Density on the Compressive Behavior of Dry Sand Under Confinement at High Strain Rates. Exp. Mech. 2011, 51, 1499–1510. [Google Scholar] [CrossRef]
- Martin, B.E.; Chen, W.; Song, B. Moisture effects on the high strain-rate behavior of sand. Mech. Mater. 2009, 41, 786–798. [Google Scholar] [CrossRef]
- Bragov, A.M.; Lomunov, A.K.; Sergeichev, I.V.; Tsembelis, K.; Proud, W.G. Determination of physicomechanical properties of soft soils from medium to high strain rates. Int. J. Impact Eng. 2008, 25, 967–976. [Google Scholar] [CrossRef]
- Liu, J.X.; Chen, Z.F.; Xu, W.F.; Chen, G. Experimental Study on Dynamic Mechanical Properties of Compacted Clay under Different Compaction Degrees and Water Contents. Rock Soil Mech. 2012, 33, 1631–1639. [Google Scholar]
- Yang, R.S.; Chen, J.; Yang, L.Y.; Fang, S.Z.; Liu, J. An experimental study of high strain-rate properties of clay under high consolidation stress. Soil Dyn. Earthq. Eng. 2017, 92, 46–51. [Google Scholar] [CrossRef]
- Hao, Y.; Hao, H.; Li, Z.X. Influence of end friction confinement on impact tests of concrete material at high strain rate. Int. J. Impact Eng. 2013, 60, 82–106. [Google Scholar] [CrossRef]
- Zhong, W.A.; Rusinek, A.; Jankowiak, T.; Abed, F.; Bernier, R.; Sutter, G. Influence of interfacial friction and specimen configuration in Split Hopkinson Pressure Bar system. Tribol. Int. 2015, 90, 1–14. [Google Scholar] [CrossRef]
- Kim, Y.B.; Kim, J. Influence of Specimen Thickness on the Acquisition of Al6061-T6 Material Properties Using SHPB and Verified by FEM. Materials 2021, 14, 205. [Google Scholar] [CrossRef]
- Prabhu, S.; Qiu, T. Simulation of Split Hopkinson Pressure Bar Tests on Sands Using the Discrete-Element Method. Int. J. Geomech. 2022, 22, 1–6. [Google Scholar] [CrossRef]
- Xu, D.S.; Zhang, Z.J.; Qin, Y.; Yang, Y. Effect of particle size on the failure behavior of cemented coral sand under impact loading. Soil Dyn. Earthq. Eng. 2021, 149, 106884. [Google Scholar] [CrossRef]
- Baranowski, P.; Janiszewski, J.; Malachowski, J. Study on computational methods applied to modelling of pulse shaper in split-Hopkinson bar. Arch. Mech. 2014, 66, 429–452. [Google Scholar]
- Maassen, S.F.; Niekamp, R.; Bergmann, J.A.; Pöhl, F.; Schröder, J.; Wiederkehr, P. Modeling of the Split-Hopkinson-Pressure-Bar experiment with the explicit material point method. Comput. Part. Mech. 2022, 9, 153–166. [Google Scholar] [CrossRef]
- Nyström, U.; Gylltoft, K. Comparative numerical studies of projectile impacts on plain and steel-fibre reinforced concrete. Int. J. Impact Eng. 2011, 38, 95–105. [Google Scholar] [CrossRef]
- Sliseris, J.; Korjakins, A. Numerical modeling of the casting process and impact loading of a steel-fiber-reinforced high-performance self-compacting concrete. Mech. Compos. Mater. 2019, 55, 29–40. [Google Scholar] [CrossRef]
- Yamamuro, J.A.; Abrantes, A.E. Behavior of Medium Sand Under Very High Strain Rates. In Proceedings of the 1st Japan-U.S. Workshop on Geomechanics: Testing, Modeling, and Simulation; 2025. Available online: https://ascelibrary.org/doi/abs/10.1061/40797(172)2 (accessed on 6 March 2025).
- Zwiessler, R.; Kenkmann, T.; Poelchau, M.H.; Nau, S.; Hess, S. On the use of a split Hopkinson pressure bar in structural geology: High strain rate deformation of Seeberger sandstone and Carrara marble under uniaxial compression. J. Struct. Geol. 2017, 97, 225–236. [Google Scholar] [CrossRef]
- Sherif, A.Y.A.; Ahmed, K.; Mostafa, S.; Mostafa, A. Testing and modeling clay behavior subjected to high strain rate loading in a tunneling problem. Ain Shams Eng. J. 2022, 13, 101764. [Google Scholar]
- Sulsky, D.; Chen, Z.; Schreyer, H.L. A particle method for history-dependent materials. Computer Methods Appl. Mech. Eng. 1994, 118, 179–196. [Google Scholar] [CrossRef]
- Bardenhagen, S.G.; Kober, E.M. The Generalized Interpolation Material Point Method. Comput. Model. Eng. Sci. 2004, 5, 477–496. [Google Scholar]
- Zhang, D.Z.; Ma, X.; Giguere, P.T. Material point method enhanced by modified gradient of shape function. J. Comput. Phys. 2011, 230, 6379–6398. [Google Scholar] [CrossRef]
- Lian, Y.P.; Zhang, X.; Liu, Y. An adaptive finite element material point method and its application in extreme deformation problems. Comput. Methods Appl. Mech. Eng. 2012, 241–244, 275–285. [Google Scholar] [CrossRef]
- He, L.; Gan, Y.; Chen, Z. Preliminary effort in developing the smoothed material point method for impact. Comput. Part. Mech. 2019, 6, 45–53. [Google Scholar] [CrossRef]
- Yerro, A.; Alonso, E.E.; Pinyol, N.M. The material point method for unsaturated soils. Geotechnique 2015, 65, 201–217. [Google Scholar] [CrossRef]
- Genuchten, V.M. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Sun, D.A.; You, G.; Zhou, A.N.; Sheng, D.C. Soil–water retention curves and microstructures of undisturbed and compacted Guilin lateritic clay. Bull. Eng. Geol. Environ. 2016, 75, 781–791. [Google Scholar] [CrossRef]
- Zhang, R.; Sun, Y.; Song, E. Simulation of dynamic compaction and analysis of its efficiency with the material point method. Comput. Geotech. 2019, 116, 103218.1–103218.19. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).