1. Introduction
LPG cylinders are increasingly being used in our daily lives, particularly in domestic heating [
1,
2], fuel storage for LPG vehicles [
3] and during welding work. These devices require special attention because they are located close to humans and any issues related to structural integrity can cause significant material and human damage. The design and development of these devices requires several levels of mechanical studies and physical tests (the burst pressure test, fatigue test, shock and impact test and leak test) to preserve their structural integrity and ensure their safety according to international approval standards (ISO 9162 [
4], UNECE R67, UNECE R115). In the literature, several works interested in the study of LPG cylinders in the field of mechanics [
5,
6,
7] and the field of CFD [
8] and also concerning the process and method of mechanical manufacturing [
9] can be found. As an example, the authors of [
10] investigated the mechanical and microstructural properties of liquefied petroleum gas (LPG) cylinders from local sources, assessing their compliance with ISO 4706 standards [
11]. Experimental tests were performed on three samples including tensile, bending, hardness, hydrostatic pressure, and microstructural analyses.
Finite element method(FEM) is an important step after mechanical design. It allows the mechanical structure to be verified and validated before starting the manufacturing process. The authors of [
12] presented a technical investigation into the design, stress analysis, and damage assessment of fiber-lined composite gas cylinders using Abaqus software 2020. Ardayfio et al. [
13] analyzed the mechanical and microstructural properties of welding regions of LPG cylinder materials from various local sources. Experimental and numerical analyses focus on tensile strength, hardness, burst pressure, fracture toughness, and microstructure. This study demonstrates the importance of the precise control of materials and manufacturing processes to ensure the durability and safety of LPG cylinders.
The modeling of curved structures still remains a pertinent research topic because the finite element method shows limitations in approximating curved structures by meshing. In the literature, several researchers [
14,
15,
16,
17] have demonstrated interest in the development of new numerical methods capable of approximating geometry exactly or with less approximation error, notably the IGA method, which is based on the Non-Uniformal Rational B-Splines function [
18,
19]. The IGA method with NURBS functions provides good results in geometric approximation and numerical analysis compared to the FEM [
20,
21].
In another sense, the integration of the T-Splines function has corrected some limitations of the NURBS function [
21,
22]; T-Splines mesh is flexible and uses fewer control points and therefore less computation time compared to the NURBS function. The literature shows that T-Splines functions are rarely used or used only in a few particular studies. As an example, Du et al. [
23,
24] present an isogeometric analysis in linear and nonlinear cases of thin-walled structures, applying Bézier extraction tools for the use of T-Splines and NURBS functions in finite element analysis. In this work, they support the Kirchhoff–Love and Reissner–Mindlin hypotheses for the analysis of plates and shells. Large deformations, including several models of hyperplastic materials, are also treated. This work introduces new perspectives in isogeometric analysis based on the new T-Splines function that comes with positive points, especially in localized mesh with fewer control points compared to NURBS, which will reduce the computation time. El Fakkoussi et al. [
25] integrate and adapt the IGA approach with the T-Splines function for research on the mechanical analysis of a 3D pipe with a preformed hole issue under compression loading with linear elasticity behavior for untrimmed surfaces to study structural engineering issues. Zhang et al. [
26] have introduced a novel T-Splines-oriented Isogeometric topology optimization (T-ITO) method to resolve the challenges of designing shell and plate structures with arbitrary geometries. Traditional NURBS-based approaches face limitations in handling complex structures due to their tensor product nature. This research study establishes the T-ITO method as a superior approach for optimizing the topology of shell and plate structures with complex geometries in technical applications.
According to the literature review, it appears that the study of LPG cylinders by the IGA approach using the T-Splines function has not been carried out yet. In this work, we will integrate and adapt IGA with the T-Splines function for geometry modeling and numerical analysis in the linear elasticity case to study the LPG cylinder under static loading conditions. This work will make a significant contribution and enrich current research on the understanding of IGA with T-Splines, implemented for the numerical modeling of curved structures and also to evaluate the mechanical structure efficiency of LPG cylinders in comparison with other numerical methods like the FEM and IGA NURBS.
This works is structured into three sections. The primary section focuses on the mathematical background, including the T-Splines function basis, the Bézier extraction of the T-Splines function. The following section explains the steps to prepare, draw and extract geometry via the Rhino V5 and T-Splines plugin for finite element analysis. Additionally, we model an LPG cylinder subjected to a static load applying the FEM in Abaqus/Standard, and the IGA with the T-Splines method is implemented in the Matlab 2021 software. In the last section, the focus will be on the displacement and stress numerical results of a liquefied petroleum gas (LPG) cylinder subjected to a static mechanics loading issue. The numerical results obtained are examined and verified with the FEM in Abaqus/Standard.
2. Materials and Methods
In this section, we present in detail the various mathematical equations and models employed in the modeling and analysis of the mechanical performance of lithium iron phosphate (LPG) cylindrical structures. The focus will be on the application of the IGA method with T-Splines functions. A detailed formulation of the governing equations, boundary conditions, and numerical implementation will also be thoroughly discussed to highlight the effectiveness and advantages of the IGA method in this context.
2.1. T-Splines
T-Splines have been introduced as a strong candidate to replace NURBS in isogeometric analysis (IGA) with applications on curved structures [
25]. T-Splines illustrate the ability to represent complex geometries seamlessly; unlike NURBS, which enforces a rigid tensor product structure that can lead to fragmentation and discontinuities between patches, T-Splines allow for local refinement at T-junctions. This means it does not require many cross-nodal repeat patches to curve around the geometry neatly and properly without flowing over the edges of inserted shapes. Furthermore, T-Splines are used to reduce the required control points for a more efficient model and correspond to reduced degrees of freedom in analysis [
22]. These advantages allow T-Splines to be particularly good choices for the design of curved surfaces. They still preserve basic geometry while optimizing computational resources, comparing favorably with traditional NURBS-based approaches. In our previous work [
25], we clearly showed the advantage of T spline; notably, T-Splines offer several advantages over the traditional NURBS in isogeometric analysis. T-Splines also handle trimmed and untrimmed surfaces more effectively, making them particularly suitable for complex geometries. Additionally, their compatibility with Bézier extraction facilitates their integration with finite element analysis (FEA) software. Compared to NURBS-based IGA and the FEM, T-Splines improve computational efficiency while maintaining high accuracy in structural analysis, especially for mechanical structures with intricate surface details. The mathematical expression for T-Splines with the parametric coordinates
,
can be expressed as [
23]
where
is the T-Splines control point;
and
denote the rational blending function and weight of the
i-th control point;
is the B-Splines basis function defined on a topologically rectangular domain; and
n is the total number of control points.
B-Splines basis functions are constructed using the Cox–de Boor recursion formula:
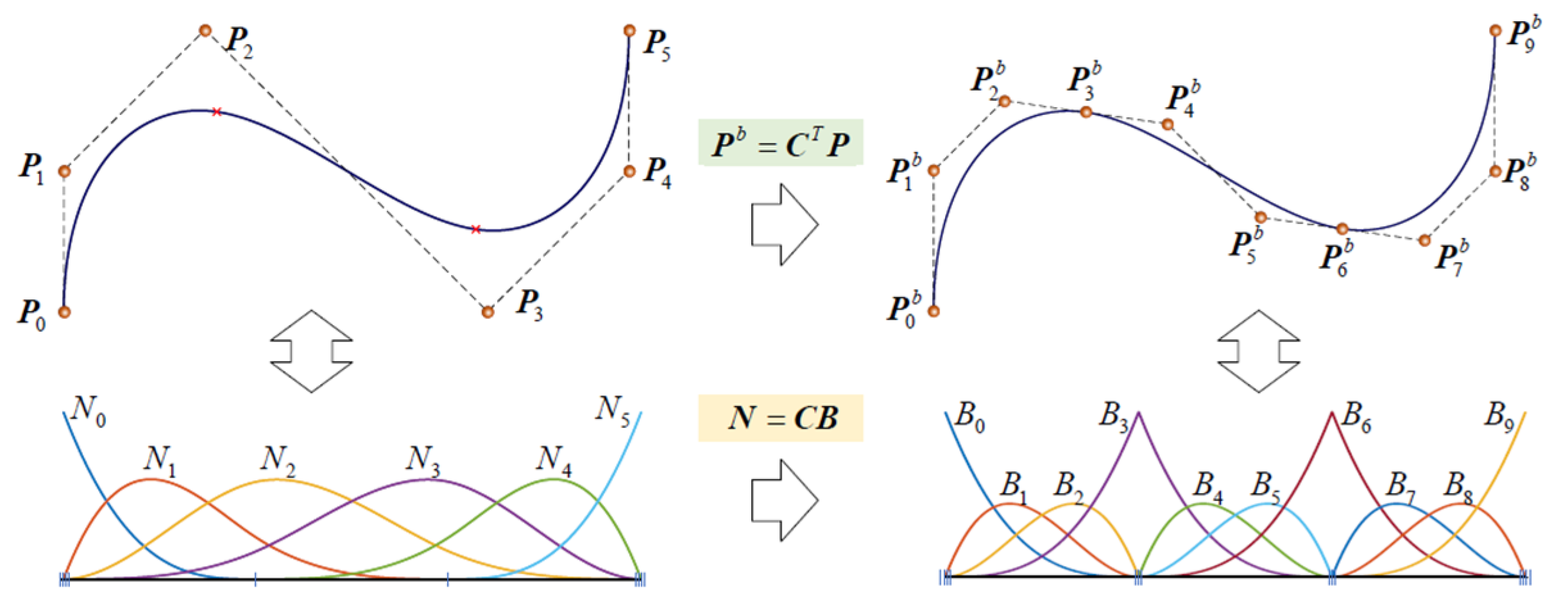
2.2. Bézier Extraction of T-Splines Functions
Similarly to the FEM, the Bézier extraction of T-Splines functions [
25] allows their basis functions to be represented as shown in
Figure 1. This process converts the T-Splines basis functions into a set of constant polynomial terms known as the Bernstein basis
, as shown in Equation (5). The Bézier elements can be processed in a similar manner to conventional finite element analysis, using existing data processing tables. In practice, only the shape function subroutine needs to be modified, while all other components of the finite element framework stay unchanged. A key outcome of the Bézier extraction process is the creation of an element extraction operator, which facilitates the transformation of T-Splines basis functions into local Bézier elements. This operator captures element-level topological information and global smoothing properties, enabling the efficient and canonical handling of T-junctions. T-junctions, often known as “hanging nodes” in finite element analysis, are a distinctive feature of T-Splines and are essential for their local refinement capability. By leveraging the extraction operator C, T-junctions are seamlessly integrated into the IGA framework, ensuring continuity and smoothness across elements while maintaining compatibility with standard finite element procedures. The Bézier extraction approach not only simplifies the integration of T-Splines into existing finite element workflows but also highlights their adaptability for modeling complex geometries and achieving higher computational efficiency.
where
is the B-Splines basis function;
is the Bezier extraction operator;
is the Bernstein basis function; and
is the point control of the B-Spline curve.
2.3. Reissner–Mindlin Shell Theorem
The most important difference between the Reissner–Mindlin shell theorem and the Kirchhoff–Love theory lies in how they account for transverse shear effects, which are crucial for accurately modeling thick shell structures. In our study, we focus on the Reissner–Mindlin shell theorem, which is widely used for shell structures where these shear effects and complex 3D geometries must be considered [
27]. This formulation is based on an exact median surface with precise normal vectors, enabling an accurate description of thick shells through a complex geometric approach.
In contrast, the Kirchhoff–Love shell theorem, which extends the Kirchhoff–Love model to thin shells, neglects transverse shear strain and is typically used for both linear and nonlinear analysis. It includes membrane strain and bending terms and utilizes covariant and contravariant tensors for nonlinear geometric analysis. The Kirchhoff–Love theorem is highly accurate for thin shells in both linear and nonlinear cases [
23]. While it provides a simplified approach suitable for thin structures, the Reissner–Mindlin theorem is more general and includes the transverse shear effects necessary for thick structures.
3. Computational Analysis and Modeling
This section describes the steps involved in preparing, drawing and extracting the geometry via the Rhino V5 and T-Splines plugin for finite element analysis. Additionally, modeling an LPG cylinder subjected to a static load applying the FEM in Abaqus/Standard, IGA with the T-Splines method is implemented in the Matlab software.
3.1. LPG Cylinder 3D Geometry and Material
The integration and modeling of geometry using NURBS or T-Splines functions in finite element analysis remains a major concern of researchers. In the literature, we did not find any tools to perform a complete IGA containing geometric preparation, NURBS or T-Splines mesh, boundary conditions and a solution of a matrix system of elastic linear equations.
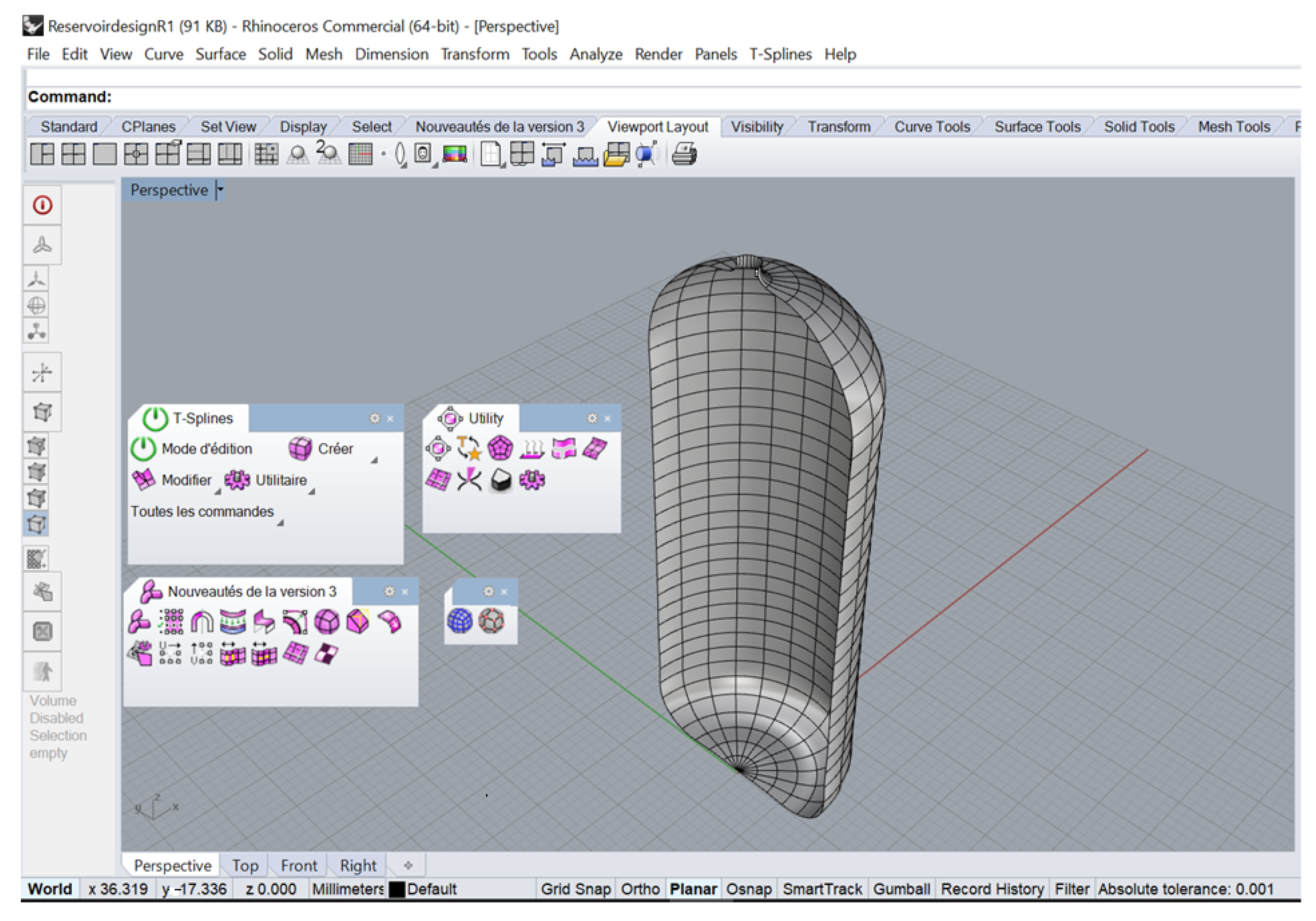
In this work, we use the T-Splines plugin [
28,
29,
30] integrated in Rhinoceros 3D V5 to realize our geometry (
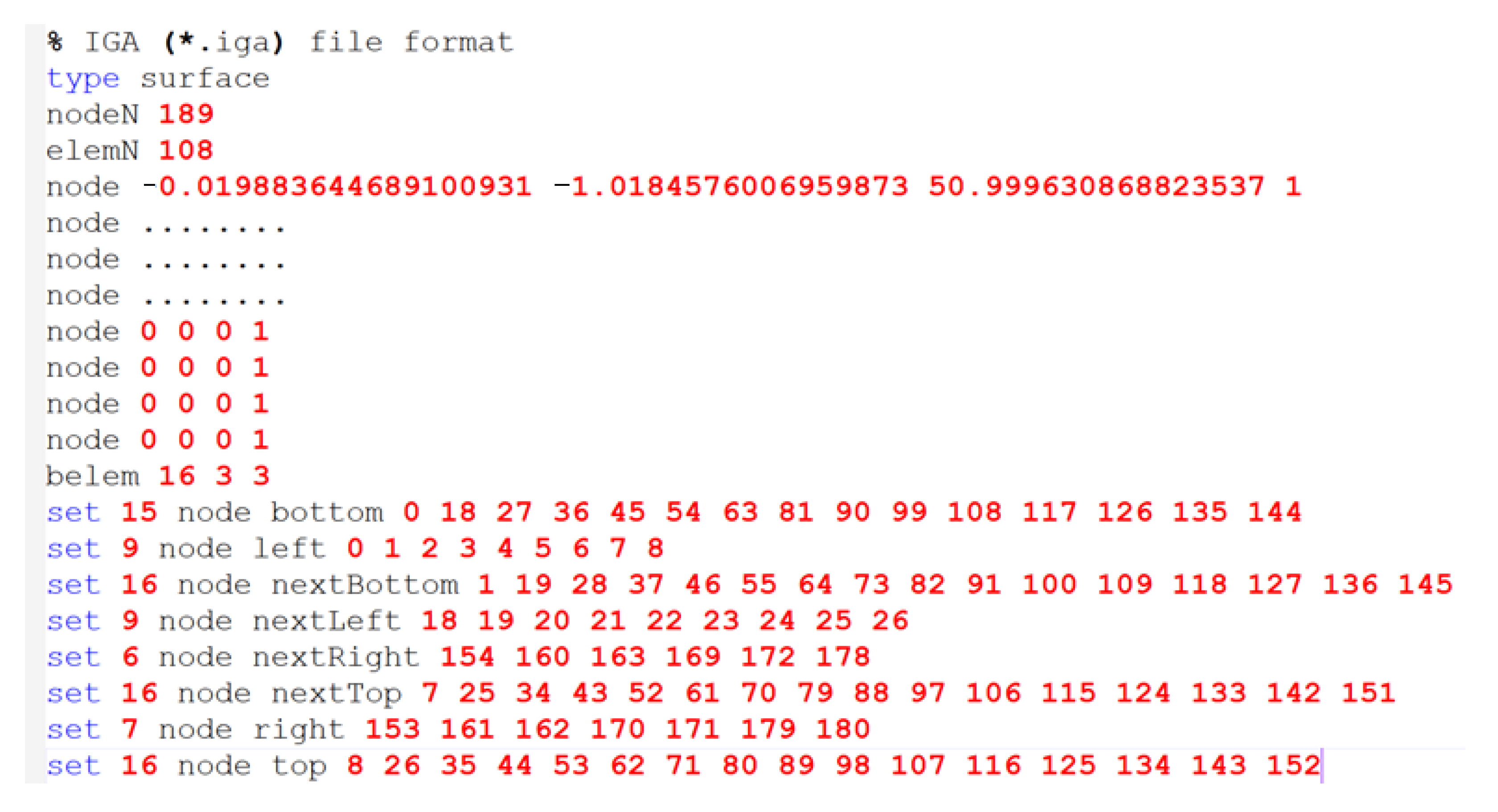
Figure 2). This part consists of three main steps: the creation of a CAD surface in Rhino V5 using the T-Splines plugin and the conversion of T-Splines surface representations into an IGA file (
Figure 3) using Bezier extraction, which contains all the necessary information used in the Matlab main code (
Figure 4), such as control points, element numbers, the degree of the T-Splines function, the T-Splines function basis and the boundary conditions of our problem, including the Dirichlet and Newman conditions.
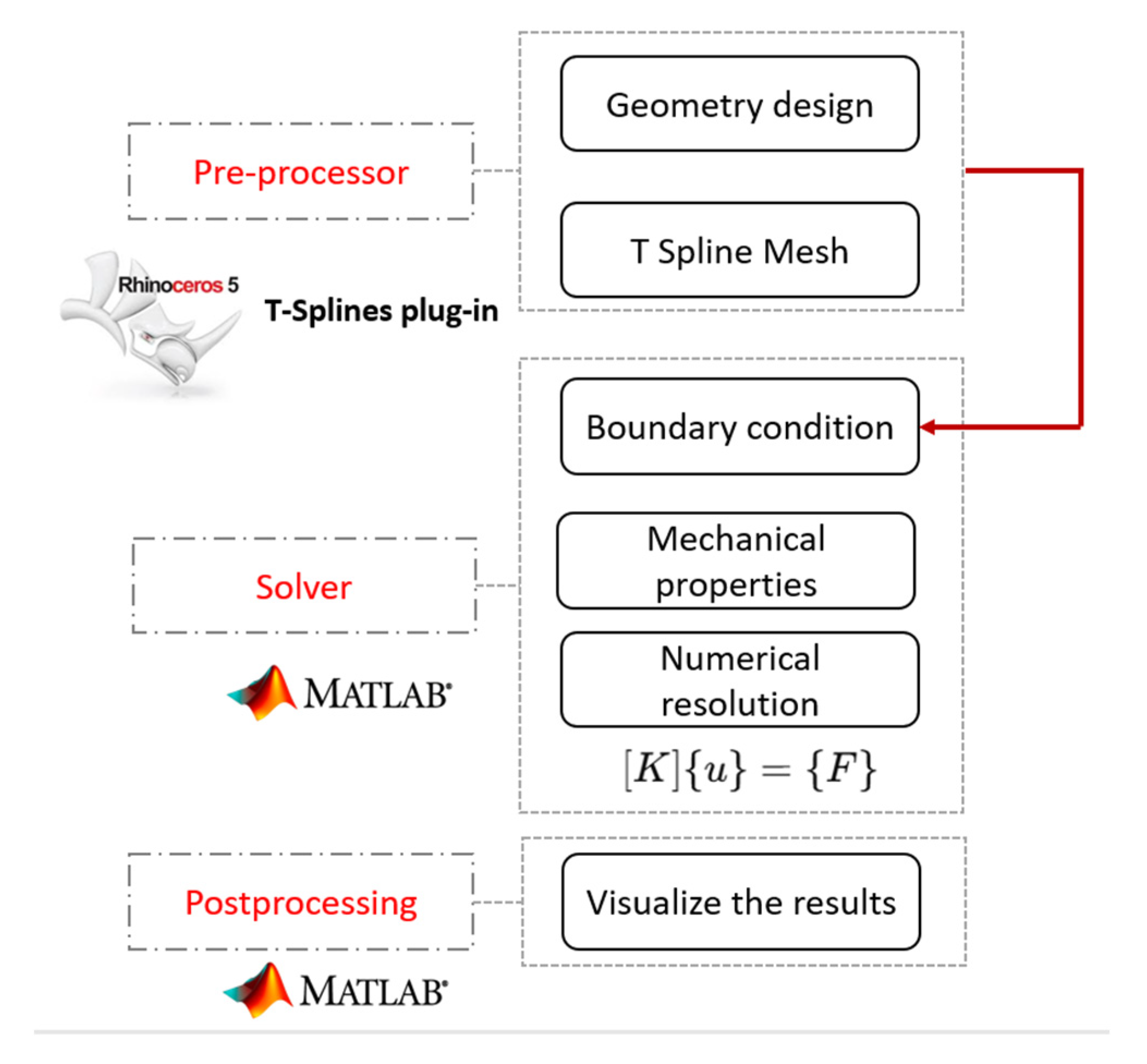
In the block diagram presented in
Figure 4, the following contributions were made:
Geometry design and T-Spline mesh: The geometry was created using the T-Splines plugin in Rhinoceros 3D V5. The mesh generation process was customized to ensure compatibility with the IGA approach, and additional scripts were developed to extract and organize the mesh data necessary for analysis.
Boundary conditions and mechanical properties: Custom MATLAB scripts were implemented to define the boundary conditions, including Dirichlet and Newman conditions, and to assign the mechanical properties of the aluminum 6061-T6 material.
Numerical resolution (Solver): The matrix system of elastic linear equations, [K]{u} = {F}, was formulated and solved using the MATLAB solver, specifically developed for the T-Splines IGA approach to study the mechanical performance of LPG cylinders.
Post-processing: The results were visualized using MATLAB, where custom plotting routines were developed to display the deformation and stress distributions. These visualizations provided a detailed analysis of the mechanical behavior of the LPG cylinder, helping to identify areas of stress concentration and regions that may be prone to failure under loading conditions.
The materials used to manufacture LPG cylinders include carbon steel alloys [
31] (
Figure 5), which are the most commonly used due to their low cost, high tensile strength and good formability, making them ideal for safely withstanding high internal pressures. We also find that the aluminum alloys [
32] (
Figure 5) are less common and are favored for lightweight applications where portability is required, offering good corrosion resistance but lower fatigue strength than steel. Finally, we found that glass fiber-reinforced polymer composites [
33,
34,
35] (
Figure 5) are mainly used for lightweight and corrosion-resistant LPG cylinders and are often favored in specialized or mobile applications due to their high pressure resistance and impact tolerance (
Figure 6).
To investigate the LPG cylinder, the aluminum alloy 6061-T6 (
Table 1) [
12] was utilized. It was used as an isotropic elastic–plastic material, and
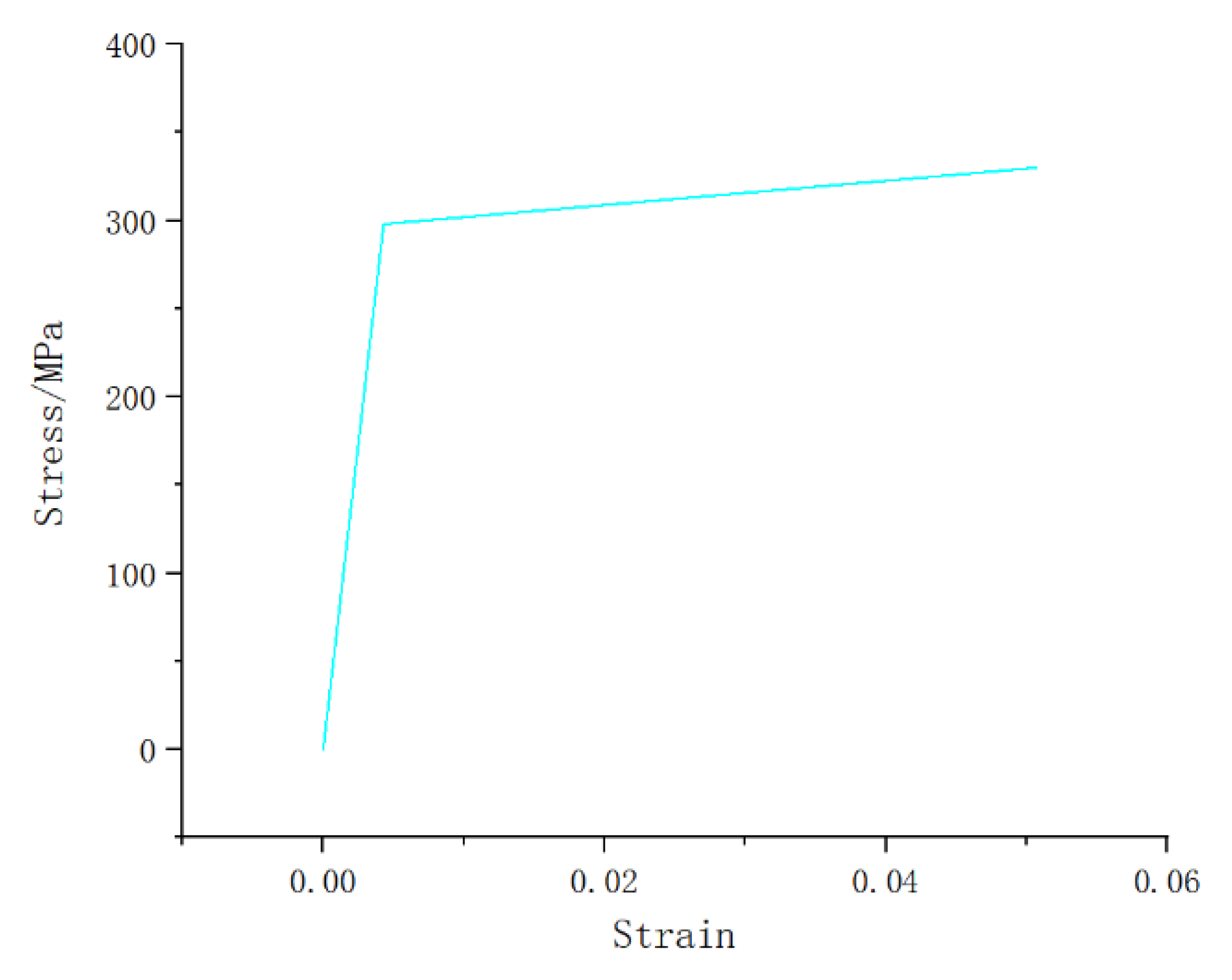
Figure 7 illustrates how a bilinear material model represents the plasticity behavior.
3.2. Meshing, Boundary Condition and Loading
For a good robust numerical convergence of the FEM analysis results in Abaqus/Standard and to promote useful comparisons with the IGA method with T-Splines results, we carried out a mesh refinement analysis for the various proposed mesh sizes. For an efficient processing time, the 1 mm mesh size was employed throughout the entire LPG cylinder, as shown in
Figure 8, for the following results in this present research.
In the present research, the aim is to employ IGA with the T-Splines method to evaluate industrial mechanical performance issues, in particular, to numerically study the storage capacity of liquefied gas (LPG) cylinders in the case of empty pressure, as well as to evaluate their mechanical performance. These studies are part of a global approach to optimizing storage space, considering geometric constraints, material properties, and safety requirements. This loading is modeled by an applied load (
F) (
Figure 9). The loading F of the empty weight of the LPG cylinder is given by
where m is the mass of the empty LPG cylinder; in our case, we take the mass 15 kg for an LPG cylinder of 13 kg of gas (one LPG cylinder is modeled with a loading of 147 Newton) and g = 9.81 m/s
2 is the gravitational acceleration.
In consideration of geometry symmetry and for a good processing time ratio, it takes half an LPG cylinder to model the storage capacity in the case of empty pressure for the two numerical methods of investigation, the finite element method (FEM) according to Abaqus/Standard and the IGA method with T-Splines.
To obtain good numerical convergence of the FEM analysis results in Abaqus/Standard, we used a linear element shell of type S4R with reduced integration to model the LPG cylinder case (
Figure 8). The S4R element is efficient in terms of good computational time savings, is less prone to negative Jacobian errors than 3D solid elements and is simpler to mesh.
4. Numerical Results and Discussion
In this part, we present the numerical results of the implementation of IGA with T-Splines and its numerical advantages to study mechanical structure issues. The LPG cylinder is subjected to a static load benchmark to check the integration and the adaptation of the IGA with T-Splines and to investigate the numerical convergence and robustness of the mechanical performance of the LPG cylinder in the case of energy storage issues. The T-Splines numerical results obtained are examined and verified with the FEM in Abaqus/Standard.
Firstly, a comparative study of computational time between the various numerical methods utilized in this study was carried out. The obtained results demonstrate that the processing time (
Table 2) of IGA with T-Splines is less than that of FEM in Abaqus/Standard. This affirms the results in studies by Du et al. [
23] and El Fakkoussi et al. [
25]. The reduced computation time of the IGA compared to the NURBS method and FEM is determined, and the T-Splines method uses less control points. And the benefits of polygonal and NURBS modeling approaches are combined in T-Splines, as well as the better numerical convergence of the results.
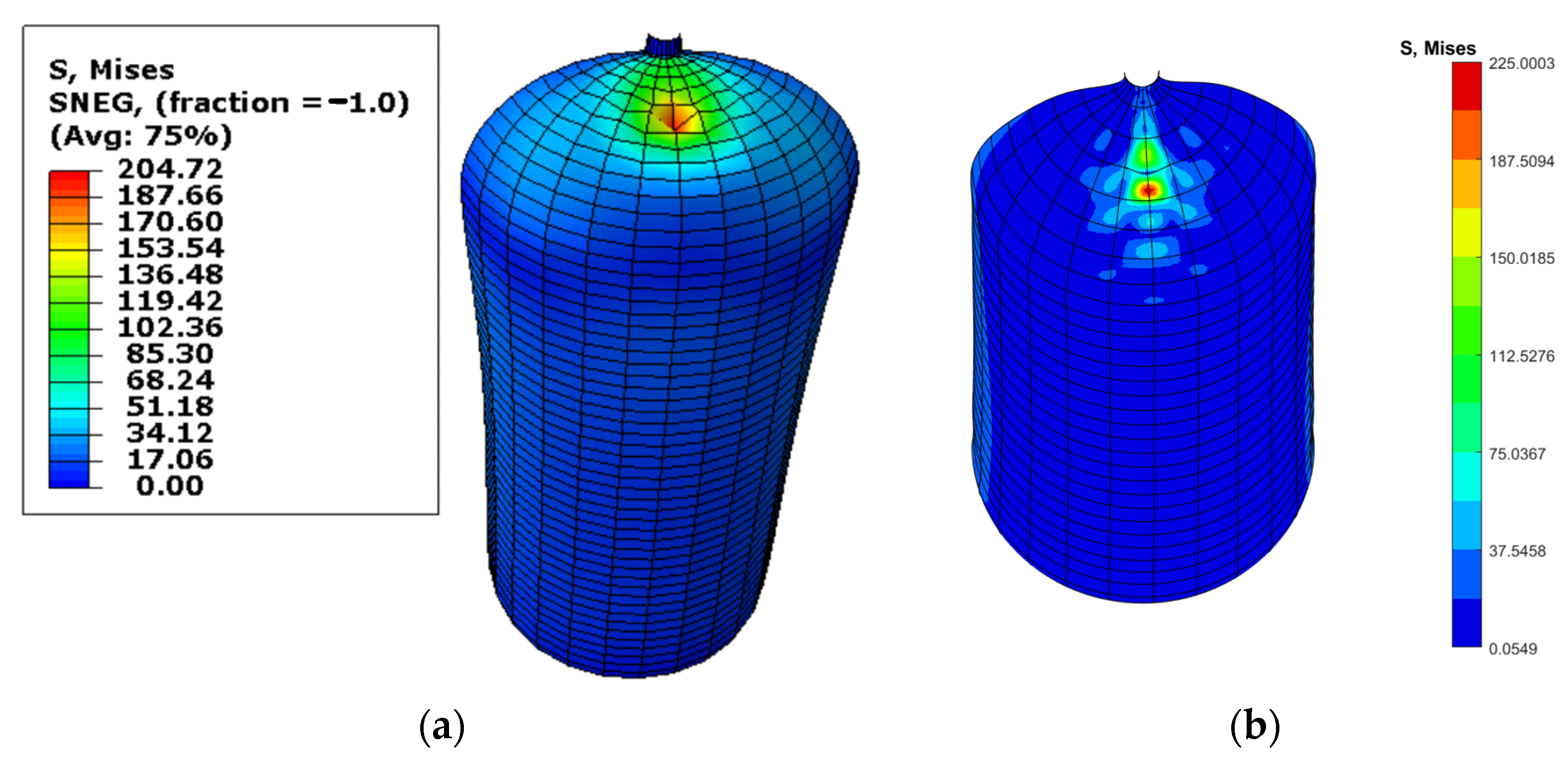
A displacement comparison was made for an LPG cylinder subjected to the force of an empty LPG cylinder during storage application, computed using the finite Element method (FEM) in Abaqus/Standard and the isogeometric analysis (IGA) T-Splines approach. As shown in
Figure 10, the displacement distribution differs between the two methods, with the T-Splines approach yielding smoother results with fewer numerical artifacts.
The comparison in
Figure 11 confirms that the IGA T-Splines method provides slightly lower displacement values than the FEM while maintaining better numerical stability and accuracy.
This difference is due to the inherent properties of T-Splines, which allow for a more flexible and continuous representation of 3D surfaces without the need for mesh refinement, unlike the FEM, which relies on structured meshing that may introduce local discretization errors (
Figure 12). The T-Splines approach also enables local refinement without increasing the global computational cost, making it advantageous for complex geometries and large deformation problems. Similar conclusions were drawn by Du et al. [
22,
23,
24], reinforcing the idea that IGA-based T-Splines outperform the traditional FEM in terms of smoothness, accuracy, and computational efficiency.
The obtained numerical results demonstrate that the IGA with T-Splines provides enhanced accuracy, particularly in capturing localized stress concentrations. The maximum Von Mises stress obtained using T-Splines is 225 MPa, whereas the result for the Abaqus/Standard FEM is 204 MPa. This enhanced precision is attributed to the ability of T-Splines to introduce local control points, refining the solution in critical zones without requiring a global mesh refinement. This feature is particularly beneficial for structural analyses where stress concentration areas are crucial for design validation.
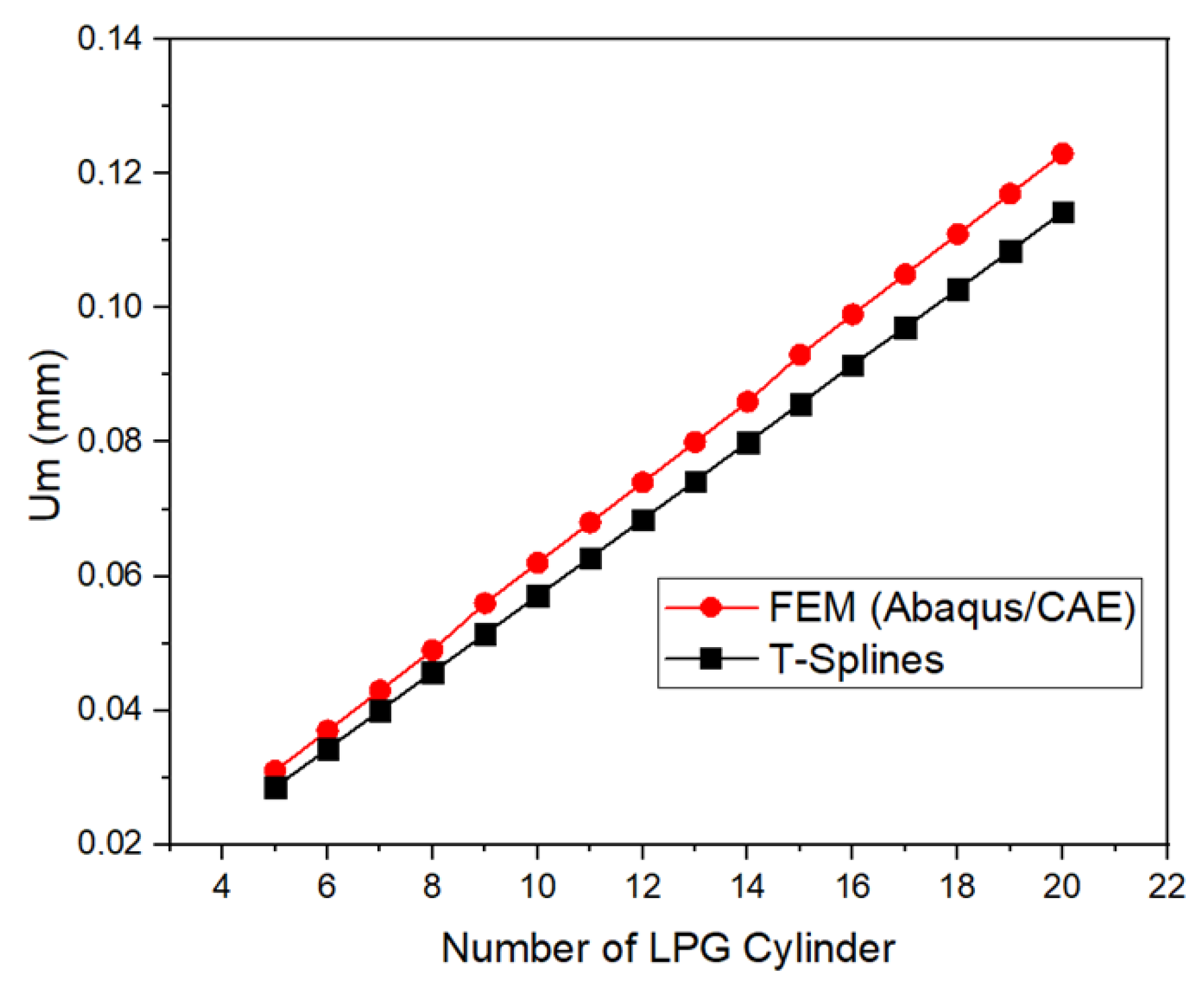
Furthermore, the structural integrity of the LPG cylinder is evaluated by varying the number of applied empty cylinders from 5 to 20.
Figure 13 shows the variation in numerical Von Mises stress results in the curve according to the number of loaded cylinders, highlighting a close correlation between the FEM and T-Splines results, with a minor but consistent difference. The curve shows that starting from the weight of 15 cylinders, the elastic limit of the aluminum alloy 6061-T6 (298 MPa) is reached. We conclude that the storage capacity of a single cylinder is equivalent to 15 empty cylinders.
Overall, the results demonstrate that the T-Splines approach provides superior numerical robustness, efficiently capturing stress variations in the loading application area while maintaining a stable and convergent solution. The method’s ability to refine specific regions without increasing computational costs makes it a powerful alternative to the conventional FEM for structural applications involving complex geometries and high stress gradients.
The results obtained demonstrated how IGA allows for rapid analyses, a very important advantage for real-time simulation. This fast processing ability is crucial in the context of digital twin, where instantaneous simulations are needed for evaluating and optimizing the performance of physical systems in real time. Furthermore, IGA offers increased accuracy in calculations, which is essential for the modeling of objects and processes in IOT simulation’s systems.
Even if this approach offers significant added values, it is very important to note that some challenges remain regarding the management of complex non-uniform geometries and computational costs for large-scale problems.
The treatment of singularities, especially in regions with high stress concentrations, is another area that requires further development. However, these challenges can be addressed through the use of extended versions of IGA (such as X-IGA), which provide greater flexibility in handling complex geometries and localized phenomena like crack growth. X-IGA, in particular, offers robust solutions for accurately capturing the initiation and propagation of cracks by using enriched basis functions that can handle singularities more effectively.
Based on all of these numerical results, confidence is held by applying the IGA with T-Splines method to numerically evaluate the mechanical performance of the LPG cylinder in energy storage applications.
5. Conclusions
The mechanical performance of an LPG cylinder for energy storage applications was successfully investigated under static loading within linear elastic, using isogeometric analysis (IGA) with the T-Splines function. The numerical results of the displacement and Von Mises stress were evaluated and verified with the FEM in Abaqus/standard. The processing time of the isogeometric analysis (IGA) with the T-Splines method is smaller in comparison to that of the FEM in Abaqus/Standard. This is confirmed by the numerical results in the studies by Du et al. and also by El Fakkoussi et al.
The Von Mises stress numerical results obtained using the T-Splines method show a close correlation with the FEM results, with a minor but consistent difference. The stress results indicate that once the weight of 15 cylinders is reached, the elastic limit of the aluminum alloy 6061-T6 (298 MPa) is exceeded. This suggests that the storage capacity of a single cylinder is equivalent to that of 15 empty cylinders.
The results demonstrate that the T-Splines approach provides superior numerical robustness, efficiently capturing stress variations in the loading application area while maintaining a stable and convergent solution. The method’s ability to refine specific regions without increasing computational costs makes it a powerful alternative to the conventional FEM for structural applications involving complex geometries and high stress gradients.
Future research could focus on further refining IGA and X-IGA techniques for crack growth simulations in multi-physics contexts, particularly in the analysis of fatigue, fracture mechanics, and failure prediction in real-world structures. Enhanced computational platforms and optimization algorithms will also be essential in making these methods more efficient and scalable, enabling their integration into real-time digital twin systems for predictive maintenance and structural health monitoring.
Another important future research direction involves a complementary investigation into LPG cylinders under internal pressure, focusing on the integration and development of isogeometric analysis with the T-Splines function. The goal is to evaluate the mechanical structure performance of LPG cylinders under internal pressure, addressing challenges in both linear elastic and plastic scenarios.
Author Contributions
Conceptualization, S.E.F., M.B.G., A.E. and M.L.S.; Methodology, M.B.G. and A.E.; Software, S.E.F., M.B.G. and A.E.; Validation, S.E.F., M.B.G., A.E. and S.V.; Formal analysis, S.E.F., M.B.G., A.E., S.V. and M.L.S.; Investigation, S.E.F., M.B.G. and A.E.; Resources, S.E.F., M.B.G. and A.E.; Data curation, S.E.F., M.B.G. and A.E.; Writing—original draft, S.E.F. and A.E.; Writing—review & editing, S.V. and M.L.S.; Visualization, S.V. and M.L.S.; Supervision, A.E., S.V. and M.L.S.; Project administration, A.E. and M.L.S.; Funding acquisition, S.V. and M.L.S. All authors have read and agreed to the published version of the manuscript.
Funding
The APC was founded by the Transilvania University of Brasov (HBS 3412/2020).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| IGA | Isogeometric analysis |
| NURBS | Non-Uniform Rational B-Splines |
| LPG | Liquefied Petroleum Gas |
| T-ITO | T-Splines-Oriented Isogeometric Topology Optimization |
| IOT | Isogeometric Optimization Technique |
References
- Barbosa, T.F.; Reis, L.; Raposo, J.; Viegas, D.X. A Protection for LPG Domestic Cylinders at Wildland-Urban Interface Fire. Fire 2022, 5, 63. [Google Scholar] [CrossRef]
- Balogun, D.; Shamim, S.; Sipai, U.; Kothari, N.; Trivedi, T.; Patel, V. LPG Smart Guard: An IoT-Based Solution for Real-Time Gas Cylinder Monitoring and Safety in Smart Homes. Eng. Proc. 2024, 82, 9. [Google Scholar] [CrossRef]
- Ajuka, L.O.; Kazeem, R.A.; Kuti, O.A.; Jen, T.C.; Afolalu, A.S.; Akinlabi, E.T. Decarbonized Automotive Fuel: Liquefied Petroleum Gas Biosynthesis, Benefits and Drawbacks. Results Eng. 2024, 21, 101889. [Google Scholar] [CrossRef]
- ISO 9162; Petroleum Products—Fuels (Class F)—Liquefied Petroleum Gases—Specifications. Available online: https://www.iso.org/standard/37164.html (accessed on 10 March 2025).
- Edward, A.B.; Okwu, M.O.; Oreko, B.U.; Ugorji, C.; Ezekiel, K.; Orikpete, O.F.; Maware, C.; Okonkwo, C.P. Development of a Smart Monitoring System for Advancing LPG Cylinder Safety and Efficiency in Sub-Saharan Africa. Procedia Comput. Sci. 2024, 232, 839–848. [Google Scholar] [CrossRef]
- Rondinella, A.; Capurso, G.; Zanocco, M.; Basso, F.; Calligaro, C.; Menotti, D.; Agnoletti, A.; Fedrizzi, L. Study of the Failure Mechanism of a High-Density Polyethylene Liner in a Type IV High-Pressure Storage Tank. Polymers 2024, 16, 779. [Google Scholar] [CrossRef]
- Kasim, M.S.; Yusof, S.N.A.; Mat Rasul, R.; Awang, R.; Abd Rahman, Z.; Mohamed, S.B.; Sahroni, T.R.; Patwari, M.A.U. Design and Optimization of LPG Safety Cap Using Finite Element Method. J. Adv. Res. Appl. Sci. Eng. Tech. 2024, 191–199. [Google Scholar] [CrossRef]
- Barbosa, T.F.; Viegas, D.X.; Modarres, M.; Almeida, M. Heat-Induced Increase in LPG Pressure: Experimental and CFD Prediction Study. Processes 2023, 11, 1930. [Google Scholar] [CrossRef]
- Wang, C.; Yu, H.; Tian, W.; Zhao, C.; Jiang, L.; Bai, Q. Research on the Integral Forming Process of Thin Walled and Thick Mouth Seamless Gas Cylinders. Sci. Rep. 2023, 13, 17021. [Google Scholar] [CrossRef]
- Fadel, A.H.; Abdullrhman, M.M.; Elsagisli, M.Y. Evaluation and Performance Analysis of Liquefied Petroleum Gas Cylinders. Iraqi J. Chem. Pet. Eng. 2024, 25, 37–47. [Google Scholar] [CrossRef]
- ISO 4706; Gas Cylinders—Refillable Welded Steel Cylinders—Test Pressure 60 Bar and Below. Available online: https://www.iso.org/standard/80380.html (accessed on 10 March 2025).
- Wu, X.; Yang, B.; Zhou, S. Strength and Failure Analysis of Fiber-Wound Composite Gas Cylinder via Numerical Simulation. Materials 2024, 17, 717. [Google Scholar] [CrossRef]
- Ardayfio, B.; Ampah-Essel, J.E.; Tetteh, W.; Tuah, J.A.; Agyei-Tuffour, B.; Annan, K.A.; Mensah, B.; Nyankson, E.; Dodoo-Arhin, D. Comparative Analyses of the Mechanical and Microstructural Properties of the Weld Region of LPG Cylinder Materials. Cogent Eng. 2023, 10, 2219096. [Google Scholar] [CrossRef]
- Farahat, A.; Verhelst, H.M.; Kiendl, J.; Kapl, M. Isogeometric Analysis for Multi-Patch Structured Kirchhoff–Love Shells. Comput. Methods Appl. Mech. Eng. 2023, 411, 116060. [Google Scholar] [CrossRef]
- Guo, M.; Wang, W.; Zhao, G.; Du, X.; Zhang, R.; Yang, J. T-Splines for Isogeometric Analysis of the Large Deformation of Elastoplastic Kirchhoff–Love Shells. Appl. Sci. 2023, 13, 1709. [Google Scholar] [CrossRef]
- El-Mekkaoui, J.; Elakkad, A.; Elkhalfi, A. Resolution of Stokes Equations with the Ca,b Boundary Condition Using Mixed Finite Element Method. WSEAS Trans. Math. 2013, 12, 586–597. [Google Scholar]
- Koubaiti, O.; El-mekkaoui, J.; Elkhalfi, A. Complete Study for Solving Navier-Lame´ Equation with New Boundary Condition Using Mini Element Method. Int. J. Mech. 2018, 12, 46–58. [Google Scholar]
- Bocko, J.; Pleško, P.; Delyová, I.; Sivák, P. Comparison of Structural Analysis of Thin-Walled Structures Accomplished by Isogeometric Analysis and the Finite Element Method. Materials 2022, 15, 6516. [Google Scholar] [CrossRef] [PubMed]
- Berrada Gouzi, M.; El Khalfi, A.; Vlase, S.; Scutaru, M.L. X-IGA Used for Orthotropic Material Crack Growth. Materials 2024, 17, 3830. [Google Scholar] [CrossRef]
- Hughes, T.J.R.; Cottrell, J.A.; Bazilevs, Y. Isogeometric Analysis: CAD, Finite Elements, NURBS, Exact Geometry and Mesh Refinement. Comput. Methods Appl. Mech. Eng. 2005, 194, 4135–4195. [Google Scholar] [CrossRef]
- El Fakkoussi, S.; Moustabchir, H.; Elkhalfi, A.; Pruncu, C.I. Application of the Extended Isogeometric Analysis (X-IGA) to Evaluate a Pipeline Structure Containing an External Crack. J. Eng. 2018, 2018, 4125765. [Google Scholar] [CrossRef]
- Du, X.; Lei, S.; Huang, Z.; Wang, W.; Zhao, G. Seamless Integration of Design and Analysis for Architected Shell Structures Using Unstructured T-Splines. Comput. Methods Appl. Mech. Eng. 2025, 435, 117619. [Google Scholar] [CrossRef]
- Du, X.; Zhao, G.; Zhang, R.; Wang, W.; Yang, J. Numerical Implementation for Isogeometric Analysis of Thin-Walled Structures Based on a Bézier Extraction Framework: NligaStruct. Thin-Walled Struct. 2022, 180, 109844. [Google Scholar] [CrossRef]
- Du, X.; Zhao, G.; Wang, W.; Guo, M.; Zhang, R.; Yang, J. NLIGA: A MATLAB Framework for Nonlinear Isogeometric Analysis. Comput. Aided Geom. Des. 2020, 80, 101869. [Google Scholar] [CrossRef]
- El Fakkoussi, S.; Koubaiti, O.; Elkhalfi, A.; Vlase, S.; Marin, M. Numerical Analysis of the Cylindrical Shell Pipe with Preformed Holes Subjected to a Compressive Load Using Non-Uniform Rational B-Splines and T-Splines for an Isogeometric Analysis Approach. Axioms 2024, 13, 529. [Google Scholar] [CrossRef]
- Zhang, X.; Xiao, M.; Gao, L.; Gao, J. A T-Splines-Oriented Isogeometric Topology Optimization for Plate and Shell Structures with Arbitrary Geometries Using Bézier Extraction. Comput. Methods Appl. Mech. Eng. 2024, 425, 116929. [Google Scholar] [CrossRef]
- Azizi, N.; Dornisch, W. A Spectral Finite Element Reissner–Mindlin Shell Formulation with NURBS-Based Geometry Definition. Comput. Mech. 2024, 74, 537–559. [Google Scholar] [CrossRef]
- Scott, M.A.; Hughes, T.J.R.; Sederberg, T.W.; Sederberg, M.T. An Integrated Approach to Engineering Design and Analysis Using the Autodesk T-Spline Plugin for Rhino3d; ICES REPORT 14-33; The Institute for Computational Engineering and Sciences, The University of Texas at Austin: Austin, TX, USA, 2014. [Google Scholar]
- Hsu, M.-C.; Wang, C.; Herrema, A.J.; Schillinger, D.; Ghoshal, A.; Bazilevs, Y. An Interactive Geometry Modeling and Parametric Design Platform for Isogeometric Analysis. Comput. Math. Appl. 2015, 70, 1481–1500. [Google Scholar] [CrossRef]
- Lai, Y.; Liu, L.; Zhang, Y.J.; Chen, J.; Fang, E.; Lua, J. Rhino 3D to Abaqus: A T-Spline Based Isogeometric Analysis Software Framework. In Advances in Computational Fluid-Structure Interaction and Flow Simulation; Bazilevs, Y., Takizawa, K., Eds.; Modeling and Simulation in Science, Engineering and Technology; Springer International Publishing: Cham, Switzerland, 2016; pp. 271–281. ISBN 978-3-319-40825-5. [Google Scholar]
- Tom, A.; Pius, G.M.; Joseph, G.; Jose, J.; Joseph, M.J. Design and Analysis of LPG Cylinder. Int. J. Eng. Appl. Sci. 2014, 6, 17. [Google Scholar] [CrossRef][Green Version]
- Meng, Z.; Jin, S.; Yu, M.; Mehari, A.; Jiang, L. Analysis of the Boss Structure of Type IV Composite Vessel for a High-Pressure Hydrogen Tube Trailer. Sustainability 2024, 16, 5098. [Google Scholar] [CrossRef]
- Panchagnula, K.K.; Panchagnula, J.S. Fabrication of Hoop-Wound Glass Fiber Reinforced Plastic Cylindrical Shells Using Filament Winding Machine. Mater. Today Proc. 2020, 27, 1315–1318. [Google Scholar] [CrossRef]
- Thanikachalam, J.; Vasiraja, N. Processing of Glass Fibre Reinforced Composite LPG Cylinder through Filament Winding Technique and Characterization. SAE Int. J. Adv. Curr. Prac. Mobil. 2020, 3, 851–855. [Google Scholar] [CrossRef]
- Bouhala, L.; Koutsawa, Y.; Karatrantos, A.; Bayreuther, C. Design of Type-IV Composite Pressure Vessel Based on Comparative Analysis of Numerical Methods for Modeling Type-III Vessels. J. Compos. Sci. 2024, 8, 40. [Google Scholar] [CrossRef]
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).