Abstract
Spatial big data about human mobility have been employed intensively in understanding human spatial activity patterns, which is a central topic in many applications. Available research on spatial clustering patterns of human activities has been investigated mainly based on similarities of locations and temporal attributes of spatial trajectories. These methods are not effective in revealing human groups who move among spaces at different locations but with the same functions. Function, as one semantic attribute of spaces, is a major driver of most human movements. This work investigates human clustering based on space functions of trajectory stay points in human mobility data using graph embedding. Firstly, typical functions of spaces are categorized into 35 types in our research area, which is a university campus. Human trajectories based on Wi-Fi networks were collected as test data. Then, human networks are built among human individuals. Each individual is taken as a node in the network, and an edge is built between two nodes if the corresponding individuals stay in spaces of the same type of function longer than a specific time duration. The graph embedding algorithm is used to calculate feature vector representations of nodes in the network, which can capture complex relationships among nodes through biased random walks. K-means clustering is applied to classify the feature vectors, which reveals potential behavioral pattern similarities of individuals concerning the functions of their staying spaces. The elbow method and silhouette score of clusters are used to determine an appropriate number of clusters. Three scenarios were designed based on three specific time durations, and random walk-biased parameters were fine-tuned to improve the clustering performance. Results reveal typical clusters and correlation between clusters and typical space functions.
1. Introduction
“Where people are” is one of the basic questions asked by researchers and practitioners in many applications, like urban planning, infrastructure management, and public health and safety [1,2,3]. With the emergence of location-aware technologies and the widespread availability of portable devices, big spatio-temporal data on human mobility, especially in urban areas, have been collected based using various instruments [4]. Data-driven approaches in mobility research have been intensively employed by academic communities, with expanding topics including moving-object data acquisition, trajectory data management and processing, trajectory analytics and clustering, and deep learning for trajectory computing [5,6]. Fundamental studies by González et al. (2008) using mobile phone data revealed universal patterns in human mobility [7], while Song et al. quantified the theoretical limits of mobility predictability through entropy analysis [8]. Researchers from many fields have been working to build an integrated science of movement and further a comprehensive understanding of human mobility and related spatial dynamics [9].
Human clustering techniques have been extended to various domains. In urban planning, clustering algorithms help in understanding pedestrian movement patterns to optimize city layouts and improve public safety [10]. Pentland’s social physics framework (2014) demonstrates how collective mobility patterns emerge from individual interactions [11], providing theoretical support for these applications. In marketing, the clustering of consumer behavior based on shopping patterns and visited locations enables businesses to target specific customer groups more effectively [12]. Recent work by Dong et al. (2016) on population-weighted network efficiency provides methodological references for analyzing commercial behavior patterns [13]. Furthermore, analyzing patient trajectories within hospital premises can enhance the management of healthcare services and improve patient care in healthcare [14]. Among trajectory data analysis and knowledge discovery methods, trajectory clustering can help to reveal underlying spatial patterns of individual and group movements across time and space, which can further be used to conduct human activity prediction and movement simulation [5,6,8,9]. In these scenarios, trajectories are taken as proxies for locations of human individuals. Spatio-temporal characteristics of one trajectory and similarities among trajectories are used to represent human behaviors and activities, as well as for human clustering and prediction, which further generate possibilities to reconstruct spatial dynamics of social communities [2,9,12].
In particular, recent studies have increasingly employed mobile phone call detail records (CDRs) to analyze human trajectories, presenting valuable insights into movement patterns, social interactions, and urban mobility at large scales [15]. Blumenstock et al. (2015) demonstrated that mobile phone data, beyond basic mobility analysis, can be leveraged to infer an individual’s socioeconomic status and social behavior [16]. Human groups can be identified further by clustering algorithms to contribute to informed urban planning [17]. Taxi trajectories generated based on global navigation satellite systems (GNSSs) are another representative instrument for understanding urban dynamics by clustering vehicle behavior and transportation demands [18]. Recent studies have mainly focused on the similarities of geometric measurements and temporal attributes of trajectories [7]. Various algorithms, such as the edit distance on real sequence, longest common subsequence (LCS), and dynamic time warping (DTW) algorithms, have been implemented to calculate similarities among trajectories. Clustering algorithms have also been used to categorize individuals into typical groups [15,19]. Recently, deep learning technologies, including recurrent neural networks, convolutional neural networks, graph neural networks, and transformer-based models, together with attention mechanisms, have been introduced into trajectory data modeling, representation learning, trajectory clustering, and mobility simulation [6,20,21]. These technologies have been intensively applied to improve the effectiveness of trajectory similarity measurement and classification, which show advantages in extracting latent characteristic patterns, estimating travel time, and detecting anomalies, in addition to mobility generation.
Most methodologies in available works adopt a data-driven trajectory approach to understand human mobility patterns and particular personal information. Most human movements are basically intentional movements with purposes [5,9]. Spaces accommodating human movements offer relevant functions that meet the requirements of these purposes [9]. To better understand human behaviors, it is necessary to incorporate more semantic information of location and space, which accommodates required and desired activities. The built environment can act as a behavioral catalyst, suggesting that space functions may fundamentally shape mobility patterns in various disciplines across scales [12]. This perspective necessitates deeper integration of semantic space information with traditional trajectory analysis. Based on home location estimation [21], researchers validated the scaling law of visitation using mobile-phone data from multiple cities, which presented an inverse pattern of human travel distance relative to the frequency of trips from home. The findings supplement the gravity law and the radiation model of human mobility. Human mobility data generated in location-based social networks (LBSNs), such as those in FourSquare, empower researchers with semantically rich information in heterogeneous dimensions coupled with raw trajectory data of position and time [22]. Semantic information can be encoded into an attribute-embedding layer in neural network models, together with stay points in trajectories. In addition, user age groups [23] can be classified based on sparse spatial–temporal clustering and aggregation of trajectory data using machine learning algorithms [17].
In urban contexts, intensive interactions happen directly among human individuals who share similar spatio-temporal trajectories or indirectly among those who may use spaces with the same functions at different locations. As indicated above, most research mainly considers the former cases, adopting approaches using spatio-temporal similarities of trajectories. Specific functions of spaces accommodating trajectory stay points underpin human movements, enriching spatio-temporal patterns of corresponding trajectories. Recent advances in spatio-temporal visualization, as summarized in Bach et al.’s systematic review of space-time cube operations [24], provide methodological foundations for the decoding of complex mobility patterns through 3D geo-visual analytics. The space function of trajectory stay points and the time that human individuals spend in spaces of specific functions reflect the purpose and drivers behind their behavior and corresponding activities. Recent advancements have shown the potential of incorporating space functions to enhance human clustering accuracy. Studies have incorporated types of buildings or areas that individuals visit to improve clustering performance for individuals with similar behavior patterns [25]. This consideration allows for a more comprehensive understanding of how individuals interact with different types of spaces. Fang et al. categorized campus life trajectories into two types based on campus access points (APs) and inferred people’s activities at different times according to the AP sets [25]. The effectiveness of mining Wi-Fi access log data to extract activity patterns in various types of space functions using K-means clustering has been demonstrated, which can reveal a deeper understanding of the spatio-temporal behaviors of students [26]. By incorporating a space function, it is possible to uncover more nuanced groups of individuals with similar spatio-temporal activity patterns. Incorporating space functions into human clustering has shown promising results within campus environments [4]. By analyzing stay points within these spaces, researchers can gain valuable insights into campus inhabitants’ behavior, optimize space utilization, and improve the effectiveness of infrastructure services. Specifically, in the context of a school campus, clustering students into groups based on their presence in different spaces can help identify spatio-temporal patterns of their study habits, social interactions, and space usages.
The basic objective of this research is to investigate what human clustering patterns are in view of space functions. In this paper, we present a methodology on human clustering based on space function data of human movement using graph embedding techniques. Human movement data were collected from Wi-Fi networks. Based on our previous efforts in geo-visualization of spatial occupancy on campus [4], this work extends available research on human clustering based on the use of spatio-temporal similarities of trajectories to address human clustering based on space function similarities of stay points in movements. After the introduction in this section, we first describe the collection of human mobility data and space data with functions. Then, we present our methodology for building a network of human individuals, employ graph embedding algorithm Node2Vec to representation learning, and generate feature vectors of individual nodes of the graph. Afterwards, the clustering algorithm and the method to determine an optimal number of clusters are elaborated. In Section 3, we present the results and conduct corresponding analysis of the clustering patterns in spaces under various scenarios. Then, discussions about our methodology and experimental results are extended. Conclusions and future research directions are summarized in the last section.
2. Methodology
2.1. Data Collection
We collected 3000 individuals’ anonymized Wi-Fi network usage data in our research region, which is the main campus of our university. The data span nine days in March 2019. There are 71,820 stay points among all trajectories in total. These data contain information about individuals’ network connection times and corresponding Wi-Fi access points (APs). Individual trajectories can be built after preprocessing the Wi-Fi network log data [4]. Figure 1 shows 3D models of the research region.

Figure 1.
3D models of the research region (coordinates in meters).
The campus is about 980,600 square meters. There are 27 buildings, including 9 teaching buildings, 11 dormitory buildings, 4 administrative buildings, 2 dining buildings, and 1 library building. In total, there are 2508 independent spaces, which are typical rooms and offices. Based on our on-site surveys and building floor plans, 35 types of space functions were identified in our research region. Figure 1 shows a 3D model of the university campus. Figure 2 shows the functions of the top-10 spaces most visited by individuals. The numbers in the figure represent the number of spatial units contained in each spatial function type that the 3000 individuals stayed in. Spaces marked as “Others” include facility control rooms, archive rooms, confidential rooms, student union offices, and cleaning rooms, where most individuals do not visit. Different functions can meet distinct behavioral purposes of campus inhabitants’ activities in the spaces, such as learning, research, office work, activities, rest, dining, training, and so on. And each stay point in human trajectories is enriched with more attributes, as shown in Table 1.
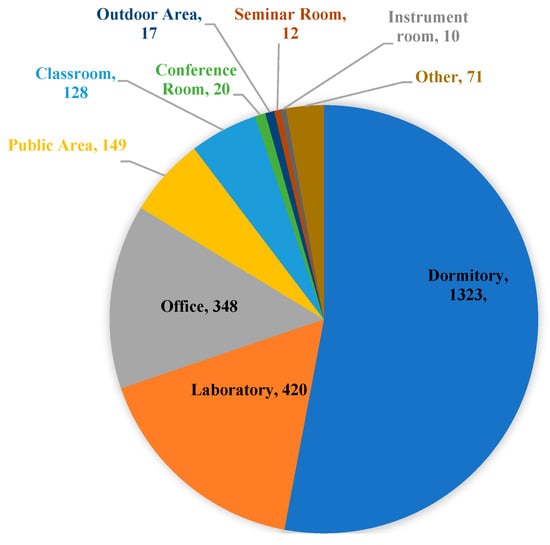
Figure 2.
Top-10 most visited space functions.

Table 1.
Stay-point attributes.
2.2. Human Network Construction
Most individuals are students, faculty members, and staff. Typical activities on campus include lecturing, self-studying, meetings, dining, sleeping, and various events. Individuals staying in spaces with the same function and similar temporal patterns can be converted to a network of individuals. The human network is constructed based on the stay-point data, with nodes representing individuals and edges reflecting their relationships. An edge is established between two individuals if they are in spaces with an identical space function and the time that the two individuals stay in such spaces exceeds a specified duration. On a university campus, two hours typically represents the duration of a class lecture for students and lecturers. Four hours represents a typical working time that research staff and graduates spend in their labs, and 24 h represents the time spent on campus by campus inhabitants. The specific duration spent in a space of a specific function is a key indicator reflecting the intention of activities, corresponding to stay points of trajectories. Consequently, three human networks are constructed with three time durations. The pseudocode used to built a human network for a specific time length is shown in Algorithm 1 below, in which the specific hour is the corresponding time duration.
| Algorithm 1 Get_Network | |
| 1: | Create an empty Network G |
| 2: | for each individual and its corresponding data group do |
| 3: | Compute AP classification statistics APClassification |
| 4: | Compute total duration for the individual Duration |
| 5: | Add node to Network G with APClassification and Duration |
| 6: | end for |
| 7: | for each pair of distinct individuals do |
| 8: | Find AP classifications common_conditions |
| 9: | if common conditions are met then |
| 10: | Compute duration for both individuals |
| 11: | if duration for both individuals > specific hours then |
| 12: | Add or update an edge in Network G between the two individuals with weight as the common duration |
| 13: | end if |
| 14: | end if |
| 15: | end for |
| 16: | Output the number of nodes and edges in the final network G |
| 17: | Extract connection information for each node and create connection_information |
| 18: | Compute connection counts for each node and merge connection_information |
| 19: | Return network G and connection_information |
2.3. Feature Representation
Graph embedding algorithms are effective in transforming high-dimensional, sparse graphs into low-dimensional and continuous feature-vector spaces. Such an algorithm encodes the relationships among nodes into feature vectors, among which distances reflect proximities in the network. These algorithms utilize biased random walks and enable us to generate low-dimensional, fix-length feature vectors that represent individuals’ interaction patterns within these space functions. With representation learning, the structure and relationships in the graph can be captured for various machine learning tasks in the vector space. Node2Vec [27] achieves this by employing the graph’s biased random walk strategy, which can effectively balance local and global structural information to generate node embeddings. The algorithm aims to learn representations for nodes so that nodes sharing similar network neighborhoods are closer together in the embedding vector space. In order to capture the complex relationships in human networks, Node2Vec can generate feature representations of individuals within a network. It can capture not only spatio-temporal activity patterns of human individuals but also the structural connections among them. Perozzi et al. (2014) used DeepWalk [28], a random walk-based method, to learn latent representations of social networks, which improved performance in community detection and link prediction tasks. Altuntaş (2024) introduced Node2Vector [29], combining network analysis and neural networks to improve the quality of node embeddings for machine learning tasks.
The algorithm is primarily based on two concepts: network neighborhoods and node similarity. A network neighborhood of a node is a fixed-size subset of neighbors of the given node. Node similarity is defined by comparing the network neighborhoods of nodes. In Node2Vec, node embeddings are obtained by generating random walk-based sequences on the graph, which can be viewed as a method of sampling nodes from the graph. The core idea is to perform multiple random walks on the nodes to capture all neighboring nodes and generate meaningful embeddings. Two transition probabilities parameters are involved (p and q), which represent whether the random walk is biased towards Breadth-First Search (BFS) or Depth-First Search (DFS). BFS sequences typically explore neighboring nodes, while DFS is more prone to exploring nodes distant from the current node. In this study, typical combinations of parameters p and q were explored to adjust the random walk’s inclination towards depth-first search (DFS) or breadth-first search (BFS) [27] and further optimize subsequent clustering and analysis of the resulting embeddings. Figure 3 shows the diagrams of BFS and DFS, and Equations (1), (2), and (3) are the formulas for the Node2Vec sampling strategies.
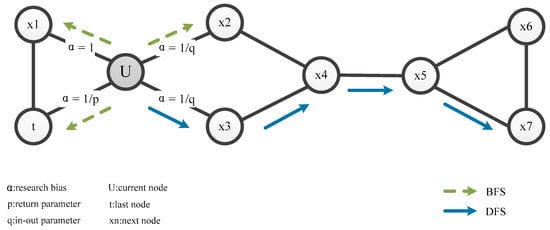
Figure 3.
Transition probabilities in Node2Vec: BFS and DFS preferences.
Given the source node () and the sampling length (), assuming the current sampling node is node , the probability of the next sampling node being is expressed as follows:
Taking Figure 2 as an example, if the current node is node and the previous step was at node , then the transition probability is πux. In this work, wux is set to 1.
and
Each node in the human network is represented by a 16-dimensional feature vector from Node2Vec, which can achieve a balance between preserving sufficient information and computational efficiency [27]. Figure 4 illustrates examples of 9 vectors generated for nodes in the human network.
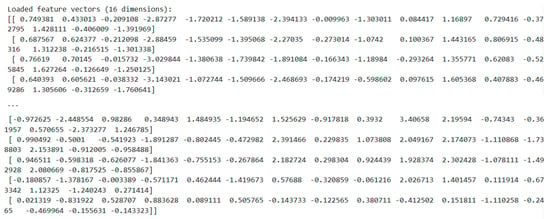
Figure 4.
Node2Vec vectors with 16 dimensions.
2.4. Clustering Analysis
Clustering is one of the important tasks in handling spatio-temporal mobility data. A basic question to answer is what groups there are. As a typical unsupervised clustering algorithm, K-means is designed to minimize the variance in each cluster and maximize differences between clusters based on one threshold value, namely the number of preferred clusters. And this algorithm can produce distinct clusters upon the number of clusters is determined. Here, we use K-means to cluster the feature vectors of nodes that are the learned results from the human network. The suitable number of clusters for each of the three specified scenarios is determined using the elbow method based on the inertia and silhouette scores of clusters.
For a specific clustering result of a given set of points, inertia represents how well the points are clustered together. It is an indicator calculating the sum of squared distances between each point and the centroid of the cluster to which the point belongs. In Equation (4), is the number of data points, is a data point, and is the centroid of cluster j to which xi belongs. A lower inertia value indicates a better clustering scheme. For each number () of K-means clustering results, changes of inertia can be plotted against . Then, an “elbow point” can be identified, where the rate of decrease in inertia slows down. The corresponding can be taken as the suitable number of clusters.
The silhouette score () is used to measure how similar a point is to its own cluster relative to other clusters. It ranges from −1 to 1, where a value close to 1 indicates that the point is well matched to a more suitable cluster and poorly matched to neighboring clusters, while a value close to −1 suggests that a point may have been assigned to a less suitable cluster. The silhouette score focuses on balancing intra-cluster cohesion and inter-cluster separation. It is calculated using Equation (5), where is the silhouette score of the ith cluster; denotes the average distance between the ith point and other data points within the same cluster; and represents the average distance between the ith point and the points in the nearest neighboring cluster, reflecting the separation between clusters.
Whereas the silhouette score is used to determine an optimized number of clusters, together with inertia, the Calinski–Harabasz score and Davies–Bouldin score are calculated to evaluate the performances of clustering results.
The Calinski–Harabasz score (CHS) evaluates the clustering quality based on the ratio of between-cluster dispersion to within-cluster dispersion. A higher Calinski–Harabasz score indicates that clusters are compact within each cluster and well separated among one another, suggesting better clustering performance. The CHS can be calculated by Equation (6), where is the number of clusters; and are the number of points and the centroid of the kth cluster, respectively; is the global centroid; and is the total number of clustering points.
The Davies–Bouldin score (DBS) measures the average similarity ratio of each cluster relative to its most similar cluster. It indicates similarity between clusters and the tightness within clusters. Lower Davies–Bouldin scores indicate better clustering, suggesting that clusters are more distinct and less similar to each other. In Equation (7), is the average Euclidean distance of the ith point to the centroid of the cluster it belongs to, and is the distance between the centroids of the ith and jth clusters:
3. Results
After constructing the network, there are 2145 nodes and 1,411,634 edges with the 2 h duration, and the average and median degrees of the nodes are 1316 and 1480, respectively. Within the 4 h duration, there are 1867 nodes and 1085,636 edges, and the average and median degrees of the nodes are 1162 and 1359, respectively. Within the 24 h duration, there are 1144 nodes and 446,469 edges, and the average and median degrees of the nodes are 780 and 922, respectively. The numbers of nodes, together with the average and median node degrees, gradually decrease as the time duration increases (from 2 h to 4 h and 24 h). The numbers of edges among nodes in the network also decrease accordingly. The sizes of these networks basically agree with our common understanding that, in general, the number of individuals staying together for short periods is greater than the number of those staying together for longer periods while engaging in social activities or at particular places.
The top row of Figure 5 below show the changes in inertia values against different clustering numbers for the 2 h, 4 h, and 24 h scenarios, from left to right. The three figures in the bottom row show the changes in silhouette score. It can be observed that the suitable number of clusters for the 2 h duration is 24, and that for the 4 h scenario is 18, while for the 24 h scenario, the suitable number is 9.
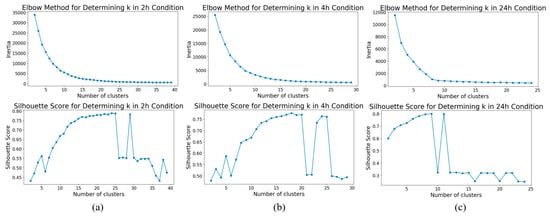
Figure 5.
Suitable numbers of clusters for (a) 2 h,(b) 4 h, and (c) 24 h scenarios.
3.1. Individuals K-Means Clustering in 2 Hours
The individuals were grouped into 24 clusters based on their feature vectors withing 2 h scenarios. Six sets of typical p and q parameters [27] were selected, considering the cluster evaluation performances of CHS and DBS, with the first three random walk strategies biased towards DFS and the last three towards BFS. The analysis explores how these biases and parameter combinations impact the clustering results, which can reveal distinct groupings that indicate diverse behavioral patterns among the individuals (Figure 5). To better visually represent clustering results, principal component analysis (PCA) was used to reduce the number of feature vectors. The subfigures (a) to (f) in Figure 6 correspond to different combinations of p and q, respectively. Figure 6 shows the clustering results, using the first two major components as horizontal and vertical axes.
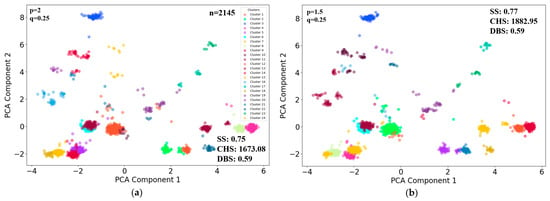
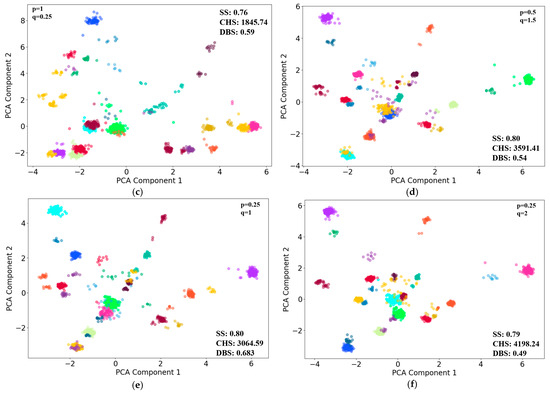
Figure 6.
Individual K-means clustering within the 2 h scenario.
In this scenario, the clustering result in Figure 6f presents the best overall metrics (p = 0.25, q = 2). Figure 7 shows a 3D visualization of the clustering result with these parameters settings, using the first three major components after PCA processing of the feature vectors.
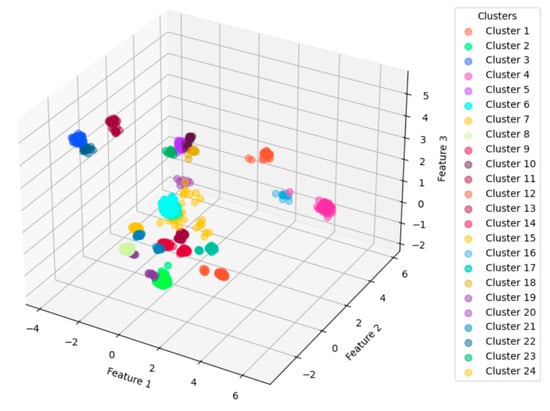
Figure 7.
Three-dimensional clustering results under the 2 h condition.
Figure 8 shows the percentage distribution of individuals in each of the 24 clusters across different space functions. Each bar comprises a percentage composition of clusters corresponding to one specific space function. The largest number of individuals is classified into Cluster 2, with the majority distributed in dormitories, classrooms, laboratories, and the student union. Notably, all records from the space function of student union fall with Cluster 2. This suggests that this group consists of students who are highly active on campus.
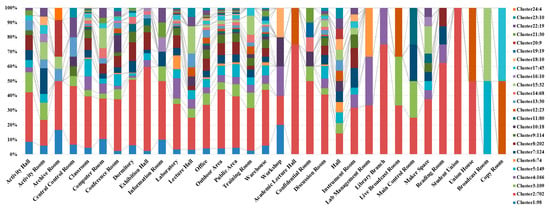
Figure 8.
Distribution of clustering results across space functions within the 2 h scenario.
Among all nodes (individuals), nodes 555, 1772, 1925, and 2293 connected to 2107 individuals, making them the nodes with the most connections among all individuals. Their records over the nine days show a certain regularity, with the majority and longest durations spent in dormitories, followed by classrooms and laboratories. This strongly suggests that these individuals are students. According to the clustering results, node 555 belongs to Cluster 6, while the other three nodes are in Cluster 2, which is the largest cluster. Through comparative analysis, we found that, aside from the dormitory, node 555′s second most frequent location was the laboratory, with fewer records in classrooms. In contrast, the other three individuals had the majority and longest records in classrooms after the dormitory. Therefore, it is likely that node 555 represents a graduate student or a senior student, while nodes 1772, 1925, and 2293 may be students with an intensive course load or who spend significant time studying in classrooms.
3.2. Individual K-Means Clustering in 4-Hour Scenario
Within the 4 h scenario, the human network size is smaller than that withing the 2 h scenario. The individuals were grouped into 18 clusters based on their feature vectors, of which there were also fewer than in the 2 h scenario. Similarly, six parameter combinations were selected, with the first three biased towards DFS and the last three towards BFS. The analysis of these combinations highlights how different biases and parameter settings influence the clustering results (Figure 9). The subfigures (a) to (f) in Figure 9 correspond to different combinations of p and q, respectively. The clustering results shown in Figure 9 are plotted against the first two major components after dimension reduction of the original feature vectors based on PCA processing.
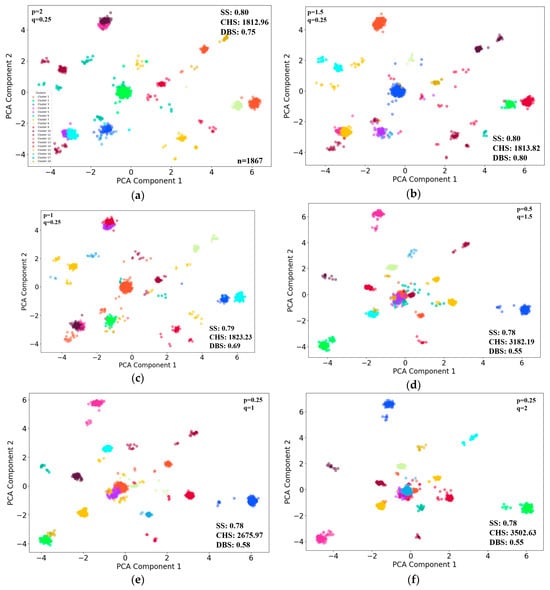
Figure 9.
Individual K-means clustering in the 4 h scenario.
Figure 10 shows a 3D visualization of the clustering results with parameter settings of p = 0.25 and q = 2, which generate the best overall cluster metrics (DBS and CHS).
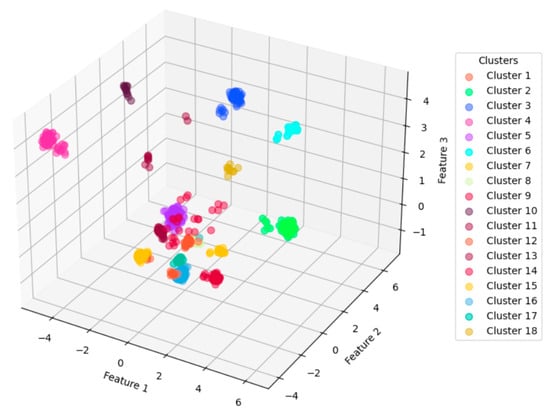
Figure 10.
Three-dimensional visualization of the clustering results under the 4 h condition.
For the overall DBS and CHS cluster metrics, Figure 9b presents the best performance. Figure 10 shows a 3D visualization of the clustering results for this parameter scenario (p = 1, q = 0.25). Similarly the corresponding result is plotted against the first three major components after PCA dimension reduction.
Within the 4 h scenario, Cluster 16 has the largest number of individuals. Most of the individuals stay in dormitories, followed by classrooms and laboratories. This cluster covers the widest range of space functions compared to other clusters. On the other hand, Cluster 18 has the fewest individuals and the fewest space functions covered by their stay points. Figure 11 shows the percentage of individuals in different functional spaces within each cluster, as well as the number of individuals in each cluster.
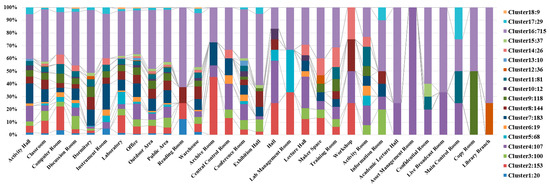
Figure 11.
Distribution of clustering results across space functions within the 4 h scenario.
The nodes with the most edges, each having 1828 connections, are nodes 985, 1772, 1892, and 2527. Compared with the 2 h scenario, nodes 985, 1892, and 2527 have 2098 connections each, which is just below the nodes with the highest number of connections. Among these four nodes, node 985 is in Cluster 8, while the remaining three were assigned to Cluster 16, which contains the most nodes. Notably, node 1892 shows regular patterns of stay in both the dormitory and laboratory over the 9-day period. Almost every half-day work shift is spent in the laboratory, with a return to the dormitory after 11 p.m., suggesting that this individual may be a graduate student. In contrast, nodes 1772 and 2527, while having fewer records in the laboratory compared to node 1892, show similar patterns, spending significant time in classrooms during the daytime and evening work hours. Node 985, however, demonstrates more diverse space function patterns compared to the other three.
3.3. Individuals K-Means Clustering in 24 Hours
With the 24 h scenario, the feature vectors of human network nodes were grouped into nine clusters. The network size and cluster numbers are smaller than in the two scenarios discussed above. Six parameter combinations were tested using the same strategy. The evaluation of these biases and parameter combinations provides insights into their effects on the clustering results, revealing significant patterns and groupings among the individuals (Figure 12). The subfigures (a) to (f) in Figure 12 correspond to different combinations of p and q, respectively. Figure 13 shows a 3D visualization of the clustering result with the best cluster metrics using the first three major components after PCA dimension reduction of corresponding feature vectors.
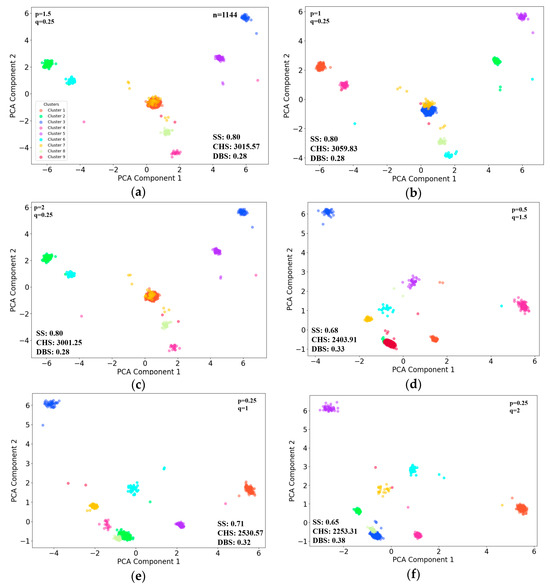
Figure 12.
Individual K-means clustering in the 24 h scenario.
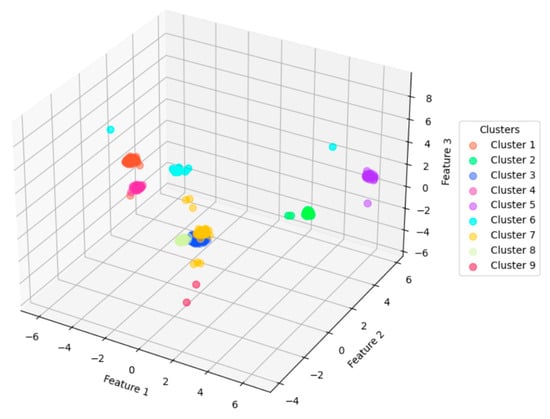
Figure 13.
Three-dimensional visualization of clustering results under the 24 h condition.
Figure 13 shows a 3D visualization of the clustering results with parameter settings of p = 1, q = 0.25, generate the best overall cluster metrics (DBS and CHS).
Among the nine clusters, Cluster 3 covers the most diverse range of space functions, with the majority of individuals spending time in dormitories, classrooms, and laboratories. Clusters 6, 7, and 9 have the fewest individuals staying in dormitories, with a proportions in classrooms and offices (Figure 14).
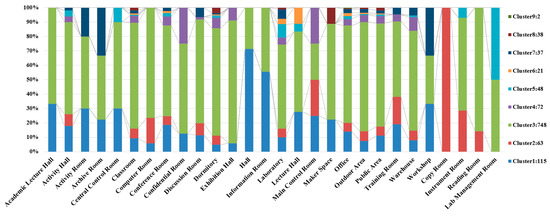
Figure 14.
Distribution of clustering results across space functions within the 24 h scenario.
The maximum number of edges connected to a single node s 1038, and there are 72 such nodes. Most of these nodes are found in Cluster 3. Analysis reveals that these individuals primarily spent their time in dormitories and laboratories over the nine days. Compared to individuals with the most connections withing the 2 h and 4 h scenarios, those in the 24 h scenario have significantly less frequent and shorter durations of classroom activities, suggesting that they are likely graduate students or research staff residing on campus.
4. Discussion
Spatio-temporal clustering based on human movement trajectories has been widely investigated based on location and time attributes in available research. Relevant clustering algorithms using geometric and temporal similarities of trajectories can reveal spatio-temporal patterns of human activities with similar location sequences. However, the space function of trajectory stay points, as one of the basic drivers of intentional human movements, has not been incorporated explicitly in previous works. It is necessary to identify individuals who visit spaces of the same type of function but at different locations. In this way, it is possible to effectively reveal the spatial dynamics of human mobility in view of space function and interactions between functions of spaces and human spatio-temporal behaviors.
In our work, human clusters were generated based on space functions and time durations spent by individuals. Thirty-five types of space functions were categorized in our research region, and three typical time durations are considered to indicate connections among individuals in spaces of the same function. With trajectory data of 3000 individuals collected from the campus Wi-Fi network over nine days, it was found that the network size and relevant statistics are inversely proportional to time duration, which agrees with common understanding of characteristics of human gathering activities. Since individuals often visit multiple spaces with different functions in a certain period, the network represents variant-dimensional connections among individual nodes. Graph embedding techniques are appropriate tools to transform network neighboring data into low-dimensional, fixed-length feature vectors. Node2Vec was introduced in this work to learn and generate continuous representations of nodes with a biased random walk strategy. K-means was then used to conduct clustering in the vector space of the learned network representation. This clustering algorithm minimizes the variance in each cluster and maximizes differences between clusters. It enables us to input a suitable number of clusters, which is more effective than other algorithms requiring more parameters. It is effective in answering questions like how many types of campus inhabitants there are. Inertia and the silhouette score are employed to determine suitable numbers of clusters based on the elbow method. Each resulting number of clusters for the corresponding time duration is inversely proportional to the time duration. This is in agreement with characteristics of human group activities. Two additional indicators measuring clustering performance are used to identify appropriate settings of biased random walk strategies.
Upon analysis and comparison of clustering results, it was found that the largest clusters across all three scenarios exhibited common characteristics. They included the widest variety of space functions, with dormitories being the most frequent, followed by laboratories, classrooms, and public areas, suggesting that these clusters likely represent student groups. These results are consistent with the characteristics of major campus inhabitants and their corresponding activity patterns.
Based on the statistical results, it can be observed that the total number of individuals in larger clusters is directly proportional to the number of individuals who stay in dormitory spaces. By examining other stay points of these clusters, it can be validated that these individuals are primarily students. A more detailed analysis of their additional stay points allows for further distinctions between different groups of students. In contrast, for smaller clusters, dormitory stays do not reveal a clear pattern, as there are few or no records of dormitory stays. Instead, the stay points of these smaller groups are concentrated in offices, classrooms, and laboratories.
5. Conclusions
In this paper, we proposed a methodology for human clustering based on feature vector representations, which are generated by the graph embedding of human networks of space functions of trajectory stay points. Using trajectory data generated from the Wi-Fi log data of 3000 individuals over nine days on a university campus, three human networks were built for typical time durations. The networks’ sizes and key statistical data of node degrees are closely related to the corresponding time duration and agree with the general pattern of public activities in the application context. With help of clustering performance indicators, appropriate biased random walk strategies were determined for K-means clustering. Corresponding analysis of the clustering results was conducted, revealing distinct behavioral patterns of typical campus inhabitants. A general pattern is that more groups of individuals can be revealed as the time duration decreases. The individuals in typical clusters are in agreement with the background information about campus inhabitants, and space usage analysis also matches individuals’ spatial and temporal activity patterns.
By incorporating space function into human mobility analysis, more research can be conducted to improve this work and further explore applicationsin wider contexts. In our research, we set three typical time durations to build the corresponding human networks. In reality, there are many other spontaneous and planned activities happening on campus, which may not last for the specific time duration we set in this research. It would be meaningful to validate patterns found in our current work by investigating clustering characteristics with a fine time duration sequence. The search strategies used in graph embedding processing of the human network could be enhanced by incorporating edge weights—for example, exact time durations or sizes of individual groups. The semantics of time attribute is also an important factor in human mobility; for example, a two-hour duration in the morning is different from one in the afternoon. This was not fully considered in our current work and can be explored further. Space function is one type of categorical information, and the resulting clusters can be taken as categorical data as well. Correspondence analysis can be introduced to explore associations based on a contingency table [30]. This research was designed to reveal the general relational patterns between human clusters and space functions by grouping each individual into a specific cluster. In the future, other clustering algorithms, such as hierarchical clustering algorithms and Density-Based Spatial Clustering of Applications with Noise (DBSCAN), can be employed to extract clusters adaptively and detect outliers. Of course, it is necessary to implement optimization algorithms to determine the suitable threshold values. In a broader urban context, a different space function system should be developed, and a fine adaptive time duration sequence should be introduced, considering very diverse human mobilities at large scales [12]. Privacy and ethical issues should be considered to protect individuals’ rights and guarantee responsible big data use. The data used in this paper were anonymized and shared with restrictions. Verification of the results can be conducted at coarse granularity levels. This work can be used to derive more individuals’ spatial and temporal characteristics and detailed interactions with spaces, with further implications for public decision making.
Author Contributions
Conceptualization, K.X. and T.W.; methodology, K.X. and T.W.; software, K.X. and P.Z.; validation, K.X., T.W., and Z.W.; formal analysis, K.X. and T.W.; investigation, K.X., P.Z. and T.W.; resources, T.W. and Z.Z.; data curation, K.X., Z.Z., P.Z. and Z.W.; writing—original draft preparation, K.X. and T.W.; writing—review and editing, K.X. and T.W.; visualization, K.X.; supervision, T.W.; project administration, T.W.; funding acquisition, T.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research is partly supported by National Natural Science Foundation of China grant number 42471464.
Data Availability Statement
The datasets presented in this article are not readily available because the original data is bounded by a non-disclosure agreement.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Eubank, S.; Guclu, H.; Anil Kumar, V.S.; Marathe, M.V.; Srinivasan, A.; Toroczkai, Z.; Wang, N. Modelling disease outbreaks in realistic urban social networks. Nature 2004, 429, 180–184. [Google Scholar] [CrossRef] [PubMed]
- Belik, V.; Geisel, T.; Brockmann, D. Human movements and the spread of infectious diseases. NetMob 2010, 2010, 44. [Google Scholar]
- Bettencourt, L.; West, G. A unified theory of urban living. Nature 2010, 467, 912–913. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Z.; Wang, T.; Zhang, Y.; Wang, Z.; Geng, R. Geo-visualization of spatial occupancy on smart campus using Wi-Fi connection log data. ISPRS Int. J. Geo-Inf. 2023, 12, 455. [Google Scholar] [CrossRef]
- Wang, S.; Bao, Z.; Culpepper, J.S.; Cong, G. A survey on trajectory data management, analytics, and learning. ACM Comput. Surv. CSUR 2021, 54, 39. [Google Scholar] [CrossRef]
- Chen, W.; Liang, Y.; Zhu, Y.; Chang, Y.; Luo, K.; Wen, H.; Li, L.; Yu, Y.; Wen, Q.; Chen, C.; et al. Deep learning for trajectory data management and mining: A survey and beyond. arXiv 2024, arXiv:2403.14151. [Google Scholar]
- González, M.C.; Hidalgo, C.A.; Barabasi, A.L. Understanding individual human mobility patterns. Nature 2008, 453, 779–782. [Google Scholar] [CrossRef] [PubMed]
- Song, C.; Qu, Z.; Blumm, N.; Barabási, A.L. Limits of predictability in human mobility. Science 2010, 327, 1018–1021. [Google Scholar] [CrossRef] [PubMed]
- Miller, H.J.; Dodge, S.; Miller, J.; Bohrer, G. Towards an integrated science of movement: Converging research on animal movement ecology and human mobility science. Int. J. Geogr. Inf. Sci. 2019, 33, 855–876. [Google Scholar] [CrossRef] [PubMed]
- Wei, H.; Songnian, L.; Shishuo, X. A three-step spatial-temporal-semantic clustering method for human activity pattern analysis. In Proceedings of the ISPRS International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Prague, Czech Republic, 12–19 July 2016; pp. 549–552. [Google Scholar]
- Pentland, A. Social Physics: How Good Ideas Spread—The Lessons from a New Science; Penguin: London, UK, 2014. [Google Scholar]
- Balsa-Barreiro, J.; Menendez, M. How cities influence social behavior. In Digital Ethology: Human Behavior in Geospatial Context; Paus, T., Kum, H.-C., Eds.; The MIT Press: Cambridge, MA, USA, 2024; Volume 33, pp. 139–157. [Google Scholar] [CrossRef]
- Dong, L.; Li, R.; Zhang, J.; Di, Z. Population-weighted efficiency in transportation networks. Sci. Rep. 2016, 6, 26377. [Google Scholar] [CrossRef] [PubMed]
- Fatema, K.M.; Kamruzzaman, M.; Kalyanaraman, A.; Lofgren, E.; Moehring, R.; Krishnamoorty, B. A visual analytics framework for analysis of patient trajectories. In Proceedings of the 15th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Niagara Falls, NY, USA, 7–10 September 2019; pp. 15–24. [Google Scholar]
- Yang, H.; Yao, X.A.; Whalen, C.C.; Kiwanuka, N. Exploring human mobility: A time-informed approach to pattern mining and sequence similarity. Int. J. Geogr. Inf. Sci. 2024, 39, 627–651. [Google Scholar] [CrossRef]
- Blumenstock, J.; Cadamuro, G.; On, R. Predicting poverty and wealth from mobile phone metadata. Science 2015, 350, 1073–1076. [Google Scholar] [CrossRef] [PubMed]
- Sun, H.; Chen, Y.; Lai, J.; Wang, Y.; Liu, X. Identifying tourists and locals by K-means clustering method from mobile phone signaling data. J. Transp. Eng. Part A Syst. 2021, 147, 04021070. [Google Scholar] [CrossRef]
- Wang, M.; Wang, J.; Song, Y. A map matching method for restoring movement routes with cellular signaling data. In Proceedings of the 2020 8th International Conference on Information Technology: IoT and Smart City, Xi’an, China, 25–27 December 2020; pp. 94–99. [Google Scholar]
- Yuan, Q.; Cong, G.; Ma, Z.; Sun, A.; Magnenat-Thalmann, N. Time-aware point-of-interest recommendation. In Proceedings of the 36th International ACM SIGIR Conference on Research and Development in Information Retrieval, Dublin, Ireland, 28 July–1 August 2013; pp. 363–372. [Google Scholar]
- Wang, W.; Osaragi, T. Learning Daily Human Mobility with a Transformer-Based Model. ISPRS Int. J. Geo-Inf. 2024, 13, 35. [Google Scholar] [CrossRef]
- Chu, C.; Zhang, H.; Wang, P.; Lu, F. Simulating human mobility with a trajectory generation framework based on diffusion model. Int. J. Geogr. Inf. Sci. 2024, 38, 847–878. [Google Scholar] [CrossRef]
- May Petry, L.; Leite Da Silva, C.; Esuli, A.; Renso, C.; Bogorny, V. MARC: A robust method for multiple-aspect trajectory classification via space, time, and semantic embeddings. Int. J. Geogr. Inf. Sci. 2020, 34, 1428–1450. [Google Scholar] [CrossRef]
- Hasan, S.; Zhan, X.; Ukkusuri, S.V. Understanding urban human activity and mobility patterns using large-scale location-based data from online social media. In Proceedings of the 2nd ACM SIGKDD International Workshop on Urban Computing, Chicago, IL, USA, 11 August 2013; pp. 1–8. [Google Scholar]
- Bach, B.; Dragicevic, P.; Archambault, D.; Hurter, C.; Carpendale, S. A review of temporal data visualizations based on space-time cube operations. In Proceedings of the Eurographics Conference on Visualization, Swansea, UK, 9–13 June 2014. [Google Scholar]
- Fang, T.; Hong, X. Discovering meaningful mobility behaviors of campus life from user-centric WiFi traces. In Proceedings of the SouthEast Conference, Kennesaw, GA, USA, 13–15 April 2017; pp. 76–80. [Google Scholar]
- Poucin, G.; Farooq, B.; Patterson, Z. Activity patterns mining in Wi-Fi access point logs. Comput. Environ. Urban Syst. 2018, 67, 55–67. [Google Scholar] [CrossRef]
- Grover, A.; Leskovec, J. node2vec: Scalable feature learning for networks. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 855–864. [Google Scholar]
- Perozzi, B.; Al-Rfou, R.; Skiena, S. Deepwalk: Online learning of social representations. In Proceedings of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, New York, NY, USA, 24–27 August 2014; pp. 701–710. [Google Scholar]
- Altuntaş, V. NodeVector: A novel network node vectorization with graph analysis and deep learning. Appl. Sci. 2024, 14, 775. [Google Scholar] [CrossRef]
- Murtagh, F. Correspondence Analysis and Data Coding with Java and R; Chapman & Hall: London, UK, 2005. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).