1. Introduction
Well completion serves as a crucial final step preceding oil and gas exploitation, pivotal in the overall process. The quality of well completion directly impacts the productivity and lifespan of oil and gas wells. Currently, perforation completion technology is extensively employed both domestically and internationally [
1]. This technique utilizes high-velocity metal jets generated by shaped charge during detonation to rapidly penetrate casing, cement ring, and formation rocks, thereby establishing efficient channels for oil and gas flow between reservoirs and wellbores. As the central component of the shaped charge, the liner plays a pivotal role in generating a metal jet to accomplish perforation and thus exerts a decisive influence on the perforating outcome [
2].
Due to the volatile global geopolitical landscape and the escalating domestic energy demand, the exploration and production activities in the oil and gas industry have progressively extended towards deep–ultra-deep reservoir buried-hill hydrocarbon, as well as offshore fields. The Bohai Bay Basin is a prominent region for the development of buried-hill hydrocarbon reservoirs in China, and it holds significant potential for expanding oil and gas resources in the country. The reservoirs in this area exhibit characteristics such as multiple structures, origins, and forms, while the rocks are composed of complex lithology with compact hard textures (hard rock). Due to various factors, such as high pressure and tight reservoir conditions in the wellbore, conventional-shaped charges are unable to effectively release oil and gas from the reservoir. Many oil and gas wells encounter challenges in fluid production post-perforation or even experience no fluid production at all. In addition, it is difficult to ascertain whether the mud contamination zone has been penetrated.
In recent years, Li et al. [
3] developed a novel powder liner by blending tungsten powder, aluminum powder, copper powder, and nickel powder in specific mass ratios based on previous studies on liners. The experimental results demonstrated excellent penetration capability in both ground-penetrating steel target tests and simulated, confining pressure, penetrating sandstone target experiments, with relatively clean perforation channels. However, due to the extremely short perforation time (on the order of microseconds), intricate processes (explosive detonation and high strain rate), and complex reservoir environment (high wellbore pressure and rock strength), the data collected by existing experimental observation methods often fragmented, rendering it arduous to comprehensively elucidate the complete physical process of perforation in hard rock [
4]. In this case, investigating the perforating process in hard rock and enhancing the performance of shaped charges is hindered by difficulties and time constraints. The numerical simulation method not only effectively circumvents such issues but also significantly enhances research efficiency. However, the constitutive parameters of the powder liner and the hard rock suitable for perforating conditions must be determined first.
The selection of constitutive parameters for liner and rock materials in finite element simulations of perforation has long been a topic of significant interest and discussion within the academic community [
5,
6,
7]. Currently, the majority of the key parameters in the material constitutive equation are acquired through experimental fitting. Liu [
8] conducted Split-Hopkinson Pressure Bar (SHPB) tests and quasi-static tests to obtain stress–strain curves of the tungsten–potassium alloy used in the liner at different strain rates. Based on these results, key parameters of its J-C constitutive model were fitted. The J-C constitutive equation of an Al-Li alloy was calibrated by Li et al. [
9] through quasi-static experiments and impact compression tests. Wen et al. [
10] determined the parameters of the HJC constitutive model for granite porphyry under varying freezing and thawing durations by analyzing model parameters, combining SHPB experiments, and conducting numerical simulations. Ling et al. [
11] established the parameters of the HJC constitutive model for sandstone through static experiments and SHPB laboratory tests.
However, there are inherent limitations in experimentally determining the constitutive parameters of powder liner (in shaped charge) and hard rock (in reservoir). First of all, in the preparation process of powder liner, usually using pressing technology, this process not only affects the microstructure of the material but also determines its macroscopic mechanical properties. Because of this, the traditional mechanical experimental methods, such as tensile tests, compression tests, etc., cannot effectively obtain its constitutive parameters. In addition, the experimental range of the strain rate cannot completely cover the actual range of the strain rate of the powder liner’s transformation from solid state to metal jet. Second, the properties of hard rock in the target reservoir and the actual downhole conditions are difficult to reproduce in these experiments. Finally, the experiment is time-consuming and laborious but also has a certain risk. These factors make the experimental method no longer suitable for fitting the constitutive parameters of powder coating and hard rock.
The present study proposes a parameter inversion method that integrates numerical simulation, multi-objective optimization, and experimental data to address the aforementioned issues. This approach aims to enhance reliability, simplicity, and universality in determining the constitutive parameters of powder liner and hard rock, thereby optimizing their applicability for hard rock perforation-related tasks.
2. Perforation Experiment
In the field of oil production engineering, perforation depth and aperture serve as crucial indicators for assessing the productivity and efficiency of oil and gas wells [
12]. Moreover, during the process of conducting perforation experiments and numerical simulations, these parameters directly reflect the performance of shaped charges. Because of this, this paper first experimented on the ground using a shaped charge to hit a steel target, obtaining the depth and aperture of the metal jet penetrating the steel target. Subsequently, the constitutive parameters of the powder liner were inverted based on these data. We conducted further simulations of the underground environment to conduct an experiment using a shaped charge to hit a hard rock target to obtain the depth and aperture of the metal jet penetrating the hard rock, and then we used these data to inverse the constitutive parameters of the hard rock.
2.1. Experiment of Penetrating Steel Target
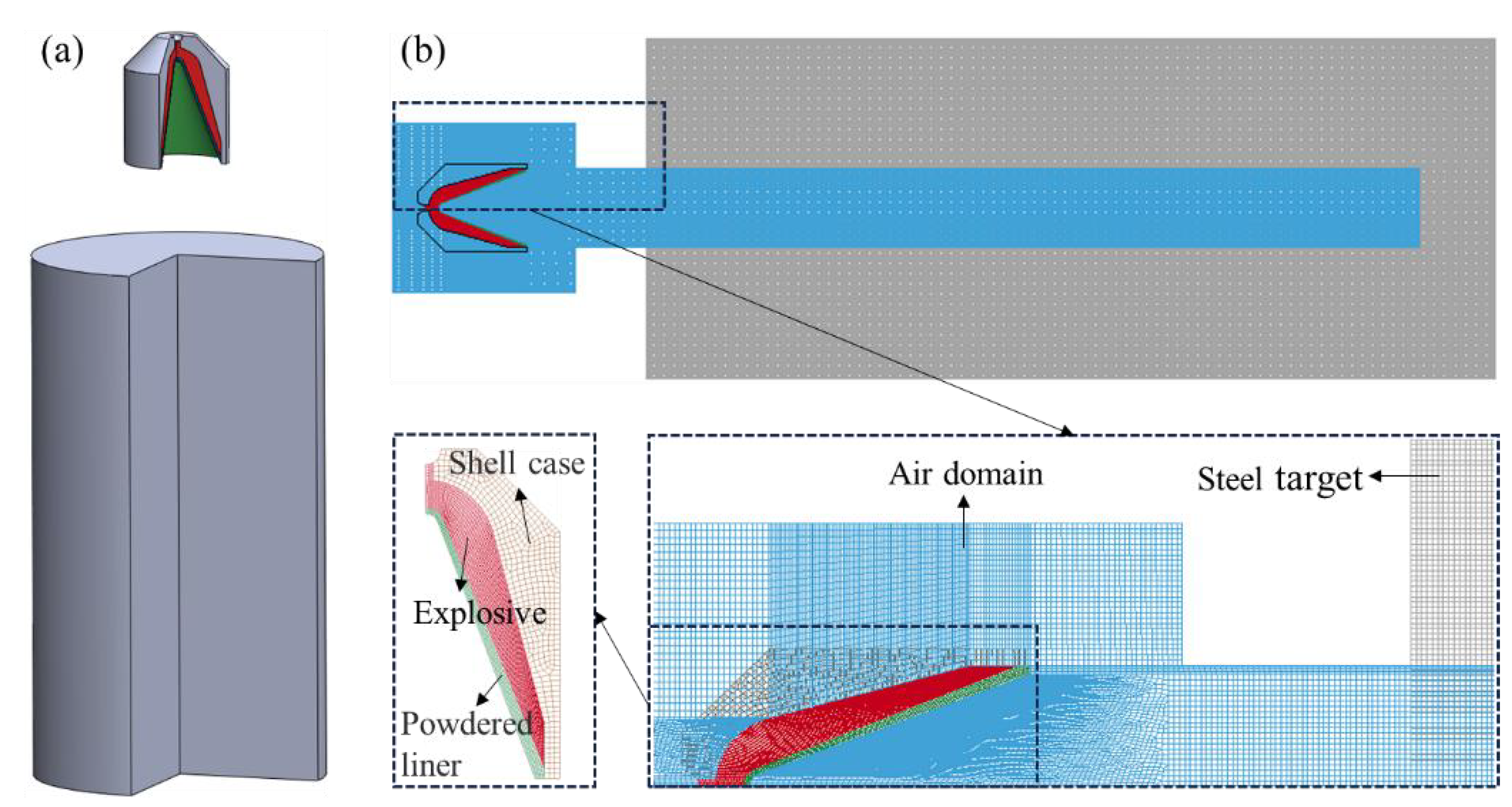
The experimental apparatus is depicted in
Figure 1, comprising primarily of shaped charge, metal sheet, blast tube, and steel target. Among them, the primary structure of the shaped charge (with a body diameter of 5.2 cm) comprises a shell case, explosive, and powder liner. A metal sheet with a thickness of 0.25 cm is utilized to simulate the wall of the perforating gun (the blind hole region), while a blast height cylinder is employed to regulate the distance (blast height) between the shaped charge and the steel target. In this experiment, the blast height remains fixed at 7 cm. The steel target consists of steel 45 and takes on a cylindrical shape with dimensions measuring 10 cm in diameter and 50 cm in height.
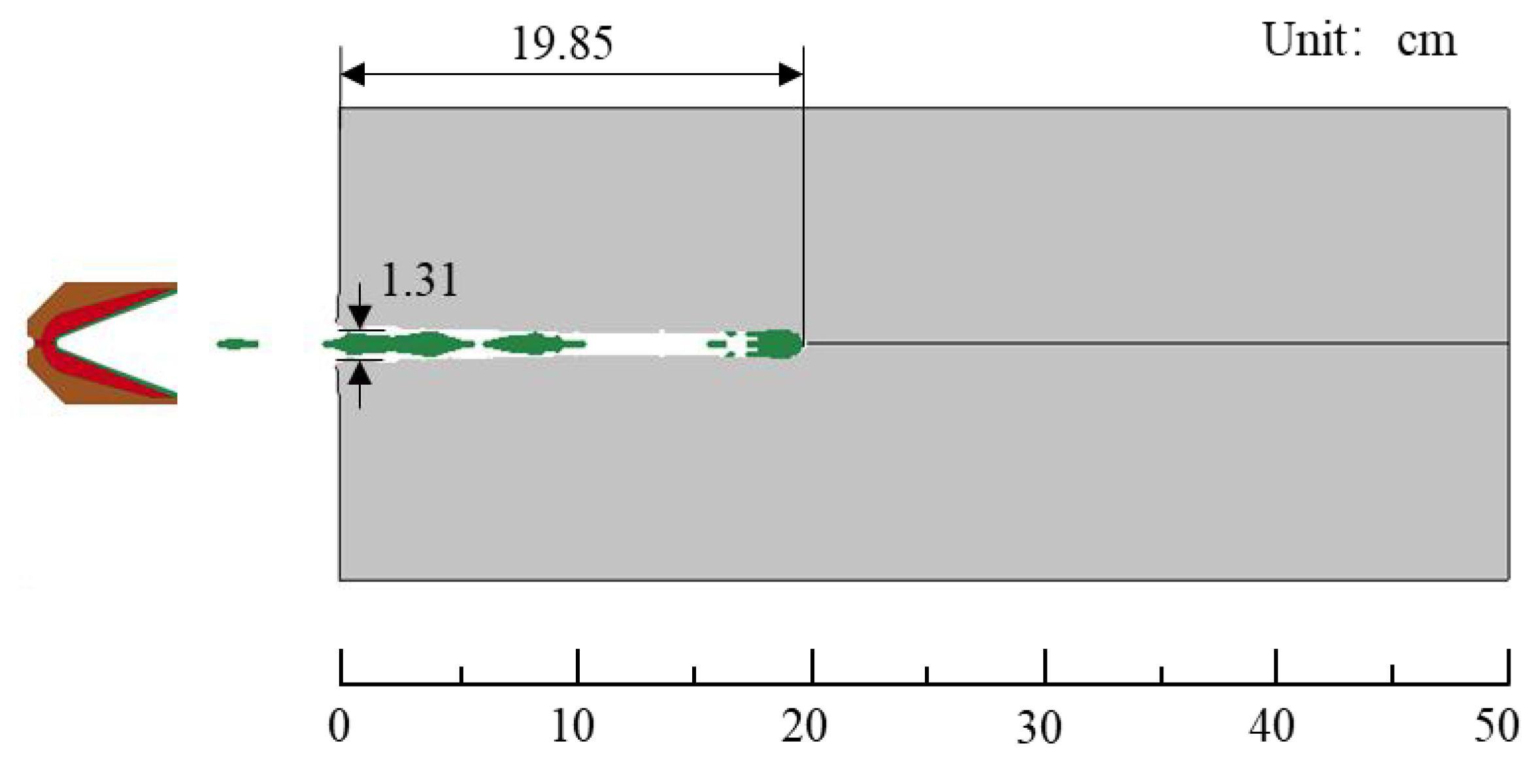
At the onset of the experiment, detonation of the explosive is initiated through a detonating cord. After the explosion, rapid oxidation of the powder liner within the shaped charge occurs under high temperature and pressure generated by the explosive detonation, resulting in the formation of a metal jet possessing substantial impact force. Once formed, this jet effectively perforates both a metal sheet and subsequently penetrates through the steel target; ultimately, a perforating channel with a certain depth and aperture is formed on said target.
Based on statistical principles and economic considerations, we repeated seven sets of targeted charge shooting experiments with the above devices. During the implementation of the experiment, we strictly controlled the experimental environment (such as temperature, humidity, etc.) and ensured that the materials (shaped charge, sheet metal, and steel target) came from the same batch to reduce the variability of the experimental results. Key parameters (such as blast height, powder liner, sheet metal thickness, etc.) were consistent in all experiments to ensure standardization of the experimental process. In addition, we calibrated the detonating equipment to ensure the accuracy of the measurements. Upon completion of each experiment, a metal probe was inserted into the perforation channel to measure the maximum depth reached, referred to as the perforation depth. Additionally, the diameter of the steel target opening was measured and recorded as the perforation aperture. The experimental results are presented in
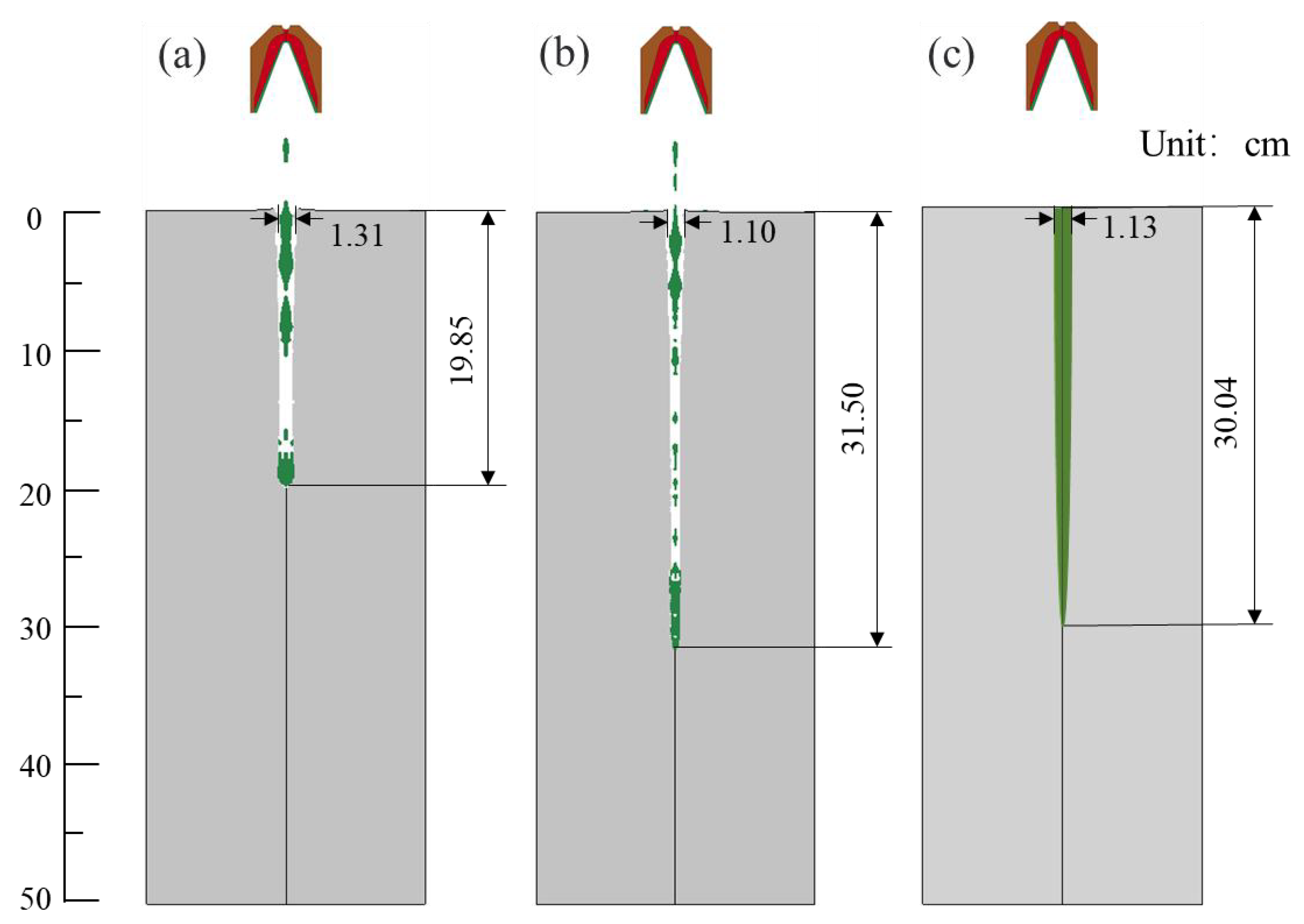
Figure 2. The perforation depth and aperture of the seven groups exhibited relatively stable characteristics. The depth ranged from 28.90 cm to 31.10 cm, averaging 30.04 cm and displaying a standard deviation of 0.80 cm. The size of the apertures varied between 1.05 cm and 1.20 cm, with an average value of 1.13 cm and a standard deviation of 0.05 cm. The statistical results indicate a low degree of data dispersion, which can provide reliable support for subsequent numerical simulations of perforation and the inversion of constitutive parameters for the powder liner.
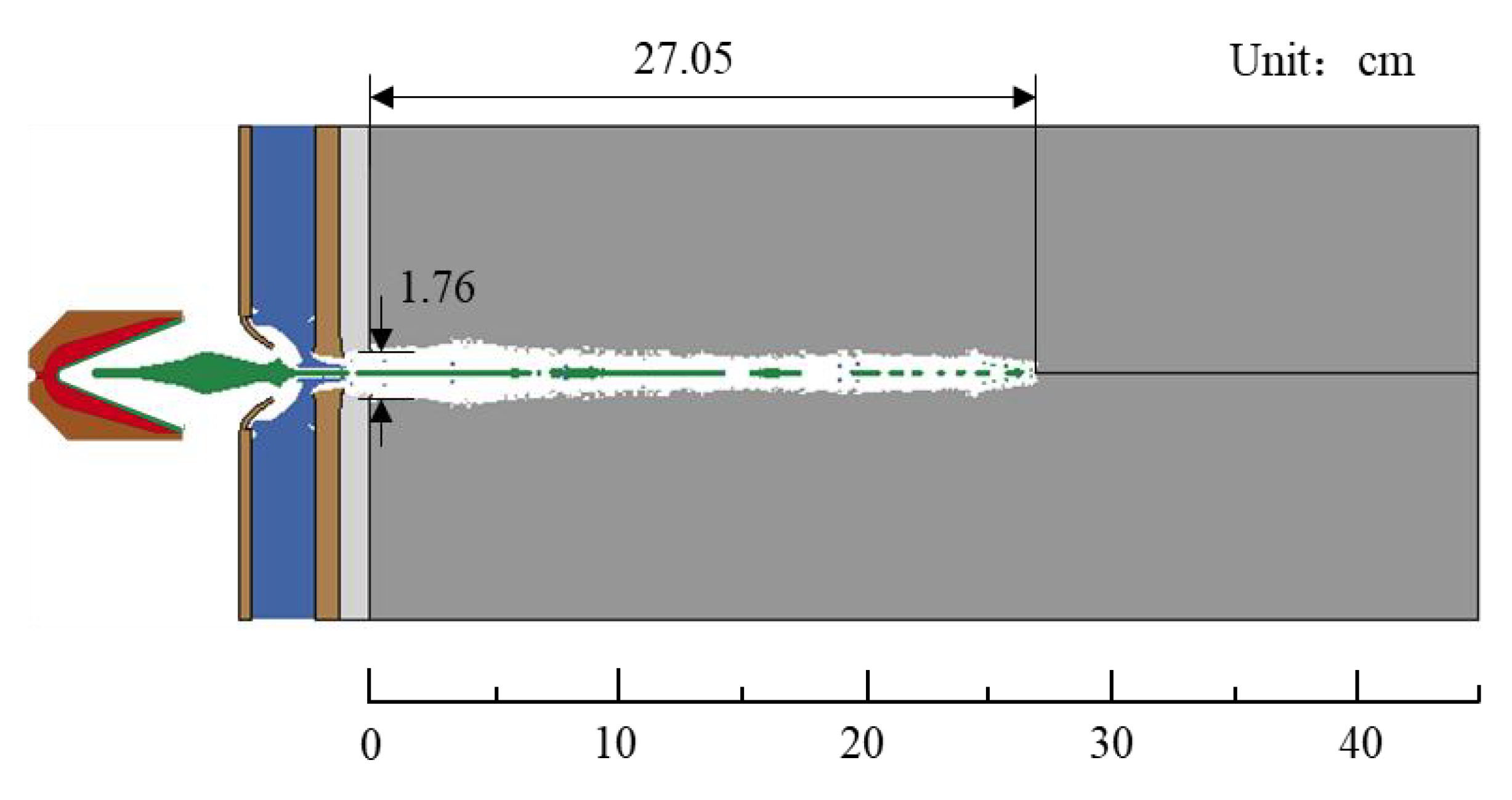
2.2. Experiment of Simulated Reservoir Penetrating Hard Rock Target
According to the Evaluation of Well Perforators issued by the American Petroleum Institute, a simulated reservoir perforation test device was designed and established according to the mechanical environment, rock properties, perforating gun parameters, and actual underground working conditions of the target reservoir. The device and test flow are illustrated in
Figure 3. The device is mainly composed of a unit gun and hard rock in two parts and a shaped charge (the same model as above) assembled in the gun, and it is connected to a detonator, placed in the upper part of the device. The hard rock (a cylinder 20 cm in diameter and 45 cm in height) is vacuum-saturated and placed under the unit gun.
At the onset of the experiment, the shaped charge is fired through the detonator. The resultant metal jet sequentially penetrates the gun holster (containing blind holes), wellbore fluid (water), casing, and cement ring, and ultimately forms a perforation channel within the hard rock. Considering the actual reservoir conditions, wellbore pressure is regulated at 25 MPa, while confining pressure is maintained at 30 MPa.
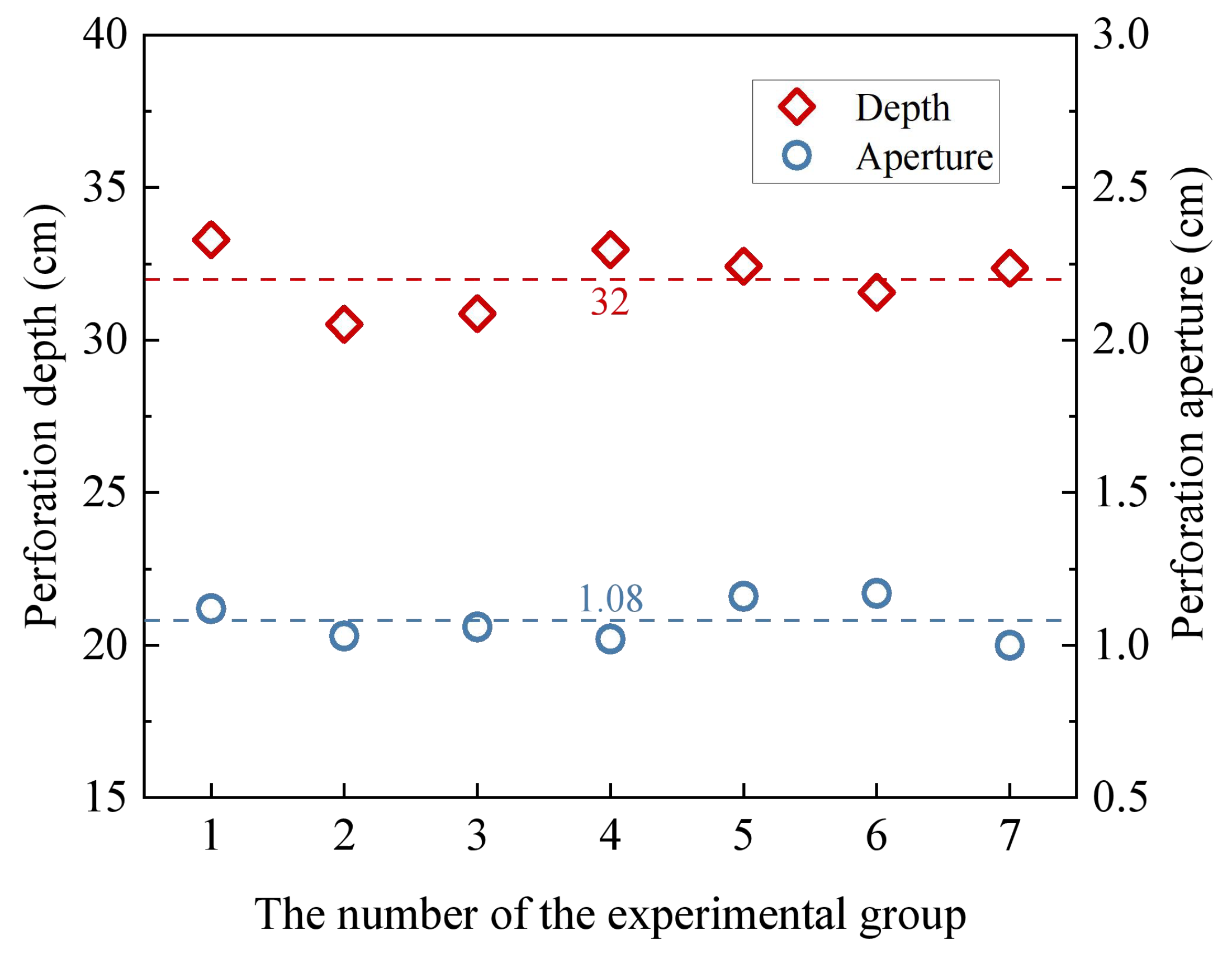
Seven groups of experiments were repeated with the above device. After the experiment was completed, the experimental target was broken, the maximum depth of the hole was recorded as the perforation depth, and the diameter of the opening of the experimental target was measured as the perforation aperture. The experimental results are illustrated in
Figure 4. The perforation depth and perforation aperture of the seven groups were relatively stable. The perforation depth fluctuated between 30.52 cm and 33.29 cm, the average depth was 32.00 cm, and the standard deviation was 1.05 cm. The perforation aperture fluctuated between 1.00 cm and 1.17 cm, with an average aperture of 1.08 cm and a standard deviation of 0.07 cm. The statistical results indicate a low degree of dispersion for each data point, thereby providing reliable support for subsequent numerical simulations of hard rock perforation and the inversion of constitutive parameters.
5. Conclusions
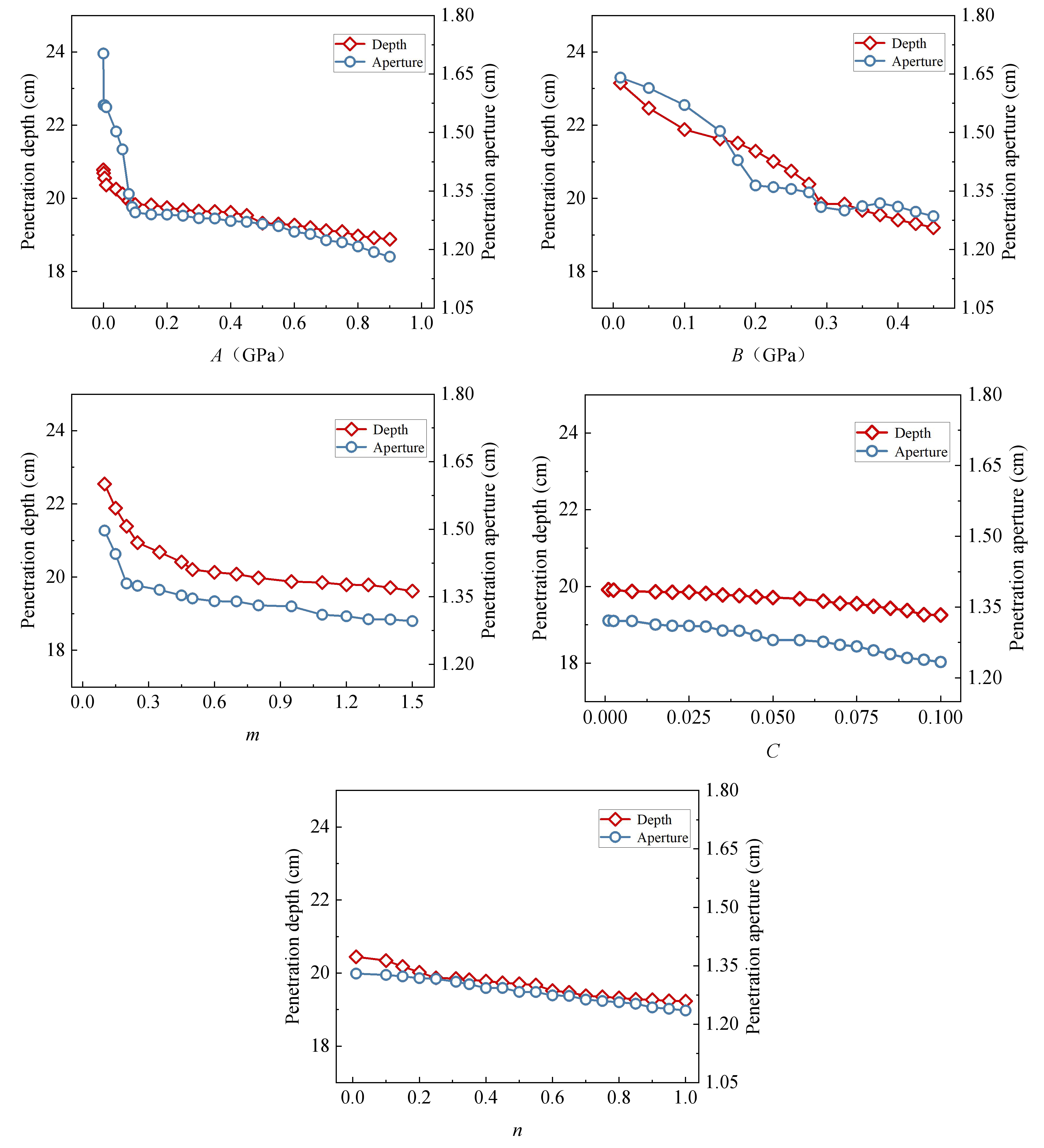
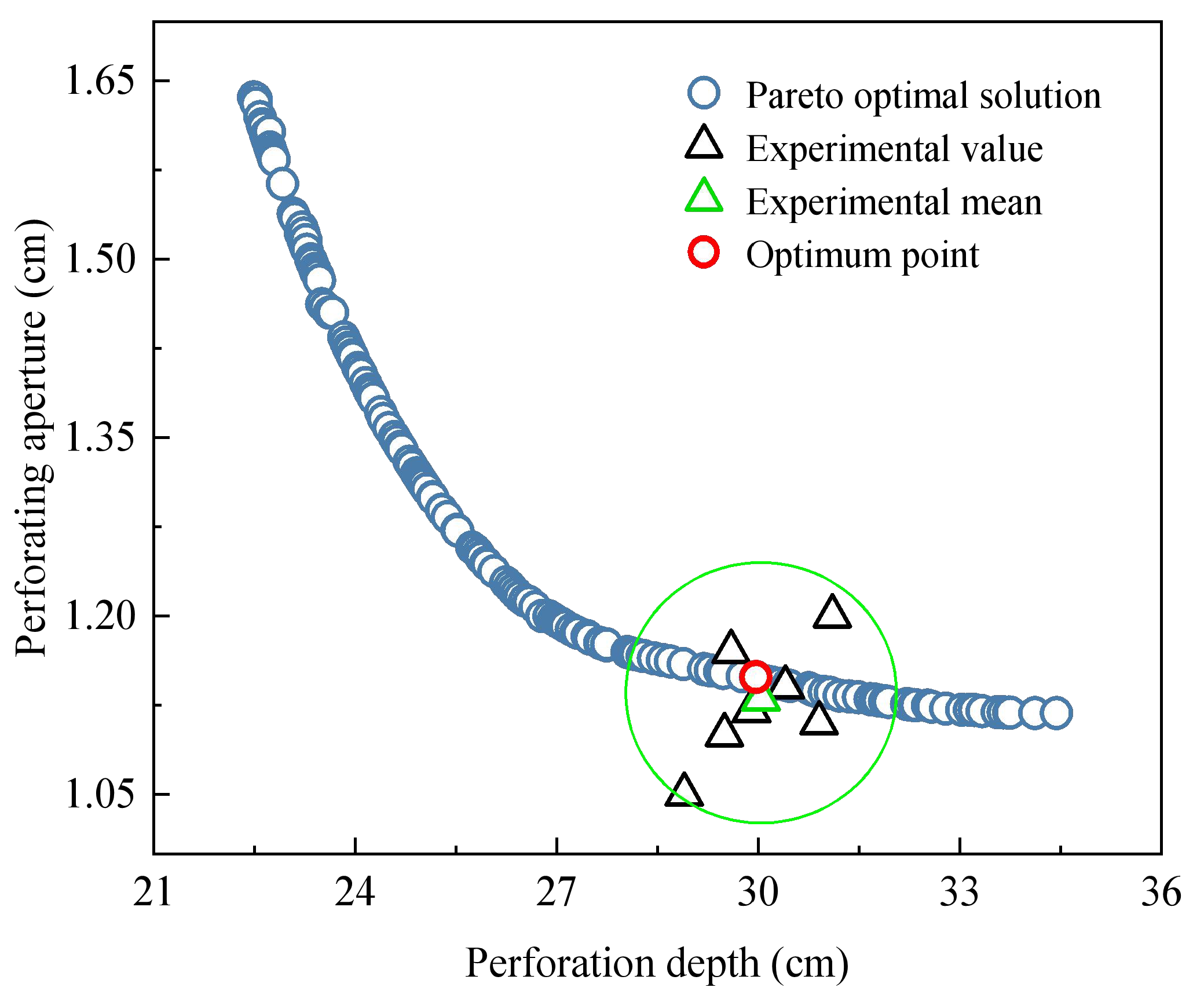
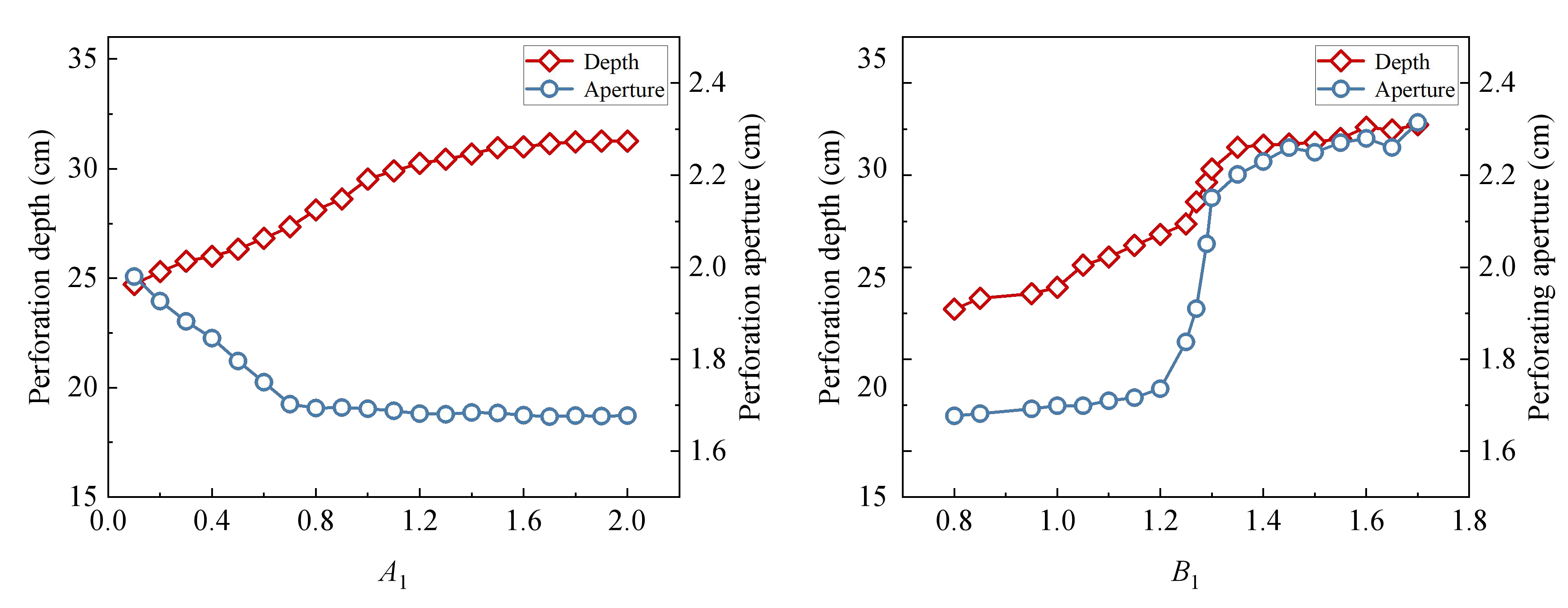
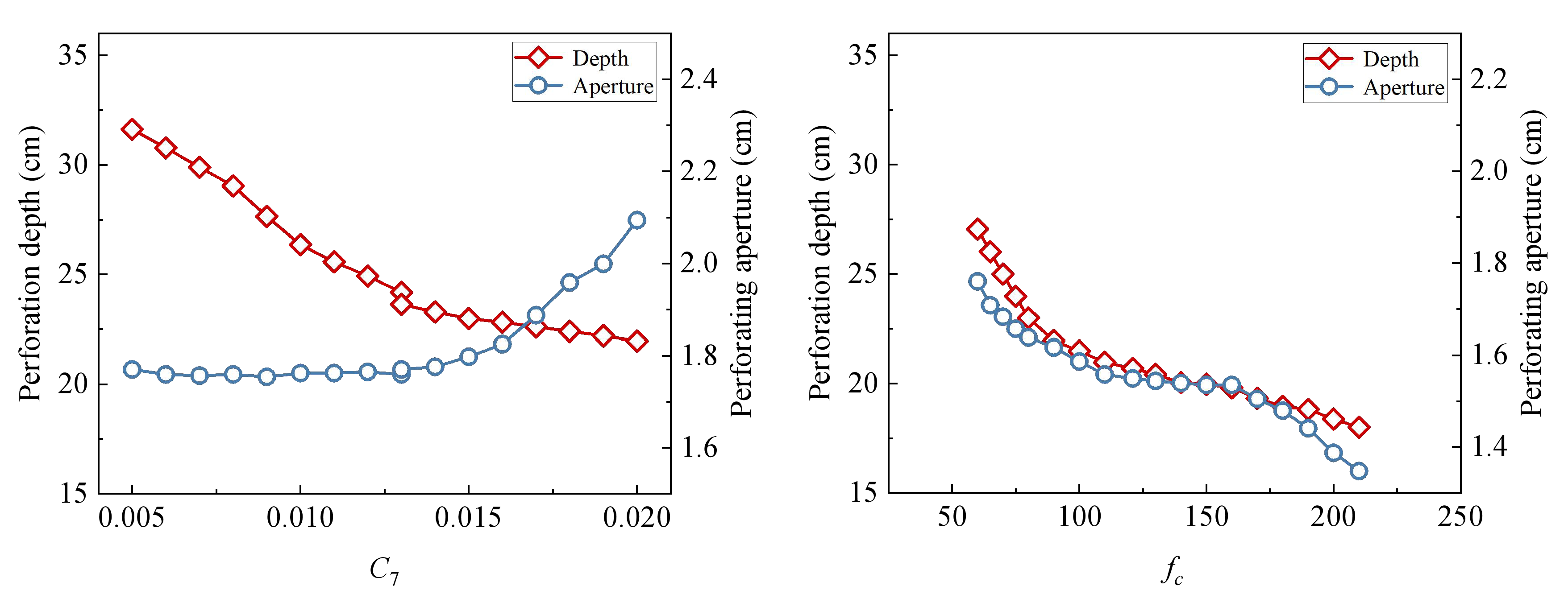
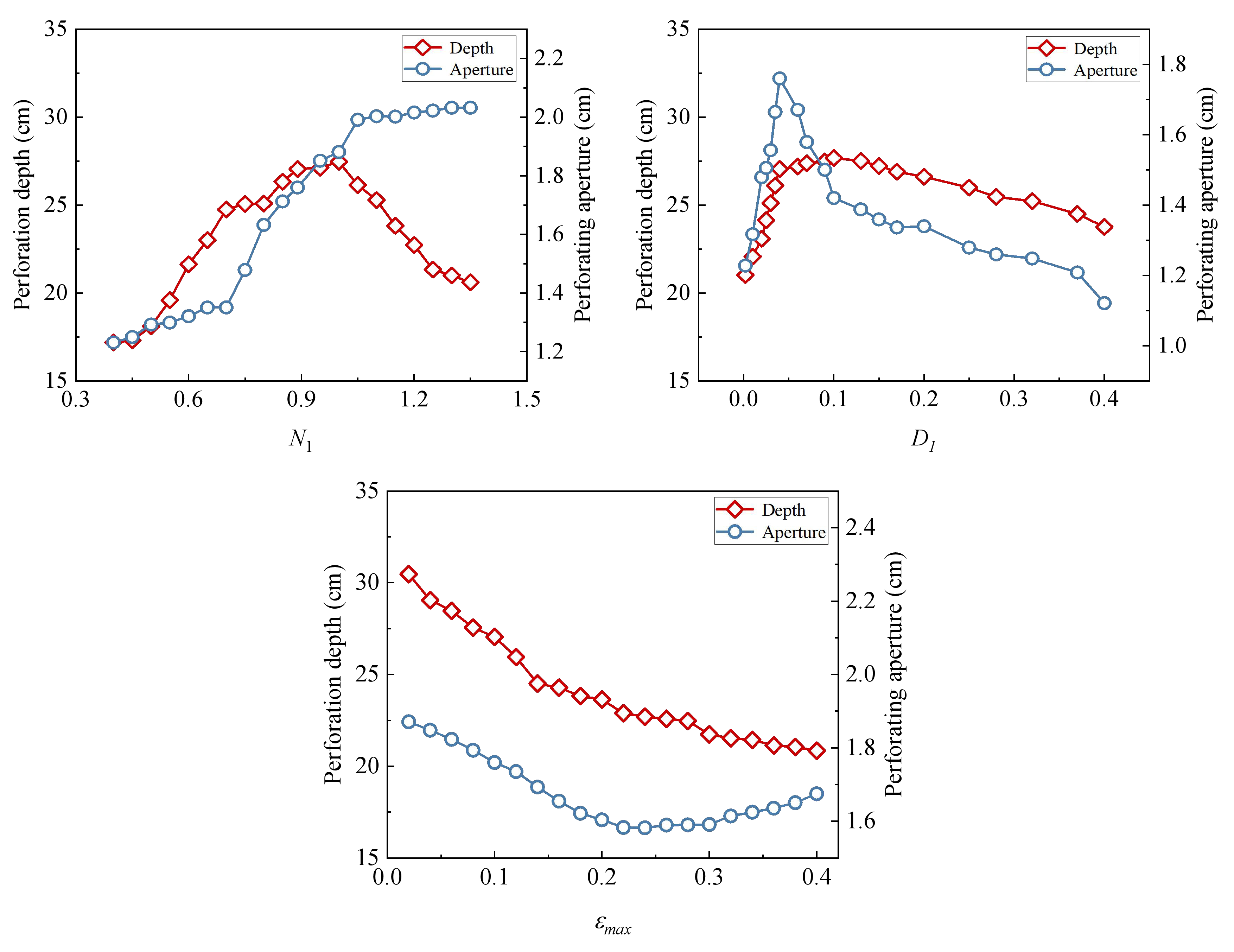
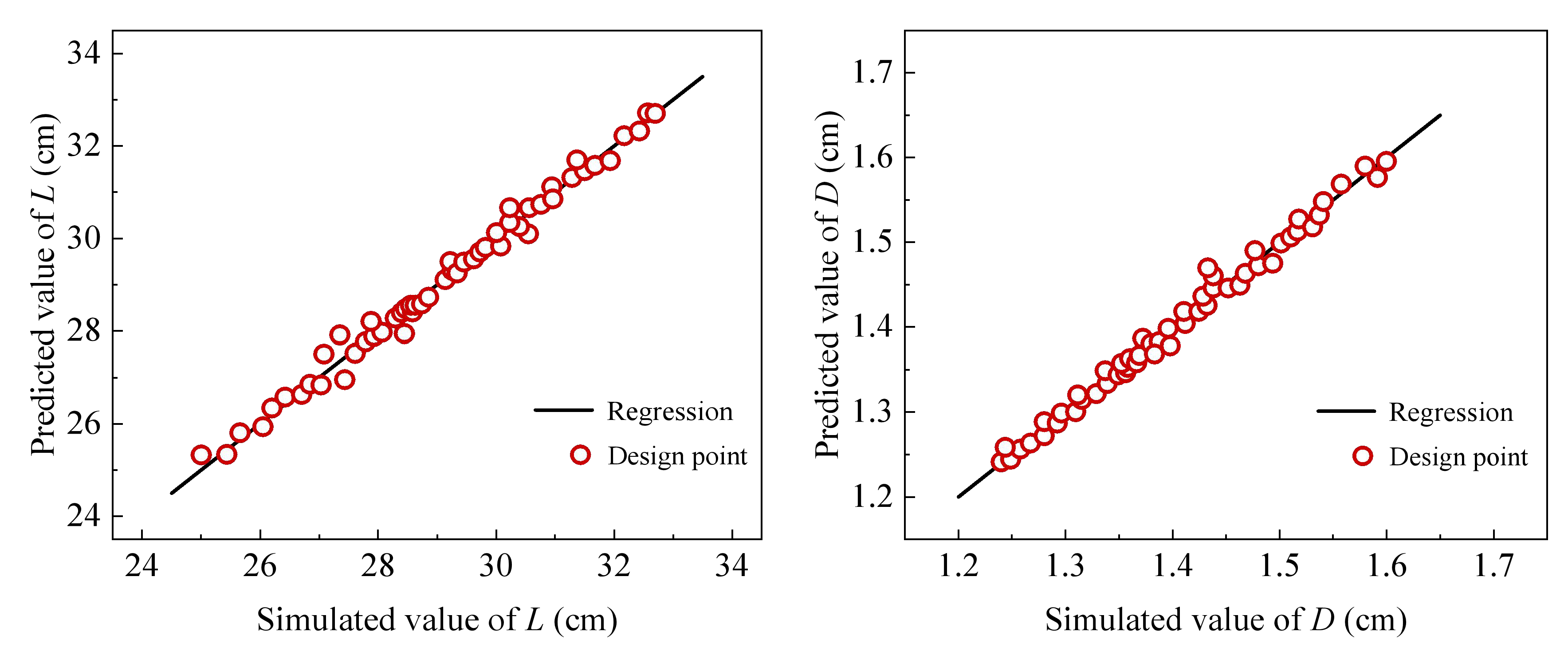
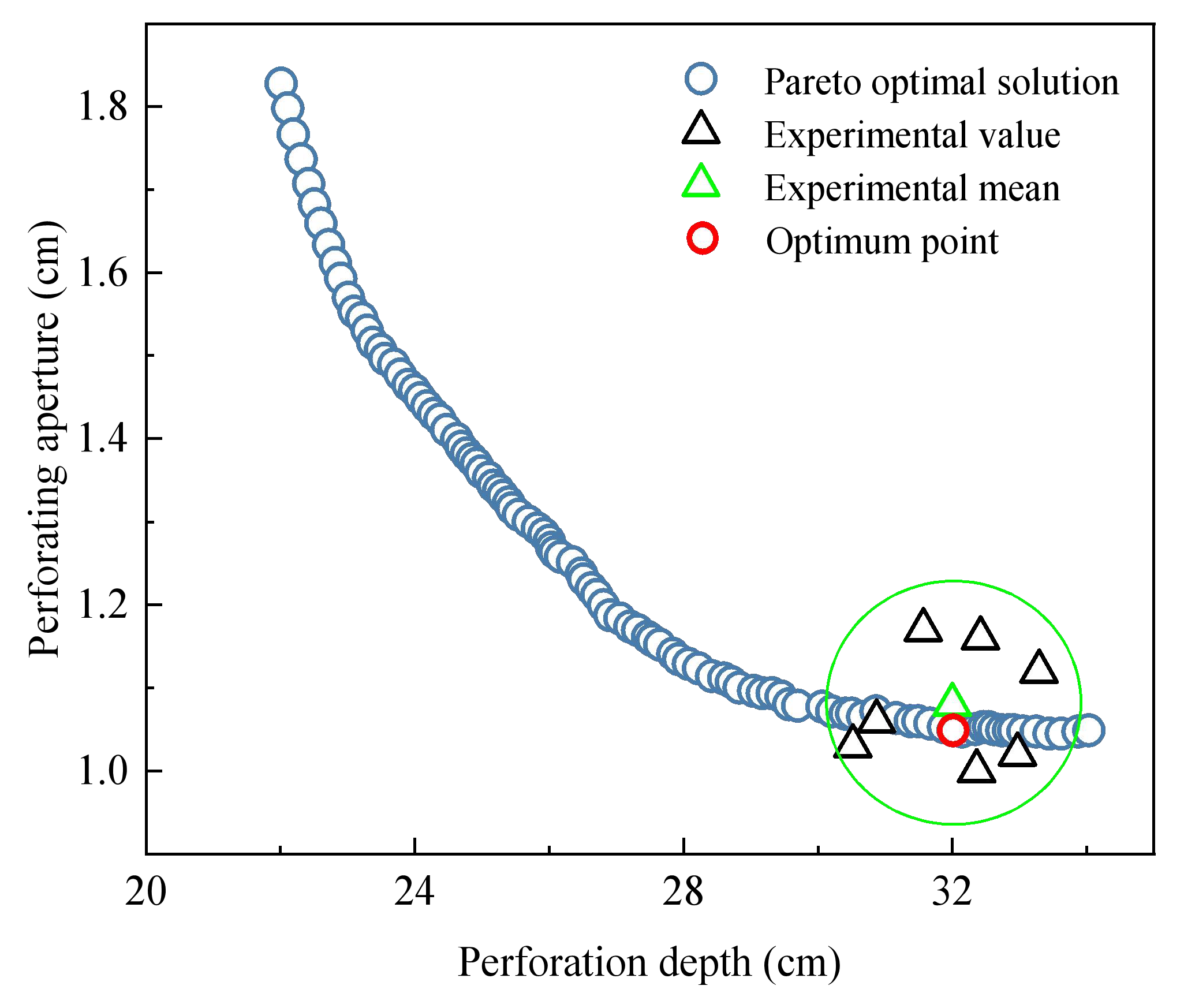
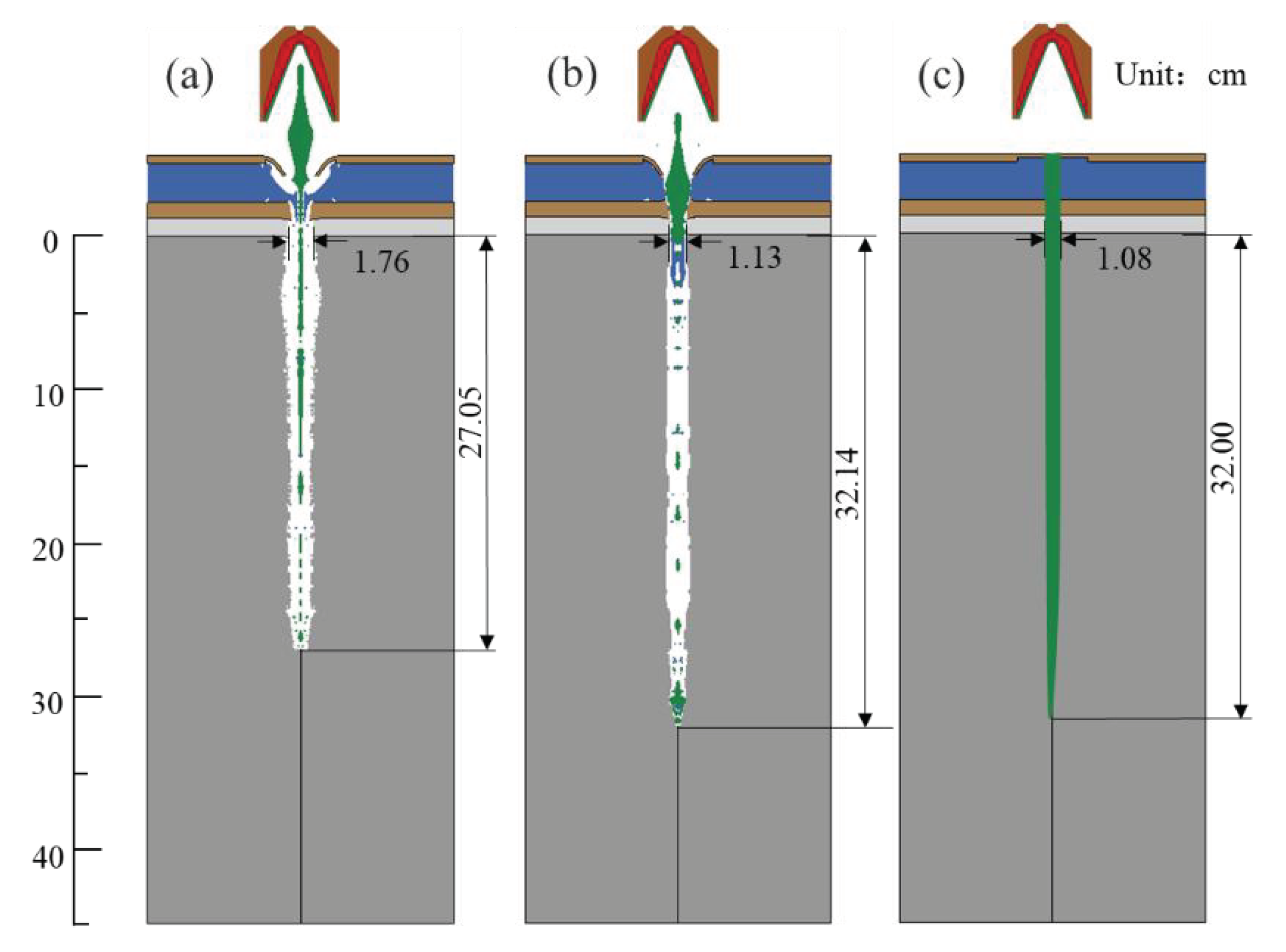
In this study, to acquire the parameters of the J-C constitutive model of powder liner in shaped charge and the parameters of the HJC constitutive model of hard rock in the reservoir, a penetrating steel target experiment and a simulated reservoir penetrating hard rock target experiment were first carried out, and the finite element software ANSYS/LS-DYNA (16.0)was used to reproduce the process of a jet penetrating a steel target and hard rock, respectively. Then, the expression of target variables (perforation depth L and perforation aperture D) regarding the parameters in the constitutive model was obtained through the utilization of the response surface method. Finally, a multi-objective genetic algorithm was employed to solve the display expression iteratively. We identified the Pareto optimal solution that closely approximated the experimental mean value by comparing it with experimental data. Then, we derived effective J-C constitutive parameters for powder liner and HJC constitutive parameters for hard rock.
The numerical simulation results, based on the reconstructed J-C constitutive parameters and HJC constitutive parameters, demonstrate that the perforation depth and aperture resemble the experimental results. This suggests that the constitutive parameters of the inversion offer a more accurate depiction of the mechanical behavior of powder liner and hard rock during actual perforation processes. Simultaneously, it was demonstrated that the perforation simulation based on the inversion of constitutive parameters could provide a more precise prediction of the damage induced by the metal jet formed through powder liner on hard rock. This finding establishes a fundamental basis for further investigation into both powdered liner and the process of hard rock perforation. At the same time, by combining numerical simulation and experimental data, the method overcomes the limitations of traditional experimental methods and reduces the dependence on experiments, thus reducing the time and economic cost that may be brought by experiments. The constitutive parameters of powder liner and hard rock can be obtained more efficiently in a short time, which also makes the results more applicable. In addition, this method not only provides a new theoretical framework for the current constitutive parameter inversion of powder liner and hard rock but also provides a new reference and inspiration for researchers in related fields in material behavior prediction, energy conversion, and transfer, etc., providing a new method for structural optimization in related engineering fields, which has great application potential. It further promotes the combination of basic research and engineering application.