Abstract
Due to the fast advancement in wireless communication technology, the demand for the modeling and generating of wireless channels is increasing. Deep learning technology is gradually applied in the wireless communication field, and the Generative Adversarial Network (GAN) framework provides a new solution for channel modeling. This paper presents a method based on Wasserstein GAN with gradient penalty (WGAN-GP) guided by an attention mechanism for wireless channel modeling and generating. The feature extraction capability of the model is enhanced by adding a channel attention mechanism in WGAN-GP, and the representation capability of the model is enhanced by adaptively recalibrating the channel feature response. The experimental results demonstrate that the proposed approach accurately models the channel distribution and generates data that closely aligns with the real channel distribution. The proposed method has been shown to achieve superior qualitative and quantitative evaluation compared to the existing method.
1. Introduction
The rapid advancement of wireless communication technology is constantly driving the development of modern society, and it has become indispensable in daily life and industrial applications. With the widespread adoption of technologies ranging from personal mobile communication to the Internet of Things, 5G networks, and the forthcoming 6G technology, the application scope of wireless communication is expanding rapidly [1]. The successful implementation of these technologies not only facilitates the instant exchange of information, but also provides the basis for innovative applications such as smart cities, telemedicine, and autonomous vehicles. In all this, the wireless channel, as the core component of the communication system, plays a crucial role. The characteristics of wireless channels and their accurate modeling have a decisive impact on the design of efficient, reliable, and forward-looking communication systems. The wireless channel plays a pivotal role in wireless communication systems. The characteristics of wireless channels and their accurate modeling have a decisive impact on the design of efficient, reliable, and forward-looking communication systems [2]. Wireless channel is the cornerstone of wireless network design and performance analysis, which in turn guides the design and optimization of wireless systems.
Traditional methods of channel modeling typically rely on large-scale field measurement data to ensure that models accurately reflect the physical and statistical characteristics of channels [3]. This reliance brings two major challenges: first, the field measurement process is often time-consuming and costly, especially in complex environments; second, as communication environments continuously evolve, the data required to update the model exponentially increases, further exacerbating resource burdens [4].
Deep learning technology has seen significant developments in recent years, and GAN provides a new approach to addressing these challenges. As shown in Figure 1, GAN can train a generative model by learning from a limited set of channel measurement data. This model learns the data distribution of the real channel dataset, obtains the channel distribution, and can generate a substantial volume of channel data consistent with the statistical characteristics of real channel environments [5]. Using GAN for channel modeling not only significantly reduces the amount of channel data required during the modeling process but also enhances the model’s adaptability and flexibility. Wasserstein GAN (WGAN) effectively improves the mode collapse problem in traditional GAN training by using Wasserstein distance as a loss function. The WGAN with gradient penalty (WGAN-GP) further stabilizes the training process and enables the model to generate more realistic and diverse data samples.
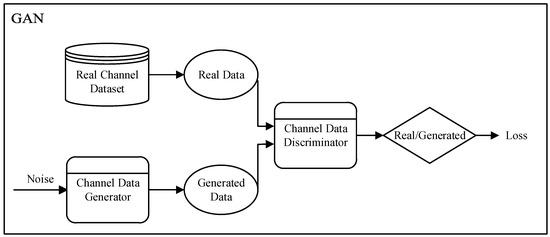
Figure 1.
Frameworks of GAN.
In the realm of this research, H. Xiao et al. [6] proposed a method named ChannelGAN based on GAN to generate a wireless channel model by learning channel measurement data. Although this study achieves significant results in the accuracy and efficiency of channel modeling, it still faces some limitations, particularly in the model’s generalization capability and the diversity of the generated channel samples. ChannelGAN performs well on specific datasets, but its ability to generalize to different environments or never-before-seen channel conditions has not been fully validated. The generated channel samples may be limited in diversity, which may result in the inadequate adaptability of the model in the face of the complex and changeable environment of the real world.
To address the above challenges, this paper introduces, for the first time, the integration of an attention mechanism with WGAN-GP in the domain of channel modeling and generating to improve the model’s capacity for learning channel characteristics. We introduce an innovative method named SE-GAN for modeling wireless channel, as illustrated in Figure 2. Based on the WGAN-GP framework, we incorporate a channel attention mechanism. This attention mechanism explicitly models the dependencies between channels, thereby enhancing the model’s capability to express and recalibrate channel features. This significantly improves the capability of the model to learn the characteristics of wireless channels and the realism of generated samples. By adaptively recalibrating the channel feature responses, the model’s ability to capture important channel features is strengthened. This approach effectively enhances the accuracy and diversity of wireless channel samples without substantially increasing computational complexity.
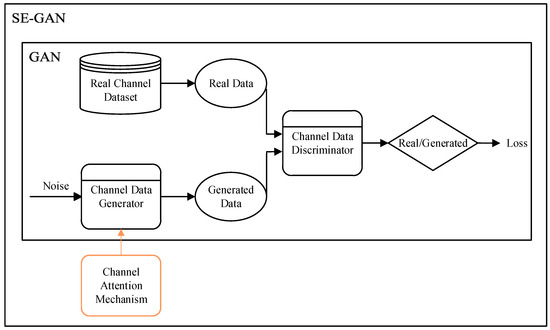
Figure 2.
Frameworks of SE-GAN.
In summary, our contributions can be concluded as follows:
- Proposing a novel approach named SE-GAN for wireless channel modeling and generating, capable of effectively modeling complex wireless environments and generating high-quality channel samples;
- Introducing the channel attention mechanism into the field of wireless channel modeling for the first time, significantly enhancing the model’s learning efficiency and the realism of generated samples;
- Demonstrating the superiority of the proposed method over the existing techniques through extensive experimental validation.
The rest of the article is organized as follows: Section 2 reviews the research status in related fields and introduces the classical methods in the field of channel modeling and generation. Section 3 describes the channel modeling and generation method proposed in this paper, focusing on the architectural details of the model used. In Section 4, the experimental simulation results are presented, and the performance of the proposed method is compared and analyzed. Finally, Section 5 concludes the paper and discusses the future research direction.
2. Related Works
In this study, clear inclusion and exclusion criteria were established to ensure that the selected literature is closely related to the latest advancements in wireless channel modeling. The inclusion criteria are as follows: first, only studies relevant to wireless channel modeling are considered, including traditional statistical models, physical models, and recent methods based on machine learning and deep learning; second, particular attention is given to the application of GAN in channel modeling and generation, especially studies published in recent years; finally, the included studies must provide a detailed description of the modeling methods, simulation processes, and experimental results, and demonstrate significant influence and citation count. The exclusion criteria include the following: first, studies unrelated to channel modeling, such as those focusing solely on communication protocols, network architectures, or other non-modeling approaches; second, early-stage studies or those not reflecting the current technological advancements, particularly those that do not consider 5G/6G environments; and finally, literature that is not publicly available, such as preprints, not peer-reviewed, or commercial reports.
Wireless channel modeling is a key link in the design and optimization of wireless communication systems, as well as a basic task for the theoretical research and practical implementation of modern wireless communication systems [7]. An accurate channel model helps to understand the specific physical effects of different wireless channels on transmitted radio signals, so as to design and deploy effective and feasible communication technologies for different transmission channels in practical application environments. However, the traditional channel modeling methods are mostly based on statistical and physical models. Although these traditional methods can accurately describe the characteristics of wireless channels in some cases, with the increasing complexity of wireless communication scenarios in the 5G and future 6G wireless communication systems [8], channel characteristics show strong time-variability and spatial heterogeneity, traditional wireless channel modeling methods are faced with many challenges. It is often difficult to adapt to the complexity and dynamics of the modern wireless communication environment and cannot provide sufficient accuracy and flexibility. In recent years, the rapid development of deep learning technology has provided new ideas and solutions for wireless channel modeling [9]. By using the powerful feature extraction and generation capabilities of deep learning models, the complex characteristics of channels can be automatically learned from channel data, and the complex characteristics of channels can be effectively captured [10] so as to achieve more accurate and flexible channel modeling and generation.
One of the channel modeling methods is to use a precision channel detector to measure various channel parameters, including direction angle, arrival angle, delay, Doppler shift, etc. These key parameters are then combined to form the channel impulse response (CIR), which will play a key role in wireless network design and performance optimization. This channel modeling method using channel detectors for channel measurement is mostly based on time division multiplexing (TDM) [11], code division multiplexing (CDM) [12], and frequency division multiplexing (FDM) [13] to describe the characteristics of the channel. Typically, such channel measurement activities using channel detectors are time-consuming and limited to a few dedicated channel measurement environments. Storing the complete impulse response requires a lot of computational resources, especially in multipath channels, where the responses of multiple different paths need to be stored. Processing and analyzing measurement data results in high computational complexity.
Deterministic channel modeling describes the input–output relationship of the channel according to the physical model and known parameters, and uses physical laws such as electromagnetic wave propagation, reflection, and refraction to describe the propagation process of signals in the channel [14]. The deterministic model assumes that the path of signal propagation is predictable and reproducible, and is not affected by random factors [15]. The shape, direction, and propagation characteristics of each path can be described by determined physical laws. Ray tracing model is a typical deterministic channel model. The ray-tracing model predicts the intensity, phase, and other characteristics of the signal at the receiving point by simulating the propagation path of electromagnetic waves (including reflection, diffraction, refraction, etc.) so as to predict the channel characteristics. Electromagnetic waves are traced as rays in a straight line [16]. This method assumes that the wave is smaller than the size of the obstacle encountered in the long run, allowing the wave effect to be ignored and only the geometric path of the ray to be considered. Ray-tracing models can provide accurate prediction of channel characteristics, but require detailed modeling of the environment, including geometric shapes and material properties of buildings, terrain, and obstacles [17]. If the environment model is not accurate, the results of the channel model may be distorted. In addition, the modeling process often requires a large amount of prior knowledge and data.
Stochastic channel modeling regards channel characteristics as random variables and describes signal propagation characteristics in the channel through a probability distribution. This modeling method is based on stochastic processes and statistical principles, and takes into account the randomness and uncertainty of channel characteristics. The geometric stochastic channel model (GSCM) is a typical stochastic channel modeling method. GSCM is obtained by using the basic laws of the reflection, diffraction, and scattering of electromagnetic waves in the environment of many scatterers with a certain distribution [18], which can reproduce the random characteristics of different types of wireless channels with time, frequency, and space. GSCM can be described in terms of the selected parameters such as departure angle and arrival angle [19]. These parameters are randomly selected according to a specific distribution. However, in the real environment, the stochastic factors of the channel are usually complex and coupled [20]. In geometric-based stochastic channel models, although these factors can be modeled separately, their coupling relationships can be difficult to accurately capture, resulting in the limited fidelity and accuracy of the model.
Channel modeling based on principal component analysis (PCA), using the PCA method to characterize and model multiple input multiple output (MIMO) channels. This method can extract some hidden features and structures from the measured channel data, and combined with the detailed information of the measurement environment and antenna configuration [21], effectively reconstruct the amplitude and phase of the CIR, which can effectively support the high antenna number of massive MIMO. PCA is a linear dimensionality reduction method, which assumes that the main information in the channel data can be extracted through linear combination [22]. However, in real wireless channels, many complex nonlinear factors may cause the channel characteristics to exhibit nonlinear behavior. PCA is unable to capture these nonlinear characteristics effectively, which may lead to a decrease in modeling accuracy.
Digital twin technology creates a virtual replica of a physical system to dynamically reflect its behavior and state in real time. The channel modeling method based on digital twin integrates sensor data, real-time monitoring, and simulation models to dynamically simulate channel characteristics in wireless communication environments, providing real-time adaptability to complex communication scenarios. In this method, a virtual model is first constructed to accurately reflect the physical properties of the communication system. The digital twin not only predicts based on historical data but also responds to environmental changes in real time, providing the system with accurate channel state information. The main advantage of digital twin technology lies in its ability to reflect changes in the physical world in real time [23]. This is particularly important for wireless communication systems, as channel conditions are often influenced by various factors, such as the environment, user behavior, and weather. Through digital twins, the communication system can dynamically adjust the channel model based on real-time data to improve communication quality and network performance. However, the real-time updating and simulation process of the digital twin model typically requires substantial computational resources.
Channel modeling based on a machine learning algorithm uses machine learning technology to analyze and model wireless communication channels. Different from traditional channel modeling methods, machine learning algorithms model and predict channel characteristics by automatically learning patterns and features from a large amount of data [24]. It can capture complex nonlinear relationships and implicit features without relying on specific physical models or preset assumptions [25]. Clustering technology is a common machine learning method. Channel modeling based on clustering technology identifies channel state groups or patterns with similar propagation characteristics through cluster analysis of channel characteristic data, thus simplifying channel modeling methods. Clustering techniques aim to divide data into multiple categories or clusters based on their similarity [26]. In wireless channel modeling, clustering technology can help find regularity or structure in channel behavior so as to better understand and predict the performance of wireless channels [27]. Clustering technology groups channel characteristics by statistical methods, but usually does not directly consider the physical propagation mechanism of the channel. This can lead to a lack of physical interpretability in the channel model, making it difficult to provide a deep physical understanding [28]. The clustering method also needs a lot of data support to ensure the reliability and validity of the clustering results. If the amount of channel data are insufficient or the quality of the data are poor, the clustering results may be inaccurate, which will affect the effect of channel modeling.
Channel modeling based on deep learning is a method that uses deep learning technology to model, predict, and optimize wireless communication channels. Deep learning builds and trains multi-layer neural network models to automatically extract features from data and make predictions [29]. Deep learning can recognize complex patterns and structures, and is widely used in speech recognition, image processing, natural language processing, and other fields. In recent years, it has been introduced into wireless communication [30], especially in channel modeling and prediction tasks. By learning the complex features of a large number of channel data, this method can more accurately simulate and predict the changes in signals in the propagation process [31], especially in a complex and dynamic wireless environment, which can improve the prediction accuracy of channels and network performance.
3. Modeling and Generating
This research focuses on a MIMO communication system. There are transmitting antennas at the base station (BS) end and receiving antennas at the user equipment (UE) end [32]. Thus, a time-domain real channel with an orthogonal frequency division multiplexing (OFDM) symbol can represent , where represents the number of delay paths. Further, the real channel is reformulated with a normalized amplitude , where represents the logarithm of the antenna, and the last dimension with a value of 2 represents the real and imaginary parts of the original complex channel, respectively.
The channel modeling involves identifying a generated channel distribution that is tailored to match the distribution of the real channel. This can be described as follows:
where is the true distribution of the real channel , but theoretically an infinite number of real channel data are needed to obtain . Therefore, a small dataset of real channel characterized by the distribution is used for channel modeling. This paper introduces a channel modeling and generating solution SE-GAN based on WGAN-GP, which can model the channel distribution more accurately by utilizing less channel data. represents the generated channel and generates the channel dataset , and . Therefore, Equation (1) can be approximated as follows:
In this study, we do not aim to explicitly find a minimum or maximum value in the traditional sense. Instead, the optimization process in the GAN is generally about approximating the optimal solution rather than directly solving for the optimal value. Therefore, related formulas do not explicitly represent the minimum or maximum, but rather depict the adversarial training process between the generator and discriminator. The objective functions in these formulas are not defined to directly minimize or maximize a particular value, but are optimized to approach an optimal generation outcome.
3.1. WGAN-GP
In order to realize complex channel modeling on complex channel dataset, WGAN-GP has strong stability during training, so this study builds upon WGAN-GP as the foundational network for SE-GAN. WGAN-GP evolved from WGAN, which itself evolved from GAN. The Generative Adversarial Network (GAN) consists of a generator (G) and a discriminator (D). The generator aims to produce data that closely mimics the distribution of real data, and the discriminator aims to distinguish between real and generated data. The training process of GAN can be conceptualized as a minimax problem, where the objective function is represented as follows:
where denotes the discriminator’s proficiency in identifying the real data from . is sampled from the real data distribution . The goal of the discriminator is to maximize the recognition probability of the real sample, that is, to maximize . represents the probability that the discriminator will judge to be the real sample, so the greater the , the greater the probability that the discriminator will judge to be the real data. denotes the discriminator’s capacity to detect the data G(z) generated by the generator. represents the data generated by the generator, [33]. The goal of the generator is to generate as much data as possible that the discriminator will judge as true, that is, to minimize the probability that , where indicates the probability that the discriminator will judge that the generated sample is generated by the generator instead of the original data. So, the smaller , the better the discriminator will judge the generator to be the real data.
WGAN introduces an approach by employing the Wasserstein distance to quantify the separation between the actual data distribution and the generated data distribution. The Wasserstein distance is defined as follows:
where represents the lower bound, finding the lowest value of the cost function of all the possible joint distributions . represents the set of all the possible joint distributions whose marginal distributions are and , respectively. said in a joint under the distribution, transfer from to average minimum cost of a data unit.
WGAN trains the models by minimizing the Wasserstein distance with the following objective function:
where represents the expected value of the discriminator output for sample in the real data distribution . represents the expected value of the discriminator output of the data generated by the generator for sample in the noise distribution . represents the set encompassing all the 1-Lipschitz functions, ensuring that the discriminator function maintains Lipschitz continuity [34].
WGAN-GP forces the discriminator to adhere to the 1-Lipschitz constraint by introducing a gradient penalty term, which is defined as follows:
where is the weight parameter of the gradient penalty, which is used to adjust the proportion of the gradient penalty term in the total loss. represents the expectation of the interpolated sample , where , and represents a weight sampled from the uniform distribution , employed to interpolate between the real sample and the generated sample . is the 2-norm (Euclidean norm) of the gradient of the discriminator output with respect to . ensures that the gradient norm of the discriminator is 1 almost everywhere in its entire input space, satisfying the 1-Lipschitz constraint [35]. In summary, the overall objective function of WGAN-GP is as follows:
This objective function aims to train the generator and discriminator by minimizing the Wasserstein distance and ensuring 1-Lipschitz constraints, thereby improving the stability of the training and the quality of the generated data. This is especially important for wireless channel modeling and generation, as such applications require highly accurate and realistic generated data to simulate real-world wireless channel conditions.
3.2. SE-GAN
This study incorporates the channel attention module (Squeeze-and-Excitation layer, SEL) into the generator of WGAN-GP, our model adaptively recalibrates the importance of each feature channel, focusing on features critical for accurate channel modeling. This method not only strengthens the model’s ability to capture channel characteristics but also elevates the quality of generated channel samples. Moreover, the introduction of the attention mechanism fosters improved training stability and efficiency, allowing the model to adeptly adjust to complex and dynamic wireless environments. Overall, this innovative combination of attention mechanisms with WGAN-GP provides a fresh perspective and an effective tool for wireless channel modeling, showcasing substantial improvements and benefits.
The channel attention module SEL is an advanced channel attention mechanism that plays a crucial role in deep neural networks by adaptively assigning varying levels of importance to different feature channels. This module is designed to enhance the representation capabilities of the network by recalibrating the channel-wise feature responses. The underlying idea is that not all feature channels contribute equally to the task at hand, and some channels may contain more valuable or task-specific information. Therefore, it is essential to focus more on these critical channels while suppressing less informative ones. It is designed to assign varying degrees of importance to different feature channels based on their contributions to the model’s outputs. Some channels may contain more valuable information for the specific task. By introducing a mechanism that adaptively adjusts the importance of each channel, the model focuses on the most critical feature channels, thereby enhancing overall performance. Figure 3 illustrates the structure of SEL, which consists of three main parts: global spatial information compression, feature channel recalibration, and feature reweighting.
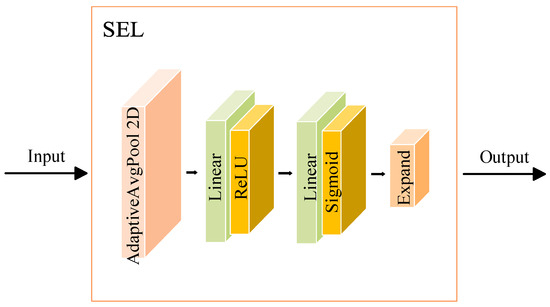
Figure 3.
Structure of SEL.
3.2.1. Global Spatial Information Compression
SEL starts by utilizing AdaptiveAvgPool2D to compress the spatial dimensions of input feature maps, thereby extracting global spatial features for each channel. The AdaptiveAvgPool2D is a module defined in the PyTorch library. It is used to perform adaptive average pooling, which automatically adjusts the output feature map size based on the input dimensions. This step aids in capturing the global statistical characteristics of each channel, providing a foundation for subsequent importance evaluations. The concrete description is given an input tensor x of shape, the layer applies a global average pooling operation using AdaptiveAvgPool2D. This operation reduces each spatial dimension of the feature map to 1, effectively obtaining a scalar value for each channel. This scalar is an aggregated representation of the global information for each feature channel. The result is a tensor y of shape, which contains the global average of each channel’s feature map. This step compresses spatial information and distills each channel’s most important features for further processing, eliminating the need for spatial positioning information in the recalibration process.
3.2.2. Feature Channel Recalibration
After obtaining the global statistics of each channel, SEL recalibrates the importance of each feature channel through a fully connected network (a simple MLP). This consists of two fully connected layers:
The first fully connected layer reduces the number of features from the original channel size to a smaller size, controlled by the parameter reduction. This reduction step reduces computational overhead and encourages the model to learn more efficient representations. The number of channels is reduced by a factor determined by the reduction parameter, typically set to 16 or other values depending on the task. The ReLU activation is applied to introduce nonlinearity and enhance the model’s expressiveness, enabling it to learn complex relationships in the data.
The second fully connected layer restores the channel dimension to its original size. This transformation concludes with the Sigmoid activation function, which outputs a set of scalar values between 0 and 1, one per channel. These scalar values represent the attention weight for each feature channel, indicating its importance in the final decision-making process.
In short, the compressed features are processed through a network consisting of two fully connected layers. The first layer, a linear layer, reduces the dimensionality of the features, decreasing parameter count and computational complexity while enhancing the model’s expressiveness through a ReLU activation function. The second linear layer restores the dimensions and concludes with a Sigmoid activation function that outputs the weight coefficients for each channel.
3.2.3. Feature Reweighting
The calculated weight coefficients are multiplied back onto the original feature channels, dynamically recalibrating the characteristics of each channel’s features. The Expand step extends the weight coefficients to match the spatial dimensions of the original feature map, ensuring that each channel’s features are appropriately scaled by the corresponding weight coefficient.
Once the weight coefficients (attention scores) have been computed, the final crucial step is to re-weight the original feature map by multiplying it with the attention values. The output tensor y from the fully connected layers has a shape. To apply these attention weights across the spatial dimensions of the input feature map, we use the Expand method to match the original size of the input feature map. This step ensures that each channel in the input feature map is multiplied by its corresponding weight across all the spatial locations.
The resulting tensor is then returned as the output of the SEL, with the feature map dynamically adjusted according to the learned attention weights. This adjustment allows the model to focus on more important features and suppress less relevant ones, ultimately improving the model’s performance by enhancing the representation of important channels.
The SE-GAN structure is depicted in Figure 4. The generator is a key component of the SE-GAN, specifically designed for channel modeling and generation tasks. The generator is responsible for transforming a latent vector, which typically represents a random noise or encoded information, into a structured output that simulates the distribution of real data. The generator is composed of linear blocks and transposed convolution blocks, incorporating a channel attention mechanism SEL. The primary function of the linear block is to map the latent vector into a high-dimensional feature space. The linear block serves as the initial stage of the generator, where the latent vector is processed to form an initial feature map that will later be up-sampled through transposed convolutions. Specifically, a fully connected layer maps the input latent vector to a feature vector of a designated dimension, helping the model learn richer feature representations. This is followed by the batch normalization of the feature vector to accelerate the training process and stabilize model training. Subsequently, a Leaky ReLU activation function introduces a nonlinear transformation, enhancing the model’s expressive capability. This activation function enhances the model’s ability to capture nonlinear relationships in the data. The transposed convolution block comprises five transposed convolution layers, each followed by a batch normalization layer, an SEL, and a Leaky ReLU activation function to adaptively recalibrate the importance of different channels during the up-sampling process. The SEL is crucial for generating high-quality outputs that capture detailed and meaningful patterns. The fifth transposed convolution layer up-samples the feature map to a single channel, and the generated channel data are output through a Tanh activation function, which normalizes the values to the range of [−1, 1]. This is a common practice in channel modeling tasks to ensure that the generated data values fall within the correct range.
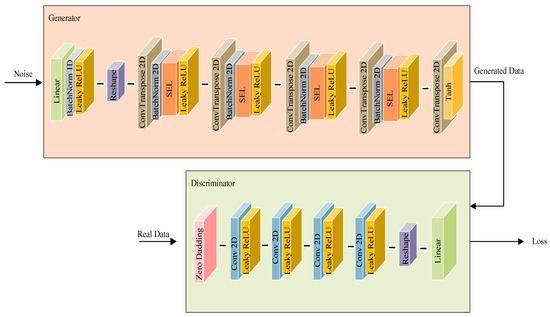
Figure 4.
Structure of SE-GAN.
The discriminator is another key component of the SE-GAN. The discriminator’s primary responsibility is to distinguish between real and generated data by learning to assign a probability score that indicates whether input data are real or fake. The discriminator achieves this through a series of convolutional layers followed by fully connected layers, enabling it to effectively capture local patterns and spatial features in the input data. The discriminator consists of three main modules: a zero-padding module, a convolution block, and a linear block. The zero-padding module preprocesses the input signal through a zero-padding function. This padding adds zeros at the bottom of the data, which ensures that the spatial information at the boundaries is maintained. This operation aims to preserve the spatial features of the signal, preventing information loss during subsequent convolution operations. The convolution block is composed of four convolution layers and four Leaky ReLU activation functions. The output of the convolution block is flattened via a view function into a high-dimensional vector, which is then fed into the linear block. These layers help the model learn hierarchical features from the input data at different levels of abstraction. The convolutional layers also progressively reduce the spatial size of the data while increasing the number of feature maps. The linear block includes a fully connected layer that projects the high-dimensional input vector into a one-dimensional output. The input signal first passes through the zero-padding module, then through the convolution block for feature extraction, and finally through the linear block for discrimination, outputting a scalar value. This scalar value indicates the probability of the input signal belonging to either real (if close to 1) or generated channel data (if close to 0).
4. Experimental Simulation Analysis
Extensive simulation experiments were performed to validate the effectiveness of the proposed algorithm, with detailed simulation parameters provided in Table 1. In our experiments, the training process was conducted on an NVIDIA GeForce RTX 4060 GPU. Each experiment involved 200 training epochs, with a total training time of approximately 16 min. To ensure the accuracy and representativeness of the proposed channel model, the simulation parameters chosen in this study must align with the parameters used in the actual communication system from which the dataset is derived. Specifically, the parameters are selected based on the settings from real-world communication environments. This alignment ensures that the generated channel model accurately reflects the behavior of the actual system during the simulation process. By maintaining consistency between the simulation parameters and the real-world system, the experimental results are better aligned with practical applications, thus enhancing the validity and reliability of the model. We numerically assessed the consistency and variability between real channel data and generated channel data using similarity and diversity metrics. The dataset employed in this study is derived from a MIMO channel environment configured with 32 transmit antennas and 4 receive antennas. It consists of 4000 distinct samples, each representing the complete channel state information for a single channel realization, making it well suited for channel estimation and modeling in MIMO systems. Specifically, the dataset is provided in a MATLAB (R2018b) file format, encompassing all the channel information matrices. The data of each sample is expressed as a complex number, and the amplitude and phase information can be obtained by the real and imaginary parts of the complex number. Each sample comprises 4096 data points, structured into a 4 × 32 matrix that captures the channel gains between the 4 receive antennas and the 32 transmit antennas. To comprehensively account for the delay spread effects in MIMO systems, each sample also incorporates 32 delay spread components. Specifically, the data dimensions are arranged in the order of 4 × 32 × 32, enabling effective characterization of the spatial and temporal properties of the channel.

Table 1.
Simulation parameter.
4.1. Similarity and Diversity Comparison
We use the similarity index and diversity index to verify the consistency and discreteness of real channel data and generated channel data, and the similarity is expressed as follows:
where denotes the number of samples generated by our model, is the number of real channel samples, is the vectorized channel of the th generated sample, and is the vectorized channels of the th real samples, respectively. is the squared magnitude of the inner product between the generated and real channel vectors, serving as a measure of their similarity.
The computation of variance is employed to produce the diversity within the channel data, and this diversity is represented as follows:
where represents the variance calculation on the vector , and each element in [, is represented as follows:
where represents the normalized squared inner product of the generated and real channel vectors, serving as a similarity measure between the two vectors.
Table 2 provides a detailed comparison of the similarity and diversity results for the channel data generated by both the SE-GAN and ChannelGAN models. The results clearly show that when the generated channel data have high similarity and low diversity compared to the actual channel data, the Multi/Sim ratio is low. A lower Multi/Sim ratio indicates that the distribution of the generated synthetic channel data closely matches the distribution of real channel data, which is a critical factor in assessing the quality of the generated data, Table A1 in Appendix A provides some of the generated data.

Table 2.
Similarity and diversity of different channel modeling and generating schemes.
From the numerical results, it is evident that SE-GAN outperforms ChannelGAN in terms of similarity. The data generated by SE-GAN shows significantly higher similarity to the real channel data, demonstrating SE-GAN’s ability to more accurately capture the key characteristics and statistical properties of the real channel. Additionally, the diversity of the data generated by SE-GAN is notably lower than that of ChannelGAN, further reinforcing SE-GAN’s superior performance. While diversity can be important in some contexts, the focus here is on the accuracy and realism of the generated data, where lower diversity aligns with a more faithful representation of real channel data.
Moreover, the overall evaluation metric, Multi/Sim, is considerably lower for SE-GAN compared to ChannelGAN, signifying that the synthetic data produced by SE-GAN is much closer to the true data distribution. This lower Multi/Sim ratio directly reflects SE-GAN’s better alignment with the real channel data, making it more suitable for applications that require high fidelity in channel modeling.
In summary, the experimental findings clearly demonstrate that the SE-GAN model proposed in this study produces higher similarity and lower diversity in the generated channel data compared to ChannelGAN. As a result, SE-GAN generates a synthetic data distribution that is much closer to the real channel data distribution. These superior outcomes confirm that SE-GAN is the more effective model for channel modeling tasks, making it the optimal choice for generating high-quality, realistic channel data.
4.2. Data Loading and Generating Time Comparison
The SE-GAN model’s network structure has been meticulously optimized to achieve higher efficiency in both the data loading and generation processes for wireless channel data. This optimization ensures that SE-GAN not only improves the accuracy of generated data but also significantly enhances computational efficiency, making it more suitable for large-scale and real-time applications.
To rigorously evaluate the time efficiency of SE-GAN, an experiment was conducted where both SE-GAN and ChannelGAN were required to generate 4000 data samples under identical conditions. The goal of this evaluation was to compare their performance in terms of processing speed during both the data loading and data generation stages. The experimental results, presented in Table 3, reveal a clear advantage for SE-GAN in terms of speed. Specifically, SE-GAN completes the data loading stage in a significantly shorter time than ChannelGAN, demonstrating its superior ability to handle and preprocess large volumes of data efficiently. Furthermore, SE-GAN also exhibits a marked improvement in the data generation stage, producing synthetic channel data at a faster rate than ChannelGAN.

Table 3.
Data loading and generating times for different channel modeling and generating schemes.
The reason behind this substantial improvement lies in the integration of the SE block within SE-GAN, which enhances the network’s focus on important features by adaptively recalibrating channel-wise feature responses. This targeted attention mechanism allows SE-GAN to allocate computational resources more effectively, leading to increased learning efficiency and reduced data processing time. By dynamically prioritizing critical features, SE-GAN not only accelerates convergence during training but also ensures that the most relevant information is retained during data generation, further improving overall performance.
These experimental findings strongly indicate that SE-GAN has a significant advantage over ChannelGAN in terms of both accuracy and efficiency. While ChannelGAN may still generate diverse data, it suffers from longer data loading and generation times, making it less suitable for scenarios requiring rapid processing and real-time performance. In contrast, SE-GAN’s optimized structure and feature recalibration mechanism allow it to achieve superior computational efficiency, making it the preferred choice for high-speed, high-accuracy wireless channel data generation tasks.
5. Conclusions
In this paper, we propose a novel wireless channel modeling and generation scheme SE-GAN. SE-GAN is based on WGAN-GP to optimize the network structure by combining attention modules, aiming to improve the efficiency and quality of wireless channel data modeling and generation. Through a large number of experiments, we comprehensively evaluated the performance of SE-GAN in terms of the similarity, diversity, and time required to generate data. As a novel wireless channel modeling and generating scheme, SE-GAN has shown remarkable advantages in these aspects, indicating that SE-GAN has a wide range of application prospects in the field of wireless channel modeling and generating.
Future research will further investigate the application of SE-GAN in various wireless communication environments, particularly focusing on its performance in complex channel models and multi-path propagation scenarios. The variations in these environments can significantly affect the accuracy and stability of the model, necessitating an in-depth exploration of how adjustments in network architecture and training strategies can enhance the model’s adaptability and robustness.
Additionally, we plan to investigate the development of fuzzy logic rule bases derived from real-world data to model channel behavior more accurately. Given the dynamic and uncertain nature of wireless communication environments, we aim to explore how these rule bases, constructed from high-quality real data, can be integrated into the system to enable real-time adjustments of channel characteristics.
Author Contributions
Conceptualization, Y.H. and N.X.; formal analysis, Y.H. and L.C.; funding acquisition, L.C.; methodology, Y.H. and L.C.; resources, Y.H. and H.Y.; software, Y.H. and H.Y.; validation, Y.H. and N.X.; writing—original draft, Y.H.; writing—review and editing, Y.H. and L.C. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by the National Natural Science Foundation of China under Grant No. 62401411 and the New Engineering Project of Hubei Province No. XGK03070, and is also supported by the Wuhan Municipal Natural Science Foundation under Grant No. 2024040801020323.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Acknowledgments
The authors would like to express their sincere thanks to the editor and the anonymous reviewers for their valuable suggestions.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this paper:
| GAN | Generative Adversarial Network |
| WGAN | Wasserstein GAN |
| WGAN-GP | Wasserstein GAN with gradient penalty |
| CIR | channel impulse response |
| TDM | time division multiplexing |
| CDM | code division multiplexing |
| FDM | frequency division multiplexing |
| GSCM | geometric stochastic channel model |
| PCA | principal component analysis |
| MIMO | multiple input multiple output |
| BS | base station |
| UE | user equipment |
| OFDM | orthogonal frequency division multiplexing |
| SEL | Squeeze-and-Excitation layer |
| SE-GAN | The model proposed in this study |
Appendix A
We provide 20 sets of data for the first transmitting antenna and the first receiving antenna under the first delay spread. These data encompass several important dimensions, including the real part, imaginary part, magnitude, and phase. By presenting these detailed datasets, we aim to offer readers a more comprehensive and in-depth perspective, thereby facilitating a better understanding of the performance and characteristics of the model we have proposed.

Table A1.
The first 20 sets of data for the first transmitting antenna and the first receiving antenna under the first delay spread.
Table A1.
The first 20 sets of data for the first transmitting antenna and the first receiving antenna under the first delay spread.
| Real | Imaginary | Magnitude | Phase |
|---|---|---|---|
| −0.340249985 | −0.129639252 | 0.364110407 | −2.777561828 |
| −0.807743013 | −0.105123891 | 0.814554975 | −3.012174847 |
| −0.74634701 | 1.830609924 | 1.976908332 | 1.9579264 |
| 2.955234469 | 0.259716469 | 2.966624919 | 0.087658327 |
| −0.052083001 | −0.844535693 | 0.846140163 | −1.632388895 |
| −0.276836008 | −0.213868771 | 0.349825709 | −2.48381706 |
| 0.472559686 | 2.263887156 | 2.31268193 | 1.365012962 |
| 1.951065774 | −1.359609416 | 2.378065478 | −0.608611925 |
| −0.855656028 | 1.682818514 | 1.887862651 | 2.041193789 |
| −0.199449003 | 2.590459286 | 2.598126097 | 1.647638409 |
| 4.937171633 | −0.350005802 | 4.949562384 | −0.070773563 |
| −1.302168012 | −0.225127801 | 1.321485549 | −2.970398022 |
| 0.670167902 | 1.109511941 | 1.296202826 | 1.027425856 |
| −0.665766001 | −0.540717236 | 0.857682632 | −2.45947304 |
| −0.051261999 | 0.006741622 | 0.051703404 | 3.010830039 |
| −0.400198996 | 0.228369327 | 0.460773031 | 2.623041632 |
| 0.894700729 | 0.44779271 | 1.000503726 | 0.464043056 |
| 2.015706484 | −0.397091996 | 2.054447537 | −0.194508246 |
| 0.862048715 | 0.521083309 | 1.007301246 | 0.543700398 |
| 0.162148225 | −0.290537894 | 0.33272258 | −1.061758138 |
References
- Tataria, H.; Shafi, M.; Molisch, A.F.; Dohler, M.; Sjöland, H.; Tufvesson, F. 6G Wireless Systems: Vision, Requirements, Challenges, Insights, and Opportunities. Proc. IEEE 2021, 109, 1166–1199. [Google Scholar] [CrossRef]
- Zhang, H.; Song, W.; Liu, X.; Sheng, M.; Li, W.; Long, K.; Dobre, O.A. Intelligent Channel Prediction and Power Adaptation in LEO Constellation for 6G. IEEE Netw. 2023, 37, 110–117. [Google Scholar] [CrossRef]
- Xie, W.; Xiao, J.; Zhu, P.; Yu, C. Multi-Task Learning-Based Channel Estimation for RIS Assisted Multi-User Communication Systems. IEEE Commun. Lett. 2022, 26, 3577–3581. [Google Scholar] [CrossRef]
- Wei, Y.; Zhao, M.-M.; Zhao, M.-J. Channel Distribution Learning: Model-Driven GAN-Based Channel Modeling for IRS-Aided Wireless Communication. IEEE Trans. Commun. 2022, 70, 74482–74497. [Google Scholar] [CrossRef]
- Yang, Y.; Li, Y.; Zhang, W.; Qin, F.; Zhu, P.; Wang, C.-X. Generative-Adversarial-Network-Based Wireless Channel Modeling: Challenges and Opportunities. IEEE Commun. Mag. 2019, 57, 322–327. [Google Scholar] [CrossRef]
- Xiao, H.; Tian, W.; Liu, W.; Shen, J. ChannelGAN: Deep Learning-Based Channel Modeling and Generating. IEEE Wirel. Commun. Lett. 2022, 11, 3650–3654. [Google Scholar] [CrossRef]
- He, R.; Schneider, C.; Ai, B.; Wang, G.; Zhong, Z.-D.; Dupleich, D.A.; Thomae, R.S.; Boban, M.; Luo, J.; Zhang, Y. Propagation channels of 5g millimeter-wave vehicle-to-vehicle communications: Recent advances and future challenges. IEEE Veh. Technol. Mag. 2020, 15, 116–126. [Google Scholar] [CrossRef]
- Wang, C.-X.; Haider, F.; Gao, X.; You, X.-H.; Yang, Y.; Yuan, D.; Aggoune, H.; Haas, H.; Fletcher, S.; Hepsaydir, E. Cellular Architecture and Key Technologies for 5G Wireless Communication Networks. IEEE Commun. Mag. 2014, 52, 2122–2130. [Google Scholar] [CrossRef]
- Paguada, S.; Batina, L.; Buhan, I.; Armendariz, I. Playing With Blocks: Toward Re-Usable Deep Learning Models for Side-Channel Profiled Attacks. IEEE Trans. Inf. Forensics Secur. 2022, 17, 2835–2847. [Google Scholar] [CrossRef]
- Zhang, J. The interdisciplinary research of big data and wireless channel: A cluster-nuclei based channel model. China Commun. 2016, 13, 14–26. [Google Scholar] [CrossRef]
- Baum, D.S.; El-Sallabi, H.; Jämsä, T.; Meinilä, J.; Kyösti, P.; Zhao, X.; Laselva, D.; Nuutinen, J.-P.; Hentilä, L.; Vainikainen, P.; et al. Commission of WINNER, release document IST-WINNER D5.4 ver 1.4. Final Report on Link and System Level Channel Models. October 2005. Available online: https://www.researchgate.net/publication/229031750_IST-2003-507581_WINNER_D5_4_v_14_Final_Report_on_Link_Level_and_System_Level_Channel_Models (accessed on 15 June 2024).
- Paschalidis, P.; Wisotzki, M.; Kortke, A.; Keusgen, W.; Peter, M. Wideband Channel Sounder for Car-to-Car Radio Channel Measurements at 5.7 GHz and Results for an Urban Scenario. In Proceedings of the 2008 IEEE 68th Vehicular Technology Conference, Calgary, AB, Canada, 21–24 September 2008. [Google Scholar]
- Talebi, F.; Pratt, T. Channel Sounding and Parameter Estimation for a Wideband Correlation-Based MIMO Model. IEEE Trans. Vehic. Technol. 2016, 65, 2499–2508. [Google Scholar] [CrossRef]
- Liu, G.; She, J.; Lu, W.; Zhang, M.; Bo, Y. 3D deterministic ray tracing method for massive MIMO channel modelling and parameters extraction. IET Commun. 2020, 14, 3169–3174. [Google Scholar] [CrossRef]
- Zhumayeva, M.; Dautov, K.; Hashmi, M.; Nauryzbayev, G. Wireless energy and information transfer in WBAN: A comprehensive state-of-the-art review. Alex. Eng. J. 2023, 85, 261–285. [Google Scholar] [CrossRef]
- Tamaddondar, M.M.; Noori, N. 3D Massive MIMO Channel Modeling With Cluster Based Ray Tracing Method. In Proceedings of the 2019 27th Iranian Conference on Electrical Engineering, Yazd, Iran, 30 April–2 May 2019; pp. 1249–1253. [Google Scholar]
- Tamaddondar, M.M.; Noori, N. 3D Cluster-Based Ray Tracing Technique for Massive MIMO Channel Modeling. Adv. Electromagn. 2021, 10, 36–45. [Google Scholar] [CrossRef]
- Wang, J.; Cheng, W.; Zhang, W.; Zhang, W.; Zhang, H. Multi-frequency access for magnetic induction-based SWIPT. IEEE J. Sel. Areas Commun. 2022, 40, 1679–1691. [Google Scholar] [CrossRef]
- Huang, C.; Wang, R.; Wang, C.-X.; Tang, P.; Molisch, A.F. A Geometry-Based Stochastic Model for Truck Communication Channels in Freeway Scenarios. IEEE Trans. Commun. 2022, 70, 85572–85586. [Google Scholar] [CrossRef]
- Li, Y.; Cheng, X. New deterministic and statistical simulation models for non-isotropic UAV-MIMO channels. In Proceedings of the 2017 9th International Conference on Wireless Communications and Signal Processing (WCSP), Nanjing, China, 1–13 October 2017. [Google Scholar]
- Ma, X.; Zhang, J.; Zhang, Y.; Ma, Z.; Zhang, Y. A PCA-Based Modelling Method for Wireless MIMO Channel. In Proceedings of the 2017 IEEE Conference on Computer Communications: Workshops (INFOCOM WKSHPS), Atlanta, GA, USA, 1–4 May 2017; pp. 874–879. [Google Scholar]
- Yang, B.; Zhang, X.; Chen, L.; Gao, Z. Principal Component Analysis-Based Visual Saliency Detection. IEEE Trans. Broadcast. 2016, 62, 4842–4854. [Google Scholar] [CrossRef]
- Zhang, Y.; He, R.; Ai, B.; Yang, M.; Chen, R.; Wang, C.; Zhang, Z.; Zhong, Z. Generative adversarial networks based digital twin channel modeling for intelligent communication networks. China Commun. 2023, 20, 832–843. [Google Scholar] [CrossRef]
- Aldossari, S.M.; Chen, K.C. Machine Learning for Wireless Communication Channel Modeling: An Overview. Wirel. Pers. Commun. 2019, 106, 41–70. [Google Scholar] [CrossRef]
- Lee, H.-S. Channel Metamodeling for Explainable Data-Driven Channel Model. IEEE Wirel. Commun. Lett. 2021, 10, 122678–122682. [Google Scholar] [CrossRef]
- Cui, Z.; Guan, K.; Oestges, C.; Briso-Rodríguez, C.; Ai, B.; Zhong, Z. Cluster-Based Characterization and Modeling for UAV Air-to-Ground Time-Varying Channels. IEEE Trans. Veh. Technol. 2022, 71, 76872–76883. [Google Scholar] [CrossRef]
- Zhou, T.; Feng, T.; Zhang, W.; Ai, B.; Liu, L.; Liang, Y. A Cluster-Based Dynamic Narrow-Beam Channel Model for Vehicle-to-Infrastructure Communications. IEEE Trans. Wirel. Commun. 2024, 23, 1115858–1115871. [Google Scholar] [CrossRef]
- Zhang, Z.; He, R.; Ai, B.; Yang, M.; Niu, Y.; Zhong, Z.; Li, Y.; Zhang, X.; Li, J. A Cluster-Based Statistical Channel Model for Integrated Sensing and Communication Channels. IEEE Trans. Wirel. Commun. 2024, 23, 911597–911611. [Google Scholar] [CrossRef]
- Yin, S.; Li, Y.; Tian, Y.; Yu, F.R. Intelligent Reflecting Surface Enhanced Wireless Communications with Deep-Learning-Based Channel Prediction. IEEE Trans. Veh. Technol. 2022, 71, 11049–11053. [Google Scholar] [CrossRef]
- Wan, W.; Chen, W.; Wang, S.; Li, G.Y.; Ai, B. Deep Plug-and-Play Prior for Multitask Channel Reconstruction Massive MIMO Systems. IEEE Trans. Commun. 2024, 72, 74149–74162. [Google Scholar] [CrossRef]
- Chen, J.; Meng, F.; Ma, N.; Xu, X.; Zhang, P. Model-Driven Deep Learning-Based Sparse Channel Representation and Recovery for Wideband mmWave Massive MIMO Systems. IEEE Trans. Veh. Technol. 2023, 72, 1216788–1216793. [Google Scholar] [CrossRef]
- Yang, Y.; Gui, Y.; Wang, H.; Zhang, W.; Li, Y.; Yin, X.; Wang, C.-X. Parallel Channel Sounder for MIMO Channel Measurements. IEEE Wireless Commun. 2018, 25, 516–522. [Google Scholar] [CrossRef]
- Goodfellow, I.J.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial nets. arXiv 2014, arXiv:1406.2661. [Google Scholar]
- Arjovsky, M.; Chintala, S.; Bottou, L. Wasserstein GAN. arXiv 2017, arXiv:1701.07875. [Google Scholar]
- Gulrajani, I.; Ahmed, F.; Arjovsky, M.; Dumoulin, V.; Courville, A. Improved training of Wasserstein GANs. arXiv 2017, arXiv:1704.00028. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).