4.1. Datasets
In this experiment, both synthetic and real-world datasets are used to validate the effectiveness of the proposed method. The synthetic data are generated using the Massive Online Analysis (MOA) toolbox [
36] to create drift data and static data (without drift). MOA (
https://moa.cms.waikato.ac.nz/(accessed on 10 May 2024)) is a software environment for evaluating algorithms and conducting online streaming data learning experiments, containing numerous stream data generators. This study selects several generators to produce single-drift and multi-drift type data, including Agrawal (AGR), SEA, Sine, Mixed, and Hyperplane (HYP). Details of the synthetic datasets can be found in
Table 1 and
Table 2.
In
Table 1, the SEA, Sine, Mixed, and AGR datasets were generated with both abrupt and gradual drift types. According to the MOA reference manual, the HYP generator is specifically used to generate incremental data, and its method of generating drift data differs from that of the other datasets. As the classification function of the data cannot be altered, multi-drift data were not generated for the HYP dataset. All datasets contain 10,000 instances and are balanced binary-class datasets. Taking the SEA dataset as an example, when the drift position is set to 5000 and the width to 1, an abrupt SEA is generated. In this case, data before point 5000 correspond to the old concept, while data after point 5000 correspond to the new concept. When the drift position is set to 4500 and the width to 1000, a gradual SEA is generated. In this scenario, data before point 4500 correspond to the old concept, and drift begins at point 4500, lasting for 1000 instances. After point 5500, the drift ends, and the remaining data correspond to the new concept.
The datasets used in
Table 2 are the same as those in
Table 1, with the distinction that each dataset contains multiple drifts points and multiple instances of abrupt or gradual drift within the same data volume. In MOA, the SEA and Sine datasets each contain four classification functions (i.e., four different concepts), so we evenly divided the ten thousand data instances among the four concepts, which included three drift points. The AGR dataset contains ten classification functions, resulting in nine drift points, and the drift width for gradual AGR is smaller than for other gradual datasets. The mixed dataset contains only two classification functions, and we utilized it to generate multiple abrupt drifts datasets. So, to maintain consistency with the data volume of the other datasets, we divided the ten thousand data instances into five parts, with four points. For datasets such as SEA that contain multiple abrupt drifts, the concepts follow a step-like progression, meaning each newly appearing concept differs from all the preceding ones, forming entirely new concepts. However, due to the mixed dataset only containing two concepts, the generated data cannot include multiple concepts. As a result, in the case of multiple abrupt drifts, the data from the mixed dataset alternate between the old and new concepts.
To validate the effectiveness of the algorithm proposed in this paper, experiments were also conducted on real-world datasets. The details of the real-world datasets are as follows:
For real-world data, we selected five real-world datasets with unknown drift points, along with one dataset (NSL-KDD) where drift can be verified, to validate the effectiveness of our proposed method. It is important to note that the original NSL-KDD dataset contains 4,898,431 instances, and the official dataset repository explicitly states that the distribution of the test set differs from that of the training set. Additionally, due to storage constraints, following the processing method in [
37], we conducted experiments using only 10% of the training data combined with the test data. Although real-world datasets commonly used for concept drift detection typically exhibit distributional changes, the exact drift locations are unknown, making it challenging to accurately assess the detection algorithm’s performance. Guo et al. [
13] evaluated the detection delay performance of the algorithm by introducing artificial drift points. Inspired by this approach, this study adopts a similar strategy of embedding drift points to assess the accuracy of drift detection algorithms on real-world datasets. Different strategies were employed for inserting drift points into real-world data with unknown drift benchmarks. When inserting a single drift point, we divided the data into three equal parts: the first one-third is used for pretraining, and this portion of the data remains unchanged. For the remaining two-thirds of the data, the first one-third is left unprocessed to ensure consistency with the distribution of the old concept (i.e., the first one-third). For the final one-third, we use a random function to select a random column and assign its feature values to random numbers between 0 and 1. Details of the datasets can be found in
Table 3.
To insert multiple drift points into real-world data, the dataset is divided into five equal parts: the first one-fifth is used for pretraining and remains unchanged, while the second one-fifth also remains unchanged. In the remaining three-fifths, a random function selects a different feature column for each portion (without repetition) and replaces its values with random numbers between 0 and 1. Details on multi-drift data can be found in
Table 4.
4.3. Evaluation Metrics
For concept drift detection, commonly used evaluation metrics are employed to assess the performance of drift detection algorithms. Specifically, we utilize the first two metrics from [
34,
39] to evaluate the algorithm’s effectiveness in terms of detection delay and accuracy. In the case of a single drift, the First Effective Drift Point (
FEDP) metric is used to quantify the effectiveness of the drift detection algorithm. The calculation is as follows:
represents the first detected drift point that is greater than or equal to the actual drift onset, while denotes the true drift start point. This metric primarily evaluates the algorithm’s ability to promptly detect drift and measure the corresponding detection delay. If no drift point is recorded in the drift list during detection, is set to 10,000 or 100,000. For instance, if the dataset in use is the abrupt SEA, is 5000, and the first detected drift point exceeding this threshold is 5012, then is calculated as FEDP = 5012 − 5000 = 12. This represents a single result. To obtain the final evaluation, the average value is computed over n experiments.
For multiple drifts, the Effective Drift Detection Rate (
) metric [
34,
39] is used to measure the number of effective detections made by the algorithm. Initially, the Effective Drift Range (
) is defined to limit the range for effective detection. For synthetic data with gradual and incremental drifts, parameters are set at the data generation stage to determine their values. Thus, the
for these datasets is tied to the drift formation width, as outlined in
Table 1. However, for abrupt synthetic datasets, where the drift width is 1, we extend the effective drift span by 100 to maintain consistency with other datasets. This results in an
of (5000, 5100). For real-world datasets, whether involving single or multiple drifts, the drift’s effective range is set to a span of 100. In cases of multiple drifts, the effective range encompasses multiple points.The Effective Detected Drift Rate (
) is used as an evaluation metric for multiple drift points. Assume DP = {DP
i, DP
i+1, …, DP
i+t}, where
represents all drift points detected within the effective range:
Let N represent the number of effective ranges. A valid detection occurs only when the detected drift points are non-empty and all detected points lie within the effective range. When both conditions are satisfied, it is counted as 1. If only one or a few of the effective ranges contain valid detected drift points, the value is recorded as , which represents the number of detected drift points within the effective range (with each range counted only once) divided by the total number of effective ranges. When no drift points in the are within the effective range, the value is recorded as 0. This metric evaluates whether the detection algorithm can identify all drift points when multiple drifts are present, thereby assessing the sensitivity of the detection algorithm.
To measure the significant differences between algorithms, the statistical tests proposed in [
40,
41]—the Friedman test and its subsequent Bonferroni-Dunn test—are employed to compare the overall performance of the algorithms. First, the Friedman test is applied to verify whether all algorithms perform similarly. Suppose there are
k algorithms tested on
N datasets, and the variable
When both
k and
N are large,
follows a chi-squared distribution with
degrees of freedom. To improve the rigor of the test, we employ the following statistic:
where
is calculated using Equation (
7). The statistic
follows an F-distribution with degrees of freedom
and
.
If the null hypothesis that “all algorithms perform equally” is rejected, we proceed with the Bonferroni–Dunn test to identify significant differences between pairs of algorithms. The Bonferroni–Dunn test determines the critical difference for the mean rank differences as follows:
where
is determined by the significance level
and and the number of algorithms
k.
The false detection rate (
) is an important metric for evaluating the drift detection method’s ability to detect and identify drifts. Following the metric proposed in [
13], the calculation of
is given by
where
represents the length of all drift detection output results and
represents the actual inserted drift points. The
measures the proportion of invalid detections in the drift detection output, with smaller values indicating better drift detection performance.
4.4. Experiment Results and Analysis
To maintain consistency in the data distribution between the pretraining phase and the data before the drift, synthetic data for the pretraining phase are generated using the generators shown in
Table 1. For the real data, the first 1/5 of the original dataset is used as pretraining data. The experiment is implemented using Python 3.6.5, and the neural network architecture is built with PyTorch 2.4.0. Details of the hyperparameter values involved in the construction of the neural network can be found in
Table 5.
To validate the effectiveness of the proposed method, its performance is evaluated using the metrics discussed in
Section 4.3. The detection methods mentioned in
Section 4.2 all require the base classifier to classify the data and generate the error rate. To avoid the potential bias of relying on a single classifier, which may not fully utilize the performance of the drift detection algorithm, we use two classical classifiers from skmultiflow, namely Hoeffding Tree and Naive Bayes, as baseline classifiers for comparison, providing input for the detection algorithms. The parameter settings for each detector are set to their default values. To ensure fairness, each metric is computed with n set to 100, and the average of 100 experiments is taken.
It is important to note that during the pretraining phase, we first generate non-drift data for all datasets listed in
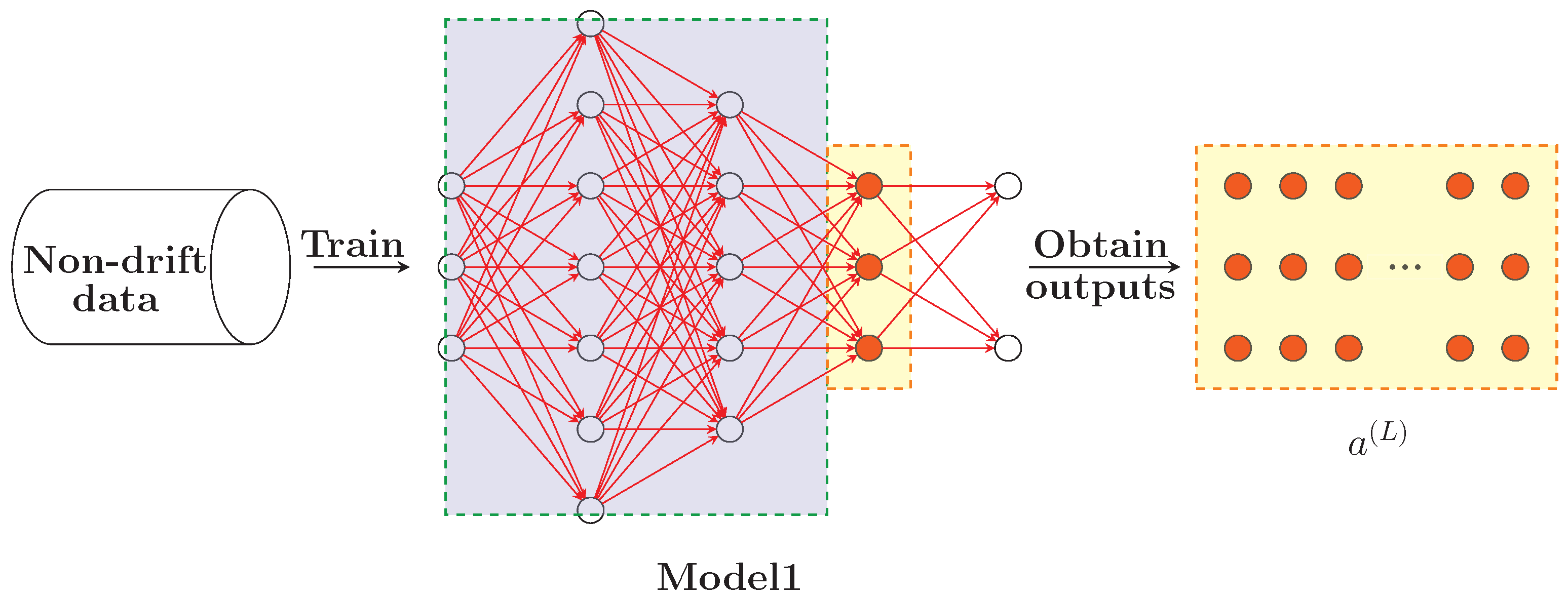
Table 1. Taking SEA_a as an example, its generation command in MOA is “WriteStreamToARFFFile -s (ConceptDriftStream -s (generators.SEAGenerator -f 3 -b -n 5000 -p 0) -d (generators.SEAGenerator -f 2 -b -n 5000 -p 0) -p 5000 -w 1) -f E:\Dataset\dataset.arff -m 10,000 -h”. The key parameter here is the value of ‘f’. The command is designed with two phases, where ‘f’ takes different values. The parameter ‘s’ represents the currently generated data stream, and when ‘f’ is set to 3 following ‘s’, the generated data are produced using generation function 3. The parameter ‘d’ denotes drift data, and the data within its parentheses is generated using function 2. Correspondingly, the non-drift SEA data are the data produced when ‘f’ is set to 3. The same approach applies to other datasets. During the pretraining phase, Model1 in
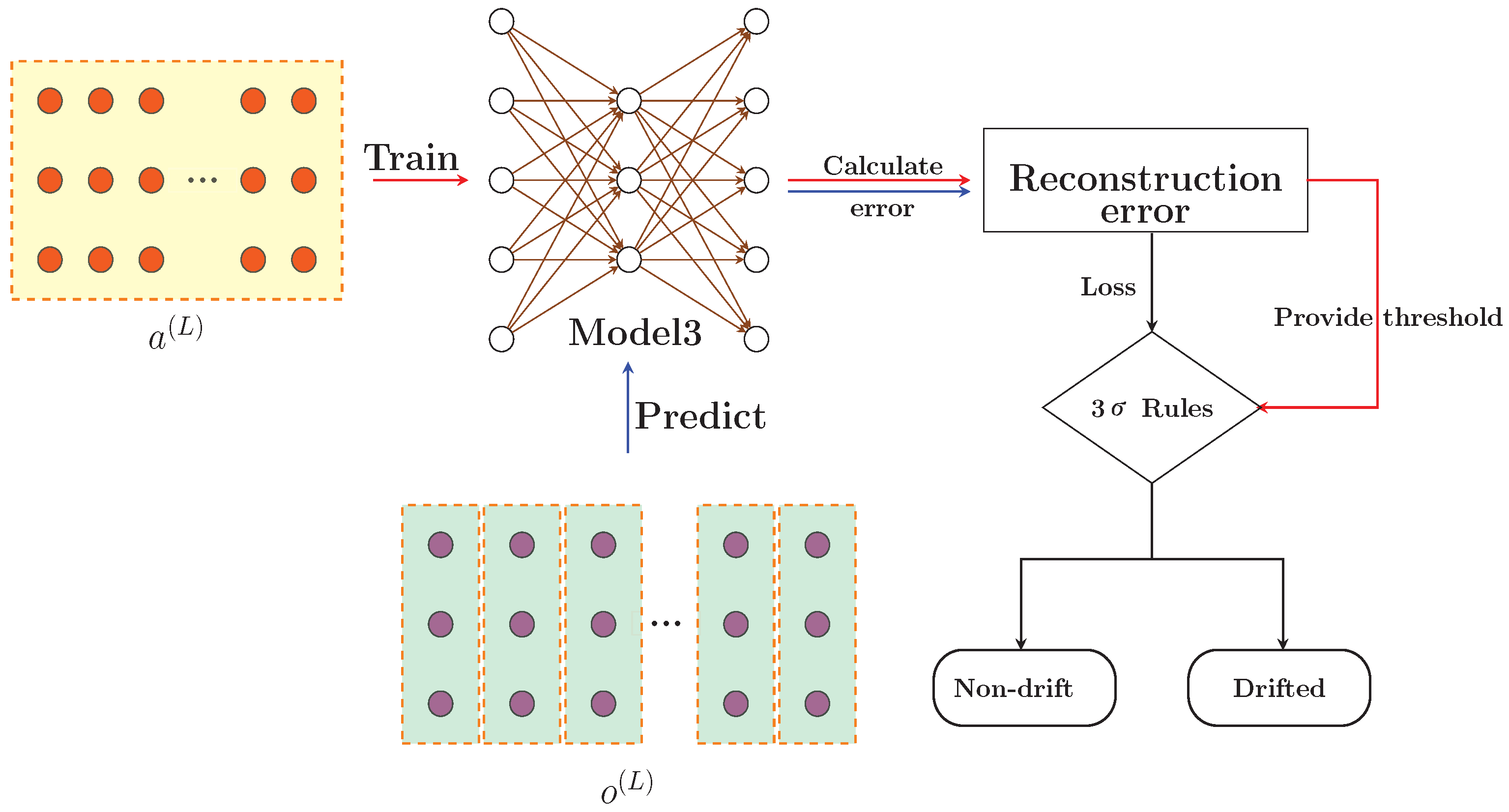
Figure 3 is trained using non-drift data generated with ‘f’ set to 3. In the streaming data processing phase, Model2 in
Figure 4 processes the drift data generated by the above command.
The detection results of synthetic data with single drift using the
metric are shown in
Table 6. The
metric represents detection delay, with smaller values being preferred. The best results in the table are highlighted in bold. From
Table 6, we can observe that the performance of the detectors varies depending on the base classifier selected for different datasets. While the DNN+AE-DD method shows slightly weaker performance on certain datasets, it outperforms other methods in overall performance. The maximum value in
Table 6 is 5500, indicating that the detector did not produce any output for this dataset. This suggests that drift occurred, but the detector failed to detect it. The inability of certain detection algorithms to detect drift on datasets such as AGR_g may be due to the inherent classification difficulty of the AGR dataset. Even with multiple classifiers trained on this dataset, the classification accuracy remains poor.
Assuming all algorithms perform equally, we obtain
based on Equation (
8). When
and
,
follows an F-distribution with degrees of freedom (8, 64), with a critical value of 2.087. Therefore, we reject the hypothesis that all algorithms perform equally. At a confidence level of
,
, resulting in a critical difference (
) value of 3.51. The statistical results are shown in
Figure 6. As observed in the figure, the proposed algorithm performs significantly better than EDDM_NB, DDM_HT, DDM_NB, and EDDM_HT in terms of delay detection.
In
Figure 7, each plot corresponds to a different dataset from
Table 6. The vertical axis represents the
metric calculated by Equation (
4), with the values on the axis represented as powers of
. The horizontal axis lists the algorithms from left to right: DNN+AE-DD, DDM_NB, DDM_HT, EDDM_NB, EDDM_HT, HDDM_W_NB, HDDM_W_HT, ADWIN_NB, and ADWIN_HT. In
Figure 7, two distinct colors are used to represent the delay, with orange indicating the best result for the current metric (for values exceeding 10,000, 10,000 is used for representation). The observation results reveal that the DNN+AE-DD algorithm performs particularly well on certain datasets, such as reducing the detection delay to a very small range on datasets like HYP. Other algorithms also demonstrate optimal performance on various datasets. Therefore, we can conclude that the DNN+AE-DD is effective in detecting concept drift in the case of a single drift occurrence.
In
Figure 7, the performance of the DNN+AE-DD in detecting abrupt concept drift is generally inferior to that of other algorithms across most datasets. The possible reason for this could be the short duration of abrupt drift events, making them harder to detect, or the overlap between the distributions of old and new concepts, which complicates detection in the short term. This hypothesis is further supported by the observation of the DNN+AE-DD’s performance on other datasets with gradual and incremental drifts. In gradual and incremental drift scenarios, there is a transitional period during which the data distribution changes over time. Specifically, in gradual drift, data points from the new distribution gradually increase, while data from the old distribution decrease. The classification boundaries between the old and new distributions may overlap during this transition, which can cause detection delays. As a result, the detection performance of the algorithm may vary across different datasets. For incremental drift data, the data in the transitional period do not belong strictly to either the new or old distribution, which allows the DNN+AE-DD to detect the drift with relatively shorter delay.
The data in
Table 7 show the performance of various algorithms on the
metric for synthetic multi-drift data. An ideal result for this metric is a value close to 1.0, with the best results highlighted in bold. This metric illustrates that each drift detection algorithm has its optimal performance at specific moments, but overall, the method proposed in this paper performs well. A value of 0.0 in
Table 7 may indicate that the current detector did not identify values within the valid detection range for a particular dataset. In such cases, the detector might have produced a result, but the detection outcome was suboptimal, or the detector might have failed to detect the occurrence of drift.
Based on Equation (
8), we obtain
. When
and
,
follows an F-distribution with degrees of freedom (8, 48), with a critical value of 2.138, leading us to reject the hypothesis that “all algorithms perform equally”. At a confidence level of
,
, yielding a critical difference (
) value of 3.99. The statistical results are shown in
Figure 8. As seen in the figure, the proposed algorithm significantly outperforms DDM_NB and DDM_HT in terms of effective detection metrics.
In
Figure 9, the different colored bars represent different effective detection ranges. SEA and Sine each have three effective detection ranges, corresponding to three colored bars, while mixed has four effective detection ranges and AGR has nine effective detection ranges. The results in
Table 7 represent the average values for each effective detection range (with an average value of 1.0 only when all bars have a value of 1.0).
Figure 9 presents detailed results for each effective detection range. From the figure, when facing multiple abrupt/gradual drift datasets, we can observe that although the DNN+AE-DD does not guarantee the best performance across all datasets, it performs well on most abrupt/gradual drift datasets. For example, in AGR_a and SEA_g, despite not achieving the best results on datasets like Sine_a, it ensures that a valid output is detected within each effective detection range. In cases where optimal performance is not achieved, this may be due to one or more detection instances failing to produce an output or providing an unsatisfactory result.
Table 8 and
Table 9 present the
and
outputs for the detection algorithm on real-world datasets with single and multiple drifts, respectively. Due to the varying sizes of the real datasets, we set the drift point outputs to 100,000 for algorithms that fail to detect drift, leading to larger values in
Table 8. The best outcomes are highlighted in bold. From these tables, it can be observed that the DNN+AE-DD algorithm demonstrates strong overall performance on both single-drift and multiple-drift real-world datasets. While our algorithm does not always achieve optimal performance on certain datasets, its results are only slightly below the best cases. These findings further validate the effectiveness of the DNN+AE-DD algorithm in detecting concept drift in streaming data.
In
Figure 10, the computed value of
is 3.28. When
and
,
follows an F-distribution with degrees of freedom (8, 40), with a critical value of 2.18. This result leads to the rejection of the null hypothesis that “all algorithms perform equally”. At a confidence level of
, the critical value
is 2.724, yielding a critical difference (
) value of 4.31. As illustrated in the figure, the proposed algorithm demonstrates significantly better performance in terms of delay detection compared to the DDM_NB, DDM_HT, ADWIN_NB, and ADWIN_HT.
In
Figure 11, the computed value of
is 6.62. When
and
,
follows an F-distribution with degrees of freedom (8,32), with a critical value of 2.244. This result also leads to the rejection of the null hypothesis that “all algorithms perform equally”. At a confidence level of
, the critical value
is 2.724, yielding a
value of 4.72. As shown in the figure, the proposed algorithm significantly outperforms the DDM_HT, ADWIN_NB, and ADWIN_HT in terms of the effective detection range.
In
Figure 12, the orange color represents the algorithm with the best detection delay performance, while the other algorithms are depicted in blue. When detecting a single drift, the DNN+AE-DD is able to significantly reduce detection delay across most real-world datasets. However, on the NSL-KDD dataset, the delay for nearly all classifiers is notably longer compared to other datasets. By analyzing
Figure 12 and
Figure 13, we observe that when detecting multiple drifts, the DNN+AE-DD algorithm performs slightly worse than detectors such as EDDM on the Electricity dataset. However, it demonstrates superior overall performance across different datasets. In the case of artificial drift points implanted in real-world datasets, the DNN+AE-DD demonstrates a clear advantage in detecting abrupt drifts. However, due to the inherent complexity of real-world data, the detection delay varies. Furthermore, we observe that the performance of the detector varies depending on the classifier chosen, highlighting the significant impact of base classifier selection on drift detection performance. For most classifiers, other detectors perform poorly, which may be attributed to the complex and dynamic nature of real-world data. Since the detector’s input relies on the predictions of the base classifier, fluctuations introduced by drift points may cause the classifier to mislabel data as noise, potentially resulting in the absence of detection outputs.
Based on the experimental results, the proposed DNN+AE-DD method effectively and promptly detects concept drift with minimal delay while demonstrating the capability to identify multiple types of drift.
Furthermore, for the synthetic datasets in
Table 10, we conducted a comparison of the false detection rates (
) across different algorithms, with the results presented in
Table 10. For cases where the algorithm did not produce detection output in all 100 experiments, we assigned the value “NaN”. The values in the table are expressed as percentages.
From
Table 10, it can be observed that the DNN+AE-DD effectively detected drift across all datasets in one hundred experiments (i.e., no “NaN” results), whereas other algorithms exhibited “NaN” on one or more datasets. This demonstrates the robustness of the proposed method in detecting drifts across various datasets and drift types. While different algorithms perform optimally on different datasets, the DNN+AE-DD maintains a balanced performance. Although the DNN+AE-DD does not achieve the lowest false detection rate when compared to all algorithms, its false detection rate is comparable or even better than the comparisons. For instance, on the AGR_a, AGR_g and HYP_i datasets, most methods fail to detect drift effectively, whereas the DNN+AE-DD successfully identifies drift in all 100 experiments with a relatively low false detection rate. In summary, although the performance of the DNN+AE-DD varies across datasets compared to other algorithms, it consistently detects drift with shorter delays and strong robustness.