The Impact of Terrain on the Planar Spatial Morphology of Mountain Settlements Studied Using Fractal Dimensions

Abstract

As urbanization progresses in China, the importance of preserving traditional settlements, particularly those located in mountainous areas, is increasingly recognized. To reveal the spatial morphology of mountain settlements influenced by topography, this study employs fractal geometry to analyze twelve mountain settlements within the Jiexiu City region. The correlation between the fractal dimensions of building structures in these settlements and those of suitable construction areas was examined, revealing a significant positive relationship. Moreover, an in-depth spatial distribution analysis of the representative village, Xingdi Village, was conducted to examine its sub-regional spatial morphology. Utilizing the Multiscale Geographically Weighted Regression (MGWR) model, this study explored the impact of slope, aspect, and elevation on the spatial form of mountainous settlements. The results indicate that the complexity of sub-spaces within Xingdi Village gradually decreases with village expansion, and there is a significant positive correlation between flat terrain and sub-spatial morphology. Based on this, a conservation framework rooted in the morphological characteristics of settlement typologies is proposed.

1. Introduction

In China, with the advancement of urbanization and the development of rural revitalization strategies, traditional settlements are confronted with the conflicting challenges of preservation and renewal. The urgency to protect these traditional settlements during the renewal process is paramount. The value of preserving traditional settlements lies in both the high-value individual buildings and courtyards within them, as well as their overall spatial configuration [1,2]. While individual structures tend to receive greater attention during renewal efforts and preservation work, the latter—namely, the overall spatial morphology of these settlements—faces a considerable risk of being compromised amidst rapid urbanization and insufficient awareness of conservation [3]. The spatial morphology of traditional settlements, in comparison to the majority of modern villages, is capable of preserving more authentic spatial information. Specifically, mountainous traditional settlements, constrained by transportation and topographical factors, experience lower levels of external interference than their plain counterparts. As a result, they retain a richer repository of embedded information, serving as critical samples and references for the study of spatial morphology conservation in traditional settlements [4]. To protect spatial morphology, it is essential to conduct both qualitative and quantitative analyses. This study aims to explore the spatial morphology of mountainous settlements from a quantitative analysis perspective, providing reference data for settlement morphology preservation. While significant foundational research has been conducted by scholars both domestically and internationally regarding qualitative analysis methods for spatial morphology, quantitative analysis primarily focuses on morphological indices and factor relationship analyses [5]. The initial exploration of spatial morphology indices relied on Euclidean geometry, which is manifested in fundamental attributes such as distance and area [5,6]. However, spatial morphology cannot be fully encapsulated by these basic properties. As complex systems, structures such as snowflakes, branching trees, and mountain ranges defy comprehensive description using suitable indices derived from Euclidean geometry. With ongoing scholarly research, fractal geometry has been increasingly demonstrated to effectively address such complex problems. By introducing fractal dimension as a mathematical tool, researchers have been able to quantify the characteristics of complex systems that are difficult to describe using traditional methods, thereby providing a scientific basis and practical means for further investigation [7].

According to existing research, fractal theory has been widely applied in urban systems. In 1985, M. Batty introduced the concept of fractal cities and utilized fractal theory to simulate urban land use and activity patterns [8]. In 1989, Longley employed four different methods to calculate the fractals of cartographic lines in Swinton, UK, and examined the functional relationships between fractal dimensions and various factors [9]. Additionally, Zhonghao Zhang investigated the expansion patterns of construction land in both urban and non-urban areas of Wentai region in Eastern China along with their related factors [10]. It is evident that the application of fractal dimensions within urban systems is extensive, encompassing a range of aspects from initial analyses of overall urban morphology to exploring influencing factors and development models.

In the realm of rural and settlement studies, scholars have introduced fractal geometry theory into the analysis of rural spatial morphology. Xincheng Pu employed fractal geometry to investigate three elements: traditional settlement boundaries, buildings, and building complexes, thereby establishing a quantitative framework [11]. Jing-Jing Zhang conducted research on the morphological differences between urban and rural settlements in mountainous and plain regions [12]. Qindong Fan utilized fractal dimensions to analyze the architectural plans and continuous facade forms of Malin Village in Henan Province, providing valuable information for village planning [13]. Yi Wang et al. applied various methods including fractal dimensions to examine diverse spatial distribution characteristics of rural settlements in Liangjiang New Area, Chongqing City, correlating factors such as elevation and slope with settlement morphology indicators [14]. Additionally, there are instances where fractal geometry has been applied to analyze changes in natural environmental development [15]. However, current research within the field of fractal geometry concerning the spatial morphology of settlements primarily focuses on calculating and analyzing the fractal dimensions of overall planar layouts and facades. The effectiveness of related factors within individual villages remains inadequately explored. In contrast, Chenming Zhang’s study on Zhengzhou identified 158 unit grids as objects for analysis; this approach effectively examined how road networks and land use patterns influence fractal dimensions at a grid level [16]. These studies provide new insights into analyzing internal spatial morphologies within settlements.

Through the establishment of regression models, it is possible to explore the impact of various factors on the spatial morphology within settlements [17,18]. Given the significant spatial heterogeneity in the topographic and geomorphic characteristics of settlements, this study employs a Multiscale Geographically Weighted Regression (MGWR) model to enable dynamic regression analysis of variables across the spatial dimension, thereby more accurately revealing the differentiated mechanisms by which various factors influence settlement spatial morphology [19]. Regarding the factors influencing the spatial morphology of mountainous settlements, scholars generally agree that slope, aspect, and elevation have the most direct effects on building and road configurations within these areas [20,21,22]. By referencing land use patterns [23], slope, aspect, and elevation are incorporated as factors in the regression analysis [24].

In summary, although scholars have applied fractal geometry to the study of urban and settlement morphology, research at the settlement level remains largely focused on holistic fractal analyses of villages. This approach does not significantly uncover the patterns and underlying logic of how various factors influence the internal spatial morphology. Furthermore, studies on mountainous settlements predominantly rely on qualitative analysis, with investigations into the impact of terrain on spatial morphology still in their infancy. Based on this context, this paper selects twelve traditional settlements within Jiexiu City in Jinzhong Prefecture, Shanxi Province as research subjects to explore the correlation between their spatial morphology and topography. Furthermore, a Multiscale Geographically Weighted Regression (MGWR) model is applied, using Xingdi Village in Jiexiu City as a case study, to deeply analyze the mechanisms by which terrain influences the internal spatial morphology of the settlement. This study aims to provide an initial analysis of the formation patterns of the planar spatial morphology of traditional mountainous settlements while investigating its underlying causes. The findings will offer a theoretical foundation for updating and protecting traditional settlements and hold certain guiding significance for rural planning efforts.

Abbreviations

In the study, some abbreviations and symbols are used, which are explained in

Table 1. Abbreviations and Symbols.

Abbreviation	Full Term or Meaning	Unit/Description
MGWR	Multiscale Geographically Weighted Regression	A regression model for multiscale analysis
GIS	Geographic Information System	A system for geographic data analysis
SPSS	Statistical Package for the Social Sciences	Statistical analysis software
SSE	Sum of Squared Errors	Used in clustering and regression
AIC	Akaike Information Criterion	A model selection criterion
GTWR	Geographically and Temporally Weighted Regression	A regression model considering spatial and temporal effects
D	Fractal dimension	Indicates spatial filling and complexity
N(r)	Number of non-empty boxes	A variable in fractal dimension calculations
r	Box side length	Unit length
X1	Ratio of flat terrain	Proportion of areas with 0–5° slope
X2	Average elevation	Unit: meters
X3	Ratio of south-facing slopes	Proportion of south-facing slope areas
β0	Constant term in regression equation	-
βk	Regression coefficient for the k-th factor	-

.

2. Materials and Methods

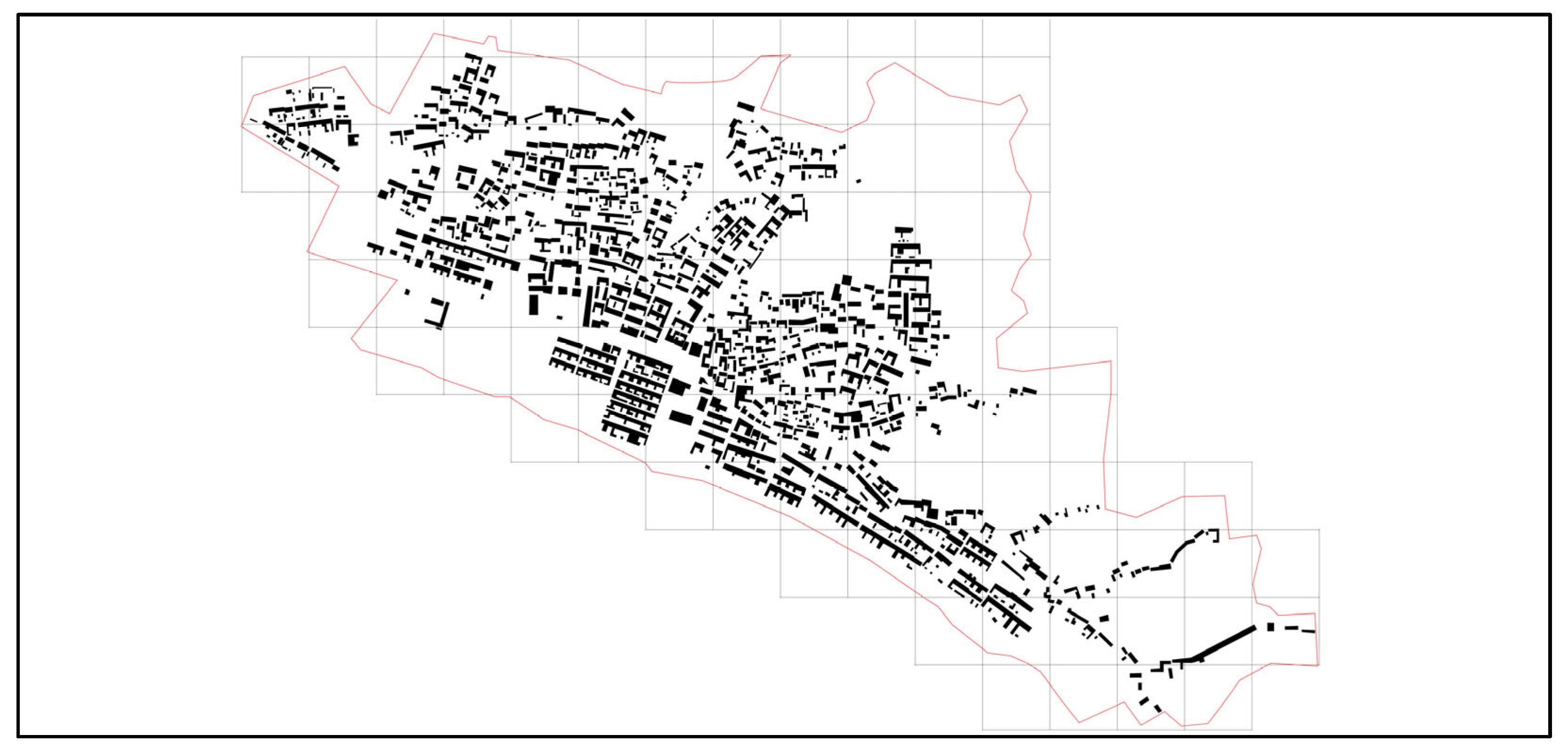
2.1. Study Area and Sample

We selected a total of 17 traditional settlements within the jurisdiction of Jiexiu City in Jinzhong, Shanxi Province, China (Figure 1). Situated near the Mianshan Mountain range, with varied terrain and an average altitude of about 800 m, the area is traversed by the ancient Tea Road, carrying significant historical and cultural heritage along with abundant traditional settlement resources [25,26]. Based on the characteristics of settlement distribution, these are categorized into mountainous, hilly, and plain types. Jiexiu City experiences a temperate continental monsoon climate with distinct seasons, an average annual temperature of approximately 10 °C, and annual precipitation ranging from 450 to 550 mm, most of which occurs in summer. The diurnal temperature variation is significant. This research focuses on 12 traditional settlements from the mountainous and hilly categories: Banyu Village, Liujiashan Village, Xingdi Village, Dajin Village, Hongshan Village, Jiaojia Fortress Village, Nanzhuang Village, Tian Village, Xialihao Village, Xiaojin Village, Zhangbi Village, and Zhangcun. The geographical locations of these settlements are situated at the foot of Mianshan Mountain and exhibit typical features characteristic of mountainous communities. The architecture within these settlements is constructed in harmony with the surrounding terrain and topography, with traditional buildings primarily made of loess, gray bricks, and timber. Walls are often built using rammed earth or masonry, and roofs are typically wooden structures covered with gray tiles or clay. To adapt to the climate, buildings generally feature thick walls and narrow windows. Some buildings are excavated directly into loess cliffs, forming structures known as yaodong (cave dwellings). Both architectural forms are representative of traditional Chinese residential structures and hold significant research value.

2.2. Research Methods

This study is divided into three processes (Figure 2). The first part involves calculating the fractal dimensions of settlement buildings and suitable construction areas, followed by a regression analysis using SPSS (Version 22) to verify their correlation. The second part focuses on selecting an individual village for in-depth analysis; specifically, we choose settlements with relatively high fractal dimensions and minimal differences between the building fractal dimension and that of suitable construction areas as samples. The boundaries of these selected villages are defined as research zones, which are further divided into 150 m × 150 m grids to compute and visualize the fractal dimensions within these subspaces. The third part employs Multiscale Geographically Weighted Regression (MGWR) for regression analysis to further investigate how internal terrain influences spatial morphology within settlements. In addition, a protection framework based on the fractal characteristics of settlements is established. Throughout this research process, we utilize fractal dimension calculations, regression analyses, and clustering analyses while also necessitating data preprocessing.

2.2.1. Fractal Dimension

The commonly used methods for calculating fractal dimensions include various approaches such as the area–perimeter relation, box-counting method, and area–radius relation [20,27,28]. In this study, we have chosen the box-counting method to compute the fractal dimension of our samples. The box-counting method is particularly well-suited for digital image processing, offering simplicity in calculating fractal dimensions for binarized images. Compared to the Hausdorff dimension, it has the advantage of lower computational complexity. Additionally, the box-counting method demonstrates strong noise resistance, ensuring reliable results. The specific calculation involves covering the sample with squares of side length r and counting the number of non-empty boxes $N\left(r\right)$. The value of $N\left(r\right)$ changes as $r$ decreases. The fractal dimension $D$ is determined by the slope in a double logarithmic plot [29,30], as shown in Equation (1).

$$D=-\underset{r\to 0}{\lim }{\displaystyle \frac{\lg N(r)}{\lg r}}$$

(1)

The $D$ value calculated in this process represents the degree of spatial filling and complexity. In this study, we utilized the fraclab toolbox in MATLAB (Version 2020a) to substitute for the aforementioned calculation process. The underlying principles remain consistent with Equation (1); however, this approach allows for faster computation and more accurate results while enabling finer variations of r. Scholars have indicated that fractal dimension calculations can encompass all data rather than being limited to a specific scale-invariant region; therefore, we selected all data from the double-logarithmic plot as the source for calculating the $D$ value [31].

2.2.2. Multiscale Geographically Weighted Regression

Multiscale Geographically weighted regression (MGWR) is a localized regression model that establishes a regression equation for each spatial point [32], reflecting the influence of independent variables on the dependent variable at specific scales [33]. The primary distinction between GWR and traditional least squares models is given in Equation (2):

$${\mathrm{Y}}_i={\mathsf{\beta }}_0+{\displaystyle \sum _{i=1}{\mathsf{\beta }}_k{X}_{ik}+{\mathsf{\epsilon }}_i}$$

(2)

$${\mathrm{Y}}_i={\mathsf{\beta }}_0(u_i+v_i)+{\displaystyle \sum _{i=1}{\mathsf{\beta }}_k(u_i+v_i)X_{ik}+{\mathsf{\epsilon }}_i}$$

(3)

The distinction lies in the incorporation of spatial coordinates into the independent variables. This allows GWR to capture the spatial heterogeneity of independent variables, as illustrated in Equation (3).

The expression involves the following variables: $i$ represents the $i$-th sample, $Y_i$ denotes the corresponding dependent variable value for the $i$-th sample, ${\mathsf{\beta }}_0$ indicates the constant term of the regression equation, ${\mathsf{\beta }}_k$ signifies the regression coefficient for the k-th influencing factor, and $X_{ik}$ refers to the i-th influencing factor of the k-th sample. Additionally, $(u_i,v_i)$ represents the spatial coordinates of the i-th sample, and ${\mathsf{\epsilon }}_i$ accounts for random error [34]. In this study, we utilized the main software to perform calculations on the Multiscale Geographically Weighted Regression (MGWR) model. This software can be downloaded from “https://sgsup.asu.edu/sparc/multiscale-gwr” (accessed on 10 July 2024).

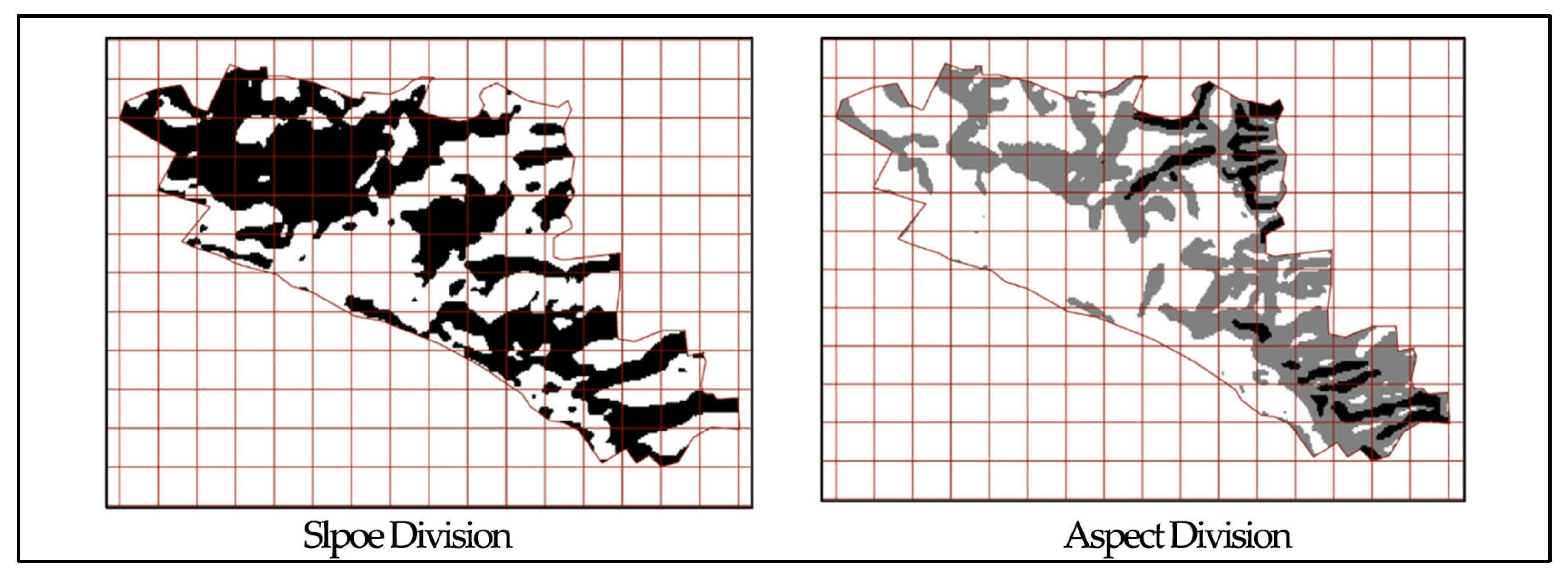
2.2.3. Data Preprocessing

In this study, data preprocessing is divided into three parts. The first part involves the preprocessing of research samples from 12 settlements within Jiexiu City using satellite imagery and GIS technology. Based on the site plans from settlement protection planning documents, the settlement buildings were precisely located, and raster base maps of settlement buildings with 1 m precision were created using AutoCAD software (Version 2018), with building areas filled in black. Meanwhile, 5 m precision elevation data from Jiexiu City were used to conduct the slope analysis, identifying suitable construction areas with slopes of less than 10°. Raster base maps of these suitable construction areas, also with 5 m precision, were generated and filled in black as well. This step aims to generate settlement building distribution maps and suitable construction area distribution maps (Figure 3) where the slope is less than 10° [35], which will facilitate subsequent calculations of fractal dimensions and correlation validation.

The second part focuses on the subspace regional division of Xingdi Village, which is characterized by a relatively high fractal dimension among the 12 settlements and a minimal difference in fractal dimension compared to the suitable construction areas. This village is divided into 67 regions using a grid size of 150 m × 150 m (Figure 4), and the fractal dimensions of building patches within each grid cell are calculated accordingly.

After verification, it was found that the explanatory power of independent variables in sub-regions derived from a 100 m × 100 m grid segmentation is insufficient for the dependent variable. Conversely, excessively large grids may lead to an inadequate sample size during MGWR regression [16]. The third part involves mapping the independent and dependent variables of MGWR regression. We selected the fractal dimension values of subspace grid building patches as the dependent variable, while different levels of slope and aspect distribution ratios were utilized as independent variables (Figure 5). The classification of slopes is defined as follows: flat (0–5°), gentle slope (5–10°), and unsuitable for construction (above 10°) [35]. Additionally, only the proportion of south-facing areas is considered for the aspect ratio. X₁ is defined as the ratio of flat areas (0–5°) to the total grid area, X₂ represents the average elevation of each grid, and X₃ is the ratio of south-facing slope areas to the total grid area. Compared to the average slope, the slope–area ratio better reflects topographical characteristics, as the average slope may obscure terrain details. For example, steep regions may also contain flat areas, which cannot be captured by the average value. Meanwhile, the slope–area ratio is less sensitive to extreme values and is less affected by outliers. The inclusion of elevation height considers the vertical height factor of mountain settlements, making the results closer to 3D analysis.

Data source: The settlement layout maps are derived from the traditional village protection plans of each settlement, with the diagrams accurately drawn based on coordinate systems to ensure high precision. Elevation data were obtained from a third-party online platform, featuring a spatial resolution of 5 m. The temporal coverage of the elevation data corresponds to the year 2022, and the acquisition date was March 2024. To meet the specific requirements of this study, the data underwent additional preprocessing, including cropping and refinement.

3. Results

3.1. Calculation Results of Fractal Dimension for Urban Settlements

Through the preprocessing of data, we conducted a fractal dimension calculation on the building distribution maps and suitable construction area distributions of 12 research samples. The results are presented in

Table 2. Fractal dimension results of urban settlements.

Village	Architectural Fractal Dimension	Suitable Construction Area Fractal Dimension	Difference
Dajin	1.630	1.920	0.290
Xingdi	1.650	1.930	0.280
Nanzhuang	1.583	1.860	0.277
Jiaojiabao	1.585	1.850	0.265
Xiaojin	1.620	1.880	0.260
Zhangbi	1.660	1.918	0.258
Xialihou	1.690	1.930	0.240
Zhang	1.720	1.950	0.230
Banyu	1.470	1.690	0.220
Tian	1.584	1.880	0.216
Liujiashan	1.590	1.790	0.200
Hongshan	1.710	1.900	0.190

.

Through calculations, the average fractal dimension of settlement buildings reached 1.624, while the average fractal dimension of suitable construction areas was 1.868. Both values are considered relatively high within the jurisdiction of Jiexiu City. Generally, the fractal dimension of settlement buildings is lower than that of suitable construction areas. Among them, Banyu Village has a smaller settlement with a dispersed building distribution; its fractal dimensions for both settlements and suitable construction areas are the lowest recorded, with a minimal difference of only 0.220. In contrast, Zhangcun Village features a larger settlement characterized by dense building arrangements and higher building volume ratios; it exhibits the highest fractal dimensions for both categories, 1.720. The smallest difference between these two indices is found in Hongshan Village, which shows a discrepancy of merely 0.190, whereas Dajin Village displays the largest gap at 0.290. Using SPSS to conduct correlation analysis on the fractal dimensions of the study sample buildings and those in suitable construction areas yielded the results shown in

Table 3. SPSS regression results.

	Architectural Fractal Dimension	Suitable Construction Area Fractal Dimension
Architectural fractal dimension	1 (0.000 ***)	0.841 (0.001 ***)
Suitable construction area fractal dimension	0.841 (0.001 ***)	1 (0.000 ***)

Note: *** represent significance levels of 1%.

.

The analysis results indicate a strong positive correlation between the two variables, with a correlation coefficient reaching as high as 0.841, which is statistically significant (p < 0.001). This suggests that as the fractal dimension of settlement architecture increases, the fractal dimension of suitable construction areas also rises concurrently. This preliminary finding reveals the intrinsic relationship between topography and the spatial morphology of settlement architecture, providing data support and a research foundation for further exploration of the interaction mechanisms between the two.

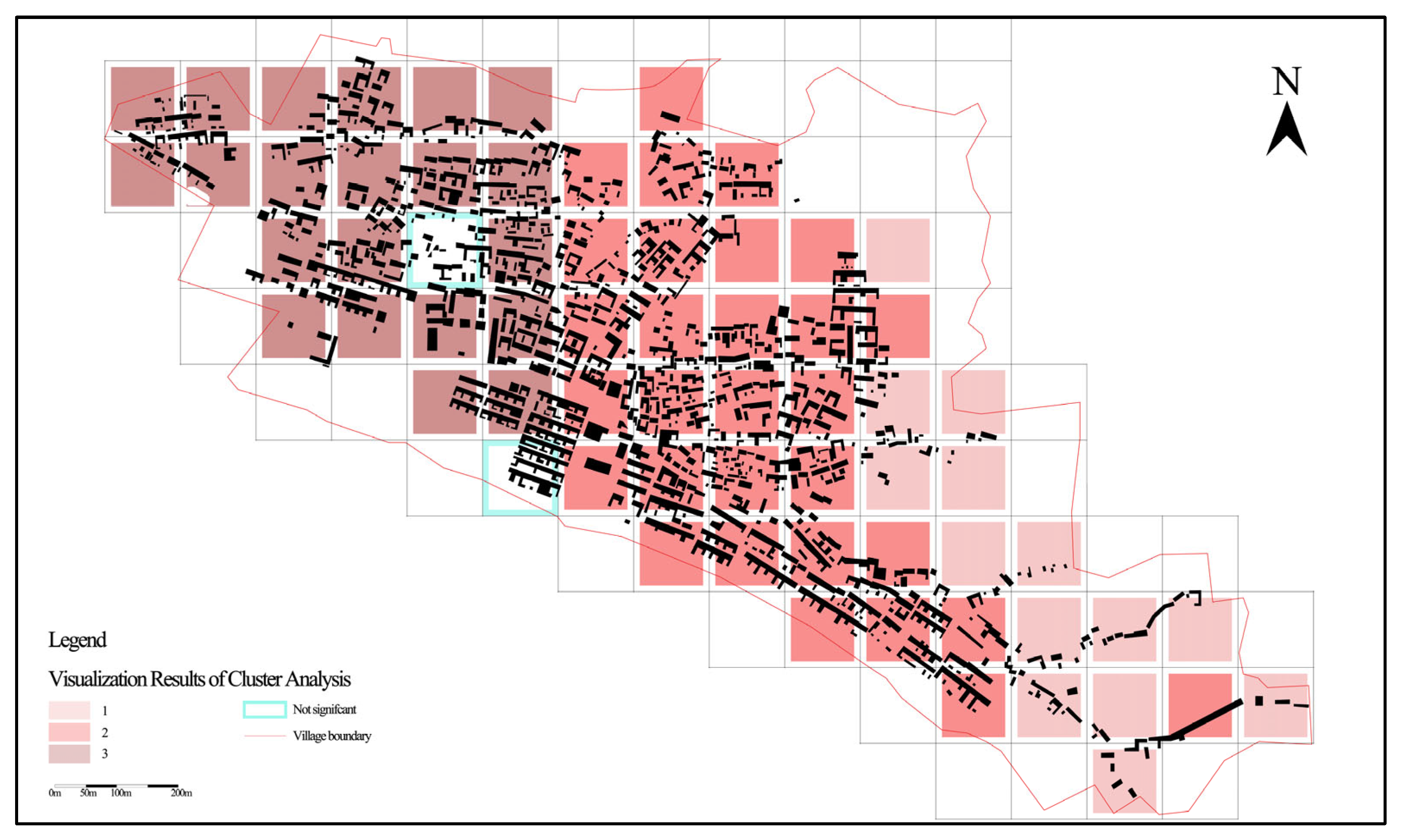
3.2. Distribution Results of Spatial Fractal Dimension in Xingdi Village

The analysis of the fractal dimension of settlement subspaces requires the selection of 12 research samples. The selected study objects must meet two criteria: first, the settlement area should be sufficiently large to facilitate segmentation using appropriately sized grids; second, both the fractal dimensions of settlement buildings and suitable construction land should rank at a relatively high level within the sample. A higher fractal dimension value indicates greater overall spatial complexity of the village, making it more suitable as a subject for subsequent research. As indicated by the results in Section 3.1, Xingdi Village meets both conditions mentioned above. Its building fractal dimension is 1.650, which ranks above average within the sample, while its suitable construction area has a fractal dimension of 1.930, placing it at a high level. Additionally, this village covers a considerable area and is located at the foot of Mianshan Mountain, being recognized as the largest village in Mianshan Town. Within the settlement, there are distinct sections representing new and old villages, with new constructions situated to the south and older structures concentrated in central areas and along the western foothills. By employing a grid size of 150 m × 150 m for subspace division, we delineated 67 regions within this settlement. The calculation and visualization results for each grid’s fractal dimension are presented below (Figure 6).

The calculation results indicate that the minimum fractal dimension of the settlement subspace is 1.326, while the maximum value reaches 1.763, with an average of 1.633. This demonstrates that the fractal dimensions of the settlement subspace are at a relatively high level. In terms of distribution, it can be observed that:

• Overall, the subspace fractal dimensions of the settlement are predominantly concentrated in its central area, which serves as the core of the settlement. This region retains a diverse array of traditional architecture and fortifications while also representing a transitional zone between old and new structures within the settlement. As one moves toward the periphery of the settlement, there is a noticeable decrease in subspace fractal dimensions. The lowest fractal dimensions can be observed at both the easternmost and northernmost edges of the settlement. Analyzing topographical features reveals that to the southwest, there is a trend towards flatter terrain, whereas to the northeast, it gradually approaches the Mianshan Mountain range. Consequently, subspace fractal dimensions exhibit a radial decline towards this northeastern direction.
• The settlement comprises two distinct parts: new villages and old villages. The boundary between these two areas is located along a main road situated to the south of the settlement, with old villages lying to its north and new villages to its south. Analysis indicates that on average, the subspace fractal dimensions in new village areas exceed those found in old village regions.
• Focusing on specific notable zones within the settlement—such as well-preserved courtyards, fortress walls, and temples—reveals that these locations possess higher covering subregion fractal dimensions compared to their surrounding areas; for instance, regions like Huiluan Temple and East Fort exhibit significantly elevated fractal dimensions relative to nearby locales.
• By overlaying these data with slope maps of the settlement’s terrain (Figure 7), we can derive insights into potential correlations between fractal dimension values and topography. It becomes apparent that in areas characterized by relatively gentle slopes, subspace fractal dimensions tend to be larger; conversely, steeper terrains correspond with lower dimensional values. This observation suggests a possible relationship between topographic features and subspace fractal dimensions—a hypothesis warranting further investigation in subsequent studies.

3.3. MGWR Regression Results

3.3.1. General Effect of MGWR Regression

After determining the fractal dimension of each subspace in Xingdi Village, this study employs a Multiscale Geographically Weighted Regression (MGWR) model to further investigate the influencing factors and patterns associated with mountainous settlements. MGWR can account for multi-scale effects in regression calculations by assigning independent spatial bandwidths to different influencing factors, thereby capturing the spatial heterogeneity characteristics among factors with greater precision. The previously calculated fractal dimensions of subspaces are utilized as the dependent variable. The graded proportions of slope and aspect within the subspace grids, along with elevation, are employed as independent variables for the MGWR regression. All independent variables have passed multicollinearity detection. The model fit is presented in

Table 4. Regression results of the MGWR model.

Model Parameter	MGWR
Residual sum of squares	33.239
AIC	161.880
AICc	165.299
R2	0.504
Adjusted R2	0.432

.

The MGWR model demonstrates favorable values for RSS and AIC. The R² value of 0.504 is attributed to the insufficient explanatory power of the independent variable (aspect) on the dependent variable (fractal dimension). In the MGWR model, different bandwidths are assigned to factors based on their spatial characteristics to more accurately reflect their spatial influence. Specifically, the slope factor is allocated a local bandwidth of 45, indicating that the influence of slope exhibits strong spatial heterogeneity and is more suitable for medium-scale analysis. In contrast, the effects of elevation and aspect are more extensive and display global consistency, thus being assigned global bandwidths for computation. The statistical data for the MGWR regression can be found in

Table 5. Descriptive statistics of the coefficients of the MGWR model.

	p-Value	Mean	STD	Min	Median	Max
X1 (Slope)	<0.001	0.592	0.221	0.263	0.554	0.918
X2 (Elevation)	0.077	0.318	0.032	0.271	0.312	0.384
X3 (Aspect)	0.335	0.051	0.010	0.034	0.051	0.067

.

The statistical analysis reveals that the slope variable (X₁) and the elevation variable (X₂) exert significant positive influences on the dependent variable (fractal dimension), with mean regression coefficients of 0.592 and 0.318, respectively. In contrast, the aspect variable (X₃) exhibits a p-value exceeding 0.05, indicating that its effect on the dependent variable is not statistically significant.

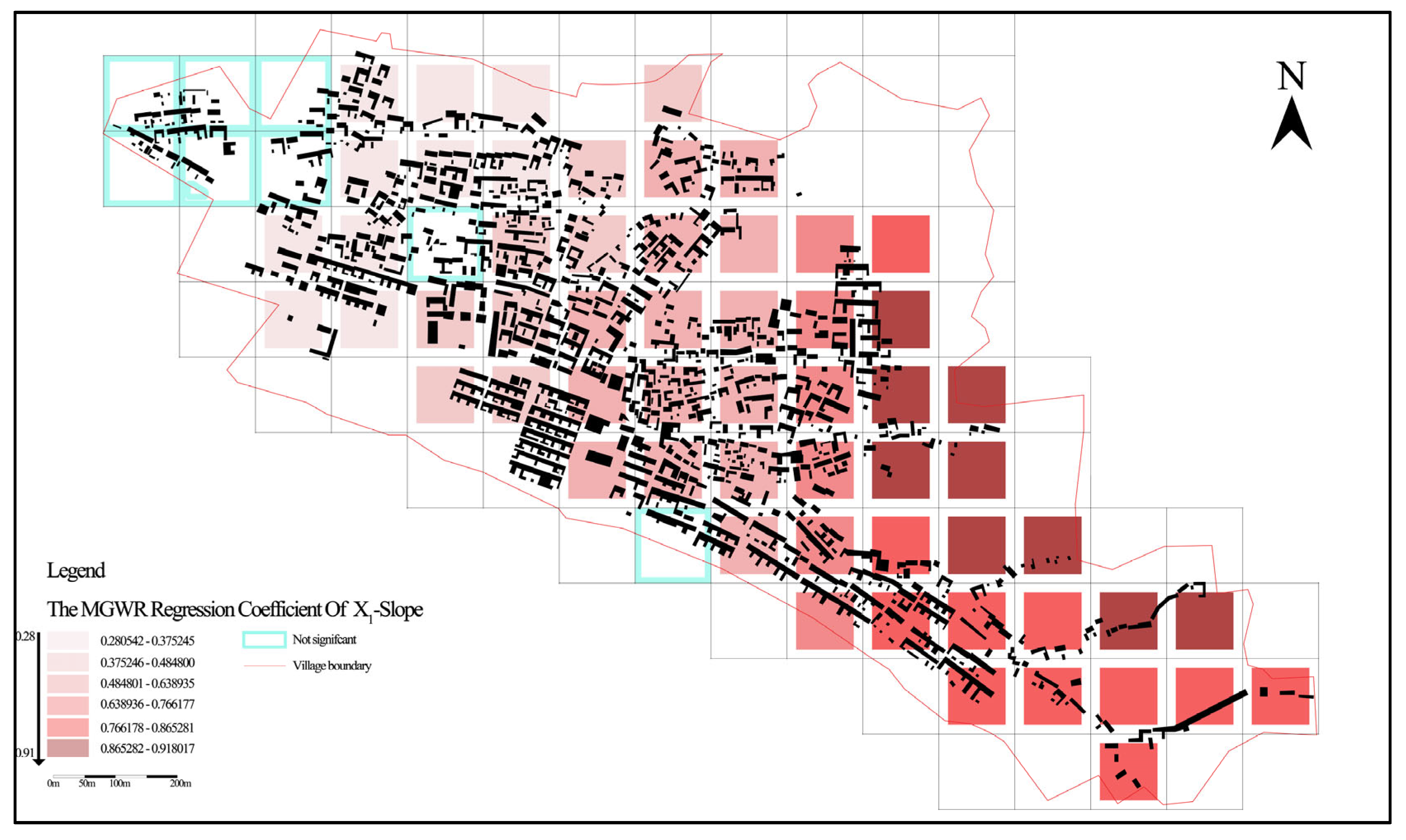
3.3.2. MGWR Visualization Results

After obtaining the MGWR regression results, we filtered the available data and represented them in spatial coordinates. The magnitude of the regression coefficients is illustrated using hue variations, as shown in Figure 8 and Figure 9.

The X₁ slope factor exhibits a positive impact on the dependent variable (fractal dimension). However, its influence on the northwestern side of the settlement is not statistically significant. The distribution pattern of regression coefficients follows these principles:

• The regression coefficients are relatively lower in the northwestern part of the settlement and higher in the northeastern part.
• The average value of regression coefficients is higher in steep mountainous regions.

The X₂ elevation factor has a positive impact on the dependent variable, fractal dimension. However, in certain areas on the northern side of the settlement, its influence is not statistically significant. The distribution pattern of the regression coefficients is as follows:

• From the village center to the periphery, the positive impact of elevation on the subspace fractal dimension becomes progressively stronger.
• Both higher and lower elevations exert a stronger positive impact on the subspace fractal dimension of the settlement.

4. Discussion

4.1. Discussion on the Fractal Dimension of Settlements and the Fractal Dimension of Suitable Construction Areas

In the study of settlement morphology, researchers primarily focus on utilizing fractal dimensions for comprehensive analysis of settlements. Fractal dimensions reflect the intrinsic spatial order of complex systems and reflect self-similarity at both macro and micro levels [36]. The objects of fractal dimension analysis extend beyond merely the planar distribution patterns of settlement buildings; previous studies have also investigated building facades and street frontages within settlements to analyze their aesthetic forms [13,37]. For mountainous settlements, construction is significantly influenced by topography, resulting in limited suitable areas for development that are often not contiguous. Consequently, village morphology tends to exhibit a dispersed point-like distribution [38,39]. Suitable construction areas can effectively reflect the characteristics of the terrain and landforms. Based on the above points, we selected suitable construction areas as one of the subjects for fractal dimension analysis and sought to establish its correlation with the fractal dimensions of settlements.

The fractal dimension of settlement building distribution reflects the spatial filling degree and complexity of settlements. The fractal dimension suitable for construction areas indicates the richness of land resource forms in mountainous settlements. Research has shown that traditional mountain settlements within the jurisdiction of Jiexiu City exhibit high spatial complexity. Villages with higher fractal dimensions, such as Zhang Village and Hongshan Village, have fractal dimensions of 1.72 and 1.71, respectively. These villages share certain common characteristics in their settlement morphology; both Zhang Village and Hongshan Village feature relatively organized new village areas that develop around ancient village regions, occupying a significant proportion of space. The well-planned new village areas demonstrate higher utilization rates due to their relative completeness in planning, which translates into greater spatial filling degrees and complexities. This significantly impacts the overall fractal dimension. Furthermore, constructing new villages around core ancient villages also influences the fractal dimension; this approach is more effective than rebuilding new villages in other areas, as it better complements settlement boundaries and enhances the spatial integrity of ancient villages. In our study, we found that while there are substantial proportions of new village areas adjacent to ancient villages—such as Jiaojia Fortress Village—their fractal dimensions do not reach similarly high levels. In terms of the fractal dimensions of suitable construction areas, all surveyed villages exhibited remarkably high fractal dimension values. This is primarily because the morphology of suitable construction areas in mountainous settlements is constrained and shaped by natural systems, which are inherently regarded as exemplary fractal systems [40]. Furthermore, a strong linear positive correlation was observed between the planar complexity of the twelve samples and the complexity of suitable construction areas. This suggests an intrinsic relationship between the planar morphology of settlement buildings and topographical features. In other words, the complexity of the terrain may significantly influence the spatial layout of settlement buildings, and the morphological characteristics of settlements, to some extent, reflect the complexity of their geographical environment.

This finding further supports the hypothesis of a correlation between topography and the spatial morphology of settlements, laying a solid foundation for exploring the interaction mechanisms between settlements and their natural environment. Such conclusions are highly consistent with existing qualitative analyses of mountainous settlements [41], providing robust mathematical support for these studies and offering valuable insights for determining research samples and advancing subsequent investigations.

4.2. Discussion on the Spatial Morphology of Xingdi Village Settlement

The analysis of the overall fractal dimension in the study area represents only a small part of fractal dimension analysis. Previous research has indicated that urban areas exhibit fractal structures and characteristics, and similarly, sub-regions within cities also display these traits. Therefore, it is feasible to conduct detailed studies on different directions and regions within urban settings [16,42]. In contrast, prior spatial analyses within settlements have utilized methods such as space syntax [43] without incorporating fractal dimensions into their evaluations. This study shifts its focus from densely populated and extensive urban systems to relatively discrete settlement systems characterized by smaller village areas. Compared to urban environments, settlements are smaller in scale but exhibit similarly complex spatial forms. They can also be regarded as complex systems, making them appropriate for conducting fractal dimension analysis at sub-regional scales. By performing such analyses, the complexity of spatial forms within sub-regions of settlements can be effectively revealed.

The distribution pattern of the fractal dimension in subspaces reflects more internal spatial morphological characteristics compared to the overall fractal dimension of the settlement. The study of Xingdi Village reveals that the core area of this settlement, due to its developed and optimized morphology, exhibits a higher degree of spatial filling and complexity. Similar to urban models, it is observed that the filling degree deteriorates as one approaches the boundary of the settlement. Throughout the development process of settlements, there inevitably arises a need for morphological renewal. This progression has led to two distinct developmental pathways—one involves continuous improvement upon existing settlements, leading to new ones, while the other entails establishing new zones in newly designated areas. Xingdi Village has opted for the latter approach, resulting in a clear demarcation between old and new villages along north–south axes. The newly constructed village benefits from well-planned designs and relatively complete infrastructure support, featuring more organized courtyard spaces with higher overall space utilization rates. In contrast, although older villages exhibit greater complexity within their core areas, there exists a significant disparity between their edge regions and core areas. Overall, it can be concluded that the spatial filling degree in new villages surpasses that found in old ones. Furthermore, we have observed that near Dongzhai and Xibao regions within Xingdi Village, spatial patterns are well-preserved; traditional courtyards remain largely intact with favorable configurations and have not undergone substantial modernization alterations. Consequently, these areas demonstrate significantly better spatial filling degrees compared to other ancient village regions.

4.3. Discussion on Influencing Factors of Subspace Morphology

In the context of mountainous settlements, the natural terrain and topography significantly determine the direction, development model, and overall framework of settlement growth [39]. Taking Xingdi Village as an example, the mountainous areas to the northeast directly influence its development towards the southwest. The demand for relatively flat terrain in new village construction necessitates a site-selection approach for new buildings. Additionally, the orientation of mountain ranges affects the layout of roads within the settlement, thereby impacting its overall spatial structure. This study aims to reveal how topography influences internal subspace morphology in Xingdi Village. The regression results indicate that in most areas of Xingdi Village, flatter plots with smaller slopes positively influence the complexity and density of the planar distribution of settlement buildings, with an even greater impact in mountainous regions. Settlement construction and development exhibit a certain reliance on flat areas; modern practices in building, developing, renewing, and preserving settlements are largely dependent on level terrain. Flat land facilitates transportation convenience, ease of construction, and accessibility for utilities—all factors that contribute to enhancing spatial morphology within settlements. In steep terrains, building layouts exhibit higher sensitivity. Flat plots in such areas are relatively scarce and hold significant importance, making building arrangements highly dependent on them. The abundance or scarcity of flat plots can substantially alter the complexity of building layouts. In contrast, in gentler terrains, the widespread availability of flat plots reduces their constraints on building distribution, resulting in a relatively weaker influence on subspace complexity and density. Moreover, the boundary effects of flat plots are more pronounced in steep terrains, where flat plots often exhibit irregular shapes, exerting a greater impact on the spatial organization patterns of building layouts. The limited availability of flat terrains also constrains planning and construction activities, encouraging more rational considerations. The shape of flat plots directly affects the morphology of building layouts, significantly influencing their complexity and spatial density. Regarding slope orientation, traditional units in Jiexiu District predominantly consist of residential structures designed in courtyard styles that benefit from four-directional exposure; thus, north–south slopes have minimal impact on settlement spatial morphology. For elevation, the regression results indicate that in most areas of Xingdi Village, the average elevation of subregions has a positive impact on the complexity and density of building layouts, with a stronger effect in both higher and lower elevation areas. In high-elevation and low-elevation regions, building layouts are more sensitive to changes in elevation, primarily due to transportation and natural factors. In contrast, transitional areas are more influenced by social factors.

4.4. Discussion on Development Planning Recommendations

Based on the findings of this study, and in conjunction with existing planning frameworks, it is essential to supplement spatial morphology aspects. At the same time, a heritage conservation system is established based on the fractal characteristics of the settlement and influencing factors. Using subspace fractal dimensions and their influencing factors as the basis, the settlement is partitioned for protection. The goal is to maintain the stability of fractal dimension values both locally and across the entire settlement, optimize the layout characteristics of local areas, and guide the spatial morphology of newly developed areas based on fractal characteristics. This study primarily introduces the core components of the system, namely the classification of spatial conservation zones based on fractal characteristics and the corresponding renewal strategies for each category.

4.4.1. Protection Zoning Based on Fractal Characteristics

The zoning must be based on objective data and multiple variables. Evidently, cluster analysis is well-suited for integrating various variables for classification. Additionally, cluster analysis can classify settlements according to similar morphological patterns, revealing local characteristics and spatial heterogeneity.

In this study, subspace fractal dimensions, slope influence factors, and elevation influence factors were selected as clustering factors. Z-score standardization was applied to eliminate the effects of dimensional differences. K-means clustering was used for the analysis, requiring the determination of the value of K. The elbow method was employed to calculate the sum of squared errors (SSE) for K values ranging from 2 to 8 (

Table 6. Sum of Squared Errors (SSE) corresponding to different K values.

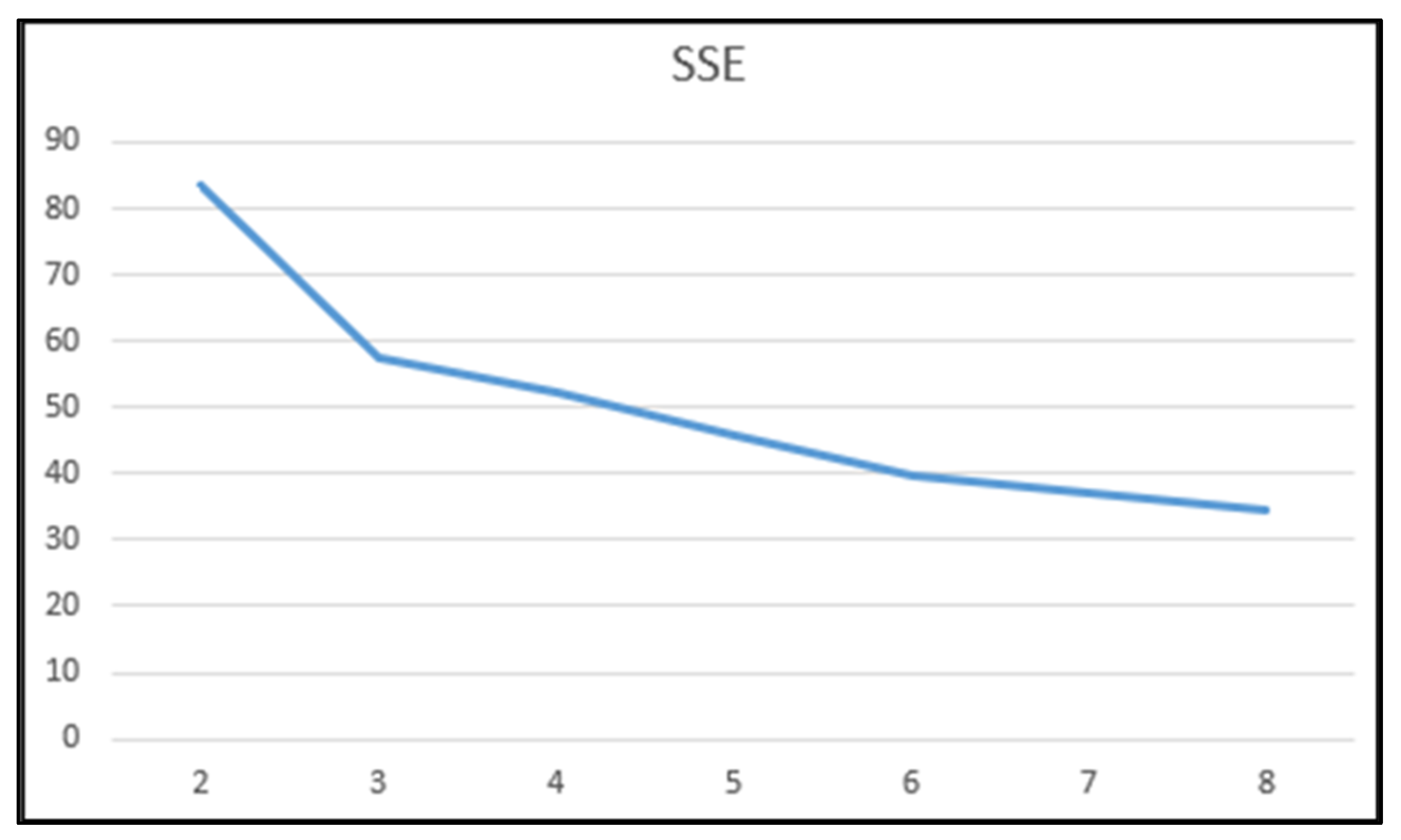
K	2	3	4	5	6	7	8
SSE	83.275802	57.619362	52.125689	45.686388	39.778818	36.945142	34.558358

). A line chart was plotted (Figure 10), and the inflection point was identified at K = 3.

Based on the above calculations, the clusters were divided into three categories. Cluster analysis was conducted, resulting in cluster centroids (

Table 7. Final cluster centers.

	Clustering
	1	2	3
Z-score: fractal dimension	−1.35942	0.43210	0.25622
Z-score: slope	1.26056	0.24549	−1.14809
Z-score: altitude	−0.24554	−0.76269	1.23095
Effective	14	31	22
Invalid	0	0	0

) and an ANOVA table (

Table 8. ANOVA.

	Clustering		Error		F	Significance
	MS	DF	MS	DF
Z-score: fractal dimension	16.552	2	0.514	64	32.204	<0.001
Z-score: slope	26.557	2	0.201	64	131.887	<0.001
Z-score: altitude	26.106	2	0.215	64	121.179	<0.001

Since clustering has been selected to maximize the differences between cases in different clusters, the F-test should only be used for descriptive purposes. The observed significance levels have not been adjusted accordingly and therefore cannot be interpreted as tests of the hypothesis that cluster means are equal.

). The number of samples in each category was reasonable and statistically significant.

In addition, the clustering analysis retained the classification results of each subspace region and visualized them (Figure 11).

All subspace regions are grouped into three categories. According to the results, the first category is characterized by low fractal dimensions, the highest slope influence factor, and a relatively low elevation influence factor. This corresponds to areas with low-complexity building layouts, significantly influenced by slope, and located in the steeper northeastern part of the settlement. The second category exhibits moderately low fractal dimensions, a moderately low slope influence factor, and the lowest elevation influence factor. These correspond to areas with medium-complexity building layouts, situated in relatively flat transitional elevation zones. The third category is marked by the highest fractal dimensions, the lowest slope influence factor, and the highest elevation influence factor. These areas correspond to high-complexity building layouts, significantly influenced by elevation, with dense and complex building arrangements.

4.4.2. Core Construction of Genetic Conservation Systems

The conservation system’s core is centered on devising differentiated conservation planning strategies for three distinct regional categories, guided by the results of cluster analysis. These strategies are subsequently integrated with existing conservation plans to construct a settlement conservation framework rooted in morphological typology. This system exhibits its advantages in two primary dimensions: first, by reclassifying existing architectural structures to delineate conservation boundaries based on typological systems; and second, by imposing restrictions on new construction and development activities within various regions to mitigate potential disruptions to fractal characteristics. For the first type of region, characterized by relatively low building layout complexity but significant slope constraints, it is deemed suitable for low-density development and ecological preservation. Accordingly, this region is designated as an environmental coordination zone. For the second type of region, which exhibits moderate building layout complexity and relatively flat terrain, it is appropriate for controlled development and utilization, leading to the establishment of a construction control zone. For the third type of region, distinguished by high building layout complexity, pronounced elevation influences, and gentle terrain, a core conservation zone is instituted to ensure robust protection. Moreover, the integration of existing conservation plans is imperative, necessitating the consideration of cultural factors and the intrinsic value of architectural heritage. This involves consolidating core conservation zones, expanding construction control zones, and redefining environmental coordination zones to achieve a comprehensive and cohesive conservation framework.

5. Conclusions

Through the results and analyses generated in this study, the following conclusions can be drawn: (1) When examining traditional villages within the jurisdiction of Jiexiu City, there is a certain correlation between topography and the spatial morphology of mountainous settlements. (2) Hongshan Village and its subspaces exhibit distinct typological characteristics; as the village expands, the degree of spatial filling diminishes, with higher levels observed within both new villages and traditional courtyards. (3) Flat terrain facilitates the optimization of spatial configurations in mountainous settlements, a phenomenon that becomes particularly pronounced in steep terrains where flat land is scarce. Additionally, the spatial layout of buildings at higher and lower altitudes demonstrates a greater sensitivity to elevation changes. (4) A heritage conservation system was established based on fractal dimensions and the influencing factors of slope and altitude, providing a scientific enhancement to the existing conservation plans. This research provides reliable data support and directional recommendations for planning mountainous settlements, demonstrating practical significance.

Limitations

This study has several limitations that warrant further discussion in subsequent research: (1) Mountain settlements represent a complex three-dimensional system, and the spatial morphology of these settlements holds research value in the vertical dimension as well. Some scholars have employed three-dimensional models to calculate fractal dimensions for analyzing spatial morphology in this context. However, this study exhibits shortcomings in its exploration along the z-axis; future research will establish three-dimensional models of settlements and compute their fractal dimensions for analysis. (2) The development of villages is a protracted process, and changes in settlement spatial morphology over time, as well as the influence of terrain on this morphology, should be considered temporally. Future studies will sample different significant morphological nodes during the historical formation process of settlements and employ Geographically Weighted Temporal Regression (GTWR) for analysis [44]. (3) The analysis conducted herein regarding the fractal dimensions of subspaces within a settlement is limited to basic visualizations without delving into multifractal analyses. As a function, multifractals can provide deeper insights into the spatial organizational patterns of such systems [45]. Subsequent research will focus on analyzing multifractal functions to achieve a more profound understanding of settlement spatial morphology. (4) The current analysis is somewhat constrained by its limited scope; to summarize mountain settlement spatial morphologies comprehensively, it is essential to increase the sample size for further investigation. (5) The spatial morphology of mountainous settlements cannot be solely attributed to topographical factors. Future research should incorporate considerations of social factors and other natural factors to provide a more comprehensive analysis. This approach would help to uncover the dynamic balance between geographical constraints and socio-economic factors, thereby offering deeper insights into the interplay between natural and human influences.