Research on Quasi-Zero Stiffness Vibration Isolation System of Buckled Flexural Leaf Spring Structure for Double Crystal Monochromator
Abstract
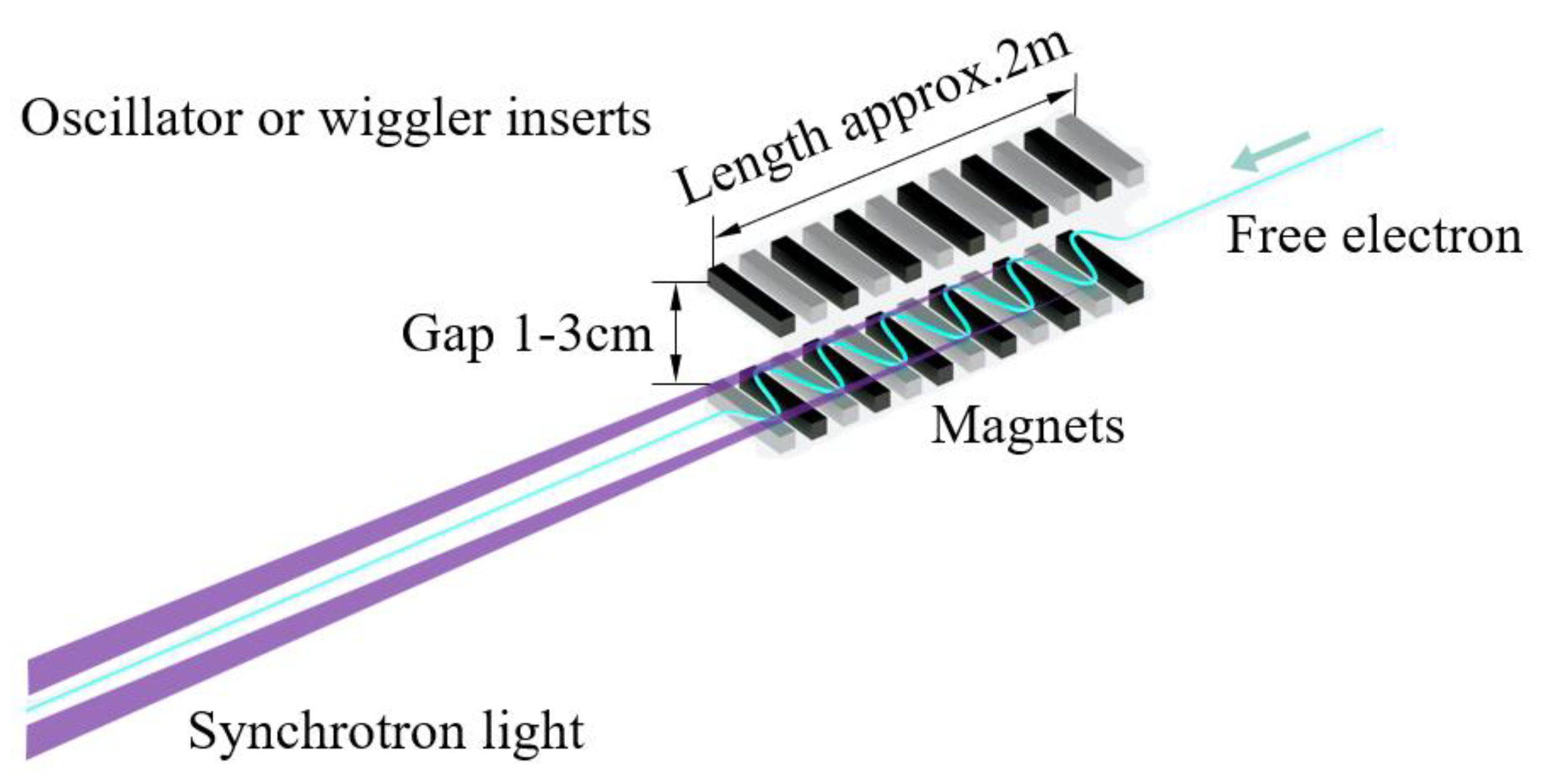
1. Introduction
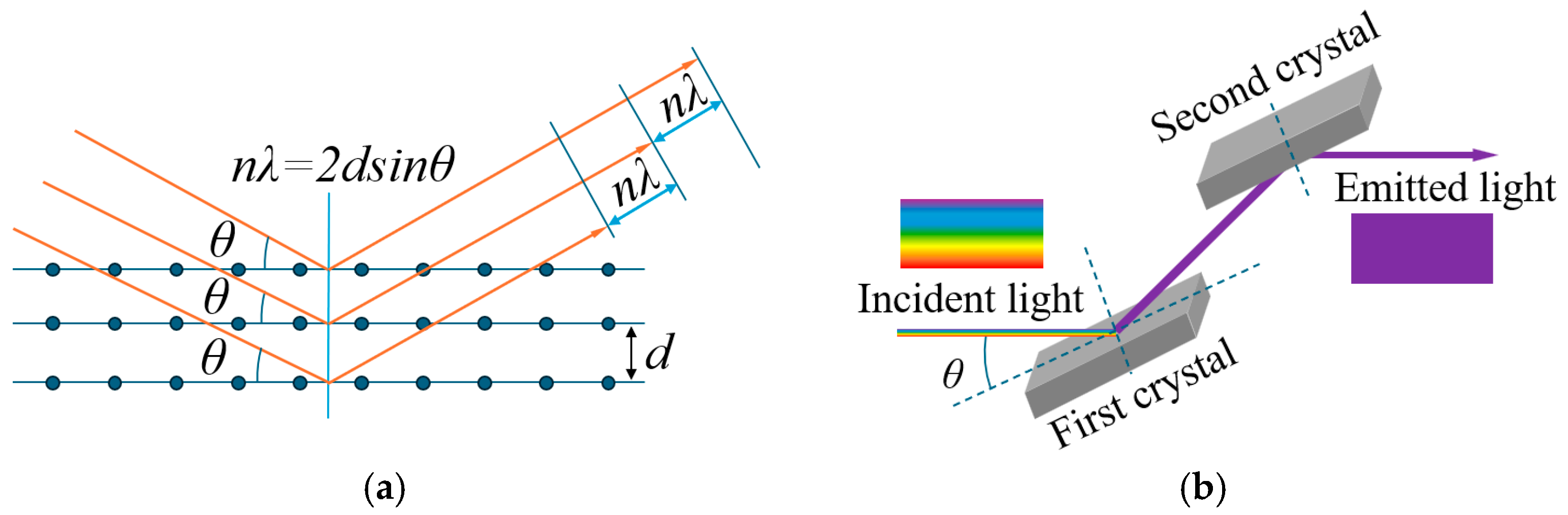
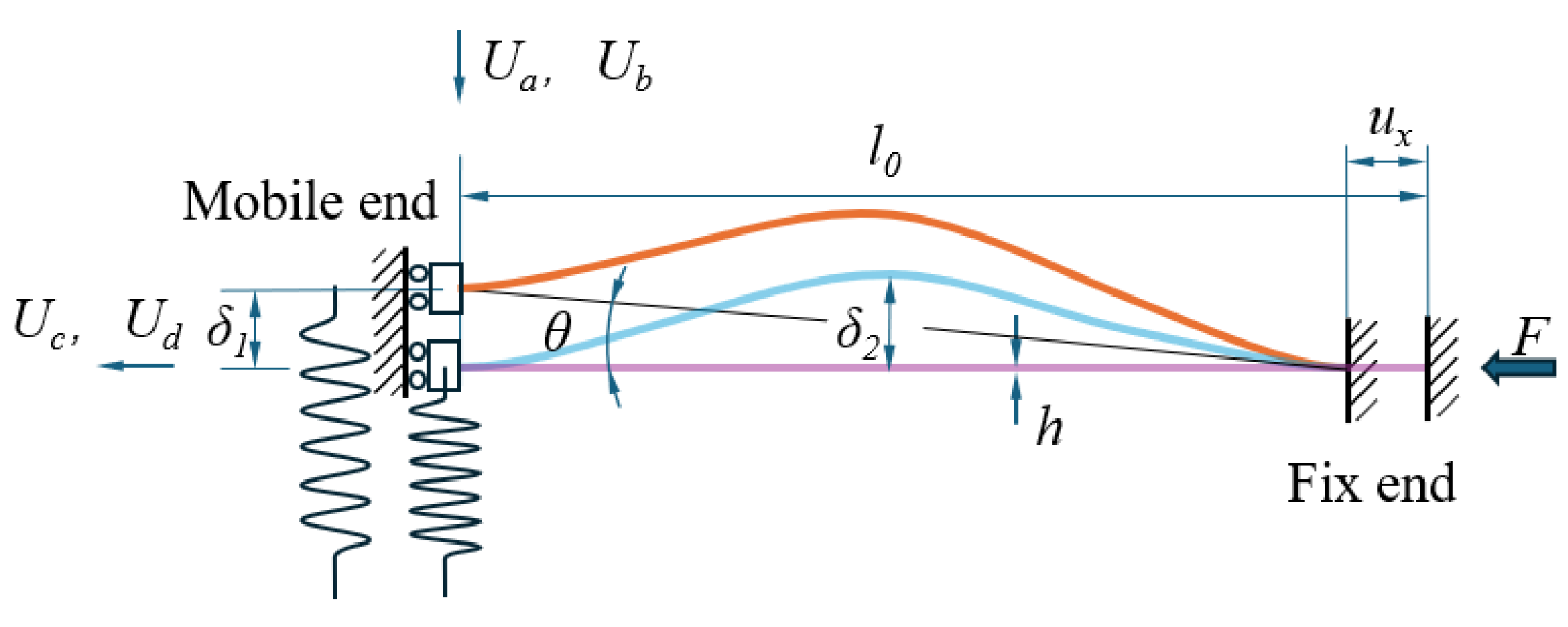
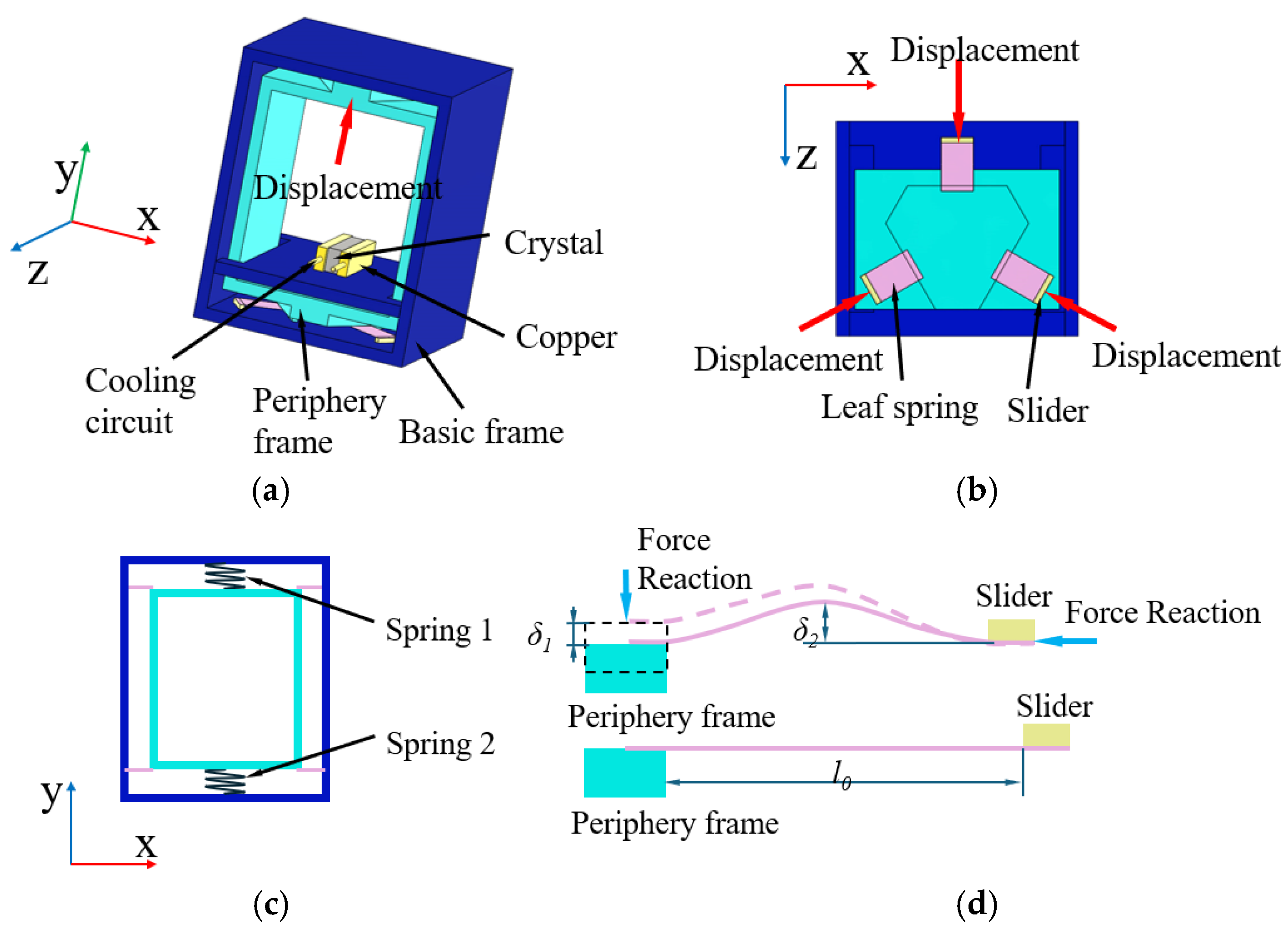
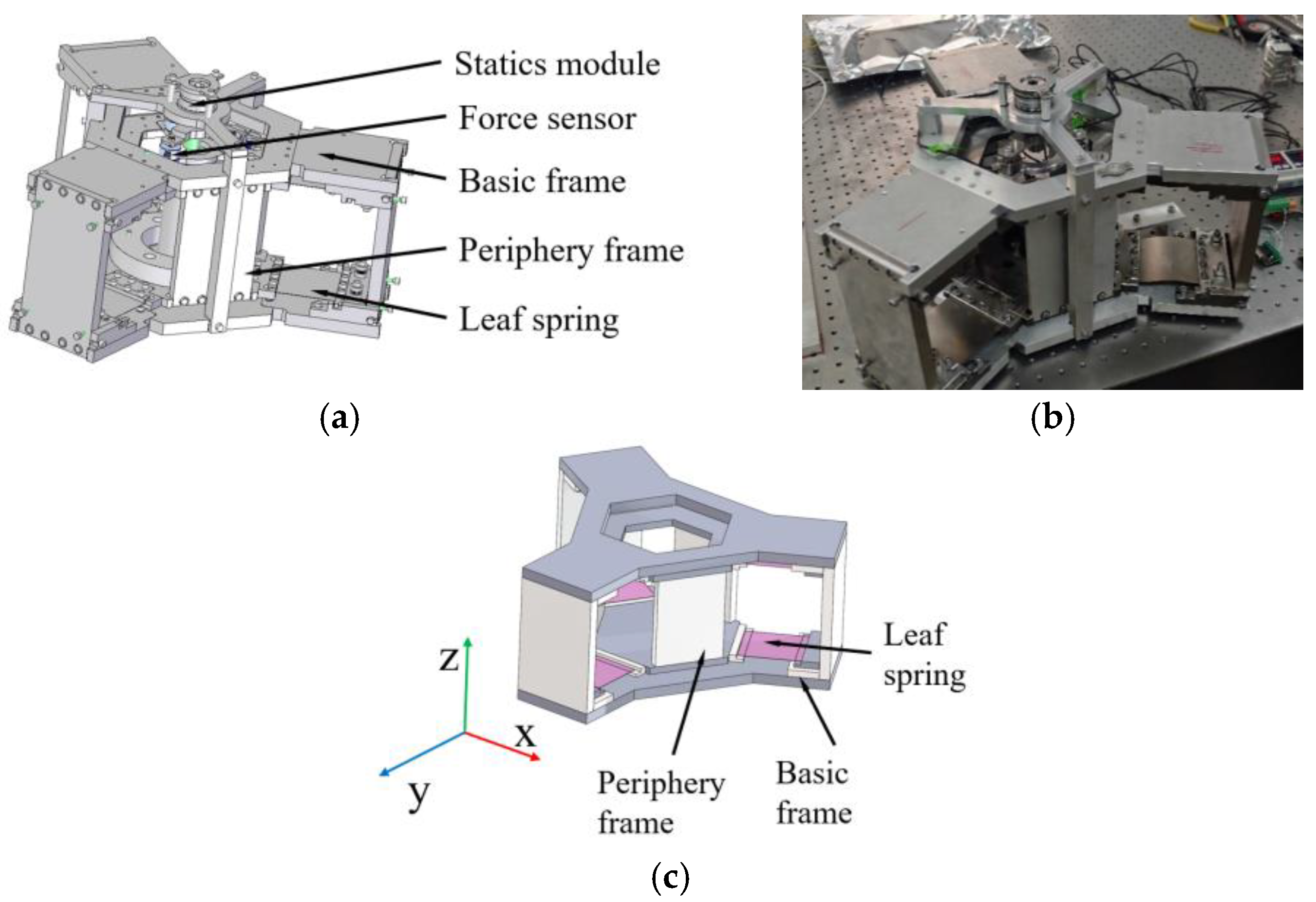
2. Vibration Isolation System of the DCM
3. Structural Design and Analysis of QZS Vibration Isolation Systems
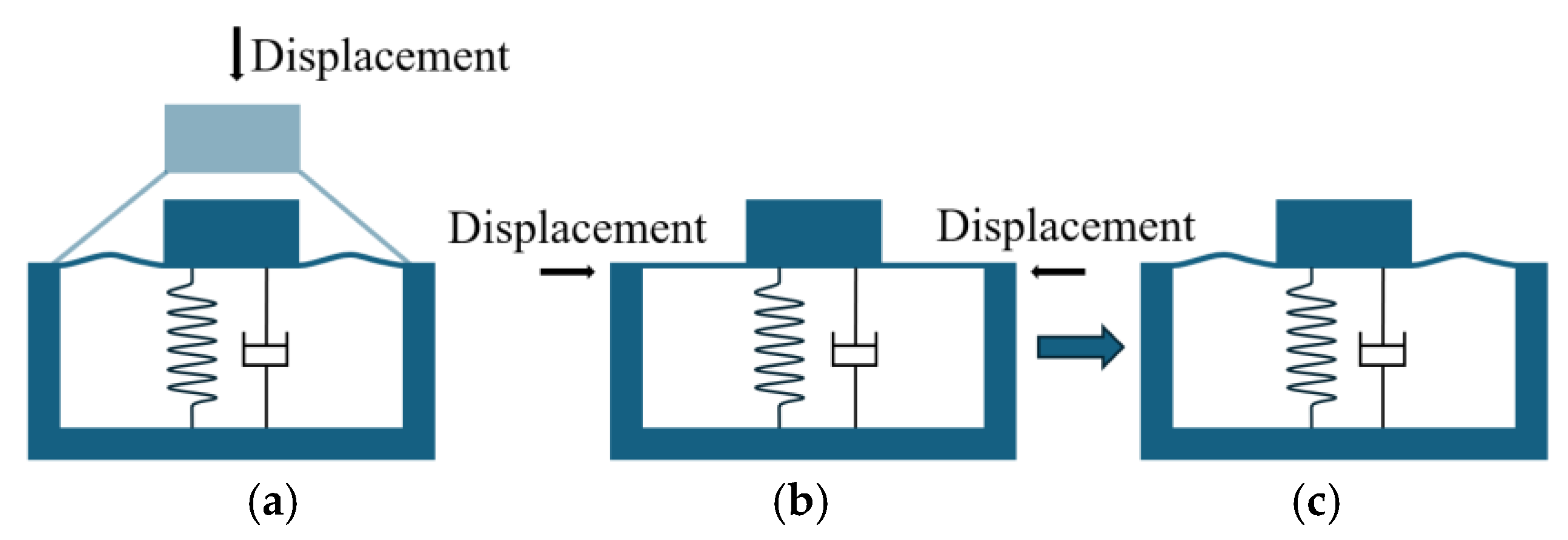
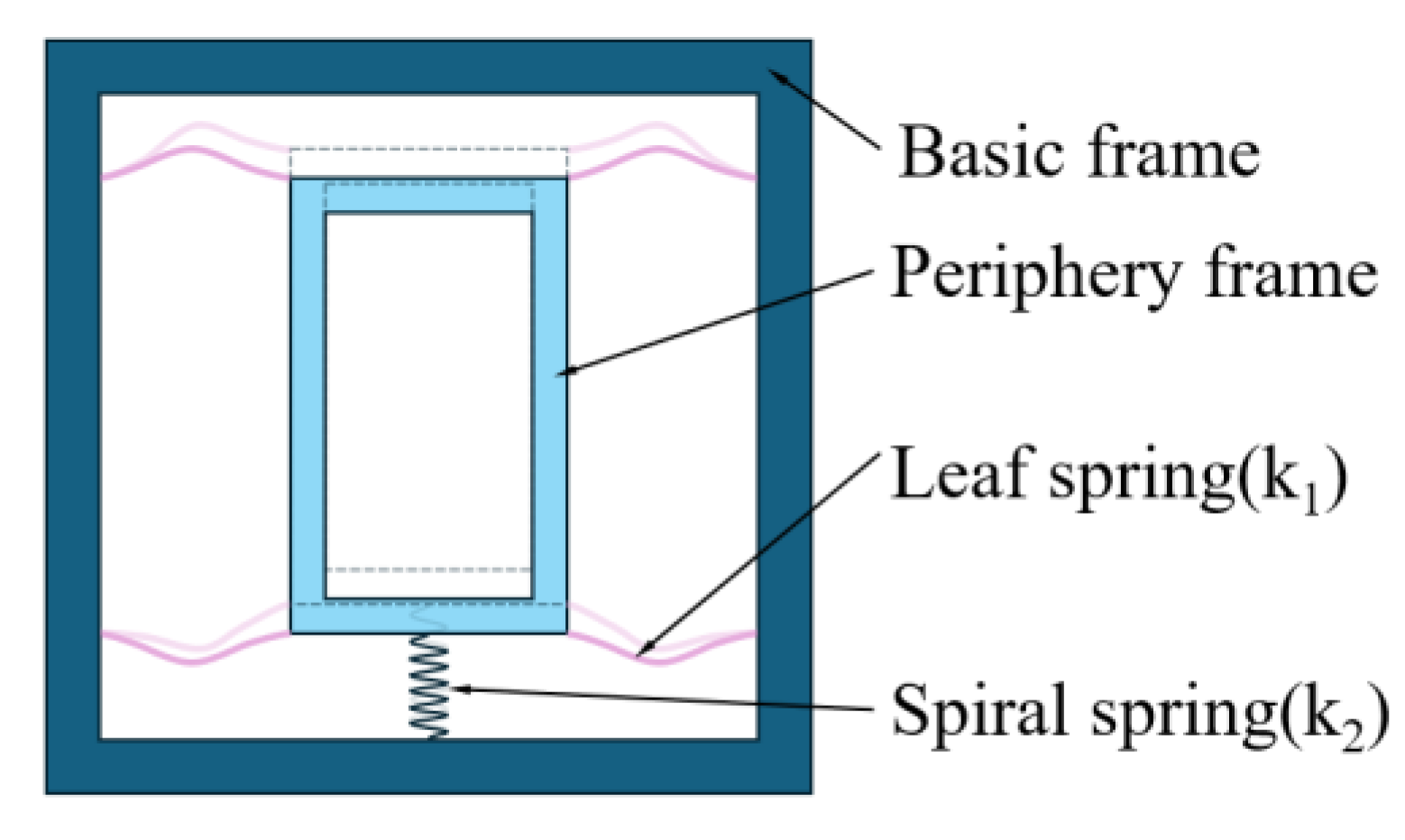
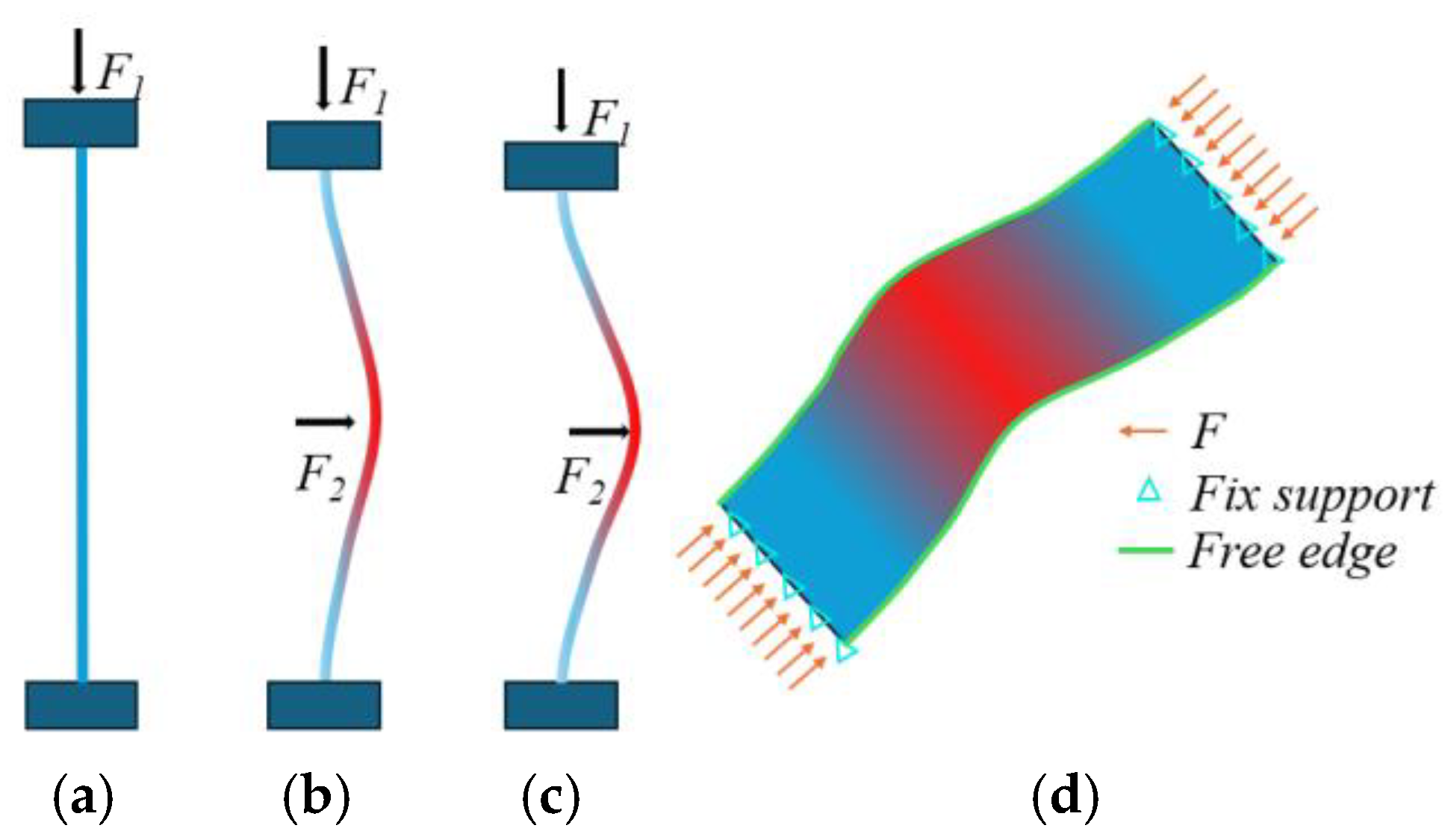
3.1. Negative Stiffness Element Design
3.2. The Analysis of the Compression of the Leaf Spring
3.3. Potential Energy and Negative Stiffness Derivation
4. Finite Element Analysis
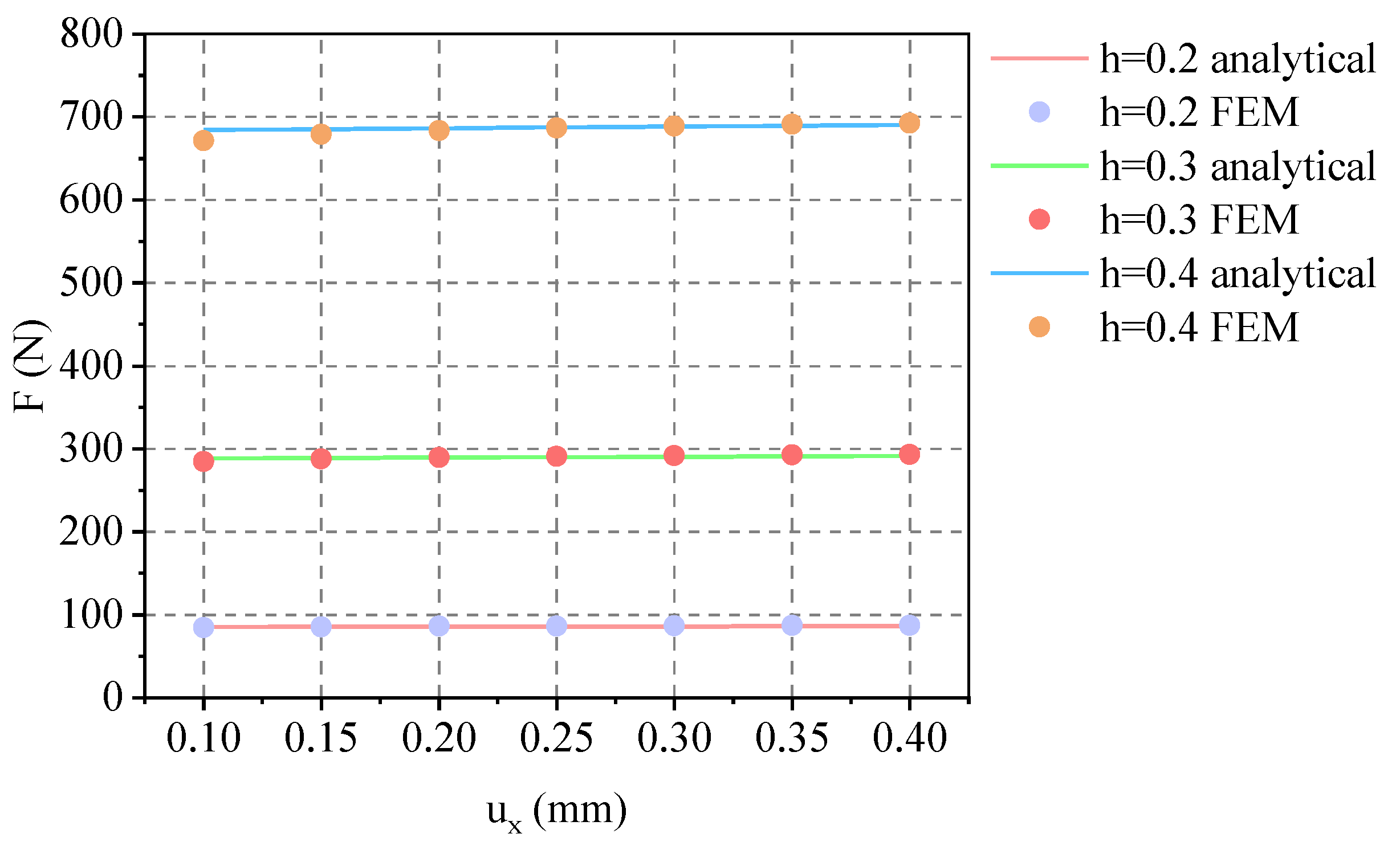
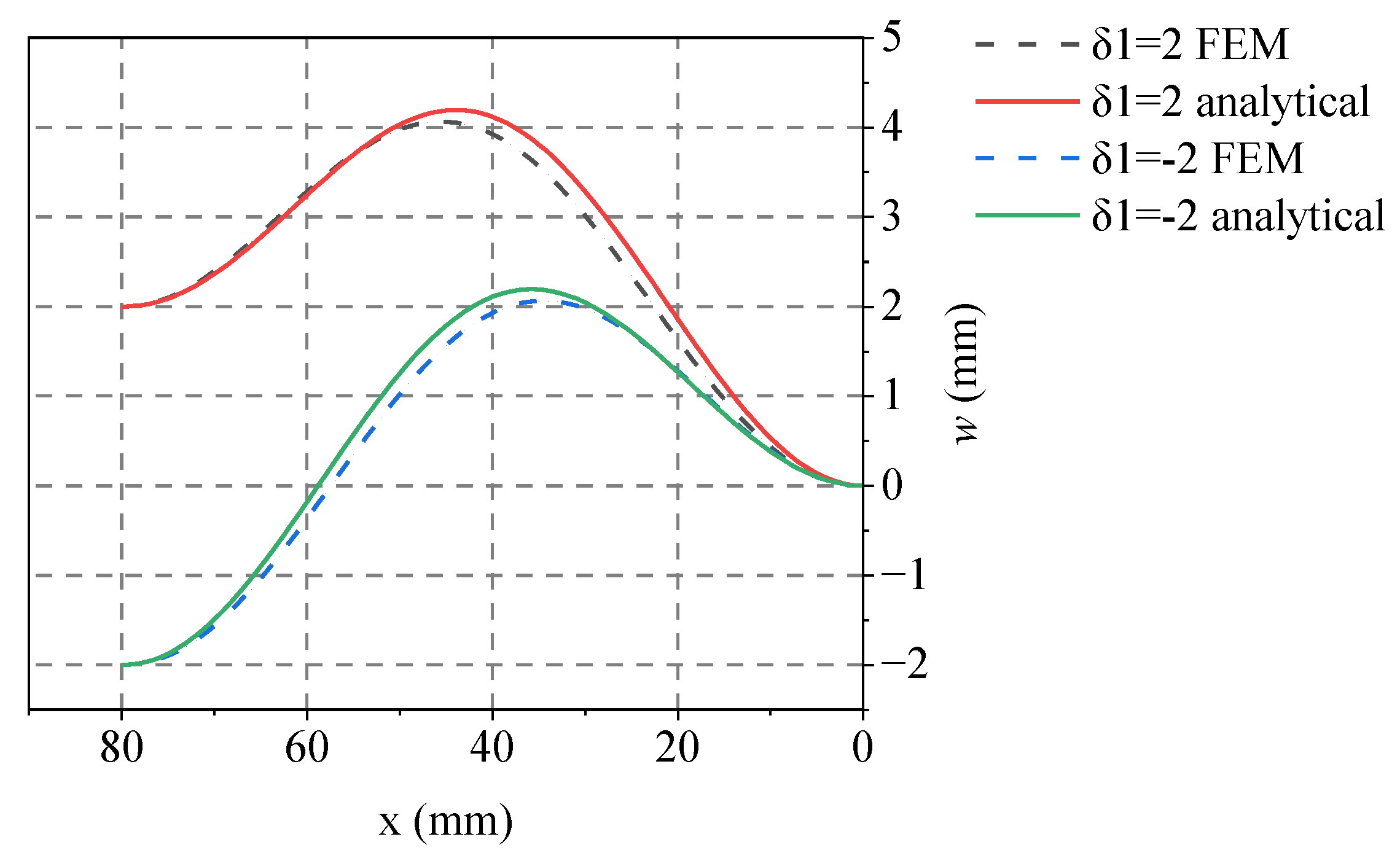
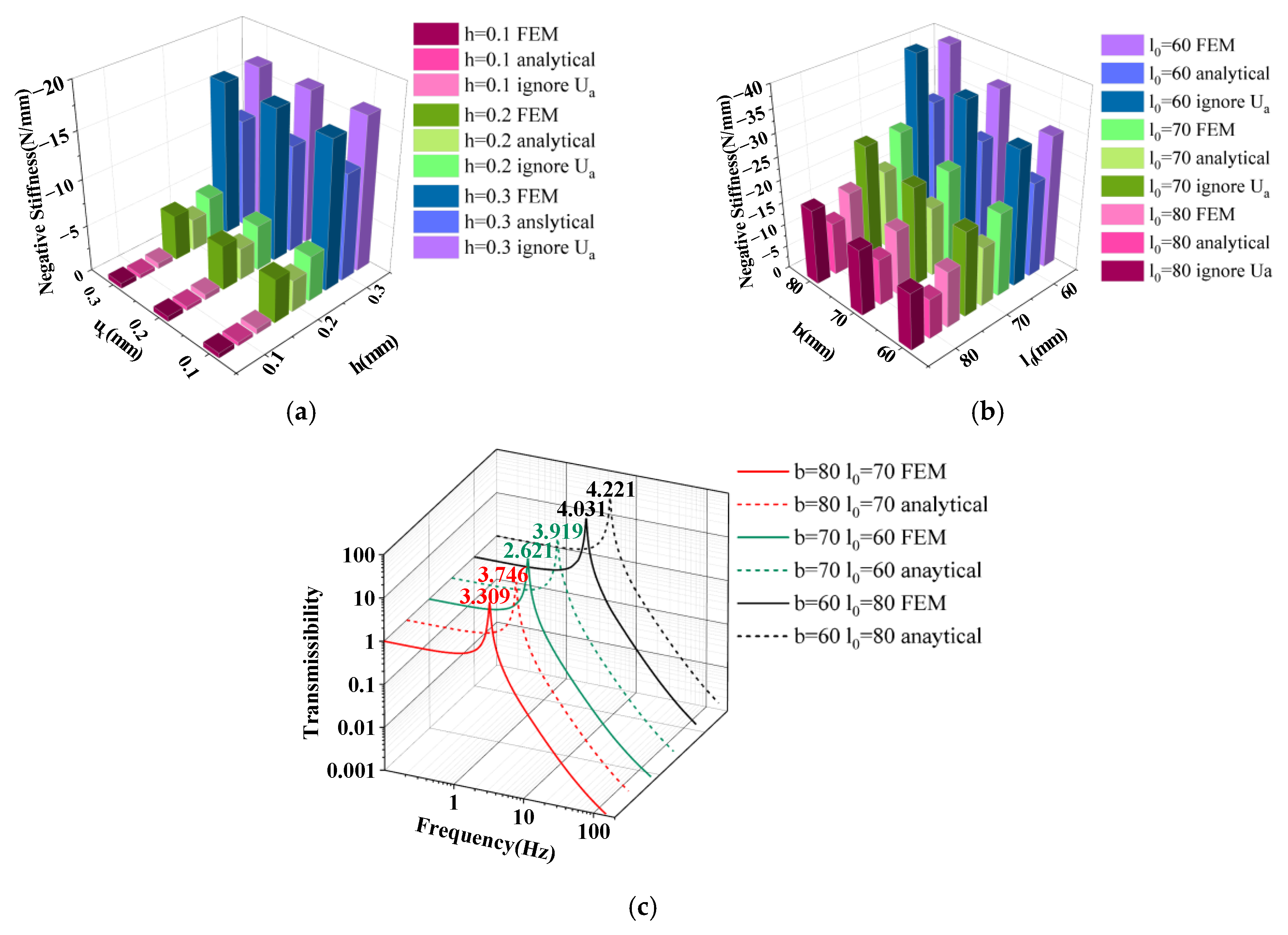
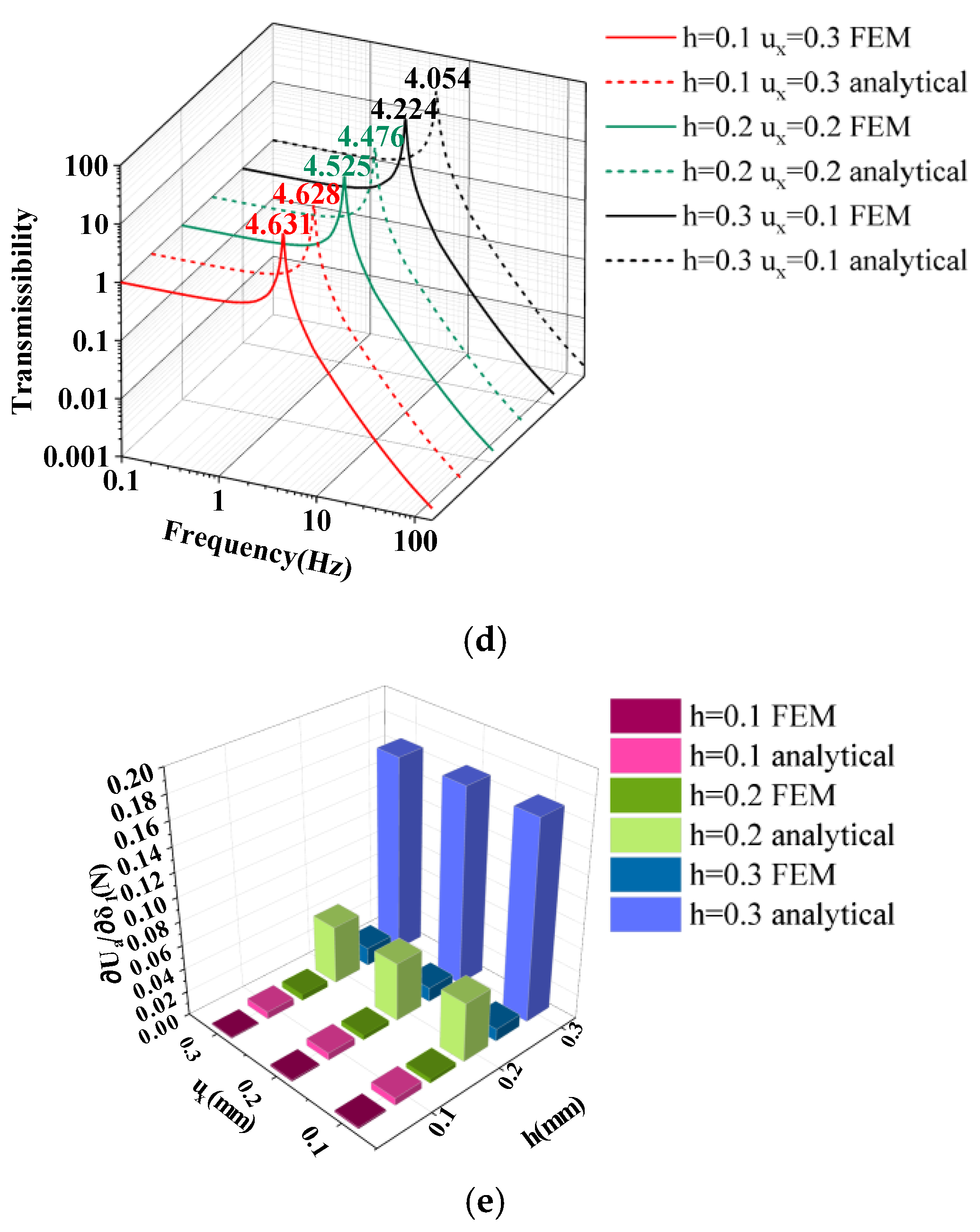
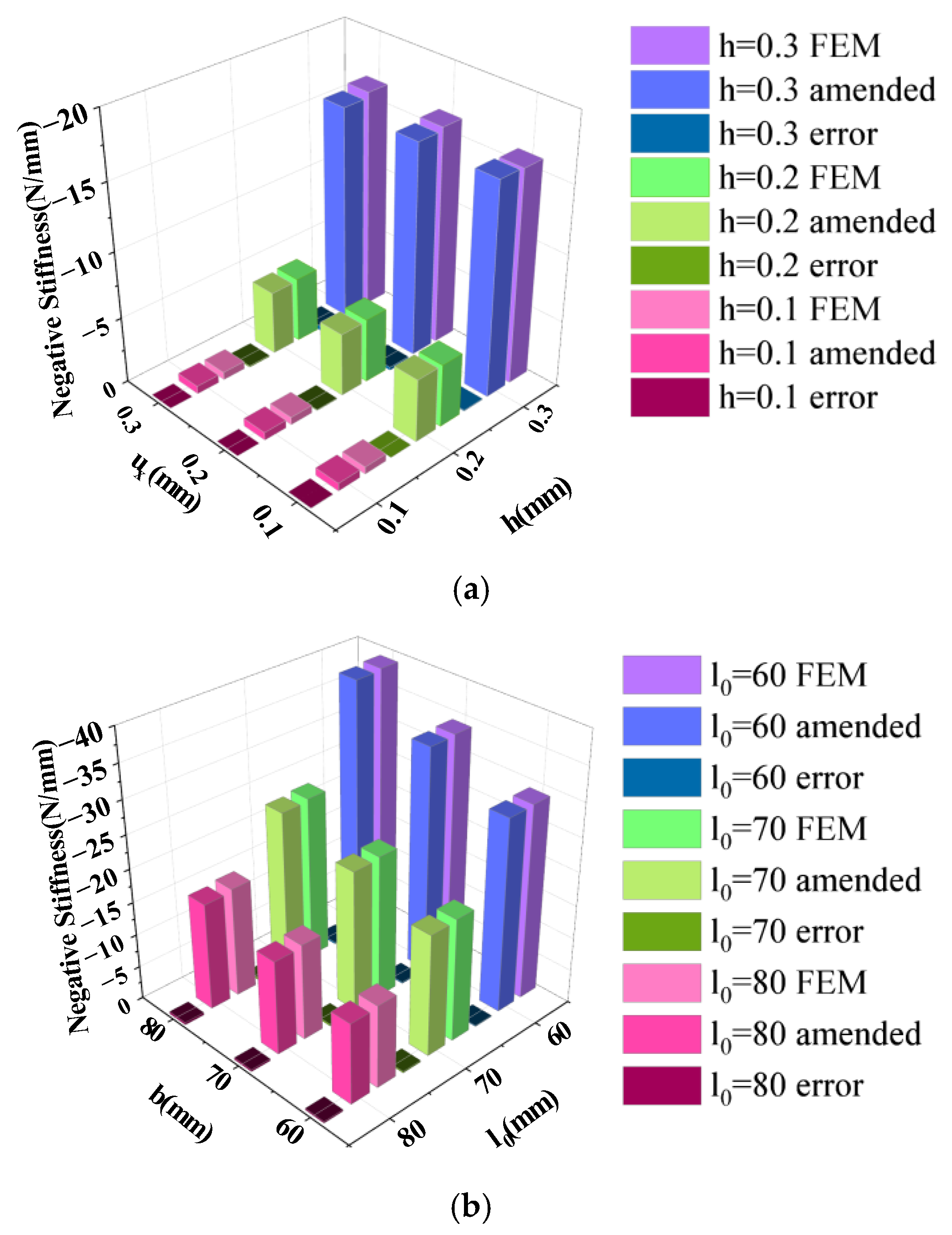
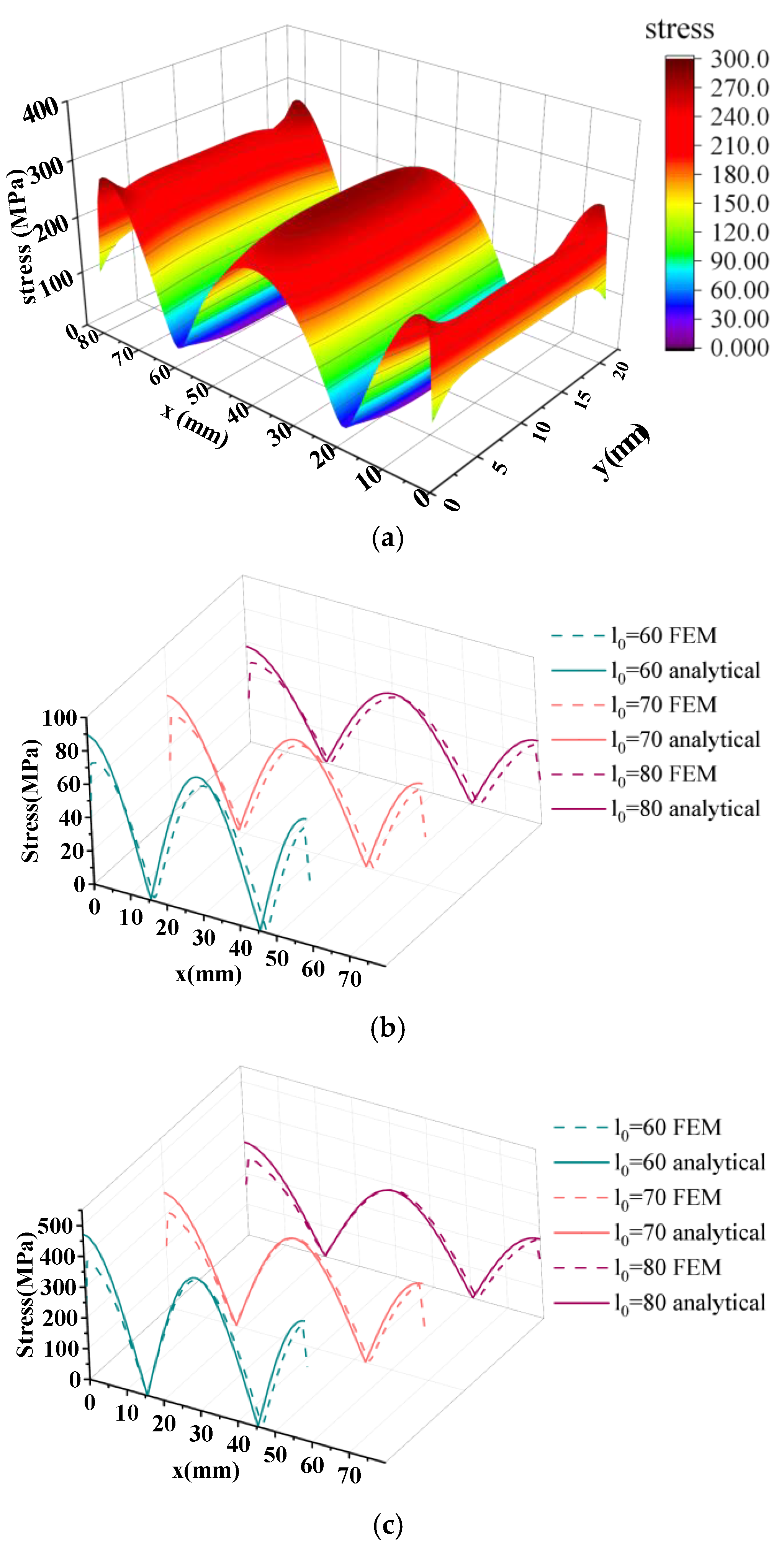
4.1. Accuracy of Formulas
4.2. Stress Field Analysis
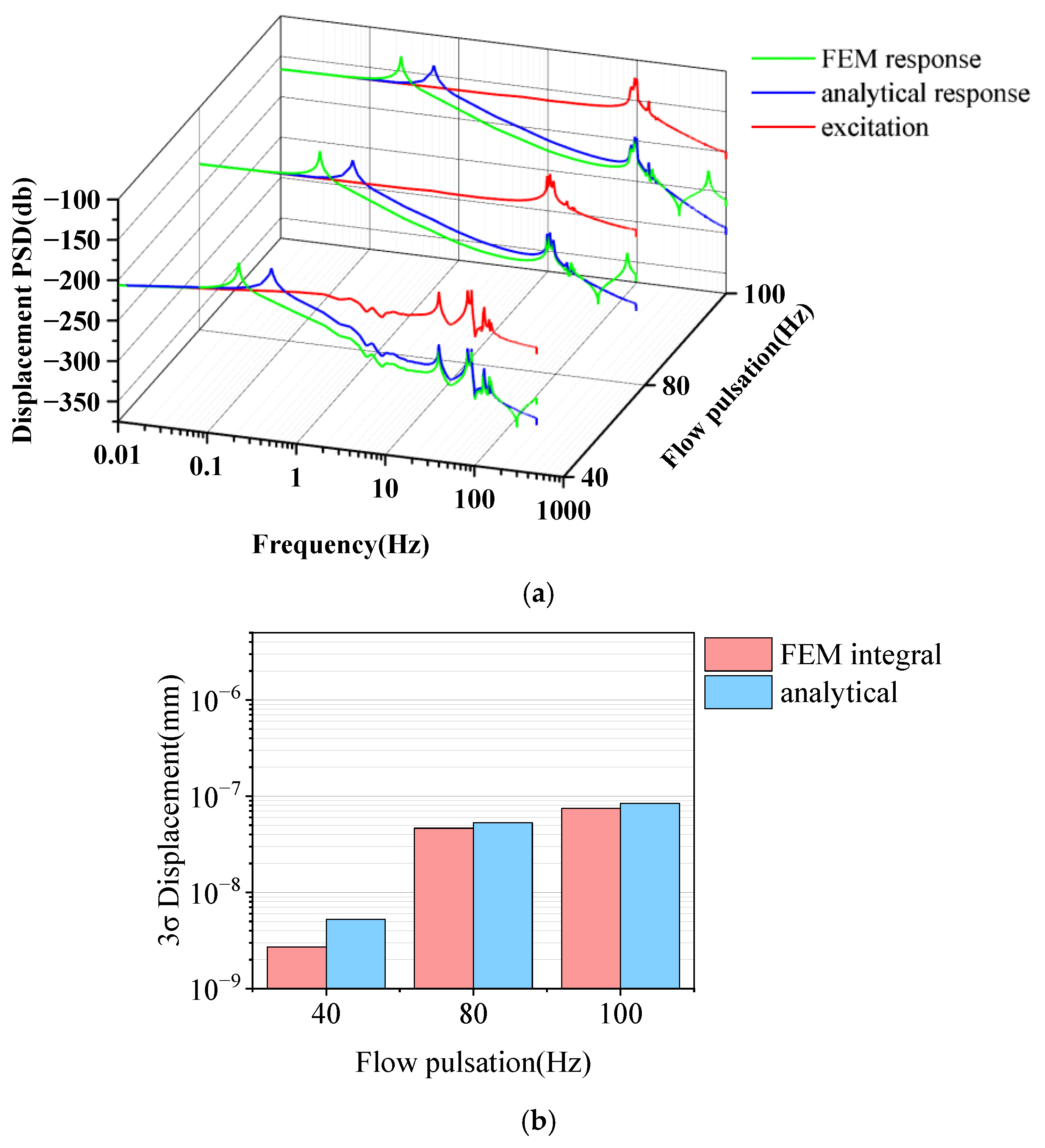
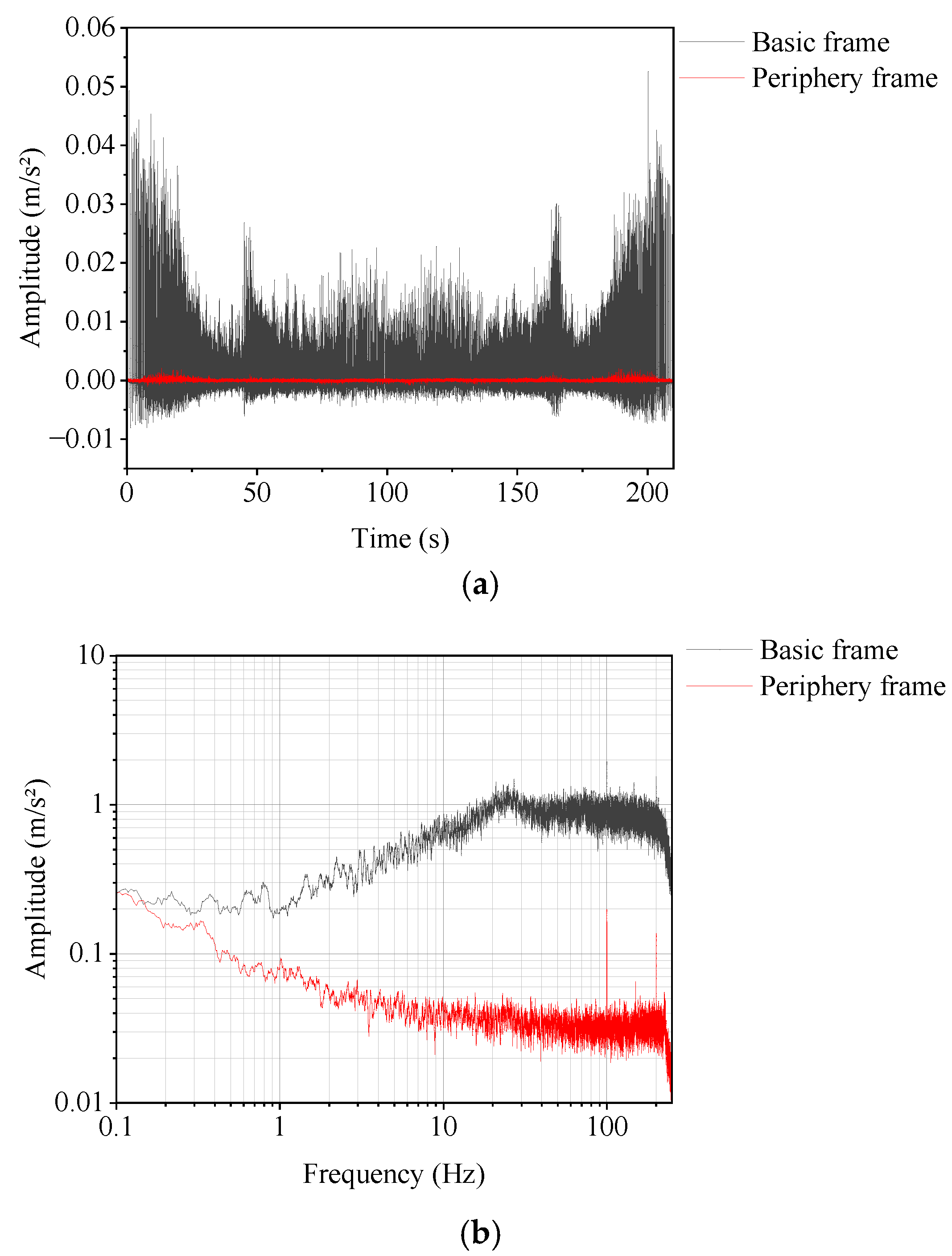
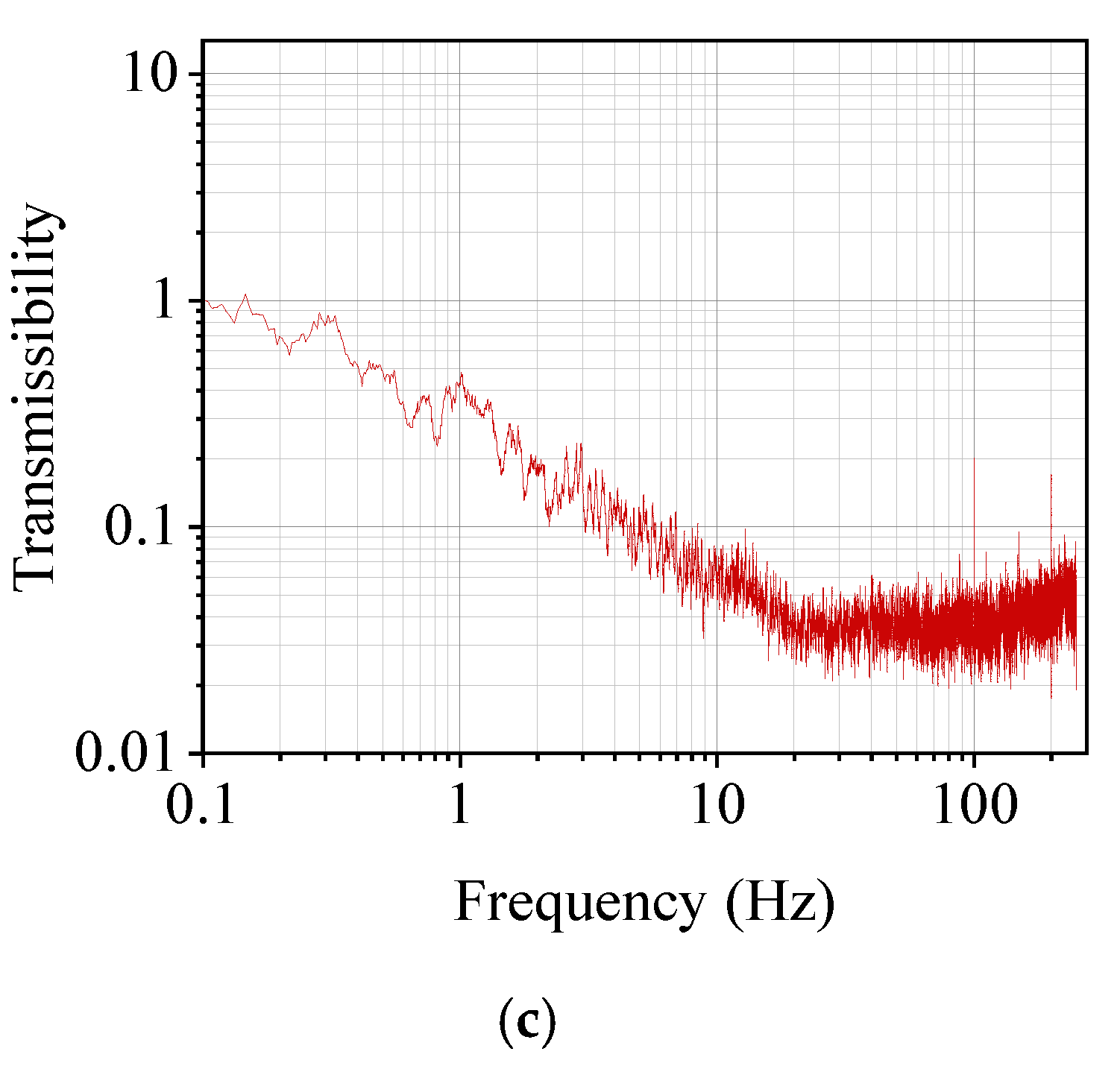
4.3. Vibration Isolation Performance Analysis
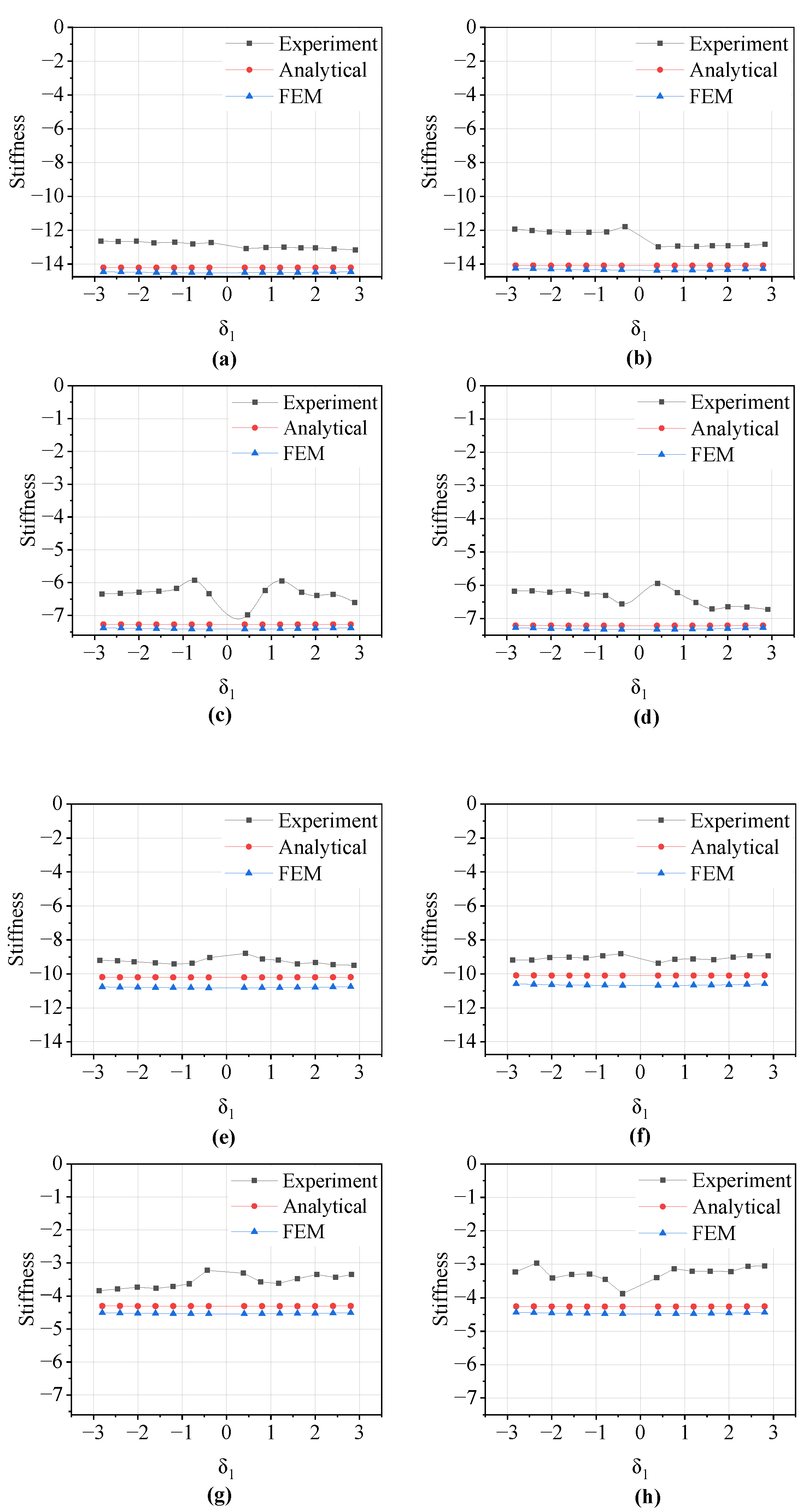
5. Experimental Verification
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tsoutsouva, M.G.; Regula, G.; Ryningen, B.; Vullum, P.E.; Mangelinck-Noël, N.; Stokkan, G. Dynamic observation of dislocation evolution and interaction with twin boundaries in silicon crystal growth using in–situ synchrotron X-ray diffraction imaging. Acta Mater. 2021, 210, 116819. [Google Scholar] [CrossRef]
- Li, A.; Gong, X.; Bai, Y.; Lu, Q.; Li, S.; Zhang, W.; Chai, K. Research on the Mechanism of Flow-Induced Vibration in the Cooling System of a Double Crystal Monochromator. Appl. Sci. 2024, 14, 2767. [Google Scholar] [CrossRef]
- Soares, T.R.S.; Furtado, J.P.S.; de Albuquerque, G.S.; Saveri Silva, M.; Geraldes, R.R. Dynamical modelling validation and control development for the new High-Dynamic Double-Crystal Monochromator (HD-DCM-Lite) for Sirius/LNLS. In Proceedings of the 19th International Conference on Accelerator and Large Experimental Physics Control Systems (ICALEPCS 2023), Cape Town, South Africa, 7–13 October 2023. [Google Scholar]
- Ciatto, G.; Chu, M.H.; Fontaine, P.; Aubert, N.; Renevier, H.; Deschanvres, J.L. SIRIUS: A new beamline for in situ X-ray diffraction and spectroscopy studies of advanced materials and nanostructures at the SOLEIL Synchrotron. Thin Solid Film. 2016, 617, 48–54. [Google Scholar] [CrossRef]
- Shuo, C.; WanQian, Z.; ZhanFei, Z.; LiMin, Z.; Song, X. Research and optimization of flow-induced vibrations in a water-cooled monochromator. Rev. Sci. Instrum. 2024, 95, 035124. [Google Scholar]
- Siming, G.; Dongjie, H.; Eryan, W.; Ruiqiang, S.; Pengyue, Z. Structure improvement and stability research of double crystal monochromator. Metrol. Sci. Technol. 2021, 65, 8–13. [Google Scholar]
- Hiroshi, Y.; Yasuhisa, M.; Yasuhiro, S.; Ichiro, T.; Yuki, I.; Tomoyuki, T.; Masayuki, T.; Takanori, M.; Hikaru, K.; Yasunori, S.; et al. Challenges toward 50 nrad-stability of x-rays for a next generation light source by refinements of SPring-8 standard monochromator with cryo-cooled Si crystals. In AIP Conference Proceedings; AIP Publishing: Melville, NY, USA, 2019; Volume 2054. [Google Scholar]
- Yichen, F.; Hongliang, Q.; Wanqian, Z.; Wenhong, J.; Yun, L.; Jie, W.; Zhongliang, L. Angular stability measurement of a cryocooled double-crystal monochromator at SSRF. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2020, 983, 164636. [Google Scholar]
- Li, S. Analysis of foundation vibration pattern and coherence of Shanghai Light Source Experimental Hall. Noise Vib. Control. 2016, 36, 108–111+159. (In Chinese) [Google Scholar]
- Ma, Z.; Rui, Z.; Yang, Q. Recent advances in quasi-zero stiffness vibration isolation systems: An overview and future possibilities. Machines 2022, 10, 813. [Google Scholar] [CrossRef]
- Hamzehei, R.; Bodaghi, M.; Wu, N. Mastering the art of designing mechanical metamaterials with quasi-zero stiffness for passive vibration isolation: A review. Smart Mater. Struct. 2024, 33, 083001. [Google Scholar] [CrossRef]
- Ge, Y.; Zhi-Yuan, W.; Xin-Sheng, W.; Sen, W.; Hong-Xiang, Z.; Lin-Chuan, Z.; Wen-Hao, Q.; Wen-Ming, Z. Nonlinear compensation method for quasi-zero stiffness vibration isolation. J. Sound Vib. 2022, 523, 116743. [Google Scholar]
- Carrella, A.; Brennan, M.J.; Waters, T.P. Static analysis of a passive vibration isolator with quasi-zero-stiffness characteristic. J. Sound Vib. 2007, 301, 678–689. [Google Scholar] [CrossRef]
- Carrella, A.; Brennan, M.J.; Kovacic, I.; Waters, T.P. On the force transmissibility of a vibration isolator with quasi-zero-stiffness. J. Sound Vib. 2009, 322, 707–717. [Google Scholar] [CrossRef]
- Wei, Z.; Chun, C.; Ran, M.; Yan, H.; Weiping, W. Performance analysis of a quasi-zero stiffness vibration isolation system with scissor-like structures. Arch. Appl. Mech. 2021, 91, 117–133. [Google Scholar]
- Wang, J.; Guo, Y. Multi-directional vibration isolation performances of a scissor-like structure with nonlinear hybrid spring stiffness. Nonlinear Dyn. 2024, 112, 8871–8888. [Google Scholar] [CrossRef]
- Linchuan, G.; Axconny, K.; Rang-Lin, F.; Xu, W. Analysis of a passive scissor-like structure isolator with quasi-zero stiffness for a seating system vibration-isolation application. Int. J. Veh. Des. 2020, 82, 224–240. [Google Scholar]
- Jiaxi, Z.; Xinlong, W.; Daolin, X.; Steve, B. Nonlinear dynamic characteristics of a quasi-zero stiffness vibration isolator with cam–roller–spring mechanisms. J. Sound Vib. 2015, 346, 53–69. [Google Scholar]
- Song, Z.; Dayang, W.; Yongshan, Z.; Quantian, L. Design and testing of a parabolic cam-roller quasi-zero-stiffness vibration isolator. Int. J. Mech. Sci. 2022, 220, 107146. [Google Scholar]
- Yonglei, Z.; Hao, W.; Haiyan, H.; Dongping, J. A novel quasi-zero stiffness isolator with designable stiffness using cam-roller-spring-rod mechanism. Acta Mech. Sin. 2025, 41, 524210. [Google Scholar]
- Lian, X.; Deng, H.; Han, G.; Jiang, F.; Zhu, L.; Shao, M.; Liu, X.; Hu, R.; Gao, Y.; Ma, M.; et al. A low-frequency micro-vibration absorber based on a designable quasi-zero stiffness beam. Aerosp. Sci. Technol. 2023, 132, 108044. [Google Scholar]
- Changqi, C.; Jiaxi, Z.; Linchao, W.; Kai, W.; Daolin, X.; Huajiang, O. Design and numerical validation of quasi-zero-stiffness metamaterials for very low-frequency band gaps. Compos. Struct. 2020, 236, 111862. [Google Scholar]
- Zeyi, L.; Kai, W.; Tingting, C.; Li, C.; Daolin, X.; Jiaxi, Z. Temperature controlled quasi-zero-stiffness metamaterial beam for broad-range low-frequency band tuning. Int. J. Mech. Sci. 2023, 259, 108593. [Google Scholar]
- Robertson, W.S.; Kidner, M.R.F.; Cazzolato, B.S.; Zander, A.C. Theoretical design parameters for a quasi-zero stiffness magnetic spring for vibration isolation. J. Sound Vib. 2009, 326, 88–103. [Google Scholar] [CrossRef]
- Yang, W.; Yuanping, X.; Lu, Y.; Jin, Z.; Jarir, M.; Chaowu, J. An ultra-sensitive diamagnetic levitation accelerometer with quasi-zero-stiffness structure. Measurement 2025, 245, 116651. [Google Scholar]
- Chaoran, L.; Yuewu, W.; Wei, Z.; Kaiping, Y.; Jia-Jia, M.; Huan, S. Nonlinear dynamics of a magnetic vibration isolator with higher-order stable quasi-zero-stiffness. Mech. Syst. Signal Process. 2024, 218, 111584. [Google Scholar]
- Lei, X.; Xiang, S.; Li, C.; Xiang, Y. A 3D-printed quasi-zero-stiffness isolator for low-frequency vibration isolation: Modelling and experiments. J. Sound Vib. 2024, 577, 118308. [Google Scholar]
- Xin, L.; Shuai, C.; Bing, W.; Xiaojun, T.; Liang, Y. A compact quasi-zero-stiffness mechanical metamaterial based on truncated conical shells. Int. J. Mech. Sci. 2024, 277, 109390. [Google Scholar]
- Chunyu, Z.; Guangdong, S.; Yifeng, C.; Xiaobiao, S. A nonlinear low frequency quasi zero stiffness vibration isolator using double-arc flexible beams. Int. J. Mech. Sci. 2024, 276, 109378. [Google Scholar]
- Haodong, Z.; Jiangjun, G.; Yao, C.; Zhengliang, S.; Hengzhu, L.; Pooya, S. A quasi-zero-stiffness vibration isolator inspired by Kresling origami. Structures 2024, 69, 107315. [Google Scholar]
- Xiaolong, Z.; Xuhao, L.; Changcheng, L.; Ruilan, T.; Luqi, C.; Minghao, W. Design of hyperbolic quasi-zero stiffness metastructures coupled with nonlinear stiffness for low-frequency vibration isolation. Eng. Struct. 2024, 312, 118262. [Google Scholar]
- Size, A.; Jianzheng, W.; Zhimin, X.; Huifeng, T. Analysis of negative stiffness structures with B-spline curved beams. Thin-Walled Struct. 2024, 195, 111418. [Google Scholar]
- Changqi, C.; Xin, G.; Bo, Y.; Kai, W.; Yongsheng, Z.; Wei, Y.; Jiaxi, Z. Modelling and analysis of the quasi-zero-stiffness metamaterial cylindrical shell for low-frequency band gap. Appl. Math. Model. 2024, 135, 90–108. [Google Scholar]
- Wu, Q.; Qiao, J.; Li, X.; Wang, S.; Li, B.; Wu, S.; Wang, Z.; Ji, J. NiTi Alloy Quasi-Zero Stiffness Vibration Isolation Structure with Adjustable Mechanical Properties. Machines 2025, 13, 92. [Google Scholar] [CrossRef]
- Ji, L.; Yanhui, W.; Shaoqiong, Y.; Tongshuai, S.; Ming, Y.; Wendong, N. Customized quasi-zero-stiffness metamaterials for ultra-low frequency broadband vibration isolation. Int. J. Mech. Sci. 2024, 269, 108958. [Google Scholar]
- Fossat, P.; Kothakota, M.; Ichchou, M.; Bareille, O. Dynamic bending model describing the generation of negative stiffness by buckled beams: Qualitative analysis and experimental verification. Appl. Sci. 2023, 13, 9458. [Google Scholar] [CrossRef]
- Fulcher, B.A.; Shahan, D.W.; Haberman, M.R.; Conner Seepersad, C.; Wilson, P.S. Analytical and experimental investigation of buckled beams as negative stiffness elements for passive vibration and shock isolation systems. J. Vib. Acoust. 2014, 136, 031009. [Google Scholar] [CrossRef]
- Geraldes, R.; Witvoet, G.; Vermeulen, J. The mechatronic architecture and design of the High-Dynamic Double-Crystal Monochromator for Sirius light source. Precis. Eng. 2022, 77, 110–126. [Google Scholar] [CrossRef]
- Gere, J.M.; Goodno, B.J. Mechanics of Materials Translation; Machinery Industry Press: Norwalk, CT, USA, 2017; pp. 328–335, 710–761. (In Chinese) [Google Scholar]




| Parameter | Value | ||
|---|---|---|---|
| Length (mm) | 60 | 70 | 80 |
| Width (mm) | 60 | 70 | 80 |
| Thickness (mm) | 0.1 | 0.2 | 0.3 |
| Compression (mm) | 0.1 | 0.2 | 0.3 |
| Elastic Modulus (GPa) | 193 | ||
| Poisson’s Ratio | 0.28 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, S.; Gong, X.; Bai, Y.; Lu, Q.; Li, A.; Song, Y.; Zhang, W.; Chai, K.; Shen, W. Research on Quasi-Zero Stiffness Vibration Isolation System of Buckled Flexural Leaf Spring Structure for Double Crystal Monochromator. Appl. Sci. 2025, 15, 3024. https://doi.org/10.3390/app15063024
Li S, Gong X, Bai Y, Lu Q, Li A, Song Y, Zhang W, Chai K, Shen W. Research on Quasi-Zero Stiffness Vibration Isolation System of Buckled Flexural Leaf Spring Structure for Double Crystal Monochromator. Applied Sciences. 2025; 15(6):3024. https://doi.org/10.3390/app15063024
Chicago/Turabian StyleLi, Shengchi, Xuepeng Gong, Yang Bai, Qipeng Lu, Ao Li, Yuan Song, Wenbo Zhang, Kewei Chai, and Wenhao Shen. 2025. "Research on Quasi-Zero Stiffness Vibration Isolation System of Buckled Flexural Leaf Spring Structure for Double Crystal Monochromator" Applied Sciences 15, no. 6: 3024. https://doi.org/10.3390/app15063024
APA StyleLi, S., Gong, X., Bai, Y., Lu, Q., Li, A., Song, Y., Zhang, W., Chai, K., & Shen, W. (2025). Research on Quasi-Zero Stiffness Vibration Isolation System of Buckled Flexural Leaf Spring Structure for Double Crystal Monochromator. Applied Sciences, 15(6), 3024. https://doi.org/10.3390/app15063024





