Integrated Analysis of Optimization and Settlement Characteristics in Hybrid Pile Systems for Reused Foundations
Abstract
1. Introduction
2. Research Overview
3. Pile-Soil Numerical Model
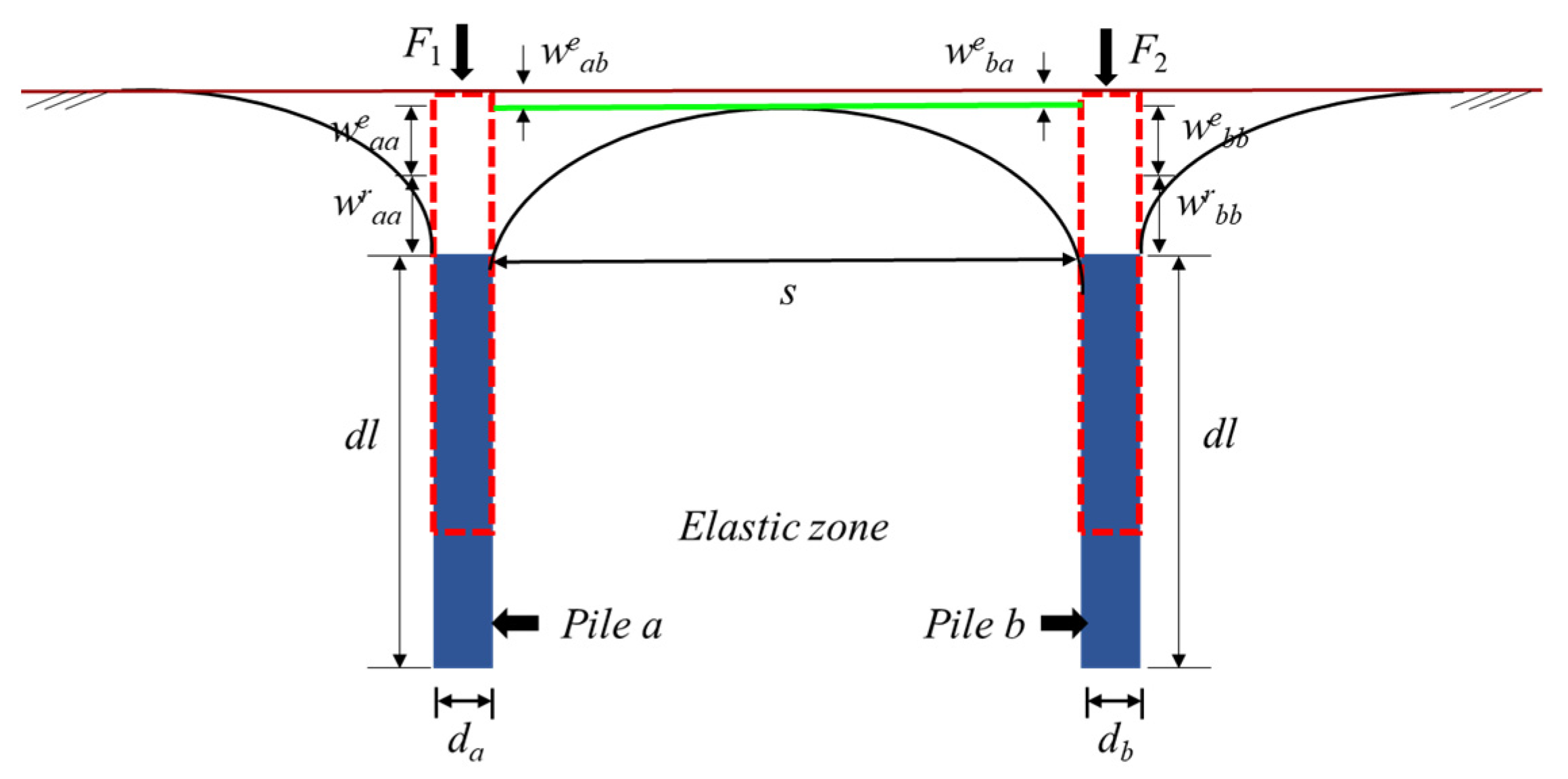
3.1. Pile-Soil Mechanical Model
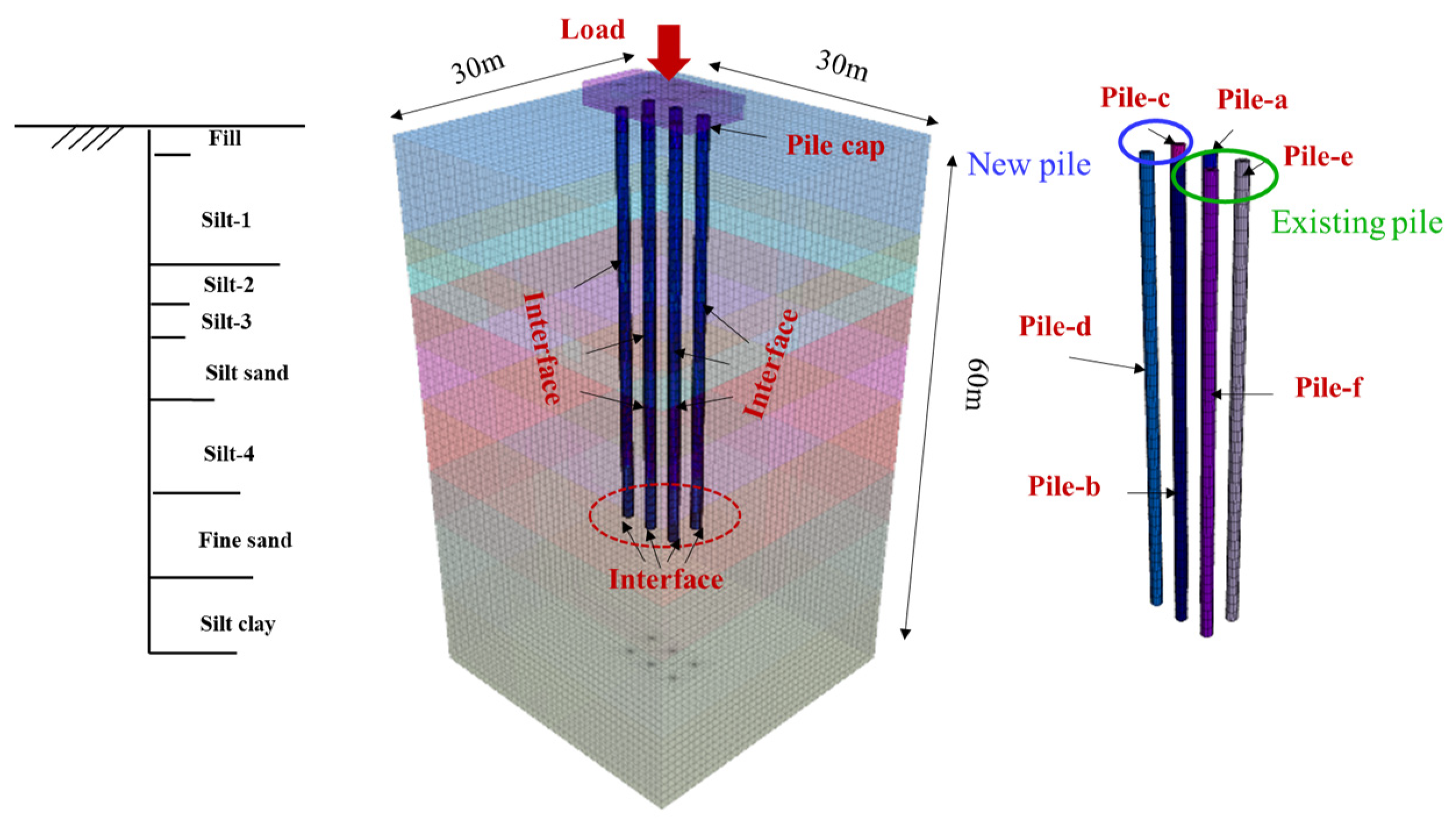
3.2. Pile-Soil Numerical Model
3.2.1. Model and Boundary Conditions
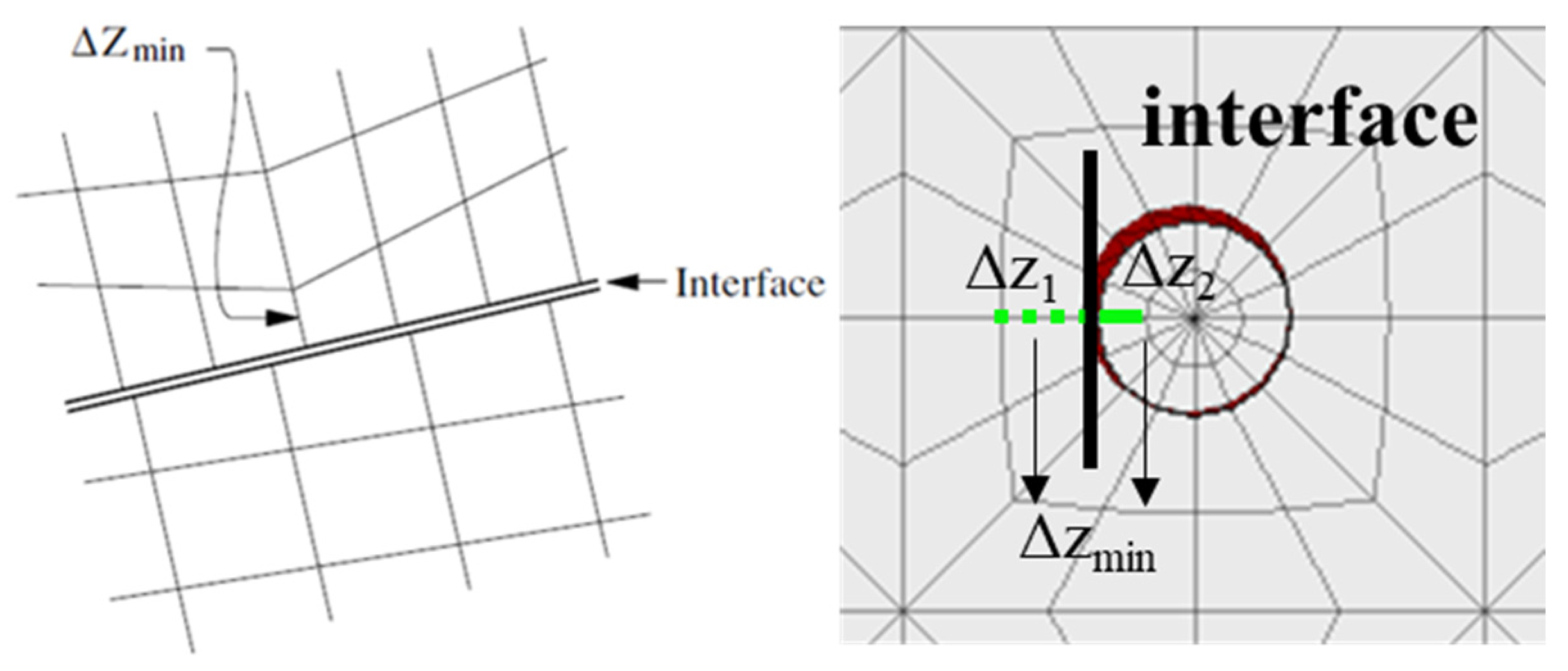
3.2.2. Contact Settings
3.2.3. Loading Process
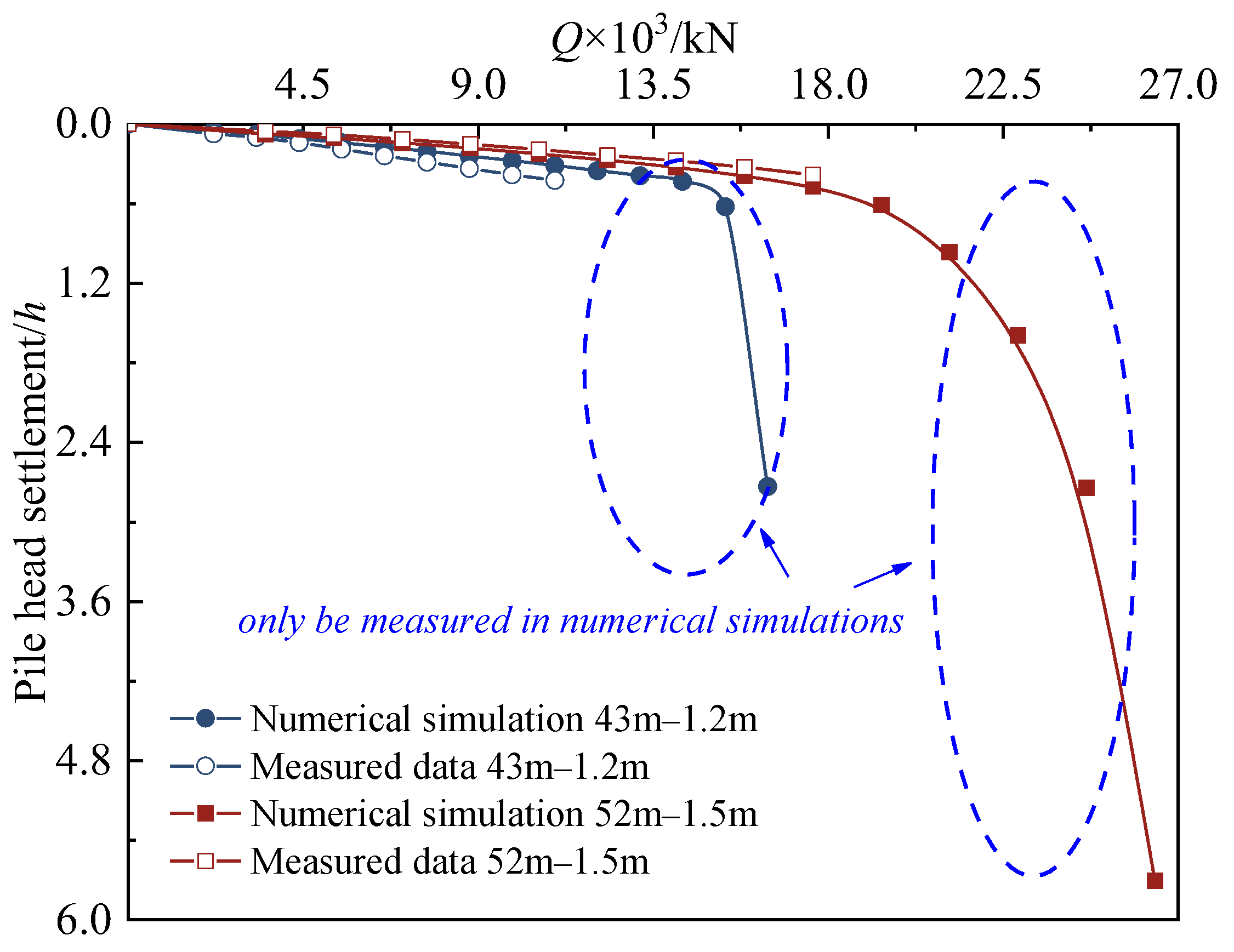
3.3. Verification of the Numerical Model
4. Interaction Between Parameters of New and Existing Piles
4.1. Behavior of New Piles
4.2. Behavior of Existing Piles
5. Study on the Behavior Parameters of Existing Piles
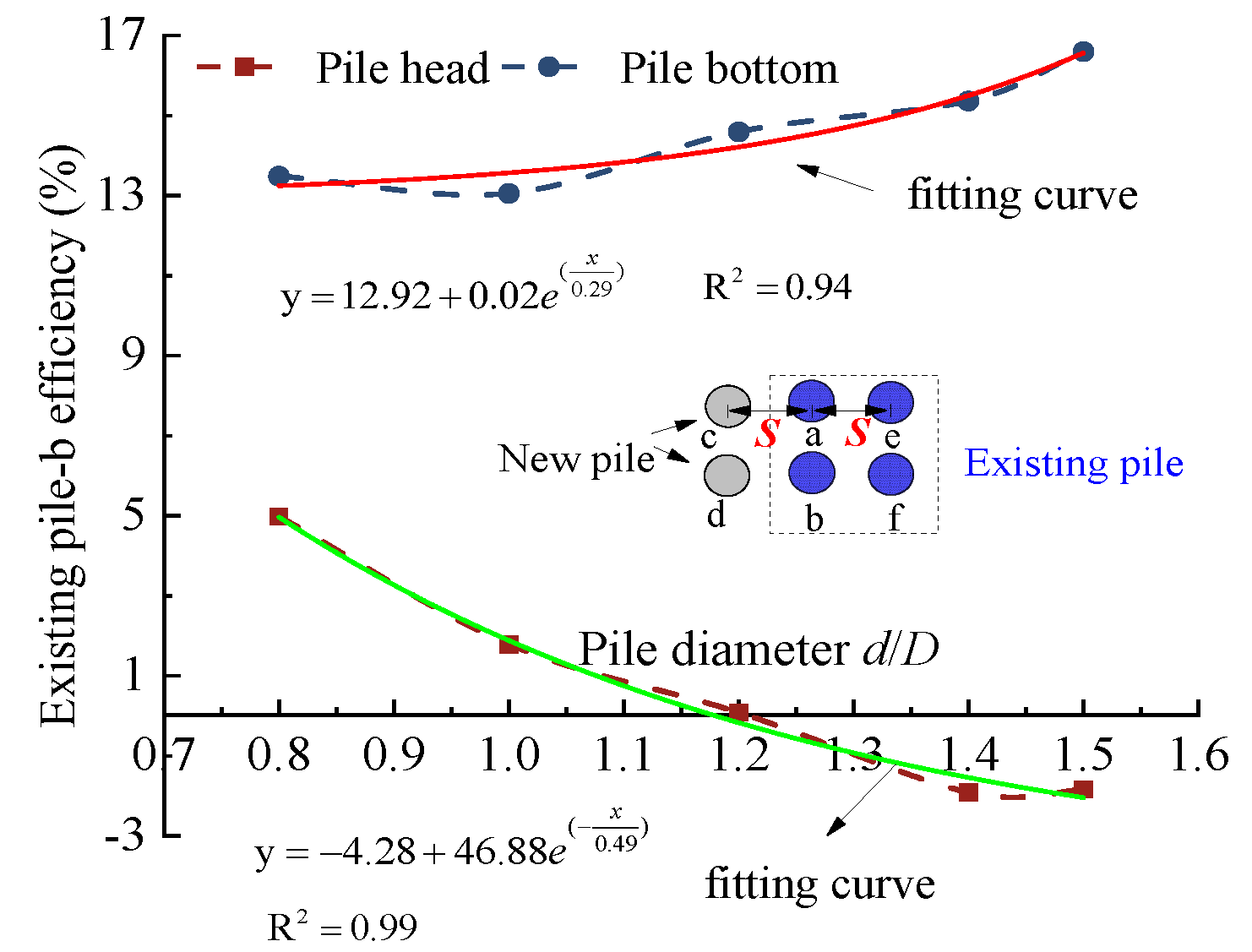
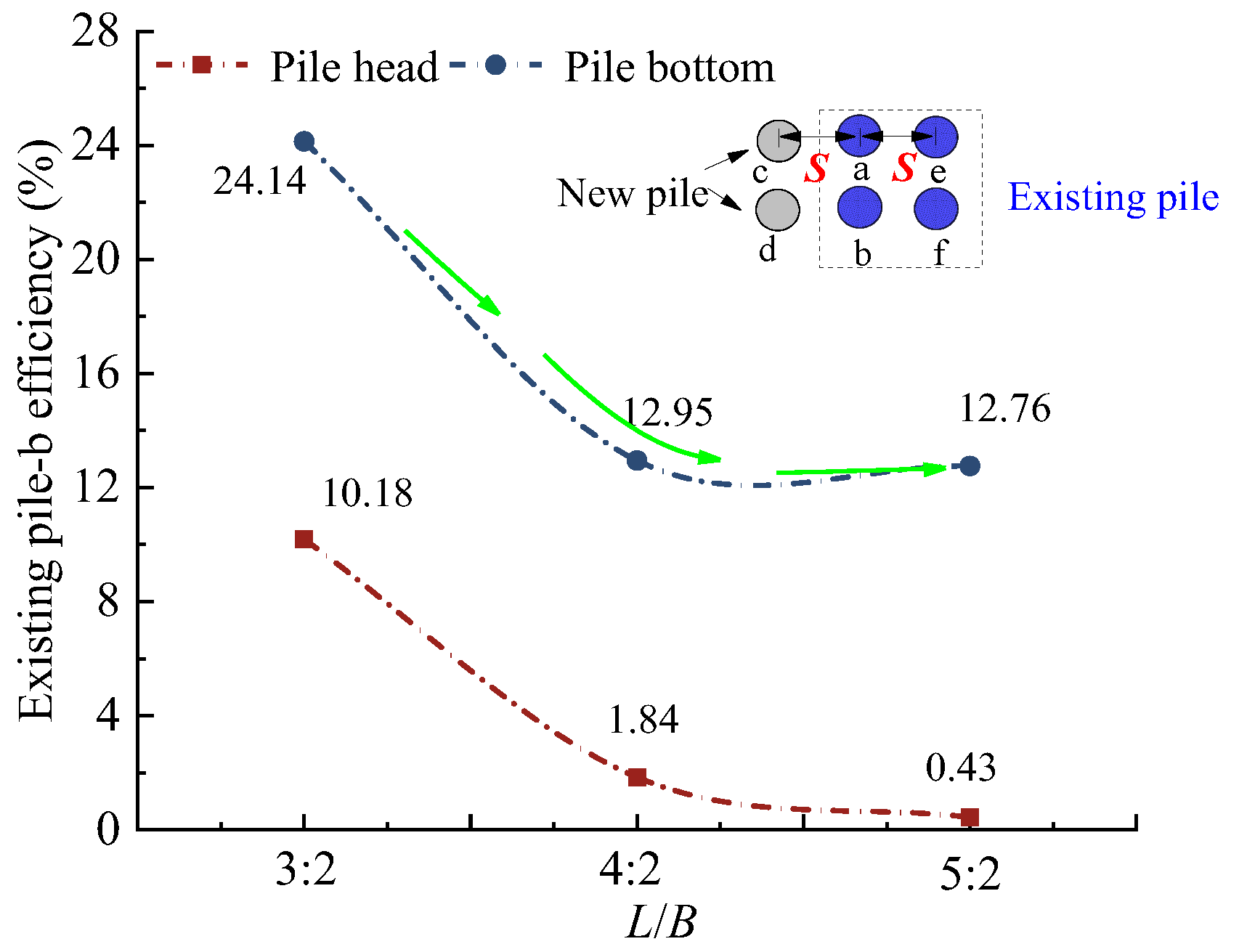
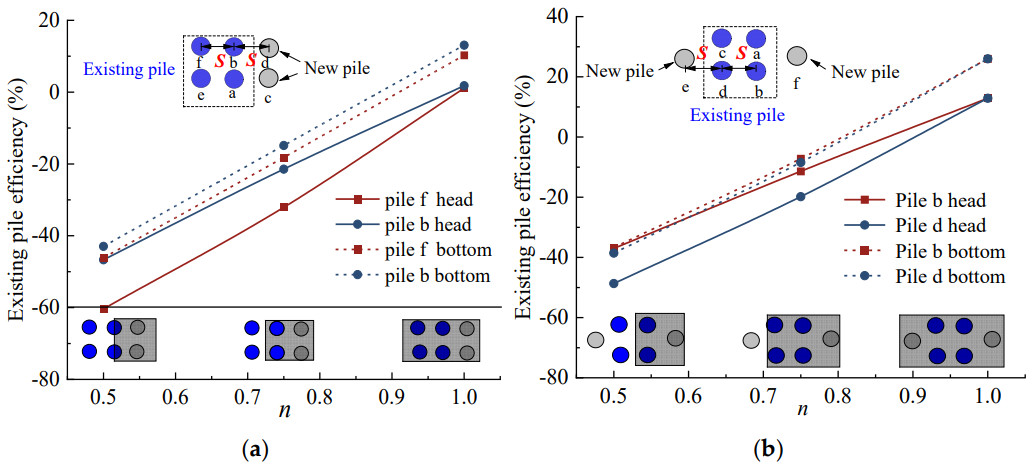
5.1. Pile Arrangement
5.2. Pile Cap
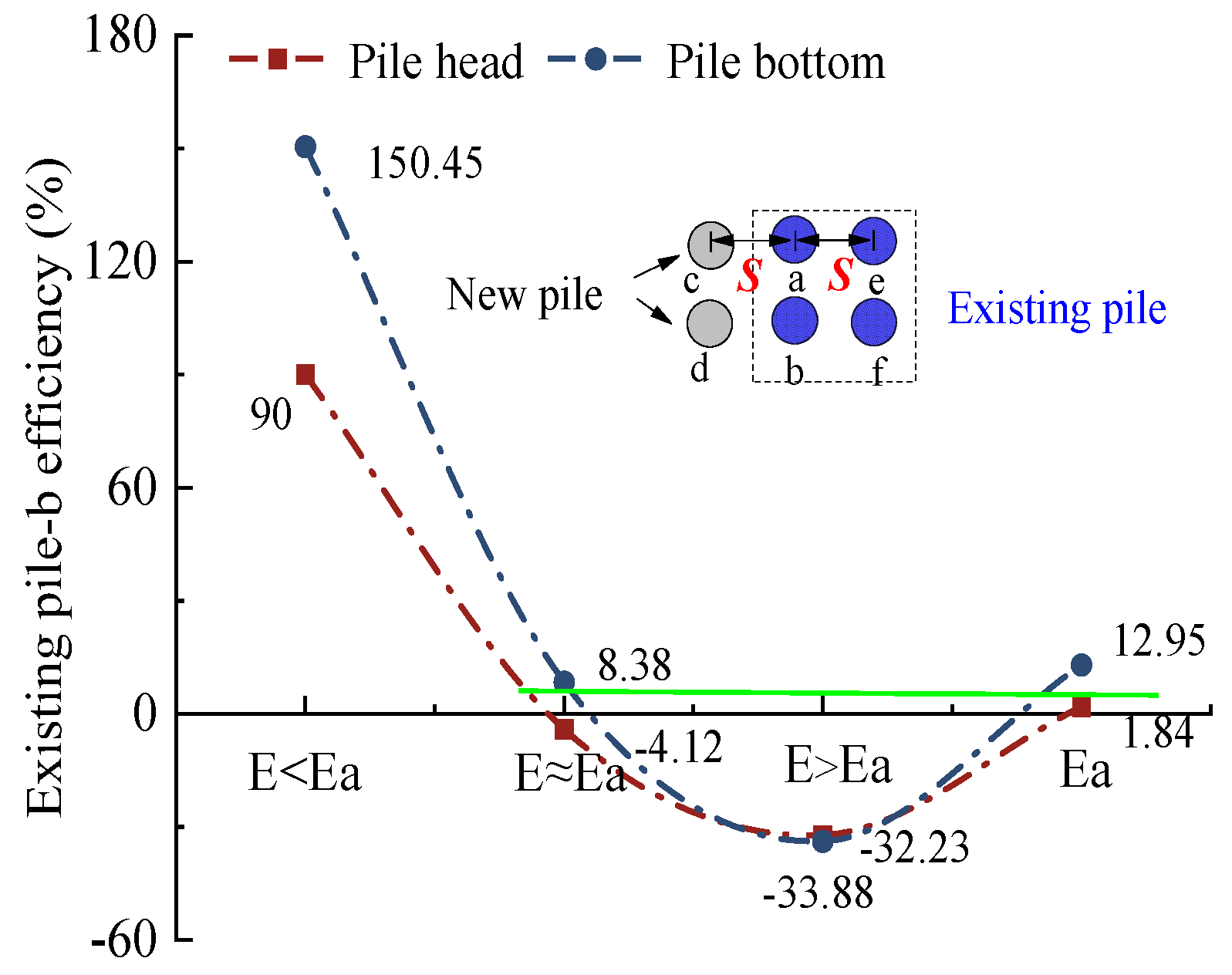
5.3. Soil Layer Properties
6. Discussion
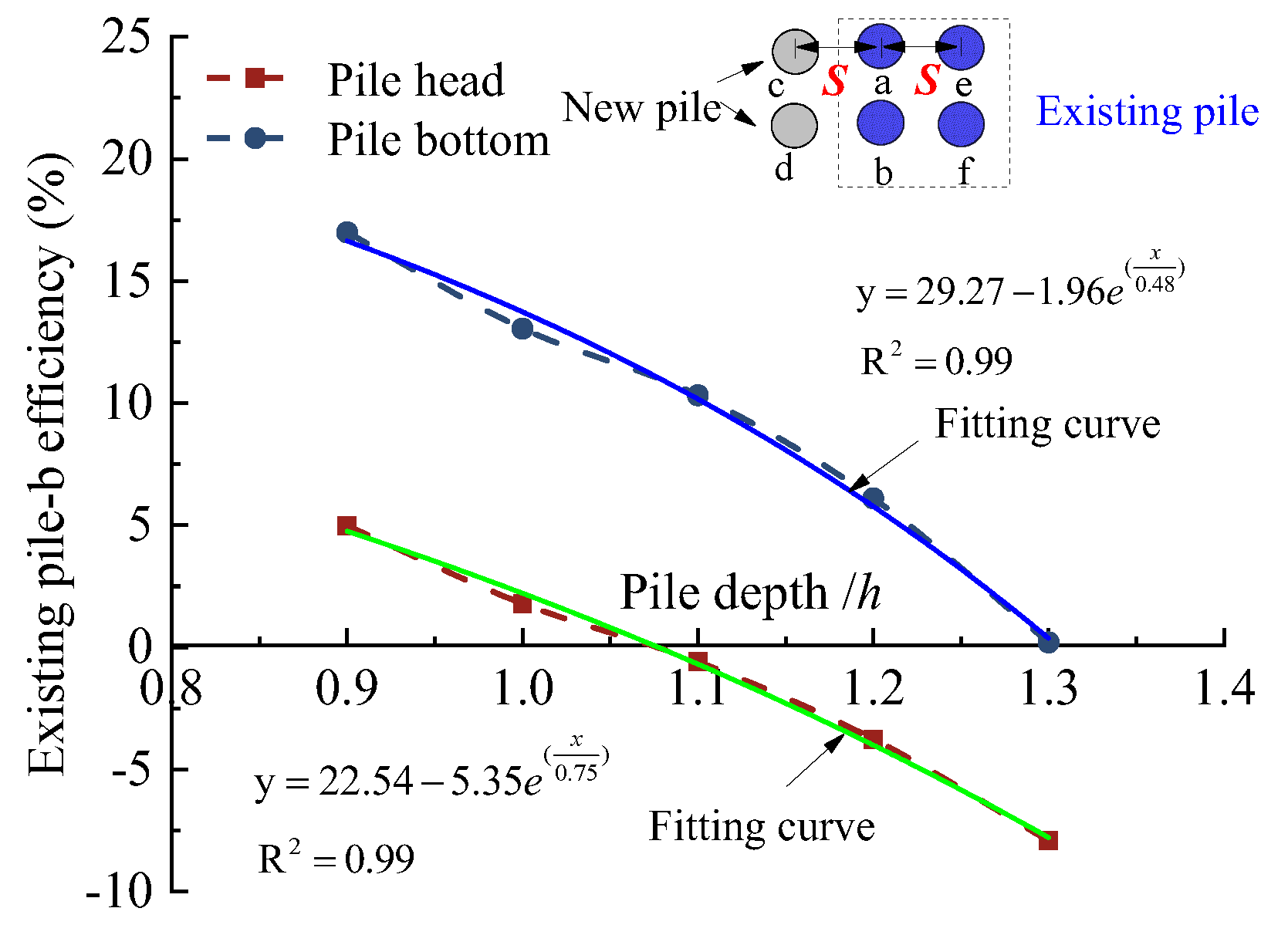
6.1. New Pile Parameters and Existing Pile Efficiency
6.2. External Factors and Existing Pile Efficiency
7. Conclusions
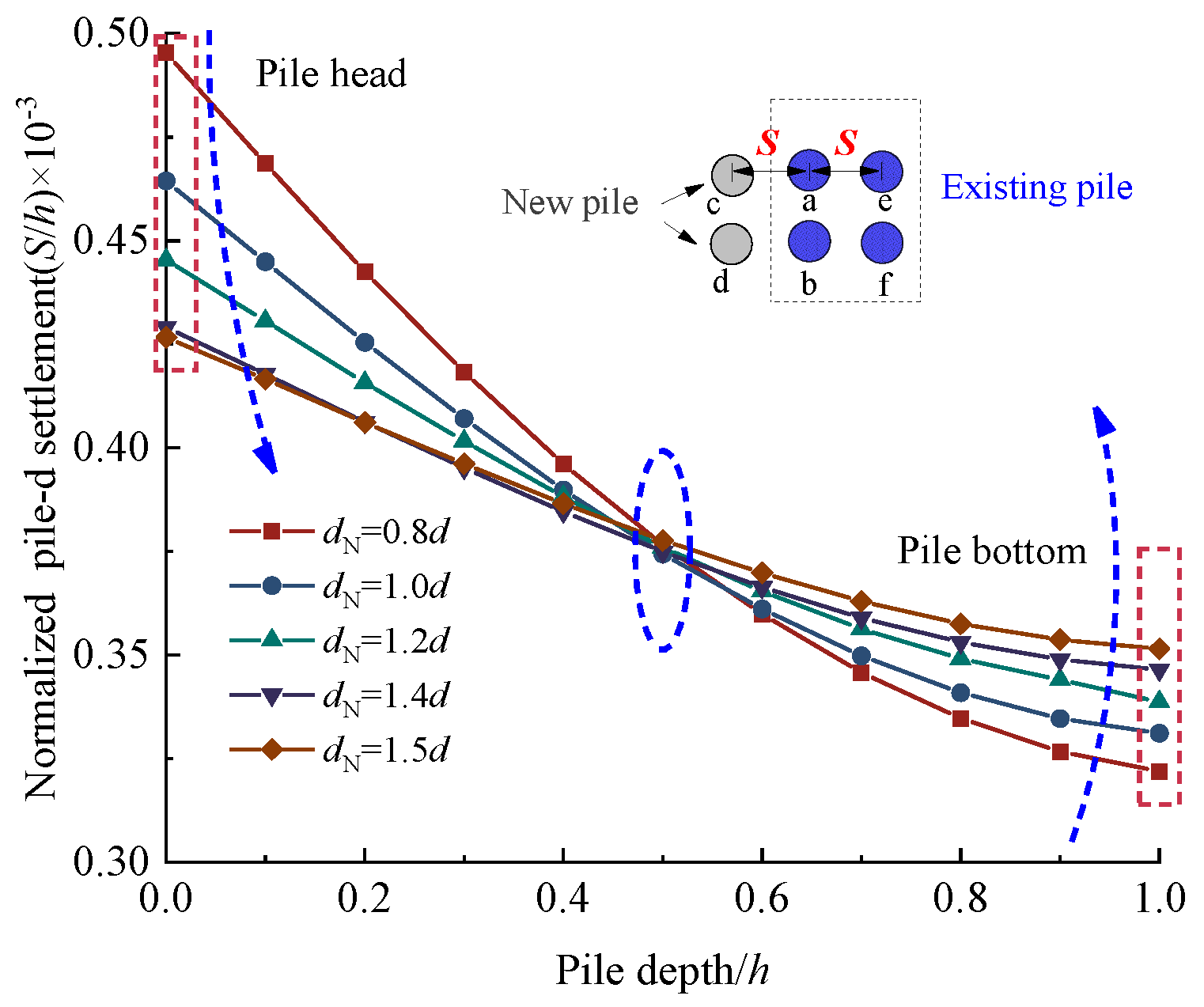
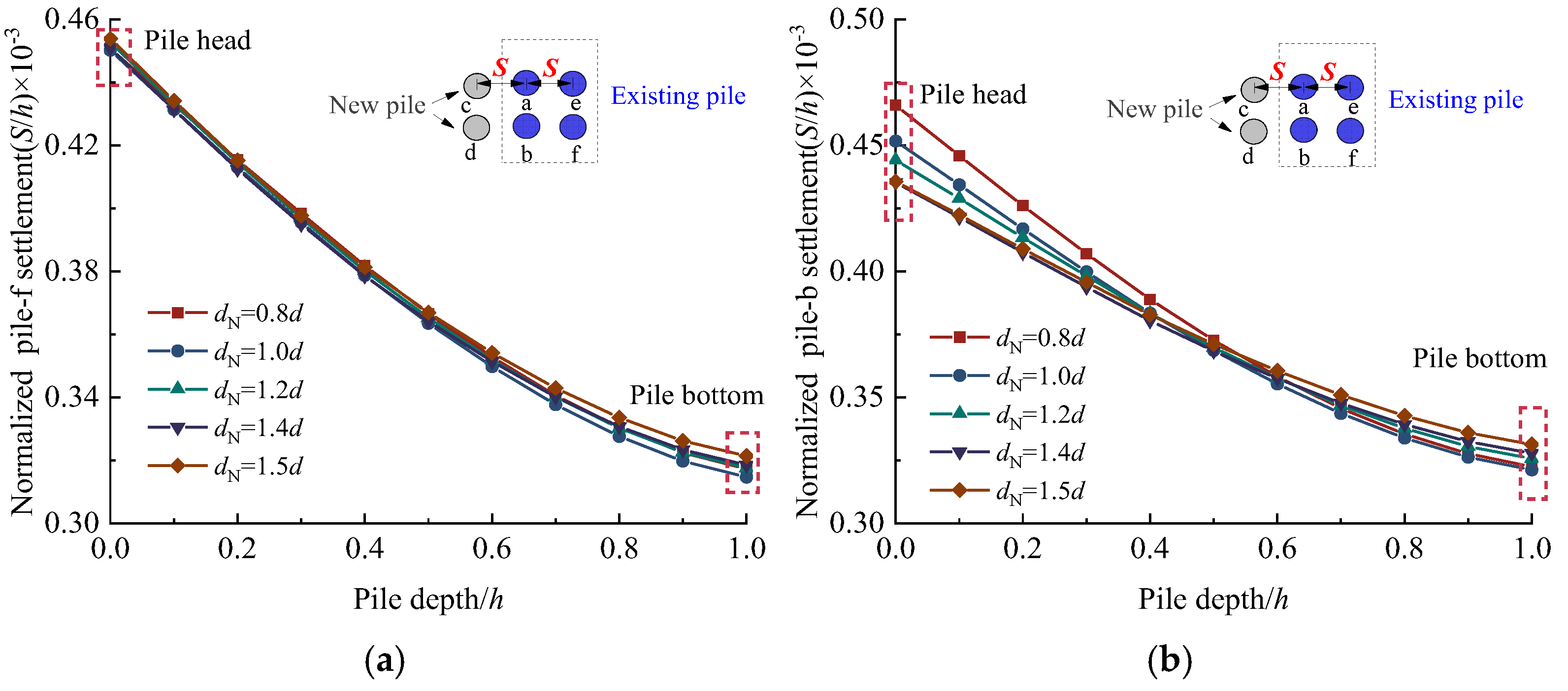
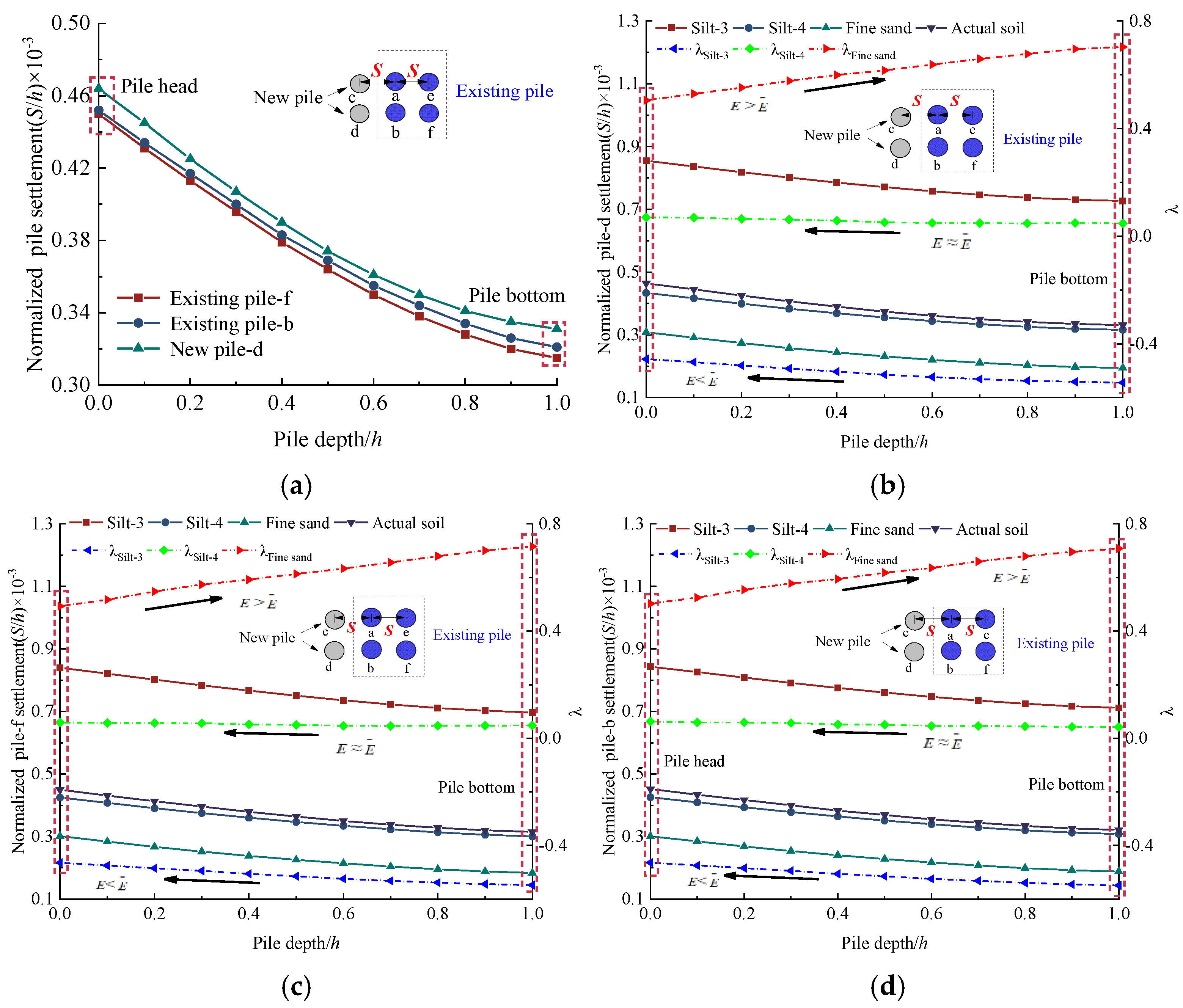
- The settlement of new piles decreases exponentially with increasing pile spacing (dN). As dN increases, the settlement in the upper half of both new and adjacent existing piles decreases, while settlement in the lower half increases. The settlement behavior of new and nearby existing piles exhibits significant segmented characteristics as dN varies.
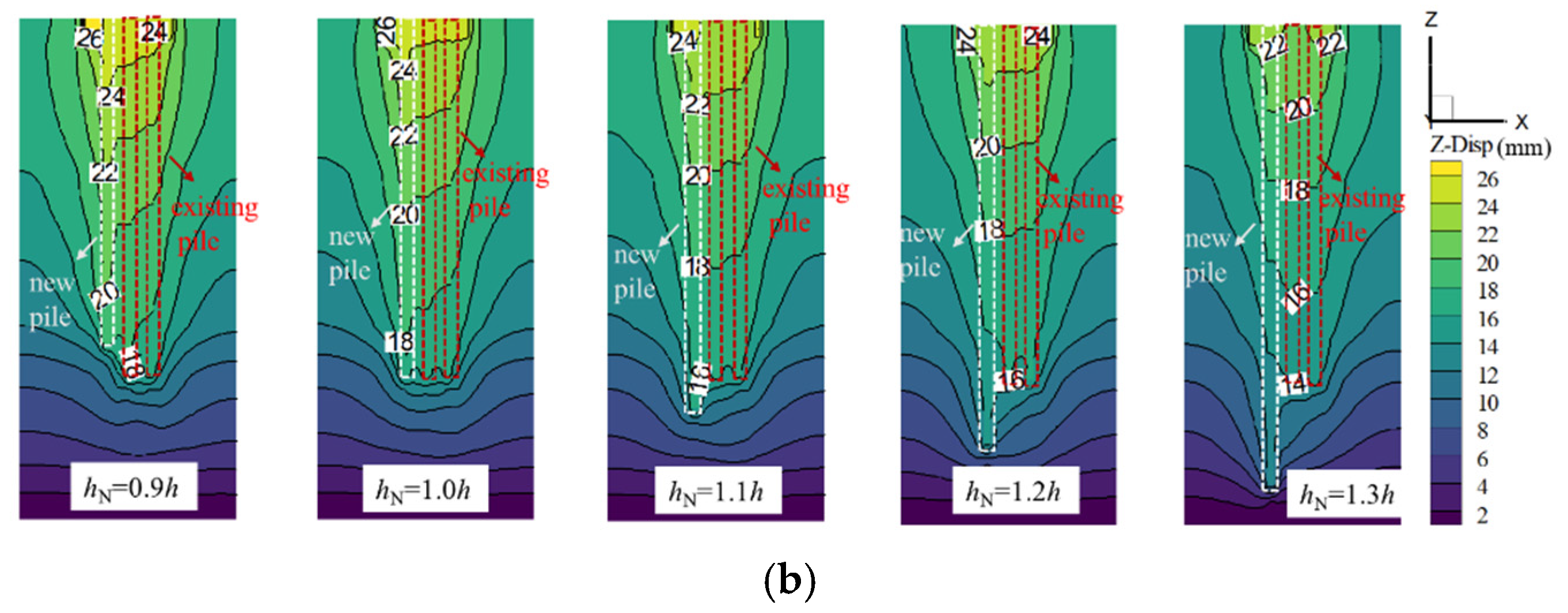
- The installation of new piles induces bidirectional displacement in existing piles. To minimize this impact, it is recommended to select dN and hN within the ranges of 1.0–1.1h and 1.0–1.2d, respectively.
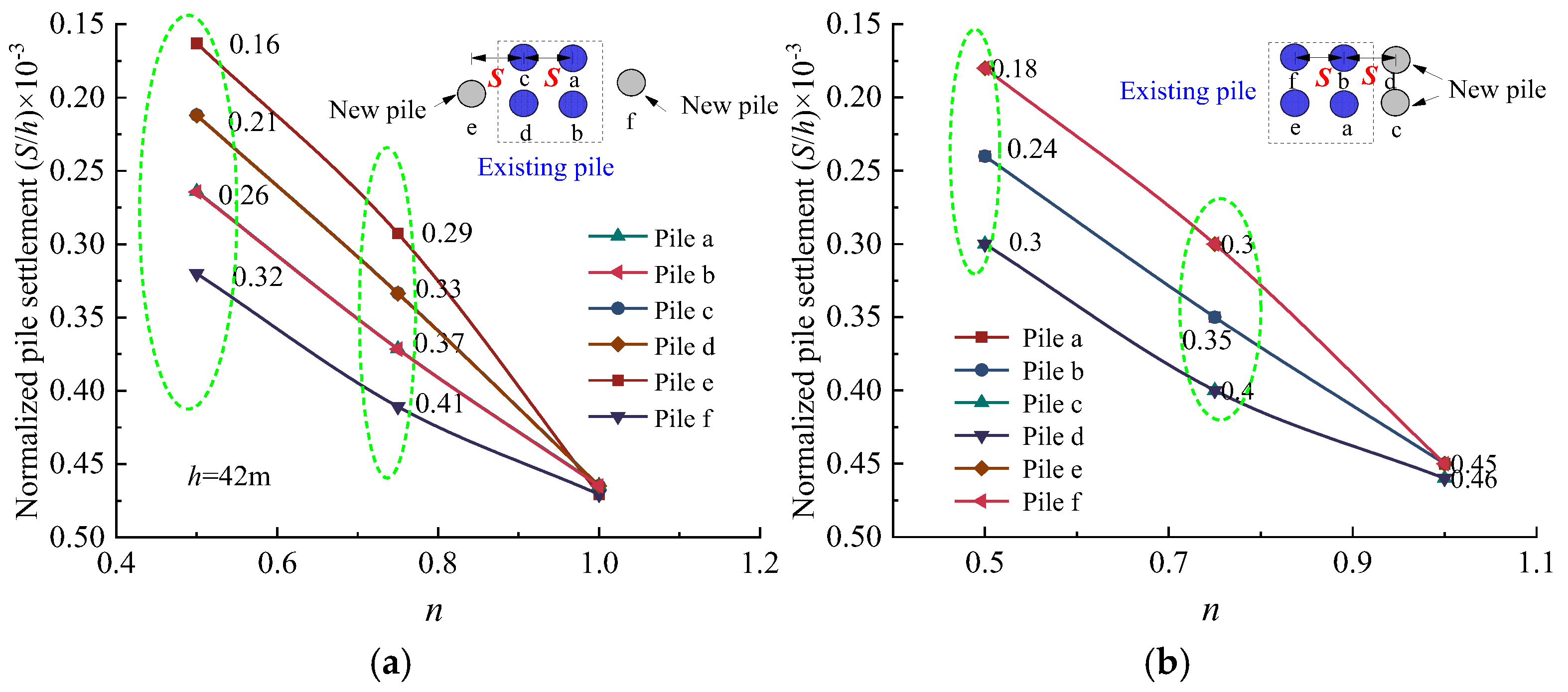
- Compared to symmetrical arrangements, lateral arrangements of new and existing piles demonstrate slightly greater stability in settlement behavior under varying load distributions, making them a preferable design choice for certain loading scenarios.
- Besides pile height and diameter, pile caps exhibit a size effect on the settlement behavior of new and existing piles. When the cap ratio (L/B) is approximately 4:2, the settlement difference between new and existing piles tends to stabilize.
- An existing pile efficiency parameter (η) is introduced, and sensitivity analysis reveals that the most significant factors affecting the settlement behavior are geological properties, load distribution, pile arrangement, hN, dN and L/B, in that order. This parameter provides a practical approach to assessing pile interactions.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chow, Y.K.; Thevendran, V. Optimisation of pile groups. Comput. Geotech. 1987, 4, 43–58. [Google Scholar] [CrossRef]
- Cao, M.; Chen, L. Analysis of interaction factors between two piles. J. Shanghai Jiaotong Univ. 2008, 13, 171–176. [Google Scholar] [CrossRef]
- Kim, Y.; Jeong, S. Analysis of soil resistance on laterally loaded piles based on 3D soil–pile interaction. Comput. Geotech. 2011, 38, 248–257. [Google Scholar] [CrossRef]
- Martin, C.M.; Randolph, M.F. Upper-bound analysis of lateral pile capacity in cohesive soil. Géotechnique 2006, 56, 141–145. [Google Scholar] [CrossRef]
- Livneh, B.; Naggar, M.E. Axial testing and numerical modeling of square shaft helical piles under compressive and tensile loading. Can. Geotech. J. 2008, 45, 1142–1155. [Google Scholar] [CrossRef]
- Elsherbiny, Z.H.; El Naggar, M.H. Axial compressive capacity of helical piles from field tests and numerical study. Can. Geotech. J. 2013, 50, 1191–1203. [Google Scholar] [CrossRef]
- Lueprasert, P.; Jongpradist, P.; Jongpradist, P.; Schweiger, H.F. Structural Responses of a Tunnel Lining Due to an Adjacent Loaded Pile. Int. J. Civ. Eng. 2023, 21, 1027–1043. [Google Scholar] [CrossRef]
- Butcher, A.P.; Powell, J.J.M.; Skiner, H.D. Reuse of Foundations for Urban Sites: A Best Practice Handbook; BRE Press: Watford, UK, 2006. [Google Scholar]
- Tamura, S.; Adachi, K.; Sakamoto, T.; Hida, T.; Hayashi, Y. Effects of existing piles on lateral resistance of new piles. Soils Found. 2012, 52, 381–392. [Google Scholar] [CrossRef]
- Brian, S. Numerical simulations of the reuse of piled raft foundations in clay. Acta Geotech. 2017, 12, 1047–1059. [Google Scholar] [CrossRef][Green Version]
- Hertlein, B.H.; Walton, W.H. Assessment and Reuse of Old Foundations. Transp. Res. Rec. 2000, 1736, 48–52. [Google Scholar] [CrossRef]
- Leung, Y.F.; Leung, Y.F.; Soga, K.; Klar, A. Multi-objective foundation optimization and its application to pile reuse. In Proceedings of the Geo-Frontiers 2011, Dallas, TX, USA, 13–16 March 2011; pp. 75–84. [Google Scholar] [CrossRef]
- Horii, Y.; Nagao, T.; Kawata, M.; Ishizawa, S.; Ono, S. Reuse of existing piles using flexible connection at pile head. J. Archit. Build. Sci. AIJ 2007, 13, 81–84. (In Japanese) [Google Scholar] [CrossRef]
- Watanabe, T.; Ishizaki, S.; Tomita, N.; Kawamoto, S.; Tatsuno, S. Reuse of existing bored piles for high-rise building foundation. Jpn. Geotech. Soc. Spec. Publ. 2015, 2, 158–161. [Google Scholar] [CrossRef]
- Li, L.; Li, J.P.; Sun, D.A.; Gong, W.B. Analysis of time-dependent bearing capacity of a driven pile in clayey soils by total stress method. Int. J. Geomech. 2017, 17, 04016156. [Google Scholar] [CrossRef]
- Augustesen, A.H. The Effects of Time on Soil Behaviour and Pile Capacity. Ph.D. Thesis, Aalborg University, Aalborg, Denmark, 2006. [Google Scholar]
- Roy, M.; Blanchet, R.; Tavenas, F.; La Rochelle, P. Behaviour of a sensitive clay during pile driving. Can. Geotech. J. 1981, 18, 67–85. [Google Scholar] [CrossRef]
- Poulos, H.G. Effect of pile driving on adjacent piles in clay. Can. Geotech. J. 1994, 31, 856–867. [Google Scholar] [CrossRef]
- Li, L.; Gong, W. Prediction of nonlinear vertical settlement of a pile group consisting of new and existing displacement piles in clay strata. Soils Found. 2019, 59, 1336–1348. [Google Scholar] [CrossRef]
- Reda, A.; Amaechi, C.V.; Shahin, M.A. Case study for effects of pile installation on existing offshore facilities in brownfields. Appl. Ocean Res. 2023, 138, 103651. [Google Scholar] [CrossRef]
- Shan, H.; Xia, T.; Yu, F.; Tao, H.; He, S.; Giosuè, B.; Boscato, G. Influence of Underpinning Pile Drilling Construction on the Bearing Behavior of Existing Loaded Foundation Piles: Case Study. Adv. Civ. Eng. 2020, 2020, 9568279. [Google Scholar] [CrossRef]
- Zhou, P.; Liu, H.L.; Zhou, H.; Cao, G.W.; Ding, X.M. A simplified analysis approach for the effect of the installation of adjacent XCC pile on the existing single XCC pile in undrained clay. Acta Geotech. 2022, 17, 5499–5519. [Google Scholar] [CrossRef]
- Wu, W.; Yang, Z.; Liu, X.; Zhang, Y.; Liu, H.; El Naggar, M.H.; Xu, M.; Mei, G. Horizontal dynamic response of pile in unsaturated soil considering its construction disturbance effect. Ocean Eng. 2022, 245, 110483. [Google Scholar] [CrossRef]
- Begaj, L.; McNamara, A.M. Centrifuge model testing for pile foundation reuse. Int. J. Phys. Model. Geotech. 2011, 11, 166–177. [Google Scholar] [CrossRef]
- Tamura, S.; Higuchi, Y.; Hayashi, Y.; Yamzasaki, M. Centrifuge studies on the effects of existing piles on the end resistance and shaft friction of a new pile. Soils Found. 2012, 52, 1062–1072. [Google Scholar] [CrossRef]
- Li, H.; Tamura, S. An existing pile efficiency method for the design of lateral new pile behavior in sites with existing piles. Can. Geotech. J. 2023, 60, 1188–1201. [Google Scholar] [CrossRef]
- Li, H.; Liu, S.; Tong, L.; Zhang, D. Influence of the head fixity adjustment of existing piles on the lateral load response of new piles. Géotechnique 2023, 75, 56–67. [Google Scholar] [CrossRef]
- Zhou, J.; Li, G.; Liu, L.; Li, Y.; Nie, Y. Investigation of the Load-Settlement Response of Piles in Sand Using an Interface Constitutive Model. Int. J. Geomech. 2022, 22, 04022198. [Google Scholar] [CrossRef]
- Huang, M.; Zhang, C.; Li, Z. A simplified analysis method for the influence of tunneling on grouped piles. Tunn. Undergr. Space Technol. 2009, 24, 410–422. [Google Scholar] [CrossRef]
- Jawad, S.; Han, J. Numerical Analysis of Laterally Loaded Single Free-Headed Piles within Mechanically Stabilized Earth Walls. Int. J. Géoméch. 2021, 21, 04021038. [Google Scholar] [CrossRef]
- Tomlinson, M.; Woodward, J. Pile Design and Construction Practise, 5th ed.; Taylor & Francis Group: London, UK; New York, NY, USA, 2007. [Google Scholar]
- Cook, R.D.; Malkus, D.S.; Plesha, M.E.; Witt, R.J. Concept and Applications of Finite Elements Analysis, 4th ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2001. [Google Scholar]
- Li, Z.; Chen, Z.; Wang, L.; Zeng, Z.; Gu, D. Numerical simulation and analysis of the pile underpinning technology used in shield tunnel crossings on bridge pile foundations. Undergr. Space 2021, 6, 396–408. [Google Scholar] [CrossRef]
- Gu, X.; Chen, F.; Zhang, W.; Wang, Q.; Liu, H. Numerical investigation of pile responses induced by adjacent tunnel excavation in spatially variable clays. Undergr. Space 2022, 7, 911–927. [Google Scholar] [CrossRef]
- Liu, X.Z.; Sang, Y.L.; Zhao, F.; Shi, G.; Heng, Y. Evaluation of effects of static pile driving on existing metro tunnel structure. J. Perform. Constr. Facil. 2019, 33, 04019045. [Google Scholar] [CrossRef]
- Deb, P.; Debnath, B.; Reang, R.B.; Pal, S.K. Structural analysis of piled raft foundation in soft soil: An exp erimental simulation and parametric study with numerical method. Ocean Eng. 2022, 261, 112139. [Google Scholar] [CrossRef]
- Chen, Y.; Xu, D. FLAC/FLAC3D Foundation and Engineering Example; China Water Resources and Hydropower Press: Beijing, China, 2009. [Google Scholar]
- Liu, H.; Gu, S.; Duan, S.; Hou, S. Load Settlement Response of Composite Foundation of Variable Pile Diameters. Int. J. Geomech. 2024, 24, 04024202. [Google Scholar] [CrossRef]
- Li, L.; Gong, W.B.; Li, J.P. Effects of clay creep on long-term load-carrying behaviors of bored piles: Aiming at reusing existing bored piles. Int. J. Geomech. 2020, 20, 04020132. [Google Scholar] [CrossRef]
- Randolph, M.F.; Carter, J.P.; Wroth, C.P. Driven piles in clay—The effects of installation and subsequent consolidation. Géotechnique 1979, 29, 361–393. [Google Scholar] [CrossRef]
- Bond, A.J.; Jardine, R.J. Effects of installing displacement piles in a high OCR clay. Géotechnique 1991, 41, 341–363. [Google Scholar] [CrossRef]






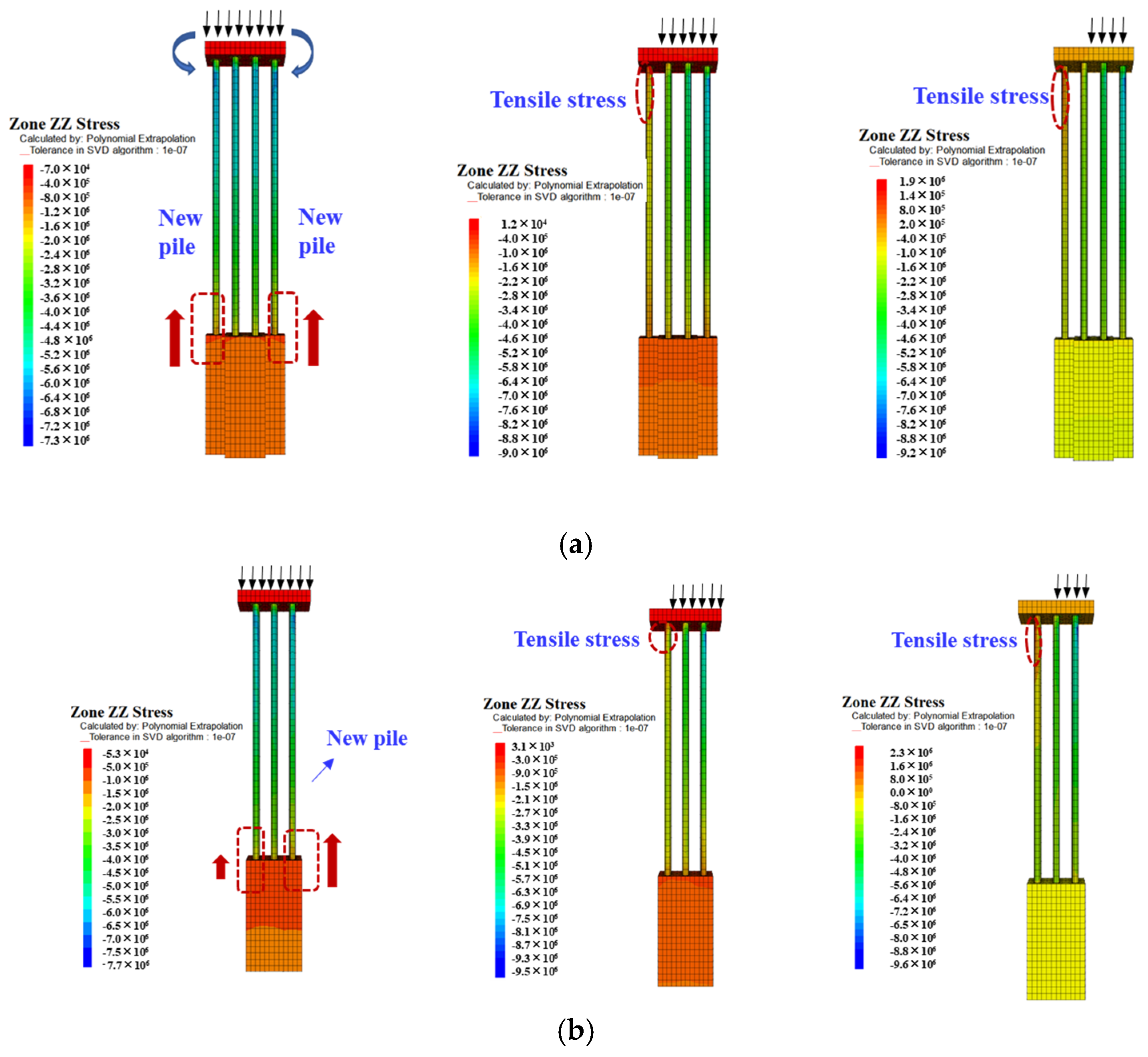
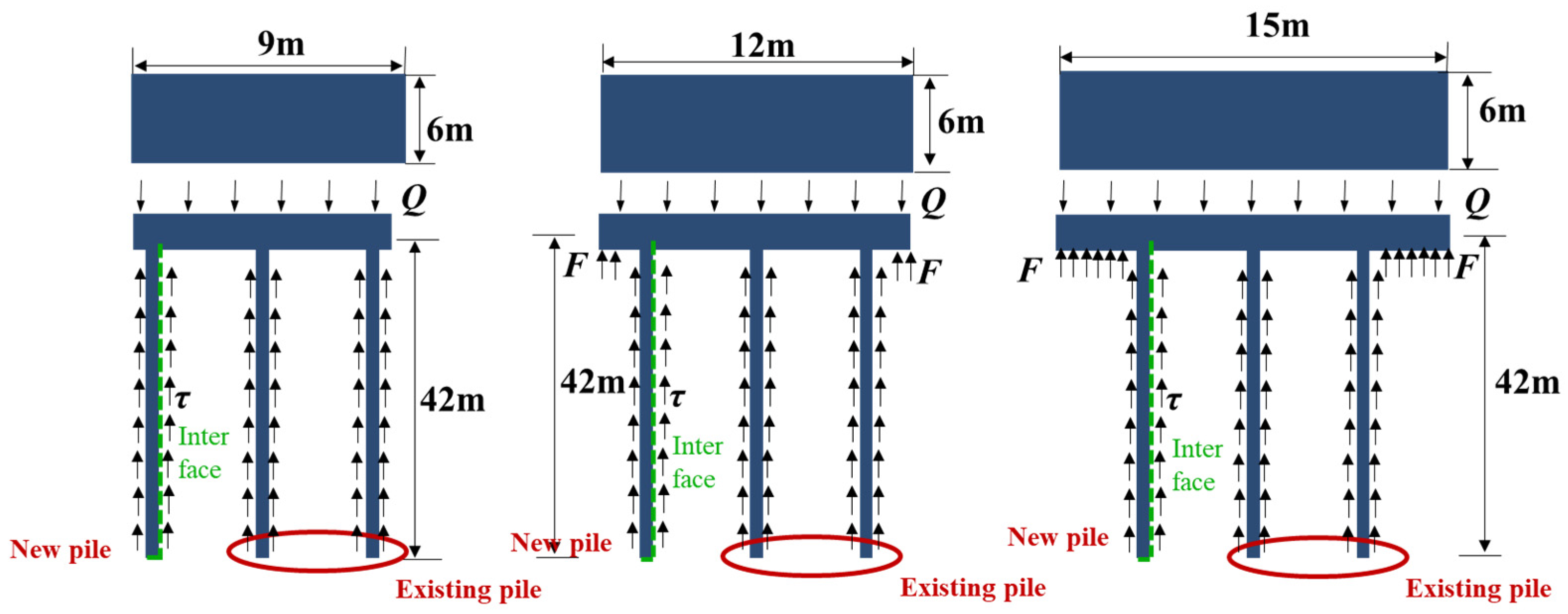

| Layer | Depth (m) | c (kPa) | ρ (kg/cm3) | φ (°) | E (Mpa) | ν |
|---|---|---|---|---|---|---|
| Fill | 0.0–1.8 | 5 | 1800 | 25 | 5 | 0.35 |
| Silt-1 | 1.8–11.0 | 12.6 | 1792 | 20.1 | 10. 7 | 0.35 |
| Silt-2 | 11.0–14.0 | 12.9 | 1730 | 20.4 | 9.2 | 0.31 |
| Silt-3 | 14.0–16.7 | 13.2 | 1760 | 21.4 | 6.5 | 0.30 |
| Silt sand | 16.7–21.7 | 0 | 1850 | 25.0 | 16.0 | 0.25 |
| Silt-4 | 21.7–28.1 | 14.1 | 1847 | 21.8 | 13.8 | 0.30 |
| Fine sand | 28.1–35.6 | 0 | 1850 | 30.0 | 23.0 | 0.25 |
| Silt clay | 35.6–42.4 | 33.8 | 1958 | 13.3 | 8.5 | 0.34 |
| Silt + clay | 42.4–51.0 | 15.2 | 1960 | 22.5 | 14.5 | 0.31 |
| Clay + silt | 51.0–60.0 | 33.5 | 1947 | 13.3 | 11.0 | 0.31 |
| Parameter | Value | Description | |
|---|---|---|---|
| New pile (as dN = 1.2 m) | EI | 3.53 × 106 | Bending stiffness (kN·m2) |
| ν | 0.3 | Poisson’s ratio | |
| Head condition | - | Restrained by pile cap | |
| Existing pile | EI | 1.47 × 106 | Bending stiffness (kN·m2) |
| ν | 0.3 | Poisson’s ratio | |
| Head condition | - | Restrained by pile cap | |
| Pile cap | E | 3.15 × 107 | Elastic modulus (kPa) |
| ν | 0.3 | Poisson’s ratio |
| Pile Head | Pile Bottom | Pile Head | Pile Bottom | ||
|---|---|---|---|---|---|
| dN | 0.8~1.5d | 0.8~1.5d | hN | 0.9~1.3h | 0.9~1.3h |
| 4.98~−1.84% | 13.49~16.60% | 4.97~−7.92% | 17~0.20% | ||
| L/B | 9:6~15:6 | 9:6~15:6 | Soil layer | 0.56Ea~1.95Ea | 0.56Ea~1.95Ea |
| 10.18~0.43% | 24.14~12.76% | 90~−32.23 | 150.45~−33.88 | ||
| Symmetric arrangement | 0.5~1 | 0.5~1 | Lateral arrangement | 0.5~1 | 0.5~1 |
| −42.67~2.75 | −43.07~13.33 | −60.36~1.10 | −46.12~10.26 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Niu, J.; Yang, Z.; Yin, S.; Cheng, S. Integrated Analysis of Optimization and Settlement Characteristics in Hybrid Pile Systems for Reused Foundations. Appl. Sci. 2025, 15, 3016. https://doi.org/10.3390/app15063016
Niu J, Yang Z, Yin S, Cheng S. Integrated Analysis of Optimization and Settlement Characteristics in Hybrid Pile Systems for Reused Foundations. Applied Sciences. 2025; 15(6):3016. https://doi.org/10.3390/app15063016
Chicago/Turabian StyleNiu, Jingsen, Zheng Yang, Siyu Yin, and Shengzhao Cheng. 2025. "Integrated Analysis of Optimization and Settlement Characteristics in Hybrid Pile Systems for Reused Foundations" Applied Sciences 15, no. 6: 3016. https://doi.org/10.3390/app15063016
APA StyleNiu, J., Yang, Z., Yin, S., & Cheng, S. (2025). Integrated Analysis of Optimization and Settlement Characteristics in Hybrid Pile Systems for Reused Foundations. Applied Sciences, 15(6), 3016. https://doi.org/10.3390/app15063016





