Abstract
The efficiency of a metro station is determined by the transfer capacity it has on the platform. This is the critical area and the primary motivation for this research. This study analyzed the impact of platform typology on the efficiency and capacity of metro stations. Through the study, the simulation of different typologies, the design logic of the station was analyzed from the ground up, examining each of its components from both a physical and operational perspective. To evaluate the efficiency and capacity of a platform configuration, Fruin’s level of service or LOS is used to compare the efficiency across different platform typologies, allowing for the quantification of constraints within the platform configuration. The platform configuration, access points, and connectors impact the station’s transfer capacity. This configuration must align with the environmental conditions and the station’s role within the system as a whole. The mixed-platform station configuration is twice as efficient as a central platform station and slightly more efficient than a side-platform station, with variations depending on station usage, environment, and position within the network. Under symmetric flow conditions, the side platform is more efficient, reaching a LOS D (density between 1.54 and 3.57 passengers/m2). Under asymmetric flow conditions, the central platform is more efficient, reaching a LOS D. However, under both symmetric and asymmetric flow conditions, the mixed platform is more efficient than the two previous configurations, and this design is proposed as the most suitable for transfer station designs, reaching a LOS D. A modular station design is proposed, where a mixed station is built with the capacity to expand based on increased passenger demand. This means constructing a central-platform station initially, and when the capacity is reached (LOS = E or density of 5.26 passengers/m2), the second phase is built, adding lateral platforms, thus converting it into a mixed station and doubling its capacity.
1. Introduction
In nature, every circuit has constraints. In transportation circuits or circular transportation systems such as buses, railways, subways, trams, cable cars, etc., their main constraints are the stations. In the case of a railway system like the subway, the station is the main constraint on the circuit’s speed, which directly impacts the system’s transport capacity [1]. To maintain a high circuit speed, it is necessary to minimize the train’s dwell time at the station, which involves maximizing the transfer of passengers between the platform and the train in the shortest time possible while maintaining high service levels.
The physical and operational designs of a railway system are matters of engineering, but until today, the design of stations has been the responsibility of architectural offices, which are more concerned with the form than the function of the station. Thus, in Latin America, we have managed to build beautiful but useless subway stations. The efficiency of a station is determined by the transfer capacity of the platform [2]. This is the critical area of the station and the subject of the present research.
In this research, the roots of the station design logic are analyzed, and each component is studied from both a physical and operational perspective (see example in Figure 1). The aim is to analyze, model, simulate, and evaluate the efficiency and capacity of each component individually, as well as in an integrated systemic manner. The behavior of passengers is studied from an operational perspective in corridors, stairs, elevators, platforms, and train access points. The passenger behavior within the station is modeled by establishing an algorithm that describes the interaction between the passenger and different infrastructures, and various scenarios will be simulated. With this, the efficiency and capacity of different platform configurations are evaluated by analyzing their characteristics, and the research concluded by describing which station configuration is ideal for specific environmental and operational conditions.

Figure 1.
Different types of platform typologies at underground metro stations in Chile: (a) central island platform in Metro de Santiago; (b) side platform in EFE Valparaiso metro system.
2. Literature Review
Until the mid-20th century, the theory of subway station design relied almost entirely on railway design. However, the population increase and the greater densification of cities due to migration from rural areas to urban centers began to impact the capacity of subway stations. This forced designers to seek solutions to optimize their classic railway stations, transforming them into stations that optimize the flow and transfer of urban passengers. In China, the design parameters for railways and subways were based on the Soviet standard until 1992, when China introduced the GB50157-92 standard [3]. This standard optimized the dimensions and designs of stations based on the behavior of Chinese users. Later, in 2003, the GB50157-2003 standard [4] was created, implementing optimizations in station area dimensions and incorporating technological solutions such as screendoors, dynamic segregators, reversible turnstiles, improvements in accessibility, and risk reduction. In 2014, the GB50157-2013 update was released [5].
In 2008, Wang [6] presented a methodology for calculating and dimensioning subway stations based on passenger flows and counter-flows. In 2012, Yao et al. [7] compared the design parameters of subway stations in China, from the Soviet standard to the current one. They used stations built under these different standards and compared their operational conditions. One of the key parameters in station design is the evacuation conditions in case of an emergency. Cheng and Yang [8] developed a methodology for optimizing station designs for emergency conditions, and Li et al. [9] specialized it for the evacuation of transfer stations.
The depth, lighting, and design of a station affect the psychological perception of users. La Vigne [10] developed a methodology for designing stations that reduces the feeling of insecurity. In China, Xiao-Xia et al. [11] investigated the psychological factors and behavior of users under stress during station evacuations.
From a regional perspective of influence, European metros, heavily influenced by the London Underground, use the design methodology of British railway stations [12]. Countries influenced by the Paris Metropolitan, such as Chile, Mexico, and Venezuela, use the design methodology of Alstom [13]. In the United States, design recommendations, access dimensions, and service levels for subway stations are described in the WMATA publication [14]. Capacity calculations for stations are recommended by Rail [15], and evaluation tools for stations are published by Rail [16]. Accessibility and pedestrian facilities in stations are recommended by the Metropolitan Council [17].
The typologies of stations are diverse and conditioned by the environmental variables of the station: building lines, the height or depth of the railway line, climate, geology, seismic conditions, hydrogeology, construction system, and operational design, among others. However, regardless of the various variables that determine the stations, they can be grouped according to height and platform arrangement. Cui and Hu [18] document the typical station sections present in China, and Wang [19], in his study on the architectural, functional, and structural design of the Hujialou Station of the Beijing Subway, details the general characteristics of different station typologies.
The functional characteristics of stations with a central island platform configuration were studied by Xu [20], based on the Tuanjiehu Station of the Beijing Subway. He concluded that this type of station with a central island platform behaves similarly to side-platform stations, but with the structural benefits of the island platform station, as it shares common stairs and elevators with side platforms.
Lebedev [21] details the different typologies, configurations, and construction systems used in Russia. Xu [22] specifies the most common station typologies in China. One of the important constraints in station design is the limited room for making structural modifications to subway stations, especially underground ones, which reduces their potential for expansion and optimization, among other factors. This leads to highly inefficient stations when expanded or converted into transfer stations due to construction limitations. This is because structural modifications in the construction of the station can affect the tunnel, adjacent buildings, or pre-existing stations. Liu et al. [23] studied how to control deformations in buildings close to subway stations. Another design constraint in stations is related to the operational design of the line and the subway service exploitation strategy, which directly affects the system’s capacity and impacts the station design. Hui [24] studied how the operational design of maneuvers affects the behavior of the station.
With respect to capacity, one of the classic areas of study in transportation is the relationship between flow, speed, and density. Chen et al. [25] studied the relationship between speed and density of passenger flow on the platforms and stairs of Line 1 of the Beijing Subway. In their study, they developed a linear regression model that allows for the determination of capacity and service level. Leurent et al. [26] designed a passenger traffic assignment model with capacity constraints, which enables the evaluation of the interaction between capacity and comfort both inside the train and on the platforms. The Capacity and Service Quality Manual [27], in Chapter 10, specifies the capacities within a station, namely the access points, horizontal circulation, vertical circulation, platforms, and waiting areas, as well as the interaction between the various elements of a station.
To measure the level of comfort in stations, the level of service (LOS) is used. The LOS is a quality measure employed to determine comfort levels under different conditions of flow, speed, and density in metro stations. Initially, the level of service only considered physical flow variables such as density and speed. However, in the area of pedestrian flows and subway services, new objective and subjective variables related to the infrastructure, the crowd, and the user in particular have been incorporated. These include factors such as lighting, climate control, perceived insecurity, and the perception of time, among others. The level of service, service quality, or passenger comfort has become an extremely important variable today, as congestion is frequent in cities and users demand higher quality in transportation services. D’Acierno et al. [28] studied how the degradation of subway service affects users and proposed strategies to minimize passenger dissatisfaction. Hermant and De Gersigny [29] conducted an analysis of the level of service and space requirements in stations in South Africa. For the purpose of this research, the study will focus solely on the components of the platform.
Pedestrian flow behavior has various models derived from vehicular flows and hydraulic models of fluids and gases [30]. The similarity between the behavior of pedestrian crowds and that of gases or fluids was materialized and simulated by Helbing et al. [31] and Xi et al. [32]. The conceptual foundations of the pedestrian level of service (LOS) were developed by Fruin [33], and various studies on speed and free-flow walking have been researched and compiled by Daamen and Hoogendoorn [34]. The behavior of pedestrian crowds in counterflow with self-organization has been described by Rangel-Huerta [35].
In the specific context of pedestrian flow behavior in subway stations, pedestrian behavior and self-organization in subway corridors using social force models and cellular automata have been studied by González [36]. The optimization of transfer flows in subway stations was studied by Nai et al. [37] and Li and Zhou [38], while the study of pedestrian queues on subway platforms was researched by Xu et al. [39]. The simulation of pedestrian behavior at subway doors was examined by Zhang et al. [40]. The reaction of users and changes in pedestrian behavior with different platform widths was explored by Wang et al. [41], and the pedestrian congestion index in stations was proposed by Wang et al. [42]. The simulation of pedestrian behavior at the Omonia Station of the Athens Metro was conducted by Anagnostopoulos [43].
As can be seen, the studies on the analysis and optimization of pedestrian flow in subway stations date back to the last decade. Previously, pedestrian flows were only considered in emergency evacuation conditions, such as accidents, fires, or wartime scenarios. This last parameter is a crucial design aspect in the Soviet Union’s subway station design standard, and it was also present in China’s standards until 1992. In this regard, pedestrian behavior in emergency conditions has been modeled by Wang et al. [44], and the most commonly used pedestrian parameters can be found in the Capacity and Service Quality Manual [45].
Recent studies [46] reported that key factors should be considered in the design of metro stations, such as track alignment, tunneling strategy, station typology, operations and maintenance, procurement strategy, and environmental aspects. The station typology is a relevant factor, being a critical engineering choice that involves balancing conflicting constraints such as subsea tunneling [47].
The planning of green infrastructure should consider its overall contribution to the sustainable development of the city, with special attention to the design of the metro station considering the interaction between public sectors, metro operators, and logistics companies, among others [48].
It is important to note that the vitality of underground spaces in metro stations is influenced by different factors, such as accessibility, visibility, spatial scale, business distribution, and the physiological and traffic environments [49]. Therefore, the type of station is a relevant factor when designing these underground spaces. Other factors, such as connectivity, temporality, and interdependency, should be also considered [50].
Several architectural characteristics influence the passenger experience, including the configuration of the concourse level, the geometry of the platform hall, and the use of art elements [51]. The authors found that accessibility and the station’s position within the city and neighborhood also affect comfort and safety.
In some cases, the design of metro stations tends to focus primarily on functionality, with many stations having similar designs that lack innovation. This has led to a failure in promoting urban culture and enhancing city visibility. The authors [52] explored design concepts for metro station entrances, considering both exterior and interior spaces, with the goal of creating more innovative and culturally significant designs for future metro stations. Therefore, metro stations should be designed and considered as a node place [53]. These spaces are not only points or junctions in which flows of passengers are attracted or generated, but also places where they interact with the city
Despite the progress in studies, there is a noticeable gap in knowledge regarding the typology of subway stations, which this study aims to address through passenger simulation, including their behavior in spaces such as platforms.
3. Methodology
3.1. Typology of Stations
The methodology presents different types of stations that were used in this study. These types are divided into three categories (see Figure 2):
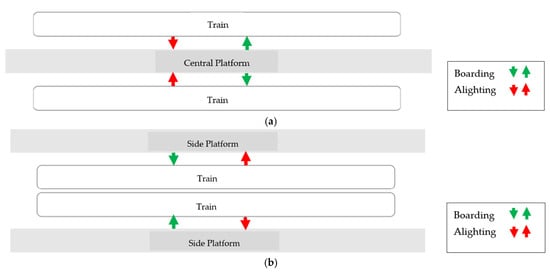
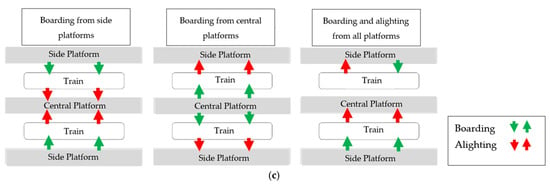
Figure 2.
Typology of the infrastructure used in metro stations: (a) central island platform; (b) side platform; (c) mixed platform.
- station with a central platform;
- station with side platforms;
- station with mixed platforms (side and central).
The central platform consists of a single platform that serves two train lines simultaneously. These can either be the same line with services in both directions or a transfer station between two unidirectional services. The train operation takes place on one side of the train, utilizing only 50% of the total doors of each carriage. The platform serves passengers heading in both directions of the train, with a common area that accommodates both groups of passengers, as well as those disembarking from the trains. As a result, four passenger flows converge on the same platform (see Figure 2a).
On the other hand, the side-platform configuration is one of the most common worldwide due to its simplicity in construction from the perspective of railway alignment. It consists of two side platforms with separate access points and stairs, as each platform serves one direction of travel, with two converging passenger flows: those entering and those exiting (see Figure 2b).
The mixed platform, also known as the “Spanish solution,” consists of a central platform accompanied by two lateral platforms. Its configuration is the combination of a central platform and two side platforms, which makes its capacity and operation superior to the sum of its individual parts. This is primarily because the transfer capacity at the doors is 100%, utilizing both sides of the carriage without pedestrian counterflow at the train doors (see Figure 2c).
3.2. Simulation Variables
The following describes the physical and operational conditions for the three different platform configurations that will be used in the simulation. The total platform width [a], as well as the total stair width [e], are identical for all three platforms. Likewise, the platform length and the dimensions of the trains are the same for all evaluated configurations. Therefore, the station dimensions are exactly the same for all the configurations to be simulated (see Table 1). As a result of the above, the platform configuration for the station simulation can be seen in the following figure using AnyLogic 2023 (see Figure 3).

Table 1.
Dimensions and configuration used in the simulation at the platforms.
Figure 3.
Simulated scenarios: (a) side platform; (b) central island platform; (c) mixed platform.
AnyLogic unifies all modern modeling and simulation approaches, as it simultaneously integrates agent-based simulation, system dynamics, and discrete event systems, with macro-, meso-, and microscopic-scale levels. It allows work with flow diagrams, state diagrams, action diagrams, and process flow diagrams. It operates in Linux, Apple, and Windows environments, and is integrable with Java engines and editing tools such as Eclipse. It enables the export of simulation models into small Java applications to be used from any web browser. Additionally, it has a pedestrian library that describes pedestrian behavior and a railway library that allows for the programming of train operations. Both pedestrians and trains can be visualized in 3D. For all of these reasons, AnyLogic includes all the necessary features to carry out the simulations for this research.
The pedestrian library of AnyLogic allows the simulation of pedestrian flows in physical environments, such as areas with high pedestrian traffic like subway or train stations. It enables the collection of statistical data on pedestrian density and the estimation of wait times. It is a powerful library for detecting potential problems arising from the interaction between pedestrians and their environment or with other pedestrians. Pedestrian models have two design areas: the environment and the behavior. The environment incorporates walls, areas, stairs, ramps, queues, and service areas. The behavior defines the physical rules of pedestrian conduct.
The train library of AnyLogic allows for the modeling, simulation, and visualization of train operations at various levels of scale and complexity. The library enables the creation of accurate designs for trains, carriages, dimensions, door widths, seating arrangements, density, route topology, and train accelerations and decelerations, in addition to all types of train operations and switching yards.
In the AnyLogic simulation tool, the physical environment must be designed, and the agents that interact within it, their characteristics, and the relationships between them need to be defined. The characteristics of the pedestrians, namely their origins and destinations, behaviors, and interaction relationships are established. Additionally, the topology of the trains and carriages, along with the operating conditions of the train, are defined.
AnyLogic, by integrating all modern simulation methods, allows for the simulation of everything from the pedestrian seated in their seat, their behavior inside the train, the platform, and the station to the operation of the entire line. This enables visualization from the macro-, meso-, and microscopic levels.
In AnyLogic, the operation of the trains must be designed, configured, and parameterized. During the physical design phase, the train, carriages, doors, and other components are dimensioned. Then, the operational relationships, variables, and parameters for each are created (see Figure 4). These include the train arrival, frequency, carriage capacity, passenger arrival rate, door capacity, door opening time, passenger loading time, unloading time (for sequential operation), and conditions for train entry and exit, such as speed, acceleration, and timings.
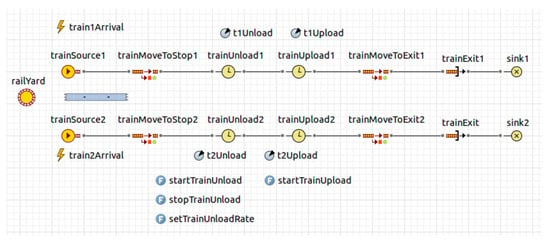
Figure 4.
Sequence of parameters for the train design using AnyLogic software.
AnyLogic allows for programming pedestrians with a high degree of artificial intelligence. In this study, it focuses on behaviors and decision-making within a train station. It will be limited to programming parameterizable behavior variables such as maximum speed, speed under free flow conditions, tolerance levels to obstacles and other pedestrians, crowd behavior, influx rates, and behavior on stairs, escalators, and corridors, among others (see Figure 5).
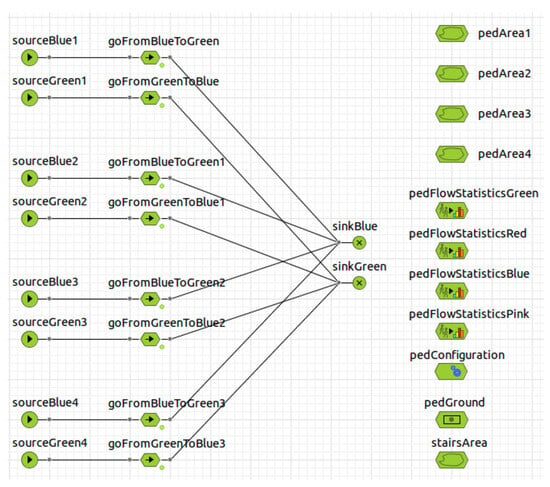
Figure 5.
Sequence of parameters for passengers using AnyLogic software.
For the purposes of this simulation, the station dimensions are:
- total platform width = 18 [m];
- total stair width = 6 [m];
- platform length = 150 [m];
- station width = 24 [m].
The physical characteristics of the train are:
- number of carriages = 7 [carriages];
- length of each carriage = 20 [m];
- width of each carriage = 3 [m];
- door width = 1.5 [m];
- doors per carriage = 8 [doors];
- doors per side = 4 [doors];
- doors per train = 56 [doors].
Four types of behaviors can be identified for the same platform:
- Symmetric entry flows in both directions: the number of passengers entering the station is distributed evenly along the platform from each staircase. The number of passengers waiting to board the train is equal on each platform;
- Asymmetric entry flows: the opposite of the symmetric entry flow. The flow in one platform has been reduced by half, while the flow in the opposite platform has been doubled;
- Symmetric exit flows from both trains: the number of passengers exiting the station is distributed evenly along the platform from each staircase. The number of passengers alighting the train is equal on each platform;
- Asymmetric exit flows: the opposite of the symmetric exit flow. The flow in one platform has been reduced by half, while the flow in the opposite platform has been doubled.
As a result, the AnyLogic software provides an efficient use of the space map, in which the blue color means a low use of space while the red color means a high use of space. In between those colors, there are other mapping colors, such as light blue, green, and yellow, which represent the medium use of the space. This space map is represented by the level of service defined by Fruin [27,33], in which LOS = A is equivalent to free flow conditions and LOS = F represents an overcrowded situation. In the case of LOS = E, the capacity is reached (see Table 2).

Table 2.
Level of service (LOS) at the platforms used in the simulations.
4. Results
4.1. Central Platform
The central platform has a single platform with a width of 18 m, where passengers waiting for trains in both directions are located, and passengers disembark from both trains. The platform has a stair axis consisting of two double bidirectional staircases, and each staircase has a width of 6 m, with bidirectional pedestrian traffic.
For the stairs, a configuration is used that physically segregates the bidirectional flows, preventing counterflow on the staircases. This staircase setup yielded the best capacity index in the simulation.
The platform has four potential pedestrian counterflows, as there are two entry flows and two exit flows on the platform.
In the simulation, a platform 18 m in width and 150 m in length is modeled, with a stair axis that occupies one-third of the platform and has a width of 6 m. This configuration includes four staircases located in the center of the platform.
Four types of behaviors can be identified for the same platform:
- (a)
- symmetric entry flows in both directions;
- (b)
- asymmetric entry flows;
- (c)
- symmetric exit flows from both trains;
- (d)
- asymmetric exit flows.
In the case of symmetric entry flows in both directions, the pedestrian flow entering the platform through the staircases is uniform for both trains. The platform is spacious, allowing for smooth flow without complications for pedestrians. When stress testing the station by increasing the passenger flow entering the station, it is observed that the critical areas are the access points to the staircases located at the platform level. As the flow increases, appropriate density levels are observed on the platform, with lower service levels on the staircases, reaching LOS = C (i.e., density between 1.08 and 1.54 passengers/m2). When the staircase capacity is exceeded (LOS = F or a density over 5.26 passengers/m2), a collapse occurs at the staircase access points, rapidly increasing the density on the platform and the mezzanine level (see Figure 6a).

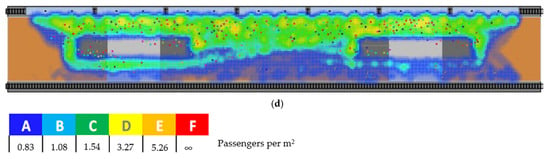
Figure 6.
Simulated behaviors considering a central platform: (a) symmetric entry flows in both directions; (b) asymmetric entry flows; (c) symmetric exit flows from both trains; (d) asymmetric exit flows.
For the situation of asymmetric entry flow, the pedestrian flow entering the platform through the staircases is uniform but asymmetric for both trains. The flow in one platform has been reduced by half, while the flow in the opposite platform has been doubled. When conducting a stress test on the station by proportionally increasing the passenger flow entering the station, it is observed that the critical areas are once again the access points to the staircases, located at the platform level. As the flow increases, appropriate density levels are observed on the platform (LOS = C), with lower service levels on the staircases. This configuration allows us to observe that when the flow is asymmetric—meaning passengers predominantly use the station in one direction—the use of platform space becomes more efficient. This is because the entire platform area can be utilized by the passengers, as the flow in one direction allows for a better distribution of space (see Figure 6b).
When the exit flow for both exits is symmetric, the pedestrian exit flow to the staircases is not uniform, as it strongly depends on train frequency, passenger load by direction, and the number of passengers disembarking at the station. As the flow increases, appropriate density levels are observed on the platform, with lower service levels on the staircases (LOS = C). When conducting a stress test on the station by proportionally increasing the flow of passengers disembarking from the trains, it is observed that the critical areas are once again the entry points to the staircases from the platform (see Figure 6c), reaching, at some points, LOS = E (i.e., capacity is reached, reaching a density between 3.27 and 5.26 passengers/m2). However, the overall station’s behavior is similar to the behavior observed in Figure 6a, where the platform remains at good service levels.
Finally, in the asymmetrical exit flow configuration, the station is the destination for many passengers at certain times of the day, in which the behavior is largely influenced by the number of passengers disembarking from the trains. If the station is located at the end of the network, passengers arriving at it will primarily come from one direction of the line. A scenario was simulated where a large portion of the passengers disembark at the station from only one of the two lines. As the flow increases, appropriate density levels are observed on the platform (LOS = C), with lower service levels on the staircases. When conducting a stress test on the station, by proportionally increasing the flow of passengers disembarking from the trains, it is observed that the critical areas are once again the entry points to the staircases from the platform (see Figure 6d), reaching LOS = E. The entire platform is used for the circulation of passengers disembarking from the trains, allowing for a free flow across the platform. The staircases facilitate a proper exit for pedestrians, provided that the counterflows with incoming passengers are not moderately high.
4.2. Side Platform
The lateral platform consists of two platforms with a width of a/2 (9 m) each. On each platform, passengers wait in one direction, and passengers disembark from the train coming from that direction. The platforms have two stair axes, each consisting of two double bidirectional staircases. Each staircase has a width of e/2 (3 m), with bidirectional pedestrian traffic.
As in the previous simulation, the staircases use a configuration that physically segregates bidirectional flows, preventing counterflow on the staircases. The platform has two potential pedestrian counterflows, as each platform faces the entry flow to the train and the exit flow from the train to the platform.
The same four types of behaviors in the previous simulation can be identified for the same platform.
The platform is modeled with a width of 9 m and a length of 150 m, with a stair axis that occupies one-third of the platform and is 3 m wide. The platform consists of four staircases, which are located at the sides of the lateral platforms.
In the case of symmetric entry flows in both directions, when conducting a stress test on the station by increasing the flow of passengers entering the station, it is observed that the critical areas are the access points to the staircases located at the platform level, reaching LOS = D (see Figure 7a). Low train frequencies or very high passenger inflows on the platform create conflicts with passengers disembarking from the trains, resulting in strong counterflow (LOS E or F). In general, the density remains normal and is evenly distributed across both platforms (LOS = C). With a platform width of a/2 and staircases of e/2, the access points to the staircases become separated and reduced, allowing for better passenger operation. This configuration helps mitigate congestion and improves overall flow, as the distribution of passengers is more efficient due to the physical separation of flows.


Figure 7.
Simulated behaviors considering a side platform: (a) symmetric entry flows in both directions; (b) asymmetric entry flows; (c) symmetric exit flows from both trains; (d) asymmetric exit flows.
On the other hand, in the case of asymmetric flow, the pedestrian flow entering the station is uniform but asymmetric. The number of passengers arriving at the station to board the train in one direction has been doubled, while the passengers in the opposite direction have been reduced by half. When conducting a stress test on the station by proportionally increasing the flow of passengers entering, it is observed that the critical areas are the access points on one of the platforms (see Figure 7b). As the flow increases, low-density levels are observed on one platform, while high-density levels are seen on the opposite platform, reaching more than 5.26 passengers/m2 or LOS = F. This lateral platform configuration shows that when the flow is asymmetric—meaning passengers primarily use the station in one direction—the use of platform space becomes inefficient. While one platform is heavily congested and its passengers experience low service levels (LOS = F), the opposite platform remains almost empty (LOS = A). This imbalance highlights the inefficiency of the layout in handling asymmetric flows, as the platform space is not utilized optimally.
When considering symmetrical exit flow, the flows descending at the station are uniform and symmetric, meaning the station receives an equal number of passengers from both directions of the line. When conducting a stress test on the station by proportionally increasing the passenger flow, the station performs well, with the platform density being moderately high but the flow remaining constant, reaching LOS = D (see Figure 7c). However, when the disembarking of passengers coincides with high passenger inflows to the trains, a strong counterflow is generated at the train doors. This counterflow creates congestion as passengers entering and exiting the trains try to use the same access points, leading to potential delays or a decrease in service efficiency (LOS = F).
Finally, when a station is a destination for a large number of users coming from only one side of the line, asymmetric exit flows are observed at the station. The condition where most passengers disembark at the station from only one of the two lines has been simulated. As the flow increases, uneven density levels are observed, where one platform becomes heavily congested (LOS = F) while the opposite platform remains in normal conditions, reaching LOS = A (see Figure 7d). When performing a stress test on the station by proportionally increasing the flow of passengers disembarking from the trains, it is observed that the critical areas are the train doors, where a strong counterflow of passengers occurs, as well as the areas at the entrances to the staircases. This results in congestion at the access points, making it difficult for passengers to move efficiently through the station and potentially reducing service levels (LOS = F).
4.3. Mixed Platform
The lateral platform has three platforms with a width of a/3 [6 m]. On each platform, passengers wait in one direction only, while on the third platform, passengers disembark from trains coming from both directions. The platforms have three sets of stairways, each consisting of two double bidirectional stairs. Each stairway is 2 m wide (e/3), with unidirectional pedestrian flow. Unlike previous simulations, unidirectional flows are used on the stairways, preventing counterflow.
The platform does not have any counterflow pedestrian areas, as each platform operates with unidirectional pedestrian traffic. In the simulation conducted in Anylogic, a platform with a width of 6 m and a length of 150 m is used, with a staircase axis that takes up one-third of the platform and is 2 m wide. The stairways are located on the sides of the lateral platforms and in the center of the central platform.
Four types of behaviors can be identified for the same platform, based on the previous different pedestrian flow scenarios.
In the case of symmetric entry flows, the pedestrian flow is symmetric and uniform for both lateral platforms. Passengers enter through the lateral platforms and disembark via the central platform, effectively avoiding any pedestrian counterflow at the train doors, platforms, or stairways. When conducting a stress test by increasing the flow of passengers entering the station, it becomes evident that the critical zones are the access points to the stairways located at the platform level, reaching LOS = F (see Figure 8a). Since the platform has a width of a/3 and the stairways are e/3 wide, the access points to the stairways are separated and reduced, allowing for better passenger operation. When the inflow to the station is high, it is observed that passengers should enter via the lateral platforms and disembark via the central platform. However, when the pedestrian volume is medium, entry can be made via the central platform. This is because the lateral platforms have double the capacity in both platform space and stairways compared to the central platform. This configuration optimizes the station’s operation by ensuring smooth pedestrian flow and minimizing bottlenecks, especially during high inflows. The use of the central platform for disembarking, combined with the lateral platforms for entry, ensures better space usage and flow management.

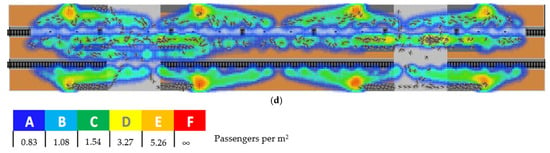
Figure 8.
Simulated behaviors considering a mixed platform: (a) Symmetric entry flows in both directions; (b) Asymmetric entry flows; (c) Symmetric exit flows from both trains; (d) Asymmetric exit flows.
When the pedestrian flow entering the station is uniform but asymmetric, the number of passengers arriving at the station to board the train in one direction has been doubled, while the passengers in the opposite direction have been halved. Upon conducting a stress test on the station by proportionally increasing the flow of passengers entering the station, we observe that the critical areas are low, with the point of maximum stress occurring at the stairway access points (see Figure 8b). As the flow increases, acceptable density levels are observed at both the loading and unloading platforms, reaching LOS = D. Due to the asymmetry of the ingress, the third platform has a low density of passengers (LOS = A). This lateral platform configuration shows that, when the flow is asymmetric, the use of the platform space is efficient, as passenger loading occurs without counterflow on one platform and passenger unloading takes place on the second platform. This optimizes the space usage by concentrating two-thirds of the total platform area on the higher-demand operation. For instance, this configuration also allows Platform 1 to be dedicated to loading Train A, while Platform 2 is used for passenger disembarkation, keeping Platform 3 exclusively for Train B. In this way, the configuration allows modular allocation of platform capacity, responding flexibly to varying passenger demands.
In the case of uniform and symmetrical flows descending at the station, the station receives an equal number of passengers from both directions of the line. The operational configuration of the platform is maintained, where passengers enter through the lateral platforms and disembark via the central platform. During a stress test of the station, when the flow of passengers is increased proportionally, the station performs well until the access points to the central stairways collapse (LOS = F), resulting in increased density on the central platform (see Figure 8c). This configuration allows for the allocation of two-thirds of the platform’s operational capacity to serve one direction (either ingress or egress), utilizing the lateral platforms, and one-third for the other service, using the central platform. Under these conditions, the most demanded service is the egress of passengers from both trains, meaning that the lateral platforms must be used for passenger disembarkation. When the passenger operation is reversed, with entry via the central platform and disembarking via the lateral platforms, the station maintains good service levels (LOS = B). This operational configuration enables efficient use of the platforms, allocating the greater capacity of the lateral platforms to meet the higher demand of passengers disembarking from the trains.
Finally, a simulation has been conducted where the majority of passengers disembark at the station from only one of the two lines in which the exit flows are asymmetrical. Disembarking occurs via the central platform, while passengers entering the station use the lateral platforms. When a stress test is performed on the station, increasing the flow of passengers descending from the trains, the critical areas are identified as the access points to the stairways and their surrounding areas (see Figure 8d). This configuration has an efficient operational design, as it allows the platform and stair capacity to be dynamically utilized to meet passenger demand, reaching LOS = C.
5. Discussion
5.1. Comparison of Platform Layout
The central-platform layout leads to counterflows of passengers, mainly between those heading towards the trains and those exiting the trains. The station allows for efficient flow at low-to-medium volumes. For higher flows, it is necessary to channel the traffic by segregating pedestrian pathways to avoid counterflow. In this type of platform, narrow platforms are not recommended. To increase the platform’s capacity, side platforms can be implemented, converting it into a high-capacity mixed-platform station. In other words, the station accommodates moderate passenger levels with flow in both directions. Medium-to-high flow levels mainly impact the access points to the staircases. Low train frequencies or very high inflows of passengers entering the station cause high levels of counterflow on the platform. It is observed that the station performs well under asymmetric operating conditions, compared to its symmetric operation.
In the case of the side platform, when the flow is high, counterflow occurs at the doors, platforms, and access points. Train operations are carried out on one side of the train, utilizing only 50% of the total doors on each carriage. This type of station allows for normal flow at low-to-medium volumes and can handle medium-to-high flows if its access points are segregated and the counterflow at the train doors is properly managed. Unlike the central platform, this type of platform cannot expand its capacity due to space limitations. In other words, the station can handle medium-high levels of passengers, with flow in both directions. High flow levels mainly impact the access points to the staircases. Low train frequencies or very high passenger inflows cause high levels of counterflow on the platform, particularly at the train doors. It is observed that the station performs well under symmetric operational conditions, compared to its performance under asymmetric conditions. In asymmetric flow conditions, the station’s performance becomes deficient, as passengers concentrate on one side of the platform, leading to high density levels. This imbalance results in congestion and inefficiencies in platform usage, reducing overall service quality.
When the mixed solution is considered, the station is divided into three platforms, which allows for the physical segregation of pedestrian flows, completely preventing counterflow. It is designed so that access to the train is on one side of the carriage, while disembarking occurs on the opposite side. This setup eliminates counterflow at the train doors and also utilizes 100% of the train doors, doubling its transfer capacity and allowing for shorter door opening times compared to the previously described platform configurations. This platform configuration has no counterflow at any of its levels, including train doors, the platform, access points, or stairs, enabling it to operate efficiently with very high passenger flows. Depending on the surrounding conditions, the station can function dynamically with varying passenger flows. If operational conditions require high demand in one direction, the central platform can operate in a mixed mode, using one side platform and the central platform for entry and exit of a single service, while the other lateral platform (with lower demand) operates with entry and exit through a single platform with counterflow. The mixed platform’s adaptable nature allows it to meet the operational needs of the metro system and maintain very high flow levels with efficiency and a good service level. It also allows for major maintenance work on the platforms without disrupting station operations, as two of the three platforms can be used alternately. Or, the station can operate as either a central platform or as lateral platforms. Compared to other platform configurations, the mixed platform is the most versatile, dynamic, and modular, capable of adapting to different demands and operational needs.
The mixed type of station supports very high passenger volumes because the platform layout ensures that there is no conflict or contraflow in any of the four critical areas: stairways, stair access points, platforms, and train doors. The station can be used dynamically, with the lateral platforms handling two-thirds of the operational capacity and the central platform handling one-third. This modular use of the platforms allows for flexible responses to changing demands, offering the following operation alternatives:
- (a)
- Ingress via lateral platforms, egress via central platform
When the main demand is for passengers entering the station in both directions, two-thirds of the operational capacity is allocated to passengers entering the trains;
- (b)
- Ingress via central platform, egress via lateral platforms
When the main demand is for passengers disembarking from the trains, two-thirds of the operational capacity is allocated to passenger disembarkation and egress from the station;
- (c)
- Combined operation
When the operation is extremely high for a train (e.g., Train A) in both directions, it is recommended to use two platforms to meet the demand for Train A. One platform is used for passenger ingress to the train and the second for passenger disembarkation. The third platform operates bidirectionally to serve another train (e.g., Train B). This approach allows for focused operation during peak hours with unidirectional demand.
Due to its modular design and dynamic operation, this platform configuration offers the highest operational capacity of all the studied configurations (see Figure 9).
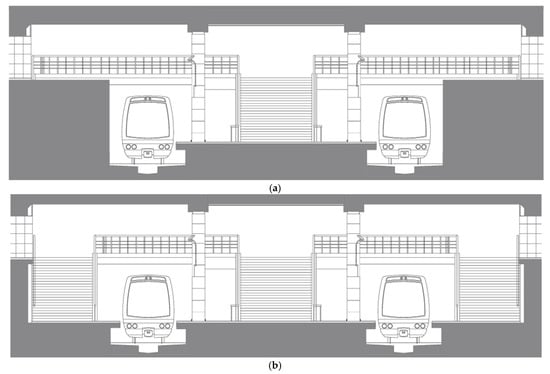
Figure 9.
Modular construction of underground stations toward a mixed layout according to the demand level: (a) Phase 1: building a central platform for a low-medium demand; (b) Phase 2: building lateral platforms to accommodate a higher demand.
5.2. Comparison with Existing Empirical Studies and Best Practices
When comparing our findings with existing empirical studies and best practices, we observe several points of convergence, as well as areas where this research either diverges from or contributes beyond the current literature:
- Convergence with best practices:
- ○
- Mixed platform (“Spanish Solution”): Our conclusion that a mixed-platform configuration tends to outperform either a central or lateral platform aligns with experiences in cities like Barcelona and on some lines of the Mexico City Metro, where the so-called “Spanish solution” is used to reduce door conflicts and shorten train dwell times. Empirical observations in these systems support the idea that physically separating boarding and alighting flows lowers congestion both on the platform and at the train doors;
- ○
- Use of the level of service (LOS) scale: By employing Fruin’s framework to measure pedestrian density, we align with the quality-of-service assessment methods widely adopted in various transport systems. Many metro operators apply density-based indices, so our findings regarding LOS thresholds are consistent with well-established station design practices.
- Contributions and divergences:
- ○
- Phased or modular construction: Our study goes beyond many empirical investigations by proposing a modular growth strategy: starting with a central platform and later adding lateral platforms to achieve a mixed design. Although there are isolated instances of stations that have been urgently expanded in an ad hoc manner, few studies systematically describe how to carry out such a progressive and controlled expansion. In this regard, our work deviates from the common approach of static or single-phase station design. It enables planners and designers to build stations with reserve capacity so that, when facing an unexpected future surge in demand, they can increase the station’s capacity—effectively doubling it—without replicating the entire structure;
- ○
- Analysis of asymmetric flows: Many empirical studies concentrate on station performance during relatively symmetrical peak hours, but they do not always explore situations characterized by high levels of asymmetry. Such asymmetry is quite common in stations located on the outskirts of cities, where the flow is predominantly outbound in the morning and inbound in the afternoon. Our research emphasizes how certain station types respond to markedly unbalanced demand. This focus highlights a gap in best-practice guidelines, which generally address “bidirectional” peak-hour surges rather than flows concentrated in one direction (due to specific events or other factors). This contribution is valuable for planners, as it enables more efficient use of available space and resources.
By contrasting our results with operational data from real stations and recognized industry standards, our proposal provides a comparative lens through which to better understand the advantages, limitations, and opportunities for improvement across different platform configurations. Furthermore, we encourage additional empirical validation—especially in stations recently expanded or those facing highly asymmetric demand—so as to strengthen the practical value of a phased or modular strategy in metro platform design.
Therefore, the method employed in this work is appropriate for several reasons:
- Comparative approach: Our aim was to analyze three platform configurations (central, lateral, and mixed) under different flow scenarios. A pedestrian simulation method provides a consistent framework for simultaneously evaluating metrics such as passenger density, waiting times, and counterflows;
- Flexibility of the simulation tool: By using modeling software that integrates both the train dimension and the pedestrian dimension, a comprehensive analysis of platform behavior was achieved—an aspect that many previous studies address separately (either focusing solely on pedestrian flow or exclusively on train frequencies);
- Reference to recognized standards: Basing our work on Fruin’s level of service (LOS) scale and density metrics validated by the literature ensures that the parameters used are compatible with internationally accepted evaluation methods, allowing us to compare our findings with those of other studies;
- Representation of real-world scenarios: By considering both symmetric and asymmetric flows, a broader spectrum of potential operational conditions was considered, thus facilitating comparisons with empirical research that examines maximum occupancy situations, peak hours, or unidirectional demand.
Thus, the methodology used is well-suited to the requirements of comparative analysis and, furthermore, allows us to identify points of alignment with studies that yield similar outcomes, while still recognizing discrepancies that arise when demand levels, cultural conditions, or growth assumptions differ from those in our model.
However, with respect to the limitations of this study, the model is a simplified abstraction of reality, aiming to compare the benefits of different platform configurations under various conditions. There are potential limitations and biases worth discussing to ensure the applicability of the results to broader contexts:
- Heterogeneity of passengers: The model treats users in a relatively homogeneous manner, assuming they all behave similarly in terms of walking speed, reactions to congestion, or boarding/alighting methods. In reality, however, there is great variability (people with reduced mobility, passengers with large luggage, children, groups, etc.). Failing to account for this diversity of passenger profiles can introduce bias by overestimating the station’s real efficiency or, conversely, by overlooking specific bottlenecks (for example, slower queues on stairways or elevators). Nonetheless, since it is a comparative analysis, these biases and limitations would appear similarly in all scenarios;
- Fixed-demand assumptions: The study begins with predefined flow scenarios (symmetric/asymmetric, high/low). While these scenarios cover a reasonable range of conditions, real station demand can fluctuate due to seasonal factors, large-scale events, extended rush hours, failures in other transportation modes, etc. Consequently, the limitation of using fixed-demand patterns makes it difficult to extrapolate the findings to unforeseen or highly volatile situations. However, these constraints would apply equally to all scenarios;
- Lack of exhaustive empirical validation: Although the model is calibrated according to parameters from the literature (for example, Fruin’s guidelines, maximum densities, and level of service), ideally one would have broad empirical data from operational stations to assess how well the simulations match reality (e.g., comparing observed vs. simulated densities and travel times). Without such validation, the results remain an approximation that may differ in real-life situations, especially in infrastructures with unique architectural features or variations in users’ physical characteristics (societies with higher obesity rates or older populations may exhibit different behaviors and interactions with the infrastructure);
- Specific geographic and cultural context: Station usage and circulation conditions may vary depending on local culture and pedestrian norms (e.g., queuing customs, attitudes toward congestion, accessibility regulations). The same platform design may be more or less efficient in different cities or countries, depending on factors such as train punctuality, passenger aggression/cooperation, the presence of personnel directing flows, physical distancing among passengers, or environmental conditions (e.g., an airport station, a major rail hub, or a commercial or educational setting, where travelers might carry more luggage or walk at different speeds). This reality limits the automatic transfer of conclusions to other regions;
- Partial scope in station modeling: Although the study examines platform areas and staircases in detail, a complete metro system includes mezzanines, street-level entrances, interconnecting corridors, and even internal commercial spaces that affect pedestrian flow. A partial model focusing on the platform may underestimate (or ignore) upstream or downstream bottlenecks, affecting the accuracy of predictions regarding the station’s overall efficiency.
Nevertheless, it is important to note several challenges that could arise in practical implementation:
- ○
- Geotechnical and structural conditions: In highly seismic areas, or regions with complex soil conditions or systems subject to high vibration (taking into account the inherent vibration of an operational metro system), expanding a station to add lateral platforms may require significantly reinforcing the original structure. This could entail large-scale underground works, with greater-than-anticipated costs and timelines. For this reason, in practice, stations are not usually expanded directly. Rather, they tend to be duplicated at a reasonable distance;
- ○
- Space constraints in built-up environments: In dense urban areas, the additional construction of platforms or the widening of circulation corridors may be limited by adjacent buildings or existing installations (utility ducts, other transit lines, underground parking structures, etc.). This lack of space can hinder expansion. However, had the station originally been designed with modular capacity in mind, a reserve area could have been left for lateral platform growth;
- ○
- Financial planning and investment phases: While the modular concept aims to optimize long-term investment by building only what is necessary for current and medium-term projected demand, this approach directly addresses a very common issue: the inability to accurately predict actual long-term demand (50 years). Facing this reality, the modular system allows for maintaining a capacity reserve that could eventually be built out in the future when justified by demand, thus avoiding unnecessary expenses at the system’s outset and only incurring them when truly required. Retaining this reserve capacity from the start of the project is highly efficient for long-term investment, ensuring a high level of service over time;
- ○
- Operational disruptions: Carrying out expansion work while the station remains in service presents a logistical challenge. Partial or total closure of key areas can affect passenger flow and cause inconvenience. For this reason, construction phases must consider temporary detours and safety measures to keep operations at acceptable levels. A phased construction model, by placing lateral platforms outside the main operational areas, enables the station to be expanded without negatively impacting its day-to-day operation.
Overall, these challenges underscore that adopting a modular design requires not only the proper physical and operational layout of the station but also an integrated planning process that addresses technical, financial, and urban considerations. This ensures that the second phase of construction effectively meets actual demand as it evolves. Nonetheless, factoring in the possibility of modular construction from the project’s inception makes it possible to anticipate and prepare for uncertain future scenarios without incurring additional costs, while still providing the potential for future capacity increases without disrupting service operations.
6. Conclusions
The main objective of this research was to analyze the impact of platform typology on the efficiency and capacity of the metro station. To achieve this, all the relationships and interactions within the platform were analyzed, and its behavior was modeled and evaluated under different design scenarios. This allowed for an understanding of how the various variables interact with each other and how they impact efficiency and capacity.
It was observed that the platform configuration, its accesses, and connectors strongly affect the station’s transfer capacity, and this configuration must be aligned with the environmental conditions and the station’s role within the metro network.
The average operating speed of the metro network linearly determines the network’s capacity. The stations, however, are the main restrictions on the operating speed. Therefore, the impact on the network’s capacity is strongly influenced by the efficiency with which each and every station operates. The average speed of the network is conditioned by the least efficient station within the circuit, which is usually the transfer stations. Improving the efficiency of a station enhances its operation, reduces the train’s dwell time at the station, increases the average speed, and thus, increases the overall transportation capacity of the entire network.
It is often mistakenly believed that an efficient station is a larger one. But in fact, even a station that is larger than necessary becomes less efficient, as the passengers have to travel longer distances, increasing their dwell and travel times.
By using the same volume of space, platform width, and stairways, it has been demonstrated that a station with mixed platforms is almost twice as efficient as a central-platform station. The central platform station is slightly more efficient than a station with lateral platforms, but this difference varies depending on the station’s usage, its surroundings, and its position within the network.
Station design should allow for phased construction, with the goal of expanding it to increase its capacity as passenger demand grows over the years. A modular station design will enable a generic station to be transformed into a high-capacity or transfer station.
The lateral platform station or the mixed-platform station is capable of handling medium-to-high passenger flows, but only the latter allows for transformation into a mixed station, thus doubling its capacity to handle very high passenger flows
This research also contributed to solving an urban-planning issue related to the current planning tools’ inability to predict passenger demand at a station over the long term. By using the tools applied in this research, the design of modular stations with phased construction is proposed, allowing stations to adapt in a planned manner to future requirements.
Further studies will expand upon the current study to analyze passengers both entering and exiting the station simultaneously by considering the most unfavorable passenger flow patterns for different types of platforms.
Author Contributions
Conceptualization, A.L., S.S. and V.A.; Methodology, A.L., S.S., V.A. and A.P.; Software, A.L.; Validation, A.L. and S.S.; Formal analysis, A.L.; Investigation, A.L. and S.S.; Resources, A.P.; Data curation, A.L. and B.A.; Writing—original draft, S.S.; Writing—review and editing, A.L., V.A., A.P. and B.A.; Visualization, A.L. and B.A.; Supervision, S.S.; Project administration, S.S.; Funding acquisition, A.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors upon request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Fernández, R.; Zegers, P.; Weber, G.; Tyler, N. Influence of platform height, door width, and fare collection on bus dwell time: Laboratory evidence for Santiago de Chile. Transp. Res. Rec. 2010, 2143, 59–66. [Google Scholar] [CrossRef]
- Seriani, S.; Fernández, R. Planning guidelines for metro–bus interchanges by means of a pedestrian microsimulation model. Transp. Plan. Technol. 2015, 38, 569–583. [Google Scholar] [CrossRef]
- GB50157-92; Code for Metro Design. China Planning Press: Beijing, China, 1992.
- GB50157-2003; Code for Design of Metro. China Planning Press: Beijing, China, 2003.
- GB50157-2013; Code for Design of Metro. China Planning Press: Beijing, China, 2014.
- Wang, L.H. Subway station platform design. North. Jiaotong 2008, 4, 220–222. [Google Scholar]
- Yao, L.; Sun, L.; Wang, W.; Xiong, H. Adaptability Analysis of Service Facilities in Transfer Subway Stations. Math. Probl. Eng. 2012, 2012, 701852. [Google Scholar] [CrossRef]
- Cheng, H.; Yang, X. Emergency Evacuation Capacity of Subway Stations. Procedia Soc. Behav. Sci. 2012, 43, 339–348. [Google Scholar] [CrossRef]
- Li, Y.; Sun, X.; Feng, X.; Wang, C.; Li, J. Study on Evacuation in Subway Transfer Station Fire by STEPS. Procedia Eng. 2012, 45, 735–740. [Google Scholar] [CrossRef]
- La Vigne, N.G. Safe Transport: Security by Design on the Washington Metro. In Preventing Mass Transit Crime; Criminal Justice Press: Monsey, NY, USA, 1996. [Google Scholar]
- Ge, X.; Dong, W.; Jin, H. Study on the Social Psychology and Behaviors in a Subway Evacuation Drill in China. Procedia Eng. 2011, 11, 112–119. [Google Scholar]
- GC/TT0196; BRB, Station Platform Design Requirements. British Railways Board: London, UK, 1993.
- Metro de Caracas Normas de Proyectos, Capitulo 15; Estaciones: Caracas, Venezuela, 2007.
- WMATA. Station Site and Access Planning Manual; Washington Metropolitan Area Transit Authority: Washington, DC, USA, 2008. [Google Scholar]
- Network Rail. Station Capacity, Assessment Guidance; Network Rail: London, UK, 2011. [Google Scholar]
- Network Rail. Guide to Station Planning and Design; Network Rail: London, UK, 2011. [Google Scholar]
- Metropolitan Council. Station and Suppport Facility Design Guidelines User Guide. In Regional Transitway Guidelines; Metropolitan Council: Minneapolis, MN, USA, 2012. [Google Scholar]
- Cui, Z.; Hu, J. Subway station type selection. Tunn. Constr. 2005, 25, 18–20. [Google Scholar]
- Wang, Z. Selection of Architectural and Structural Types of Hujialou Station on No 10 Line of Beijing Metro. Tunn. Constr. 2006, 26, 22–26. [Google Scholar]
- Xu, J. Architectural design Analysis of Separated Island-type Metro Station. Tunn. Constr. 2009, 29, 290–294. [Google Scholar]
- Lebedev, A. Metrogiprotrans. 70 Years–One Love, One Project; Art. Lebedev Publishing House: Moscow, Russia, 2003; p. 206. [Google Scholar]
- Xu, R.L. Design and construction of subway. In Collected Works in Contemporanry Civil Engineering and Architectural Science and Technology; Shaanxi Science and Technology Press: Xianyang, China, 1997; ISBN-13: 978-7-5369-2584-7; ISBN 7-5369-2584-0. (In Chinese) [Google Scholar]
- Liu, H.; Li, L.; Wang, C.; Wei, H. Design and deformation control of excavation support project close to a subway station. Chin. J. Geotech. Eng. 2010, 34, 654–658. [Google Scholar]
- Hui, L. Case Analysis on Platform Design of Urban Rail Transit System. J. Transp. Syst. Eng. Inf. Technol. 2008, 8, 167–173. [Google Scholar]
- Chen, F.; Wu, Q.; Zhang, H.; Li, S.; Zhao, L. Relationship analysis on station capacity and passenger flow: A case of Beijing subway line 1. J. Transp. Syst. Eng. Inf. Technol. 2009, 9, 93–98. [Google Scholar] [CrossRef]
- Leurent, F.; Chandakas, E.; Poulhes, A. A passenger traffic assignment model with capacity constraints for transit networks. Procedia Soc. Behav. Sci. 2012, 54, 772–784. [Google Scholar] [CrossRef]
- TRB; HCM. Station Capacity Transit Capacity and Quality of Service Manual, Third Edition Transportation Research Board; National Research Council: Washington, DC, USA, 2013. [Google Scholar]
- D’Acierno, L.; Gallo, M.; Montella, B.; Placido, A. Evaluation of Travel Demand Impacts in the Case of Rail System Failure. Procedia Soc. Behav. Sci. 2013, 87, 75–84. [Google Scholar] [CrossRef][Green Version]
- Hermant, L.F.L.; De Gersigny, M.R. Microscopic assessment of pedestrian space requirements within railway stations in South Africa. In Proceedings of the 29th Southern African Transport Conference SATC 2010, Pretoria, South Africa, 6–19 August 2010. [Google Scholar]
- Guio, F. Flujos peatonales en infraestructuras continuas: Marco conceptual y modelos representativos. Rev. Virtual Univ. Catol. Norte 2010, 29, 179–203. [Google Scholar]
- Helbing, D.; Molnar, P.; Farkas, I.J.; Bolay, K. Self-organizing pedestrian movement. Environ. Plan. B 2001, 28, 361–384. [Google Scholar] [CrossRef]
- Xi, H.; Lee, S.; Son, Y.J. An integrated pedestrian behavior model based on extended decision field theory and social force model. In Proceeding of the 2010 Winter Simulation Conference, Baltimore, MD, USA, 5–8 December 2011; IEEE: New York, NY, USA, 2011; pp. 829–836. [Google Scholar]
- Fruin, J. Metropolitan Association of Urban Designers and Environmental Planners. In Pedestrian Planning and Design; Springer: Berlin/Heidelberg, Germany, 1971. [Google Scholar]
- Daamen, W.; Hoogendoorn, S.P. Free Speed Distributions for Pedestrian Traffic; TRB-Annual Meeting: Washington, DC, USA, 2006. [Google Scholar]
- Rangel-Huerta, A. Ecuacion de Boltzmann de discos rigidos auto-impulsados para peatones en contraflujo. Rev. Mex. Fis. 2013, 59, 153–159. [Google Scholar]
- Gonzalez, J. Estudio de Modelos Para Trafico Peatonal y Su Aplicacion a Pasillos en Diferentes Escenarios. Master’s Thesis, Universidad Autonoma Metropolitana, Mexico City, Mexico, 2011; p. 103. [Google Scholar]
- Nai, W.; Dong, D.; Chen, S.; Zheng, W.; Yang, W. Optimizing the Usage of Walking Facilities between Platform and Concourse Layer in L-Shaped Interchange Metro Station. Procedia Soc. Behav. Sci. 2012, 43, 748–757. [Google Scholar] [CrossRef][Green Version]
- Li, W.; Zhou, J. The Optimize Management of Passenger Organization in Transfer Station Based on Dynamic Passenger Flow Analysis. Procedia Soc. Behav. Sci. 2013, 96, 1322–1328. [Google Scholar] [CrossRef]
- Xu, X.Y.; Liu, J.; Li, H.Y.; Zhou, Y.F. Probabilistic model for remain passenger queues at subway station platform. J. Cent. South Univ. 2013, 20, 837–844. [Google Scholar] [CrossRef]
- Zhang, Q.; Han, B.; Li, D. Modeling and simulation of passenger alighting and boarding movement in Beijing metro stations. Transp. Res. Part C Emerg. Technol. 2008, 16, 635–649. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, F.; Li, X. Modification and Pedestrian Simulation or Platform width Calculation method of urban rail transit. J. Transp. Syst. Eng. Inf. Technol. 2012, 12, 168–173. [Google Scholar]
- Wang, S.W.; Sun, L.S.; Rong, J.; Yang, Z.F. Transit Station Congestion Index Research Based on Pedestrian Simulation and Gray Clustering Evaluation; Hindawi Publishing Corporation: Cairo, Egypt, 2013. [Google Scholar]
- Anagnostopoulos, D.; Karlaftis, M.G.; Nikolaidou, M. Development of an object oriented pedestrian traffic flow simulation-environment for transport terminal planning. J. Adv. Transp. 2003, 37, 83–103. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, F.; Li, X. Comparative analysis and pedestrian simulation evaluation on emergency evacuation test methods for urban rail transit stations. PROMET Traffic Transp. 2012, 24, 535–542. [Google Scholar] [CrossRef][Green Version]
- Kittelson & Associates, Inc.; KFH Group, Inc.; Parsons Brinckerhoff Quade & Douglass, Inc.; Zaworski, K. Transit Capacity and Quality of Service Manual (TCRP Report 100), 2nd ed.; Transportation Research Board: Washington, DC, USA, 2003; Available online: http://onlinepubs.trb.org/onlinepubs/tcrp/docs/tcrp100/Part0.pdf (accessed on 9 January 2025).
- Mitelman, A.; Giat, Y. Key Factors in the Design of Urban Underground Metro Lines. Sustainability 2024, 16, 9293. [Google Scholar] [CrossRef]
- Yang, L.; Yang, Y.; Yang, M.; Zhang, Y.; Sheng, X. Numerical Investigation of the Long-Term Service Performance of Subsea Tunnel Lining Structure Considering Ion Erosion Deterioration. Sustainability 2024, 16, 10539. [Google Scholar] [CrossRef]
- Gong, D.; Tian, J.; Hu, W.; Dong, J.; Chen, Y.; Ren, R.; Chen, Z. Sustainable Design and Operations Management of Metro-Based Underground Logistics Systems: A Thematic Literature Review. Buildings 2023, 13, 1888. [Google Scholar] [CrossRef]
- Xu, Y.; Chen, X. The spatial vitality and spatial environments of urban underground space (UUS) in metro area based on the spatiotemporal analysis. Tunn. Undergr. Space Technol. 2022, 123, 104401. [Google Scholar] [CrossRef]
- Debrock, S.; Van Acker, M.; Admiraal, H. Design recommendations for sustainable urban underground spaces. Tunn. Undergr. Space Technol. 2023, 140, 105332. [Google Scholar] [CrossRef]
- Jasińska, K.; Kłosek-Kozłowska, D. Passengers’ experience in underground non-transfer metro stations: The impact of spatial characteristics. Tunn. Undergr. Space Technol. 2024, 143, 105482. [Google Scholar] [CrossRef]
- Liang, X.; Lu, Z.; Ye, F.; Zhang, W. Investigation of design of independent metro station entrances in China. In Proceedings of the Institution of Civil Engineers-Municipal Engineer; Thomas Telford Ltd.: London, UK, 2023; Volume 176, pp. 10–31. [Google Scholar]
- Khalid, N.S.; Samsudin, N.A.; Abdullah, Y.A. Application of the Node-Place Model to Explore the Spatial Development of KL Sentral in Malaysia. MCRJ Spec. Issue 2023, 20, 52–66. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).