Abstract
The presence of water-filled ruts during rainy conditions poses dual risks to driving safety: extended braking distances and sudden lateral vehicle deflection. When using maximum depth alone to describe the severity of the rut, it is impossible to obtain the three-dimensional rut morphology, let alone describe its effect on the water distribution on the road. To address this limitation, this study integrates the behavioral characteristics of the road surface with the three-dimensional rut morphology to calculate the water film thickness distribution of the road surface and develop a predictive model for the adhesion coefficient of the entire road surface. Based on the CarSim 2019 dynamics software and the road surface adhesion coefficient model, a water-filled rut driving safety simulation model was established. Key evaluation indicators are identified to quantify the effects of the three-dimensional rut morphology on braking and side deflection behavior, leading to the establishment of a comprehensive safety assessment model. This framework enables the correlation between three-dimensional rut morphology detection and driving risk evaluation, providing valuable insights for traffic safety management on rainy days, particularly in sections with existing ruts.
1. Introduction
Good road conditions are an important guarantee for safe vehicle driving. Asphalt pavement is subjected to the combined effect of vehicle load, high temperature, rainfall, and other unfavorable conditions for a long time in the process of use, and the spatial position of the pavement material deforms and evolves year by year to produce rutting. Rubbing will cause the vehicle to bump in the process of driving and changing lanes and affect driving safety, and it is easy to form water on rainy days, resulting in an uneven distribution of the thickness of the water film on the road surface. When the vehicle is driving on the road section with water-filled ruts, not only will the braking distance be lengthened, but it will also cause a large sideways deviation in a short period of time, which will aggravate the driving risk. The pattern of water rutting on the road surface is closely related to driving safety. The adhesion coefficient of the tire and road surface is an important factor affecting the safety of driving on rainy days; this is due to the increase in the thickness of the road surface water film and the consequent reduction of vehicle stability. Therefore, comprehensively and accurately analyzing the safety risk of driving in water-filled ruts and establishing a driving safety evaluation model are important ways to improve driving safety in water-filled ruts.
For road sections with rutting disease, the distribution pattern of pavement water on rainy days is closely related to the morphology of ruts in the three-dimensional space of the road surface. At present, the identification of road water accumulation areas mainly relies on the on-site observation of road management personnel to observe the depth and scope of road water accumulation after precipitation. This method is not only work-intensive, but is also affected by people’s subjective experience. It is difficult to accurately identify the depth and area of water-filled areas, and it is impossible to accurately grasp the impact of changes in rainfall intensity on water-filled areas. John Anderson (1995) [1] measured the depth of accumulated water on different road surfaces under different rainfall conditions, and summarized the relationship between the thickness of the water film and the slope of the road surface, rainfall intensity, and pavement drainage length. Luo Jing (2015) [2] established a model of the friction coefficient that changed with the water film thickness when the water film thickness is 0–5 mm according to the test results. Wang Yizuo (2017) [3] established and verified the water film thickness prediction model through the water film test on an indoor cement concrete pavement. Li Yingxia (2017) [4] improved the existing Sass road ponding physical model based on road data and meteorological data such as rainfall, and used the improved model to conduct experiments. Ma (2017) [5] established a water film thickness prediction model based on the artificial neural network considering the pavement width, but the calculated value depends on the range of the sample size. Brufau (2004) [6] made a one-dimensional assumption on the pavement, and predicted the steady-state runoff depth of the pavement under uniform rainfall conditions, but the one-dimensional pavement ignored the influence of the three-dimensional morphology of the pavement on the water flow. Geng Yanfen (2019) [7] established a numerical model of asphalt pavement runoff in the straight section based on the hydrodynamic method of the two-dimensional shallow water equation. The spatiotemporal effect of pavement runoff is analyzed under comprehensive consideration of pavement width, slope, drainage, and other influencing factors, but the influence of rutting and other pavement diseases on pavement surface water distribution is not considered. To sum up, the three-dimensional morphology of ruts has a non-negligible impact on the distribution of pavement water depth, but the current pavement water identification methods cannot be directly used to identify diseased pavement water areas; the close link between pavement conditions and vehicle safety has not yet been systematically incorporated into models for predicting the risk of hydroplaning.
For the safety analysis of water-filled pavement, T.F. Fwa (2008) [8,9,10,11] and Ji Tianjian (2010) [12] established the tire–water flow pavement model and CFD simulation, and found that the tire inflation pressure, tread pattern, and load have a significant effect on the critical hydroplaning speed. And through simulation analysis, a critical hydroplaning speed prediction model considering the above mentioned various influencing factors was obtained. Zhang Chi (2015) [13,14] quantitatively analyzed the influence of water film thickness and vehicle speed on vehicle side-turning angle on water-filled roads and proposed a safety evaluation method, considering driving safety under water-filled rutting conditions. According to the Euler coupling algorithm, Zhu Shengze (2016) [15] simulated and analyzed the influence of the spacing, width, and depth of the transverse grooves on the hydroplaning speed of the tire. Wang Weifeng (2017) [16] took the vehicle dynamics analysis software ADAMS 2016 as the simulation platform, and proposed to use tire parameters, vehicle parameters, and road coefficient parameters to construct a coupled vehicle–tire–road model. Cao Qingqing (2018) [17] built a set of rainy and sunny car driving stability evaluation systems based on the full-car model, and used the braking distance and lateral distance to conduct stability research for straight roads and curves in rainy days. Yan Jiao (2019) [18] detected and reconstructed the rutting section based on three-dimensional laser technology, calculated and obtained the water distribution of the section, and used the CarSim vehicle model to analyze the lateral stability. Tao Ma (2022) [19] analyzed the effect of water film thickness on the tire adhesion coefficient based on a three-phase coupled model. However, the study did not consider the effect of rutting geometric features on water film thickness. Yan Jiao et al. (2022) [20] constructed an adhesion coefficient whole vehicle model. However, the study did not address the dynamic calculation of water film thickness and its effect on the adhesion coefficient. In order to address the safety issue of slippery road surfaces, some researchers have also carried out studies on the calculation and dynamic correction of water film thickness, e.g., Jennifer Cai et al. (2023) [21] proposed a water film thickness prediction method based on the correction of measured data, which improved the calculation accuracy of the model by optimizing the Manning’s coefficient. However, this study mainly focused on airport runways and did not consider the influence of rutting geometric features on water film thickness and traffic safety.
Scholars at home and abroad have conducted research on road surface water film, road surface runoff, adhesion between tires and road surfaces under water-filled conditions, the impact of water-filled roads on vehicles, and evaluation indicators of water-filled ruts, and have established a series of mathematical models and simulation models. Despite these advancements, current studies still have notable shortcomings, such as a lack of integration between rut-induced ponding and vehicle safety assessment. Many studies tend to treat rutting and ponding in pavements as isolated phenomena rather than considering the interactions between rutting three-dimensional morphology, water film thickness, and vehicle behavior. In addition, real-time risk prediction is inadequate. Existing waterlogging identification methods are unable to dynamically predict hazardous areas under different rainfall conditions, which limits their practical application in real-world driving environments. Finally, most of the water strike risk models rely on simplifying assumptions that do not fully capture the effects of rut geometry and three-dimensional water accumulation on vehicle stability. In the study of vehicle driving safety on water-filled roads, the questions of how to integrate more road parameters into the impact of tires and water-filled roads and how to consider the consequences of different motion states of the vehicle under complex road conditions need to be solved.
Therefore, in order to make up for these deficiencies and improve driver safety, a new method is proposed in this study: Firstly, the calculation method of the water catchment process of rutted pavements based on grid division is used to extract the three-dimensional morphology of rutted puddle space, and the calculation of pavement water film thickness is realized. Then, an improved waterlogged-rut driving safety simulation model is proposed to realize the waterlogged-rut driving safety evaluation and early warning. The length of dangerous braking zone and critical side deviation time are taken as the driving safety evaluation indexes of a waterlogged rut, and the linkage between rut 3D morphology detection and the driving safety evaluation of a waterlogged rut is directly established through the simulation analysis of the rut 3D morphology indexes and different working conditions. By filling these critical research gaps, this study will help to improve the safety of wet weather driving on rutted roads and traffic safety control.
2. Analysis of Water Accumulation in Rutted Roads
2.1. Water Flow Calculation
In order to study the impact of pavement water on driving safety under the influence of a rutted road surface, this paper proposes an automatic recognition method based on grid division. The technological route that has been conceptualized is shown in Figure 1:
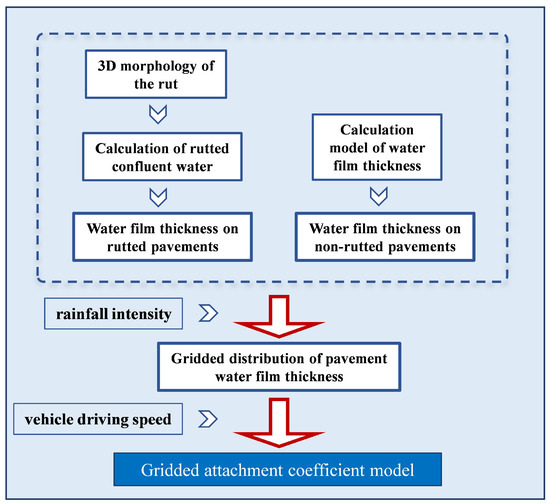
Figure 1.
Flow chart for rutted road surface water analysis.
The length of the waterlogged section of rutted roadway is divided according to the coordinates of the start and end locations of the ruts. Since the water at any point on the pavement flows in the direction of the synthetic longitudinal slope, the synthetic longitudinal slope of the well-graded area is represented by calculating the value of the synthetic longitudinal slope, which is the direction of water flow in that area. As shown in Figure 2, the section of roadway surrounded by the tangent line between the start and end points of the rut and the synthetic longitudinal slope of the pavement is the section of roadway used for the calculation of the rutted ponding area applicable to this study.
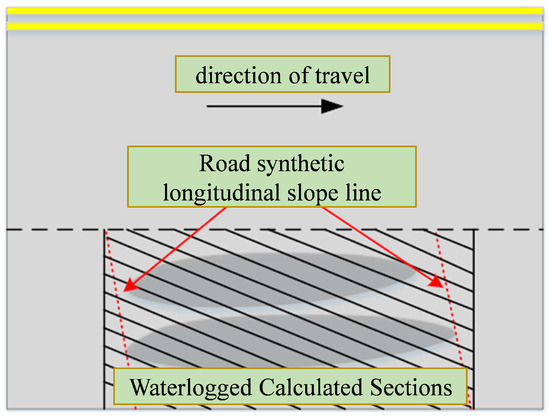
Figure 2.
Applicable road sections for water in the rutted water area calculations.
After reconstructing the 3D model of the pavement for the entire water road section, we divide the road section into grid units based on the research needs. According to the retention, infiltration, and evaporation of water flow on the pavement, the water flow from each grid to another in a certain period of time can be calculated by
where is the total rainfall in the grid, is the amount of accumulated water left in the grid by the pavement structure, is the amount of water infiltrated through the pavement, and is the rainfall evaporated during this period of time. The variables are determined as follows:
: Calculated based on the average rainfall intensity (I), rainfall duration (T), and grid area (A) over a certain period of time (see Equation (2)).
: This amount of water remains in the grid due to the road surface structure. Only when the depth of the road surface structure is filled does the water flow to other grids. The MTD index is a common index to characterize the macroscopic texture of pavement; this paper draws on the principle of an approximate equivalent sand-laying method to calculate the macroscopic texture MTD of the 3D reconstruction of a pavement. Its volume is equal to that of the road surface structure (see Equation (3)).
: For pavement surfaces using different grades of asphalt mixtures, the water permeability is different, and for different stages of use, the pavement surface aging and the gap between the particles of the pavement structural material are also different. Therefore, for different pavements, grid penetration experiments under different synthetic slopes are used to obtain corresponding data. For the convenience of calculation, the water seepage of the grids is divided into different grades according to the specific slope.
After calculating the water flow from each grid to other grids, we determine the catchment path of the water flow in each grid. According to the horizontal and vertical 3D laser elevation point cloud information in the grid, the trend line is fitted in MATLAB R2018a to obtain the transverse slope and longitudinal slope of each section in the grid. As shown in Figure 3, the slope of the trend line equation is the value to be determined. The average value of all cross−section fitting slopes in the grid is used as the transverse slope and longitudinal slope of the measured grid.
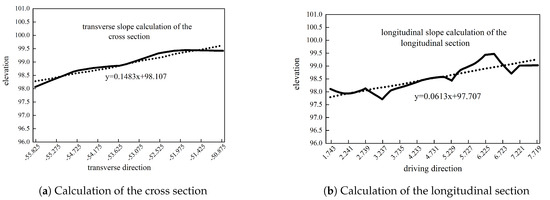
Figure 3.
The calculation of transverse and longitudinal slopes in the grids.
Based on the calculated transverse and longitudinal slope values, the composite slope is determined for each grid, as shown in Figure 4a. In each grid, the composite slope is indicated by an arrow. The starting point of the arrow is the center of the grid, and the length is 10 cm. The size of the composite slope is marked next to the arrow. The direction of the composite slope is the angle between the arrow and the driving direction. Finally, the trend of the composite slope distribution of the measured road surface is obtained, and Figure 4b is a partial composite slope distribution trend chart; the diagram identifies how standing water converges and flows in and around the rutted area, thereby analyzing the effect of water film thickness on driving safety. This water flow schematic allows for the further calculation of the volume of standing water in the rutted area and, combined with road gradient information, predicts the pattern of standing water under different rainfall intensities in order to assess the safety of driving during rainy days.
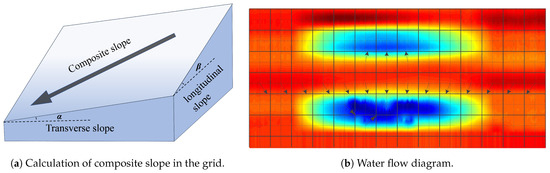
Figure 4.
Calculation and distribution of composite slopes.
In order to facilitate the calculation of confluence water volume distribution according to direction, a rectangular coordinate system is established with the horizontal direction of the road as the x-axis and the driving direction as the y-axis. The water volume within each grid is distributed along the X and Y directions according to Equations (4) and (5), respectively, and the water flowing from each grid to neighboring grids is divided into two portions with a direction symbol.
where and are the amount of water approaching the confluence of the grid in the X and Y directions, respectively; and is the angle between the composite slope and the driving direction.
The amount of water in each grid is superimposed and summarized separately in the X and Y directions. When the water volume symbol of neighboring grids is the same (or the direction is the same), it is distributed in that direction. If the symbol is the opposite, it is not distributed in that direction. Then, the water remains in the current grid, and the amount of accumulated water within the grid is calculated according to Equation (6).
where is the total amount of accumulated water in the grid, and is the amount of water flowing from other grids.
The volume of accumulated water in the rut is calculated based on the rut area (that is, the plane where the upper bottom of the rut is located). Using the outline of the bottom surface of the rut as the boundary, the volume of water accumulated by each grid in the rut area is calculated according to Equation (6). The total volume () of water within the rut can be obtained by adding the volume of water accumulated in all grids. The calculation method is shown in Equation (7), where m is the number of grids of the car, and is the amount of accumulated water in the i-th grid.
2.2. Road Surface Water Morphology Under the Influence of Ruts
Within half of the rut, the accumulated water from the grids will be integrated and filled from the bottom of the rut to the top until it is flat with the road surface. Therefore, based on the 3D contour of the rut and the principle of volume equality, we let the accumulated water volume of the rut () under current rainfall conditions be equal to the volume of the rut () used to store the accumulated water. As shown in Figure 5, according to the volume calculation principle, it is possible to find the area of accumulated water () of the vehicle rut under current working conditions and the distance () between the plane and the next nearest calculated surface.
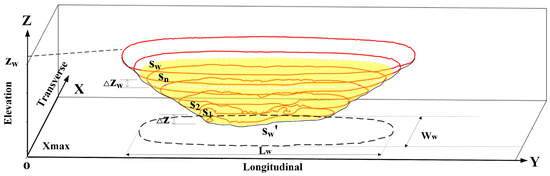
Figure 5.
Schematic diagram of finding depth distribution of half rut in accumulated water.
According to and the superposition of the various contoured line intervals, the maximum depth of water accumulation () within half of the rut can be determined under current rainfall conditions.
where is the maximum depth of water accumulation within the rut, is the calculated spacing of rut volume, and is the height difference between the surface of the rut and the nearest rut surface.
After identifying the elevation of the lowest point of the rut, we can find the elevation of water surface () based on the maximum depth of water accumulation.
where is the elevation of the water surface, is the elevation of any point within the rut, and is the maximum depth of water accumulation.
Then, based on the difference between the elevation of the plane and any point within the outline surface inside the rut, the depth of water () at any point in the accumulated water area can be calculated.
where is the depth of water accumulation at any point in the rut, is the elevation of accumulated water surface, and is the elevation of any point within the rut.
By projecting the identified contour lines onto the plane, it is possible to calculate the width () and length () of the accumulated water in half of the rut based on the maximum horizontal and vertical coordinates. The specific method is the same as that of the rut width and length.
If the 3D morphology of the left and right half of the rut is different, the state of water accumulation is different as well. On the basis of 3D road surface reconstruction and rut water accumulation recognition, the road surface is divided into a water surface and a non-water surface by identifying the elevation and location of the left and right half of the rut. For the non-water surface, a prediction model is used to calculate the average water film thickness of the road surface. For the water surface, the water accumulation identification method proposed in this section is used to identify the average water film thickness within each grid (Equation (12)). When calculating the water film thickness, if the grid has both a water surface and non-water surface at the same time, the water film thickness is calculated using the method for a larger area within the grid.
where is the average thickness of water film within the k-th grid of the road surface, is the thickness of water film at any point within the grid, and m and n are the number of point clouds in the driving direction and the horizontal direction of the road, respectively.
2.3. Method for Calculating Adhesion Coefficient of Accumulated Water Pavement
On the basis of tire–road contact characteristics and water skiing analysis, the influencing factors of the road surface adhesion coefficient are analyzed. It was found that the depth of pavement structure, tire tread depth, driving speed, and water film thickness all have a certain effect on the adhesion coefficient of a rainy day waterlogged pavement, and the focus of this paper is to evaluate the driving safety of rainy day pavement, on the one hand, to provide drivers with rainy day safety speed warning, and on the other hand, to provide support for the decision-making of pavement maintenance. Therefore, this paper selects two indicators of driving speed and water film thickness to estimate and analyze the adhesion coefficient of pavement.
The water film thickness and driving speed are taken into account, and an adhesion coefficient prediction model is established through finite element analysis. In the simulation, we select the ‘C-class’ two-car as a simulation model with a weight of 1270 kg, which is more suitable for China’s common small car technical rutting driving safety analysis, in order to match the road surface input to the model of the road surface adhesion coefficient calculations; a width of 225 mm for a 225/60 R18 tire type is chosen. The driving trajectory of the simulated vehicle is set to be along the center line of the lane.
According to the calculated water film thickness, the road adhesion coefficient at different vehicle speeds can be calculated. After calculating the adhesion coefficient of the road surface water film thickness (h) and vehicle driving speed (v), the adhesion coefficient model is obtained as shown in Equation (13) through regression analysis.
where —road surface adhesion coefficient under some skiing conditions; v—vehicle driving speed (km/h); h—water film thickness (mm).
The study further analyzed the variation in roadway attachment coefficients at different vehicle speeds and water film thicknesses as shown in Figure 6; each section unit represents the change in ponding form and adhesion coefficient in the cell. The rainfall intensity of 25 mm/h was used to calculate the real-time water film thickness at different roadway locations, and the empirical regression formula was used to calculate the attachment coefficients at different vehicle speeds. The results show that the adhesion coefficient decreases as the water film thickness increases, and the adhesion coefficient in the rutted waterlogged area is significantly lower than that in the non-rutted area, showing obvious spatial differences. The effect of vehicle speed on the adhesion coefficient was relatively small. The study calculates the coefficient of adhesion by means of rainfall intensity, the water film thickness prediction model, and empirical regression formula, and proposes a method that can be used to evaluate the adhesion performance of roadways under different rainfall conditions and driving speeds, which can provide a reference for the safe of roadways.
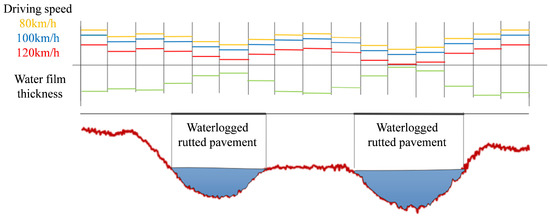
Figure 6.
Adhesion coefficient varies with vehicle speed and water film thickness.
3. Establishment of Water Rut Safety Model and Analysis of Braking and Side Deflection
3.1. Simulation Model Establishment
3.1.1. Simulation Steps
In order to carry out the simulation analysis of driving safety in waterlogged ruts, according to the data characteristics and research requirements of this paper, a waterlogged-rut driving safety simulation model is established. First, we build the full-car model in CarSim. The Vehicle Module in CarSim contains different types of vehicles, which can be selected according to the research needs. Secondly, we establish a road surface model and input road surface point cloud data through the Geometry Module. The adhesion coefficient of each road grid is input to CarSim through the Road Friction Map module. Finally, based on the analysis of vehicle braking and handling stability, the braking distance and side deflection distance are selected as the output variables of water rut safety simulation to analyze the impact of water-filled ruts on driving safety.
To verify that the CarSim simulation model established in this article can be used for the accurate and comprehensive evaluation of driving safety in waterlogged ruts, the simulation model established in this article is first validated. The difference between the model input used in this article and the previous scholars’ simulation analysis of waterlogged ruts is that the previous scholars used a single adhesion coefficient converted from the maximum waterlogged depth of the ruts, while the adhesion coefficient input in this article is a matrix library based on road grid partitioning. For comparative verification, this article conducts simulation analysis on braking distance and offset distance based on the same waterlogged rutting under the two types of adhesion coefficient inputs mentioned above. In addition, braking and lateral deviation simulation analysis is performed on the waterlogged ruts at speeds of 60 km/h, 80 km/h, 100 km/h, 110 km/h, and 120 km/h. Figure 7 shows the variation curves of braking distance and lateral deviation distance with speed.
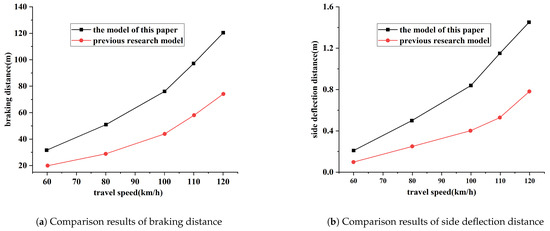
Figure 7.
Simulation results of two models.
From Figure 7, it can be seen that under the condition of water accumulation in the ruts, the braking distance and lateral deviation distance of both simulation models increase with the increase in speed, which is consistent with previous research conclusions. The braking distance and lateral deviation distance output by the model in this article are both smaller than the output values of previous models. This is because previous models used the maximum water depth to represent the water depth of the entire road section, while the grid adhesion coefficient input in this article is a gradually changing adhesion coefficient converted based on the actual water depth in each cell, which is closer to the actual state of the road surface.
The flowchart for the establishment of the water rut safety model and analysis of braking and side deflection is shown in Figure 8.
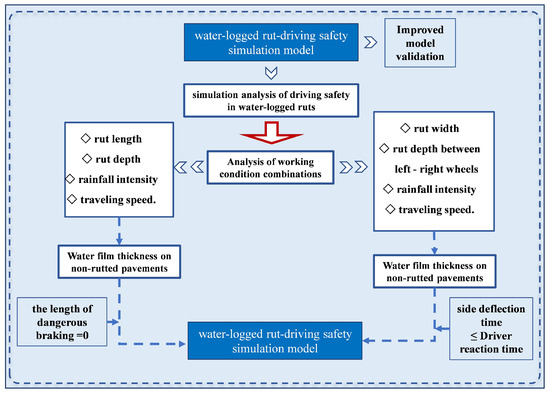
Figure 8.
The flowchart for the establishment of the safety model and the analysis of braking and side deflection.
3.1.2. Selection of Safety Evaluation Indicators
- Safety evaluation indicators of brakingFurther, when combined with the rut waterlogged state of the braking results for in-depth analysis, with different braking starting points for simulation analysis, the braking distance of the the vehicle in relation to the waterlogged rut positional relationship is as shown in Figure 9. From the figure, it can be seen that the braking distance with 180 m as the braking starting point is the smallest; this is due to its braking path and the fact that the rut has no contact, with the rest of the braking starting points of the braking path completely in contact with the rut or partially in contact with the braking path. In the initial braking action, where the braking path is in contact with the thickness of the water film, the larger the vehicle, the longer the braking distance. Therefore, the length and depth of the rutted water is an important factor affecting the safety of vehicle braking on waterlogged rutted pavement.
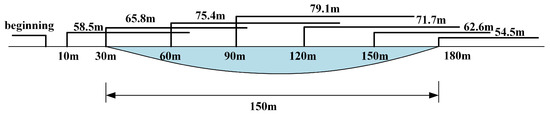 Figure 9. Braking distances for different starting points in waterlogged ruts.Combining the previous studies and the braking distances at different braking starting points in Figure 9, according to the contact state between the vehicle and the rut, there exists a region between 30 m and 120 m in which the braking distance is greater than the prescribed safety distance. To summarize, on a road with accumulated water, when braking starts at a point and the braking distance is greater than the specified safe distance at the current driving speed, the length along the driving direction is defined as a dangerous braking zone. We select a point on the road as the starting point for car simulation, and define it as the 0 point of coordinate. Then, a point away from the starting point is chosen as the braking point for simulation, and the result curves are shown in Figure 10a. The x-axis is the braking starting point coordinate and the y-axis is the braking distance. We find that the coordinates of the starting point of braking at the braking distance are equal to the safe vehicle distance at the corresponding driving speed, and the length between the two is the length of the dangerous braking zone.
Figure 9. Braking distances for different starting points in waterlogged ruts.Combining the previous studies and the braking distances at different braking starting points in Figure 9, according to the contact state between the vehicle and the rut, there exists a region between 30 m and 120 m in which the braking distance is greater than the prescribed safety distance. To summarize, on a road with accumulated water, when braking starts at a point and the braking distance is greater than the specified safe distance at the current driving speed, the length along the driving direction is defined as a dangerous braking zone. We select a point on the road as the starting point for car simulation, and define it as the 0 point of coordinate. Then, a point away from the starting point is chosen as the braking point for simulation, and the result curves are shown in Figure 10a. The x-axis is the braking starting point coordinate and the y-axis is the braking distance. We find that the coordinates of the starting point of braking at the braking distance are equal to the safe vehicle distance at the corresponding driving speed, and the length between the two is the length of the dangerous braking zone.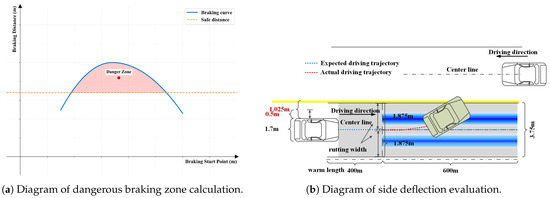 Figure 10. Schematic diagram of safety evaluation indicators.For the same rut, under different rainfall intensity and traveling speed, the water accumulation pattern is different, and the length of hazardous braking zone is different; under the same rainfall intensity and traveling speed, the water accumulation pattern is also different for ruts of different lengths, widths, and depths, thus affecting the length of hazardous braking zone. Therefore, this paper selects the length of dangerous braking zone as the safety evaluation index of waterlogged rut braking.
Figure 10. Schematic diagram of safety evaluation indicators.For the same rut, under different rainfall intensity and traveling speed, the water accumulation pattern is different, and the length of hazardous braking zone is different; under the same rainfall intensity and traveling speed, the water accumulation pattern is also different for ruts of different lengths, widths, and depths, thus affecting the length of hazardous braking zone. Therefore, this paper selects the length of dangerous braking zone as the safety evaluation index of waterlogged rut braking. - Safety evaluation index of side deflectionThe side deflection distance is used as an index for the results of the lateral safety simulation analysis in this paper. The occurrence of the side deviation of a vehicle in a waterlogged rut is mainly due to the different friction states of the left and right wheels in contact with the road surface, resulting in an imbalance of the lateral forces on the wheels, and thus the risk threshold for the amount of side deviation of a rut can be defined as half of the width of the rut waterlogged rut. But for car ruts, if uneven water accumulation occurs, the width of the water area of different ruts is not the same. For the same rut, the width of the accumulated water is not the same for different rainfall intensities and time periods. Therefore, it is impossible to directly characterize the lateral safety of a section with accumulated water. For a rut with accumulated water, the side risk threshold is half the width of the water accumulation, but the time (T) to reach the risk threshold is not the same under different conditions. If the driver is still unable to respond when the time reaches T, then the vehicle will be in danger (Figure 10b).Since the lateral deviation amount and lateral deviation time are the most simple and intuitive, this paper selects the lateral deviation time at which the lateral deviation amount reaches half of the rut width, i.e., the critical lateral deviation time, as the safety evaluation index of lateral deviation. This index can be applied to different models, different water depths, and different speeds, so that it is comparable between different working conditions, thus improving the applicability and universality of the evaluation system.
3.2. Simulation Condition Analysis
3.2.1. Selection of Simulation Conditions
This section simulates and analyzes a combination of operating conditions from the three aspects of rut morphology, rainfall intensity, and vehicle speed.
Among them, the rut morphology includes four indicators: rut length, rut width, maximum rut depth, and left–right depth difference. The rut length is the maximum of the left and right half of the rut, and the rut width is the sum of the average of the left and right half of the rut. The maximum rut depth is the average of the maximum depth of the left and right half, and the left–right depth difference is the difference between the maximum depth of the left and right rut. In order to better control the variables, a rutted road section with the actual rut length × width × depth × difference between the left and right depths of 450 m × 2 m × 18 mm × 8 mm was interpolated and transformed in the longitudinal, transverse, and vertical directions, respectively. Based on this, this paper selects different rutting morphology for simulation analysis, in which the rut lengths are 150 m, 300 m, 450 m, and 600 m, the rut widths are 0.8 m, 1.4 m, 2.0 m, and 2.4 m, the maximum rut depth is 6 mm, 12 mm, 18 mm, and 24 mm, and the left–right depth differences are 2 mm, 4 mm, and 8 mm, 12 mm, respectively, in order to comprehensively characterize the impact of different waterlogged ruts on traffic safety.
The same rutting pattern of the rainy day water distribution pattern is affected by rainfall intensity; in order to facilitate the study in the western region of China, the 5-year 10 min rainfall intensity of 150 mm/h was used for the maximum limit, while the other rainfall intensities of different heavy rainfall levels were converted to a 1-h rainfall intensity value for simulation analysis. Therefore, the rainfall intensity levels selected in this paper are 150 mm/h, 100 mm/h, 50 mm/h, and 10 mm/h for the calculations. At present, the maximum speed on the highway in China is 120 km/h. In order to better analyze the safety of high-speed driving, 120 km/h is used as the maximum braking initial speed and driving speed in the simulations. The driving speed is increased at an interval of 20 km/h, and 100 km/h, 80 km/h, and 60 km/h are used as the simulation speeds.
This paper analyzes 19 simulation conditions under the rut index values, rainfall intensity, and vehicle speed to perform braking simulation and side deflection simulation. These conditions can comprehensively reflect the impact of waterlogged rutting on driving safety and provide reliable data support for the subsequent evaluation system. The simulation conditions are shown in Table 1.

Table 1.
Simulation conditions of car rut with accumulated water.
3.2.2. Correlation Analysis of Indicators
In order to ensure the accuracy of the proposed model while improving its simplicity and practicality, it is necessary to perform correlation analysis of the indicators; then highly relevant indicators can be selected to establish models for braking and side deflection. Multiple linear regression analysis was performed based on the dangerous braking zone length and side deflection time thresholds of the 19 operating conditions shown in Table 1. At a confidence level of 95%, the p−values for the t statistics are given in Figure 11.
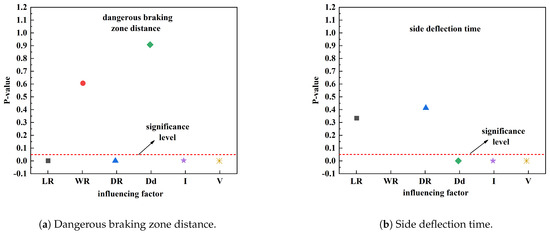
Figure 11.
Correlation analysis of influencing factors.
In multiple linear regression analysis, the p−value is used to evaluate the significance of various influencing factors on driving safety. If , it indicates that the factor has a significant impact on the length of the dangerous braking zone or lateral deviation time, and should be included in the model; if , the impact is relatively small and can be eliminated. Figure 10 visually displays the p-value distribution of different factors and indicates the significance level. The results indicate that the rut length, rut width, rainfall intensity, and driving speed significantly affect the length of the dangerous braking zone and should be included in the braking safety evaluation model. The rut width, the difference in depth between the left and right ruts, rainfall intensity, and driving speed significantly affect the lateral deviation time, indicating that vehicle stability is more affected by these factors.The regression coefficient is used to measure the degree of influence of independent variables on dependent variables. The regression coefficient analysis shows that there is a positive correlation between driving speed and braking zone length (), and a negative correlation between rainfall intensity and lateral deviation time (), indicating that the stronger the rainfall, the more likely the vehicle is to experience lateral deviation. Further analysis shows that the significance of the influencing factors may fluctuate with the change in rainfall intensity, and the influence of rut depth may increase under rainstorm conditions. The analysis results can provide data support for highway safety management and optimize driving speed limit strategies under different rainfall conditions.
Different working conditions were selected to evaluate the safety of waterlogged rutted vehicle braking, and the results are shown in Figure 12.
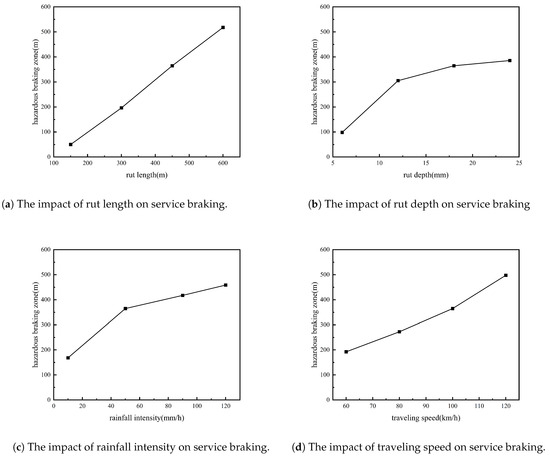
Figure 12.
Evaluation of the safety of waterlogged rutted vehicle braking.
From the Figure 12, it can be seen the hazardous braking zone is affected by rut length, rut depth, rainfall intensity, and traveling speed. The braking hazard zone increases roughly linearly as the rut length is extended; this is mainly due to the expansion of deeper water at the front and rear of the vehicle, which lengthens the braking danger zone. An increased rut depth results in longer braking zones, but the effect diminishes after a certain depth is reached; rainfall intensity also expands the danger zone, but once the ruts are filled, the rate of growth slows. The travel speed has the greatest effect, as higher speeds reduce the coefficient of adhesion, lengthen braking distances, and widen the danger zone due to the fixed distribution of the water film.
3.3. Driving Safety Evaluation Model for Water Rut
3.3.1. Braking Safety Evaluation Model
By analyzing the impact of the above factors on the length of the dangerous braking zone of water rut, it can be seen that rut length, rut depth, rainfall intensity, and driving speed all have a good linear correlation with the length of the dangerous braking zone. Therefore, it is possible to establish multiple linear regression models of dangerous braking zone length, rut length, rut depth, rainfall intensity, and driving speed based on the calculation results of 13 operating conditions (1, 2, 3, 4, 8, 9, 10, 14, 15, 16, 17, 18, and 19). We assume the model relationship between the length of the dangerous braking zone and these four indicators is as follows:
If we set the confidence level to be 95% and perform multiple linear regression analysis with a significance level of 0.05 on the selected operating conditions and results, the obtained regression coefficients are as follows:
Then, we obtain a regression equation as shown in Equation (14) for the driving safety evaluation model based on dangerous braking length.
where S is the dangerous braking zone length (m), is the rut length (m), is the rut depth (m), I is the rainfall intensity (mm/h), and V is the driving speed (km/h).
Different working conditions were selected to evaluate the safety of the side deflection of the waterlogged rut, and the results are shown in Figure 13.
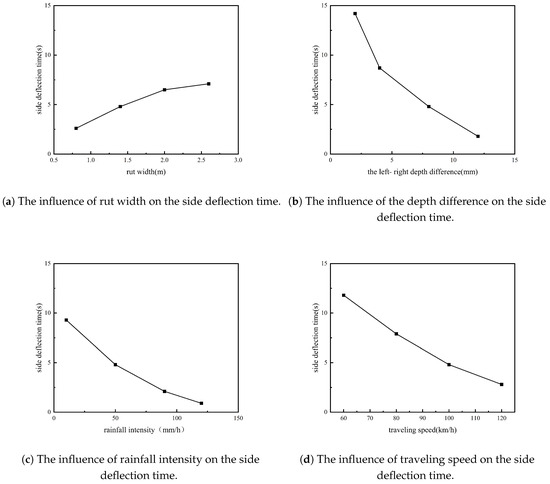
Figure 13.
Evaluation of the safety of the side deflection of a waterlogged rut.
According to the results of conditions 3, 5, 6, and 7, increasing the rut width prolongs the lateral deviation time and improves safety. This is because as the width increases, both wheels will contact the water film more evenly, thus reducing the risk of deviation; according to the results of Case 3, 11, 12, and 13, the greater the difference in rut depth between the left and right wheels, the shorter the lateral deviation time and the higher the safety risk. This is because the depth difference will cause an uneven thickness of water film, resulting in unbalanced tire adhesion and increased lateral instability. Through the simulation results of Case 3, 14, 15, and 16, the higher the rainfall intensity, the shorter the lateral deviation time, but the effect will be stabilized after exceeding a certain critical value. By analyzing the results of Case 3, 17, 18, and 19, the higher the vehicle speed, the shorter the lateral deviation time, and the more abrupt and dangerous the deviation is. Increased vehicle speed reduces traction, increases the likelihood of skidding, and makes it more difficult to maintain control.
Differences in rut width and depth are key structural factors affecting lateral deviation, while rainfall intensity and travel speed have dynamic effects. Higher speeds and deeper rutting imbalances can seriously affect driving safety, so careful road maintenance and adaptive driving strategies are needed on waterlogged roads.
3.3.2. Side Deflection Safety Evaluation Model
Similarly, multiple linear regression models of side deflection time thresholds and rut width, left and right rut depth difference, rainfall intensity, and driving speed can be established based on the simulation results of 13 operating conditions (3, 5, 6, 7, 11, 12, 13, 14, 15, 16, 17, 18, and 19). The obtained vehicle safety evaluation model based on side deflection time thresholds is a regression equation as shown in Equation (15):
where T is critical side deflection time (m), is the rut width (m), is the left and right rut depth difference (mm), I is the rainfall intensity (mm/h), and V is the driving speed (km/h).
An analysis of variance was performed on the model and the results are shown in Table 2.

Table 2.
Analysis of variance of the factors affecting traveling side deviation.
The p-value of the F-statistic of the regression equation of this model is , which is much smaller than the significance level of 0.05. Therefore, the evaluation model of the waterlogged rut traveling side deviation (Equation (15)) constructed in this paper has a significant regression effect at a confidence level of 95%.
4. Case Analysis of Driving Safety Evaluation of Water-Filled Ruts
4.1. Data Collection
This road section studied in this article is located in the K1423+250 tK1426+2503 at Xishang Expressway in Shaanxi Province. Three rutted road sections were detected using a 3D laser detection vehicle developed by Chang’an University, and 3D laser point cloud data of a 1000 m full vehicle road surface were collected. The collected 3D laser point cloud of the entire lane road surface was processed, and the MATLAB platform was used to conduct 3D modeling based on regular grids for three road sections. The length, width, depth, and three-dimensional shape of the ruts on the three road sections are different. Among them, the K1243+250 K1244+250 section (Rut 1 #) has the shortest rut length and the shallowest maximum depth; the K1245+250 K1246+250 section (Rut 3 #) has the longest rut and the deepest maximum depth.
Compared with Rut 1 #, the length of Rut 2 # increased by 151.6 m, the width increased by 0.9 m, the maximum depth increased by 6.4 mm, and the difference in depth between left and right increased by 2.6 mm; compared with Rut 2 #, the length of Rut 3 # increased by 105.7 m, the width increased by 0.6 m, the maximum depth increased by 5.9 mm, and the difference in depth between left and right increased by 1.6 mm, which is a significant change. According to the Technical Specification for Highway Asphalt Pavement Maintenance (JTJ073.2-2001) [22], rutting depth exceeding 15 mm should be repaired by overlaying, so Rut 3 # needs to take maintenance measures. The multi-dimensional index calculation method of pavement rutting proposed in this study can quantitatively describe and compare different rutting and provide a basis for further analyzing its impact on traffic safety.
4.2. Driving Safety Evaluation on Roads with Water-Filled Ruts
Based on the calculation results of the multi-dimensional rut index above, it is possible to evaluate the braking and side deflection safety on any road section using models established in this paper. For the water-filled rut, its safety evaluation model is shown in Table 3.

Table 3.
Safety and side deflection evaluation models on different road sections.
As can be seen from the table, under different rainfall intensities, it is possible to control the dangerous braking length and critical side deflection time of the water-filled rut by controlling the driving speed. Using the braking safety evaluation model and side deflection safety evaluation model in Table 2, the length of the dangerous braking area and critical side deflection time under different rainfall intensities and different driving speeds are calculated. For Rut 1#, Rut 2#, and Rut 3#, the changes in the length of the dangerous braking zone and the critical deflection time are shown in Figure 14.
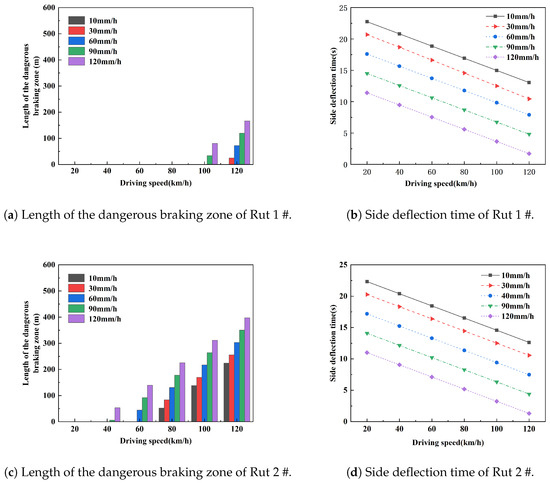
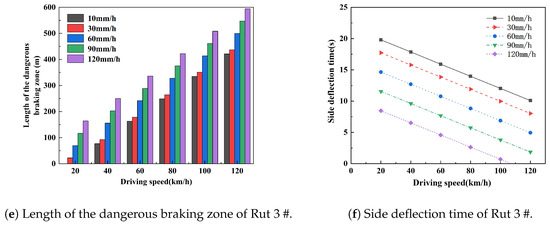
Figure 14.
Dangerous braking zone length and critical side deflection time under different rainfall intensities.
As far as braking is concerned, for Rut 1#, when the driving speed is 120 km/h or less, there are no dangerous braking zones. When the rainfall intensity is 30 mm/h and 60 mm/h, there are no dangerous braking zones at driving speeds below 100 km/h. When the rainfall intensity is 90 mm/h and 120 mm/h, there are no dangerous braking zones at driving speeds below 80 km/h. For Rut 2#, when the rainfall intensity is 10 mm/h and 30 mm/h, there are no dangerous braking zones at driving speeds below 60 km/h. When the rainfall intensity is 60 mm/h, there will be no dangerous braking zone at driving speeds below 40 km/h. When the rainfall intensity is 90 mm/h and 120 mm/h, there will be no dangerous braking zone when the driving speed drops to 20 km/h. For Rut 3#, when the rainfall intensity is 10 mm/h, dangerous braking zones do not occur only when the driving speed drops to 20 km/h. When the rainfall intensity is 30 mm/h or more, dangerous braking zones occur at any speed. Therefore, in order to ensure driving safety during heavy rain and road capability during light to medium rain, Rut 3# should be repaired. As far as side deflection is concerned, the higher the driving speed or the greater the rainfall intensity, the shorter the critical side deflection time. Therefore, it can be found that under specific rainfall conditions, the driving speed can be controlled to eliminate the length of the dangerous braking zone or increase the critical side deflection time.
In this paper, the length of the dangerous braking zone is 0, as the safety limit of the braking zone length, and the time to reach the critical side deviation is 5 s, as the safety threshold of the side deviation time. The results of calculating the critical safe vehicle speed based on the braking hazard length and side deflection time are shown in Table 4.

Table 4.
Critical safe vehicle speed based on braking hazard length and side deflection time.
The results of the analysis in this section can be directly used for rainy day traffic management and road safety optimization. By calculating the critical safe speeds under different rainfall conditions, recommendations for rainy day travel speed management are provided. From the figure, it can be seen the safe driving limits within different rutted sections are different. For example, for the road section K1244+250 K1245+250, when the rainfall intensity exceeds 80 mm/hour in one hour, it is no longer possible to ensure safe driving by controlling the speed. Speed control is critical for safety on slippery roads, but extreme rainfall conditions may render speed control ineffective, and additional road design measures may be required to prevent accidents. In addition, increased rut depth can significantly reduce the coefficient of adhesion, so it is recommended that rut depth be reduced and drainage design be optimized through proper road maintenance. Alternatively, high permeability pavement can be used to reduce water accumulation and improve driving safety in rainy days. In the future, the results of the study can be used in intelligent driving systems to optimize driving strategies in rainy days to provide automatic deceleration warning in rutted areas. Combined with the calculation of water film thickness, it can optimize the triggering conditions of the automatic braking system to reduce the risk of uncontrolled braking in rainy days.
5. Conclusions
Based on the rut detection and the three-dimensional shape of the rut, this paper conducts road surface water shape recognition and driving safety impact analysis, establishes a water-filled rut driving safety simulation model, and then evaluates the water rut driving safety. The main research conclusions are as follows:
- We realized the distribution calculation of the water film thickness of the whole road area of the rutted road section. According to the characteristics of pavement runoff and the three-dimensional shape of ruts, a calculation method for the water catchment process of rutted pavement based on grid division is proposed, and the pavement is divided into rutted pavement and non-rutted pavement. According to the three-dimensional shape and distribution characteristics of rutting water, the water film thickness of rutting water pavement is calculated. The water film thickness of the non-rutting water pavement is calculated, and the gridded water film thickness of the whole lane road surface under the influence of rutting is obtained.
- The length of the dangerous braking zone and the side deflection time are proposed as the driving safety evaluation indexes of water-filled ruts. The three-dimensional morphological indicators of ruts, such as rut length, width, depth, and depth difference between left and right ruts, were selected together with rainfall intensity and driving speed to establish a combination of control variable simulation conditions. According to the correlation analysis of influencing factors, the results show that the rut length, rut depth, rainfall intensity, and driving speed are strongly correlated with the braking distance, and the rut width, left and right rut depths, rainfall intensity, and driving speed are strongly correlated with the side deflection distance.
- The effects of rut length, rut depth, rainfall intensity, and driving speed on the braking distance are analyzed, and a safety evaluation model for driving in water-filled ruts is established. The influence of rut width, left and right rut depth difference, rainfall intensity, and driving speed on the side deflection distance is analyzed, and a vehicle lateral safety evaluation model for water-filled ruts is established.
- On this basis of the establishment of a waterlogged rut driving brake safety evaluation model and waterlogged rut driving side deviation safety evaluation model, the actual waterlogged rut in different sections of the road is calculated, as is the critical safe speed under different rainfall intensities, and the real-time early warning of waterlogged rut driving safety is realized. In the future, the results of the study can be used in intelligent driving systems to optimize driving strategies in rainy days, providing automatic deceleration warnings in rutted areas of pavement that are experiencing ponding.
Author Contributions
Conceptualization, Y.L. and J.Y.; methodology, Y.L.; investigation, J.Y.; writing—original draft preparation, Y.L.; writing—review and editing, Y.L. and J.Y.; funding acquisition, J.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the Fundamental Research Funds for the Central Universities, CHD, China, under Grant 300102214504, and the Natural Science Foundation of Shaanxi Province, China, under Grant 2022J0-547, and 2024JC-YBQN-0429.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Anderson, J. Depth of Rain Water on Road Surface. Highw. Transp. 1995, 5, 45–49. [Google Scholar]
- Luo, J.; Liu, J.; Wang, Y. Validation test on pavement water film depth prediction model. China J. Highw. Transp. 2015, 28, 57–63. [Google Scholar]
- Wang, Y.; Li, G.; Zhang, Z. Verification of water film depth model and highway traffic safety in rainy day. Sci. Technol. Eng. 2017, 17, 128–132. [Google Scholar]
- Li, Y.; Jiao, S.; Bao, Y. Dry and Wet State Discrimination and the Application of Water/Snow Accumulation Model on the Road Surface of Expressway. Sci. Technol. Eng. 2017, 33, 558–567. [Google Scholar]
- Ma, Y.; Geng, Y.; Chen, X.; Lu, Y. Prediction for asphalt pavement water film thickness based on artificial neural network. J. Southeast Univ. Engl. Ed. 2017, 33, 490–495. [Google Scholar]
- Brufau, P.; García-Navarro, P.; Vázquez-Cendón, M. Zero mass error using unsteady wetting–drying conditions in shallow flows over dry irregular topography. Int. J. Numer. Methods Fluids 2004, 45, 1047–1082. [Google Scholar] [CrossRef]
- Geng, Y.; Chen, X.; Chen, Y.; Ma, Y.; Huang, X. Runoff characteristics for straightline segment asphalt pavement based on two-dimensional shallow water equations. J. Traffic Transp. Eng. 2019, 19, 9–16. [Google Scholar]
- Ong, G.P.; Fwa, T. Prediction of wet-pavement skid resistance and hydroplaning potential. Transp. Res. Rec. 2007, 2005, 160–171. [Google Scholar] [CrossRef]
- Fwa, T.; Kumar, S.S.; Ong, G.P.; Huang, C. Analytical modeling of effects of rib tires on hydroplaning. Transp. Res. Rec. 2008, 2068, 109–118. [Google Scholar] [CrossRef]
- Ong, G.P.; Fwa, T. Wet-pavement hydroplaning risk and skid resistance: Modeling. J. Transp. Eng. 2007, 133, 590–598. [Google Scholar] [CrossRef]
- Fwa, T.; Ong, G.P. Wet-pavement hydroplaning risk and skid resistance: Analysis. J. Transp. Eng. 2008, 134, 182–190. [Google Scholar] [CrossRef]
- Ji, T.; Gao, Y.; Chen, R. Dynamic hydroplaning analysis of car tire. J. Traffic Transp. Eng. 2010, 10, 57–60. [Google Scholar]
- Zhang, C.; Guo, X.; Cue, B. Influence of uneven wet pavement surface condition on driving safety. J. Highw. Transp. Res. Dev. 2014, 31, 104–111. [Google Scholar]
- Min, Z.; Guo, X.; Chi, Z. Simulation analysis of rutting length based on driving safety under condition of road waterlogging. J. Syst. Simul. 2020, 27, 747–754. [Google Scholar]
- Zhu, S.; Huang, X. Numerical simulation of tire hydroplaning speed on transverse grooved concrete pavements. J. Southeast Univ. (Nat. Sci. Ed.) 2016, 46, 1296–1300. [Google Scholar]
- Wang, W. A Simulation Analysis of Pavement Skid Resistance Against Driving Safety on Curve Roads. J. Transp. Inf. Saf. 2017, 35, 32–37. [Google Scholar]
- Cao, Q. Analysis of Vehicle Stability Influenced by Skid Resistance of Asphalt Pavement. Ph.D. Thesis, Southeast University, Nanjing, China, 2018. [Google Scholar]
- Yan, J.; Li, Y.; Hui, B. Simulation analysis of rutting section unevenness with respect to vehicle driving safety. Automob. Technol. 2019, 47, 47–51. [Google Scholar]
- Ma, T.; Tang, J.; Zheng, B.; Huang, X. Adhesion Characteristics Between Vehicle Tires and Asphalt Pavement Under Rainy Conditions. J. Beijing Univ. Technol. 2022, 48, 635–643. [Google Scholar]
- Yan, J. Driving Safety Analysis Using Grid-Based Water-Filled Rut Depth Distribution. J. Saf. Environ. 2022, 22, 1759–1767. [Google Scholar] [CrossRef]
- Cai, J.; Zhao, H.; Qian, X.; Wu, M.; Qian, J. A Real-Time Correction Method for Airport Runway Water Film Thickness Distribution Prediction Using Measured Data. J. Traffic Transp. Eng. 2023, 23, 105–114. [Google Scholar]
- JTJ073.2-2001; Technical Specifications for Maintenance of Highway Asphalt Pavement. Ministry of Communications of the People Republic of China: Beijing, China, 2001.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).