A Generalized Shape Function for Vibration Suppression Analysis of Acoustic Black Hole Beams Based on Fractional Calculus Theory
Abstract
1. Introduction
2. Fundamental Theory
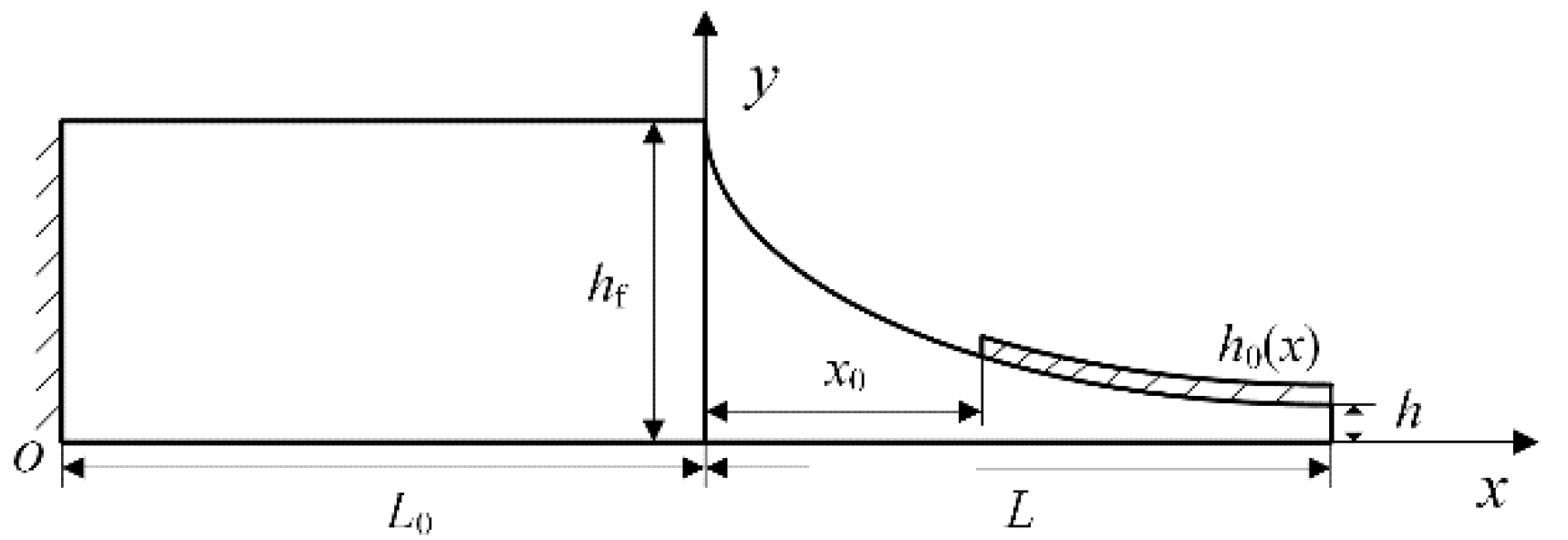
2.1. The Vibration Equation of Traditional ABH Structure
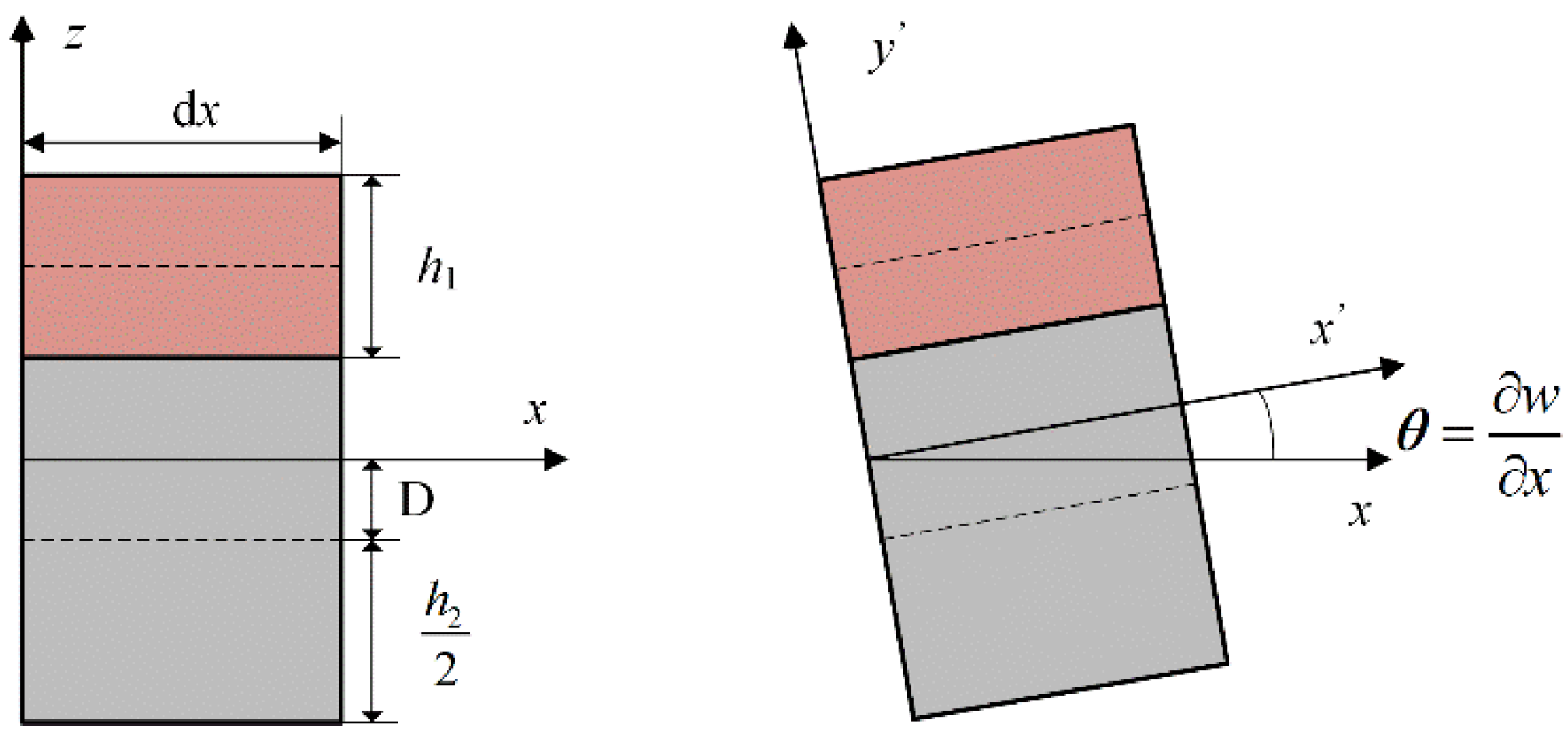
2.2. A Generalized Fractional-Order Model for Viscoelastic ABH Composite Beams
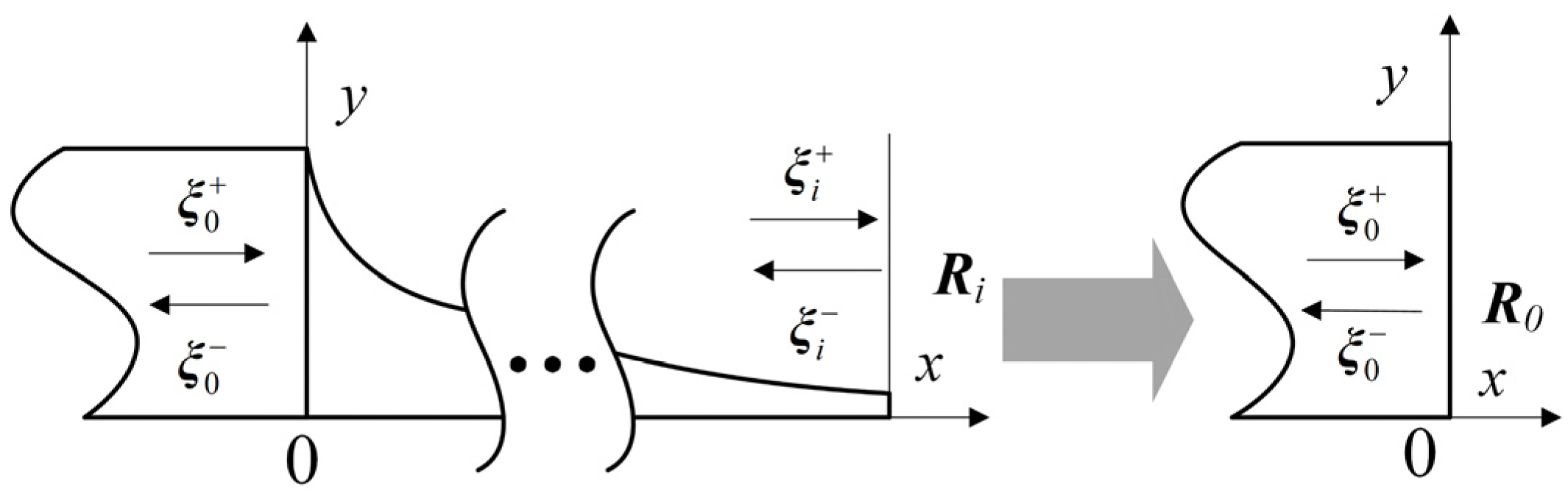
2.3. Analysis Process of the Wave Method
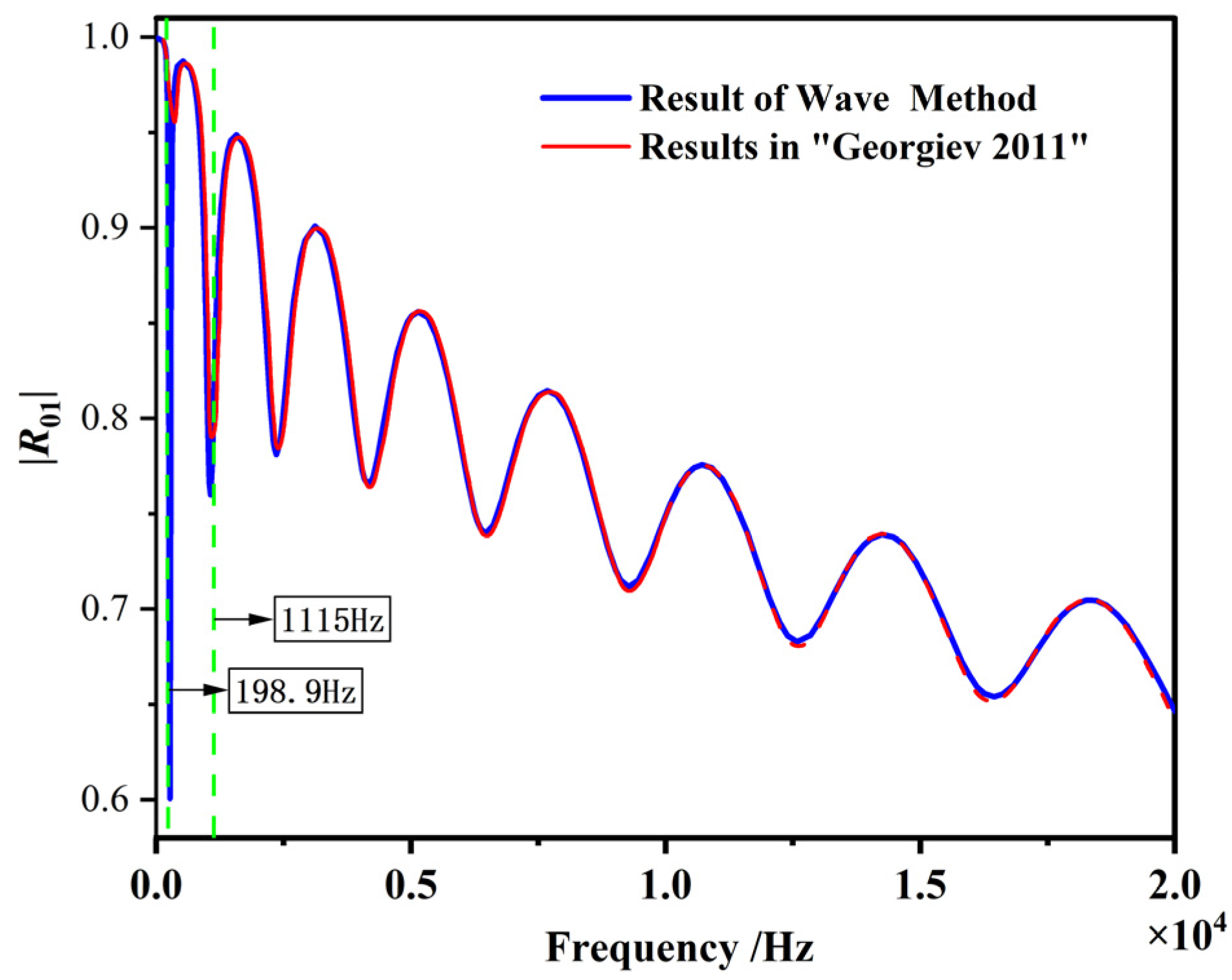
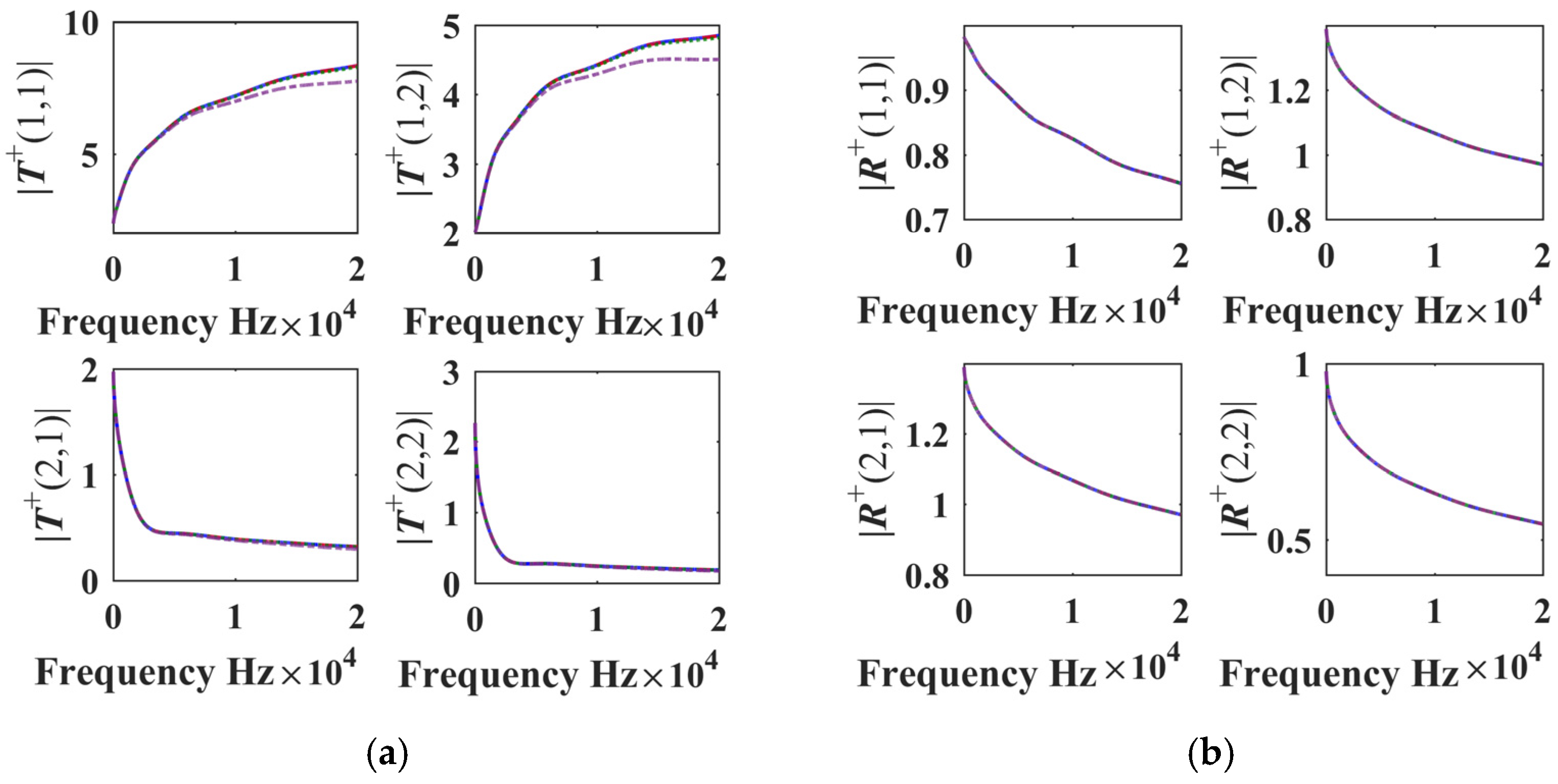
3. Validation
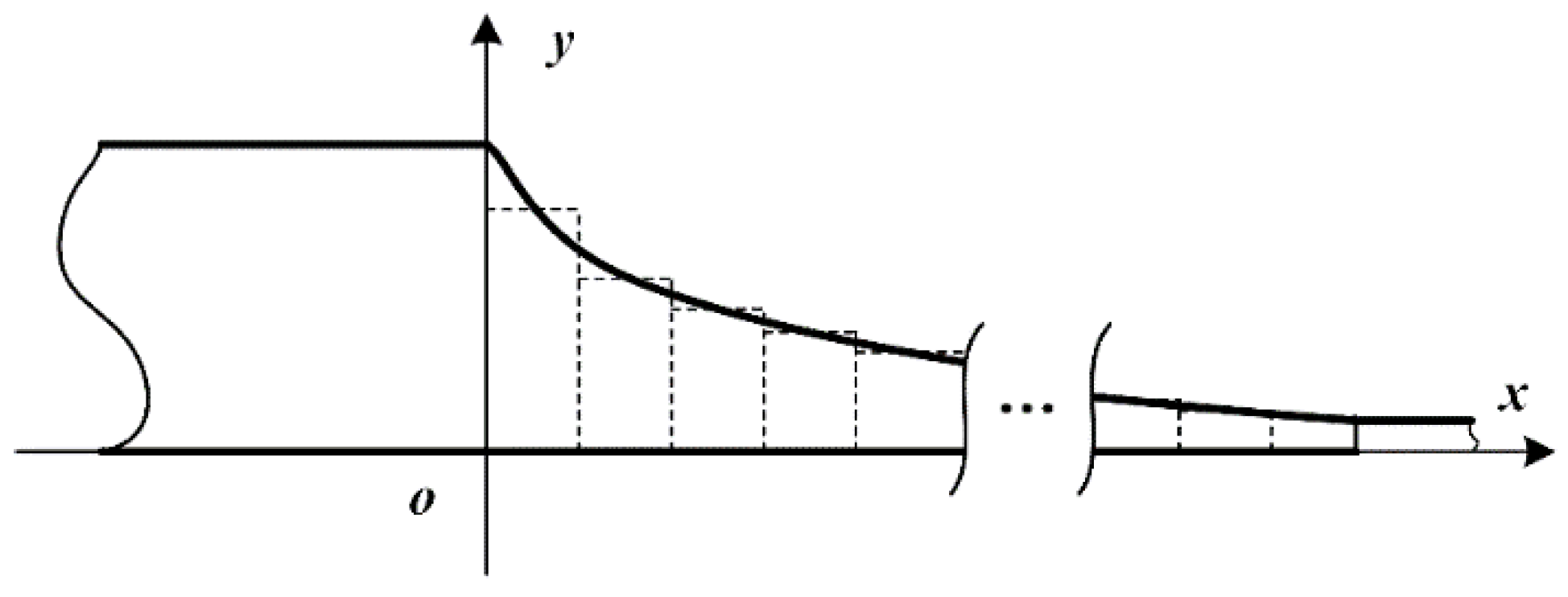
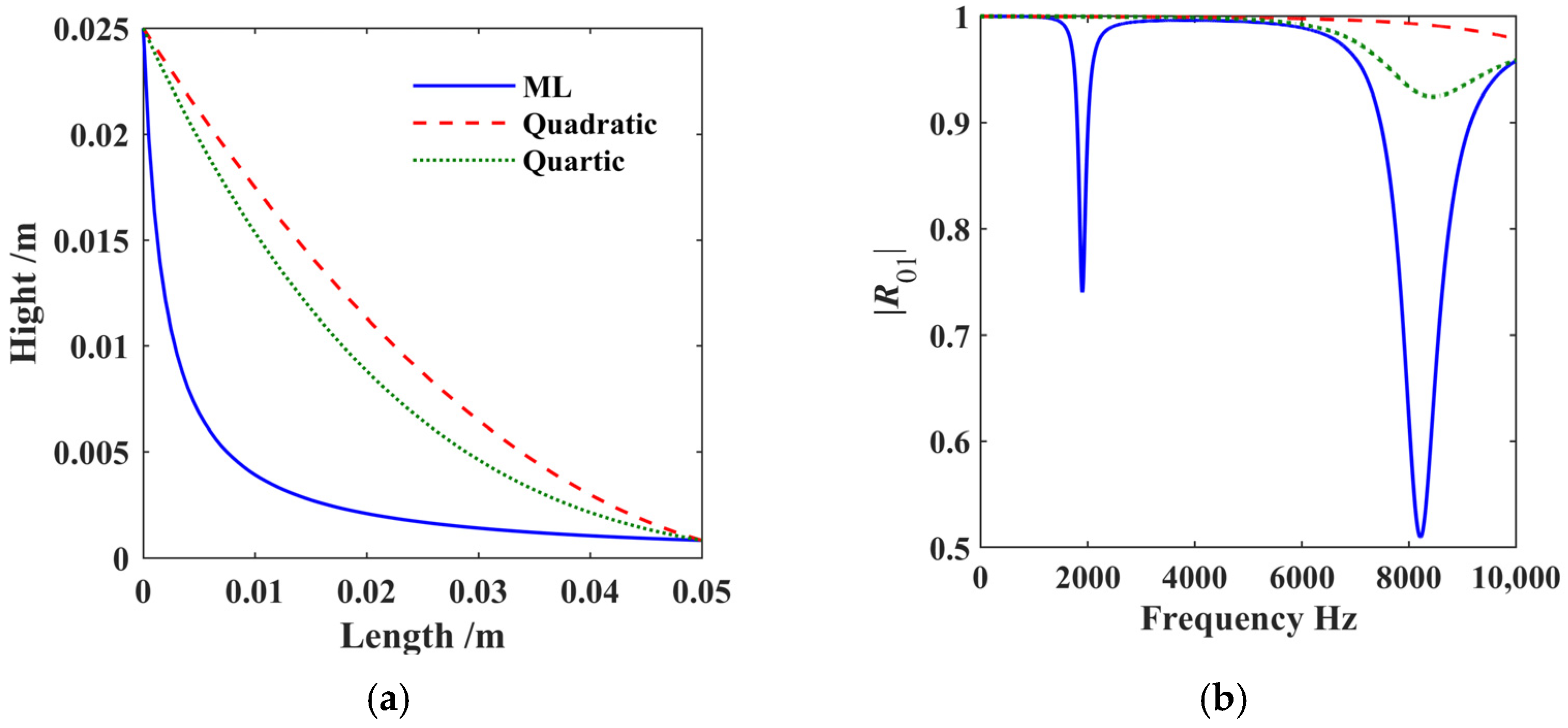
4. New Shape Function of ABH Structures
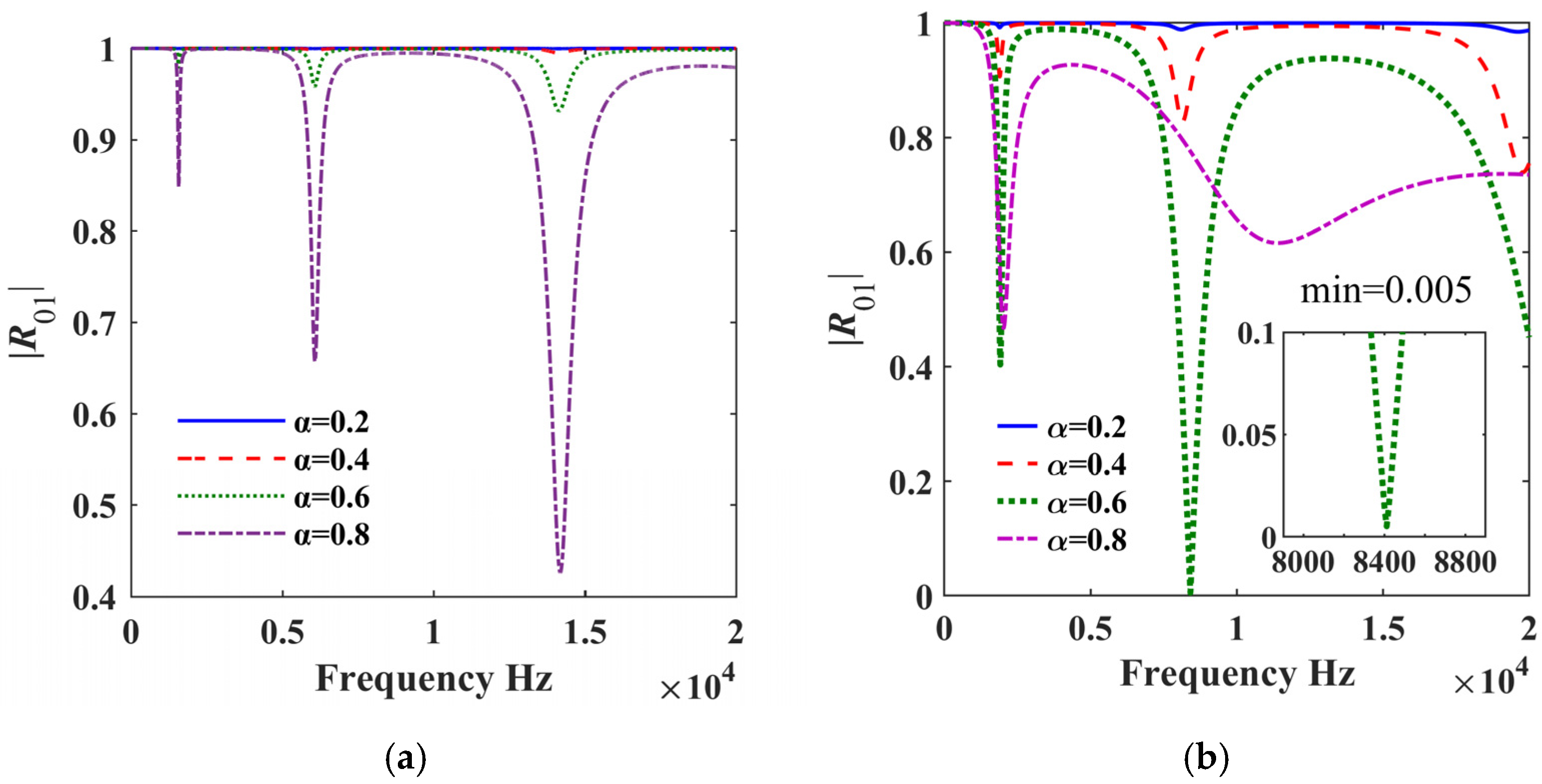
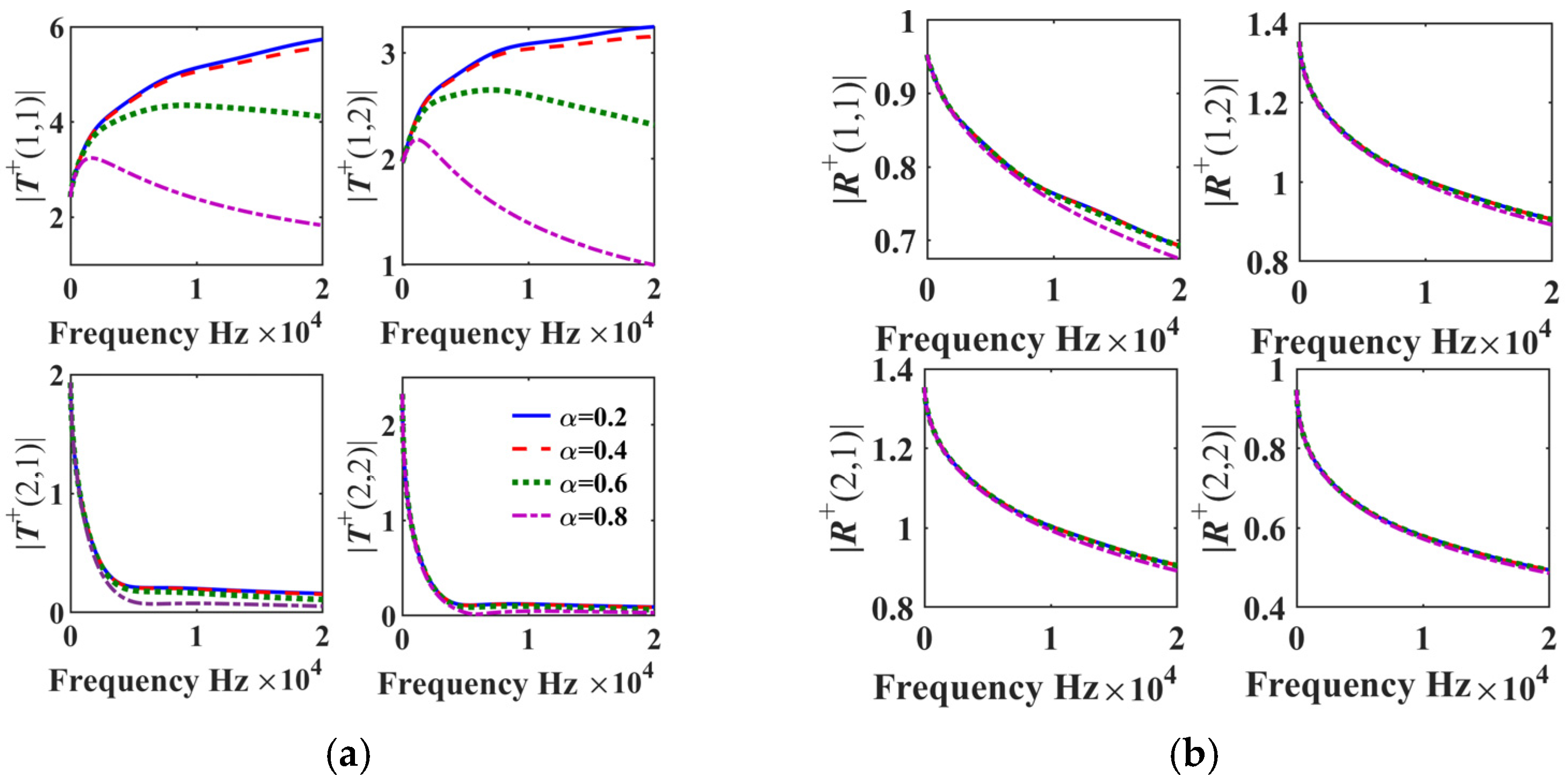
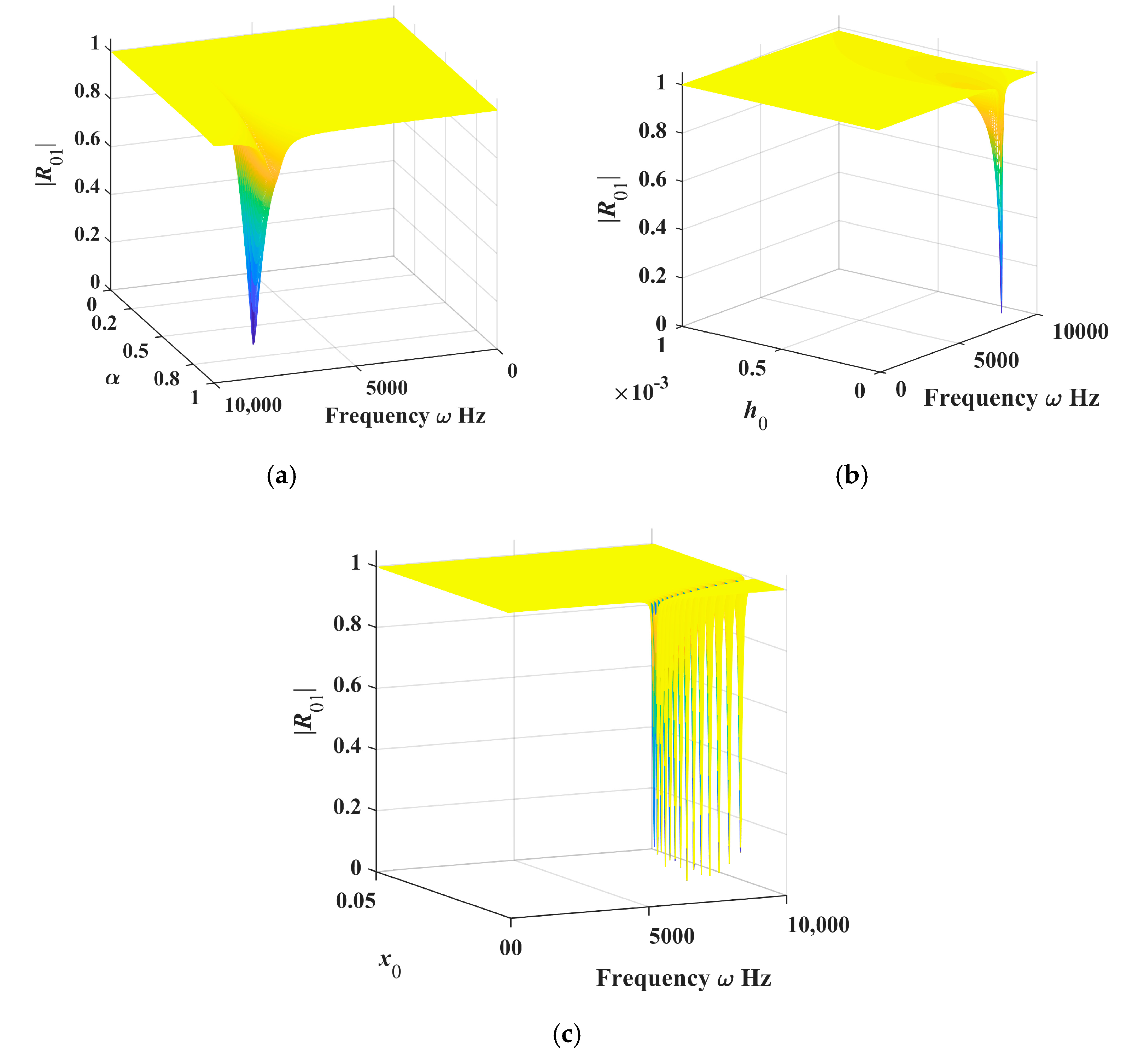
5. Results Discussion
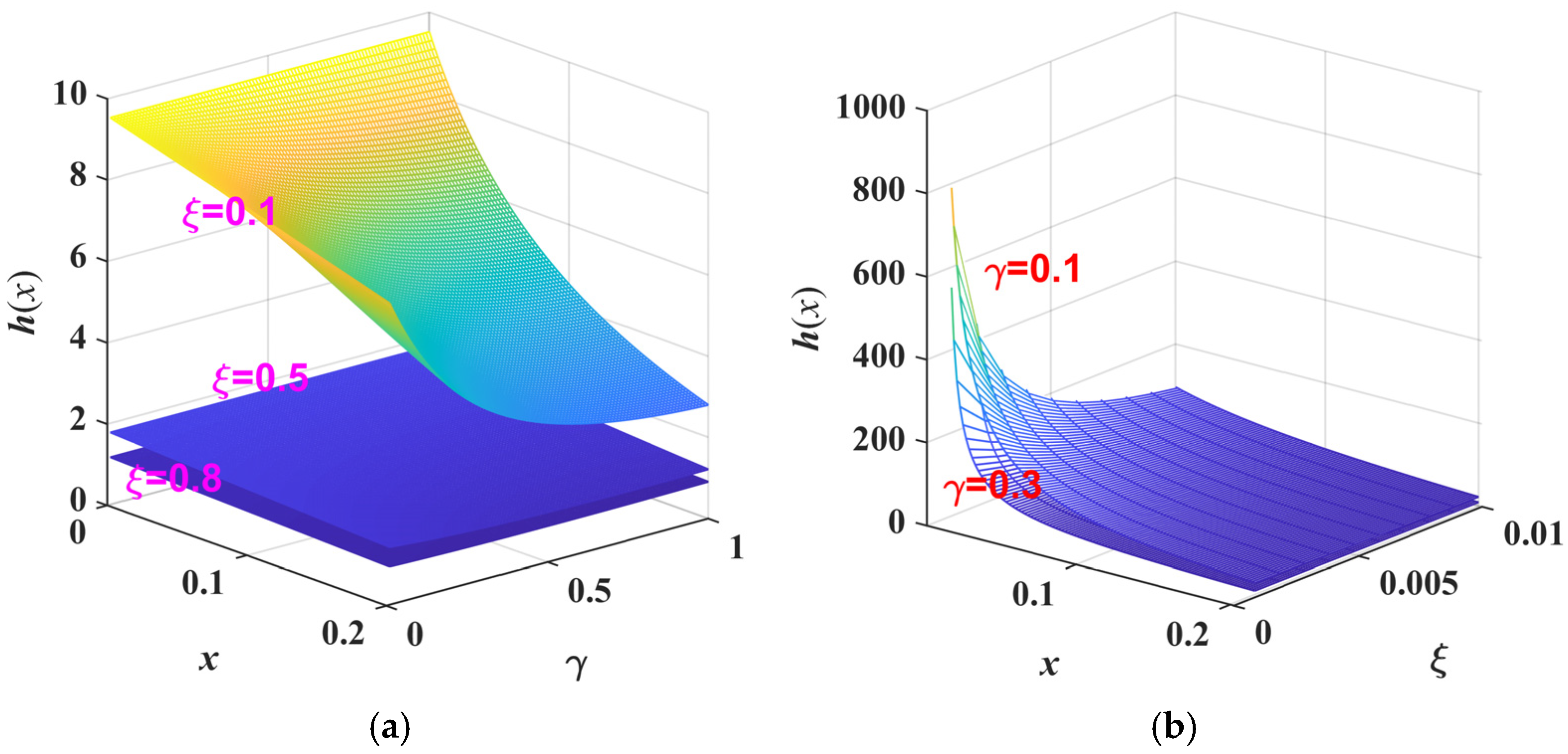
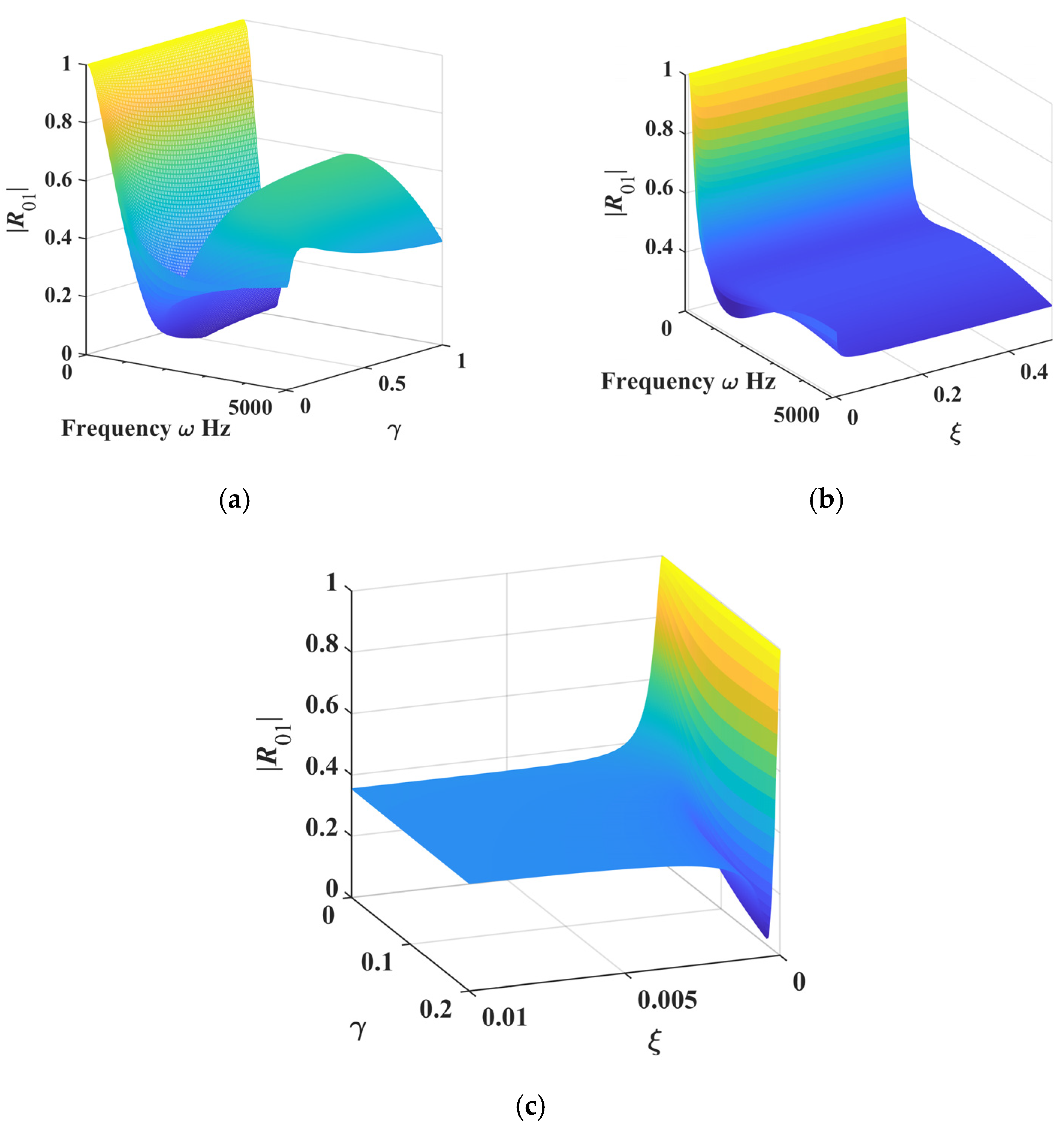
5.1. The Results and Analysis of the Fractional Model of ML-ABH Structure
5.2. Analysis of PSO Algorithm Optimization Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mironov, M.A. Propagation of a flexural wave in a plate whose thickness decreases smoothly to zero in a finite interval. Sov. Phys. Acoust. USSR 1988, 34, 318–319. [Google Scholar]
- Krylov, V.V. New type of vibration dampers utilising the effect of acoustic ‘black holes’. Acta Acust. United Acust. 2004, 90, 830–837. [Google Scholar]
- Li, X.; Ding, Q. Sound radiation of a beam with a wedge-shaped edge embedding acoustic black hole feature. J. Sound Vib. 2019, 439, 287–299. [Google Scholar] [CrossRef]
- Huang, W.; Zhang, H.; Inman, D.J.; Qiu, J.; Cesnik, C.E.; Ji, H. Low reflection effect by 3D printed functionally graded acoustic black holes. J. Sound Vib. 2019, 450, 96–108. [Google Scholar] [CrossRef]
- Li, X.; Ding, Q. Analysis on vibration energy concentration of the one-dimensional wedge-shaped acoustic black hole structure. J. Intell. Mater. Syst. Struct. 2018, 29, 2137–2148. [Google Scholar] [CrossRef]
- Ji, H.; Liang, Y.; Qiu, J.; Cheng, L.; Wu, Y. Enhancement of vibration based energy harvesting using compound acoustic black holes. Mech. Syst. Signal Process. 2019, 132, 441–456. [Google Scholar] [CrossRef]
- Deng, J.; Guasch, O.; Zheng, L.; Song, T.; Cao, Y. Semi-analytical model of an acoustic black hole piezoelectric bimorph cantilever for energy harvesting. J. Sound Vib. 2021, 494, 115790. [Google Scholar] [CrossRef]
- Zhang, L.; Kerschen, G.; Cheng, L. Electromechanical coupling and energy conversion in a PZT-coated acoustic black hole beam. Int. J. Appl. Mech. 2020, 12, 2050095. [Google Scholar] [CrossRef]
- Li, H.; Doaré, O.; Touzé, C.; Pelat, A.; Gautier, F. Energy harvesting efficiency of unimorph piezoelectric acoustic black hole cantilever shunted by resistive and inductive circuits. Int. J. Solids Struct. 2022, 238, 111409. [Google Scholar] [CrossRef]
- Park, S.; Jeon, W. Concave-shaped acoustic black holes with asymmetric arrangement for suppression and amplification of structural vibration. J. Sound Vib. 2025, 600, 118885. [Google Scholar] [CrossRef]
- Yang, M.; Chen, C.; Wei, L.; Chen, X.; Sun, X.; Fu, H. Semi-analytical model and vibrational energy recovery efficiency of piezoelectric beams with quasi-periodic additional acoustic black holes. Appl. Phys. A 2024, 130, 928. [Google Scholar] [CrossRef]
- Wang, Y.; Du, J.; Cheng, L. Power flow and structural intensity analyses of acoustic black hole beams. Mech. Syst. Signal Process. 2019, 131, 538–553. [Google Scholar] [CrossRef]
- Deng, J.; Zheng, L.; Zeng, P.; Zuo, Y.; Guasch, O. Passive constrained viscoelastic layers to improve the efficiency of truncated acoustic black holes in beams. Mech. Syst. Signal Process. 2019, 118, 461–476. [Google Scholar] [CrossRef]
- McCormick, C.A.; Shepherd, M.R. Optimization of an acoustic black hole vibration absorber at the end of a cantilever beam. J. Acoust. Soc. Am. 2019, 145, EL593–EL597. [Google Scholar] [CrossRef]
- Deng, J.; Guasch, O.; Zheng, L. A semi-analytical method for characterizing vibrations in circular beams with embedded acoustic black holes. J. Sound Vib. 2020, 476, 115307. [Google Scholar] [CrossRef]
- Cao, S.; Lee, H.P.; Lim, K.M. Estimation of Wave Reflection Coefficient by Semi-Analytical Method in an Acoustic Black Hole Beam. Int. J. Appl. Mech. 2020, 12, 2050004. [Google Scholar] [CrossRef]
- He, M.-X.; Ding, Q. Data-driven optimization of the periodic beam with multiple acoustic black holes. J. Sound Vib. 2021, 493, 115816. [Google Scholar] [CrossRef]
- Li, P.; Biwa, S. Flexural waves in a periodic non-uniform Euler-Bernoulli beam: Analysis for arbitrary contour profiles and applications to wave control. Int. J. Mech. Sci. 2020, 188, 105948. [Google Scholar] [CrossRef]
- Li, W.; Wen, H.; Guo, J. A multiscale Gaussian expansion method for low-frequency multimodal damping analysis of variable stiffness acoustic black hole beams. Thin-Walled Struct. 2025, 206, 112619. [Google Scholar] [CrossRef]
- Gao, N.; Wei, Z.; Hou, H.; Krushynska, A.O. Design and experimental investigation of V-folded beams with acoustic black hole indentations. J. Acoust. Soc. Am. 2019, 145, EL79–EL83. [Google Scholar] [CrossRef]
- Li, H.; Touzé, C.; Pelat, A.; Gautier, F. Combining nonlinear vibration absorbers and the Acoustic Black Hole for passive broadband flexural vibration mitigation. Int. J. Non-Linear Mech. 2021, 129, 103558. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, K.; Zhou, S.; Wei, Z. An ultralight phononic beam with a broad low-frequency band gap using the complex lattice of acoustic black holes. Appl. Phys. Express 2019, 12, 077002. [Google Scholar] [CrossRef]
- Gao, N.; Wei, Z.; Zhang, R.; Hou, H. Low-frequency elastic wave attenuation in a composite acoustic black hole beam. Appl. Acoust. 2019, 154, 68–76. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, K.; Cheng, Y.; Wei, Z. Lightweight-high-stiffness vibration insulator with ultra-broad band using graded double-leaf acoustic black holes. Appl. Phys. Express 2020, 13, 17007. [Google Scholar] [CrossRef]
- Park, S.; Kim, M.; Jeon, W. Experimental validation of vibration damping using an Archimedean spiral acoustic black hole. J. Sound Vib. 2019, 459, 114838. [Google Scholar] [CrossRef]
- Kim, S.-Y.; Lee, D. Numerical simulation of characteristics of wave propagation and reflection coefficient in a helix-acoustic black hole. J. Vib. Control 2020, 28, 615–625. [Google Scholar] [CrossRef]
- Xu, J.; Chen, Y.; Tai, Y.; Xu, X.; Shi, G.; Chen, N. Vibration analysis of complex fractional viscoelastic beam structures by the wave method. Int. J. Mech. Sci. 2020, 167, 105204. [Google Scholar] [CrossRef]
- Xu, J.; Chen, Y.; Tai, Y.; Shi, G.; Chen, N. Vibration analysis of sandwich beams with viscoelastic coating described by fractional constitutive equation. Mech. Adv. Mater. Struct. 2022, 29, 429–439. [Google Scholar] [CrossRef]
- Oskouie, M.F.; Ansari, R. Linear and nonlinear vibrations of fractional viscoelastic Timoshenko nanobeams considering surface energy effects. Appl. Math. Model. 2017, 43, 337–350. [Google Scholar] [CrossRef]
- Hollkamp, J.P.; Semperlotti, F. Application of fractional order operators to the simulation of ducts with acoustic black hole terminations. J. Sound Vib. 2020, 465, 115035. [Google Scholar] [CrossRef]
- Georgiev, V.; Cuenca, J.; Gautier, F.; Simon, L.; Krylov, V.V. Damping of structural vibrations in beams and elliptical plates using the acoustic black hole effect. J. Sound Vib. 2011, 330, 2497–2508. [Google Scholar] [CrossRef]



| Geometrical Characteristics | Characteristics of Material |
|---|---|
| L = 0.05 m h = 0.0015 m | Beam |
| E1 = 210 Gpa | |
| b = 0.0015 m m = 4 | Absorbing film |
| E2 = 0.5 Gpa | |
| Thickness of Film | α | Length of Film | ML Parameters | Fitness Value | ||
|---|---|---|---|---|---|---|
| h0 | ξ | γ | a | |||
| 0.01 mm | 0.2 | 0.8 L | 0.5886 | 0.6468 | 2.7745 × 10−5 | 0.4845 |
| 0.5 L | 0.6556 | 0.6830 | 1.1889 × 10−4 | 0.9638 | ||
| 0.2 L | 0.6562 | 0.6827 | 7.7302 × 10−6 | 0.11 | ||
| 0.8 | 0.8 L | 0.5694 | 0.4231 | 0.0012 | 0.0086 | |
| 0.5 L | 0.6512 | 0.4369 | 6.2344 × 10−4 | 0.4313 | ||
| 0.2 L | 0.6529 | 0.4184 | 5.2108 × 10−5 | 0.9066 | ||
| 0.7 mm | 0.2 | 0.8 L | 0.7765 | 0.4625 | 0.0003 | 0.0605 |
| 0.5 L | 0.7765 | 0.4625 | 0.0003 | 0.0640 | ||
| 0.2 L | 0.7462 | 0.3927 | 0.0001 | 0.9494 | ||
| 0.8 | 0.8 L | 0.8564 | 0.4014 | 0.0012 | 0.9752 | |
| 0.5 L | 0.8759 | 0.3678 | 0.0006 | 0.9944 | ||
| 0.2 L | 0.8658 | 0.4034 | 0.0009 | 0.999 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, J.; Chen, N. A Generalized Shape Function for Vibration Suppression Analysis of Acoustic Black Hole Beams Based on Fractional Calculus Theory. Appl. Sci. 2025, 15, 2768. https://doi.org/10.3390/app15052768
Xu J, Chen N. A Generalized Shape Function for Vibration Suppression Analysis of Acoustic Black Hole Beams Based on Fractional Calculus Theory. Applied Sciences. 2025; 15(5):2768. https://doi.org/10.3390/app15052768
Chicago/Turabian StyleXu, Jun, and Ning Chen. 2025. "A Generalized Shape Function for Vibration Suppression Analysis of Acoustic Black Hole Beams Based on Fractional Calculus Theory" Applied Sciences 15, no. 5: 2768. https://doi.org/10.3390/app15052768
APA StyleXu, J., & Chen, N. (2025). A Generalized Shape Function for Vibration Suppression Analysis of Acoustic Black Hole Beams Based on Fractional Calculus Theory. Applied Sciences, 15(5), 2768. https://doi.org/10.3390/app15052768






