Abstract
Nano-structures play a crucial role in advancing technology due to their unique properties and applications in various fields. This study examines the forced vibration behavior of an orthotropic nano-system consisting of an elastically connected nanoplate and a doubly curved shallow nano-shell. Both nano-elements are simply supported and embedded in a Winkler-type elastic medium. Utilizing the Eringen constitutive elastic relation, Kirchhoff–Love plate theory, and Novozhilov’s linear shallow shell theory, we derive a system of four coupled nonhomogeneous partial differential equations (PDEs) describing the forced transverse vibrations of the system. We perform forced vibration analysis using modal analysis. The developed model is a novel approach that has not been extensively researched by other authors. Therefore, we provide insights into the nano-system of an elastically connected nanoplate and a doubly curved shallow nano-shell, offering a detailed analytical and numerical analysis of the PDEs describing transverse oscillations. This includes a clear insight into natural frequency analysis and the effects of the nonlocal parameter. Additionally, damping proportional coefficients and external excitation significantly influence the transverse displacements of both the nanoplate and nano-shell. The proposed mathematical model of the ECSNPS aids in developing new nano-sensors that respond to transverse vibrations based on the geometry of the nano-shell element. These sensors are often used to adapt to curved surfaces in medical practice and gas sensing.
1. Introduction
Developing a suitable mathematical model is crucial to obtain the accurate response for the sandwich nano-structures. Generally, an appropriate type of coupling layer is responsible for the stiffness of the sandwich nano-system. For this reason, this study aims to demonstrate how geometric and material parameters can affect the stiffness of nano-systems by analyzing the amplitude values of forced vibrations of nano-systems. In recent years, nonlocal elastic theory has attracted much attention because of the necessity for modeling and analyzing very small mechanical structures in the development of nanotechnologies [1,2]. It is known that the size effect of nano-structures is important for their mechanical behavior because their dimensions are small and comparable to molecular distances. There are various higher-order continuum theories involving material length scale parameters. Among them are strain gradient elasticity theory [3] and nonlocal theory [4,5,6]. In these theories, the phenomenon known as material size effects arises because internal material properties, such as inhomogeneity and interatomic interactions, significantly influence elastic behaviors. Due to the expanding applications of nano-sized structures, this consideration has gained increasing interest in fields such as sandwich nano-structures, which have been widely used in various applications in aerospace, biomedicine, and mechanical and civil engineering [7,8]. Many researchers have shown that the advantage of these structures is their high strength and stiffness-to-weight ratios [9,10,11,12]. The mechanical and geometrical properties of the nano-sandwich system significantly influence the system’s behavior [13,14,15,16]. For this reason, this study aims to show how the stiffness of the system would change if one element (a nanoplate) in the nano-system were replaced with another corresponding element of the same surface area, only with a radius of curvature (nano-shell). Additionally, researchers have previously questioned the effect of curvature upon the vibration frequencies of rectangular shallow shells [17]. Open shallow shells have large radii of curvatures compared to other shell parameters. A shallow shell can be doubly curved, and more applications can be found in engineering practice. Bhimaraddi [18] investigated the free vibration analysis of homogeneous and laminated doubly curved shells on a rectangular planform using three-dimensional elasticity equations. In a paper by Dereli, E. et al. [19], an extensive investigation into the deformation, shear, and normal stress values of sandwich structures with lattice cores of varying aspect ratios is presented. Their findings suggest potential for optimization in lightweight structures, which could lead to innovative advancements in design and manufacturing processes within the aerospace and automotive sectors. The nonlocal electro-elastic bending analysis of a doubly curved nano-shell was studied in a paper by Arefi [20] based on nonlocal elasticity theory and first-order shear deformation theory. In a paper by Karami and Shahsavari [21], the forced resonate vibration of nano-shells, which included four different geometries of shells—spherical, elliptical, hyperbolic, and cylindrical—was studied. The comprehensive free vibration analysis of doubly curved shallow shells, which are made of an orthotropic material, was presented in a paper by Ghavanloo and Fazelzadeh [22]. In a paper by Hosseini-Hashemi et al. [23], the influences of changing geometrical parameters and scale parameters on the natural frequency of the micro-/nano-spherical shell based on first-order shear deformation theory were investigated. The increased use of orthotropic shells in the design of various devices, including their mechanical behavior, has attracted the attention of many researchers. As fundamental elements, shells are used in many fields of modern engineering technologies because they provide dynamic stability. A study by Turan, F. et al. [24] deals with the free vibration and buckling responses of porous orthotropic doubly curved shallow shells subjected to edge compressions that are non-uniformly distributed. In this paper, parametric studies were developed to discuss the influence of various factors, such as different porosity coefficients, aspect ratios, arc length-to-thickness ratios, radius-to-arc length ratios, orthotropy ratios, and shell types, on the free vibration and buckling behavior of porous orthotropic doubly curved shallow shells. The free vibration of composite sandwich plates and cylindrical shells, composed of two composite laminated faces and an ideally orthotropic elastic core, was considered by Hwu [25]. Based on several different numerical mathematical methods, the natural frequencies of composite sandwich plates and cylindrical shells [25] were obtained. It was shown that the values of the natural frequencies of such a system agree well with each other.
In the present study, the authors analyze in detail a nano-system composed of an elastically connected nanoplate and nano-shell. The nanoplate and the doubly curved shallow nano-shell are made of orthotropic materials. Both nano-elements (the plate and shell) are simply supported and connected by an elastic layer, which is approximated by the Winkler model of discretely distributed springs of linear stiffness, , acting on the surface of the nanoplate and nano-shell. In this paper, the forced vibration analysis was conducted for an elastically connected system composed of a nanoplate and nano-shell (ECSNPS). Based on Eringen’s constitutive elastic relation, Kirchhoff–Love plate theory [26,27,28], and Novozhilov’s linear shallow shell theory [29], a system of four coupled nonhomogeneous PDEs for the transverse vibrations of an ECSNPS was derived. The forced transverse vibration analysis was solved by modal analysis. The effect of the nonlocal parameter on the values of the amplitudes of the forced vibration of the ECSNPS is presented. Additionally, the effects of external excitations, damping proportional coefficients, and radius curvatures of nano-shell on the ECSNPS are analyzed in detail. We rigorously examine the effects of nano-shell curvature on nano-systems, with a particular focus on its role in reducing the amplitude of transverse vibrations in the upper nanoplate. The advanced mathematical model of the sandwich nano-structure proposed here holds significant promise for the dynamic analysis of nano-sensors. These applications leverage the unique geometry of the nano-shell element to precisely tune and optimize transverse responses, thereby driving significant advancements in the field of nanotechnology.
The model developed in this paper is not sufficiently researched by other authors. For this reason, the authors provide insights into the nano-system of an elastically connected nanoplate and a doubly curved shallow nano-shell and give a detailed analysis of the solution of partial differential equations describing transverse oscillations. It also provides clear insight into natural frequency analysis and how the nonlocal parameter affects them. Also, the analysis of the impact of changing the radius of curvature of the lower element (nano-shell) in this model yields significant results.
2. Brief Review of Eringen’s Constitutive Elasticity
It is known that the effect of nano-structures’ size is important for their mechanical behavior because their dimensions are small and comparable to molecular distances. There are various higher-order continuum theories involving material length scale parameters. Among them are a couple of stress elasticity theories, such as those by Koiter [30], Toupin [31], and Mindlin and Tiersten [32], strain gradient elasticity theory by Lam et al. [3], and Eringen’s nonlocal theory [4,5,6]. All these theories provide extensions of the classical equations of elasticity with additional higher-order strain gradient terms based on the assumption that the materials cannot be modeled as collections of points, but they have to be considered as atoms with a higher-order deformation mechanism at the micro- or nano-scale. Nonlocal strain gradient theory uses two independent short length scale parameters. Unlike the nonlocal elasticity theory that will be used in this paper, nonlocal strain gradient theory takes into account both the interatomic forces and higher-order microstructure deformation mechanism. This work provides an opportunity for the same model to be used by applying multiple methods.
It is worth noting that the state of stress and strain depends on the external load, the shape of the profile, and the type of material, but the relationship between them is directly linearly proportional under conditions of ideal elasticity at stresses below the elastic limit. According to Eringen’s nonlocal elasticity theory [4,5,6], the state of stress at some point in the domain is defined as a function of the state of strain not only at that point but as a function of the state of strain at all points in the observed domain. This assumption accounts for long-range intermolecular interactions and leads to a size-dependent theory of elasticity, which aligns well with the atomic theory of lattice dynamics.
Using the fundamental equations of the nonlocal elasticity theory from papers written by Eringen and co-workers [4,5,6], Eringen’s constitutive elastic relation from the stress and strain is given as
where is the nonlocal parameter, describes the internal characteristic length, and is a constant corresponding to each material that can be identified from atomistic simulations or by using the dispersive curve of the Born–Karman model of lattice dynamics. is the elastic modulus tensor for classical isotropic elasticity, and and are the stress and strain tensors, respectively.
Using Equation (1), the constitutive relations can be written for one-dimensional structures in the following forms:
where is Young’s modulus of elasticity and is the shear modulus.
By applying relation (1), the constitutive relation for orthotropic two-dimensional nano-structures can be expressed as follows:
where is the Laplacian, and denote Poisson’s ratios (), , and are the normal and shear stresses, , , and are the normal and shear strains, and is the shear modulus. The internal characteristic lengths, , are often assumed to be in the range 0–3 [nm], and Poisson’s ratio is in the range 0–0.5. When the nonlocal constitutive relation is reduced to the classical constitutive relation of the elastic body.
The nonlocal parameter describes the internal characteristic length, and is a constant corresponding to each material that can be identified from atomistic simulations or by using the dispersive curve of the Born–Karman model of lattice dynamics. Also, nonlocality refers to the effects on the measurement of two particles characterized by quantum entanglement. There are only a few laboratories equipped with the expensive and demanding apparatus required for this quantum-level experiment. Therefore, we had to take values that had already been used by many authors before us. For this purpose, we used the nonlocal parameter range 0–3 specified in these references [33,34,35]. Our model in the numerical code allows for the use of different parameter ranges. The corresponding author can provide the Mathematica numerical code upon reasonable request, allowing for the input of any other material and geometric characteristics of the system. The requirement would be to cite our work so that the results can be compared with other experimentally applied models.
3. Mathematical Formulations of the Equations of Motion for an Orthotropic Nanoplate
Based on Kirchhoff’s plate theory [26,27], the displacement components, , and , for an arbitrary point on the middle plane of the nanoplate along the x, y, and z axes can be written in the following forms:
The strain–displacement relations for linear strain theory are
The nonlocal constitutive relation between the stress and strain of one orthotropic nanoplate, as expressed in the form of (4), based on nonlocal stresses, ,, and , can be written as follows:
Based on Newton’s second law for the infinitesimal element of the nanoplate, equilibrium equations can be obtained in the following form:
where , and are the in-plane stress variables, and , and are the moment variables, defined as
and is the external force caused by the transverse force f:
Using expression (6), (13) and (14) and taking into account Equations (7)–(9) yields
and
where are extensional and are the bending stiffnesses of the orthotropic elastic nanoplate, expressed as
By using Equations (10)–(12), (16)–(18) and (19)–(21), the PDEs describing the displacements in the xOy plane and the transverse displacement in the z-axis direction of a nanoplate subjected to an external load, f(x,y,t), have the forms
4. Mathematical Formulation of the Equations of Motion for an Orthotropic Doubly Curved Shallow Nano-Shell
According to Novozhilov’s linear shell theory presented by Amabili [29], the strain components at an arbitrary point in the panel are related to the middle surface strains, , , and , and changes in the curvature and torsion of the middle surface, , , and which are defined by the following relationships:
where
The nonlocal constitutive relation between stress and strain is defined by expression (4). For the nano-shell, the constitutive relation between stress and strain can be written in the following form:
From Equation (33), the nonlocal stresses are written in the following forms:
Integrating Equations (34)–(36) and taking into account expressions (13) and (14) yields
and
The extensional and bending stiffnesses are expressed by expressions (22) and (23).
According to Novozhilov’s linear shell theory presented by Amabili [29], the equilibrium equations of the orthotropic doubly curved shallow shell can be written in the following form:
The displacements in the xOy plane and the transverse displacement in the z-axis direction of a nano-shell have the following forms:
In all three presented Equations (46)–(48), the displacement is denoted as w. For this reason, all equations must be taken into account to describe the vibration analysis of an orthotropic doubly curved shallow nano-shell. In a paper by Ghavanloo E. et al. [22], PDEs of the orthotropic doubly curved shallow shell based on the gradient elasticity were presented.
5. Formulation of Model ECSNPS
We perform a detailed analysis for the nano-system shown in Figure 1, which is composed of an elastically connected nanoplate and nano-shell (ECSNPS). The nanoplate and the doubly curved shallow nano-shell are made of orthotropic materials. Both nano-elements (the plate and shell) are simply supported and connected by an elastic layer, which is approximated by the Winkler model of discretely distributed springs of linear stiffness , which act on the surface of the nanoplate and nano-shell. The material characteristics of the nano-shell are the same as those of the nanoplate, with the same elastic modulus , Poison coefficients , shear modulus and mass density . The geometrical characteristics, namely the length , width , and thickness , are the same for the nanoplate and nano-shell, where, for the shell, and are the principal radii of curvature. We assume that the transversal displacement of the nanoplate is ; the displacement of the nano-shell is in direction x and in direction y; and the transversal displacement of the nano-shell in direction z is .
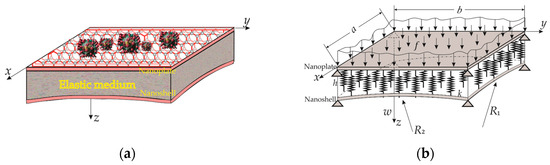
Figure 1.
The double graphene nano-system is composed of a nanoplate and a nano-shell and coupled by a Winkler-type elastic layer: (a) physical model; (b) mechanical model.
The material properties in Table 1 were taken from a study by Pouresmaeeli et al. [33]. The value for the stiffness coefficient k was obtained from a paper by Radić et al. [36].

Table 1.
Material and geometrical properties for nanoplate and doubly curved shallow nano-shell.
If we use the PDEs of transverse oscillations ((26) and (46)–(48)) and if we take into account the elastic layer connecting the nanoplate and the nano-shell via the displacement of the ends of the springs, , (where 1 denotes the nanoplate and 2 denotes the nano-shell), we obtain the PDEs of the coupled system, which represent the small transverse displacements of the mid-plane of the nanoplate and nano-shell in the following forms:
The transverse displacements of the midplane of the nanoplate are described by in Equation (49). In Equations (50)–(52), it can be observed that the displacement components in all three directions, , and appear. Therefore, all equations must be considered when describing the small transverse oscillations of an orthotropic doubly curved shallow nano-shell. The mathematical analysis was conducted using the Cartesian coordinate reference system.
The boundary conditions of a simply supported nanoplate and nano-shell, of length a and width b, are
where i = 1 denotes a nanoplate, while i = 2 denotes a double-curved shallow nano-shell.
In this paper, Eringen’s method in differential form is used. The application of different boundary conditions using Eringen’s method in differential form would not allow us to obtain the accuracy of the results of this presented model. The results are valid and coincide only with the simply supported boundary conditions when using both forms of Eringen’s equation (integral and differential) [37,38,39]. Eringen’s constitutive relation in integral form should be applied to other boundary conditions in future publications, and it is worthwhile to compare the results with those from the paper [40]. For this reason, due to the detailed methodology presented in this paper, using Eringen’s differential form, only simply supported boundary conditions of the system are considered.
6. Solution Methodology for Determining the Natural Frequencies of the ECSNPS
Governing Equations (49)–(52) can be solved by assuming displacements in the following forms:
where , m = 1,2,3,…; n = 1,2,3,….
Unknown time functions are marked by and .
By substituting the assumed solutions (56)–(59) into Equations (49)–(52) and applying the orthogonality conditions, a system of ordinary differential equations (ODEs) of free vibrations is obtained in the following form:
where are the mass and extensional and bending stiffness constants presented in Appendix A.
Taking into account the presented differential Equations (49)–(52), the ODEs (60)–(63) of the time modes of the transverse oscillations that describe the free vibration of the undamped observed ECSNPS have the following matrix form:
or for a more concise form, see Kelly [41]:
where
The free vibrations of the ECSNPS described by Equation (65) are periodic. Thus, when free vibrations at a single frequency are initiated for a particular system, the ratio of any two dependent variables is independent of time. These assumptions lead to hypothesizing the normal-mode solution of Equation (65) in the form
where is the m-dimensional vector of constants (according to mode shapes) and represents the natural frequencies of the ECSNPS.
Substituting Equation (68) into Equation (65) gives
Since is valid for any real value of time t,
The mass matrix is nonsingular, and thus exists. Multiplying Equation (70) by and rearranging gives
where is the identity matrix. Thus, the trivial solution is obtained unless
By solving the determinant (72) for the unknown , using Kelly’s study [41] and the programming language Wolfram Mathematica 9.0, four natural frequencies were obtained for each pair (m, n) and for the chosen set of parameters presented in part of natural frequency analysis. These four natural frequencies correspond to four different vibration modes.
7. Forced Vibration of the Damped ECSNPS
In this section, the forced vibrations of the damped system for the considered nano-system are analyzed. Damping is implemented using the assumption of Rayleigh-type proportional damping, defined by the coefficients α and β. Specifically, the damping matrix is a linear combination of the mass matrix βM and the stiffness matrix αK; see Kelly’s study [41].
Considering the PDEs of the nanoplate (49) and nano-shell (50)–(52), the PDEs for the time modes of the transverse vibrations, which describe the forced vibrations of the damped ECSNPS, can be presented in the following matrix form, as shown in Kelly’s study [41]:
where M, K, and are presented in expressions ((66) and (67)) and
To determine the forced vibration response of the presented system (73), the standard procedure of modal analysis was used based on the principal coordinates from Kelly [41]. For the natural frequencies, obtained from expression (72), the matrix P presents the system’s modal matrix, a matrix whose columns are normalized mode shapes:
The system of n-differential equations corresponding to the generalized coordinates can be transformed into a system with the principal coordinates by introducing the modal matrix of the system, P. The columns of this matrix represent the normalized mode shapes. The transformation is given by
which is equivalent to a linear transformation between the generalized and the principal coordinates of the system:
Substituting of Equation (39) into Equation (36) yields
By applying the mode-shape orthogonality condition and multiplying Equation (78) by a scalar , for an arbitrary value of r = 1, 2, 3, 4, we find that only one term in each of the sums is non-zero, specifically when . With the mode shapes normalized, Equation (78) can be expressed as follows:
Equation (79) can also be written in the form
where
For load in expression (74), we take the uniformly distributed surface harmonic load in the following form:
By substituting (82) into expression (74), we obtain
Equation (80) can be written in the form
where
The general solution of Equation (80) can be developed as a sum of homogeneous, and particular, solutions in the form
Each nonhomogeneous version of Equation (80) has a corresponding homogeneous equation:
The homogeneous solution is assumed to be in the form
where A and B are the arbitrary constants obtained from the initial conditions and
Based on the nonhomogeneous term given in Equation (84), we can predict the type of function that the particular solution would be, given as
where C and D are coefficients that are easy to determine.
By substituting and into Equation (84), we obtain two equations:
From the system of Equations (91) and (92), the coefficients are determined in the following forms:
where N is the amplitude of the vibration.
From Equations (93) and (94), it is easy to obtain the unknowns N and in the following form:
Now, the particular and general solutions have the following forms:
For the arbitrary initial condition and , it is possible to obtain the constants A and B in the following form:
Finally, the general solution of Equation (84) is obtained:
When the solution from Equation (99) is resubstituted into Equation (77), we obtain
Finally, the solutions of Equation (73) for the damped ECSNPS are given in the following forms:
In this section, we focused on linearly dependent Rayleigh damped oscillations as part of our effort to emphasize the significance of our linear model and assumptions. While we acknowledge that damping in nano-structures is generally nonlinear and scale-dependent, we believe our model provides a solid foundation for further research. The presumed proportionality might not always be valid, which could influence the accuracy of our results. However, this aspect can be expanded upon in future research to refine the assumptions and achieve more realistic results. Our linear model represents an important step towards a better understanding of damped oscillations in nano-structures and can serve as a starting point for further studies in this field.
The entire modeling approach, from the physical and mathematical aspects to the solution of the plate–shell system’s displacement, is presented in the flow chart shown in Figure 2.
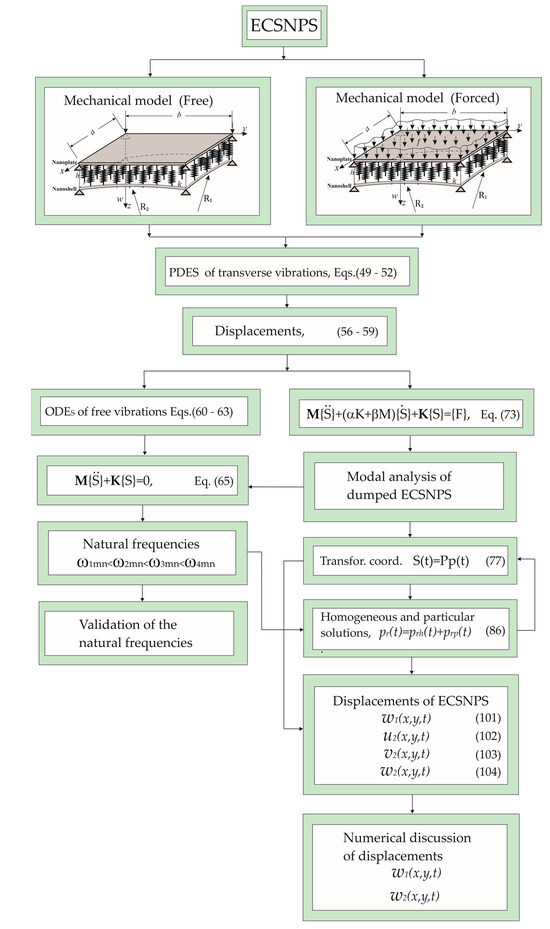
Figure 2.
Flow chart illustrates the procedures for obtaining the solutions of the presented nano-model.
8. Results and Discussion
This section is divided into two parts. In the first part, the natural frequencies of the nano-system presented in this study are analyzed. The second part presents the results of the forced vibrations of the nano-system created from an elastically connected nanoplate and nano-shell (ECSNPS). Most importantly, a comparison of the transverse response of forced vibrations between the nano-system elastically composed of a nanoplate and a nano-shell (ECSNPS) and the nano-system elastically composed of two nanoplates (ECSTNP) is presented.
8.1. Natural Frequency Analysis
For the material and geometrical characteristics given in Table 1, the natural frequencies of the presented nano-system, are given in Table 2. The values of the natural frequencies of the presented nano-system (ECSNPS) are denoted by for the first three eigenmodes,

Table 2.
Natural frequencies of ECSNPS, for .
In Table 2, the values of the natural frequencies are compared based on changes in the nonlocal parameter. It can be observed that the natural frequencies decrease as the values of the nonlocal parameter increase.
The general mode shapes of the vibrations of the two coupled plates are presented in a paper by Oniszczuk [42,43]. Assuming that the nonlocal parameter is equal to zero, μ = 0, and the radius of curvature of the doubly curved shallow shell tends to infinity, i.e., and in Equations (49)–(52), the equations are reduced to two-plate equations, as in the paper by Oniszczuk [42,43].
Then, the system of four coupled differential Equations (49)–(52) is reduced to a system of two coupled differential equations, which represent the transverse displacements of two elastically coupled plates, as shown in Oniszczuk’s study [42,43]. In this way, the considered nano-system is reduced to a system of two nanoplates interconnected by a Winkler-type elastic layer.
The values of the natural frequencies of the observed nano-system (ECSNPS) are compared with the results from the paper by Oniszczuk [42,43]. In Equations (49)–(52), the geometric and material parameters from the paper by Oniszczuk [42,43] are used. By neglecting the nonlocal parameter and assuming that the radii of curvature of the shallow shell tend to infinity, a very good agreement between our results and the values of the frequencies obtained from the work by Oniszczuk [42,43] is obtained, as shown in Table 3.

Table 3.
Comparison of natural frequencies, of doubly curved plate system from Oniszczuk’s study [42,43] when and R1 = R2 = ∞.
If we omit the upper nanoplate and the elastic medium, the validity of the derived equations is assessed by comparing them with published findings for a doubly curved shell from [22], as shown in Table 4. From Table 4, it can be seen that the natural frequency values are close to those obtained in [22]. The differences in values arise due to the application of gradient elasticity theory in [22].

Table 4.
Validation of the frequency parameters, of the shallow spherical shells, where .
8.2. Forced Vibration of the ECSNPS
The main objective of this research is to observe the expected occurrence of dynamic absorption or decreased amplitudes in the excited upper nanoplate of the ECSNPS in comparison with the results for the ECSTNP. Figure 3 presents the two analyzed nano-systems. This section also examines the material and geometrical influences on the ECSNPS for the first three pairs of forced vibration modes.
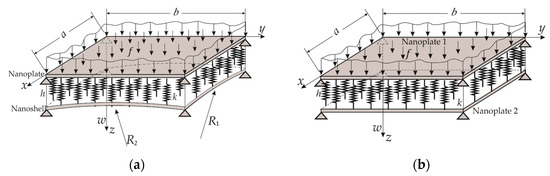
Figure 3.
The nano-systems coupled by a Winkler-type elastic layer: (a) elastically connected system composed of nanoplate and nano-shell (ECSNPS); (b) elastically connected system from two nanoplates (ECSTNP).
In this section, the forced transverse vibration response at the mid-points of the nano-systems is analyzed. The ECSNPS is excited with a periodic force in the form F0cos (Ωt), where F0 = 10 [nN] and Ω = 0.8ω11. The value of the nonlocal parameter is chosen to be in an analysis that does not include the influence of this parameter. The values of the damping proportional coefficients are chosen to be α = β = 1 nNs/m. All the parameters for the material and geometrical characteristics used are given in Table 1. The varied parameters are listed in the corresponding figures.
The model developed in this paper has not been sufficiently researched by other authors, and it could only be concretely compared with the plate–plate nano-model if we used the material and geometric characteristics from [11]. Assuming that the radii of curvature of the doubly curved shallow shell tends to infinity, i.e., in Equations (49)–(52), the equations are reduced to two-plate equations, as in the paper by Atanasov et al. [11]. In this case, the transverse displacements would match those reported in the mentioned paper.
As already mentioned during the frequency analysis, assuming that the nonlocal parameter is equal to zero, μ = 0, and the radii of curvature of the doubly curved shallow shell tend to infinity, i.e., in Equations (49)–(52), the equations are reduced to two-plate equations, as in the paper by Oniszczuk [43]. Similarly, in that case, the transverse displacements would match those reported in the paper by Oniszczuk [43].
The main novelty and goal of this research are the development of a model and the proof that the upper excited element of the nano-system (nanoplate) exhibits smaller amplitude transverse vibrations when the lower element is curved (nano-shell).
A comparison of the amplitude values of the transverse vibrations of the ECSNPS and ECSTNP nano-systems is shown in Figure 4. The transverse displacements as a function of time for the plate–plate (ECSTNP) system are shown in gray, while those for the plate–shell system (ECSNPS) are shown in blue. Figure 4a presents a comparison of the amplitude of the forced transverse vibrations of the upper nanoplate in the ECSNPS with that of the upper nanoplate in the ECSTNP. The most important observation is that the amplitude values of the upper elements in the plate–shell system (ECSNPS) are lower than those in the plate–plate system (ECSTNP), as indicated by the blue line. This decrease in amplitude values in the ECSNPS is one of the primary findings of this study. In Figure 4, the radius of curvature values for the nano-shell are R1 = ∞ and R2 = 450 [nm].
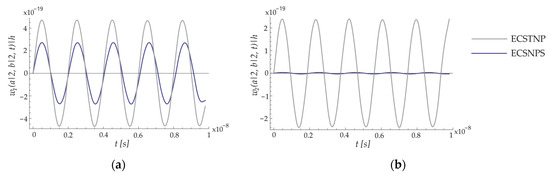
Figure 4.
Comparison of the amplitude values of the forced vibrations of the ECSNPS and the ECSTNP: (a) the upper nanoplate of the ECSNPS with the upper nanoplate of the ECSTNP; (b) the lower nano-shell of the ECSNPS with the lower nanoplate of the ECSTNP.
Additionally, Figure 4b compares the amplitude values of the forced transverse vibrations of the nano-shell in the ECSNPS with those of the lower nanoplate in the ECSTNP. It was observed that the amplitude value is significantly smaller for the nano-shell in the ECSNPS compared to the vibration amplitude of the lower nanoplate in the ECSTNP.
It can be concluded that, with a change in geometric shape, the transverse response decreases, and consequently, the stiffness of the nano-system increases.
The influence of the radius of curvature , for , on the transverse displacement of the forced vibration for the first three modes of the ECSNPS is presented in Figure 5. The values of the radius of curvature R2 vary from 150 to 850, while the radius of curvature R1 tends to infinity. Lower values of the radius of curvature R2 lead to a decrease in the amplitude of forced vibrations in both the nanoplate and nano-shell of the ECSNPS. Notably, the amplitude of forced vibrations in the nano-shell significantly decreases as the radius of curvature decreases, as illustrated in Figure 5b.
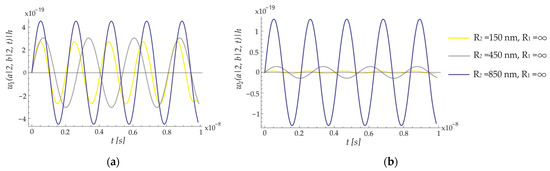
Figure 5.
Effect of the radius of curvature R2 on the transverse displacement for the first three modes of the ECSNPS: (a) nanoplate; (b) nano-shell.
It can be observed that as the radii of curvature decrease, the transverse displacement of the forced vibration for both the upper nanoplate and lower nano-shell of the ECSNPS also decreases.
The effect of the one-sided and double-sided curved nano-shells on the transverse displacement for the first three modes of the ECSNPS is presented in Figure 6. The doubly curved shallow nano-shell has radii of curvature of , while the one-sided-curved nano-shell has radii of curvature of . The transverse displacement of one-side-curved nano-shell is marked in blue, while the transverse displacement of the double-sided-curved nano-shell of the ECSNPS is marked in gray. From Figure 6a, it can be seen that the vibration amplitude of the nanoplate is smaller in the ECSNPS with a one-sided-curved nano-shell. Figure 6b also shows that the amplitude of the forced vibration for the nano-shell of the ECSNPS is smaller with the one-sided-curved nano-shell.
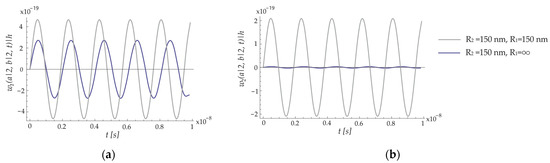
Figure 6.
Effect of the one-sided- and double-sided-curved nano-shell on the transverse displacement for the first three modes of the ECSNPS: (a) nanoplate; (b) nano-shell.
The conclusion is that the amplitude of the forced vibration is smaller for both the nanoplate and the nano-shell for the ECSNPS with the one-sided-curved nano-shell.
The effect of the external excitation on the transverse displacement for the first three modes of the ECSNPS is presented in Figure 7. The following magnitude values of the uniformly distributed surface harmonic loads are used: It is observed that increasing the magnitude values of the external load increases the vibration amplitude of both the nanoplate and nano-shell of the ECSNPS.
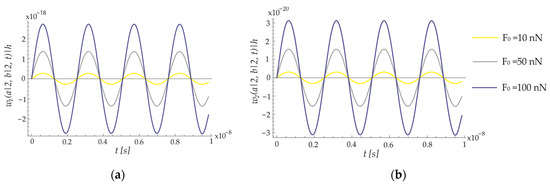
Figure 7.
Effect of the external excitation on the transverse displacement for the first three modes of the ECSNPS: (a) nanoplate; (b) nano-shell.
The effect of the nonlocal parameter on the transverse displacement for the first three modes of the ECSNPS is presented in Figure 8. The transverse displacements for the nanoplate of the ECSNPS are shown in Figure 8a, while those for the nano-shell of the ECSNPS are shown in Figure 8b. It is observed that the vibration amplitude of the nanoplate in the ECSNPS decreases with an increase in the nonlocal parameter, as seen in Figure 8a. Conversely, the amplitude of the forced vibration of the nano-shell in the ECSNPS increases with an increase in the nonlocal parameter, as shown in Figure 8b. Similar observations regarding the effect of the nonlocal parameter on a doubly curved nano-shell are also noted in [20].
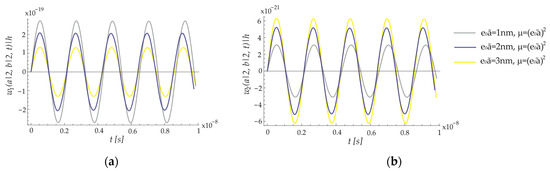
Figure 8.
Effect of the nonlocal parameter on the transverse displacement for the first three modes of the ECSNPS: (a) nanoplate; (b) nano-shell.
The effect of the damping proportional coefficients on the transverse displacement for the first three modes of the ECSNPS is presented in Figure 9. It can be observed that an increase in the damping proportionality coefficients decreases the amplitude of transverse vibrations in both nano-elements of the ECSNPS.
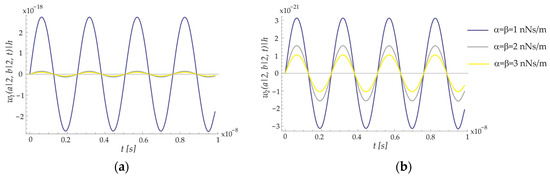
Figure 9.
Effect of the damping proportional coefficients on the transverse displacement for the first three modes of the ECSNPS: (a) nanoplate; (b) nano-shell.
This manuscript provides a comprehensive study numerically alongside essential information, which could serve as an experimental analysis. There are parametric studies investigating the influence of geometry [44,45,46,47], which could be of use for experimental research in combination with new knowledge from this paper.
The analysis of the impact of changing the radius of curvature of the lower element (nano-shell) in this model yields significant results. It is observed that as the radius of curvature decreases, the transverse displacement of the forced vibration of the presented system also decreases. Therefore, it can be concluded that with a change in geometric shape, the transverse response decreases, and consequently, the stiffness of the nano-system increases. Furthermore, by comparing the amplitudes of transverse displacement in the plate–plate system (ECSTNP) with the plate–shell system (ECSNPS) under the unchanged effect of the external force, we can conclude that the amplitude value is significantly smaller for the ECSNPS compared to the vibration amplitude of the ECSTNP. This observation can be effectively demonstrated in nano-sensors, for which a more accurate determination of the response is required in so-called curved sensors. Such sensors are most often used to adapt to curved surfaces and can be applied in medical practice [48,49] and gas sensing [50].
Experimental investigation and comparison with numerical findings are always interesting aspects of research. It would be highly beneficial to investigate such a nano-system with geometric properties that affect oscillation amplitudes in real-world experiments. We hope that future experimental research in this field will validate our analytical and numerical findings.
9. Conclusions
This work presents a detailed analytical and numerical analysis of the forced vibration behavior of an orthotropic nano-system composed of an elastically connected nanoplate and a doubly curved shallow nano-shell. The main novelty is the discovery that the upper excited element of the nano-system (the nanoplate) exhibits smaller amplitude transverse vibrations when the lower element is curved (the nano-shell).
This study demonstrates how the stiffness in such a nano-system changes based on variations in geometric and material parameters. Both nano-elements are simply supported and embedded into a Winkler-type elastic medium.
Using Eringen’s constitutive elastic relation, Kirchhoff–Love plate theory, and Novozhilov’s linear shallow shell theory, a system of four coupled nonhomogeneous PDEs for the transverse vibration of the system was derived. The numerical method for solving these PDEs is presented in detail, with forced vibration analysis solved using modal analysis.
The effects of the nonlocal parameter, external excitation, proportional damping coefficients, and radii of curvature of the nano-shell on the ECSNPS were examined in detail. The amplitude decrease of the excited upper nanoplate was related to the increasing nonlocal parameter and the decreasing radii of curvature of the nano-shell.
The phenomenon of smaller amplitude vibrations was observed by comparing the amplitude of forced transverse responses in a system composed of two nanoplates (ECSTNP) to a system composed of a nanoplate and a nano-shell (ECSNPS).
An increase in proportional damping coefficients results in decreased transverse displacements of the nanoplate and nano-shell. An increase in external excitation to the upper plate results in increased transverse displacements.
The proposed ECSNPS model aids in developing nano-sensors that respond to transverse vibrations based on nano-shell geometry. The results can be used for the development of Nano-Electromechanical Devices (NEMDs), providing engineers with better insight into the behavior of the ECSNPS under the influence of the considered parameters. In particular, adaptable NEMDs that require specific geometrical shapes with different curvatures could benefit from such an analysis.
Additionally, it would also be possible and useful to extend such an analysis to other configurations, such as a shell–shell elastically coupled system, which will be the subject of our future research.
This paper provides a solid framework for future research to extend the analysis to similar elastically coupled nano-configurations, to compare the results with our numerical findings, and to conduct experimental measurements to validate our numerical results.
Author Contributions
Conceptualization, M.S.A., I.R.P., J.S., C.B., A.P. and R.P.; methodology, M.S.A.; software, M.S.A.; formal analysis, M.S.A., J.S., I.R.P., C.B., A.P. and R.P.; writing—original draft, M.S.A.; writing—review and editing, M.S.A., J.S. and I.R.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research was financially supported by the ERASMUS+Partnerships for cooperation and exchanges of practices (KA220)—“Biomedical Innovations through Digital Transformation of Additive Technologies and Knowledge Exchange-BIOMEDIX”—Project No. 2024-1-LV01-KA220-HED-000255929. Also, this research was financially supported by the Ministry of Science, Technological Development and Innovation of the Republic of Serbia (Contract No. 451-03-136/2025-03/200109).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study, including the review protocol, are available upon request from the corresponding author.
Acknowledgments
This research is a revised and expanded version of a doctoral dissertation titled “Stability and Forced Vibration of Coupled Nano-Structures” by the corresponding author M.S.A., which was defended at the Faculty of Mechanical Engineering, University of Niš, on 4 September 2023. Also special thanks to the ERASMUS+Partnerships for cooperation and exchanges of practices (KA220)—“Biomedical Innovations through Digital Transformation of Additive Technologies and Knowledge Exchange-BIOMEDIX”—Project No. 2024-1-LV01-KA220-HED-000255929 for supporting.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ECSNPS | Elastically connected system of a nanoplate and nano-shell; |
| ECSTNP | Elastically connected system of two nanoplates; |
| PDE | Partial differential equation; |
| ODE | Ordinary differential equations. |
Appendix A
References
- Li, X.; Warzywoda, J.; McKenna, G.B. Mechanical responses of a polymer graphene-sheet nano-sandwich. Polymer 2014, 55, 4976–4982. [Google Scholar] [CrossRef]
- Li, H.; Wang, W.; Yao, L. Analysis of the vibration behaviors of rotating composite nano-annular plates based on nonlocal theory and different plate theories. Appl. Sci. 2021, 12, 230. [Google Scholar] [CrossRef]
- Lam, D.C.; Yang, F.; Chong, A.C.M.; Wang, J.; Tong, P. Experiments and theory in strain gradient elasticity. J. Mech. Phys. Solids 2003, 51, 1477–1508. [Google Scholar] [CrossRef]
- Eringen, A.C.; Edelen, D.G.B. On nonlocal elasticity. Int. J. Eng. Sci. 1972, 10, 233–248. [Google Scholar] [CrossRef]
- Eringen, A.C. On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves. J. Appl. Phys. 1983, 54, 4703–4710. [Google Scholar] [CrossRef]
- Eringen, A.C. Nonlocal Continuum Field Theories; Springer Science & Business: Berlin, Germany, 2002; Volume 56. [Google Scholar]
- Cheng, N.; Juntian, T.A.N.G.; Peng, F.E.N.G.; Zhihao, H.A.O.; Zhang, Y.; Chang, M. Experimental and theoretical study on flexural performance of lightweight sandwich panels using FRP connectors. Case Stud. Constr. Mater. 2024, 21, 03947. [Google Scholar] [CrossRef]
- Zhou, S.; Qi, L.; Zhang, R.; Li, A.; Ren, F.; Zheng, Z.; Qiao, J.; Sun, Y.; Zhou, S. Analysis of the electromechanical responses of sandwich circular nano-plate based on flexoelectric nano-ultrasonic transducer. Appl. Math. Model. 2025, 137, 115697. [Google Scholar] [CrossRef]
- Marchetti, F.; Ege, K.; Leclere, Q.; Roozen, N.B. On the structural dynamics of laminated composite plates and sandwich structures; a new perspective on damping identification. J. Sound Vib. 2020, 474, 115256. [Google Scholar] [CrossRef]
- Di Sciuva, M.; Sorrenti, M. Bending, free vibration and buckling of functionally graded carbon nanotube-reinforced sandwich plates, using the extended Refined Zigzag Theory. Compos. Struct. 2019, 227, 111324. [Google Scholar] [CrossRef]
- Atanasov, M.S.; Karličić, D.; Kozić, P. Forced transverse vibrations of an elastically connected nonlocal orthotropic double-nanoplate system subjected to an in-plane magnetic field. Acta Mech. 2017, 228, 2165–2185. [Google Scholar] [CrossRef]
- Safarpour, M.; Rahimi, A.; Noormohammadi, A.O.; Rabczuk, T. Frequency characteristics of multiscale hybrid nanocomposite annular plate based on a Halpin–Tsai homogenization model with the aid of GDQM. Appl. Sci. 2020, 10, 1412. [Google Scholar] [CrossRef]
- Wang, Y.; Guo, Y.; Zhang, J. Dynamic response of double-layer rectangular sandwich plates with graded foam cores under blast loading. Int. J. Impact Eng. 2025, 195, 105141. [Google Scholar] [CrossRef]
- Fu, T.; Wang, X.; Hu, X.; Rabczuk, T. Impact dynamic response of stiffened porous functionally graded materials sandwich doubly-curved shells with Arc-type auxetic core. Int. J. Impact Eng. 2024, 191, 105000. [Google Scholar] [CrossRef]
- Atanasov, M.S. Stability and Forced Vibration of Coupled Nano-Structures. Ph.D. Thesis, University of Niš, Niš, Serbia, 2023. [Google Scholar]
- Pavlovic, I.R.; Pavlovic, R.; Janevski, G.; Despenic, N.; Pajkovic, V. Dynamic behavior of two elastically connected nanobeams under a white noise process. Facta Univ. Ser. Mech. Eng. 2020, 18, 219–227. [Google Scholar] [CrossRef]
- Leissa, A.W.; Kadi, A.S. Curvature effects on shallow shell vibrations. J. Sound Vib. 1971, 16, 173–187. [Google Scholar] [CrossRef]
- Bhimaraddi, A. Free vibration analysis of doubly curved shallow shells on rectangular planform using three-dimensional elasticity theory. Int. J. Solids Struct. 1991, 27, 897–913. [Google Scholar] [CrossRef]
- Dereli, E.; Mbendou, J., II; Patel, V.; Mittelstedt, C. Analytical and numerical analysis of composite sandwich structures with additively manufactured lattice cores. Compos. Part C Open Access 2024, 14, 100484. [Google Scholar] [CrossRef]
- Arefi, M. Analysis of a doubly curved piezoelectric nano shell: Nonlocal electro-elastic bending solution. Eur. J. Mech A Solids 2018, 70, 226–237. [Google Scholar] [CrossRef]
- Karami, B.; Shahsavari, D. On the forced resonant vibration analysis of functionally graded polymer composite doubly-curved nanoshells reinforced with graphene-nanoplatelets. Comput. Methods Appl. Mech. Eng. 2020, 359, 112767. [Google Scholar] [CrossRef]
- Ghavanloo, E.; Fazelzadeh, S.A. Free vibration analysis of orthotropic doubly-curved shallow shells based on the gradient elasticity. Compos. Part B Eng. 2013, 45, 1448–1457. [Google Scholar] [CrossRef]
- Hosseini-Hashemi, S.; Sharifpour, F.; Ilkhani, M.R. On the free vibrations of size-dependent closed micro/nano-spherical shell based on the modified couple stress theory. Int. J. Mech. Sci. 2016, 115, 501–515. [Google Scholar] [CrossRef]
- Turan, F.; Karadeniz, M.; Zeren, E. Free vibration and buckling behavior of porous orthotropic doubly-curved shallow shells subjected to non-uniform edge compression using higher-order shear deformation theory. Thin-Walled Struct. 2024, 205, 112522. [Google Scholar] [CrossRef]
- Hwu, C.; Hsu, H.W.; Lin, Y.H. Free vibration of composite sandwich plates and cylindrical shells. Compos. Struct. 2017, 171, 528–537. [Google Scholar] [CrossRef]
- Reddy, J.N. Mechanics of Laminated Composite Plates and Shells: Theory and Analysis; CRC Press: Boca Raton, FL, USA, 2004. [Google Scholar]
- Reddy, J.N. Theory and Analysis of Elastic Plates And Shells; CRC Press: Boca Raton, FL, USA, 2006. [Google Scholar]
- Karličić, D.; Murmu, T.; Adhikari, S.; McCarthy, M. Non-Local Structural Mechanics; John Wiley Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Amabili, M. Nonlinear Vibrations and Stability of Shells and Plates; Cambridge University Press (CUP): Cambridge, UK, 2008. [Google Scholar]
- Koiter, W. Couple stresses in the theory of elasticity, I and II. Koninklijke Nederlandse Akademie van Wetenschappen. Proc. Roy. Soc. B 1964, 67, 17–44. [Google Scholar]
- Toupin, R. Elastic materials with couple-stresses. Arch. Ration. Mech. Anal. 1962, 11, 385–414. [Google Scholar] [CrossRef]
- Mindlin, R.D.; Tiersten, H. Effects of couple-stresses in linear elasticity. Arch. Ration. Mech. Anal. 1962, 11, 415–448. [Google Scholar] [CrossRef]
- Pouresmaeeli, S.; Ghavanloo, E.; Fazelzadeh, S.A. Vibration analysis of viscoelastic orthotropic nanoplates resting on viscoelastic medium. Comp. Struct. 2013, 96, 405–410. [Google Scholar] [CrossRef]
- Ansari, R.; Sahmani, S.; Arash, B. Nonlocal plate model for free vibrations of single-layered graphene sheets. Phys. Lett. A 2010, 375, 53–62. [Google Scholar] [CrossRef]
- Ansari, R.; Rajabiehfard, R.; Arash, B. Nonlocal finite element model for vibrations of embedded multi-layered graphene sheets. Comput. Mater. Sci. 2010, 49, 831–838. [Google Scholar] [CrossRef]
- Radić, N.; Jeremić, D.; Mijatović, B. Vibration analysis of orthotropic double-nanoplate system subjected to unidirectional in-plane magnetic field with various boundary conditions. IOSR J. Mech. Civ. Eng. 2018, 15, 59–76. [Google Scholar]
- Fernández-Sáez, J.; Zaera, R.; Loya, J.A.; Reddy, J.N. Bending of Euler–Bernoulli beams using Eringen’s integral formulation: A paradox resolved. Int. J. Eng. Sci. 2016, 99, 107–116. [Google Scholar] [CrossRef]
- Eptaimeros, K.G.; Koutsoumaris, C.C.; Tsamasphyros, G.J. Nonlocal integral approach to the dynamical response of nanobeams. Int. J. Mech. Sci. 2016, 115, 68–80. [Google Scholar] [CrossRef]
- Batra, R.C. Misuse of Eringen’s nonlocal elasticity theory for functionally graded materials. Int. J. Eng. Sci. 2021, 159, 103425. [Google Scholar] [CrossRef]
- Kiani, K. A meshless approach for free transverse vibration of embedded single-walled nanotubes with arbitrary boundary conditions accounting for nonlocal effect. Int. J. Mech. Sci. 2010, 52, 1343–1356. [Google Scholar] [CrossRef]
- Kelly, S.G. Mechanical Vibrations: Theory and Applications; Cengage Learn: Tokyo, Japan, 2012. [Google Scholar]
- Oniszczuk, Z. Free transverse vibrations of an elastically connected rectangular simply supported double-plate complex system. J. Sound Vib. 2000, 236, 595–608. [Google Scholar] [CrossRef]
- Oniszczuk, Z. Forced transverse vibrations of an elastically connected complex rectangular simply supported double-plate system. J. Sound Vib. 2004, 270, 997–1011. [Google Scholar] [CrossRef]
- Zhou, Y.; Chen, Y.; Jin, L. Three-dimensional postbuckling analysis of thick hyperelastic tubes. J. Mech. Phys. Solids 2023, 173, 105202. [Google Scholar] [CrossRef]
- Chen, Y.; Liu, T.; Jin, L. Pseudo-bistability of viscoelastic shells. Philos. Trans. R. Soc. A 2023, 381, 20220026. [Google Scholar] [CrossRef]
- Wang, T.; Fu, C.; Potier-Ferry, M.; Xu, F. Morphomechanics of growing curled petals and leaves. J. Mech. Phys. Solids 2024, 184, 105534. [Google Scholar] [CrossRef]
- Yang, Y.; Xu, F. Computational morphology and morphogenesis for empowering soft-matter engineering. Nat. Comput. Sci. 2024, 4, 388–390. [Google Scholar] [CrossRef]
- Li, J.; Liu, B.; Liu, J.; Shi, J.L.; He, X.D.; Yuan, J.; Wu, Q. Low-cost wearable device based D-shaped single mode fiber curvature sensor for vital signs monitoring. Sens. Actuators A Phys. 2022, 337, 113429. [Google Scholar] [CrossRef]
- Chowdhury, M.K.H.; Anik, H.R.; Akter, M.; Hasan, S.M.M.; Tushar, S.I.; Mahmud, S.; Nahar, N.; Tania, I.S. Sensing the Future with Graphene-based Wearable Sensors: A review. Results Mater. 2024, 25, 100646. [Google Scholar] [CrossRef]
- Chandel, V.S.; Wang, G.; Talha, M. Advances in modelling and analysis of nano structures: A review. Nanotechnol. Rev. 2020, 9, 230–258. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).