Forced Dynamics of Elastically Connected Nano-Plates and Nano-Shells in Winkler-Type Elastic Medium
Abstract
1. Introduction
2. Brief Review of Eringen’s Constitutive Elasticity
3. Mathematical Formulations of the Equations of Motion for an Orthotropic Nanoplate
4. Mathematical Formulation of the Equations of Motion for an Orthotropic Doubly Curved Shallow Nano-Shell
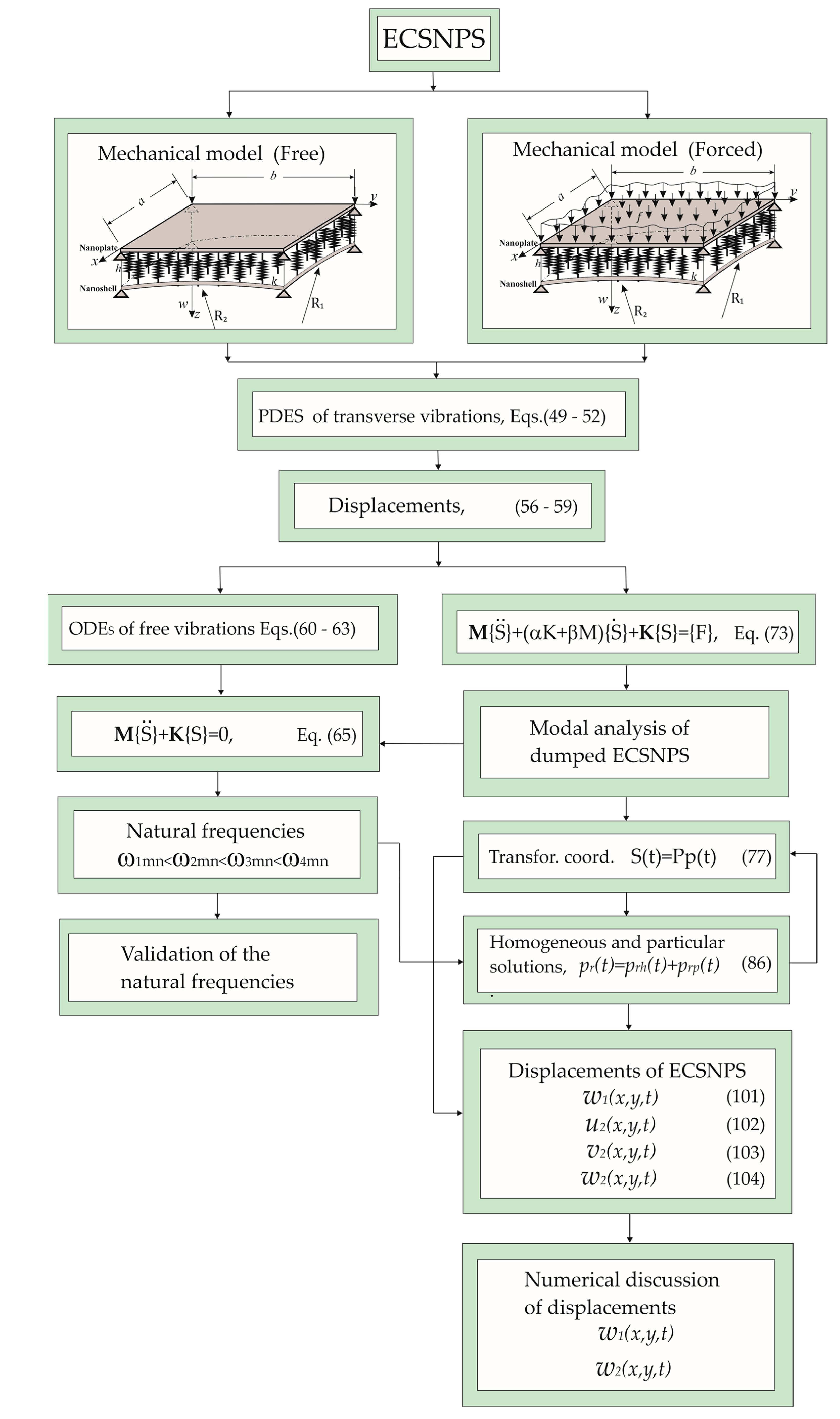
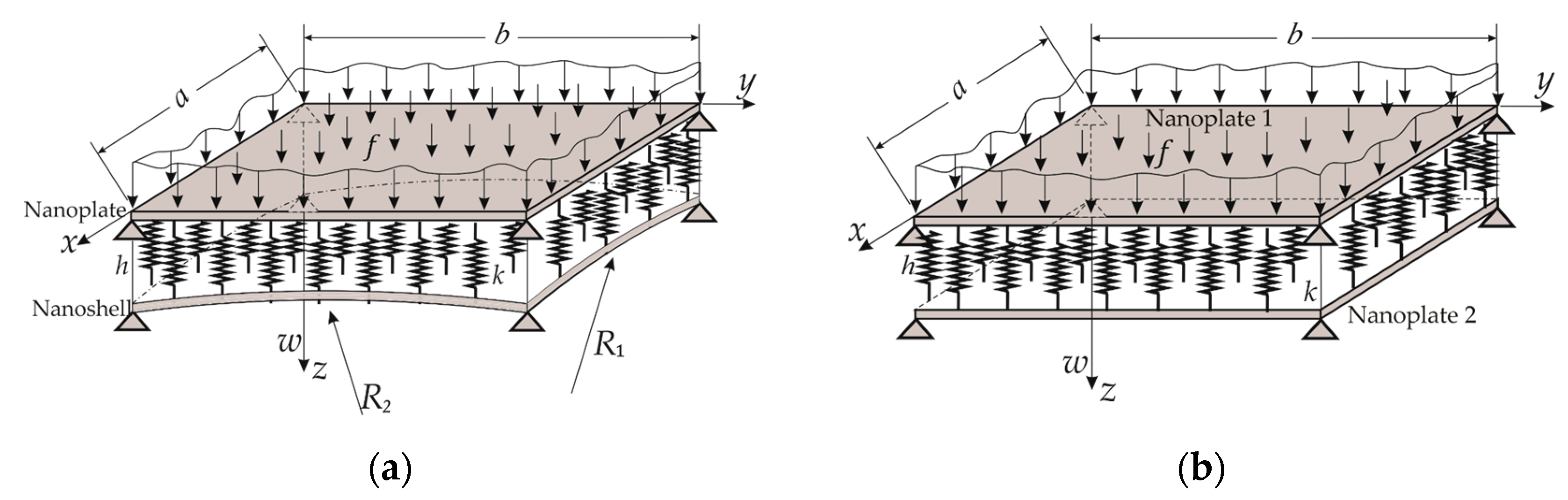
5. Formulation of Model ECSNPS
6. Solution Methodology for Determining the Natural Frequencies of the ECSNPS
7. Forced Vibration of the Damped ECSNPS
8. Results and Discussion
8.1. Natural Frequency Analysis
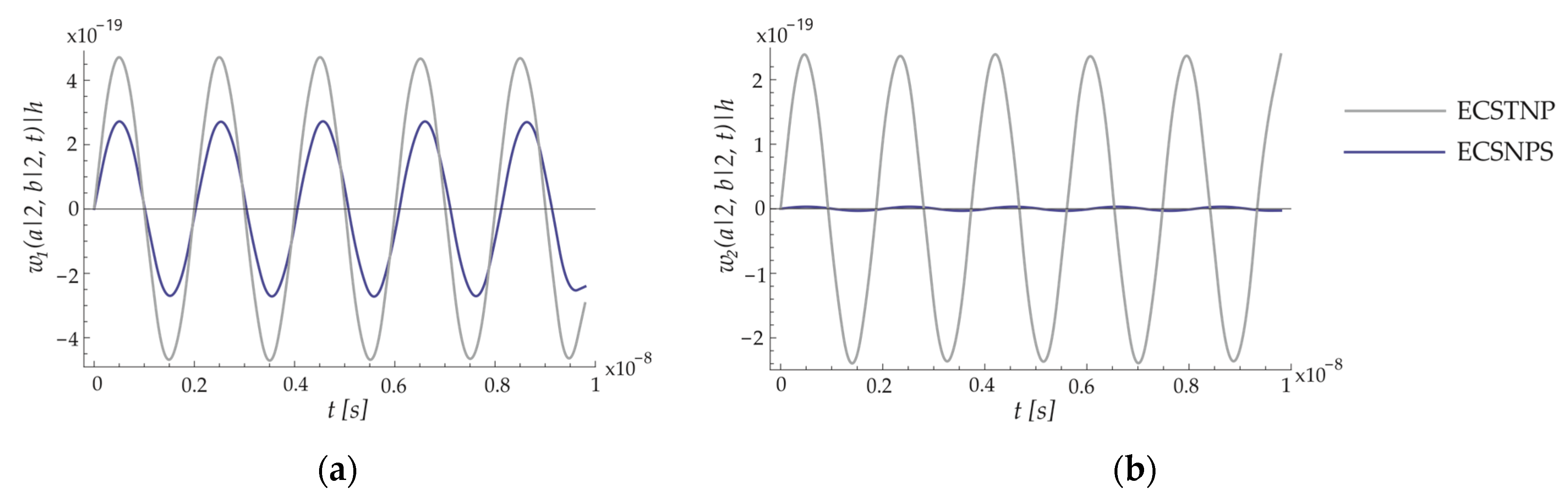
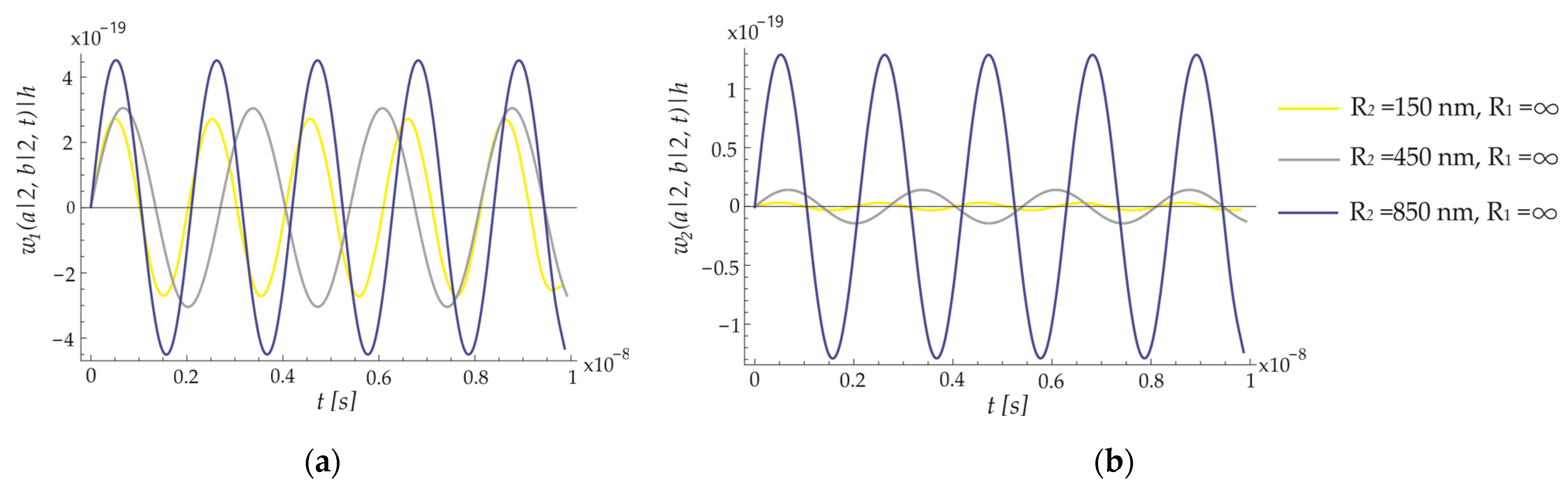
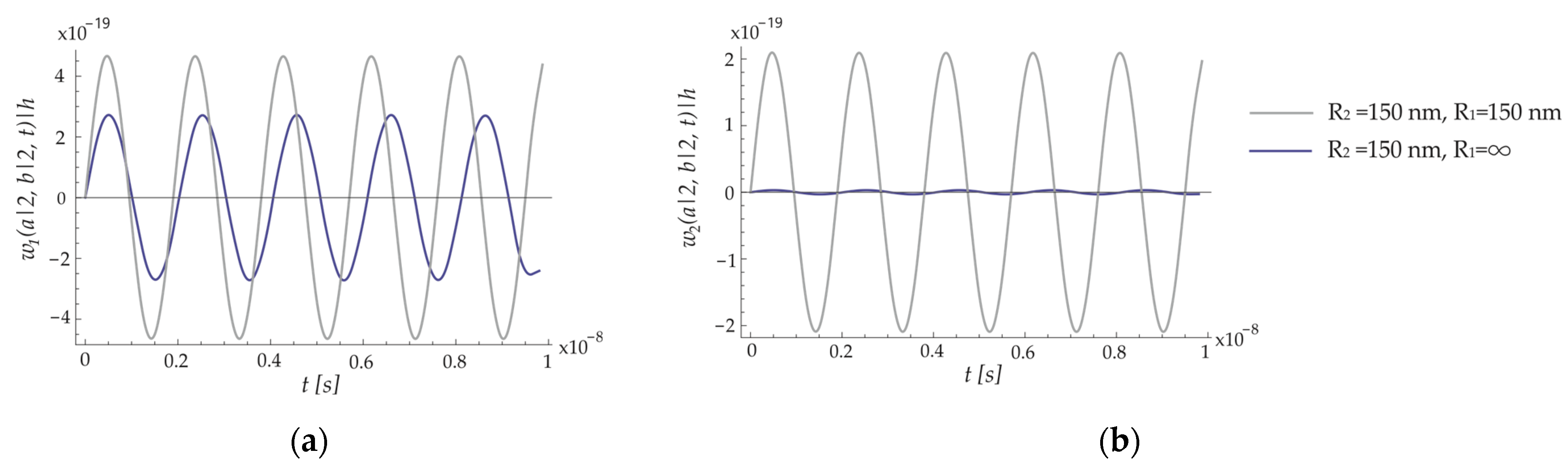
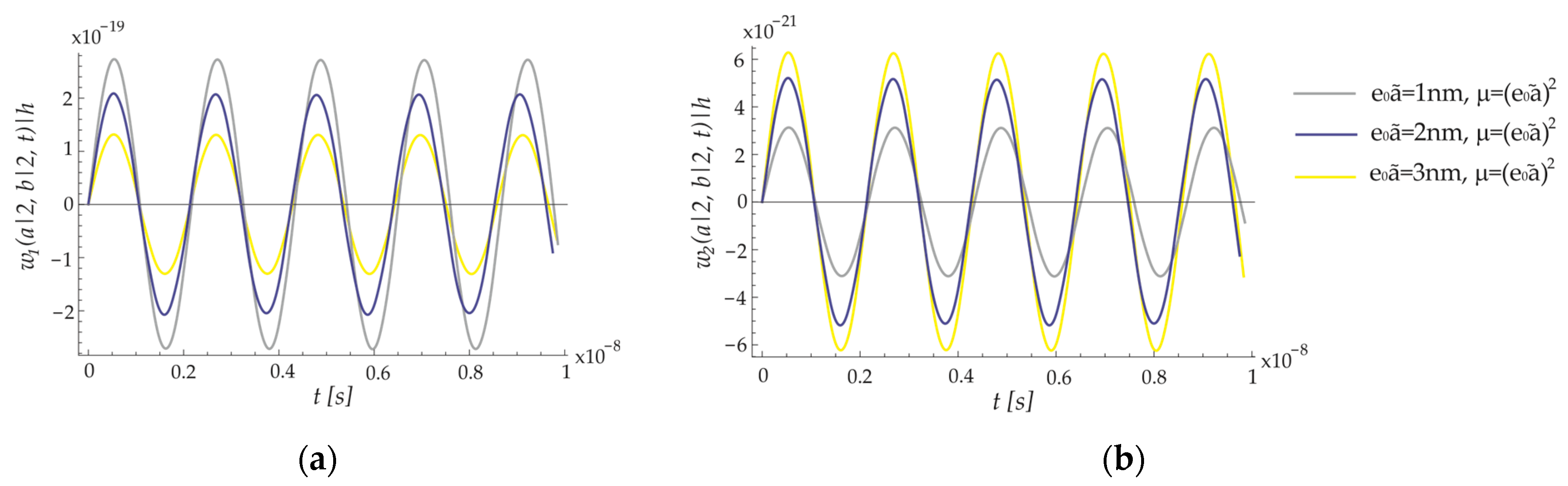
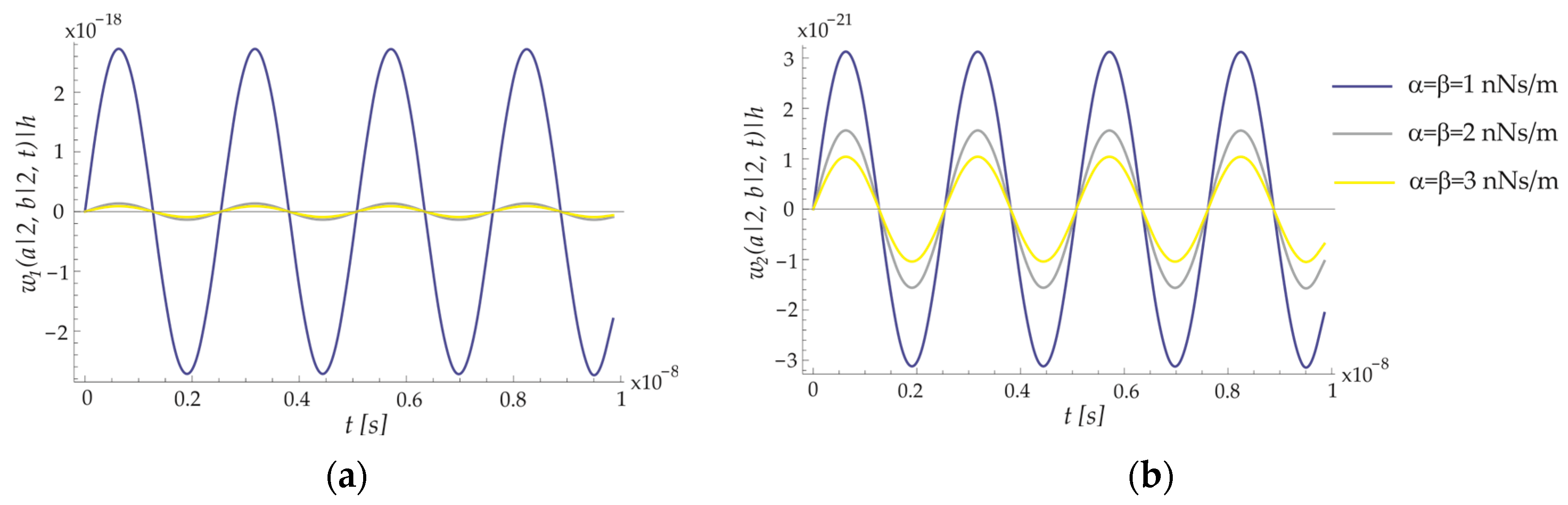
8.2. Forced Vibration of the ECSNPS
9. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ECSNPS | Elastically connected system of a nanoplate and nano-shell; |
| ECSTNP | Elastically connected system of two nanoplates; |
| PDE | Partial differential equation; |
| ODE | Ordinary differential equations. |
Appendix A
References
- Li, X.; Warzywoda, J.; McKenna, G.B. Mechanical responses of a polymer graphene-sheet nano-sandwich. Polymer 2014, 55, 4976–4982. [Google Scholar] [CrossRef]
- Li, H.; Wang, W.; Yao, L. Analysis of the vibration behaviors of rotating composite nano-annular plates based on nonlocal theory and different plate theories. Appl. Sci. 2021, 12, 230. [Google Scholar] [CrossRef]
- Lam, D.C.; Yang, F.; Chong, A.C.M.; Wang, J.; Tong, P. Experiments and theory in strain gradient elasticity. J. Mech. Phys. Solids 2003, 51, 1477–1508. [Google Scholar] [CrossRef]
- Eringen, A.C.; Edelen, D.G.B. On nonlocal elasticity. Int. J. Eng. Sci. 1972, 10, 233–248. [Google Scholar] [CrossRef]
- Eringen, A.C. On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves. J. Appl. Phys. 1983, 54, 4703–4710. [Google Scholar] [CrossRef]
- Eringen, A.C. Nonlocal Continuum Field Theories; Springer Science & Business: Berlin, Germany, 2002; Volume 56. [Google Scholar]
- Cheng, N.; Juntian, T.A.N.G.; Peng, F.E.N.G.; Zhihao, H.A.O.; Zhang, Y.; Chang, M. Experimental and theoretical study on flexural performance of lightweight sandwich panels using FRP connectors. Case Stud. Constr. Mater. 2024, 21, 03947. [Google Scholar] [CrossRef]
- Zhou, S.; Qi, L.; Zhang, R.; Li, A.; Ren, F.; Zheng, Z.; Qiao, J.; Sun, Y.; Zhou, S. Analysis of the electromechanical responses of sandwich circular nano-plate based on flexoelectric nano-ultrasonic transducer. Appl. Math. Model. 2025, 137, 115697. [Google Scholar] [CrossRef]
- Marchetti, F.; Ege, K.; Leclere, Q.; Roozen, N.B. On the structural dynamics of laminated composite plates and sandwich structures; a new perspective on damping identification. J. Sound Vib. 2020, 474, 115256. [Google Scholar] [CrossRef]
- Di Sciuva, M.; Sorrenti, M. Bending, free vibration and buckling of functionally graded carbon nanotube-reinforced sandwich plates, using the extended Refined Zigzag Theory. Compos. Struct. 2019, 227, 111324. [Google Scholar] [CrossRef]
- Atanasov, M.S.; Karličić, D.; Kozić, P. Forced transverse vibrations of an elastically connected nonlocal orthotropic double-nanoplate system subjected to an in-plane magnetic field. Acta Mech. 2017, 228, 2165–2185. [Google Scholar] [CrossRef]
- Safarpour, M.; Rahimi, A.; Noormohammadi, A.O.; Rabczuk, T. Frequency characteristics of multiscale hybrid nanocomposite annular plate based on a Halpin–Tsai homogenization model with the aid of GDQM. Appl. Sci. 2020, 10, 1412. [Google Scholar] [CrossRef]
- Wang, Y.; Guo, Y.; Zhang, J. Dynamic response of double-layer rectangular sandwich plates with graded foam cores under blast loading. Int. J. Impact Eng. 2025, 195, 105141. [Google Scholar] [CrossRef]
- Fu, T.; Wang, X.; Hu, X.; Rabczuk, T. Impact dynamic response of stiffened porous functionally graded materials sandwich doubly-curved shells with Arc-type auxetic core. Int. J. Impact Eng. 2024, 191, 105000. [Google Scholar] [CrossRef]
- Atanasov, M.S. Stability and Forced Vibration of Coupled Nano-Structures. Ph.D. Thesis, University of Niš, Niš, Serbia, 2023. [Google Scholar]
- Pavlovic, I.R.; Pavlovic, R.; Janevski, G.; Despenic, N.; Pajkovic, V. Dynamic behavior of two elastically connected nanobeams under a white noise process. Facta Univ. Ser. Mech. Eng. 2020, 18, 219–227. [Google Scholar] [CrossRef]
- Leissa, A.W.; Kadi, A.S. Curvature effects on shallow shell vibrations. J. Sound Vib. 1971, 16, 173–187. [Google Scholar] [CrossRef]
- Bhimaraddi, A. Free vibration analysis of doubly curved shallow shells on rectangular planform using three-dimensional elasticity theory. Int. J. Solids Struct. 1991, 27, 897–913. [Google Scholar] [CrossRef]
- Dereli, E.; Mbendou, J., II; Patel, V.; Mittelstedt, C. Analytical and numerical analysis of composite sandwich structures with additively manufactured lattice cores. Compos. Part C Open Access 2024, 14, 100484. [Google Scholar] [CrossRef]
- Arefi, M. Analysis of a doubly curved piezoelectric nano shell: Nonlocal electro-elastic bending solution. Eur. J. Mech A Solids 2018, 70, 226–237. [Google Scholar] [CrossRef]
- Karami, B.; Shahsavari, D. On the forced resonant vibration analysis of functionally graded polymer composite doubly-curved nanoshells reinforced with graphene-nanoplatelets. Comput. Methods Appl. Mech. Eng. 2020, 359, 112767. [Google Scholar] [CrossRef]
- Ghavanloo, E.; Fazelzadeh, S.A. Free vibration analysis of orthotropic doubly-curved shallow shells based on the gradient elasticity. Compos. Part B Eng. 2013, 45, 1448–1457. [Google Scholar] [CrossRef]
- Hosseini-Hashemi, S.; Sharifpour, F.; Ilkhani, M.R. On the free vibrations of size-dependent closed micro/nano-spherical shell based on the modified couple stress theory. Int. J. Mech. Sci. 2016, 115, 501–515. [Google Scholar] [CrossRef]
- Turan, F.; Karadeniz, M.; Zeren, E. Free vibration and buckling behavior of porous orthotropic doubly-curved shallow shells subjected to non-uniform edge compression using higher-order shear deformation theory. Thin-Walled Struct. 2024, 205, 112522. [Google Scholar] [CrossRef]
- Hwu, C.; Hsu, H.W.; Lin, Y.H. Free vibration of composite sandwich plates and cylindrical shells. Compos. Struct. 2017, 171, 528–537. [Google Scholar] [CrossRef]
- Reddy, J.N. Mechanics of Laminated Composite Plates and Shells: Theory and Analysis; CRC Press: Boca Raton, FL, USA, 2004. [Google Scholar]
- Reddy, J.N. Theory and Analysis of Elastic Plates And Shells; CRC Press: Boca Raton, FL, USA, 2006. [Google Scholar]
- Karličić, D.; Murmu, T.; Adhikari, S.; McCarthy, M. Non-Local Structural Mechanics; John Wiley Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Amabili, M. Nonlinear Vibrations and Stability of Shells and Plates; Cambridge University Press (CUP): Cambridge, UK, 2008. [Google Scholar]
- Koiter, W. Couple stresses in the theory of elasticity, I and II. Koninklijke Nederlandse Akademie van Wetenschappen. Proc. Roy. Soc. B 1964, 67, 17–44. [Google Scholar]
- Toupin, R. Elastic materials with couple-stresses. Arch. Ration. Mech. Anal. 1962, 11, 385–414. [Google Scholar] [CrossRef]
- Mindlin, R.D.; Tiersten, H. Effects of couple-stresses in linear elasticity. Arch. Ration. Mech. Anal. 1962, 11, 415–448. [Google Scholar] [CrossRef]
- Pouresmaeeli, S.; Ghavanloo, E.; Fazelzadeh, S.A. Vibration analysis of viscoelastic orthotropic nanoplates resting on viscoelastic medium. Comp. Struct. 2013, 96, 405–410. [Google Scholar] [CrossRef]
- Ansari, R.; Sahmani, S.; Arash, B. Nonlocal plate model for free vibrations of single-layered graphene sheets. Phys. Lett. A 2010, 375, 53–62. [Google Scholar] [CrossRef]
- Ansari, R.; Rajabiehfard, R.; Arash, B. Nonlocal finite element model for vibrations of embedded multi-layered graphene sheets. Comput. Mater. Sci. 2010, 49, 831–838. [Google Scholar] [CrossRef]
- Radić, N.; Jeremić, D.; Mijatović, B. Vibration analysis of orthotropic double-nanoplate system subjected to unidirectional in-plane magnetic field with various boundary conditions. IOSR J. Mech. Civ. Eng. 2018, 15, 59–76. [Google Scholar]
- Fernández-Sáez, J.; Zaera, R.; Loya, J.A.; Reddy, J.N. Bending of Euler–Bernoulli beams using Eringen’s integral formulation: A paradox resolved. Int. J. Eng. Sci. 2016, 99, 107–116. [Google Scholar] [CrossRef]
- Eptaimeros, K.G.; Koutsoumaris, C.C.; Tsamasphyros, G.J. Nonlocal integral approach to the dynamical response of nanobeams. Int. J. Mech. Sci. 2016, 115, 68–80. [Google Scholar] [CrossRef]
- Batra, R.C. Misuse of Eringen’s nonlocal elasticity theory for functionally graded materials. Int. J. Eng. Sci. 2021, 159, 103425. [Google Scholar] [CrossRef]
- Kiani, K. A meshless approach for free transverse vibration of embedded single-walled nanotubes with arbitrary boundary conditions accounting for nonlocal effect. Int. J. Mech. Sci. 2010, 52, 1343–1356. [Google Scholar] [CrossRef]
- Kelly, S.G. Mechanical Vibrations: Theory and Applications; Cengage Learn: Tokyo, Japan, 2012. [Google Scholar]
- Oniszczuk, Z. Free transverse vibrations of an elastically connected rectangular simply supported double-plate complex system. J. Sound Vib. 2000, 236, 595–608. [Google Scholar] [CrossRef]
- Oniszczuk, Z. Forced transverse vibrations of an elastically connected complex rectangular simply supported double-plate system. J. Sound Vib. 2004, 270, 997–1011. [Google Scholar] [CrossRef]
- Zhou, Y.; Chen, Y.; Jin, L. Three-dimensional postbuckling analysis of thick hyperelastic tubes. J. Mech. Phys. Solids 2023, 173, 105202. [Google Scholar] [CrossRef]
- Chen, Y.; Liu, T.; Jin, L. Pseudo-bistability of viscoelastic shells. Philos. Trans. R. Soc. A 2023, 381, 20220026. [Google Scholar] [CrossRef]
- Wang, T.; Fu, C.; Potier-Ferry, M.; Xu, F. Morphomechanics of growing curled petals and leaves. J. Mech. Phys. Solids 2024, 184, 105534. [Google Scholar] [CrossRef]
- Yang, Y.; Xu, F. Computational morphology and morphogenesis for empowering soft-matter engineering. Nat. Comput. Sci. 2024, 4, 388–390. [Google Scholar] [CrossRef]
- Li, J.; Liu, B.; Liu, J.; Shi, J.L.; He, X.D.; Yuan, J.; Wu, Q. Low-cost wearable device based D-shaped single mode fiber curvature sensor for vital signs monitoring. Sens. Actuators A Phys. 2022, 337, 113429. [Google Scholar] [CrossRef]
- Chowdhury, M.K.H.; Anik, H.R.; Akter, M.; Hasan, S.M.M.; Tushar, S.I.; Mahmud, S.; Nahar, N.; Tania, I.S. Sensing the Future with Graphene-based Wearable Sensors: A review. Results Mater. 2024, 25, 100646. [Google Scholar] [CrossRef]
- Chandel, V.S.; Wang, G.; Talha, M. Advances in modelling and analysis of nano structures: A review. Nanotechnol. Rev. 2020, 9, 230–258. [Google Scholar] [CrossRef]


| E1 | E2 | a | b | h | ||||
|---|---|---|---|---|---|---|---|---|
| TPa | TPa | TPa | kg/m3 | nm | nm | nm | GPa/nm | |
| 2.434 | 2.473 | 1.039 | 0.197 | 6316 | 0.129 | 10 | 4.5 | 0.075 |
| m = 1 | n = 1 | 4.61953 × 1011 | 2.99085 × 1012 | 7.38604 × 1012 | 1.21507 × 1013 |
| n = 2 | 9.31595 × 1011 | 2.30851 × 1012 | 1.03814 × 1013 | 1.64871 × 1013 | |
| n = 3 | 1.46995 × 1012 | 2.15757 × 1012 | 1.15336 × 1013 | 1.82203 × 1013 | |
| m = 2 | n = 1 | 5.70087 × 1011 | 5.67846 × 1012 | 6.99782 × 1012 | 1.36309 × 1013 |
| n = 2 | 1.01025 × 1012 | 4.20984 × 1012 | 1.01672 × 1013 | 1.67344 × 1013 | |
| n = 3 | 1.52519 × 1012 | 3.45108 × 1012 | 1.13942 × 1013 | 1.82509 × 1013 | |
| m = 3 | n = 1 | 7.34647 × 1011 | 6.85678 × 1012 | 7.19172 × 1012 | 1.51839 × 1013 |
| n = 2 | 1.13034 × 1012 | 5.94912 × 1012 | 9.69245 × 1012 | 1.71264 × 1013 | |
| n = 3 | 1.61201 × 1012 | 4.78913 × 1012 | 1.11226 × 1013 | 1.83239 × 1013 | |
| m = 1 | n = 1 | 3.84471 × 1011 | 2.07360 × 1012 | 5.08588 × 1012 | 8.36769 × 1012 |
| n = 2 | 5.86577 × 1011 | 1.35492 × 1012 | 5.97785 × 1012 | 9.49374 × 1012 | |
| n = 3 | 8.24879 × 1011 | 1.19378 × 1012 | 6.20668 × 1012 | 9.80507 × 1012 | |
| m = 2 | n = 1 | 4.33619 × 1011 | 3.68099 × 1012 | 4.50109 × 1012 | 8.78749 × 1012 |
| n = 2 | 6.24265 × 1011 | 2.40523 × 1012 | 5.77111 × 1012 | 9.49987 × 1012 | |
| n = 3 | 8.54911 × 1011 | 1.86919 × 1012 | 6.10670 × 1012 | 9.78197 × 1012 | |
| m = 3 | n = 1 | 5.04771 × 1011 | 4.25083 × 1012 | 4.25083 × 1012 | 9.17758 × 1012 |
| n = 2 | 6.77858 × 1011 | 3.33059 × 1012 | 5.40006 × 1012 | 9.54656 × 1012 | |
| n = 3 | 8.95666 × 1011 | 2.56714 × 1012 | 5.92601 × 1012 | 9.76398 × 1012 | |
| m = 1 | n = 1 | 3.44521 × 1011 | 1.53112 × 1012 | 3.71222 × 1012 | 6.10881 × 1012 |
| n = 2 | 4.49233 × 1011 | 9.63276 × 1011 | 4.11125 × 1012 | 6.52950 × 1012 | |
| n = 3 | 5.85347 × 1011 | 8.49677 × 1011 | 4.19978 × 1012 | 6.63473 × 1012 | |
| m = 2 | n = 1 | 3.73072 × 1011 | 2.64494 × 1012 | 3.19060 × 1012 | 6.25442 × 1012 |
| n = 2 | 4.78425 × 1011 | 1.66611 × 1012 | 3.95389 × 1012 | 6.50982 × 1012 | |
| n = 3 | 6.15194 × 1011 | 1.28667 × 1012 | 4.12822 × 1012 | 6.61318 × 1012 | |
| m = 3 | n = 1 | 4.11932 × 1011 | 2.96932 × 1012 | 2.96932 × 1012 | 6.39772 × 1012 |
| n = 2 | 5.11162 × 1011 | 2.28870 × 1012 | 3.68065 × 1012 | 6.51242 × 1012 | |
| n = 3 | 6.42609 × 1011 | 1.75086 × 1012 | 4.00041 × 1012 | 6.59264 × 1012 |
| Oniszczuk [42,43] | Present Study | ||||
|---|---|---|---|---|---|
| m = 1 | n = 1 | 52.8 | 72.0 | 52.7975095047 | 72.0248360629 |
| n = 2 | 84.5 | 97.7 | 84.4760152075 | 97.6534543441 | |
| n = 3 | 137.3 | 145.8 | 137.2735247122 | 145.7532867105 | |
| m = 2 | n = 1 | 179.5 | 186.1 | 179.5115323161 | 186.0763021839 |
| n = 2 | 211.2 | 216.8 | 211.1900380189 | 216.7976756296 | |
| n = 3 | 264.0 | 268.5 | 263.9875475236 | 268.4947397018 | |
| m = 3 | n = 1 | 390.7 | 393.8 | 390.7015703349 | 393.7609897669 |
| n = 2 | 422.4 | 425.2 | 422.3800760378 | 425.2116280556 | |
| n = 3 | 475.2 | 477.7 | 475.1775855425 | 477.6962819637 |
| Ghavanloo E. et al. [22] | Presented Study | |
|---|---|---|
| Ω1 | 5.0843 | |
| Ω2 | 12.2689 | |
| Ω3 | 13.4459 | |
| Ω4 | 20.1542 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Atanasov, M.S.; Pavlović, I.R.; Simonović, J.; Borzan, C.; Păcurar, A.; Păcurar, R. Forced Dynamics of Elastically Connected Nano-Plates and Nano-Shells in Winkler-Type Elastic Medium. Appl. Sci. 2025, 15, 2765. https://doi.org/10.3390/app15052765
Atanasov MS, Pavlović IR, Simonović J, Borzan C, Păcurar A, Păcurar R. Forced Dynamics of Elastically Connected Nano-Plates and Nano-Shells in Winkler-Type Elastic Medium. Applied Sciences. 2025; 15(5):2765. https://doi.org/10.3390/app15052765
Chicago/Turabian StyleAtanasov, Marija Stamenković, Ivan R. Pavlović, Julijana Simonović, Cristina Borzan, Ancuţa Păcurar, and Răzvan Păcurar. 2025. "Forced Dynamics of Elastically Connected Nano-Plates and Nano-Shells in Winkler-Type Elastic Medium" Applied Sciences 15, no. 5: 2765. https://doi.org/10.3390/app15052765
APA StyleAtanasov, M. S., Pavlović, I. R., Simonović, J., Borzan, C., Păcurar, A., & Păcurar, R. (2025). Forced Dynamics of Elastically Connected Nano-Plates and Nano-Shells in Winkler-Type Elastic Medium. Applied Sciences, 15(5), 2765. https://doi.org/10.3390/app15052765








