Abstract
In this study, we present the Response-Based Key Encapsulation Mechanism (R-KEM), an ephemeral key encapsulation and recovery scheme tailored for cryptographic systems in high-noise, high-jamming network environments. By adopting the Challenge–Response Pair (CRP) mechanism for both key encapsulation and authentication, R-KEM eliminates the need to store secret keys on the device, favoring on-demand key generation. By maintaining only encrypted data on the device, R-KEM significantly enhances security, ensuring that in the event of an attack, no sensitive information can be compromised. Its novel error-correcting strategy efficiently corrects 20 to 23 bits of errors promptly, eliminating the need for redundant helper data and fuzzy extractors. R-KEM is ideally suited for terminal devices with constrained computational resources. Our comprehensive performance analysis underscores R-KEM’s ability to recover error-free cryptographic keys in noisy networks, offering a superior alternative to conventional methods that struggle to maintain secure data transmission under such challenges. This work not only demonstrates R-KEM’s efficacy but also paves the way for more resilient cryptographic systems in noise-prone environments.
1. Introduction
Key recovery, in the context of session keys, traditionally refers to the process of retrieving a key that was previously stored on a device but may have been lost or compromised. In contrast, our approach focuses on recovering session keys that are never stored locally. Instead, these keys are encapsulated and transmitted over a noisy communication channel, eliminating the need for persistent key storage and enhancing the security of the cryptographic system.
In noisy communication environments, the accurate retrieval of these ephemerally generated session keys presents unique challenges. Our solution leverages innovative search algorithms to facilitate key recovery, ensuring secure communication continuity even when noise is introduced during key encapsulation and transmission.
Unlike conventional methods that rely on retrieving previously stored keys, our technique ensures that no sensitive data are ever saved on a device. Our approach employs a dynamic verification mechanism that not only facilitates key recovery but also enables device authentication.
This paper outlines the foundational principles of our method and presents a comprehensive performance analysis, demonstrating its effectiveness in key recovery under challenging conditions.
2. Background
Error-correcting codes (ECCs) are widely used in many cryptographic protocols, in particular across unreliable noisy networks to enhance data integrity and confidentiality. Their role is to detect and correct errors in data transmission or storage, thus safeguarding the information from corruption or unauthorized alterations [1,2,3]. The authors of [4] extend classical error correction methods to distributed communication networks, introducing network error correction. It leverages network coding principles that require redundant data to correct errors and ensure reliable communication in the presence of noise. Paper [5] addresses the challenges of reliable UAV-to-ground communication and relies on iterative message-passing techniques in the decoding process to enhance error correction and ensure robust data transmission. Paper [6] presents a novel method combining cryptography and error correction to detect and correct transmission errors in wireless communication. The method in [6], termed Joint Channel Coding and Cryptography, uses cryptographic check values for error recovery, achieving a coding gain of 0.72 dB while maintaining security requirements. This approach addresses the inherent error-proneness and security challenges in wireless transmission, providing a significant improvement over traditional convolutional coding methods. The authors in [7] use multi-path capillary routing combined with forward error correction to enhance the reliability of real-time streaming over unreliable networks. By leveraging redundant packets and a dynamic feedback mechanism, they adjust forward error correction overhead as needed to combat packet losses effectively. The authors of [8] present a pilot-free polar-coded transmission scheme that leverages frozen bits for joint channel state information estimation and decoding, significantly improving performance over traditional pilot-assisted transmission. In paper [9], a general framework for error detection in symmetric cryptography ciphers that proposes an operation-centered approach is presented. It enumerates and analyzes arithmetic and logic operations within ciphers to apply suitable error-detecting codes (EDCs) for efficient fault detection. Paper [10] reviews various error control techniques in bio-cryptography, focusing on methods such as score-based thresholding, quantization, and error correction coding. The findings in [10] highlight the challenges of biometric variability and the need for robust error control mechanisms in bio-cryptographic systems to ensure secure and accurate authentication. The authors of [10] also discuss the importance of selecting appropriate error correction methods tailored to specific biometric modalities and their error characteristics. Similarly, the authors of [11] examine the vulnerability of biometric encryption systems, particularly focusing on the security of ECCs in these systems. This study reveals how the error-correcting scheme, which relies on zero insertions, is susceptible to attacks, demonstrating that an attacker could reconstruct the entire key with minimal knowledge of zero locations in the ECC.
Fuzzy extractors enable consistent repeatable cryptographic keys from noisy data such as physically unclonable functions (PUFs), corrupted databases, and biometric information. By employing ECCs, fuzzy extractors compensate for the variability inherent in these data sources, ensuring that a user can reliably regenerate the same key despite slight differences in input [12,13,14,15,16]. A fuzzy extractor that leverages the Learning Parity with Noise (LPN) problem to efficiently correct errors in noisy biometric sources is presented in [17]. The authors of [18] introduce a new cryptographic concept where private keys in asymmetric systems are subject to noise similar to biometric data variability. The authors of [18] propose methods for public key encryption and digital signatures using noisy keys leveraging a computational version of the fuzzy vault scheme for key generation and management. The approach is grounded in graded encoding schemes offering solutions to previous limitations in biometric-based cryptography by allowing multiple public keys from a single noisy biometric source while maintaining user privacy and security.
The work presented in [19] provides an extensive analysis of error correction methods for PUFs, focusing on linear and pointer-based schemes. This work compares various designs on algorithmic levels, emphasizing their implementation complexity, error probabilities, and Field Programmable Gate Array (FPGA) resource utilization. This comprehensive study aims to optimize error correction in key generation from PUFs, balancing between security, resource efficiency, and error rates in different scenarios.
The authors of [20] propose an innovative approach to enhance the reliability and efficiency of cryptographic key generation from static random access memory (SRAM) PUFs. They introduce a soft decision helper data algorithm that significantly reduces the number of SRAM cells required for key generation. This method leverages the variability in individual cell error probabilities to optimize error correction, offering a more efficient alternative to hard decision decoding techniques traditionally used in this context. The work focuses on enhancing the efficiency and reliability of key generation from SRAM PUFs using a low-overhead soft decision helper data algorithm (HDA). This approach significantly reduces resource usage and the size of the PUF needed, resulting in a more practical and efficient solution for secure key storage in cryptographic systems, especially in hardware-constrained environments. The research carried out in [21] provides a comprehensive review of various HDAs used for key generation in PUFs. The authors discuss the challenges in ensuring key reproducibility, uniformity, and control in PUF-based systems and analyze different approaches to helper data generation, including error correction schemes and entropy compression methods. The study attempts to identify new threats and open problems in the field, contributing to the advancement of secure and efficient key generation techniques for PUFs.
The collective work of [22,23,24,25] explores a novel approach to cryptographic key generation using PUFs and response-based cryptography (RBC). It shifts the computational burden of error correction to the server side in distributed systems, using a parallel Message Passing Interface (MPI)-based implementation for efficient key recovery. This method is particularly beneficial for Internet of Things (IoT) devices with limited processing power, enhancing both security and computational efficiency. The work presented in [26] proposes a novel method to create cryptographic keys from PUFs by replacing traditional error correction with key fragmentation and efficient search engines. This approach minimizes the error rates and computational requirements, making the key generation process more efficient and secure, particularly suitable for environments with constrained computing resources.
We suggest error detection and key recovery methods that are fundamentally different from the error-correcting schemes presented in the reference papers above. Our approach provides a novel perspective on the integration of error correction in cryptographic systems that can operate without data helpers in noisy and jammed communication networks. Our findings underscore the potential of this method in enhancing the reliability and security of cryptographic key generation, particularly in scenarios where traditional error correction methods may fall short. Our work opens new avenues for research in cryptography and error correction, promising more secure and efficient solutions for data integrity and confidentiality in the presence of errors (and noise) in transmission or storage.
The structure of our work is outlined as follows. Section 3 delves into the role of noise in cryptography, explaining how it is used to conceal data to prevent potential attacks over unsecured networks. Section 4 delves into the concept of the Challenge–Response Pair (CRP) mechanism. It explains how CRPs can be generated through various methods, particularly focusing on the use of biometric protocols and digital files. Section 5 describes a novel cryptographic protocol called Response-Based Key Encapsulation Mechanism (R-KEM) that uses a CRP mechanism to encapsulate ephemeral keys with a subset of the responses. This section provides a comprehensive explanation of the protocol’s operation via illustrative examples and methods for improvement. Section 6 presents the experimental work. The results showcase the relationship between error rates and noise levels, the efficiency of key recovery in terms of throughput per second, the duration required for key recovery as a function of error occurrences, and the likelihood of failure in identifying a match. Section 7 discusses the findings and the efficacy of the proposed protocol. Section 8 outlines directions for future research.
3. Noise Injection in Cryptography
Noise injection in cryptographic keys refers to the intentional introduction of random changes into the key generation or key handling process. The purpose of injecting noise is to enhance the security and resilience of cryptographic systems against various attacks, including side-channel attacks, differential power analysis, and fault attacks [27,28]. By adding noise to cryptographic keys, the keys become less predictable and exhibit increased entropy, making it more challenging for an attacker to derive the original key. The noise acts as a form of obfuscation that masks the underlying key data, thus increasing the level of difficulty in exploiting vulnerabilities in cryptographic algorithms or implementations.
There are several techniques for injecting noise into cryptographic keys. One common approach is to use physical properties such as heavy magnetic noise, random electrical noise, a random number generator, quantum effects, or thermal noise (as a source of randomness during key generation [29,30,31,32]). This ensures that the resulting keys have a high degree of entropy and are resistant to deterministic attacks. Another method is to apply random noise injection during key handling or cryptographic operations. For example, in key exchange protocols, random noise can be introduced to obscure the exchanged key material, preventing eavesdroppers from gaining information about the shared secret. Additionally, noise injection is used to protect cryptographic keys stored in hardware devices by introducing difficulty for an attacker attempting to extract or analyze the key through side-channel attacks or invasive probing.
The effectiveness of noise injection depends on the quality and randomness of the introduced noise. It is important to ensure that noise does not compromise the security of keys or create unintended vulnerabilities. Additionally, noise injection techniques should be carefully designed to prevent reverse engineering or statistical analysis, making sure the noise remains unpredictable and does not expose any sensitive information.
4. CRP Mechanism
CRPs are a fundamental component in the domain of cryptography, particularly in authentication protocols. The mechanism is based on the principle of proving one’s identity or authenticity without revealing the actual secret or key involved in the process. This method aids in mitigating the risks associated with the direct transmission of sensitive information over potentially insecure channels.
Challenge: The verifier (which could be a server, system, or any entity requiring authentication of another entity) issues a challenge to the requestor (the entity attempting to prove its identity, such as a user or a device). This challenge is typically a randomly generated value or a specific query designed to produce a unique response based on a shared secret. Figure 1 illustrates how the challenge is generated from the crypto table shared between the user and the server. The challenge is designed to ensure that the response will be dynamic and unique for each session, thus preventing replay attacks where an attacker might reuse a previously intercepted response to gain unauthorized access.
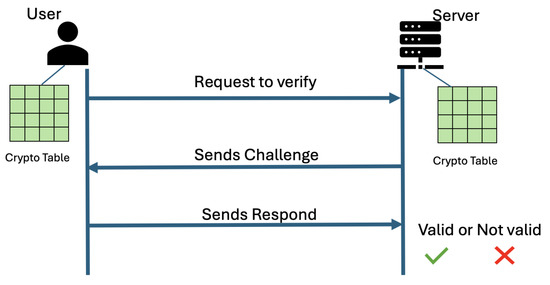
Figure 1.
Challenge response pair mechanism for authentication. The user requests to verify itself. The server, having access to the same crypto table, issues a challenge, and the user utilizes the crypto table to generate a response unique to that challenge. The server can verify the user’s authenticity by generating the corresponding response on its own and comparing it with the received one.
Response: Upon receiving the challenge, the requestor computes a response using a pre-shared secret or a cryptographic key that both the requestor and verifier have agreed upon in advance. This computation often involves cryptographic algorithms that ensure the response is securely tied to the challenge. The key aspect here is that the response should be impossible (or computationally infeasible) to generate without possessing the secret, thereby ensuring that only the legitimate requestor can produce the correct response.
CRPs can be derived from a variety of sources, including PUFs, digital files, or biometric data. During the enrollment phase, the verifier leverages these sources of randomness to generate unique responses tailored to each entity. In the subsequent verification cycles, the CRP mechanism is repeated to produce the corresponding responses, which are essential for both authentication and decryption processes.
The overview of how these CRPs can be generated from digital files and biometric information is provided next in Example of CRP Generation for Noise-Tolerant Cryptographic Protocols.
Example of CRP Generation for Noise-Tolerant Cryptographic Protocols
Operating a terminal device in noisy networks: Before releasing the terminal device (a rover, a drone, some other kind of robot, etc.) in the noisy network, a fixed set of encrypted commands are downloaded during what is called the enrollment cycle, which is described below. The commands can be anything that is appropriate to the application, like a set of navigational waypoints, a simple directional movement, or anything else of arbitrary complexity. The command files can be encrypted with a symmetric cipher, each with its own separate key. Only the cipher texts are saved onto the terminal device, while the plain texts and keys are kept in the server driving the device. The CRP mechanism needed to encapsulate these keys with a subset of responses, as presented in Section 5, is directly based on the encrypted commands.
During the initial key encapsulation cycle, which is done during enrollment, the system hashes each encrypted command (that is, it hashes the cipher text) using the extended output Secure Hash Algorithms; SHA3-256 cryptographic hash function. A password that is shared between the two devices produces sets of challenges, which the system uses to query the hash digests of the cipher texts and from those queries produce sets of responses. Finally, for each set of responses, the key used to encrypt the associated command data produces a subset of responses, where the responses that are kept correspond to the set positions of the key. Responses corresponding to unset key positions are discarded, along with the key once the process is completed.
The terminal device loaded with the encrypted command data and the shared password, which go out into the field is deployed.When the device operator wishes to issue a particular command to the terminal device, they transmit the response subset associated with the required command. This transmission can be corrupted in transit; alone, this transmission can tolerate up to 40% noise. Combined with additional ECCs that we discuss, we expect that this technology can exchange bit-perfect keys at staggering levels of corruption. To recover the command, the terminal device receives a corrupted response subset. The device uses its shared password, the cipher text of the command file, and the same CRP mechanism to produce a full set of responses from the cipher text; this response set will be a pristine version of the responses computed during enrollment. The device then runs the matching algorithm described in Section 5, matching the full set of responses with their received subset, thereby reconstructing the set and unset bit positions and recovering the key despite the noise injected in the subset of responses.
Template-less key generation from biometric images: An additional application involves the use of biometric images for the CRP mechanism. Each biometric image is used as a PUF, which represents an innovative framework within the realm of security technologies, leveraging distinctive and inherent physical traits of individuals to construct resilient and non-replicable digital identifiers. As opposed to conventional security systems that preserve sensitive data in centralized databases, such as passwords, fingerprints, or facial features, the idea of using biometric PUFs to generate keys without storing facial information is an exciting concept.
This innovative methodology not only mitigates the vulnerabilities associated with the centralized storage of biometric information but also augments overall security. Biometric PUFs find diverse applications, notably in secure access control systems, identity verification for financial transactions, as well as safeguarding sensitive data within healthcare and governmental contexts.
In the key generation process, facial enrollment initiates the collection of facial landmarks through multiple iterations. To generate unique responses, various techniques (such as landmarking techniques) where the Euclidian distances between a substantial landmark point on the face and a random point are utilized. Another technique known as the Johnson–Lindenstrauss lemma algorithm can also be used to project a higher dimensional face to a lower dimension.
In the key recovery procedure, one facial scan is performed and the challenge is used to compute distances between landmarks and the fixed point, thereby producing a subset of responses essential in key recovery. Potential errors arising from variations in lighting conditions or facial expressions are mitigated through the application of the key recovery mechanism discussed in Section 5.
5. Key Encapsulation and Recovery Method Using CRP
In this protocol, the initial step involves the generation of a key with a length of N Bits with a random number generator (RNG). This key is called an ephemeral key (K). To encapsulate this key, we use a CRP mechanism that generates a set of N P-bit long responses from N Challenges. One example of a protocol is where the N challenges are generated from an RNG; they point at a memory array programmed with randomly selected zeros and ones to generate the N responses or one of the examples mentioned in Example of CRP Generation for Noise-Tolerant Cryptographic Protocols. A subset of responses is generated from the set of N responses by keeping only the positions in K where the bit value is 1 and discarding the positions with a bit value of 0. On average, this results in N/2 responses. An example of the protocol of interest is to introduce noise into the system by randomly flipping T out of P bits with the responses of the subset. T has to be kept within an acceptable threshold. This noisy subset, along with the cipher text of any secret message that was generated using K as the key, is transmitted over the communication channel, which can also increase the noise level. See Algorithm 1.
| Algorithm 1 R-KEM Key Encapsulation | |
| 1: | ▹ Generate N-bit ephemeral key K |
| 2: | |
| 3: | |
| 4: | |
| 5: for in S do | |
| 6: | |
| 7: end for | |
| 8: Transmit | |
Upon receiving the transmitted data, the receiver reconstructs the set of N responses with the same CRP mechanism and initiates the search process. To recover K, the receiver compares the received subset with the complete set of responses. For each response of the subset, a match is considered successful when only one match is found within the search window (); in such a case, the receiver identifies and saves the position as 1. However, if multiple matches are detected, a collision is indicated; all the positions that matched are stored for later analysis and error-correcting schemes. Conversely, if no match is found within the window, a failure to detect is indicated, and all corresponding positions are marked for the error-correcting schemes. The full algorithm is explained in Algorithms 2 and 3.
| Algorithm 2 R-KEM Error Detection |
| 1: Input: Subset of responses , full set of responses , and threshold T 2: Initialize , , and 3: Initialize lists: NoMatches[], OneMatch[], Collisions[] 4: while do 5: Compute Hamming distance for all with 6: if for all k then 7: for all k do 8: Append to NoMatches[] 9: end for 10: Increment i and j by 1; set 11: else if for exactly one k then 12: Append to OneMatch[] 13: Increment j by 1, , set 14: else 15: Find the smallest and largest k values where 16: for all k values found do 17: Append to Collisions[] 18: end for 19: Increment j by 1; set ; set 20: end if 21: end while 22: Output: NoMatches[], OneMatch[], Collisions[] |
Throughout the search process, the receiver accumulates information regarding the positions that resulted in matches, as well as those that had collisions or failures to detect. The matched positions are retained as a “1”, whereas the positions associated with collisions or failures are used to discover the correct key.
| Algorithm 3 R-KEM Key Recovery |
| 1: Input: NoMatches[], OneMatch[], Collisions[], N, C (Cipher Text) 2: Initialize K as an array of zeros with length N 3: for each position in OneMatch[] do 4: Flip the bit at position in K 5: end for 6: if NoMatches[] and Collisions[] are empty then 7: Attempt to decrypt C with K to obtain M 8: Output: K if M is a valid plaintext 9: else 10: Combine NoMatches[] and Collisions[] into a list of lists 11: for each combination of bits from do 12: Flip the bits in K according to 13: Attempt to decrypt C with new K to obtain M 14: if M is a valid plaintext then 15: Output: K 16: break 17: end if 18: end for 19: end if 20: Output: Failed to find the key |
This protocol incorporates a step-by-step approach that enables the receiver to recover the correct key by iteratively analyzing the responses, identifying matches, and addressing collisions and failures to detect. By the conclusion of the search process, the receiver will possess the necessary information to determine the positions that correspond to successful matches and those requiring further investigation by flipping one bit at a time.
A collision occurs when two randomly selected responses, ra and rb (each consisting of P bits), share at least P-T common bits. The assumption made in this protocol is that all responses follow a binomial distribution, where the probability (q) of obtaining a state “0” is equal to the probability of obtaining a state “1” (q = 0.5). To ensure the protocol’s effectiveness, it is necessary to ensure that the probability of collision between the responses of the orderly subset and randomly chosen responses remains sufficiently low [33].
A model based on binomial distribution has been developed that focuses on three key variables within the algorithm: the rate of injected noise in the subset of responses, the length of the responses (P), and the threshold (T) in terms of the number of bits. The number t represents the number of erratic bits below the threshold T. This model seeks to find the optimal values for these variables, striking a balance that minimizes collision probabilities while maintaining the protocol’s efficiency and reliability.
The formula is expressed as
5.1. Search Space Needed for Key Recovery
Once Algorithms 2 and 3 have been executed, the worst-case scenario required to find the correct key can be quantified mathematically. This calculation is based on the length of the sublists within the Collisions and Nomatch lists. The size of the sublist is multiplied together to obtain the total number of possible key combinations. If we denote the Collisions list as A and Nomatch list as B, we will have the following:
Let and , where and are the sublists, and and are the lengths (number of elements) of the sublists in lists A and B, respectively. The total number of possible combinations C can be represented as the product of the lengths of each sublist, as follows:
5.2. Example
Consider the ephemeral key represented by a 6-bit sequence 011010. In Figure 2, bit positions are labeled with white squares denoting “0”s and black squares denoting “1”s. The full set of responses, each of length P bits where P is elective, correspond in black to the “1” positions in the ephemeral key, forming the subsets of responses. After noise injection, these subsets are transmitted to the receiver. Utilizing the CRP mechanism, the receiver generates a full set of responses and uses the search algorithm. This algorithm assesses the hamming distance between each subset and response in the search window against a threshold to determine matches, categorizing them into OneMatch, NoMatch, and Collisions. For instance, the initial search window may detect positions 0 and 1 as matches, thus recording them in the Collisions list. The second window may reveal a single match at position 2 classified into OneMatch, and the last search, finding no matches, adds positions 3, 4, and 5 to NoMatch. The recovery algorithm first utilizes OneMatch to generate a preliminary key. It then combines Collisions and NoMatch to exhaustively produce all possible key combinations, designated as keys (1) through (7).
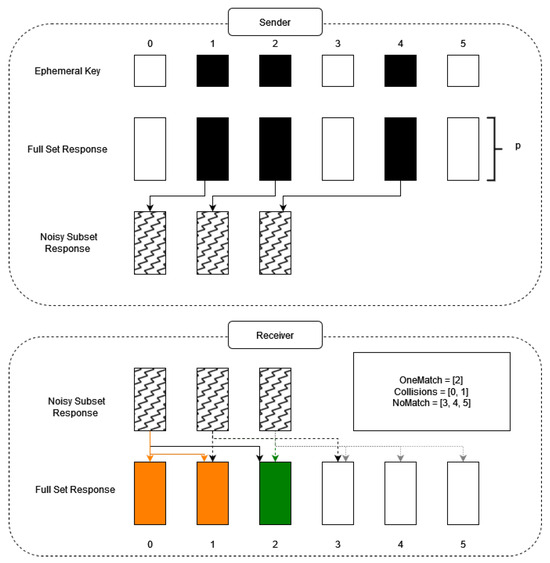
Figure 2.
Simplified illustration of key encapsulation on the sender side and error detection process on the receiver side. The orage responses represent the collision, green represents one match, and white represents the no match responses. The numbers in front of the OneMatch, Collisions, and NoMatch variable represents the positions of the responses that showed the characteristics of these variables.
(1) 001000
(2) 101100
(3) 101010
(4) 101001
(5) 011100
(6) 011010
(7) 011001
(2) 101100
(3) 101010
(4) 101001
(5) 011100
(6) 011010
(7) 011001
In the process of key recovery, although key (6) is the actual correct key, the receiver determines the correct key through a process of elimination. This involves decrypting the ciphertext with each potential key, in sequence, until a readable plaintext is obtained. This method ensures that even without prior knowledge of the correct key, the receiver can systematically identify it by testing each one against the ciphertext.
Enhanced List Processing
The key recovery protocol is refined by incorporating additional comparison steps after collecting the OneMatch, Collision, and NoMatch lists. By cross-referencing the OneMatch list with both the Collision and NoMatch lists, any common positions should be removed from the latter two. If this elimination results in a sublist with a single element, then this position should be reallocated to the OneMatch list, as it represents the sole possible match for its corresponding search window. This strategy not only streamlines the search space but also enhances the efficiency of the key recovery process. A step-by-step approach of this method is shown in Algorithm 4.
| Algorithm 4 Enhanced List Processing |
| 1: Input: OneMatch[], Collisions[], NoMatch[] 2: Procedure: RefineKeyRecovery(OneMatch, Collisions, NoMatch) 3: for each position in OneMatch[] do 4: if is in Collisions[] then 5: Remove from Collisions[] 6: end if 7: if is in NoMatch[] then 8: Remove from NoMatch[] 9: end if 10: end for 11: for each list L in {Collisions[], NoMatch[]} do 12: if Length of L is 1 then 13: Move element from L to OneMatch[] 14: end if 15: end for 16: Output: Updated OneMatch[], Collisions[], NoMatch[] |
This collection of scatter plots presented in Figure 3 presents a comparative analysis of error rates before and after the implementation of the enhancement technique (segmented by varying response lengths of 8 to 512). Each subplot correlates the pre-enhancement error rates on the x-axis with the post-enhancement error rates on the y-axis; thus, the presence of a trend line in each plot bearing a positive slope of less than 45 degrees suggests an overall reduction in errors. The data points predominantly reside below the line y = x, implying that for most instances, the enhancement method has successfully lowered the error rates. Although there is a scattering of points on this line indicating cases of unsuccessful enhancement, the overall distribution indicates a clear trend of improvement. Notably, the effect of the enhancement does not appear to be uniform across all response lengths (as indicated by the varying density of points below the trend line in each subplot), yet it consistently indicates a tendency towards error reduction. This pattern demonstrates the general efficacy of the enhancement process. This reduction is substantial, considering that the number of potential keys to be generated is contingent upon the sizes of the generated lists, as shown in Equation (2).
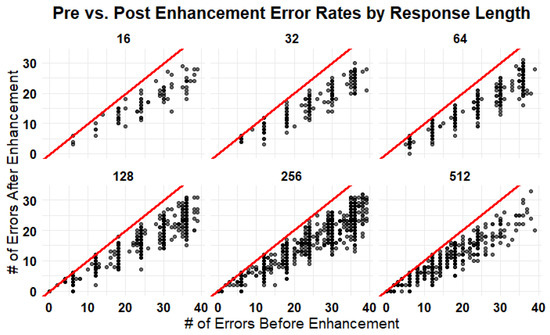
Figure 3.
Reduction in error rates following enhancement across various response lengths. This preliminary enhancement step significantly lowers error rates, particularly in instances with initially high error counts, thereby streamlining the key recovery process. Without this crucial enhancement, cases with large error quantities might be deemed infeasible for key recovery due to the excessive computational effort required to sift through numerous possible key combinations. The red line represents y = x. Dots on the line indicate no difference in error rate before and after the enhancement, while dots below the red line represent a lower error rate after the enhancement.
6. Experimental Results
This section presents the outcomes of our experiments conducted on a 12th Generation Intel® Core™ i7-12700K processor operating at 3600 MHz featuring 12 cores and 20 threads. The system is equipped with 32 GB of RAM and runs on Windows 11. For each response length and noise level, the protocol was executed 10,000 times to collect data. Random noise in the responses was simulated using random sampling and a normal distribution to introduce variability into each response. Key performance metrics—such as collision rate, key recovery latency, key recovery throughput, and failure rate—were recorded. These metrics were evaluated across various noise levels and different values of the parameter P to assess the protocol’s resilience and efficiency under various conditions.
Furthermore, increasing the length of P leads to improved performance, particularly in handling higher levels of noise. As the response length is extended, the protocol becomes more resilient to noise-induced errors and maintains successful key recovery at increasingly higher noise levels. This suggests that longer response lengths enhance the protocol’s overall performance and reliability, enabling effective operation, even in noisy environments.
Figure 4 compares the theoretical model depicted in Equation (1) with the empirical data collected from our experiments. This comparison assesses the alignment between the theoretical predictions and the observed performance under different noise levels and response lengths. The experimental data closely align with the model’s predictions, which shows a significant correlation between the two. This alignment can be attributed to the use of a random number generator for simulating noise injection within the protocol. However, it is important to note that actual noise conditions might exhibit variations from the model due to the complex nature of physical phenomena and experimental environments. The results demonstrate that longer responses exhibit greater resilience to higher noise levels because there is less likelihood of finding exact same responses, which reduces collision rates. The close match between the theoretical and experimental results validates the effectiveness and accuracy of our model in predicting the protocol’s performance. Furthermore, this graph provides valuable insights for configuring the system based on specific use cases and environmental conditions. By analyzing the relationship between noise levels and collision rates, we can determine the optimal response length to balance performance and resource constraints.
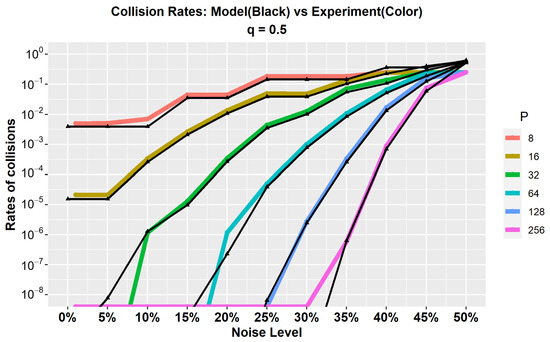
Figure 4.
Comparative analysis of collision rates: model predictions vs. experimental results across different noise levels. The plot demonstrates the relationship between collision rates and varying noise levels where the black lines represent the theoretical model and the colored lines depict the experimental data for different values of parameter P.
Figure 5 depicts the key recovery throughput measured in keys-per-second across different noise levels and response lengths (P). As anticipated, the bar graph reveals a clear relationship between the noise level and the effectiveness of key recovery for varying response lengths.
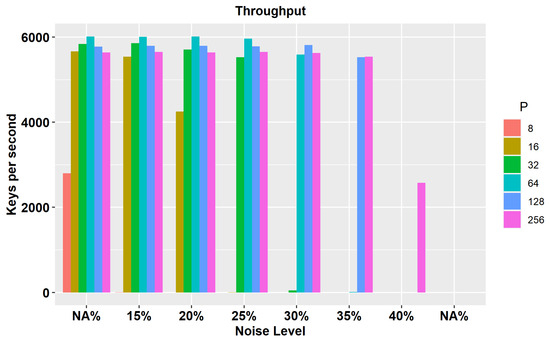
Figure 5.
Key recovery throughput. This bar graph highlights the rate at which keys are successfully recovered per second thus illustrating the impact of different response lengths and noise levels on recovery efficiency.
As the noise level increases, the shorter response lengths show decreased capability in recovering keys, resulting in reduced efficiency. This observation aligns with expectations since shorter response lengths are more susceptible to the adverse effects of noise interference and higher error rates. However, it is noteworthy that, even with higher noise levels, longer response lengths can still remain effective for key recovery until the threshold reaches slightly above 40 percent noise. This behavior is due to the minimal or zero collisions found in longer responses. Equation (1) explains how longer responses can tolerate higher noise levels without collisions. Consequently, key recovery can be performed more efficiently, increasing throughput for longer responses. At 50 percent noise, the response becomes almost random and indistinguishable from each other. Below 40 percent, the probability of collisions remains very low because longer responses are still distinguishable.
These findings show the importance of response length selection when considering noise levels in the system. Shorter response lengths may be suitable in low-noise environments (where key recovery throughput remains efficient). On the other hand, longer response lengths are more advantageous in scenarios where noise levels are expected to be high, since they provide a greater degree of resilience and enable the successful recovery of keys despite the presence of significant noise interference.
Figure 6 demonstrates the efficiency of the key recovery protocol in managing error correction under varying levels of injected noise. The vertical lines in the figure represent the levels of noise introduced into the system, illustrating the protocol’s tolerance to high percentages of noise. The curve plotted shows that the protocol rapidly corrects up to slightly more than 20 erratic bits, maintaining a latency of less than 2 to 3 s. However, when the noise level approaches slightly below 40%, the number of errors begins to exceed 20, which delays the key recovery process. This result is attributed to the searching mechanism discussed in Algorithm 2 which identifies the precise locations of errors. By streamlining the search process for key recovery, the system effectively bypasses the computationally intensive approach of “brute force” searching, which results in fast and accurate error correction even in the presence of high noise levels.

Figure 6.
Key recovery latency versus error count in noisy cryptographic environments. This plot demonstrates the protocol’s capacity to quickly correct a substantial quantity of errors found in the ephemeral key. It shows the efficiency of key recovery processes. The vertical bars represent the noise injection rate, illustrating how varying error rates impact the recovery latency. The red line represents the latency and the dots are the data points.
Figure 7 illustrates the effect of noise injection on the failure rate in correctly identifying matches. Specifically, it highlights the frequency at which the system fails to pinpoint the matching position across all three lists (Onematch, Collisions, and Nomatch). Such failures result in unsuccessful key recovery attempts since the potential key combinations do not align with the correct key due to these errors. However, note that the plot shows the resilience of longer response lengths to errors, indicating their ability to maintain lower failure rates despite increasing noise levels.
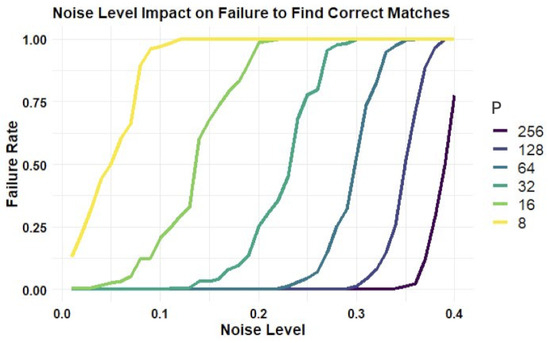
Figure 7.
The impact of noise levels on match detection failure. This plot illustrates how high noise levels contribute to the increased likelihood of failing to identify a matching position within `Collisions’ or `NoMatch’ lists (which leads to unsuccessful key recovery attempts). Notably, extending the response length tends to reduce these failure rates, thus enhancing the reliability of match detection (even in the presence of noise).
Comparison with Other Works
As illustrated in Figure 8, our methodology, R-KEM, demonstrates a significant enhancement in performance compared to the RBC protocol, as described in the works of [22,24]. Similar to our approach, RBC is a CRP-based error detection and correction scheme implemented on the server side. However, while RBC relies on exhaustive search methods for key recovery, RBC_4 and RBC_8 incorporate a fragmentation approach that divides the key into n fragments, adds padding, and then proceeds with key recovery. As n increases, key recovery becomes faster; for instance, RBC_8 is relatively fast due to higher fragmentation. Nevertheless, increasing n further can compromise security, as attackers can more easily gain information about the key when the fragmented portions are smaller, making it easier to find a match. In contrast, the R-KEM protocol’s advanced error correction capability is attributed to its innovative erratic position detection technique, which identifies the correct key faster without the need for fragmentation, even with a high number of errors. While RBC may be suited for servers with abundant computational resources, our approach is tailored to endpoint devices, which may be limited in computational power. This capability to effectively correct errors in noisy environments using average computing resources, without sacrificing security, distinctively positions our protocol as advantageous over conventional methods.
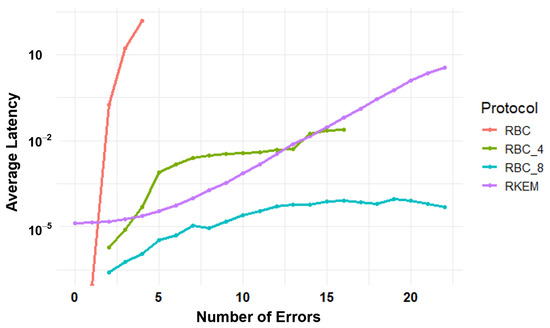
Figure 8.
Comparative analysis of latency in error correction: RBC protocol versus R-KEM protocol on a logarithmic scale. Note: in the R-KEM protocol, the number of errors represents the number of collisions (with each collision requiring correction of at least 2 positions). Thus, two collisions equate to correcting at least four positions.
Table 1 compares the search spaces needed for key recovery in RBC and R-KEM. The RBC search space is calculated using the binomial coefficient formula, which illustrates the combinatorial nature of RBC’s error correction process for a space of 256 potential error positions. This search space represents the total number of unique pairs of error positions that RBC can process when correcting several errors.

Table 1.
Comparison of error correction capabilities and search space sizes for RBC and R-KEM protocols derived from theoretical formulas.
On the other hand, the R-KEM search space is derived from the formula based on the product of lengths of sublists (Equation (2)). This method reveals a consistently sized search space despite an increase in the number of errors that can be corrected. In the context of this comparison, each collision is considered equivalent to a single error, with the understanding that each collision involves the need to examine at least two positions. Therefore, when the table indicates that R-KEM is correcting for 15 errors, it is implied that a minimum of 30 positions require examination. The search space presented in the table reflects the minimum possible combinations, under the assumption that each collision involves only two positions to be checked.
This highlights the efficiency of R-KEM in environments prone to high noise levels, where error susceptibility is greater. Such a robust error correction capability demonstrates R-KEM’s potential for significantly improving reliability in adverse conditions.
7. Discussion
The analysis of the protocol shows its robustness and efficiency in key recovery, even in substantial noise interference, which is a common challenge in cryptographic systems operating within networks affected by poor coverage or jamming. Our results in collision rate and throughput illustrate how response lengths can be tailored to the demands of the application.
The strength of our protocol lies in its error detection mechanism, which compares responses within a predefined search window. With longer responses, this approach significantly reduces collisions while providing valuable positional information about any mismatches. This, in turn, accelerates key recovery by eliminating the need for brute-force searching, requiring only a few bit-flipping corrections to reconstruct the original key.
In terms of memory usage, at higher noise levels, longer responses consume less memory than shorter responses during the key recovery process. This is because longer responses result in fewer collisions, reducing the space required for searching the matching key. In contrast, shorter responses have a higher collision rate, necessitating more bit-flipping operations to identify the correct key, which in turn increases both memory consumption and processing time.
With no noise, the scenario changes significantly. For shorter response lengths (below 64 bits), occasional collisions still occur due to the higher probability of generating identical responses. In this range, both time complexity and space complexity decrease as response length increases, since longer responses reduce collision rates and minimize the need for additional computations. However, beyond a certain response length, the complexity begins to increase. This is because, with longer responses, no errors are encountered, and the primary factor influencing computational cost becomes the length of the response itself. As a result, once collisions stop appearing in our key recovery protocol, both time and space complexity follow a linear growth of .
One limitation of our approach is that the error correction mechanism is specifically designed for CRP-based key encapsulation protocols. As a result, while our method effectively recovers cryptographic keys encapsulated using our scheme, it does not detect errors in conventionally transmitted data over standard communication channels. This specificity highlights the need for further evaluation in diverse real-world scenarios.
While our simulated implementation has produced promising results, real-world deployment is essential for a more accurate assessment of performance. The findings presented in this paper offer valuable insights into expected outcomes and potential limitations in practical settings. However, deviations from our results are anticipated, particularly due to the unpredictable nature of noise in certain environments. In such cases, the protocol may not maintain performance at noise levels up to 40 percent as demonstrated here. This limitation, however, can be mitigated by increasing response lengths or adjusting other critical parameters that may prove influential during real-world implementation.
8. Future Work
Building on the findings of this work, we will focus on two key areas to further develop and refine the error correction system. First, we will improve its integration with biometric cryptosystems by implementing adaptive techniques to counteract environmental noise and template variability, ensuring more reliable key recovery. Second, we will improve its application in noise-resistant key exchange mechanisms by analyzing its performance under various error models and jamming conditions.
Biometric responses, in particular, are subject to relatively high amounts of response noise compared to items more consistent such as a memory PUF, to the point that brute-force keyspace search algorithms like RBC cannot feasibly correct enough key error to be useful in a biometric application. Whereas an RBC approach can correct four-to-six bit errors in a key recovery process, our new system is capable of correcting up to 20 or 25 bit errors promptly, rendering our system an ideal choice for a templateless biometry application. To empirically evaluate the efficacy of this protocol, we plan to test it using a variety of front-facing face image databases, including a large set of faces purpose-generated by Artificial Intelligence (AI), which contains a great deal of diversity across age, gender, and ethnicity. Due to the uniqueness of facial images generated through AI, this dataset is optimal for testing this key recovery protocol to its limit. For instance, as the images will have variations, i.e., an individual gaining weight and/or changing facial hair over a period of time, it will create an impact on regenerating the right key during the authentication phase to match it with enrollment, which will have been taken before this transformation has occurred. Also, lighting conditions have an impact on landmark placing technology, as they are sensitive and would result in error bits in the recovered key. For this, we need a robust key recovery scheme that will operate efficiently in a noisy environment. The source of this noise can be any factor, and the protocol should withstand all sorts of situations. These circumtances show the effectiveness and importance of noisy key recovery protocol in the field of templateless biometry, where most of the current research is focused, as it enables biometric authentication without retaining any biometric information of an individual.
The ability to withstand significant response noise is crucial in the design of response-based key exchange systems that are robust against substantial signal corruption, such as poor signal reception or the presence of military jamming. By applying this technology to systems that conduct ephemeral key recoveries from hash-based challenge–response mechanisms, the performance of these systems can be significantly enhanced, surpassing their conventional capabilities. To rigorously evaluate the resilience of this approach, we plan to conduct both simulated and physical tests on rovers or drones configured to operate using the hash-based challenge–response system. These tests will be designed to assess how these systems will perform under actual (realized) conditions. This empirical testing will provide valuable insights into the systems’ robustness and their ability to maintain operational integrity in environments with high levels of signal interference.
9. Conclusions
In this study, we conducted a comprehensive analysis of the R-KEM Mechanism. Our findings demonstrate the protocol’s ability to securely encapsulate ephemeral keys in significant environmental noise or deliberate noise injections, ultimately facilitating the generation of error-free cryptographic keys for decryption on endpoint devices. This protocol outperforms other CRP-based error detection mechanisms, such as RBC, rendering it particularly useful for devices constrained by computational resources.
Author Contributions
Conceptualization, B.C. and D.G.M.; methodology, B.C. and D.G.M.; software, D.G.M.; validation, D.G.M.; formal analysis, D.G.M.; investigation, D.G.M. and B.C.; resources, D.G.M.; data curation, D.G.M.; writing—original draft preparation, D.G.M.; writing—review and editing, D.G.M., M.L.G., S.J., M.A. and S.A.; visualization, D.G.M.; supervision, B.C.; project administration, B.C.; funding acquisition, B.C. All authors have read and agreed to the published version of the manuscript.
Funding
Research was sponsored by the Army Research Laboratory and was accomplished under Cooperative Agreement Number W911NF-23-2-0014. The views and conclusions contained in this document are those of the authors and should not be interpreted as representing the official policies, either expressed or implied, of the Army Research Laboratory or the U.S. Government. The U.S. Government is authorized to reproduce and distribute reprints for Government purposes notwithstanding any copyright notation herein.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Datasets will be made available upon request through the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| CRP | Challenge–Response Pair |
| ECC | Error-Correcting Code |
| EDC | Error-Detecting Code |
| HDA | Helper Data Algorithm |
| IoT | Internet of Things |
| PUF | Physically Unclonable Function |
| RBC | Response-Based Cryptography |
| R-KEM | Response-Based Key Encapsulation Mechanism |
References
- Carlet, C.; Crama, Y.; Hammer, P.L. Boolean Functions for Cryptography and Error-Correcting Codes; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Bruen, A.A.; Forcinito, M.A. Cryptography, Information Theory, and Error-Correction: A Handbook for the 21st Century; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Júnior, W.G.; Júnior, D.P. A proposal of a cryptography algorithm with techniques of error correction. Comput. Commun. 1997, 20, 1374–1380. [Google Scholar]
- Yeung, R.W.; Cai, N. Network error correction, I: Basic concepts and upper bounds. Commun. Inf. Syst. 2006, 6, 19–36. [Google Scholar]
- Dong, P.; Xiang, X.; Liang, Y.; Wang, P. A Block-Based Concatenated LDPC-RS Code for UAV-to-Ground SC-FDE Communication Systems. Electronics 2023, 12, 3143. [Google Scholar] [CrossRef]
- Ziviae, N.; Ruland, C.; Rehman, O.U. Error correction over wireless channels using symmetric cryptography. In Proceedings of the 2009 1st International Conference on Wireless Communication, Vehicular Technology, Information Theory and Aerospace & Electronic Systems Technology, Aalborg, Denmark, 17–20 May 2009; IEEE: Piscataway, NJ, USA, 2006; pp. 752–756. [Google Scholar]
- Gabrielyan, E.; Hersch, R.D. Rating of Routing by Redundancy Overall Need. In Proceedings of the 2006 6th International Conference on ITS Telecommunications, Chengdu, China, 21–23 June 2006; IEEE: Piscataway, NJ, USA, 2006; pp. 786–789. [Google Scholar]
- Yuan, P.; Coşkun, M.C.; Kramer, G. Polar-coded non-coherent communication. IEEE Commun. Lett. 2021, 25, 1786–1790. [Google Scholar] [CrossRef]
- Breveglieri, L.; Koren, I.; Maistri, P. An operation-centered approach to fault detection in symmetric cryptography ciphers. IEEE Trans. Comput. 2007, 56, 635–649. [Google Scholar] [CrossRef]
- Pussewalage, H.S.G.; Hu, J.; Pieprzyk, J. A survey: Error control methods used in bio-cryptography. In Proceedings of the 2014 11th International Conference on Fuzzy Systems and Knowledge Discovery (FSKD), Xiamen, China, 19–21 August 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 956–962. [Google Scholar]
- Stoianov, A. Security of error correcting code for biometric encryption. In Proceedings of the 2010 Eighth International Conference on Privacy, Security and Trust, Ottawa, OA, Canada, 17–19 August 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 231–235. [Google Scholar]
- Boyen, X. Reusable cryptographic fuzzy extractors. In Proceedings of the 11th ACM conference on Computer and Communications Security, Washington, DC, USA, 25–29 October 2004; pp. 82–91. [Google Scholar]
- Dodis, Y.; Ostrovsky, R.; Reyzin, L.; Smith, A. Fuzzy extractors: How to generate strong keys from biometrics and other noisy data. SIAM J. Comput. 2008, 38, 97–139. [Google Scholar] [CrossRef]
- Arakala, A.; Jeffers, J.; Horadam, K.J. Fuzzy extractors for minutiae-based fingerprint authentication. In Proceedings of the Advances in Biometrics: International Conference, ICB 2007, Seoul, Republic of Korea, 27–29 August 2007; Springer: Berlin/Heidelberg, Germany, 2007; pp. 760–769. [Google Scholar]
- Fuller, B.; Meng, X.; Reyzin, L. Computational fuzzy extractors. Inf. Comput. 2020, 275, 104602. [Google Scholar] [CrossRef]
- Li, N.; Guo, F.; Mu, Y.; Susilo, W.; Nepal, S. Fuzzy extractors for biometric identification. In Proceedings of the 2017 IEEE 37th International Conference on Distributed Computing Systems (ICDCS), Atlanta, GA, USA, 5–8 June 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 667–677. [Google Scholar]
- Herder, C.; Ren, L.; Van Dijk, M.; Yu, M.D.; Devadas, S. Trapdoor computational fuzzy extractors and stateless cryptographically-secure physical unclonable functions. IEEE Trans. Dependable Secur. Comput. 2016, 14, 65–82. [Google Scholar] [CrossRef]
- Herder, C.; Fuller, B.; van Dijk, M.; Devadas, S. Public key cryptosystems with noisy secret keys. Cryptol. Eprint Arch. 2017. Available online: https://eprint.iacr.org/2017/210 (accessed on 20 February 2025).
- Hiller, M.; Kürzinger, L.; Sigl, G. Review of error correction for PUFs and evaluation on state-of-the-art FPGAs. J. Cryptogr. Eng. 2020, 10, 229–247. [Google Scholar] [CrossRef]
- Maes, R.; Tuyls, P.; Verbauwhede, I. A soft decision helper data algorithm for SRAM PUFs. In Proceedings of the 2009 IEEE International Symposium on Information Theory, Montreal, QC, Canada, 22–26 June 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 2101–2105. [Google Scholar]
- Delvaux, J.; Gu, D.; Schellekens, D.; Verbauwhede, I. Helper data algorithms for PUF-based key generation: Overview and analysis. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2014, 34, 889–902. [Google Scholar] [CrossRef]
- Philabaum, C.; Coffey, C.; Cambou, B.; Gowanlock, M. A response-based cryptography engine in distributed-memory. In Intelligent Computing: Proceedings of the 2021 Computing Conference; Springer: Berlin/Heidelberg, Germany, 2021; Volume 3, pp. 904–922. [Google Scholar]
- Lee, K.; Gowanlock, M.; Cambou, B. SABER-GPU: A response-based cryptography algorithm for SABER on the GPU. In Proceedings of the 2021 IEEE 26th Pacific Rim International Symposium on Dependable Computing (PRDC), Perth, Australia, 1–4 December 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 123–132. [Google Scholar]
- Cambou, B.; Philabaum, C.; Booher, D.; Telesca, D.A. Response-based cryptographic methods with ternary physical unclonable functions. In Advances in Information and Communication: Proceedings of the 2019 Future of Information and Communication Conference (FICC); Springer: Berlin/Heidelberg, Germany, 2020; Volume 2, pp. 781–800. [Google Scholar]
- Cambou, B.; Gowanlock, M.; Yildiz, B.; Ghanaimiandoab, D.; Lee, K.; Nelson, S.; Philabaum, C.; Stenberg, A.; Wright, J. Post quantum cryptographic keys generated with physical unclonable functions. Appl. Sci. 2021, 11, 2801. [Google Scholar] [CrossRef]
- Cambou, B.; Philabaum, C.; Booher, D. Replacing Error Correction by Key Fragmentation and Search Engines to Generate Error-Free Cryptographic Keys from PUFs; CryptArchi2019: Prague, Czech Republic Northern Arizona University: Flagstaff, AZ, USA, 2019. [Google Scholar]
- Veyrat-Charvillon, N.; Medwed, M.; Kerckhof, S.; Standaert, F.X. Shuffling against side-channel attacks: A comprehensive study with cautionary note. In Proceedings of the Advances in Cryptology–ASIACRYPT 2012: 18th International Conference on the Theory and Application of Cryptology and Information Security, Beijing, China, 2–6 December 2012; Proceedings 18. Springer: Berlin/Heidelberg, Germany, 2012; pp. 740–757. [Google Scholar]
- Jain, S.; Partridge, M.; Cambou, B. Noise injection techniques in cryptographic keys to enhance security of autonomous systems. In Proceedings of the Autonomous Systems: Sensors, Processing and Security for Ground, Air, Sea, and Space Vehicles and Infrastructure 2023, Orlando, FL, USA, 14–15 April 2025; SPIE: Washington, DC, USA, 2023; Volume 12540, pp. 97–111. [Google Scholar]
- Petrie, C.S.; Connelly, J.A. A noise-based IC random number generator for applications in cryptography. IEEE Trans. Circuits Syst. Fundam. Theory Appl. 2000, 47, 615–621. [Google Scholar] [CrossRef]
- Tuyls, P.; Škoric, B.; Kevenaar, T. Security with Noisy Data: On Private Biometrics, Secure Key Storage and Anti-Counterfeiting; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Alibeigi, I.; Amirany, A.; Rajaei, R.; Tabandeh, M.; Shouraki, S.B. A Low-Cost Highly Reliable Spintronic True Random Number Generator Circuit for Secure Cryptography; World Scientific Publishing Company: London, UK, 2020; Volume 10, p. 2050003. [Google Scholar]
- Ingvarsson, S.; Xiao, G.; Parkin, S.S.; Gallagher, W.J.; Grinstein, G.; Koch, R.H. Low-frequency magnetic noise in micron-scale magnetic tunnel junctions. Phys. Rev. Lett. 2000, 85, 3289. [Google Scholar] [CrossRef] [PubMed]
- Cambou, B.; Philabaum, C.; Hoffstein, J.; Herlihy, M. Methods to Encrypt and Authenticate Digital Files in Distributed Networks and Zero-Trust Environments. Axioms 2023, 12, 531. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).