Abstract
In modern processor architecture, a branch predictor is an important module whose design influences the performance of the processor. Nowadays, the factors affecting the performance of branch predictors have changed from common branches to hard-to-predict branches, which rarely show up but have low prediction accuracy. In particular, the data-related branches are a difficult problem to be handled by the current predictors. In this paper, we continue to study Zangeneh’s BranchNet CNN neural network branch predictor to explore the solution. Due to the observation that some data-related branches are associated with register values, we add BranchNet, a sub-network that handles register values in the offline training phase and modify the above sub-network according to the feedback from the preliminary experiments by adjusting the network parameters and redesigning the network structure. Through that process, it can better learn the relationship between register values and branch results. The experiments were carried out on the SPEC 2017 integer benchmarks. The network was trained and validated on the top five H2P branches of all benchmarks. The results show that the addition of register information reduces the MPKI rate of the top five H2P branches on average, compared to the BranchNet, by 17.32%. Analyzing the results, we find that the network with the addition of register value information has significantly improved the prediction accuracy of certain H2P branches, indicating that the addition of register values is effective in H2P branch prediction.
1. Introduction
Modern processors use techniques like pipelining, cache, superscalar, etc., to improve processor performance [1], and the techniques above require the continuous flow of instructions. In pipeline processors, the next instruction of the branch instructions needs to be fetched before executing. In order not to block the instruction flow, a branch predictor is required to judge which instruction is to be fetched. If the instruction is fetched incorrectly, the processor must waste about 14 to 25 clock cycles to recover the correct instruction flow [2]. Therefore, the branch predictor is a key structure in processor design that affects the performance of the processor.
Branch predictors, developed from static predictors, have shared the latest TAGE predictor and its variants [3,4,5] for decades and are nearly perfect in predicting static branches. According to statistical results [6], today’s state-of-the-art predictors achieve not less than 99% accuracy for 99% of static branch predictions on the SPEC 2017 benchmarks. In that situation, people have shifted their attention from overall prediction accuracy to those specific branches with low accuracy and high MPKI, which have deep impacts on programs. These branches are difficult for predictors which have the inputs of branch history and program counter to predict and have significant influence on program execution and have been called hard-to-predict (H2P) branches.
Neural network branch predictors have been studied since the beginning of this century. In the last decade, the neural network has shown its power in the fields of image recognition, video processing, etc. Researchers have also begun to study branch prediction with machine learning and neural networks, which they regard as a binary classification problem. Through features such as stronger pattern recognition and deeper input history length, the neural network branch predictor shows similar or even higher prediction accuracy than the traditional predictor; for H2P branches, it can also dig deeper into the prediction information hidden in the branching history to improve prediction.
In the proposed neural network branch predictor, the input is still the branch execution history. For some H2P branches, digging deeper into the branch execution history can learn their complex relationship between history and direction so that improving their prediction is achieved. However, for other H2P branches, their execution relies on other information, such as the value of specific registers or data in memory. This is what is not available from the branch history and is one of the reasons why all the current predictors can hardly give the right predictions. But, the neutral predictor’s feature of offline training allows us to collect additional content from other parts of the processor and add it to the predictor’s inputs. Through that process, the predictor will have the potential ability to improve the prediction of the aforementioned H2P branches. In this paper, we explore the impact of adding register values to CNN neural branch predictors for predicting H2P branch prediction.
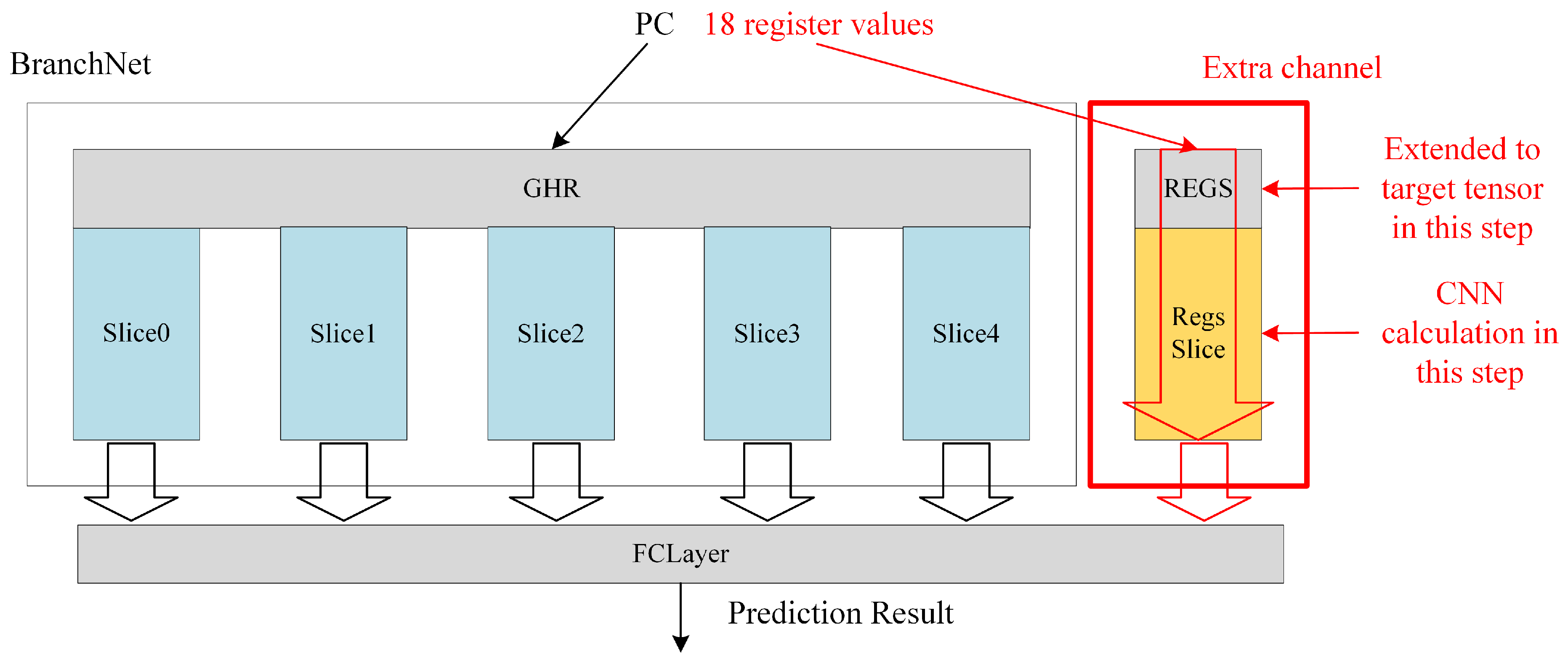
The contributions of this paper are the following: based on the previous BranchNet [7] neural network branch predictor, additional channels for processing register values are added, the network channel parameters are modified according to the need of analyzing register values, and its structure diagram is shown in Figure 1; trace files containing the register values are generated on the SPEC2017 benchmarks using Intel Pintool for training and tests; and finally, through experiments, the results are obtained and the effect of adding register values to branch prediction is analyzed.
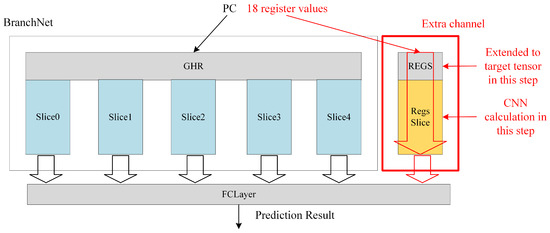
Figure 1.
Structure of the CNN neural network branch predictor with the addition of the register value channel.
2. Recent Branch Predictor Developments
The representation of traditional network branch predictors in recent years is the variants of the TAGE predictor. The TAGE predictor uses the idea of the previous PPM-like predictor design [8]. It contains two tables; one is a bimodal [3] table indexed with a pc, and the other table combines multiple columns which are indexed by using different lengths of history hashed with a pc.
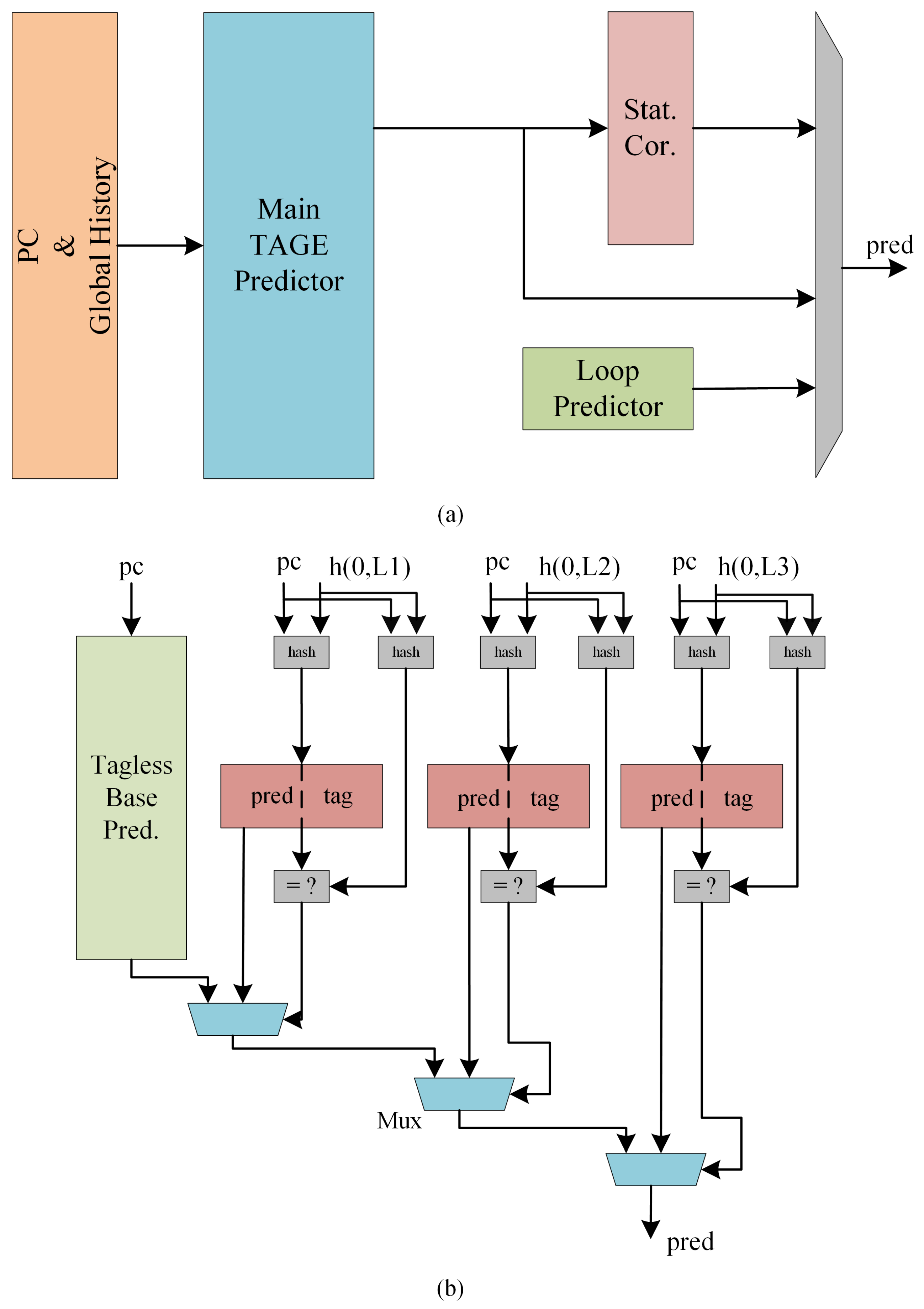
Since TAGE was proposed, most of the research on improving TAGE predictors focused on the additional prediction module. The structure of the representative TAGE-SC-L predictor [5] is shown in Figure 2, which contains a TAGE predictor as the main part, supplemented with a static error corrector, plus a loop predictor. When a prediction is to be made, the results of each part are combined in order to give the most possible result.
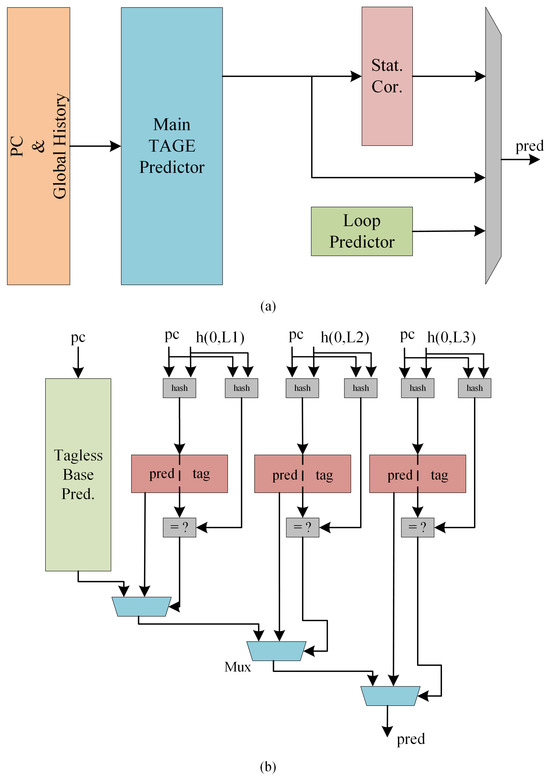
Figure 2.
(a) shows TAGE-SC-L predictor [5] and (b) shows the main tage predictor’s structure.
The BATAGE [9] predictor proposed in 2018 modified the TAGE predictor by using a new state transfer register called a dual-counter and proposing a new prediction and updating algorithm for this transfer register, which improves the accuracy of the TAGE predictor. It provides new ideas and directions for research on the TAGE predictor.
Zhao [10] et al. reported a new design of branch predictor for non-volatile processors; their work reduced backup costs while maintaining prediction ability.
At the beginning of this century, Jimenez proposed a perceptron branch predictor model based on a single-layer perceptron network [11,12]. Since machine learning and deep learning had wide usages in fields such as image video language from 2016, researchers have also tried to introduce deep learning into branch prediction. Mao [13,14] first explored branch prediction based on a deep confidence network (DBN), and the author also tried to apply some common convolutional neural network (CNN) structures to branch predictors. Zhao [15] reported a neural predictor based on the parallel structure of the SRNN.
Zangeneh [7] proposed the BranchNet predictor on the basis of previous research on CNN neural network branch predictors. It absorbed the TAGE predictor’s characteristics of multiple history paths and took offline training as the main strategy, which was used for optimizing H2P branch prediction. The author found that BranchNet has better prediction accuracy for branches that are difficult to predict perfectly with the TAGE predictor after experiments; it is also demonstrated that the offline-trained model also has good prediction results when facing first-encountered branches. The authors also propose a simplified neural network and a new convolutional computational mechanism for hardware deployment.
Chaudhary [16] et al. proposed a hybrid branch predictor design by combining a global branch prediction strategy with Learning Vector Quantization (LVQ). The authors continued optimizing the LVQ branch predictor [17] by applying the backpropagation algorithm to the branch prediction domain. Dang [18] et al. proposed a hybrid predictor design by combining the BATAGE predictor with a neural network predictor. He also designed a runahead mechanism for the data-dependent branches. Luis [19] et al. addressed the problem of large input size of the neural network branch predictor. He applied Weightless Neural Networks (WNNs) to the branch predictor and achieved a neural network predictor with small inputs.
In general, the development of traditional branch predictors represented by the TAGE has slowed down in recent years. Thanks to the development of neural network research, many studies on neural network branch predictors have been published recently, but most of these are only attempts to apply various types of neural networks to branch prediction, lacking in-depth research and optimization of the network. The paper [6] points out that in the case where the TAGE predictor is already accurate enough to correctly predict 99% of static branches, it is the H2P branch that is the key factor affecting metrics such as MPKI and IPC. Therefore, we believe that optimization for specific behavioral branches is the focus of research on branch predictors.
3. Background
3.1. CNN-Based Neural Network Branch Predictor Structure
The work in this paper builds on the BranchNet predictor proposed in paper [7]. It is a branch predictor using a CNN neural network with offline training mode. Its structure was inspired by the structure proposed in the paper [20], but it has the following two changes:
- (1)
- Each H2P branch was trained in separate modules. For the experiments in this paper, it is better and easier to observe the effect on H2P branches after introducing register information.
- (2)
- BranchNet absorbs the characteristics of multiple history paths of the TAGE predictor and uses three to five slices to train histories of different lengths and finally outputs the results into a fully connected layer.
The slice is the smallest network unit in BranchNet, which is used to perform feature extraction on the branch history. It consists of an embedding layer, a convolutional layer, a BatchNorm layer, and a pooling layer. The results of multiple slice operations are output to a fully connected layer, which is then computed to give branch prediction results.
Our work was carried out in the BigNet parameter of BranchNet, whose specific parameters are shown in the following text.
3.2. Training and Predicting Process
The first step in training a neural network branch predictor is to create datasets. One option is using an architecture runtime simulator. It can run the program without too much additional processing, process the branch instructions, and train the neural network. At this point, the data that make up the datasets are given by the simulator runtime. This approach has the benefit that it is easy to add the information used for training, but the disadvantage is the high overhead of the simulator and the slow speed of training. Another option is the trace-driven simulator, whose input trace file can be extracted by specific tools during the program runtime or generated by an architecture simulator. The trace-driven simulator runs faster than the runtime simulator, but the disadvantage of using trace files is that the trace file has to be regenerated if additional content is needed.
We use a trace-based simulation program to conduct our experiments because it runs faster. We run the program to train only one branch and one model at one time. The program reads the trace file with the organizational structure described below and runs from the beginning until the last branch has completed training and then proceeds with the validation and test step. When training, the program reading trace stops when it encounters the branch being trained. After that, the program expands the values of the 18 registers to the length required by the current training model and puts them into the model calculation to obtain a prediction. The program compares it with the actual result and then completes the backpropagation computation. That is how simulation the program works.
Our experiment uses Pintool to collect the information to generate trace files. Pintool can be used to perform program analysis on user space applications, and by calling the API it provides, it can record the data, such as jump direction and address and register values, which are needed for the research. The data we need to run the experiments are shown in Table 1.

Table 1.
Trace file content structure.
The type of registers in the table was chosen as a 32-bit unsigned integer, with the reasons explained below. We attached Pintool to the benchmarks program to collect all the data in Table 1. Each time the benchmark program executes a branch instruction, Pintool will save the information into a file; thus, we can obtain the original trace file. Trace files record 200 million instructions for each benchmark.
The dataset for training the neural network consists of a training set, validation set, and test set, and Table 2 shows the programs chosen for each set of this experiment.

Table 2.
The input of each set for training and testing the neural predictor.
In order to find the H2P branch in each trace, our experiment uses the trace file generated by the method described above and runs through the TAGE-SC-L branch predictor provided by the 5th Championship Branch Prediction competition to filter out the top five branch with the highest MPKI, saving the addresses of these branches.
The next step is to convert the original trace file into an HDF5 file read by the actual training program. The whole HDF5 file consists of the following data parts: the first one is the data structure described in Table 1, and the training program uses the pc value, jump direction and register value. For convenience, the pc value needs to be additionally processed and is obtained by left shifting the pc value 1 bit and setting the lowest bit to the jump direction. The second step is locating all hard-to-predict branches in the trace file, and this information is collected in order to quickly locate the hard-to-predict branch. The last one is the number of jumps in that hard-to-predict branch. We use the python h5py library to accomplish hdf file generation. All the above datasets are compressed using gzip to reduce the size.
Finally, the actual training process can be carried out. The start point for training is not the first instruction but the location where the H2P branch first appears. To do so, it is necessary to process each H2P branch before beginning the training, extracting its corresponding branch history from the lowest bit of the pc processed above and splicing it into the desired history length.
After the training is completed, the effects of the hard-to-predict branch processed by BranchNet are tested with the testing set. These procedures complete the training and test process for a hard-to-predict branch. Multiple H2P branches can be trained at the same time, the number of which is limited by the resources of the computer used for the experiment.
4. Reasons for Introducing Register Values
Paper [6] points out that simply increasing the size of the predictor does not improve the H2P branch prediction very well. Two reasons exist for this: first, H2P branches have high history variation and have no stable behavioral mode, which leads to much of the overhead used being wasted. The second is that some rare branches are not stable enough for the predictor to grasp their behavior and give correct predictions, which also leads to the uselessness of increasing the size. New prediction mechanisms are needed to address these H2P branches.
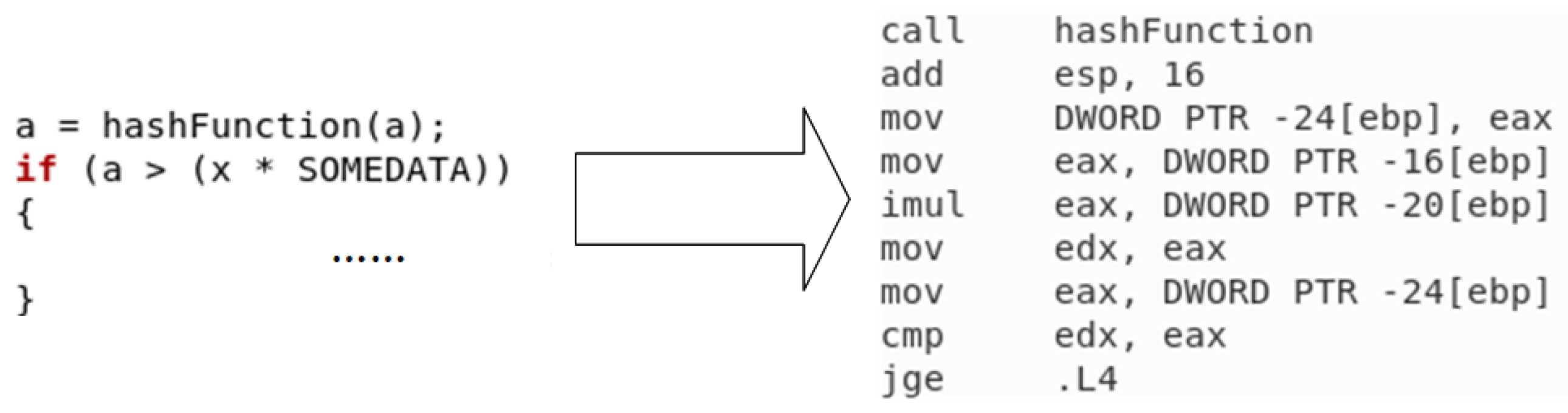
The data-dependent branch which showed in Figure 3 is the main variety of H2P branching, and there have been some previous studies in dealing with this problem. In the paper [22], the data-dependent branch is proposed to be solved by recording the dependency chain of branch instructions, and it is pointed out in the paper that if a branch has the same register value as the previous branch in the dependency chain, the jump result of the previous branch can also be used in the current branch. Paper [23] designed a runahead mechanism based on the dependency chain to solve the data-dependent branch jump by running instructions in advance.
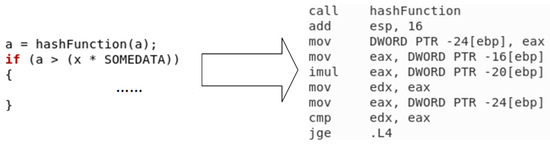
Figure 3.
Simple data dependency branch.
All the above methods use some additional structure to handle data-dependent branches, but for CNN-based branch predictors, adding register value information in offline training mode is very easy and does not require additional mechanisms or structures. For BranchNet, an additional data path just needs to be added to handle register values and then extract the register values saved in the trace file during the training process.
The question of whether there is a regularity in the statistical distribution of register values is addressed in the paper [6]. The authors studied the relationship between register values and the number of instructions in the SPECint2017 benchmarks, where the authors recorded the lower 32 bits of the register values for the 18 registers. By observing the results, the authors have two conclusions: (1) The distribution of register values varies between different benchmarks. (2) The distribution of register values is complex, but a recognizable structure can be found. So, we can say that the CNN has the ability to recognize the underlying patterns.
In summary, the current predictor works in a way that makes it difficult to predict H2P branches represented by data-dependent branches, whereas neural network branch predictors have an excellent ability to uncover potential pattern matches and it is easy to incorporate register information into the offline training process. Therefore, we believe that it is feasible and effective to introduce register values to the neural network branch predictor training process.
5. Network Structure for Processing Register Values
Figures compiled of more than one sub-figure presented side by side or stacked. If a multipart figure is made up of multiple figure types (one part is linear and another is grayscale or color), the figure should meet the stricter guidelines.
In order to add the register values to the training, the register values first need to be added to the trace file. As described in Section 4, the lower 32 bits of the 18 registers are added to the training for this experiment, and the added registers are as follows.
Register list: RDI, RSI, RBP, RSP, RBX, RDX, RCX, RAX, R8, R9, R10, R11, R12, R13, R14, R15, RIP, RFLAGS.
The register values were stored by modifying the trace structure used in the Pintool script to include an array of 32-bit unsigned integers, length 18. The training and test sets are equivalent to those described above. The trace files and hdf5 files are regenerated too. After that, we completed the training preparation.
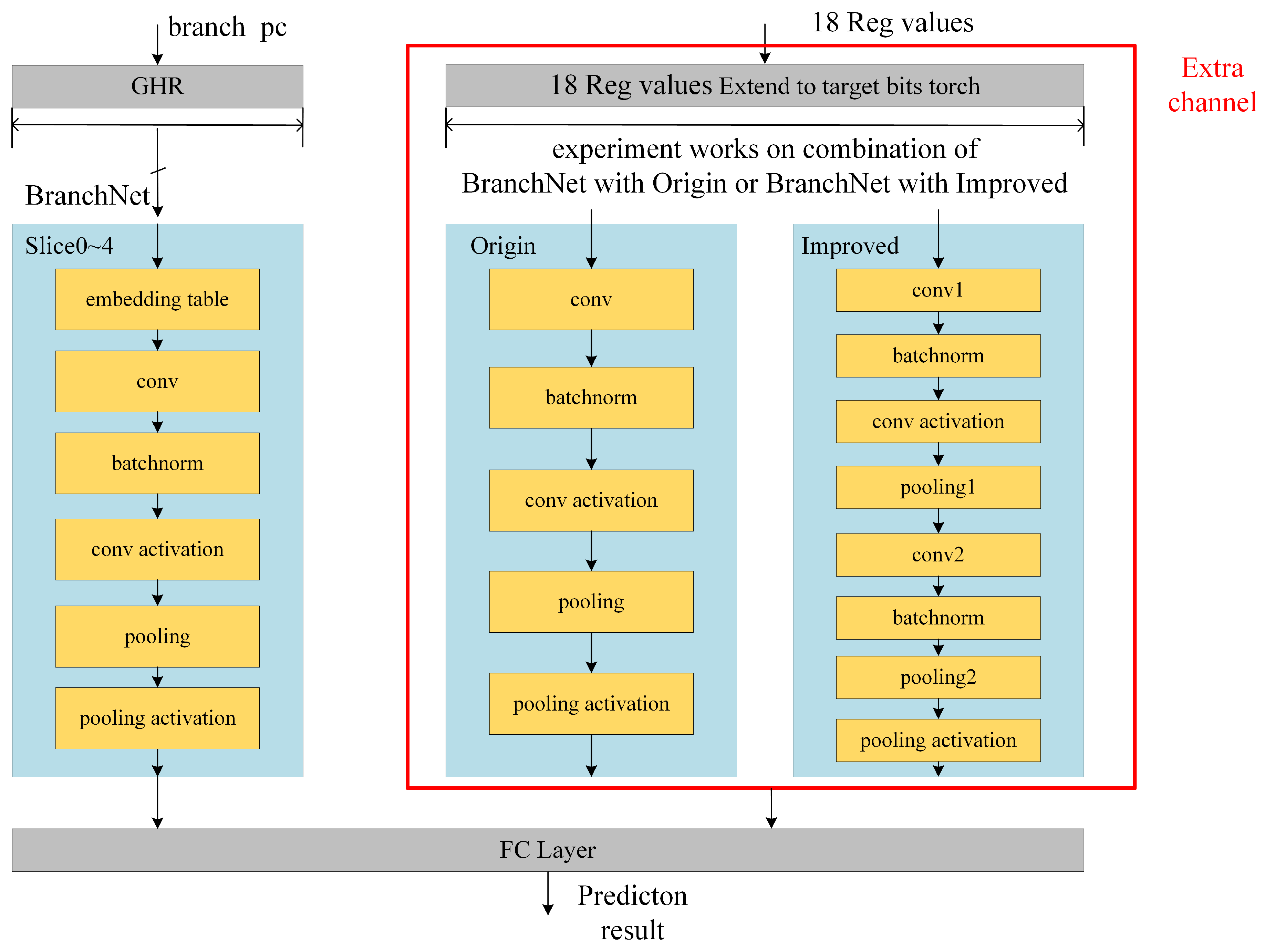
The next step is to modify the network. We add a new register value datapath to BranchNet. The datapath has two types of structures.
The first slice structure, called the origin, for processing register values is the same as that of the history slices, but the embedding layer is removed for simplicity. It consists of a 1D convolution layer, BatchNorm, and a sum-pooling layer.
After some experiments with the first slice structure, we found that its effect was not obvious, and the reason may be that the origin slice has insufficient recognition ability. Therefore, a new slice structure for processing register values is proposed. In order to improve the recognition ability, the depth of the network is increased, and the parameter is modified. It has an extra 1D convolutional layer, BatchNorm, and a pooling layer. We call it improved.
The Table 3 shows the parameters of the two slices structures and BranchNet slice in detail.

Table 3.
Two types of processing register value slice and BranchNet-Big parameter table. Origin is the slice parameter referencing the BranchNet slice, and improved is the modified slice parameter.
Figure 4 shows the origin, improved, and BranchNet slice structures in the experiment framework diagram of the whole experiment. In the experimental phase, we set up three control groups: BranchNet alone, BranchNet with the origin sllice structure, and BranchNet with the improved slice structure. In the experiment, all register data are to be expanded into a 576-length tensor and then input into the register slice.
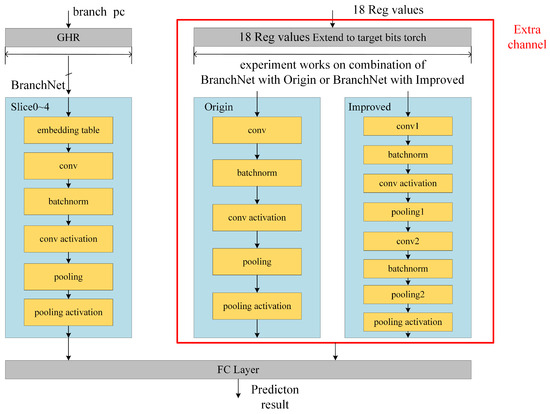
Figure 4.
Comparison of origin, improved, and BranchNet slice structures.
Due to the increased network depth and considering the network complexity, we also considered the width of the input register values in the experiments to verify their effect on the prediction results so that the tensor width will be 150.
6. Results and Discussion
6.1. Results
Our experiment was carried out on an NVIDIA 3060Ti GPU with VRAM 8G. The operating system is Ubuntu 22.04 in WSL2, python version 3.10.12 pytorch version 2.2.1, and CUDA version 12.5. We verify the experiments by computer simulation program. The source code can be found in [24].
Using the methodology described in Section 3, experiments were conducted on all benchmarks of the SPECcrate2017 integer test, recording the results of the BranchNet, the origin, and the improved slice structures in an attempt to optimize the results of the top five H2P branches given by the TAGE predictor. Results are shown in Table 4.

Table 4.
Two types of processing register value slice and BranchNet-Big parameter table, Origin is the slice parameter referencing the BranchNet slice, and improved is the modified slice parameter.
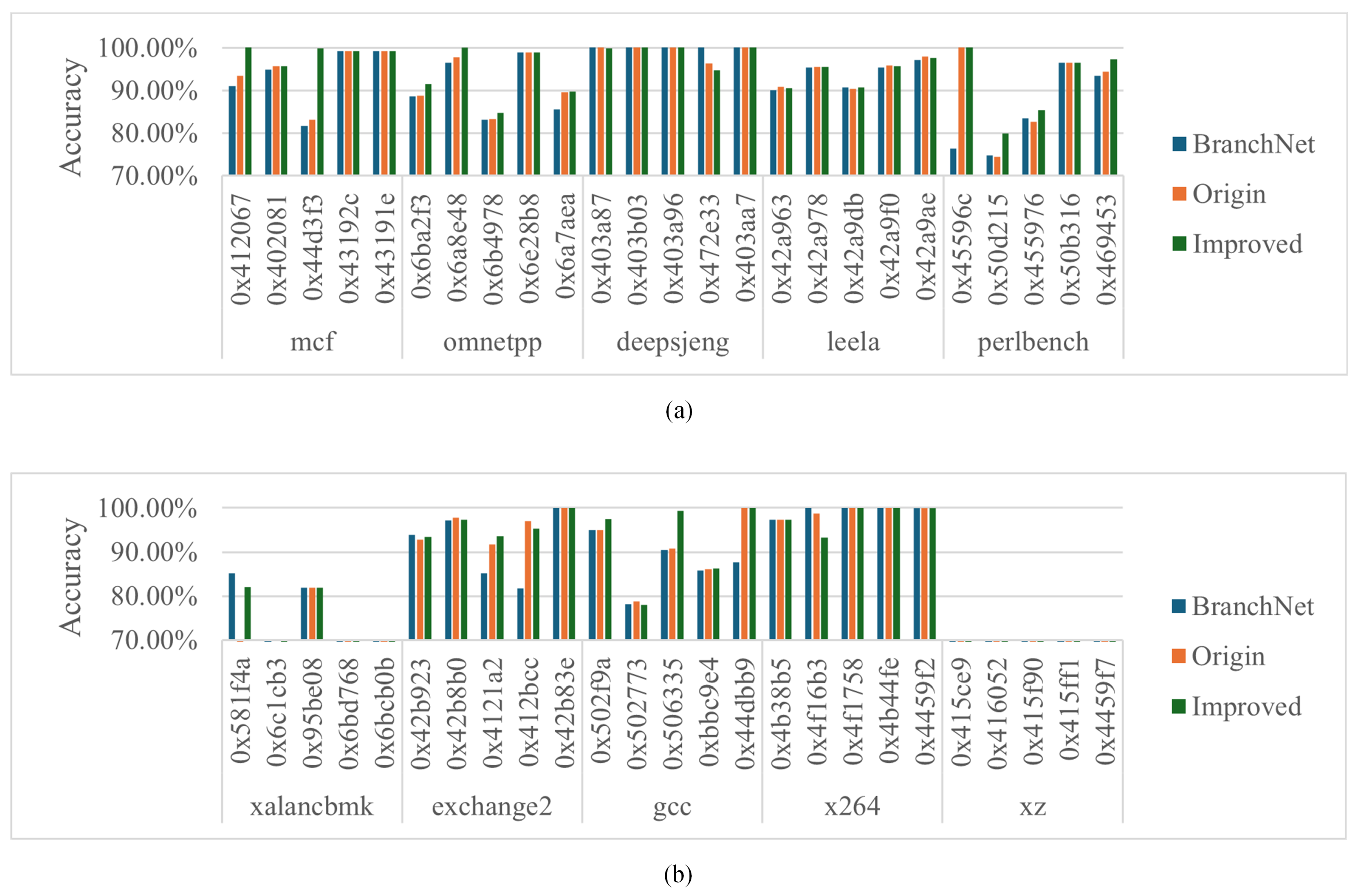
As shown in Figure 5 and Table 4, predictive accuracy was improved in more than half of the branches (31 out of 50). In particular, eight branches have significant improvement in prediction accuracy after adding register value information, and most of these branches are strongly correlated with register value information. And the improved slice can better explore the relationship between branch direction and register value, which can generally improve the prediction accuracy more.
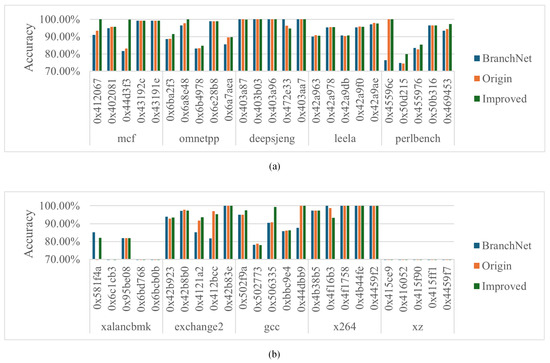
Figure 5.
(a,b) show the results on 45 H2P branches of 10 benchmarks.
The remaining branches have decreased in accuracy after the addition of the BranchNet. Most of them are unrelated or weakly related to the input register values, and adding extra information rather reduces the correct rate of BranchNet’s prediction, or the relationship between the jump direction and the register values is complicated, and the neutral predictor has difficulty in learning. And the improved slice causes more negative effects compared to the origin slice dealing with register values. For example, xalancbmk’s 0x6bcb0b branch first takes a value from memory to a register and then obtains the value from the register-addressed memory to compare with a constant number, which is not very relevant to the register value, so the slice performs poorly. x264’s 0x4f16b3 branch reads a value from memory and saves it in a register and then calculates the jump direction based on the lower 8 bits of the register, so the upper 24 bits of the input register values are invalid. Using the improved slice to make the judgment may be interfered with by this useless information, resulting in a decrease in the correct prediction rate.
Next, We will take a look at the comparison between the results of the original slice and the improved slice. In most of the branches, the two slices behave in a consistent way; i.e., they either simultaneously increase or decrease the prediction accuracy. There are a few exceptions: xalancbmk’s 0x6c1cb3 branch significantly improves the accuracy of the origin slice but the improved slice does not perform as well as the origin slice. The 0x581f4a branch performs poorly for the origin slice. Although the improved slice gets better, it still does not perform as well as the BranchNet itself. exchange2’s 0x412bcc branch, for which the origin slice has better performance than the improved slice.
We read three branches’ source code and tried to find the reason: 0x6c1cb3 uses only the lower 8 bits of the register value, while we input 32-bit register values. The improved slice over-exploits the register value information, resulting in useless bits of data interfering with the judgment of the branch prediction. 0x581f4a uses the register value to address the memory value and compares it with a constant to obtain the prediction result. The complexity of the relationship between the jump direction and the register value causes the origin slice to fail to explore their correlation, while the improved slice works better, but the accuracy decreases compared to the BranchNet because the jump result still is related to the memory value. The 0x412bcc branch reads data from the memory into the register, and if it does not equal 0, then the result is jump. Its unusual behavior may be due to the register’s actual data not being particularly relevant, so that deeper improved slice learning leads to misunderstandings.
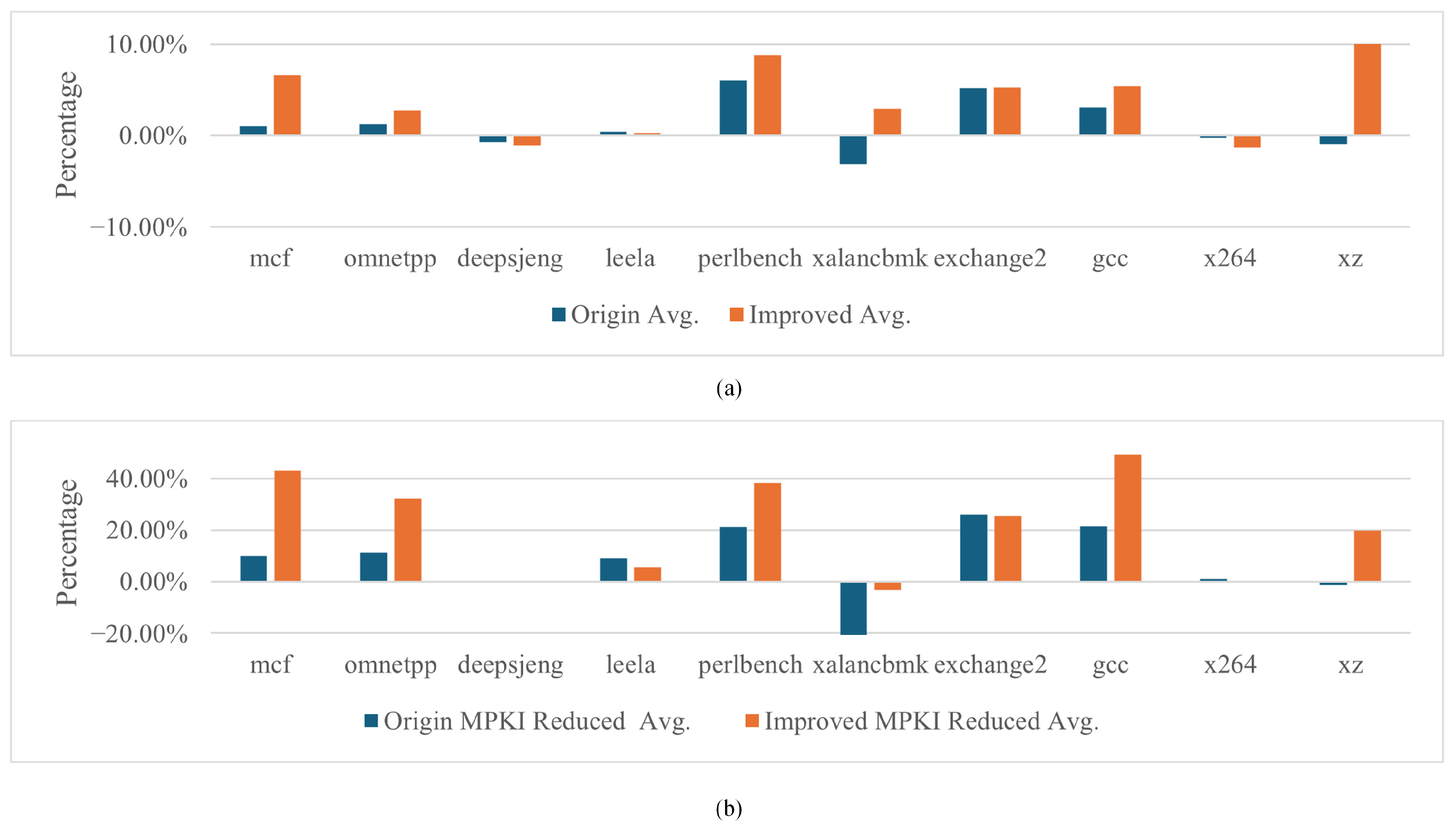
Figure 6 shows the average accuracy and MPKI rate of the two slices with the addition of register information compared to the BranchNet network. deepsjeng and x264 have decreased in accuracy and the origin slice facing xalancbmk has decreased in accuracy, while the improved slice has increased. The prediction accuracy values for the remaining benchmarks were all improved.
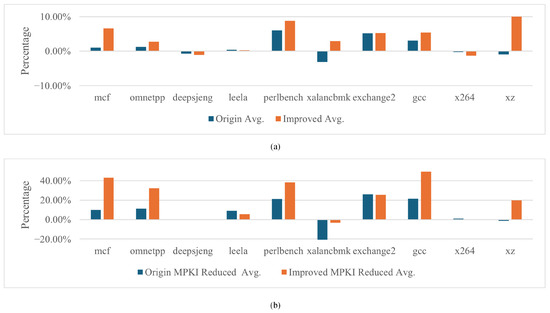
Figure 6.
(a) shows the increased accuracy rate of both networks for BranchNet, and (b) shows the decreased MPKI rate of both networks for BranchNet.
In terms of the average reduced MPKI rate, only xalancbmk’s MPKI rate was elevated, and the average MPKI of deepsjeng and x264 remained nearly unchanged, while all the other benchmarks reduced their MPKI rates, with both the mcf and gcc benchmarks reducing theirs by nearly 40%.
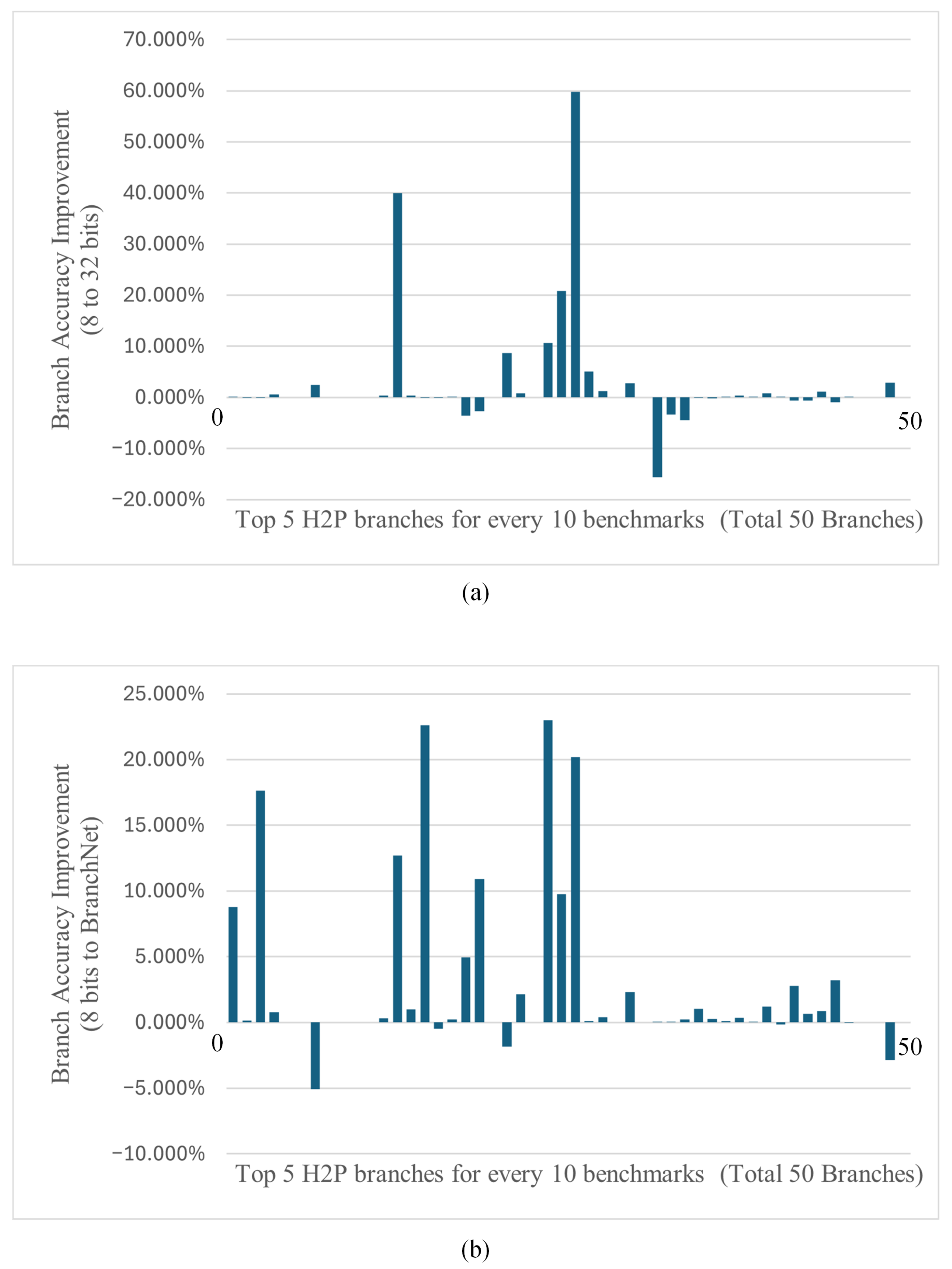
Finally, we compared the results of training with register values of 32 bits and with register values of 8 bits in both cases. As shown in Figure 7, 8-bit improves branch accuracy by 46% and decreases it in 28% of the branches compared to the 32-bit. Against BranchNet, the 8-bit improved branch accuracy by 62%, which is the same as the results for the 32-bit. Branch accuracy decreased in 12% of the branches, which is lower than the 16% in the 32-bit.
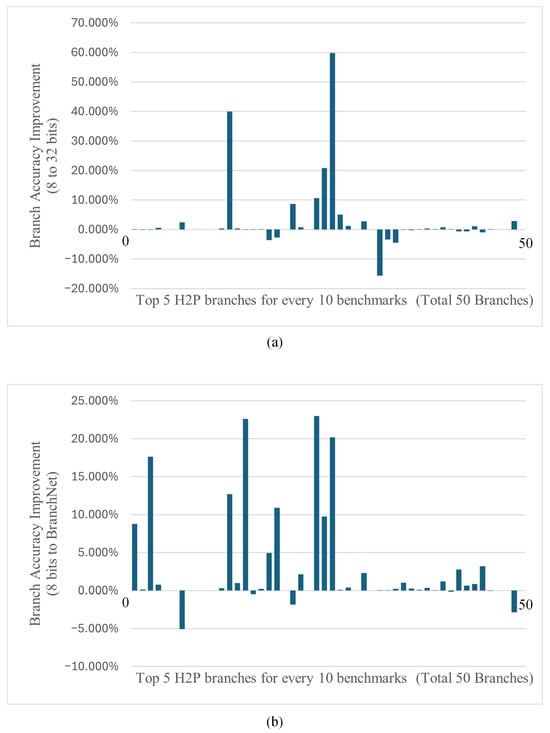
Figure 7.
(a) shows the variation of 8-bit to 32-bit accuracy for all branches and (b) shows the variation of 8-bit to BranchNet accuracy for all branches.
6.2. Improvement Is Not Randomized
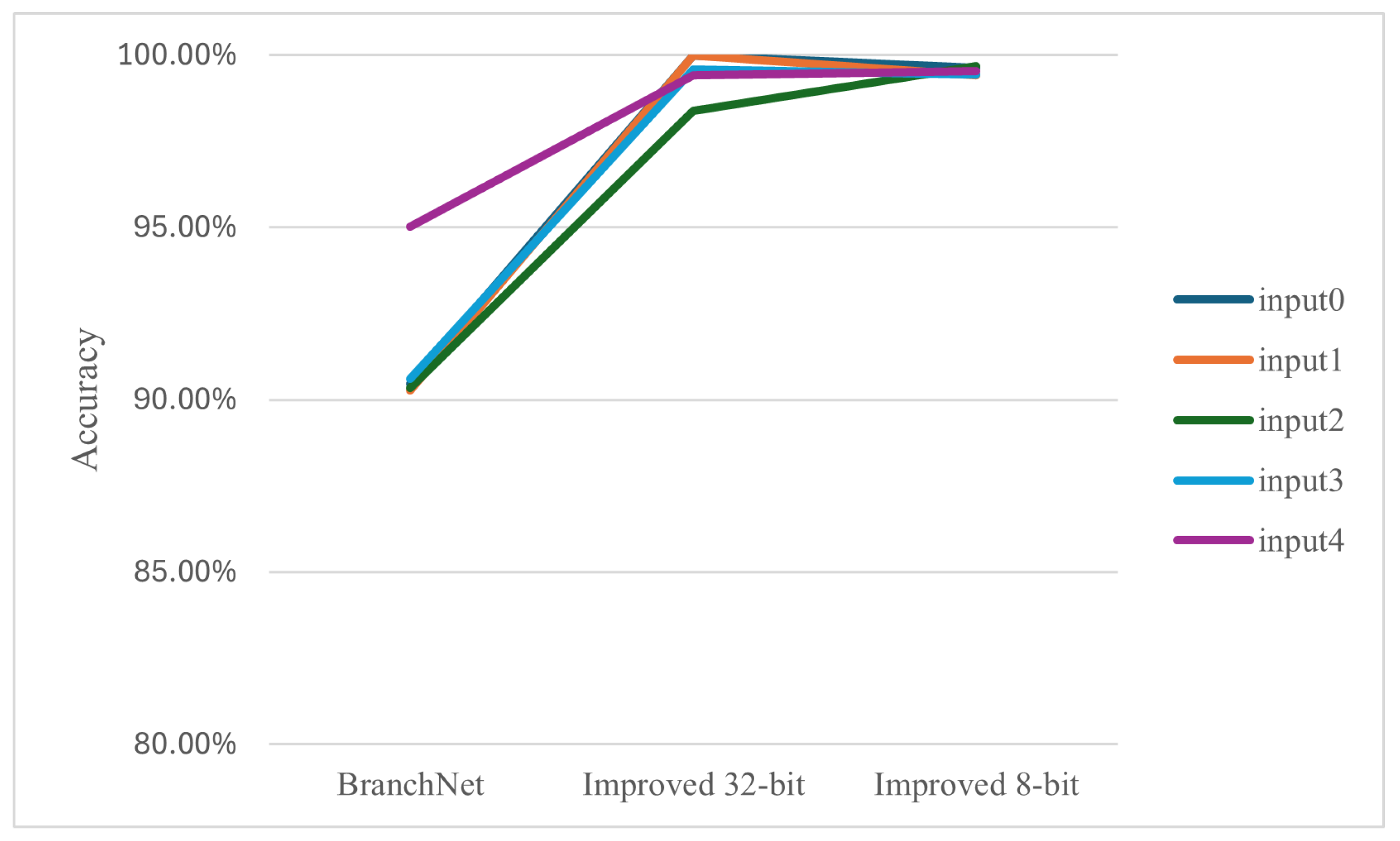
We also designed a simple experiment to illustrate that the slice’s improvement for prediction is not random under different inputs of the benchmark. We chose the branch 0x506335, which gains a significant improvement in the improved slice, and gave gcc 5 different input files and parameters to observe the prediction accuracy of the BranchNet alone and the improved 32- and 8-bit for this branch. As shown in Figure 8, the improved slice 32- and 8-bit show near-uniform accuracy on five different inputs, which could indicate that the improved slice’s improvement in prediction accuracy is not random.
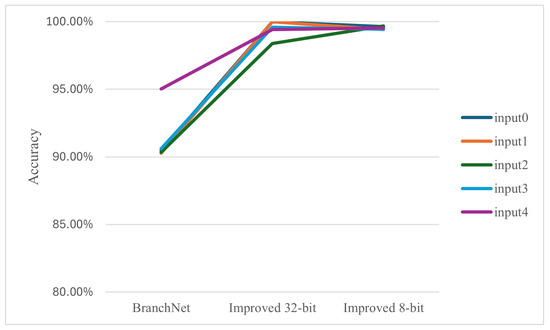
Figure 8.
Prediction accuracy for gcc’s different inputs with BranchNet and improved slice with 32 and 8 bits.
6.3. Discussion
At the beginning of the research, we first tried value prediction with BranchNet itself, i.e., the origin slice in the article, but found that it improved the prediction minimally, so we followed up with the improved slice with boosted parameters and it works well. Finally, for the improved slice, we investigated the effect of different widths of inputs on the prediction, and the 32-bit register value was found to have an effect on the branch using the lower 8 bits, so an 8-bit size register value was also chosen for the comparison experiments.
In the experiments, we ran CNN prediction by computer. For the prediction of the actual processor, the CNN computation requires extra time and also extra silicon area, which are limiting factors for the future applications of this paper. According to the paper [7], the latency of BranchNet under mini-parameter is 1.1 times that of the 64 KB TAGE-SC-L, so we believe that the latency of the improved slice will be larger than the 64 KB TAGE-SC-L.
Overall, the improved slice can better tap into the association between register values and branch directions compared to the origin slice, and more than half of the H2P branches have improved accuracy. Moreover, reducing the input register width to 8 bits has a slight impact on the prediction network and saves resource consumption. We can conclude that the introduction of register values in the neural network branch predictor can improve the prediction accuracy of H2P branches, especially those associated with register value data.
7. Conclusions and Future Works
This paper addresses the problem of how to improve the prediction accuracy of data-dependent H2P branches. Based on the previously proposed CNN branch predictor BranchNet, we added the register-value-processing sub-network and modified it to adapt to its more complex recognition needs. And the effectiveness of the work was evaluated in the top five H2P branches filtered by the TAGE-SC-L predictor on each integer benchmark of SPEC2017. Through experiments, the H2P branch MPKI was reduced for more than half of the benchmarks. Further research on related aspects can be carried out in the future in the following areas:
- In response to the phenomenon that the addition of register values negatively affects the prediction of a few irrelevant branches, it can be introduced as an additional independent predictor, and mechanisms for determining the register values of relevant branches can be further studied to minimize the negative impact.
- Very few H2P branches that depend on register values are difficult to predict with both slices used in this paper, and there exists room for further optimization of these networks. Given the speed of development of neural networks, the next step could be to choose a more efficient network to handle register values or to continue optimizing the existing CNN branch predictor.
- In terms of how to introduce register values into the branch predictor in a real processor design, additional data paths can be designed to introduce register values into the branch predictor, or another register table can be maintained in the branch predictor, or other plausible methods can be investigated. It also needs to be investigated how to deploy the neural network branch predictor into the processor.
Author Contributions
Conceptualization, Y.T.; methodology, Y.T.; software, Y.T.; validation, Z.C. and W.F.; writing, Y.T.; review and editing, Z.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| CNN | Convolutional Neural Network |
| H2P | Hard to Predict |
| MPKI | Mispredictions per Kilo Instructions |
References
- Kessler, R.E.; McLellan, E.J.; Webb, D.A. The Alpha 21264 microprocessor architecture. In Proceedings of the International Conference on Computer Design. VLSI in Computers and Processors (Cat. No. 98CB36273), Austin, TX, USA, 5–7 October 1998; IEEE: Piscataway, NJ, USA, 1998; pp. 90–95. [Google Scholar]
- Seznec, A.; Felix, S.; Krishnan, V.; Sazeides, Y. Design tradeoffs for the Alpha EV8 conditional branch predictor. ACM SIGARCH Comput. Archit. News 2002, 30, 295–306. [Google Scholar] [CrossRef]
- McFarling, S. Combining Branch Predictors; Technical Report TN-36; Technical Report; Western Research Laboratory: Palo Alto, CA, USA, 1993. [Google Scholar]
- Kulkarni, K.N.; Mekala, V.R. A Review of Branch Prediction Schemes and a Study of Branch Predictors in Modern Microprocessors. 2016. Available online: https://www.researchgate.net/publication/266891966 (accessed on 23 February 2024).
- Seznec, A. TAGE-SC-L Branch Predictors. In JILP-Championship Branch Prediction. 2014. Available online: https://inria.hal.science/hal-01086920/ (accessed on 23 February 2024).
- Lin, C.K.; Tarsa, S.J. Branch prediction is not a solved problem: Measurements, opportunities, and future directions. arXiv 2019, arXiv:1906.08170. [Google Scholar]
- Zangeneh, S.; Pruett, S.; Lym, S.; Patt, Y.N. Branchnet: A convolutional neural network to predict hard-to-predict branches. In Proceedings of the 2020 53rd Annual IEEE/ACM International Symposium on Microarchitecture (MICRO), Athens, Greece, 17–21 October 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 118–130. [Google Scholar]
- Michaud, P. A PPM-like, tag-based branch predictor. J. Instr.-Level Parallelism 2005, 7, 10. [Google Scholar]
- Michaud, P. An alternative tage-like conditional branch predictor. ACM Trans. Archit. Code Optim. (TACO) 2018, 15, 1–23. [Google Scholar] [CrossRef]
- Zhao, M.; Xu, S.; Dong, L.; Xue, C.J.; Yu, D.; Cai, X.; Jia, Z. Branch Predictor Design for Energy Harvesting Powered Nonvolatile Processors. IEEE Trans. Comput. 2023, 73, 722–734. [Google Scholar] [CrossRef]
- Jiménez, D.A.; Lin, C. Dynamic branch prediction with perceptrons. In Proceedings of the HPCA Seventh International Symposium on High-Performance Computer Architecture, Monterrey, Mexico, 19–24 January 2001; IEEE: Piscataway, NJ, USA, 2001; pp. 197–206. [Google Scholar]
- Jiménez, D.A. Fast path-based neural branch prediction. In Proceedings of the 36th Annual IEEE/ACM International Symposium on Microarchitecture, MICRO-36, San Diego, CA, USA, 5 December 2003; IEEE: Piscataway, NJ, USA, 2003; pp. 243–252. [Google Scholar]
- Mao, Y.; Shen, J.; Gui, X. A study on deep belief net for branch prediction. IEEE Access 2017, 6, 10779–10786. [Google Scholar] [CrossRef]
- Mao, Y.; Zhou, H.; Gui, X.; Shen, J. Exploring convolution neural network for branch prediction. IEEE Access 2020, 8, 152008–152016. [Google Scholar] [CrossRef]
- Zhang, L.; Wu, N.; Ge, F.; Zhou, F.; Yahya, M.R. A dynamic branch predictor based on parallel structure of SRNN. IEEE Access 2020, 8, 86230–86237. [Google Scholar] [CrossRef]
- Sweety; Chaudhary, P. Improving branch prediction by combining perceptron with learning vector quantization neural network in embedded processor. Int. J. Inf. Technol. 2021, 13, 1815–1821. [Google Scholar] [CrossRef]
- Nain, S.; Chaudhary, P. A neural network-based approach for the performance evaluation of branch prediction in instruction-level parallelism processors. J. Supercomput. 2022, 78, 4960–4976. [Google Scholar] [CrossRef]
- Dang, N.M.; Cao, H.X.; Tran, L. BATAGE-BFNP: A High-Performance Hybrid Branch Predictor with Data-Dependent Branches Speculative Pre-execution for RISC-V Processors. Arab. J. Sci. Eng. 2023, 48, 10299–10312. [Google Scholar] [CrossRef]
- Villon, L.A.; Susskind, Z.; Bacellar, A.T.; Miranda, I.D.; de Araújo, L.S.; Lima, P.M.; Breternitz, M., Jr.; John, L.K.; França, F.M.; Dutra, D.L. A conditional branch predictor based on weightless neural networks. Neurocomputing 2023, 555, 126637. [Google Scholar] [CrossRef]
- Tarsa, S.J.; Lin, C.K.; Keskin, G.; Chinya, G.; Wang, H. Improving branch prediction by modeling global history with convolutional neural networks. arXiv 2019, arXiv:1906.09889. [Google Scholar]
- Amaral, J.N.; Borin, E.; Ashley, D.R.; Benedicto, C.; Colp, E.; Hoffmam, J.H.S.; Karpoff, M.; Ochoa, E.; Redshaw, M.; Rodrigues, R.E. The alberta workloads for the spec cpu 2017 benchmark suite. In Proceedings of the 2018 IEEE International Symposium on Performance Analysis of Systems and Software (ISPASS), Belfast, UK, 2–4 April 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 159–168. [Google Scholar]
- Chen, L.; Dropsho, S.; Albonesi, D.H. Dynamic data dependence tracking and its application to branch prediction. In Proceedings of the Ninth International Symposium on High-Performance Computer Architecture, HPCA-9 2003, Anaheim, CA, USA, 12 February 2003; IEEE: Piscataway, NJ, USA, 2003; pp. 65–76. [Google Scholar]
- Pruett, S.; Patt, Y. Branch runahead: An alternative to branch prediction for impossible to predict branches. In Proceedings of the MICRO-54: 54th Annual IEEE/ACM International Symposium on Microarchitecture, Athens, Greece, 18–22 October 2021; pp. 804–815. [Google Scholar]
- Branchnet with Register Value. Available online: https://github.com/chnjstyj/branchnet_with_register_value (accessed on 23 February 2024).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).