Fréchet-Derivative-Based Global Sensitivity Analysis and Its Physical Meanings in Structural Design
Abstract
1. Introduction
2. Primary Concepts and Assumptions in This Work
- (a)
- The computational model is square-integrable, and the output PDF is continuously differentiable with respect to the distribution parameters of the input PDF.
- (b)
- The model inputs are independently distributed.
- (c)
- The model output is univariate.
3. Review of Three Classical Global Sensitivity Indices
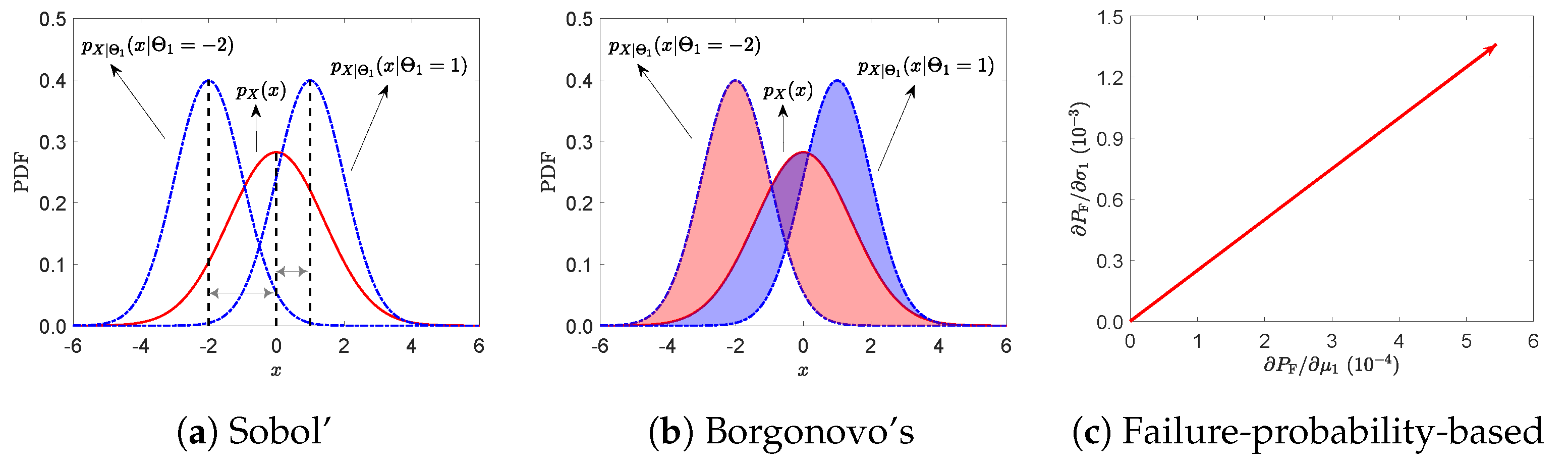
3.1. Variance-Based GSI
3.2. Moment-Independent GSI
3.3. Failure-Probability-Based GSI
3.4. Objectives of This Research and Adopted Methods
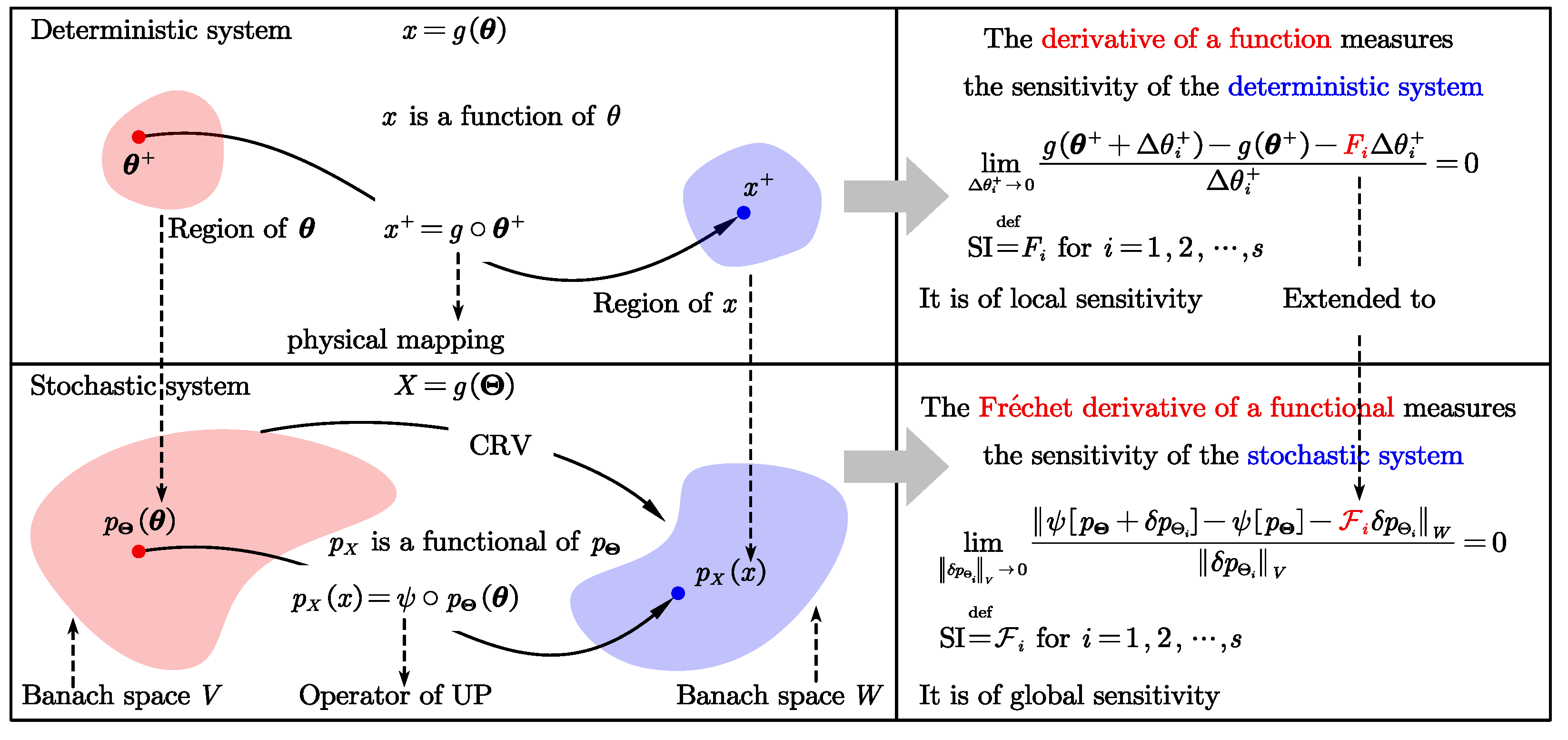
4. Fréchet-Derivative-Based GSI
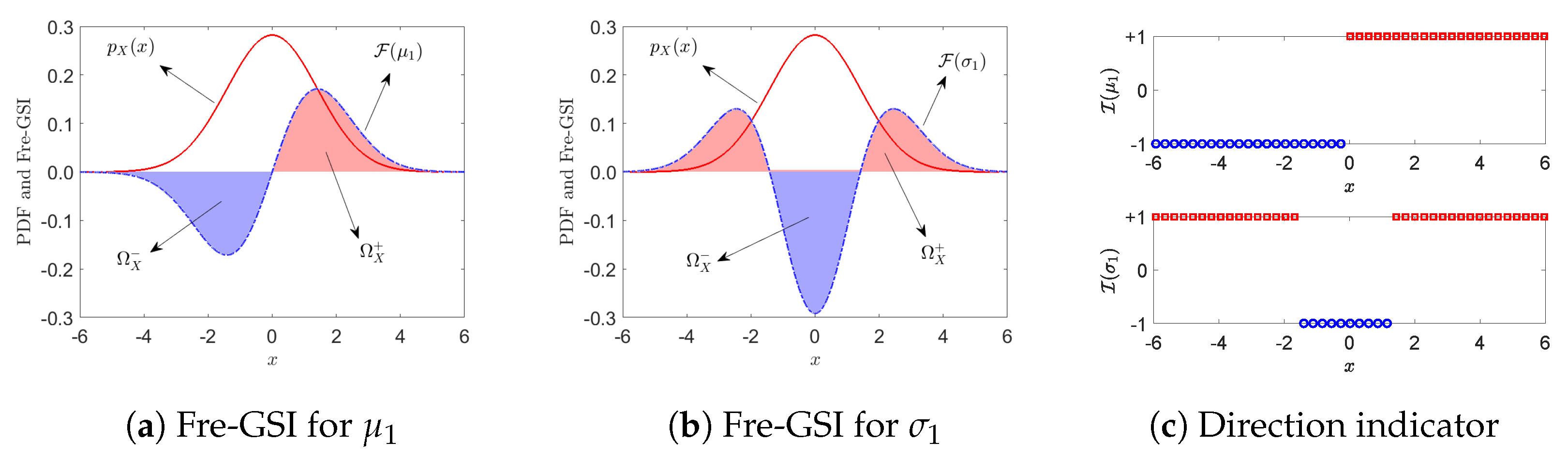
4.1. Definition of the Fréchet-Derivative-Based GSI and Its Parametric Expression
4.2. Importance Measure and Direction Indicator of the Fre-GSI
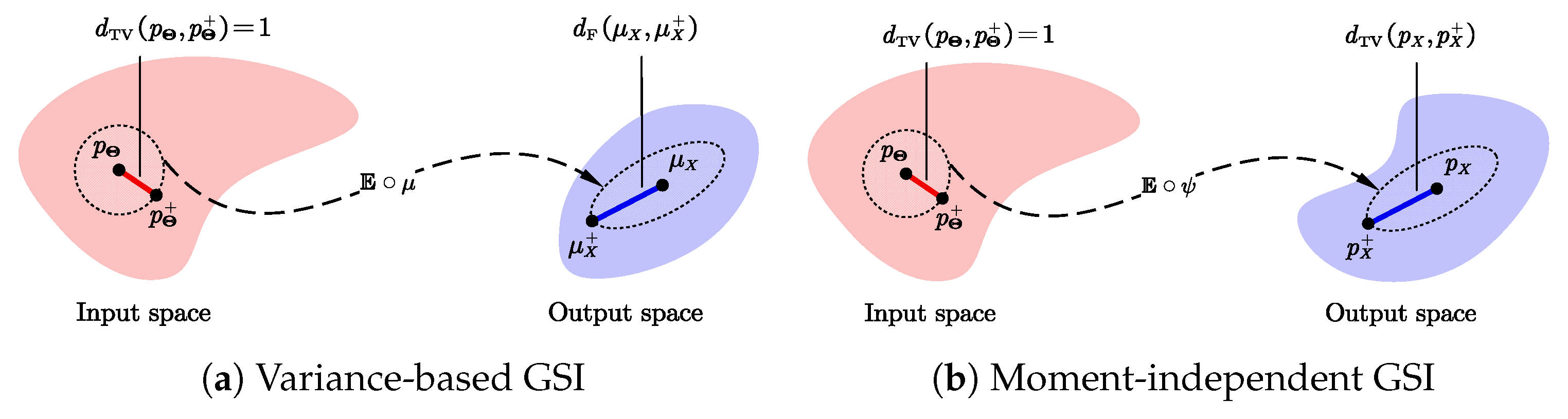
4.3. Links of the Fréchet-Derivative-Based GSI with the Three Classical GSIs
4.3.1. On the Concept of the Output from a Functional Perspective
4.3.2. On the Concept of the How from a Functional Perspective
4.3.3. Links Between the Fre-GSI to the Three Classical GSIs
5. Test Examples
5.1. Example 1: A Similar Toy Model
5.2. Example 2: An Analytical and Nonlinear Model
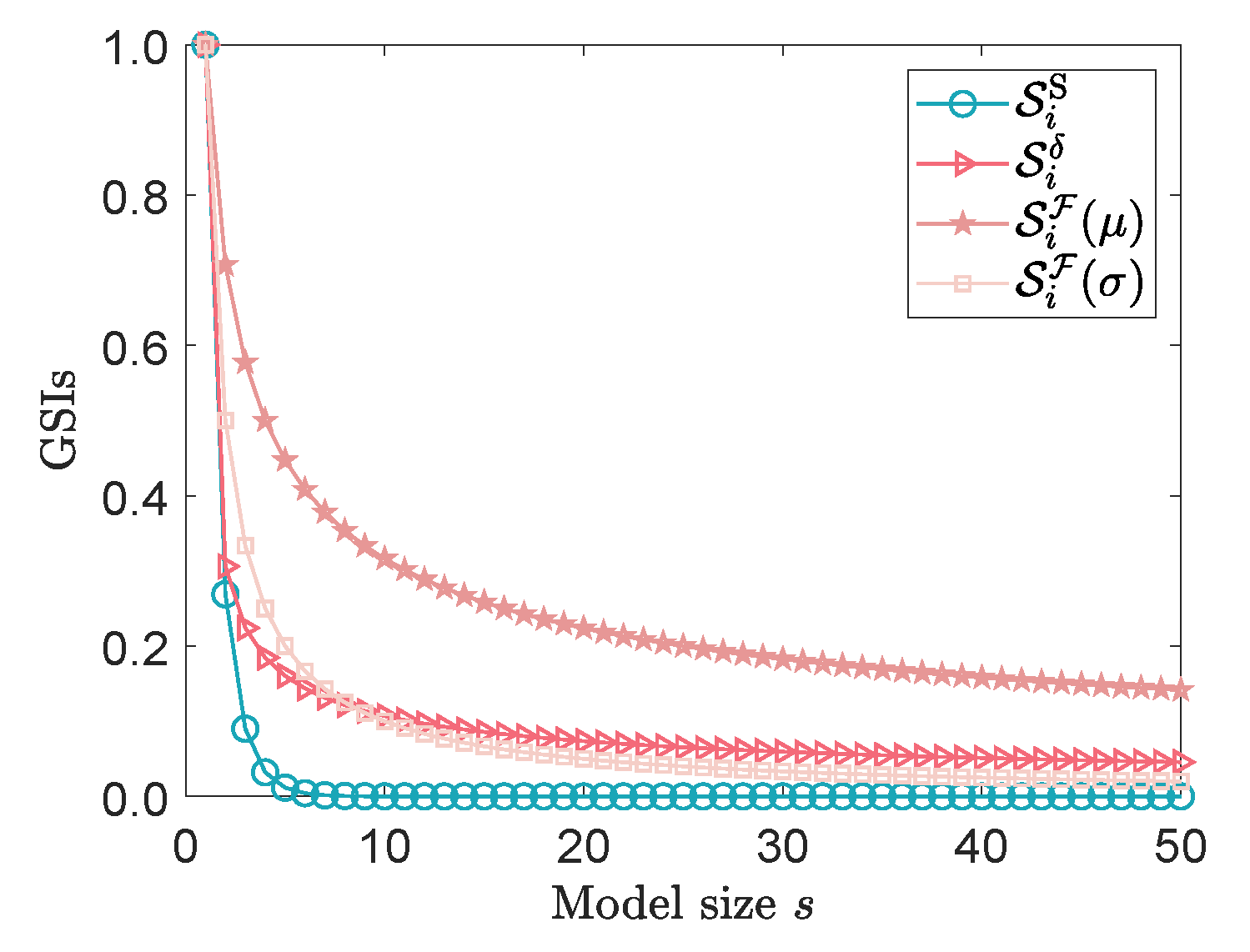
5.3. Example 3: Borgonovo’s Growing Size Model
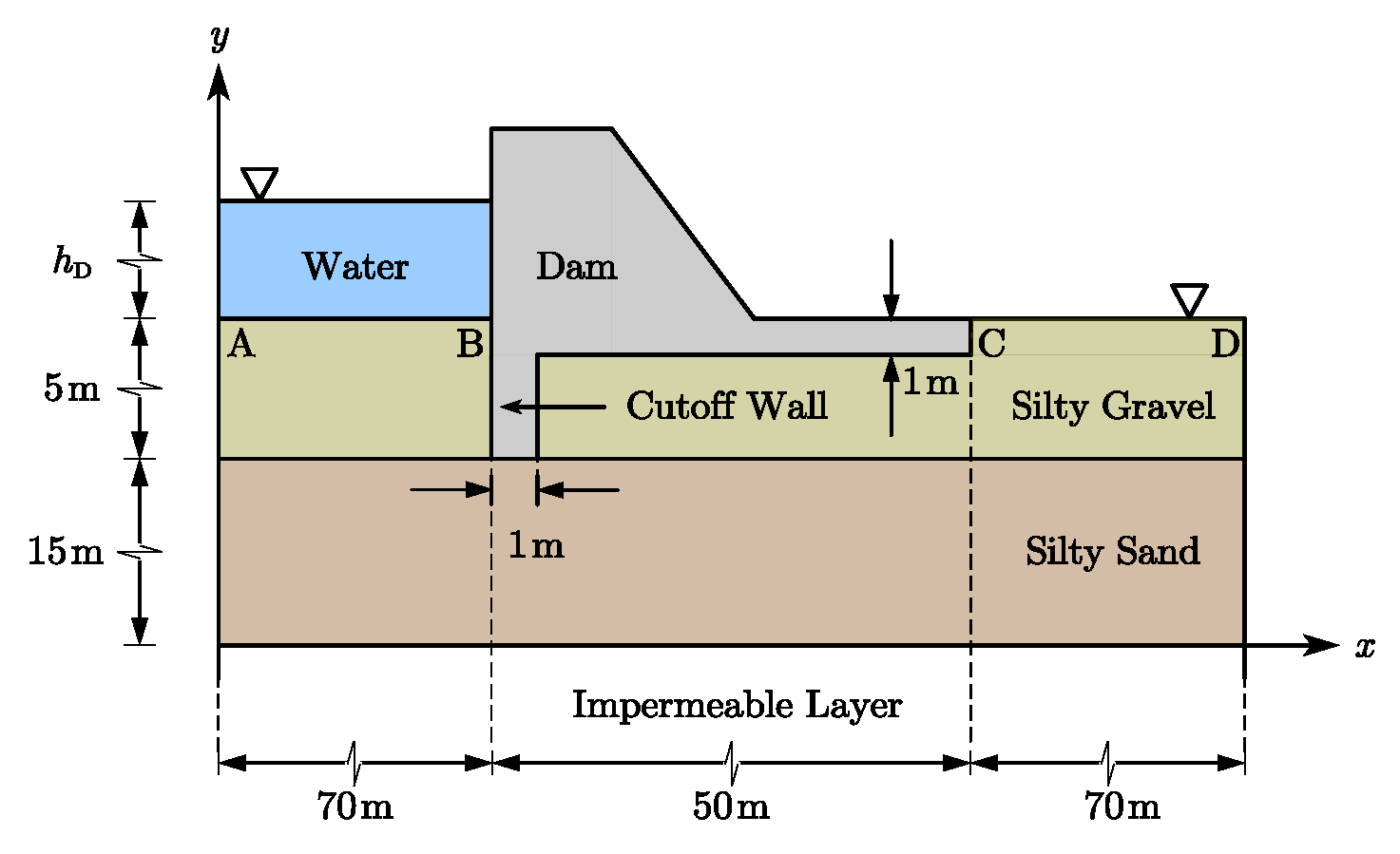
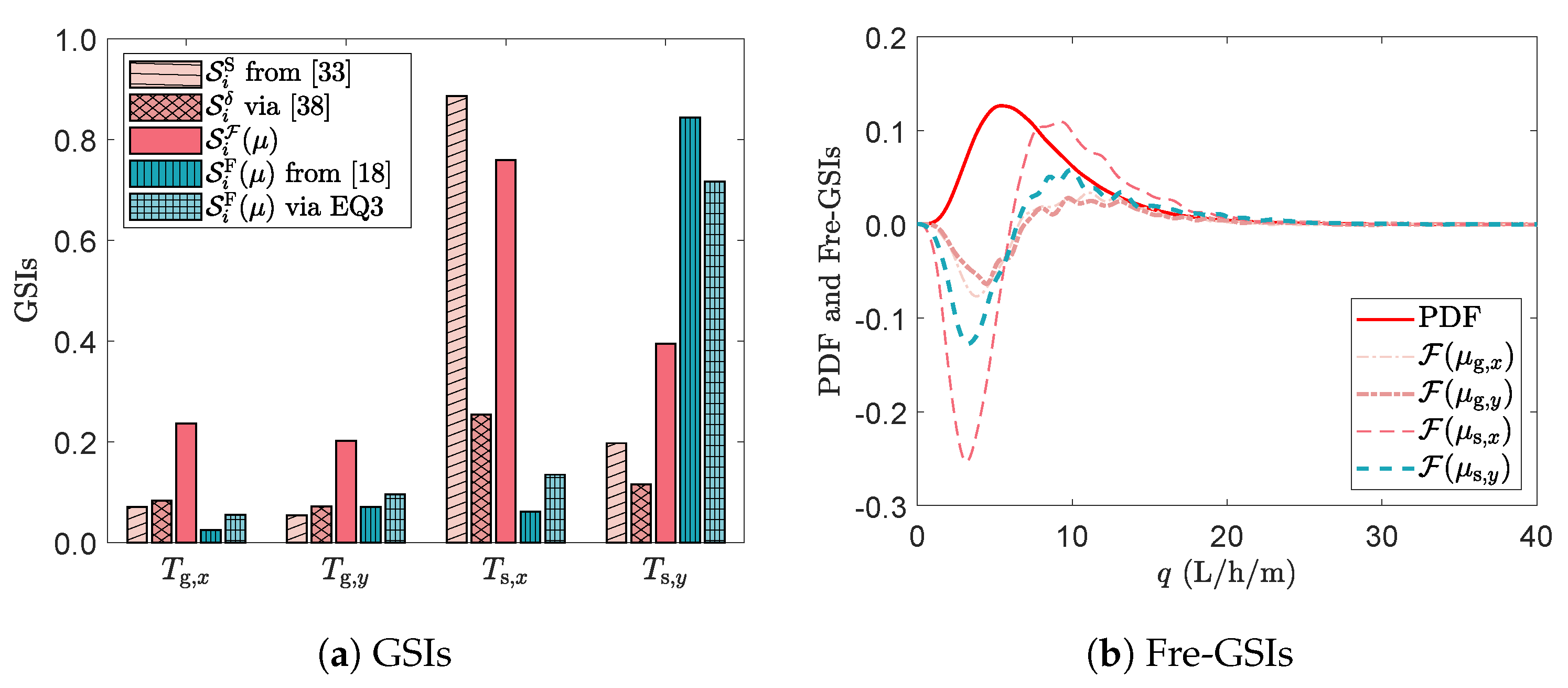
5.4. Example 4: A Dam Seepage Model
6. Conclusions
- The importance measure and direction indicator are obtained from the Fre-GSI, whose basic properties are studied to illustrate the ability of Fre-GSI for global sensitivity analysis.
- The four GSIs can be clearly comprehended through a functional description, wherein the distinctions among the four GSIs stem from the definitions of stochastic distances computed by different operators.
- Some practical links of the Fre-GSI with other GSIs are analytically derived and verified numerically.
- The complementary nature of the four GSIs is revealed. The variance-based GSI can effectively reflect the model structure, while the moment-independent GSI can reflect the uncertainty in distribution. The failure-probability-based GSI is useful for quantifying the impact of different failure criteria, while the Fre-GSI has robust capabilities on the importance measure and the direction of sensitivity.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| CRV | change of random variables |
| Fre-GSI | Fréchet-derivative-based global sensitivity index |
| GSI | global sensitivity index |
| KDE | kernel density estimation |
| MCS | Monte Carlo simulation |
| probability density function | |
| QoI | quantity of interest |
| SD | standard deviation |
| UP | uncertainty propagation |
Appendix A. Proof of Some Properties of the Fre-GSI
Appendix A.1. Proof of Property 1
Appendix A.2. Proof of Property 2

Appendix A.3. Link of the Fre-GSI with the Variance-Based GSI
Appendix A.4. Link of the Fre-GSI with the Moment-Independent GSI
Appendix A.5. Link of the Fre-GSI with the Failure-Probability-Based GSI
References
- Ehre, M.; Papaioannou, I.; Straub, D. Global sensitivity analysis in high dimensions with PLS-PCE. Reliab. Eng. Syst. Saf. 2020, 198, 106861. [Google Scholar] [CrossRef]
- Papaioannou, I.; Straub, D. Variance-based reliability sensitivity analysis and the FORM α-factors. Reliab. Eng. Syst. Saf. 2021, 210, 107496. [Google Scholar] [CrossRef]
- Wan, Z.Q.; Tao, W.F.; Ding, Y.Q.; Xin, L.F. Fréchet-derivative-based global sensitivity analysis of the physical random function model of ground motions. Dis. Prev. Res. 2023, 2, 8. [Google Scholar] [CrossRef]
- Hong, X.; Wan, Z.Q.; Chen, J.B. Parallel assessment of the tropical cyclone wind hazard at multiple locations using the probability density evolution method integrated with the change of probability measure. Reliab. Eng. Syst. Saf. 2023, 237, 109351. [Google Scholar] [CrossRef]
- Jung, W.H.; Taflanidis, A.A. Efficient global sensitivity analysis for high-dimensional outputs combining data-driven probability models and dimensionality reduction. Reliab. Eng. Syst. Saf. 2023, 231, 108805. [Google Scholar] [CrossRef]
- Shang, Y.; Nogal, M.; Teixeira, R.; Wolfert, A. Extreme-oriented sensitivity analysis using sparse polynomial chaos expansion. Application to train–track–bridge systems. Reliab. Eng. Syst. Saf. 2024, 243, 109818. [Google Scholar] [CrossRef]
- Derennes, P.; Morio, J.; Simatos, F. Simultaneous estimation of complementary moment independent and reliability-oriented sensitivity measures. Math. Comput. Simulat. 2021, 182, 721–737. [Google Scholar] [CrossRef]
- Ma, Y.Z.; Jin, X.X.; Zhao, X.; Li, H.S.; Zhao, Z.Z.; Xu, C. Reliability-oriented global sensitivity analysis using subset simulation and space partition. Reliab. Eng. Syst. Saf. 2024, 242, 109794. [Google Scholar] [CrossRef]
- Torii, A.J.; Novotny, A.A. A priori error estimates for local reliability-based sensitivity analysis with Monte Carlo Simulation. Reliab. Eng. Syst. Saf. 2021, 213, 107749. [Google Scholar] [CrossRef]
- Chen, J.B.; Wan, Z.Q.; Beer, M. A global sensitivity index based on Fréchet derivative and its efficient numerical analysis. Probabilistic Eng. Mech. 2020, 62, 103096. [Google Scholar] [CrossRef]
- Chen, J.B.; Yang, J.S.; Jensen, H. Structural optimization considering dynamic reliability constraints via probability density evolution method and change of probability measure. Struct. Multidiscip. Optim. 2020, 62, 2499–2516. [Google Scholar] [CrossRef]
- Saltelli, A.; Tarantola, S.; Campolongo, F.; Ratto, M. Sensitivity Analysis in Practice: A Guide to Assessing Scientific Models; John Wiley & Sons: Chichester, UK, 2004. [Google Scholar]
- Sobol’, I.M. Sensitivity estimates for nonlinear mathematical models. Math. Model. Comput. Exp. 1993, 1, 407–414. [Google Scholar]
- Mara, T.A.; Tarantola, S. Variance-based sensitivity indices for models with dependent inputs. Reliab. Eng. Syst. Saf. 2012, 107, 115–121. [Google Scholar] [CrossRef]
- Borgonovo, E. A new uncertainty importance measure. Reliab. Eng. Syst. Saf. 2007, 92, 771–784. [Google Scholar] [CrossRef]
- Borgonovo, E.; Castaings, W.; Tarantola, S. Moment independent importance measures: New results and analytical test cases. Risk Anal. 2011, 31, 404–428. [Google Scholar] [CrossRef]
- Wu, Y.T. Computational methods for efficient structural reliability and reliability sensitivity analysis. AIAA J. 1994, 32, 1717–1723. [Google Scholar] [CrossRef]
- Valdebenito, M.A.; Jensen, H.; Hernández, H.B.; Mehrez, L. Sensitivity estimation of failure probability applying line sampling. Reliab. Eng. Syst. Saf. 2018, 171, 99–111. [Google Scholar] [CrossRef]
- Perrin, G.; Defaux, G. Efficient evaluation of reliability-oriented sensitivity indices. J. Sci. Comput. 2019, 79, 1433–1455. [Google Scholar] [CrossRef]
- Lemaître, P.; Sergienko, E.; Arnaud, A.; Bousquet, N.; Gamboa, F.; Iooss, B. Density modification-based reliability sensitivity analysis. J. Stat. Comput. Simul. 2015, 85, 1200–1223. [Google Scholar] [CrossRef]
- Helton, J.C.; Johnson, J.D.; Sallaberry, C.J.; Storlie, C.B. Survey of sampling-based methods for uncertainty and sensitivity analysis. Reliab. Eng. Syst. Saf. 2006, 91, 1175–1209. [Google Scholar] [CrossRef]
- Ghanem, R.; Higdon, D.; Owhadi, H. (Eds.) Handbook of Uncertainty Quantification; Springer International Publishing: Cham, Switzerland, 2017. [Google Scholar]
- Borgonovo, E. Measuring uncertainty importance: Investigation and comparison of alternative approaches. Risk Anal. 2006, 26, 1349–1361. [Google Scholar] [CrossRef] [PubMed]
- Iooss, B.; Le Gratiet, L. Uncertainty and sensitivity analysis of functional risk curves based on Gaussian processes. Reliab. Eng. Syst. Saf. 2019, 187, 58–66. [Google Scholar] [CrossRef]
- Lamboni, M.; Kucherenko, S. Multivariate sensitivity analysis and derivative-based global sensitivity measures with dependent variables. Reliab. Eng. Syst. Saf. 2021, 212, 107519. [Google Scholar] [CrossRef]
- Vuillod, B.; Montemurro, M.; Panettieri, E.; Hallo, L. A comparison between Sobol’s indices and Shapley’s effect for global sensitivity analysis of systems with independent input variables. Reliab. Eng. Syst. Saf. 2023, 234, 109177. [Google Scholar] [CrossRef]
- Li, J.; Chen, J.B. The principle of preservation of probability and the generalized density evolution equation. Struct. Saf. 2008, 30, 65–77. [Google Scholar] [CrossRef]
- Grigoriu, M. Stochastic Systems: Uncertainty Quantification and Propagation; Springer: London, UK, 2012. [Google Scholar]
- Wan, Z.Q.; Chen, J.B.; Beer, M. Functional perspective of uncertainty quantification for stochastic parametric systems and global sensitivity analysis. Chin. J. Theor. Appl. Mech. 2021, 53, 837–854. [Google Scholar]
- Rubinstein, R.Y. Sensitivity analysis and performance extrapolation for computer simulation models. Oper. Res. 1989, 37, 72–81. [Google Scholar] [CrossRef]
- Homma, T.; Saltelli, A. Importance measures in global sensitivity analysis of model output. Reliab. Eng. Syst. Saf. 1996, 52, 1–17. [Google Scholar] [CrossRef]
- Da Veiga, S.; Gamboa, F.; Iooss, B.; Prieur, C. Basics and Trends in Sensitivity Analysis; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2021. [Google Scholar]
- Liu, Q.; Homma, T. A new importance measure for sensitivity analysis. J. Nucl. Sci. 2010, 47, 53–61. [Google Scholar] [CrossRef]
- Wan, Z.Q.; Chen, J.B.; Li, J.; Ang, A.H.-S. An efficient new PDEM-COM based approach for time-variant reliability assessment of structures with monotonically deteriorating materials. Struct. Saf. 2020, 82, 101878. [Google Scholar] [CrossRef]
- Borgonovo, E.; Plischke, E. Sensitivity analysis: A review of recent advances. Eur. J. Oper. Res. 2016, 248, 869–887. [Google Scholar] [CrossRef]
- Torii, A.J. On sampling-based schemes for probability of failure sensitivity analysis. Probabilistic Eng. Mech. 2020, 62, 103099. [Google Scholar] [CrossRef]
- Chen, J.B.; Wan, Z.Q. A compatible probabilistic framework for quantification of simultaneous aleatory and epistemic uncertainty of basic parameters of structures by synthesizing the change of measure and change of random variables. Struct. Saf. 2019, 78, 76–87. [Google Scholar] [CrossRef]
- Zhao, Y.G.; Zhang, X.Y.; Lu, Z.H. A flexible distribution and its application in reliability engineering. Reliab. Eng. Syst. Saf. 2018, 176, 1–12. [Google Scholar] [CrossRef]
- Li, J.; Chen, J.B. Stochastic Dynamics of Structures; John Wiley & Sons: Singapore, 2009. [Google Scholar]
- Wan, Z.Q. Global sensitivity evolution equation of the Fréchet-derivative-based global sensitivity analysis. Struct. Saf. 2024, 106, 102413. [Google Scholar] [CrossRef]
- Wainwright, H.M.; Finsterle, S.; Jung, Y.; Zhou, Q.L.; Birkholzer, J.T. Making sense of global sensitivity analyses. Comput. Geosci. 2014, 65, 84–94. [Google Scholar] [CrossRef]
- Atkinson, K.; Han, W.M. Theoretical Numerical Analysis: A Functional Analysis Framework; Springer Science & Business Media: New York, NY, USA, 2009. [Google Scholar]

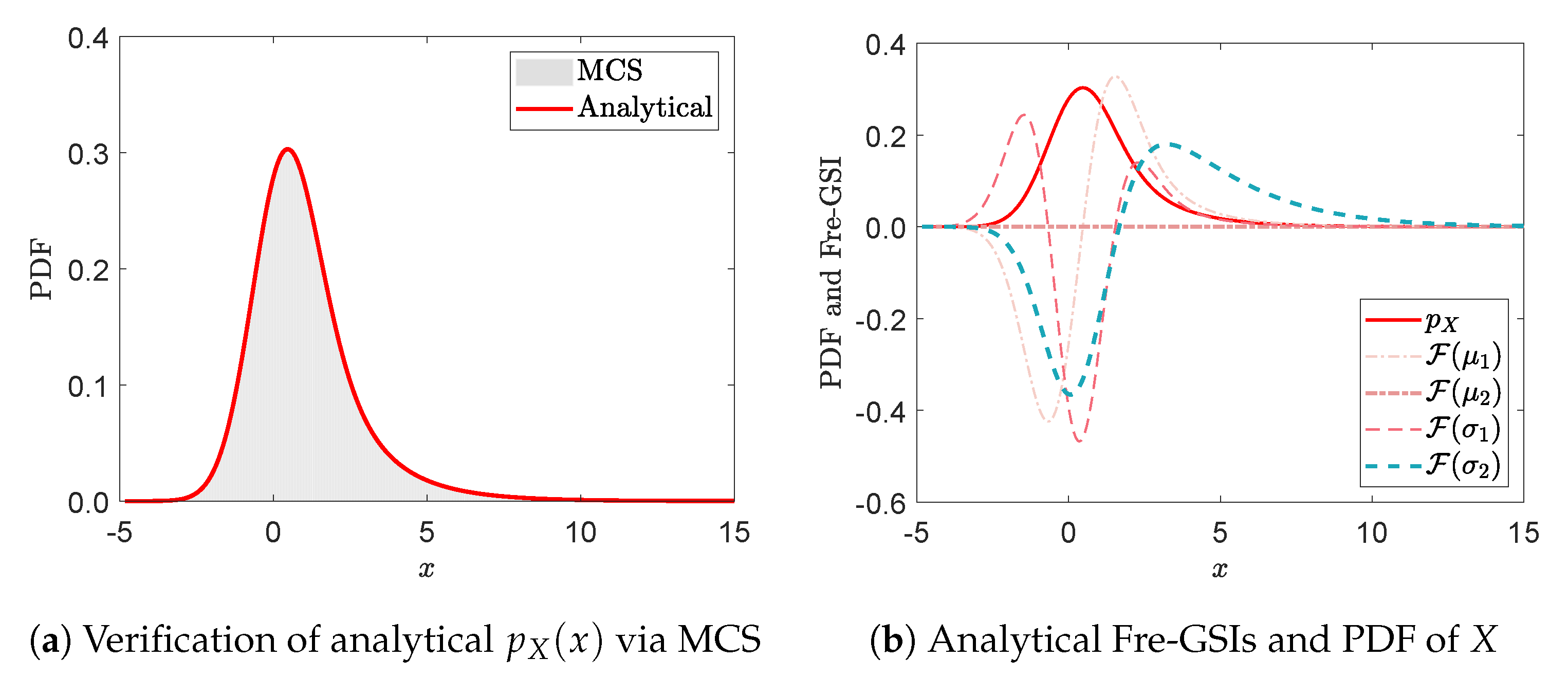
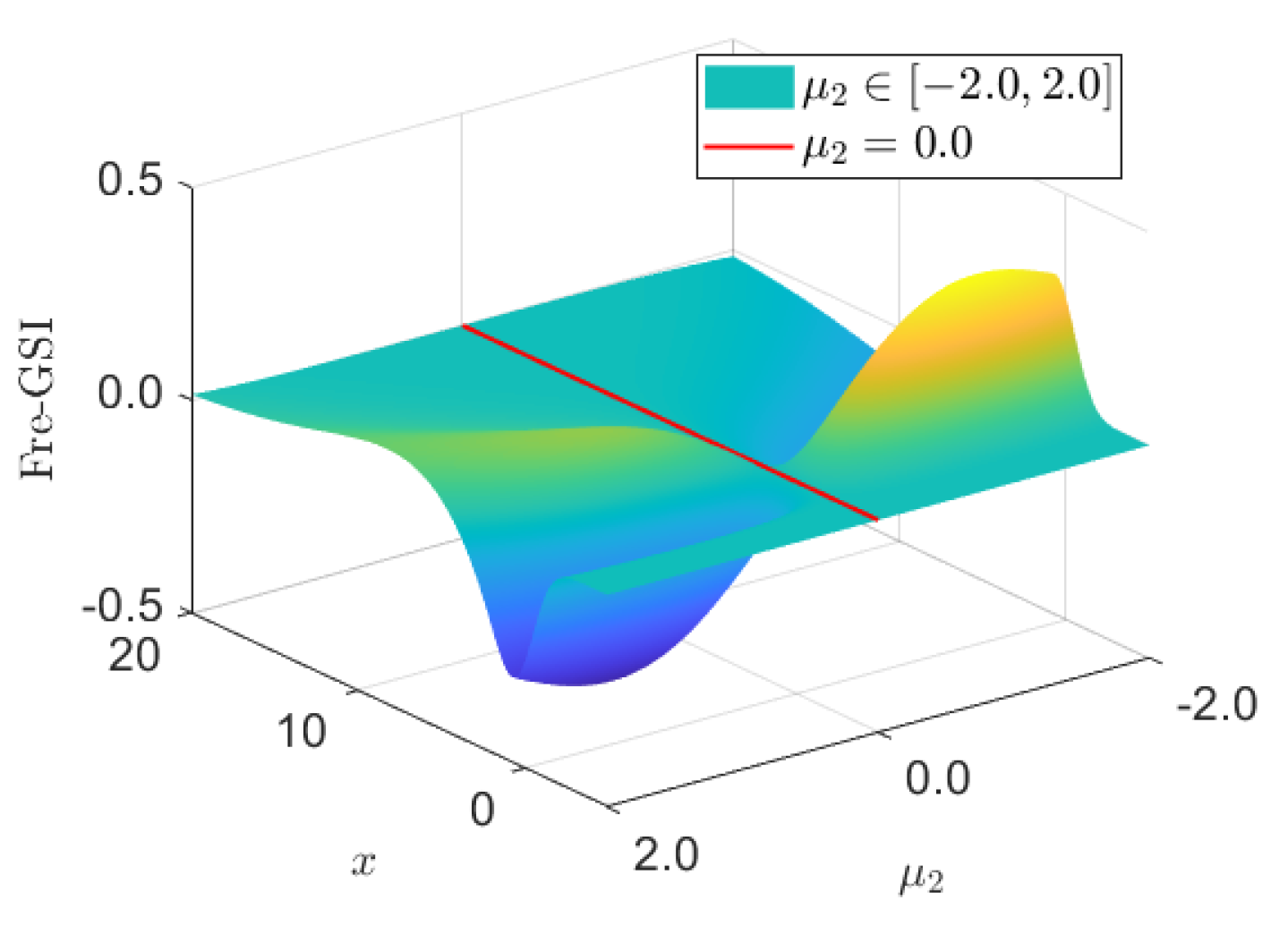
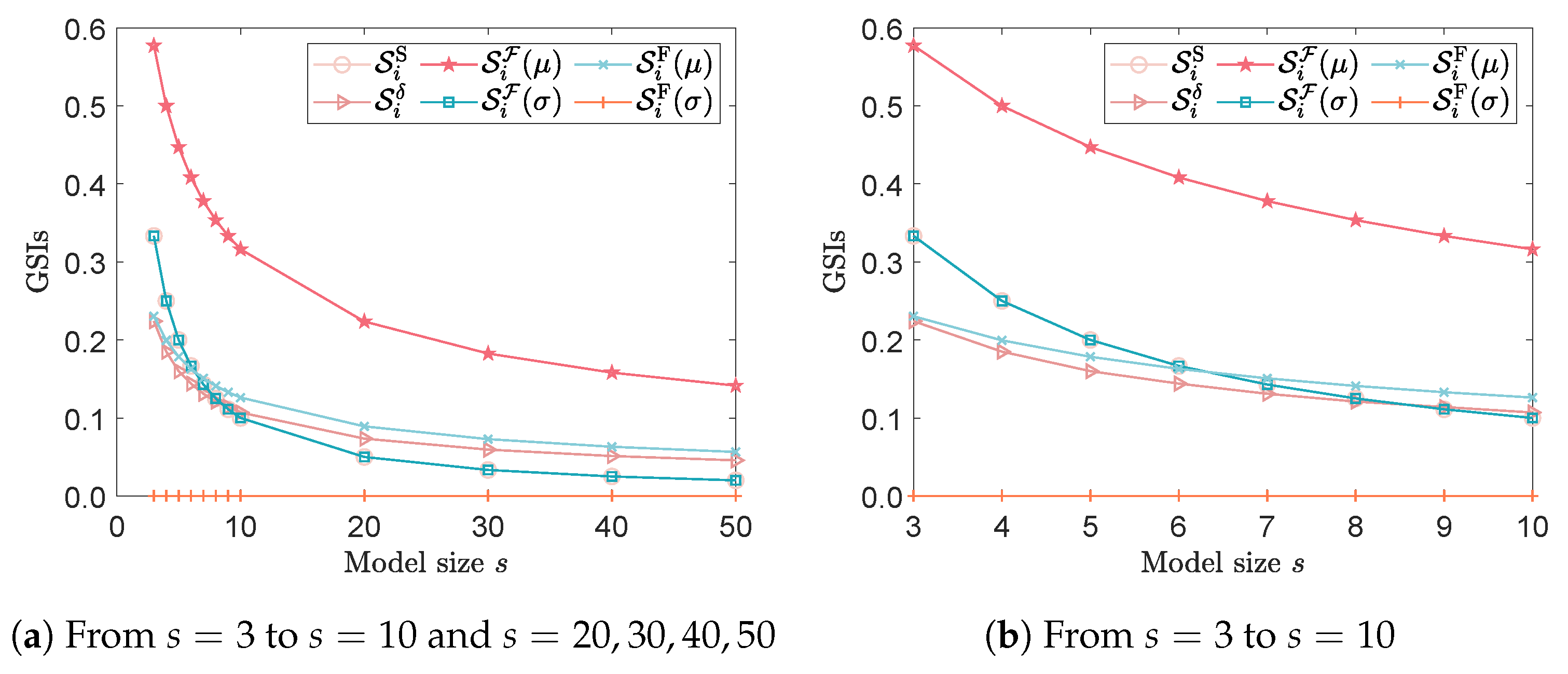

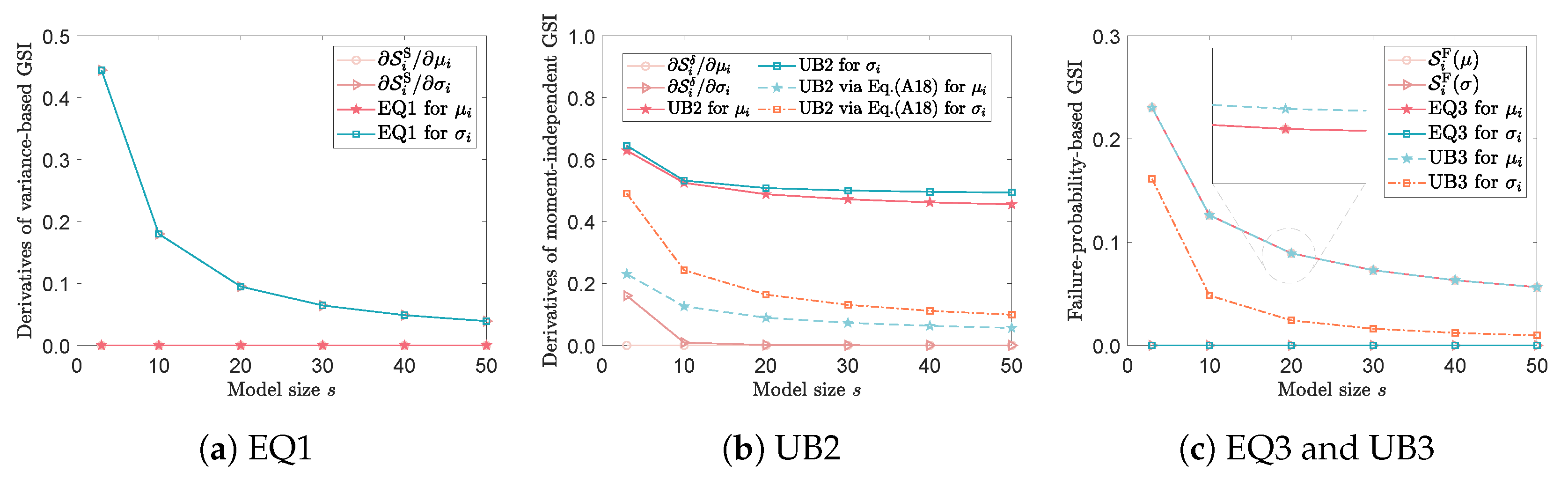
| EQ1 | UB2 | EQ3 | UB3 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Parameters | Distribution | (Mean, SD) |
|---|---|---|
| Lognormal | (m/s) | |
| Lognormal | (m/s) | |
| Lognormal | (m/s) | |
| Lognormal | (m/s) | |
| Uniform | (m) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tao, W.; Wan, Z.; Wang, X. Fréchet-Derivative-Based Global Sensitivity Analysis and Its Physical Meanings in Structural Design. Appl. Sci. 2025, 15, 2703. https://doi.org/10.3390/app15052703
Tao W, Wan Z, Wang X. Fréchet-Derivative-Based Global Sensitivity Analysis and Its Physical Meanings in Structural Design. Applied Sciences. 2025; 15(5):2703. https://doi.org/10.3390/app15052703
Chicago/Turabian StyleTao, Weifeng, Zhiqiang Wan, and Xiuli Wang. 2025. "Fréchet-Derivative-Based Global Sensitivity Analysis and Its Physical Meanings in Structural Design" Applied Sciences 15, no. 5: 2703. https://doi.org/10.3390/app15052703
APA StyleTao, W., Wan, Z., & Wang, X. (2025). Fréchet-Derivative-Based Global Sensitivity Analysis and Its Physical Meanings in Structural Design. Applied Sciences, 15(5), 2703. https://doi.org/10.3390/app15052703







