Enhancing Security and Efficiency in IoT Assistive Technologies: A Novel Hybrid Systolic Array Multiplier for Cryptographic Algorithms

Abstract

The incorporation of Internet of Things (IoT) edge nodes into assistive technologies greatly improves the daily lives of individuals with disabilities by facilitating real-time data processing and seamless connectivity. However, the increasing adoption of IoT edge devices intended for individuals with disabilities presents significant security challenges, particularly concerning the safeguarding of sensitive data and the heightened risk of cyber vulnerabilities. To effectively mitigate these risks, advanced cryptographic protocols, including those based on elliptic curve cryptography, have been proposed to establish robust security measures. While these protocols are effective in reducing the risk of data exposure, they often demand considerable computational resources, which poses challenges for cost-effective IoT devices. Therefore, it is essential to prioritize the effective execution of cryptographic algorithms, as they rely on finite field operations such as multiplication, inversion, and division. Among these computations, field multiplication is particularly critical, serving as the backbone for the other operations. This study intends to create an innovative hybrid systolic array design for the Dickson basis multiplier, which integrates both serial and parallel inputs to enhance overall performance. The proposed design is anticipated to significantly reduce space and power consumption, thereby enabling the secure execution of complex cryptographic algorithms on resource-limited IoT devices designed for disabled people. By addressing these pressing security issues, the study aspires to fully leverage IoT technologies to enhance the living standards of individuals with disabilities, while ensuring that their privacy and security are meticulously maintained.

1. Introduction

The integration of Internet of Things (IoT) edge nodes into assistive devices marks a significant advancement in improving the daily experiences of individuals with disabilities. These edge nodes facilitate real-time data processing and connectivity, enabling assistive devices to respond more effectively to the needs of users. For example, smart wheelchairs equipped with IoT edge nodes improve mobility by providing features such as obstacle detection and navigation assistance, empowering individuals with disabilities to navigate their environments safely and independently [1,2]. Similarly, hearing aids with IoT capabilities enable individuals with hearing impairments to filter sounds and adjust settings via smartphone connectivity, thus enhancing their ability to communicate in diverse settings [3,4].

Smart home systems designed for individuals with disabilities utilize IoT edge nodes to offer voice control or remote operation of lights, thermostats, and door locks, thereby increasing autonomy and comfort [5]. Wearable health monitors are capable of tracking vital signs and activity levels, providing real-time alerts to users and caregivers, which is particularly important for those with health concerns [6]. Additionally, smart prosthetics leverage edge nodes to analyze movement patterns, facilitating adaptive responses that enhance both functionality and user comfort [7,8].

Assistive robots developed to support individuals with disabilities can navigate and perform tasks using IoT edge nodes, thereby facilitating daily activities and improving user interaction [9]. Telehealth devices equipped with edge nodes enable remote consultations, ensuring that individuals with disabilities can access medical support without the necessity of travel [10]. Furthermore, environmental control systems empower users to manage their surroundings through IoT technology, promoting independence and enhancing overall quality of life [11].

Despite the integration of Internet of Things (IoT) devices into assistive technologies has significantly enhanced the lives of individuals with disabilities, their widespread adoption brings significant security challenges that must be thoroughly addressed. The sensitive data collected by these devices, coupled with their vulnerability to cyberattacks, raises critical concerns regarding personal privacy and the protection of essential infrastructure. For instance, smart home assistants such as Amazon Echo and Google Home are capable of storing sensitive voice recordings. If these recordings are not adequately secured, they could be accessed by unauthorized users, leading to potential violations of privacy and misuse of personal information [12]. Furthermore, wearable health monitors designed to track vital signs and other health metrics often lack effective authentication mechanisms. This shortcoming leaves personal health data exposed to unauthorized access, significantly jeopardizing the privacy and security of disabled users who rely on these devices for health management [13]. Additionally, smart wheelchairs face risks associated with physical tampering; if compromised, their navigation systems could be manipulated, posing severe safety risks to users. Remote monitoring systems also present challenges, as they may transmit sensitive data without sufficient encryption, making them susceptible to interception and exploitation [14].

The vulnerabilities extend to assistive communication devices and environmental control systems, which frequently rely on insecure communication channels. Such vulnerabilities can facilitate unauthorized access and manipulation of users’ home environments, undermining their safety and autonomy [15]. Location tracking devices, while essential for enhancing safety, can introduce significant privacy risks if the tracking information is intercepted by malicious actors [16]. Furthermore, IoT-enabled prosthetics may be vulnerable to firmware flaws that can lead to operational failures, while emergency alert systems are at risk of denial of service attacks, which could prevent timely notifications [17].

To ensure these devices can operate effectively and securely, it is imperative to address these pervasive security concerns. In this regard, cryptographic protocols are essential for bolstering the security of IoT edge devices. These protocols provide a robust framework for mitigating key vulnerabilities across various functionalities. For example, end-to-end encryption is crucial for safeguarding data privacy, ensuring that sensitive information—such as voice recordings and health data—remains confidential and inaccessible to unauthorized parties. Secure communication protocols, including Transport Layer Security (TLS), are vital for protecting data in transit, effectively preventing eavesdropping and man-in-the-middle attacks. Such measures are particularly important for remote monitoring systems and assistive communication devices, where the integrity and confidentiality of data are paramount. Moreover, the implementation of robust authentication methods, such as public key infrastructure (PKI) and digital signatures, is critical for ensuring that only authorized users can access and control devices like smart wheelchairs and environmental control systems. By significantly mitigating the risks associated with unauthorized access, these methods enhance user trust in IoT technologies. Additionally, secure firmware update protocols, such as code signing, are necessary to confirm that only verified updates are applied to IoT-enabled prosthetics, thereby protecting against the exploitation of known vulnerabilities.

Cryptographic techniques also play a pivotal role in verifying the authenticity of requests sent to emergency alert systems, thereby reducing the likelihood of false alerts and mitigating the risks of denial of service attacks. Furthermore, cryptographic hashing algorithms help maintain data integrity by ensuring that information collected by environmental control systems remains intact and unaltered. Collectively, these protocols establish a comprehensive security framework that ensures the reliable and safe operation of IoT devices while safeguarding the privacy and well-being of individuals with disabilities.

Implementing robust security measures is essential to fully harness the potential of IoT technologies in enhancing the independence and quality of life for individuals with disabilities. Given that these individuals often depend heavily on such devices, it is crucial to address the security vulnerabilities associated with them. The limited resources available in IoT edge nodes complicate the deployment of effective cryptographic protocols necessary for protecting user data. These protocols rely on finite field arithmetic operations, with finite field multiplication serving as a fundamental component in various arithmetic processes used within them [18,19,20]. Thus, advancements in these protocols are closely tied to improvements in this particular operation. Therefore, this research mainly focuses on developing a compact hybrid systolic multiplier architecture to enable the implementation of cryptographic protocols in resource-constrained IoT edge nodes, thereby bolstering the security of IoT assistive devices. By tackling these security challenges, we can unlock the full potential of IoT technologies to empower individuals with disabilities.

Table 1. Comparison of current traditional designs to the proposed solution.

Aspect	Transitional Designs	Our Proposal
Resource Efficiency	High computational demand, unsuitable for IoT devices	Optimized hybrid systolic array with reduced power and space requirements
Complexity	Quadratic complexity leading to integration challenges	Linear complexity for easier implementation in compact devices
Miniaturization	Limited capability for miniaturization in existing designs	Compact design tailored for resource-constrained environments

presents a summary of the challenges encountered by existing traditional multiplier designs and demonstrates how our proposed compact hybrid systolic multiplier architecture addresses these issues. This approach is intended to enhance both the security and efficiency of IoT assistive devices.

1.1. Literature Review

The selection of base representation for components in GF($2^m$) plays a crucial role in determining the multiplication efficiency within finite fields. Various representations, such as polynomial basis (PB), normal basis (NB), dual basis (DB), and redundant basis (RB), each offer unique advantages tailored to different applications [18,19,20]. Notably, the normal basis (NB) stands out as particularly advantageous for cryptographic applications. One of the key benefits of normal bases is their proficiency in executing squaring operations efficiently. This efficiency is achieved by utilizing simple cyclic shifts for squaring, which require fewer computational demands and processing time. This characteristic is especially important in security protocols, where squaring occurs frequently, underscoring the normal basis’s suitability for rapid processing. In addition, normal bases ensure a uniform representation of components. This uniformity results in predictable patterns during arithmetic operations, facilitating easier hardware optimization. Such predictability is essential for crafting high-performance digital circuits, as it helps maintain stable operation and resource management. Conversely, other representations, like polynomial basis (PB), can lead to inconsistencies in task complexity, making the design and refinement of hardware solutions more challenging [21,22,23,24,25].

Although normal bases present numerous benefits, they also come with certain limitations, particularly in the multiplication of components. The multiplication procedure using a normal basis tends to be more complex than with other representations, which can hinder performance, especially in scenarios that require frequent multiplication operations. To address these challenges, advanced versions of normal bases, including optimal normal basis (ONB) and Gaussian normal basis (GNB), have been introduced. These modifications aim to improve multiplication efficiency while preserving the beneficial characteristics that make normal bases advantageous.

Considering the drawbacks of normal bases, the Dickson basis emerges as a promising substitute for developing effective finite field multipliers in various applications [18]. The space complexity related to Dickson-based multipliers typically aligns well with that of optimal normal basis (ONB) multipliers, rendering this option especially appealing for resource-limited settings, such as embedded systems and IoT devices. Scholars, including Hasan and Negre [18], have explored lightweight Dickson polynomials, including binomials and trinomials, to enhance the performance of these multipliers further. Additionally, Chiou et al. [19] have made significant strides by creating high-throughput bidirectional systolic array multipliers that leverage the Dickson basis, showcasing its relevance and effectiveness in cryptographic applications. However, the bidirectional architecture frequently observed in existing designs, such as those by Chiou [19], poses notable challenges when it comes to incorporating effective error-detection strategies. These strategies are essential for safeguarding systems against side-channel attacks that may exploit weaknesses in elliptic curve cryptography. This situation underscores the pressing need for resilient architectures capable of embedding robust security functionalities without compromising overall efficiency. Alternatively, the researchers in [20] proposed a unidirectional systolic array design for the Dickson basis multiplier, enabling the effective incorporation of robust error-detection mechanisms. Nevertheless, its quadratic area complexity renders it impractical for compact, ultra-low-power IoT edge nodes, highlighting the ongoing challenge of balancing performance and resource constraints in this field.

The selection of irreducible polynomials plays a vital role in optimizing finite field multipliers, as they underpin the arithmetic operations executed. This decision can have a profound effect on overall performance [21,22,23,24,25]. Although irreducible trinomials and pentanomials are frequently favored for their operational advantages, the flexibility and effectiveness of finite field multiplication are enhanced by a diverse range of polynomial choices. Additionally, some irreducible polynomials, though less commonly adopted, can offer considerable advantages in specific contexts, thereby facilitating the creation of efficient multipliers [26,27,28]. This range of polynomial options enriches the versatility and efficiency of finite field multiplication across various technological applications.

Different design techniques can lead to a variety of multiplier architectures, each exhibiting distinct characteristics that impact their performance and suitability for specific applications. For instance, bit-serial multipliers are renowned for their compact design and remarkable energy efficiency, making them ideal for low-power devices; however, they necessitate multiple clock cycles to complete a single multiplication operation, which can hinder speed in high-performance settings [29,30,31]. In contrast, bit-parallel multipliers can produce results in just one clock cycle, significantly improving throughput, but they often come with greater expenses related to hardware and power usage, making them more suitable for applications where speed is critical and budget constraints are less stringent [32,33,34,35,36,37,38,39,40]. Moreover, in the field of Very Large Scale Integration (VLSI), systolic and semi-systolic array designs are increasingly favored due to their modular nature and ability to process data concurrently. These architectures are particularly advantageous for high-speed applications, such as digital signal processing and real-time computing, as they effectively optimize the utilization of available hardware resources while enhancing overall performance and scalability. By leveraging parallelism, they can significantly reduce latency and improve throughput, making them a compelling choice for modern computational demands.

A considerable number of researchers have focused on enhancing systolic and semi-systolic multipliers tailored for binary extension fields GF($2^m$), which play a vital role in various computational applications. For example, Lee and Chiou [29,41] have developed advanced semi-systolic array multipliers that include error-detection features to improve the reliability of computations. In a similar vein, Huang et al. [42] have concentrated on optimizing both time and space efficiency in their designs, addressing the limitations of hardware resources. Furthermore, Choi and Lee [33] have contributed to the field by designing systolic array architectures that enable simultaneous multiplication and squaring operations. This innovation significantly enhances the performance of modular exponentiation, a crucial process in many algorithms, while reducing the associated resource requirements. Their methodology also employs least significant bit (LSB)-first multiplication techniques, which additionally improve computing efficiency by optimizing the computation sequence.

Recent developments in multiplier designs have primarily concentrated on enhancing both efficiency and speed, particularly in the context of cryptographic systems that necessitate fast and accurate computations. For instance, Chiou et al. [19] engineered a semi-systolic array multiplier that significantly diminishes time complexity, enabling it to handle rapid multiplication tasks with impressive performance metrics. This innovation is especially valuable in environments where quick calculations are vital, such as digital signatures and encryption algorithms. Expanding upon this foundational work, Lee [43,44] proposed semi-systolic Montgomery modular multipliers that utilize a two-tiered approach to systolic computation. This design not only enhances area utilization by effectively managing hardware resources but also substantially reduces latency, making it a critical advancement for high-performance VLSI implementations. The two-tiered methodology facilitates a robust capacity for parallel processing and pipelining, allowing multiple operations to be executed simultaneously. As a result, this approach leads to a marked increase in the efficiency of modular multiplication operations, which are essential for a range of contemporary cryptographic applications.

Additionally, Mathe and Boppana [45] introduced an innovative and versatile multiplier architecture that adeptly manages both parallel and serial input formats. This flexibility allows for optimal performance across a diverse range of operand types, enhancing adaptability in various computational scenarios. Building on this foundation, Ibrahim [46] designed one-dimensional bit-serial and bit-parallel systolic array structures specifically aimed at computations in the Galois Field GF($2^m$). These structures improve resource utilization, ensuring that hardware resources are deployed effectively and achieving greater processing efficiency. This design is particularly beneficial for applications such as error correction codes and cryptographic systems, where the demand for speed and efficiency is critical in today’s digital landscape.

Pillutla and Boppana [23] have made notable contributions to the field through the introduction of a polynomial basis systolic multiplier specifically engineered for designated field sizes. This advancement signifies a shift towards specialized architectures that are adept at addressing the distinct requirements of various computational tasks. In a related context, Lee’s implementation of a Toeplitz matrix-vector representation has effectively reduced the complexities associated with Montgomery-based bit-parallel multipliers. This methodological refinement has resulted in designs that demonstrate enhanced efficiency and practicality, as documented in [38]. Moreover, Sarmadi’s development of a two-dimensional parallel systolic multiplier [39], grounded in the Montgomery algorithm, achieves impressive performance while maintaining minimal spatial requirements. This architecture facilitates the simultaneous execution of multiple operations, thereby significantly increasing throughput and establishing itself as an essential asset in high-demand computational environments.

Mathe [40] has significantly advanced the field by integrating interleaving multiplication techniques into a two-dimensional parallel systolic multiplier architecture. This innovative approach facilitates effective resource utilization while simultaneously ensuring high performance levels. The implementation of interleaving techniques allows for the concurrent processing of multiple operations, thereby substantially enhancing throughput. These developments collectively signify a concerted effort to establish flexible multiplier architectures that can adapt to the evolving requirements of modern cryptographic applications. Furthermore, they contribute to improved performance and resource efficiency in hardware implementations. Such advancements are imperative for sustaining the integrity and efficacy of cryptographic systems within an increasingly complex technological landscape.

1.2. Paper Contribution

This paper introduces a groundbreaking compact hybrid systolic array architecture specifically developed for the Dickson basis multiplier, showcasing remarkable improvements in both space and power efficiency when compared to traditional designs. By seamlessly integrating serial and parallel inputs, the proposed systolic array enhances data processing flexibility while maintaining a streamlined structure that effectively consolidates input types into parallel outputs.

A key feature of this architecture is its linear complexity, which contrasts sharply with the quadratic complexity typically found in many existing designs. Linear complexity means that the resources needed for computation increase directly with the size of the input; for instance, if the input size doubles, the resources required also approximately double. In contrast, quadratic complexity indicates that the resources required grow at a rate proportional to the square of the input size, leading to a fourfold increase in resource demands when the input size doubles. By maintaining linear complexity, the architecture minimizes the number of processing elements (PEs) and connections needed, which directly contributes to lower space and power usage. The streamlined design reduces the overall number of active components during operation, leading to further energy savings. Consequently, the proposed architecture not only occupies less physical space but also operates more efficiently, making it particularly suitable for applications where power efficiency is critical.

Crucially, even with this reduction in area and power consumption, the multiplier’s performance remains intact, achieving timing delays that are comparable to those of conventional two-dimensional multipliers. Furthermore, the modular design and close connectivity among PEs greatly enhance its suitability for VLSI implementation. These tight interconnections not only improve overall performance but also minimize wire delays, which can considerably impact circuit efficiency. Consequently, this multiplier structure is particularly well-suited for compact IoT edge nodes designed for disabled people, providing substantial advantages in terms of space efficiency and power savings. The characteristics of this approach render it an attractive option for applications tailored specifically to individuals with disabilities, particularly in environments where high efficiency is essential. This innovation holds the potential to significantly benefit those who rely on assistive technologies. The experimental analysis strongly supports the advantages of this design, laying the groundwork for the effective implementation of cryptographic algorithms on IoT edge nodes designed for people with special needs. Moreover, the success in deploying these cryptographic algorithms within resource-constrained environments will not only enhance security but also ensure safe access to vital assistive devices. This improvement is instrumental in promoting a better quality of life for individuals with disabilities, empowering them to navigate their daily lives with greater confidence and independence.

1.3. Paper Organization

This study is organized in the following manner: Section 2 offers a comprehensive overview of the Dickson basis, underscoring its vital importance in multiplier design. In Section 3, we undertake a detailed examination of the combined dependency graph (DG) associated with Dickson-based multipliers. This analysis explores the complex interrelationships and dependencies among different operations, providing insights into how these interactions impact overall performance metrics. Section 4 delves into the architecture and implementation details of the proposed hybrid systolic Dickson basis multiplier. Here, we highlight its innovative characteristics and discuss the expected performance benefits that distinguish it from traditional architectures. In Section 5, we carry out a thorough comparison of performance metrics across a range of multipliers, focusing on those that employ the Dickson basis. Attention is given to their efficiency in the context of IoT applications aimed at assisting individuals with disabilities. Finally, Section 6 summarizes our principal findings and suggests avenues for future research initiatives.

2. Exploring Dickson Basis Multiplication in GF($2^m$)

Consider ℜ as a ring, with ℏ being a specific element contained in ℜ (i.e., $\hslash \in \Re$). The $k^{th}$ Dickson polynomial of the ${(k+1)}^{th}$ type, represented as ${\mathbb{D}}_{\mathsf{\ell },k}(\rho ,\hslash )$, serves as a significant entity in algebra and number theory. These polynomials are recognized for their fascinating characteristics and numerous applications. Their formulation enables various computations and theoretical investigations, making them essential tools in both theoretical and applied mathematics. The polynomial can be expressed using the following formula [18,19,20]:

$$\begin{array}{c}\hfill {\mathbb{D}}_{\mathsf{\ell },k}(\rho ,\hslash )=\sum _{i=1}^{\lfloor {\displaystyle \frac{\mathsf{\ell }}{2}}\rfloor }{\displaystyle \frac{\mathsf{\ell }-ki}{\mathsf{\ell }-i}}\left({\displaystyle \genfrac{}{}{0pt}{}{\mathsf{\ell }-i}{i}}\right){(-\hslash )}^i{\rho }^{\mathsf{\ell }-2i}\end{array}$$

(1)

In this context, $\lfloor {\displaystyle \frac{\mathsf{\ell }}{2}}\rfloor$ refers to the floor function applied to the value of ${\displaystyle \frac{\mathsf{\ell }}{2}}$, effectively rounding down to the nearest integer. Meanwhile, the notation $\left({\displaystyle \genfrac{}{}{0pt}{}{\mathsf{\ell }-i}{i}}\right)$ calculates the count of possible selections of i elements from a total of $\mathsf{\ell }-i$ distinct items, highlighting its combinatorial significance. To simplify our analysis, we will concentrate on the ${\mathsf{\ell }}^{th}$ Dickson polynomial of the first kind, which corresponds to the case where $k=0$. This particular polynomial plays a foundational role in the study of algebraic structures and can be expressed through a specific formula that captures its essential characteristics and relationships within the broader framework of Dickson polynomials. The polynomial can be expressed as follows:

$$\begin{array}{c}\hfill {\mathbb{D}}_{\mathsf{\ell }}(\rho ,\hslash )=\sum _{i=1}^{\lfloor {\displaystyle \frac{\mathsf{\ell }}{2}}\rfloor }{\displaystyle \frac{\mathsf{\ell }}{\mathsf{\ell }-i}}\left({\displaystyle \genfrac{}{}{0pt}{}{\mathsf{\ell }-i}{i}}\right){(-\hslash )}^i{\rho }^{\mathsf{\ell }-2i}\end{array}$$

(2)

In this context, ${\mathbb{D}}_0(\rho ,\hslash )=2$ and ${\mathbb{D}}_1(\rho ,\hslash )=\rho$ serve as the initial conditions for the cases when $\mathsf{\ell }=0$ and $\mathsf{\ell }=1$, respectively. Expanding on these foundational equations, the Dickson polynomials are defined recursively by by the subsequent expressions:

$${\mathbb{D}}_i(\rho ,\hslash )=\left\{\begin{array}{cc}2\hfill & \mathrm{if}i=0,\hfill \\ \rho \hfill & \mathrm{if}i=1,\hfill \\ \rho {\mathbb{D}}_{i-1}(\rho ,\hslash )-\hslash {\mathbb{D}}_{i-2}(\rho ,\hslash )\hfill & \mathrm{if}i\ge 2\hfill \end{array}\right.$$

(3)

In the context of the finite field GF(2), we are particularly interested in the ${\mathsf{\ell }}^{th}$ Dickson polynomial where $\hslash =1$, denoted as ${\mathbb{D}}_{\mathsf{\ell }}(\rho ,1)$. For each integer i, we can represent this as ${\omega }_i={\mathbb{D}}_i(\rho ,1)$. The Dickson basis, which is derived from an irreducible polynomial K of degree r within GF(2), can be characterized as follows:

In the context of the finite field $GF\left(2\right)$, we delve into the study of Dickson polynomials, specifically focusing on the polynomial of order ℓ when $\hslash =1$. This is denoted as ${\mathbb{D}}_{\mathsf{\ell }}(\rho ,1)$. Considering any integer i, we designate ${\omega }_i$ as ${\mathbb{D}}_i(\rho ,1)$. When analyzing an irreducible polynomial K with degree r in $GF\left(2\right)$, we can establish a Dickson basis, represented by the collection: $\mathsf{\Omega }=\{{\omega }_1,{\omega }_2,\dots ,{\omega }_r\}$. To illustrate the concept, we can consider ${\omega }_1=\rho$, ${\omega }_2={\rho }^2$, and ${\omega }_3={\rho }^3+\rho$ demonstrate the construction of the basis elements. As a result, any element X in the field GF($2^r$) can be represented in the form: $E=e_1{\omega }_1+e_2{\omega }_2+\cdots +e_r{\omega }_r$, where $e_i\in GF\left(2\right)$ for i index ranging from 1 to r.

By leveraging the fundamental characteristics of GF($2^r$), it is possible to reformulate Equation (3) to underscore these features more effectively. This reformulation can be expressed as:

$${\omega }_i=\left\{\begin{array}{cc}0\hfill & \mathrm{if}i=0,\hfill \\ \rho \hfill & \mathrm{if}i=1,\hfill \\ \rho {\omega }_{i-1}+{\omega }_{i-2}\hfill & \mathrm{if}i\ge 2\hfill \end{array}\right.$$

(4)

A Dickson binomial is characterized as an irreducible polynomial K that can be expressed in the following simple two-component expression: $K={\omega }_r+1$. This particular representation is noteworthy due to its efficiency and straightforward nature, making it highly applicable in various cryptographic scenarios. Conversely, a polynomial K is considered a Dickson trinomial when it assumes the structure $K={\omega }_r+{\omega }_n+1$, with the stipulation that $1\le n\le {\displaystyle \frac{r}{2}}$. This configuration facilitates more intricate interactions among terms, thereby enhancing overall security measures. Dickson polynomials, encompassing both binomials and trinomials, are integral to the field of lightweight cryptography. This domain seeks to enhance efficiency while maintaining robust security, particularly in environments characterized by limited resources. The present study aims to examine the application of Dickson binomials in cryptographic frameworks. It will underscore their significant contributions and advantages, highlighting their efficacy in achieving efficient and secure cryptographic solutions.

Multiplication Technique Using the Dickson Basis: As previously stated, let the Dickson basis be represented as $\mathsf{\Omega }=\{{\omega }_1,{\omega }_2,\cdots ,{\omega }_r\}$. Additionally, we will consider the irreducible binomial given by $K={\omega }_r+1$, which facilitates the generation of various elements within the finite field. The elements E, F, and H in the finite field GF($2^r$) are represented in relation to this basis as follows: $E=e_1{\omega }_1+e_2{\omega }_2+\cdots +e_r{\omega }_r$, $F=f_1{\omega }_1+f_2{\omega }_2+\cdots +f_r{\omega }_r$, $H=h_1{\omega }_1+h_2{\omega }_2+\cdots +h_r{\omega }_r,$ where the coefficients $e_i$, $f_i$, and $h_i$ are elements of GF(2) for each index i ranging from 1 to r. Moreover, the element H is defined as the result of multiplying E and F, followed by taking the computation modulo K. This relationship can be succinctly expressed as $H=E\times FmodK$. Such an operation plays a vital role in various applications within cryptography, enabling efficient computations while ensuring security in environments with limited resources.

As highlighted in the works of [18,20], the irreducible binomial $K={\omega }_r+1$ plays a pivotal role in the generation of elements within a finite field GF($2^r$). It has been demonstrated that for all integers $i\ge 0$, the equation ${\omega }_{r+i}={\omega }_i+{\omega }_{r-i}$ is satisfied. Utilizing this equation, one can derive the product H more effectively. Specifically, when calculating H, the elements can be expressed in terms of their corresponding basis components, allowing for a streamlined process of multiplication. By leveraging the established relationship, the computation of H can be simplified as follows:

$$\begin{array}{c}\hfill H=EF=\underbrace{\sum _{i,j=1}^r{e}_i{f}_j{\omega }_{i+j}}+\underbrace{\sum _{i,j=1}^r{e}_i{f}_j{\omega }_{|i-j|}}\end{array}$$

(5)

Equation (5) can be reformulated in matrix notation, a representation that is essential for the accurate synthesis of the systolic multiplier. This matrix representation facilitates a more systematic approach to performing calculations, ensuring that the operations can be efficiently executed in parallel. The product H is obtained from three separate matrix-vector products, identified as $H_1$, $H_2$, and $H_3$ [18,20]. These products are essential components in the overall computation and can be expressed as follows:

$$\begin{array}{c}H=\underset{H1}{\underbrace{\left[\begin{array}{ccccc}{e}_r& e_{r-1}& e_{r-2}& \cdots & e_1\\ e_1& e_r& e_{r-1}& \cdots & e_2\\ e_2& e_1& e_r& \cdots & e_3\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ e_{r-1}& e_{r-2}& e_{r-3}& \cdots & e_r\end{array}\right]\times \left[\begin{array}{c}{f}_1\\ f_2\\ f_3\\ ⋮\\ f_r\end{array}\right]}}\\ +\underset{H2}{\underbrace{\left[\begin{array}{ccccc}0& e_1& e_2& \cdots & e_{r-1}\\ 0& 0& e_1& \cdots & e_{r-2}\\ 0& 0& 0& \cdots & e_{r-3}\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ 0& 0& 0& \cdots & 0\end{array}\right]\times \left[\begin{array}{c}{f}_1\\ f_2\\ f_3\\ ⋮\\ f_r\end{array}\right]}}\\ +\underset{H3}{\underbrace{\left[\begin{array}{ccccc}{e}_{r-1}& 0& e_{r-1}& \cdots & e_2\\ e_{r-2}& e_{r-1}& 0& \cdots & e_3\\ e_{r-3}& e_{r-2}& e_{r-1}& \cdots & e_4\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ 0& e_1& e_2& \cdots & e_{r-1}\end{array}\right]\times \left[\begin{array}{c}{f}_r\\ f_{r-1}\\ f_{r-2}\\ ⋮\\ f_1\end{array}\right]}}\end{array}$$

(6)

3. Dependency Graph

To attain a more profound comprehension of the computational interdependencies and structures outlined in Equation (6), a dependency graph (DG) can be utilized for illustration. In examining the three matrix-vector products $H_1$, $H_2$, and $H_3$ delineated in Equation (6), it is evident that they operate within a common processing framework, yet they exhibit distinct variations in the organization and presentation of input components to the computational system. Figure 1 exhibits the DG corresponding to the matrix-vector products detailed in Equation (6), employing a two-dimensional integer domain $\mathcal{D}$ characterized by indices i and j. The DG comprises $r\times r$ nodes, with each node signifying the operations specified by the formula in Equation (6). Importantly, the coefficients for the matrix-vector products $H_1$, $H_2$, and $H_3$ are calculated sequentially, commencing with the coefficients for $H_1$. The resultant product H can be obtained after a latency of $r+2$ clock cycles, by aggregating the outcomes from the three product vectors $H_1$, $H_2$, and $H_3$.

The flow of signals in the DG depicted in Figure 1 can be characterized as follows: From the left side, the signals $f_i$, $f_i$, and $f_{r-i+1}$ are introduced sequentially, with i taking values from 1 to r. In addition, signals $e_{r-i+1}$, $e_{i-1}$, and $e_{r-i}$ are introduced from the left corners of the nodes along the DG’s left edge, following a similar sequential order. From the top of the DG, the signals $e_{j-1}$, 0, and $e_{r-j}$ are introduced in succession, where j ranges from 1 to r. Additionally, the zero values of the signals $h_j$ are introduced from the top of DG. It is essential that these signals are entered in the correct sequence from the upper part of the DG at designated timings. As processing occurs at each node, the intermediate coefficient results of the matrix-vector products $H_1$, $H_2$, and $H_3$ are computed and transmitted to the subsequent row of nodes. Ultimately, the result H is derived by summing the coefficients from $H_1$, $H_2$, and $H_3$, with this summation executed using XOR gates.

4. Derivation of the Hybrid Compact Systolic Multiplier

This section delineates the methodology employed to examine the development of the hybrid systolic multiplier. Central to this approach is the application of particular scheduling and projection functions on the dependency graph (DG), which facilitates the design of the proposed multiplier layout [47,48,49].

4.1. Scheduling Function

Let us denote any node in the DG by the point $\mathbf{\Gamma }(i,j)=\left[ij\right]$. Furthermore, we apply the following scheduling function to the scheduling vector $\mathbf{{\rm Y}}=\left[{\upsilon }_0{\upsilon }_1\right]$ in order to determine the time scheduling for each node.

$$\Delta \left(\mathbf{\Gamma }\right)=\mathbf{{\rm Y}}\mathbf{\Gamma }-\delta =i{\upsilon }_0+j{\upsilon }_1-\delta$$

(7)

To ensure that no nodes in the DG are assigned negative time values, a scalar parameter $\delta$ has been introduced in the previous formula. In the specific scenario under consideration, selecting $\delta \equiv 0$ results in the DG nodes depicted in Figure 1 receiving only positive time values. This choice of $\delta$ effectively eliminates any negative time allocations during the execution of the algorithm.

The scheduling vector operates within a predetermined range and adheres to specific constraints that govern its functionality. Specifically, nodes positioned at $\mathbf{\Gamma }=[i,j]$ are mandated to run only following the activation of nodes at $\mathbf{\Gamma }=[i-1,j]$. This requirement is crucial, as it establishes a clear sequential order of execution. Consequently, it ensures that the essential dependency relationships between the nodes are preserved throughout the process. Such an organized approach is imperative for maintaining the integrity of the scheduling framework.

$$\Delta (\mathbf{\Gamma }=[i,j\left]\right)>\Delta (\mathbf{\Gamma }=[i-1,j\left]\right)$$

(8)

Taking into account the coordinate values of $\mathbf{{\rm Y}}$, the previously mentioned formula can be represented as follows:

$$\begin{array}{ccc}\hfill i{\upsilon }_0+j{\upsilon }_1& >& (i-1){\upsilon }_0+j{\upsilon }_1\hfill \\ \hfill {\upsilon }_0& >& 0\hfill \end{array}$$

(9)

By examining Equation (6), we can expand our timing constraints by noting that the operations linked to nodes $\mathbf{\Gamma }=[i,j+1]$ must be executed only after those associated with nodes $\mathbf{\Gamma }=[i-1,j]$ have been completed. This means that the execution sequence is critical, as it ensures that the necessary dependencies are respected and that the overall scheduling framework operates efficiently.

$$\Delta (\mathbf{\Gamma }=[i,j+1\left]\right)>\Delta (\mathbf{\Gamma }=[i-1,j\left]\right)$$

(10)

Based on the coordinate values of $\mathbf{{\rm Y}}$, the previously mentioned formula can be articulated as follows:

$$\begin{array}{ccc}\hfill i{\upsilon }_0+j{\upsilon }_1+{\upsilon }_1& >& i{\upsilon }_0-{\upsilon }_0+j{\upsilon }_1\hfill \\ \hfill {\upsilon }_1& >& -{\upsilon }_0\hfill \end{array}$$

(11)

By utilizing the inequality pairs, Equations (9) and (11), we can identify the most effective scheduling vectors. An illustrative example of a fitting scheduling vector is the next vector $\mathbf{{\rm Y}}$, which aids in deriving the planned hybrid systolic design.

$$\begin{array}{ccc}\hfill \mathbf{{\rm Y}}& =\hfill & \hfill \left[\begin{array}{cc}1& 0\end{array}\right]\end{array}$$

(12)

By inserting the derived scheduling vector $\mathbf{{\rm Y}}$ into Equation (7), we can formulate the corresponding scheduling function as:

$$\begin{array}{c}\hfill \Delta \left(\mathbf{\Gamma }\right)=i\end{array}$$

(13)

Figure 2 illustrates the scheduling times in the dependency graph (DG) after applying the derived function to each node. It is evident that the nodes within each row can be computed simultaneously, while the partial results from one row are transferred to the nodes of the subsequent row with a delay of one time instance. Given that the DG remains consistent for the three matrix-vector products specified in Equation (6), it will be utilized to compute $H_1$, $H_2$, and $H_3$ sequentially. Consequently, the aggregated output H can be available after $r+2$ time instances. This latency can be achieved by employing a conventional two-dimensional systolic array to compute the aggregated product. However, to develop a compact one-dimensional systolic array suitable for integration into resource-constrained IoT nodes, it is essential to ensure that the DG computes each matrix-vector product separately over r time instances. Consequently, this approach will result in the aggregated product H being available at the output after $3r$ time instances, thereby optimizing the design for resource efficiency while maintaining functionality as will be described later.

4.2. Projection Function

The projection function, as detailed in [47], plays a critical role in the optimization of dependency graphs (DGs) by merging multiple vertices $\mathbf{\Gamma }(i,j)$ into a unified processing element (PE), referred to as $\overline{\mathbf{\Gamma }}$. This consolidation simplifies the computational architecture, enabling more efficient processing. Once these PEs are formed, they are interconnected to construct a systolic or semi-systolic array, which facilitates streamlined data flow and computation. The projection function can be represented in different ways, one of which is presented below:

$$\overline{\mathbf{\Gamma }}=\mathbf{\Xi }\mathbf{\Gamma }$$

(14)

In the earlier discussed equation, the projection matrix is represented by $\mathbf{\Xi }$. To effectively ascertain this projection matrix, it is crucial to first determine the corresponding projection vector $\mathbf{\Gamma }$. As noted in [47], the projection vector $\mathbf{\Gamma }$ functions as the null vector of the projection matrix $\mathbf{\Xi }$. This relationship is vital for the effective execution of computations. Furthermore, to ensure that each resulting PE finishes its tasks at different times, certain constraint must be imposed on the projection vector. This constraint is outlined in [47] and are essential for optimizing the performance of the system. The details of this constraint is as follows:

$$\mathbf{{\rm Y}}\mathbf{\Gamma }\ne \mathbf{0}$$

(15)

Considering the limitations placed on $\mathbf{\Gamma }$, Equation (15), and using the scheduling vector $\mathbf{{\rm Y}}=\left[10\right]$, the projection vector that leads to the hybrid systolic design can be expressed as follows:

$$\begin{array}{ccc}\hfill \mathbf{\Gamma }& =\hfill & \hfill \left[\begin{array}{cc}1& 0\end{array}\right]\end{array}$$

(16)

Since $\mathbf{\Gamma }$ represents the null space of the projection matrix $\mathbf{\Xi }$, The projection matrix can be formulated in the following way.

$$\begin{array}{ccc}\hfill \mathbf{\Xi }& =\hfill & \hfill \left[\begin{array}{cc}0& 1\end{array}\right]\end{array}$$

(17)

This formulation is essential for understanding how the projection vector influences the overall system’s behavior. By employing the properties of the null space, we can derive a clearer representation of the projection matrix, which is critical for the subsequent analysis and implementation of the hybrid systolic design.

By substituting the obtained projection vector $\mathbf{\Xi }=\left[01\right]$ into Equation (14), we can derive the related projection function. The formulation of the projection function provides insights into the behavior of the system under the specified constraints, enabling us to express it as follows:

$$\begin{array}{c}\hfill \overline{\mathbf{\Gamma }}\left(\mathbf{\Gamma }\right)=j\end{array}$$

(18)

This implies that the nodes of the dependency graph (DG) can be aligned along the j direction, allowing for computation through a one-dimensional systolic array. This configuration simplifies the architecture, making it well-suited for applications in resource-constrained environments.

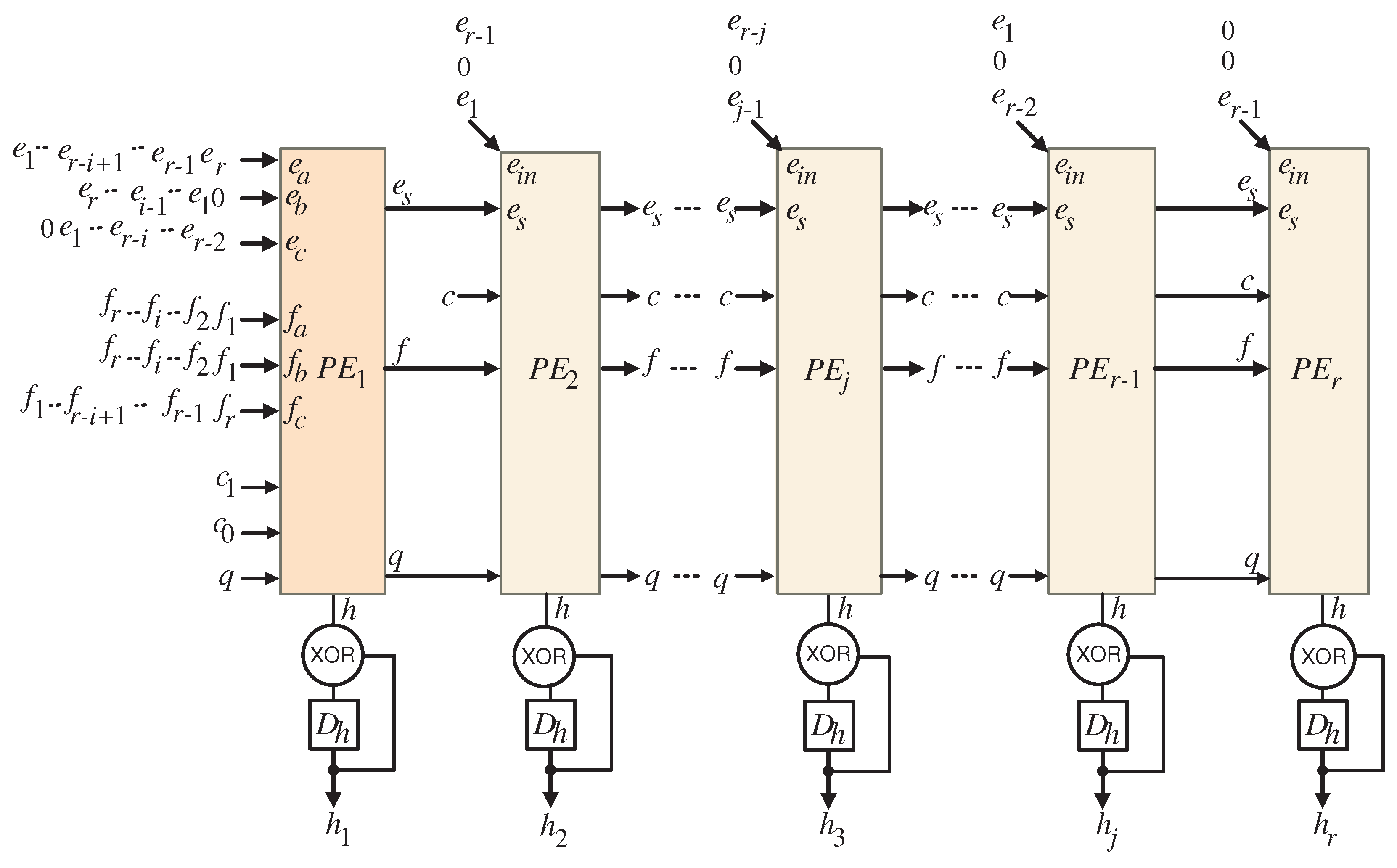
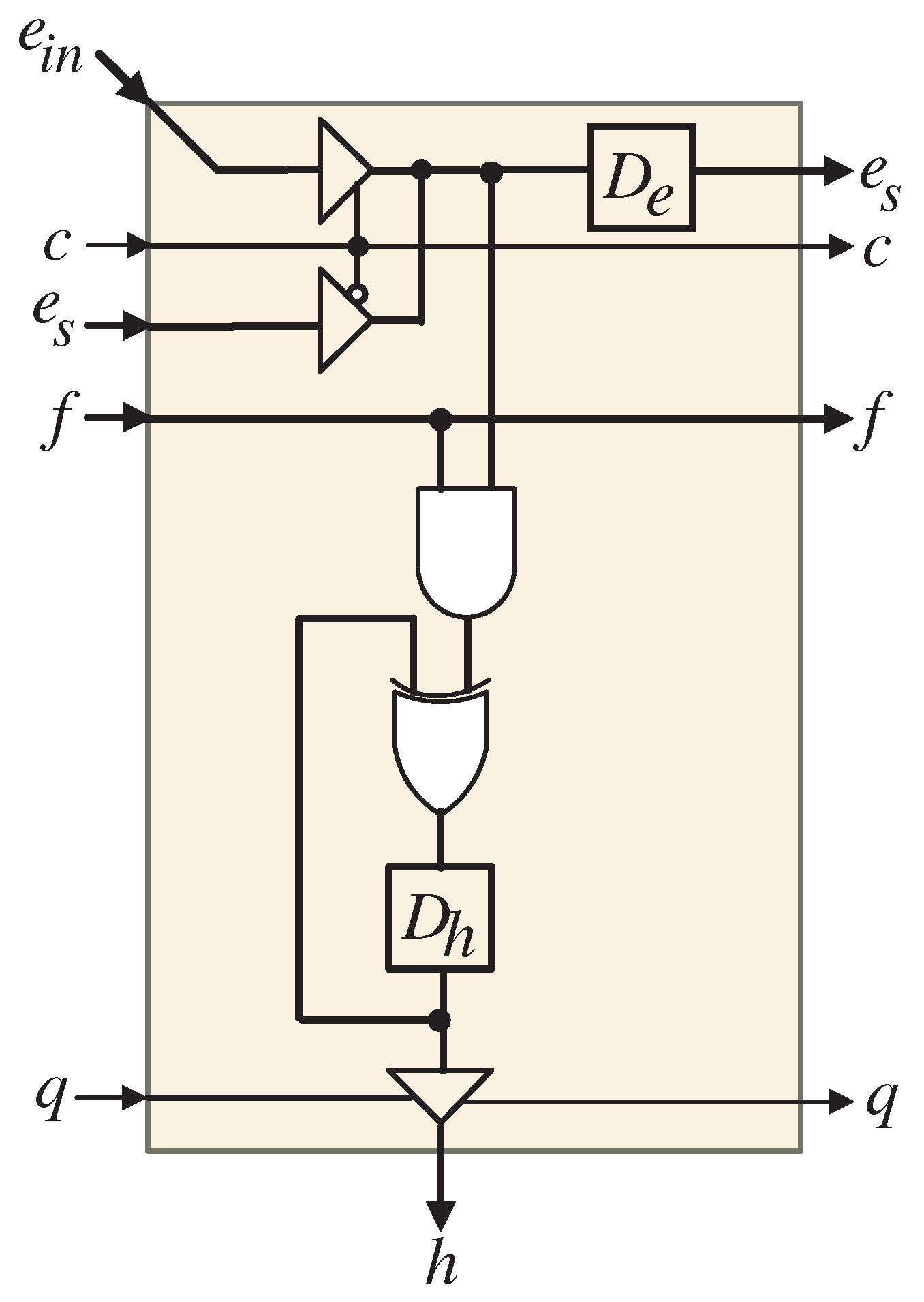
4.3. The Explored Multiplier Layout

The hybrid systolic multiplier architecture, as illustrated in Figure 3, is constructed by applying the derived scheduling and projection functions, $\Delta \left(\mathbf{\Gamma }\right)$ and $\overline{\mathbf{\Gamma }}\left(\mathbf{\Gamma }\right)$, to the DG nodes. This systematic approach enables an efficient mapping of operations across the PEs. In Figure 3, the systolic structure consists of r PEs, each designed to perform specific tasks in parallel. Notably, the functional design of the first processing element (${\mathrm{PE}}_1$) is illustrated in Figure 4, highlighting its unique capabilities. In contrast, the functional design for the regular processing elements (${\mathrm{PE}}_j$) is shown in Figure 5, demonstrating the consistent design principles applied across the architecture.

Unlike earlier two-dimensional systolic and semi-systolic implementations, the proposed one-dimensional hybrid systolic multiplier demonstrates a significant reduction in area complexity, attaining a linear complexity instead of a quadratic complexity. This reduction not only enhances area efficiency but also contributes to overall performance optimization. Furthermore, when compared to the Dickson two-dimensional systolic designs detailed in [18,19,20], the resulting architecture exhibits improved space complexity, making it a compelling choice for resource-constrained applications. As illustrated in the findings section, the proposed multiplier configuration significantly surpasses multipliers that utilize traditional field multiplication techniques, such as those presented in [18,19,20,32,39,42,50,51]. This emphasizes the outstanding performance and efficiency of the proposed architecture, solidifying its potential for enhancing multiplication operations in various computational contexts.

By examining Figure 3, Figure 4 and Figure 5, one can systematically analyze the developed hybrid systolic multiplier architecture, which is specifically designed to enhance area and power consumption while delivering moderate speed for resource-constrained IoT edge nodes tailored for individuals with disabilities.

The hybrid systolic multiplier employs dedicated input ports for efficient data handling. Input ports $e_a$, $e_b$, and $e_c$ are allocated to the first processing element (${\mathrm{PE}}_1$) and are sequentially fed by the signals $e_{r-i+1}$, $e_{i-1}$, and $e_{r-i}$ for each i ranging from 1 to r. Initially, input port $e_a$ receives the $e_{r-i+1}$ signals. After r clock cycles, input port $e_b$ is similarly fed the $e_{i-1}$ signals, and after another r clock cycles, input $e_c$ is fed with the $e_{r-i}$ signals. In conjunction, input ports $f_a$, $f_b$, and $f_c$ are also assigned to ${\mathrm{PE}}_1$ and are sequentially fed using the signals $f_i$ and $f_{r-i+1}$ for each i ranging from 1 to r. Initially, input port $f_a$ receives the $f_i$ signals. After r clock cycles, input port $f_b$ follows suit, utilizing the same $f_i$ signals, and subsequently, after another r clock cycles, input $f_c$ is fed sequentially, this time with the $f_{r-i+1}$ signals.

The output signal $e_s$ from ${\mathrm{PE}}_1$ is designed to pipeline through all subsequent PEs, while the output signal f from ${\mathrm{PE}}_1$ must also be propagated through all PEs. Additionally, the signal h is computed within each PE and is made available at the output every r clock cycles. Control signals $c_1$ and $c_0$ are specifically allocated to ${\mathrm{PE}}_1$ to manage certain tri-state buffers within this PE, as will be elaborated in subsequent sections.

Control signal c is employed to facilitate the selection between signal $e_s$ and those assigned to port $e_{in}$, as demonstrated in Figure 5. This control signal must propagate through the regular PEs (${\mathrm{PE}}_j$) to ensure its availability in each of these elements. Furthermore, control signal q is broadcast to all PEs and must remain active every r clock cycles to enable the h outputs to pass through the tri-state buffers to the XOR gates located at the outputs of each PE, as illustrated in Figure 3.

Ultimately, the final output bits of $h_j$, for each j ranging from 1 to r, are delivered in parallel through latches $D_h$ at the outputs of the systolic array after a duration of $3r$ clock cycles, as depicted in Figure 3.

The operation of the examined hybrid systolic multiplier structure can be outlined through a series of systematic steps, each of which contributes to the overall functionality of the design, as detailed below.

• In the initial clock period, the latches $D_h$ are reset to zero ($D_h=0$), ensuring that the input bits of $h_j$, for j ranging from 1 to r, are initialized appropriately at the inputs of the XOR gates located both within and outside each processing element. This initialization is critical for maintaining data integrity, as depicted in Figure 3, Figure 4 and Figure 5. Concurrently, the control signal c is activated ($c=1$), allowing the input signals $e_{j-1}$ to pass through the input port $e_{in}$ of the regular PEs (${\mathrm{PE}}_j$), where j is within the range from 1 to r. This enables the utilization of these signals within each processing element. Additionally, during this clock period, control signals $c_1$ and $c_0$ are deactivated ($c_1=0$ and $c_0=0$), permitting the first bits of the $e_{r-i+1}$ and $f_i$ signals, for i ranging from 1 to r, to traverse the input ports $e_a$ and $f_a$ of the first PE (${\mathrm{PE}}_1$).
• From the second clock period up to the $r^{th}$ clock period, control signal c is deactivated ($c=0$), allowing the sequential passage of signals $e_{r-i+1}$ through the input port $e_s$ of the regular PEs (${\mathrm{PE}}_j$). This step is essential for their effective use within each processing element. During this interval, control signals $c_1$ and $c_0$ remain deactivated ($c_1=0$ and $c_0=0$), facilitating the passage of all remaining sequential bits of the $e_{r-i+1}$ and $f_i$ signals through the input ports $e_a$ and $f_a$ of the first PE (${\mathrm{PE}}_1$), thereby ensuring their availability for processing.
• Upon completing the first r clock cycles, control signal q is activated ($q=1$), enabling the transfer of the intermediate bits of h to the accumulator, which comprises XOR gates and $D_h$ latches positioned at the output of each PE, as illustrated in Figure 3. These accumulated bits are stored in the $D_h$ latches and are intended to be combined with the output bits generated after the next set of r clock cycles, marking the beginning of the second operational phase of the systolic array.
• Following the completion of the first r clock cycles, the systolic array transitions into a second computation phase. At the first clock cycle of this phase, the latches $D_h$ within each PE are reset to initialize the input bits of $h_j$, for j ranging from 1 to r, to zero at the inputs of the XOR gates, as shown in Figure 4 and Figure 5. Simultaneously, control signal c is activated ($c=1$) to facilitate the utilization of zero input signals assigned to input port $e_{in}$ within each regular PE (${\mathrm{PE}}_j$). During this clock period, control signals $c_1$ and $c_0$ are set to 1 and 0, respectively ($c_1=1$ and $c_0=0$), allowing the first bits of the $e_{i-1}$ and $f_i$ signals, for i ranging from 1 to r, to pass through the input ports $e_b$ and $f_b$ of the first PE (${\mathrm{PE}}_1$).
• From the second clock period until the $r^{th}$ clock period of the second computation phase, control signal c is deactivated ($c=0$), enabling the sequential passage of signals $e_{i-1}$ through the input port $e_s$ of the regular PEs (${\mathrm{PE}}_j$). This allows for their effective use within each processing element. During this period, control signals $c_1$ and $c_0$ maintain their states ($c_1=1$ and $c_0=0$), ensuring that all remaining sequential bits of the $e_{i-1}$ and $f_i$ signals pass through the input ports $e_b$ and $f_b$.
• At the conclusion of the second r clock cycles, control signal q is activated ($q=1$) to transfer the intermediate bits of h to the accumulator (XOR gates and $D_h$ latches) located at the output of each PE, as shown in Figure 3. These bits are added to the previously stored output bits from the first computation phase. The accumulated bits are retained in the $D_h$ latches for subsequent addition to the next output bits produced after the third r clock cycles, marking the beginning of the third operational phase of the systolic array.
• After the second r clock cycles, the systolic array enters the third computation phase. At the first clock cycle of this phase, the latches $D_h$ within each PE are reset to initialize the input bits of $h_j$, for j ranging from 1 to r, to zero at the inputs of the XOR gates inside each PE, as shown in Figure 4 and Figure 5. Concurrently, control signal c is activated ($c=1$) to facilitate the use of the input signals $e_{r-j}$, for j ranging from 1 to r, assigned to input port $e_{in}$ within each regular PE (${\mathrm{PE}}_j$). Furthermore, during this clock period, control signals $c_1$ and $c_0$ are both activated ($c_1=1$ and $c_0=1$), allowing the first bits of the $e_{r-i}$ and $f_{r-i+1}$ signals, for i ranging from 1 to r, to pass through the input ports $e_c$ and $f_c$ of the first PE (${\mathrm{PE}}_1$).
• From the second clock period until the $r^{th}$ clock period of the third computation phase, control signal c is deactivated ($c=0$), facilitating the sequential passage of the signals $e_{r-i}$, for i ranging from 1 to r, through the input port $e_s$, thereby allowing their effective use within each of the regular PEs (${\mathrm{PE}}_j$). During these clock periods, control signals $c_1$ and $c_0$ retain their states ($c_1=1$ and $c_0=1$), enabling all remaining sequential bits of the $e_{r-i}$ and $f_{r-i+1}$ signals, for i ranging from 1 to r, to traverse the input ports $e_c$ and $f_c$, respectively. This ensures their availability for processing throughout these clock cycles.
• At the conclusion of the third computation phase, control signal q is activated ($q=1$) to facilitate the transfer of the resulting intermediate bits of h to the accumulator (XOR gates and $D_h$ latches) located at the output of each PE, as depicted in Figure 3. The obtained bits are added to the output bits previously stored in the $D_h$ latches following the second computation phase. The output bits from the third computation phase will likewise be stored in the $D_h$ latches, culminating in the final computation result of the hybrid systolic multiplier.

5. Findings and Analysis

This portion emphasizes a comparative evaluation of the examined hybrid systolic multiplier in relation to various notable systolic and semi-systolic multiplier configurations from existing research [19,20,43,44,50]. The evaluation is structured into two portions to provide a comprehensive understanding of the proposed design’s performance. The first portion explores the resource consumption and execution time of the proposed framework in relation to competing designs, highlighting the qualitative aspects. Through an in-depth analysis of these factors, we seek to offer valuable observations regarding resource consumption and performance speed, which are critical factors in the design of efficient computational systems.

In the following section, we will validate our complexity assessment through practical implementation. By executing the proposed design in a real-world environment, we can evaluate its actual efficiency and contrast it with the anticipated features derived from our theoretical analysis, highlighting the quantitative aspects. This execution will ensure our analysis accurately represents the function of the multiplier in practical scenarios, allowing us to identify any discrepancies between expected and observed outcomes. Moreover, the results from this implementation will serve to inform future enhancements to the design, potentially leading to improved efficiency and effectiveness in IoT applications tailored for individuals with disabilities.

5.1. Complexity Examination

In analyzing the presented hybrid systolic design depicted in Figure 3, it becomes evident that the structure comprises multiple processing elements (PEs), amounting to r in number. The implemented systolic array is comprised of $2r+6$ tri-state buffers, r AND gates, $2r$ XOR gates, no MUXes, and $3r$ latches. A thorough analysis of the computational logic within PEs allows for the calculation of the critical path delay (CPD) of the proposed multiplier. The CPD represents the cumulative propagation delays through two tri-state buffers ($2{\lambda }_{tri}$), a two-input AND gate (${\lambda }_A$), and a two-input XOR gate (${\lambda }_X$). These components are essential in shaping the overall performance and efficiency of the architecture, as they directly influence the speed at which data can be processed and the system’s responsiveness in real-time applications.

In the analysis of the multiplier setup, it is imperative to underscore that the proposed design achieves its ultimate outcome within $3r$ clock intervals. This duration signifies that the entire calculation sequence—starting with the beginning of the multiplication process and finishing with the output being delivered—transpires within these $3r$ clock intervals. Understanding this timeframe is vital for assessing the multiplier’s efficiency and speed, thus enabling a thorough appraisal of its effectiveness in real-world applications.

Table 2. Assessment of Resource Utilization and Execution Time in Proposed and Rival Multipliers.

Multiplier Layout	Tri-State	AND	XOR	MUX	Latch	Latency	CPD	Area Complexity	Time Complexity
Chiou [19]	0	$r^2$	$3r^2+2r$	0	$3r^2+4r$	$r+1$	${\lambda }_A+3{\lambda }_X$	$\mathcal{O}\left(r^2\right)$	$\mathcal{O}\left(r\right)$
Chiou [20]	0	$r^2$	$r^2+r$	0	$3r^2$	$r+2$	${\lambda }_A+{\lambda }_X$	$\mathcal{O}\left(r^2\right)$	$\mathcal{O}\left(r\right)$
Lee [43]	0	$r^2+r$	$r^2+2r$	0	$1.6r^2+4r$	$(r+7)/2$	${\lambda }_A+{\lambda }_X$	$\mathcal{O}\left(r^2\right)$	$\mathcal{O}\left(r\right)$
Lee [44]	0	$r^2+r$	$r^2+(7r+1)/2$	0	$2.1r^2+6.5r$	$(r+7)/2$	${\lambda }_A+{\lambda }_X$	$\mathcal{O}\left(r^2\right)$	$\mathcal{O}\left(r\right)$
Chiou [50]	0	$r^2$	$r^2+r$	r	$2r^2+3r$	$r+1$	${\lambda }_A+{\lambda }_X+{\lambda }_M$	$\mathcal{O}\left(r^2\right)$	$\mathcal{O}\left(r\right)$
Proposed	$2r+6$	r	$2r$	0	$3r$	$3r$	$2{\lambda }_{tri}+{\lambda }_A+{\lambda }_X$	$\mathcal{O}\left(r\right)$	$\mathcal{O}\left(r\right)$

presents a detailed comparison of the newly introduced hybrid systolic multiplier with several established systolic and semi-systolic multiplier designs [19,20,43,44,50]. This comparison is structured around three key criteria. First, the analysis evaluates the utilization of essential components, such as gates, multiplexers, and latches. These components are critical for the functionality of each multiplier design. Second, the study examines the latency associated with each multiplier. Latency refers to the time taken for the multiplier to produce its output after the input is provided. This metric is vital for understanding the efficiency of the design in practical applications. Finally, the critical path delay (CPD) is assessed. CPD is a significant factor that influences the overall performance of the multiplier, as it determines the maximum time required for the signal to propagate through the circuit. By analyzing these aspects, the study aims to demonstrate the benefits of the hybrid approach and identify potential improvements in the efficiency and effectiveness of multipliers in real-world scenarios.

The results of the analysis reveal a significant disparity in area utilization between the newly introduced multiplier architecture and the previously referenced architectures. Multiplier architectures discussed in existing research typically exhibit a quadratic space complexity. This means that as the field size r increases, the number of components required expands quadratically. Specifically, if the field size doubles, the number of components may increase by a factor of four, leading to substantial increases in resource demands. This rapid growth in resource requirements poses challenges for various applications, particularly in environments where space and power are at a premium. In contrast, the hybrid systolic multiplier offers a more favorable linear space complexity. This linear relationship means that the increase in resource consumption is directly proportional to the increase in the field size. For instance, if the field size doubles, the number of components required also approximately doubles. This characteristic enables a significant reduction in resource consumption for the proposed design compared to existing designs with quadratic complexity, making the hybrid systolic architecture a more efficient alternative. This improved spatial utilization is particularly valuable for Internet IoT solutions aimed at individuals with disabilities, who often face considerable constraints related to limited resource access and physical space. By employing a design that scales linearly, the proposed architecture can fit into more compact spaces while still delivering the necessary computational power. Moreover, the analysis demonstrates that all systems evaluated share a comparable time complexity, which is linear. This finding suggests that the operational efficiency of the hybrid systolic multiplier is similar to that of current architectures in terms of processing speed. However, it achieves this efficiency while requiring significantly fewer resources. The ability to maintain linear complexity in both space and time reinforces the advantages of this architecture, making it particularly well-suited for applications where efficient use of resources is critical. This combination of low area utilization and power consumption, alongside comparable performance, positions the hybrid systolic multiplier as an optimal choice for modern IoT applications. This balance between performance and resource optimization makes the proposed configuration an appealing choice for practical applications. It is especially relevant in contexts where effective resource management is crucial, especially in the development of assistive technologies for individuals with disabilities. By addressing both performance standards and resource limitations, the hybrid systolic multiplier represents a promising solution for modern computational challenges.

The hybrid systolic multiplier setup offers several advantages that greatly enhance its suitability for IoT solutions designed to assist individuals with disabilities. One of the key benefits of this design is its compact nature, which minimizes space demands while maximizing the use of available hardware resources. This efficient arrangement not only leads to a more compact physical form but also positively influences essential performance indicators. By reducing the overall footprint, the hybrid systolic multiplier allows for easier integration into various devices, making it an ideal choice for assistive technologies. Additionally, the optimized use of resources contributes to improved efficiency and effectiveness in operation, further supporting the needs of individuals with disabilities. Overall, this design represents a significant step forward in creating accessible and efficient solutions in the IoT landscape.

The enhancements in space efficiency result in improved values for both the area-delay product (ADP) and the power-delay product (PDP) of the multiplier. These improvements enhance overall functionality and promote better energy conservation, making the proposed configuration an attractive option for scenarios that demand efficient resource management and low power usage. This combination of efficiency and performance makes it particularly relevant in contexts where optimizing both space and energy usage is paramount.

The merits of the suggested multiplier design are compellingly demonstrated through the implementation results outlined in

Table 3. Analysis of Efficiency in Various Multiplier Designs for $r=283$.

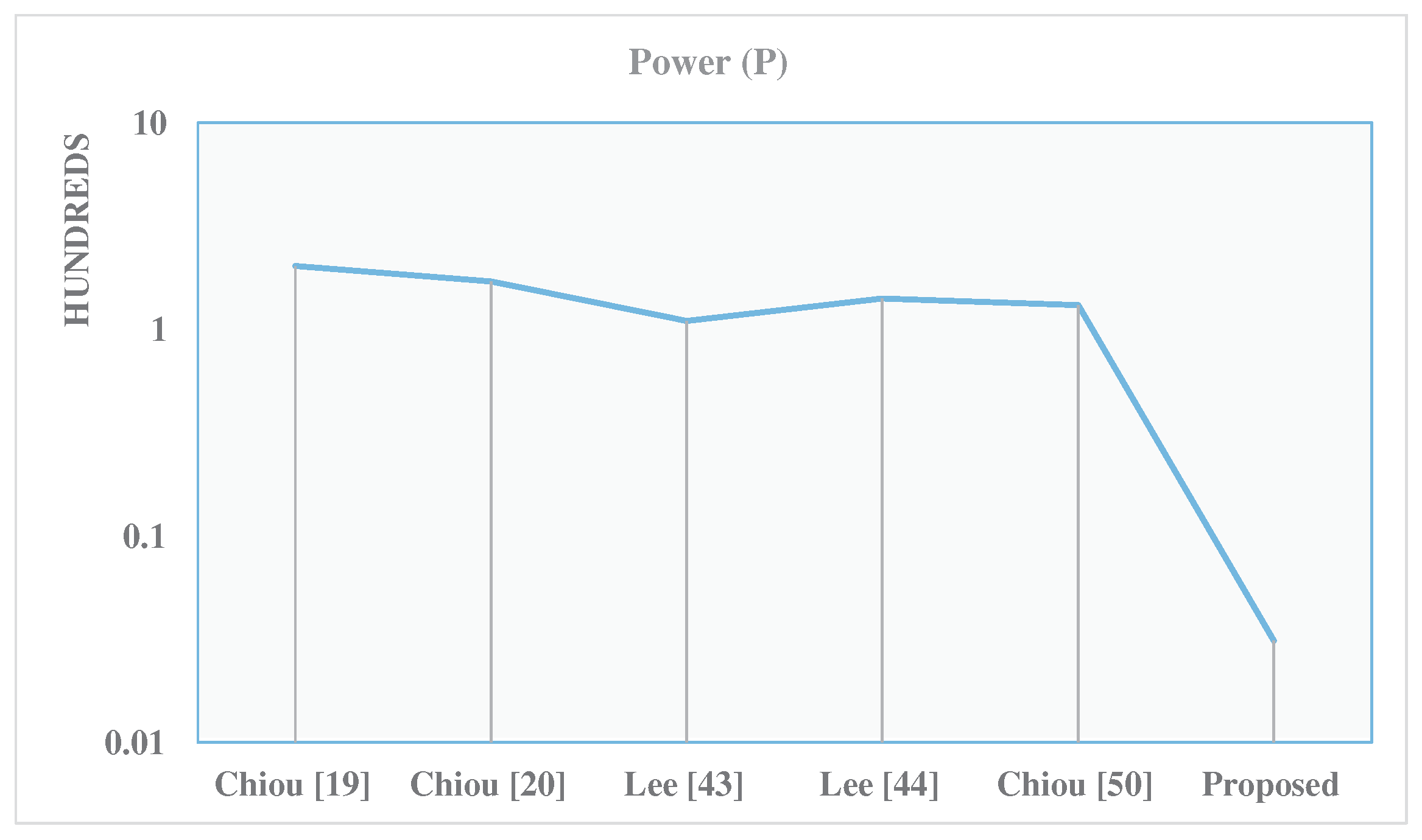
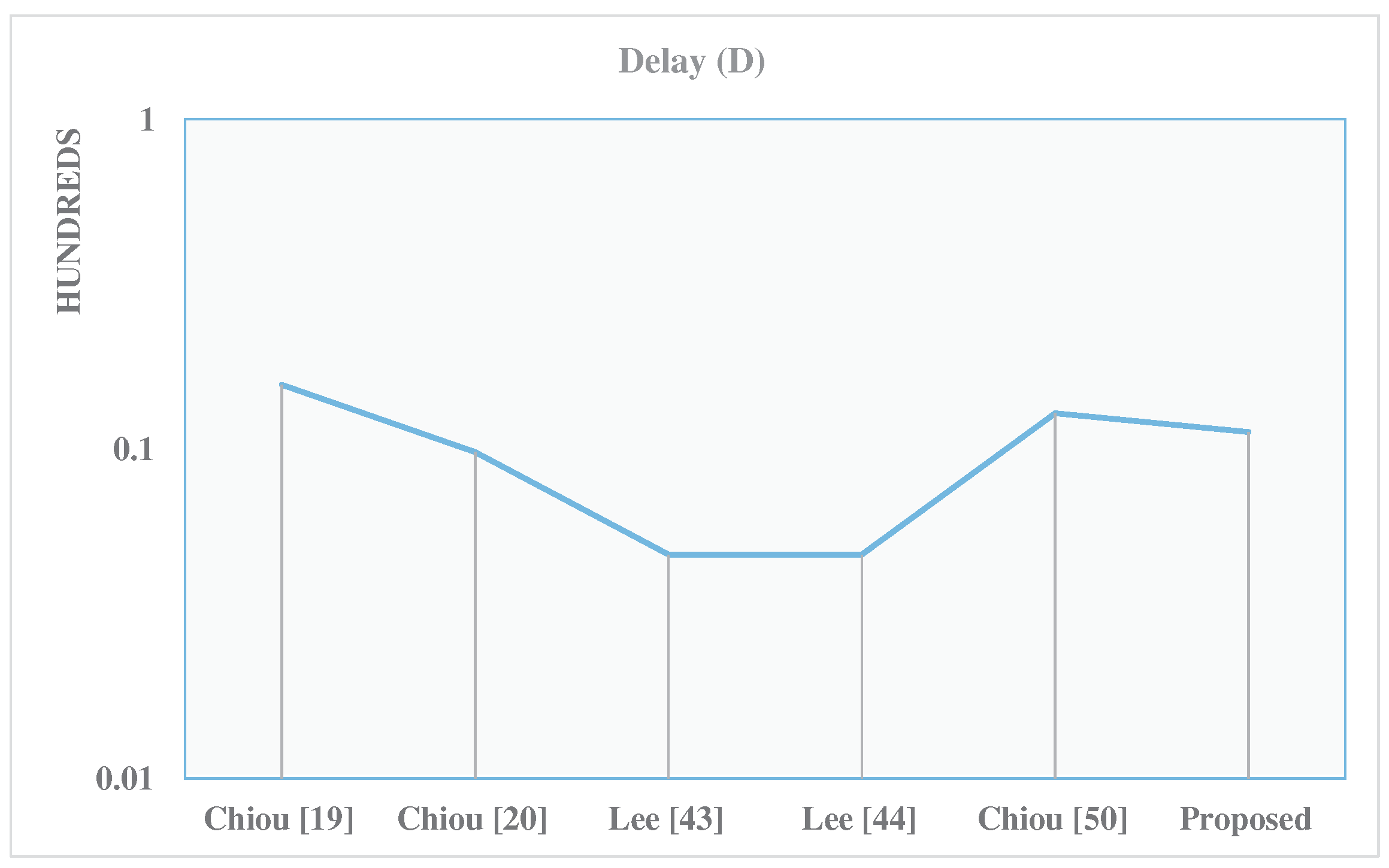
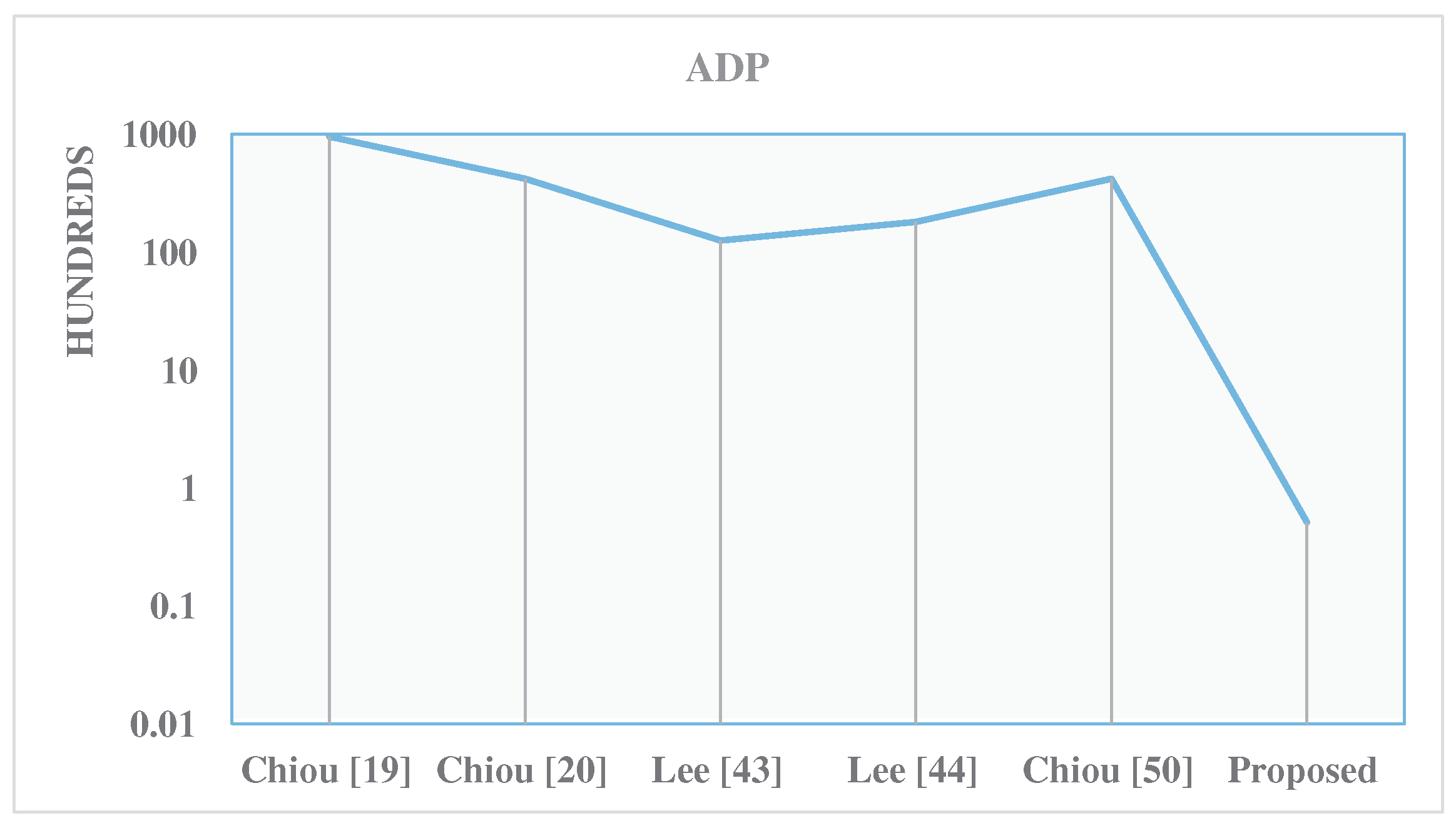
Design	r	A [Kgates]	D [ns]	P [mW]	ADP	PDP	A Saving (%)	P Saving (%)	ADP Saving (%)	PDP Saving (%)
Chiou [19]	283	6083	15.6	202	95,117	3163	99.8	96.9	99.9	98.8
Chiou [20]	283	4276	9.8	170	41,720	1655	99.7	96.2	99.8	97.7
Lee [43]	283	2631	4.8	109.5	12,562	523	99.6	94.2	99.5	92.8
Lee [44]	283	3771.2	4.8	140	18,005	670	99.7	95.5	99.6	94.3
Chiou [50]	283	3274	12.8	131	41,904	1671	99.7	95.1	99.8	97.7
Proposed	283	4.5	11.2	3	51	34	-	-	-

. These results provide strong evidence for the assertions regarding decreased area complexity, as well as significant improvements in the ADP and PDP. By successfully minimizing resource consumption without compromising performance, the suggested design offers noteworthy practical advantages. This is especially crucial for IoT applications designed for individuals with disabilities, where essential factors such as energy efficiency, effective use of space, and overall operational performance are critically important. These enhancements underscore the configuration’s capability to meet the challenges of resource-limited settings.

5.2. Implementation Insights and Results

The newly developed systolic multiplier design underwent a thorough evaluation compared to current systolic and semi-systolic multiplier implementations [19,20,43,44,50]. This assessment was carried out using a systematic methodology. The modelling and realization of the various multiplier architectures were conducted with the VHDL programming language, which is well-suited for detailed hardware representation. During the synthesis phase, the framework employed the Synopsys Design Compiler alongside the Nangate library (15 nm, 0.8 V), a reputable tool known for its accuracy in estimating area, delay, and power consumption. This comprehensive methodology ensures that the performance of the proposed design is effectively compared to established implementations in the field.

To ensure that the designs met their performance criteria, a comprehensive assessment procedure was conducted utilizing ModelSim’s simulation capabilities. This phase involved creating intricate testbenches specifically designed to evaluate a wide range of operational scenarios, thereby verifying the consistency and reliability of outputs across various conditions. The meticulous nature of this validation effort was crucial for identifying potential issues early on, ensuring that only designs meeting all performance requirements progressed to the synthesis phase. This structured approach not only streamlined the overall development process but also significantly enhanced the quality and integrity of the final designs.

The synthesis phase represents a crucial step in the design workflow, as it converts VHDL code for each multiplier design into a gate-level netlist, a task efficiently handled by the synthesis tool. This significant process translates abstract design specifications into a format that is ready for physical implementation, ensuring that the designs can be successfully realized in hardware. The produced gate-level netlists provide a comprehensive depiction of the circuit architecture, which is instrumental for additional refinement and evaluation in the following stages of the design process.The synthesis phase stands as a pivotal moment in the design workflow, transforming the intricate VHDL code of each multiplier design into a tangible gate-level netlist. This essential process, deftly executed by the synthesis tool, breathes life into abstract design specifications, converting them into a format primed for physical implementation. As the netlists emerge, they unveil a comprehensive depiction of the circuit architecture, revealing the intricate connections and relationships that will ultimately be realized in hardware. This detailed representation serves not only as a blueprint but also as a foundation for further refinement and meticulous evaluation in the subsequent stages of the design process, ensuring that every aspect aligns with the intended performance and functionality.

To facilitate this conversion, the compiler harnesses the power of the Nangate library, which is meticulously designed to account for critical environmental factors affecting circuit performance. This library provides essential parameters that are tailored to the specific technology, including gate sizes, signal propagation delays, and power characteristics. Importantly, it incorporates considerations for noise margins, thereby ensuring that circuits can withstand signal fluctuations without compromising their functionality. Moreover, the library models temperature variations, enabling designers to predict the impact of temperature changes on performance metrics such as propagation delays and power consumption. Additionally, it accommodates voltage fluctuations to guarantee reliable operation across a range of supply voltages. The library also emphasizes electromagnetic effects, which can disrupt circuit performance through issues like crosstalk and signal integrity degradation, particularly in densely packed designs. These comprehensive parameters are indispensable for achieving a synthesis process that is both precise and efficient, finely tuned to the designated technology node. During this phase, the synthesis tool rigorously refines the netlist while adhering to established constraints, including area and power requirements. This meticulous approach ensures that the final implementation not only meets performance benchmarks but also aligns with specified design criteria. Ultimately, this focus on environmental factors, significantly enhances the overall performance and reliability of multiplier designs, thereby ensuring their effectiveness in practical applications.

Upon completing the synthesis phase, it becomes imperative to extract vital performance metrics—area, delay, and power consumption—from the synthesized netlists. This quantitative analysis is not just beneficial; it is essential for understanding the operational efficiency of each design. By conducting a systematic comparison, we can uncover the benefits and drawbacks of various multiplier configurations, providing clear insights that are invaluable for real-world applications. Understanding these metrics is essential for accurately evaluating the performance of each design under practical conditions. Consequently, this thorough assessment informs subsequent modifications and optimizations aimed at significantly enhancing overall performance and effectiveness. Such insights are crucial in the design process, ensuring that the chosen configurations align seamlessly with the specific requirements of their intended applications.

The compiled findings for the proposed hybrid systolic multiplier design are systematically summarized in Table 3, where they are compared against established configurations [19,20,43,44,50] for a field size of $r=283$. This comprehensive table details several key evaluation criteria, including area, delay, power consumption, ADP, PDP, all of which have been meticulously derived from the synthesis outputs to reflect the design’s operational characteristics. Furthermore, Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10 present graphical representations plotted on a logarithmic scale, which enhances the clarity of the comparative analysis by allowing for a more intuitive understanding of these metrics. These representations effectively underscore the strengths and weaknesses of the new design, providing critical insights into its performance across various evaluation criteria that are essential for assessing its suitability for the IoT applications tailored for disabled individuals.

A thorough examination of the data presented in Table 3 and Figure 6 and Figure 7 compellingly demonstrates that the proposed hybrid systolic multiplier outshines existing designs in terms of area usage and power consumption. The evidence is striking: area requirements have drastically decreased by an astonishing 99.6% to 99.8%. This remarkable reduction signifies not just a minor improvement but a transformative shift in the physical components required for implementation. Equally impressive are the advancements in power consumption. The proposed design achieves reduction in power consumption ranging from 94.2% to 96.9%. These substantial advancements in energy efficiency are not simply quantitative figures; they signify a design that is genuinely impactful in real-world contexts. This is especially vital in scenarios where resource constraints—like limited physical space and power supply—are critical factors. In summary, these outstanding results confirm that the new design not only optimizes area usage but also dramatically improves energy efficiency. This powerful combination makes it an outstanding choice for addressing the specific needs of resource-constrained IoT edge devices designed for individuals with disabilities. For those pursuing innovative solutions to improve accessibility and functionality, this hybrid systolic multiplier stands out as a compelling option that effectively tackles the challenges presented by modern assistive technologies.

A notable characteristic of the new architecture is its slightly increased delay when compared to various reference designs as illustrated in Figure 8. This increase in delay primarily results from a modest rise in latency and an elevated Critical Path Delay (CPD) within the new layout. The CPD defines the longest delay path in the multiplier circuit and is essential for overall performance as it directly influences the speed of operation execution. Nonetheless, it is crucial to highlight that despite this moderate increase in delay, the new architecture maintains a level of computational effectiveness that is comparable to existing options in terms of time complexity. This indicates that the design can still execute tasks efficiently even in light of the increased delay. Such efficiency renders the new architecture particularly suitable for a wide array of practical applications in real-time IoT scenarios that assist individuals with disabilities. In these vital contexts, achieving a balance among performance, resource efficiency, and design considerations is imperative for success.Thus, while the delay may be somewhat increased, the overall effectiveness and adaptability of this architecture position it as a strong candidate for tackling the security challenges in resource-constrained IoT edge nodes designed for individuals with disabilities. Its design specifically addresses the need for safe and reliable technological solutions that cater to the unique vulnerabilities of this community.

The analysis presented in Table 3 and illustrated in Figure 9 and Figure 10 indicates that the suggested hybrid systolic multiplier arrangement offers substantial benefits regarding the ADP and PDP. These two performance metrics are critical as they encapsulate the compromises among area, delay, and power consumption, which are essential considerations in modern circuit design. Remarkably, the new architecture achieves ADP reductions ranging from 99.5% to 99.9% when compared to existing designs, signifying a considerable enhancement in overall efficiency and improved resource utilization, thereby allowing for more compact circuit implementations. Moreover, the advancements noted in PDP are particularly noteworthy, with decreases ranging from 92.8% to 98.8%. Such results highlight the significant energy efficiency improvements of the proposed architecture, which can lead to lower operational costs and reduced heat generation during function. Consequently, this hybrid systolic multiplier emerges as an excellent option for deployment in limited-resource IoT applications tailored for individuals with disabilities, in which optimizing resource efficiency is crucial for ensuring functionality and accessibility in these vital technologies.

The analysis indicates that the offered multiplier architecture successfully integrates substantial space and power savings while maintaining a delay that comparable to that of alternative designs, which is crucial for maintaining competitive performance. This equilibrium is vital for ensuring effective computation and quick response times in critical applications, where even minor delays can significantly impact functionality. Additionally, the design achieves significant reductions in both the ADP and PDP, which reflect enhanced overall performance and efficiency in practical scenarios. These improved metrics not only signify effective resource management but also highlight increased power efficiency, thereby reducing operational costs and minimizing heat generation. Consequently, this design is particularly well-suited for resource-constrained IoT devices specifically tailored for individuals with disabilities, where optimized performance and prolonged battery life are essential to meet their unique requirements and enhance their overall user experience.

The constructed hybrid systolic multiplier presents a compelling solution for efficient cryptographic implementations in resource-constrained IoT devices, maximizing space and energy efficiency while delivering robust performance. This innovative architecture is particularly well-suited for IoT applications designed to assist individuals with disabilities, as it effectively balances the need for performance and minimal energy use, making it an ideal choice for devices that must operate efficiently over extended periods. This enhancement is crucial for devices like assistive technology tools and remote health monitoring solutions, as it safeguards user information—preventing serious consequences for privacy and safety—while also ensuring energy efficiency to prolong device usage. Furthermore, the design’s compact nature enables its seamless integration into small, user-friendly IoT devices tailored for disabled individuals, fostering intuitive interactions and facilitating features like real-time location tracking and personalized assistance services that can greatly benefit users in their daily lives. This innovative multiplier not only enhances security in resource-constrained IoT edge devices, but also significantly improves the overall daily experiences of disabled individuals. By fostering greater independence and enhancing overall quality of life, the design of the multiplier serves to deliver secure assistive technologies that are specifically tailored to address individual needs. This targeted customization enables users to navigate their environments with increased ease and confidence, ultimately contributing to their enhanced autonomy.

6. Findings Overview and Conclusions

This research introduces a novel hybrid systolic array design specifically optimized for Dickson-basis multiplication in the context of binary extension fields. This advancement is significant for enhancing cryptographic applications that require high levels of efficiency and security. The study leverages a dependency graph to systematically organize multiplication operations, employing sophisticated scheduling and node projection functions. This methodological approach results in a highly efficient multiplier that optimizes computational processes. A key attribute of this design is its reduction in space complexity, transitioning from a quadratic to a linear scale. This reduction is particularly advantageous VLSI applications, where efficient resource utilization is critical for both performance and cost-effectiveness. Performance evaluations utilizing the ASIC CMOS library reveal significant reductions in both area and power consumption. These results illustrate the multiplier’s capacity to minimize physical space while achieving lower energy usage, thereby rendering it suitable for energy-sensitive environments. Moreover, key performance metrics such as the power-delay product and area-delay product indicate substantial improvements in overall efficiency when compared to traditional multiplier architectures. The proposed multiplier framework is particularly well-suited for cryptographic protocols deployed in resource-constrained Internet of Things (IoT) devices targeting individuals with disabilities, where optimizing both space and power is essential for effective implementation. Additionally, this design contributes to the functionality of assistive technologies aimed at individuals with disabilities, ensuring reliable and efficient operation. Future work will concentrate on enhancing the design’s resistance to side-channel attacks, a significant vulnerability in cryptographic systems. By employing a unidirectional systolic architecture, we aim to simplify modifications and facilitate the integration of robust error-detection mechanisms, crucial for safeguarding elliptic curve cryptography against such attacks. Additionally, we will investigate the trade-offs associated with increasing the field size in our proposed systolic multiplier, examining its impact on performance, area usage, and power consumption. This thorough analysis will enable us to address both the benefits and challenges of scalability in our future developments.