Analysis of the Impact of the New Two-Lane Shield Tunnel Underpass on the Existing Tunnels
Abstract
1. Introduction
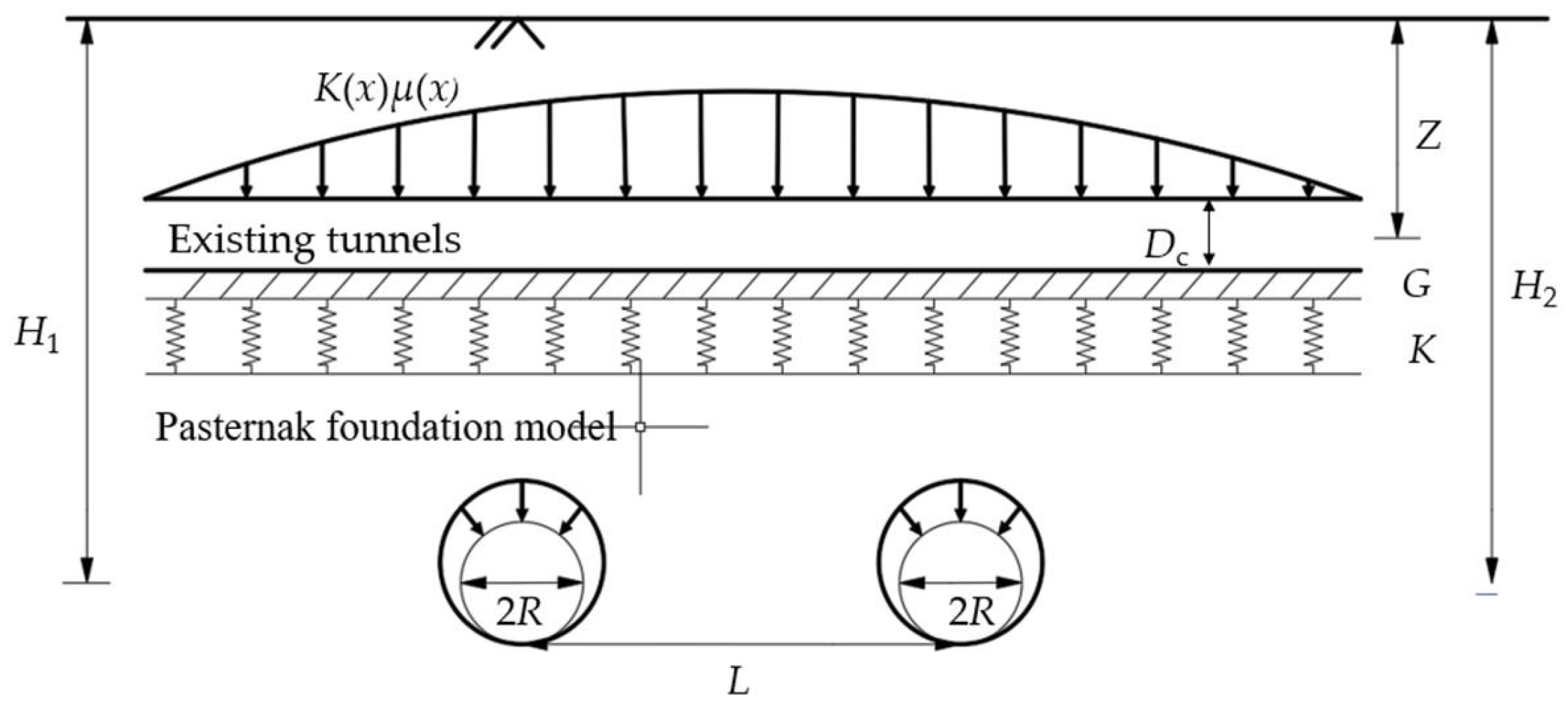
2. Theoretical Analysis of Vertical Settlement in Underpass Tunnels
2.1. Underlying Assumption
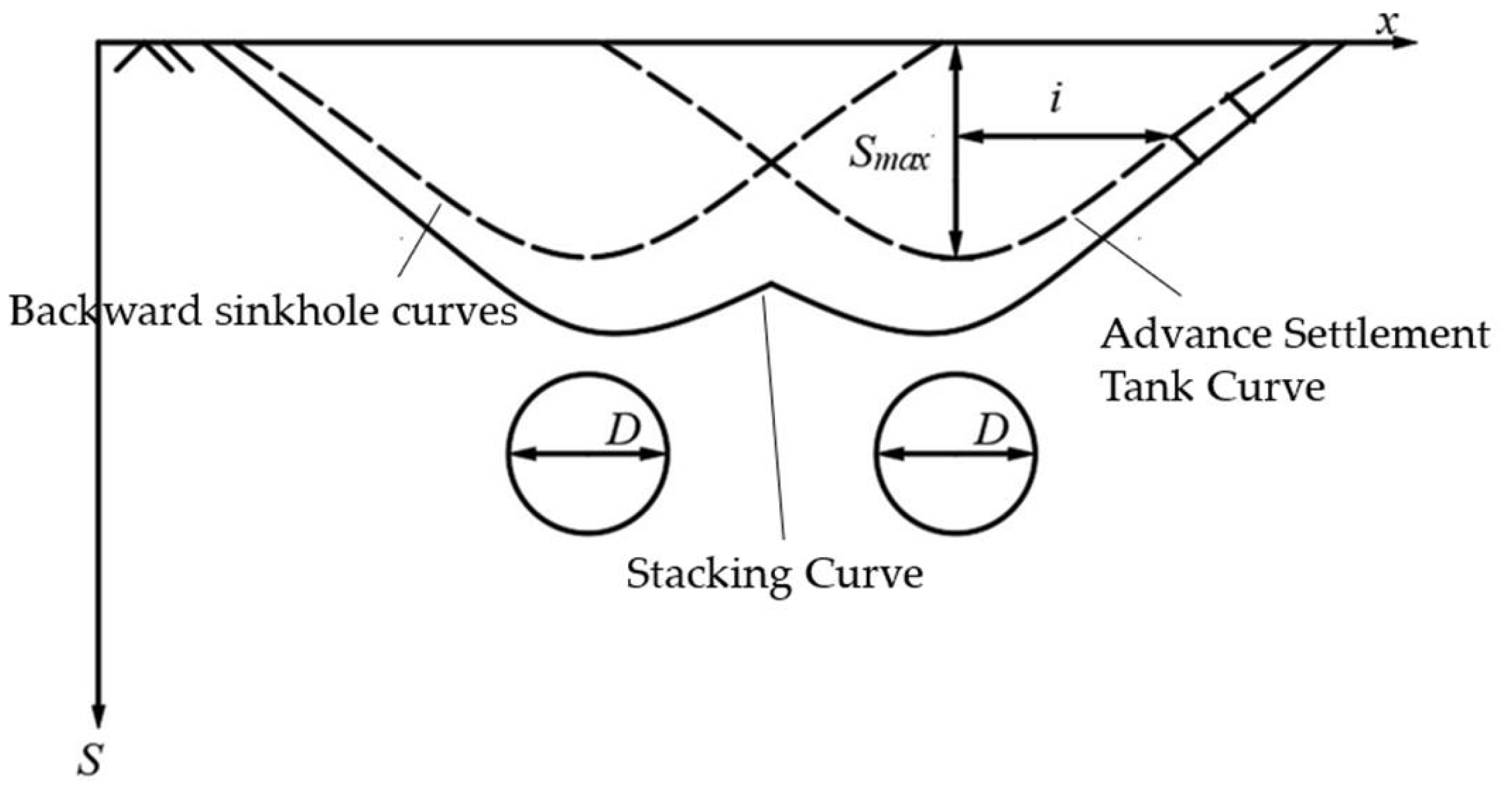
2.2. Modification of Peck’s Formula
2.3. Two-Lane Tunnel Excavation Prediction of Settlement Calculation for Existing Tunnels
3. Numerical Simulation of Underpass Construction
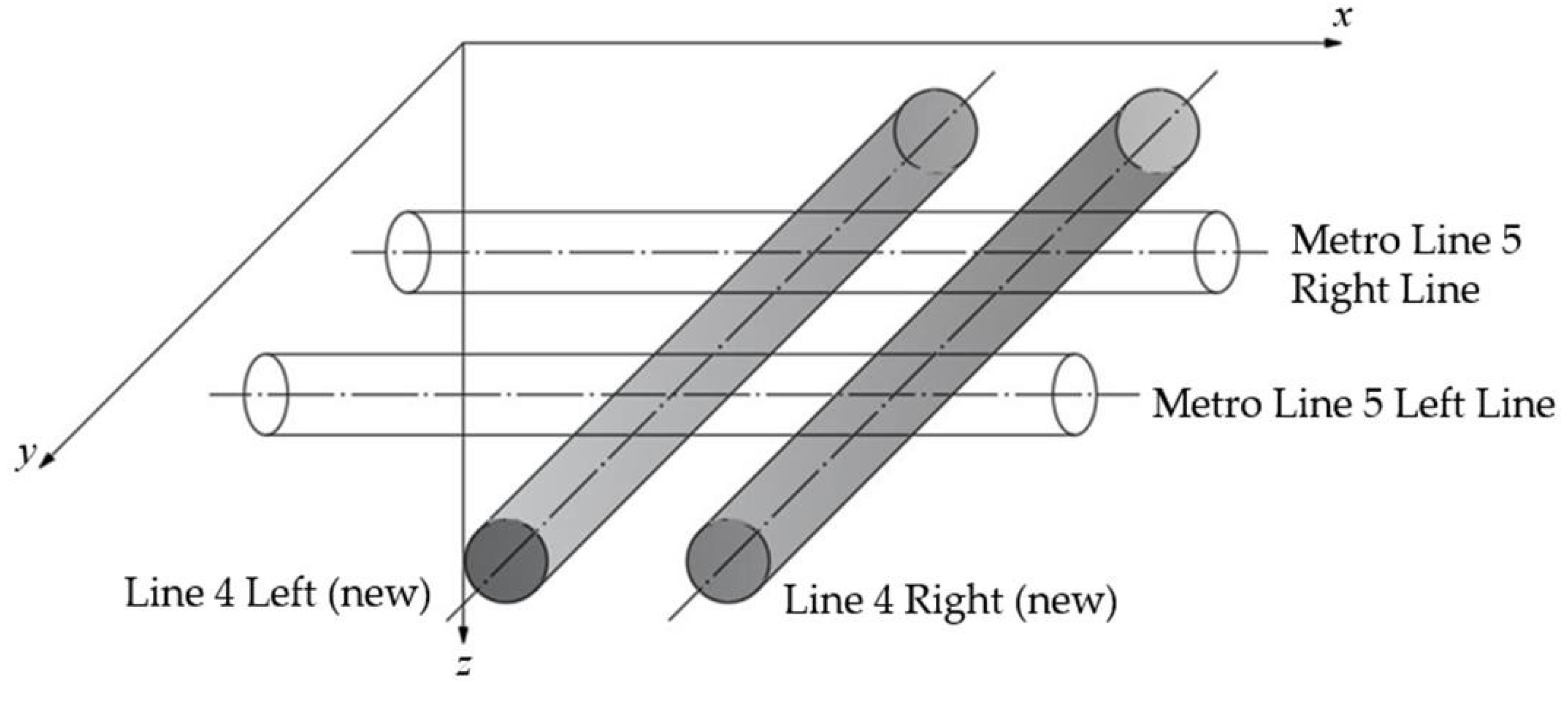
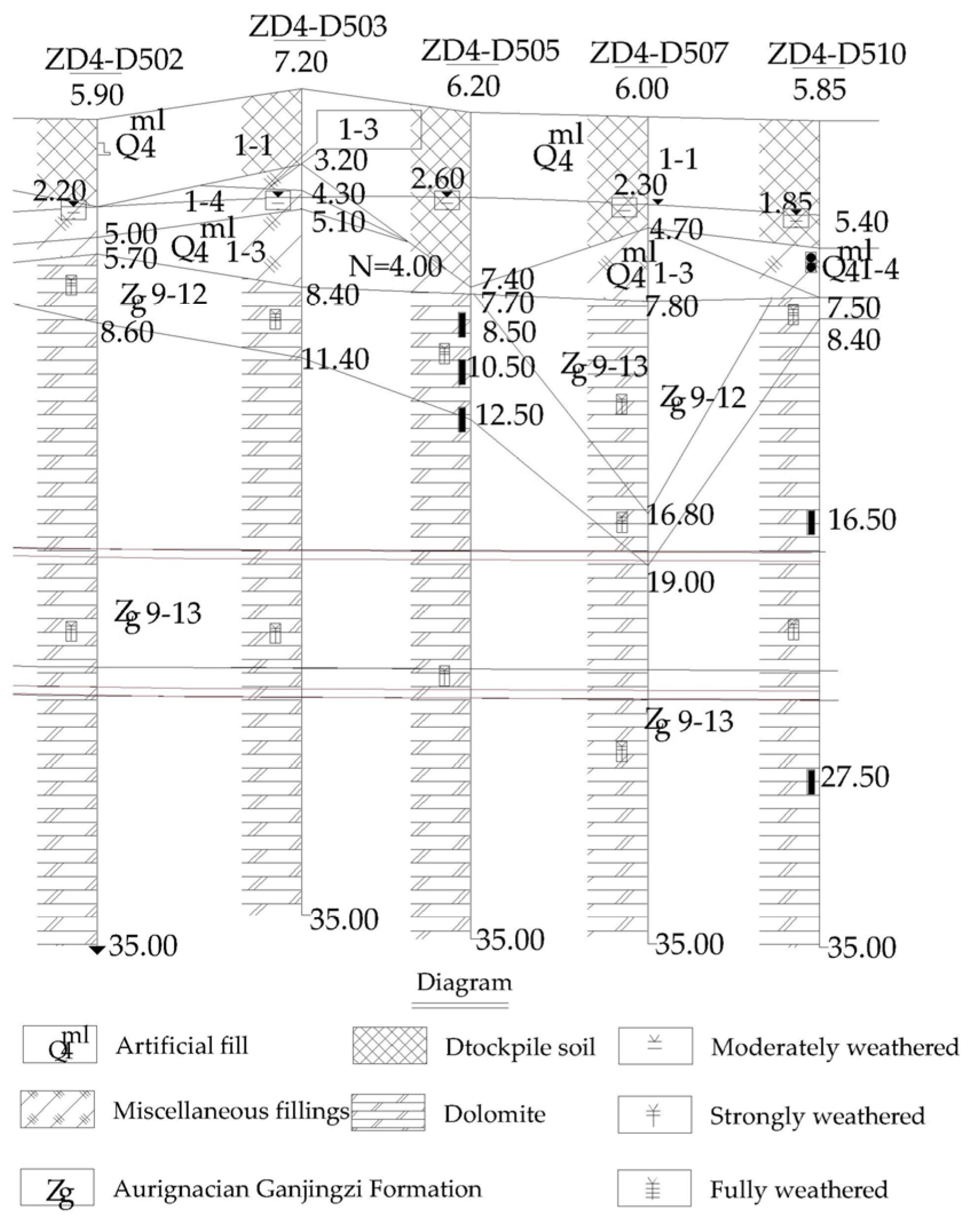
3.1. Project Overview
3.2. Numerical Model and Parameter Selection
3.3. Shield Construction Process Simulation
3.4. Analysis of Simulation Results
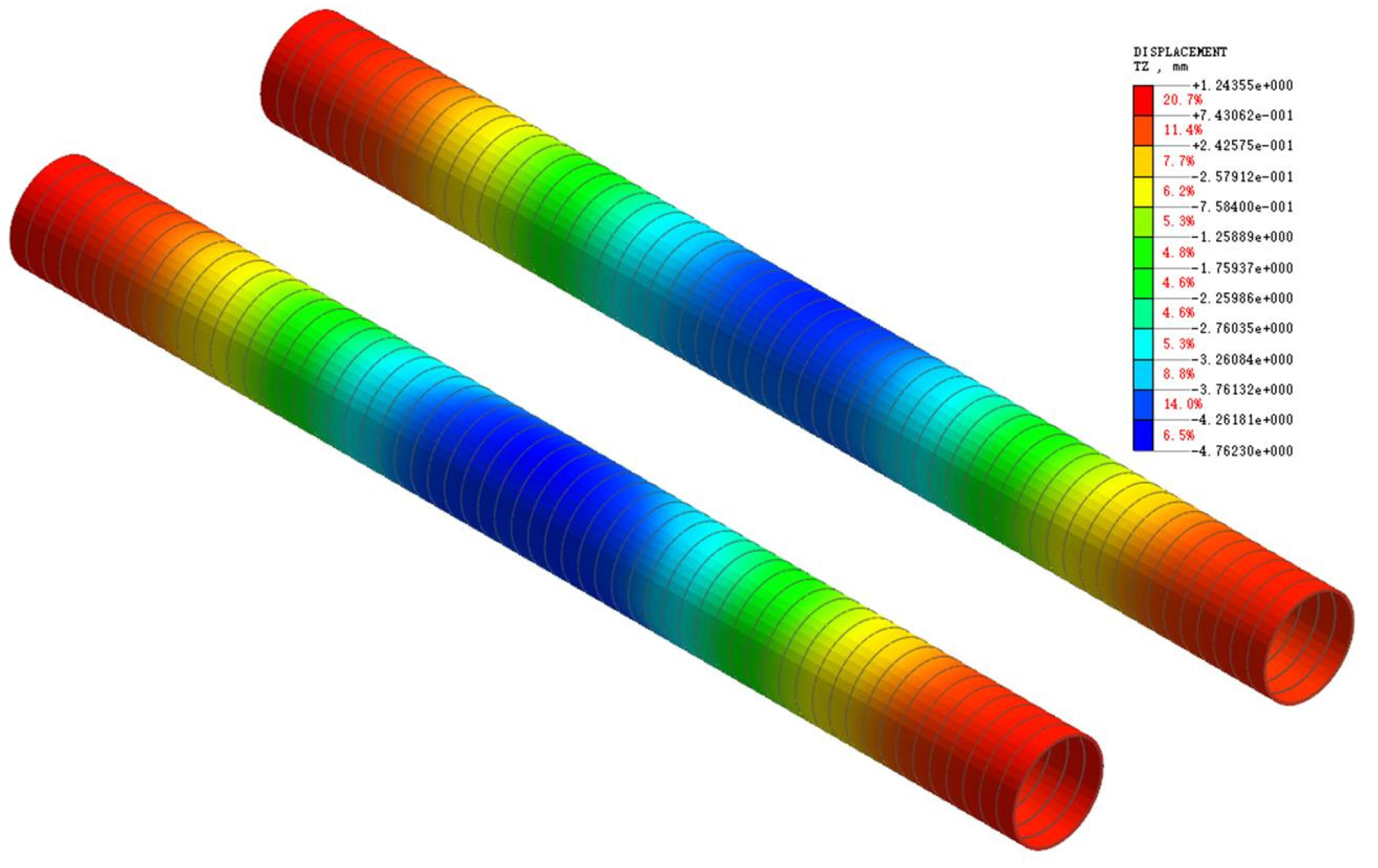
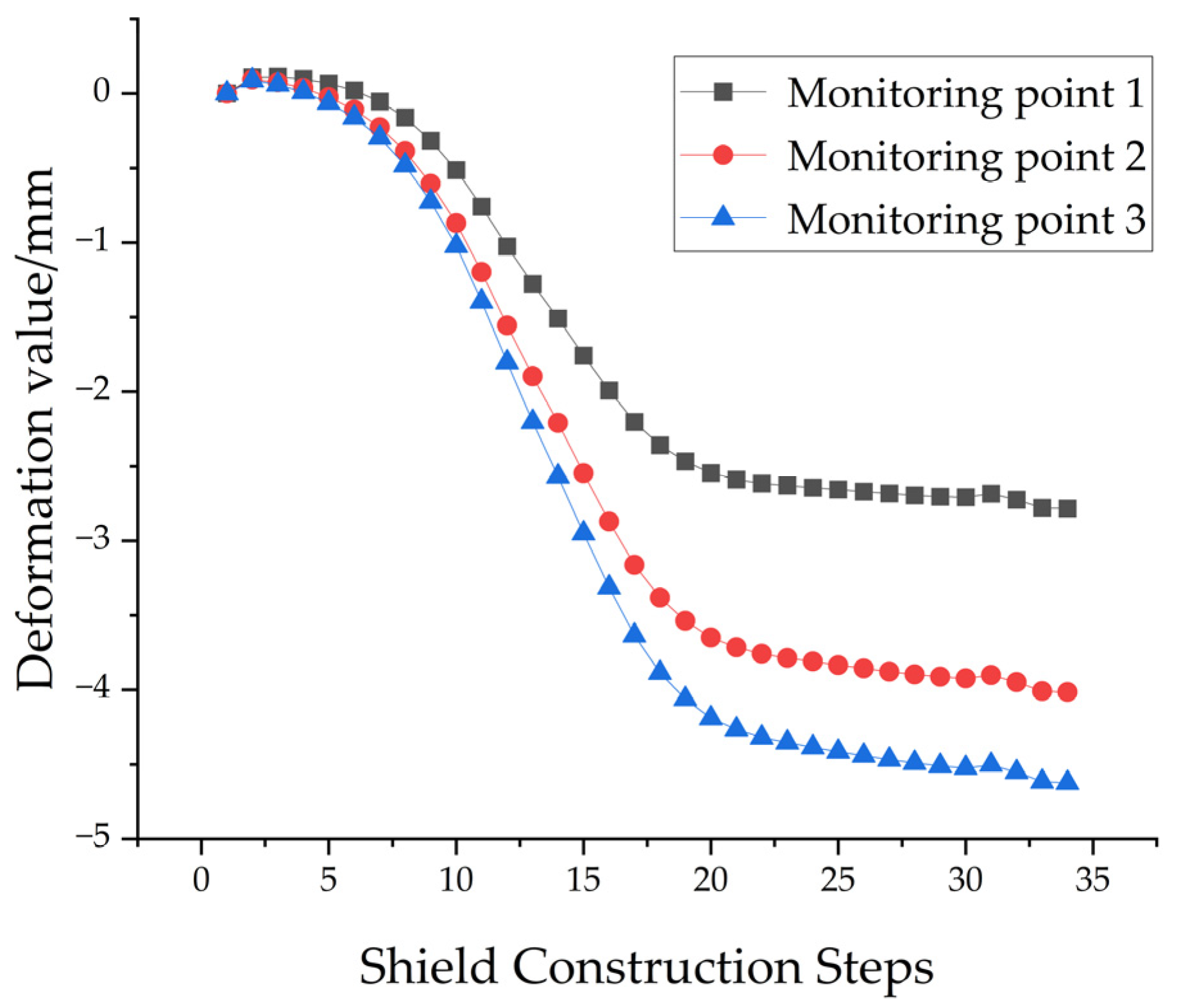
3.4.1. Influence of Two-Lane Shield Underpass on Vertical Settlement of Existing Tunnels
3.4.2. Analysis of Additional Stresses on Existing Tunnels by Double-Line Shield Penetration
3.5. Influence of Construction Parameters on the Deformation of Existing Tunnels
3.5.1. Influence of Soil Compartment Pressure on the Deformation of Existing Tunnels
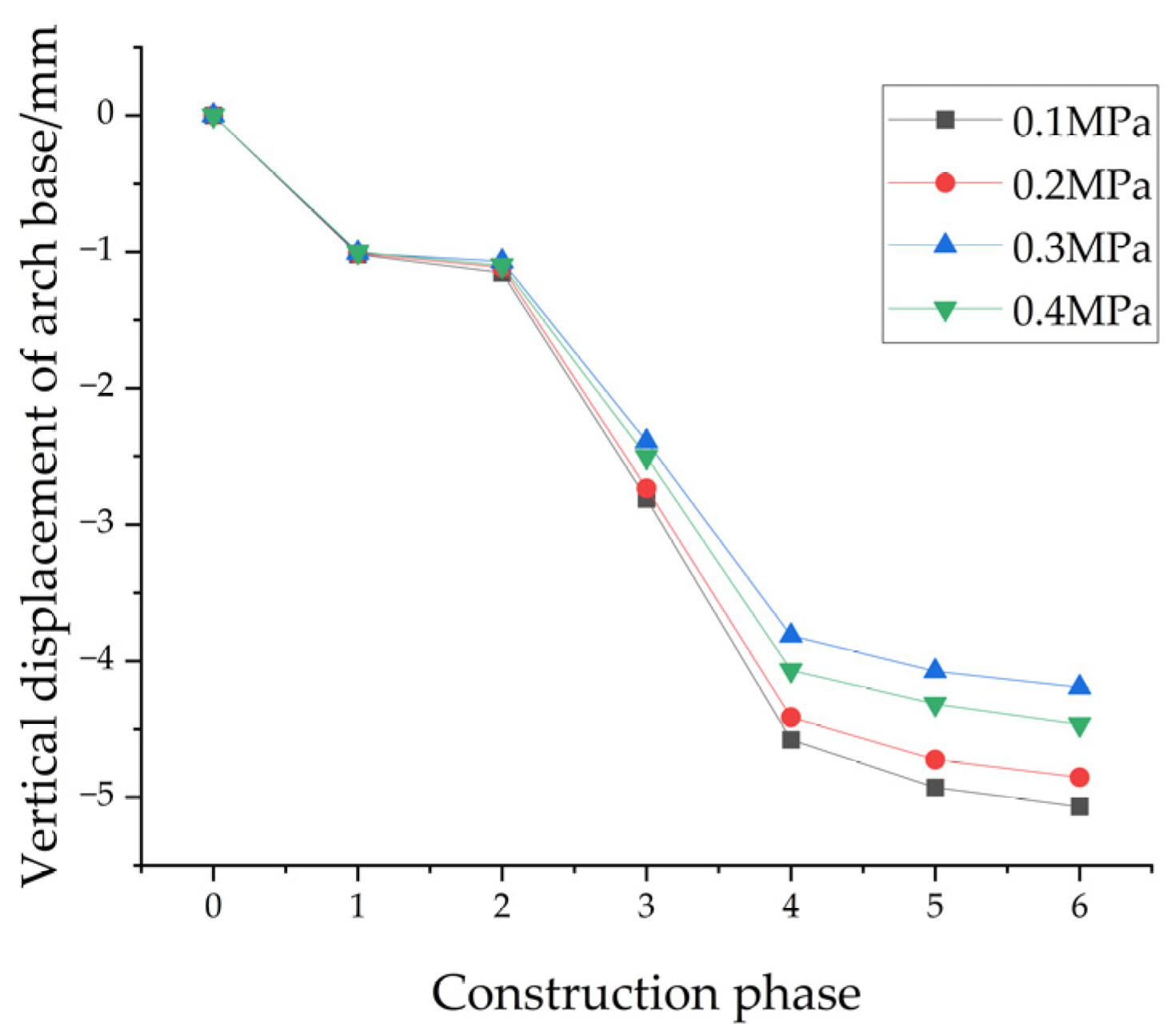
3.5.2. Influence of Grouting Pressure on Deformation of the Existing Tunnels
4. Analysis of Settlement Monitoring Results
4.1. On-Site Monitoring
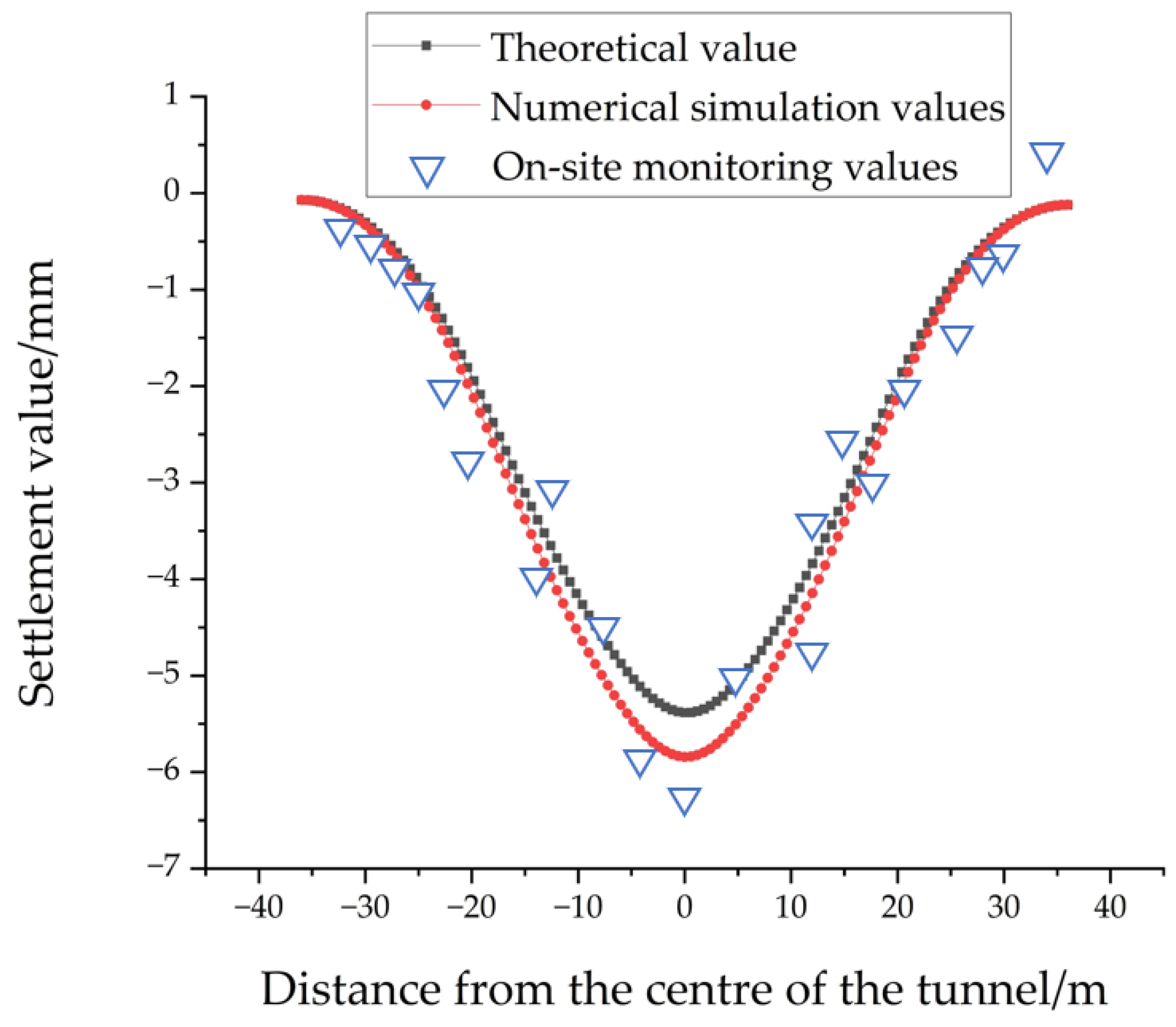
4.2. Theoretical Calculation, Numerical Simulation, and Monitoring Data Comparison
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sagaseta, C. Analysis of undrained soil deformation due to ground loss. Geotechnique 1987, 37, 301–320. [Google Scholar] [CrossRef]
- Wei, G.; Zhao, D.G.L.; Qi, Y.J. Research on the calculation method of vertical displacement of existing tunnel caused by similar rectangular shield tunnel tunneling. Tunn. Constr. 2022, 42, 960–966. [Google Scholar]
- Gan, X.L.; Yu, J.L.; Gong, X.N. Study on the influence of new double-track tunnel underpass on existing shield tunnel. Chin. J. Rock Mech. Eng. 2019, 39, 3586–3594. [Google Scholar]
- Zhang, Z.G.; Chen, J.; Zhu, Z.G. Analysis of longitudinal deformation of existing discontinuous tunnel induced by shield tunneling based on Kerr foundation model. Chin. J. Geotech. Eng. 2019, 45, 2238–2247. [Google Scholar]
- Wang, L.X.; Liu, S.J.; Wang, J. Research on settlement deformation of existing tunnel caused by shield tunneling. Chin. Q. Mech. 2019, 45, 855–866. [Google Scholar]
- Fan, W.H.; Xie, S.H.; Zhou, F.C. Case study on proximity impact zoning and control measures of new double-track shield tunnel under existing tunnel. Mod. Tunn. Technol. 2019, 60, 43–57. [Google Scholar]
- Zhang, Q.F.; Xia, T.; Ding, Z. Displacement influence and construction control of the existing subway tunnel by shield tunneling at a short distance. Rock Soil Mech. 2016, 37, 3561–3568. [Google Scholar]
- Si, J.B.; Zhu, Y.H.; Ji, C. Measurement and analysis of vertical deformation caused by rectangular shield tunneling in soft soil. Chin. J. Rock Mech. Eng. 2017, 36, 1551–1559. [Google Scholar]
- Gan, X.L.; Yu, J.L.; Gong, X.N. Characteristics and countermeasures of tunnel heave due to large-diameter shield tunneling underneath. J. Perform. Constr. Facil 2020, 34, 04019081. [Google Scholar] [CrossRef]
- Lin, Q.T.; Lu, D.C.; Lei, C.M. Model test study on the interaction between shield, pebble stratum, and existing tunnel during underpass construction. J. Beijing Univ. Technol. 2021, 47, 328–337. [Google Scholar]
- Zhao, D.G.L.; Wei, G.; Liang, L.J. Model test study on the influence of similar rectangular shield construction on adjacent existing tunnels in sandy soil. Tunn. Constr. 2019, 44, 1000–1011. [Google Scholar]
- Liu, Y.; Cao, Y.Z.; Wu, X.L. Model test research on the existing open-cut tunnel under subway shield construction. Chin. J. Railway Sci. 2024, 45, 110–121. [Google Scholar]
- Michael, K.; Dimitris, L.; Ioannis, V. Development of a 3D finite element model for shield EPB tunneling. Tunn. Underground Space Technol. 2017, 65, 22–34. [Google Scholar]
- Golpasand, M.R.B.; Do, N.A.; Dias, D. Effect of the lateral earth pressure coefficient on settlements during mechanized tunneling. Geomech. Eng. 2018, 16, 643–654. [Google Scholar]
- Moosavi, E.; Shirinabadi, R.; Rahimi, E. Numerical modeling of ground movement due to twin tunnel structure of Esfahan subway, Iran. J. Min. Sci. 2018, 53, 663–675. [Google Scholar] [CrossRef]
- Wu, X.G.; Yang, S.; Tian, J.K. Analysis of influence parameters of shield proximity construction on existing tunnels and study on proximity zoning. J. Civ. Eng. Manag. 2021, 38, 96–109+114. [Google Scholar]
- Zhou, Z.; Zhong, C.P.; Xie, W.D. Study on the influence of normal pressure bulkhead opening in mudstone formation on the deformation of existing tunnel structure. Mod. Tunn. Technol. 2023, 60, 205–212. [Google Scholar]
- Liu, B.; Tao, L.G.; Ding, C.G. Prediction and application of ground subsidence induced by double tunnel construction. J. China Univ. Mining Technol. 2006, 3, 356–361. [Google Scholar]
- Mair, R.J.; Taylor, R.N.; Bracegirdle, A. Subsurface settlement profiles above tunnels in clays. Géotechnique. 1993, 43, 315–320. [Google Scholar] [CrossRef]
- Qi, J.; Wang, Z.J.; Chen, Z.J. Analysis on the width parameter of deep soil settlement trough caused by shield tunnel excavation. Mod. Tunn. Technol. 2019, 61, 29–41. [Google Scholar]
- Zhang, Q.; Wu, K.; Cui, S.; Yu, Y.; Zhang, Z.; Zhao, J. Surface settlement induced by subway tunnel construction based on modified peck formula. Geotech. Geol. Eng. 2019, 37, 2823–2835. [Google Scholar] [CrossRef]
- Lin, C.G.; Huang, M.S. Deflection of discontinuous underground pipeline in shield tunnel excavation based on Pasternak foundation. Chin. J. Geotech. Eng. 2019, 41, 1200–1207. [Google Scholar]
- Zhang, X.Q.; Zhang, M.X.; Li, L. Study on construction disturbance mechanism of multi-line overlapping shield tunnel in short distance crossing. Rock Soil Mech 2017, 38, 1133–1140. [Google Scholar]




| Name of Soil Layer | Thickness/m | Heaviness/(kN·m−3) | Cohesion/(kPa) | The Angle of Internal Friction/(°) | Modulus of Elasticity/(MPa) | Poisson’s Ratio |
|---|---|---|---|---|---|---|
| Plain fill | 2.5 | 17 | 10 | 15 | 8 | 0.3 |
| Gravel | 4 | 20 | 0 | 36 | 12,000 | 0.28 |
| Fully weathered dolomite | 10 | 22 | 38 | 15 | 20,000 | 0.3 |
| Strongly weathered dolomite | 20 | 22 | 45 | 16 | 35,000 | 0.3 |
| Moderately differentiated dolomite | 23.5 | 23 | 70 | 30 | 50,000 | 0.3 |
| Material Name | Weight (kN·m−3) | Modulus of Elasticity/GPa) | Poisson’s Ratio |
|---|---|---|---|
| Shield shell | 78 | 250 | 0.2 |
| Pipe sheet | 22.5 | 20 | 0.3 |
| Grouting | 24 | 21 | 0.25 |
| Construction | Phase Maximum Von Mises Stress/(kN·m−2) | Minimum Von Mises Stress/(kN·m−2) |
|---|---|---|
| (1) | 2468 | 796 |
| (2) | 32,478 | 691 |
| (3) | 2774 | 556 |
| (4) | 2960 | 504 |
| (5) | 3109 | 480 |
| (6) | 3164 | 473 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Fang, X.; Yang, Y. Analysis of the Impact of the New Two-Lane Shield Tunnel Underpass on the Existing Tunnels. Appl. Sci. 2025, 15, 2642. https://doi.org/10.3390/app15052642
Li J, Fang X, Yang Y. Analysis of the Impact of the New Two-Lane Shield Tunnel Underpass on the Existing Tunnels. Applied Sciences. 2025; 15(5):2642. https://doi.org/10.3390/app15052642
Chicago/Turabian StyleLi, Jinkui, Xinxia Fang, and Yu Yang. 2025. "Analysis of the Impact of the New Two-Lane Shield Tunnel Underpass on the Existing Tunnels" Applied Sciences 15, no. 5: 2642. https://doi.org/10.3390/app15052642
APA StyleLi, J., Fang, X., & Yang, Y. (2025). Analysis of the Impact of the New Two-Lane Shield Tunnel Underpass on the Existing Tunnels. Applied Sciences, 15(5), 2642. https://doi.org/10.3390/app15052642





