Abstract
Reinforcement learning is a machine learning framework that relies on a lot of trial-and-error processes to learn the best policy to maximize the cumulative reward through the interaction between the agent and the environment. In the actual use of this process, the computing resources possessed by a single user are limited so that the cooperation of multiple users are needed, but the joint learning of multiple users introduces the problem of privacy leakage. This research proposes a method to safely share the effort of multiple users in an encrypted state and perform the reinforcement learning with outsourcing service to reduce users calculations combined with the homomorphic properties of cryptographic algorithms and multi-key ciphertext fusion mechanism. The proposed scheme has provably security, and the experimental results show that it has an acceptable impact on performance while ensuring privacy protection.
1. Introduction
Artificial intelligence has become the frontier of human exploration [1] and it has been widely applied into different scenarios. With more complicated problems wish to be solved by artificial intelligence, reinforcement learning is noticed. In the process of reinforcement learning, the agent optimize its policy through the award or punish obtained form different interactions with environment under different states. Due to this characteristic, it is considered to be an effective method for dealing with continuous decision-making problems. But the performance of reinforcement learning is limited by computing power in early stage.
With the rapid development of computing and information technology, deep learning helps the reinforced learning to perform better so that it is used in more and more aspects [2] such as Industrial manufacturing, robot control, logistics management, national defense and military, intelligent transportation, intelligent healthcare, etc. The training of famous large language model like ChatGPT [3] and Deepseek-R1 [4] also uses reinforcement learning. With artificial intelligence used more in science research [5], reinforcement learning is used in many fields of basic scientific research such as the control of tokamak plasmas [6] and to discover algorithms which can get matrix multiplication faster [7].
Due to the complexity of problems in reality, researchers have enhance the reinforcement learning with only one agent to a system with multiple agent. Multi-agent reinforcement learning have provides strong supports for modeling and solving the problems in autonomous driving [8], intelligent inventory management [9], wireless networks [10] etc.
All the developments above make the reinforcement learning model more complex, which need more data to train the model. For the data of a single user is often insufficient to train a complex model, the cooperation of multiple users using their private data is needed in training of complex model, which makes privacy leakage a major risk factor in the Artificial Intelligence model training process as is mentioned in [11].
This dilemma is especially evident in reinforcement learning, because the trial-and-error cost that a single user can afford is often not enough to train a model which can perform well. Therefore, a method of fusing the attempt records of multiple users for reinforcement learning training is necessary. At the same time, this approach needs to be able to protect the privacy of users and support outsourced computing to make reasonable use of computing resources.
In order to protect the privacy of different users and perform secret computations while protecting privacy, we have successfully built a data sharing system in which users can encrypt their data using their unique keys and can later provide conversion keys to confirm the server’s use of the data. We have designed a secret computations process which can be done by the server without user interaction.
There are two main challenges to keep privacy protected while improve speed of computition in encrypted state. Firstly, since it is necessary to count the numbers of times of taking different actions under different states, we need to determine whether a ciphertext is equal to another one while ensuring security, which poses a challenge to data security. Second, we cannot allow the server to establish a connection between the ciphertext and the plaintext, which results in the policy maintained by the server being out of order. This affects the performance of the model.
Corresponding to the first challenge, we redesigned the operational details of proxy re-encryption so that it is impossible to determine whether the ciphertext is equal before conversion, and the converted ciphertext shows hash-like consistency. Similarly, ciphertext conversion can only be performed with the permission of the owner. To address the second challenge, we prioritize the state according to the action with the highest probability in the existing strategy, which increases the possibility of retrieving the corresponding state first, thereby determining the corresponding action more quickly. The main contributions of this paper are as follows:
- Our solution can firmly maintain user rights, and different users can encrypt their data with unique keys to and control their use. We use partially homomorphic encryption (PHE) to improve the versatility of the system. At the same time, the ciphertext under the same mechanism can meet the special needs of reinforcement learning tasks.
- Our solution takes into account both security and computational efficiency. It makes the efficiency of reinforcement learning in an encrypted state similar to that in plain text and user privacy are protected, which greatly improves the usability of the solution.
- Our design does not affect the dynamic learning characteristics of the reinforcement learning model. The continuously iteration process does not require additional communication, and the policy can adapt to new changes during use.
2. Related Works
To protect user privacy, there are a variety of tools available, such as homomorphic encryption, secret sharing, oblivious transfer, and garbled circuits. In general, homomorphic encryption requires more computing power, while secret sharing incurs a lot of communication overhead. Oblivious transfer and garbled circuit rely on specific hardware implementations, so they are not universal. In this privacy-preserving outsourced policy iteration method, both statistics and policy updates should be run on the server side. The specific values of states and behaviors should be encrypted by the user, which raises the need to perform calculations in a secret state. In order to minimize unnecessary communication and user-side computing overhead, we consider using homomorphic encryption to protect user privacy.
Homomorphic encryption is the algorithms supporting calculations on encrypted data. While the operations supported by homomorphic encryption can usually not include all operations available on plaintext, homomorphic encryption is divided into three categories: Fully Homomorphic Encryption (FHE), Somewhat Homomorphic Encryption (SWHE) and Partially Homomorphic Encryption (PHE).
The first proposed FHE scheme introduced by Gentry et al. in [12], with which any polynomial functions could be calculated under encrypted state but the calculation cost it needed is too much to become usable in actual scene. Therefore, BGN algorithm [13] is more used to keep its efficiency with the supported operation is reduced into a limited times of addition and multiplication and become SWHE.
Moreover, PHE is another way to keep efficiency which only supports a single type of operations. This supported operation is usually addition or multiplication. If a PHE support addition, we have homomorphic add operation on ciphertext and ciphertext so that . Similarly, we have homomorphic multiple operation on ciphertext and ciphertext so that , if multiplication is supported. The detail operation in or is defined individually in each PHE algorithms. The most used is Paillier brought out in [14].
The basic way to calculate encrypted data with different key is to make it able to be compute by keep their homomorphism under different keys like what the [15,16] have done. This way is called multi-key homomorphic encryption (MKHE), but will not be adopted by us for their heavy computing cost.
Therefore a way to switch the key of a ciphertext is needed, as is introduced by Zhang et al. in [17]. They uses a key-switching matrices to change keys into a unified one, which is efficient but, in essence, this method reduces the security of multiply keys to a single key. That is to say the matrix weakened the security of the original scheme, which is not good.
To keep the security the same while considering the efficiency, many methods like [18,19] introduce two servers. In [18], the ciphertexts are decrypted and than encrypted again by the Second server, which is a brief way but the Second server keeps all keys and its royalty and invincibility must be ensured. In [19,20], they divide the proxy re-encrypt and calculate into different server, but they still need interactions between them to accomplish the conversion and calculation process, which is complicated and significantly increased the consumption on communication.
Since the communication cost is huge, refs. [21,22] tried remove the process of ciphertext conversion, but they can not reduce that in process of calculation. To canceling the Second server, the scheme proposed by Ma et al. in [23] perform the re-encryption with server and users, but the communicate cost is still high. In summary, they can not solve the problems they aim to by avoid the problem itself.
Concentrate to the accrual scene similar to us, ref. [24] shows a solution to aggregate a group of numbers from many participants, but the privacy can be hurt for the users may keep some information and the retreated users could violate the privacy of those users left. To protect this privacy, DeePAR in [25] proposed by Zhang et al. realize a complete way under different keys, but the secret key of users is needed to be used during the re-encryption process. To avoid this use, Xiaoyin Shen et al. proposed a scheme in [26]. This method introduces fog nodes so that calculate can be done with only one server and it keeps the communication cost relatively low. but it introduces a new step of the Second time gathering, which brings new cost.
In general, most of related works aiming to perform some calculation on separated dataset only take arithmetic operations like add, subtract, multiply and divide into consideration or even a part of them. While our scheme supports the judgment of equality additionally. The detailed difference of our scheme with other methods which can perform the similar fusion and calculation on different encrypted data is shown in Table 1. Obviously, our scheme can act individual function with the least number of server.

Table 1.
Comparison among related works and our scheme.
In [15,16], they directly realize a homomorphic encryption under multiply key. They do not need to convert a ciphertext, but A high calculation cost is needed. Ref. [17] introduces a matrix to change a key into another for higher efficiency but the safety is degrade. Refs. [18,19] reduces the calculation cost. But instead of that, they introduced too mach communication cost. Refs. [21,22] delete the step of ciphertext transformation to reduce communication between two servers, but the communication is still unavoidable during calculation. Ref. [26] finally get rid of the second server the same to our scheme. But our scheme additionally supports safety judgment on equality.
3. Preliminaries
The main techniques involved in proposed scheme can be summarized into two aspects as proxy re-encryption and homomorphic encryption. There are introductions of these two techniques and that of policy iteration.
3.1. Proxy Re-Encryption
Proxy re-encryption offers a method that can convert a ciphertext into a different one but they could be decryped and get the same plaintext m. This enhances the security of cryptographic algorithm by avoiding the repeated use of one ciphertext. Since it was first proposed in [27]. With this, people could avoid the decryption and re-encryption process but transform a ciphertext into another, so that the possibility of expose to plaintext m could be minimized.
The typical scenario of proxy re-encryption can be described as follows: Alice wants to send its data m to several users safely. To ensure the security, it is needed to ecrypt the data m with the public keys of each user. With a large amount of them, it need too much computation for Alice so that it could encrypt data with a intermediate key and offers transform keys to receivers instead of encrypt same data by many times. After that, receivers can convert the text to which it can decrypt with their secret keys. This proxy of convert process is completed by receivers, which transfers the computing cost from single sender to multiple receivers without the expose of plaintext m so that the privacy is protected.
In our scheme, a variant of proxy re-encryption is used in Section 5.4, it converts a ciphertext from secret key to the secret key with a re-encryption key correspond to . The correctness is verified in Section 6.
3.2. Homomorphic Encryption
Homomorphic encryption stands for those cryptographic algorithms which owns homomorphism. As a concept from abstract algebra, homomorphism means a mapping from an algebraic structure to an algebraic structure of the same kind, which keeps all relevant structures unchanged. That is, all properties such as identity, inverse, and binary operations remain the same. A homomorphism suit (1).
In which “·” presents an operation on X and “∘” presents an operation on Y. Similarly, a homomorphic encryption means a encryption method that suit (2).
In which “·” presents an operation on plaintext group M and “∘” presents an operation on ciphertext group C, which allows people to act operations on ciphertexts and directly get the ciphertext corresponding to the plaintext of results to preset operation corresponding plaintexts to those ciphertext.
3.3. BCP and BCP Enhance Method
Accodring to the actual demand of target scenario, the basic PHE algorithm chose in our scheme is BCP proposed by [28]. The supported homomorphic operation of this scheme contains only addition, which is also called to own the attribute of linear homomorphism. The supported operations and specific processes defined by [28] is showed as below:
- Algorithm Initialization: choose two large primes p and q, compute and randomly select ;
- Key Generation: Randomly choose secret key , the public key ;
- Encryption: The plaintext m should be . To encrypt m, firstly select a random . And the ciphertext can be calculate as (3):
- Linear Homomorphism: If we have two ciphertext , under the same secret key s, we can calculate as (5):
To be noticed, the multiple operations on each part of ciphertexts are all modular operations based on .
Except from the operations it already defined, we can also use the Proxy Re-encryption technique on this cryptographic algorithm as follows: If there are three secret key and they conform to the relationship shown as (6), the Proxy Re-encryption process between and by them can be acted.
To keep the efficiency of BCP while supporting more necessary operations, a framework proposed by Catalano and Fiore in [29] is used in our scheme. By using this method, we could support homomorphic multiplication and keep all system fast. This scheme build a construction with basic encryption so that it can calculate the . Although, the multiplication operations is not used in this passage, we keep it for better security. The necessity of using this method will be explained in Section 6.3. In contrast, a realign operation supported by [29] mechanism is needed. We can realign its plaintext part as (7).
To be noticed, the encryption process must be done with the same key of original ciphertext and . Otherwise, the Equation (7) does not hold. Of course we can also align the plaintext part of and to a new value by the same key of them like (8).
If , should be equal to . Of cause, this is not obvious in our scenario, a special method will be used in Section 5.5 to show whether they are equal.
3.4. Policy Iteration
Policy Iteration is a basic method to solve Markov Decision Problem, which is suitable for our research. It uses an iterative way to avoid solving the inverse matrix, so it has high computational efficiency. If we could build an efficient outsourcing policy iteration, it will become a solid foundation for follow-up research.
In policy iteration we usually initialize the policy to choose each actions fairly. After an attempt, we can evaluate the policy with its performance and update our policy. This iteration process is often expressed as (9):
In which presents the value last round and can be the new one. In fact, (9) actually shows an attempt process. The policy could be iterated like (10):
The best policy for fixed environment must be greed determined policy and our policy could approach it gradually.
4. Model Description
The system model introduces the participates and their need with ability, and the threat model implicate the potential threats in this system, which are also what we aim to deal with.
4.1. System Model
There are three types of characters as shown in Figure 1 in our system. Users offer their attempt histories to join in the training of policy for same problem or only ask for the policy on server for operation suggestions. If it is needed, users could also ask for trained policy. These different actions are shown in Figure 1 as UserA, UserB and UserC.
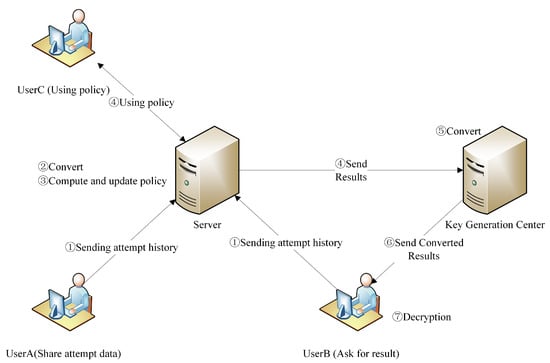
Figure 1.
System model.
Server collects encrypted data from users offering it, and fuse those data from different users and protected by different secret key to a unified encrypted state database. After that, the Server could act further calculation to update the policy matrix. This policy matrix is usable but only generate encrypted results so that it can not be used by the person who do not hold the correct secret key.
Key Generation Center (KGC) is also the manager for this system and act as a trusted third party but it did not join in the operation too much. After the collecting of encrypted data from users by the Server, the KGC should help the Server to transform ciphertext that can support the needed calculation. It also helps to convert results set for those users who legally ask for calculation result. Except what mentioned above, KGC do not undertake the calculation cost. It would distribute keys for all participators including itself and tasks. In fact, the data from users are converted to a domain protected by the key of KGC by default by the Server, which offers the right of decrypt them to KGC.
4.2. Threat Model
KGC is considered to be reliable. In contrast, Server and Users may launch attacks to the system.
Server is considered to be honest-but-curious. It will follow the preset behavior honestly, but they are curious about the contents of encrypted data.
Users are likely to collude with other Users so that there they can know the content of ciphertext from other users including data and request. For the Server would frequently return results for users, the method to deal with the collusion between Users and Servers can obviously need the participation of KGC or another non collusive server. So the collusion between Users and Server is now not considered. Two type of possible attacks in our system.
- Some Users try to know the content of ciphertext of other users;
- Some Users try to know the content of ciphertext returned from the Server to specific User;
- The Server tries to know the content of ciphertest it received and calculated on;
- An attacker from the cloud (maybe server or other users) tries to reach data from users by observing the input, intermediate results or final output.
5. Proposed Scheme
The proposed scheme is constructed by seven steps as follows: system initialization, parameter negotiation, user data encryption, ciphertext conversion, calculation and model iteration, using of encrypted policy and policy providing to specific users.
5.1. System Initialization and Participator Registration
In initialization step of this system, the encryption system for all this system would be established by the KGC, and it should generate and transfer pairs of public key and secret key for each User as well as Server.
The secret key for User i , Server and Key Generation Center are all kept by Key Generation Center.
5.2. Parameter Negotiation for Data Sharing Task
To share attempt history for policy iteration, Users individually choose its , calculate out the corresponding negotiate parameter as (11). The Server and Key Generation Center would both receive it and the public parameter of this task can be calculate as (12):
The Server will release to the Key Generation Center and all Users joined in this task. Once the KGC confirm the correctness of , it generates a secret key for this task. Everyone who join in this data fusion including Users and Server can get this secret key , which would be used to realize the re-encrypted process in following step.
5.3. User Encryption
Before the User encryption, User should randomly choose to build the authorization for conversion like (13).
As for each plaintext m. User would built the ciphertext stricture introduced in Section 3.3. The First part of it needs a randomly choosed bias and the Second part needs a random number . The ciphertext c for plaintext m is built as (14) to (16).
After encryption of all attempt histories, they will be send to Server. The authorization is needed for the Servers to fuse all encryptions to a united encrypted data set. Once the User decide to start the training, its should be sent to the Server through secret channel. This mechanism ensures power of User permission.
5.4. Ciphertext Conversion
With ciphertext c, authorization from the corresponding user , the Server can convert the ciphertext c to a united one . Ciphertext conversion process can be calculated like (17) and (18):
The Second part of ciphertext c and united ciphertext are actually ciphertexts under BCP algorithm for the random chosen bias value b. By this proxy re-encryption process the secret key on them are converted to the secret key of KGC , which complete the fusion of User data. If is needed, this target secret key could be replaced to any other one and the owner of this secret key can manage all training process. In our scheme, this target key for data fusion is temporary set to be the key of Key Generation Center.
5.5. Ciphertext Calculations and Policy Update
To initialize and update the policy matrix, the alignment of bias b and random number r is needed. For a pair of converted ciphertexts for and like (19):
In order to verify whether the corresponding plaintext and are equal to each other only by action on their ciphertexts and safely, the server firstly aligns the first part of and to a unified value as is introduced in Section 3.3. The server realigns the first part of and to as follows:
If the plaintext values corresponding to and are equal to each other, the plaintext corresponding to should be equal to that corresponding to . But they are encrypted with different r, so whether they are equal to each other is still invisible. Assume a pair of and as (21):
To unify the random number and used in these two ciphertext, the server should send all the first part of ciphertext to Key Generation Center for help. The Key Generation Center can use its secret key to get and . To make the equation of and visible, Key Generation Center can calculate and so that (22) is meeted, the unified result of is kept by the Key Generation Center.
Receiving and , the Server can infer those ciphertexts whose corresponding plaintext the same with the same Second part of ciphertext for the aligned bias. For more ciphertexts the needed can be as many as the amount of ciphertexts.
Finally Server can count the number of every encrypted pairs and update the policy matrix. After traversing n attempt histories, the policy matrix would updates n times. More updates finished, the policy can become usable.
5.6. Policy Using
If some users need to use the policy on Server, it should ask the Key Generation Center for task secret key and the unified value . The task secret key and the unified value should be distribute through secret channel.
Received unified value the unified ciphertext for each state and action can be calculated as (23).
Actually all this value act as hash value. To make requests, User encrypt it by the secret key it chosen by itself, and send the authorization secretly to server like Section 5.3. The returned action from Server is corresponding to the one chosen by policy. Server will record the pair and encrypt it by the authorization for this user. Once the user decrepted the returned ciphertext, it will get one of the Unified . After it tried the action, the user can get a new state and request for a new action. After continuously repeating the above process, the user can reach the target state and Server can get a new attempt history for updating the policy.
5.7. Results Conversion and Decryption
With mentioned steps multiply users can already train and use a policy under encrypted state on a Server. If it is needed, a user can ask for the policy matrix, Server S can encrypt the labels of policy matrix just the same way as is used during the use of policy and send its policy matrix to this user. The user can naturally map each label to the plaintext it present to.
6. Security Analysis
To ensure the security of this system, the correctness of introduced operations is proved. And it is necessary to ensure that one user or multiple colluding users are unable to decrypt other encrypted data according to the threat model. Besides, it is necessary to ensure that the Server or an adversary could not obtain the plaintext to all ciphertext in this system. And we would explain the usage of BCP enhance method to deal with probabilistic forgery attacks.
6.1. Correctness
The new introduced step on this encryption is only a variant of proxy re-encryption on ciphertext introduced in Section 5.4. In this step, the first part of ciphertext c is not changed and the second part is assumed to become the one under the secret key of Key Generation Center . The prove that the secret key to ciphertext is the secret key of Key Generation Center is given in (24):
For the already existing calculation process under ciphertext is separately proved to be correct in the source paper [28,29]. Therefore, all steps in proposed scheme are proved correct and they could output the exactly right result.
6.2. Security
The security of basic BCP algorithm and the building method from a linear homomorphic encryption to a homomorphic encryption in degree-2 functions are individually proved in their resources paper [28,29], so this passage mainly analyze the security of parameter negotiation for data sharing task, ciphertext conversion and policy using steps in proposed scheme. To prove the security of our scheme, we prove it with the method of real and ideal paradigm proposed in [30]. And the following theorems are needed.
Theorem 1.
In process Section 5.2, it is computationally infeasible for every participators including users, server and Key Generation Center to get from others and r.
Proof.
Even the Key Generation Center is acting as a trusted third party. We could set up a Semi-Honest adversary who could get the view of server , Key Generation Center and multiply users and as . the view of includes all and the and of and . Based on Discrete logarithm Problem (DLP), all chosen by except the one from and are computationally infeasible except those completely identical to or , which can obviously be probability neglected. Therefore, the probability to gather all part of r is negligible. It indicates that r is computationally infeasible too. □
Theorem 2.
In processes of Section 5.4, Section 5.5, Section 5.6 and Section 5.7, it is computationally infeasible for server or several Users colluded with each other and to obtain the plaintext from another User based on the semantically security of BCP algorithm witch is proved in [28].
Proof.
To discuss this, we should assume two Semi-Honest adversary for server and users and as and . Firstly, the view of could contains and c from all users. To get the plaintext of m, the value of b is needed while it is encrypted into , as is shown in (15) and (16), which constitute a variant of BCP ciphertext for the can be seen as in which presents the second part of a BCP ciphertext corresponding to plaintext of b under the secret key of . For , is obviously unfeasible so that is computationally undecryptble based on the semantically secure of BCP. Even is removed in following steps, the structure of is still kept. □
Secondly, the map from to corresponding action is given by Key Generation Center to all user such as so that it can infer the actual means of the returned result from server after decryption by the secret key chosen by itself. But the removed version of encrypted data from other user such as is not included in the view of . That is to say, is needed to investigate the plaintext of uploaded by , which needed or . However, as is designed by proposed scheme, is not sent out and is sent in secret channel as authorization credentials, which is all unfeasible for .
6.3. Necessity of BCP Enhance Method
Taken the actual scenario into account, the options of actions is often relatively less. For example, the actions can be chosen in a two-dimension maze are usually only four as . To encrypt them by BCP algorithm, the ciphertext looks like (15) and (16). By randomly choose two ciphertext of actions from one user such as and divide the corresponding part of them to each other, there is a non negligible probability up to 25% to get a pair of so that adversary can successfully forge a fake attempt history under this probability to server.
By changing the encryption of plaintext m to encryption of randomly chosen bisa value b, the possibility of this collision become negligible. At the same time, there are align method available for server to recover the equality. Also as is said in Section 6.2, the complex key used by is composed by public key of Key Generation Center and secret key . Both part of them is designed unfeasible for others and they are even encrypted with different random number, which further makes the aforementioned attack methods impossible.
7. Experimental Results
7.1. Introduction of Experiment Environment
The experiment is run under a classical task of Reinforcement learning called Grid World. In this game, an environment, an agent and the relationship of state, actions with reward are built up, which constitute a Markov Decision Process that the policy iteration process could run to solve. There are two typical solutions of a Grid World problem as shown in Figure 2, which shows different solutions by different policy.
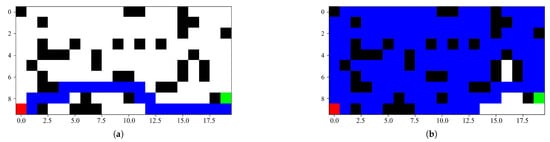
Figure 2.
This is a wide figure. Schemes follow the same formatting. If there are multiple panels, they should be listed as: (a) A solution by policy after 6000 iterations. (b) A solution by random policy.
In a game of Grid World, the different states are expressed in different grids like Figure 2. We fill the start state into red color and the target state, also is known as finish state into green color. The wall grid is filled by black color, which is unable to reach or cross. The blue grids show the states the agent have reached by following different policy. Obviously the policy of in Figure 2 performs better than that of in Figure 2.
In each state the agent can try an action belonging to set , which mean to go upward, downward, leftward or rightward. But if the next state in chosen direction is out of range or is the wall, the agent would be kept the same state as that the action did not act. Once the agent reach the goal state, it finish an attempt the number of actions it take is seen as a punishment, and the goal for policy iteration is to minimize this punishment. All these mechanisms above compose a Markov Decision Problem.
7.2. Performances Comparison with Original Policy Iteration
This experiment is done in a virtual machine with Ubuntu 22.04.1 LTS deployed on computer with 16GB DDR5 memory with frequency of 4000 MHz and Intel Core I7-14700K CPU and encrypted-state computing is run in PyCharm 2024.3.1.1 with Charm-Crypto 0.50.
To set up maze environment, we set the space of maze as a grid matrix. The environment build system would randomly choose a grid at the leftmost column to be the beginning and one of the rightmost column as goal. Then, some grid would be set as the wall. In order to ensure a high probability of the existence of a path from the beginning to the goal, we set the probability of a grid to be the wall as 20%.
In theory, the number of iterations needed for the policy to generate the best action chain in our scheme is the same that without encryption. We still run this algorithm under encrypted state of our scheme and original way for 100 times, and the result of both way is shown in Table 2.

Table 2.
The performance of our scheme and original policy iteration method.
In Table 2, the maze size and wall probability are fixed so that the experiments could be successfully conducted without be stopped by an unsolvable maze frequently. Because the maze is randomly generated, the average steps and number of iterations are not completely equal in our scheme with the original policy iteration without encryption. But they are quite close to each other.
For the time cost for each round is not evenly distributed as is shown in Figure 3. The difference in time costs is relatively apparent at the beginning but reduced during the policy iteration. At the beginning, the policy is not optimized so that the attempt history is composed by a large number of steps, which leads to a longer time of updating for both method. With the continuous updating of policy, the steps of attempt histories become stable and better, which result in a similar time of proposed scheme and original policy iteration algorithm.
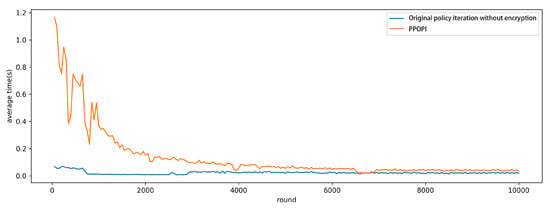
Figure 3.
Time costs under different times of iterations.
As is shown in Figure 3, our scheme shows sensitivity to the actual number of stage-action pairs in attempt history, but the time cost of our scheme is not too much comparing to original policy iteration process. Considering that the computation and conversion on ciphertext in our scheme are almost done by server, we can announce that our scheme is usable for actual scenario.
8. Conclusions
In conclusion, we focus on the security of policy iteration with multiple users. And a scheme of fusion encrypted data into a united database is designed. The proposed solution can complete ciphertext conversion and subsequent reinforcement learning using only one server.After the outsourced training, the encrypted policy in server can be used by making requests without downloading the complete policy and a complete decision chain generated during the use of encrypted policy can also be used in further training of policy on the server without additional communication. Using of this scheme can get users rid of heavy computational cost and servers can concentrate on computation instead of waiting for communication and wastes its computing resources.
For further research, we noticed that there are more complex computations in practical application, while the calculating are all done in plaintext. Researchers can continue to expand relevant cryptographic mechanisms to support computations on ciphertexts with more complex artificial intelligence algorithms, which will make the training and using process of artificial intelligence safer.
Author Contributions
Conceptualization, B.C.; methodology, B.C.; software, B.C.; validation, B.C. and J.Y.; formal analysis, B.C. and J.Y.; investigation, B.C. and J.Y.; writing—original draft preparation, B.C.; writing—review and editing, B.C.; visualization, B.C.; supervision, J.Y.; funding acquisition, J.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by National Natural Science Foundation of China, grant number No. 62162020 and the Haikou Science and Technology Special Fund, grant number 2420016000142.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author(s).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Zhu, S.; Yu, T.; Xu, T.; Chen, H.; Dustdar, S.; Gigan, S.; Gunduz, D.; Hossain, E.; Jin, Y.; Lin, F.; et al. Intelligent Computing: The Latest Advances, Challenges, and Future. Intell. Comput. 2023, 2, 0006. [Google Scholar] [CrossRef]
- Shakya, A.K.; Pillai, G.; Chakrabarty, S. Reinforcement learning algorithms: A brief survey. Expert Syst. Appl. 2023, 231, 120495. [Google Scholar] [CrossRef]
- Liu, Y.; Han, T.; Ma, S.; Zhang, J.; Yang, Y.; Tian, J.; He, H.; Li, A.; He, M.; Liu, Z.; et al. Summary of ChatGPT-Related Research and Perspective Towards the Future of Large Language Models. Meta-Radiology 2023, 1, 100017. [Google Scholar] [CrossRef]
- DeepSeek-AI; Guo, D.; Yang, D.; Zhang, H.; Song, J.; Zhang, R.; Xu, R.; Zhu, Q.; Ma, S.; Wang, P.; et al. DeepSeek-R1: Incentivizing Reasoning Capability in LLMs via Reinforcement Learning. arXiv 2025, arXiv:2501.12948. [Google Scholar]
- Wang, H.; Fu, T.; Du, Y.; Gao, W.; Huang, K.; Liu, Z.; Chandak, P.; Liu, S.; Van Katwyk, P.; Deac, A.; et al. Scientific discovery in the age of artificial intelligence. Nature 2023, 620, 47–60. [Google Scholar] [CrossRef] [PubMed]
- Degrave, J.; Felici, F.; Buchli, J.; Neunert, M.; Tracey, B.; Carpanese, F.; Ewalds, T.; Hafner, R.; Abdolmaleki, A.; De Las Casas, D.; et al. Magnetic control of tokamak plasmas through deep reinforcement learning. Nature 2022, 602, 414–419. [Google Scholar] [CrossRef] [PubMed]
- Fawzi, A.; Balog, M.; Huang, A.; Hubert, T.; Romera-Paredes, B.; Barekatain, M.; Novikov, A.; R. Ruiz, F.J.; Schrittwieser, J.; Swirszcz, G.; et al. Discovering faster matrix multiplication algorithms with reinforcement learning. Nature 2022, 610, 47–53. [Google Scholar] [CrossRef] [PubMed]
- Zhang, R.; Hou, J.; Walter, F.; Gu, S.; Guan, J.; Röhrbein, F.; Du, Y.; Cai, P.; Chen, G.; Knoll, A. Multi-Agent Reinforcement Learning for Autonomous Driving: A Survey. arXiv 2024, arXiv:2408.09675. [Google Scholar]
- Zhang, C.; Wang, X.; Jiang, W.; Yang, X.; Wang, S.; Song, L.; Bian, J. Whittle Index with Multiple Actions and State Constraint for Inventory Management. In Proceedings of the Twelfth International Conference on Learning Representations, Vienna, Austria, 7–11 May 2024. [Google Scholar]
- Bellouch, M.; Zitoune, L.; Lahsen-Cherif, I.; Vèque, V. DQL-MultiMDP: A Deep Q-Learning-Based Algorithm for Load Balancing in Dynamic and Dense WiFi Networks. In Proceedings of the 2024 IEEE Wireless Communications and Networking Conference (WCNC), Dubai, United Arab Emirates, 21–24 April 2024; pp. 1–6. [Google Scholar]
- Ren, J.; Xu, H.; He, P.; Cui, Y.; Zeng, S.; Zhang, J.; Wen, H.; Ding, J.; Huang, P.; Lyu, L.; et al. Copyright Protection in Generative AI: A Technical Perspective. arXiv 2024, arXiv:2402.02333. [Google Scholar]
- Gentry, C. Fully homomorphic encryption using ideal lattices. In Proceedings of the Forty-First Annual ACM Symposium on Theory of Computing, Bethesda, MD, USA, 31 May–2 June 2009; pp. 169–178. [Google Scholar]
- Boneh, D.; Goh, E.J.; Nissim, K. Evaluating 2-DNF Formulas on Ciphertexts. In Theory of Cryptography; Kilian, J., Ed.; Springer: Berlin/Heidelberg, Germany, 2005; Volume 3378, pp. 325–341. [Google Scholar]
- Paillier, P. Public-Key Cryptosystems Based on Composite Degree Residuosity Classes. In Advances in Cryptology—EUROCRYPT ’99; Stern, J., Ed.; Springer: Berlin/Heidelberg, Germany, 1999; Volume 1592, pp. 223–238. [Google Scholar]
- López-Alt, A.; Tromer, E.; Vaikuntanathan, V. On-the-fly multiparty computation on the cloud via multikey fully homomorphic encryption. In Proceedings of the Forty-Fourth Annual ACM Symposium on Theory of Computing, New York, NY, USA, 19–22 May 2012; pp. 1219–1234. [Google Scholar]
- Chen, H.; Dai, W.; Kim, M.; Song, Y. Efficient Multi-Key Homomorphic Encryption with Packed Ciphertexts with Application to Oblivious Neural Network Inference. In Proceedings of the 2019 ACM SIGSAC Conference on Computer and Communications Security, London, UK, 11–15 November 2019; pp. 395–412. [Google Scholar]
- Zhang, J.; Wang, X.; Yiu, S.M.; Jiang, Z.L.; Li, J. Secure Dot Product of Outsourced Encrypted Vectors and its Application to SVM. In Proceedings of the Fifth ACM International Workshop on Security in Cloud Computing, Abu Dhabi, United Arab Emirates, 2 April 2017; pp. 75–82. [Google Scholar]
- Peter, A.; Tews, E.; Katzenbeisser, S. Efficiently Outsourcing Multiparty Computation Under Multiple Keys. IEEE Trans. Inf. Forensics Secur. 2013, 8, 2046–2058. [Google Scholar] [CrossRef]
- Wang, B.; Li, M.; Chow, S.S.M.; Li, H. A tale of two clouds: Computing on data encrypted under multiple keys. In Proceedings of the 2014 IEEE Conference on Communications and Network Security, San Francisco, CA, USA, 29–31 October 2014; pp. 337–345. [Google Scholar]
- Wang, B.; Li, M.; Chow, S.S.M.; Li, H. Computing encrypted cloud data efficiently under multiple keys. In Proceedings of the 2013 IEEE Conference on Communications and Network Security (CNS), Washington, DC, USA, 14–16 October 2013; pp. 504–513. [Google Scholar]
- Zhang, J.; He, M.; Zeng, G.; Yiu, S.M. Privacy-preserving verifiable elastic net among multiple institutions in the cloud. J. Comput. Secur. 2018, 26, 791–815. [Google Scholar] [CrossRef]
- Zhang, J.; Hu, S.; Jiang, Z.L. Privacy-Preserving Similarity Computation in Cloud-Based Mobile Social Networks. IEEE Access 2020, 8, 111889–111898. [Google Scholar] [CrossRef]
- Ma, X.; Ji, C.; Zhang, X.; Wang, J.; Li, J.; Li, K.C.; Chen, X. Secure multiparty learning from the aggregation of locally trained models. J. Netw. Comput. Appl. 2020, 167, 102754. [Google Scholar] [CrossRef]
- Li, T.; Li, J.; Chen, X.; Liu, Z.; Lou, W.; Hou, T. NPMML: A Framework for Non-interactive Privacy-preserving Multi-party Machine Learning. IEEE Trans. Dependable Secure Comput. 2020, 18, 2969–2982. [Google Scholar] [CrossRef]
- Zhang, X.; Chen, X.; Liu, J.K.; Xiang, Y. DeepPAR and DeepDPA: Privacy Preserving and Asynchronous Deep Learning for Industrial IoT. IEEE Trans. Ind. Inform. 2020, 16, 2081–2090. [Google Scholar] [CrossRef]
- Shen, X.; Luo, X.; Yuan, F.; Wang, B.; Chen, Y.; Tang, D.; Gao, L. Privacy-preserving multi-party deep learning based on homomorphic proxy re-encryption. J. Syst. Archit. 2023, 144, 102983. [Google Scholar] [CrossRef]
- Blaze, M.; Bleumer, G.; Strauss, M. Divertible protocols and atomic proxy cryptography. In Advances in Cryptology—EUROCRYPT’98; Nyberg, K., Ed.; Springer: Berlin/Heidelberg, Germany, 1998; Volume 1403, pp. 127–144. [Google Scholar]
- Bresson, E.; Catalano, D.; Pointcheval, D. A Simple Public-Key Cryptosystem with a Double Trapdoor Decryption Mechanism and Its Applications. In Advances in Cryptology—ASIACRYPT 2003; Laih, C.S., Ed.; Springer: Berlin/Heidelberg, Germany, 2003; Volume 2894, pp. 37–54. [Google Scholar]
- Catalano, D.; Fiore, D. Using Linearly-Homomorphic Encryption to Evaluate Degree-2 Functions on Encrypted Data. In Proceedings of the 22nd ACM SIGSAC Conference on Computer and Communications Security, Denver, CO, USA, 12–16 October 2015; pp. 1518–1529. [Google Scholar]
- Goldreich, O. Foundations of Cryptography; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).