Compact Multi-Channel Long-Wave Wideband Direction-Finding System and Direction-Finding Analysis for Different Modulation Signals
Abstract
1. Introduction
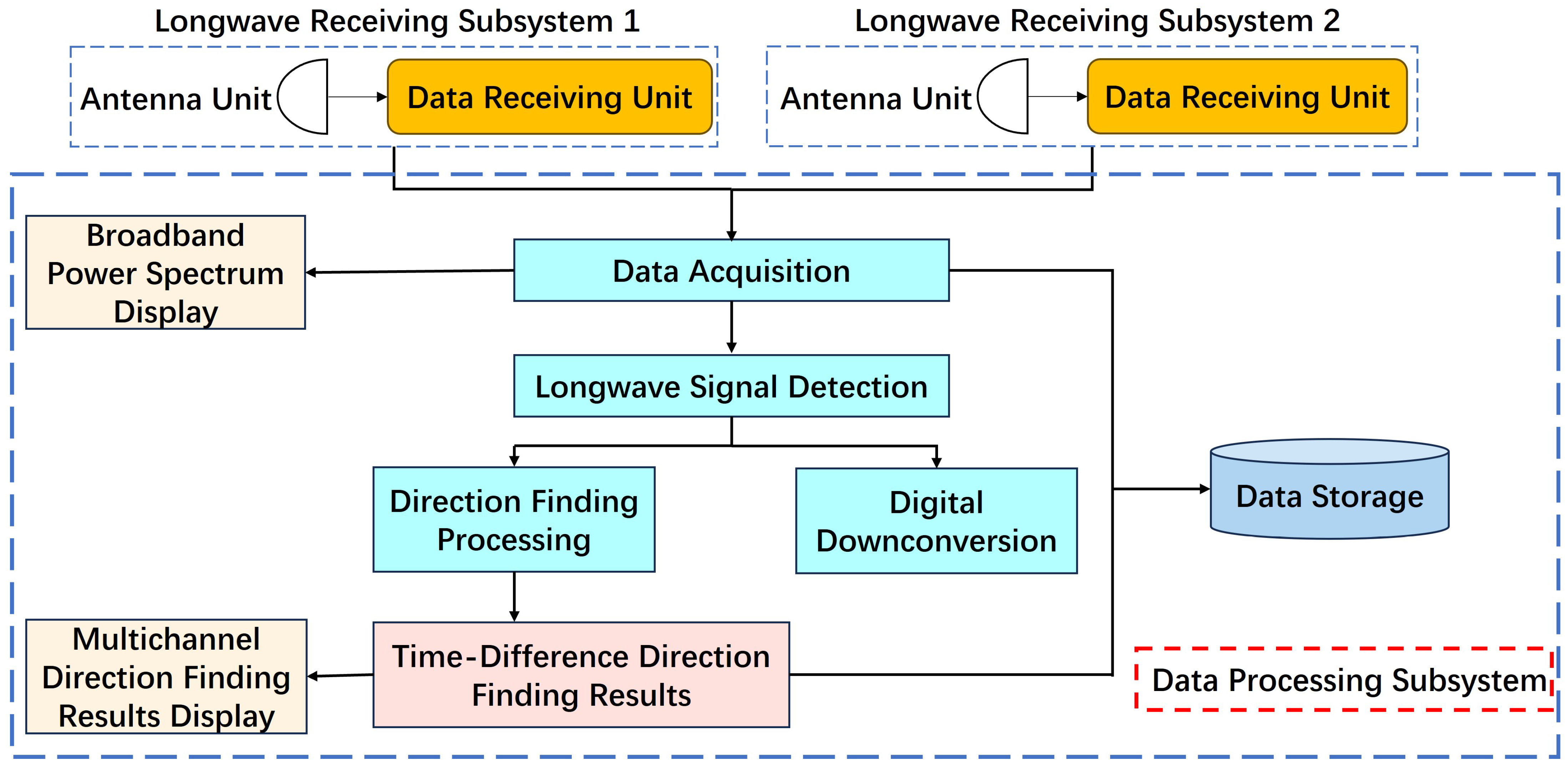
2. System Description
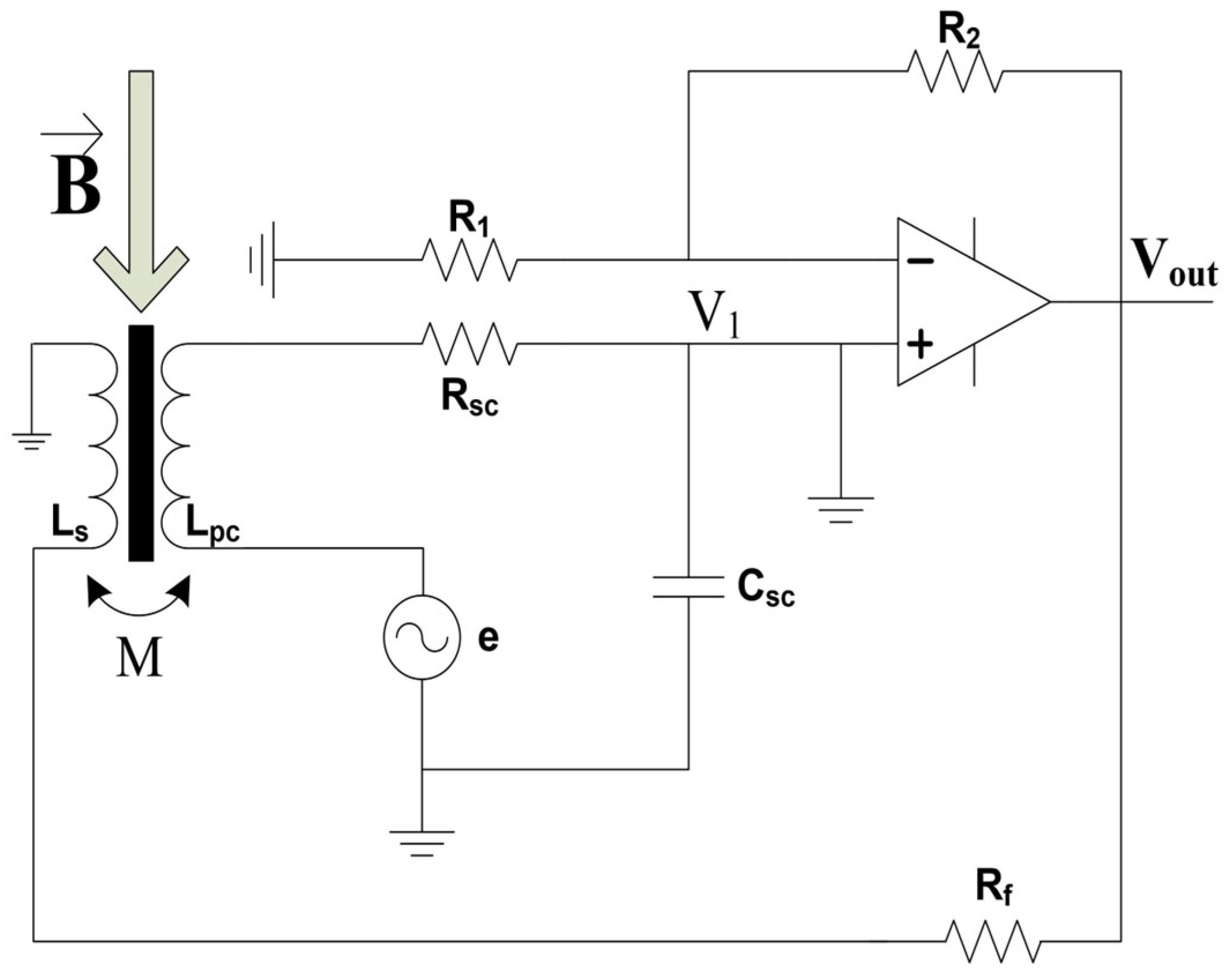
2.1. Horizontal Magnetic Field Sensor
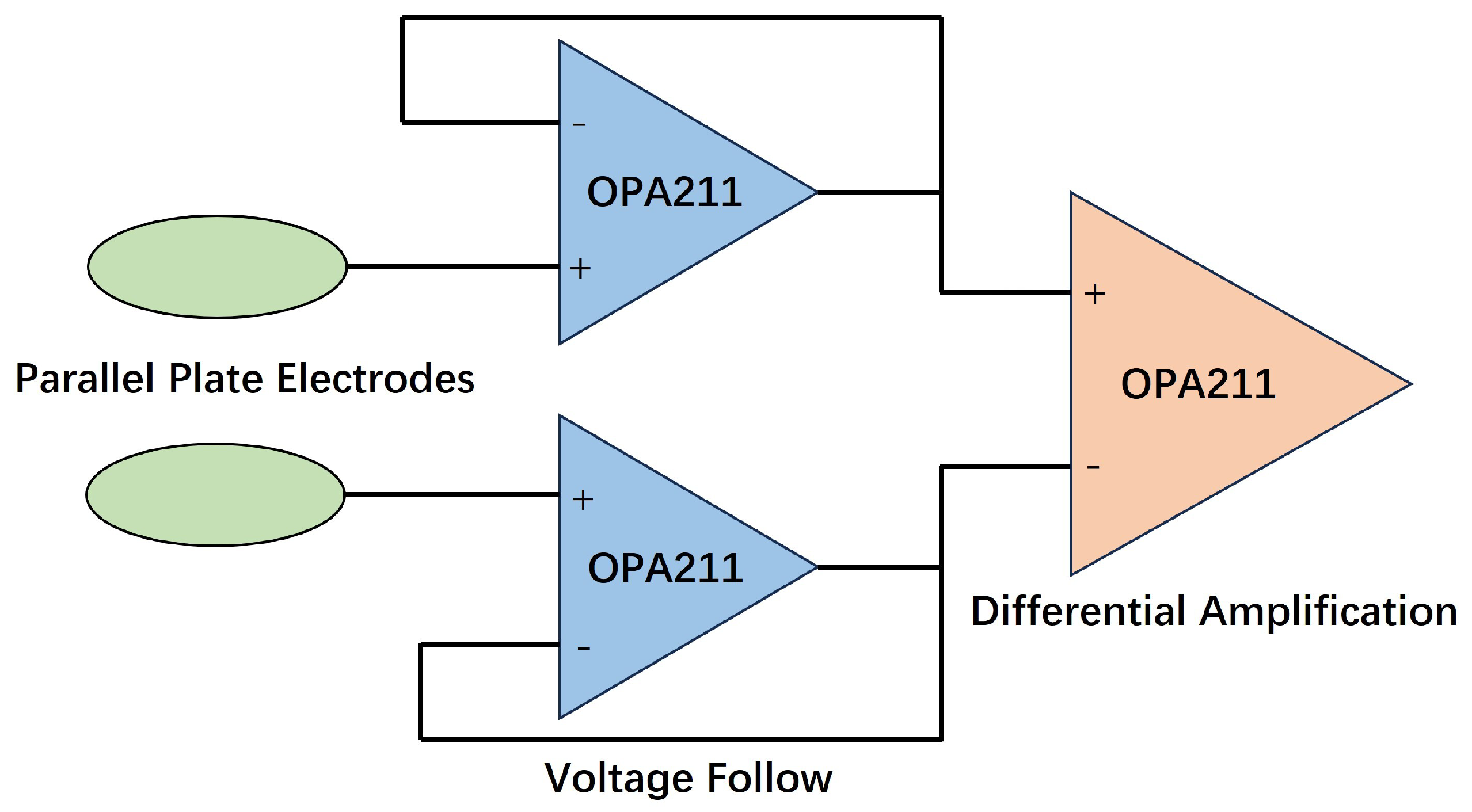
2.2. Vertical Electric Field Sensor
2.3. Sensitivity Analysis
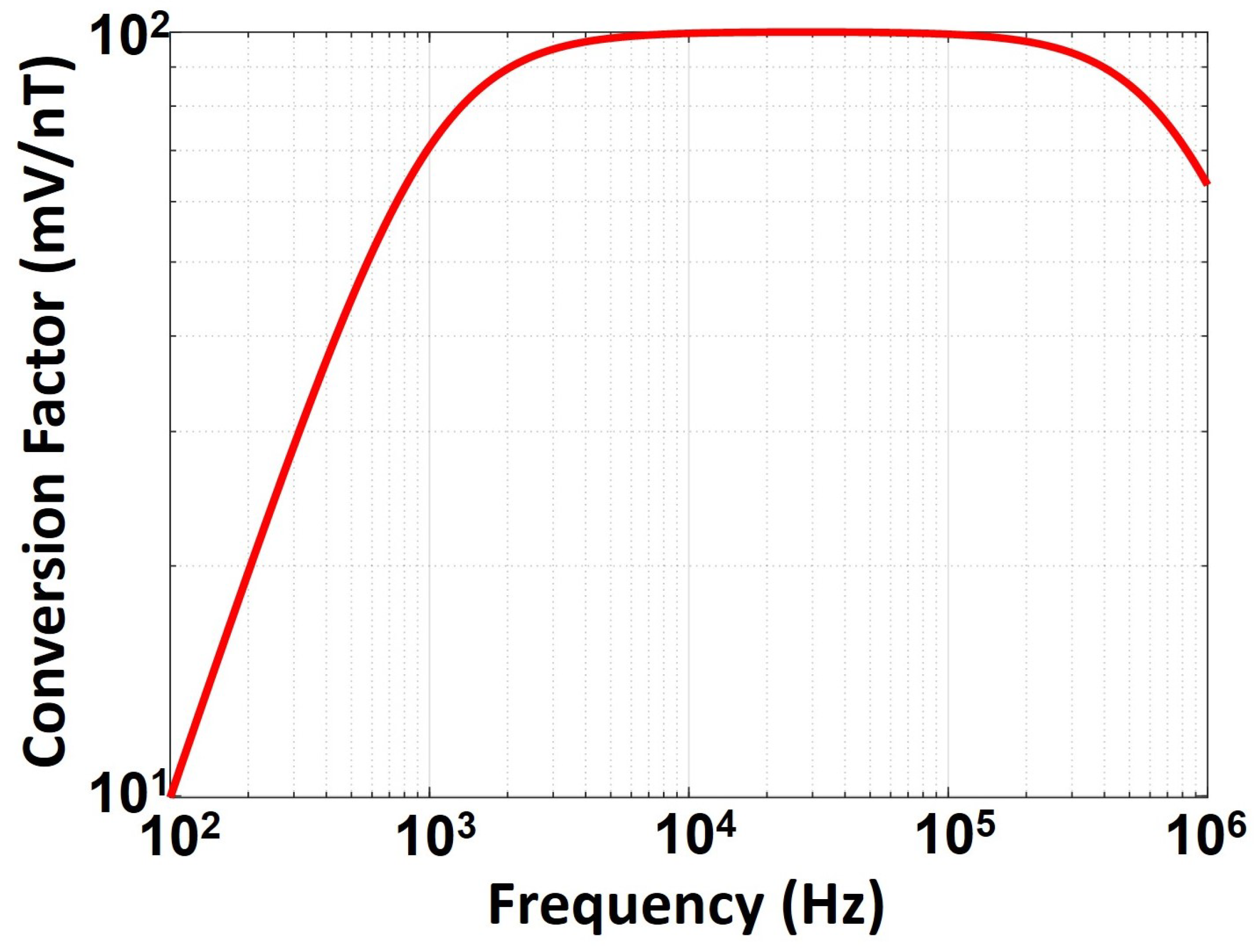
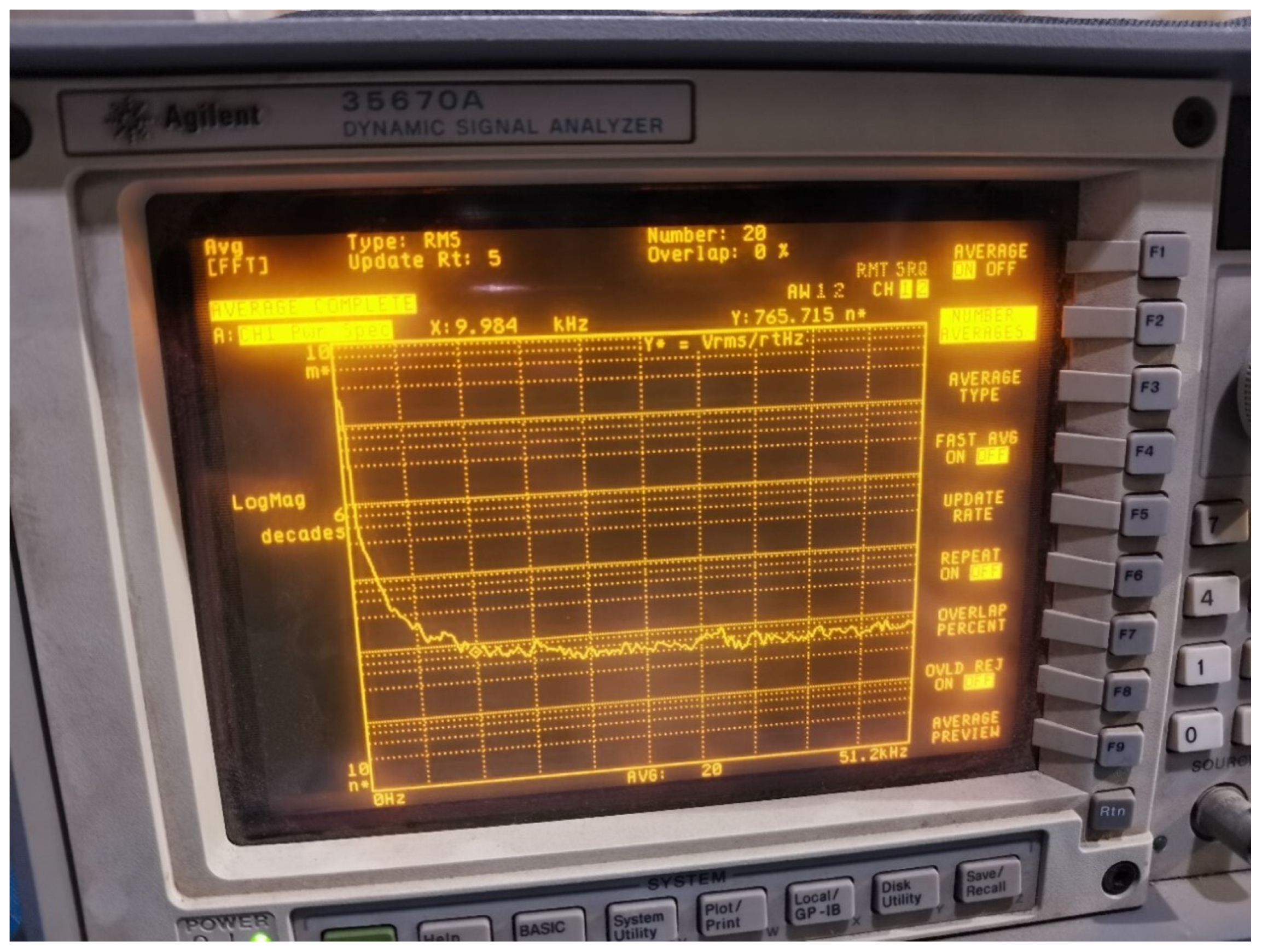
2.3.1. Magnetic Field Sensor Measurement Sensitivity Analysis
- Coil Noise
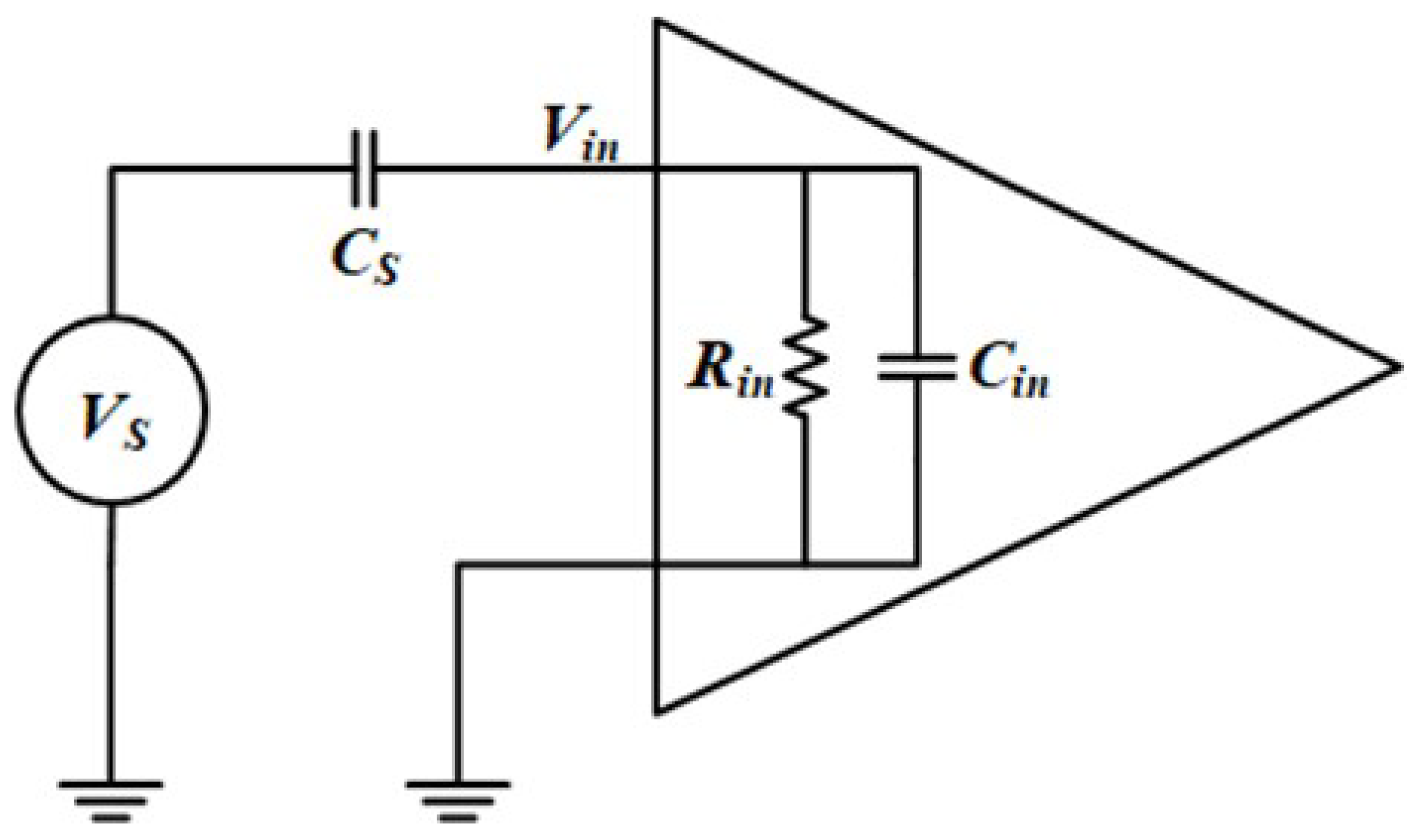
- Circuit-Induced Noise
2.3.2. Electric Field Sensor Measurement Sensitivity Analysis
2.3.3. Receiver Sensitivity Analysis
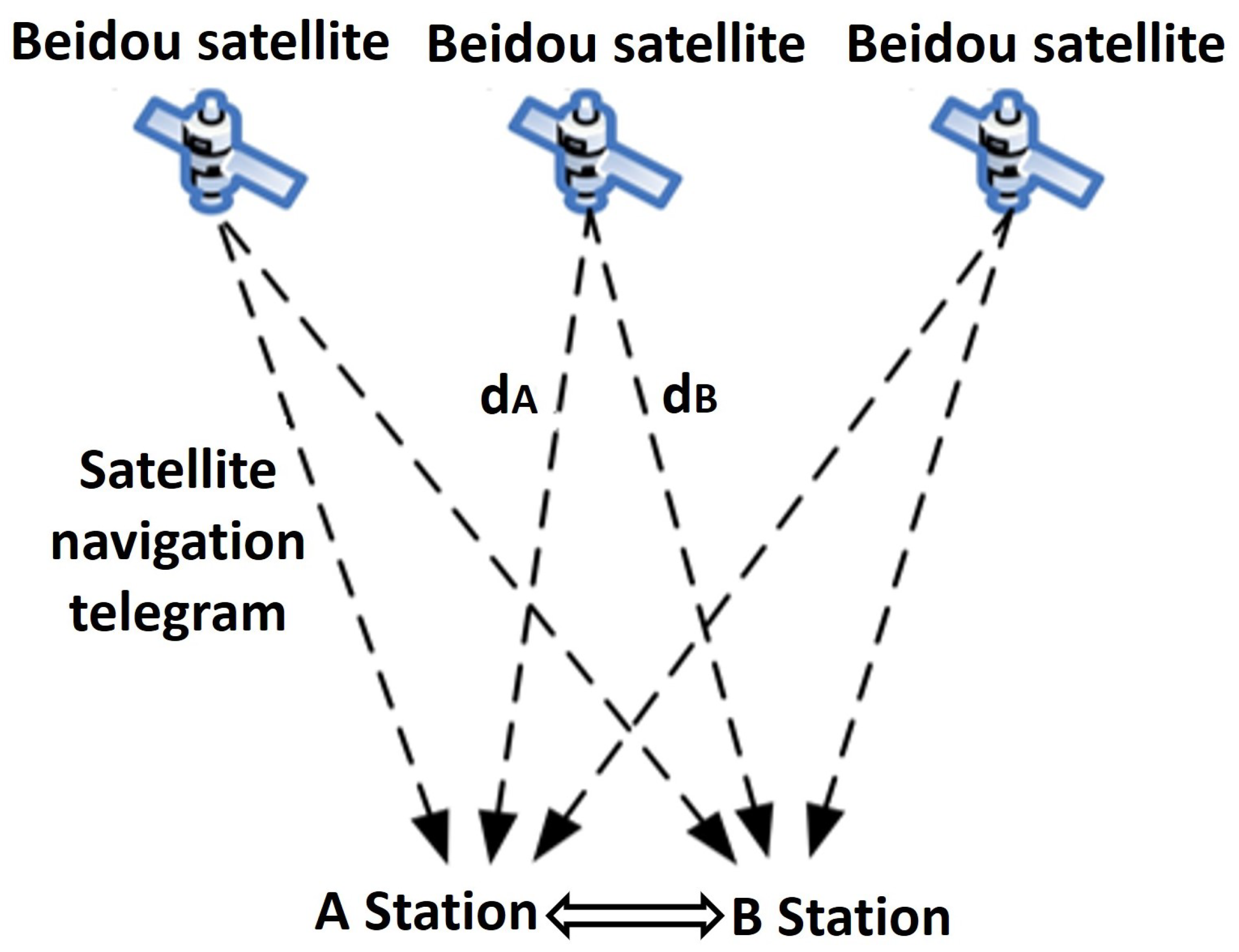
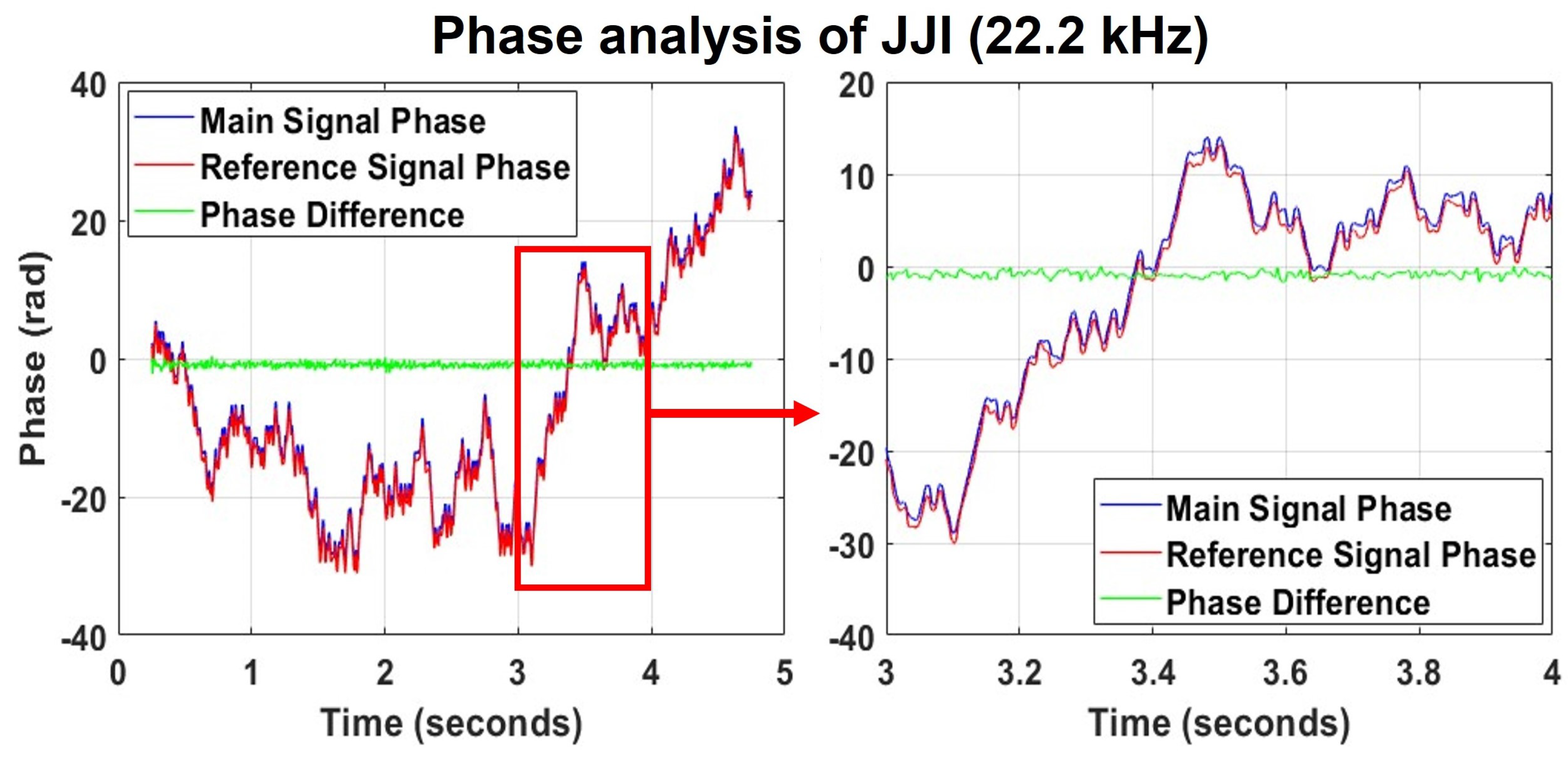
2.4. Time Synchronization Precision
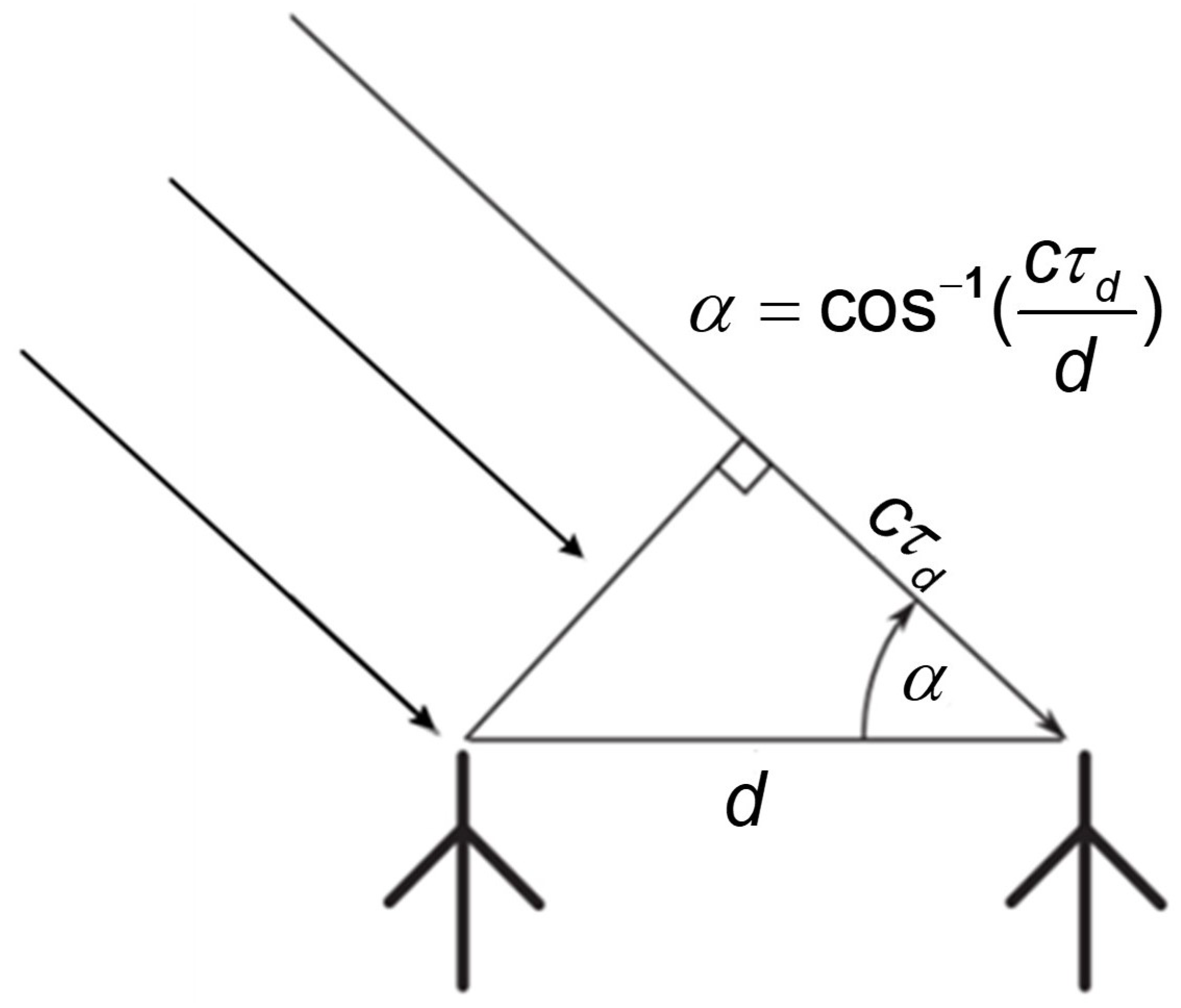
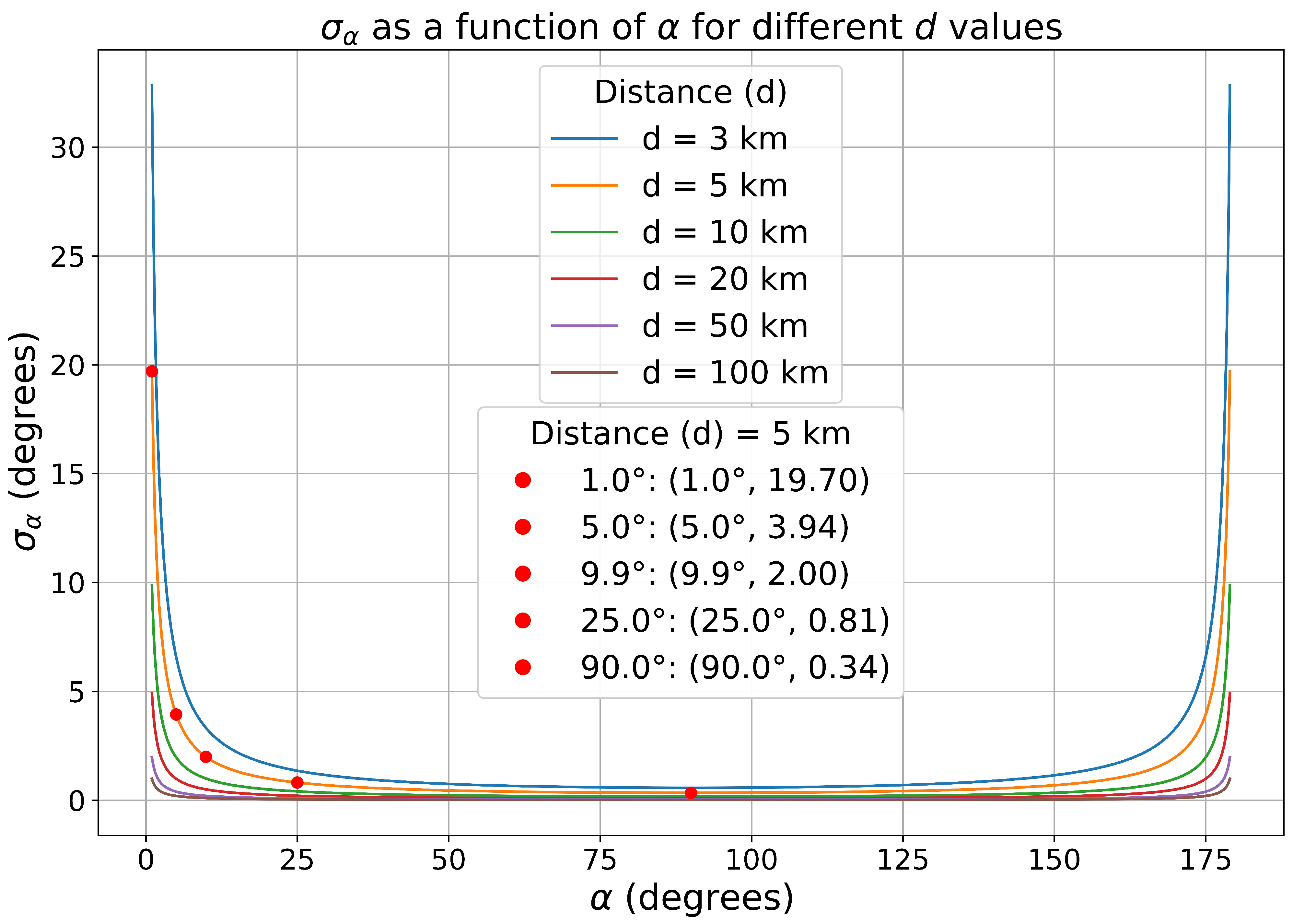
2.5. Direction-Finding Accuracy
2.6. Direction Finding of ASK and MSK Modulated Signals
3. Results and Discussion
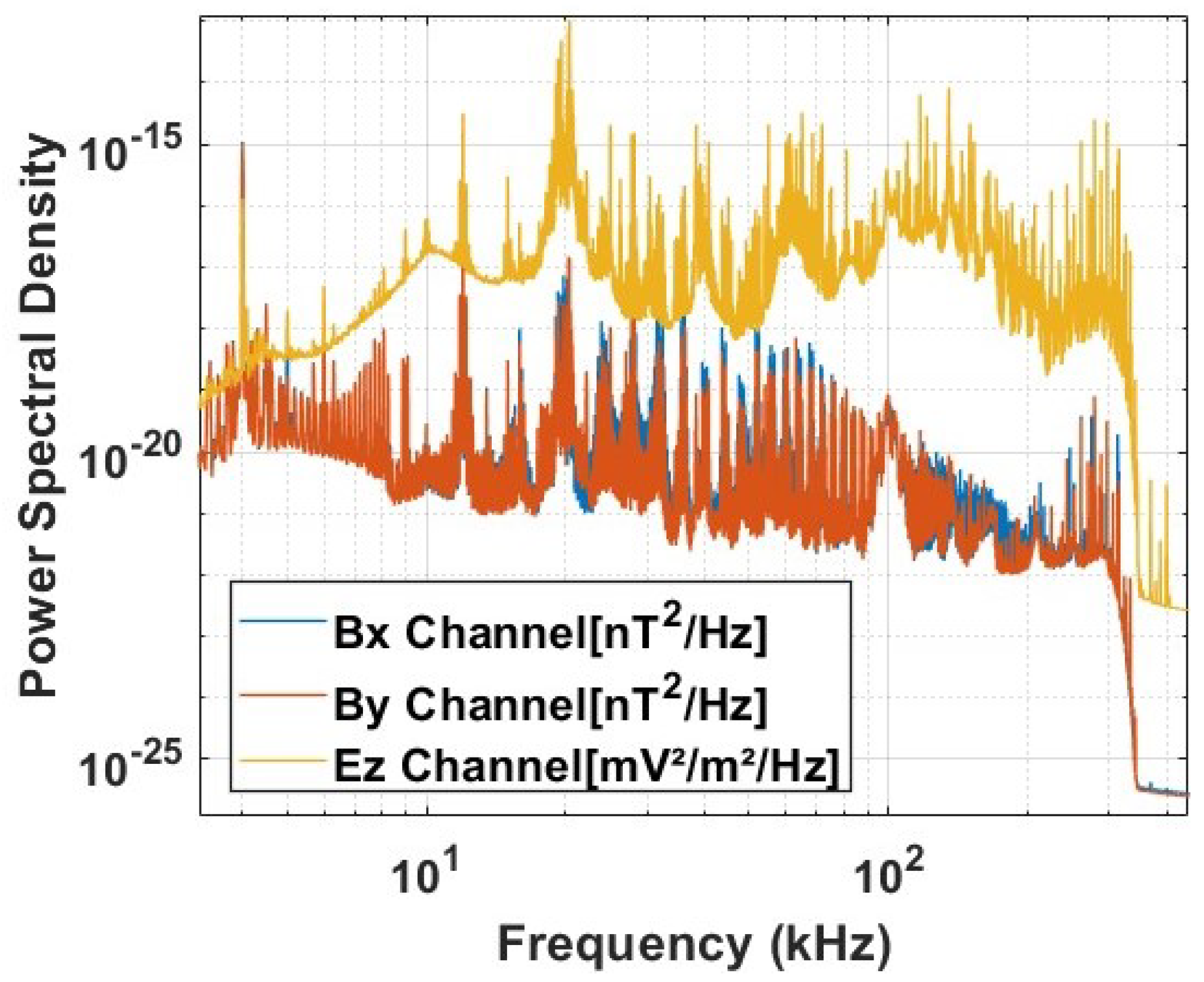
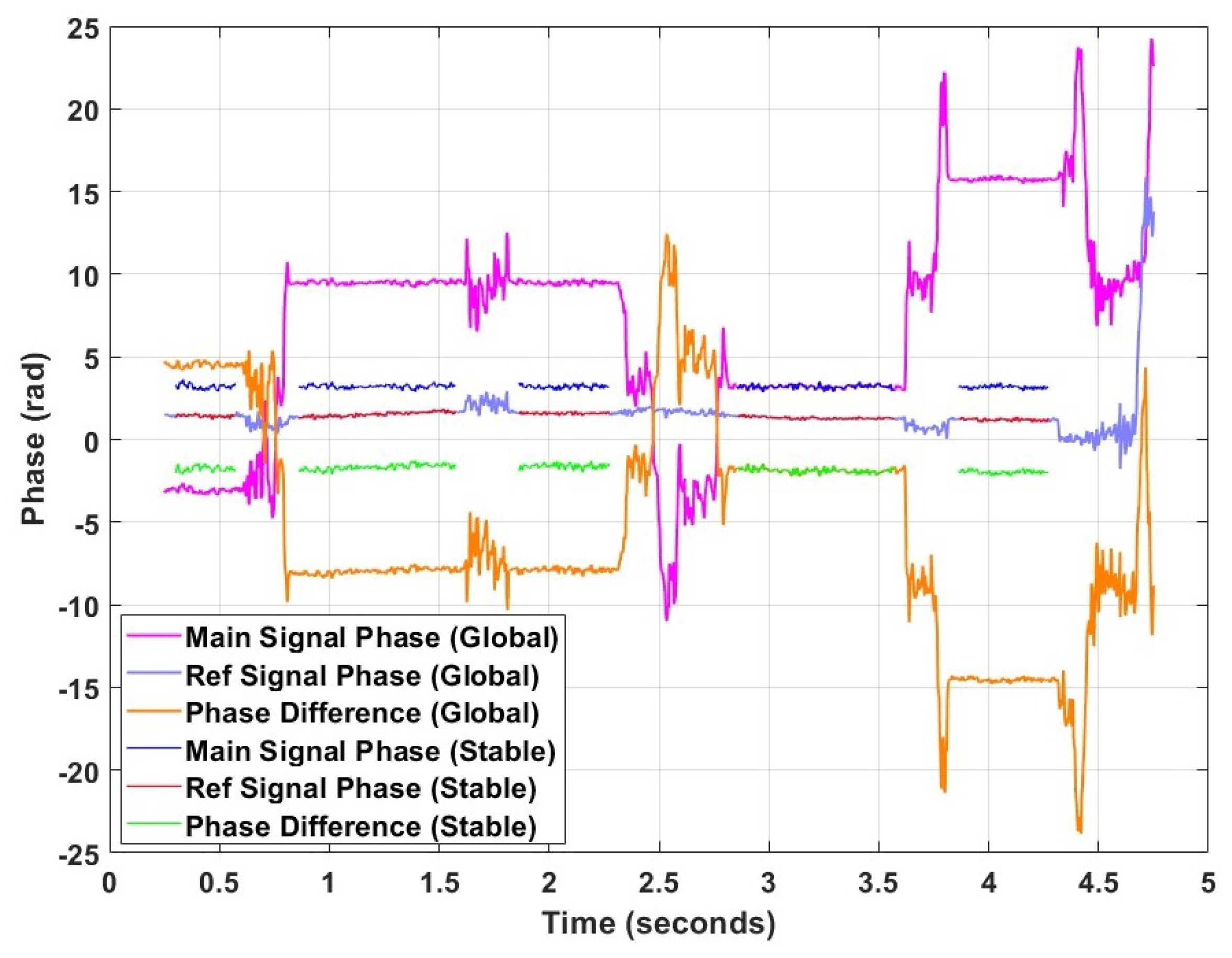
3.1. Measured Wideband Data Analysis
3.2. Narrowband Signal Analysis and Direction Finding
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| MSK | Minimum Shift Keying |
| ASK | Amplitude Shift Keying |
| ELF | Extremely Low Frequency |
| VLF | Very Low Frequency |
| LF | Low Frequency |
| GPS | Global Positioning System |
| ADC | Analog-to-Digital Converter |
| SNR | Signal-to-Noise Ratio |
| TR Noise | Thermal Noise of the Coil Resistor |
| CV Noise | Circuit Equivalent Input Voltage Noise |
| CI Noise | Circuit Equivalent Input Current Noise |
| PPS | Pulse Per Second |
References
- Preece, W.H. Earth currents. Nature 1894, 49, 554. [Google Scholar] [CrossRef]
- Barr, R.; Jones, D.; Rodger, C. ELF and VLF radio waves. J. Atmos. Sol. Terr. Phys. 2000, 62, 1689–1718. [Google Scholar] [CrossRef]
- Batlló, J. La Radiació ElectromagnèTica: CièNcia, TèCnica, Guerra I Pau. Quad. D’HistÒRia L’Eng. 2004, 6, 331–333. [Google Scholar]
- Swanson, E. Omega. Proc. IEEE 1983, 71, 1140–1155. [Google Scholar] [CrossRef]
- Thomson, N. Experimental daytime VLF ionospheric parameters. J. Atmos. Sol. Terr. Phys. 1993, 55, 173–184. [Google Scholar] [CrossRef]
- Thomson, N.R.; Clilverd, M.A.; McRae, W.M. Nighttime ionospheric D region parameters from VLF phase and amplitude. J. Geophys. Res. Space Phys. 2007, 112, 271. [Google Scholar] [CrossRef]
- Sechrist, C. Comparisons of techniques for measurement of D-region electron densities. Radio Sci. 1974, 9, 137–149. [Google Scholar] [CrossRef]
- Kelley, M.C.; Siefring, C.L.; Pfaff, R.F.; Kintner, P.M.; Larsen, M. Electrical measurements in the atmosphere and the ionosphere over an active thunderstorm: 1. Campaign overview and initial ionospheric results. J. Geophys. Res. Space Phys. 1985, 90, 9815–9823. [Google Scholar] [CrossRef]
- Betz, H.; Schmidt, K.; Oettinger, P.; Wirz, M. Lightning detection with 3-D discrimination of intracloud and cloud-to-ground discharges. Geophys. Res. Lett. 2004, 31, 11. [Google Scholar] [CrossRef]
- Pessi, A.T.; Businger, S.; Cummins, K.L.; Demetriades, N.W.S.; Murphy, M.; Pifer, B. Development of a Long-Range Lightning Detection Network for the Pacific: Construction, Calibration, and Performance. J. Atmos. Ocean. Technol. 2009, 26, 145–166. [Google Scholar] [CrossRef]
- Marshall, R.A.; Inan, U.S. Two-dimensional frequency domain modeling of lightning EMP-induced perturbations to VLF transmitter signals. J. Geophys. Res. Space Phys. 2010, 115, 761. [Google Scholar] [CrossRef]
- Liu, Z.; Koh, K.L.; Mezentsev, A.; Enno, S.; Sugier, J.; Füllekrug, M. Variable phase propagation velocity for long-range lightning location system. Radio Sci. 2016, 51, 1806–1815. [Google Scholar] [CrossRef]
- Li, J.; Dai, B.; Zhou, J.; Zhang, J.; Zhang, Q. Preliminary Application of Long-Range Lightning Location Network with Equivalent Propagation Velocity in China. Remote. Sens. 2022, 14, 560. [Google Scholar] [CrossRef]
- Li, J.; Song, L.; Zhang, Q.; Wang, S.; Yang, J.; Ge, Q. Optimizing lightning location accuracy: A study of propagation velocity and time of arrival in long-range lightning location algorithms. Measurement 2024, 234, 114754. [Google Scholar] [CrossRef]
- Bertoni, F.C.P.; Raulin, J.; Gavilán, H.R.; Kaufmann, P.; Rodriguez, R. Lower ionosphere monitoring by the South America VLF Network (SAVNET): C region occurrence and atmospheric temperature variability. J. Geophys. Res. Space Phys. 2013, 118, 6686–6693. [Google Scholar] [CrossRef]
- Gross, N.C.; Cohen, M.B.; Said, R.K.; Gołkowski, M. Polarization of Narrowband VLF Transmitter Signals as an Ionospheric Diagnostic. J. Geophys. Res. Space Phys. 2018, 123, 901–917. [Google Scholar] [CrossRef]
- McCormick, J.C.; Cohen, M.B.; Gross, N.C.; Said, R.K. Spatial and Temporal Ionospheric Monitoring Using Broadband Sferic Measurements. J. Geophys. Res. Space Phys. 2018, 123, 3111–3130. [Google Scholar] [CrossRef]
- Richardson, D.K.; Cohen, M.B. Seasonal Variation of the D-Region Ionosphere: Very Low Frequency (VLF) and Machine Learning Models. J. Geophys. Res. Space Phys. 2021, 126, e2021JA029689. [Google Scholar] [CrossRef]
- Füllekrug, M. Wideband digital low-frequency radio receiver. Meas. Sci. Technol. 2010, 21, 015901. [Google Scholar] [CrossRef]
- Shao, X.M.; Stanley, M.; Regan, A.; Harlin, J.; Pongratz, M.; Stock, M. Total Lightning Observations with the New and Improved Los Alamos Sferic Array (LASA). J. Atmos. Ocean. Technol. 2006, 23, 1273–1288. [Google Scholar] [CrossRef]
- Wood, T.G.; Inan, U.S. Localization of individual lightning discharges via directional and temporal triangulation of sferic measurements at two distant sites. J. Geophys. Res. Atmos. 2004, 109, 5204. [Google Scholar] [CrossRef]
- Inan, U.S.; Cohen, M.B.; Said, R.K.; Smith, D.M.; Lopez, L.I. Terrestrial gamma ray flashes and lightning discharges. Geophys. Res. Lett. 2006, 33, 2085. [Google Scholar] [CrossRef]
- Cohen, M.B.; Said, R.K.; Paschal, E.W.; McCormick, J.C.; Gross, N.C. Broadband longwave radio remote sensing instrumentation. Rev. Sci. Instruments 2018, 89, 094501. [Google Scholar] [CrossRef] [PubMed]
- Gurses, B.V.; Whitmore, K.T.; Cohen, M.B. Ultra-sensitive broadband “AWESOME” electric field receiver for nanovolt low-frequency signals. Rev. Sci. Instruments 2021, 92, 024704. [Google Scholar] [CrossRef] [PubMed]
- Cohen, M.; Inan, U.; Paschal, E. Sensitive Broadband ELF/VLF Radio Reception with the AWESOME Instrument. IEEE Trans. Geosci. Remote. Sens. 2010, 48, 3–17. [Google Scholar] [CrossRef]
- Gurses, B.V.; Whitmore, K.T.; Cohen, M.B. Electric Field Sensor Design for Longwave Radio Reception. In Proceedings of the 2019 SoutheastCon, Huntsville, AL, USA, 11–14 April 2019; pp. 1–2. [Google Scholar] [CrossRef]
- Krupka, M.A.; Matthews, R.; Say, C.; Hibbs, A.D.; Delory, G.D. Development and Test of Free Space Electric Field Sensors with Microvolt Sensitivity. Nasa Sti/Recon Tech. Rep. 2001, 3, 14007. [Google Scholar]
- Lu, X.; Chen, L.; Shen, N.; Wang, L.; Jiao, Z.; Chen, R. Decoding PPP corrections from BDS B2b signals using a software-defined receiver: An initial performance evaluation. IEEE Sensors J. 2020, 21, 7871–7883. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, L.; Li, J.; Yang, Y.; Zhang, T. Featured services and performance of BDS-3. Sci. Bull. 2021, 66, 2135–2143. [Google Scholar] [CrossRef]
- Dong, D.P.; Wu, H.S.; Guo, Q.F.; Yang, J.W.; Li, X. Research on high-precision time synchronisation technology for sea mobile platforms. Int. J. Inf. Commun. Technol. 2024, 24, 57–70. [Google Scholar] [CrossRef]
- Feng, P.; Wu, G.; Bai, Y.; Ding, X. Additional spread spectrum modulation timing method in BPC. In Proceedings of the Sixth International Symposium on Precision Engineering Measurements and Instrumentation, Hangzhou, China, 8–10 August 2010; Volume 7544, pp. 500–505. [Google Scholar] [CrossRef]
- Wu, C.; Qiu, S.; Wang, N.; Denisov, O.; Qiu, J.; Molebny, V. A Simple Analysis of The Development and Future of Long-wave Transmitting Antenna. In Proceedings of the 2023 6th International Conference on Electronics Technology (ICET), Chengdu, China, 12–15 May 2023; pp. 277–281. [Google Scholar] [CrossRef]
- Basak, T.; Hobara, Y.; Pal, S.; Nakamura, T.; Izutsu, J.; Minatohara, T. Modeling of Solar Eclipse effects on the sub-ionospheric VLF/LF signals observed by multiple stations over Japan. Adv. Space Res. 2024, 73, 736–746. [Google Scholar] [CrossRef]
- Yamazaki, S.; Onishi, K.; Goto, T.n.; Mikada, H.; Konishi, N. Feasibility study of subsurface electromagnetic exploration using longwave radio-clock time-signal. In Proceedings of the 9th SEGJ International Symposium. Society of Exploration Geophysicists of Japan, Sapporo, Japan, 12–14 October 2009; pp. 1–4. [Google Scholar] [CrossRef]
- Ohya, H.; Suzuki, T.; Tsuchiya, F.; Nakata, H.; Shiokawa, K. Variation in the reflection height of VLF/LF transmitter signals in the D-region ionosphere and the possible source: A 2018 meteoroid in Hokkaido, Japan. Radio Sci. 2024, 59, 1–10. [Google Scholar] [CrossRef]





| Reference | Year | Bandwidth | Electric/Magnetic Sensitivity | Antenna Size | Time Precision |
|---|---|---|---|---|---|
| Ref1 [19] | 2009 | 4 Hz–400 kHz | N/A * | 1.55 m | ns |
| Ref2 [25] | 2010 | 300 Hz–30 kHz | 2.6 m | ns | |
| Ref3 [23] | 2018 | 17–120 kHz | 56 cm | 15–20 ns | |
| Ref4 [26] | 2019 | 1–500 kHz | 1 m | 15–20 ns | |
| Ref5 [24] | 2021 | DC-470 kHz | 2 m | 15–20 ns | |
| This work | 2025 | 10–300 kHz | , | 20 cm(E-sensor), 35 cm (B-sensor) | <10 ns |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, H.; Wang, S.; Xu, X.; Ji, Y.; Liu, X. Compact Multi-Channel Long-Wave Wideband Direction-Finding System and Direction-Finding Analysis for Different Modulation Signals. Appl. Sci. 2025, 15, 2570. https://doi.org/10.3390/app15052570
Lu H, Wang S, Xu X, Ji Y, Liu X. Compact Multi-Channel Long-Wave Wideband Direction-Finding System and Direction-Finding Analysis for Different Modulation Signals. Applied Sciences. 2025; 15(5):2570. https://doi.org/10.3390/app15052570
Chicago/Turabian StyleLu, Hangyu, Shun Wang, Xin Xu, Yicai Ji, and Xiaojun Liu. 2025. "Compact Multi-Channel Long-Wave Wideband Direction-Finding System and Direction-Finding Analysis for Different Modulation Signals" Applied Sciences 15, no. 5: 2570. https://doi.org/10.3390/app15052570
APA StyleLu, H., Wang, S., Xu, X., Ji, Y., & Liu, X. (2025). Compact Multi-Channel Long-Wave Wideband Direction-Finding System and Direction-Finding Analysis for Different Modulation Signals. Applied Sciences, 15(5), 2570. https://doi.org/10.3390/app15052570






