Personalized Federated Learning with Progressive Local Training Strategy and Lightweight Classifier

Abstract

Data heterogeneity poses a significant challenge in federated learning (FL), which has become a central focus of contemporary research in artificial intelligence. Personalized federated learning (pFL), a specialized branch of FL, seeks to address this issue by tailoring models to the unique data distributions of individual clients. Despite its potential, current pFL frameworks face critical limitations, particularly in handling client training discontinuity. When clients are unable to engage in every training round, the resulting models tend to diverge from their local knowledge, leading to catastrophic forgetting. Moreover, existing frameworks often separate the model from the local classifier used for personalization, keeping the classifier local for extended periods. This inherent characteristic of classifiers frequently leads to overfitting on local training data, thereby impairing the generalization capability of the local models. To tackle these challenges, we propose a novel personalized federated learning framework, PFPS-LWC (Personalized Federated Learning with a Progressive Local Training Strategy and a Lightweight Classifier). Our approach introduces local knowledge recall and employs regularized classifiers to mitigate the effects of local knowledge forgetting and enhance the generalization of the models. We evaluated the performance of PFPS-LWC under varying degrees of data heterogeneity using the CIFAR10 and CIFAR100 datasets. Our method outperformed the state-of-the-art approach by up to 4.22% and consistently achieved the best performance across various heterogeneous environments, further demonstrating its effectiveness and robustness.

1. Introduction

Federated learning (FL) is a distributed learning framework that enables collaborative training across multiple clients while preserving privacy, thereby possessing vast potential for application across numerous domains, such as healthcare [1,2,3], security [4,5], intelligent driving [6,7], and recommender systems [8,9,10,11].

Data heterogeneity is an inevitable problem in federated learning. Currently, there is a significant body of work that recognizes this issue, and considerable efforts have been directed towards addressing it. Model-based methods [12,13,14] correct the training direction of the model by introducing an auxiliary model or adding regular losses to constrain the training direction of the local model. Several works have addressed this issue from a data perspective by altering the distribution of local data to make it more similar to global distribution, thereby mitigating the problem. For instance, works have utilized Generative Adversarial Networks (GANs) [15] or other specialized and traditional data augmentation methods such as [16,17,18,19] to generate missing categories of data locally.

The traditional federated learning approach struggles with data heterogeneity, making it difficult to generate a globally effective model. Personalized federated learning (pFL) was proposed to address this by creating a personalized model for each client, improving adaptation to local data. Rather than relying on a single global model, pFL introduces personalized components locally. For example, FedPer [20] uses the last layer of a convolutional neural network, while FedTP [21] uses the self-attention layer of a transformer [22] network and FedBN [23] uses a BN (batch normalization) layer to personalize the model. Other pFL approaches, like FedALA [24] and HPFL [25], improve model training and aggregation by enhancing local model personalization. They achieve this by creating personalized feature extractors for each client instead of using a shared one. Another promising approach [26,27] leverages knowledge distillation [28], where intermediate or global models act as teacher models, guiding local student models trained on local data, thus improving performance.

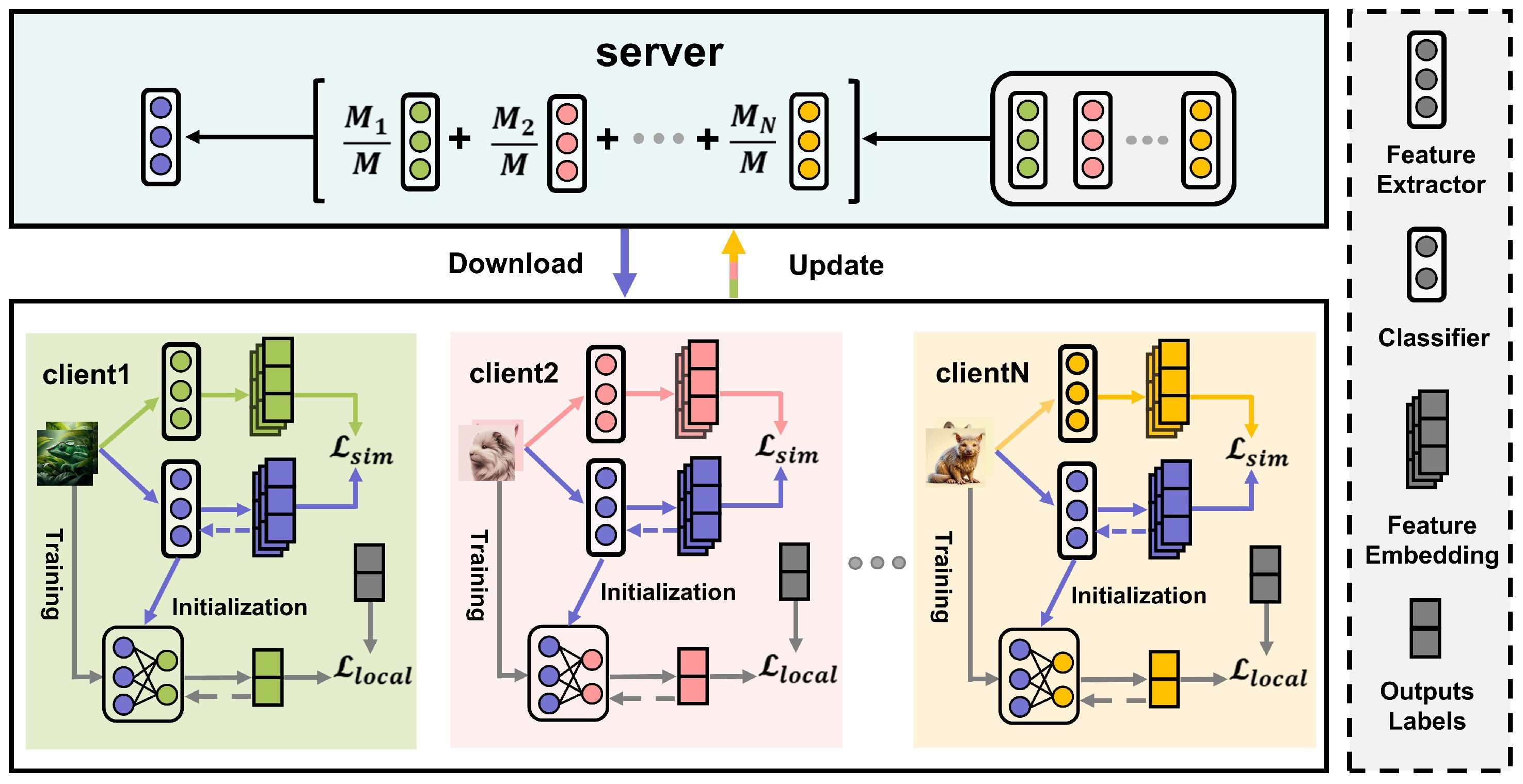
Existing pFL frameworks typically decouple the model into a feature extractor and classifier. The local feature extractor is initialized with the globally aggregated one in each round, mitigating data heterogeneity. However, this approach overlooks the continuity of local model training. As shown in Figure 1, the reinitialization of the local feature extractor each round leads to inconsistency between the global model and local knowledge, especially for clients missing multiple rounds of training, referred to as “stragglers”. These clients experience a growing deviation from their local knowledge, disrupting consistent learning. Additionally, while the global aggregation helps the feature extractor generalize, the local classifier tends to overfit after several rounds, reducing the generalization and performance on new data. We summarize the challenges of the current pFL framework as two main issues: training discontinuity and classifier overfitting.

To address the training discontinuity problem, we introduce a local knowledge recall mechanism designed to retain the model from the previous training round on the client side. This mechanism ensures that when the client receives the updated global model in the subsequent iteration, it can enhance the similarity between the outputs of the global feature extractor and the retained local feature extractor. As shown in Figure 2, we add a stage for knowledge recall before the local model initialization phase. By doing so, the mechanism effectively achieves the goal of knowledge recall, allowing the model to retain and leverage previously acquired local knowledge.

To address the classifier overfitting problem, we propose adding a regularization term to the loss function during the local model training phase. The regularization term aims to mitigate the classifier’s tendency to overfit the local training data by making the classifier parameters sparser, making it a lightweight classifier. By incorporating this regularization, we aim to enhance the generalizability of the lightweight classifier, ensuring that it performs well not only on the local training data but also on unseen data. This approach helps to balance the benefits of local training with the need for a globally robust feature extractor, ultimately improving the overall performance of the pFL system.

In this paper, we propose Personalized Federated Learning with a Progressive Local Training Strategy and a Lightweight Classifier (PFPS-LWC). The key contributions of our work are as follows:

• We propose a Progressive Local Training Strategy that enables a smooth transition from a global model to an initial model with local knowledge and mitigates discontinuity in customer training.
• We propose a lightweight classifier strategy, which reduces the parameter density and overfitting tendency of the original classifier and alleviates the overfitting problem of the original pFL framework.
• We conducted extensive evaluations under varying online rates and data distributions, demonstrating the effectiveness of PFPS-LWC through a series of rigorous experiments. These evaluations showed that our proposed method outperforms existing approaches, providing strong evidence of its practical applicability and benefits.

The remainder of this paper is structured as follows: Section 2 reviews related work on federated learning and personalized federated learning. Section 3 presents our proposed method, PFPS-LWC, in detail. Section 4 describes the experimental setup and results, highlighting the effectiveness of our approach. Finally, Section 5 provides a summary and discussion.

2. Related Works

2.1. Federated Learning Under Data Heterogeneity

Data heterogeneity is an inevitable problem due to the diverse sources of data from clients, leading to variations in federated learning. These differences can affect model updates, slowing convergence and reducing the performance of the global model. When there is significant heterogeneity, the aggregation process may incorporate these disparities into the global model, causing local knowledge to be forgotten, especially when initializing local models. This deviation from local data characteristics results in a loss of relevant information for each client.

As the importance of data privacy protection continues to grow, traditional methods of collecting and centrally training data are no longer feasible. For example, in healthcare, data from various hospitals may differ due to variations in equipment, imaging protocols, and patient demographics, resulting in Non-IID data distributions. Similarly, IoT devices, such as smartwatches, home security cameras, and fitness trackers, generate data with significant variations in format, scale, and relevance to users’ activities. These discrepancies can affect local model training after aggregation, as well as the overall performance of the global model. This issue extends to other domains like smart homes, where devices like thermostats and security cameras process data locally and contribute to model improvements through aggregated updates. In autonomous vehicles, cars collect data for navigation and safety, training models on local data while ensuring privacy. In the finance sector, bank branches train fraud detection models on transaction data, with updates aggregated to enhance model accuracy while preserving customer privacy. The edge devices mentioned in the examples above, such as in hospitals, IoT devices, smart homes, autonomous vehicles, and bank branches, all correspond to the “clients” depicted in Figure 3.

This shift has led to the introduction of the federated learning paradigm, which enables collaborative training across multiple parties without the need to share raw data. Federated learning allows each client to train a model locally on their own data and then share only the model updates with a central server, thereby preserving data privacy. However, federated learning faces significant challenges due to the differences in data distribution among different clients. These differences, collectively known as data heterogeneity, can arise from variations in feature distribution, label distribution, or the data volume. This inconsistency can cause the models to converge at different rates, making it difficult to achieve a unified global model that performs well across all clients. As a result, the overall convergence speed and performance of the federated learning system are adversely affected. Addressing the challenges posed by data heterogeneity is crucial for the successful development and deployment of federated learning systems.

The earliest federated learning paradigm was FedAvg [29]. It achieves model aggregation by simply aggregating the model parameters trained locally on different clients. However, this paradigm has a significant drawback: it relies on the assumption that the data are IID (independently and identically distributed). When the data are Non-IID, its performance is suboptimal. FedProx [14] recognized the impact of data heterogeneity, specifically when data are Non-IID, on global model training. To mitigate this heterogeneity, it introduced a regularization term. This regularization term helps to mitigate the effects of data heterogeneity by stabilizing the training process and ensuring that the model updates from different clients are more aligned. By incorporating this regularization, FedProx aimed to improve the convergence speed and overall performance of the global model, making it more robust to the variations in data distributions across clients.

Various methods have been proposed to address this challenge. For instance, techniques introducing regularization terms such as FedDyn [30], FedDC [31], SCAFFOLD [12], FedDecorr [32], and [33] aim to reduce the gap between local and global models or correct the direction of local model training. These regularization terms help align the local models with the global model, thereby improving the overall consistency and performance of the federated learning system. In addition to regularization-based methods, several approaches have focused on improving federated model aggregation, such as pFedSim [34] and FedDisco [35]. They consider factors like the distribution similarity of local data and the model similarity to generate global models that are more suitable for each client. By taking into account these similarities, these approaches help create global models that better reflect the diverse data distributions across clients, thereby mitigating the impact of data heterogeneity to some extent. In addition, the work based on data enhancement methods, such as FedAug [16], FedM-UNE [19], and FedDA [36], has also alleviated the problem of Non-IID data to a certain extent. These methods aim to balance the classes for clients, reduce the degree of data heterogeneity, and enhance the diversity of the training data, which helps improve the generalizability of the models. Although the aforementioned approaches can learn useful features from heterogeneous data to some extent, they often fail to achieve satisfactory performance when the degree of heterogeneity is high. This is because the variations in data distributions can be too significant for these methods to handle effectively. Therefore, in this paper, we propose to address this issue using a personalized federated learning paradigm. Our approach focuses on tailoring the learning process to the specific characteristics of each client’s data, thereby improving the overall performance and robustness of the federated learning system.

2.2. Personalized Federated Learning

Personalized federated learning has garnered significant attention for its outstanding performance on Non-IID data by incorporating personalized factors for each local model. This approach is particularly effective in scenarios where data distributions vary significantly across different clients. The mainstream strategy in pFL is model decoupling, which involves splitting the model into two distinct parts: the feature extractor (also known as the backbone network) and the classifier (or head). These two components are trained using different strategies to achieve a high degree of personalization.

In neural networks, the deeper layers of the network have a stronger correlation with the data distribution. Based on this conclusion, more recent works have taken an approach that uses the classifier as the personalized component. These works primarily use the classifier as the personalized component while treating the feature extractor as the shared component. For example, FedPer [20] treats the classifier as the personalized component, keeping it local, while the feature extractor is treated as the shared component. In this design, each client customizes its own classification standards, which allows for better feature extraction while avoiding discrepancies caused by the classifier. Other methods based on using classifiers as personalization components such as PFedMe [37], Ditto [38], and FedRep [39] promote the learning of global feature extractors by adjusting local training. These approaches ensure that the feature extractor can generalize well across different clients, while the classifier remains tailored to the specific data of each client. The more personalized approaches, like FedFomo [40] and FedALA [24], achieve personalization for each client by combining weighted models for each client and correcting class embedding gradients by injecting cross-client gradient terms. This helps in aligning the learning process across clients and improving the overall model performance. There is also an approach [11] that uses federated graph learning to capture user preferences based on distributed multi-domain data and improve the recommendation performance across all domains without compromising privacy. This method leverages the unique characteristics of graph data to enhance personalization. FedProto [41] employs a prototype learning approach, improving tolerance to heterogeneity by transmitting abstract class prototypes between clients and the server instead of gradients. This reduces the communication overhead and enhances the model’s ability to handle diverse data distributions. Fed-RoD [42] balances general performance and personalized performance by training a general predictor and a personalized predictor through a dual prediction task framework. This approach ensures that the model can perform well on both local and global data.

As opposed to using a classifier as a personalized component, LG-FedAvg [43] proposed using the feature extractor as the personalized component while sharing the classifier among all clients. This strategy provides a unified standard for classification across all models, ensuring consistency in the classification process. At the same time, the feature extractor is tailored to better align with the local data distribution of each client. By doing so, the extracted features are more representative of the local data, thereby mitigating the impact of data heterogeneity to some extent. This decoupling approach allows the feature extractor to capture the unique characteristics of each client’s data, enhancing the model’s ability to generalize across different data distributions.

The aforementioned works have made efforts in different directions to mitigate the impact of data heterogeneity to varying degrees. However, they often lack consideration of the inherent flaws within the pFL frameworks themselves. These flaws can include issues such as the complexity of model training, the communication overhead, and the difficulty in balancing personalization with generalization. Addressing these inherent flaws is crucial for the further development and effectiveness of personalized federated learning systems.

2.3. Comparison with Existing Methods

In this section, we compare our proposed method with existing representative studies in the field, focusing on key aspects such as the model architecture, method categories, training strategies, and their respective advantages and disadvantages. To facilitate a clear and detailed analysis, we provide tables summarizing the relevant comparisons. As shown in

Table 1. Comparison of federated learning and personalized federated learning methods.

Method	Architecture	Categories	Strategies	Advantages	Disadvantages
FedAvg [29]	CNN	FL	Simple aggregation	Simple and efficient	Sensitive to data heterogeneity
FedProx [14]	CNN	FL	Regularization	Robust to data heterogeneity	More computational costs
FedPer [20]	CNN	pFL	Model peronalization	High adaptability	Prone to overfitting
pFedMe [37]	CNN	pFL	Personalized loss	High personalization	More computional costs
FedBN [23]	CNN	pFL	Batch normalization	Fast convergence	More computional costs
FedProto [41]	CNN	pFL	Prototype learning	High communication efficiency	Slow training
PFPS-LWC	CNN	pFL	Feature alignment and regularization	Efficient and robust	More computional costs

, the comparison highlights the key differences across various methods.

The table provides a comprehensive comparison of various federated learning methods, highlighting the trade-offs between efficiency, personalization, robustness, and computational costs. While methods like FedAvg [29] offer simplicity and efficiency, they struggle in heterogeneous environments. FedProx [14] addresses data heterogeneity through regularization, but with added computational complexity. Personalized methods such as FedPer [20], pFedMe [37], and FedBN [23] offer better adaptation to local data but are more prone to overfitting and incur higher computational costs. PFPS-LWC balances robustness and efficiency, making it a strong choice for environments with data heterogeneity. FedProto [41], focusing on communication efficiency, comes with the downside of slower training. Overall, the choice of method depends on the balance between the need for model personalization, computational resources, and the desired robustness to data heterogeneity.

3. Methodology

3.1. Preliminaries

Personalized federated learning is an important branch of federated learning that aims to address the issue of data heterogeneity among different clients. In a pFL system, assume there are N clients and one server. Each client, $i\in \left\{1,2,\dots ,N\right\}$, holds a private dataset, $D_i={\left\{(x_j,y_j)\right\}}_{j=1}^{M_i}$, where $M_i$ represents the data volume of client i. Additionally, define $M={\displaystyle \sum _{i=1}^N}{M}_i$ as the total volume of all data. Each client’s decoupled model parameters are $w_i=({\theta }_i,{\varphi }_i)$, where ${\theta }_i$ is the parameters of the feature extractor and ${\varphi }_i$ is the parameters of the classifier. On the server side, the aggregation of the shared feature extractor is completed, and the parameters of the aggregated feature extractor are denoted as ${\theta }_g$.

There are two processes in pFL, the local update process and the global aggregation process. Let E denote the total number of epochs for local training in a global round, t, and T represent the total number of global training rounds, while e denotes an intermediate epoch during local training. For client i, it first updates the local feature extractor using the global aggregated feature extractor ${\theta }_g^{(t-1)}$, and the updated local feature extractor is ${\theta }_i^t$. Then, ${\theta }_i^t$ is concatenated with ${\varphi }_i^t$ to form the initialized model $w_i^t=({\theta }_i^t,{\varphi }_i^t)$. This model is trained locally for E epochs, resulting in $w_i^{t+E}=({\theta }_i^{t+E},{\varphi }_i^{t+E})$. The updated local feature extractor ${\theta }_i^{t+E}$ is then uploaded to the server. In an ideal scenario, assuming all clients participate in training and updating and the model parameters are aggregated in proportion to the data volume, the updated global feature extractor is ${\theta }_g^t={\displaystyle \sum _{i=1}^N}{\displaystyle \frac{M_i}{M}}{\theta }_i^{t+E}$, and the aggregated feature extractor is distributed to each client. Under the pFL framework, the overall optimization objective is as follows:

$$\underset{\theta ,{\varphi }_i}{min}\left\{F(\theta ,{\varphi }_i):=\sum _{i=1}^N{\displaystyle \frac{M_i}{M}}\mathcal{L}(\theta ,{\varphi }_i;D_i)\right\}$$

(1)

where $\mathcal{L}$ is the loss of client i on its private dataset, $D_i$.

3.2. Progressive Local Training Strategy

Current personalized federated learning frameworks decouple models into personalized headers and shared feature extractors. At the beginning of each round, they directly initialize the local feature extractor using the global feature extractor and concatenate it with the personalized head (which always resides locally) to complete the initialization of the local model. Essentially, they ignore the continuity of local training and cause the local knowledge to be forgotten directly. For a certain local client, if it does not participate in the global training for many rounds, the continuity of its local training will be severely damaged, leading to the direct forgetting of local knowledge. Additionally, in cases where there is high data heterogeneity among clients, this heterogeneity is transferred to the local models through the global model. As a result, clients may receive a model that significantly differs from their own data, which is detrimental to local training. To address this issue, we propose a Progressive Local Training Strategy which preserves the local model from the client’s last participation in global training. This preserved model is then used to recall knowledge when initializing the global model in the next participating round.

In prior personalized federated learning frameworks, the stage where the global feature extractor is concatenated with the local classifier was commonly referred to as the model initialization stage. This stage is crucial as it sets the foundation for the subsequent training process by combining the global and local components of the model. However, we propose to introduce a new stage prior to this, called the local knowledge recall stage. This additional stage aims to leverage the knowledge gained from previous training rounds, ensuring that the model retains valuable local information before integrating the global feature extractor.

By incorporating the local knowledge recall stage, we aim to enhance the model’s ability to utilize previously learned local information, thereby improving its overall performance and stability. The approach helps to mitigate the issue of discontinuity in local training and ensures a smoother transition to the model initialization stage. We refer to this overall strategy as a Progressive Local Training Strategy. This strategy not only improves the alignment between local and global models but also enhances the model’s ability to generalize across diverse data distributions.

In this stage, we denote the local feature extractor from the most recent round of participation in the federated process as ${\theta }_i^l$, where ‘l’ refers to ‘local’. The global feature extractor obtained in the current round is ${\theta }_g$, and the output of the data after passing through the feature extractor $\theta$ is $z_j=f(\theta ,x_j)$, where f represents the mapping function from the data to the features. Next, for $x_j^i\in D_i$ belonging to client i, we utilize $z_j^i=f({\theta }_i^l,x_j^i)$ as the soft label for $x_j^i$. Correspondingly, the output of $x_j^i$ on ${\theta }_g$ is $z_j^g$. Based on the above definition, we establish the following objective to realize the knowledge of the ${\theta }_i^l$ transfer to ${\theta }_g$:

$$\underset{{\theta }_g}{min}\left\{F({\theta }_g,{\theta }_i^l):={\mathcal{L}}_{sim}({\theta }_g,{\theta }_i^l,x_i^j),where x_i^j\in D_i\right\}$$

(2)

We employ the cosine similarity function to maximize the similarity between the two outputs and establish the following loss function:

$${\mathcal{L}}_{sim}=1-{\displaystyle \frac{z_j^i·z_j^g}{\left|\right|z_j^i\left|\right|\times \left|\right|z_j^g\left|\right|}}=1-{\displaystyle \frac{f({\theta }_i^l,x_j^i)·f({\theta }_i^g,x_j^i)}{\left|\right|f({\theta }_i^l,x_j^i)\left|\right|\times \left|\right|f({\theta }_i^g,x_j^i)\left|\right|}},$$

(3)

Then, the update process for ${\theta }_g^{t+e}$ is as follows:

$${\theta }_g^{t+e}\leftarrow {\theta }_g^{t+e-1}-\nabla {\mathcal{L}}_{sim}({\theta }_g,{\theta }_i^l,x_i^j), where{x}_i^j\in D_i$$

(4)

Through the mechanism described above, we facilitate the transfer of knowledge from the local model parameters, denoted as ${\theta }_i^l$, to the global model parameters, ${\theta }_g$, by maximizing the similarity between the outputs of two distinct networks when they process an identical dataset. This strategy enables ${\theta }_g$ to assimilate the learning knowledge accumulated by each client during previous training rounds, thereby ensuring the seamless continuation of the local training process, and after the process is finished, we use the updated ${\theta }_g$ to initialize the local feature extractor, establishing the initial local model to carry out subsequent local training. Specially, the initial model establishes a strong connection with local knowledge at this stage, providing a good starting point for local training, making later local training more efficient and effective. After the local training process has been completed, the updated local feature extractor ${\theta }_i^{t+E}$ is used to further refine the local parameters ${\theta }_i^l$ and continue to the next stage.

3.3. Local Training with Lightweight Classifier

The model’s ability to generalize is a key factor that directly influences its performance and can be effectively enhanced by reducing the upper bound on its generalization. To quantify the upper bound on generalization, we apply the theory of Rademacher complexity as outlined in [44]. Let $\mathcal{G}$ be a set of functions mapping $\mathcal{Z}\to [a,b]$, and let S = $(Z_1,\dots ,Z_n)$ be i.i.d. random variables on $\mathcal{Z}$, drawn from some distribution, P. The empirical Rademacher complexity of $\mathcal{G}$ with respect to the sample $(Z_1,\dots ,Z_n)$ is defined as

$$\widehat{{\mathfrak{R}}_S}\left(\mathcal{G}\right):={\mathbb{E}}_{\sigma }\left[{\displaystyle \underset{g\in \mathcal{G}}{sup}\frac{1}{n}\sum _{i=1}^n{\sigma }_{i}g\left(x_i\right)}\right],$$

(5)

where $\sigma ={({\sigma }_1,\dots ,{\sigma }_n)}^T$ and ${\sigma }_i\backsim unif\left\{-1,1\right\}$, which are known as Rademacher random variables. Moreover, with a probability of at least $1-\delta$, we have, with respect to that drawn from S,

$${\displaystyle \forall g\in \mathcal{G},\mathbb{E}\left[g\left(\mathcal{Z}\right)\right]\le \frac{1}{n}\sum _{i=1}^{n}g\left(x_i\right)+2\widehat{{\mathfrak{R}}_S}\left(\mathcal{G}\right)+3(b-a)\sqrt{\frac{log(2/\delta )}{2n}},}$$

(6)

where the right-hand side of the equation is the upper bound on the generalization of the model. As evident from Equation (6), the upper bound on the model’s generalization capability is determined by three key factors: the empirical risk, the Rademacher risk, and the combined effect of the sample size and the number of categories. For neural networks, the Rademacher risk has a bound with an explicit dependence on the dimension, which is primarily influenced by the model complexity [45].

Inspired by the above theory, reducing the model’s complexity can lower the Rademacher risk and improve the model’s generalization ability. The classifier head, located at the end of a deep learning model, is responsible for mapping extracted features to class predictions. While it can fit local data distributions and features well, it is prone to overfitting local data [46]. In the pFL framework, the classifier is locally trained and updated, causing its parameters to become overly complex and leading to a significant increase in the model complexity. This increase in complexity tends to raise the Rademacher risk and exacerbate the overfitting phenomenon. To address this issue, we propose to introduce lightweight classifiers to limit the complexity of the model and thus reduce the Rademacher risk and then improve the generalization performance of the model.

Regularization techniques, commonly used in machine learning, help reduce overfitting and improve model generalization. Therefore, we propose adding a classifier regularization term during the local training process in pFL to alleviate the degree of overfitting of the classifier and improve the model performance. In this section, we propose utilizing L2 regularization to enhance the training process of local models. By applying the L2 norm to the classifier, we can control its parameter density, making it relatively sparse. This approach helps achieve the goal of creating lightweight classifiers. Building on the original loss function, we add an L2 regularization term for the lightweight classifier, controlled by the hyperparameter $\lambda$. Thus, the local loss consists of two parts: the empirical loss, which we use the cross-entropy loss for, and the regularization loss. For the total loss, we define it as follows:

$${\mathcal{L}}_{local}={\mathcal{L}}_{CE}+\lambda {\mathcal{L}}_{REG},$$

(7)

In the above equation, ${\mathcal{L}}_{CE}$ represents the cross-entropy loss, and ${\mathcal{L}}_{REG}$ represents the regularization loss.

Here, we define the mapping function from the features to the classifier as h. Thus, the classification output for data x can be represented as $h_{\varphi }\left(f_{\theta }\left(x\right)\right)$. The definition of ${\mathcal{L}}_{CE}$ and ${\mathcal{L}}_{REG}$ are as follows:

$${\mathcal{L}}_{CE}(h_{\varphi }\left(f_{\theta }\left(x\right)\right),y)=-{\displaystyle \frac{1}{M_i}}\sum _{j=1}^{M_i}{h}_{\varphi }\left(f_{\theta }\left(x_j\right)\right)log\left(y_j\right),$$

(8)

$${\mathcal{L}}_{REG}={\left|\right|\varphi \left|\right|}_2=\sqrt{{\displaystyle \sum _{k=1}^{\left|\varphi \right|}{\varphi }_k^2}},$$

(9)

$\left|\varphi \right|$ represents the number of $\varphi$’s parameters and ${\varphi }_k$ is the kth parameter of $\varphi$. Then, the update process of the local model is

$$w_i^{t+e}({\theta }_i^{t+e},{\varphi }_i^{t+e})\leftarrow w_i^t({\theta }_i^t,{\varphi }_i^t)-\nabla {\mathcal{L}}_{local}.$$

(10)

We modify the locally trained loss function and control the regularization degree of the lightweight classifier head by adjusting the weight of the $\lambda$ regularization term in the loss function. By regularizing the classifiers, the parameters of the local classifiers can be made sparse, which reduces the Rademacher risk of the model to some extent and improves the generalization ability of the model.

3.4. The Convergence of PFPS-LWC

To prove the convergence of PFPS-LWC, we begin by introducing the following assumptions.

Assumption 1.

$Lipschitz$ $Smoothness.$ The gradients of client i’s local complete heterogeneous model $w_i$ are $L1-Lipschitzsmooth$:

$$\begin{array}{cc}\hfill \parallel \nabla {\mathcal{L}}_i^{t_1}\left(w_i^{t_1};x,y\right)-\nabla {\mathcal{L}}_i^{t_2}\left(w_i^{t_2};x,y\right)\parallel & \le L_1\parallel w_i^{t_1}-w_i^{t_2}\parallel ,\hfill \\ \hfill \forall t_1,t_2>0,i\in \left\{0,1,\dots ,N-1\right\},& \left(x,y\right)\in D_i\hfill \end{array}$$

(11)

The above formulation can be further derived as

$$\begin{array}{c}\hfill {\mathcal{L}}_i^{t_1}-{\mathcal{L}}_i^{t_2}⩽〈\nabla {\mathcal{L}}_i^{t_2},\left(w_i^{t_1}-w_i^{t_2}\right)〉+{\displaystyle \frac{L_1}{2}}{\parallel w_i^{t_1}-w_i^{t_2}\parallel }_2^2\end{array}$$

(12)

The smoothness assumption guarantees that the gradient updates are controlled and do not cause erratic or unstable model updates, which could hinder convergence. It provides a theoretical foundation for maintaining stability during federated model aggregation and facilitates the model’s smooth convergence.

Assumption 2.

$Unbiased$ $Gradient$ $and$ $Bounded$ $Variance.$ Client i’s random gradient $g_t^{w,i}=\nabla {\mathcal{L}}_i^t\left(w_i^t,{\mathcal{B}}_i^t\right) (\mathcal{B}$ is a batch of local data) is unbiased:

$$\begin{array}{c}\hfill {\mathbb{E}}_{{\mathcal{B}}_i^t\subseteq D_i}\left[g_t^{w,i}\right]=\nabla {\mathcal{L}}_i^t\left(w_i^t\right)\end{array}$$

(13)

and the variance of the random gradient $g_t^{w,i}$ is bounded by

$$\begin{array}{c}\hfill {\mathbb{E}}_{{\mathcal{B}}_i^t\subseteq D_i}\left[{\parallel \nabla {\mathcal{L}}_i^t\left(w_i^t;{\mathcal{B}}_i^t\right)-\nabla {\mathcal{L}}_i^t\left(w_i^t\right)\parallel }_2^2\right]\le {\sigma }^2\end{array}$$

(14)

This assumption ensures that the model’s optimization process is based on correct and stable gradient updates. It also prevents the introduction of large variance during training, which would otherwise affect the stability of the global model aggregation and hinder convergence.

Assumption 3.

$Bounded$ $Prameter$ $Variation.$ The parameter variations of the homogeneous feature extractor ${\theta }_i^t$ and ${\theta }^t$ before and after aggregation are bounded as

$$\begin{array}{c}\parallel {\theta }^t-{\theta }_i^t\parallel \le {\delta }^2\end{array}$$

(15)

This assumption ensures that despite local data heterogeneity, the model updates remain manageable and do not cause large disparities between local and global models. It helps in maintaining the stability of the federated learning system by ensuring that parameter updates are consistently within a reasonable range, facilitating convergence and preventing instability during model aggregation.

Using Assumptions 1 and 2, we can establish the following lemma.

Lemma 1.

There is an upper bound on the loss range of any client’s local model, w, in the t local training round.

$$\begin{array}{c}\hfill {\displaystyle \mathbb{E}\left[{\mathcal{L}}_{t+1}^{E+0}\right]\le {\mathcal{L}}_t^{E+0}+(\frac{L_1{\eta }^2}{2}-\eta )\sum _{e=1}^E{\parallel \nabla {\mathcal{L}}_t^{E+e}\parallel }_2^2+\frac{L_{1}E{\eta }^2{\sigma }^2}{2}}\end{array}$$

(16)

Leveraging Assumption 3 and Lemma 1, we derive Lemma 2.

Lemma 2.

For the $(t+1)$ local training round, the loss of any client before and after aggregating local homogeneous small feature extractors on the server is bounded by

$$\begin{array}{c}\hfill \mathbb{E}\left[{\mathcal{L}}_{t+1}^{E+0}\right]\le \mathbb{E}\left[{\mathcal{L}}_t^{E+1}\right]+\eta {\delta }^2\end{array}$$

(17)

By synthesizing Lemma 1 and 2, we ultimately arrive at the following conclusion:

$$\begin{array}{c}\hfill \eta <{\displaystyle \frac{2(ϵ-{\delta }^2)}{L_1(ϵ+E{\sigma }^2)}}\end{array}$$

(18)

Given that $ϵ$, $L1$, ${\delta }^2$, ${\sigma }^2$, and E are all positive constants, it follows that $\eta$ has well-defined solutions. Consequently, when the learning rate $\eta$ satisfies the aforementioned condition, convergence is assured for any client’s local complete heterogeneous model. The detailed certification process is presented in Appendix A.

3.5. An Overview of PFPS-LWC

To provide a concise overview of the proposed method, we present the algorithm in a pseudocode format below, as shown in Algorithm 1. The algorithm is divided into two parts: one for the client-side operations and the other for the server-side operation. Before local training begins on the client side, the model needs to undergo an initialization process. In this step, we optimize the global feature extractor by minimizing the discrepancy between its output and the output of the previous round’s feature extractor for this client. The optimized feature extractor is concatenated with the classifier to form the initial model for local training, which is then used in this process. On the server side, we perform aggregation based on the proportion of data from each client. By calculating the data proportion for each client, we determine their aggregation weights, which are then used to aggregate the global feature extractor.

Algorithm 1 PFPS-LWC.

1: Input: Global feature extractor ${\theta }_g$, local feature extractor that participated in the last round of global training ${\theta }_i^l$, local classifier ${\varphi }_i^t$, dataset $D_i$, local epoch E, global round T, the number of participating clients $N_t$, learning rate $\eta$.  2: Client Training:  3: for $i=1$ to $N_t$ do  4:     if ${\theta }_i^l\ne NULL$ then  5:         Localize global feature extractor ${\theta }_g$:  6:         ${\theta }_g^{t+e}\leftarrow {\theta }_g^{t+e-1}-\nabla {\mathcal{L}}_{sim}({\theta }_g,{\theta }_i^l,D_i)$  7:     end if  8:     Initialize local model: $({\theta }_i^t,{\varphi }_i^t)=({\theta }_g,{\varphi }_i^t)$  9:     for $e=1$ to E do 10:         $({\theta }_i^{t+e},{\varphi }_i^{t+e})\leftarrow \left(({\theta }_i^{t+e-1},{\varphi }_i^{t+e-1})\right)-\eta \nabla {\mathcal{L}}_{local}$ 11:    end for 12:    Get trained local feature extractor: ${\theta }_i^{t+E}$ 13:    Update the local feature extractor in the last round 14:    of global training: ${\theta }_i^l={\theta }_i^{t+E}$ 15:    return ${\theta }_i^{t+E}$ to server 16: end for 17: Server Aggregation: 18: for $t=1$ to T do 19:    $\left\{{\theta }_1^{t+E},{\theta }_2^{t+E},\dots ,{\theta }_{N_t}^{t+E}\right\}\leftarrow$ Client Training() 20:    Compute aggregation weights $\left[{\alpha }_1,{\alpha }_2,...,{\alpha }_{N_t}\right]$ 21:    Get the aggregated global feature ${\theta }_g$ 22:    Send ${\theta }_g$ to clients who are selected in round t + 1. 23: end for

3.6. Discussion of the Proposed PFPS-LWC Method

PFPS-LWC introduces several key innovations that enhance the personalization and robustness of federated learning. One of the most significant contributions is the Progressive Local Training Strategy combined with the local knowledge recall stage, which ensures that each client retains and utilizes its local knowledge across multiple rounds of global training. Unlike traditional methods, where local models are initialized using global feature extractors without consideration for previous local training, PFPS-LWC allows clients to recall previous local knowledge before integrating new global information. This effectively reduces catastrophic forgetting and enables a smoother transition between local and global training phases, significantly improving the model’s ability to adapt to the unique characteristics of each client’s data.

Additionally, PFPS-LWC improves model generalization through the use of lightweight classifiers. By limiting the classifier complexity, the method reduces the risk of overfitting to local data, which is a common challenge in federated learning systems. This lightweight classifier not only enhances personalization but also mitigates the model complexity, helping to maintain a balance between personalization and generalization.

4. Experiments

4.1. Experiment Setup

• Datasets. To evaluate the effectiveness of the proposed federated learning method, we conducted comprehensive experiments on two widely adopted and challenging visual benchmark datasets:

• Cifar10 [47]: The CIFAR10 dataset contains 60,000 32 × 32 color images, evenly distributed across 10 different classes, with each class comprising 6000 images. Among them, 5000 were used for training and 1000 for testing.
• Cifar100 [47]: An extension of CIFAR10, the CIFAR100 dataset includes 60,000 32 × 32 color images, evenly distributed across 100 classes, with each class containing 600 images. Among them, 500 were used for training and 100 for testing.

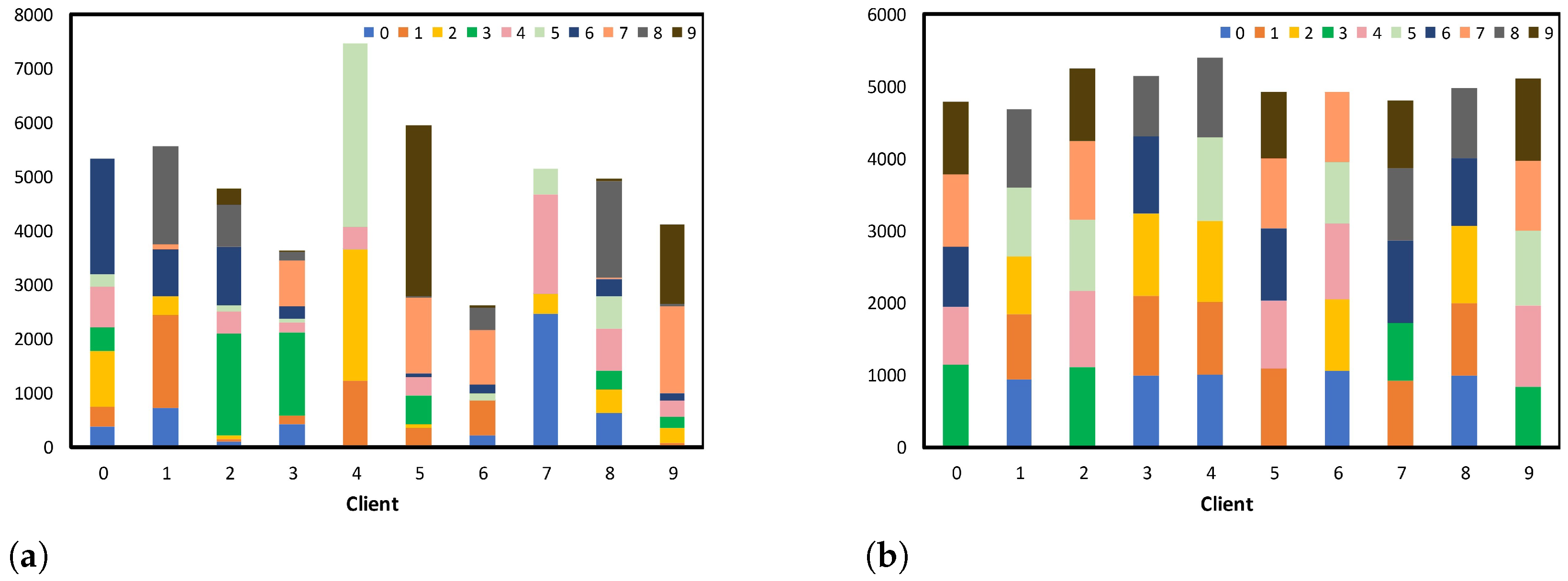
For each dataset, we employed two data partitioning methods. The first method used the Dirichlet distribution to partition the data, which were then allocated to each client. In Dirichlet partitioning, the parameter controlling the Dirichlet distribution, denoted as $\beta$, can be adjusted to control the degree of Non-IID data among different clients. A smaller $\beta$ indicated a higher degree of Non-IID data, allowing us to simulate varying levels of heterogeneity by adjusting the value of $\beta$. The second method was pathological Non-IID partitioning, a manually designed Non-IID data partitioning method. This method involved dividing the dataset into multiple small shards and randomly assigning these shards to different clients, resulting in significant heterogeneity in the data distribution across clients. We conducted experiments under these two heterogeneity simulation settings. This extensive experimental setup simulated real-world scenarios and ensured a comprehensive evaluation of the robustness of our method. In order to more intuitively understand the two partitioning methods, we present a figure showing two data distributions created using Dirichlet partitioning and pathological Non-IID partitioning on the cifar10 dataset below, where the number of clients, N, was 10 and the Dirichlet distribution parameter $\beta$ = 0.5. The specific distribution after partitioning is shown in Figure 4 below.

• Models. For classification tasks on the above datasets, we used a five-layer CNN network. The first four layers of the CNN served as feature extractors, while the final layer functioned as the classifier. For the CIFAR10 dataset, the output dimension of the final layer was set to 10, while for the CIFAR100 task, the output dimension of the final layer was set to 100.
• Counterparts. To demonstrate the effectiveness of the proposed method, we select a representative and superior personalized federated learning method including FedPer [20], FedBN [23], pFedMe [37] and FedProto [41]. Additionally, to showcase the superiority of personalized federated learning on Non-IID data, we also compared our method with the representative of traditional personalized federated learning methods such as FedAvg [29] and FedProx [14].
• Implementation details. To ensure the fairness of the comparison methods, we used the same hyperparameters in our experiments. In the experiments, we set the number of clients, N, to 10, the number of global training rounds, T, to 20, and the number of local training epochs, E, to 5. We used an SGD optimizer with a learning rate of 0.01 and a batch size of 64. Additionally, we set the parameter $\lambda$ in the PFPS-LWC method to 0.02. The top-one accuracy was used for the evaluation.

4.2. A Comparison with State-of-the-Art Methods

To validate the effectiveness of our method, we compared it with several state-of-the-art methods in the field of federated learning and conducted a comprehensive evaluation. We used P to represent the proportion of clients participating in training each round. The smaller the P, the fewer clients participated in training, increasing the likelihood of clients being offline for extended periods. In our experiments, we set P to [0.3, 0.5, 0.7] to simulate collaborative training scenarios under different participation rates. This variation in participation rates helped us understand how our method performs under different levels of client availability.

Additionally, for the Dirichlet partitioning method, the smaller the $\beta$, the greater the degree of data heterogeneity. We set $\beta$ to [0.1, 0.3, 0.5] to simulate different levels of data heterogeneity using Dirichlet partitioning methods. These parameter settings effectively simulated environments with high data heterogeneity at different participation rates, allowing us to thoroughly evaluate the robustness of our method. For the pathological Non-IID partitioning method, we set the number of classes to 5 for cifar10 and 30 for cifar100. This approach involved dividing the dataset into multiple small shards and randomly assigning these shards to different clients, resulting in significant heterogeneity in the data distribution across clients. This setup was designed to mimic real-world scenarios where data distributions can vary widely among different clients.

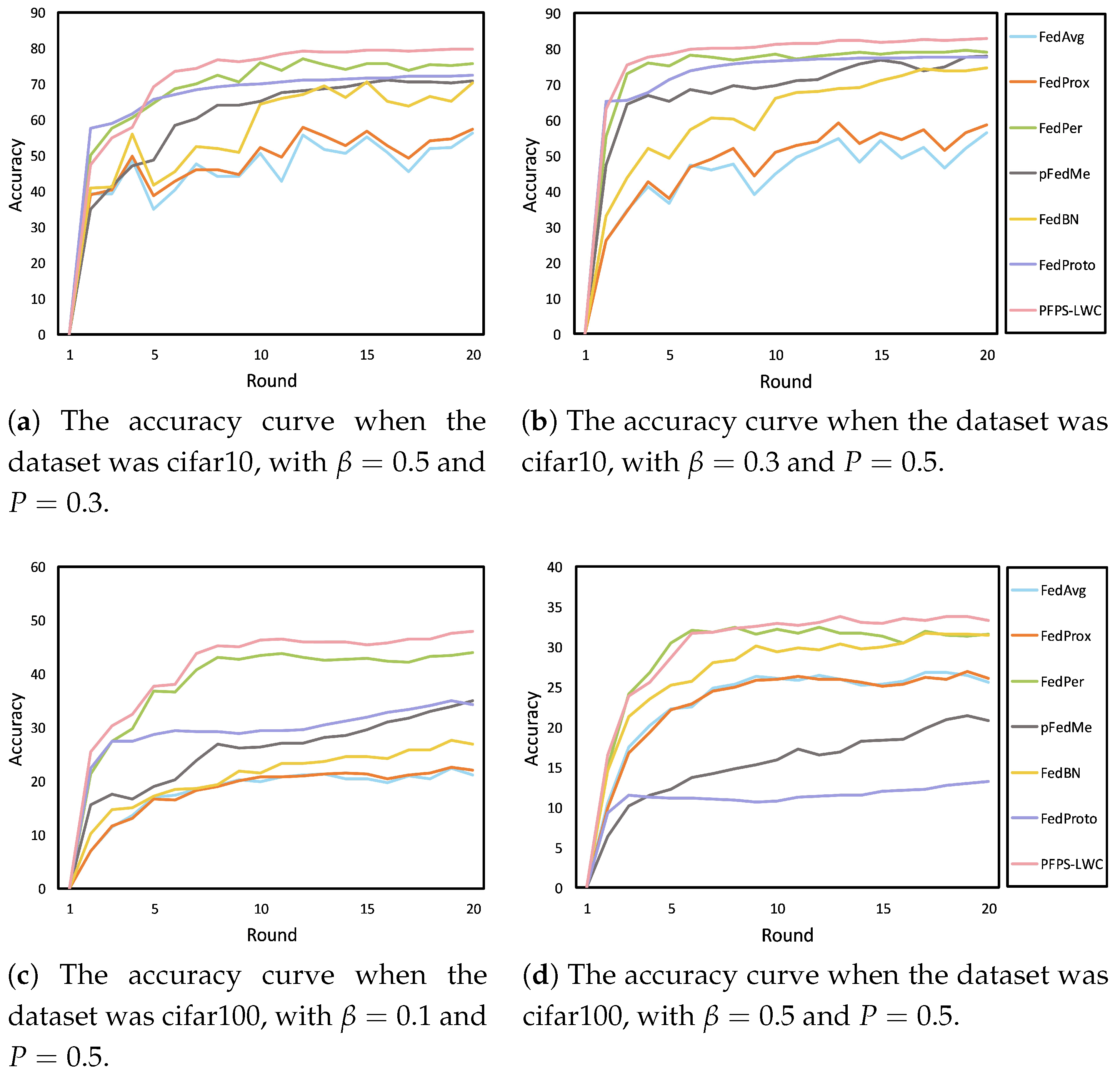
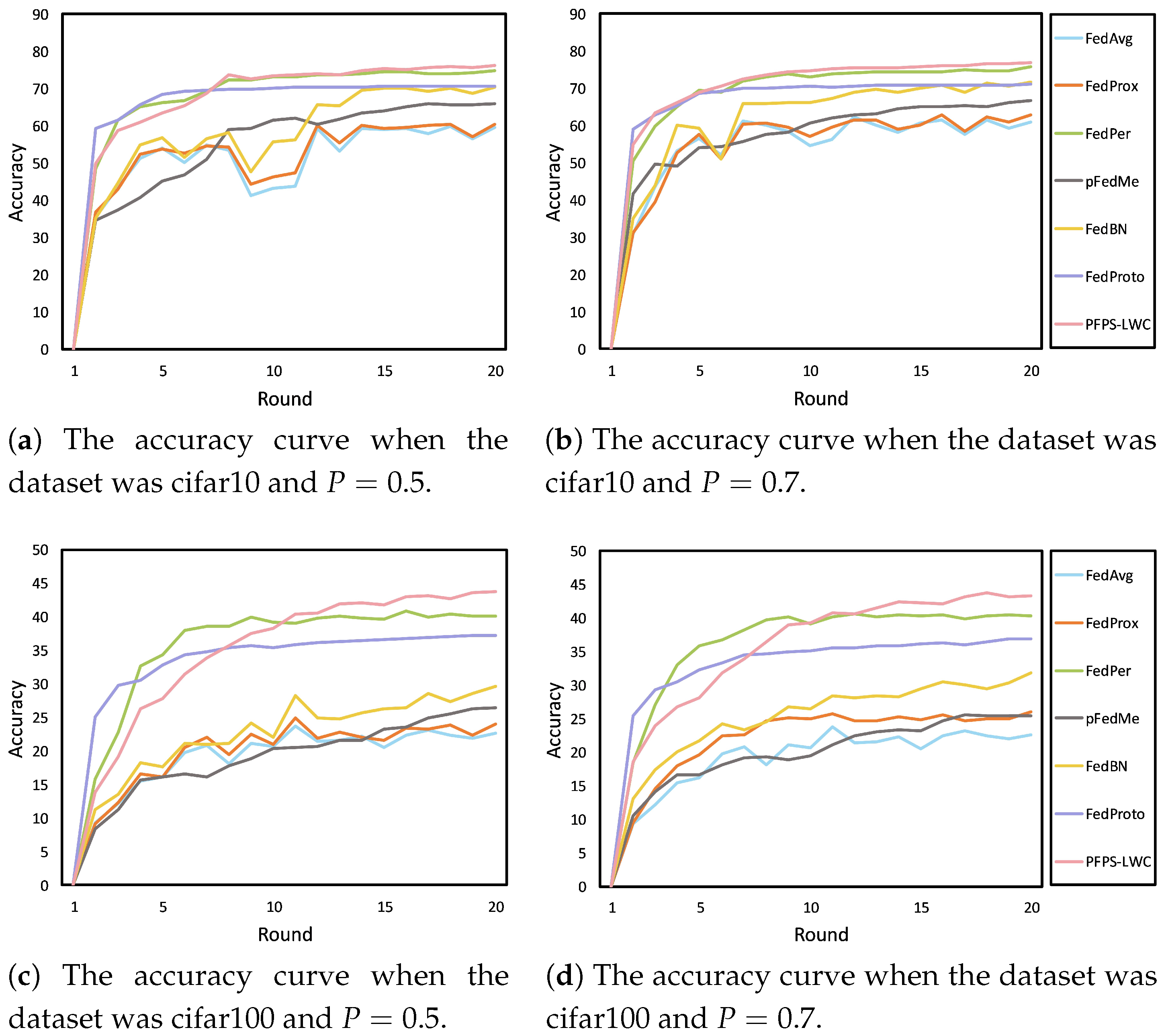
Extensive experiments were conducted in the above simulated environments. The results are shown in

Table 2. Prediction accuracy of the proposed method compared with that of state-of-the-art methods on Cifar10 using different Dirichlet settings.

Method	Accuracy⇑ Predicted with Different Settings of $\mathit{\beta }$ and P on Cifar10.
	$\mathit{\beta }=\mathbf{0.1}$			$\mathit{\beta }=\mathbf{0.3}$			$\mathit{\beta }=\mathbf{0.5}$
	$\mathit{P}=0.3$	$\mathit{P}=\mathbf{0.5}$	$\mathit{P}=\mathbf{0.7}$	$\mathit{P}=\mathbf{0.3}$	$\mathit{P}=\mathbf{0.5}$	$\mathit{P}=\mathbf{0.7}$	$\mathit{P}=\mathbf{0.3}$	$\mathit{P}=\mathbf{0.5}$	$\mathit{P}=\mathbf{0.7}$
FedAvg [29]	$33.03$	$34.54$	$52.3$	$49.17$	$56.5$	$58.95$	$56.15$	$56.36$	$54.14$
FedProx [14]	$36.35$	$40.03$	$53.84$	$52.59$	$58.79$	$59.2$	$57.34$	$58.67$	$56.86$
FedPer [20]	89.36	87.09	87.48	79.74	79.01	79.94	75.59	76.21	76.4
pFedMe [37]	87.68	86.08	86.04	77.59	75.73	69.67	70.8	71.8	71.16
FedBN [23]	67.91	84.66	85.29	72.72	74.61	73.85	70.27	72.41	72.96
FedProto [41]	88.56	88.42	89.11	76.96	77.71	77.08	72.31	72.15	72.36
PFPS-LWC	90.58	91.03	90.91	82.36	82.81	83.18	79.77	80.43	80.33
$\Delta$	1.22	3.94	3.43	2.62	3.8	3.24	4.18	4.22	3.93

,

Table 3. Prediction accuracy of the proposed method compared with that of state-of-the-art methods on Cifar100 using different Dirichlet settings.

Method	Accuracy⇑ Predicted with Different Settings of $\mathit{\beta }$ and P on Cifar100.
	$\mathit{\beta }=\mathbf{0.1}$			$\mathit{\beta }=\mathbf{0.3}$			$\mathit{\beta }=\mathbf{0.5}$
	$\mathit{P}=\mathbf{0.3}$	$\mathit{P}=\mathbf{0.5}$	$\mathit{P}=\mathbf{0.7}$	$\mathit{P}=\mathbf{0.3}$	$\mathit{P}=\mathbf{0.5}$	$\mathit{P}=\mathbf{0.7}$	$\mathit{P}=\mathbf{0.3}$	$\mathit{P}=\mathbf{0.5}$	$\mathit{P}=\mathbf{0.7}$
FedAvg [29]	$18.68$	$21.22$	$23.64$	$22.81$	$25.55$	$26.73$	$24.05$	$25.6$	$27.76$
FedProx [14]	$19.5$	$22.03$	$24.31$	$23.45$	$25.72$	$24.77$	$23.78$	$26.11$	$27.25$
FedPer [20]	43.18	43.97	44.92	37.57	37.55	36.71	31.23	31.05	31.32
pFedMe [37]	32.89	34.98	34.04	22.34	24.41	24.58	19.01	20.84	21.19
FedBN [23]	21.17	26.88	29.57	25.71	30.05	32.03	28.36	31.45	32.51
FedProto [41]	35.57	34.31	35.43	20.66	21.5	21.18	13.14	13.27	13.8
PFPS-LWC	46.84	48	48.69	40.32	39.86	40.57	33.59	34.1	33.72
$\Delta$	3.66	4.03	3.77	2.75	2.31	3.86	2.36	3.05	2.4

and

Table 4. Prediction accuracy of the proposed method compared with that of state-of-the-art methods on Cifar10 and Cifar100 using different pathological settings.

Method	Accuracy⇑ Predicted with Different Pathological Settings
	Cifar10			Cifar100
	$\mathit{P}=\mathbf{0.3}$	$\mathit{P}=\mathbf{0.5}$	$\mathit{P}=\mathbf{0.7}$	$\mathit{P}=\mathbf{0.3}$	$\mathit{P}=\mathbf{0.5}$	$\mathit{P}=\mathbf{0.7}$
FedAvg [29]	$44.78$	$59.55$	$60.99$	$20.35$	$22.64$	$25.12$
FedProx [14]	$49.28$	$60.48$	$62.76$	$20.68$	$23.94$	$26.01$
FedPer [20]	74.68	74.68	74.66	39.12	40.13	40.32
pFedMe [37]	65.17	65.9	66.78	24.68	26.43	25.38
FedBN [23]	65.16	70.5	71.75	26.6	29.56	31.88
FedProto [41]	71.05	70.74	71.01	37.19	34.31	36.86
PFPS-LWC	76.06	76.29	76.64	41.9	43.7	43.35
$\Delta$	1.38	1.61	2.22	2.78	3.57	3.03

. We report the accuracy of different methods on the cifar10 and cifar100 datasets under various conditions. These tables provide a comprehensive comparison of our method against existing approaches, highlighting its effectiveness in handling data heterogeneity and varying participation rates. In Table 2, we show the experimental results in the case where the dataset was cifar10 and the data partitioning method was Dirichlet partitioning. Notably, when $\beta$ = 0.5 and P = 0.3, PFPS-LWC surpassed the baseline by an impressive 4.18%. Moreover, PFPS-LWC achieved optimal performance in all settings, compared to other methods. When the dataset was cifar100, with $\beta$ = 0.1 and P = 0.5, as shown in Table 3, our method surpassed the baseline by an impressive 4.03%. This significant improvement highlights the effectiveness of our approach in scenarios with strong data heterogeneity and lower client participation rates.

In Table 4, we present the experimental results for cifar10 and cifar100 under pathological data partitioning. As shown in the table, our method achieved optimal results in this scenario. Specifically, when the dataset was cifar100 with $p=0.5$, PFPS-LWC surpassed FedPer’s accuracy by up to 3.57%. This demonstrates that our method is effective when the data volume is similar but the types of data differ. It also highlights the importance of retaining local knowledge to mitigate the interference from other types of knowledge.

A thorough examination of Table 2, Table 3 and Table 4 reveals a compelling observation: under various environmental settings, PFPS-LWC consistently achieved the best results on both the cifar10 and cifar100 datasets, outperforming other methods. This substantial evidence demonstrates the robustness of PFPS-LWC in highly heterogeneous environments and with varying client participation rates. Under different environmental settings, PFPS-LWC also significantly outperformed the baseline, further validating its versatility and robustness. This remarkable advantage underscores the necessity of PFPS-LWC’s improvements to the original pFL framework. It supports our viewpoint that simply using the global model to initialize local models is unreasonable. Instead, our approach, which focuses on improving the continuity of local training and alleviating local knowledge forgetting, proves to be more effective. By ensuring that local models retain valuable knowledge from previous training rounds and seamlessly integrate global information, PFPS-LWC enhances the overall effectiveness of federated model training.

Additionally, compared to traditional federated learning methods like FedAvg [29] and FedProx [14], our method significantly outperformed them. In extreme heterogeneous conditions with $\beta =0.1$ and $P=0.3$, as shown in Table 3, our method exceeded their accuracy on the cifar10 dataset by an impressive 57.55% and 54.23%, respectively. These substantial improvements highlight the effectiveness of our approach in handling highly heterogeneous data distributions and low client participation rates. This further underscores the potential of PFPS-LWC as a robust solution for federated learning in extremely heterogeneous environments. The ability of our method to maintain high accuracy under such challenging conditions demonstrates its versatility and robustness.

In addition, we present the accuracy curves of different methods during the training process in Figure 5 and Figure 6. These figures provide a direct comparison of the convergence behavior and stability of our method versus those of others across different heterogeneous environments. As shown in both figures, our method achieved faster convergence compared to that of the other methods, highlighting its efficiency in reaching optimal performance. This is particularly evident in the rapid rise in accuracy in the early stages of training, which suggests that our model is able to quickly adapt to local data distributions.

Moreover, both figures consistently demonstrate smaller fluctuations in the accuracy curves for our method. This stability across both figures is a key feature indicating that our model maintains consistent performance throughout the training process, avoiding common issues such as overfitting or underfitting. The reduced fluctuations across both figures can be interpreted as a result of incorporating more local knowledge into the model, which helps it better adapt to the specific characteristics of each client’s data. This dual advantage, faster convergence and improved stability, further reinforces the effectiveness and robustness of our approach, making it well suited to handle the challenges posed by data heterogeneity in federated learning environments.

4.3. Ablation Experiments

To validate the effectiveness of Module 3.2 (the Progressive Local Training Strategy) and Module 3.3 (the lightweight classifier), we conducted a series of ablation experiments. These experiments were performed on the cifar10 dataset with $\beta =0.5$ and $P=[0.3,0.5,0.7]$, as well as on the cifar100 dataset with $\beta =0.5$ and $P=[0.3,0.5,0.7]$. By varying these parameters, we aimed to simulate different levels of data heterogeneity and client participation rates, providing a comprehensive evaluation of our proposed modules.

The results of these ablation experiments are presented in

Table 5. Ablation study: ✓ indicates module usage, × indicates module non-usage.

Module		Cifar10 ($\mathit{\beta }=\mathbf{0.5}$)			Cifar100 ($\mathit{\beta }=\mathbf{0.1}$)
PLT	LWC	$\mathit{P}=\mathbf{0.3}$	$\mathit{P}=\mathbf{0.5}$	$\mathit{P}=\mathbf{0.7}$	$\mathit{P}=\mathbf{0.3}$	$\mathit{P}=\mathbf{0.5}$	$\mathit{P}=\mathbf{0.7}$
×	×	75.59	76.21	76.4	43.18	43.97	44.92
✓	×	79.13 (3.54)	79.32 (3.11)	78.9 (2.52)	45.87 (2.69)	45.9 (1.93)	46.64 (1.72)
×	✓	76.87 (1.28)	77.15 (0.94)	78.26 (1.86)	44.31 (1.13)	46.12 (2.15)	46.95 (2.03)
✓	✓	79.77 (4.18)	80.43 (4.22)	80.33 (3.93)	46.84 (3.66)	48 (4.03)	48.69 (3.77)

below. This table illustrates the overall effectiveness of the different modules, highlighting the contributions of each component to the performance of our method. By isolating the impact of the Progressive Local Training Strategy and the lightweight classifier, we could better understand their individual and combined effects on the model accuracy and stability.

From the table, we can observe that both modules improved the algorithm’s performance to varying degrees. For instance, on the cifar10 dataset, the Progressive Local Training (PLT) module, with $\beta =5$ and $P=0.3$, showed a 3.53% improvement over the baseline. This improvement highlights the effectiveness of the PLT module in enhancing the model’s ability to retain and utilize local knowledge, thereby improving its performance in heterogeneous environments. On the cifar100 dataset, the lightweight classifier (LWC) module, with $\beta =0.1$ and $P=0.5$, demonstrated a 2.15% improvement over the baseline. This result underscores the importance of regularizing the classifier head, which undergoes prolonged local training. By incorporating an LWC, the classifier’s generalization capability is enhanced, leading to better overall performance.

These experiments demonstrate that both modules significantly enhance the performance of our method, particularly in environments with high data heterogeneity and varying client participation rates. The Progressive Local Training Strategy helps to maintain continuity in local training, while the LWC improves the generalization capability of the classifier. Together, these modules contribute to a more robust and effective federated learning framework.

4.4. Hyperparameter Sensitivity Analysis

Our method involves only one hyperparameter, $\lambda$, which controls the weight of the L2 regularization term in the LWC. To determine the optimal value of $\lambda$, we conducted a series of experiments on the cifar10 dataset with $\beta =0.5$ and $P=0.5$. We explored a range of values for $\lambda$ to observe its impact on the model performance. In the range [0, 0.1], we used a step size of 0.02 to finely tune the regularization weight. For the range [0.1, 0.3], we increased the step size to 0.05 to cover a broader spectrum of values. Finally, in the range [0.3, 1], we used a step size of 0.1 to efficiently explore higher values of $\lambda$. This systematic approach allowed us to comprehensively evaluate the effect of $\lambda$ on the model’s accuracy.

As illustrated in Figure 7, the algorithm exhibited relatively stable performance and notable improvement when the $\lambda$ parameter fell within the range of [0, 0.2]. This indicates that moderate regularization helps enhance the model’s generalization capability without overly constraining it. However, as $\lambda$ increased beyond this range, the performance showed a fluctuating decline. This degradation in performance with larger $\lambda$ values can be primarily attributed to the increased weight of the regularization term, which causes the optimization of the overall loss function to overly favor the regularization of the classifier. This excessive regularization can hinder the model’s ability to learn effectively from the local data.

Therefore, it is recommended to utilize $\lambda$ values within a smaller range to achieve optimal performance. Furthermore, the overall fluctuation range of the algorithm’s performance remained relatively small across different ranges of $\lambda$, indicating the algorithm’s stability and providing a higher fault tolerance for the selection of the $\lambda$ parameter. This stability is crucial for ensuring consistent performance across different training scenarios and data distributions.

4.5. Discussion of Other Parameters

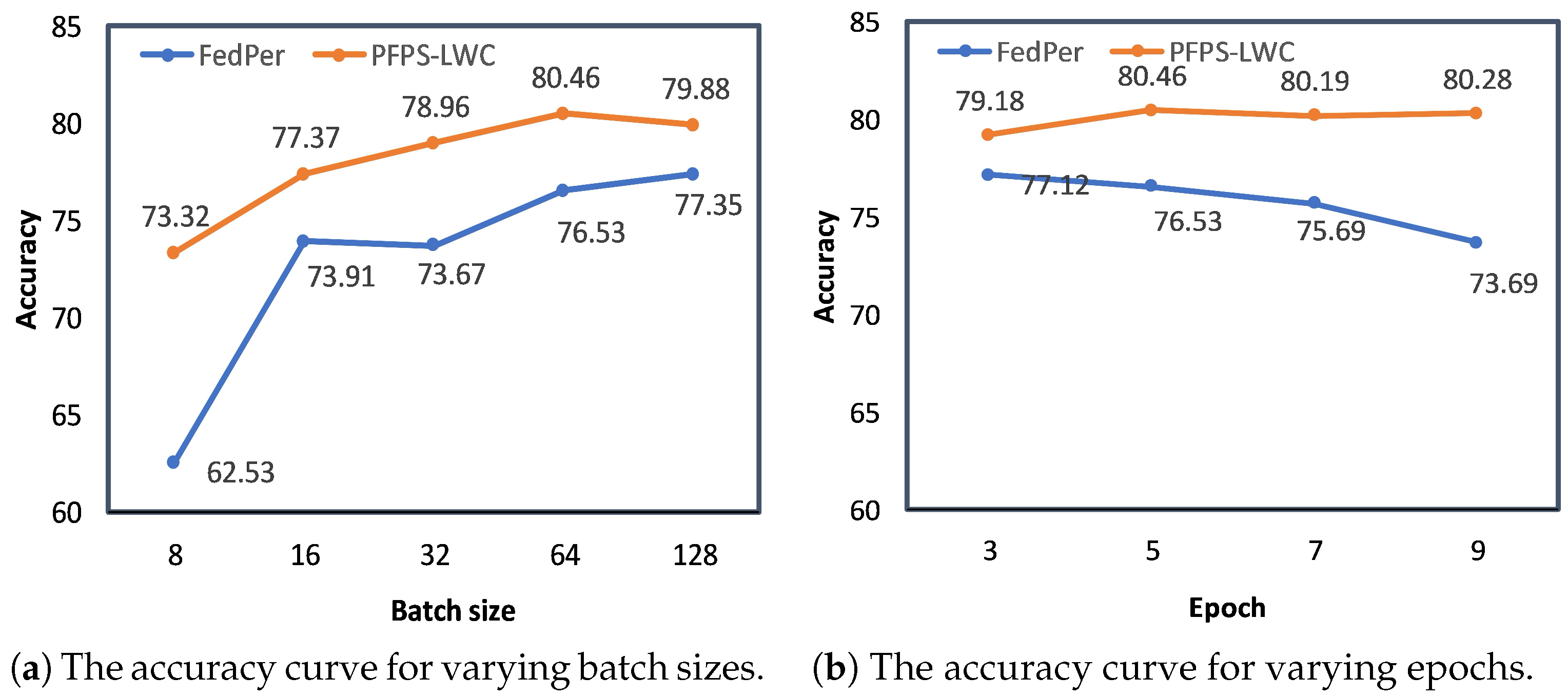
To further validate the robustness of our method under highly heterogeneous conditions, we conducted experiments with parameter settings that were independent of our algorithm. Specifically, we chose the parameters batch size and local training epochs, E. By varying the ranges of the batch size and E, we assessed the performance of the algorithm under different conditions. These experiments were conducted on the CIFAR10 dataset with $\beta$ set to 0.5 and P set to 0.5. In the experiments, the $batch-sizes$ were set to [8, 16, 32, 64, 128], and the values for E were set to [3, 5, 7, 9]. By exploring these different configurations, we aimed to understand how our method performs with varying batch sizes and training epochs, which are critical factors in the training process. The results of the experiment are shown in the figure below. These results provide insights into the stability and effectiveness of our method across different training settings.

Firstly, the batch size has a significant impact on model training. Generally, larger batch sizes lead to better training performance; however, this can be difficult to achieve for clients with limited computational resources. As shown in Figure 8a, when the batch size was small, the traditional personalized federated learning method FedPer performed poorly in local training. In contrast, PFPS-LWC significantly improved the local training performance with smaller batch sizes, surpassing FedPer in accuracy by 10.79%. This indicates that our method effectively mitigates the shortcomings of traditional personalized federated learning frameworks in resource-constrained environments. Furthermore, PFPS-LWC consistently outperformed FedPer across different batch sizes, demonstrating the robustness of our method under various settings.

The local epochs also play a crucial role in the local training performance. As shown in Figure 8b, the performance of traditional personalized federated learning was highly sensitive to the number of local epochs, with FedPer’s accuracy fluctuating significantly across different ranges. In contrast, PFPS-LWC exhibited much smaller fluctuations and consistently outperformed FedPer in terms of accuracy. Notably, when E = 9, PFPS-LWC surpassed FedPer by 6.59% in terms of accuracy. This not only highlights the stability of PFPS-LWC across different numbers of local epochs but also demonstrates its superiority over FedPer.

These findings underscore the effectiveness of our method in various training scenarios. By maintaining high performance with smaller batch sizes and exhibiting stable accuracy across different numbers of local epochs, PFPS-LWC proves to be a robust and adaptable solution. This robustness is particularly valuable in real-world federated learning environments, where computational resources and data distributions can vary widely among clients.

4.6. Analysis of Results and Future Research

Through extensive experiments, we have validated the effectiveness of the PFPS-LWC approach in personalized federated learning, particularly in addressing critical challenges such as data heterogeneity and fluctuations in client participation rates. We conducted experiments on the cifar10 and cifar100 datasets, using various data partitioning methods, including Dirichlet and pathological Non-IID partitioning. The results show that PFPS-LWC performs exceptionally well across different environmental settings, significantly outperforming existing methods, thus demonstrating the robustness of our approach.

In scenarios with varying data distributions and participation rates, PFPS-LWC exhibits greater adaptability compared to traditional federated learning methods. By employing Progressive Local Training Strategies and lightweight classifiers, PFPS-LWC effectively enhances the client’s local model performance and significantly improves the accuracy and stability of the global model. Moreover, in environments with limited computational resources and high data heterogeneity, PFPS-LWC shows notable advantages, demonstrating its strong robustness and generalization capability.

Despite its strong performance, PFPS-LWC has some limitations. In scenarios with extremely high data heterogeneity, there is still potential for further performance improvements. Future work could focus on refining the knowledge recall mechanism to enhance the model’s adaptability and stability in such challenging environments. Additionally, while PFPS-LWC has been evaluated on visual datasets like cifar10 and cifar100, its applicability could be extended to more complex, domain-specific datasets, such as medical or IoT data, to assess its broader effectiveness.

Regarding changes in the model architecture, we recognize that different network architectures can impact both the results and conclusions of the model. The five-layer CNN architecture we are currently using performed well in our experiments and is widely applied in related research. However, with changes in the network architecture (such as adding or removing layers or altering the number of neurons per layer), the model’s performance and the convergence speed of the global model may vary. Altering the architecture could lead to improvements or declines in performance, depending on the model’s complexity, the nature of the training data, and computational resource limitations. Theoretically, however, the PFPS-LWC method is a systematic approach, and its performance is less affected by structural changes. Therefore, future research could explore the impact of different architectures on the effectiveness of PFPS-LWC and further optimize the architectural design to enhance performance across different data distributions and application scenarios.

Future research can focus on several key areas: first, further optimizing the knowledge recall mechanism to address challenges posed by extreme data heterogeneity; second, enhancing the computational efficiency of the model, particularly for edge computing and IoT devices, to reduce computational and storage burdens; and finally, exploring the potential of PFPS-LWC in cross-domain applications (such as healthcare, autonomous driving, etc.), with a focus on data privacy protection and real-time adaptability.

5. Conclusions

In this paper, we explored the critical issues of local knowledge discontinuity and local classifier overfitting in existing personalized federated learning frameworks. These challenges can significantly hinder the performance and generalizability of federated learning models, especially in environments with highly heterogeneous data. To address these problems, we introduced the PFPS-LWC method, which specifically targets and alleviates these challenges. By employing a Progressive Local Training Strategy, we achieved the local correction of the global model’s parameters, thereby enhancing the continuity of local knowledge. This strategy ensures that the model retains valuable local information across training rounds, improving its ability to generalize and perform well on diverse data distributions. Additionally, we incorporated a lightweight classifier by adding a regularization term to the loss function. This approach mitigates the overfitting of local classifiers, ensuring that they do not become overly specialized to the local training data. By balancing the regularization term, we enhanced the generalization capability of the classifiers, leading to more robust and effective models.

Through extensive experiments, we comprehensively validated the effectiveness and robustness of PFPS-LWC. Our experimental results demonstrated significant improvements in the model performance across various settings, highlighting the method’s ability to handle data heterogeneity and varying client participation rates. We hope that our work provides new insights for future research on personalized federated learning in the context of highly heterogeneous data. By addressing the inherent flaws in existing frameworks and proposing a robust solution, we aim to advance the field and contribute to the development of more effective federated learning systems.