Abstract
The accurate prediction of structural performance in sheet-metal components is critical for optimizing design and ensuring reliability in engineering applications. This study emphasizes the necessity of incorporating non-uniformities induced by stamping processes, such as thickness variation and work-hardening effects, into Finite Element Method (FEM) simulations. Experimental and computational analyses reveal that neglecting these variations results in significant discrepancies, particularly in displacement predictions, where deviations exceeding 50% were observed at specific points. While elastic behavior showed reasonable agreement with experimental results, plastic deformation predictions were notably less accurate due to the inherent inhomogeneities of the real work-hardening model compared to the uniform assumptions in standard FEM models. These findings underscore the need for improved methodologies in mapping stamping-induced material properties and validating simulation results. Further refinement of mapping accuracy and validation techniques is essential for enhancing the predictive capabilities of FEM simulations for complex sheet-metal components.
1. Introduction
The accurate prediction of mechanical behavior in sheet-metal components is crucial for the design and validation of safety-critical structures in industries such as transportation, automotive, and aerospace [1,2]. Since simulations with Finite Element Method (FEM) can accurately model complicated geometries and loading conditions, they are frequently used for this purpose [3,4]. However, traditional FEM models assume homogeneous material properties, failing to implement the local variations that occur during manufacturing processes such as stamping [5]. This simplification causes discrepancies between simulated and experimental results, particularly for components with large deformations and complex loading scenarios [6,7,8,9]. In fact, sheet-metal stamping introduces significant non-uniformities in mechanical properties, including localized thinning, strain hardening, and anisotropy [10,11,12,13], which can impact the structural performance of the component, especially under high loads where yield strength and thickness variations play a crucial role [14,15,16].
Nonlinear FEM has proven to be accurate, offering the capability to account for anisotropy and yield criteria, and to model the springback phenomenon [17]. There are also many studies investigating the different types of plane stress and strain in sheet-metal forming. Andersen et al. [18] analyzed the ductile fracture of thin metal plates, showing that fracture strain is significantly higher in plane strain bending than in far-field tension due to differences in localization mechanisms and stress states, with implications for material design and predictive modeling. Tekkaya et al. [19] investigates the potential of metal forming processes not only to shape products but also to predict and control their mechanical and physical properties throughout the manufacturing chain. The paper highlights how advancements in analytical and measurement techniques allow for accurate prediction and deterministic setting of properties such as hardness, residual stress, formability, and anisotropy during forming processes. Wang et al. [20] introduced a Lode-dependent anisotropic–asymmetric hardening model (LAA-Yld91) for metals to precisely characterize anisotropic hardening and tension–compression asymmetry under diverse loading conditions. By coupling two Yld91 anisotropic functions with a Lode-dependent weight function and optimizing parameters via a neural network, the model demonstrates high accuracy in predicting yield surface evolution for various alloys, including Ti-6Al-4V, DP980, and AA 5754-O, with applications in advanced metal forming simulations. A detailed study on simple shear tests demonstrates their effectiveness in characterizing the plastic anisotropy of rolled metal sheets under large strains. By optimizing specimen geometry and clamping techniques, the research improves stress and strain homogeneity, leading to more accurate evaluations of anisotropic hardening behavior essential for constitutive modeling and forming process simulations [21]. Tardif and Kyriakides [22] emphasized the significance of a systematic approach that integrates experimental methods with FEM analysis to determine material properties under large strains. In fact, sheet-metal subjected to plastic deformation during stamping is not characterized by uniform properties due to the inherent anisotropies introduced during the rolling process of the sheet. The study calibrates the parameters of a non-quadratic yield function, which is subsequently used to enhance the accuracy of tensile test simulations. Ailinei et al. [23] examine the impact of anisotropy on the vibration behavior of S600Mc sheet-metal, highlighting its importance in plastic deformation simulations. Their study combines experimental vibration tests at various orientations with finite element analysis, demonstrating the influence of anisotropy on structural damping and its implications for high-cycle fatigue performance. Ignoring these variations can result in over-designs or unexpected failures during physical testing. As a result, bridging the gap between simulations and structural analyses is essential for improving simulation accuracy and reducing the number of expensive experimental validations.
This paper presents a novel approach to improve FEM structural simulations by integrating non-uniform mechanical properties derived from stamping simulations, focusing on a railway passenger seat structure, which is a critical component governed by strict safety standards such as AFNOR NF F 31-119 [24]. The methodology involves simulating the stamping process to predict local variations in thickness and yield stress, mapping these properties into the structural FEM model, and validating the results against experimental static tests. By incorporating real-world material behavior into FEM analyses, this approach provides more realistic predictions of deformation, stress distribution, and residual plasticity.
The objectives of this work are threefold:
- To develop a robust workflow for mapping stamping-induced property variations into structural FEM models;
- To evaluate the impact of mapped properties on the accuracy of FEM simulations compared to uniform-property models;
- To validate the mapped FEM simulations against experimental data, highlighting improvements in predictive capability.
2. Materials and Methods
This study focuses on enhancing the accuracy of structural FEM simulations by incorporating the material property variations introduced during the stamping process. The methodology integrates multiple steps, as shown in Figure 1, starting with the simulation of the stamping process, which forms the foundation for accurately extracting non-uniform properties, such as thickness and strain distributions. These properties are critical for understanding the material behavior of the component. The stamping simulation was performed using specialized software to model the deformation of sheet-metal under realistic manufacturing conditions. The material’s behavior was assumed to be elastic–plastic, and we recorded changes in thickness and strain accurately. The simulation outputs provided key insights into localized thinning and stress variations, which were crucial for the upcoming analysis. To ensure reliability, the simulation results were validated using simplified calculations and comparisons with published studies.
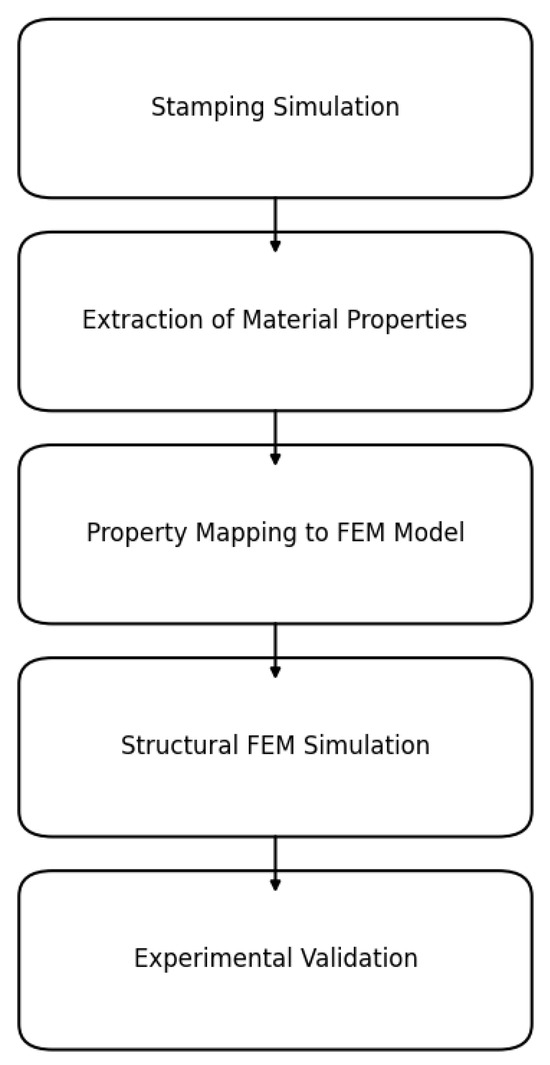
Figure 1.
Workflow for integrating stamping simulation with FEM analysis and experimental validation.
The next step was property mapping, which was used as a connection between the stamping simulation and the structural FEM analysis, where we implemented the non-uniform properties obtained from the stamping simulation directly in the FEM model. Then, a custom script was developed to process the simulation outputs and convert them into a format compatible with FEM software Altair Hyperworks 2021.1. Afterward, the mapped properties were assessed for accuracy using visualization methods, ensuring that critical regions of high deformation were accurately represented in the structural model.
Considering mapped material properties, the structural FEM model was developed to simulate the performance of the stamped component under static loading conditions defined by relevant standards. The model included precise geometry and boundary conditions to replicate experimental setups, where two types of material behavior were considered: linear elastic and nonlinear with plastic deformation and strain hardening. The nonlinear model captured the residual plasticity and stress redistributions, providing more accurate predictions of structural performance.
Finally, experimental validation was conducted to compare the FEM predictions with physical tests. The stamped component was subjected to static loads, and displacement measurements were taken at key points using precise instrumentation. The experimental data were then compared with FEM results to evaluate the accuracy of the simulations.
3. Stamping Simulation and Property Mapping
The stamping simulation forms the foundation for integrating non-uniform mechanical properties into structural FEM models. This simulation was conducted using Altair HyperForm with the Radioss One-Step solver, a tool well suited for efficiently predicting deformation and strain distributions in sheet-metal forming processes.
3.1. Material Specifications
Low-carbon steel, the composition of which is reported in Table 1, is commonly used in railway seat structures due to its favorable mechanical properties, and was selected as the material. The mechanical properties are reported in Table 2.

Table 1.
Chemical composition of the material.

Table 2.
Mechanical properties of the low-carbon steel.
3.2. Simulation Setup
The simulation assumed idealized stamping conditions, including a friction coefficient of 0.15 between the sheet and the die, an approximated blank holder force to provide sufficient constraint, and a simplified die geometry to match the seat’s key features while ensuring computational efficiency. Uniform material properties were used initially, with no pre-existing strain or stress. The sheet-metal was modeled with a quadrilateral mesh optimized to capture local thinning and strain concentrations while maintaining computational efficiency, and the mesh size was carefully selected to balance accuracy and computational cost, as shown in Figure 2a. Critical regions expected to experience high deformation, such as corners and edges, were assigned to a finer mesh with an average element size of 1.0 mm, while regions with lower strain gradients were meshed more coarsely with an element size of up to 5.0 mm. This controlled local mesh refinement method ensures sufficient resolution in high-stress areas without increasing computational time. Other solid elements are meshed using a hexahedral mesh element.
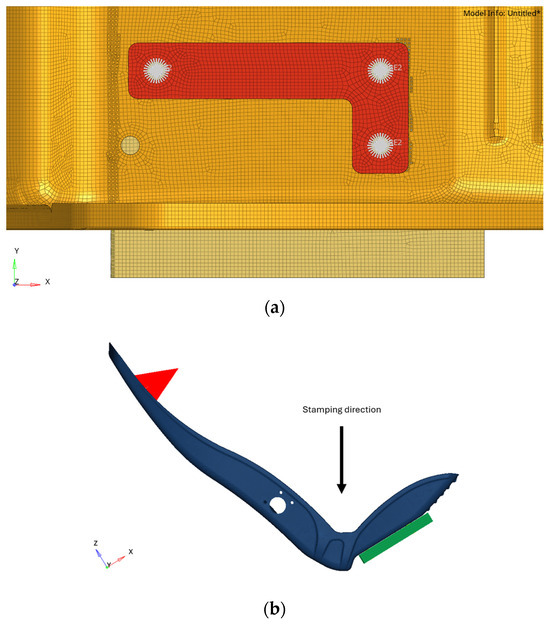
Figure 2.
Stamping simulation, (a) mesh part and (b) stamping direction.
The solver employed an implicit time-stepping method, treating the stamping operation as a quasi-static process with negligible dynamic effects. Key assumptions included elastic–plastic material behavior modeled with an isotropic hardening law, the simplification of the process to a single stamping step approximating the final geometry, as shown in Figure 2b, and the exclusion of thermal effects by assuming room-temperature stamping. This method is particularly beneficial during the initial stages of product design, as it simplifies the simulation process and enhances speed [25,26].
3.3. Simulation Outputs
The simulation outputs provided essential data for downstream FEM modeling, including the following:
- The thickness distribution map reveals localized thinning and thickening, as shown in Figure 3a, ranging from −23.4% to +43.3%, relative to the initial sheet thickness of 1.2 mm. This means that in the most deformed regions, the local thickness is reduced to approximately 0.92 mm (1.2 mm × 0.77), while in thickened areas, it reaches a maximum of approximately 1.72 mm (1.2 mm × 1.43). The red areas (thinning above 37.3%) are concentrated around sharp bends and edges, indicating significant stretching and potential failure risks. In contrast, blue areas (thinning below 6.9%) represent flatter regions with minimal deformation. The major strain distribution confirms these findings, as shown in Figure 3b, with strain values from −6.87 × 10−2 to 8.77 × 10−1, showing high-strain zones at upper edges and corners subjected to tensile forces. Together, these maps identify critical areas prone to thinning and stress, essential for evaluating structural integrity.
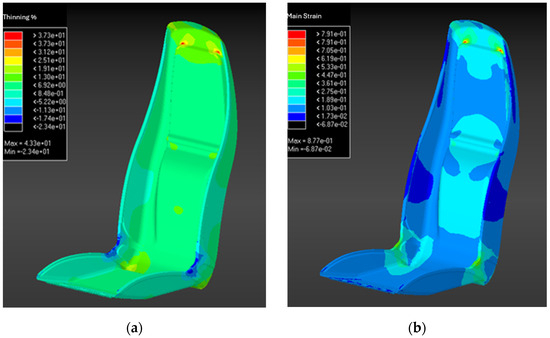 Figure 3. Stamping simulation, (a) thickness distribution and (b) strain values.
Figure 3. Stamping simulation, (a) thickness distribution and (b) strain values.
- Figure 4 displays the effective stress distribution across the stamped seat, highlighting regions of varying stress intensity under simulated loading conditions. The stress values range from a minimum of 14.5 MPa (blue regions) to a maximum of 567 MPa (red regions), as indicated by the color gradient in the scale. Regions experiencing the highest stress concentrations, represented by red and yellow zones, are primarily located around sharp bends, edges, and connection points. These areas are subjected to significant tensile and compressive forces during the stamping process, making them critical zones for potential material failure or yielding. On the other hand, blue and green regions, which exhibit lower stress levels, correspond to relatively flat areas or sections with less deformation, where the material retains its original integrity more effectively.
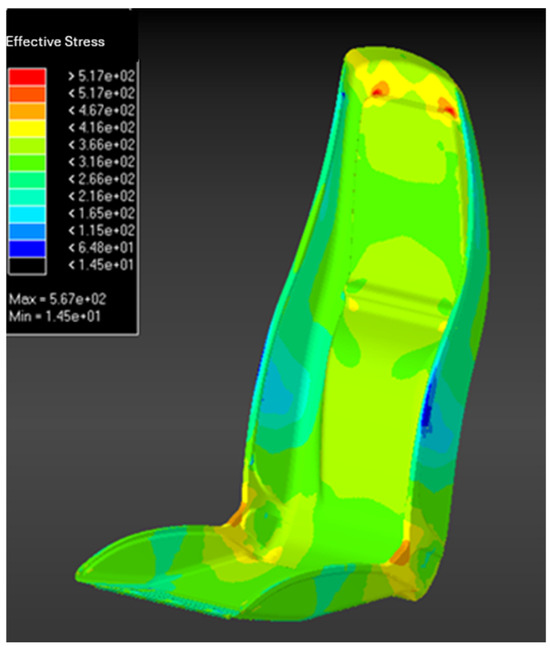 Figure 4. Effective stress resulting from the stamping simulation.
Figure 4. Effective stress resulting from the stamping simulation.
3.4. Validation and Quality Control
The validation of the stamping simulation was performed using the Gom Argus system by Zeiss Spa, Oberkochen, Germany, which combines optical measurement with dedicated software for accurate strain analysis. This process began with the preparation of the sheet-metal, where a pattern of equidistant points was engraved using laser technology to serve as markers for orientation during the analysis, as shown in Figure 5a. After stamping the part under the same conditions as those of the simulation, the surface was cleaned to ensure accurate data acquisition, as shown in Figure 5b. The Gom Argus system captured images from multiple angles, constructing a 3D representation of the part’s surface in real time, highlighting any areas requiring further imaging for completeness. The acquired data were then compared to the simulation results in a post-processing phase. As shown in Figure 6, the comparison between the scanned and simulated strain distributions revealed that while the overall correlation was within ±0.5%, significant localized differences were observed, particularly in high-strain regions. These discrepancies are evident in the red zones of the scanned model, which indicate higher strain concentrations compared to the simulation results. The primary reason for this deviation is that the simulation model assumes idealized boundary conditions and material behavior, while the physical stamping process introduces localized effects such as strain localization, friction variations, and microstructural anisotropies, which are difficult to fully replicate in a numerical model.

Figure 5.
Sheet-metal: (a) raw sheet with engraved equidistant points and (b) stamped part.
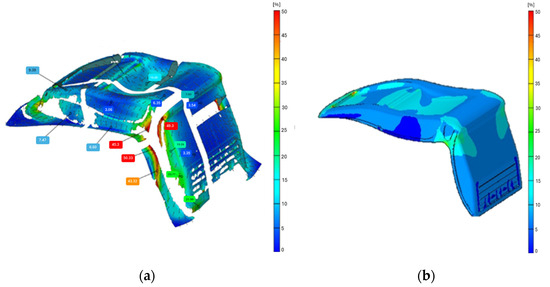
Figure 6.
Comparison between (a) scanned and (b) simulated strains.
Additionally, the simulation does not account for secondary deformations or slight misalignments that may occur during the physical stamping process. The optical strain measurement system captures real-world irregularities, whereas the FEM model relies on idealized constraints that may lead to a slightly more uniform strain distribution. While these localized discrepancies are present, the overall accuracy remains within acceptable engineering limits, and the simulation results are still considered representative for structural performance assessments. Future refinements may include more detailed modeling of friction effects, anisotropic hardening, and secondary deformation mechanisms to further reduce these discrepancies.
This validation confirms the reliability of the stamping simulation for predicting the material behavior of the component, ensuring sufficient alignment with real-world conditions to optimize the design and manufacturing processes.
3.5. Property Mapping
The process of mapping the stamping simulation results in the structural FEM model is illustrated in Figure 7. The process began with the use of the Result Mapper tool in Hypercrash software of Altair Hyperworks 2021.1, which automatically maps thicknesses, stresses, and strains directly onto the FEM mesh. To simplify the process, the same FEM mesh was used for both stamping and structural models, ensuring seamless compatibility. The stamping simulation outputs were exported into two separate files: the first, in OptiStruct format (.fem), contained nodal and element thickness data, while the second, in Radioss format (.sta), held the strain data for each element. These files were processed using a custom Octave/Matlab script, referred to as the Mesh program. The script extracted the element IDs, thicknesses, and strain results from the stamping simulation data and calculated the corresponding stress vector based on the elastoplastic hardening model. This allowed for the adjustment of yield strength at the element level, accounting for localized hardening effects induced during stamping. To ensure accurate mapping, a comparison mechanism was incorporated into the script, analyzing individual elements and assigning material properties through Property Cards and Mat Cards. These cards defined the mechanical behavior of each element, including parameters such as Young’s modulus, Poisson’s Ratio, material density, hardening slope, and yield stress. By organizing material properties in ascending order and visually inspecting the results, the mapping ensured that each element accurately reflected the stamping-induced changes in geometry and material behavior. The complete workflow is represented in Figure 7.
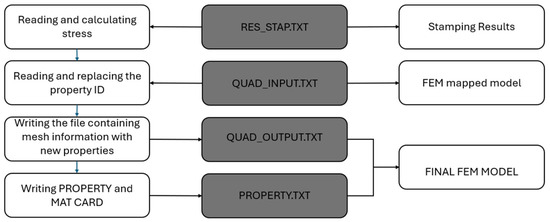
Figure 7.
Workflow for stress calculation, property mapping, and FEM model generation.
The mapped model was validated through visual representation, where each element was color-coded based on its assigned material properties. This visualization facilitated quick checks to confirm the correct assignment of properties.
4. Method Validation
4.1. Simulation
Based on the seat geometry and material property distribution obtained from the stamping forming in Section 3, a structural FEM model was developed to conduct a virtual verification of structural performance and simulate the static and dynamic tests required by the AFNOR NF F 31-119 and EN 12663-1 standards [24,27]. The AFNOR NF F 31-119 standard defines the test conditions for approving both passenger and driver seats, applying conventional loads at specific points on the seat. Conversely, the EN 12663-1 standard provides guidelines for additional equipment and their fixation, with loads applied at the center of gravity and scaled proportionally to the total weight of the seat, including the occupant. For the tests focusing solely on the sheet-metal part, the AFNOR NF F 31-119 standard was used as the primary reference.
The test procedure defined by the AFNOR NF F 31-119 standard involves applying a constant force of 1500 N to the center of the upper backrest in a front-to-back direction, as shown in Figure 8. The yellow sheet-metal seat is bolted to the red base floor of the test room using six virtual screws, while vertical movements are restricted by purple L-plates connected to the base. The load is applied via a blue pad, simulating realistic loading conditions. This setup tests the unreinforced sheet-metal part under particularly high forces, pushing it to the limits of its structural integrity. In the stamping simulation, the holes in the component remain unfilled, as these regions are critical for capturing stress concentrations and serve as interfaces for connections or constraints. Around these holes, elements are thickened to form washers, enhancing local stiffness and accommodating increased stress. The meshing process begins with a two-dimensional (2D) mesh created on one face of the component. Using the Solidmap tool, this mesh is extruded into a 3D hexahedral (brick) element mesh, providing precise geometric representation and ensuring accurate stress and deformation analysis during simulation. Table 3 summarizes the material properties and mathematical models used for different structural components, including steel sheet-metal, solid parts, and M8 screws.
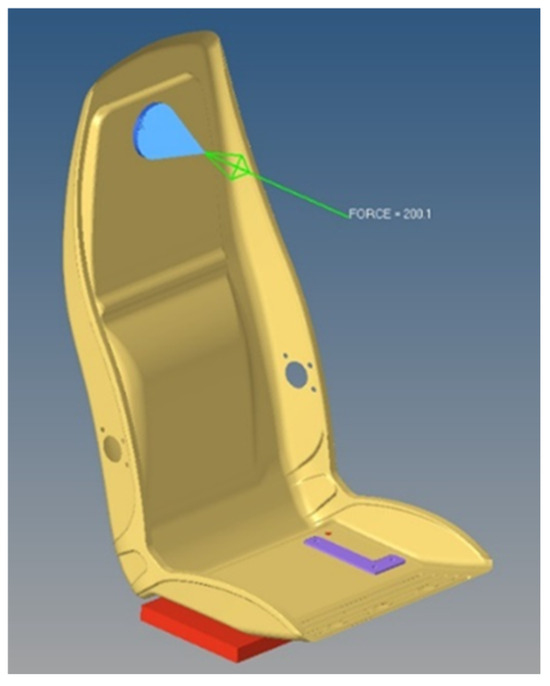
Figure 8.
Simulation setup with respect to AFNOR NF F 31-119 standard.

Table 3.
Material properties and mathematical models for structural components.
Figure 9 illustrates the balance of forces and reactions on the seat’s sheet-metal. A blocked constraint contact, simulating a welded connection between components, significantly increases stiffness, effectively treating the seat as if it were welded to the base. The base, with a thickness of 20 mm, is modeled as particularly rigid. However, this type of contact overlooks stress hot spots, especially those near the edge of the base and the L-Plate, where constraint reactions occur. In practice, the screws do not create constraint reactions but instead generate significant friction forces through tightening, which induce large reaction forces between the components. In the FEM model, relative translation along the X-axis between the body and the L-Plate is constrained using a TIE contact. This contact is connected to the base through Beam and RBE2 elements, ensuring that it remains rigidly constrained. The nonlinear modeling captures these behaviors, providing a more realistic representation of stress distributions and yielding in critical regions.
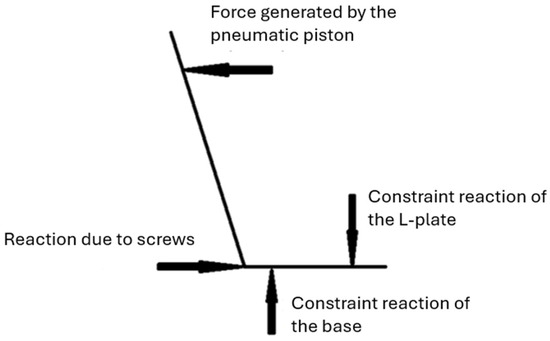
Figure 9.
Free body diagram showing forces and reactions.
The structural analysis involves two primary loads: a force applied along the negative X-direction and the gravitational force. The gravitational force primarily serves to simulate springback behavior in the unloaded state, ensuring that the model reflects real-world relaxation effects post-deformation. Constraints were applied to the plate by selecting all nodes on its lower surface and blocking translations in the X, Y, and Z directions, as detailed in Table 4. This constraint setup accurately represents the physical conditions of the test, allowing the model to simulate the component’s response under applied loads while maintaining stability and structural integrity during the analysis. Table 5 also summarizes the loading details.

Table 4.
Contact definition and constrained degrees of freedom (DOFs) for structural parts.

Table 5.
Load and constraint definitions with linear and nonlinear modules.
The evaluation of the structural performance of the stamped sheet-metal component was conducted using two distinct modeling approaches: linear and nonlinear models. These models were designed to investigate the impact of thickness mapping and material property definitions on the accuracy and reliability of the FEM predictions. Comparing the results of linear and nonlinear analyses provided insights into the elastic and elastoplastic behavior of the component, enabling a more comprehensive understanding of its response to applied loads. The linear models focused on the elastic range of the material, while the nonlinear models captured yielding and stress redistribution in critical areas, incorporating localized effects derived from the stamping simulation data.
Two linear models were developed to assess the influence of thickness mapping on the component’s elastic behavior. The linear simulation model used two different thickness assumptions: one assuming a uniform initial thickness of 1.2 mm, and the other incorporating thickness variations obtained from the stamping simulation, which ranged approximately from 0.92 mm to 1.72 mm in extreme cases. However, to simplify the analysis and maintain computational efficiency, only thickness variations within the range of 1.1 mm to 1.2 mm were considered in the structural FEM model. This conservative range captures the majority of the sheet’s deformation while excluding extreme thinning/thickening effects that would require additional refinement in the meshing process. Both models utilized a linear elastic material definition with identical Young’s modulus values. The loads were intentionally kept small to ensure that the material remained in the elastic range, even during physical tests. This approach was necessary due to the presence of hardened areas in the stamped component, which still contained zones with lower yield stresses. The mapped model exhibited higher compliance due to the reduced thickness in some areas, consistent with experimental observations. The exclusion of L-Plates in these models, justified by the low magnitude of the applied loads, simplified the analysis without introducing significant errors. The results highlighted the importance of incorporating thickness variations, as the mapped model provided a more accurate representation of the component’s elastic behavior.
The nonlinear models extended the analysis to include material yielding and stress redistribution. The standard model utilized elastoplastic hardening properties derived from the stamping simulation but assumed a constant thickness of 1.2 mm (Figure 10). In contrast, the mapped model employed an elastic–plastic material definition with thickness variations. In the nonlinear simulation, a conservative approximation is employed by modeling the exponential part of the stress–strain relation with a straight line. This approximation assumes perfect plastic behavior after yielding, without considering strain hardening effects. While this approach enhances numerical efficiency and stability, it does not accurately capture the progressive hardening that real materials exhibit. As a result, the simulation may underestimate the material’s resistance to further deformation in the plastic region. To improve post-yield predictions, future refinements could incorporate a more advanced hardening law, such as isotropic–kinematic hardening. Additionally, while thickness variations and local yield strength distributions from the stamping simulation were integrated into the structural FEM model, the complete deformation history was not directly transferred. This decision was primarily driven by computational limitations and challenges in ensuring compatibility between forming and structural simulations. The omission of pre-strain effects and residual stresses may introduce discrepancies in structural analysis, particularly in regions where significant strain path changes influence material response. Future efforts will explore methods to incorporate the full deformation history into FEM analyses to enhance predictive accuracy.
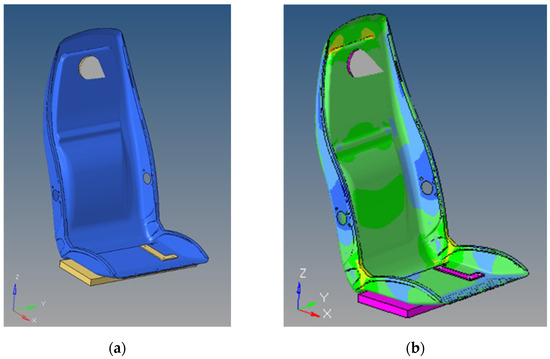
Figure 10.
Visualization of the (a) standard and the (b) nonlinear By-Prop models.
By explicitly acknowledging these approximations and their implications, this work aims to strike a balance between computational efficiency and predictive accuracy, while continuously improving material modeling approaches in structural FEM simulations.
The nonlinear models incorporated additional numerical controls to enhance solution accuracy, as reported in Table 6. Key parameters included NINC, the number of load increments, typically set between 10 and 20 for quasi-static simulations, and DTMAX, the maximum time step, which ensured detailed results. The NINT parameter enabled the post-processing analysis of incremental loads, allowing evaluations of both linear and nonlinear phases. Unlike the linear models, the nonlinear setups included L-Plates to account for stress hotspots at component edges, where yielding was most likely to occur. These models provided a comprehensive understanding of structural behavior under higher loading conditions, accurately capturing critical stress and deformation patterns.

Table 6.
Numerical control details of loading and unloading steps.
4.2. Experiments
Static tests were carried out to validate the structural simulation and the complete process of mapping the material model from the stamping to the structural simulations. These tests were based on the AFNOR NF F 31-119 standard. The experimental setup, shown in Figure 11, included two dial indicators with 0.01 mm precision and an up to 80 mm range, another dial indicator with 0.001 mm precision and an up to 80 mm range, a pneumatic cylinder, and a load cell with 0.1 kg precision and an up to 200 kg range.

Figure 11.
Experiment setup in the tests of the thrust of (a) the backrest along the x-negatives, (b) the backrest along the x-positive and (c) the armrest along the y-positives.
The setup was organized as follows. The sheet-metal seat was fixed to the platform by the base, which was also virtually modeled, and lifted by two additional 10 mm thick plates to prevent the lower edge from touching the floor during loading. The body was tightened between the base and the L-Plates using six bolts, which provided the main anchorage. To anchor the pneumatic piston and the comparator, two beams were used, which were positioned transversely to the direction of the load.
First, several tests were carried out in the linear field before the destructive ones:
The first load case was also used for the destructive test. Loads were applied step-by-step in small units, with each step repeated three times. The force was applied slowly to avoid shocks, and sufficient resting time was allowed before reading the numbers from the dial comparators. After each step, the force was removed, and the setup was inspected to confirm its complete return to the zero position, ensuring the reliability of the instruments and the procedure.
A similar procedure was implemented for the destructive test, gradually increasing the load until the sheet-metal seat reached its breaking point. Deformations at important points were recorded as a function of the load cell values and then were compared with FEM simulation results for validation.
For conciseness, only the results of the initial tests are included in this paper. The validation was conducted at three primary measurement points: Point A, situated at the application point of the pneumatic cylinder at a height of 652 mm from the floor; Point B, positioned approximately halfway up the backrest at a 204 mm height; and Point C, located at the folding junction between the backrest and the seat, representing the lowest part of the backrest. Points A and B measured deformations along the X-axis, while Point C captured deformation along the Z-axis, as shown in Figure 12.

Figure 12.
Positioning of the (a) first and second, and (b) third dial comparators. (c) Measurement points.
As previously described, several tests were conducted, exceeding those strictly required to validate the structural simulation.
The first subtest (backrest push along the X-positive direction) is identical to the test described in previous subchapters, except for the opposite direction of the load application. The workstation setup remained unchanged; the body was simply rotated 180°, and the instrumentation was repositioned while maintaining the comparator heights. The first loading is always regarded as “invalid” as it allows the body to settle into position. Following this initial step, the comparators are reset, and the official measurements commence. The test results are presented in Table 7.

Table 7.
X-positive backrest push test results.
In this test, the loads were kept lower than those applied along the negative X direction, as the body exhibited greater compliance. The observed residual deformations were relatively “high,” potentially indicating a failure risk. However, in the elastic range, residual deformations should theoretically return to zero after the spring back phase. According to the AFNOR NF F 31-119 standard, the residual deformations must remain below 5% of the maximum deformation under load. The standard explicitly states the following: “The residual deformation must always be negligible”, i.e., at most, 5% of the maximum deformation in the presence of stress reached at the moment of the application of the forces.
Table 8 outlines the threshold values specified by the AFNOR regulation, demonstrating that the maximum residual deformations observed during testing remain well below the allowable limits. This confirms the validity of the measurements for the body test.

Table 8.
Maximum displacement and threshold values in first and secondary tests.
The second and third tests follow a similar procedure, differing only in the direction of the applied force and the corresponding positioning of the comparators. These tests involve loading the armrest in both positive and negative directions along the Y-axis, while the reference system remains consistent with the automotive coordinate system. Due to the change in test configuration, the sampling points differ from those specified in previous tests (as shown in Figure 12). Point A, located near the pneumatic piston’s application area, remains conceptually unchanged. However, Points B and C are now positioned along the external edge of the body in decreasing order of height. Specifically, Point C is located at the center of the ribs in the lower part of the seat, where the seat cushion and backrest meet. Table 9 and Table 10 show the measurements taken during the tests for Y-positive armrest push and Y-negative armrest push, respectively.

Table 9.
Y-positive armrest push test results.

Table 10.
Y-negative armrest push test results.
Table 8, Table 11 and Table 12 validate the accuracy and reliability of the measurements performed during the tests. However, from the other tables, it can be seen that the residual deformation measurements are not exactly increasing. This irregularity is attributed to settlement “bumps”, which occurred due to the lifting of the probe shaft using the lifting knob. The data clearly indicates when these settlement bumps began, a phenomenon that was not anticipated in earlier tests. Despite this, the overall measures remain consistent and within acceptable thresholds, confirming the validity of the testing process.

Table 11.
Maximum displacement and threshold values Y-positive armrest push test.

Table 12.
Maximum displacement and threshold values for Y-negative armrest push test.
5. Results and Discussion
5.1. Linear Models
To evaluate the structural behavior of the seat component, the results from the linear models were analyzed first. These models provided insights into the elastic response of the structure, highlighting the impact of mapped thickness variations compared to uniform thickness assumptions.
The stamping simulation revealed a general thinning of the sheet-metal, along with a slight increase in thickness in the intersection area between the backrest and the seat. These results show that the calculations were completed successfully, with the ε index achieving convergence to eight decimal orders. The ε index represents the error that is computed to solve the matrix equation that gives the displacement vector. The lower the index the lower the error of the solution reached with the FEM model.
On average, the mapped model exhibited greater flexibility, primarily due to the reduced overall thickness caused by stretching during the stamping process.
Compared to the real data, the FEM models generally demonstrated greater stiffness, except at Point B, where the deviations were relatively minor. The deviations were particularly pronounced at Point C, highlighting limitations in the model’s ability to capture the deformation in this area accurately. The following points are specifically relevant to note:
- At Point A, the measured displacement was 5.60 mm, while the uniform thickness model simulated a displacement of 4.88 mm (a 12.90% deviation); the mapped thickness model simulated the value 5.11 mm, reducing the deviation to 8.70%.
- At Point B, the measured displacement was 1.26 mm, with the uniform thickness model simulating a displacement of 1.35 mm (a 7.30% deviation); the mapped model produced the value 1.42 mm, resulting in a 12.60% deviation.
- At Point C, the measured displacement was 0.413 mm, but the uniform thickness model simulated a displacement of only 0.175 mm (a 57.60% deviation); the mapped model, though slightly better, simulated a displacement of 0.194 mm, still resulting in a high deviation of 53.10%.
All the details mentioned above are summarized in Table 13.

Table 13.
Difference between Measured and Simulated data in points A, B, C in Uniform and Mapped model.
The strain distributions, shown in Figure 13, revealed slight differences in the deformation contour lines. The regions of deformation were marginally larger in the mapped model than in the uniform thickness model, indicating the influence of localized thinning on the structural response. Stress distributions, shown in Figure 14, highlight significant stress concentrations around the anchor holes. These high localized stresses are primarily attributed to the discretization method of the constraint elements. Specifically, rigid-body element 2 (RBE2) introduced considerable stiffness, generating stress hot spots just outside the application points. To ensure that yielding does not occur in these areas, further analysis of the potential indentation of the bolted connections is recommended. Overall, the results demonstrate the need for mapped thickness models to better capture the deformation and stress behavior of the stamped sheet-metal component. While the mapped model showed improvements over the uniform thickness model, particularly at Points A and C, further refinements in the FEM setup are necessary to address discrepancies in areas with complex stress and strain distributions.

Figure 13.
Strain of the sheet-metal seat from the (a) uniform and (b) mapped thickness models.

Figure 14.
Stresses of the sheet-metal seat from the (a) uniform and (b) mapped thickness models.
5.2. Nonlinear Models
To develop a deeper understanding of the plastic behavior of the seat component, nonlinear models were analyzed. These models incorporated both geometric and material nonlinearities, with one assuming uniform properties and the other utilizing mapped thickness and mechanical properties derived from the stamping simulation. By considering localized yield stresses and the effects of work hardening, the nonlinear models provided a more accurate representation of the structural behavior under high loads, capturing stress redistributions and plastic deformations in critical regions.
The results of the nonlinear simulations reveal that all the predicted values are lower than those observed in real experiments, indicating that the models exhibit greater rigidity compared to the actual sheet-metal. A detailed comparison of the two nonlinear models highlights key differences. At Points A and B, the uniform property model deforms more than the mapped model. This behavior is attributed to the assumption that the uniform model’s material is equivalent to virgin sheet-metal, with yielding occurring above 153 MPa, which increases displacement. Conversely, at Point C, the uniform model predicts lower values, likely due to localized breakage in an area above the sampling point. This failure prevents further downward transmission, reducing the measured displacement.
Despite higher relative errors, the mapped model provides results that align more closely with real-world observations. The relative errors in the mapped model’s predictions are more consistent across sampling points, while those in the uniform property model vary significantly, with deviations spanning approximately thirty percentage units. However, the magnitudes of the measurements differ significantly across sampling points, ranging from 12 mm at larger displacements to just 0.5 mm at smaller ones. The similarity in displacement at Points A and B in the uniform property model appears coincidental, stemming from the elasto-plastic hardening material behavior assumed in this model. In this approach, once the yield strength is exceeded, the tension continues to increase, enhancing the resistance. In contrast, the mapped model incorporates elasto-plastic material behavior, reacting with a constant resistant load once the yield value is reached. This distinction results in differing deformation trends between the two models.
Residual data analysis indicates that both simulations underestimate the real-world behavior, showing weaker and more deformable characteristics. The material models used in the simulations allow for earlier failure compared to that observed in reality. Notably, the uniform property model poorly represents the experimental results, as evidenced by significant virtual deformation and compromised elastic return, indicating inappropriate material model and reference data choices. In contrast, the mapped model demonstrates better agreement with real behavior at Points A and B, though it deviates more significantly at Point C. The discrepancies at Point C may arise from experimental errors or limitations in the simulation data, particularly when dealing with displacement on the order of hundredths of a millimeter, which are negligible relative to the overall body size. Figure 15 and Figure 16 compare the plastic strain and deformation contours for both simulations. The iso-strain areas in the mapped property model are significantly smaller than those in the uniform model, reflecting localized yielding near the base and L-Plate edges, which are expected regions for constraint reaction interfaces. The legend scale was standardized across both models for the direct comparison of plastic deformations and strains, further highlighting the differences in behavior between the models. These findings emphasize the need for accurate material modeling and refined stamping simulation data to improve alignment with real-world behavior.

Figure 15.
Plastic strain of the sheet-metal seat from the (a) uniform and (b) mapped nonlinear material properties.
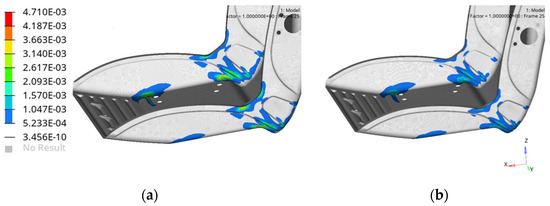
Figure 16.
Deformations of the sheet-metal from (a) uniform and (b) mapped nonlinear material properties.
The red areas on the left in the simulation results represents the regions where stress has exceeded the yield value. Interestingly, in the mapped model, multiple areas reach maximum stress, but only subset transitions into the plastic deformation field. This distinction highlights the effects of localized material behavior. For example, the ribbed area, which experienced significant deformation during the stamping process, exhibits a high level of hardening. As a result, its yield stress exceeds the maximum stress observed, as shown in Figure 17.
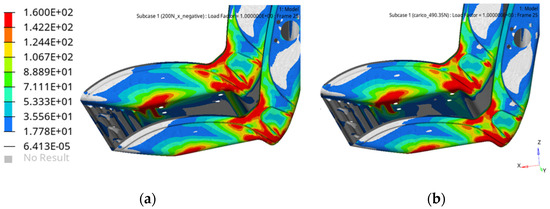
Figure 17.
Stresses on the sheet-metal seat in different views from the (a) uniform and (b) mapped nonlinear material properties.
Overall, the mapped model demonstrates a more realistic and robust performance compared to the standard model. While the mapped model does exhibit a high error, it remains consistent and stable, making it a more reliable approximation of real-world behavior under complex loading conditions, as summarized in Table 14. This underscores the importance of incorporating accurate material and geometric properties derived from stamping simulations into FEM analyses.

Table 14.
Comparison of measured and simulated displacement and residual values at key points.
6. Conclusions
The primary aim of this work was to demonstrate the necessity of accounting for the phenomenon of work hardening in simulating components derived from cold stamping processes of sheet-metal. Work hardening introduces localized material properties that depend directly on the degree of deformation that occurs during manufacturing. To address this, a stamping simulation was performed to extract deformation data, which were then mapped onto the body using a semi-automatic method.
The comparison of the two linear models, one with constant thickness and the other with thickness derived from the stamping simulation, revealed minimal differences in the elastic field. Both models showed similar global behavior, with deviations in displacement measurements at Point C being excessively high and failing to accurately represent real behavior. Specifically, the measured displacement at Point C was 0.413 mm, whereas the uniform thickness model simulated a displacement of 0.175 mm (a deviation of 57.60%) and the mapped thickness model simulated a displacement of 0.194 mm (a deviation of 53.10%). Differences the in iso-strain and iso-stress curves were negligible. Ultimately, thickness mapping alone did not provide a significant improvement in linear simulations for this specific case, as both models converged to reality with comparable precision.
In contrast, the nonlinear models demonstrated more substantial differences. The model with uniform geometric and mechanical properties consistently over-predicted the yield, leading to excessive deviations, particularly at Point C, where results were considered unacceptable. The mapped model, while also exceeding the 10% error threshold, showed greater consistency across all sampling points, with errors typically in the range of 10–20%. For example, at Point A, the measured displacement was 5.60 mm, while the uniform model simulated a displacement of 4.88 mm (a deviation of 12.90%) and the mapped model simulated a displacement of 5.11 mm (a deviation of 8.70%).
Residual measurements further emphasized the limitations of the standard model, which exhibited excessive yielding and poor agreement with experimental results. The mapped model, however, provided a better approximation of the real shell’s behavior. While the errors were higher than desired, they remained stable and within a predictable range, suggesting that the mapped model converged to reality with an offset caused by factors such as simulation approximations or data quality from the stamping process.
This work highlights that predicting the plastic behavior of a hardened component using a model with uniform properties is not feasible. The excessive approximations inherent in uniform models fail to capture the inhomogeneities caused by work hardening. The mapped model demonstrated the necessity of incorporating data from stamping simulations, particularly for regions with localized variations in material properties. However, the process requires further refinement, particularly in mapping accuracy and validation methodologies, to achieve greater reliability and alignment with real-world behavior.
In conclusion, while the results presented some approximations, they provide encouraging insights into the potential of mapped property models. These models are a step forward in accurately simulating the complex mechanical behavior of components derived from cold stamping processes, laying the foundation for further research and optimization of the mapping process. To conclude, while the percentage of deviations are significant, the actual residual values remain lower than predicted, showing that the material’s real mechanical properties surpass initial expectations based on traditional modeling approaches. These enhanced properties cannot be overlooked from an engineering perspective, as they contribute to improved structural performance. Although this study represents a significant advancement in the state of the art, further research is necessary to fully integrate non-uniform material properties into FEM models, ensuring greater accuracy and predictive reliability
Author Contributions
Conceptualization, D.C. and F.C.; methodology, B.E., D.C. and F.C.; software, B.E.; investigation, B.E. and H.R.; writing—original draft preparation, review and editing, H.R. and A.V.; supervision, A.V. All authors have read and agreed to the published version of the manuscript.
Funding
This research was internally funded by FISA Fabbrica Italiana Sedili Autoferroviari Srl, who is hosting Elia Burello for his Master’s thesis.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Raw data supporting the conclusions of this article will be made available by the authors upon request.
Conflicts of Interest
Authors Dario Cimolino and Francesco Capaccioli was employed by the company FISA Fabbrica Italiana Sedili Autoferroviari Srl. The authors declare that this study received funding from FISA Fabbrica Italiana Sedili Autoferroviari Srl. The funder was not involved in the study design, collection, analysis, interpretation of data, the writing of this article or the decision to submit it for publication. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Raabe, D.; Tasan, C.C.; Olivetti, E.A. Strategies for improving the sustainability of structural metals. Nature 2019, 575, 64–74. [Google Scholar] [CrossRef] [PubMed]
- Traphöner, H.; Clausmeyer, T.; Tekkaya, A.E. Material characterization for plane and curved sheets using the in-plane torsion test—An overview. J. Mater. Process. Technol. 2018, 257, 278–287. [Google Scholar] [CrossRef]
- Lorenzini, M.; Giacopini, M.; Barbieri, S.G. Thermo-mechanical analysis of the exhaust manifold of a high performance turbocharged engine. Key Eng. Mater. 2018, 774, 307–312. [Google Scholar] [CrossRef]
- Panthi, S.K.; Ramakrishnan, N.; Pathak, K.K.; Chouhan, J.S. An analysis of springback in sheet metal bending using finite element method (FEM). J. Mater. Process. Technol. 2007, 186, 120–124. [Google Scholar] [CrossRef]
- Marretta, L.; Di Lorenzo, R. Influence of material properties variability on springback and thinning in sheet stamping processes: A stochastic analysis. J. Adv. Manuf. Technol. 2010, 51, 117–134. [Google Scholar] [CrossRef]
- Barbieri, S.G.; Mangeruga, V.; Giacopini, M.; Mantovani, S. Structural analysis of the forming process for hairpin windings for electric motor applications: Torsional-flexural instability issues. In Proceedings of the 2022 International Conference on Electrical Machines (ICEM), Valencia, Spain, 5–8 September 2022. [Google Scholar]
- Mantovani, S.; Presti, I.L.; Cavazzoni, L.; Baldini, A. Influence of manufacturing constraints on the topology optimization of an automotive dashboard. Procedia. Manuf. 2017, 11, 1700–1708. [Google Scholar] [CrossRef]
- Pepelnjak, T.; Sevsek, L.; Luzanin, O.; Milutinovic, M. Finite Element Simplifications and Simulation Reliability in Single Point Incremental Forming. Materials 2022, 15, 3707. [Google Scholar] [CrossRef]
- Liu, S.C.; Hu, S.J. Variation simulation for deformable sheet metal assemblies using finite element methods. J. Manuf. Sci. Eng. 1997, 119, 368–374. [Google Scholar] [CrossRef]
- Esener, E.; Akşen, T.A.; Ünlü, A.; Firat, M. On the prediction of strength and deformation anisotropy of automotive sheets for stamping formability analysis. J. Braz. Soc. Mech. Sci. Eng. 2021, 43, 551. [Google Scholar] [CrossRef]
- Abe, Y.; Mori, K.-I.; Maeno, T.; Ishihara, S.; Kato, Y. Improvement of sheet metal formability by local work-hardening with punch indentation. Prod. Eng. 2019, 13, 589–597. [Google Scholar] [CrossRef]
- Pham, Q.T.; Islam, M.S.; Barlo, A.; Sigvant, M.; Caro, L.P.; Trana, K. Modeling the strain localization of shell elements subjected to combined stretch–bend loads: Application on automotive sheet metal stamping simulations. Thin-Walled Struct. 2023, 188, 110804. [Google Scholar] [CrossRef]
- Mirone, G.; Barbagallo, R.; Bua, G.; De Caro, D.; Ferrea, M.; Tedesco, M.M. True stress-strain identification accounting for anisotropy of sheet metals. IOP Conf. Ser. Mater. Sci. Eng. 2024, 1306, 012005. [Google Scholar] [CrossRef]
- Raulea, L.V.; Goijaerts, A.M.; Govaert, L.E.; Baaijens, F.P.T. Size effects in the processing of thin metal sheets. J. Mater. Process. Technol. 2001, 115, 44–48. [Google Scholar] [CrossRef]
- Li, J.C.; Chong, L.I.; Zhou, T.G. Thickness distribution and mechanical property of sheet metal incremental forming based on numerical simulation. Trans. Nonferrous Met. Soc. China 2012, 22, s54–s60. [Google Scholar] [CrossRef]
- Altinbalik, T.; Tonka, A. Numerical and experimental study of sheet thickness variation in deep drawing processes. Int. J. Mod. Manuf. Technol. 2012, 4, 9–16. [Google Scholar]
- Ablat, M.A.; Qattawi, A. Numerical simulation of sheet metal forming: A review. J. Adv. Manuf. Technol. 2017, 89, 1235–1250. [Google Scholar] [CrossRef]
- Andersen, R.G.; Londono, J.G.; Woelke, P.B.; Nielsen, K.L. Fundamental differences between plane strain bending and far-field plane strain tension in ductile plate failure. J. Mech. Phys. Solids 2020, 141, 103960. [Google Scholar] [CrossRef]
- Tekkaya, A.E.; Allwood, J.M.; Bariani, P.F.; Bruschi, S.; Cao, J.; Gramlich, S.; Groche, P.; Hirt, G.; Ishikawa, T.; Löbbe, C.; et al. Metal forming beyond shaping: Predicting and setting product properties. CIRP Ann. 2015, 64, 629–653. [Google Scholar] [CrossRef]
- Wang, S.; Shang, H.; Han, M.; Zhou, C.; Chen, Q.; Lou, Y. Lode-dependent Yld91 function for anisotropic-asymmetric hardening modeling of metals under non-associated flow rule. J. Mater. Process. Technol. 2024, 325, 118298. [Google Scholar] [CrossRef]
- Bouvier, S.; Haddadi, H.; Levée, P.; Teodosiu, C. Simple shear tests: Experimental techniques and characterization of the plastic anisotropy of rolled sheets at large strains. J. Mater. Process. Technol. 2006, 172, 96–103. [Google Scholar] [CrossRef]
- Tardif, N.; Kyriakides, S. Determination of anisotropy and material hardening for aluminum sheet metal. Int. J. Solids Struct. 2012, 49, 3496–3506. [Google Scholar] [CrossRef]
- Ailinei, I.-I.; Galatanu, S.-V.; Madroane, D.-F.; Marsavina, L. The Influence of anisotropy on the vibration behaviour of S600Mc sheet metal. Procedia Struct. Integr. 2022, 42, 1422–1427. [Google Scholar] [CrossRef]
- AFNOR NF F 31-119; Railway Rolling Stock. Behaviour of Rolling Stock’s Seats at Statics Stress, Fatigue Stress, Vibrations Stress and Shocks Stress. Associazione Francese di Standardizzazione (AFNOR): Paris, France, 1995.
- Jingxin, N.A.; Wei, C. One step positive approach for sheet metal forming simulation based on quasi-conjugate-gradient method. Chin. J. Mech. Eng. 2013, 26, 730–736. [Google Scholar] [CrossRef]
- Xiaoda, L.; Xiangkui, Z.; Ping, H.; Weijie, L.; Xianghui, Z. One-step Inverse Forming Simulation on Hot Forming Process of High-strength Food-can Tinplate. Adv. J. Food Sci. Technol. 2016, 10, 26–30. [Google Scholar] [CrossRef]
- Dansk Standard DS/EN 12663-1:2010+A1:2015; Railway Applications—Structural Requirements of Railway Vehicle Bodies—Part 1: Locomotives and Passenger Rolling Stock (and Alternative Method for Freight Wagons). International Arbejdsgruppe WG CEN/TC 256, Danish Committee DS/S-268, Danish Standards Foundation: Copenhagen, Denmark, 2015.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).