Abstract
The vulnerability of existing buildings to recent earthquakes underscores the critical need to explore effective retrofit solutions thoroughly. This study presents a comprehensive methodology for ranking seismic retrofit alternatives for reinforced concrete beams with shear deficiencies. It evaluates five alternatives to ensure a 50-year service life, meeting current seismic standards and incorporating specific preventive maintenance measures for each option. A cradle-to-grave life cycle assessment was used to analyze the impacts associated with the sustainability of each alternative. Hybridization of emerging multi-criteria decision-making methods was applied for criteria weighting and final ranking, and a hierarchical model including economic, environmental, social, and functional criteria was developed. The results highlight carbon fiber reinforcements and steel plates with epoxy adhesives as optimal solutions due to their lower environmental and social impact, along with improvements in execution time and minimal architectural impact. This study underscores the necessity of a comprehensive approach to identifying optimal retrofitting alternatives, demonstrating the imperative to complement the conventional structural engineering objective of ensuring safety while minimizing investment.
1. Introduction
The past decade’s seismic events underscore societies’ persistent vulnerability to earthquakes. Despite increased efforts by governments, academia, and international organizations to mitigate seismic risks, recent earthquakes reveal that significant challenges remain []. Much of the aging building stock was constructed under outdated seismic design standards and fails to meet current seismic resistance codes []. As more buildings near the end of their intended service life, additional risks related to material durability emerge; this creates a substantial societal risk, as evidenced by the susceptibility of existing structures to recent earthquakes, which have caused structural damage, significant economic losses, serious injuries, and loss of life [].
Informal, self-managed housing construction—typically undertaken by residents or builders without formal training and often without permits or adherence to building codes—constitutes a significant proportion of residential construction in low- and middle-income countries []. Post-earthquake assessments have consistently highlighted structural vulnerabilities and a high incidence of collapses in informally constructed reinforced concrete and masonry housing []. One of the most devastating recent earthquakes, the April 2016 Pedernales earthquake on the northwest coast of Ecuador, had a moment magnitude (MW) of 7.8. Official statistics reported 668 fatalities, 12 missing persons, 6274 injuries, 113 rescues, and 28,775 individuals displaced to shelters. Approximately 30,000 homes were severely damaged or destroyed, with urban (13,962) and rural (15,710) areas experiencing nearly equal levels of destruction []. The widespread damage to low- and mid-rise reinforced concrete buildings revealed that inadequate seismic detailing and poor-quality control contributed to their partial or total collapse []. Limited economic resources further exacerbate these problems, as most construction practices in informal buildings do not comply with seismic codes.
Post-earthquake studies worldwide have highlighted the significant impact of shear failures in beams, columns, and beam-column joints on the seismic performance of existing reinforced concrete buildings []. Pre-code reinforced concrete structures are particularly susceptible to shear failures during seismic events, underscoring the critical importance of accurately estimating the shear capacity of these elements. Many existing reinforced concrete buildings were designed using outdated standards that often overestimated the shear strength of beams. Unlike flexural damage, shear damage is brittle and far more detrimental to structural performance. Furthermore, poor reinforcement practices—such as insufficient transverse reinforcement and overlapping splices in the plastic hinge region—heighten vulnerability by promoting brittle failure modes, including shear failures. These deficiencies compromise structural integrity, posing significant risks to property and human life [].
Increasing the shear capacity of reinforced (RC) concrete beams is crucial, as shear failure is sudden and typically accompanied by poor energy dissipation. Numerous parameters influence the shear strength of reinforced concrete beams, and predicting shear capacity is an ongoing area of research. Current design standards employ either empirical or semi-empirical methods. ACI-318 uses a semi-empirical approach based on truss models for shear reinforcement contribution and an empirical factor for the concrete contribution []. In contrast, Eurocode 2 adopts the variable strut inclination method []. Additionally, other researchers have proposed models based on the modified compression field theory and the general stress field approach [].
Localized preventive interventions can help mitigate potential damage. Several methods for enhancing the shear strength of reinforced concrete beams have been developed, with the most common being the addition of reinforced concrete jacketing, steel jacketing, and composite jacketing (fiber-reinforced polymers) [,]. RC cladding is particularly effective in improving shear performance and is a relatively easy-to-apply reinforcement method []. It is also a well-established technique for retrofitting structural elements. The success of the jacketing process largely depends on achieving a strong bond between the old and new materials, with reinforced concrete being highly effective at the interface, making it a reliable material for U-shaped reinforcement of shear-critical beams []. Steel jacketing offers the advantage of requiring less space, being lightweight, and easy to install []. On the other hand, externally bonded fiber-reinforced polymer (FRP) composites have emerged as an efficient solution, enhancing bending, shear, torsion, and confinement capabilities. FRP composites are characterized by their low invasiveness, high strength-to-weight ratio, and ease of application [].
Structural engineering has traditionally focused on achieving maximum safety with minimal investment. However, growing concerns about sustainability have elevated the importance of its three pillars: economic, environmental, and social. A circular economy (CE) presents a promising approach to addressing sustainability challenges by extending the useful life of the built environment through the retrofit and refurbishment of buildings and infrastructure []. In the building and construction industry, the economic dimension of sustainability has historically received the most attention, while environmental impacts have gained increasing research interest in recent years. Seismic retrofitting of reinforced concrete buildings typically involves the production of new materials and implementing construction processes, contributing to the industry’s already significant environmental impact. Given the large number of buildings with seismic deficiencies, these retrofitting activities may exacerbate negative environmental consequences []. Meanwhile, the social dimension of sustainability in the construction sector faces substantial challenges due to its relative development and lack of maturity [].
Multi-criteria decision-making methods (MCDM) are valuable tools for tackling complex engineering problems, particularly when selecting optimal solutions under conflicting criteria []. Multiple attribute decision-making methodologies (MADMs) have received much attention recently. MADMs have evolved into comprehensive operations research methods integrating computational and mathematical tools to identify optimal solutions []. MADMs enable a holistic assessment of safety and sustainability by addressing conflicting dimensions and criteria. Recent research has applied decision-making methods to rank seismic retrofitting alternatives, incorporating economic, functional, and environmental criteria. These studies include contributions from references [,,,,]. However, many building retrofit studies lack social life cycle analysis, leaving a significant gap. Despite the availability of advanced MADMs, their application in seismic retrofit remains limited []. Classical decision-making methods continue to dominate the research landscape. With the proliferation of innovative decision-making approaches in recent years, there is considerable potential to improve accuracy and applicability, offering robust solutions to current challenges. The term “postpone effect” aptly describes the state of the field, reflecting the lag in adopting and applying modern MCDMs in research [].
The scientific community has made significant strides in utilizing MCDM methods to select optimal seismic retrofitting alternatives. However, there is still a need to thoroughly explore retrofit strategies with a holistic approach that can effectively minimize seismic risk. While established MCDM methods have been widely applied, newer methodologies developed in recent years may yield improved results in the weighting of criteria and the final ranking of alternatives. This study addresses these gaps by introducing a methodology that integrates the three pillars of sustainability—economic, environmental, and social—through life cycle assessments alongside a functional dimension. The primary objective is to propose a comprehensive framework for classifying seismic retrofit strategies for reinforced concrete beams with shear deficiencies at the local level. Additionally, two secondary objectives are pursued: first, to evaluate the sustainability dimensions through life cycle assessments, and second, to employ emerging MCDM methods for criteria weighting and ranking alternatives.
The article is structured to achieve these objectives: Section 2 reviews the literature on life cycle assessments and emerging MCDM approaches. Section 3 contains materials and methods and details the proposed methodology. Section 4 and Section 5 analyze and discuss the results, including a sensitivity analysis. Finally, Section 6 concludes with the key findings of the study.
2. Literature Review
2.1. Life Cycle Assessment
The life cycle assessment (LCA) framework is a powerful tool for assessing the environmental impacts of products, systems, or processes throughout their life cycle. Life cycle sustainability assessment is increasingly applied in the building and construction sector, with significant economic, environmental, and social impacts []. Recent studies have focused on analyzing the environmental aspects of seismic retrofitting of buildings using LCA. For example, a group of researchers compared the environmental performance of reinforced concrete column jacketing and dissipation devices, concluding that the latter is more environmentally friendly than traditional solutions []. Similarly, another study evaluated three seismic retrofitting methods for an old RC building: concrete shear wall reinforcement, RC column jacketing with shear wall reinforcement, and base isolation using high-damping rubber bearings and viscous fluid dampers. Of these, the base isolation method was found to have the least environmental impact []. Another group of researchers conducted an LCA of three seismic retrofitting alternatives for a reinforced concrete building: RC column jacketing, beam weakening, and shear walls. Among them, shear walls were found to have the highest environmental impact []. Similarly, another research analyzed and compared the environmental performance of four seismic retrofitting strategies: FRP-based strengthening solution, FRP-RC jacketing-based strengthening solution, installation of RC shear walls, and base isolation. Their results indicate that base isolation has the lowest environmental impact []. Another study conducted an LCA of seismic retrofitting of RC columns, comparing three traditional methods: concrete jacketing, steel jacketing, and carbon fiber incorporation; steel jacketing proved to be the best alternative from an economic and environmental point of view [].
The building and construction sector faces significant challenges on the social sustainability front. The criteria for assessing social sustainability in the built environment vary considerably, highlighting the need for a standardized framework []. This lack of consistency can be attributed to the ambiguity surrounding the definition of social sustainability criteria. Notably, no relevant studies currently address social life cycle assessments of seismic retrofitting alternatives, underscoring a significant knowledge gap.
2.2. Decision-Making Methods
Selecting the most appropriate multi-criteria decision-making methods from the existing literature is complex. No single MCDM model can address all the multifaceted challenges encountered in the construction industry []. Among the approaches employed to select retrofit alternatives, the joint application of the Analytical Hierarchy Process (AHP) for criteria weighting and the Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS) for ranking alternatives has gained widespread acceptance within the scientific community. This combined approach generates a comprehensive ranking of alternatives with minimal parameters required from the decision-maker (DM) []. However, research on the application of MCDM in the construction industry remains limited. Researchers and decision-makers must integrate emerging MCDM methods to fill this gap.
The weighting stage of criteria is a critical step in the decision-making process. According to the literature, the Best-Worst Method (BWM) outperforms both the AHP and the Analytical Network Process (ANP) []. BWM offers a systematic approach that requires fewer pairwise comparisons than AHP, leading to more consistent judgments []. For the ranking of alternatives, several state-of-the-art methods have gained prominence. These include EDAS (Evaluation Based on Distance to Average Solution), MABAC (Multi-Attribute Boundary Approximation Area Comparison), CODAS (Combinatorial Distance-Based Assessment), and MARCOS (Measurement of Alternatives and Ranking According to Compromise Solution). These advanced techniques offer robust frameworks for evaluating and ranking alternatives effectively.
2.2.1. Best-Worst Method
The pairwise comparison method proposed by Rezaei in 2015 [] is based on identifying the best and worst criteria from a set of evaluation criteria, followed by pairwise comparisons between these criteria and all others. The stages of the Best-Worst Method are briefly outlined below: (a) Determine the set of decision criteria; (b) Determine the best criterion (the most desirable, the most important) and the worst criterion (the least desirable, the least significant); (c) Determine the preference of the best criterion over the other criteria, using a number between 1 and 9; (d) Determine the preference of all criteria over the worst criterion, using a number between 1 and 9; (e) Calculate the optimal weights determined from the maximum absolute differences:
For all, j is minimized, which results in the following min-max model:
This model is equivalent to the following model:
The solution of this model could lead to multiple optimal solutions; a new model is proposed that minimizes the maximum between the set of . The problem can be formulated as follows:
This problem is transformed into the following linear programming problem:
This problem has only one solution, and we obtain the optimal weights and ; . It is regarded as an indicator of comparison consistency, with values close to zero reflecting a high degree of consistency.
2.2.2. Evaluation Based on Distance to Average Solution
Proposed by Ghorabaee et al. in 2015 [], it ranks alternatives based on the distance to the median solution, eliminating the need to calculate both the ideal and nadir solutions. Two measures are used to assess the desirability of alternatives: positive distance to the mean (PDA) and negative distance to the mean (NDA). These measures indicate the difference between each alternative and the mean solution. Higher PDA and lower NDA values mean the alternative is better than the median solution. Their application is summarized in the following steps:
- 1.
- Construct the decision matrix , Xij is the value of the performance of alternative i in criterion j.
- 2.
- Determine the average solution according to all criteria:
- 3.
- Calculate the distance matrices according to the type of benefit or cost criterion:
Benefit:
Cost:
- 4.
- Determine the weighted sum for all alternatives:
wj is the weight of the criterion j.
- 5.
- Normalize SP and SN values:
- 6.
- Calculate the evaluation score (AS) of all alternatives:
Alternatives are ranked in descending order of values (AS).
2.2.3. Multi-Attribute Boundary Approximation Area Comparison
Proposed by Pamucar and Cirovic in 2015 [], it is based on the definition of the distance of the criterion function of each alternative to the edge approximation area; the method is applied in six steps:
- 1.
- Formation of the decision matrix ;
- 2.
- Normalization of the elements of the initial matrix X, ;
Benefit:
Cost:
- 3.
- Determine the weighted matrix, wi criteria weighting coefficients;
- 4.
- Determine the edge approximation area matrix , formed by edge approximation area (BAA);
- 5.
- Determine the matrix :
Alternative Ai could belong to the border approach area G, the upper approach area G+, or the lower approach area G−, G+ contains the ideal alternative A+, and G− contains the anti-ideal alternative A−. Membership is determined according to the following:
For Ai to be selected as the best, it must have as many criteria as possible belonging to the upper approximation zone G+.
To rank the alternatives, the values of the criterion functions for the other options Si are determined as the sum of the distance of the alternatives from the boundary approach areas qi.
2.2.4. Combinatorial Distance-Based Assessment
Proposed by Ghorabaee et al. in 2016 [], it evaluates the desirability of alternatives using Euclidean and taxonomic distances. The primary metric is the Euclidean distance between the alternatives and the negative ideal solution, while the secondary metric is the Taxicab distance. The alternative farthest from the negative ideal solution is deemed the most desirable. The method is implemented as follows:
- 1.
- Definition of the decision matrix ;
- 2.
- Normalization of the decision matrix:
- 3.
- Calculating the weighted normalized decision matrix:
- 4.
- Determine the ideal negative solution (point):
- 5.
- Calculate the Euclidean and taxicab distances of the alternatives with respect to the negative ideal solution:
- 6.
- Construct the relative evaluation matrix :
ψ is a threshold function to recognize the equality of the Euclidean distances of two alternatives:
τ is the threshold that can be set by the decision-maker. Its value can be between 0.01 and 0.05; usually τ = 0.02 is used.
- 7.
- Calculate the evaluation score for each alternative:
The alternatives are ranked according to the degressive values of Hi.
2.2.5. Measurement of Alternatives and Ranking According to Compromise Solution
The method proposed by Steviç et al. in 2020 [] measures and ranks alternatives relative to a compromise solution; utility functions must be determined based on the distances to the ideal and anti-ideal solutions and their aggregations. The best alternative is the one closest to the perfect solution and farthest from the anti-ideal benchmark. The method is applied by following these steps:
- 1.
- Determining the decision matrix;
- 2.
- Determine the extended matrix defining the ideal (IA) and anti-ideal (AAI) solution:
B group of benefit criteria, and C group of cost criteria;
- 3.
- Normalize the extended matrix :
- 4.
- Determine the weighted matrix ; ;
- 5.
- Calculate each alternative’s utility relative to the ideal and anti-ideal solutions:
- 6.
- Determine the utility function of the alternatives:
The utility functions of the ideal and anti-ideal solutions are calculated according to the following:
The higher the value of the utility function, the better.
3. Materials and Methods
A comprehensive methodology is proposed for selecting the optimal seismic retrofitting solution for reinforced concrete beams with shear deficiencies, adopting a holistic approach. Figure 1 illustrates the methodology, organized into four clearly defined stages: Stage 1: Define the problem and the dimensions to analyze for the strengthening alternatives: economic, environmental, social, and functional. Stage 2: Present five strengthening alternatives to enhance the shear strength of the beam under study. Stage 3: Quantify the economic, environmental, and social impacts using life cycle assessments—Life Cycle Cost Assessment (LCCA), Environmental Life Cycle Assessment (LCA), and Social Life Cycle Assessment (S-LCA). Additionally, two criteria representing the functionality of the strengthening alternatives will be evaluated. Stage 4: Develop a decision model through expert input, structured hierarchically into four dimensions, eight criteria, and 16 specific indicators. Employ the BWM for subjective criteria weighting and the EDAS, MABAC, CODAS, and MARCOS methods to rank the alternatives. This approach identifies the optimal seismic retrofitting solution for reinforced concrete beams with shear deficiencies.
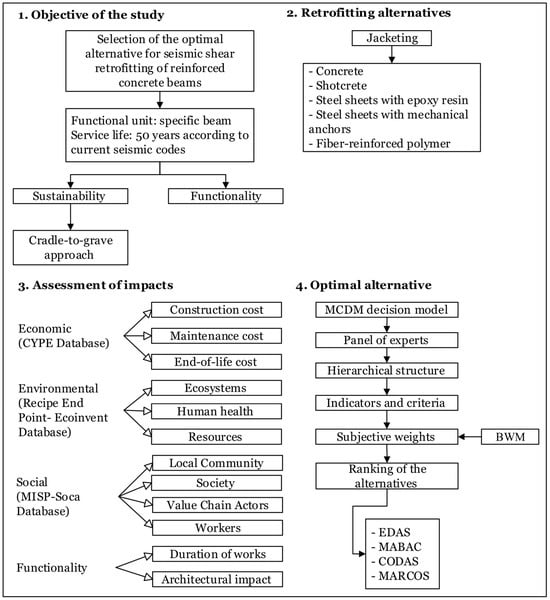
Figure 1.
Methodology of the study.
3.1. Description of the Problem and Retrofit Alternatives
This study aims to determine the optimum seismic retrofitting solution for a reinforced concrete beam with shear deficiencies. The analyzed beam has a span of 6.0 m. It presents material properties and longitudinal and transverse reinforcement, typical of beams built according to obsolete standards or non-designed practices. In order to comply with current seismic regulations, the retrofit of the beam includes a 22% increase in shear strength within the intended plastic hinge zone. The analysis assumes a service life of 50 years for the retrofit beam, which ensures compliance with modern seismic requirements and improves the durability of the structural element. The seismic strengthening alternatives are evaluated using a “cradle-to-grave” life cycle analysis, which incorporates economic, environmental, and social dimensions while assessing functionality.
Optimal seismic retrofitting is selected from five alternatives: concrete jacketing (CJ), shotcrete jacketing (SCJ), steel jacketing with structural epoxy adhesive (STE), steel jacketing with anchor bolts (STA), and use of carbon fiber reinforced polymer (CFRP). The methods for the design of retrofitting alternatives are considered to be an additive approach.
The equations in the Ecuadorian standard NEC-15 [], which are based on ACI-318, were used for the concrete jacketing alternatives. The nominal shear strength considers the contribution of the concrete (Vc) and the shear reinforcement (Vs), according to Equation (45).
The contribution of concrete to shear was determined using Equation (46).
where f′c is the compressive strength of the concrete cylinder in MPa, bw is the width of the beam, and d is the effective depth of the beam. For the contribution of the vertical stirrup, ACI-318 considers the truss model represented by Equation (47).
where Av is the effective area of the stirrup legs, fy is the steel yield strength, and s is the spacing between the stirrups.
For the alternatives incorporating steel plates, equation 48 followed the reference guidelines []. This expression considers the shear strength of reinforced concrete beams with continuous horizontal steel plates attached to the web, the addition of the contributions of the concrete, the internal shear reinforcement, and the external steel plates. Equation (49) determines the contribution of shear stress (Vp), considering the sum of the shear stresses along its depth and thickness.
where τavg is the average shear stress in the steel plates, hp is the depth of the plates, and tp is the thickness of the plates on either side of the beam’s web. For the quadratic distribution of shear stress over the depth of the plate, the average stress is calculated using Equation (50):
τmax is the maximum shear stress in a steel plate, which can be determined from Tresca’s maximum shear stress theory. This theory considers the yield strength of the material fyp, as indicated in Equation (51):
Thus, when considering Equations (49)–(51), the contribution of the plates becomes Equation (52):
For the design of the CFRP, the Guide for the Design and Construction of Externally Bonded FRP Systems for Reinforcing Concrete Structures (ACI 440) was used, where the contribution of the FRP shear stress (Vf) in Equation (53) is affected by the coefficient f with a value of 0.85 for U-shaped wraps.
The contribution of the shear stress of the FRP is given by Equation (54):
where for rectangular sections, Afv is determined by Equation (55):
where n is the number of FRP reinforcement layers, tf is the nominal thickness of a reinforcing sheet, wf is the nominal width of a reinforcing sheet, ffe is the effective stress in the FRP reinforcement, α is the angle formed by the extreme fiber in traction with the FRP strip, dfv the depth of the FRP shear reinforcement, and sf the distance between the centers of the FRP strips.
Specific preventive maintenance measures based on material properties were incorporated to ensure that the retrofit alternatives achieve the expected service life of 50 years from installation or until structural damage due to an earthquake occurs. Table 1 summarizes the general characteristics of the beam analyzed and the shear strength values of the five retrofit alternatives considered.

Table 1.
General information about the original beam and the retrofitting alternatives.
The beam requiring retrofit is assumed to be part of a reinforced concrete building in northern Quito, classified as a high seismic hazard zone under Ecuador’s current seismic regulations. The following transport distances were considered: 8.0 km from the concrete factory, 42.3 km for steel, 40.2 km for structural adhesives and materials used in preventive maintenance, and 13.2 km to the landfill for waste disposal. For CFRP and epoxy resin, transport distances include 3800 km by air and 37.3 km by land, as these materials are imported into Ecuador. Figure 2 shows the schematics of the retrofitting alternatives. A detailed description of the alternatives to retrofit is provided.
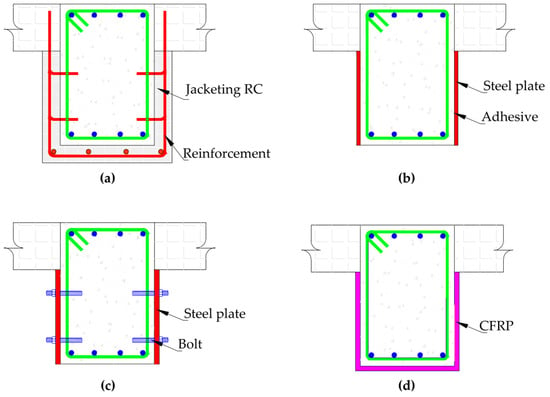
Figure 2.
Alternative reinforcement schemes. (a) CJ and SCJ; (b) STE; (c) STA; (d) CFRP.
CJ Alternative: A 75 mm thick layer of concrete is applied to the bottom and side faces of the beam. The concrete, with a compressive strength of 24 MPa and a soft consistency, is pre-mixed at the plant and pumped on-site. Before application, a continuous layer of two-component, thixotropic, epoxy resin-based structural adhesive is applied to the hardened concrete surface. The reinforcement consists of four longitudinal bars 12 mm in diameter and stirrups 10 mm in diameter, spaced at 150 mm and anchored to the slab using chemicals. Preventive maintenance includes the application of an anti-carbonation paint.
SCJ Alternative: A 75 mm thick shotcrete jacket is applied to the bottom and side faces of the beam. The shotcrete has a compressive strength of 24 MPa and fluid consistency. It is applied using a wet spraying technique. The reinforcement is identical to that used in the CJ alternative. Preventive maintenance consists of the application of anti-carbonation paint.
STE Alternative: 4 mm thick A572 Gr50 hot-rolled steel plates are applied to the lateral faces of the beam and secured using a two-component thixotropic epoxy resin adhesive. Preventive maintenance includes the application of a two-component epoxy resin-based anticorrosive paint and passive fire protection achieved by spraying cement-based fireproof mortar.
STA Alternative: 4 mm thick A572 Gr50 hot-rolled steel plates are secured to the beam’s lateral faces using mechanical anchorage with bolts. Preventive maintenance includes the application of two-component epoxy resin-based anticorrosive paint and passive fire protection provided by the projection of cement-based fireproof mortar.
CFRP Alternative: The CFRP is applied using a U-wrap method with two layers of unidirectional carbon fabric, each 0.165 mm thick. The fabric has a tensile strength of 4900 MPa, an elasticity modulus of 230,000 MPa, an ultimate elongation of 2.10%, and a 300 g/m2 weight. Preventive maintenance includes passive fire protection through the projection of cement-based fireproof mortar.
3.2. Implementation of Life Cycle Assessment
The LCCA includes construction, preventive maintenance, and end-of-life (EoL) costs. Construction costs cover the supply of materials, equipment and machinery usage, labor, and minor tools. For the CJ alternative, this also includes the cost of the recoverable formwork system. Preventive maintenance costs encompass anti-carbonation paint for CJ and SCJ, anti-corrosion paint for STE and STA, fireproof mortar for STE, STA, and CFRP, and decennial maintenance for the first 10 years. EoL costs involve demolition, sorting, and transportation to recycling plants or landfills as appropriate. Future costs are converted to present value using a 2% social discount rate, which aligns with long-term sustainability objectives []. The LCCA used unit price analyses from the CYPE construction cost database, which included specific costs for Ecuador with a cutoff date of January 2025.
The environmental and social dimensions are evaluated across four distinct phases. First, the objective and scope of the study are to assess five seismic retrofitting alternatives for reinforced concrete beams with shear deficiencies. The functional unit is the seismic retrofitting of a specific reinforced concrete beam, ensuring structural safety over a 50-year service life. A cradle-to-grave approach is adopted, covering material fabrication, transportation to the site, construction, preventive maintenance, and end-of-life. The end-of-life stage includes pre-treatment of concrete, transporting steel and concrete to recycling plants, and final disposal of CFRP to a landfill.
The second phase consisted of conducting an inventory analysis for each alternative. Environmental impacts were assessed using the Ecoinvent database, while social impacts were assessed using SOCA v2, with both analyses modeled in OpenLCA version 2.3 software. By using SOCA, which integrates data from the PSILCA social database, the same processes applied in the environmental impact assessment were used, ensuring consistency in the results. As the global SOCA data are complete but region-specific data may be missing, the global average was used for process modeling, following the reference recommendation []. The energy required for machinery operations during construction was obtained from the BEDEC database. For the SCJ alternative, the additional energy required for shotcrete application was considered and extracted from BEDEC. For the STA alternative, the energy values for machinery operations during construction were adapted from reference []. For carbon fiber, the energy results for virgin carbon fiber production from reference [] were adapted to Ecoinvent’s carbon fiber reinforced plastic process used in aircraft manufacturing. Table 2 presents the inventory by functional unit and the associated processes from the Ecoinvent database, which were also used in SOCA. A zero discount rate was applied for future end-of-life quantifications.

Table 2.
Life cycle inventory.
In the third phase, the Endpoint Recipe method was employed to assess environmental impacts. At the same time, the Social Impact Weighting Methodology (MISP) was used to evaluate social impacts, and both models were modeled using OpenLCA software. Pedigree matrix approaches were incorporated to account for uncertainty based on five indicators: reliability, completeness, temporal correlation, geographical correlation, and technological correlation.
In the final phase, the environmental results were interpreted by grouping the impacts into three damage categories: ecosystems (measured in species per year), human health (measured in disability-adjusted life years), and resource availability (measured in US dollars). A hierarchical approach was used for a long-term scenario (H), with the three damage categories normalized using the WORLD ReCiPe methodology, following H/H hierarchies (person/year). The Final Recipe method was then applied to calculate each retrofit alternative’s full life-cycle environmental impact score. For social impacts, the MISP methodology translates the 55 indicators into four stakeholder categories: Workers, Value Chain Actors, Society, and the Local Community. These impacts are measured using a unit average mean risk per hour (MRH).
3.3. Decision Model
The decision model incorporated four dimensions represented by eight criteria and 16 specific indicators, as shown in Table 3. The criteria reflect the impacts identified through life cycle analysis using a cradle-to-grave approach for the economic, environmental, and social dimensions. The functionality dimension includes two criteria commonly employed by researchers in selecting optimal building retrofitting solutions using MCDM: the duration of construction works and the architectural impact of the retrofit alternative [].

Table 3.
Hierarchical tree of the decision model.
The economic dimension is represented by two criteria: C1: Construction costs, which include construction costs, materials, equipment, machinery, labor, and minor tools. C2: Maintenance and EoL, which include preventive maintenance, such as carbonation protection for CJ and SCJ, anti-corrosion paint for STE and STA, and fireproof mortar for STE, STA, and CFRP. This criterion also includes decennial maintenance and EoL costs, such as crushing for CJ, transportation to material plants for CJ, STE, and STA for recycling, and transportation to landfills for CFRP. According to the LCCA, all costs are measured in dollars. Future costs consider a social discount rate of 2% to reflect long-term sustainability issues.
Environmental dimensions encompass two criteria reflecting the environmental impacts throughout the life cycle: C3: Production and Construction covers the impacts associated with the production of materials, transportation to the site, and energy consumed by machinery during the installation of the retrofit alternative. C4: Maintenance and EoL consider the impacts of producing raw materials required for preventive maintenance of each alternative and the end-of-life phase, including treatment before recycling CJ and SCJ and transport to recycling facilities or landfills. These criteria are evaluated using indicators that measure impacts within three damage categories: Ecosystems, Human Health, and Resources. Impacts are quantified in points derived from the Endpoint ReCiPe method.
The social dimension includes two criteria grouping four stakeholder categories: C5: Local community and society and C6: Stakeholders and value chain workers. Social impacts are measured in Mean Risk per Hour (MRH).
The Functionality dimension is represented by two criteria: C7: Duration of works, evaluated using a scale based on CYPE cost analysis performances. C8: Architectural impact, evaluated by a scaling approach translating the qualitative judgments of the decision-makers using the AHP and pairwise comparisons of the five alternatives. Six decision-makers with professional experience in civil engineering and architecture were consulted to ensure a diversity of perspectives and approaches. These experts have between 10 and 35 years of academic and professional experience in structural engineering, construction, and sustainability.
4. Analysis of Results
4.1. Results of Life Cycle Assessments
Figure 3 illustrates the results of the LCCA for alternatives to retrofit the beam with shear deficiencies. The costs are expressed as present values as of January 2025. Construction costs are the most significant component of the total costs, accounting for an average of 82% across all alternatives. The CFRP alternative incurs the highest construction costs due to the expensive raw materials. CJ ranks second, mainly due to the high cost of the formwork system required. The STE and STA alternatives have the highest costs in the maintenance stage. This is attributed to the inclusion of two types of preventive maintenance: anti-corrosion paint with fireproofing mortar, which represents a 2.3 times increase compared to the preventive maintenance cost of the CJ alternative. In the EOL phase, the costs are especially significant for the CJ and SCJ alternatives due to the requirements for the pretreatment of concrete waste. The percentages shown in Figure 3 represent the total LCCA values, with the CJ alternative as the benchmark. The SCJ alternative has the lowest total costs, with a 45% reduction, while the CFRP alternative has an increase of 1%.
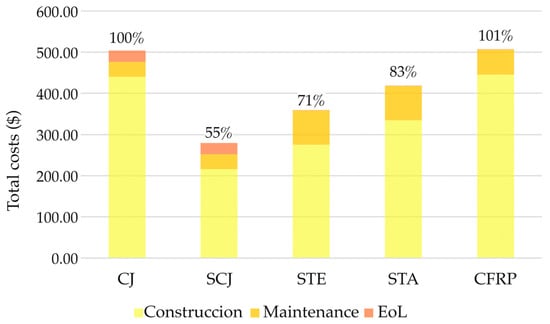
Figure 3.
Economic life cycle assessment.
The ReCiPe endpoint approach provides straightforward LCA results for environmental impacts, offering a clear overview of the effects associated with each alternative. Figure 4 highlights the impacts across damage categories: Ecosystems, Human Health, and Resources. The manufacturing phase has the highest impact in all damage categories, with the exception of the STE alternative, which has the highest values for the preventive maintenance stage in the Ecosystems category. In the EoL phase, impacts are substantial for CJ and SCJ. Regarding total impact values measured in points, the Resources category has the highest representation, followed by Human Health and Ecosystems. Among all alternatives, CJ exhibits the highest environmental impact. SCJ ranks second but achieves the most significant reduction in the Resources damage category, with a 21% decrease compared to CJ. Despite requiring higher energy consumption for machinery operations during the manufacturing and application of shotcrete, SCJ benefits from the reduction of structural adhesives, which helps lower its overall environmental impact. STE and STA alternatives offer substantial ecological advantages, particularly in the Human Health category, with reductions of 69% for STE and 79% for STA compared to CJ. Similarly, CFRP presents significant benefits with reductions of 54% in the Ecosystems category, 70% in Human Health, and 56% in Resources compared to CJ. Similarly, the Figure 4d) summarizes the total environmental impacts of the retrofit alternatives. CJ has the highest overall impact, while SCJ achieves a 19% reduction. CFRP shows a 59% decrease, and the lowest environmental impacts are observed for the STE and STA alternatives, with decreases of 62% and 77%, respectively, compared to CJ.
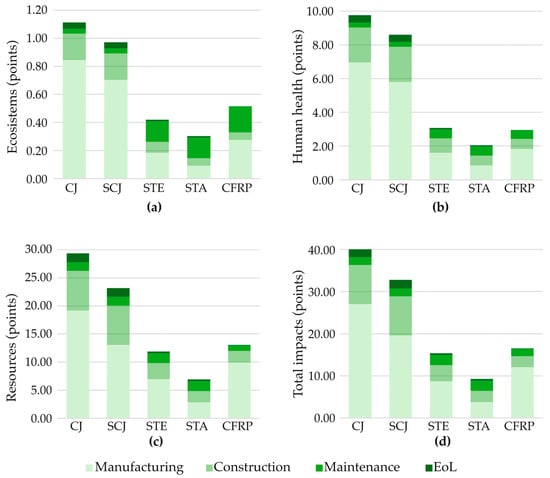
Figure 4.
Environmental life cycle assessment. (a) ecosystems; (b) human health; (c) resources; (d) total impacts.
The impacts associated with the S-LCA are represented in Figure 5, where the highest values are for the Workers and Society stakeholders of the alternatives. The most significant social impacts are found in the CJ alternative. SCJ presents a total decrease in social impacts of 21% regarding CJ, and the STE alternative is 61%. The most significant reductions correspond to the CFRP alternative, with a reduction of 68%, and STA, with the most significant reduction of 75%.
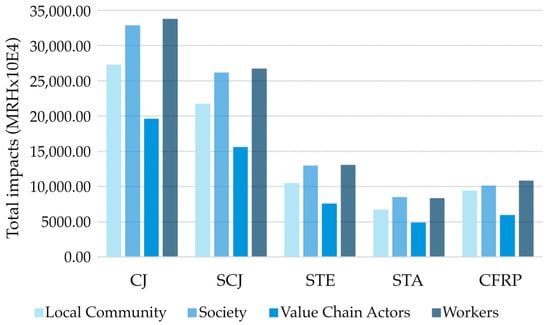
Figure 5.
Social life cycle assessment.
4.2. Selecting the Optimal Retrofit Alternative
Table 4 presents the values of indicators representing the economic, environmental, social, and functional dimensions for the five retrofit alternatives considered. Costs are expressed in dollars, environmental indicators in points, social indicators in average mean risk per hour, and functionality on a standardized scale. Based on these values, the eight criteria were determined for use in the decision-making process. Figure 6 illustrates the normalized values for each criterion across all alternatives. The CJ alternative shows the highest values for environmental, social, and functional criteria, while the CFRP alternative scores highest for criterion C1. STE and STA exhibit the highest values for criterion C2, corresponding to preventive maintenance costs and end-of-life impacts. SCJ has the lowest construction cost, STE achieves the lowest value for criteria C7, and STA for criteria C3, C5, and C6. Lastly, the CFRP alternative demonstrates the weakest values for criteria C2, C4, and C8.

Table 4.
Values of the indicators for each alternative.
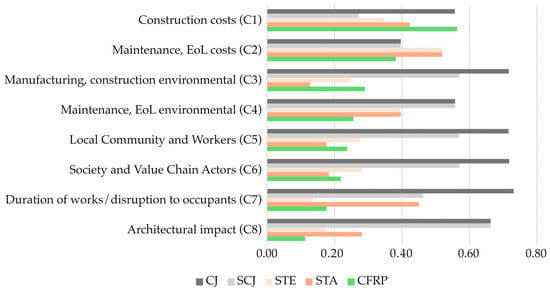
Figure 6.
Normalized values of the criteria.
Table 5 presents the geometric mean values of the weights derived using the BWM method for both the criteria and dimensions analyzed. The criterion with the lowest weighting was the environmental impact of the maintenance and EoL phases, followed by the costs associated with maintenance and EoL and the social impacts on the local community and workers. In contrast, architectural impact and construction cost were identified as the most important criteria. Table 6 shows the results of the ranking methods applied in this study. The CJ alternative was the worst-rated in all cases, followed by the SCJ alternative. The STA alternative ranked third in all methods. The EDAS and MABAC methods identified the STE alternative as the best option for seismic retrofitting of shear-deficient beams, with CFRP ranking second. CODAS and MARCOS methods ranked CFRP as the best option, followed by the STA alternative.

Table 5.
Weights derived from BWM.

Table 6.
Classification of alternatives with MCDM.
5. Discussion
In the search for optimal seismic retrofit strategies, the scientific community has predominantly relied on traditional MCDM methods, often overlooking innovative approaches that could provide better solutions. This study presents a comprehensive methodology for ranking seismic retrofit alternatives using emerging MCDM techniques. The methodology integrates functionality with the three pillars of sustainability-economic, environmental, and social life cycle analysis. The proposed approach is applied to evaluate and rank five seismic retrofit alternatives for a reinforced concrete beam with shear deficiencies. These retrofit alternatives were designed to achieve the same increase in shear strength to meet seismic regulations. The analysis considers a time frame beginning from the implementation of the retrofit and extending up to a useful life of 50 years or until the beam sustains damage from an earthquake. The inclusion of specific preventive maintenance, tailored to the material characteristics of each alternative, ensures the validity of this time frame. This approach eliminates the possibility of one retrofit alternative having a longer lifespan, allowing for a fair comparison [].
Determining the shear capacity of reinforced concrete beams remains an evolving area of research. Most shear design methods use an additive approach, combining the contributions of concrete and steel. However, Eurocode 2 considers only the steel contribution to shear strength [], which can lead to an underestimation of the shear capacity in lightly shear-strengthened beams where the concrete contribution is more significant []. This manuscript’s methods for designing the retrofitting alternatives are based on an additive approach that considers the contributions of concrete, steel, and composites. This approach resulted in comparable increases in shear strength capacity across the different retrofit alternatives, assuming that all resistance mechanisms reach their maximum values simultaneously without any interaction between them. Although this additive approach is widely accepted, recent research has indicated potential interactions between the experimental strength contributions of FRP shear reinforcement [].
The relatively high increase in shear force observed in the concrete-based alternatives is mainly due to construction limitations, as additional concrete is required even when it is not structurally necessary []. For alternatives involving steel plates, the contribution to shear stress is considered a function of the depth and thickness of the continuous plates. However, in the case of STE, where the plates are not fully anchored to the concrete, they may not reach maximum strength at the elastic limit. To take this into account, previous studies [,] have introduced modification factors that consider the tensile capacity of the concrete at the concrete-adhesive interface, with a reduction factor of 0.76 being applicable in this case. For the STA, the contribution of the bolts to the shear capacity could also be considered []; however, theoretical models to accurately predict shear capacity are still under development [].
The depth of the beam below the slab limits the bond length or connection length of the steel and CFRP coatings. As a result, the bond length can be shorter than the required development length, leading to premature failure of the rehabilitation system and limiting the effective utilization of the high-strength properties of the laminates. For the STE alternative, steel plates contribute more significantly to the shear resistance of the beam when the ratio of plate depth to beam depth reaches its maximum feasible value. Studies have shown that, for ratios greater than 0.75, the contribution of the plate remains unchanged, which is particularly advantageous for T beams and beams located under slabs []. In this study, the ratio was 0.70. On the other hand, shear reinforcement using CFRP laminates with anchors can increase shear capacity by approximately 20% or more compared to CFRP laminates without anchors [,]. However, the ACI 440 design guidelines provide conservative and reliable predictions, guaranteeing safe retrofitting designs for beams with a shear deficiency with CFRP laminates []; there are currently no standardized guidelines for anchor design.
By analyzing the cost-effectiveness of the retrofitting alternatives, their economic viability can be assessed by determining the cost required to achieve a 1% increase in shear strength []. Table 7 presents the retrofitting costs obtained through LCCA for a 1% increase in shear strength in the different alternatives. Among the alternatives, the SCJ method demonstrates the lowest cost per 1% increase in shear strength, making it the most cost-effective option. In contrast, the CFRP alternative incurs the highest costs. However, despite its cost-effectiveness, concrete jacketing has certain drawbacks, especially in labor-intensive construction processes, long execution times, and reduced usable space inside the building []. The viability of the retrofitting strategies was evaluated using two criteria: C7–Duration of the work and C8–Architectural impact. The results indicate that CJ has the highest value for C7, while both CJ and SCJ have the highest values for C8.

Table 7.
Cost-effectiveness of the alternatives.
Retrofitting alternatives involving the use of concrete generate significant environmental, social, and functional impacts. These high environmental impacts and associated social consequences are primarily due to concrete production, further exacerbated by the large quantities required for these retrofit methods, even when not structurally necessary. The environmental and social impacts of SCJ are lower than CJ due to the reduction of structural adhesive in the retrofit process. Although the shotcrete and equipment required for SCJ are more expensive than conventional concrete, the cost of SCJ is reduced by avoiding extensive formwork systems and the reduction of structural adhesives required for CJ. Alternatives that include concrete have notable architectural impacts, but CJ has the highest execution time, contributing to its lower ranking. Consequently, CJ and SCJ are ranked fifth and fourth among the retrofit alternatives.
Steel jacketing alternatives significantly reduce environmental and social impacts and lower construction costs; this is attributed to the efficient use of materials by placing continuous steel plates on both sides of the beam web. This retrofitting technique effectively enhances shear strength and ductility, achieving higher shear capacity by increasing the height of the plates rather than their thickness []. However, the highest preventive maintenance costs for steel jacketing alternatives are due to the need for anti-corrosion paint and fireproof mortar. The STA alternative shows reduced environmental and social impacts compared to STE, primarily because it eliminates using epoxy resin-based thixotropic adhesives. Nevertheless, STA involves higher construction costs, longer execution times, and more significant architectural impacts due to the anchor bolts required, ranking it third among the alternatives. The incorporation of carbon fibers presents reductions in environmental and social impacts, shorter execution times, and minimal architectural impacts, although its construction costs are high. The STE and CFRP retrofit alternatives lead the alternatives in the ranking.
In construction engineering, decision-making often involves conflicting criteria. In the search for optimal seismic retrofit solutions, economic, environmental, and social impacts, lead times, and architectural considerations can result in conflicting criteria for different retrofit alternatives. Various MCDM methods are available in the literature to address such complexities. Among them, the widely used AHP and TOPSIS combine antiquity and ease of application. However, little attention has been given to exploring newer, more advanced decision-making methods. AHP remains the most commonly applied method for criteria weighting. However, the BWM has emerged as a robust alternative in the MCDM field, offering reliable and relevant results. Unlike the arbitrary pairwise comparisons in AHP, BWM employs a systematic approach []. It requires fewer pairwise comparisons, reducing inconsistencies and producing more reliable outcomes than AHP []. One of the concerns in applying different MCDM methods is the rank reversal problem. This issue occurs when the ranking of alternatives changes depending on the method used, leading to inconsistencies in decision-making [].
The STE alternative ranks first in the EDAS and MABAC methods, followed closely by CFRP. In the MARCOS method, CFRP ranks first, narrowly edging out STE. In contrast, the CODAS method places CFRP in first place, with a significant advantage over STE in second place. This study has considered input from diverse experts to capture different professional, academic, and research perspectives. However, the weighting of criteria often introduces uncertainty in the application of MCDM methods, which can significantly influence decision-making results. The results indicate that STE is the highest-ranked alternative in the two methods, while CFRP leads in the remaining two. An important step in the application of MCDM is the sensitivity analysis of aspects that can significantly alter the results, thus ensuring consistency in the final decision []. In order to support the robustness of these results, a sensitivity analysis was performed to examine how variations in the weighting of the criteria might affect the rankings. The analysis included positive and negative weighting variations of 10% and 15%, resulting in 16 scenarios. An additional scenario was considered in which all criteria had the exact weighting. Rankings were then generated for each scenario across all MCDM methods, providing valuable information on the consistency and reliability of the decision-making process.
Figure 7 presents the results for a ±15% variation in the criteria weights, as no significant changes were observed with a 10% variation. Across the 68 scenarios analyzed, CJ consistently ranks last, while SCJ occupies fourth place in all MCDM rankings. In the EDAS method, STE ranks first in 14 scenarios. CFRP leads the ranking when the weight of the construction cost criterion is reduced when the architectural impact criterion is increased and in the scenario with equal weights for all criteria. Similarly, in the MABAC method, STE ranks first in 15 scenarios. At the same time, CFRP emerges as the best option when construction costs are lower and in the equal-weight scenario. CFRP is consistently ranked as the best option across all scenarios analyzed for the CODAS and MARCOS methods. Notably, STA ranks second when the environmental impact weight during the manufacturing stage is increased in the CODAS method and when equal weights are applied in both the CODAS and MARCOS methods. Based on the results from the four MCDM methods and the weight variations applied in the sensitivity analysis, CFRP emerges as the best option in 57% of cases. At the same time, STE is the top choice in 43% of cases.
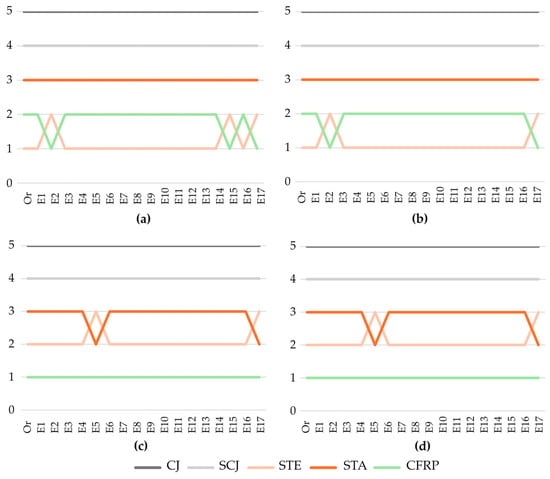
Figure 7.
Sensitivity analysis. (a) EDAS; (b) MABAC; (c) CODAS; (d) MARCOS.
Traditional retrofit techniques, which consist of increasing the concrete section and using steel profiles, are widely used worldwide []. Applying U-jacketing reinforced concrete sleeves to retrofit beams with shear deficiencies is an ongoing development within the scientific community to address key challenges, such as limited section increase. A group of researchers conducted an experimental study using thin layers of U-shaped reinforced concrete to retrofit shear-critical beams, evaluating the performance of these jackets []. Similarly, another group explored the effectiveness of U-shaped reinforced cementitious mortar liners for repairing damaged shear-critical beams []. In another study, they analyzed beams representing older construction practices with inadequate stirrup spacing, which leads to premature shear failure. They applied a three-sided coating method using thin sleeves of self-compacting reinforced concrete [].
The retrofitting alternatives in this study focus on improving shear strength in reinforced concrete beams. However, concrete jackets allow the sections to behave similarly to conventional sections of the exact dimensions. A group of researchers analyzed the load-displacement curves and the corresponding ductilities, concluding that retrofitting reinforced concrete beams exhibits mechanical behavior comparable to and slightly better than ordinary reinforced concrete beams of the same size []. As for CFRP, significant improvements in ductility have been determined up to the point of lamina detachment []. Similarly, another group studied the retrofitting of shear-critical reinforced concrete beams using various FRP systems. It concluded that retrofitting improved shear capacity and transformed shear failure into more ductile flexural failure []. In addition, an experimental study examined the effects of steel plates attached to the web of the beam, either with adhesives or bolts, showing significant improvements in beam stiffness—by 29% and 42%, respectively—as well as more excellent ductility when more bottomless plates are used [].
This study classified five retrofit alternatives based on coating techniques for jacketing beams with shear deficiencies. However, the literature highlights additional techniques that achieve the same retrofit objective. One such method is shear beam retrofit through external prestressing, where a restoring force is applied via externally placed, non-adhered tendons. This approach is known for its ease of application, cost-effectiveness, and straightforward maintenance [,]. In recent years, ultra-high-performance concrete (UHPC) has been proposed to retrofit reinforced concrete structural elements. In beams, UHPC has been shown to prevent shear failure and enhance flexural performance, increasing strength by 40% to 125%, making it a promising emerging alternative [].
The durability of the retrofitting alternatives is considered within the time frame of this study, starting from implementation and extending up to 50 years or until the retrofitting beam sustains damage due to an earthquake. While seismically retrofit structures typically perform well under expected earthquake scenarios, this does not guarantee their continued operability after a seismic event []. For the CJ and SCJ alternatives, the brittle shear failure mode is effectively mitigated. In shallow beam jacketing with a span-to-depth ratio greater than 2.5, the retrofitted section can achieve ductile flexural failure modes [], improving flexural strength, energy dissipation, and ductility []. The STE alternative effectively controls cracking under the steel plate; however, its anchoring capacity is limited by the tensile strength of the concrete under the adhesive. This limitation can lead to a risk of explosive detachment of the steel plate. In the case of the STA alternative, stresses at the fixing points can cause localized creep of the steel plate and crushing of the adjacent concrete. However, with adequate anchoring, more excellent ductility can be achieved at the point of failure []. Finally, the CFRP alternative improves crack resistance, promoting a shift to a ductile failure mode. However, two main failure modes are observed: detachment from the concrete surface and rupture of the CFRP. In the first scenario, the beams may fail prematurely under the initial load before the CFRP reaches its maximum capacity. In the second scenario, rupture governs the shear capacity [,]. Future research could focus on the need for resilient buildings that account for the challenges posed by seismic damage, including restoring functionality amidst physical, social, and economic disruptions over time [].
6. Conclusions
This paper presents a comprehensive methodology for selecting seismic retrofitting solutions for reinforced concrete beams with shear deficiencies. Five retrofit alternatives designed to improve the shear capacity in the expected plastic hinge formation zone were evaluated to ensure compliance with current seismic regulations. A service life of 50 years was considered for each alternative, with preventive maintenance adapted to the specific properties of the material. The retrofit alternatives evaluated include concrete jacket (CJ), shotcrete jacket (SCJ), steel jacket with structural epoxy adhesive (STE), steel jacket with mechanical anchors (STA), and incorporation of carbon fiber reinforced polymer (CFRP). A hierarchical decision-making model encompassed four dimensions-functionality, economic, environmental, and social- and was analyzed through eight criteria and measured by 16 specific indicators. The BWM method was applied to weigh the criteria and rank the reinforcement alternatives. At the same time, four new MCDM methods were used for the final ranking: EDAS, MABAC, CODAS, and MARCOS.
Life cycle assessments of the economic, environmental, and social dimensions were conducted using a “cradle to grave” approach. The SCJ and STE alternatives demonstrate cost reductions compared to the traditional CJ option. The STE, STA, and CFRP alternatives offer substantial environmental and social advantages over the concrete-based CJ and SCJ alternatives. Compared to the CJ alternative, the STA alternative achieves the most significant reductions in environmental and social impacts, with decreases of 76% and 73%, respectively. STE shows reductions of 61% and 59%, while CFRP achieves reductions of 58% and 66%, respectively, in environmental and social impacts. In addition, STE and CFRP show the shortest execution times and lowest architectural impacts among the alternatives evaluated.
Based on the assumptions of this study, the CFRP and STE alternatives emerge as the preferred options when economic, environmental, social, and functional criteria are considered together. Retrofitting with carbon fiber significantly reduces environmental and social impacts while enhancing functionality despite the high costs associated with the raw materials. Steel jacketing with structural epoxy adhesive is also viable, providing balanced performance across all criteria and outperforming the alternative incorporating structural steel with mechanical anchors. In contrast, alternatives involving concrete are the least favorable due to their high environmental and social impacts coupled with lower functionality.
This study evaluated five commonly used alternatives for seismic retrofitting shear-deficient beams. Future research could explore additional options, including fiber-reinforced polymeric materials and innovative composite materials, such as concrete composite linings and fiber-reinforced cement mortars. Further studies could also incorporate criteria that address the final capacity characteristics of the retrofit element and address the need for resilient buildings capable of recovering quickly after an earthquake to maintain functionality in a shorter time frame. Additionally, the application of MCDM methods could be improved by integrating approaches to manage the uncertainty inherent in expert opinion and considering interactions between criteria, ultimately improving the robustness of solutions.
Author Contributions
This study represents a result of teamwork Conceptualization, P.V., B.G. and V.Y.; methodology, P.V., B.G. and V.Y.; validation, P.V. and B.G.; writing—original draft, P.V. and B.G.; writing—review and editing, V.Y.; resources, V.Y.; supervision, V.Y.; project administration, V.Y.; funding acquisition, V.Y. All authors have read and agreed to the published version of the manuscript.
Funding
Grant PID2023-150003OB-I00 funded by MCIN/AEI/10.13039/501100011033 and by “ERDF A way of making Europe”.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data will be made available on request.
Acknowledgments
The first two authors are grateful to the Universidad Central del Ecuador for funding to pursue a doctoral program at the Universitat Politècnica de València.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| RC | Reinforced concrete |
| FRP | Fiber-reinforced polymer |
| CE | Circular economy |
| MCDM | Multi-criteria decision-making |
| MADM | Multiple attribute decision-making |
| LCA | Life cycle assessment |
| AHP | Analytical Hierarchy Process |
| TOPSIS | Technique for Order of Preference by Similarity to Ideal Solution |
| DM | Decision-maker |
| ANP | Analytical Network Process |
| BWM | Best-Worst Method |
| EDAS | Evaluation Based on Distance to Average Solution |
| MABAC | Multi-Attribute Boundary Approximation Area Comparison |
| CODAS | Combinatorial Distance-Based Assessment |
| MARCOS | Measurement of Alternatives and Ranking According to Compromise Solution |
| LCCA | Life Cycle Cost Assessment |
| S-LCA | Social Life Cycle Assessment |
| CJ | Concrete jacketing |
| SCJ | Shotcrete jacketing |
| STE | Steel jacketing with structural epoxy adhesive |
| STA | Steel jacketing with anchor bolts |
| CFRP | Carbon fiber-reinforced polymer |
| EoL | End-of-life |
| MISP | Social Impact Weighting Methodology |
| MRH | Mean risk per hour |
References
- Hoyos, M.C.; Silva, V. Exploring benefit cost analysis to support earthquake risk mitigation in Central America. Int. J. Disaster Risk Reduct. 2022, 80, 103162. [Google Scholar] [CrossRef]
- Harirchian, E.; Jadhav, K.; Mohammad, K.; Hosseini, S.E.A.; Lahmer, T. A Comparative Study of MCDM Methods Integrated with Rapid Visual Seismic Vulnerability Assessment of Existing RC Structures. Appl. Sci. 2020, 10, 6411. [Google Scholar] [CrossRef]
- Pohoryles, D.A.; Bournas, D.A.; Da Porto, F.; Caprino, A.; Santarsiero, G.; Triantafillou, T. Integrated seismic and energy retrofitting of existing buildings: A state-of-the-art review. J. Build. Eng. 2022, 61, 105274. [Google Scholar] [CrossRef]
- Murray, P.B.; Feliciano, D.; Goldwyn, B.H.; Liel, A.B.; Arroyo, O.; Javernick-Will, A. Seismic safety of informally constructed reinforced concrete houses in Puerto Rico. Earthq. Spectra 2023, 39, 5–33. [Google Scholar] [CrossRef]
- Goldwyn, B.; Vega, Y.G.; Javernick-Will, A.; Liel, A.B. Identifying misalignments between the informal construction sector’s perceptions and engineering assessments of housing safety in future disasters for capacity development. Int. J. Disaster Risk Reduct. 2022, 77, 103105. [Google Scholar] [CrossRef]
- Carrillo, J.; Arteta, C.A.; Vera, X. Post-earthquake safety assessment of schools after the 2016 Ecuador M7.8 earthquake. Soil Dyn. Earthq. Eng. 2024, 179, 108561. [Google Scholar] [CrossRef]
- Goretti, A.; Hutt, C.M.; Hedelund, L. Post-earthquake safety evaluation of buildings in Portoviejo, Manabi province, following the Mw7.8 Ecuador earthquake of April 16, 2016. Int. J. Disaster Risk Reduct. 2017, 24, 271–283. [Google Scholar] [CrossRef]
- Scala, S.A.; De Risi, M.T.; Verderame, G.M. Code-based brittle capacity models for seismic assessment of pre-code RC buildings: Comparison and consequences on retrofit. Bull. Earthq. Eng. 2024, 22, 6643–6674. [Google Scholar] [CrossRef]
- Liu, X.; Thermou, G.E. A review on the shear performance of reinforced concrete (RC) beams strengthened with externally bonded mortar-based composites. Structures 2023, 58, 105474. [Google Scholar] [CrossRef]
- Olalusi, O.B.; Viljoen, C. Assessment of simplified and advanced models for shear resistance prediction of stirrup-reinforced concrete beams. Eng. Struct. 2019, 186, 96–109. [Google Scholar] [CrossRef]
- De Domenico, D.; Ricciardi, G. Shear strength of RC beams with stirrups using an improved Eurocode 2 truss model with two variable-inclination compression struts. Eng. Struct. 2019, 198, 109359. [Google Scholar] [CrossRef]
- Chung, P.-T.; Chou, C.-C. One-sided shear retrofit of reinforced concrete beams in existing high-rise buildings. Eng. Struct. 2022, 252, 113634. [Google Scholar] [CrossRef]
- Liu, X.; Lu, Z.-D.; Li, L.-Z. The Use of Bolted Side Plates for Shear Strengthening of RC Beams: A Review. Sustainability 2018, 10, 4658. [Google Scholar] [CrossRef]
- Naoum, M.C.; Papadopoulos, N.A.; Sapidis, G.M.; Chalioris, C.E. Advanced Structural Monitoring Technologies in Assessing the Performance of Retrofitted Reinforced Concrete Elements. Appl. Sci. 2024, 14, 9282. [Google Scholar] [CrossRef]
- Gonzalez-Libreros, J.H.; Sneed, L.H.; D’Antino, T.; Pellegrino, C. Behavior of RC beams strengthened in shear with FRP and FRCM composites. Eng. Struct. 2017, 150, 830–842. [Google Scholar] [CrossRef]
- Lei, H.; Li, L.; Yang, W.; Bian, Y.; Li, C.-Q. An analytical review on application of life cycle assessment in circular economy for built environment. J. Build. Eng. 2021, 44, 103374. [Google Scholar] [CrossRef]
- Salgado, R.A.; Apul, D.; Guner, S. Life cycle assessment of seismic retrofit alternatives for reinforced concrete frame buildings. J. Build. Eng. 2020, 28, 101064. [Google Scholar] [CrossRef]
- Dong, Y.; Ng, S.T.; Liu, P. Towards the principles of life cycle sustainability assessment: An integrative review for the construction and building industry. Sustain. Cities Soc. 2023, 95, 104604. [Google Scholar] [CrossRef]
- Munoz-Medina, B.; Ordonez, J.; Romana, M.G.; Lara-Galera, A. Typology Selection of Retaining Walls Based on Multicriteria Decision-Making Methods. Appl. Sci. 2021, 11, 1457. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Govindan, K.; Antucheviciene, J.; Turskis, Z. Hybrid multiple criteria decision-making methods: A review of applications for sustainability issues. Econ. Res.-Ekon. Istraz. 2016, 29, 857–887. [Google Scholar] [CrossRef]
- Formisano, A.; Castaldo, C.; Chiumiento, G. Optimal seismic upgrading of a reinforced concrete school building with metal-based devices using an efficient multi-criteria decision-making method. Struct. Infrastruct. Eng. 2017, 13, 1373–1389. [Google Scholar] [CrossRef]
- Fiore, P.; Donnarumma, G.; Falce, C.; D’Andria, E.; Sicignano, C. An AHP-Based Methodology for Decision Support in Integrated Interventions in School Buildings. Sustainability 2020, 12, 181. [Google Scholar] [CrossRef]
- Santa-Cruz, S.; Cordova-Arias, C.; Brioso, X.; Vazquez-Rowe, I. Transparency-based protocol for decision-making regarding seismic rehabilitation projects of public buildings. Int. J. Disaster Risk Reduct. 2021, 55, 102116. [Google Scholar] [CrossRef]
- Clemett, N.; Gallo, W.W.C.; O’Reilly, G.J.; Gabbianelli, G.; Monteiro, R. Optimal seismic retrofitting of existing buildings considering environmental impact. Eng. Struct. 2022, 250, 113391. [Google Scholar] [CrossRef]
- Villalba, P.; Sánchez-Garrido, A.J.; Yepes, V. Life cycle evaluation of seismic retrofit alternatives for reinforced concrete columns. J. Clean. Prod. 2024, 455, 142290. [Google Scholar] [CrossRef]
- Villalba, P.; Sánchez-Garrido, A.J.; Yepes, V. A review of multi-criteria decision-making methods for building assessment, selection, and retrofit. J. Civ. Eng. Manag. 2024, 30, 465–480. [Google Scholar] [CrossRef]
- Zhu, X.; Meng, X.; Zhang, M. Application of multiple criteria decision making methods in construction: A systematic literature review. J. Civ. Eng. Manag. 2021, 27, 372–403. [Google Scholar] [CrossRef]
- Cavalieri, F.; Bellotti, D.; Caruso, M.; Nascimbene, R. Comparative evaluation of seismic performance and environmental impact of traditional and dissipation-based retrofitting solutions for precast structures. J. Build. Eng. 2023, 79, 107918. [Google Scholar] [CrossRef]
- Pushkar, S.; Halperin, I.; Ribakov, Y. Life-Cycle Assessment of Contemporary and Classical Seismic Retrofitting Approaches Applied to a Reinforced Concrete Building in Israel. Buildings 2022, 12, 1854. [Google Scholar] [CrossRef]
- Vitiello, U.; Salzano, A.; Asprone, D.; Di Ludovico, M.; Prota, A. Life-Cycle Assessment of Seismic Retrofit Strategies Applied to Existing Building Structures. Sustainability 2016, 8, 1275. [Google Scholar] [CrossRef]
- Passos Neto, G.d.M.; Alencar, L.H.; Valdes-Vasquez, R. Multiple-Criteria Methods for Assessing Social Sustainability in the Built Environment: A Systematic Review. Sustainability 2023, 15, 16231. [Google Scholar] [CrossRef]
- Sánchez-Garrido, A.J.; Navarro, I.J.; Yepes, V. Multi-criteria decision-making applied to the sustainability of building structures based on Modern Methods of Construction. J. Clean. Prod. 2022, 330, 129724. [Google Scholar] [CrossRef]
- Goldani, N.; Ishizaka, A. A hybrid fuzzy multi-criteria group decision-making method and its application to healthcare waste treatment technology selection. Ann. Oper. Res. 2024, 1–26. [Google Scholar] [CrossRef]
- Rezaei, J. Best-worst multi-criteria decision-making method. Omega-Int. J. Manag. Sci. 2015, 53, 49–57. [Google Scholar] [CrossRef]
- Ghorabaee, M.K.; Zavadskas, E.K.; Olfat, L.; Turskis, Z. Multi-Criteria Inventory Classification Using a New Method of Evaluation Based on Distance from Average Solution (EDAS). Informatica 2015, 26, 435–451. [Google Scholar] [CrossRef]
- Pamucar, D.; Cirovic, G. The selection of transport and handling resources in logistics centers using Multi-Attributive Border Approximation area Comparison (MABAC). Expert Syst. Appl. 2015, 42, 3016–3028. [Google Scholar] [CrossRef]
- Ghorabaee, M.K.; Zavadskas, E.K.; Turskis, Z.; Antucheviciene, J. A new combinative distance-based assessment (codas) method for multi-criteria decision-making. Econ. Comput. Econ. Cybern. Stud. Res. 2016, 50, 25–44. [Google Scholar]
- Stevic, Z.; Pamucar, D.; Puska, A.; Chatterjee, P. Sustainable supplier selection in healthcare industries using a new MCDM method: Measurement of alternatives and ranking according to COmpromise solution (MARCOS). Comput. Ind. Eng. 2020, 140, 106231. [Google Scholar] [CrossRef]
- MIDUVI, Norma Ecuatoriana de la Construcción, 2015, NEC; Ministerio de Desarrollo Urbano y Vivienda: Quito, Ecuador, 2015.
- Adhikary, B.B.; Mutsuyoshi, H. Shear strengthening of RC beams with web-bonded continuous steel plates. Constr. Build. Mater. 2006, 20, 296–307. [Google Scholar] [CrossRef]
- Allacker, K. Environmental and economic optimisation of the floor on grade in residential buildings. Int. J. Life Cycle Assess. 2012, 17, 813–827. [Google Scholar] [CrossRef]
- Jiang, T.; Yin, P.; Jin, Q. Performances of typical photovoltaic module production from the perspective of life cycle sustainability assessment. Sustain. Energy Technol. Assess. 2024, 64, 103703. [Google Scholar] [CrossRef]
- Palacios-Munoz, B.; Gracia-Villa, L.; Zabalza-Bribian, I.; Lopez-Mesa, B. Simplified structural design and LCA of reinforced concrete beams strengthening techniques. Eng. Struct. 2018, 174, 418–432. [Google Scholar] [CrossRef]
- Akbar, A.; Liew, K.M. Multicriteria performance evaluation of fiber-reinforced cement composites: An environmental perspective. Compos. Part B-Eng. 2021, 218, 108937. [Google Scholar] [CrossRef]
- Bertolli, V.; Sneed, L.H.; Focacci, F.; D’Antino, T. Shear Strengthening of RC Beams with U-Wrapped FRCM Composites: State of the Art and Assessment of Available Analytical Models. J. Compos. Constr. 2025, 29, 4024091. [Google Scholar] [CrossRef]
- Rakib, M.A.; Morshed, A.Z. Shear strengthening design of pre-cracked reinforced concrete beams using bonded and bolted steel plates. Aust. J. Struct. Eng. 2023, 24, 159–172. [Google Scholar] [CrossRef]
- Li, L.Z.; Cai, Z.W.; Lu, Z.D.; Zhang, X.L.; Wang, L. Shear performance of bolted side-plated reinforced concrete beams. Eng. Struct. 2017, 144, 73–87. [Google Scholar] [CrossRef]
- Mhanna, H.H.; Hawileh, R.A.; Abdalla, J.A. Shear strengthening of reinforced concrete T-beams using CFRP laminates anchored with bent CFRP splay anchors. Procedia Struct. Integr. 2020, 28, 811–819. [Google Scholar] [CrossRef]
- Kalfat, R.; Jumaah, R.; Al-Mahaidi, R.; Abdouka, K.; Hashemi, J. Post-Tensioned Concrete Beams Strengthened in Shear Using Fiber-Reinforced Polymer Laminates and Patch Anchors. J. Compos. Constr. 2020, 24, 4019065. [Google Scholar] [CrossRef]
- Mhanna, H.H.; Hawileh, R.A.; Abdalla, J.A.; Salama, A.S.D.; Alkhrdaji, T. Shear Strengthening of Reinforced Concrete T-Beams with Anchored CFRP Laminates. J. Compos. Constr. 2021, 25, 4021030. [Google Scholar] [CrossRef]
- Lee, S.-H.; Lee, H.-D. Shear strengthening effect by external post-tensioning steel rods in damaged reinforced concrete beams. Structures 2024, 62, 106327. [Google Scholar] [CrossRef]
- Chalioris, C.E.; Kytinou, V.K.; Voutetaki, M.E.; Papadopoulos, N.A. Repair of Heavily Damaged RC Beams Failing in Shear Using U-Shaped Mortar Jackets. Buildings 2019, 9, 146. [Google Scholar] [CrossRef]
- Balali, A.; Valipour, A. Prioritization of passive measures for energy optimization designing of sustainable hospitals and health centres. J. Build. Eng. 2021, 35, 101992. [Google Scholar] [CrossRef]
- Pamucar, D.; Ecer, F.; Cirovic, G.; Arlasheedi, M.A. Application of Improved Best Worst Method (BWM) in Real-World Problems. Mathematics 2020, 8, 1342. [Google Scholar] [CrossRef]
- Navarro, I.J.; Yepes, V.; Marti, J.V. A Review of Multicriteria Assessment Techniques Applied to Sustainable Infrastructure Design. Adv. Civ. Eng. 2019, 2019, 6134803. [Google Scholar] [CrossRef]
- Chalioris, C.E.; Thermou, G.E.; Pantazopoulou, S.J. Behaviour of rehabilitated RC beams with self-compacting concrete jacketing—Analytical model and test results. Constr. Build. Mater. 2014, 55, 257–273. [Google Scholar] [CrossRef]
- Altun, F. An experimental study of the jacketed reinforced-concrete beams under bending. Constr. Build. Mater. 2004, 18, 611–618. [Google Scholar] [CrossRef]
- Waqas, R.M.; Elahi, A.; Kırgız, M.S. Experimental and finite element analysis of shear deficient of reinforced concrete beam retrofitted externally with carbon fiber reinforced polymer sheet. Structures 2025, 72, 108232. [Google Scholar] [CrossRef]
- Baggio, D.; Soudki, K.; Noël, M. Strengthening of shear critical RC beams with various FRP systems. Constr. Build. Mater. 2014, 66, 634–644. [Google Scholar] [CrossRef]
- Giuseppe Santarsiero, V.P.; Masi, A. Structural rehabilitation of half-joints in RC bridges: A state-of-the-art review. Struct. Infrastruct. Eng. 2025, 21, 227–250. [Google Scholar] [CrossRef]
- Li, C.; Aoude, H. Blast retrofit of shear-deficient high-strength concrete beams with ultra-high performance concrete. Eng. Struct. 2024, 304, 117619. [Google Scholar] [CrossRef]
- Gallo, W.W.C.; Clemett, N.; Gabbianelli, G.; O’Reilly, G.; Monteiro, R. Seismic Resilience Assessment in Optimally Integrated Retrofitting of Existing School Buildings in Italy. Buildings 2022, 12, 845. [Google Scholar] [CrossRef]
- Chalioris, C.E.; Pourzitidis, C.N. Rehabilitation of Shear-Damaged Reinforced Concrete Beams Using Self-Compacting Concrete Jacketing. Int. Sch. Res. Not. 2012, 2012, 816107. [Google Scholar] [CrossRef]
- Tahsiri, H.; Sedehi, O.; Khaloo, A.; Raisi, E.M. Experimental study of RC jacketed and CFRP strengthened RC beams. Constr. Build. Mater. 2015, 95, 476–485. [Google Scholar] [CrossRef]
- Barnes, R.A.; Baglin, P.S.; Mays, G.C.; Subedi, N.K. External steel plate systems for the shear strengthening of reinforced concrete beams. Eng. Struct. 2001, 23, 1162–1176. [Google Scholar] [CrossRef]
- Askar, M.K.; Hassan, A.F.; Al-Kamaki, Y.S.S. Flexural and shear strengthening of reinforced concrete beams using FRP composites: A state of the art. Case Stud. Constr. Mater. 2022, 17, e01189. [Google Scholar] [CrossRef]
- Chen, J.F.; Teng, J.G. Shear capacity of FRP-strengthened RC beams: FRP debonding. Constr. Build. Mater. 2003, 17, 27–41. [Google Scholar] [CrossRef]
- Hao, H.; Bi, K.; Chen, W.; Pham, T.M.; Li, J. Towards next generation design of sustainable, durable, multi-hazard resistant, resilient, and smart civil engineering structures. Eng. Struct. 2023, 277, 115477. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).