Fast Path Generation Algorithm for Mobile Robot Navigation Using Hybrid Map

Abstract

In this paper, we address the challenge of memory consumption in mobile robot navigation, particularly when using grid-based maps for accurate environment representation. While grid-based maps are widely used, their large memory requirements make them unsuitable for embedded systems. To overcome this limitation, we propose a novel path planning algorithm that rapidly generates secure paths using a hybrid map. This hybrid map significantly reduces memory usage compared to grid-based maps while maintaining the efficiency of a topological map. Experimental results demonstrate that the proposed method requires only 1.5% of the computation time needed for grid-based path planning, ensuring faster and more efficient navigation. Furthermore, the approach provides robust and secure paths, making it ideal for mobile robot applications. This method holds promise for advancing autonomous navigation in resource-constrained environments.

1. Introduction

The rapid advancement of modern society has significantly increased the importance of security and surveillance in various sectors. As the demand for enhanced security measures grows, the number of areas and environments requiring constant monitoring has risen sharply. This has created a substantial reliance on human resources to maintain safety and security. To address these challenges, numerous studies have explored the potential of intelligent mobile robots to enhance surveillance efficiency and reduce the dependence on manual labor [1,2,3,4,5].

Intelligent mobile robots can perform continuous monitoring, detect anomalies, and respond to security threats with minimal human intervention [6,7,8]. These robots are equipped with advanced sensors and decision-making algorithms, enabling them to navigate complex environments and provide real-time feedback. Recent advancements in artificial intelligence and robotics have further improved their capabilities, including better path planning, object recognition, and obstacle avoidance [9,10,11]. Furthermore, the integration of IoT technology allows these robots to collaborate with existing security infrastructure, offering a more comprehensive approach to modern surveillance. This development not only reduces operational costs but also enhances the reliability and consistency of security systems [12,13].

To effectively utilize intelligent mobile robots for security and patrol tasks, navigation challenges must be addressed [14,15,16]. For mobile robots to solve these challenges, several key issues need to be resolved. First, mobile robots require a map that accurately represents their surrounding environment and a path planning algorithm to perform various service tasks [17,18]. The robot must independently navigate to its destination using the environment map. Second, mobile robots must be equipped with an obstacle avoidance algorithm. When encountering obstacles while following a path generated from the environment map, the robot must utilize its sensors to analyze the surroundings and safely avoid the obstacle [19,20].

Additionally, the robot must be capable of dynamically updating its environment map in real time to adapt to changes in its surroundings [21,22,23,24]. This capability ensures reliable navigation in dynamic or unknown environments. Furthermore, the integration of robust decision-making algorithms enables mobile robots to prioritize tasks efficiently, ensuring optimal performance in complex security and patrol operations. These features are essential for the deployment of intelligent robots in real-world applications, where unpredictability and rapid decision-making are common.

Numerous studies have been conducted to develop algorithms that generate safe paths for robots [25,26,27,28]. Path generation algorithms can generally be categorized into two types: those that utilize occupancy grid-based maps and those that rely on topology maps. One widely used approach in grid-based methods is the distance transform algorithm, which creates paths by calculating distance values from the destination to the robot’s starting position. In this algorithm, the robot follows the path by moving toward locations with progressively lower distance values until it reaches its destination. While grid-based path search algorithms are capable of generating precise paths, they present significant limitations. One major drawback is their inability to adapt to new obstacles that may appear during the robot’s movement. Additionally, the computational time required for path calculation increases significantly as the size of the map grows. These challenges highlight the need for more efficient and adaptive approaches to path planning, particularly in dynamic and large-scale environments. Advanced algorithms that combine the precision of grid-based methods with the adaptability of topological approaches could offer a promising solution to these issues.

A commonly used path generation algorithm that utilizes a topological map is Depth First Search (DFS). To apply the DFS algorithm, the environment must first be converted into a graph-type data structure. In the DFS algorithm, the path search time is proportional to the square of the number of nodes in the graph. Despite this, it offers faster path generation compared to grid-based map algorithms. However, a significant drawback is that the robot may struggle to move accurately using the path information generated by the algorithm [29,30,31]. This limitation arises because topological maps often lack the detailed spatial information needed for precise navigation, particularly in complex environments. As a result, additional optimization or hybrid approaches may be required to enhance the accuracy of robot movement while maintaining the efficiency of topological path planning methods.

The previously mentioned occupancy grid-based path generation algorithm and topology map-based path generation algorithm have the following issues. First, both algorithms assume that the robot has access to a pre-generated map before it begins to move. As a result, the robot cannot generate a path if pre-generated map information is unavailable. Second, when using an occupancy grid-based map, the time required for path generation increases significantly with the size of the map.

The rest of this paper is organized as follows. Section 2 describes the research related to the paper. Section 3 describes the structure of the hybrid map and shows the fast path planning using the hybrid map. Section 4 describes the experimental results. Finally, Section 5 describes the conclusion and future plans.

2. Related Works

This paper examines the environment map and path generation algorithm used by mobile robots for path planning. Existing path generation algorithms primarily focus on creating paths that minimize travel time and distance from a specific location to the destination.

2.1. Path Planning

The A* algorithm is one of the most widely used path planning algorithms in mobile robotics [32,33,34]. It efficiently finds the shortest path by combining the cost from the starting point to a node and an estimated cost from that node to the destination. A major advantage of A* is its ability to guarantee an optimal path if the heuristic is admissible and consistent. Additionally, it is flexible and can be adapted to different environments and constraints by modifying the heuristic function. However, A* can be computationally expensive, especially in large maps with high resolution, as it explores a significant number of nodes. This leads to increased memory usage and slower performance in real-time applications. Moreover, it does not handle dynamic obstacles well, requiring a complete re-computation of the path when the environment changes. Despite its limitations, A* is ideal for static environments where precision and optimality are critical.

The Rapidly Exploring Random Tree (RRT) algorithm is a sampling-based path planning method that is particularly effective in high-dimensional and complex environments [35]. It generates a path by randomly sampling points in space and incrementally building a tree that connects the robot’s starting position to the goal. One of its strengths is its ability to handle non-linear constraints and dynamic environments, making it suitable for real-time applications. Additionally, RRT requires less memory and computational resources compared to grid-based methods like A*. However, the paths generated by RRT are often suboptimal and may require additional post-processing to smoothen them. Furthermore, the randomness of the algorithm can lead to inconsistent results, with the quality of the path depending on the sampling process. Despite these drawbacks, RRT is highly versatile and well suited for navigating in complex or unknown environments.

The Distance Transform algorithm is a grid-based path planning method that calculates the shortest path by propagating distance values from the destination to the robot’s starting position [36]. One of its primary advantages is its simplicity and ease of implementation, making it a popular choice for straightforward environments. Additionally, it generates precise paths by taking the exact geometry of obstacles into account, which is useful for environments with static and well-defined boundaries. The algorithm also guarantees optimal paths in terms of distance when no dynamic changes occur in the environment. However, the Distance Transform algorithm has notable drawbacks. It requires a high-resolution occupancy grid map, which can significantly increase memory consumption and computational load. This makes it less efficient for large or complex environments, particularly when used in real-time applications. Another limitation is its inability to handle dynamic obstacles, as it relies on a pre-generated map. If the environment changes during navigation, the entire path needs to be recalculated, leading to delays. Despite these challenges, the algorithm is well suited for static environments where precision is more important than adaptability.

2.2. Mapping

Simultaneous Localization and Mapping (SLAM) is a critical algorithm in robotics that enables a robot to build a map of an unknown environment while simultaneously determining its position within it [37]. SLAM integrates sensor data, such as lidar, cameras, or ultrasonic sensors, to create a representation of the environment in real time. A key component of SLAM is solving the data association problem, which involves matching current sensor observations with previously recorded data to ensure map accuracy. Modern SLAM algorithms leverage techniques like probabilistic methods, such as particle filters or extended Kalman filters, to account for uncertainty in sensor data and robot motion. SLAM is widely used in applications like autonomous vehicles, drones, and mobile robots, where accurate navigation in dynamic environments is essential. Recent advancements in SLAM, including visual SLAM and deep learning-based approaches, have further enhanced its robustness and efficiency in complex and large-scale environments.

For an intelligent mobile robot to generate a map on its own, it must utilize the SLAM algorithm. The environment map generated by the SLAM algorithm primarily employs an occupancy grid-type map. Occupancy grid maps are widely used in mobile robots for mission planning and navigation due to their ability to represent an environment with fine-grained spatial details. One key advantage is their flexibility, as they can accurately represent both free spaces and obstacles by dividing the environment into small grid cells. This makes them particularly effective for algorithms that require precise path planning, such as A* or Distance Transform. Additionally, occupancy grids are straightforward to update with new sensor data, allowing for incremental map-building in static or semi-dynamic environments. The occupancy grid method involves dividing the entire target space into a grid and classifying each cell as Free (empty space), Occupied (obstacle), or Unknown (unexplored area).

However, there are notable limitations to using occupancy grid maps [38]. High-resolution grids require significant memory, which can be a challenge for embedded systems or robots with limited resources. The computational complexity of processing these maps increases with their size, making real-time performance in large-scale environments difficult to achieve. Moreover, occupancy grids struggle with dynamic obstacles, as constant updates to the grid can be computationally expensive. Another drawback is that these maps often lack higher-level abstraction, such as connectivity or semantic information, which can be useful for long-term planning. Despite these challenges, occupancy grids remain a reliable choice for many robotic applications due to their simplicity and accuracy.

Topological decomposition maps are an efficient approach to address some limitations of occupancy grid maps in mobile robot navigation [17,39]. These maps rely on extracting key environmental features, such as walls, corners, and obstacles, to build a graph-based representation of the environment. One major advantage is their reduced memory requirement, as they do not store fine-grained spatial data but rather abstract connections between significant features. This results in faster computation for path planning, making them ideal for large-scale environments where computational efficiency is critical. Additionally, topological maps simplify navigation tasks by focusing on connectivity between nodes, which ensures that the robot can move along predefined paths with less processing overhead.

Despite these advantages, topological decomposition maps have certain limitations. Since they focus on abstract representations, they lack the precision needed to accurately depict the surrounding environment. This can lead to challenges in navigation, especially in tight spaces or areas with complex obstacles. Furthermore, the robot may struggle with precise localization and obstacle avoidance when relying solely on topological maps, as they do not provide detailed spatial resolution. Constructing an accurate topological map also requires robust feature detection algorithms, which may not perform well in unstructured or highly dynamic environments. Nevertheless, these maps remain a valuable tool for high-level navigation, particularly when combined with other methods to address their limitations.

3. Proposed Methods

In this section, we describe a hybrid map that takes advantage of both the occupancy grid map and the topology map. The proposed RC-Map (Rectangle Map) is a hybrid map that analyzes the occupancy grid map of Figure 1 generated by the robot to generate a fast path with less memory usage. When a robot equipped with the RC-Map algorithm is given a space, it acquires surrounding information using its own sensors, generates a map based on this, and updates it. The algorithm to generate RC-Map was described in a previous study [40].

3.1. Hybrid Map

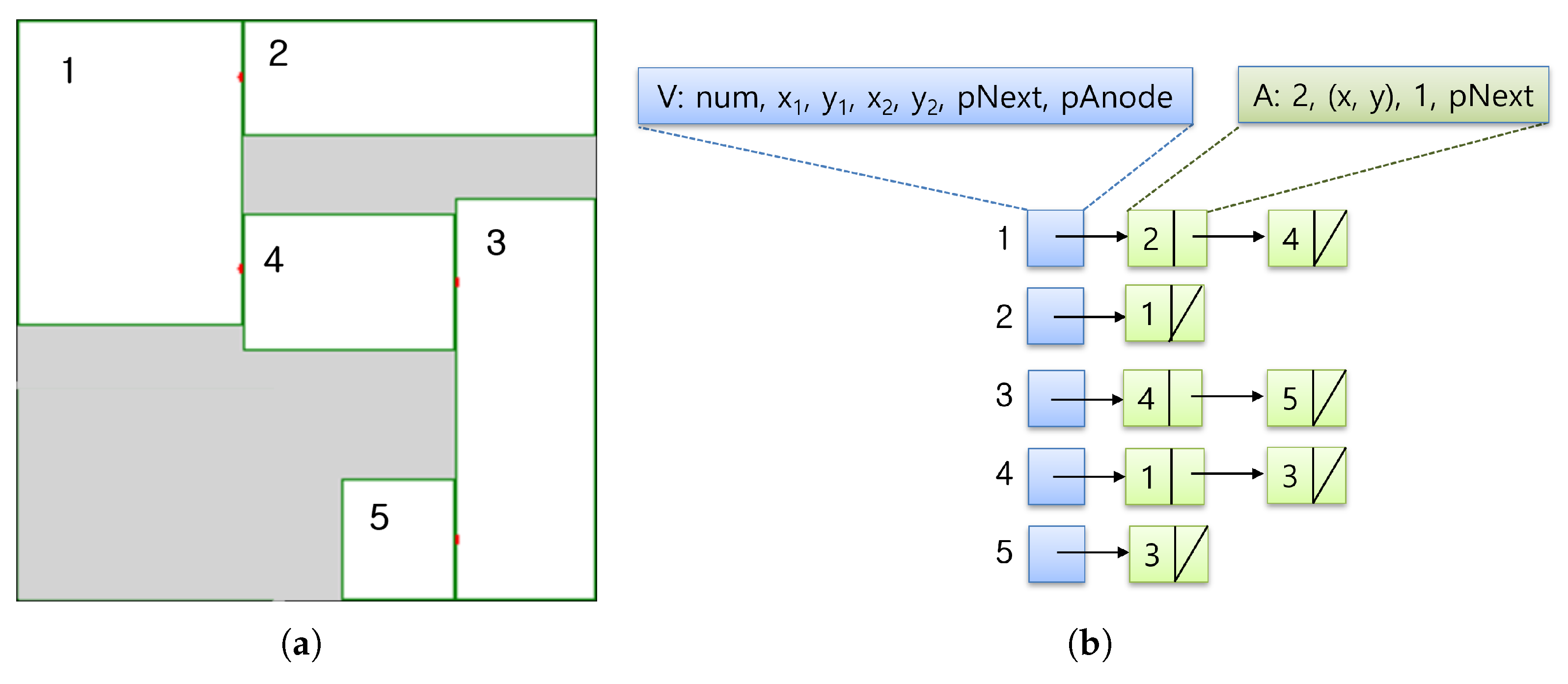
In this paper, we describe the structure of Hybrid RC-Map and show that it can be used to quickly patrol a given space by making a path plan. Figure 1 shows the difference between RC-Map and an occupied grid map. Hybrid RC-Map divides the free area of the occupied grid map into squares and expresses each square as a node. Since RC-Map maintains only the coordinate information of squares, it can express the environment using less memory than a cell-based occupied grid map.

Figure 2a shows a visual representation using the data structure of RC-Map. In the actual implementation, RC-Map is stored as a graph-type data structure as shown in Figure 2b. This structure was chosen for its low memory usage and fast search. RC-Map uses V and A nodes as internal data structures. V node means an empty space in the hybrid map where the robot can move. TV-nodes maintain node numbers, coordinates on the environmental map, and pointer information pointing to a list of adjacent nodes to accurately represent environmental information. An A node means a node adjacent to a V node. A node has the node number, AP (Adjacent Point), V node number, and a pointer to the next A node. The proposed hybrid map RC-Map functions as follows from the existing topology map. In a general topology map, a node only maintains basic information about the area it wants to express, but in RC-Map, a square is referred to as a node, and coordinate information about the area is maintained to maintain the accurate expression of the grid map. In addition, an AP is used to indicate the connection between nodes and to generate a movement path between nodes. AP is explained in the next subsection, Path Generation.

3.2. Path Generation

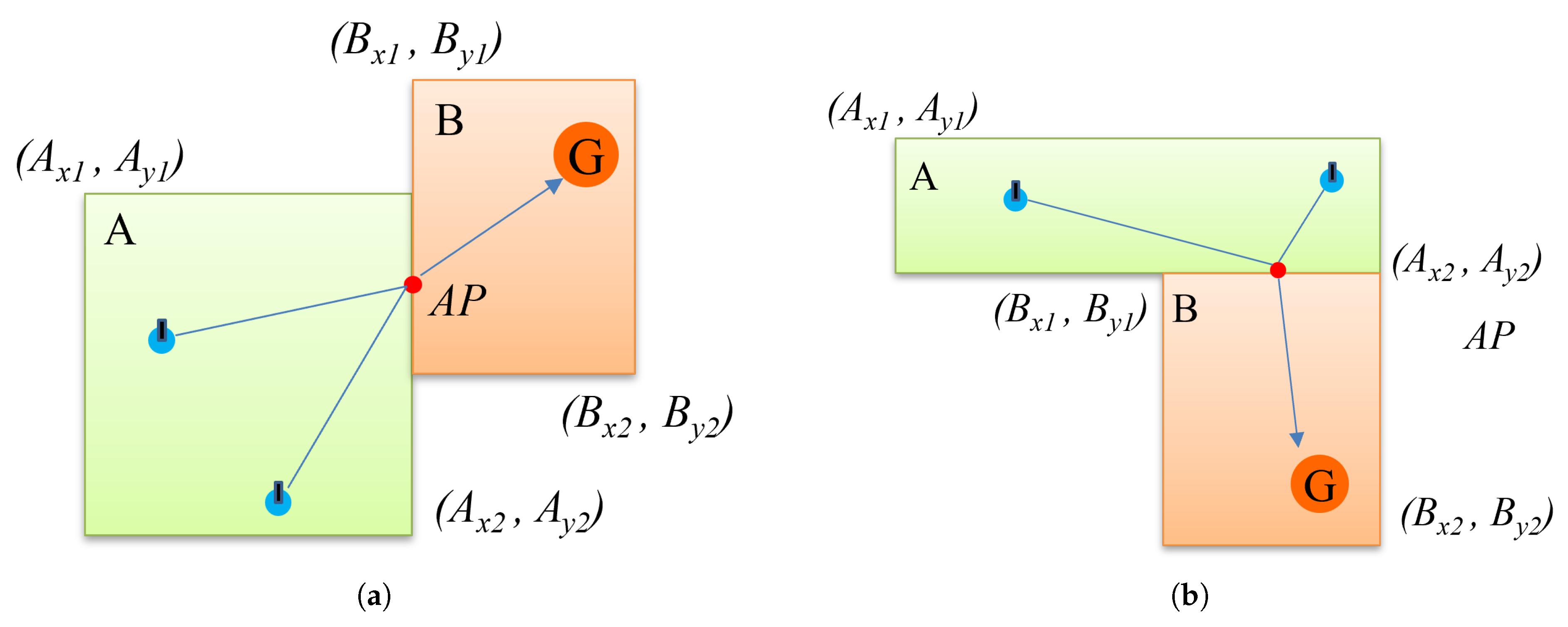
In RC-Map, the concept of AP (Adjacent Point) is introduced for fast path generation. An AP refers to the center point of the adjacent parts when two areas are adjacent. In the actual implementation of the method, one area is expressed as a node. Assume that two nodes A and B are as in Equations (1) and (2). As in Figure 3a, the AP of the adjacent nodes can be expressed by Equation (3), and the AP of two nodes adjacent to each other vertically, as in Figure 3b, can be expressed by Equation (4).

$$CoordinatesofareaA:A(A_{x1},A_{y1},A_{x2},A_{y2})$$

(1)

$$CoordinatesofareaB:B(B_{x1},B_{y1},B_{x2},B_{y2})$$

(2)

$$AP(x,y)=\left(B_{x1},{\displaystyle \frac{A_{y1}+B_{y2}}{2}}\right)$$

(3)

$$AP(x,y)=\left({\displaystyle \frac{A_{x1}+B_{x2}}{2}},B_{y1}\right)$$

(4)

After RC-Map is generated, the mobile robot can utilize the AP to move through the area. If the AP is obtained through Equations (3) and (4), a path can be quickly generated that can pass through the AP and arrive at position G regardless of where it is in area A. For example, when there is a robot in area A on the left of Figure 3a and the robot moves to position G of node B, the robot in node A can move directly to the AP and then to position G. Using this method, faster path generation is possible compared to grid-based path generation. Figure 3 visually shows the path created using the generated AP.

In RC-Map, the movement of a mobile robot from the current space to the next final destination can be viewed as a movement between nodes. It can move from the current location to the AP of the immediately adjacent space, and then to the AP of the adjacent node, and repeat this process to reach the final destination. At that time, moving to the AP may not be the shortest path. However, considering the safe movement of the robot, moving from a node in a free space to the AP is an appropriate choice in the robot’s situation.

The fast path generation algorithm using RC-Map requires data in the form of the topology of G(V, A) and a start node and a destination node to find the optimal path. RC-Map is in the form of general graph data, so various graph search algorithms can be utilized. In this paper, Dijkstra’s algorithm, which is widely used to solve the shortest path problem in graphs, was modified to operate according to the RC-Map data structure [40]. Algorithm 1 demonstrates how to generate a fast shortest path by utilizing RC-Map.

Algorithm 1:Shortest path generation using RC-MAP

4. Results

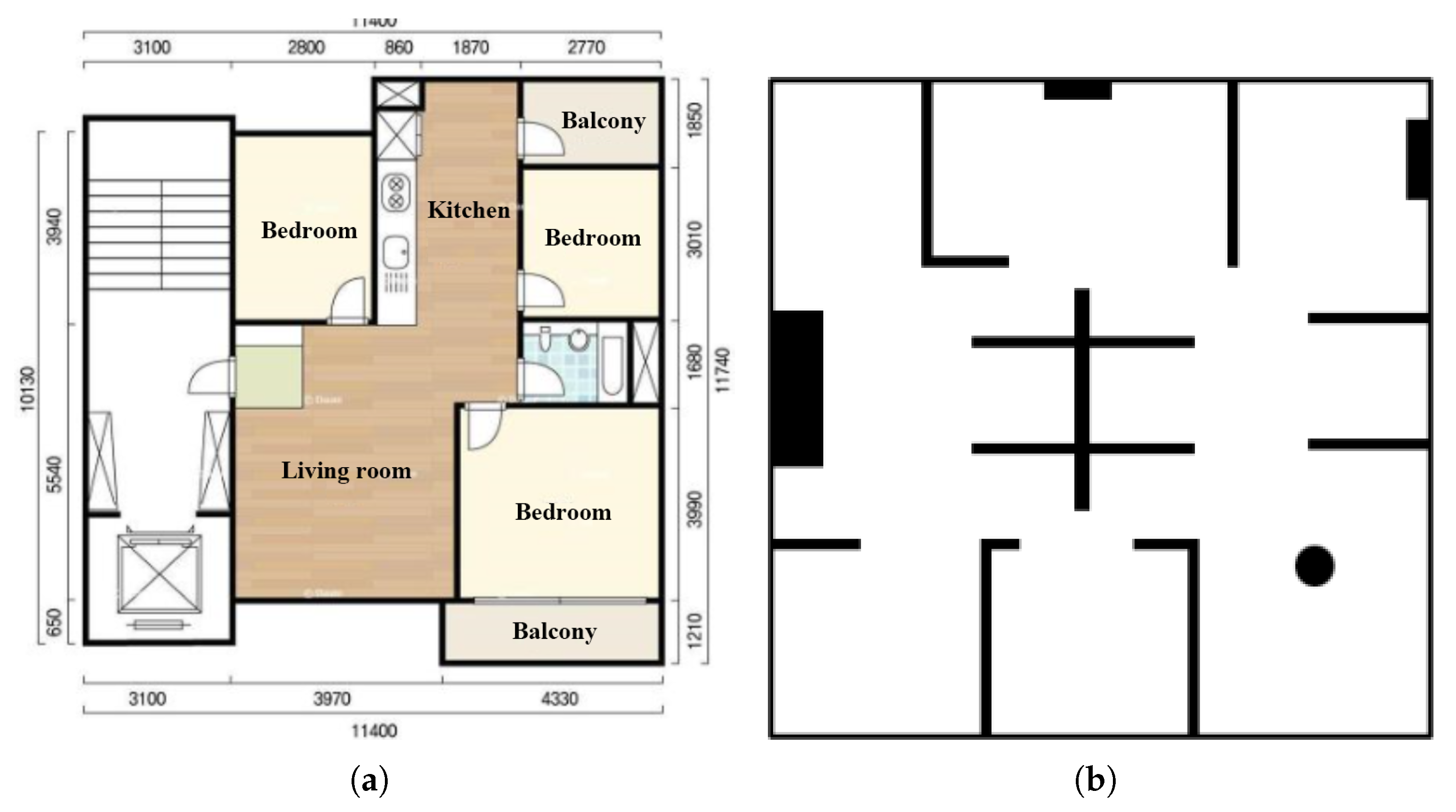
In order to demonstrate that fast path generation is possible using the RC-Map proposed in this paper, a simulation experiment was performed. Figure 4a is a floor plan of an actual residential environment, and mapping was performed using a robot in that space. Figure 4b is a virtual residential space created for simulation, and it was used to check the robot’s movement path.

Figure 5 shows the experimental environment of Figure 4a expressed in RC-Map. About 80 V nodes and 204 A nodes were used, and 8768 bytes of memory were used. This corresponds to about 3% of the (300 × 300)-sized grid map.

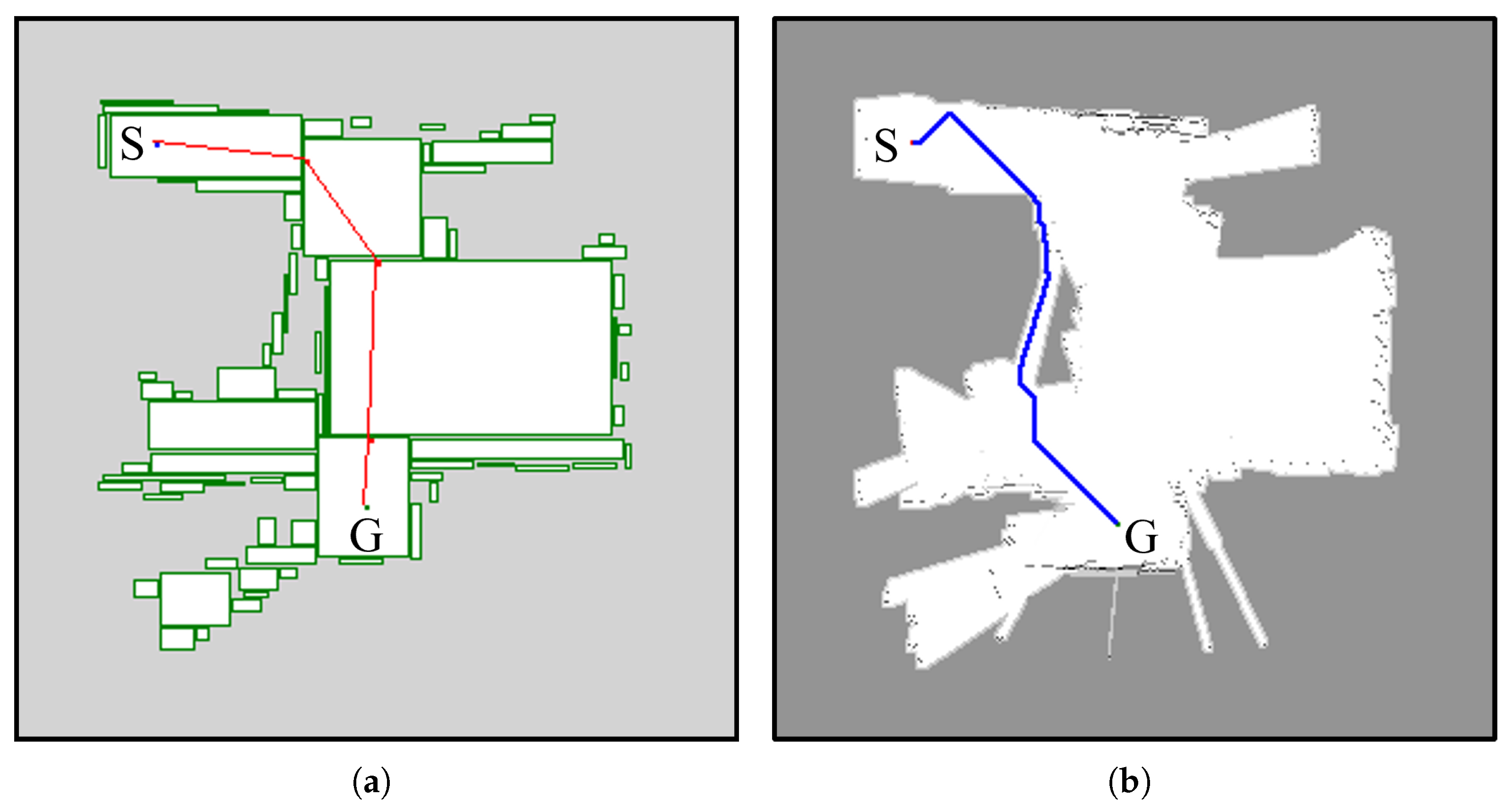
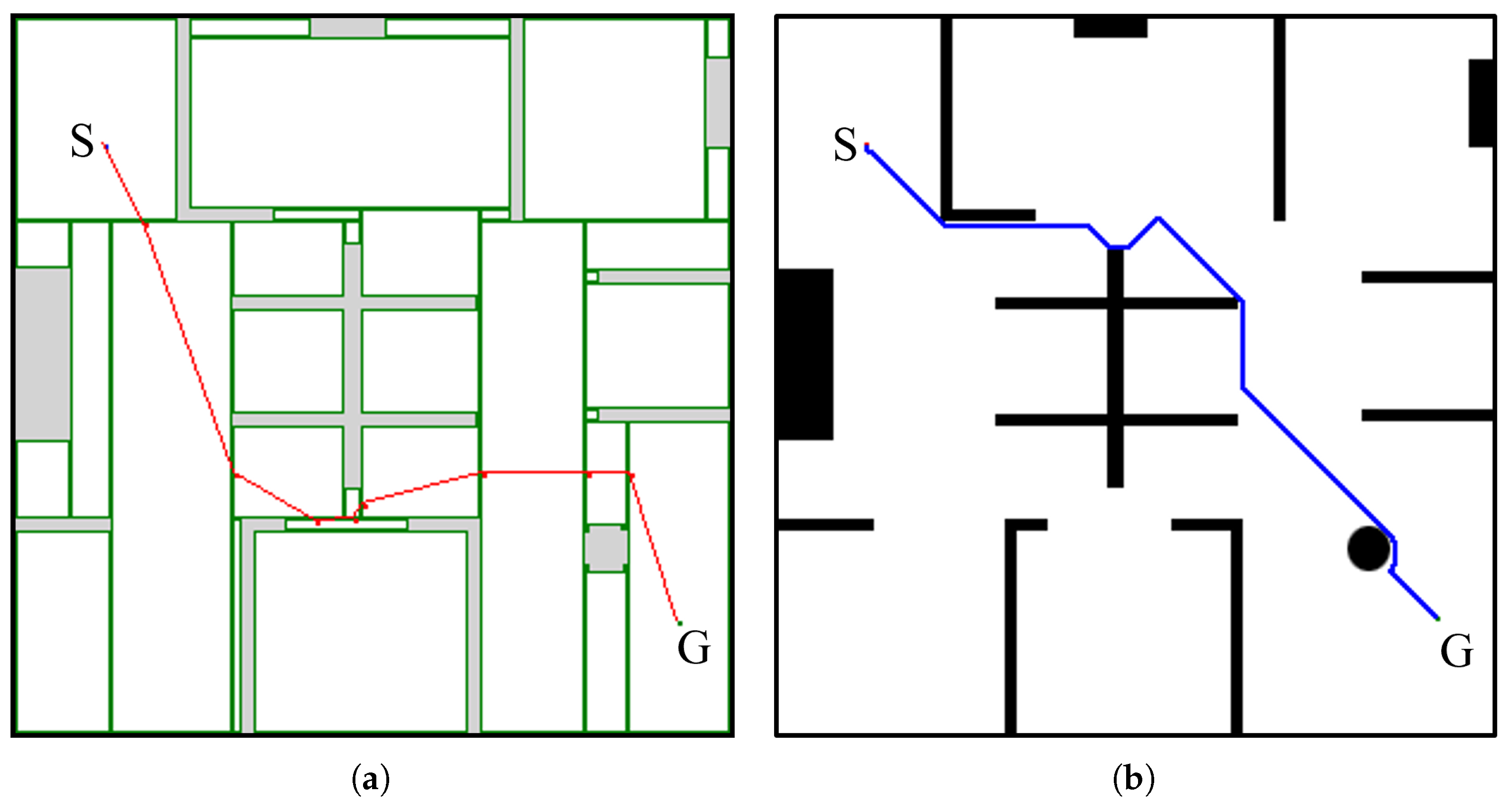
Figure 6 shows the path generation results using RC-Map and the path generation results using Distance Transform path generation in the experimental environment of Figure 4a. The total moving distance was 7.19 m when RC-Map was used, and the total moving distance was 6.18 m when the Distance Transform method was used. In terms of total moving distance, RC-Map moved a longer distance, but the number of turns during the movement was 6 for RC-Map and 40 for Distance Transform. This shows that the robot using Distance Transform moved along a narrow path and made many turns, as in the middle part of Figure 6b. This caused the robot to use more battery. In contrast, RC-Map moved to the destination by moving nodes in the empty area where the robot could move freely, as in Figure 6a. In order to generate the path in Figure 6, RC-Map took a total of 10 ms and Distance Transform took 740 ms. This can be an important issue for mobile robots using embedded boards.

Figure 7 shows the path generation results using RC-Map and Distance Transform path generation in the experimental environment of Figure 4b. When RC-Map was used, the total moving distance was 18.87 m, the total number of turns was 10, and the path generation time was 15 ms. When Distance Transform was used, the total moving distance was 9.64 m, the total number of turns was 19, and the path generation time was 1238 ms. The experimental results show the same results as in Figure 6 above. However, depending on the complexity of the grid map, the path generation calculation time of Distance Transform showed a large difference compared to RC-Map. When using a grid map like this, you can see that the Distance Trans path generation time also increased as the map resolution and complexity increased.

5. Conclusions

In this paper, we proposed a hybrid map that can be used in mobile robots. The proposed hybrid map can generate fast paths and can be used in mobile robots and service robots. The proposed path generation method uses a graph-type hybrid map and consumes less memory than the existing grid map. It solves the problem of path generation time increasing due to the resolution and complexity of the grid map. Additionally, the RC-Map introduces the concept of Adjacent Points (APs), enabling faster and safer path planning for mobile robots. This approach not only reduces computational complexity but also ensures efficient traversal of large spaces.

In the future, we plan to apply RC-Map to various fields, including dynamic and real-time navigation systems. We also aim to enhance the adaptability of RC-Map for environments with irregular obstacles or dynamically changing layouts. Furthermore, we plan to modify RC-Map so that it can generate more optimized paths while maintaining a balance between efficiency and safety.