Optimal Allocation of Water Resources in Irrigation Areas Considering Irrigation Return Flow and Uncertainty
Abstract
1. Introduction
2. Materials and Methods
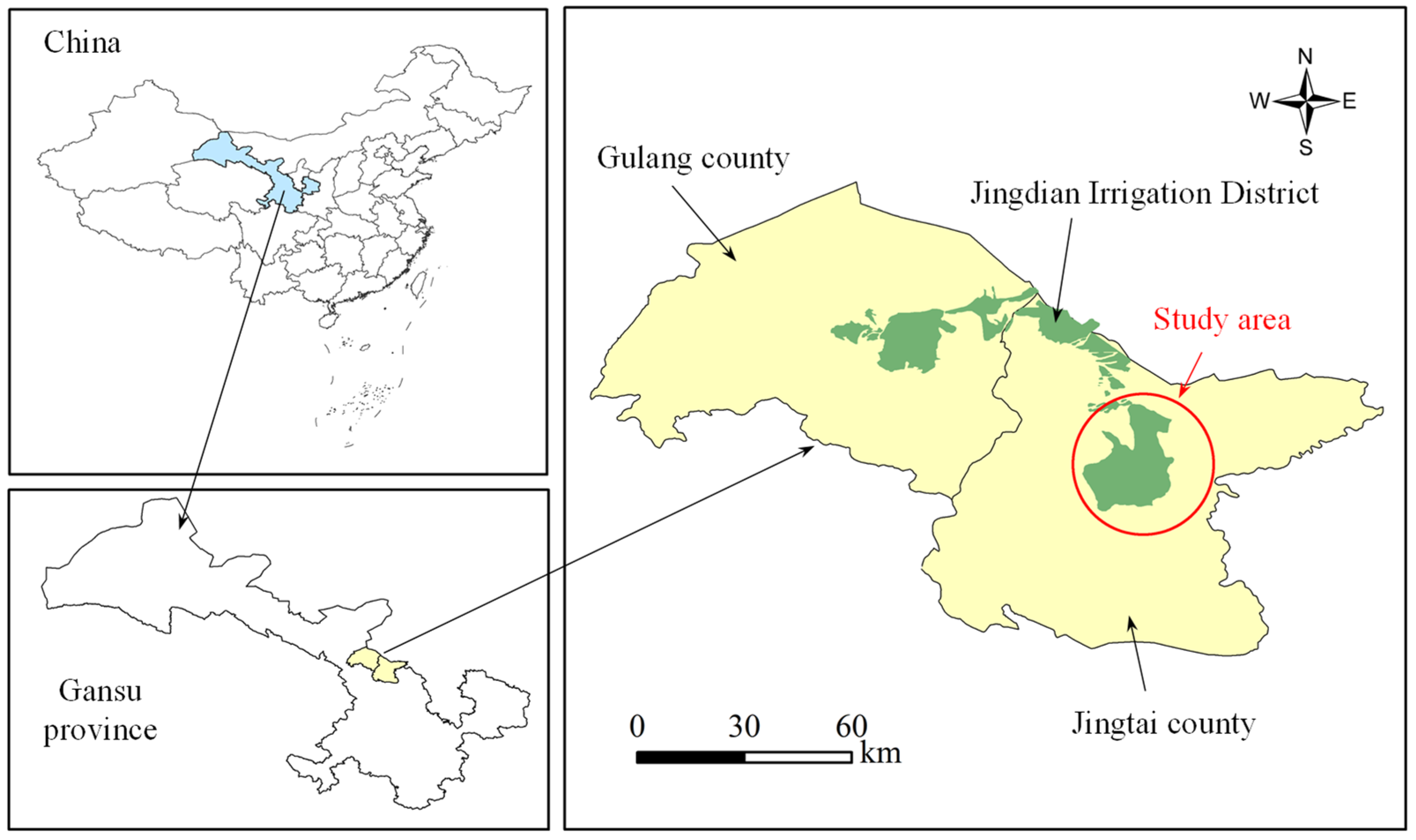
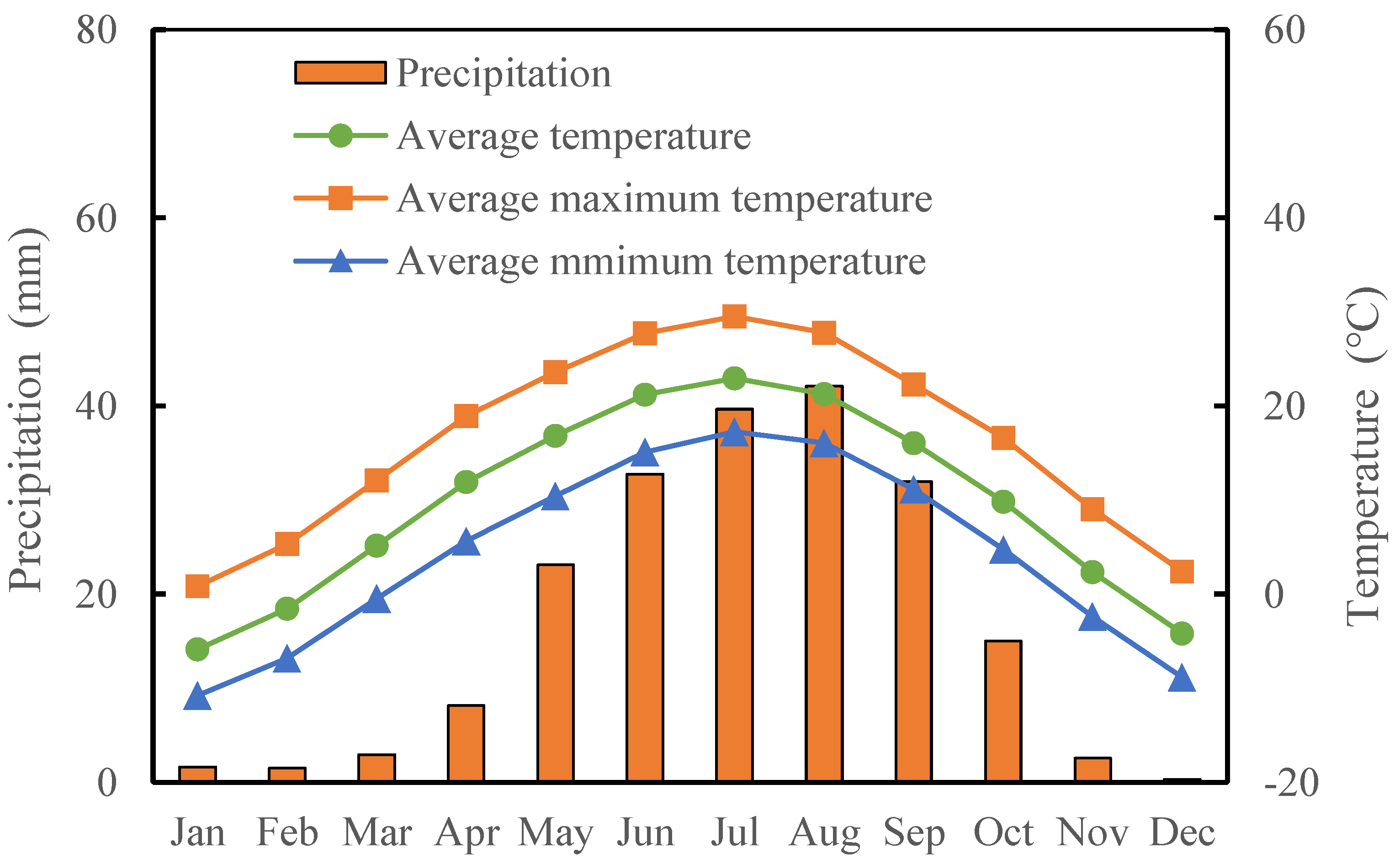
2.1. Study Area
2.2. Optimal Allocation of Water Resources
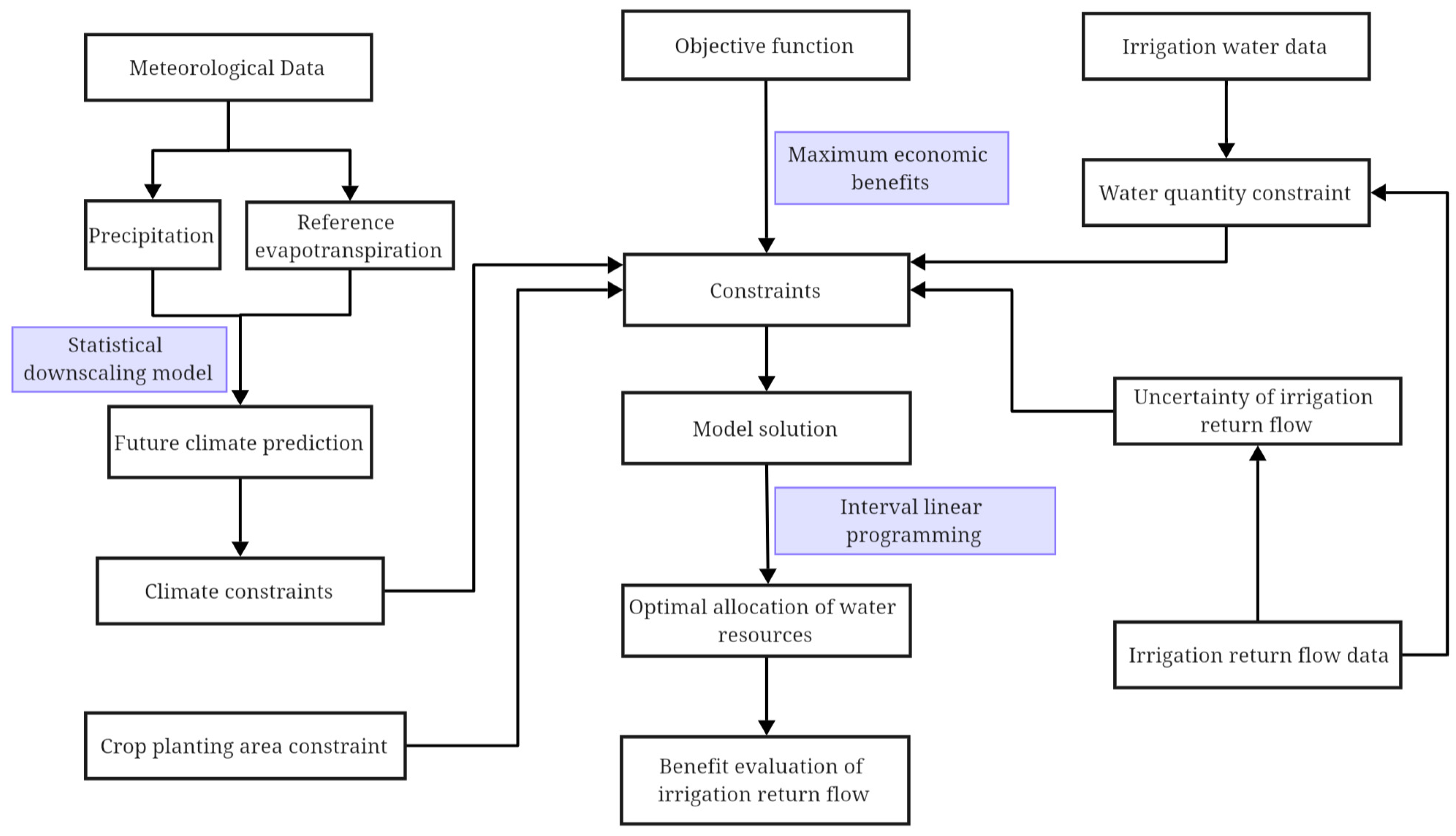
2.2.1. Process of Optimal Allocation
2.2.2. Statistical Downscaling Model
2.2.3. Interval Linear Programming
- (1)
- Objective function:
- (2)
- Constraints:
- (1)
- Upper linear programming model
- Objective function:
- Constraints:
- (2)
- Lower-level linear programming model
- Objective function:
- Constraints:where Sign() represents the sign function; and represent interval variables with positive and negative coefficients in the objective function, respectively.
2.2.4. Establishment of Optimal Allocation Model of Water Resources
- (1)
- Objective function:
- (2)
- Constraints:
- a.
- Irrigation water constraint
- b.
- Water balance constraint
- c.
- Crop area constraint
- d.
- Non-negative constraint
2.2.5. Model Parameter
- (1)
- Effective precipitation
- (2)
- Reference evapotranspiration and crop water demand
- (3)
- Return flow
- (4)
- Crop parameters
- (5)
- Other parameters of the model
3. Results and Discussion
3.1. Future Climate Change
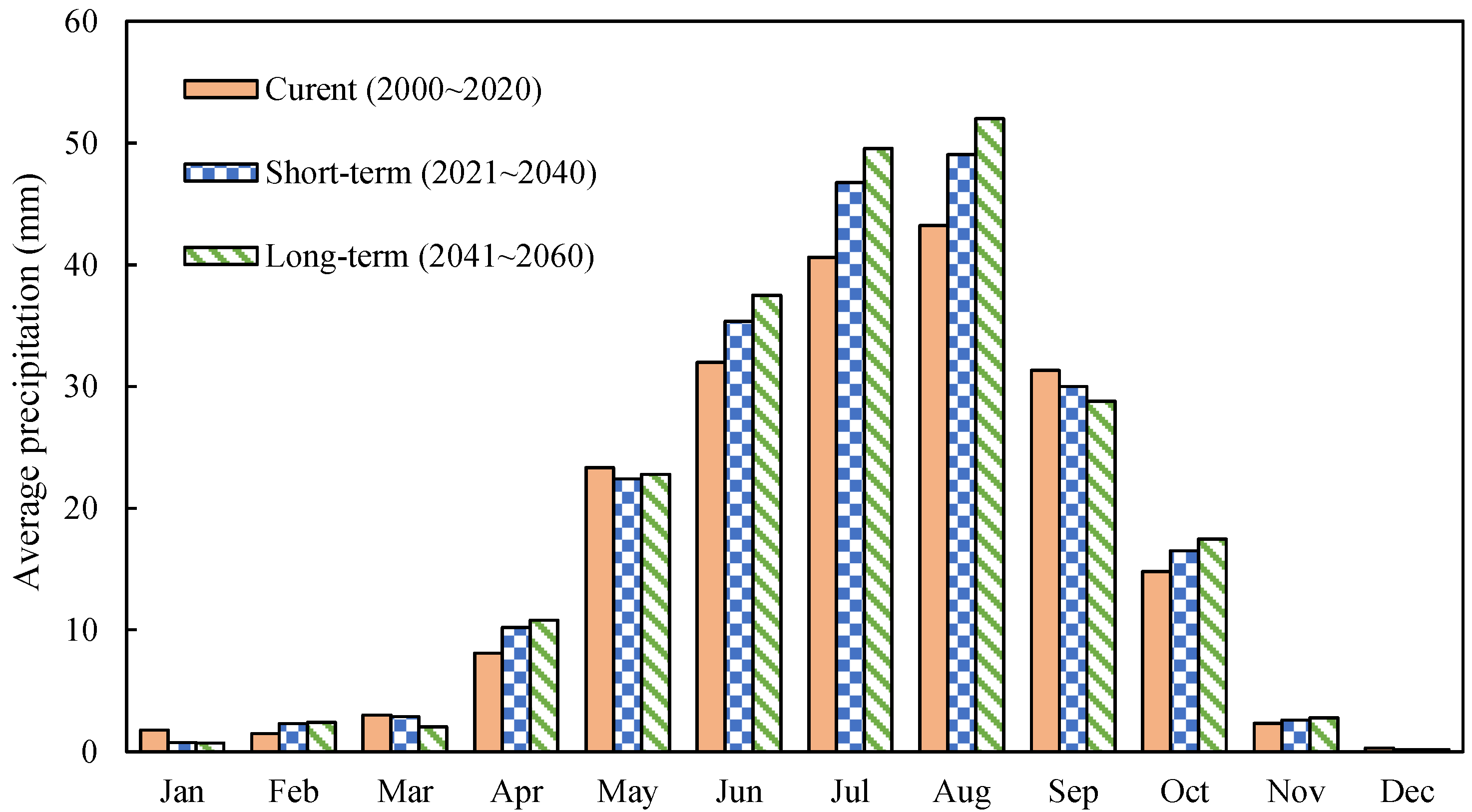
3.1.1. Change Characteristics of Precipitation
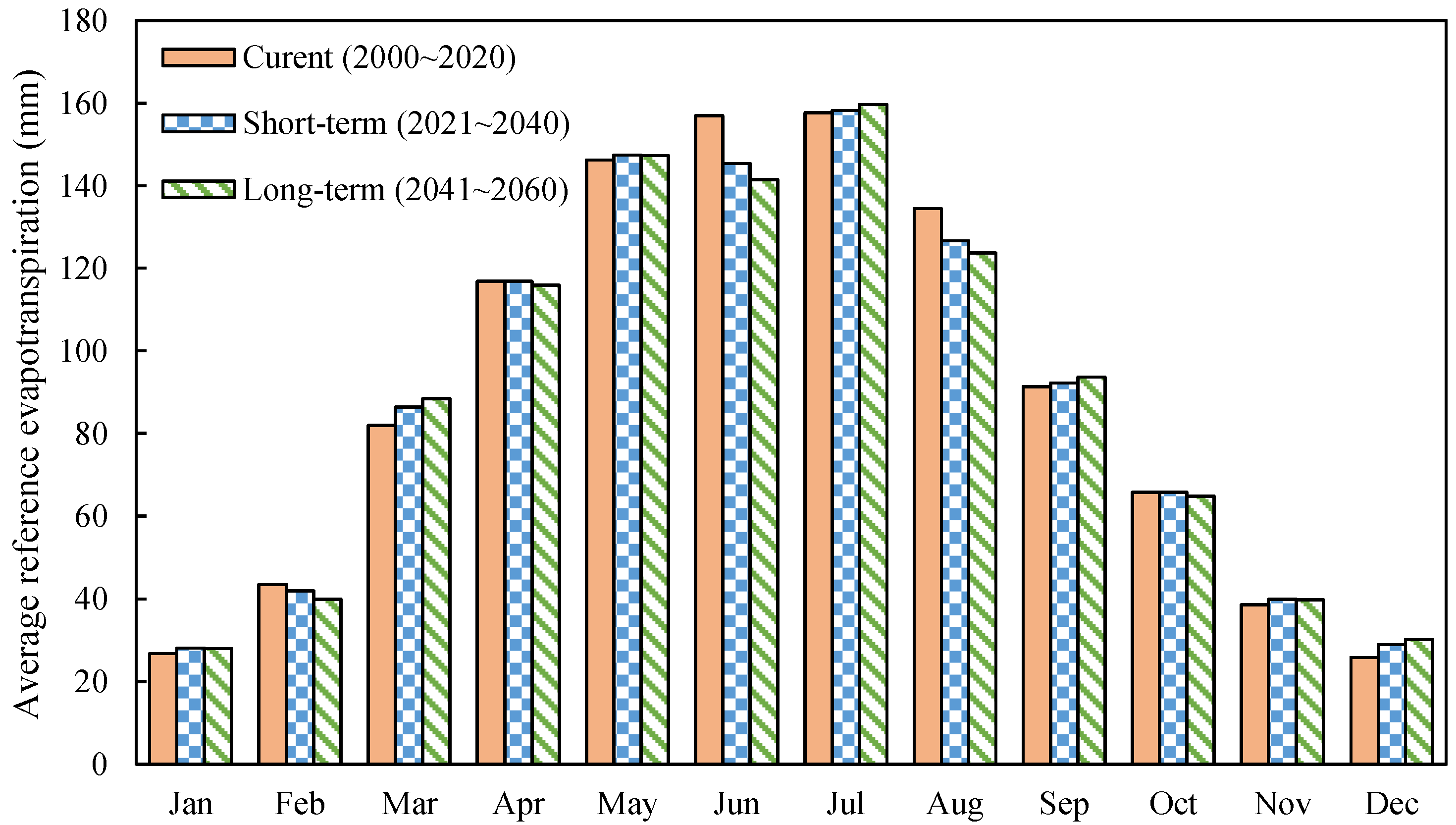
3.1.2. Change Characteristics of Reference Evapotranspiration
3.2. Optimal Allocation of Irrigation Water Diversion (Model I)
3.2.1. Optimization Results of Irrigation Benefits (Model I)
3.2.2. Optimization Results of Crop Planting Structure (Model I)
3.2.3. Results of Optimal Allocation of Water Resources (Model I)
3.3. Optimal Allocation Considering Return Flow (Model II)
3.3.1. Optimization Results of Irrigation Benefits (Model II)
3.3.2. Optimization Results of Crop Planting Structure (Model II)
3.3.3. Results of Optimal Allocation of Water Resources (Model II)
4. Conclusions
- (1)
- The precipitation in the study area shows an increasing trend. The annual precipitation in the short-term years and long-term years increases by 6.1 mm and 8.9 mm, respectively. The reference evapotranspiration showed a decreasing trend. The reference evapotranspiration in the short-term years and long-term years decreases by 8.2 mm and 13.3 mm respectively.
- (2)
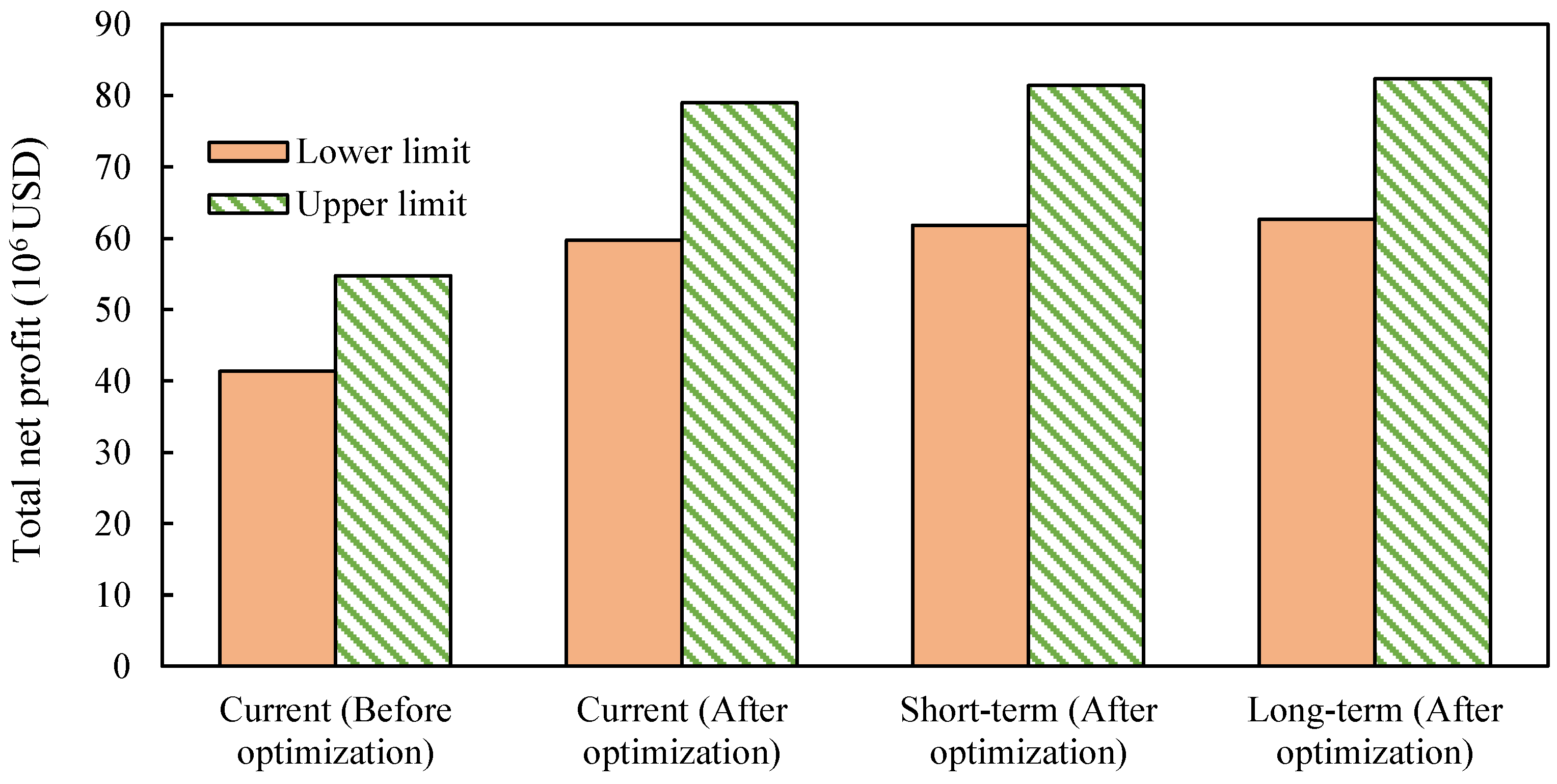
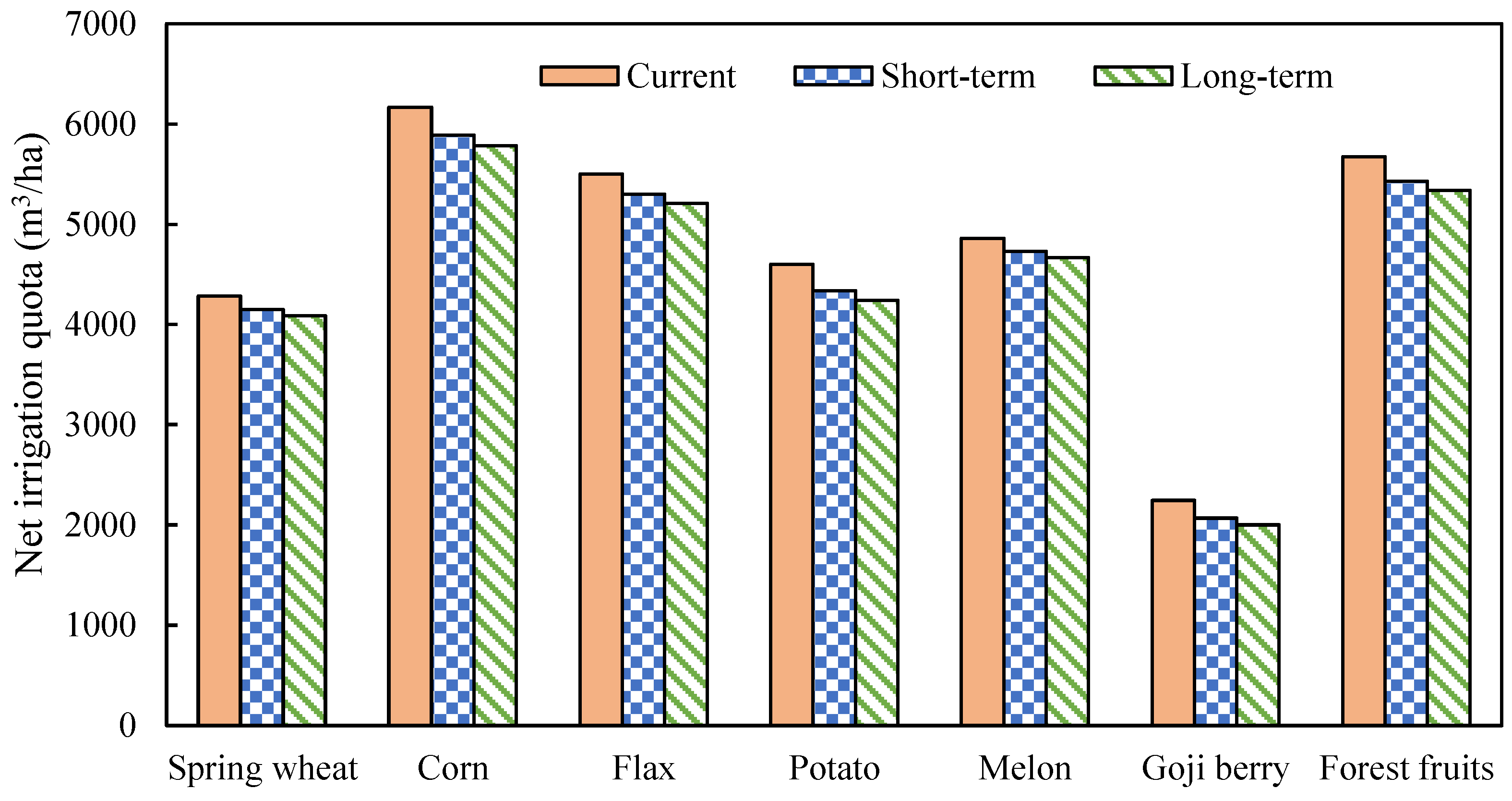
- After optimizing the optimal allocation of irrigation water diversion (model I) in the current years, the net profit increased by USD [18.27, 24.18] million, and the total planting area increased by 900 ha. The crop planting structure changes significantly, with a decrease in the planting proportion of low water productivity crops (spring wheat, corn, and flax) and an increase in the planting proportion of high water productivity crops (potato, melon, goji berry, and forest fruits). After optimizing for the upcoming years, the net profit for both the short-term and long-term years saw an increase of USD [2.20, 2.47] and [3.02, 3.43] million respectively. Additionally, the total planting area expands by 700 hectares and 1000 hectares respectively. Due to limitations in irrigation water diversion, the irrigation area faces a shortage of water resources. However, there is potential to increase the crop planting area in both the current years and the planning years. By effectively utilizing the return flow, the crop planting area can be expanded even further.
- (3)
- When optimizing the allocation of return flow (model II), the net profit of the current years, short-term years, and the long-term years increased by USD [7.14, 7.97], [5.08, 5.63] and [4.4, 4.81] million, respectively, compared with the net profit of model I. The total planting area also increased by 2.6 thousand ha, 1.9 thousand ha, and 1.6 thousand ha, respectively, compared with the total planting area of model I. Additionally, the amount of irrigation water diversion was reduced by [12, 18] million m3, [18, 24] million m3, and [20, 26] million m3, respectively, compared with that of model I. The use of return flow resources for farmland irrigation can not only improve irrigation efficiency and avoid the pollution of return flow discharge on the water quality of the Yellow River, but also reduce water diversion from the Yellow River, play a water-saving role, and reduce the cost of water extraction to a certain extent.
- (4)
- The application of interval linear programming models can effectively optimize the allocation of irrigation return flow under conditions of uncertainty. This study also serves as a reference for the reuse and optimization of irrigation return flow in other arid regions, contributing positively to the efficient utilization of water resources and the protection of water environments. In addition to irrigation return flow, the method proposed in this study can also be applied for the optimal allocation of the reuse of treated industrial and domestic wastewater. However, it is important to determine a reasonable interval number as a constraint condition.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ren, C.; Li, Z.; Zhang, H. Integrated multi-objective stochastic fuzzy programming and AHP method for agricultural water and land optimization allocation under multiple uncertainties. J. Clean. Prod. 2019, 210, 12–24. [Google Scholar] [CrossRef]
- Zhuang, X.W.; Li, Y.P.; Nie, S.; Fan, Y.R.; Huang, G.H. Analyzing climate change impacts on water resources under uncertainty using an integrated simulation-optimization approach. J. Hydrol. 2018, 556, 523–538. [Google Scholar] [CrossRef]
- Zhang, J.X.; Deng, M.J.; Li, P.; Li, Z.B.; Huang, H.P.; Shi, P.; Feng, C.H. Security pattern and regulation of agricultural water resources in Northwest China from the perspective of virtual water flow. Strateg. Study CAE 2022, 24, 131–140. [Google Scholar] [CrossRef]
- Song, W. The Research on Runoff Evolution and Allocation of Water Resources in the Area of Qianzhong Water Diversion Project. Master’s Thesis, Tianjin University, Tianjin, China, 2016. [Google Scholar]
- Gao, Z. Progresses and challenges in the study of Eco-fluvial dynamics. J. Hydraul. Eng. 2019, 50, 88–96. [Google Scholar]
- Shi, Y.W. Study on the Regularity of Drainage Water Volume of Qingtongxia Irrigation Area of Ningxia. Master’s Thesis, Xi’an University of Technology, Xi’an, China, 2005. [Google Scholar]
- Li, J.; Song, J.; Li, M.; Shang, S.; Mao, X.; Yang, J.; Adeloye, A.J. Optimization of irrigation scheduling for spring wheat based on simulation-optimization model under uncertainty. Agric. Water Manag. 2018, 208, 245–260. [Google Scholar] [CrossRef]
- Li, M.; Jiang, Y.; Guo, P.; Li, J. Irrigation water optimal allocation considering stakeholders of different levels. Trans. Chin. Soc. Agric. Mach. 2017, 48, 199–207. [Google Scholar]
- Montazar, A.; Riazi, H.; Behbahani, S.M. Conjunctive water use planning in an irrigation command area. Water Resour. Manag. 2010, 24, 577–596. [Google Scholar] [CrossRef]
- Feng, J. Optimal allocation of regional water resources based on multi-objective dynamic equilibrium strategy. Appl. Math. Model. 2021, 90, 1183–1203. [Google Scholar] [CrossRef]
- Habibi, D.M.; Banihabib, M.E.; Nadjafzadeh, A.A.; Hashemi, S.R. Multi-objective optimization model for the allocation of water resources in arid regions based on the maximization of socioeconomic efficiency. Water Resour. Manag. 2016, 30, 927–946. [Google Scholar] [CrossRef]
- Afzal, J.; Noble, D.H.; Weatherhead, E.K. Optimization model for alternative use of different quality irrigation waters. J. Irrig. Drain. Eng. 1992, 118, 218–228. [Google Scholar] [CrossRef]
- Guo, P.; Chen, X.; Li, M.; Li, J. Fuzzy chance-constrained linear fractional programming approach for optimal water allocation. Stoch. Environ. Res. Risk Assess. 2013, 28, 1601–1612. [Google Scholar] [CrossRef]
- Yang, G.Q.; Guo, P.; Li, R.H.; Li, M. Optimal allocation model of surface water and groundwater based on queuing theory in irrigation district. Trans. Chin. Soc. Agric. Eng. 2016, 32, 115–120. [Google Scholar]
- Cui, L.; Li, Y.; Huang, G. Double-sided fuzzy chance-constrained linear fractional programming approach for water resources management. Eng. Optim. 2016, 48, 949–965. [Google Scholar] [CrossRef]
- Karamouz, M.; Kerachian, R.; Zahraie, B. Monthly water resources and irrigation planning: Case study of conjunctive use of surface and groundwater resources. J. Irrig. Drain. Eng. 2004, 130, 391–402. [Google Scholar] [CrossRef]
- Bazargan-Lari, M.R.; Kerachian, R.; Mansoori, A. A conflict-resolution model for the conjunctive use of surface and groundwater resources that considers water-quality issues: A case study. Environ. Manag. 2009, 43, 470–482. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.X. Multi-Water Conjunctive Optimal Allocation Model of Irrigation Area Research Under Uncertainty. Master’s Thesis, Northeast Agricultural University, Harbin, China, 2016. [Google Scholar]
- Zhang, C.; Guo, P.; Huo, Z. Irrigation water resources management under uncertainty: An interval nonlinear double-sided fuzzy chance-constrained programming approach. Agric. Water Manag. 2021, 245, 106658. [Google Scholar] [CrossRef]
- Maqsood, I.; Huang, G.; Huang, Y.; Chen, B. ITOM: An interval-parameter two-stage optimization model for stochastic planning of water resources systems. Stoch. Environ. Res. Risk Assess. 2005, 19, 125–133. [Google Scholar] [CrossRef]
- Fu, Q.; Li, J.H.; Liu, D.; Li, T.X. Allocation optimization of water resources based on uncertainty stochastic programming model considering risk value. Trans. Chin. Soc. Agric. Eng. 2016, 32, 136–144. [Google Scholar]
- Huang, Y.; Li, Y.P.; Chen, X.; Ma, Y.G. Optimization of the irrigation water resources for agricultural sustainability in Tarim River Basin, China. Agric. Water Manag. 2012, 107, 74–85. [Google Scholar] [CrossRef]
- Yang, G.; Guo, P.; Huo, L.; Ren, C. Optimization of the irrigation water resources for Shijin irrigation district in north China. Agric. Water Manag. 2015, 158, 82–98. [Google Scholar] [CrossRef]
- Li, M.; Guo, P.; Singh, V.P. Biobjective optimization for efficient irrigation under fuzzy uncertainty. J. Irrig. Drain. Eng. 2016, 142, 05016003. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, L.; Ping, G.; Zhang, C.; Fan, Z.; Guo, S. An inexact irrigation water allocation optimization model under future climate change. Stoch. Environ. Res. Risk Assess. 2019, 33, 271–285. [Google Scholar] [CrossRef]
- Yue, Q.; Zhang, F.; Zhang, C.; Zhu, H.; Tang, Y.; Guo, P. A full fuzzy-interval credibility-constrained nonlinear programming approach for irrigation water allocation under uncertainty. Agric. Water Manag. 2020, 230, 105961. [Google Scholar] [CrossRef]
- Guo, S.; Zhang, F.; Zhang, C.; An, C.; Wang, S.; Guo, P. A multi-objective hierarchical model for irrigation scheduling in the complex canal system. Sustainability 2018, 11, 24. [Google Scholar] [CrossRef]
- Gong, X.; Zhang, H.; Ren, C.; Sun, D.; Yang, J. Optimization allocation of irrigation water resources based on crop water requirement under considering effective precipitation and uncertainty. Agric. Water Manag. 2020, 239, 106264. [Google Scholar] [CrossRef]
- Yan, W.B.; Yu, L.H.; Cheng, H.Z. Simulation and prediction of future precipitation and temperature change in Poyang Lake Basin—Based on the SDSM statistical downscaling method. China Rural. Water Hydropower 2015, 7, 36–43. [Google Scholar]
- Feng, Y.; Cui, N.B.; Gong, D.Z.; Wei, X.P. Projection of reference evapotranspiration in hilly area of central Sichuan using statistical downscaling model. Trans. Chin. Soc. Agric. Eng. 2016, 31 (Suppl. S1), 71–79. [Google Scholar]
- Li, Q.Q.; Li, Y.P.; Huang, G.H.; Wang, C.X. Risk aversion based interval stochastic programming approach for agricultural water management under uncertainty. Stoch. Environ. Res. Risk Assess. 2017, 32, 715–732. [Google Scholar] [CrossRef]
- Guo, S.; Zhang, F.; Zhang, C.; Wang, Y.; Guo, P. An improved intuitionistic fuzzy interval two-stage stochastic programming for resources planning management integrating recourse penalty from resources scarcity and surplus. J. Clean. Prod. 2019, 234, 185–199. [Google Scholar] [CrossRef]
- Zhang, F.; Zhang, C.; Yan, Z.; Guo, S.; Wang, Y.; Guo, P. An interval nonlinear multiobjective programming model with fuzzy-interval credibility constraint for crop monthly water allocation. Agric. Water Manag. 2018, 209, 123–133. [Google Scholar] [CrossRef]
- Huang, G.H.; Baetz, B.W.; Patry, G.G. A grey fuzzy linear programming approach for municipal solid waste management planning under uncertainty. Civ. Eng. Syst. 1993, 10, 123–146. [Google Scholar] [CrossRef]
- Chen, N.S. Study on the Prediction of Return Water and the Temporal and Spatial Variation Characteristics of Water Quality in Large-Scale Yellow River Diversion Irrigation Area. Master’s Thesis, Xi’an University of Technology, Xi’an, China, 2021. [Google Scholar]
- Rodríguez-Pérez, A.M.; Rodríguez-Gonzalez, C.A.; López, R.; Hernández-Torres, J.A.; Caparrós-Mancera, J.J. Water Microturbines for Sustainable Applications: Optimization Analysis and Experimental Validation. Water Resour. Manag. 2024, 38, 1011–1025. [Google Scholar] [CrossRef]
- Zhao, M.; Guo, P.; Zhang, Y. Study on the water optimal allocation in irrigation district based on considering soil water balance. J. China Agric. Univ. 2020, 25, 91–102. [Google Scholar]
- Fu, Y.H.; Guo, P.; Fang, S.Q. Optimal water resources planning based on interval-parameter two-stage stochastic programming. Trans. Chin. Soc. Agric. Eng. 2014, 30, 73–81. [Google Scholar]



| Period. | Mar. | Apr. | May | Jun. | Jul. | Aug. | Sep. | Oct. |
|---|---|---|---|---|---|---|---|---|
| Current | 3.0 | 8.1 | 23.3 | 32.0 | 40.6 | 43.2 | 31.3 | 14.8 |
| Short-term | 2.9 | 10.2 | 22.4 | 35.4 | 46.7 | 49.0 | 30.0 | 16.5 |
| Long-term | 2.0 | 10.8 | 22.8 | 37.5 | 49.5 | 52.0 | 28.8 | 17.5 |
| Crop type | Mar. | Apr. | May | Jun. | Jul. | Aug. | Sep. | Oct. |
|---|---|---|---|---|---|---|---|---|
| Spring wheat | 0.46 | 0.33 | 0.51 | 0.42 | 0.21 | 0.00 | 0.00 | 0.00 |
| Corn | 0.00 | 0.49 | 0.51 | 0.49 | 0.72 | 0.66 | 0.50 | 0.32 |
| Flax | 0.47 | 0.32 | 0.51 | 0.51 | 0.55 | 0.27 | 0.00 | 0.00 |
| Potato | 0.00 | 0.03 | 0.65 | 0.50 | 0.72 | 0.66 | 0.48 | 0.00 |
| Melon | 0.47 | 0.32 | 0.51 | 0.44 | 0.29 | 0.00 | 0.00 | 0.00 |
| Goji berry | 0.00 | 0.02 | 0.62 | 0.48 | 0.69 | 0.57 | 0.35 | 0.00 |
| Forest fruits | 0.47 | 0.32 | 0.51 | 0.48 | 0.72 | 0.66 | 0.41 | 0.14 |
| Period | Crop Period | Mar. | Apr. | May | Jun. | Jul. | Aug. | Sep. | Oct. |
|---|---|---|---|---|---|---|---|---|---|
| Current | Spring wheat | 1.4 | 2.7 | 11.9 | 13.4 | 8.5 | 0.0 | 0.0 | 0.0 |
| Corn | 0.0 | 4.0 | 11.9 | 15.7 | 29.2 | 28.5 | 15.7 | 4.7 | |
| Flax | 1.4 | 2.6 | 11.9 | 16.3 | 22.3 | 11.7 | 0.0 | 0.0 | |
| Potato | 0.0 | 0.2 | 15.1 | 16.0 | 29.2 | 28.5 | 15.0 | 0.0 | |
| Melon | 1.4 | 2.6 | 11.9 | 14.1 | 11.8 | 0.0 | 0.0 | 0.0 | |
| Goji berry | 0.0 | 0.2 | 14.4 | 15.4 | 28.0 | 24.6 | 11.0 | 0.0 | |
| Forest fruits | 1.4 | 2.6 | 11.9 | 15.4 | 29.2 | 28.5 | 12.8 | 2.1 | |
| Short-term | Spring wheat | 1.3 | 3.4 | 11.4 | 14.9 | 9.8 | 0.0 | 0.0 | 0.0 |
| Corn | 0.0 | 5.0 | 11.4 | 17.3 | 33.6 | 32.3 | 15.0 | 5.3 | |
| Flax | 1.4 | 3.3 | 11.4 | 18.1 | 25.7 | 13.2 | 0.0 | 0.0 | |
| Potato | 0.0 | 0.3 | 14.6 | 17.7 | 33.6 | 32.3 | 14.4 | 0.0 | |
| Melon | 1.4 | 3.3 | 11.4 | 15.6 | 13.5 | 0.0 | 0.0 | 0.0 | |
| Goji berry | 0.0 | 0.2 | 13.9 | 17.0 | 32.2 | 27.9 | 10.5 | 0.0 | |
| Forest fruits | 1.4 | 3.3 | 11.4 | 17.0 | 33.6 | 32.3 | 12.3 | 2.3 | |
| Long-term | Spring wheat | 0.9 | 3.6 | 11.6 | 15.8 | 10.4 | 0.0 | 0.0 | 0.0 |
| Corn | 0.0 | 5.3 | 11.6 | 18.4 | 35.6 | 34.3 | 14.4 | 5.6 | |
| Flax | 0.9 | 3.5 | 11.6 | 19.1 | 27.2 | 14.0 | 0.0 | 0.0 | |
| Potato | 0.0 | 0.3 | 14.8 | 18.8 | 35.6 | 34.3 | 13.8 | 0.0 | |
| Melon | 0.9 | 3.5 | 11.6 | 16.5 | 14.4 | 0.0 | 0.0 | 0.0 | |
| Goji berry | 0.0 | 0.2 | 14.1 | 18.0 | 34.2 | 29.6 | 10.1 | 0.0 | |
| Forest fruits | 0.9 | 3.5 | 11.6 | 18.0 | 35.6 | 34.3 | 11.8 | 2.5 |
| Period | Mar. | Apr. | May | Jun. | Jul. | Aug. | Sep. | Oct. |
|---|---|---|---|---|---|---|---|---|
| Current | 82.0 | 116.9 | 146.2 | 156.9 | 157.7 | 134.4 | 91.4 | 65.9 |
| Short-term | 86.4 | 116.9 | 147.4 | 145.3 | 158.2 | 126.6 | 92.2 | 65.9 |
| Long-term | 88.4 | 115.9 | 147.3 | 141.4 | 159.6 | 123.7 | 93.6 | 64.9 |
| Period | Crop Type | Mar. | Apr. | May | Jun. | Jul. | Aug. | Sep. | Oct. | Total |
|---|---|---|---|---|---|---|---|---|---|---|
| Current | Spring wheat | 13.9 | 63.1 | 193.0 | 174.2 | 22.1 | 0.0 | 0.0 | 0.0 | 466.3 |
| Corn | 0.0 | 46.8 | 128.7 | 161.6 | 162.4 | 138.4 | 67.6 | 21.1 | 726.6 | |
| Flax | 16.4 | 119.2 | 185.7 | 199.3 | 74.1 | 21.5 | 0.0 | 0.0 | 616.2 | |
| Potato | 0.0 | 2.3 | 76.0 | 155.3 | 156.1 | 130.4 | 43.9 | 0.0 | 564.1 | |
| Melon | 23.8 | 121.6 | 179.8 | 166.3 | 36.3 | 0.0 | 0.0 | 0.0 | 527.8 | |
| Goji berry | 0.0 | 1.2 | 43.9 | 86.3 | 100.9 | 68.5 | 17.4 | 0.0 | 318.2 | |
| Forest fruits | 21.3 | 83.0 | 131.6 | 141.2 | 141.9 | 121.0 | 29.2 | 2.0 | 671.2 | |
| Short-term | Spring wheat | 14.7 | 63.1 | 194.6 | 161.3 | 22.1 | 0.0 | 0.0 | 0.0 | 455.8 |
| Corn | 0.0 | 46.8 | 129.7 | 149.7 | 162.9 | 130.4 | 68.2 | 21.1 | 708.8 | |
| Flax | 17.3 | 119.2 | 187.2 | 184.5 | 74.4 | 20.3 | 0.0 | 0.0 | 602.9 | |
| Potato | 0.0 | 2.3 | 76.6 | 143.8 | 156.6 | 122.8 | 44.3 | 0.0 | 546.5 | |
| Melon | 25.1 | 121.6 | 181.3 | 154.0 | 36.4 | 0.0 | 0.0 | 0.0 | 518.3 | |
| Goji berry | 0.0 | 1.2 | 44.2 | 79.9 | 101.2 | 64.6 | 17.5 | 0.0 | 308.6 | |
| Forest fruits | 22.5 | 83.0 | 132.7 | 130.8 | 142.4 | 113.9 | 29.5 | 2.0 | 656.7 | |
| Long-term | Spring wheat | 15.0 | 62.6 | 194.4 | 157.0 | 22.3 | 0.0 | 0.0 | 0.0 | 451.3 |
| Corn | 0.0 | 46.4 | 129.6 | 145.6 | 164.4 | 127.4 | 69.3 | 20.8 | 703.5 | |
| Flax | 17.7 | 118.2 | 187.1 | 179.6 | 75.0 | 19.8 | 0.0 | 0.0 | 597.4 | |
| Potato | 0.0 | 2.3 | 76.6 | 140.0 | 158.0 | 120.0 | 44.9 | 0.0 | 541.8 | |
| Melon | 25.6 | 120.5 | 181.2 | 149.9 | 36.7 | 0.0 | 0.0 | 0.0 | 513.9 | |
| Goji berry | 0.0 | 1.2 | 44.2 | 77.8 | 102.1 | 63.1 | 17.8 | 0.0 | 306.1 | |
| Forest fruits | 23.0 | 82.3 | 132.6 | 127.3 | 143.6 | 111.3 | 30.0 | 1.9 | 652.0 |
| Year | Return Flow (106 m3) | Irrigation Diversion (106 m3) | Return Flow Coefficient |
|---|---|---|---|
| 2018 | 46.571 | 137.859 | 0.338 |
| 2019 | 47.691 | 147.839 | 0.323 |
| 2020 | 44.406 | 162.358 | 0.274 |
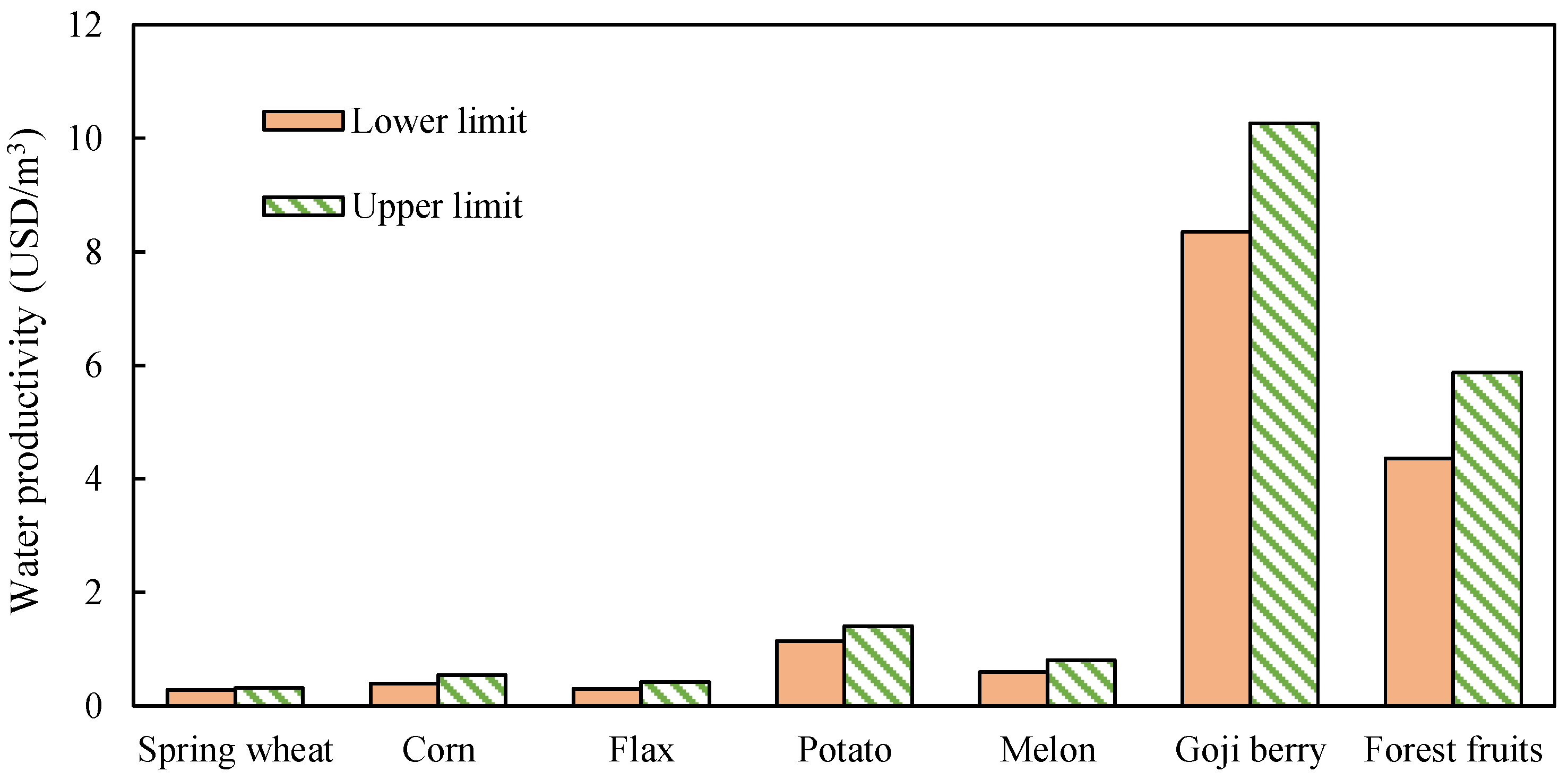
| Crop Type | Crop Yield (kg/ha) | Crop Price (USD/kg) | Planting Cost (USD/ha) | Minimum Planting Area (ha) | Maximum Planting Area (ha) |
|---|---|---|---|---|---|
| Spring wheat | 6750 | [0.33, 0.36] | 1442 | 2122 | 9583 |
| Corn | 11,250 | [0.22, 0.25] | 1545 | 3275 | 14,055 |
| Flax | 4050 | [0.76, 0.82] | 364 | 211 | 2871 |
| Potato | 45,000 | [0.11, 0.14] | 1580 | 393 | 2080 |
| Melon | 37,500 | [0.14, 0.16] | 2404 | 152 | 1126 |
| Goji berry | 7500 | [1.10, 1.24] | 3640 | 351 | 3339 |
| Forest fruits | 30,000 | [0.27, 0.34] | 2060 | 2239 | 5180 |
| Total Planting Area (ha) | Irrigation Water Price (USD/m3) | Irrigation Water Utilization Coefficient |
|---|---|---|
| 20,010 | 0.04 | 0.5718 |
| Crop Type | Current | Short-Term | Long-Term | |
|---|---|---|---|---|
| Before Optimization | After Optimization | |||
| Spring wheat | [2.26, 2.95] | [1.29, 1.68] | [1.30, 1.69] | [1.30, 1.70] |
| Corn | [3.34, 4.87] | [2.2, 3.22] | [2.24, 3.25] | [2.26, 3.27] |
| Flax | [2.27, 2.55] | [0.84, 0.94] | [2.82, 3.16] | [3.64, 4.08] |
| Potato | [2.79, 3.87] | [6.60, 9.18] | [6.63, 9.2] | [6.63, 9.21] |
| Melon | [2.34, 3.28] | [2.87, 4.03] | [2.87, 4.03] | [2.88, 4.03] |
| Goji berry | [8.34, 10.24] | [15.06, 18.5] | [15.08, 18.52] | [15.09, 18.53] |
| Forest fruits | [20.04, 26.98] | [30.81, 41.48] | [30.86, 41.54] | [30.88, 41.55] |
| Crop Type | Current | Short-Term | Long-Term | |
|---|---|---|---|---|
| Before Optimization | After Optimization | |||
| Spring wheat | 22.6% | 12.2% | 11.7% | 11.5% |
| Corn | 30.0% | 18.8% | 18.0% | 17.8% |
| Flax | 5.0% | 1.8% | 5.6% | 7.2% |
| Potato | 5.3% | 11.9% | 11.5% | 11.3% |
| Melon | 5.6% | 6.5% | 6.2% | 6.1% |
| Goji berry | 11.2% | 19.2% | 18.4% | 18.1% |
| Forest fruits | 20.4% | 29.7% | 28.5% | 28.1% |
| Current | Short-Term | Long-Term | |
|---|---|---|---|
| Ignore return flow | [59.62, 78.98] | [61.81, 81.46] | [62.64, 82.42] |
| Consider return flow | [66.76, 86.95] | [66.9, 87.09] | [67.03, 87.23] |
| Net profit growth | [7.14, 7.97] | [5.08, 5.63] | [4.4, 4.81] |
| Crop Type | Current | Short-Term | Long-Term | |||
|---|---|---|---|---|---|---|
| Ignore Return Flow | Consider Return Flow | Ignore Return Flow | Consider Return Flow | Ignore Return Flow | Consider Return Flow | |
| Spring wheat | [1.29, 1.68] | [1.29, 1.68] | [1.30, 1.69] | [1.30, 1.69] | [1.30, 1.70] | [1.30, 1.70] |
| Corn | [2.2, 3.22] | [2.21, 3.23] | [2.24, 3.25] | [2.25, 3.27] | [2.26, 3.27] | [2.27, 3.28] |
| Flax | [0.84, 0.94] | [7.89, 8.84] | [2.82, 3.16] | [7.91, 8.87] | [3.64, 4.08] | [7.92, 8.88] |
| Potato | [6.6, 9.18] | [6.6, 9.18] | [6.63, 9.2] | [6.63, 9.2] | [6.63, 9.21] | [6.63, 9.21] |
| Melon | [2.87, 4.03] | [2.87, 4.03] | [2.87, 4.03] | [2.87, 4.03] | [2.88, 4.03] | [2.88, 4.03] |
| Goji berry | [15.06, 18.5] | [15.06, 18.5] | [15.08, 18.52] | [15.08, 18.52] | [15.09, 18.53] | [15.09, 18.53] |
| Forest fruits | [30.81, 41.48] | [30.81, 41.48] | [30.86, 41.54] | [30.86, 41.54] | [30.88, 41.55] | [30.88, 41.55] |
| Crop Type | Current | Short-Term | Long-Term | |||
|---|---|---|---|---|---|---|
| Ignore Return Flow | Consider Return Flow | Ignore Return Flow | Consider Return Flow | Ignore Return Flow | Consider Return Flow | |
| Spring wheat | 12.2% | 10.6% | 11.7% | 10.6% | 11.5% | 10.6% |
| Corn | 18.8% | 16.4% | 18.0% | 16.4% | 17.8% | 16.4% |
| Flax | 1.8% | 14.3% | 5.6% | 14.3% | 7.2% | 14.3% |
| Potato | 11.9% | 10.4% | 11.5% | 10.4% | 11.3% | 10.4% |
| Melon | 6.5% | 5.6% | 6.2% | 5.6% | 6.1% | 5.6% |
| Goji berry | 19.2% | 16.7% | 18.4% | 16.7% | 18.1% | 16.7% |
| Forest fruits | 29.7% | 25.9% | 28.5% | 25.9% | 28.1% | 25.9% |
| Period | Ignore Return Flow | Consider Return Flow | Reduction of Irrigation Diversion | ||
|---|---|---|---|---|---|
| Irrigation Diversion | Total Water Volume | Irrigation Diversion | Return Flow | ||
| Current | 145 | 170 | [127, 133] | [37, 43] | [12, 18] |
| Short-term | 145 | 162 | [121, 127] | [35, 41] | [18, 24] |
| Long-term | 145 | 159 | [119, 125] | [34, 40] | [20, 26] |
| Crop Type | Current | Short-Term | Long-Term | |||
|---|---|---|---|---|---|---|
| Ignore Return Flow | Consider Return Flow | Ignore Return Flow | Consider Return Flow | Ignore Return Flow | Consider Return Flow | |
| Spring wheat | 15.90 | 15.90 | 15.40 | 15.40 | 15.18 | 15.18 |
| Corn | 35.34 | 35.51 | 33.73 | 33.90 | 33.13 | 33.29 |
| Flax | 2.95 | 27.61 | 9.49 | 26.60 | 12.03 | 26.16 |
| Potato | 16.73 | 16.73 | 15.77 | 15.77 | 15.43 | 15.43 |
| Melon | 9.57 | 9.57 | 9.31 | 9.31 | 9.19 | 9.19 |
| Goji berry | 13.12 | 13.12 | 12.08 | 12.08 | 11.67 | 11.67 |
| Forest fruits | 51.40 | 51.40 | 49.20 | 49.20 | 48.36 | 48.36 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jie, F.; Fei, L.; Peng, Y.; Li, S.; Ge, Y. Optimal Allocation of Water Resources in Irrigation Areas Considering Irrigation Return Flow and Uncertainty. Appl. Sci. 2025, 15, 2380. https://doi.org/10.3390/app15052380
Jie F, Fei L, Peng Y, Li S, Ge Y. Optimal Allocation of Water Resources in Irrigation Areas Considering Irrigation Return Flow and Uncertainty. Applied Sciences. 2025; 15(5):2380. https://doi.org/10.3390/app15052380
Chicago/Turabian StyleJie, Feilong, Liangjun Fei, Youliang Peng, Sheng Li, and Yanyan Ge. 2025. "Optimal Allocation of Water Resources in Irrigation Areas Considering Irrigation Return Flow and Uncertainty" Applied Sciences 15, no. 5: 2380. https://doi.org/10.3390/app15052380
APA StyleJie, F., Fei, L., Peng, Y., Li, S., & Ge, Y. (2025). Optimal Allocation of Water Resources in Irrigation Areas Considering Irrigation Return Flow and Uncertainty. Applied Sciences, 15(5), 2380. https://doi.org/10.3390/app15052380





