A Predictive Multibody Model of Paper Applied to Cash Recycling
Abstract
1. Introduction
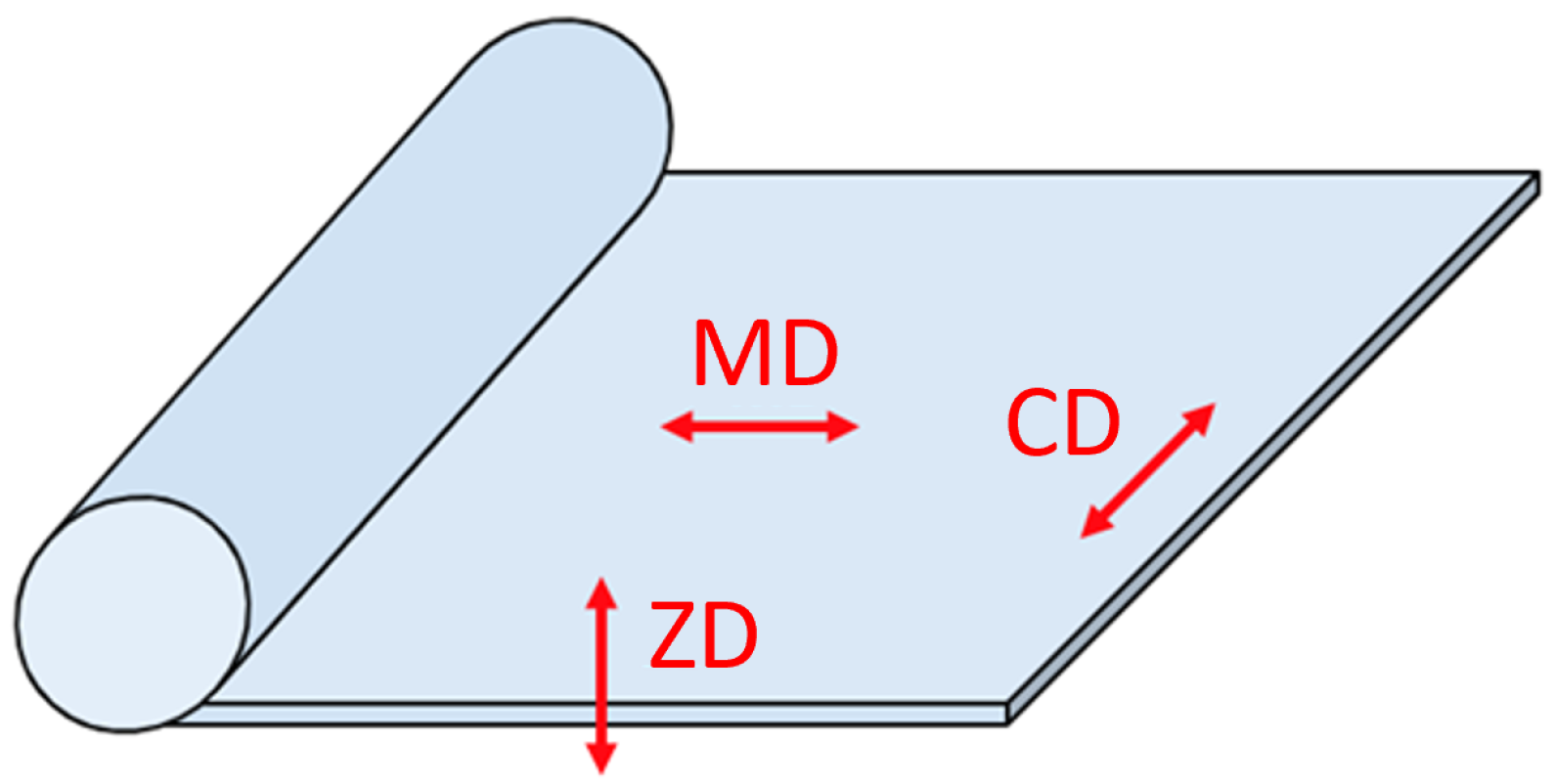
2. Modeling the Banknote
2.1. State-of-the-Art Methodologies Used to Represent Flexible Bodies in MB Simulations
- Linear flexible (LF) body obtained through a component mode synthesis (CMS) condensation method;
- Non linear finite element (NLFE) body.
2.1.1. Linear Condensation
2.1.2. Nonlinear Finite Elements
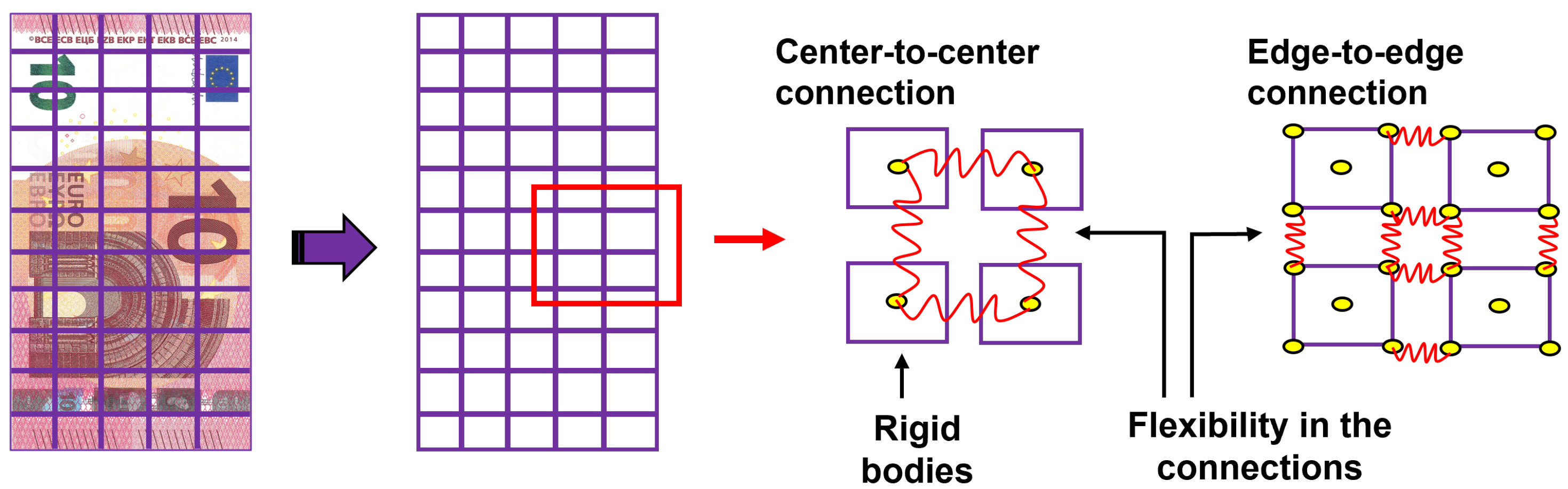
2.2. Methodology
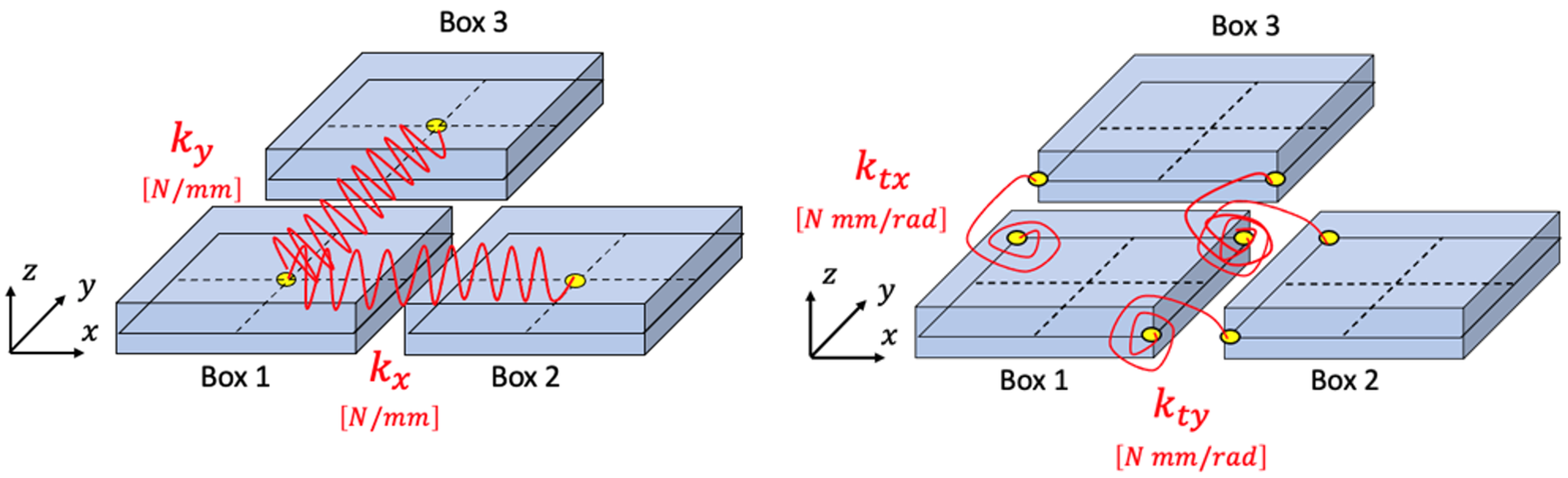
- The connections (spring+damper) are placed between the centers of mass of neighboring ‘boxes’, hereafter termed ‘center-to-center’;
- The spring/damper connect the corners of neighboring boxes, as shown in Figure 3, hereafter termed ‘edge-to-edge’.
2.2.1. Tuning Procedure
- The dimension of the boxes
- The mass of each box
- The section of each box normal to directions X and Y
2.2.2. Automated Implementation
- The points at the center and corners of each rigid body and the rigid bodies mass and inertia properties;
- The graphical elements to be associated with each body, i.e., a box; these graphics have both visualization purposes in post-processing but also play a key role in defining contacts;
- The connecting entities between all rigid bodies, i.e., bushing;
- A deformable surface that attaches to each rigid body at its midpoint in the midplane; this code is optional and is used to visualize results.
3. Modeling the Contact
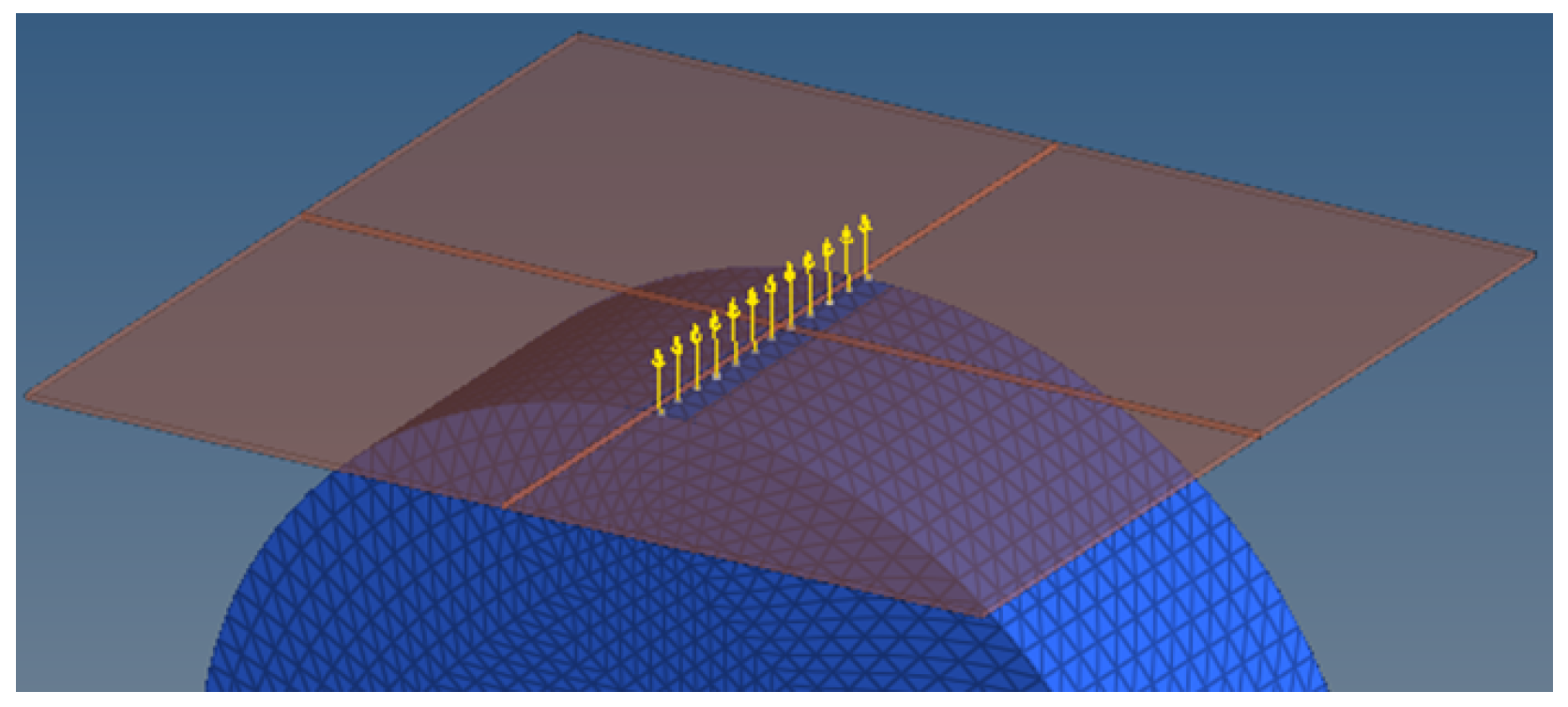
3.1. Contact Detection
- Analytical: Geometries are represented exactly by mathematical functions;
- Mesh-based: The geometries are discretized more or less finely with a mesh of first-order triangular elements; in this case, one can choose whether to evaluate the displacements, velocities, and contact forces at the nodes or at the centers of the elements.
3.2. Contact Forces Computation
3.3. Contact Implementation and Automation
4. Results and Discussion
- Model with four motor-rollers and four counter-rollers: The goal is to verify that the banknote is transported at the desired speed;
- Model with four motor-rollers and two counter-rollers: The goal is to verify that the banknote is able to reach the second row of rollers and counter-rollers;
- Model with tilted banknote: The goal is to verify the banknote tilt correction by changing roller speeds on the second row.
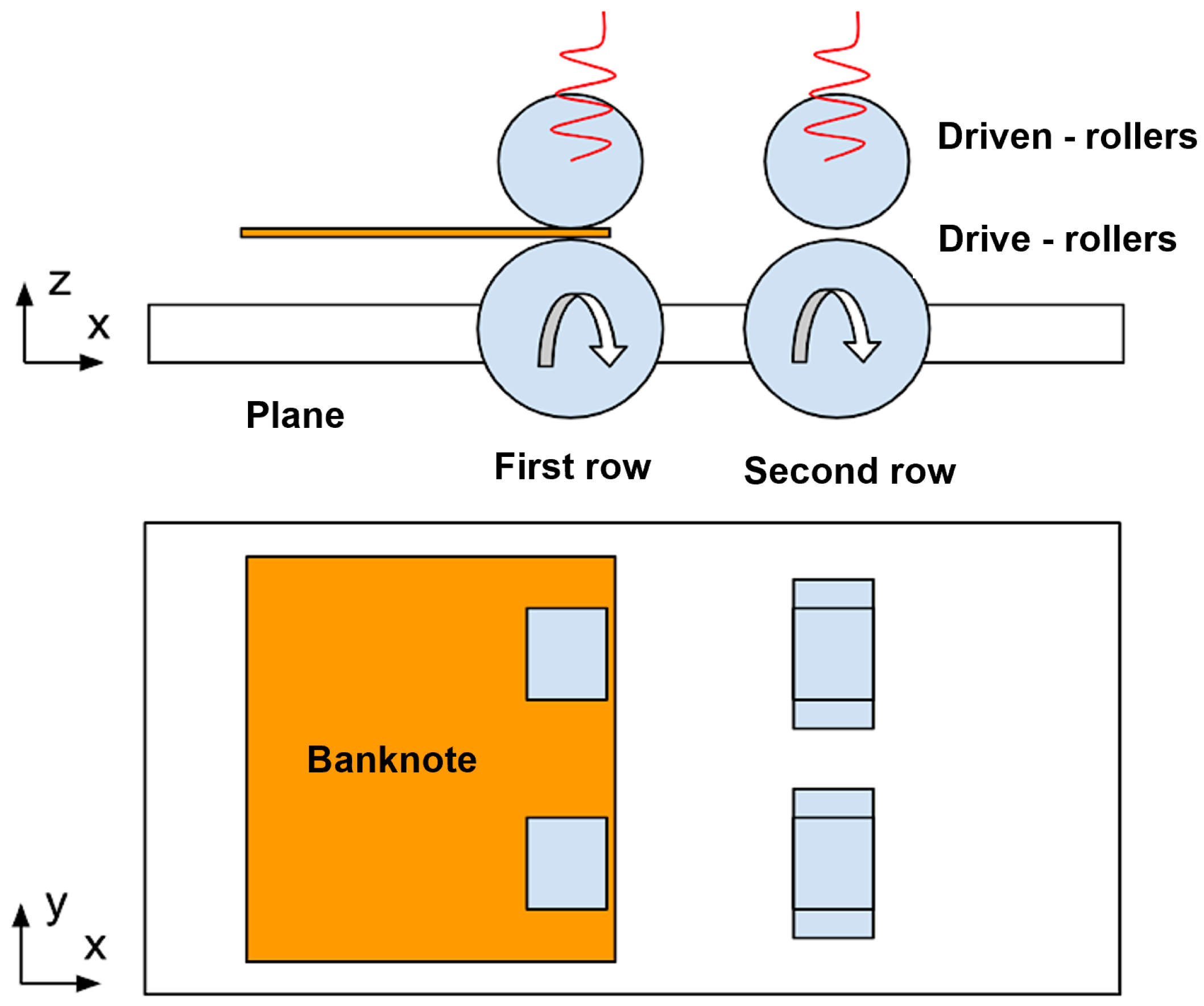
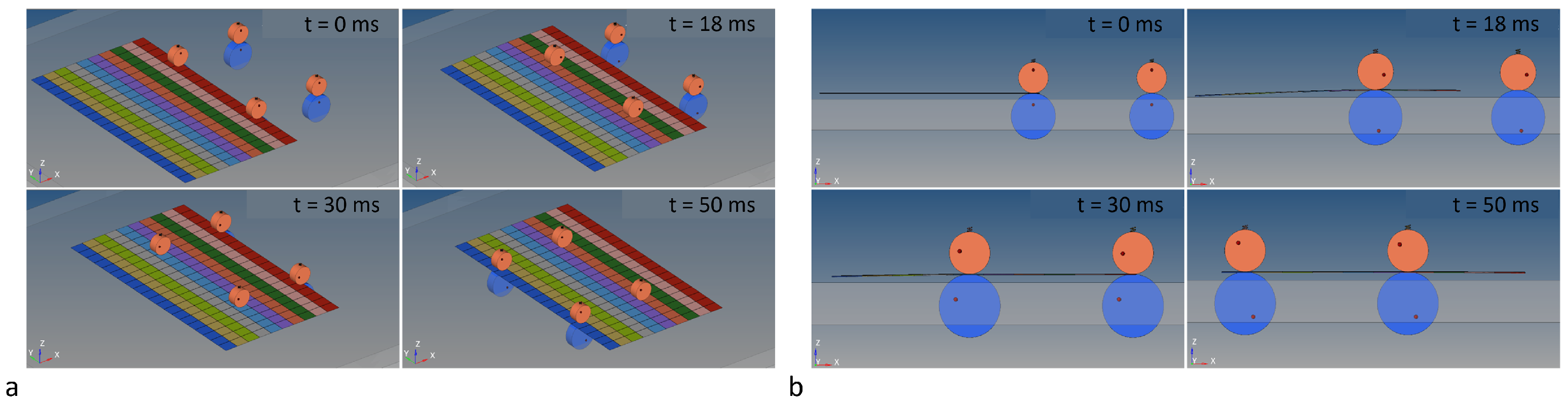
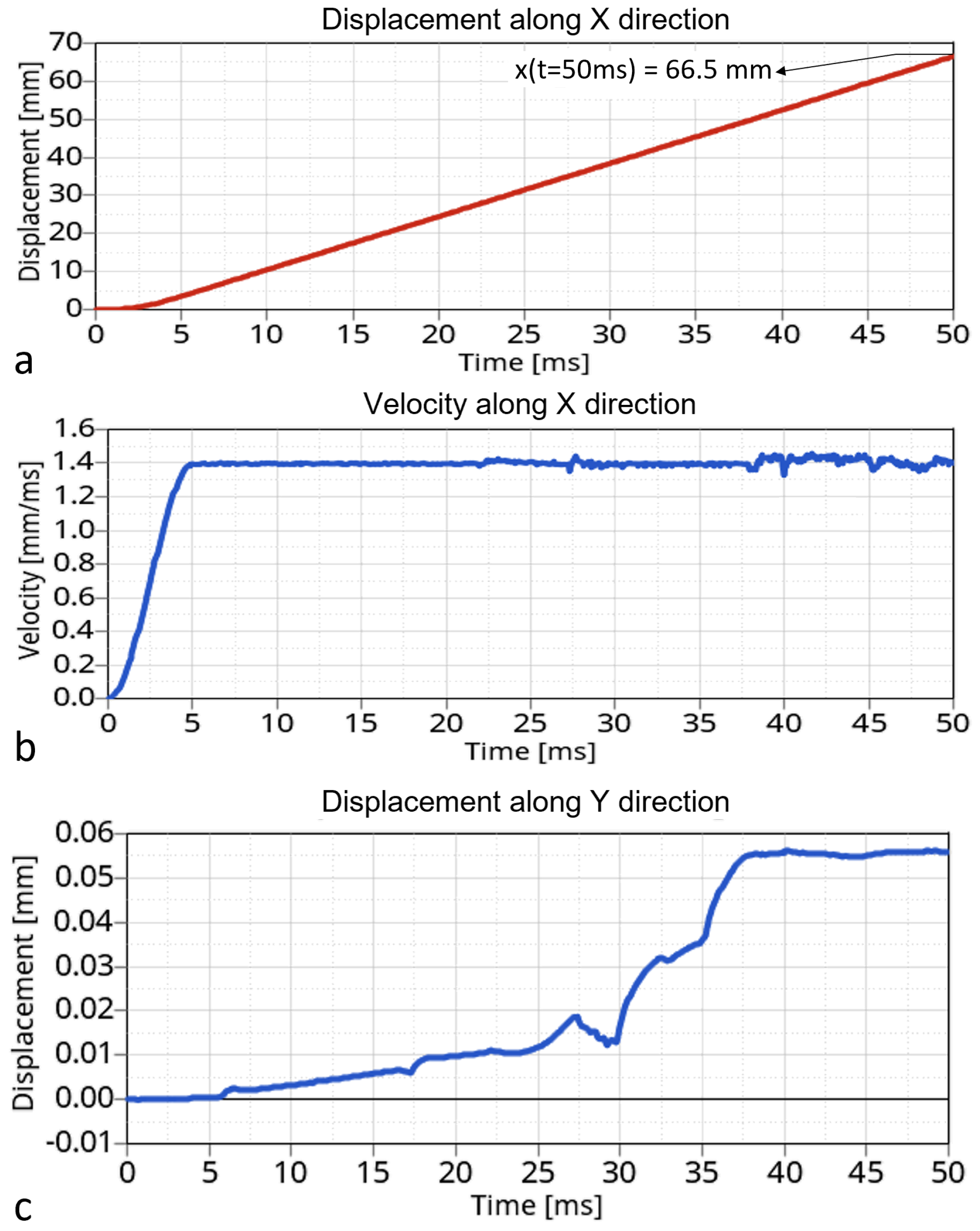
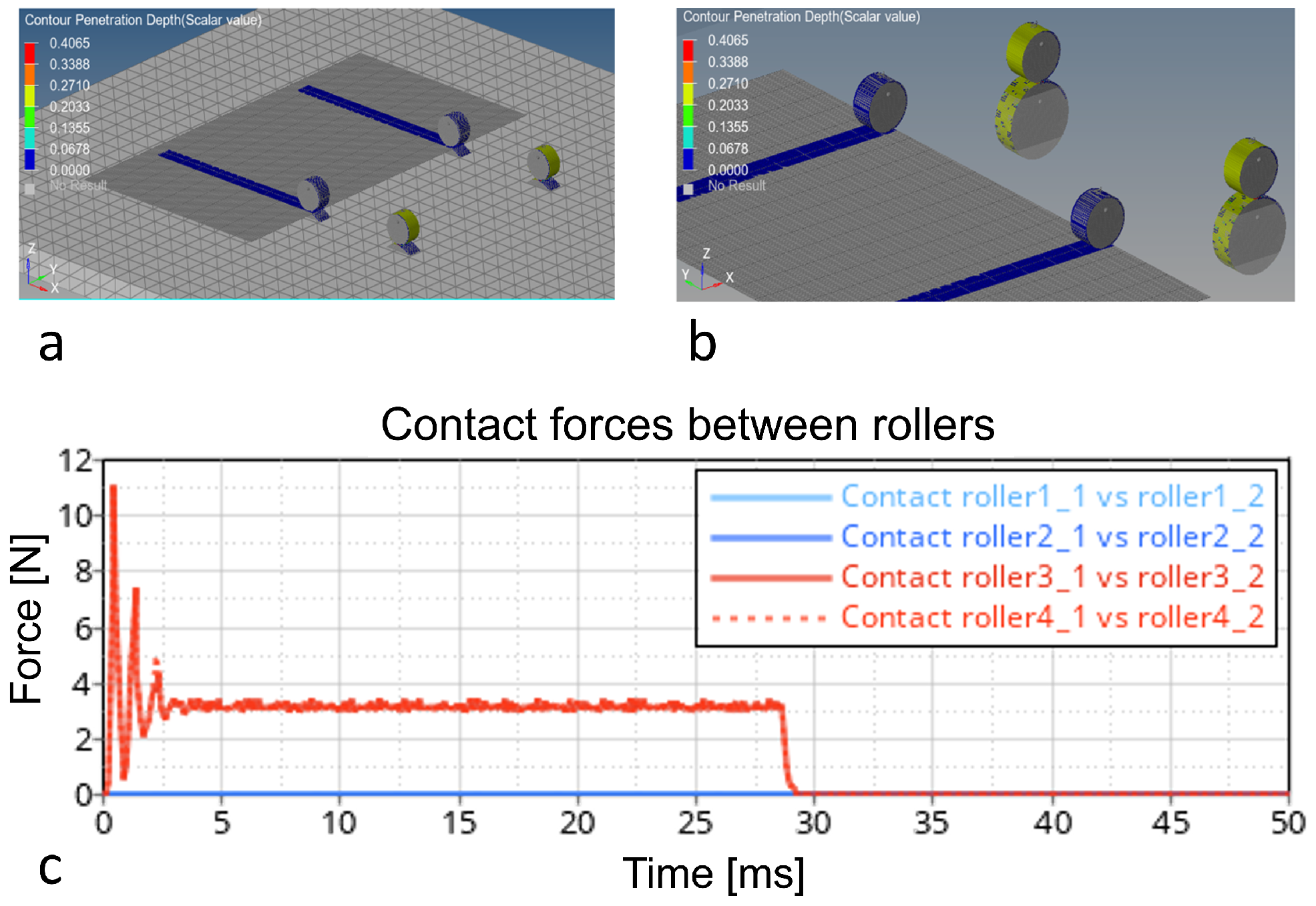
4.1. Model with Four Pairs of Motor and Counter-Rollers
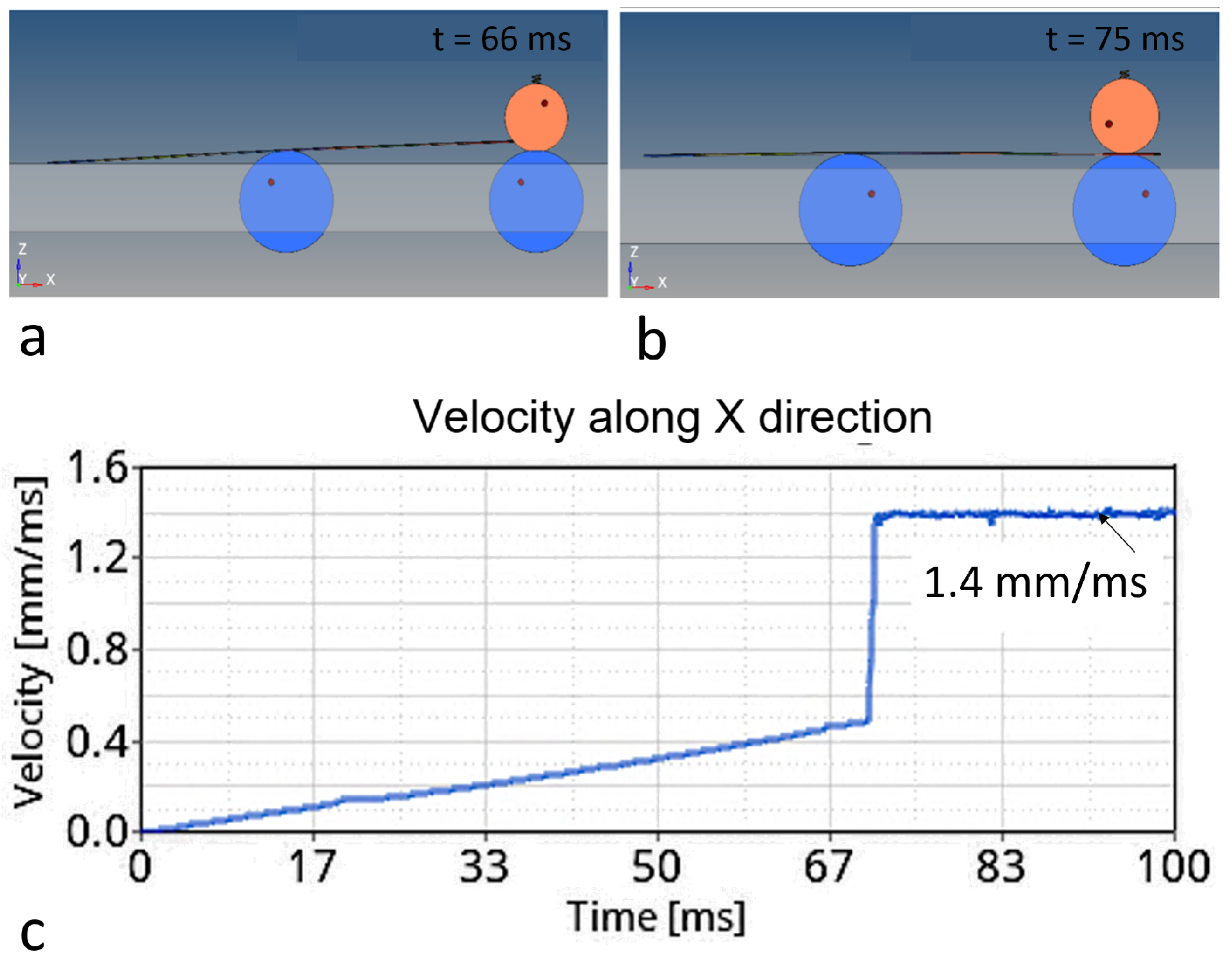
4.2. Model with Four Motor-Rollers and Two Counter-Rollers
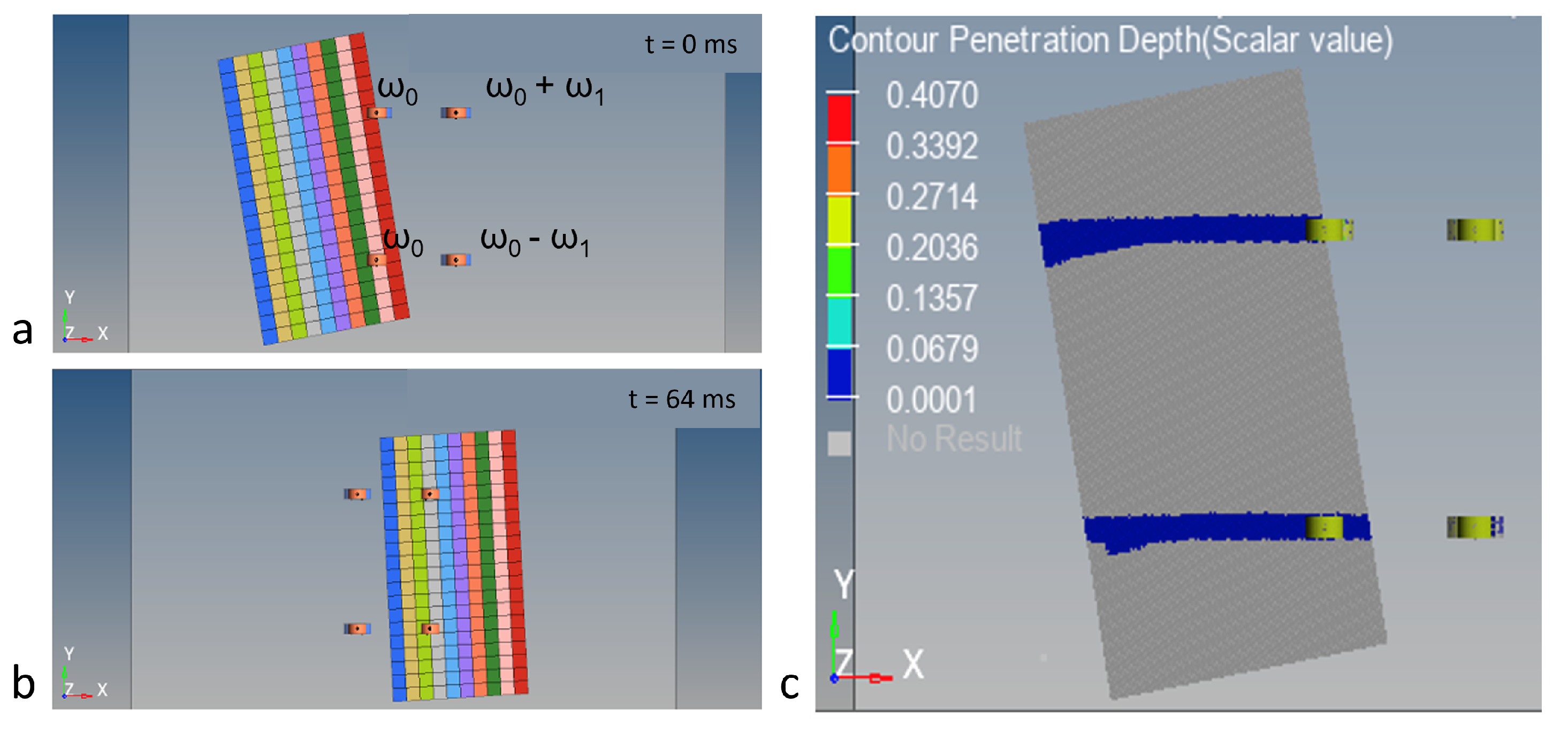
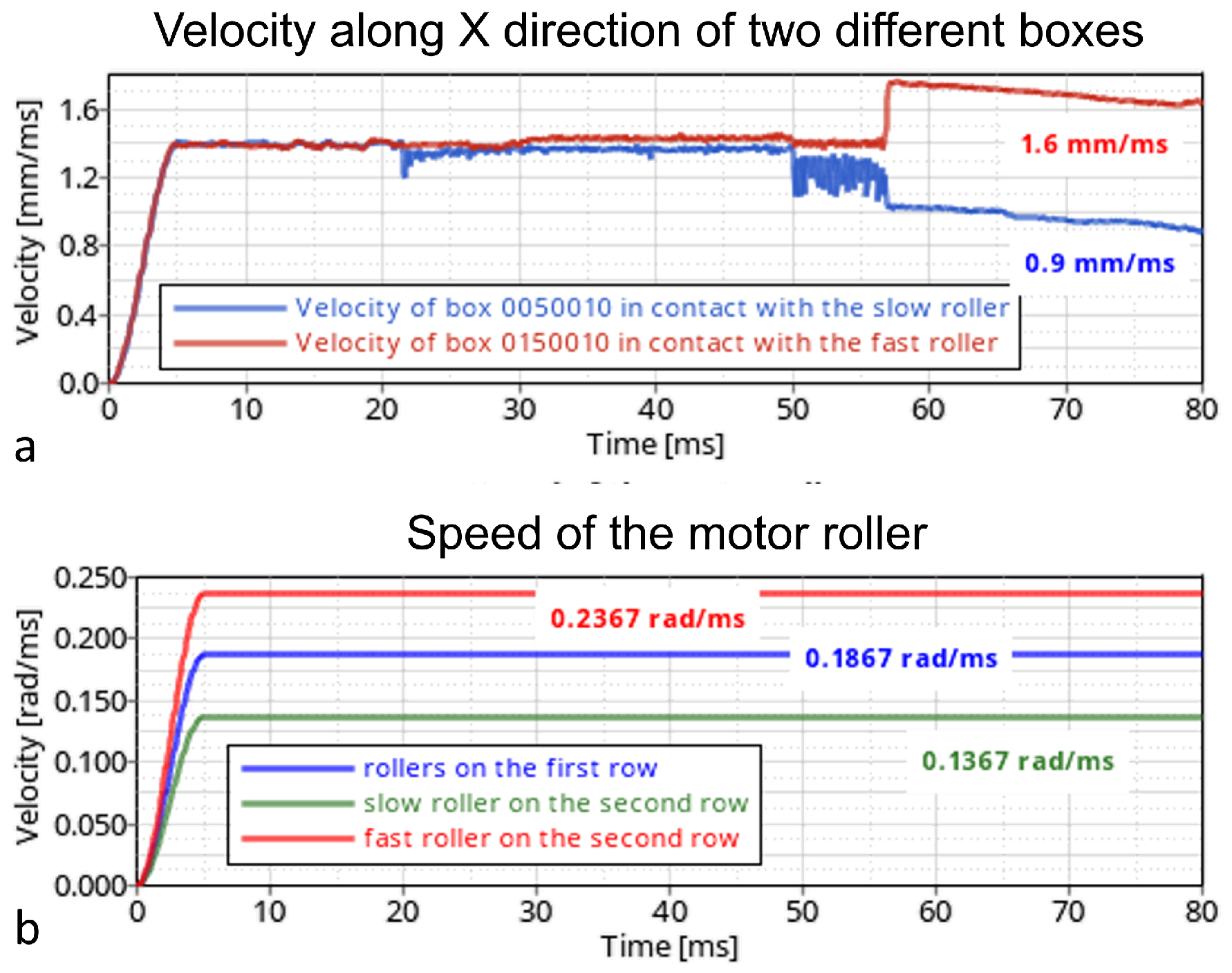
4.3. Model with Tilted Banknote
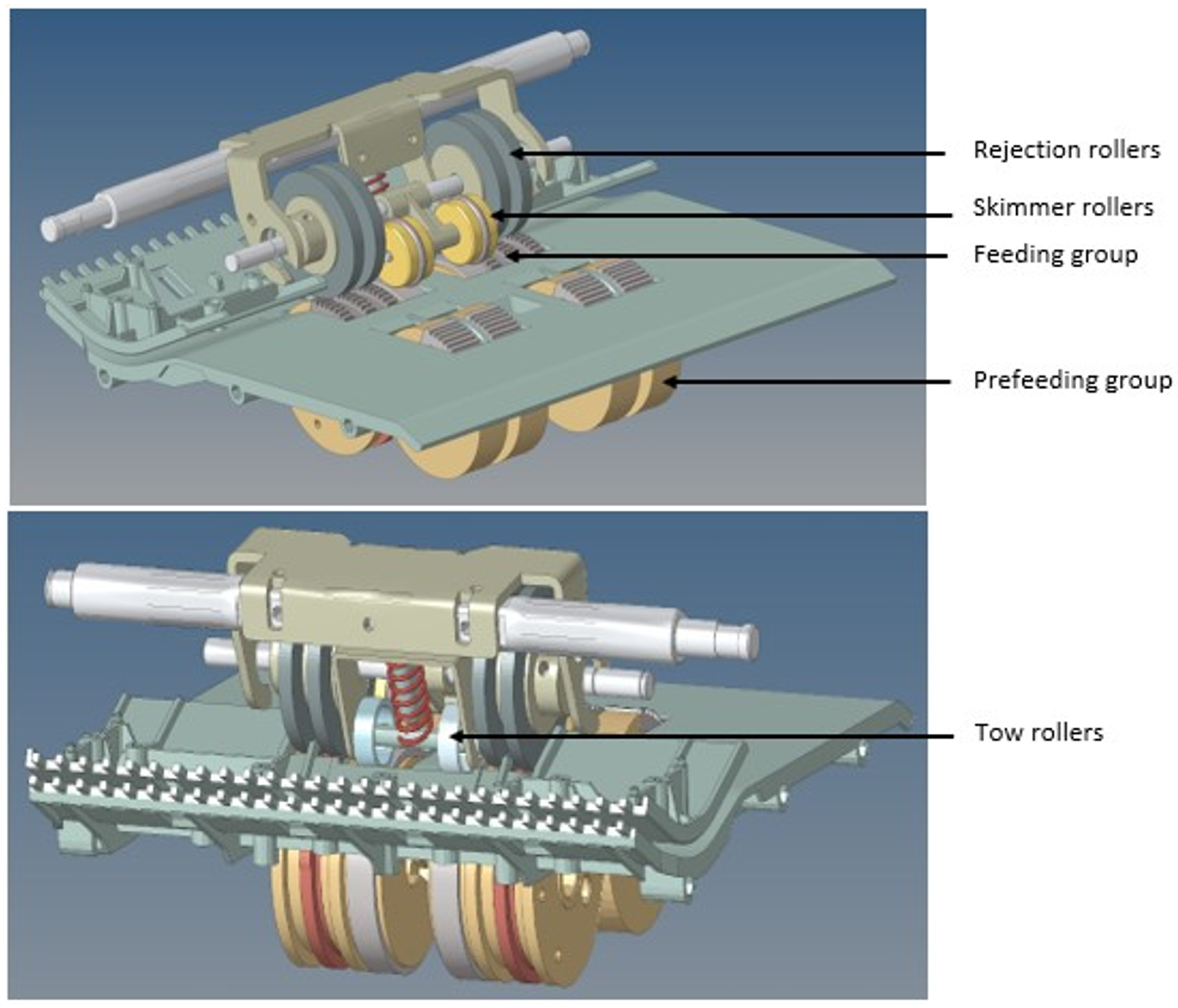
4.4. High-Fidelity Cash Recycler Model
- They align the banknote by pivoting if it arrives tilted;
- They press down on the banknote by providing the necessary drag force to get the banknote just below the rejection rollers but not past them (the feeding rollers are in charge of that).
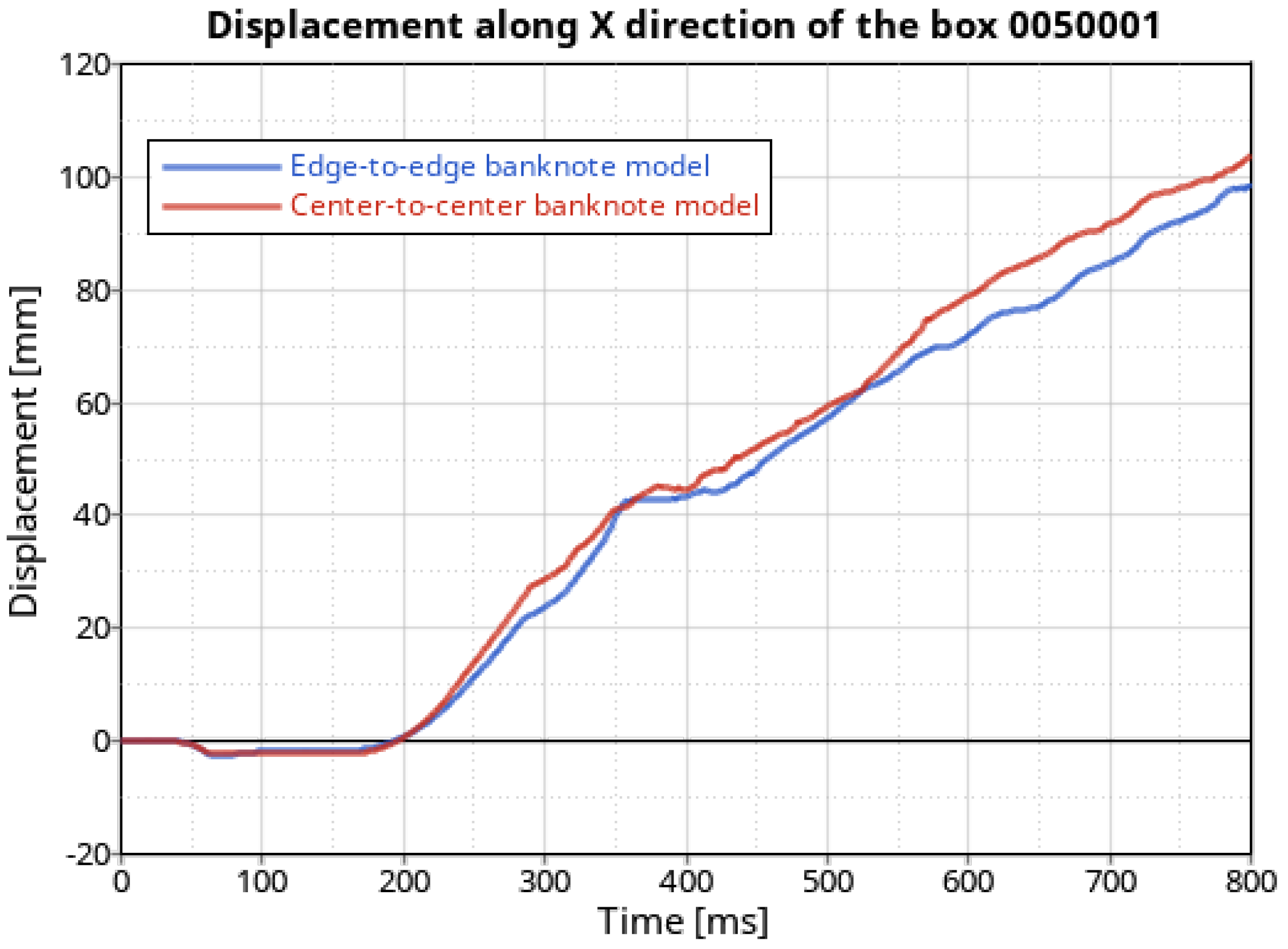
- 200 boxes banknote model with center-to-center connections;
- 200 boxes banknote model with edge-to-edge connections;
- 600 boxes banknote model with edge-to-edge connections.
5. Conclusions
- Greater simplicity in defining the contact. The contact between deformable surfaces is prone to convergence problems, especially when considering large displacements typical of transportation. Modeling the banknote as a ‘grid’ of rigid bodies allows the use of a more robust contact definition. This feature not only ensures convergence but significantly reduces computational times;
- Possibility of using the nonlinear curves characteristic of the orthotropic paper material;
- Lack of cumbersome pre-processing steps typical of dynamic condensation. In the present case, a Python code automatically creates the banknote starting from a simple set of user-defined parameters;
- Complete control and customization of the banknote system, as one can vary quantities such as thickness, friction coefficients, etc., in specific areas.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| MB | Multibody |
| LF | Linear flexible |
| NLFE | Non linear finite element |
| FE | Finite element |
| CAD | Computer-aided drawing |
References
- Tedder, K.; Huber, R. 2020 Health of Cash Study. 2020. Available online: https://javelinstrategy.com/research/2020-health-cash-study (accessed on 17 October 2022).
- Halpin, J. The Future of Retail Cash Technology; Technical Report, ACMA Currency Notes; ACMA: Melbourne, Australia, 2020. [Google Scholar]
- Bruna, A.; Farinella, G.; Guarnera, G.; Battiato, S. Forgery Detection and Value Identification of Euro Banknotes. Sensors 2013, 13, 2515–2529. [Google Scholar] [CrossRef] [PubMed]
- Simon, J.W. A Review of Recent Trends and Challenges in Computational Modeling of Paper and Paperboard at Different Scales. Arch. Comput. Methods Eng. 2021, 28, 2409–2428. [Google Scholar] [CrossRef]
- Sanjon, C.W.; Leng, Y.; Hauptmann, M.; Groche, P.; Majschak, J.P. Methods for Characterization and Continuum Modeling of Inhomogeneous Properties of Paper and Paperboard Materials: A Review. BioResources 2024, 19, 6804–6837. [Google Scholar] [CrossRef]
- Garbowski, T.; Gajewski, T.; Grabski, J.K. Estimation of the Compressive Strength of Corrugated Cardboard Boxes with Various Perforations. Energies 2021, 14, 1095. [Google Scholar] [CrossRef]
- Marin, G.; Srinivasa, P.; Nygårds, M.; Östlund, S. Experimental and Finite Element Simulated Box Compression Tests on Paperboard Packages at Different Moisture Levels. Packag. Technol. Sci. 2021, 34, 229–243. [Google Scholar] [CrossRef]
- Aduke, R.N.; Venter, M.P.; Coetzee, C.J. Numerical Modelling of Corrugated Paperboard Boxes. Math. Comput. Appl. 2024, 29, 70. [Google Scholar] [CrossRef]
- Sugiyama, H.; Kobayashi, N. Analysis of Spaghetti Problem Using Multibody Dynamics. Trans. Jpn. Soc. Mech. Eng. Ser. C 1999, 65, 910–915. [Google Scholar] [CrossRef][Green Version]
- Shabana, A.A. Flexible Multibody Dynamics: Review of Past and Recent Developments. Multibody Syst. Dyn. 1997, 1, 189–222. [Google Scholar] [CrossRef]
- Bauchau, O.A. Flexible Multibody Dynamics; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Simeon, B. Computational Flexible Multibody Dynamics; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Li, Y.; Stapleton, S.E.; Reese, S.; Simon, J.W. Anisotropic elastic-plastic deformation of paper: In-plane model. Int. J. Solids Struct. 2016, 100–101, 286–296. [Google Scholar] [CrossRef]
- Skrinjar, L.; Slavič, J.; Boltežar, M. A review of continuous contact-force models in multibody dynamics. Int. J. Mech. Sci. 2018, 145, 171–187. [Google Scholar] [CrossRef]
- Hurty, W.C. Dynamic analysis of structural systems using component modes. AIAA J. 1965, 3, 678–685. [Google Scholar] [CrossRef]
- Craig, R.R.; Bampton, M.C.C. Coupling of substructures for dynamic analyses. AIAA J. 1968, 6, 1313–1319. [Google Scholar] [CrossRef]
- MacNeal, R.H. A hybrid method of component mode synthesis. Comput. Struct. 1971, 1, 581–601. [Google Scholar] [CrossRef]
- Rubin, S. Improved Component-Mode Representation for Structural Dynamic Analysis. AIAA J. 1975, 13, 995–1006. [Google Scholar] [CrossRef]
- R. Craig, J. On the use of attachment modes in substructure coupling for dynamic analysis. In Proceedings of the AIAA/ASME 18th Structural Dynamics and Materials Conference, San Diego, CA, USA, 21–23 March 1977. [Google Scholar] [CrossRef]
- O’Shea, J.J.; Jayakumar, P.; Mechergui, D.; Shabana, A.A.; Wang, L. Reference Conditions and Substructuring Techniques in Flexible Multibody System Dynamics. J. Comput. Nonlinear Dyn. 2018, 13, 041007. [Google Scholar] [CrossRef]
- Mitra, M.; Zucca, S.; Epureanu, B.I. Adaptive Microslip Projection for Reduction of Frictional and Contact Nonlinearities in Shrouded Blisks. J. Comput. Nonlinear Dyn. 2016, 11, 041016. [Google Scholar] [CrossRef]
- Gastaldi, C.; Zucca, S.; Epureanu, B.I. Jacobian projection reduced-order models for dynamic systems with contact nonlinearities. Mech. Syst. Signal Process. 2018, 100, 550–569. [Google Scholar] [CrossRef]
- Sun, H.; Zhang, D.; Wu, Y.; Shen, Q.; Hu, D. A Semi-Analytical Multi-Harmonic Balance Method on Full-3D Contact Model for Dynamic Analysis of Dry Friction Systems. Chin. J. Aeronaut. 2024, 37, 309–329. [Google Scholar] [CrossRef]
- MotionSolve Reference Guide 2023. Available online: https://2023.help.altair.com/2023.1/hwsolvers/ms/topics/chapter_heads/msolve_ref_guide_r.htm (accessed on 5 January 2025).
- Learn Multi-Body Simulation with Altair MotionSolve. Available online: https://advanced-eng.cz/wp-content/uploads/2021/06/2021_eBook_Learn_Multi_Body_Simulation_with-Altair_Motion_Solve.pdf (accessed on 5 January 2025).
- Lagier, F.; Massicotte, B.; Charron, J.P. 3D Nonlinear Finite-Element Modeling of Lap Splices in UHPFRC. J. Struct. Eng. 2016, 142, 04016087. [Google Scholar] [CrossRef]
- Peter, B.; Sänger, N. A Nonlinear Finite Element Framework for Flexible Multibody Dynamics: Rotationless Formulation and Energy-Momentum Conserving Discretization. In Multibody Dynamics; Springer: Dordrecht, The Netherlands, 2009; pp. 119–141. [Google Scholar] [CrossRef]
- Gastaldi, C.; Berruti, T.M. Competitive Time Marching Solution Methods for Systems with Friction-Induced Nonlinearities. Appl. Sci. 2018, 8, 291. [Google Scholar] [CrossRef]
- Marques, F.; Flores, P.; Claro, J.C.P.; Lankarani, H.M. Modeling and analysis of friction including rolling effects in multibody dynamics: A review. Multibody Syst. Dyn. 2018, 45, 223–244. [Google Scholar] [CrossRef]



| Parameter | Symbol | Value |
|---|---|---|
| Banknote mass (g) | M | 0.72 |
| Banknote length short side (mm) | 67 | |
| Banknote length long side (mm) | 127 | |
| Banknote thickness (mm) | s | 0.1 |
| Number of boxes along X | 10 | |
| Number of boxes along Y | 20 | |
| Box length along X | 7.44 | |
| Box length along Y | 6.68 | |
| Box mass (g) | m | 0.0036 |
| Center-to-Center Connection | ||||
|---|---|---|---|---|
| Translational stiffness (N/mm) | Translational damping (N/mm/ms) | |||
| 317 | 0.26 | 0.12 | ||
| 124 | 0.16 | 0.12 | ||
| Rotational stiffness (N mm/rad) | Rotational damping (N mm ms/rad) | |||
| 0.27 | 7.48 | 0.12 | ||
| 0.45 | 3.22 | 0.04 | ||
| 10 | 45.5 | 0.12 | ||
| Edge-to-Edge Connection | ||||
| Translational stiffness (N/mm) | Translational damping (N/mm/ms) | |||
| 158 | 0.13 | 0.12 | ||
| 62 | 0.08 | 0.12 | ||
| Rotational stiffness (N mm/rad) | Rotational damping (N mm ms/rad) | |||
| 0.15 | 5.58 | 0.12 | ||
| 0.185 | 2.06 | 0.04 | ||
| 5 | 23 | 0.12 | ||
| Description | Mass (g) | Dimensions (mm) |
|---|---|---|
| Support plane | 681 | 227 × 300 × 10 |
| Motor-rollers | 0.88 | Diameter = 15 Thickness = 5 |
| Counter-rollers | 0.39 | Diameter = 10 Thickness = 5 |
| Parameter | Rollers/ Counter-Rollers | Plane/Banknote | Rollers/Banknote | Counter-Rollers/ Banknote |
|---|---|---|---|---|
| Stiffness k (N/) | 30.5 | 100 | 300 | 300 |
| Restitution coeff. | 0.5 | 0.5 | 0.5 | 0.5 |
| Friction coeff. | 1 | 0.3 | 1 | 0.33 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Giorio, L.; Gastaldi, C.; Delprete, C.; Libetti, S.; Eleuteri, D. A Predictive Multibody Model of Paper Applied to Cash Recycling. Appl. Sci. 2025, 15, 2283. https://doi.org/10.3390/app15052283
Giorio L, Gastaldi C, Delprete C, Libetti S, Eleuteri D. A Predictive Multibody Model of Paper Applied to Cash Recycling. Applied Sciences. 2025; 15(5):2283. https://doi.org/10.3390/app15052283
Chicago/Turabian StyleGiorio, Lorenzo, Chiara Gastaldi, Cristiana Delprete, Samuele Libetti, and Davide Eleuteri. 2025. "A Predictive Multibody Model of Paper Applied to Cash Recycling" Applied Sciences 15, no. 5: 2283. https://doi.org/10.3390/app15052283
APA StyleGiorio, L., Gastaldi, C., Delprete, C., Libetti, S., & Eleuteri, D. (2025). A Predictive Multibody Model of Paper Applied to Cash Recycling. Applied Sciences, 15(5), 2283. https://doi.org/10.3390/app15052283









