Abstract
The increasing frequency of tropical cyclones caused by global warming poses a serious threat to the safe operation of coastal power grids, making it urgent to develop methods for quantitatively assessing the risks of spatiotemporal grid anomalies. This paper proposes a risk assessment method for power grids under the influence of tropical cyclones, with a focus on the spatiotemporal evolution of grid failures. First, the abnormal impact of meteorological factors on power grid equipment is analyzed, revealing the time-varying characteristics of equipment failures. Next, by incorporating power flow redistribution, an abnormal evolution mechanism of the grid that considers the coupling effect of meteorological factors and power flow was established. Then, by identifying the abnormal propagation paths and corresponding quantitative risk assessment metrics, the evolution of system failures during tropical cyclones was analyzed, and the failure chains were evaluated for risk. Finally, simulations based on the IEEE 14 system were conducted to verify the effectiveness of the proposed method in modeling the evolution of grid anomalies and failure processes.
1. Introduction
In recent years, global warming has increased the frequency of tropical cyclones, including typhoons and extreme storm surges, in China’s coastal regions. Extreme weather conditions during tropical cyclones can disrupt offshore wind power output and trigger transmission line failures, threatening the safety and reliability of the power grid. Unlike other extreme weather events, tropical cyclones follow distinct spatiotemporal paths. As a tropical cyclone passes, the impact on grid equipment evolves over time, creating complex spatiotemporal patterns of grid anomalies that complicate risk assessment. Therefore, a quantitative risk assessment method is urgently needed that accounts for the spatiotemporal evolution of grid anomalies, which forms the basis for disaster emergency planning and strengthens resilience.
The primary cause of power grid operational risk is large-scale or significant disturbances. As distributed energy resources are increasingly integrated into modern power grids, operational risks have shifted from traditional overloads due to single equipment failures to multidimensional anomalies caused by complex, large-scale distributed energy disturbances. Random fluctuations in distributed flexible resources like electric vehicles [1], photovoltaics [2,3], and wind power [4,5] can, via the amplification effect of large-scale disturbances, push the grid’s operation beyond safe stability limits. Besides the clustering effect of large-scale distributed resources on operational indicators, major disturbances can also introduce operational risks to the grid [6]. Extreme weather events, given their frequency and destructiveness, have garnered widespread attention in power grid risk assessment in recent years [7,8,9,10].
Risk assessment of power grids under extreme weather conditions generally involves two key steps: (1) scenario set construction; and (2) risk index calculation. The first step integrates extreme weather forecasts, analyzes the abnormal characteristics of power grid equipment, and generates hypothetical scenarios describing various equipment states. The second step involves calculating risk indices such as power flow deviation, voltage deviation, and load loss under these scenarios to quantify and assess grid risk. Extreme weather factors can cause physical damage through mechanical actions, leading to equipment failures. Extreme weather factors can also cause abnormal output variations in weather-sensitive renewable energy, such as ramping in wind power. Consequently, researchers have extensively studied equipment-level mechanisms of abnormal impacts and their quantitative characterization. In studying transmission line anomalies, [11] proposed a method for assessing risk levels by constructing a hierarchical analysis model linking meteorological factors such as lightning, icing, and strong winds to risk levels. In [12], the authors analyzed how thermal stress from lightning contributes to line aging and breakage. In studying renewable energy anomalies, [13] analyzed atmospheric circulation patterns that lead to ramping of wind power, demonstrating that thermally driven land–sea wind interactions may be the primary cause. In the context of tropical cyclones, [14] quantifies the dynamic impact of extreme wind speeds on wind turbines through the analysis of offshore wind turbine results under extreme load conditions. In addition, [15] establishes a model for calculating the instantaneous failure rate of transmission lines and towers based on a tropical cyclone wind field model. After constructing such a multi-factor interaction mechanism model, subsequent fault propagation can be simulated through a cascading model.
Modeling cascading failures in power systems is crucial for assessing grid vulnerability and developing prevention and control strategies. The traditional OPA(ORNL-PSERC-Alaska) model simulates the evolution of cascading failures based on quasi-steady-state assumptions. However, it neglects the impact of system transient dynamics on the fault sequence, making it difficult to capture chain reactions triggered by equipment transients and protection actions at short time scales [16]. On the other hand, the cascading failure model based on DC power flow (DF-CFS) is widely applied in large-scale grid analysis due to its computational efficiency. However, it overlooks crucial factors such as voltage stability and angle dynamics [17].
By integrating extreme weather factors with methods for quantifying abnormal equipment states, we can establish both equipment anomalies and hypothetical scenarios for the power grid. Combining the risk index values from power flow analysis under specific scenarios with accident probabilities allows for quantifying the overall operational risk of the system [18]. A specific type of hypothetical scenario is the fault chain, where an initial disturbance leads to multiple interrelated cascading equipment failures [19]. Reference [20] examined the impact of extreme high temperatures on load and transmission line capacity, and developed an fault chain model that accounts for fault sequences. Fault chains have a broad impact and are highly destructive. Consequently, researchers are focusing on strategies to suppress the propagation of these chains or mitigate their risks during system planning and operation [21].
As tropical cyclones pass, the extreme meteorological factors affecting power grid equipment and the equipment’s abnormal states evolve continuously. Traditional fault chains, which previously considered only overloads and power flow risk factors, have evolved to account for the coupling of time-varying extreme weather conditions and power flow risks [22]. To address this, we propose a risk assessment method that incorporates the spatiotemporal evolution of grid anomalies during tropical cyclones. First, the impact mechanisms of tropical cyclones on grid equipment, including transmission lines and wind power, are analyzed to identify the time-varying abnormal states of grid equipment during cyclone events. Second, the evolution patterns of system anomalies under the coupling and interaction of time-varying extreme weather factors and power flow risks are examined. Third, alternating simulations of equipment failures induced by extreme weather and power flow redistributions are conducted based on the coupling mechanism, leading to the development of methods for constructing fault chains and scenario sets during tropical cyclones. Finally, the overall system risk assessment results are presented, incorporating uncertainties in extreme weather factors and grid parameters associated with tropical cyclones.
The main contributions of the paper include the following:
- Incorporating the spatiotemporal trajectory of typhoons, this study examined the time-varying abnormal states of source-grid equipment under typhoon impacts, revealing the spatiotemporal characteristics of grid faults. Based on these characteristics, the study further analyzed the spatiotemporal evolution mechanism of grid anomalies caused by the coupling of extreme weather factors and power flow, identifying the propagation paths of grid anomalies.
- This study utilizes a risk assessment method that considers the spatiotemporal evolution of grid anomalies. This method captures the time-varying states of grid components under extreme weather and power flow interactions. It models cascading failures, constructs fault chains, and calculates risk indicators, providing accurate risk quantification and guidance for disaster prevention.
2. Risk Assessment Research Framework Considering the Spatiotemporal Evolution of Power Grid Anomalies Under Tropical Cyclones
The core goal of this study is to deeply analyze the fault evolution process of the power grid system under the influence of extreme weather such as typhoons by combining extreme meteorological factors with the dynamic changes in power grid flow. First, the physical model of source-grid equipment under extreme meteorological factors of tropical cyclones is developed, integrating the spatiotemporal trajectory information of tropical cyclones, and analyzing the failure probabilities of lines in the system and the output characteristics of wind farms under tropical cyclones. Then, the coupling mechanism between meteorological information and power flow in the grid is analyzed to determine the abnormal propagation path of the grid under tropical cyclones, providing the theoretical foundation for subsequent risk assessment.
To quantify the risk during the system failure evolution process and the degree of system damage under tropical cyclones, a risk indicator system is established based on specific failure scenarios, reflecting the grid operation risk during the occurrence of tropical cyclones from two perspectives: the grid failure evolution stage and the post-disaster system status. Figure 1 illustrates the methodological framework of this paper.
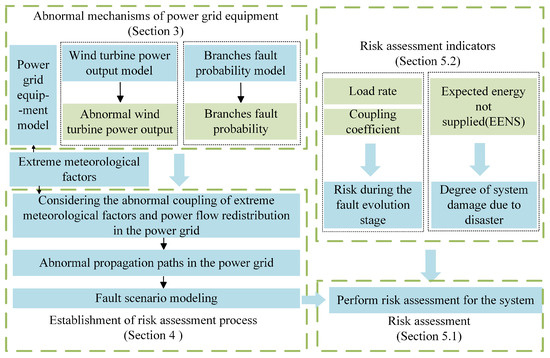
Figure 1.
Risk assessment research framework considering the spatiotemporal evolution of power grid anomalies under tropical cyclones.
3. Evolution of Power Grid Equipment Anomalies Considering Extreme Meteorological Factors Under Tropical Cyclones
3.1. Mechanisms of Abnormal Impacts of Extreme Meteorological Factors on Power Grid Equipment
Extreme weather conditions, particularly high wind speeds during tropical cyclones, can disrupt power grid equipment, including wind farms and transmission lines. High wind speeds first activate turbine protection mechanisms, disconnecting turbines from normal operation and resulting in wind power fluctuations [23]. Additionally, high wind speeds can impose uneven stress on transmission towers, causing irreversible fatigue damage and potential collapse. Tropical cyclones may also apply excessive wind pressure on overhead lines, leading to breakage. As tropical cyclones move, the changing relative positions of extreme weather factors and grid equipment create time-varying weather impacts and corresponding equipment anomalies. Based on the Rankine vortex wind field model [24], assuming that the distance between grid equipment i and the center of the tropical cyclone at time period j is , the maximum wind speed of the cyclone is , and the radius of maximum wind speed is , then the wind speed perceived by equipment i at time period j, denoted as , can be expressed as follows:
In the equation, the distance between equipment i and the center of the tropical cyclone can be expressed as follows:
In the equation, represents the coordinates of equipment i, and represents the coordinates of the tropical cyclone center during time period j.
3.1.1. Mechanism of Abnormal Effects of Extreme Meteorological Factors on Wind Power Output
The high wind speeds during tropical cyclones cause significant fluctuations in turbine output power [25]. Assuming that the wind farm i consists of N identical turbines, and based on Equations (1) and (2), the wind speed perceived by the turbine at time period j is , the output power can be expressed as follows:
In the equation, s represents the swept area; denotes the rated power of the wind turbine; indicates the cut-in wind speed; represents the rated wind speed; and signifies the cut-out wind speed. The air density can be expressed as follows:
In the equation, represents the atmospheric pressure; R denotes the atmospheric constant; and indicates the temperature.
The power coefficient can be expressed as follows:
In the equation, and represent the tip speed ratio and its optimal value, respectively, and denotes the pitch angle. The tip speed ratio and its optimal value can be expressed as follows:
3.1.2. Mechanism of Abnormal Effects of Extreme Meteorological Factors on Transmission Lines
Tropical cyclones primarily cause abnormalities in transmission lines by damaging conductors (single-span lines) or towers. This section describes the mechanism of abnormal effects of extreme meteorological factors on transmission lines by constructing a probability model for tower collapse and a probability model for conductor breakage in single-span lines.
According to the Palmgren–Miner linear fatigue damage criterion [26], the cumulative fatigue damage is obtained by summing the fatigue damage over several preceding time periods. Let be the single fatigue damage for tower i during time period j, which can be expressed as follows:
In the equation, represents the extreme wind speed perceived by tower i during time period j; a and b are the fatigue damage coefficients; denotes the critical wind speed that causes fatigue in the tower; and represents the ultimate wind speed corresponding to the damage that leads to breakage caused by a tropical cyclone in a single time period.
In practice, the collapse of a tower is related to the cumulative fatigue damage sustained throughout the entire period of a tropical cyclone’s impact. The probability that tower i will not collapse during time period j can be expressed as follows:
In this equation, denotes the duration of each time period. The probability that a tower remains intact during the first t periods is the product of the non-collapse probabilities from period 1 to period t:
Based on Equations (9) and (10), the probability that tower i does not collapse in the first t periods is as follows:
The probability that tower i collapses during the first t periods is as follows:
Tropical cyclones induce short-term faults in single-span lines through wind pressure [27]. Let represent the wind speed perceived by single-span line i during period j. The wind pressure experienced by the line can be expressed as follows:
In the equation, , , , and represent the coefficients for wind pressure non-uniformity, wind load, wind pressure height variation, and line type, respectively. denotes the angle between the wind direction and the conductor. The failure rate for single-span line i during period j can be expressed as follows:
The probability of a break occurring in single-span line i during the first j periods can be expressed as follows:
3.2. The Abnormal Evolution Process of the Power Grid Under Extreme Meteorological Conditions During Tropical Cyclones
Based on Section 3.1, the time-varying extreme weather conditions caused by a tropical cyclone not only lead to time-varying abnormal outputs in wind farm i, but also cause transmission line i to experience line faults with a specific probability at different periods. Suppose the affected wind farms are numbered from 1 to N, and the affected transmission lines are numbered from 1 to L. The tropical cyclone’s passage is divided into T periods. The abnormal grid evolution process, considering only extreme meteorological factors, can be described as a binary tuple , where element represents the spatiotemporal matrix of abnormal outputs from N wind farms:
In this equation, denotes the abnormal output of wind farm i during time period j.
The element represents the spatiotemporal matrix of failure probabilities:
In this equation, represents the probability of a fault occurring on branch l during the first j periods. Since Equation (18) does not capture the actual operational state of the branch, it is necessary to determine the spatiotemporal matrix of equipment failure states through sampling:
In this equation, represents the operational state of branch l at time period j, where 0 indicates the branch is closed, and 1 indicates the branch is open.
4. The Abnormal Evolution Mechanism of the Power Grid Considering the Coupling Effects of Meteorological Factors and Power Flows
The abnormal evolution process described by Equations (17)–(19) considers only the abnormal impacts of extreme meteorological factors on power grid equipment across different time periods. However, branch faults triggered by extreme weather may lead to overloads and further branch faults, or even cascading failures, due to power flow redistribution. As time passes, the alternating coupling of time-varying extreme weather conditions and the post-fault power flow redistribution further complicates the propagation paths of abnormalities within the grid’s branches.
4.1. Considering the Abnormal Coupling of Extreme Meteorological Factors and Power Flow Redistribution in the Power Grid
During the passage of a tropical cyclone in period t, following the abnormal state evolution method of the power grid described in Section 3, the abnormal state of the grid at period t can be represented as follows:
In the equation, represents the abnormal output vector of the wind farm in period t, and represents the operating state vector of the branch in period t. Based on Equation (20), the power flow redistribution at period t can be analyzed:
In this equation, represents the transmission power vector of all branches in the system at period t; is the branch transmission power function; is the system parameter vector. represents potential overloaded transmission power. The failure probability of the overloaded branch l () is as follows:
In this equation, represents the transmission power of overloaded branch l; represents the transmission power limit of overloaded branch l; and represents the rated transmission power of overloaded branch l. By sampling based on Equation (22), the abnormal transition state of the branch under power flow redistribution can be obtained:
Based on and the branch fault vector caused by extreme meteorological factors, the branch fault state at period t + 1 can be obtained:
In this equation, represents the following conditional function:
In this equation, represents the sampling function. If branch l is in a disconnected state () at period t, it will remain disconnected at period t + 1. Otherwise, the state will be determined by sampling based on the fault probability at period t + 1. Finally, by incorporating the abnormal output vector of the wind power at period t + 1, the abnormal system state at period t + 1 is obtained.
From Equations (20)–(25), it is evident that the system transitions from abnormal state to state , influenced not only by extreme meteorological factors at period t + 1 but also by the transition state of the branches caused by power flow redistribution at period t. The alternating coupling of extreme meteorological factors and power flow redistribution drives the system’s abnormal evolution. The coupling process of grid anomalies, considering extreme meteorological factors and power flow redistribution, can be summarized as shown in Figure 2:
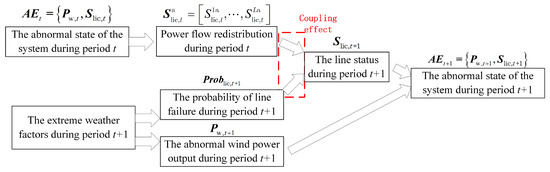
Figure 2.
Schematic diagram of the power grid anomaly coupling process considering extreme weather factors and power flow redistribution.
4.2. Abnormal Propagation Paths in the Power Grid During Tropical Cyclones
Based on Equations (20)–(25) in Section 4.1, the transition of grid abnormal states from one period to the next is a complex process governed by both power flow redistribution and extreme meteorological factors. During the T periods of a tropical cyclone, each period corresponds to a unique system state distribution, forming the abnormal propagation path illustrated in Figure 3. The fault events caused by extreme weather factors at longer time scales (minutes or hours) are denoted as in Figure 3, with representing the development time of extreme weather. At shorter time scales (seconds or milliseconds), cascading overload faults due to power flow redistribution are denoted as in Figure 3, with representing the development time of cascading faults. The radial derivatives in Figure 3 represent the power flow transfer process that occurs when an initial branch failure leads to a redistribution of system power flow. If this redistribution results in line overloads, the radial arrows illustrate the flow shift, while the blue dots indicate lines that disconnect due to these overloads.
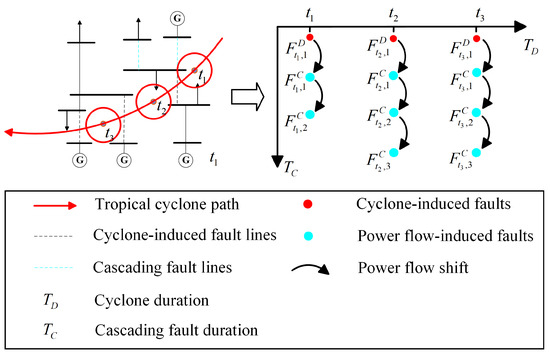
Figure 3.
Schematic diagram of the power grid anomaly propagation process, accounting for the coupling effects of meteorological factors and power flow.
Section 3 has already detailed the methods for calculating branch fault probability and wind power anomalies under extreme meteorological conditions. To derive the abnormal propagation path, the key step is to analyze the power flow redistribution process. This section focuses on two main aspects, (1) generator rescheduling and (2) islanding management, to explain the power flow redistribution in detail. Finally, the procedure for deducing the abnormal propagation path is outlined.
4.2.1. Rescheduling Considering Power Flow Redistribution
According to Equation (20), when the system experiences a fault operating state due to the impact of a tropical cyclone at time period t, rescheduling is required to restore supply-demand balance. The rescheduling process outlined in Equations (21)–(23) can be broken down into the following steps:
Step 1: Unit regulation and emergency load shedding or generator tripping
The primary goal of unit ramping and load shedding or generator tripping is to restore supply-demand balance. Since the cost of load shedding or tripping is higher than that of unit regulation, unit ramping has a higher scheduling priority than emergency load shedding or tripping. Assuming the supply-demand imbalance caused by the fault is , for the regulating unit , if the power supply is less than the load demand and the imbalance does not exceed the total upward regulation capacity , the adjusted power can be expressed as follows:
In this equation, represents the maximum power output of unit i, and represents the rated power of unit i. If, after further adjustment, , i.e., unit regulation, still fails to restore the supply-demand balance, load shedding must be implemented:
If the power supply exceeds the load demand , and the imbalance is not less than the total down-regulation capacity , the adjusted power can be expressed as follows:
In the equation, represents the minimum power output of unit i. Furthermore, if , i.e., unit regulation, still fails to restore the supply-demand balance, generator tripping should be implemented:
Step 2: Power flow analysis
After restoring the supply-demand balance through unit adjustment or generator/load shedding, the branch transmission power is determined using power flow analysis.
Step 3: Disconnection of overloaded branches
Based on the transmission power calculated in Step 2, the status of overloaded branches is determined using Equations (22)–(23).
Repeat steps 1 through 3 until the system reaches a new state of equilibrium.
4.2.2. Managing Islanded Microgrids
Considering that system redispatch and power flow redistribution may cause the interconnected system to split into multiple islands during the abnormal propagation process, the following actions are taken based on the type of island to ensure independent operation.
If the island contains no generators, all loads in the island should be shed:
If the island has only one generator and the total load demand is less than the generator’s output , the generator’s reduced power is as follows:
Furthermore, if the generator power reduction still cannot balance the total load demand , generator tripping will occur.
If the island has only one generator and the total load demand exceeds the generator’s output , the generator’s increased power is as follows:
Furthermore, if the generator’s output increase still cannot balance the total load demand , load shedding will be required.
For islands with multiple generators, the calculation process follows the same steps as in Steps 1–3.
5. Risk Assessment Considering the Coupling Effects Between Meteorological Factors and Power Flow
The analysis in Section 3 and Section 4 indicates that during the tropical cyclone passage, the power grid experiences abnormal propagation paths due to the interaction of meteorological factors and power flow. According to the law of large numbers, increasing the number of samples improves the accuracy with which the frequency of branch states reflects probability , thereby enhancing the risk assessment accuracy. In addition to being influenced by the number of branch state samples, as shown in Equations (26)–(32), different load curves produce varying time series of supply-demand imbalances, leading to distinct abnormal propagation paths through redispatching, power flow redistribution, and islanding. Assuming M load curves need to be assessed, with each requiring N branch state samples, a total of simulations are necessary. To ensure accurate branch fault probability estimation, N cannot be reduced; thus, to improve computational efficiency, M must be reduced to decrease the number of simulations.
5.1. Cascading Failure Simulation
To evaluate the impact of abnormal propagation on the power grid, the load shedding rate (LSR) is chosen as a key metric in cascade fault simulations. During the simulation of cascade fault development, this metric is used to model the cutoff. It is specifically defined as the ratio of total load loss to the initial grid load.
In this equation, D and represent the sets of buses with loads in the original network and the islanded network after decoupling, respectively. and denote the remaining loads in each respective network.
Based on the above, the evolution process of the abnormal propagation path is illustrated in Figure 4:
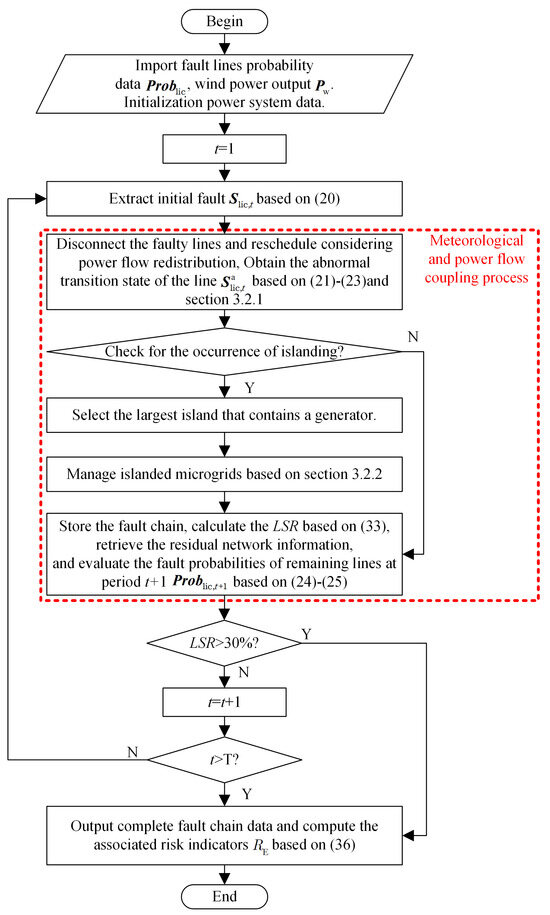
Figure 4.
Evolution flowchart of the abnormal propagation path.
5.2. Risk Assessment Indicators
The objective of quantitative risk assessment is to establish metrics that represent system risk. Various metrics can be utilized for risk analysis, including overload, voltage, and branch indicators. Branch risk indicators reflect the overload characteristics of a branch caused by power flow redistribution following a disconnection, which may result in overloads on other branches. Thus, this paper employs load rate and coupling coefficient as key metrics for risk assessment. Since the economic performance of power companies is closely linked to user power losses, this paper adopts the expected energy not supplied (EENS) [28] calculation as an additional risk metric.
(1) Load Rate
Let be the ratio of the active power of branch i at time periods t and t − 1 to its maximum allowable active power, reflecting the load level of branch i under stable operating conditions.
In the equation, and represent the power flows of branch i during the cascading failure at time periods t and t − 1, respectively, while denotes the maximum allowable power flow of branch i.
(2) Coupling Coefficient
Due to the cumulative effect of successive branch disconnections on the remaining branches, is defined as the ratio of the active power variation in branch i during stages t − 1, t, and t + 1 to the original active power of branch i. Physically, the greater the power flow fluctuation caused by the disconnection of the previous branch, the larger the coupling coefficient becomes.
In this equation, , , and represent the active power on branch i during stages t − 1, t, and t + 1 of the cascading failure, respectively.
(3) Expected Energy Not Supplied(EENS)
The expected value of reduced power supply to users due to forced unit outages indicates the severity of the fault. Therefore, EENS is used as an indicator to assess and quantify the impact of typhoons within specific fault chains.
In the equation, denotes the expected value of insufficient power in the system; denotes the probability of the system state; denotes the load reduction caused by fault state s; T denotes the evaluation time frame (typically in hours); and F denotes the set of system states.
6. Case Study Analysis
To validate the risk assessment method for spatiotemporal evolution of grid anomalies under the impact of tropical cyclones proposed in this paper, the improved IEEE 14 system is used for testing. Additionally, the feasibility of this method in large-scale power grids and under extreme disaster conditions is further validated using the enhanced IEEE 118 system.
6.1. Simulation Setup
In this case study, the tropical cyclone event is validated by simulating the path of Typhoon Maria, the eighth typhoon of 2018 in China. The typhoon’s path data are mapped onto the grid topology, yielding the modified IEEE 14 system topology, with the typhoon path annotated as shown in Figure 5. In this case study, the maximum wind speed of the wind radius (with radius ) is defined as the risk wind zone based on the critical wind speed for plastic fatigue damage. The transmission towers are constructed using Q345 material, with a unit distance of 5 km between two towers. All wind farms use the same model of wind turbine, the American NREL 5MW wind turbine. The cut-in, rated, and cut-out wind speeds of the turbine are as follows: m/s, m/s, and m/s. The specific parameters of the wind turbines, towers, and transmission lines are provided in Table 1.
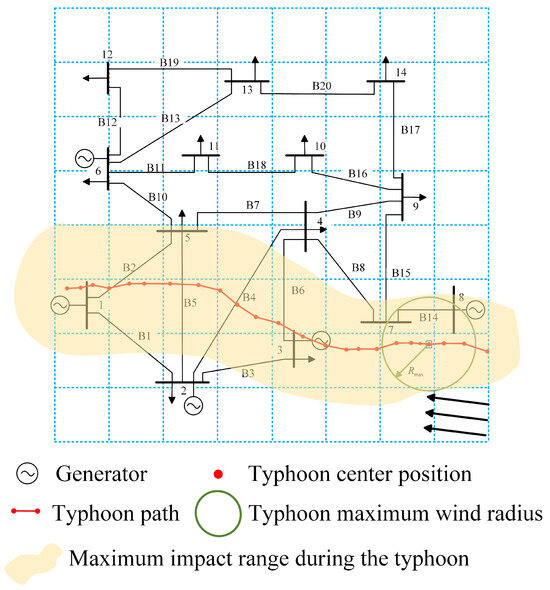
Figure 5.
Typhoon path and IEEE 14 system topology.

Table 1.
The parameters for the towers and transmission lines.
The IEEE 14 system represents a portion of the U.S. power system (located in the Midwest), including 14 buses and 20 transmission lines. In this system, the generators at nodes 2, 3, and 8 are replaced with wind farms, each with an installed capacity of 40 MW and equipped with 8 NREL 5 MW wind turbines. The load data at various time points during the passage of the typhoon are shown in Figure 6.
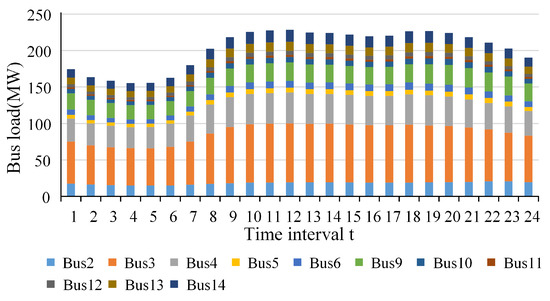
Figure 6.
Each bus load of IEEE 14 system.
6.2. Analysis of Power Grid Equipment Abnormalities Under Tropical Cyclones
Figure 7 illustrates the following trends in wind power output at bus 2: during , the output slowly increases as the typhoon approaches; during , as the wind farm nears and exits the risk wind circle, wind speed rises rapidly, resulting in fluctuations at high speeds that cause frequent start-stop operations and abnormal ramping of turbines; during , as the typhoon moves away, the wind speed decreases gradually from to , maintaining rated power output. The wind farms at buses 3 and 8 are impacted by the typhoon earlier than at bus 2, showing a similar wind power development trend but with an “advance” phenomenon.
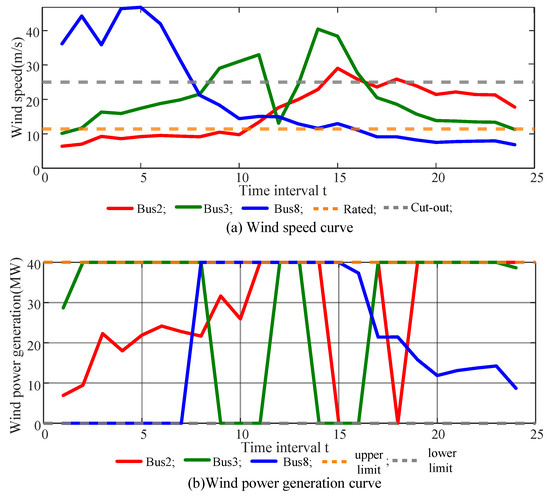
Figure 7.
Wind power curve of IEEE 14 system during typhoon.
The time-varying fault probabilities of the branches are illustrated in Figure 8. As shown in Figure 5, the branches affected by the typhoon risk circle include branches 1–6, 8, 14, and 15. Branches 8, 14, and 15 are the first to be impacted by the typhoon, being close to the wind circle’s edge. In the period , these branches experience high wind speeds, causing a sharp increase in cumulative fatigue damage, which results in fault probabilities of 0.1971, 0.8937, and 0.2699, respectively. In the interval , as the typhoon moves away, the cumulative fatigue damage no longer increases, and the fault probabilities for branches 8, 14, and 15 stabilize. Compared to branch 14, branches 1–6 are further inland, where the typhoon’s intensity has decreased, resulting in lower wind speeds and, consequently, lower cumulative fatigue damage, leading to reduced fault probabilities. The remaining branches are far from the typhoon and outside the risk wind circle, resulting in a fault probability of 0.
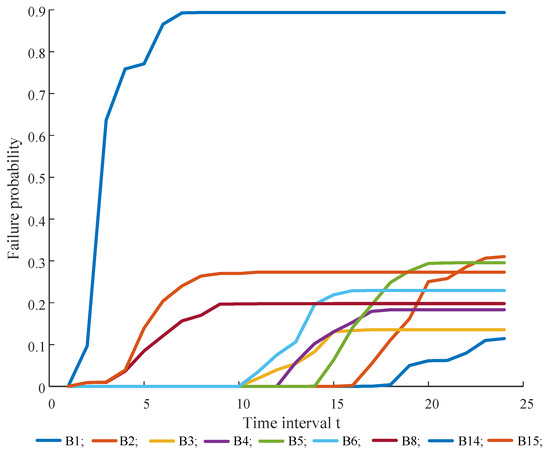
Figure 8.
Branches’ fault probability of the IEEE 14 system.
6.3. Evolution of System Failures Considering the Coupling Effects of Power Flow and Weather
To explore the evolutionary characteristics of the system during failures, this study provides a detailed analysis of the flow and meteorological coupling effects for various branch disconnections. Observing the changes in load rates and coupling coefficients following branch disconnections allows for a better understanding of flow distribution characteristics under fault conditions and the interactions between branches. The following analysis details the system’s response to disconnections of various branches, revealing key features in the fault evolution process. The high-risk fault branches under typhoon conditions are disconnected in sequence: branch 14 at period 3, branch 15 at period 4, and branch 8 at period 5, leading to the changes in load rates and coupling coefficients after disconnection as illustrated in Figure 9. Observing the changes in load rate indicators and coupling coefficients of other branches facilitates the preliminary assessment of the fault chain’s evolution trend.
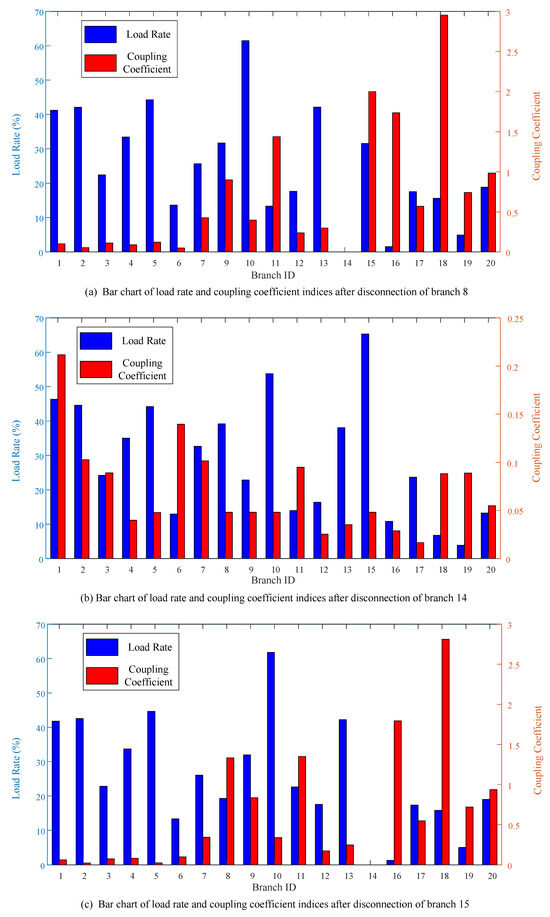
Figure 9.
Chart of branch load rates and coupling coefficients.
After disconnecting branch 8, the load rate of branch 10 reached 0.6145, the highest among all branches, indicating that this disconnection significantly impacted branch 10. Additionally, the coupling coefficient of branch 18 reached 2.9550, indicating a significant impact on its flow. Following the disconnection of branch 14, branch 15 exhibited the highest load rate of 0.6532, while branch 2 had the largest coupling coefficient at 0.2117, indicating significant impacts on these branches. Finally, after the disconnection of branch 15, the load rate of branch 10 again reached a high value of 0.6180, while the coupling coefficient of branch 18 also increased to 2.8120. These data clearly illustrate that at each stage of fault development, certain branches experienced greater flow changes, highlighting the evolution of system faults.
Figure 5 and Figure 9 indicate that disconnecting branch 14 creates a small island in the system, resulting in the failure of one generator and a significant shift in system flow. In contrast to the disconnections of branches 8 and 15, the system’s load rate and coupling coefficient indicators exhibited significant changes. Thus, in light of the impacts of extreme weather events on the power grid, particular attention should be given to critical branches that are susceptible to island effects upon disconnection, and these should be reinforced to mitigate failure risks and enhance system stability.
As the fault evolves, the fault probabilities of the lines caused by extreme weather and power flow redistribution are shown in Figure 10. The color bar and numbers on the right side of the Figure 10 indicate the total fault probability associated with the fault evolution stages caused by extreme weather and cascading failures. The red ’B’ followed by a number represents the branches in the system. Beginning at the 6th period, meteorological factors led to a gradual increase in fault probabilities for several branches. By the 12th period, the affected area within the system had significantly expanded, particularly for branches 9, 12, and 14, which exhibited fault probabilities exceeding 0.7. This indicates an intensifying impact of the typhoon on critical regions of the power grid, resulting in substantial flow transfers along these branches. During the 18th and 24th periods, the distribution of faults within the system intensified further, highlighting the increasing exposure of the power grid’s vulnerabilities due to the typhoon’s continued impact.
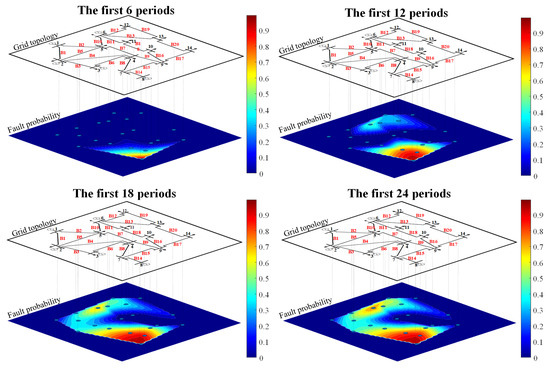
Figure 10.
Typical cascading failure on IEEE 14 system; branches affected in the cascading failure are highlight.
To tackle the problem of islands formed during typhoon passage, the maximum island handling method was implemented in the simulation. Given the high instability of island quantity and distribution during cascading failures, the maximum island handling approach effectively simplifies the problem’s complexity and ensures a reliable overall assessment of the system’s reliability. Utilizing the abnormal propagation paths outlined in Section 4.2 and the cascading failure simulation method from Section 5.1, we predicted the cascading fault chains in the power grid under tropical cyclone impacts. Through extensive sampling simulations, the 10 most frequently occurring fault chains are identified, and their risk indices are calculated, as summarized in Table 2:

Table 2.
Risk assessment results of IEEE 14 system considering the coupling effects of power flow and meteorological factors.
The analysis of the fault chain in Table 2 indicates that the entire fault chain path reflects the cascading response of the system to the severe impact of the typhoon. Extensive sampling simulations reveal that faults initially occur in key branches such as branches 14, 15, and 8, quickly spreading to secondary branches like branches 10 and 11, resulting in multiple localized power outage areas resembling islands. Particularly in the later stages of fault propagation, significant power shortages have emerged in most areas of the system, with the overall chain failure path exhibiting specific patterns, as indicated by the fault chain paths in the table. This highlights that the vulnerability of the power grid during extreme meteorological events like typhoons mainly manifests through the overload of key branches and the island effect. Therefore, in designing preventive measures, the system should prioritize these high-risk paths and fault chains, especially reinforcing branches susceptible to island formation, to improve the overall disaster resilience of the power grid.
6.4. Comparison of Grid Abnormal Evolution Under Coupled Power Flow and Weather vs. OPA Model
The traditional OPA(ORNL-PSERC-Alaska) model neglects the influence of post-fault power flow dynamics on cascading failure chains and oversimplifies the temporal arrangement of critical events. This limitation is demonstrated through simulations performed on a modified IEEE 14-bus system.Using the abnormal conditions of power grid equipment calculated in Section 5.1, fault sampling is performed to extract fault lines from all periods during the typhoon, resulting in a grid fault line set considering only meteorological effects. Based on these fault lines, power flow calculations are conducted to identify system overloads caused by the typhoon. Overloaded lines are removed to obtain cascading fault chains considering only meteorological effects. Through extensive sampling simulations, the 10 most frequently occurring fault chains are identified, and their risk indices are calculated, as summarized in Table 3.

Table 3.
Risk assessment results of the IEEE 14 system using the OPA model.
A comparative analysis of the prediction results between the proposed method, which accounts for the coupling effects of power flow and meteorological factors (Method 1), and the OPA model (Method 2), reveals that Method 1 can more accurately capture the risks of power insufficiency. Method 2 neglects the influence of power flow factors on system stability during incident development, leading to considerable deviations in expected values of power insufficiency. In scenarios with substantial wind speed fluctuations, variations in power flow can greatly impact the stability of the power system. Method 1 effectively captures these intricate dynamic changes, while Method 2 does not respond adequately, leading to an incomplete assessment of the actual risks to the power system. Method 1 more accurately represents the complexities present in real power systems, especially under conditions of strong interaction between power flow and meteorological factors, enhancing its value in power system planning and risk management. During extreme weather events, power systems may face challenges due to changes in power flow factors, which Method 2 fails to identify promptly.
6.5. Scalability Analysis of Spatiotemporal Risk Assessment Methodology for Power Grid Anomalies in Large-Scale Networks Under Extreme Disasters
The IEEE 118 system, comprising 118 buses and 186 transmission branches, is configured with topological parameters and typhoon trajectory, as depicted in Figure A1. Conventional generators at buses 87, 89, and 100 are retrofitted with equivalently rated wind farms, while new wind installations (50 MW, 50 MW, and 20 MW capacities) are deployed at buses 90, 92, and 104, respectively. Component parameters (including wind turbines, transmission towers, and line characteristics) maintain consistency with the IEEE 14 system, with detailed specifications provided in Table 1. Temporal load profiles with normalized hourly variations are illustrated in Figure A2.
The computational results reveal wind power generation profiles (Figure A3 and transmission line failure probabilities (Figure A4) under typhoon conditions. Based on the anomaly propagation pathways in Section 4.2 and cascading failure simulation methodology in Section 5.1, the cascading fault chains are predicted under tropical cyclone. From a large number of simulation results, the 10 most frequently occurring fault chains are selected and presented in Table 4.

Table 4.
Risk assessment results of IEEE 118 system considering the coupling effects of power flow and meteorological factors.
Based on the fault propagation paths shown in Table 4, when large-scale power grids face extreme weather disasters, the cascading fault evolution process exhibits the following characteristics: initial faults are concentrated in key structural branches such as 167, 169, 159, and 164, and then spread rapidly to secondary key branches like 104, 110, 30, and 106 through power flow redistribution. Notably, in the later stages of fault evolution, multi-region splitting occurs, leading to localized power supply-demand imbalances. The research results show that the risk assessment method considering the dynamic spatiotemporal evolution of the power grid can effectively handle the complex topology of large power grids. This method demonstrates strong applicability in large grid risk assessment under extreme weather conditions.
7. Conclusions
This paper proposes a spatiotemporal evolution-based risk assessment method, considering the time-varying abnormal states of source-grid equipment under the spatiotemporal trajectory of typhoons. Building on the spatiotemporal characteristics of grid faults, this study further explores the spatiotemporal evolution mechanism of grid anomalies, driven by the coupling of extreme weather factors and power flow, identifying the propagation paths of grid anomalies. This study reveals the inherent patterns of grid fault evolution under extreme weather conditions, addressing gaps in current research. The study identifies evaluation metrics that effectively reflect the grid fault evolution process and system vulnerability. Through a systematic risk assessment process, it provides a new theoretical framework and practical tools for assessing the safety of power grids during extreme weather disasters.
The proposed method outperforms traditional cascade fault models that consider only meteorological factors (e.g., the OPA model). Traditional models typically overlook the impact of power flow redistribution on grid fault evolution. In extreme weather events, the interaction between meteorological factors and power flow redistribution affects the stability of grid lines. By considering the coupling effects of meteorological factors and power flow, this study more accurately predicts the spatiotemporal evolution of grid faults, enhancing both the accuracy and timeliness of fault prediction.
The proposed method is validated through case studies of the modified IEEE 14 and IEEE 118 systems, effectively capturing the dynamic changes in grid equipment during tropical cyclone passage, particularly regarding fault characteristics under varying meteorological conditions and power flow loads. This evaluation method simulates the alternating processes of equipment failures and power flow redistribution, enabling more accurate predictions of fault chain formation and propagation. Furthermore, the method accounts for uncertainties in meteorological factors and grid parameters, enhancing the accuracy of the overall system risk assessment.
In conclusion, the method presented in this paper not only provides a scientific basis for power grid risk management under extreme weather conditions but also offers valuable insights for future disaster prevention and mitigation strategies in power grids. Future research will focus on larger-scale real-world power systems, simulating typhoons that have occurred within these systems and comparing the simulation results with actual operational data. The study will also explore fault recovery strategies during disasters, integrating recovery measures into the fault evolution scheduling process based on real grid operational patterns. Additionally, the research will extend to more tropical cyclone scenarios, including the impact of extreme weather events, such as thunderstorms, on source-grid equipment. These studies contribute to enhancing the power grid’s ability to respond to a wider range of extreme weather events.
Author Contributions
Conceptualization, C.G. and C.C.; methodology, C.G. and C.C.; software, C.G. and C.C.; validation, C.G.; formal analysis, C.G. and C.C.; investigation, C.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the National Natural Science Foundation of China (Grant No. 52207142).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
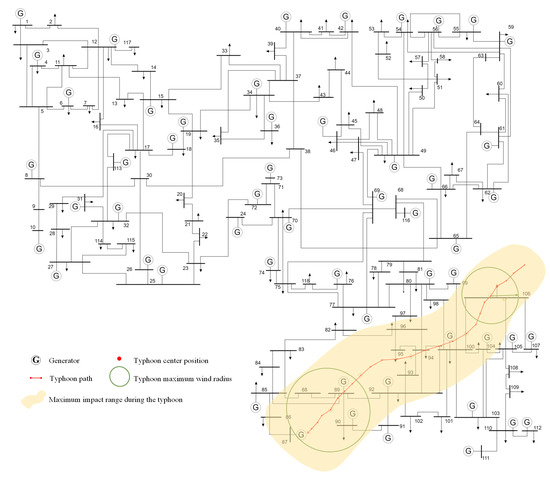
Figure A1.
Typhoon path and IEEE 118 system topology.
Figure A2.
Each bus load of IEEE 118 system.
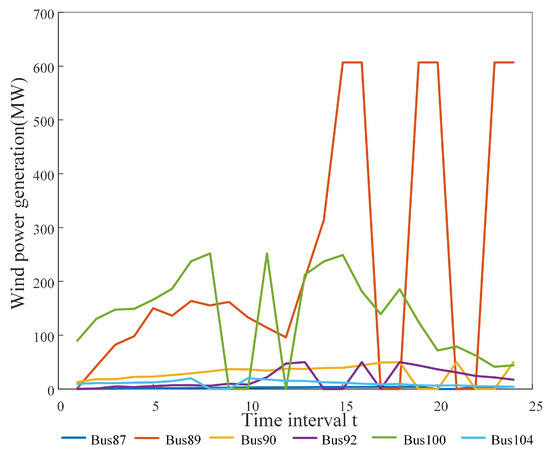
Figure A3.
Wind power curve of IEEE 118 system during typhoon.
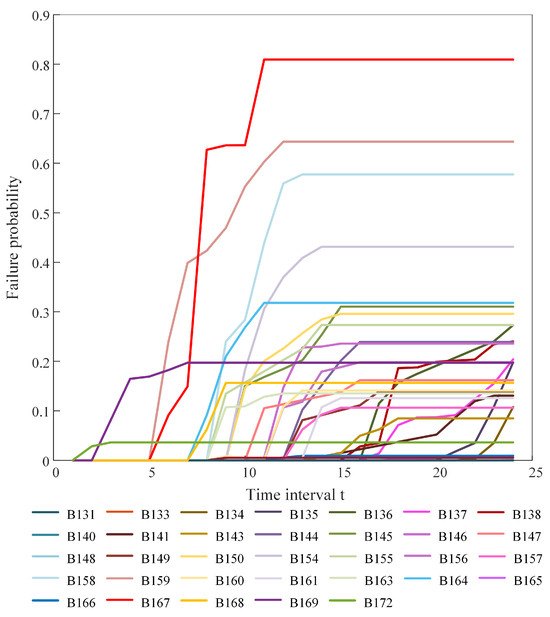
Figure A4.
Branches fault probability of the IEEE 118 system.
References
- Xu, X.; Hu, W.; Liu, W.; Du, Y.; Huang, R.; Huang, Q.; Chen, Z. Risk management strategy for a renewable power supply system in commercial buildings considering thermal comfort and stochastic electric vehicle behaviors. Energy Convers. Manag. 2021, 230, 113831. [Google Scholar] [CrossRef]
- Stringer, N.; Haghdadi, N.; Bruce, A.; Riesz, J.; MacGill, I. Observed behavior of distributed photovoltaic systems during major voltage disturbances and implications for power system security. Appl. Energy 2020, 260, 114283. [Google Scholar] [CrossRef]
- Samper, M.E.; Eldali, F.A.; Suryanarayanan, S. Risk assessment in planning high penetrations of solar photovoltaic installations in distribution systems. Int. J. Electr. Power Energy Syst. 2019, 104, 724–733. [Google Scholar] [CrossRef]
- Zhou, S.; Yang, P. Risk management in distributed wind energy implementing Analytic Hierarchy Process. Renew. Energy 2020, 150, 616–623. [Google Scholar] [CrossRef]
- Li, P.; Yang, M.; Wu, Q. Confidence Interval Based Distributionally Robust Real-Time Economic Dispatch Approach Considering Wind Power Accommodation Risk. IEEE Trans. Sustain. Energy 2021, 12, 58–69. [Google Scholar] [CrossRef]
- Deltuva, R.; Lukočius, R.; Otas, K. Dynamic stability analysis of isolated power system. Appl. Sci. 2022, 12, 7220. [Google Scholar] [CrossRef]
- Panteli, M.; Pickering, C.; Wilkinson, S.; Dawson, R.; Mancarella, P. Power System Resilience to Extreme Weather: Fragility Modeling, Probabilistic Impact Assessment, and Adaptation Measures. IEEE Trans. Power Syst. 2017, 32, 3747–3757. [Google Scholar] [CrossRef]
- Najafi Tari, A.; Sepasian, M.S.; Tourandaz Kenari, M. Resilience assessment and improvement of distribution networks against extreme weather events. Int. J. Electr. Power Energy Syst. 2021, 125, 106414. [Google Scholar] [CrossRef]
- Perera, A.; Nik, V.M.; Chen, D.; Scartezzini, J.L.; Hong, T. Quantifying the impacts of climate change and extreme climate events on energy systems. Nat. Energy 2020, 5, 150–159. [Google Scholar] [CrossRef]
- Bennett, J.A.; Trevisan, C.N.; DeCarolis, J.F.; Ortiz-García, C.; Pérez-Lugo, M.; Etienne, B.T.; Clarens, A.F. Extending energy system modelling to include extreme weather risks and application to hurricane events in Puerto Rico. Nat. Energy 2021, 6, 240–249. [Google Scholar] [CrossRef]
- Han, B.; Ming, Z.; Zhao, Y.; Wen, T.; Xie, M. Comprehensive risk assessment of transmission lines affected by multi-meteorological disasters based on fuzzy analytic hierarchy process. Int. J. Electr. Power Energy Syst. 2021, 133, 107190. [Google Scholar] [CrossRef]
- Zainuddin, N.M.; Rahman, M.A.; Kadir, M.A.; Ali, N.N.; Ali, Z.; Osman, M.; Mansor, M.; Ariffin, A.M.; Rahman, M.S.A.; Nor, S.F.M.; et al. Review of thermal stress and condition monitoring technologies for overhead transmission lines: Issues and challenges. IEEE Access 2020, 8, 120053–120081. [Google Scholar] [CrossRef]
- Dalton, A.; Bekker, B.; Koivisto, M.J. Simulation and detection of wind power ramps and identification of their causative atmospheric circulation patterns. Electr. Power Syst. Res. 2021, 192, 106936. [Google Scholar] [CrossRef]
- Ju, S.H.; Huang, Y.C.; Hsu, H.H. Parallel Analysis of Offshore Wind Turbine Structures under Ultimate Loads. Appl. Sci. 2019, 9, 4708. [Google Scholar] [CrossRef]
- Ti, B.; Li, G.; Zhou, M.; Wang, J. Resilience Assessment and Improvement for Cyber-Physical Power Systems Under Typhoon Disasters. IEEE Trans. Smart Grid 2022, 13, 783–794. [Google Scholar] [CrossRef]
- Park, B.; Su, X.; Sun, K. An Enhanced OPA Model: Incorporating Dynamically Induced Cascading Failures. IEEE Trans. Power Syst. 2022, 37, 4962–4965. [Google Scholar] [CrossRef]
- Yan, J.; Tang, Y.; He, H.; Sun, Y. Cascading Failure Analysis With DC Power Flow Model and Transient Stability Analysis. IEEE Trans. Power Syst. 2015, 30, 285–297. [Google Scholar] [CrossRef]
- Liu, X.; Shahidehpour, M.; Li, Z.; Liu, X.; Cao, Y.; Li, Z. Power system risk assessment in cyber attacks considering the role of protection systems. IEEE Trans. Smart Grid 2016, 8, 572–580. [Google Scholar] [CrossRef]
- Yang, S.; Chen, W.; Zhang, X.; Yang, W. A graph-based method for vulnerability analysis of renewable energy integrated power systems to cascading failures. Reliab. Eng. Syst. Saf. 2021, 207, 107354. [Google Scholar] [CrossRef]
- Khazeiynasab, S.R.; Qi, J. Resilience analysis and cascading failure modeling of power systems under extreme temperatures. J. Mod. Power Syst. Clean Energy 2021, 9, 1446–1457. [Google Scholar] [CrossRef]
- Qorbani, M.; Amraee, T. Long term transmission expansion planning to improve power system resilience against cascading outages. Electr. Power Syst. Res. 2021, 192, 106972. [Google Scholar] [CrossRef]
- Papic, M.; Ekisheva, S.; Cotilla-Sanchez, E. A risk-based approach to assess the operational resilience of transmission grids. Appl. Sci. 2020, 10, 4761. [Google Scholar] [CrossRef]
- Caputo, A.C.; Federici, A.; Pelagagge, P.M.; Salini, P. Scenario analysis of offshore wind-power systems under uncertainty. Sustainability 2023, 15, 16912. [Google Scholar] [CrossRef]
- Wang, X.; Liu, S.; Ban, X.; Xu, Y.; Zhou, J.; Kosinka, J. Robust turbulence simulation for particle-based fluids using the Rankine vortex model. Vis. Comput. 2020, 36, 2285–2298. [Google Scholar] [CrossRef]
- Yao, Q.; Hu, Y.; Deng, H.; Luo, Z.; Liu, J. Two-degree-of-freedom active power control of megawatt wind turbine considering fatigue load optimization. Renew. Energy 2020, 162, 2096–2112. [Google Scholar] [CrossRef]
- Weber, F.; Wu, H.; Starke, P. A new short-time procedure for fatigue life evaluation based on the linear damage accumulation by Palmgren–Miner. Int. J. Fatigue 2023, 172, 107653. [Google Scholar] [CrossRef]
- Gan, L.; Li, Y.; Chen, X.; Yu, K. A Multi-Period Reconfiguration Method of Distribution Networks Considering Spatial and Temporal Variation of Typhoon. In Proceedings of the 2020 12th IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC), Nanjing, China, 20–23 September 2020; pp. 1–5. [Google Scholar]
- Wu, H.; Liu, J.; Liu, J.; Cui, M.; Liu, X.; Gao, H. Power grid reliability evaluation considering wind farm cyber security and ramping events. Appl. Sci. 2019, 9, 3003. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).