Impact of Non-Landslide Sample Sampling Strategies and Model Selection on Landslide Susceptibility Mapping
Abstract
1. Introduction
2. Materials
2.1. Study Area
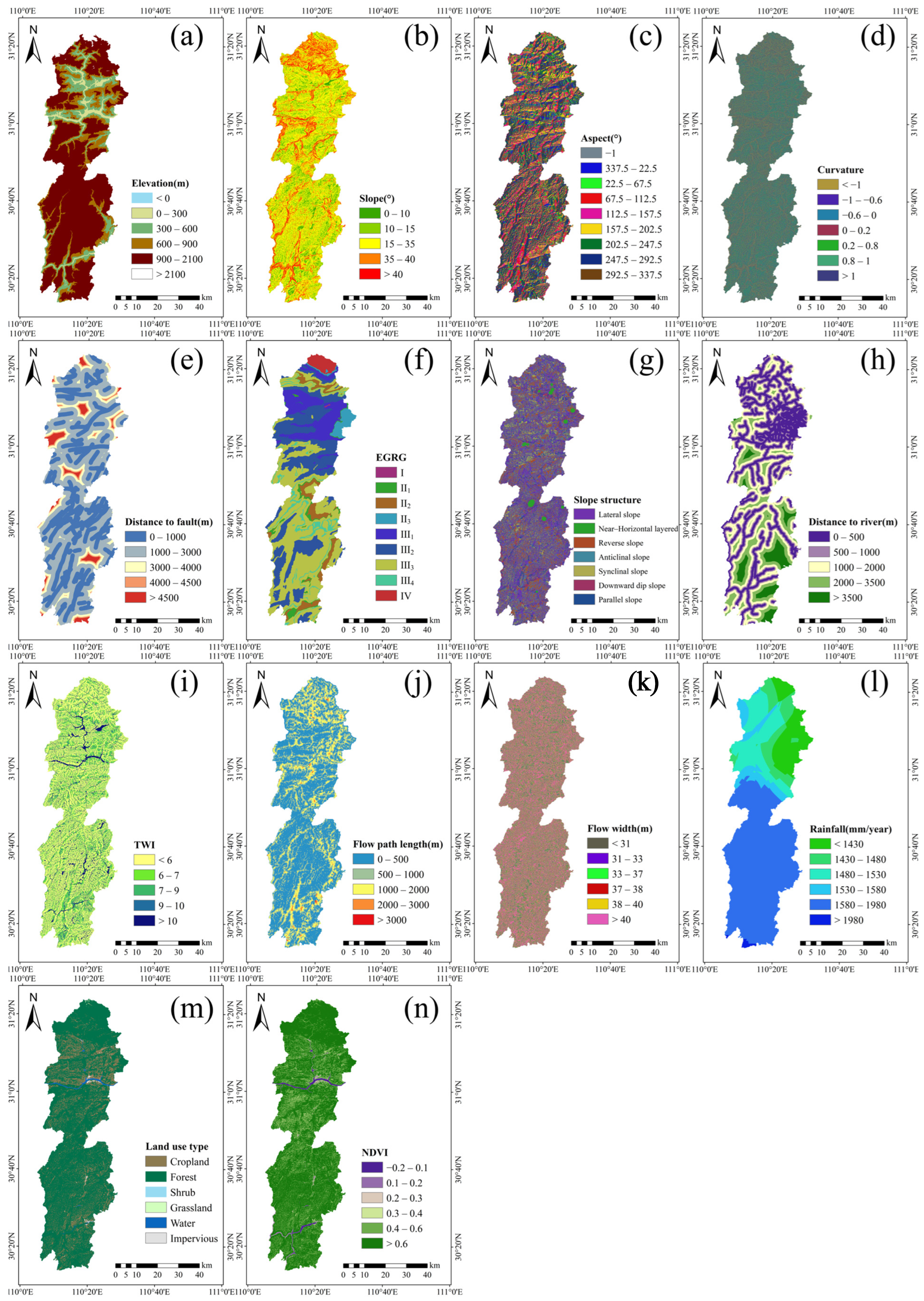
2.2. Data Source and Preparation of Influencing Factors
2.2.1. Data Source
2.2.2. Influencing Factors
3. Methodologies
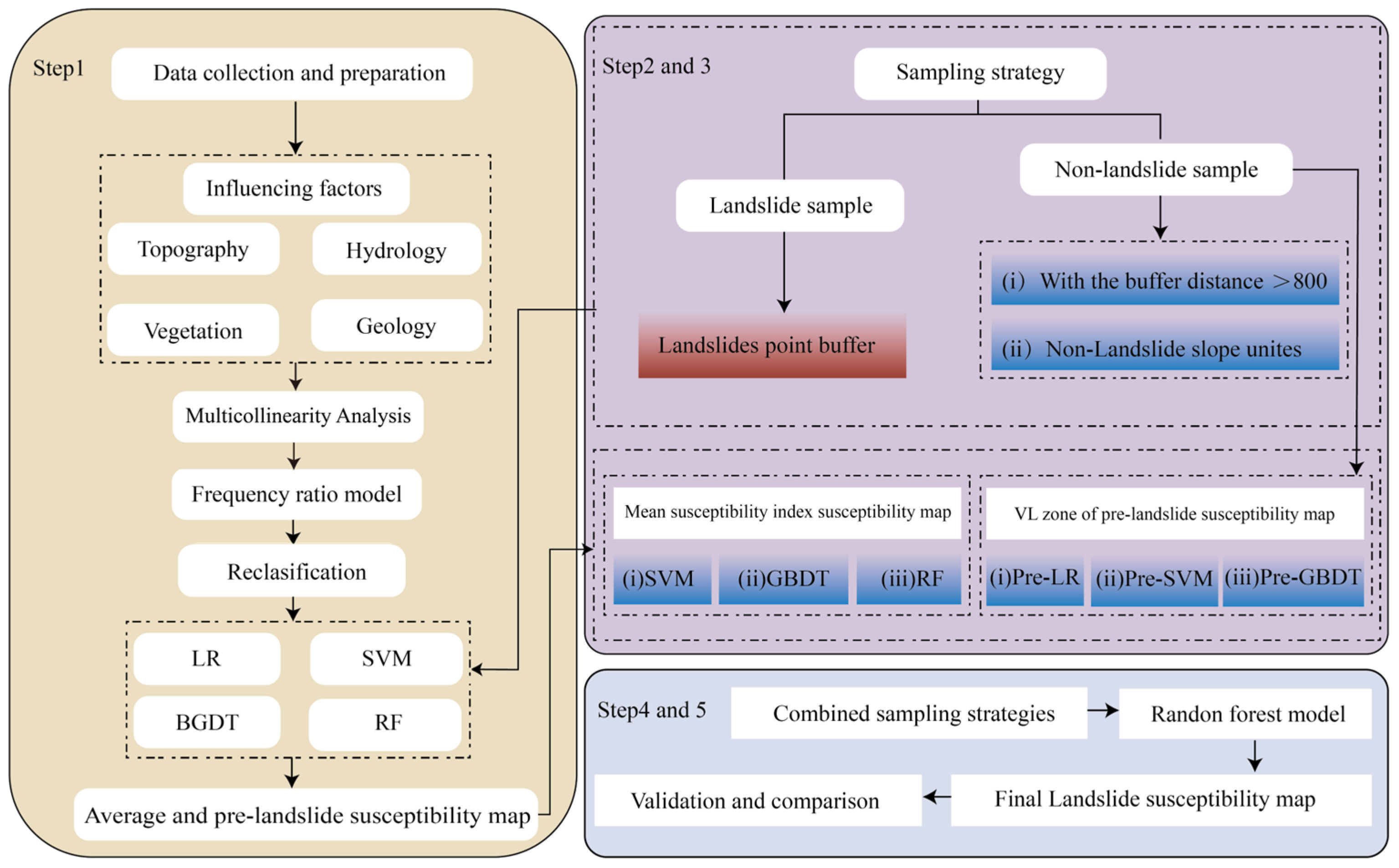
3.1. Modelling Procedure
3.2. Frequency Ratio Analysis
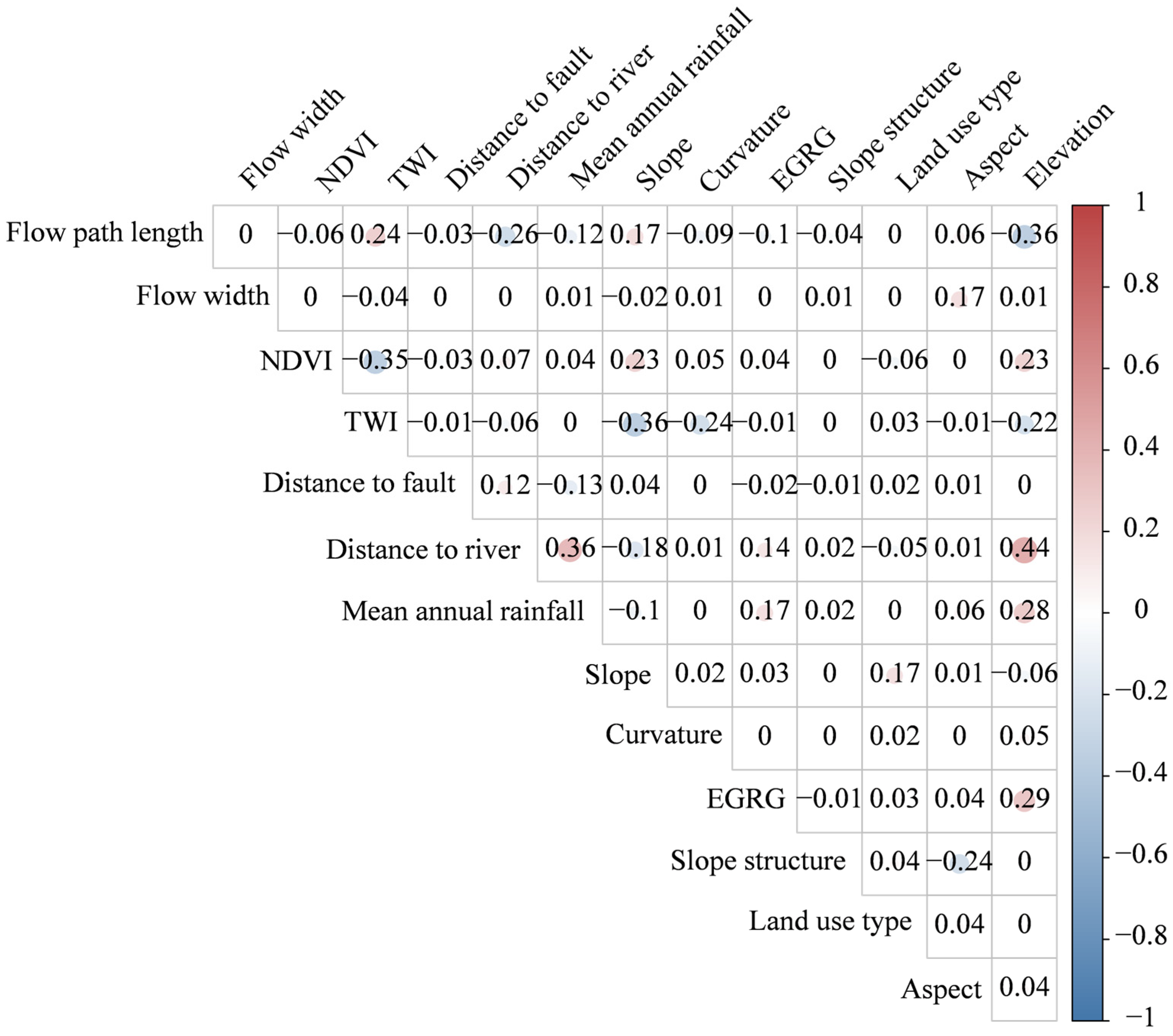
3.3. Multicollinearity Analysis
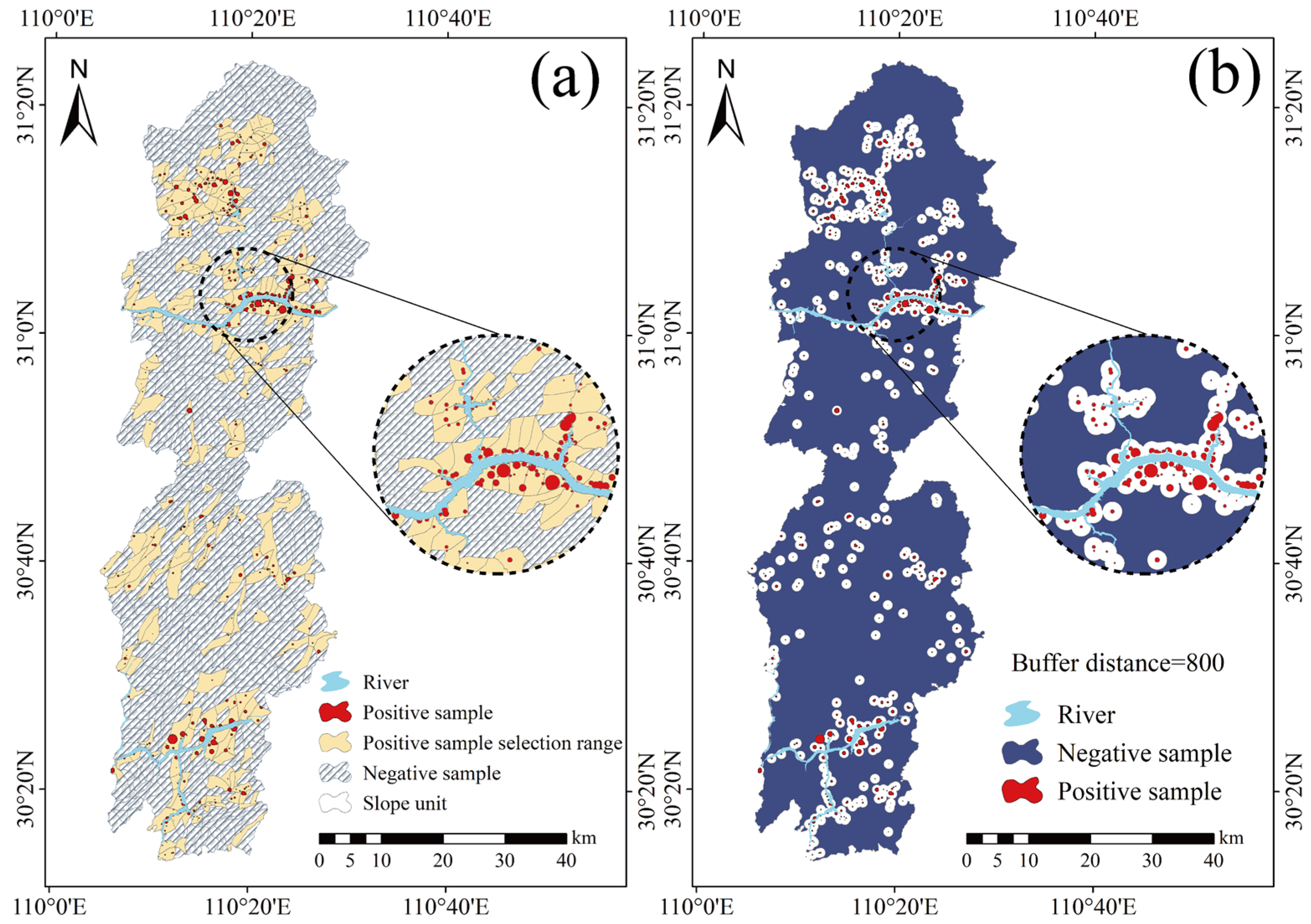
3.4. Assessment Unit and Sample Selection
3.5. Machine Learning Models
3.5.1. Logistic Regression
3.5.2. Gradient Boosting Decision Tree
3.5.3. Support Vector Machine
3.5.4. Random Forest
3.6. Model Performance Evaluation
4. Results
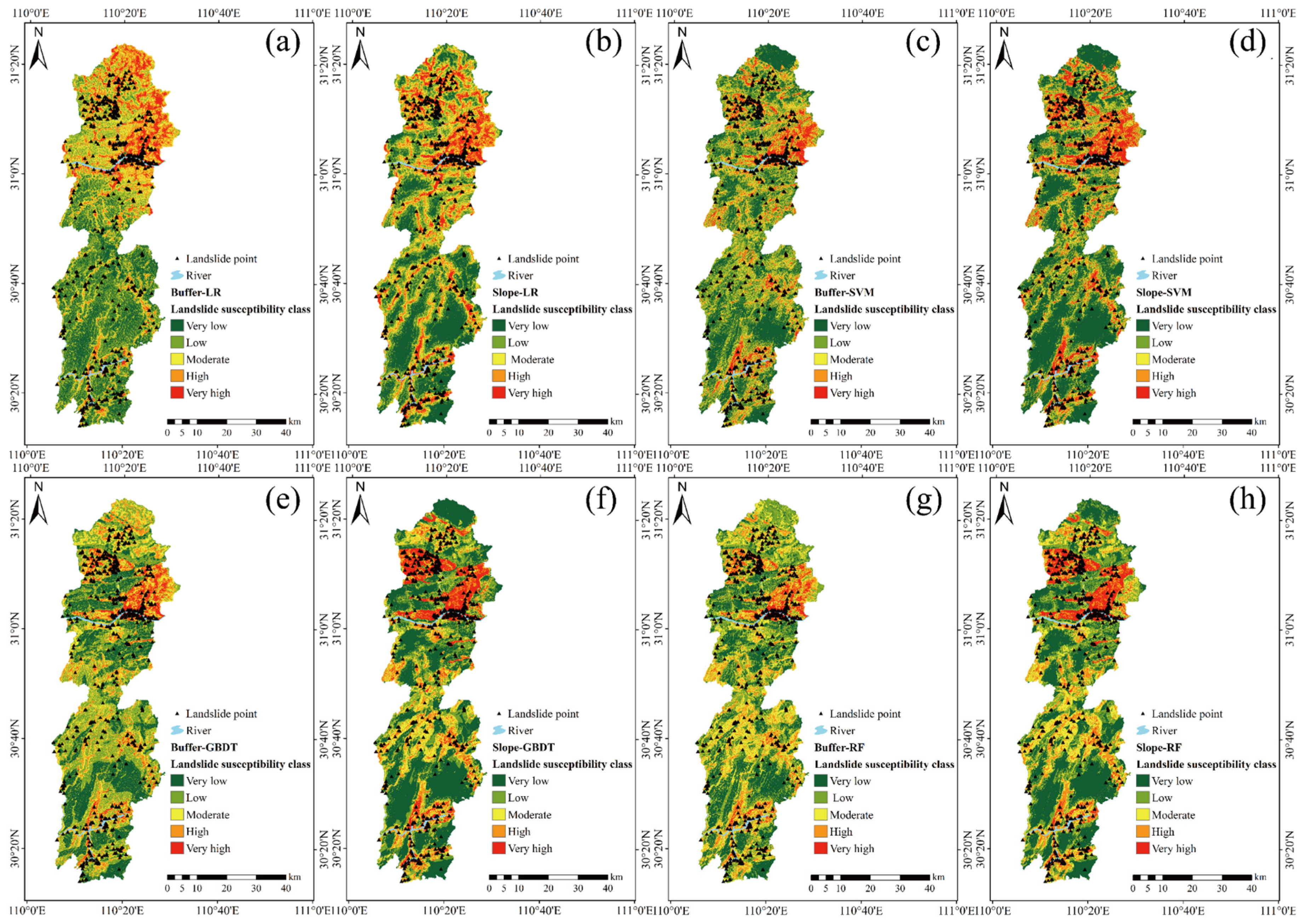
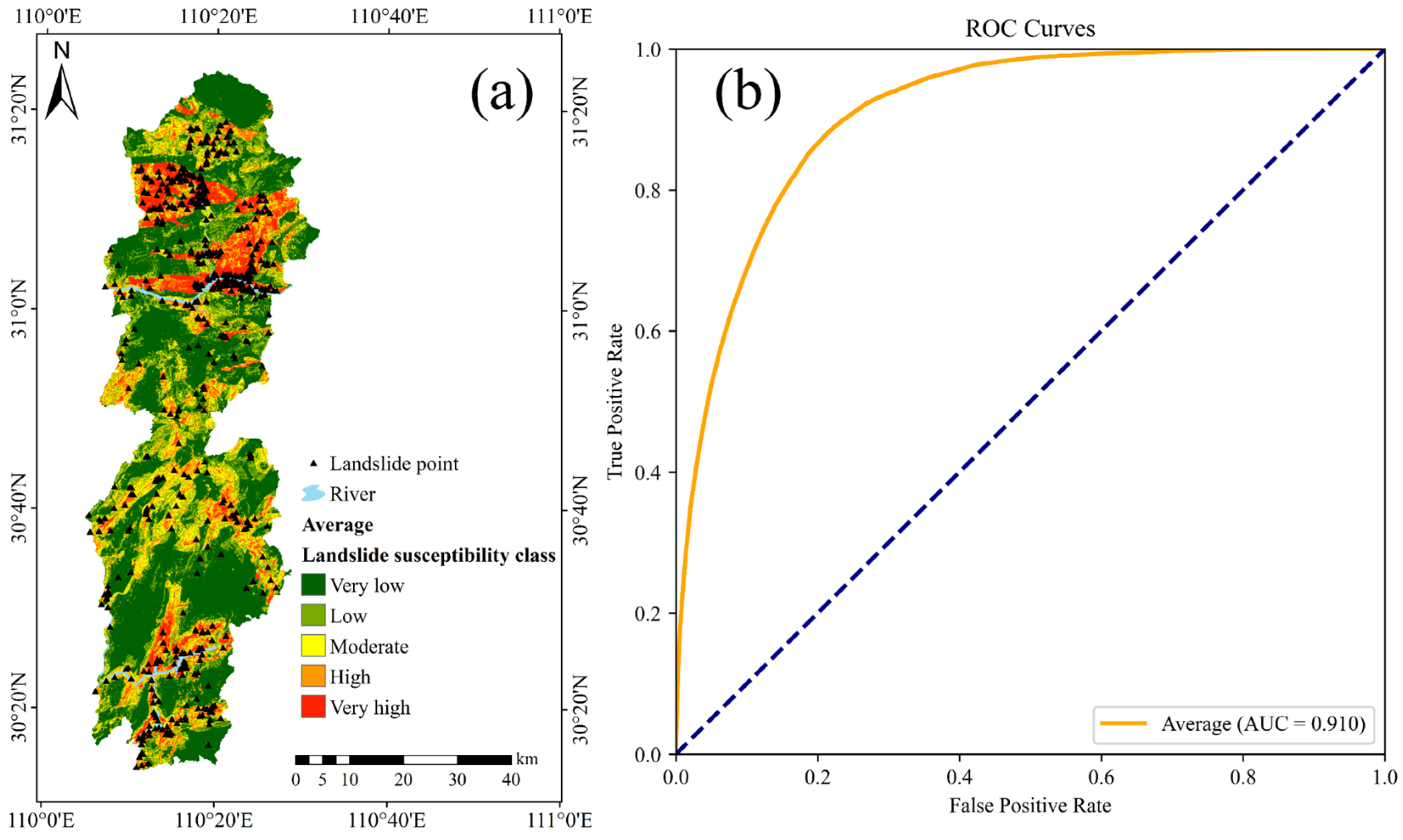
4.1. Landslide Susceptibility Assessment Results
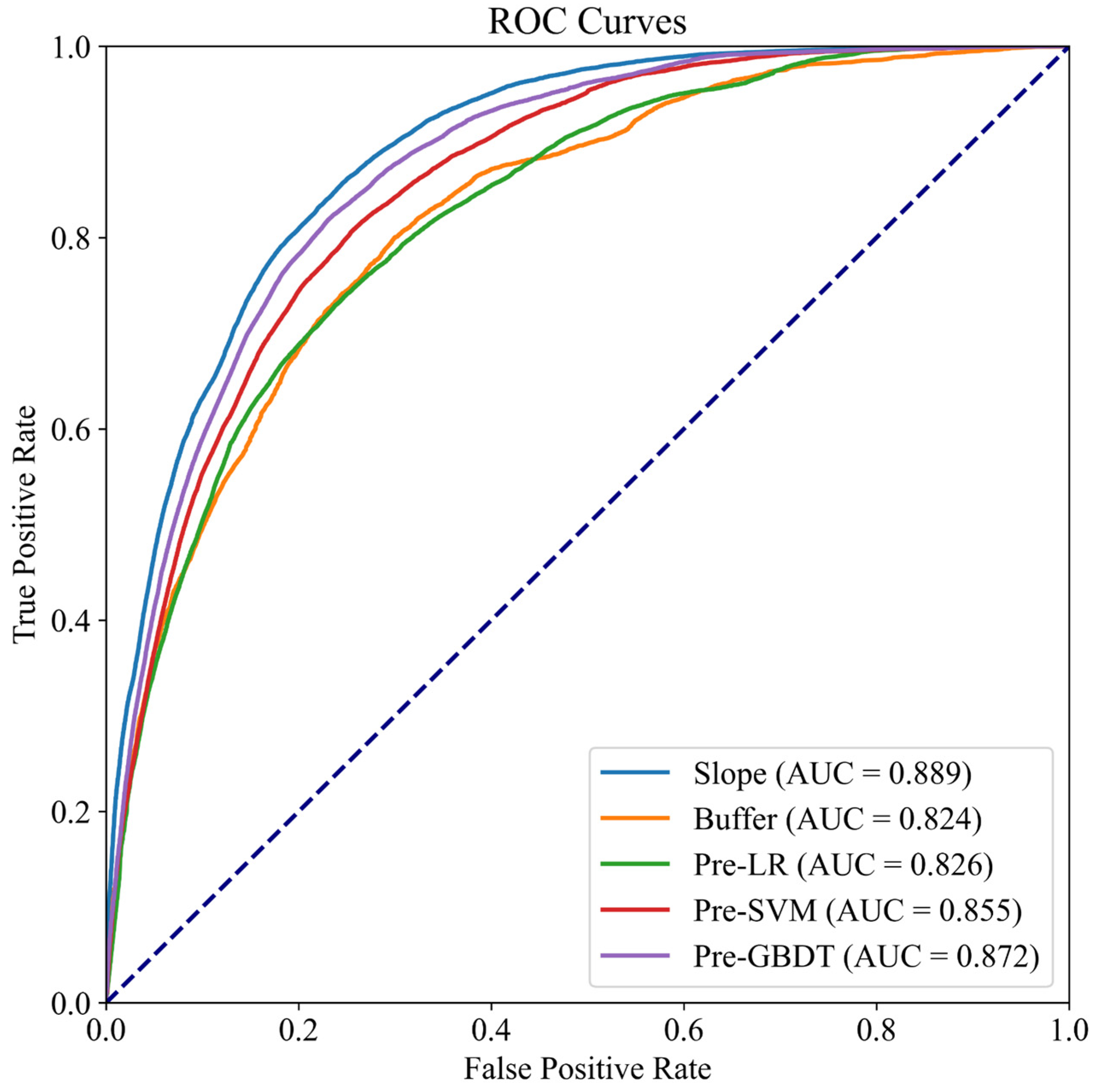
4.2. Uncertainty in Machine Learning Model Selection
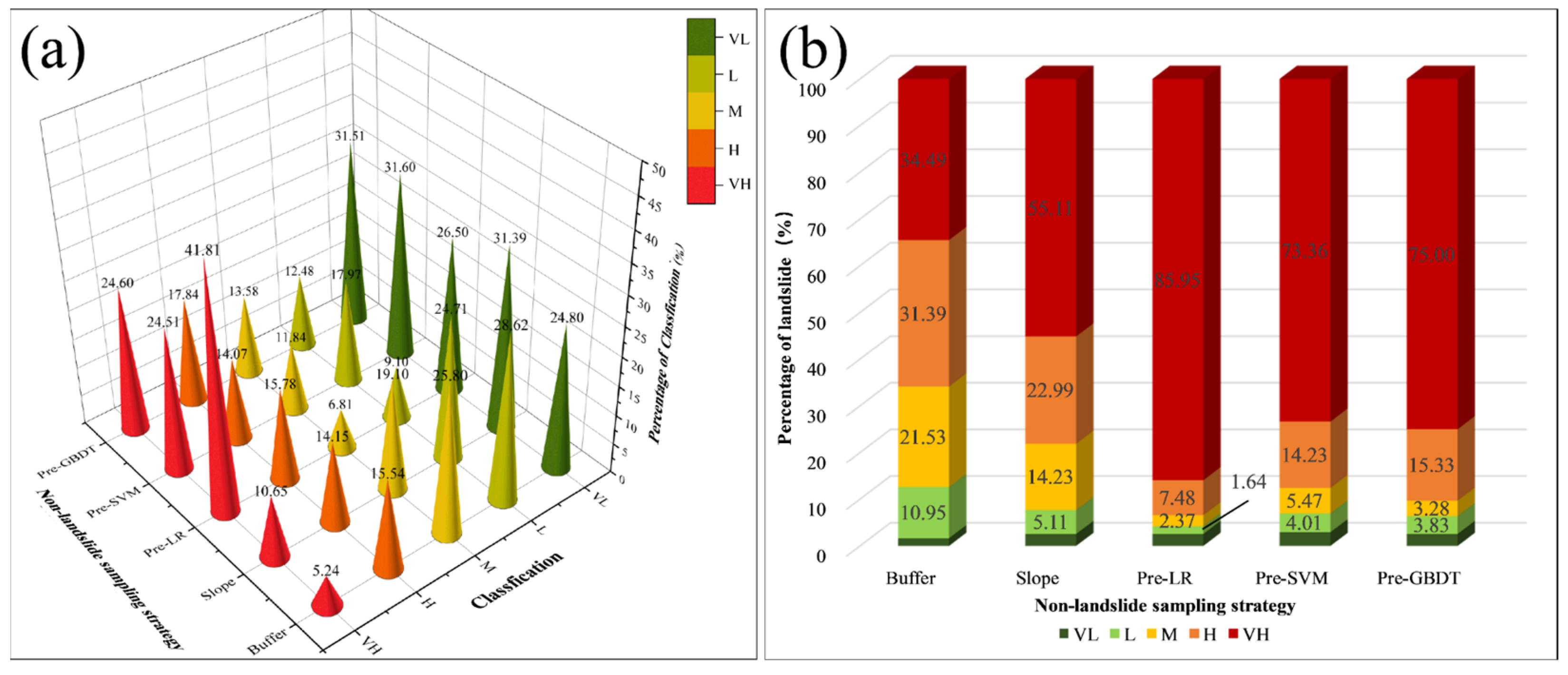
4.3. Impact of Non-Landslide Sample Sampling Strategies on Landslide Susceptibility Assessment
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Segoni, S.; Pappafico, G.; Luti, T.; Catani, F. Landslide susceptibility assessment in complex geological settings: Sensitivity to geological information and insights on its parameterization. Landslides 2020, 17, 2443–2453. [Google Scholar] [CrossRef]
- Reichenbach, P.; Rossi, M.; Malamud, B.D.; Mihir, M.; Guzzetti, F. A review of statistically-based landslide susceptibility models. Earth-Sci. Rev. 2018, 180, 60–91. [Google Scholar] [CrossRef]
- Brabb, E.E. Innovative approaches to landslide hazard mapping. In Proceedings of the 4th International Symposium on Landslides, Toronto, ON, Canada, 16–21 September 1984; Canadian Geotechnical Society: Vancouver, BC, Canada, 1984; Volume 1, pp. 307–324. [Google Scholar]
- Guzzetti, F.; Carrara, A.; Cardinali, M.; Reichenbach, P. Landslide hazard evaluation: A review of current techniques and their application in a multi-scale study. Geomorphology 1999, 31, 181–216. [Google Scholar] [CrossRef]
- Akgun, A.; Kincal, C.; Pradhan, B. Application of remote sensing data and GIS for landslide risk assessment as an environmental threat to Izmir city (West Turkey). Environ. Monit. Assess. 2011, 184, 5453–5470. [Google Scholar] [CrossRef]
- Zhang, W.; Tang, L.; Li, H.; Wang, L.; Cheng, L.; Zhou, T.; Chen, X. Probabilistic stability analysis of Bazimen landslide with monitored rainfall data and water level fluctuations in Three Gorges Reservoir, China. Front. Struct. Civ. Eng. 2020, 14, 1247–1261. [Google Scholar] [CrossRef]
- Abedini, M.; Tulabi, S. Assessing LNRF, FR, and AHP models in landslide susceptibility mapping index: A comparative study of Nojian watershed in Lorestan province, Iran. Environ. Earth Sci. 2018, 77, 405. [Google Scholar] [CrossRef]
- Pham, B.T.; Pradhan, B.; Bui, D.T.; Prakash, I.; Dholakia, M.B. A comparative study of different machine learning methods for landslide susceptibility assessment: A case study of Uttarakhand area (India). Environ. Model. Softw. 2016, 84, 240–250. [Google Scholar] [CrossRef]
- Guo, Z.; Tian, B.; Li, G.; Huang, D.; Zeng, T.; He, J.; Song, D. Landslide susceptibility mapping in the Loess Plateau of northwest China using three data-driven techniques: A case study from middle Yellow River catchment. Front. Earth Sci. 2023, 10, 1033085. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, Q.; Wang, Y.; Li, X.; Zhang, Y. Application of logistic regression for landslide susceptibility mapping in mountainous areas: A case study of the Wuling Mountains, China. Landslides 2022, 19, 87–102. [Google Scholar]
- Jafari, A.; Chai, W.; Zhang, H.; Li, M. Landslide susceptibility assessment using k-nearest neighbor algorithm in the southwestern region of China. Geomorphology 2021, 387, 107785. [Google Scholar]
- Li, P.; Yang, C.; Zhang, L.; Liu, Z. A novel landslide susceptibility mapping approach using support vector machine with the integration of geological and topographical factors. Environ. Earth Sci. 2023, 82, 345. [Google Scholar]
- Zhang, W.; Li, J.; Wang, L.; Liu, Y. Landslide susceptibility mapping using extremely randomized trees: A case study in the Qinling Mountains, China. Nat. Hazards 2022, 112, 45–61. [Google Scholar]
- Zhou, X.; Wang, L.; Zhao, Q.; Li, J. Landslide susceptibility modeling using Bayesian networks: A case study of the Sichuan Basin, China. Sci. Total Environ. 2021, 783, 146993. [Google Scholar]
- Xu, Z.; Zhao, Q.; Liu, H.; Zhang, W. Landslide susceptibility assessment using artificial neural networks in the Loess Plateau, China. Geomorphology 2022, 400, 107836. [Google Scholar]
- Wang, M.; Liu, Y.; Chen, X.; Zhang, J. Gradient boosting decision tree for landslide susceptibility modeling: A case study of the Three Gorges Reservoir Area, China. Landslides 2023, 20, 289–302. [Google Scholar]
- Zhang, X.; Chen, J.; Liu, Y.; Li, S. Landslide susceptibility mapping using random forest: Application to the Tibetan Plateau. Environ. Monit. Assess. 2023, 195, 468. [Google Scholar]
- Chang, Z.L. Regional Rainfall-Induced Landslide Hazard Assessment Method Based on Data-Driven and Forming Mechanism. Ph.D. Thesis, Nanchang University, Nanchang, China, 2023. (In Chinese). [Google Scholar]
- Xi, C.J.; Han, M.; Hu, X.W.; Liu, B.; He, K.; Luo, G.; Cao, X.C. Effectiveness of Newmark-based sampling strategy for coseismic landslide susceptibility mapping using deep learning, support vector machine, and logistic regression. Bull. Eng. Geol. Environ. 2022, 81, 174. [Google Scholar] [CrossRef]
- Guo, Z.; Tian, B.; Zhu, Y.; He, J.; Zhang, T. How do the landslide and non-landslide sampling strategies impact landslide susceptibility assessment? A catchment-scale case study from China. J. Rock Mech. Geotech. Eng. 2024, 16, 877–894. [Google Scholar] [CrossRef]
- Choi, J.; Oh, H.J.; Won, J.S.; Lee, S. Validation of an artificial neural network model for landslide susceptibility mapping. Environ. Earth Sci. 2010, 60, 473–483. [Google Scholar] [CrossRef]
- Azarafza, M.; Azarafza, M.; Akgün, H.; Atkinson, P.M.; Derakhshani, R. Deep learning-based landslide susceptibility mapping. Sci. Rep. 2021, 11, 24112. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.; Wang, Y.; Niu, R.; Peng, L. Integration of information theory, K-means cluster analysis and the logistic regression model for landslide susceptibility mapping in the Three Gorges Area, China. Remote Sens. 2017, 9, 938. [Google Scholar] [CrossRef]
- Lucchese, L.V.; de Oliveira, G.G.; Pedrollo, O.C. Investigation of the influence of nonoccurrence sampling on landslide susceptibility assessment using artificial neural networks. Catena 2021, 198, 105067. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, L.; Wang, X. Application of Digital Elevation Model (DEM) in Landslide Susceptibility Mapping: A Case Study. Landslides 2020, 15, 123–135. [Google Scholar]
- Wang, J.; Li, Z.; Yang, M. Role of Geological Data in Landslide Risk Assessment. Geol. Sci. 2019, 12, 223–234. [Google Scholar]
- Wang, Y.; Li, Q.; Zhang, Y.; Chen, L. Landslide susceptibility assessment using spatial interpolation of rainfall data: A case study of the Xijiang River Basin. Landslides 2021, 18, 665–678. [Google Scholar]
- Yang, S.; Zhao, X.; Wang, B. Relationship Between Vegetation Cover (NDVI) and Landslide Susceptibility. Environ. Earth Sci. 2020, 8, 340–350. [Google Scholar]
- Zhao, W.; Liu, Z.; Li, G. Impact of Land Use and Vegetation on Landslide Hazard Assessment. Nat. Hazards J. 2018, 30, 215–228. [Google Scholar]
- Shirzadi, A.; Chapi, K.; Shahabi, H.; Solaimani, K.; Kavian, A.; Ahmad, B.B. Rockfall susceptibility assessment along a mountainous road: An evaluation of bivariate statistic, analytical hierarchy process, and frequency ratio. Environ. Earth Sci. 2017, 76, 152. [Google Scholar] [CrossRef]
- Pearson, K. Note on Regression and Inheritance in the Case of Two Parents. Proc. R. Soc. Lond. 1895, 58, 240–242. [Google Scholar]
- Nelder, J.A.; Baker, R.J. Generalized Linear Models; Wiley Online Library: Hoboken, NJ, USA, 2006. [Google Scholar]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Cristianini, N.; Schoelkopf, B. Support vector machines and kernel methods: The new generation of learning machines. AI Mag. 2002, 23, 31–41. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Fang, K.; Wu, J.; Zhu, J. A review of technologies on random forests. Stat. Inform. Forum. 2011, 26, 32–38. [Google Scholar]
- Rodrigues, S.G.; Silva, M.M.; Alencar, M.H. A proposal for an approach to mapping susceptibility to landslides using natural language processing and machine learning. Landslides 2021, 18, 2515–2529. [Google Scholar] [CrossRef]
- van Westen, C.J.; van Asch, T.W.J.; Soeters, R. Landslide hazard and risk zonation: Why is it still so difficult? Bull. Eng. Geol. Environ. 2006, 65, 167–184. [Google Scholar] [CrossRef]
- Pham, B.T.; Jaafari, A.; Prakash, I.; Bui, D.T. A novel hybrid intelligent model of support vector machines and the MultiBoost ensemble for landslide susceptibility modeling. Bull. Eng. Geol. Environ. 2019, 78, 2865–2886. [Google Scholar] [CrossRef]
- Tang, Y.; Feng, F.; Guo, Z.; Feng, W.; Li, Z.; Wang, J.; Sun, Q.; Ma, H.; Li, Y. Integrating principal component analysis with statistically-based models for analysis of causal factors and landslide susceptibility mapping: A comparative study from the loess plateau area in Shanxi (China). J. Clean. Prod. 2020, 277, 124159. [Google Scholar] [CrossRef]
- Huang, F.; Yan, J.; Fan, X.; Zhang, Y.; Liu, Z.; Wang, Q.; Chen, J.; Liu, L. Uncertainty pattern in landslide susceptibility prediction modelling: Effects of different landslide boundaries and spatial shape expressions. Geosci. Front. 2022, 13, 101317. [Google Scholar] [CrossRef]
- Hong, H.; Miao, Y.; Liu, J.; Zhang, C.; Yang, L.; Zhao, Z. Exploring the effects of the design and quantity of absence data on the performance of random forest-based landslide susceptibility mapping. Catena 2019, 176, 45–64. [Google Scholar] [CrossRef]
- Chen, Z.; Ye, F.; Fu, W.; Wu, G.; Zhang, T.; Wang, Q. The influence of DEM spatial resolution on landslide susceptibility mapping in the Baxie River basin, NW China. Nat. Hazards 2020, 101, 853–877. [Google Scholar] [CrossRef]
- Yan, G.; Tang, G.; Li, S.; Zhang, Y.; Wang, X.; Xu, Y. Uncertainty in regional scale assessment of landslide susceptibility using various resolutions. Nat. Hazards 2023, 117, 399–423. [Google Scholar] [CrossRef]
- Yang, C.; Liu, L.L.; Huang, F.; Chen, Y.; Zhang, H.; Li, J.; Wang, F. Machine learning-based landslide susceptibility assessment with optimized ratio of landslide to non-landslide samples. Gondwana Res. 2022, 123, 198–216. [Google Scholar] [CrossRef]



| Construction Type | Lithological Unit Code | Lithological Unit Name |
|---|---|---|
| Loose soils | I | Quaternary loose soils |
| Clastic rock | II1 | Rock formation dominated by hard, thick-bedded sandstone |
| II2 | Rock formation dominated by weak, layered claystone | |
| II3 | Alternating hard and soft layered sandstone and claystone interbedded formation | |
| Carbonate rock | III1 | Slightly karstified alternating soft and hard layered clastic rock with carbonate interbedding formation |
| III2 | Highly karstified hard-layered carbonate rock formation | |
| III3 | Moderately karstified alternating soft and hard layered carbonate rock with clastic interbedding formation | |
| III4 | Moderately karstified alternating soft and hard layered carbonate and clastic rock interbedded formation | |
| Metamorphic rock | IV | Migmatite and gneiss formation |
| Category | Types of Slope Structures | Definition |
|---|---|---|
| 1 | Downward dip slope | ((|α − β|∈(0, 30°]) or (|α − β|∈[330°, 360°))) and (γ > 10°) and (δ > γ) |
| 2 | Synclinal slope | ((|α − β|∈(0, 30°]) or (|α − β|∈[330°, 360°))) and (γ > 10°) and (δ < γ) |
| 3 | Parallel slope | (|α − β|∈(30°, 60°]) or (|α − β|∈[300°, 330°)) |
| 4 | Lateral slope | (|α − β|∈(60°, 120°]) or (|α − β|∈[240°, 300°)) |
| 5 | Anticlinal slope | (|α − β|∈(120°, 150°]) or (|α − β|∈[210°, 240°)) |
| 6 | Reverse slope | (|α − β|∈(150°, 180°]) or (|α − β|∈[180°, 210°)) |
| Influencing Factors | Classification | FR | Influencing Factors | Classification | FR |
|---|---|---|---|---|---|
| Aspect (°) | Plane | 0.00 | EGRG | I | 0.00 |
| North | 1.27 | II1 | 1.61 | ||
| Northeast | 1.10 | II2 | 0.94 | ||
| East | 1.26 | II3 | 0.53 | ||
| Southeast | 1.02 | III1 | 3.98 | ||
| South | 0.98 | III2 | 0.19 | ||
| Southwest | 0.64 | III3 | 0.67 | ||
| West | 0.78 | III4 | 1.55 | ||
| West | 0.96 | IV | 0.00 | ||
| Slope structure | Near-horizontal layered | 0.76 | Curvature | <−1 | 0.88 |
| Downward dip slope | 1.07 | −1–−0.6 | 1.04 | ||
| Synclinal slope | 0.94 | −0.6–0 | 1.14 | ||
| Parallel slope | 0.93 | 0–0.2 | 1.20 | ||
| Lateral slope | 0.89 | 0.2–0.8 | 1.14 | ||
| Anticlinal slope | 1.05 | 0.8–1 | 1.04 | ||
| Reverse slope | 1.30 | >1 | 0.87 | ||
| Elevation (m) | <0 | 0.00 | Land use type | Cropland | 2.31 |
| 0–300 | 5.98 | Forest | 0.64 | ||
| 300–600 | 2.81 | Shrub | 0.36 | ||
| 600–900 | 1.19 | Grassland | 0.37 | ||
| 900–2100 | 0.30 | Water | 0.00 | ||
| >2100 | 0.00 | Impervious | 11.02 | ||
| Flow width (m) | <31 | 1.05 | Rainfall (mm/year) | <1430 | 0.00 |
| 31–33 | 1.13 | 1430–1480 | 2.57 | ||
| 33–37 | 1.06 | 1480–1530 | 0.97 | ||
| 37–38 | 1.01 | 1530–1580 | 1.39 | ||
| 38–40 | 1.04 | 1580–1980 | 0.67 | ||
| NDVI | −0.2–0.1 | 0.10 | TWI | <6 | 0.69 |
| 0.1–0.2 | 2.59 | 6–7 | 1.28 | ||
| 0.2–0.3 | 6.05 | 7–9 | 1.69 | ||
| 0.3–0.4 | 2.65 | 9–10 | 1.64 | ||
| 0.4–0.6 | 1.58 | >10 | 0.89 | ||
| Distance to river (m) | 0–500 | 1.73 | Distance to fault (m) | 0–1000 | 1.10 |
| 500–1000 | 1.30 | 1000–3000 | 0.84 | ||
| 1000–2000 | 0.56 | 3000–4000 | 1.44 | ||
| 2000–3500 | 0.17 | 4000–4500 | 1.02 | ||
| >3500 | 0.03 | >4500 | 0.73 | ||
| Slope (°) | 0–10 | 0.69 | Flow path length (m) | 0–500 | 0.46 |
| 10–15 | 0.97 | 500–1000 | 1.32 | ||
| 15–35 | 1.14 | 1000–2000 | 2.60 | ||
| 35–40 | 0.92 | 2000–3000 | 1.89 | ||
| >45 | 0.67 | >3000 | 0.00 |
| Model | Accuracy | Precision | Recall | F1 Score | ||||
|---|---|---|---|---|---|---|---|---|
| Buffer | Slope | Buffer | Slope | Buffer | Slope | Buffer | Slope | |
| LR | 0.6054 | 0.7187 | 0.6037 | 0.7138 | 0.6034 | 0.7282 | 0.6036 | 0.7209 |
| SVM | 0.7139 | 0.8040 | 0.7227 | 0.7939 | 0.6967 | 0.8227 | 0.7095 | 0.8080 |
| GBDT | 0.7222 | 0.8312 | 0.7241 | 0.8285 | 0.7202 | 0.8382 | 0.7221 | 0.8321 |
| RF | 0.7299 | 0.8385 | 0.7381 | 0.8406 | 0.7098 | 0.8341 | 0.7237 | 0.8373 |
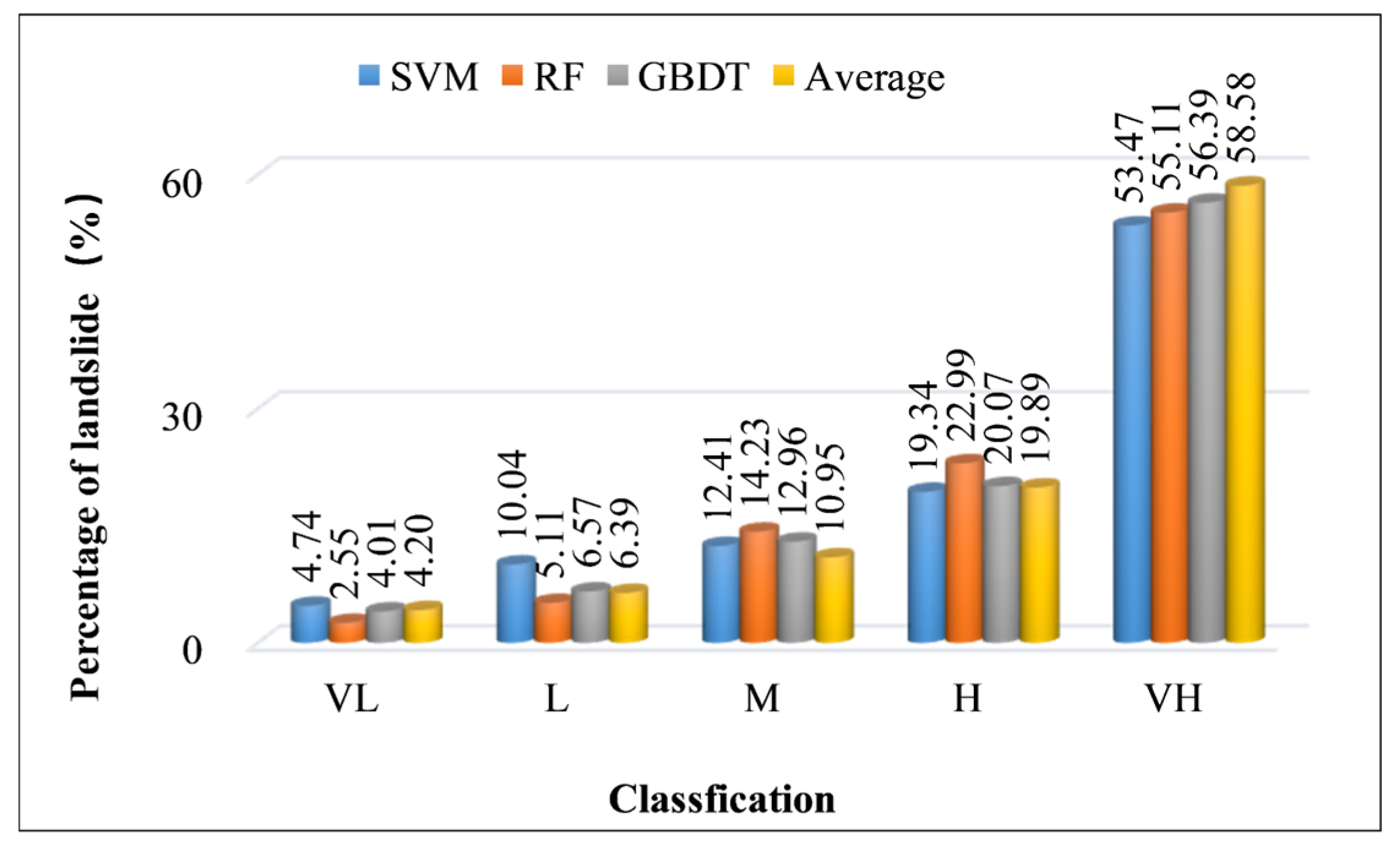
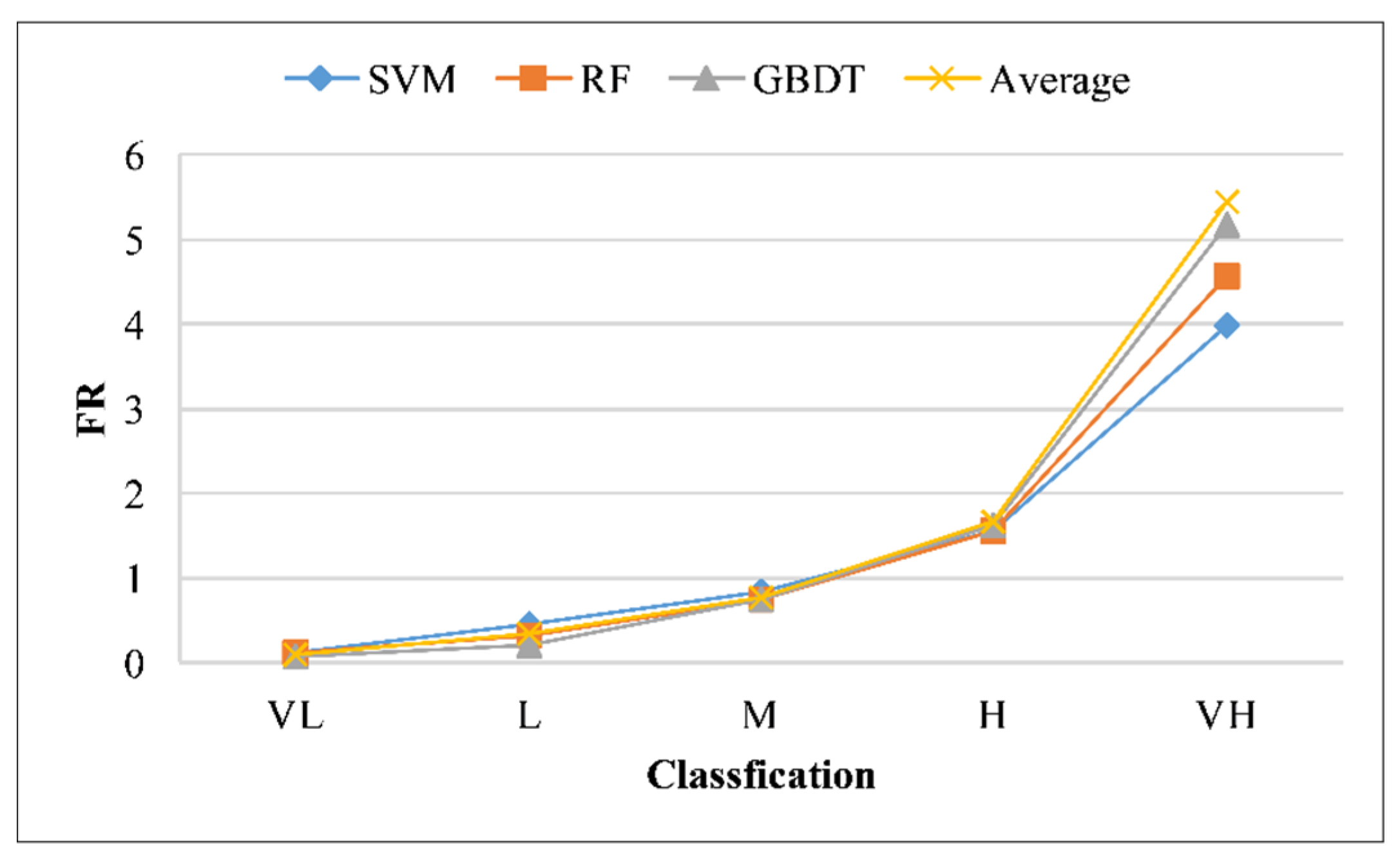
| Model | Susceptibility Zones | Raster Cells | Proportion (%) | Landslide Count | Proportion (%) | FR |
|---|---|---|---|---|---|---|
| Slope-SVM | VL | 1,371,117 | 36.84 | 26 | 4.74 | 0.13 |
| L | 827,852 | 22.25 | 55 | 10.04 | 0.45 | |
| M | 559,434 | 15.03 | 68 | 12.41 | 0.83 | |
| H | 462,794 | 12.44 | 106 | 19.34 | 1.56 | |
| VH | 500,315 | 13.44 | 293 | 53.47 | 3.98 | |
| Slope-RF | VL | 1,168,148 | 31.39 | 14 | 2.55 | 0.11 |
| L | 919,426 | 24.71 | 28 | 5.11 | 0.32 | |
| M | 710,896 | 19.10 | 78 | 14.23 | 0.75 | |
| H | 526,665 | 14.15 | 126 | 22.99 | 1.56 | |
| VH | 396,377 | 10.65 | 302 | 55.11 | 4.56 | |
| Slope-GBDT | VL | 1,381,568 | 37.12 | 22 | 4.01 | 0.08 |
| L | 757,638 | 20.36 | 36 | 6.57 | 0.21 | |
| M | 644,561 | 17.32 | 71 | 12.96 | 0.75 | |
| H | 477,588 | 12.83 | 110 | 20.07 | 1.62 | |
| VH | 460,157 | 12.36 | 309 | 56.39 | 5.17 | |
| Average | VL | 1,665,281 | 44.75 | 23 | 4.20 | 0.09 |
| L | 688,898 | 18.51 | 35 | 6.39 | 0.35 | |
| M | 524,041 | 14.08 | 60 | 10.95 | 0.78 | |
| H | 420,368 | 11.30 | 109 | 19.89 | 1.67 | |
| VH | 422,924 | 11.36 | 321 | 58.58 | 5.44 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, W.; Li, L.; Niu, R. Impact of Non-Landslide Sample Sampling Strategies and Model Selection on Landslide Susceptibility Mapping. Appl. Sci. 2025, 15, 2132. https://doi.org/10.3390/app15042132
Jiang W, Li L, Niu R. Impact of Non-Landslide Sample Sampling Strategies and Model Selection on Landslide Susceptibility Mapping. Applied Sciences. 2025; 15(4):2132. https://doi.org/10.3390/app15042132
Chicago/Turabian StyleJiang, Weijun, Ling Li, and Ruiqing Niu. 2025. "Impact of Non-Landslide Sample Sampling Strategies and Model Selection on Landslide Susceptibility Mapping" Applied Sciences 15, no. 4: 2132. https://doi.org/10.3390/app15042132
APA StyleJiang, W., Li, L., & Niu, R. (2025). Impact of Non-Landslide Sample Sampling Strategies and Model Selection on Landslide Susceptibility Mapping. Applied Sciences, 15(4), 2132. https://doi.org/10.3390/app15042132






