Mathematical Modeling and Electromagnetic Characteristics Analysis of a Six-Phase Distributed Single-Winding BPMSM with 12 Slots and 2 Poles
Abstract
Featured Application
Abstract
1. Introduction
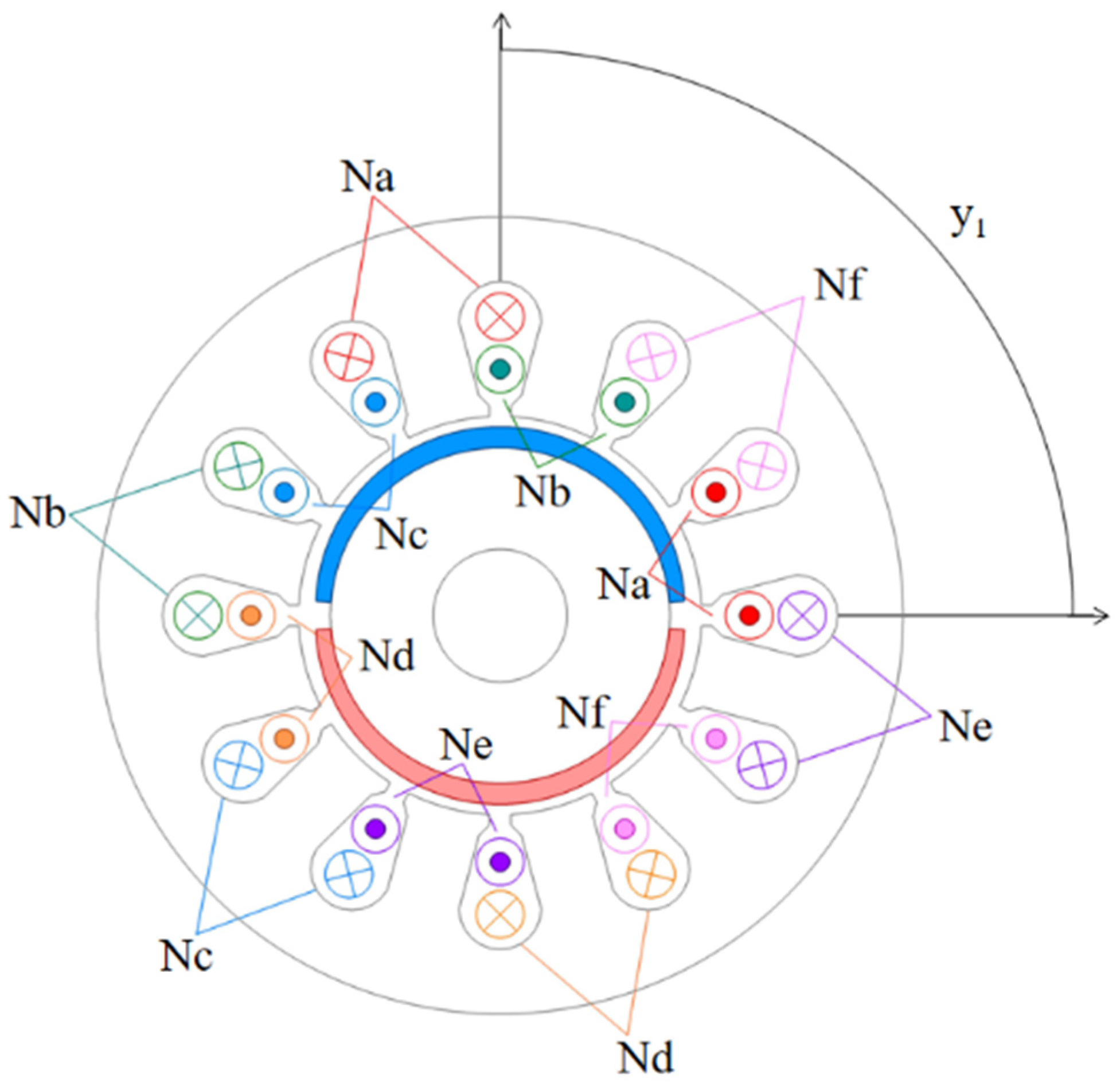
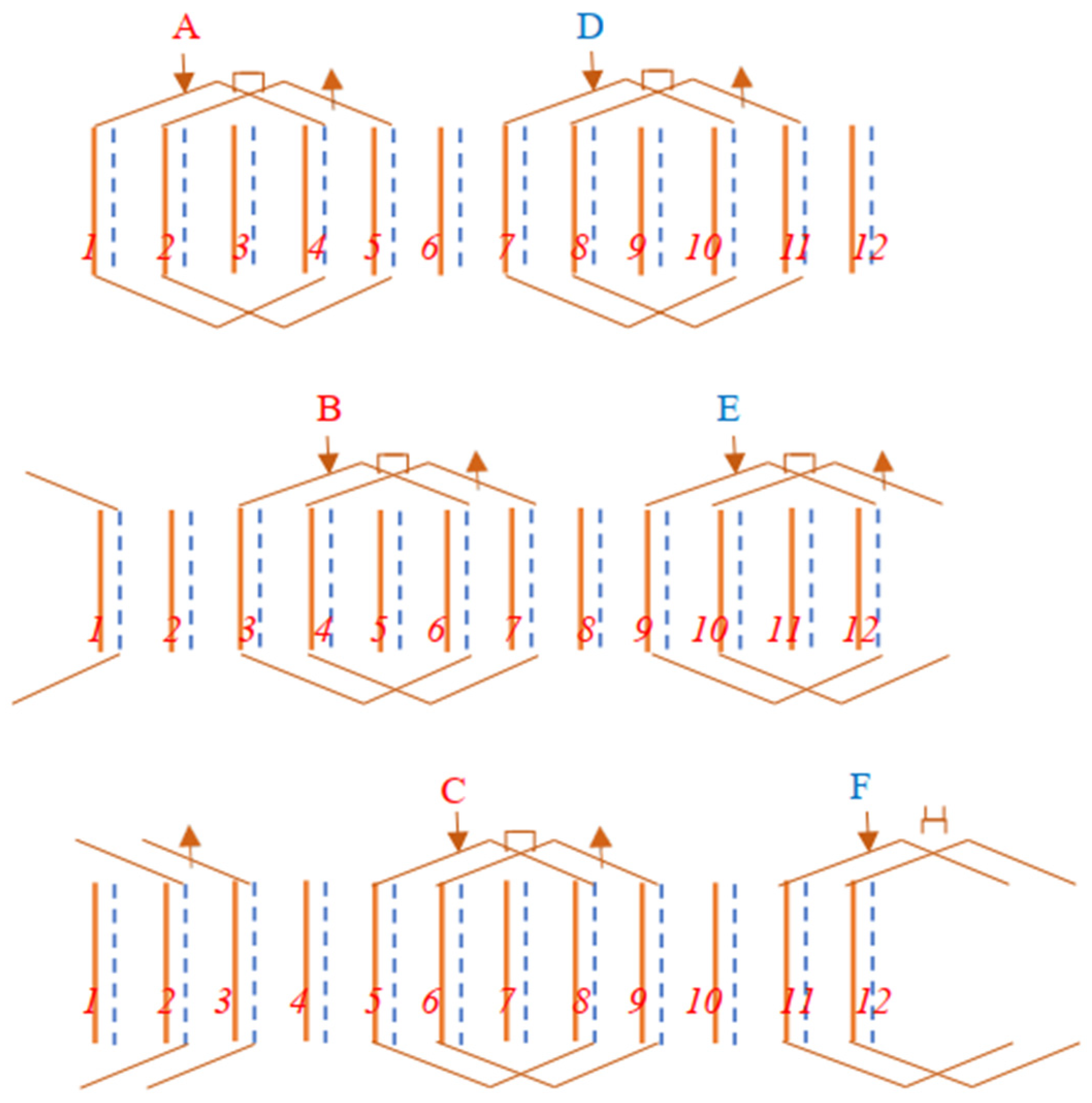
2. Structure and Working Principle of the Six-Phase DSW-12/2-BPMSM
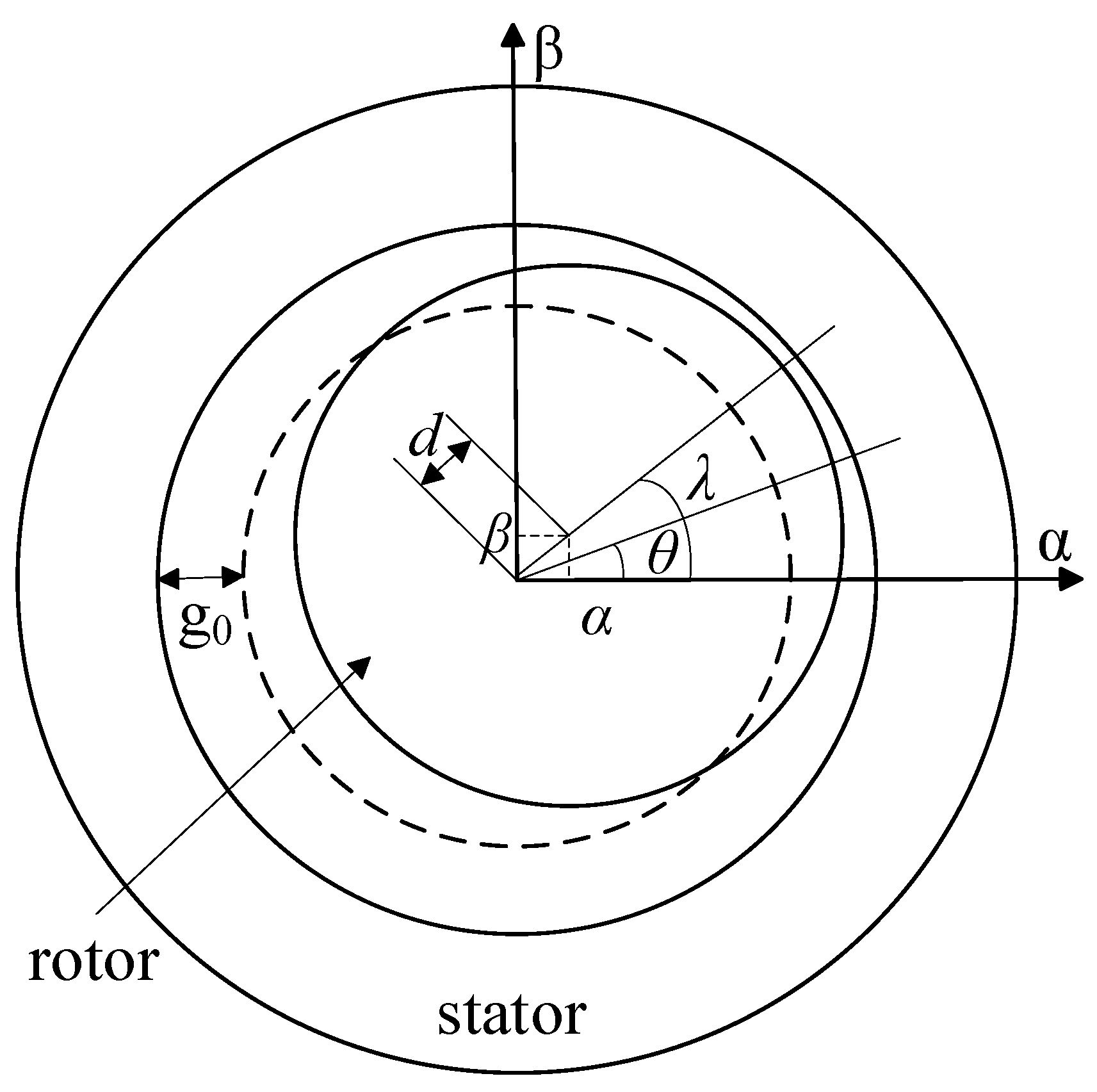
3. Mathematical Modeling of the Six-Phase DSW-12/2-BPMSM
3.1. Basic Model for Six-Phase DSW-12/2-BPMSM
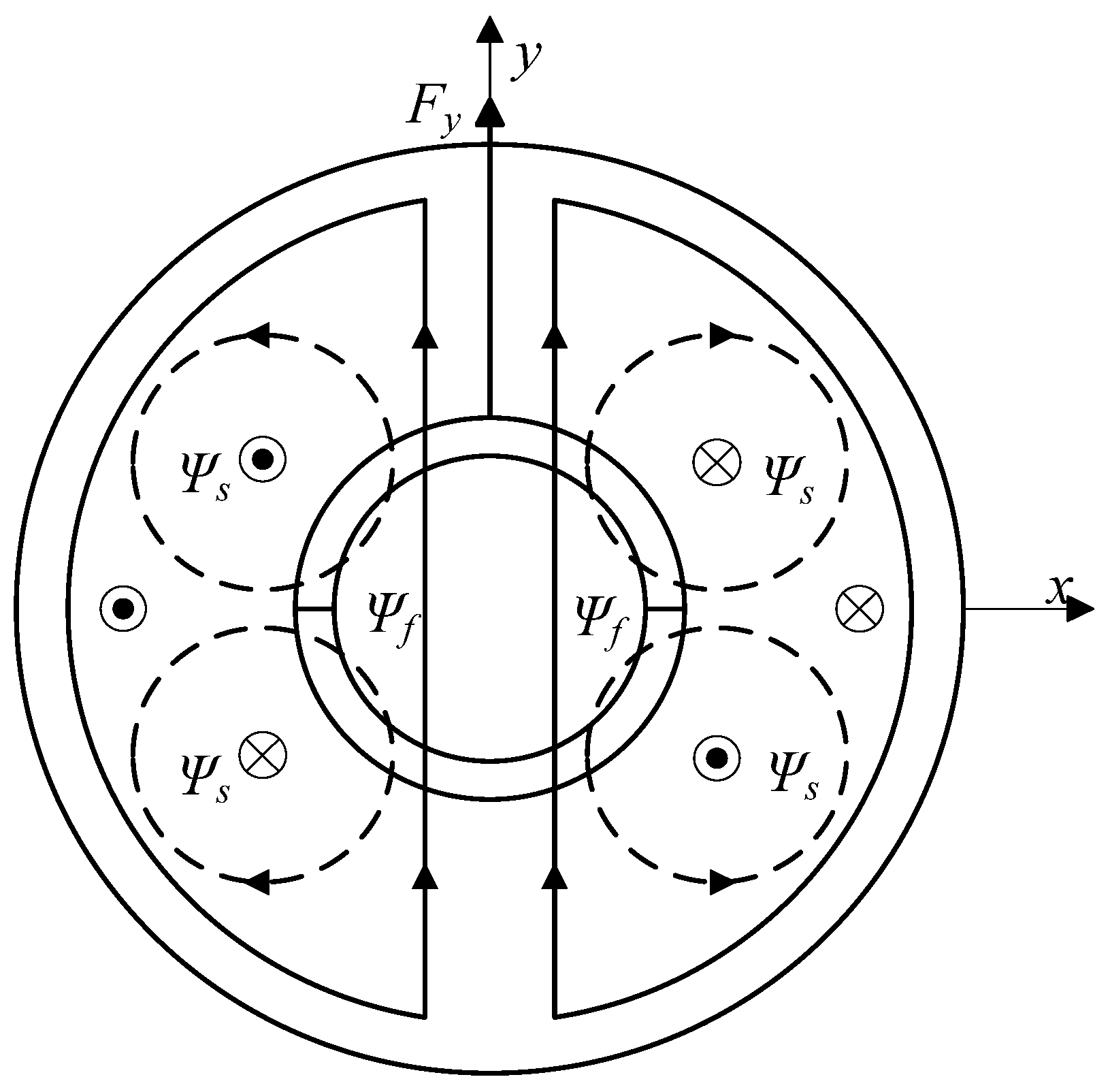
3.2. Magnetic Levitation Force Model of the Six-Phase DSW-12/2-BPMSM
4. FEM Verification and Analysis
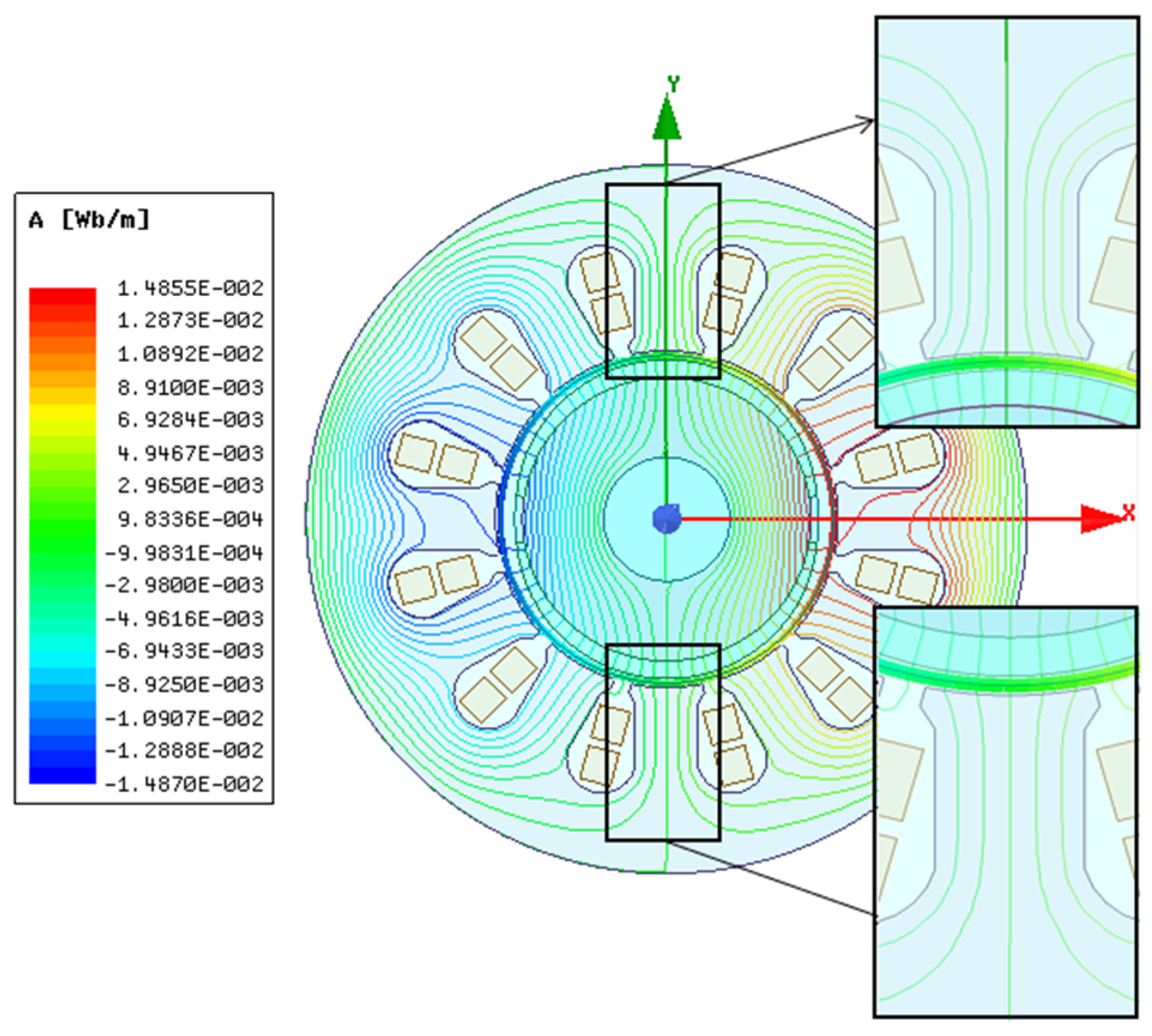
4.1. FEM Analysis Model of the Six-Phase DSW-12/2-BPMSM
4.2. Validation Analysis of Electromagnetic Torque and Magnetic Levitation Force Models
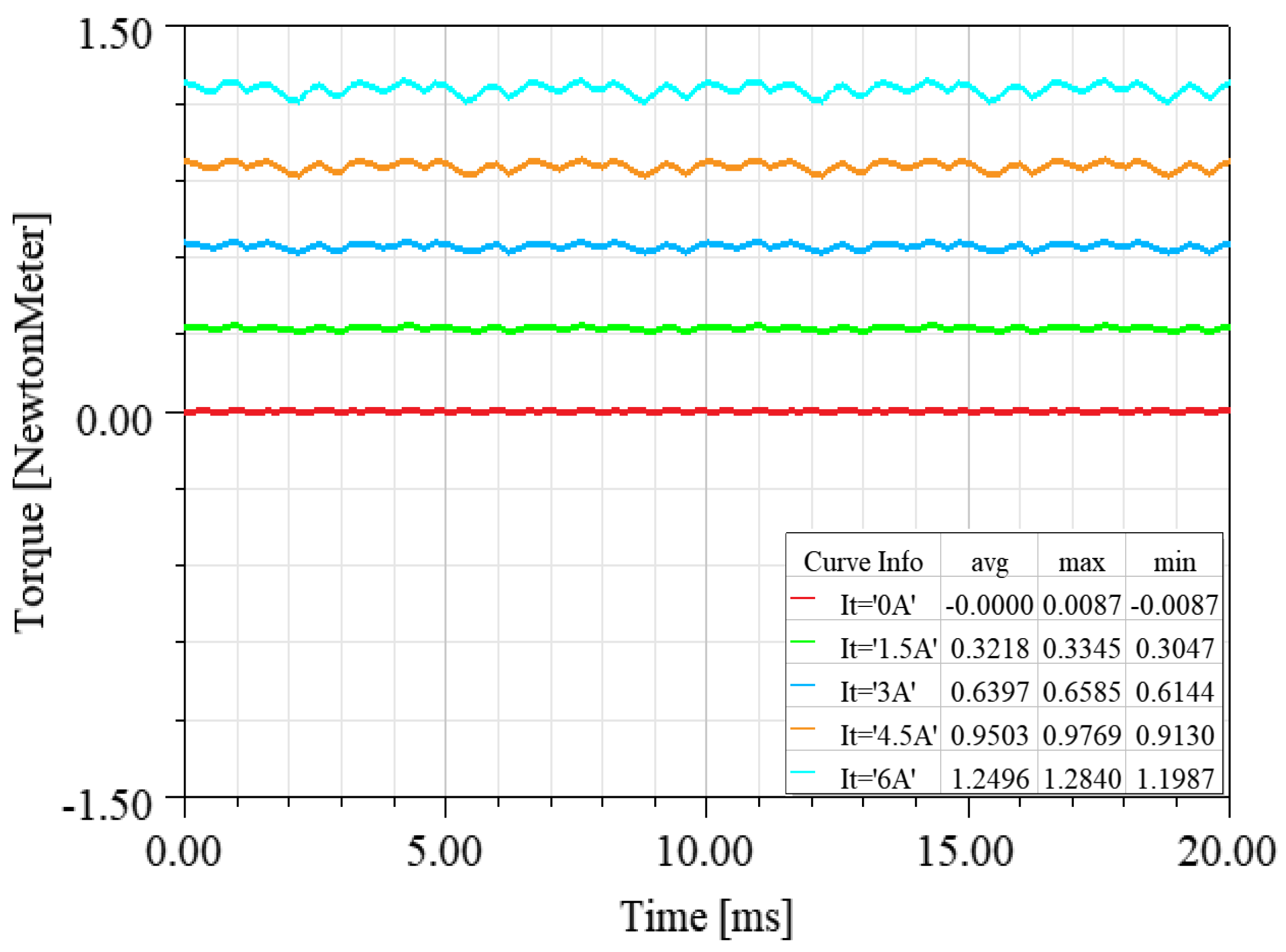
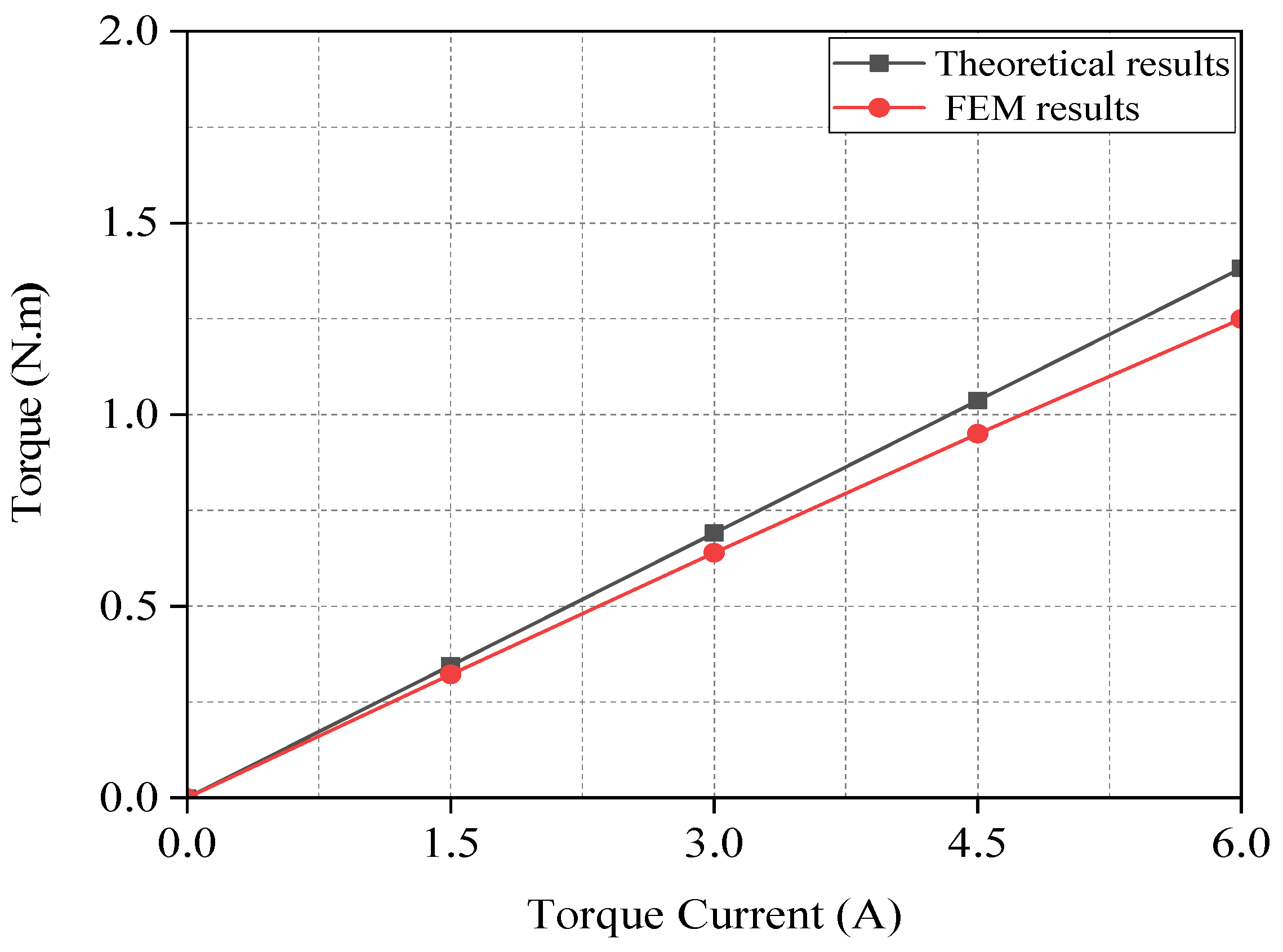
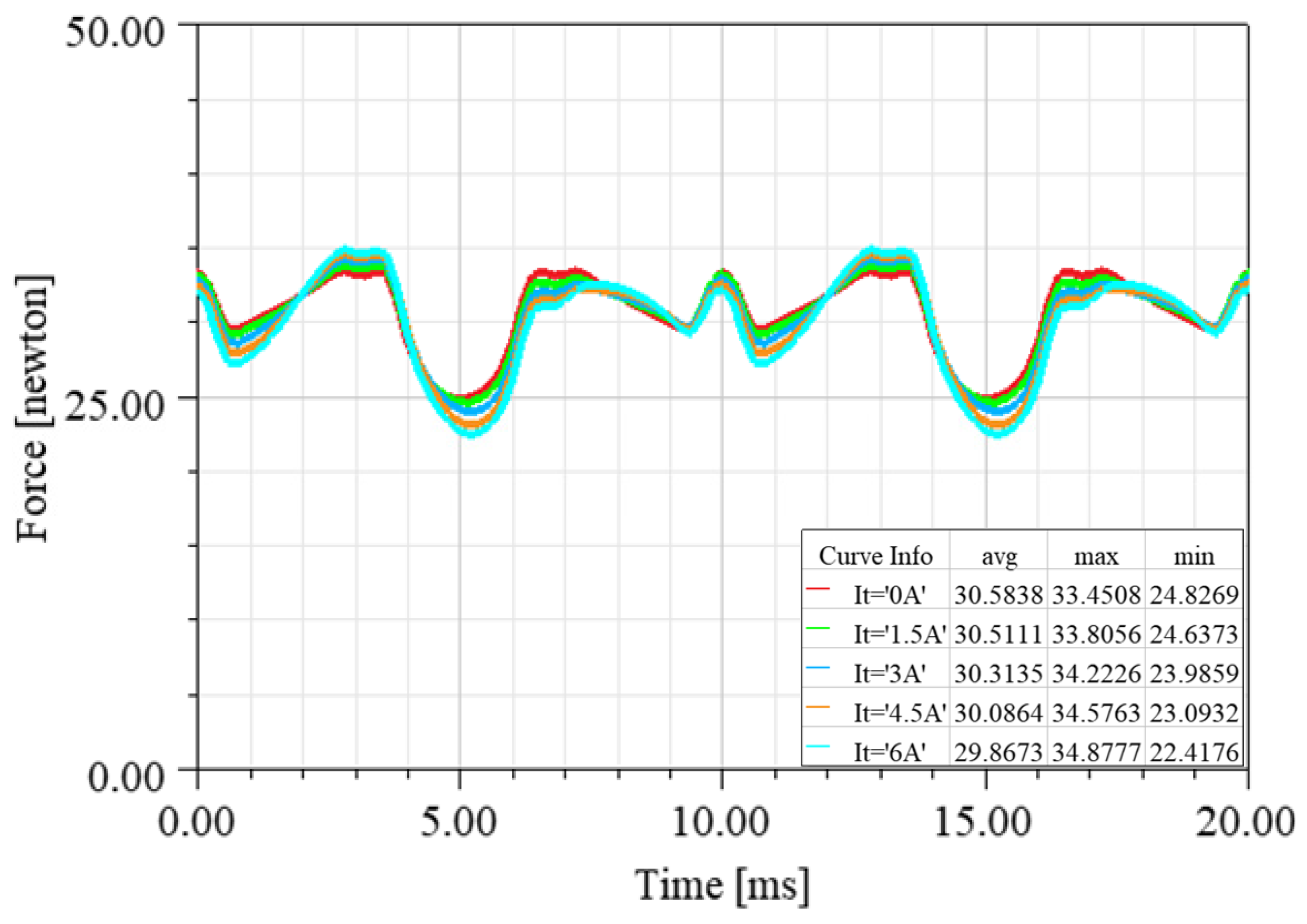
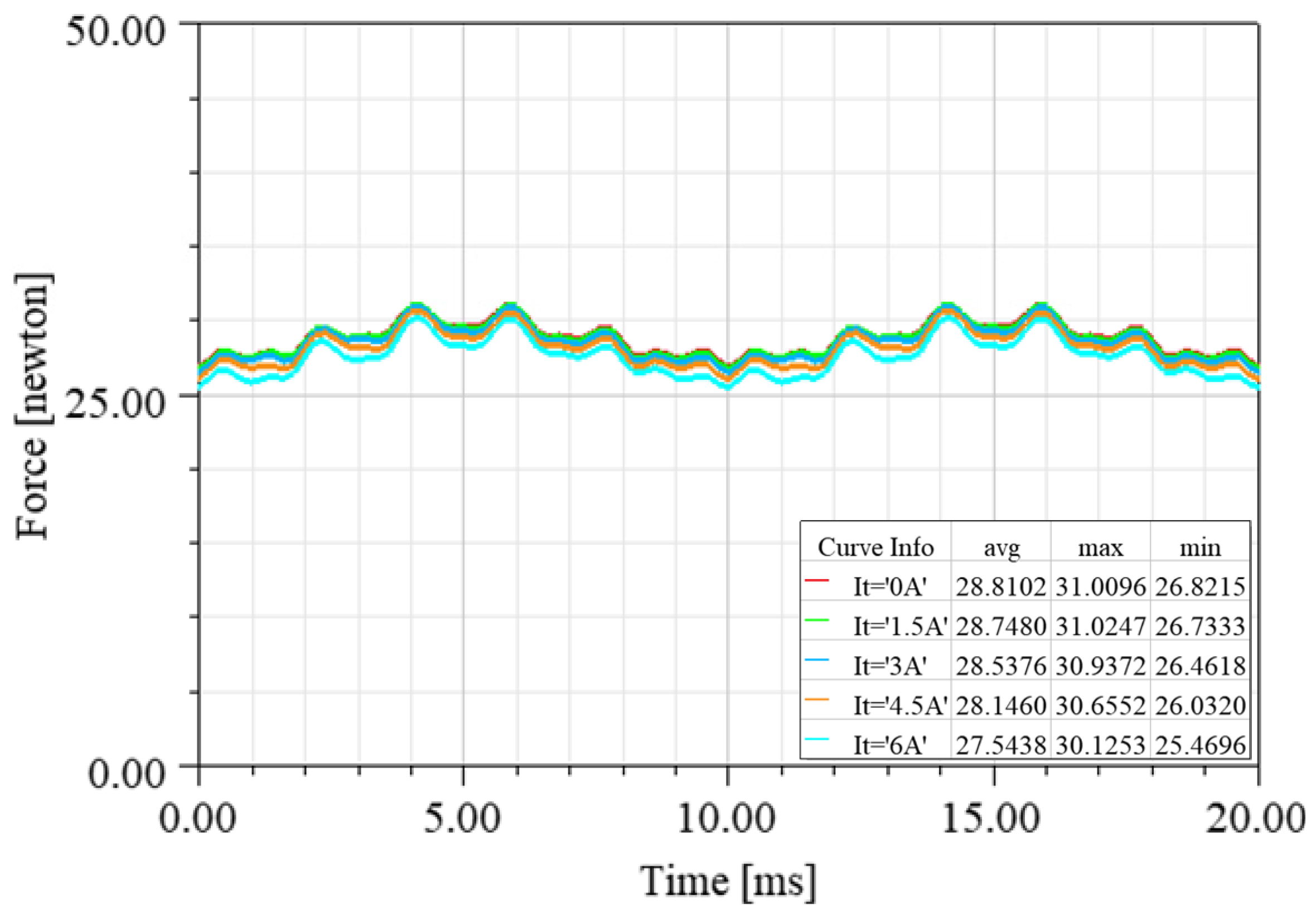
4.2.1. FEM Validation Analysis of Torque Model
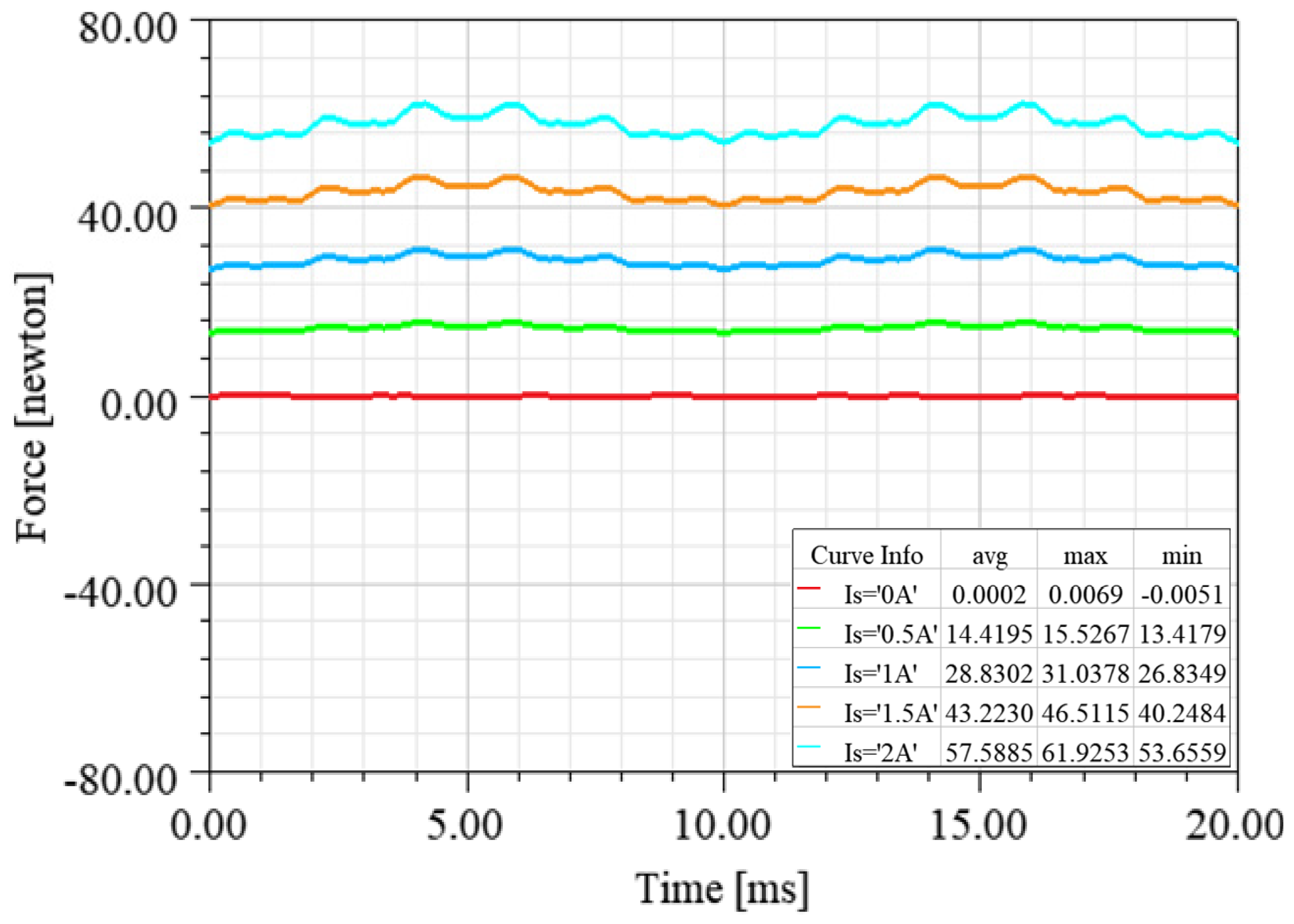
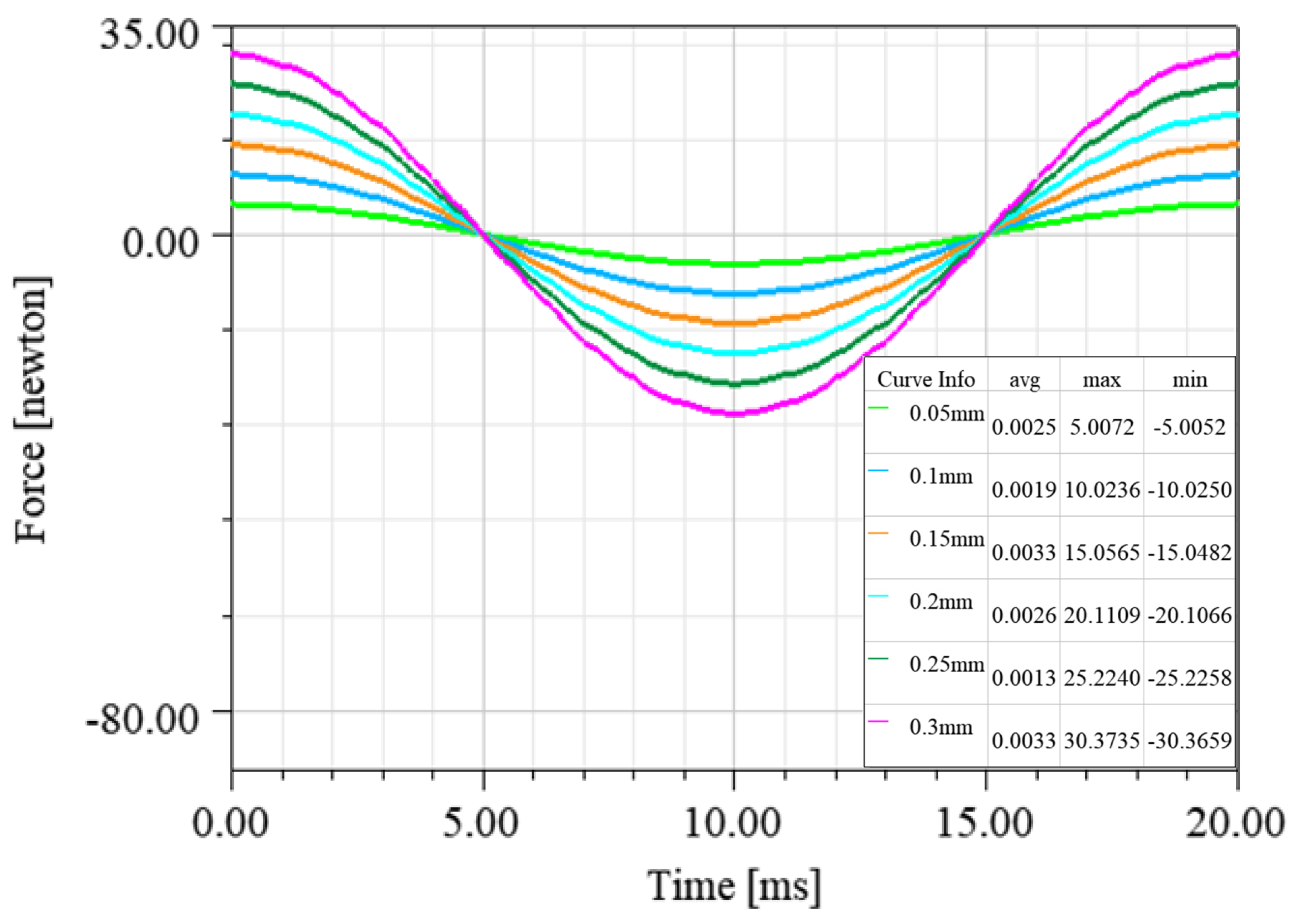
4.2.2. FEM Validation Analysis of Controlled Magnetic Levitation Force Models
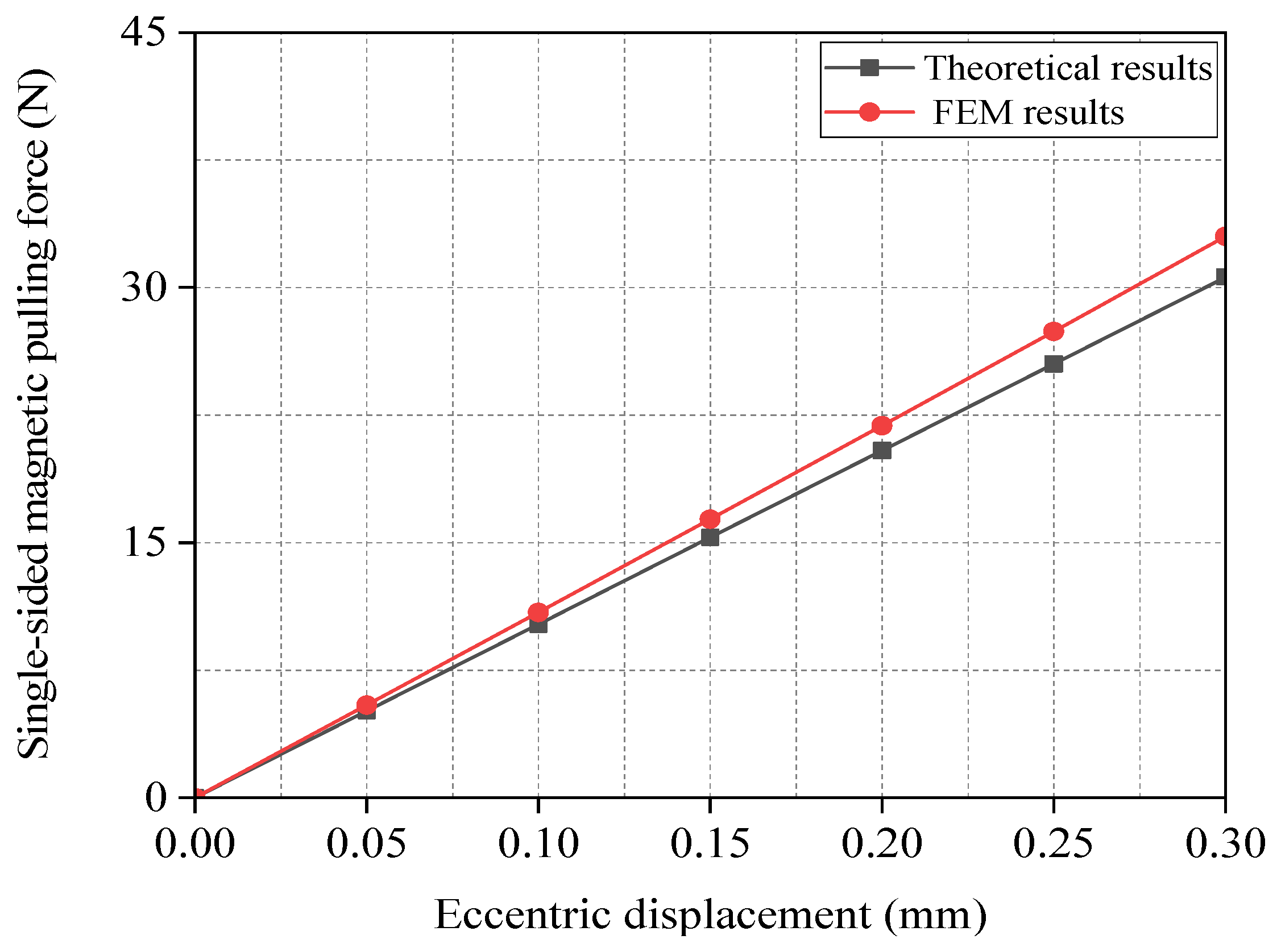
4.2.3. FEM Validation Analysis of Eccentric Magnetic Pull Force Model
4.3. Comparative Analysis with Six-Phase CSW-6/2-BPMSM
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hu, Y.F.; Taha, O.W.; Yang, K. Fault Detection in Active Magnetic Bearings Using Digital Twin Technology. Appl. Sci. 2024, 14, 1384. [Google Scholar] [CrossRef]
- Chen, J.H.; Zhu, J.W.; Eric, L. Review of bearingless motor technology for significant power applications. IEEE Trans. Ind. Appl. 2020, 56, 1377–1388. [Google Scholar] [CrossRef]
- Sun, C.; Yang, Z.B.; Sun, X.D.; Ding, Q.F. An Improved Mathematical Model for Speed Sensorless Control of Fixed Pole Bearingless Induction Motor. IEEE Trans. Ind. Electron. 2024, 71, 1286–1295. [Google Scholar] [CrossRef]
- Shen, H.; Bian, F.; Yue, Y.; Li, B.; Yu, P.; Yang, L.; Chen, G.; Hu, L. Multi-Structural Optimization of Bearingless Permanent Magnet Slice Motor Based on Virtual Prototype in Ansoft Maxwell. Appl. Sci. 2021, 11, 4740. [Google Scholar] [CrossRef]
- Bu, W.S.; Wan, S.M.; Huang, S.H.; Liu, W.S. General Analytical Model About Controllable Magnetic Suspension Force of Bearingless Motor. Proc. CSEE 2009, 29, 84–89. [Google Scholar]
- Bao, X.C.; Wang, X.L.; Ding, Q.; Shi, T.R. Design of Double Staggered Parallel Bearingless Motor Drive System. IEEE Trans. Power Electron. 2023, 38, 2230–2239. [Google Scholar] [CrossRef]
- Rao, P.N.; Kumar, N.M.; Padmanaban, S.; Subathra, M.S.P.; Chand, A.A. A Novel Sensorless Approach for Speed and Displacement Control of Bearingless Switched Reluctance Motor. Appl. Sci. 2020, 10, 4070. [Google Scholar] [CrossRef]
- Xu, K.; Guo, Y.G.; Lei, G.; Sun, X.D.; Zhu, J.G. Electromagnetic Performance Analysis of a Bearingless Permanent Magnet Synchronous Motor by Model Order Reduction. IEEE Trans. Magn. 2023, 59, 11. [Google Scholar] [CrossRef]
- Bu, W.S.; Li, H. Torque System Modeling and Electromagnetic Coupling Characteristics Analysis of a Midpoint Injection Type Bearingless Permanent Synchronous Magnet Motor. Int. Trans. Electr. Energy Syst. 2024, 2024, 3078894. [Google Scholar] [CrossRef]
- Khoo, W.K.S.; Kalita, K.; Garvey, S.D. Practical implementation of the bridge configured winding for producing controllable transverse forces in electrical machines. IEEE Trans. Magn. 2011, 47, 1712–1718. [Google Scholar] [CrossRef]
- Petersen, N.; Khamitov, A.; Slininger, T.; Severson, E.L. Machine Design and Precision Current Regulation for the Parallel DPNV Bearingless Motor Winding. IEEE Trans. Ind. Appl. 2021, 57, 7000–7001. [Google Scholar] [CrossRef]
- Li, B.N.; Huang, J.; Kang, M.; Kong, W.B. Analysis and Comparison of Inductance and Suspension Force for 2-4 Type and 4-2 Type Multiphase Permanent Magnet Bearingless Motors. Proc. CSEE 2013, 33, 106–114. [Google Scholar]
- Yuan, J.F.; Zhu, H.Q.; Zhao, Y.L.; Ding, Q. Structure principle and control of novel dual three-phase bearingless permanent magnet synchronous motor. Adv. Technol. Electr. Eng. Energy 2017, 36, 16–24. [Google Scholar]
- Wang, X.L.; Sheng, W.; Deng, Z.Q.; Ren, X.Y. Operating Characteristics Analysis of Multi-phase Bearingless Permanent Magnet Slice Motors with Faulty Phases. Proc. CSEE 2011, 31, 73–78. [Google Scholar]
- Dietz, D.; Messager, G.; Binder, A. 1kW/60,000min (-1) bearingless PM motor with combined winding for torque and rotor suspension. Iet Electr. Power Appl. 2018, 12, 1090–1097. [Google Scholar] [CrossRef]
- Qin, Y.M.; Zhu, H.Q. Torque and Suspension Force Optimization for Five-phase Bearingless PMSM with Third-order Harmonic Injection. Proc. CSEE 2018, 38, 6701–6710. [Google Scholar]
- Faiz, J.; Tabatabaei, I. Extension of winding function theory for nonuniform air gap in electric machinery. IEEE Trans. Magn. 2002, 38, 3654–3657. [Google Scholar] [CrossRef]
- Wang, H.M.; Bai, H.J.; Guo, L.Y. Design of Single-Winding Arrangement for Arbitrary Multiphase Bearingless Permanent Magnet Synchronous Motor. J. Electr. Eng. Technol. 2024, 1–11. [Google Scholar] [CrossRef]



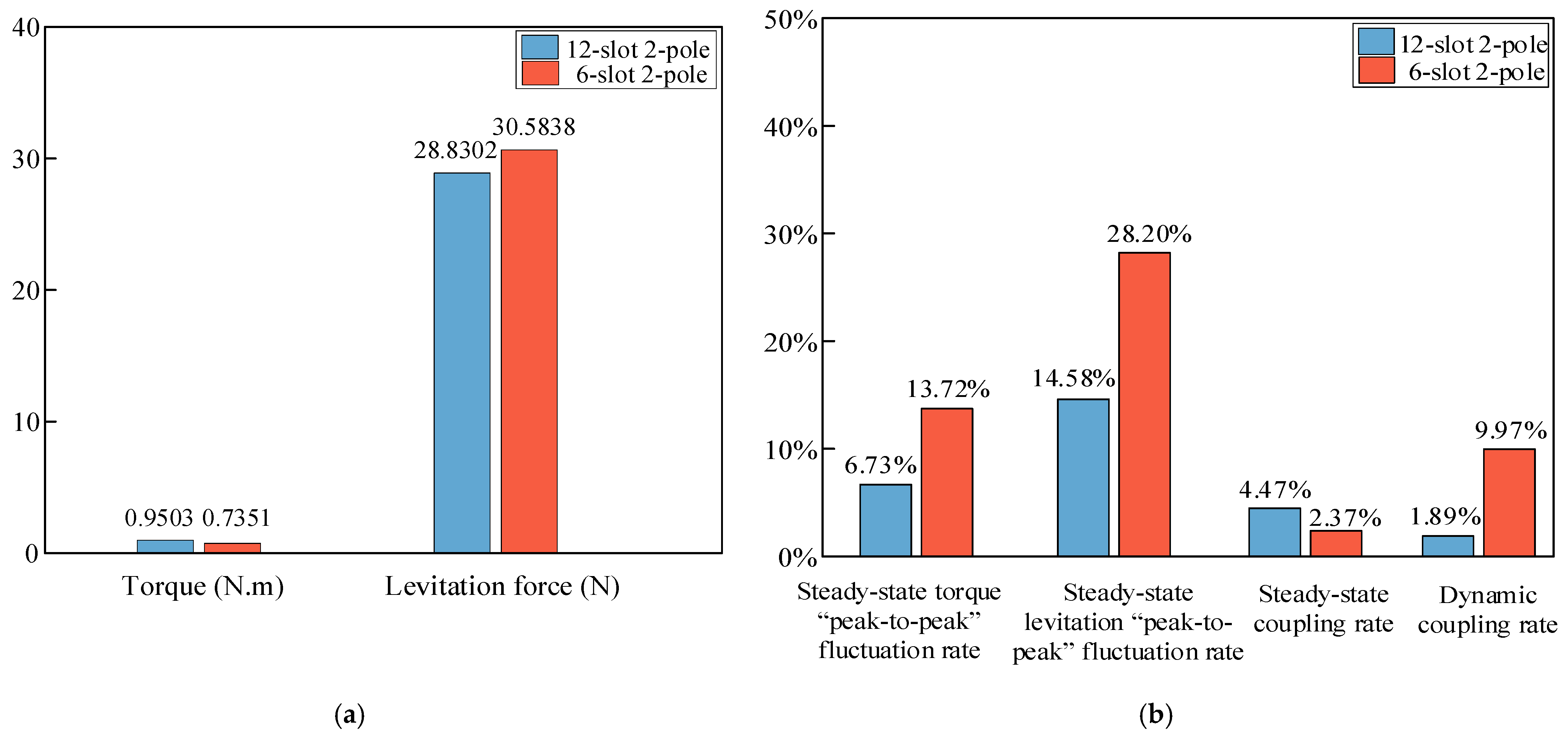
| Parameter | Value |
|---|---|
| Pole-pair number of the rotor | 1 |
| Number of stator slots | 12 |
| Stator core outer diameter (mm) | 80 |
| Stator core inner diameter (mm) | 38 |
| Rotor core outer diameter (mm) | 32 |
| Thickness of PM, Lm (mm) | 2 |
| Air gap length, g (mm) | 1 |
| L1 (mH) | 5.45 |
| L2 (mH) | 2.72 |
| M12 (H/m) | 0.6829 |
| Ψf (Wb) | 0.133 |
| Axial length (mm) | 40 |
| Residual magnetic density of PM (T) | 1.23 |
| Coercivity of PM (kA/M) | −890 |
| Turn number of coils | 100 |
| Core materials of stator and rotor | DW465_50 |
| Permanent magnet materials | NdFe35 |
| Relative permeability, μr | 1.09978 |
| Boundary condition | Natural boundary condition |
| Rated power (kw) | 1.2 |
| Rated speed (rpm) | 3000 |
| Characteristics/ Performance | Six-Phase CSW-6/2-BPMSM | Six-Phase DSW-12/2-BPMSM |
|---|---|---|
| Mechanical structure | Simple | Moderate |
| Harmonic content | High | Low |
| Torque stiffness | Moderate | High |
| Suspension force stiffness | Moderate | Moderate |
| Torque pulsation | Moderate | Small |
| Suspension force pulsation | Large | Moderate |
| Coupling | Moderate | Low |
| Efficiency | Moderate | Higher |
| Noise | Obvious | Moderate |
| Field of application | Low power | Low power |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bu, W.; Li, J.; Lu, Y. Mathematical Modeling and Electromagnetic Characteristics Analysis of a Six-Phase Distributed Single-Winding BPMSM with 12 Slots and 2 Poles. Appl. Sci. 2025, 15, 2093. https://doi.org/10.3390/app15042093
Bu W, Li J, Lu Y. Mathematical Modeling and Electromagnetic Characteristics Analysis of a Six-Phase Distributed Single-Winding BPMSM with 12 Slots and 2 Poles. Applied Sciences. 2025; 15(4):2093. https://doi.org/10.3390/app15042093
Chicago/Turabian StyleBu, Wenshao, Jiangdi Li, and Yongfang Lu. 2025. "Mathematical Modeling and Electromagnetic Characteristics Analysis of a Six-Phase Distributed Single-Winding BPMSM with 12 Slots and 2 Poles" Applied Sciences 15, no. 4: 2093. https://doi.org/10.3390/app15042093
APA StyleBu, W., Li, J., & Lu, Y. (2025). Mathematical Modeling and Electromagnetic Characteristics Analysis of a Six-Phase Distributed Single-Winding BPMSM with 12 Slots and 2 Poles. Applied Sciences, 15(4), 2093. https://doi.org/10.3390/app15042093






