Dam Deformation Monitoring Model Based on Deep Learning and Split Conformal Quantile Prediction
Abstract
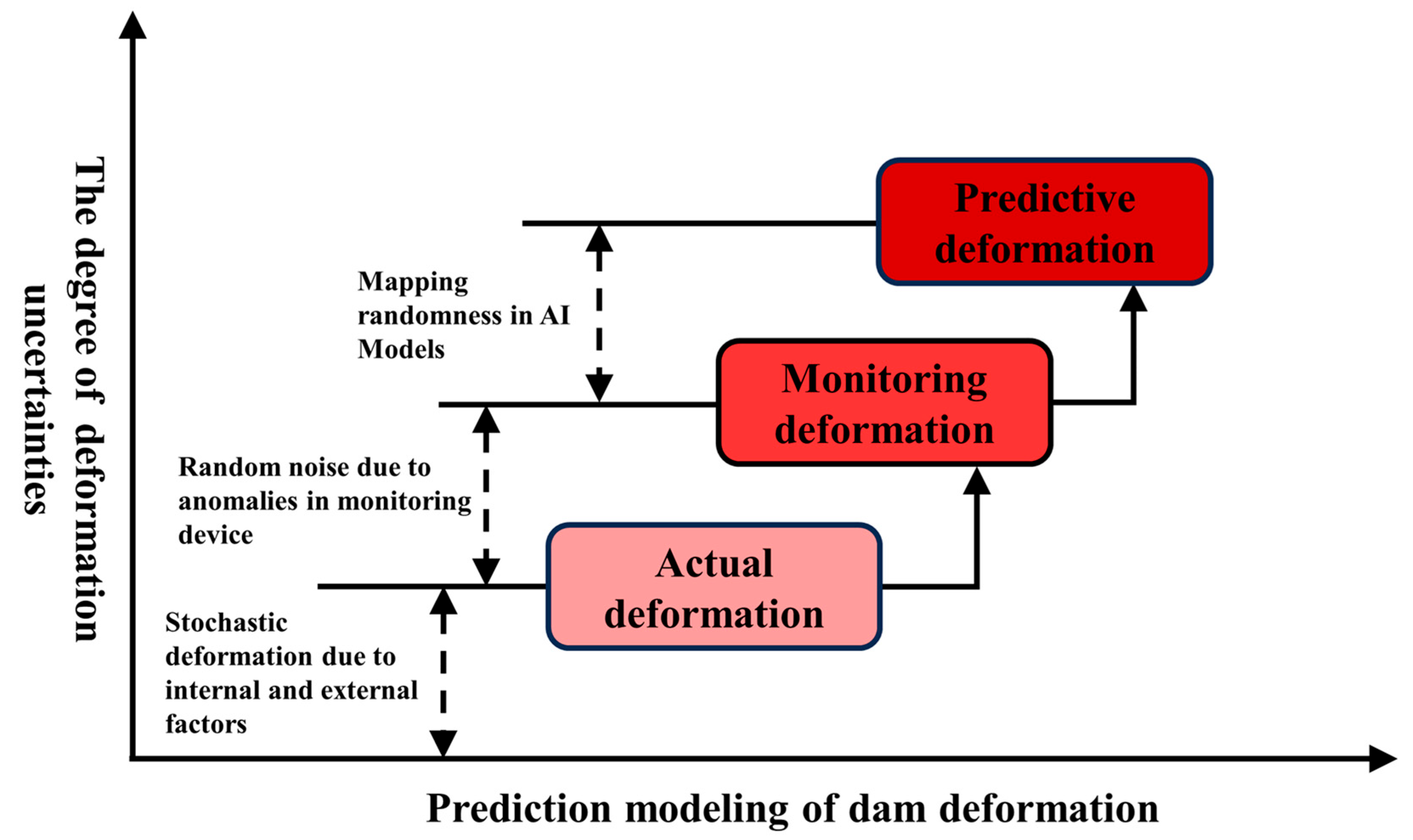
1. Introduction
- (1)
- The Bi-LSTM is used to capture the nonlinear properties of dam deformation, which ensures the generalization ability and robustness of our proposed model.
- (2)
- Split conformal quantile prediction (SCQP) is applied to quantify the uncertainties of dam deformation prediction, enabling the model to construct high-quality deformation PIs.
- (3)
- We compare the performance of point and interval predictions by mapping transformations between them. The results emphasize the importance of considering uncertainties in dam deformation prediction.
2. Methodologies
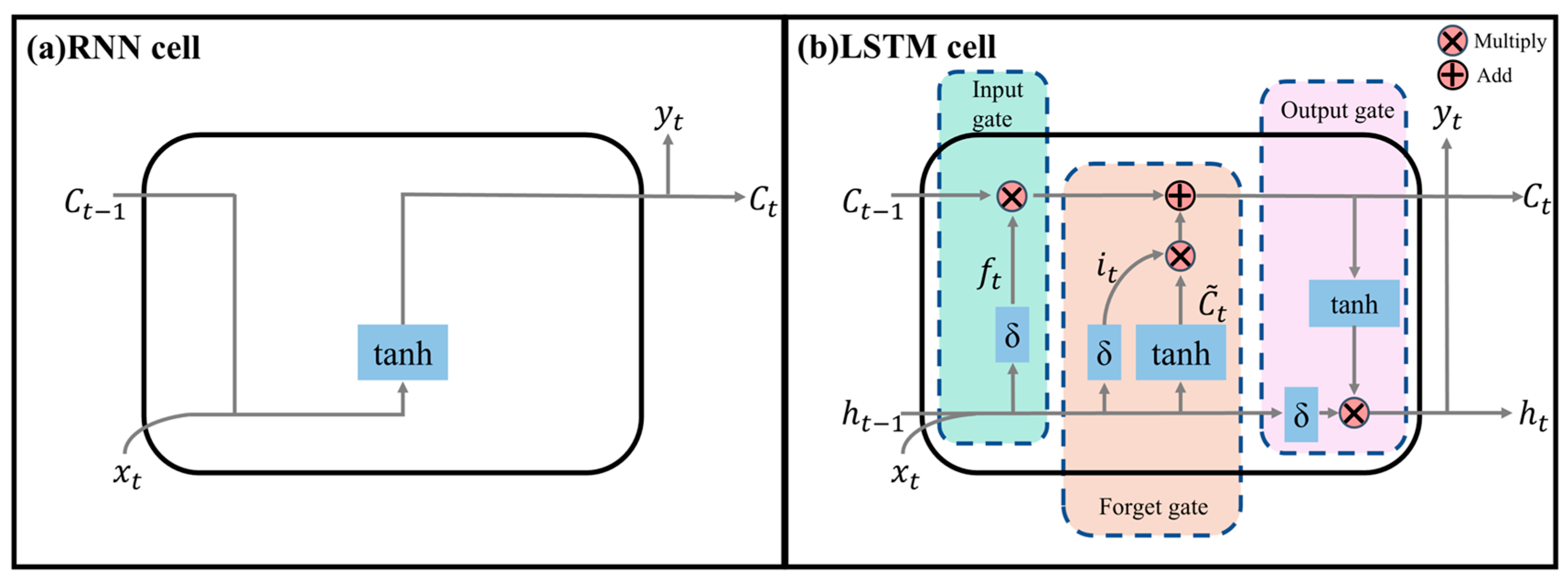
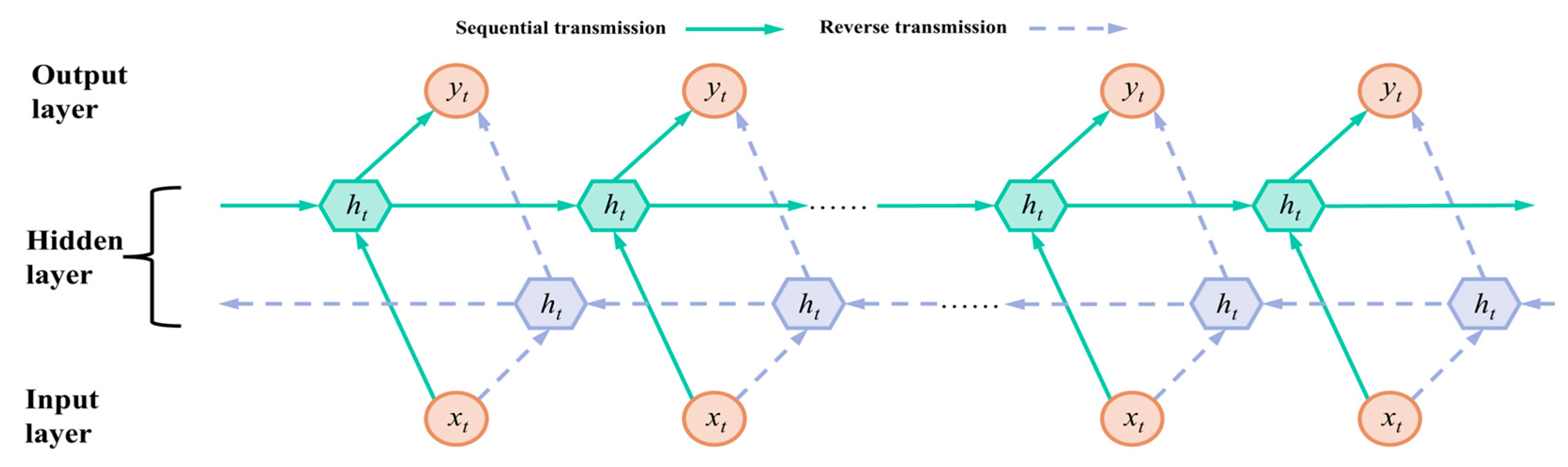
2.1. Bi-Directional Long Short-Term Memory Network
2.2. Split Conformal Quantile Prediction
2.3. The Evaluation Indicators of Model Performance
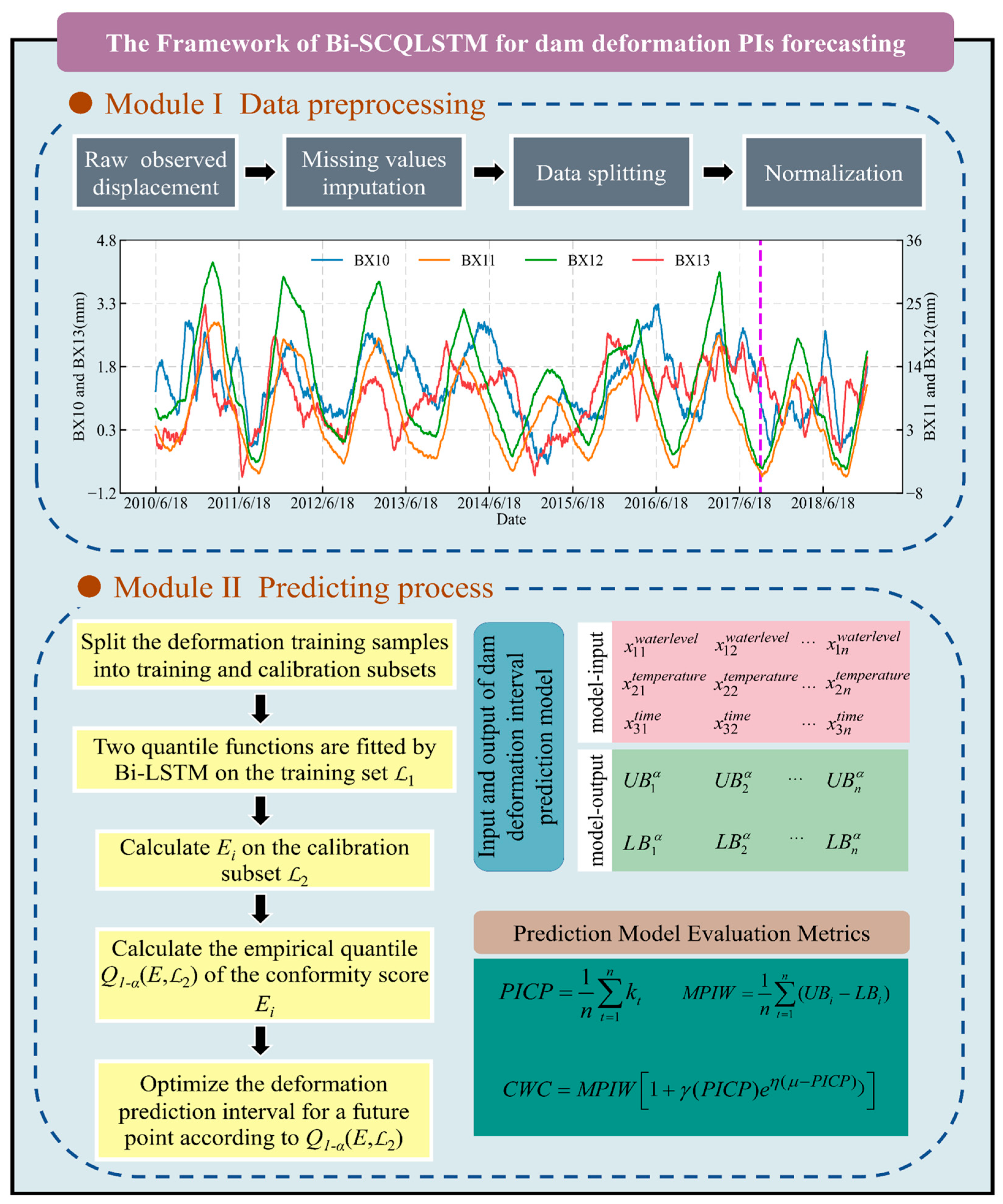
2.4. The Proposed Bi-SCQLSTM for Dam Deformation Interval Pre Diction
| Algorithm 1: Procedure of Bi-SCQLSTM |
| Input: Observation dataset , . Set: Error coverage level . |
| Process: 1. Divide the observation dataset into two disjoint subsets, the training set and the calibration set . 2. Two function curves are fitted by using a Bi-LSTM coupled with pinball loss. 3. The consistency score corresponding to a finite number of samples on the calibration set is calculated by Equation (20). 4. Compute . |
| Output: The prediction interval of the response variable corresponding to the independent variable |
- (1)
- First, a raw dam monitoring series is interpolated, and the resulting dataset is divided into training samples and test samples, and min–max normalization is performed on the two sample sets independently.
- (2)
- Secondly, the training samples are used as the input data of the Bi-SCQLSTM. During this process, the training samples are further divided into two disjoint subsets, a training subset and a calibration subset . Two function curves and are fitted to the training subset using the Bi-LSTM. The number of neurons in the output layer of the Bi-LSTM is set to 2, and the cost function is defined as pinball loss. The main idea behind this process stems from quantile regression.
- (3)
- The Bi-LSTM is then used as the underlying evaluator for the SCQP algorithm, which is used to calculate the consistency score . For finite samples from the calibration subset , the consistency score and corresponding empirical quantile will be obtained by Equation (14) and Equation (16), respectively. Then, the deformation PIs constructed by the model for the new exogenous variable will be optimized by the to further adapt to the dam deformation series with variance variability and random fluctuation.
- (4)
- Finally, the deformation PIs are evaluated and compared by using the interval evaluation indicators PICP, MPIW, and CWC.
3. Case Study
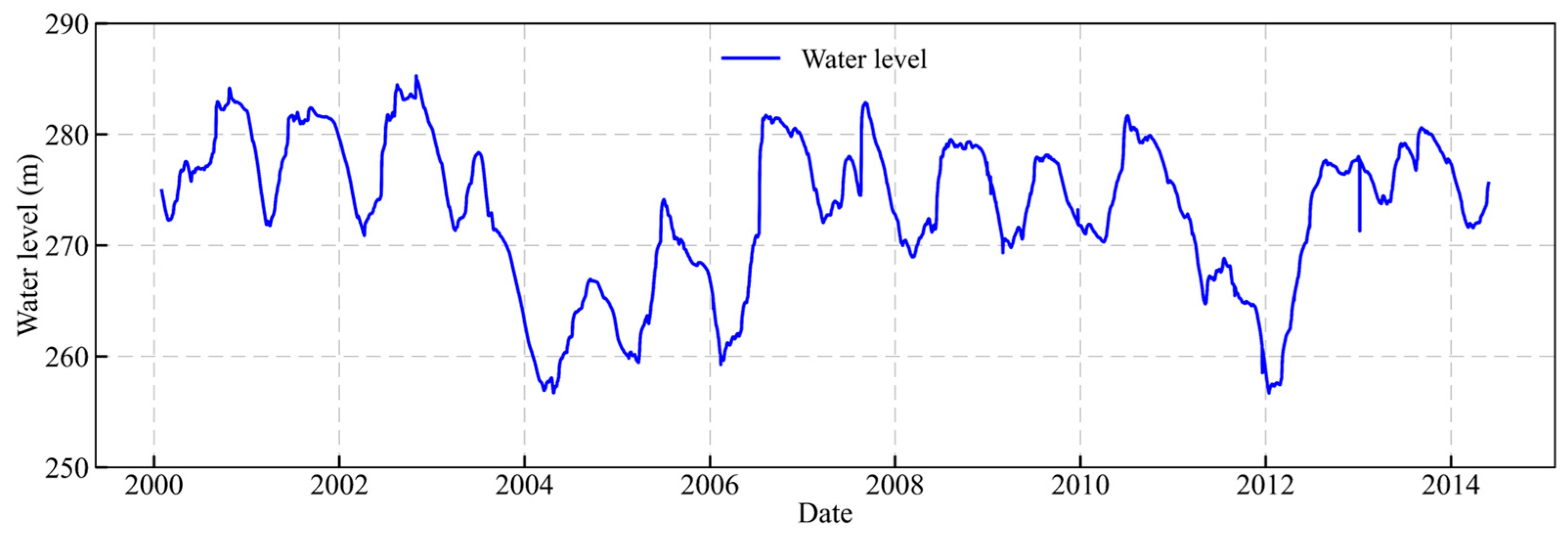
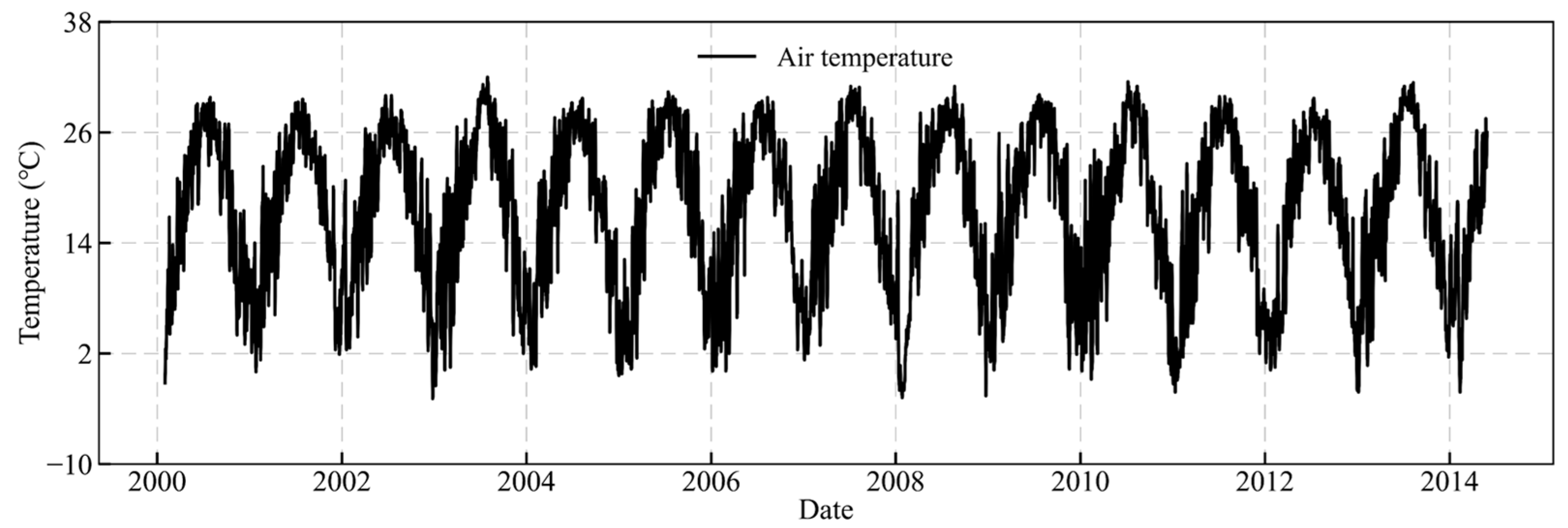
3.1. Overview of the Arch Dam Project
3.2. Model Construction and Deformation Feature Selection
3.3. Comparative Analysis of Different Interval Prediction Models
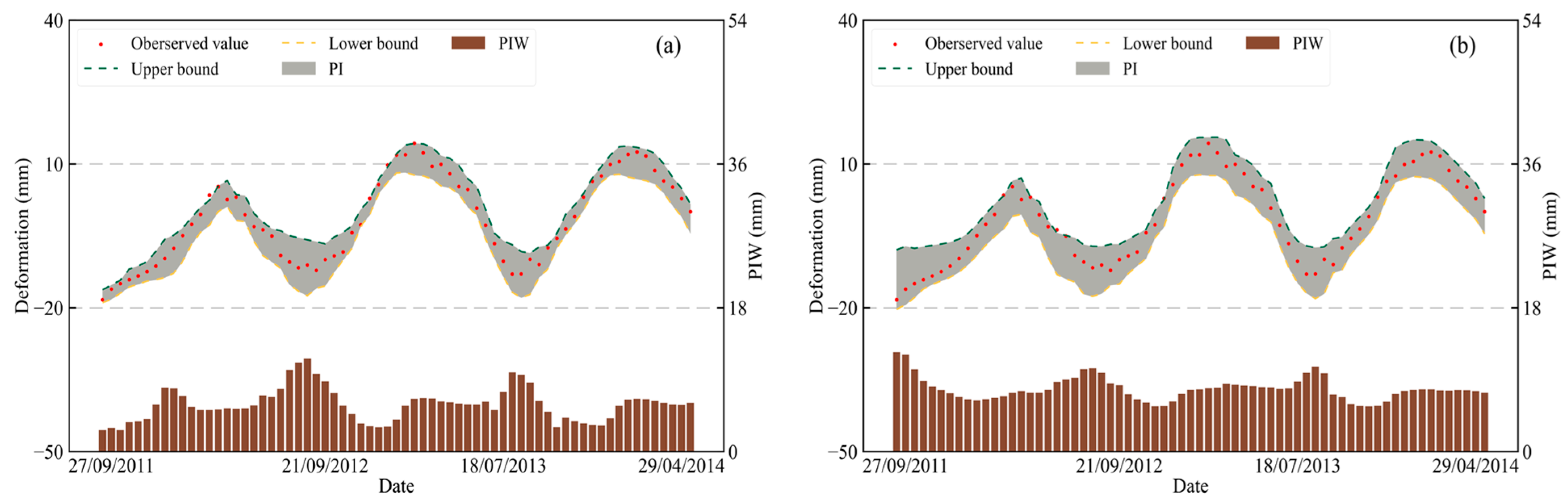
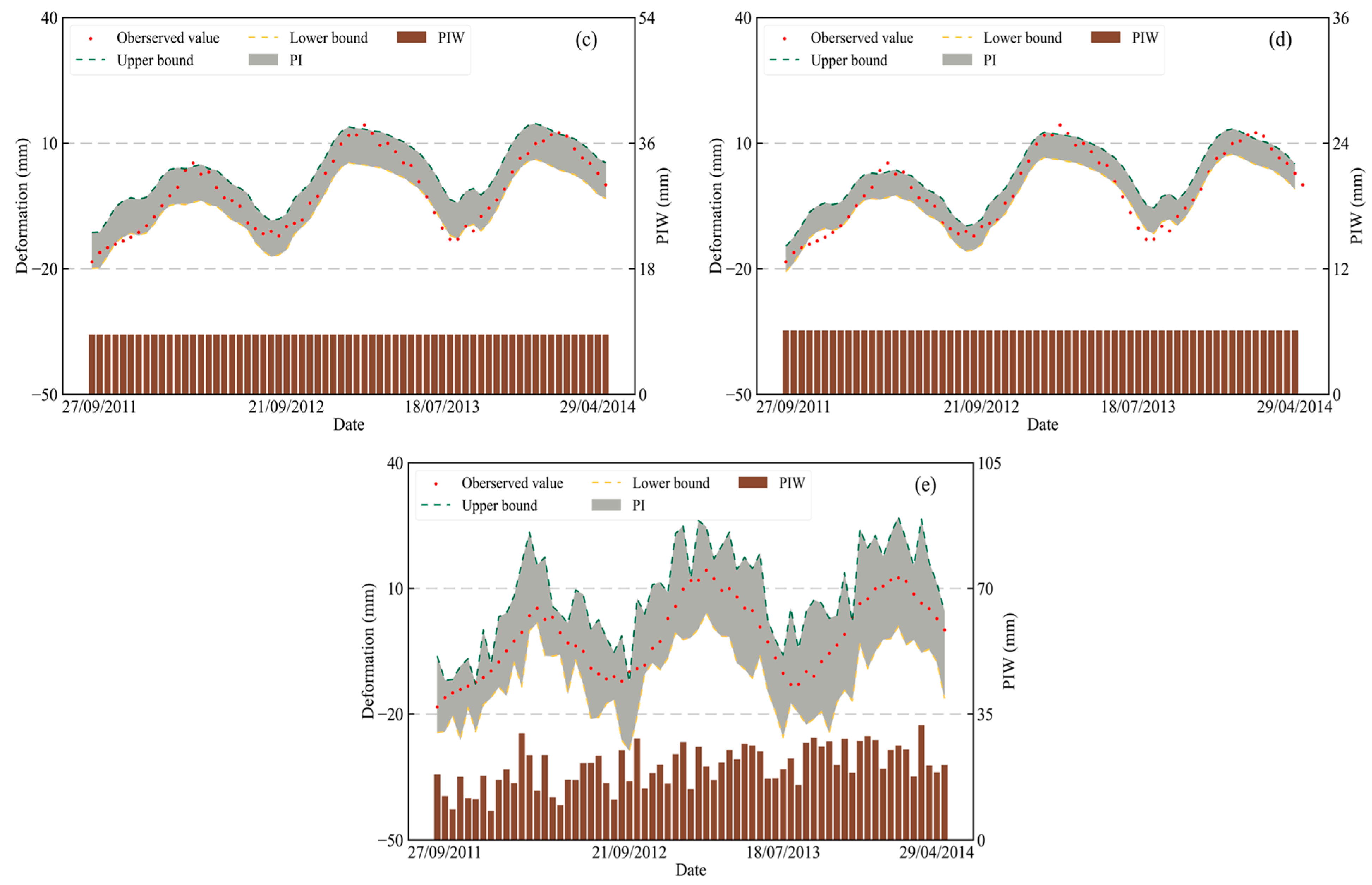
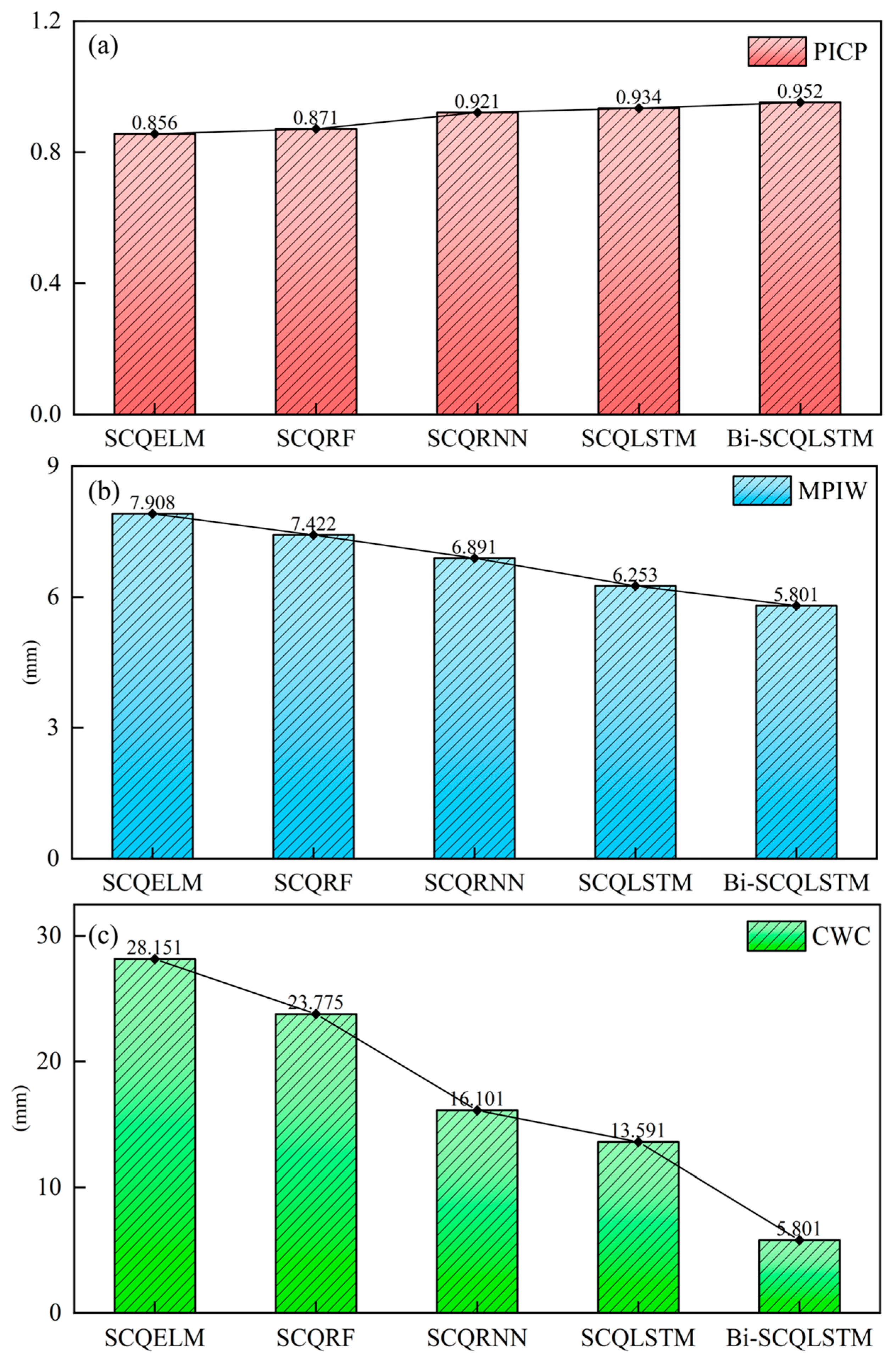
3.3.1. Interval Prediction Performance of SCQP
3.3.2. Comparison of Machine Learning (ML) and Deep Learning (DL) Models
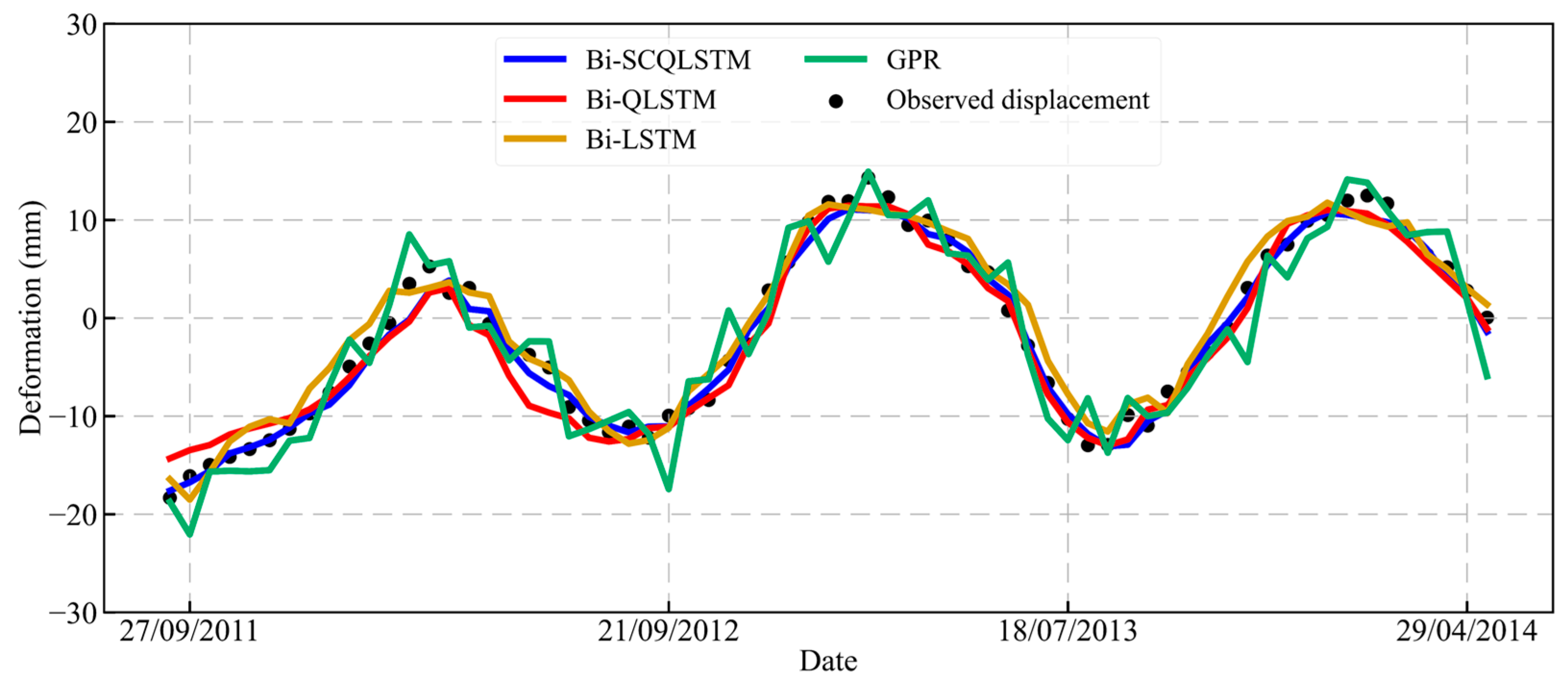
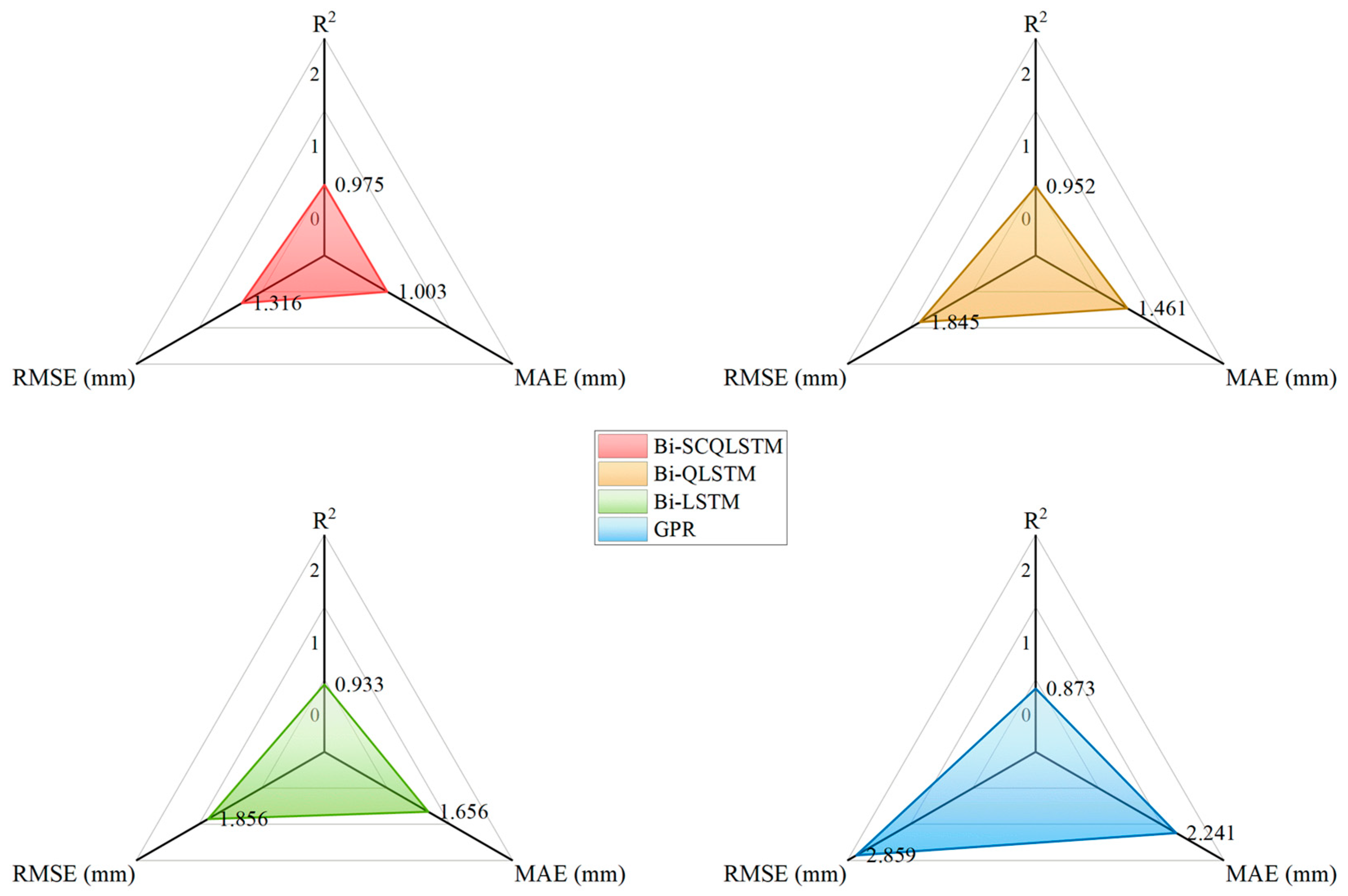
4. The Necessity of Considering the Uncertainties in Dam Deformation
5. Conclusions and Future Work
- (1)
- Dam deformation data from an arch dam are selected to test the performance of the proposed Bi-SCQLSTM. The experiment results show that, compared with the current mainstream interval prediction methods, the Bi-SCQLSTM can construct deformation PIs that meet high-quality standard.
- (2)
- Compared to ML algorithms and unidirectional DL neural networks, the Bi-LSTM also maintains a significant advantage in interval prediction with the help of hidden layer information in different time dimensions and a larger memory threshold.
- (3)
- A reasonable interval prediction paradigm can reduce the prediction error due to deformation uncertainties to some extent. As a result, point prediction results transformed from PIs have higher accuracy than standard point prediction model.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wen, Z.; Zhou, R.; Su, H. MR and stacked GRUs neural network combined model and its application for deformation prediction of concrete dam. Expert Syst. Appl. 2022, 201, 117272. [Google Scholar] [CrossRef]
- Ma, H.; Chi, F. Technical progress on researches for the safety of high concrete-faced rockfill dams. Engineering 2016, 2, 332–339. [Google Scholar] [CrossRef]
- Liu, X.; Li, Z.; Sun, L.; Khailah, E.Y.; Wang, J.; Lu, W. A critical review of statistical model of dam monitoring data. J. Build. Eng. 2023, 80, 108106. [Google Scholar] [CrossRef]
- Cao, W.; Wen, Z.; Su, H. Spatiotemporal clustering analysis and zonal prediction model for deformation behavior of super-high arch dams. Expert Syst. Appl. 2023, 216, 119439. [Google Scholar] [CrossRef]
- Cheng, L.; Zheng, D. Two online dam safety monitoring models based on the process of extracting environmental effect. Adv. Eng. Softw. 2013, 57, 48–56. [Google Scholar] [CrossRef]
- Ren, Q.; Li, M.; Song, L.; Liu, H. An optimized combination prediction model for concrete dam deformation considering quantitative evaluation and hysteresis correction. Adv. Eng. Inform. 2020, 46, 101154. [Google Scholar] [CrossRef]
- Xu, C.; Yue, D.; Deng, C. Hybrid GA/SIMPLS as alternative regression model in dam deformation analysis. Eng. Appl. Artif. Intell. 2012, 25, 468–475. [Google Scholar] [CrossRef]
- Li, B.; Yang, J.; Hu, D. Dam monitoring data analysis methods: A literature review. Struct. Control Health Monit. 2020, 27, e2501. [Google Scholar] [CrossRef]
- Su, H.; Wen, Z.; Wang, F.; Wei, B.; Hu, J. Multifractal scaling behavior analysis for existing dams. Expert Syst. Appl. 2013, 40, 4922–4933. [Google Scholar] [CrossRef]
- Sun, L.; Ji, Y.; Zhu, X.; Peng, T. Process knowledge-based random forest regression for model predictive control on a nonlinear production process with multiple working conditions. Adv. Eng. Inform. 2022, 52, 101561. [Google Scholar] [CrossRef]
- Desai, M.; Shah, M. An anatomization on breast cancer detection and diagnosis employing multi-layer perceptron neural network (MLP) and Convolutional neural network (CNN). Clin. eHealth 2021, 4, 1–11. [Google Scholar] [CrossRef]
- Huang, G.B.; Zhu, Q.Y.; Siew, C.K. Extreme learning machine: Theory and applications. Neurocomputing 2006, 70, 489–501. [Google Scholar] [CrossRef]
- Qu, X.; Yang, J.; Chang, M. A deep learning model for concrete dam deformation prediction based on RS-LSTM. J. Sens. 2019, 2019, 4581672. [Google Scholar] [CrossRef]
- Dai, B.; Gu, C.; Zhao, E.; Qin, X. Statistical model optimized random forest regression model for concrete dam deformation monitoring. Struct. Control Health Monit. 2018, 25, e2170. [Google Scholar] [CrossRef]
- Kang, F.; Liu, J.; Li, J.; Li, S. Concrete dam deformation prediction model for health monitoring based on extreme learning machine. Struct. Control Health Monit. 2017, 24, e1997. [Google Scholar] [CrossRef]
- Ren, Q.; Li, M.; Li, H.; Shen, Y. A novel deep learning prediction model for concrete dam displacements using interpretable mixed attention mechanism. Adv. Eng. Inform. 2021, 50, 101407. [Google Scholar] [CrossRef]
- Song, J.; Liu, Y.; Yang, J. Dam Safety Evaluation Method after Extreme Load Condition Based on Health Monitoring and Deep Learning. Sensors 2023, 23, 4480. [Google Scholar] [CrossRef] [PubMed]
- Kang, H.; Yang, S.; Huang, J.; Oh, J. Time series prediction of wastewater flow rate by bidirectional LSTM deep learning. Int. J. Control Autom. Syst. 2020, 18, 3023–3030. [Google Scholar] [CrossRef]
- Huang, X.; Li, Q.; Tai, Y.; Chen, Z.; Liu, J.; Shi, J.; Liu, W. Time series forecasting for hourly photovoltaic power using conditional generative adversarial network and Bi-LSTM. Energy 2022, 246, 123403. [Google Scholar] [CrossRef]
- Ren, Q.; Li, M.; Kong, R.; Shen, Y.; Du, S. A hybrid approach for interval prediction of concrete dam displacements under uncertain conditions. Eng. Comput. 2021, 39, 1285–1303. [Google Scholar] [CrossRef]
- Ren, Q.; Li, M.; Shen, Y. A new interval prediction method for displacement behavior of concrete dams based on gradient boosted quantile regression. Struct. Control Health Monit. 2022, 29, e2859. [Google Scholar] [CrossRef]
- Li, Y.; Bao, T.; Shu, X.; Chen, Z.; Gao, Z.; Zhang, K. A hybrid model integrating principal component analysis, fuzzy C-means, and Gaussian process regression for dam deformation prediction. Arab. J. Sci. Eng. 2021, 46, 4293–4306. [Google Scholar] [CrossRef]
- Hosmer, D.W.; Lemeshow, S. Confidence interval estimation of interaction. Epidemiology 1992, 3, 452–456. [Google Scholar] [CrossRef]
- Yang, X.; Xiang, Y.; Shen, G.; Sun, M. A Combination Model for Displacement Interval Prediction of Concrete Dams Based on Residual Estimation. Sustainability 2022, 14, 16025. [Google Scholar] [CrossRef]
- Jiang, J.; Zhang, W. Distribution-free prediction intervals in mixed linear models. Stat. Sin. 2002, 12, 537–553. [Google Scholar]
- Khosravi, A.; Nahavandi, S.; Creighton, D.; Atiya, A.F. Lower upper bound estimation method for construction of neural network-based prediction intervals. IEEE Trans. Neural Netw. 2010, 22, 337–346. [Google Scholar] [CrossRef]
- Jensen, V.; Bianchi, F.M.; Anfinsen, S.N. Ensemble conformalized quantile regression for probabilistic time series forecasting. IEEE Trans. Neural Netw. Learn. Syst. 2022, 35, 9014–9025. [Google Scholar] [CrossRef]
- Hu, J.; Luo, Q.; Tang, J.; Heng, J.; Deng, Y. Conformalized temporal convolutional quantile regression networks for wind power interval forecasting. Energy 2022, 248, 123497. [Google Scholar] [CrossRef]
- Yu, Y.; Si, X.; Hu, C.; Zhang, J. A review of recurrent neural networks: LSTM cells and network architectures. Neural Comput. 2019, 31, 1235–1270. [Google Scholar] [CrossRef] [PubMed]
- Ghimire, S.; Deo, R.C.; Casillas-Pérez, D.; Salcedo-Sanz, S.; Sharma, E.; Ali, M. Deep learning CNN-LSTM-MLP hybrid fusion model for feature optimizations and daily solar radiation prediction. Measurement 2022, 202, 111759. [Google Scholar] [CrossRef]
- Sherstinsky, A. Fundamentals of recurrent neural network (RNN) and long short-term memory (LSTM) network. Phys. D Nonlinear Phenom. 2020, 404, 132306. [Google Scholar] [CrossRef]
- Zhang, J.; Guo, X.; Zong, S.; Xu, H. Multiparameter estimation and LSTM-based prediction method for health state of single-layer reticulated shells. J. Build. Eng. 2023, 76, 107128. [Google Scholar] [CrossRef]
- Yan, X.; Guan, T.; Fan, K.; Sun, Q. Novel double layer BiLSTM minor soft fault detection for sensors in air-conditioning system with KPCA reducing dimensions. J. Build. Eng. 2021, 44, 102950. [Google Scholar] [CrossRef]
- Romano, Y.; Patterson, E.; Candes, E. Conformalized quantile regression. Adv. Neural Inf. Process. Syst. 2019, 32, 3543–3553. [Google Scholar]
- Lei, J.; G’sell, M.; Rinaldo, A.; Tibshirani, R.J.; Wasserman, L. Distribution-free predictive inference for regression. J. Am. Stat. Assoc. 2018, 113, 1094–1111. [Google Scholar] [CrossRef]
- Lin, Z.; Trivedi, S.; Sun, J. Conformal prediction with temporal quantile adjustments. Adv. Neural Inf. Process. Syst. 2022, 35, 31017–31030. [Google Scholar]
- Zhang, J.; Cao, X.; Xie, J.; Kou, P. An Improved Long Short-Term Memory Model for Dam Displacement Prediction. Math. Probl. Eng. 2019, 2019, 6792189. [Google Scholar] [CrossRef]
- Kang, F.; Li, J. Displacement model for concrete dam safety monitoring via gaussian process regression considering extreme air temperature. J. Struct. Eng. 2020, 146, 05019001. [Google Scholar] [CrossRef]



| Deformation Interval Prediction Models | L5H291R | ||
|---|---|---|---|
| PICP | MPIW (mm) | CWC (mm) | |
| Bi-SCQLSTM | 0.951 | 5.815 | 5.815 |
| Bi-QLSTM | 0.957 | 7.853 | 7.853 |
| Bi-SCLSTM | 0.821 | 8.577 | 39.735 |
| CIE | 0.713 | 39.735 | 100.329 |
| GPR | 0.986 | 18.429 | 18.429 |
| Deformation Interval Prediction Models | Computation Time (s) |
|---|---|
| Bi-SCQLSTM | 32.261 |
| Bi-QLSTM | 32.094 |
| Bi-SCLSTM | 28.513 |
| CIE | 28.024 |
| GPR | 20.932 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, Y.; Fu, J.; Lin, W.; Lin, C.; Lai, X.; Xie, X. Dam Deformation Monitoring Model Based on Deep Learning and Split Conformal Quantile Prediction. Appl. Sci. 2025, 15, 1960. https://doi.org/10.3390/app15041960
Su Y, Fu J, Lin W, Lin C, Lai X, Xie X. Dam Deformation Monitoring Model Based on Deep Learning and Split Conformal Quantile Prediction. Applied Sciences. 2025; 15(4):1960. https://doi.org/10.3390/app15041960
Chicago/Turabian StyleSu, Yan, Jiayuan Fu, Weiwei Lin, Chuan Lin, Xiaohe Lai, and Xiudong Xie. 2025. "Dam Deformation Monitoring Model Based on Deep Learning and Split Conformal Quantile Prediction" Applied Sciences 15, no. 4: 1960. https://doi.org/10.3390/app15041960
APA StyleSu, Y., Fu, J., Lin, W., Lin, C., Lai, X., & Xie, X. (2025). Dam Deformation Monitoring Model Based on Deep Learning and Split Conformal Quantile Prediction. Applied Sciences, 15(4), 1960. https://doi.org/10.3390/app15041960





