Research on a Wind-Energy-Harvesting Device Based on a Non-Contact Electret–Piezoelectric Coupling Structure

Abstract

Persistently and reliably harvesting wind energy to power intelligent online monitoring devices for transmission lines promotes the intelligent and sustainable development of the Internet of Things. Current small-scale wind-energy-harvesting devices, relying on a single energy conversion principle, face challenges such as low efficiency and poor performance at low wind speeds. This paper presents a coaxial rotating non-contact coupling transducer structure, and its optimization methods have been studied, which are based on electret electrostatic induction and magnetically actuated piezoelectric conversion. By analyzing the principles of alternating positive–negative unipolar electret components and constructing a finite element model, improved output capacity is demonstrated. The electric signals from electret components are more suitable for inferring the shaft and wind speeds compared to piezoelectric components. The piezoelectric components utilize frequency up-conversion theory to enhance output while addressing the low power density of the electrostatic components. Experimental results indicate that the proposed structure operates reliably at rotational speeds of 100–700 rpm, achieving a maximum output power of 6.742 mW. The output power of the electret electrostatic component’s electrodes nearly doubled, with the signal positively correlated to rotation speed. The optimized structure of the magnetically actuated piezoelectric component achieved a power increase of 11.51% at four excitations and 250 rpm. This study provides a new design approach for more durable and efficient small-scale wind-energy-harvesting devices, as well as for achieving integrated measurement and supply.

1. Introduction

Environmental energy-harvesting devices are one of the key technologies for achieving intelligent and sustainable development in the Internet of Things (IoTs) [1,2,3]. For intelligent online monitoring devices installed along transmission lines and on poles, traditional battery storage structures will eventually deplete energy and cannot meet the long-term stable power supply needs. Continuously harvesting the abundant environmental energy around monitoring equipment and converting it into electrical energy through transduction structures to form a self-powered system is advantageous for reducing the maintenance and replacement pressures of power sources [4,5,6,7].

Wind energy is a relatively abundant form of environmental energy and aligns with the principles of environmental protection. Currently, wind energy conversion technologies are mainly applied in large wind turbines, while research and application of small wind turbines for powering monitoring equipment focus on addressing issues such as low conversion efficiency, high device losses, and poor performance in low wind speed ranges [8,9,10].

Small wind turbines convert wind energy into mechanical energy through the rotation of blades induced by wind, thus converting wind energy into mechanical and then electrical energy. This process primarily includes electromagnetic (EMEH), triboelectric (TEH), piezoelectric (PEH), and electrostatic (EEH) energy harvester types [11,12,13]. Electromagnetic systems have high-excitation-frequency requirements and face challenges in miniaturization of multi-turn coil structures, making them suitable mainly for large wind turbine systems or high-speed applications in strong winds. Triboelectric converters are almost always subject to wear due to contact methods, and their impediment to the blade shaft results in higher-starting-wind-speed requirements. In contrast, piezoelectric and electrostatic systems are more conducive to miniaturization and non-contact designs. The piezoelectric structure, compared to electrostatic and triboelectric structures, is small in size and weight while being able to output considerable power and mitigate the vibration [12,13]. However, they can only output significantly higher energy near their resonant frequency, limiting their effectiveness in a broader frequency range. Expanding the operating range, utilizing non-resonant methods, and optimizing low wind speed performance are important research directions for piezoelectric converters under random excitation in natural environments. Electrostatic systems, based on the principle of electrostatic induction, offer reliable isolation and low component wear, showing significant application potential. However, low energy conversion rates and instability of the electrostatic field source remain the primary issues to be addressed.

Electret materials, capable of retaining polarized charges for extended periods, can maintain surface electric potentials ranging from several hundred volts and can be easily formed into various thin film shapes [14,15,16,17]. They are promising electrostatic field sources for wind energy conversion. Reference [18] designed a rotating electrostatic generator structure based on the advantages of electret materials, enhancing output capacity through multiple stacked electrostatic conversion components. Reference [19] further analyzed factors affecting the structure, such as duty cycle and number of electrodes, optimizing the performance of the generator. Nevertheless, the output power density and energy conversion efficiency of electrostatic converters remain relatively low.

Each type of wind energy converter has distinct characteristics with respective advantages and disadvantages. Designing coupled structures to integrate and complement different types of converters is an efficient and feasible approach. Reference [20] studied a hybrid electromagnetic–triboelectric wind energy conversion device, enhancing output power density through more complete contact while rectifying the triboelectric output to reduce overall rectification losses. Reference [21] focused on developing a wind energy hybrid converter tailored to the specific needs of an acetylene sensor, indicating that coupled structures can also be designed from a monitoring perspective.

In summary, this paper addresses the demand for durable and stable power supply devices in online monitoring systems for electrical power systems and also the issues faced by current small wind-energy-harvesting devices, such as low conversion efficiency, significant device wear, and poor performance at low wind speeds. To this end, this research designs a wind-energy-harvesting device based on a non-contact electret–piezoelectric coupled transduction structure. By employing vertically oriented curved blades to reduce drag and increase stability, the non-contact coupling structure diminishes wear on the device and extends system lifespan. The alternating arrangement of positive and negative polarities in the electret components enhances the output capacity of stacked electrodes, aligning the output magnitude with that of the piezoelectric components. The magnetically actuated variable cross-section piezoelectric cantilever array can continuously deliver substantial electrical energy across a lower and broader rotational speed range. Ultimately, the piezoelectric converter compensates for the low output power density of the electrostatic converter, while the electrostatic component’s output signal is less influenced by complex harmonic vibrations which the piezoelectric component suffers, facilitating signal inversion to deduce rotational and wind speeds, thus forming an integrated measurement and supply system that achieves synergy and complementarity.

2. Device Design

2.1. Device Model and Topology

The non-contact electret–piezoelectric coupling structure is shown in Figure 1.

In this structure, the rotor consists of curved wind blades, an electret layer, and a support layer, all of which are connected to the rotating shaft. The stator is composed of a piezoelectric layer, a copper electrode layer, and outer shell. The mechanical structure is described sequentially from top to bottom. The wind blades adopt a curved vertical-axis design, which generates relatively smaller lift and drag forces under the same wind speed, allowing for a lower starting wind speed. Additionally, vertical-axis wind blades exhibit low sensitivity to wind direction and greater structural stability. The piezoelectric layer consists of four identical optimized double-layer piezoelectric cantilever beams arranged at equal intervals. Their fixed ends are attached to the outer shell, while the active ends have magnets attached at the bottom to generate magnetically actuated vibrations. The electret support layer comprises 16 evenly spaced sector-shaped insulating supports with a sector angle of 18°. During rotation, four magnets attached to the supports at equal intervals periodically attract the piezoelectric layer, inducing vibrations and enabling output. The electret layer, composed of flexible electret films arranged in alternating positive and negative polarities, is tightly affixed to the electret support layer, which has the same surface area. The copper electrode layer shares a structure identical to that of the electret support layer. Adjacent pairs of copper plates form an electrode pair, resulting in eight parallel pairs totally. The outer shell layer serves to fix the copper electrode and piezoelectric layers while providing isolation and protection.

The outputs from the piezoelectric and electrostatic components are stored in energy storage elements via an energy management circuit and subsequently processed for external output. The topology structure of the system is illustrated in Figure 2.

The output from both the piezoelectric and electrostatic components needs to undergo rectification, voltage reduction, and voltage stabilization before charging the energy storage capacitor. Both the piezoelectric and electrostatic low loss energy management circuit is based on the LTC3588-1, which enhance charging efficiency and reduce input voltage by charging a small capacitor and then deeply discharging it to a larger capacitor, ultimately outputting at the same voltage level. The electrostatic energy management circuit is designed to accommodate its high open-circuit voltage characteristics, thus employing external rectifier bridge with better voltage-resistant components. Diodes are employed to mitigate the impact of current backflow between power sources and reduce loop losses. The enable pin detects when the energy storage capacitor reaches the threshold voltage before providing output. Notably, the super capacitor’s capacity is matched to the power level of the energy-harvesting components, supplying power to the demand device after DC/DC voltage regulation based on SX1308.

2.2. Coupling Rotation and Transmission Mode

The motion mode and structural schematic of the coupled structure rotor are shown in Figure 3.

The blades are driven by a rotating shaft, causing the electret and the electret support layer to rotate. Due to resistance, the rotation speed of the blades is not equal to the wind speed, but there is a theoretically corresponding relationship in Equation (1):

$$\lambda ={\displaystyle \frac{{\omega }_{r}R}{V}}$$

(1)

where $\lambda$ is the tip speed ratio, R is the maximum rotational radius of the wind wheel or the blade tip radius, ${\omega }_r$ is the angular velocity of the wind wheel (rad/s), representing the rotational speed, and V is the wind speed. In ideal cases, once the blade and rotor structure are determined, the tip speed ratio can be established. In practice, the tip speed ratio may vary with the range of rotational speeds, and it is generally obtained through measurements to create a speed-tip speed ratio curve.

The coupling method of the piezoelectric and electrostatic transducers during rotor rotation, as well as the vibration of the magnetically actuated piezoelectric components due to stress deformation, can be described as shown in Figure 4.

In the coupled structure, the piezoelectric component is of the magnetically actuated type and is subjected to intermittent magnetic excitation. When the magnet is rotated close to the free end of the piezoelectric cantilever beam, the magnetic force F attracts the cantilever beam, causing it to bend, thereby exciting the oscillation decay process based on the natural frequency of the piezoelectric cantilever beam, which gradually decays to stop before the next excitation arrives [22,23]. Correspondingly, the electrostatic plates experience changes in induced charge $\Delta Q$ due to the movement of the field source electret, leading to an external output.

3. Theory and Modeling

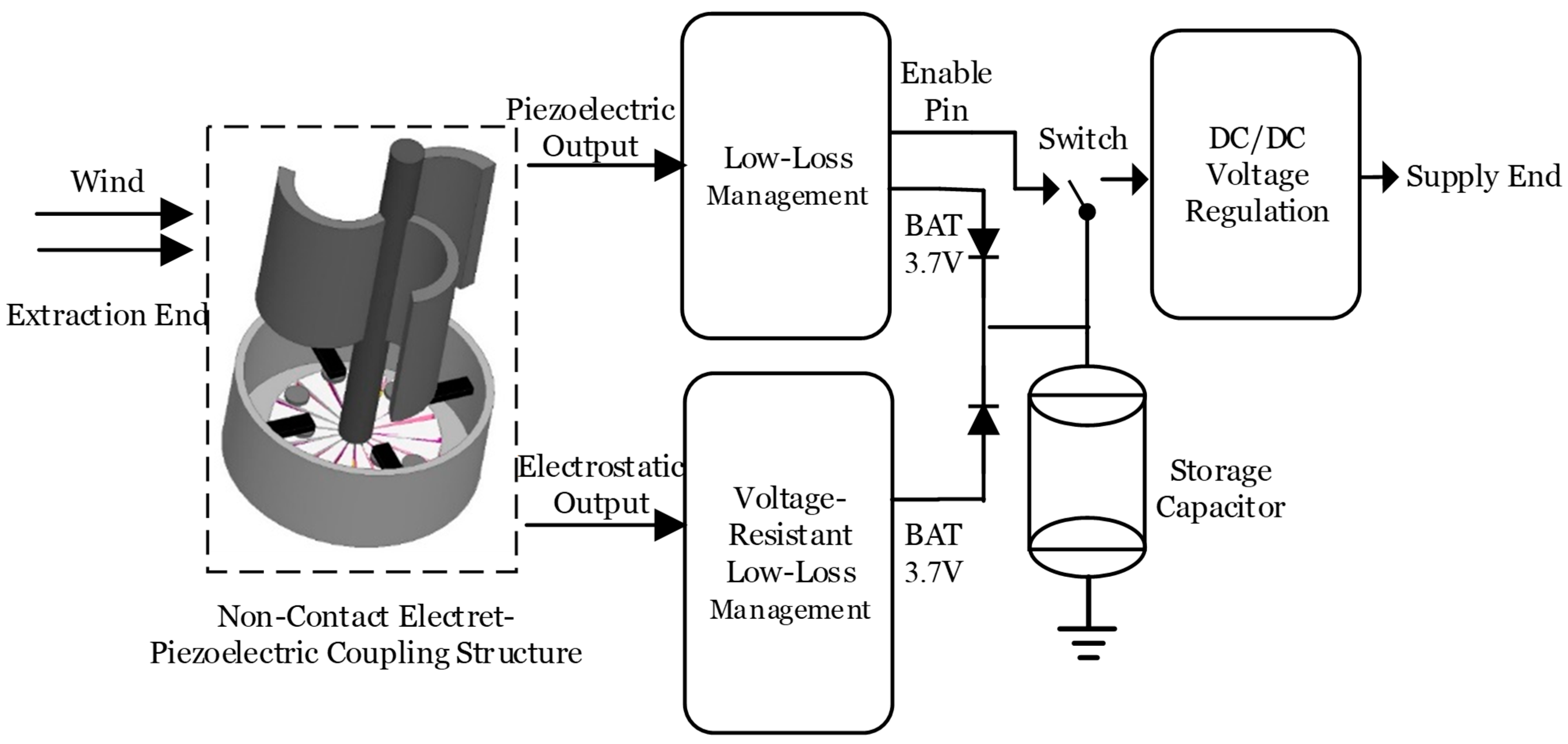
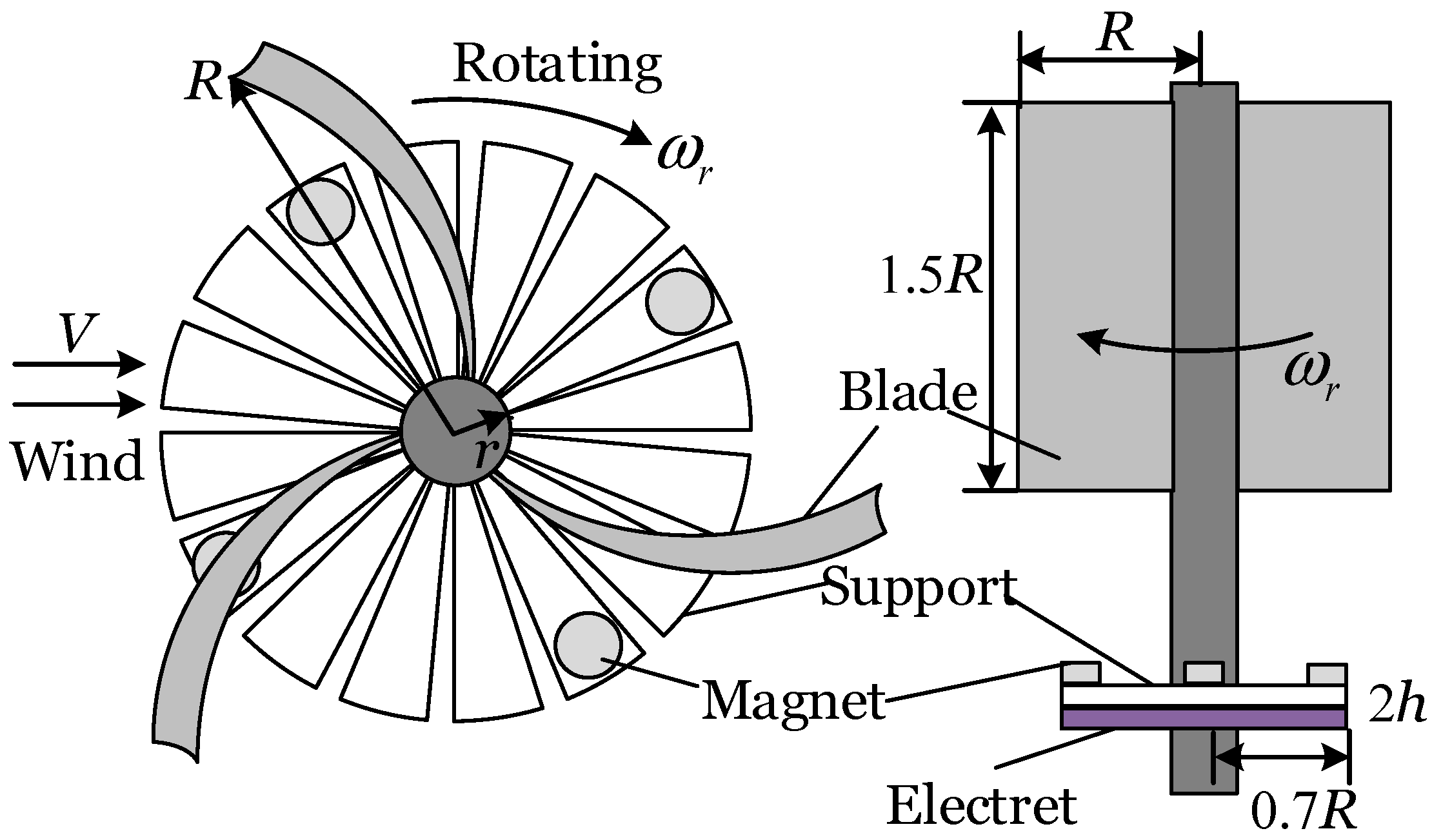
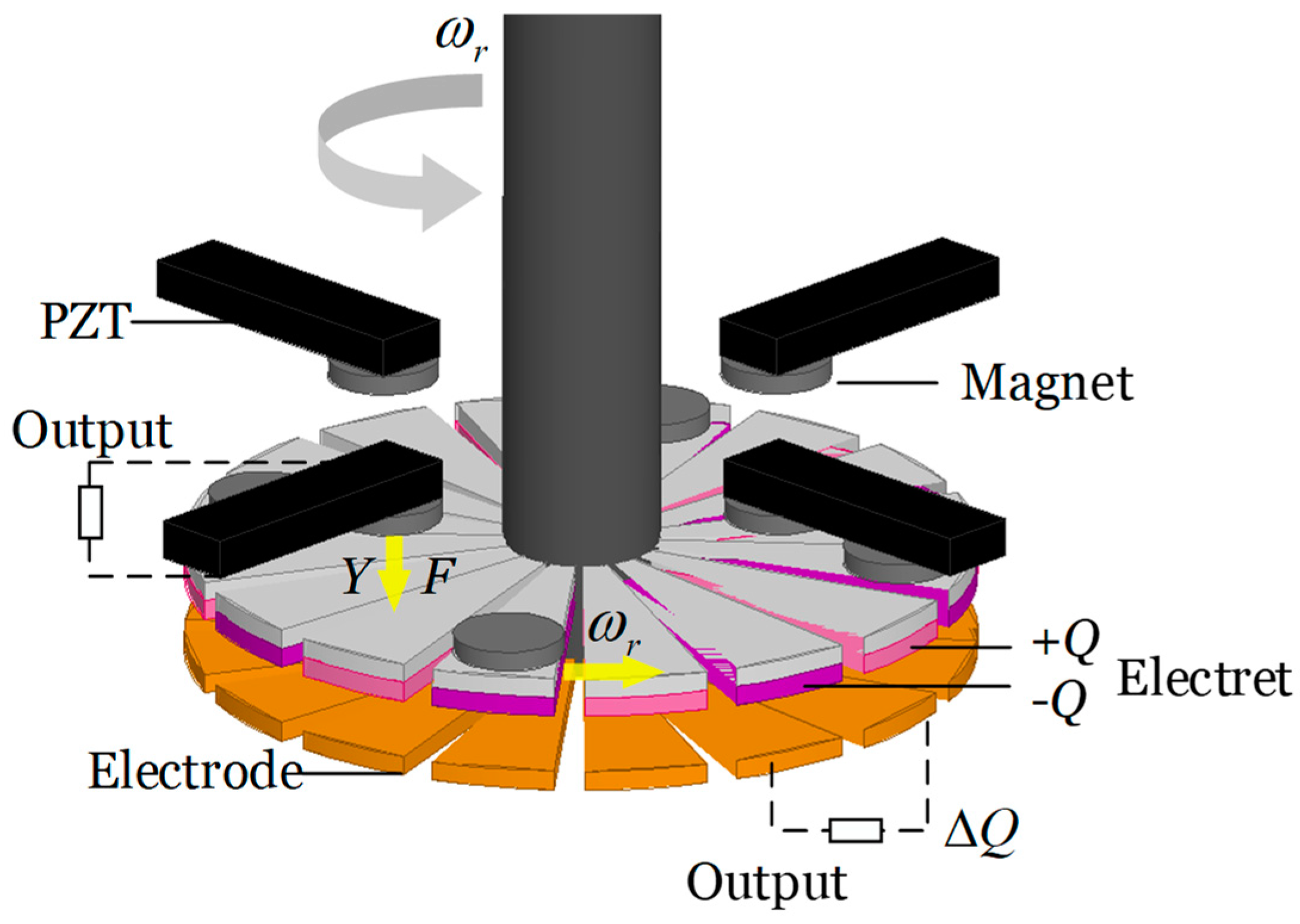
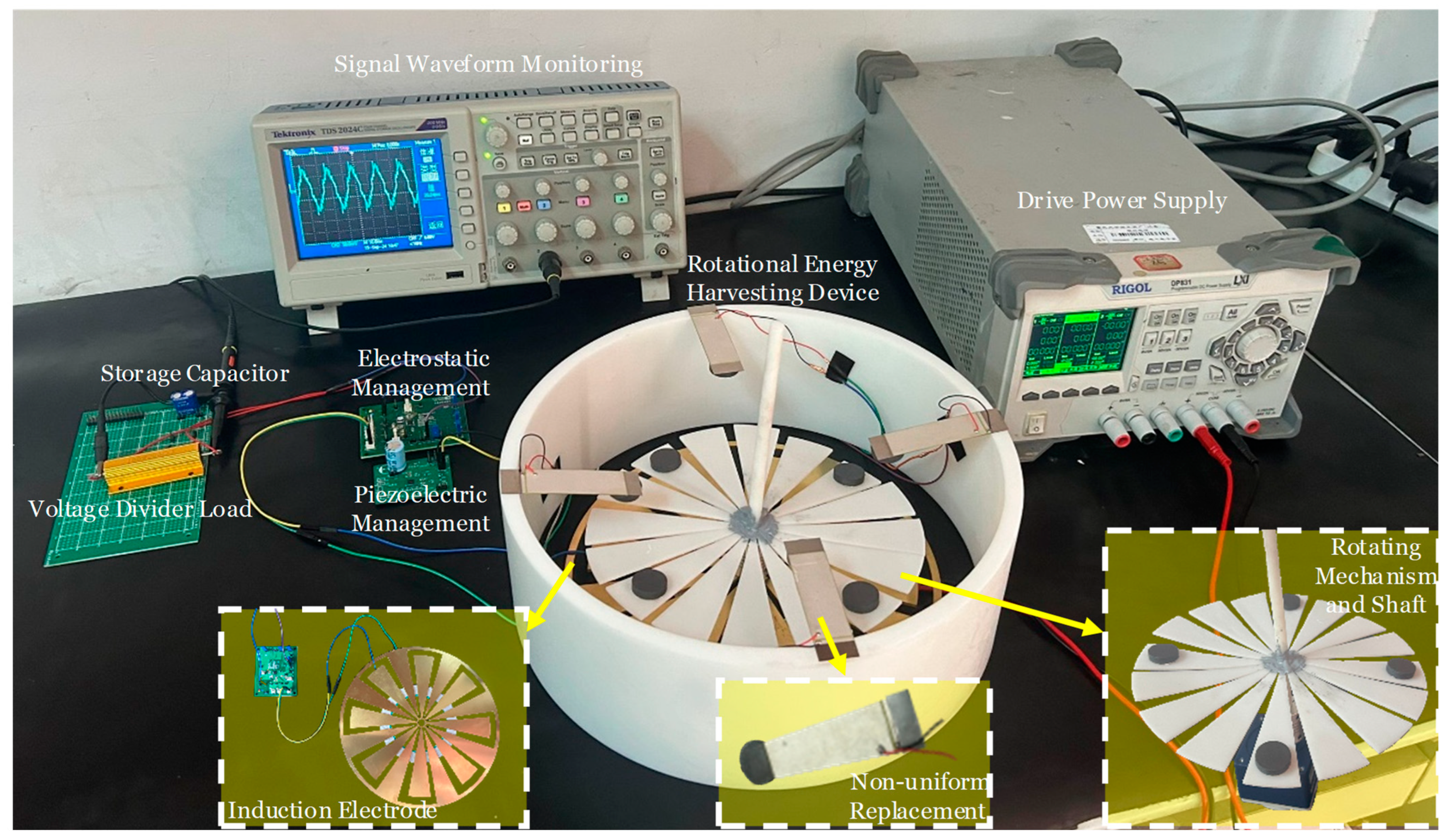
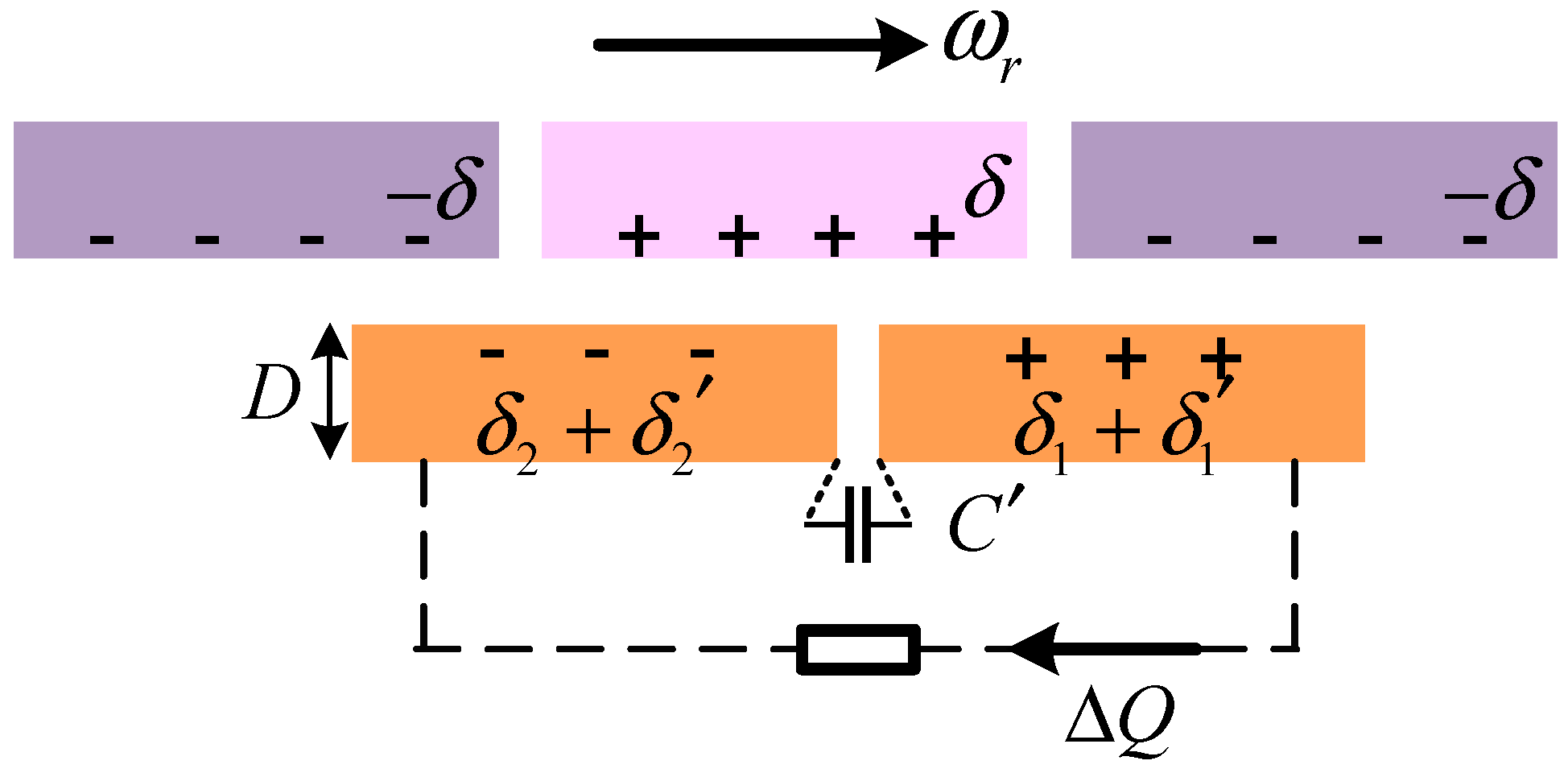3.1. Principal and Modeling of Electret Transducer Component

After polarization, the permanently polarized charges distributed on the surface of the electret serve as a source of electrostatic field, inducing surface charges on the metal plates. Relative motion causes changes in the equivalent capacitance of the electrostatic structure and the induced charge on the plates. This charge will be released into the external circuit, resulting in current output.

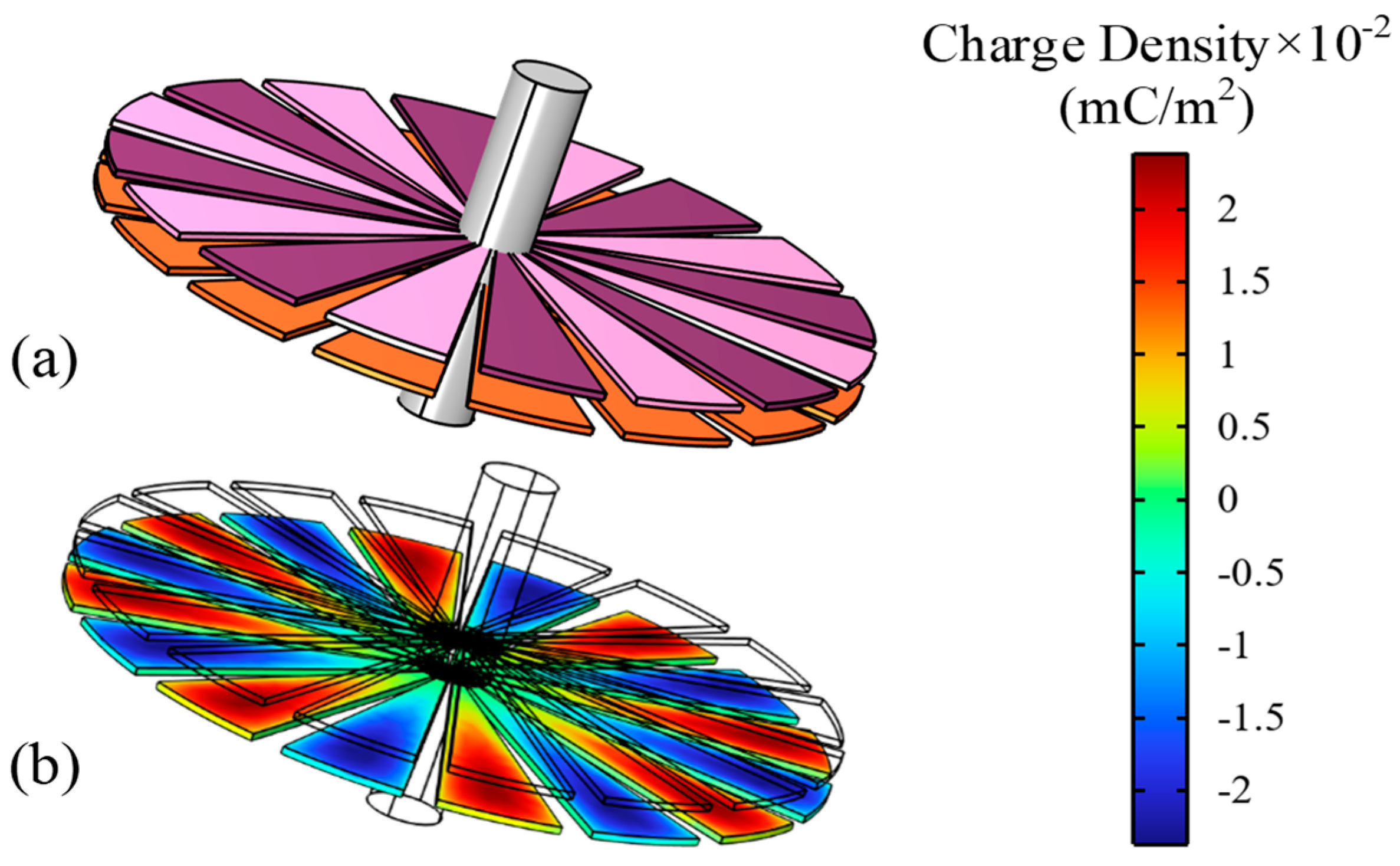
In this structure, the electret transducer component consists of 16 plates arranged in pairs, equivalent to eight pairs of electrodes in parallel, enhancing the absolute output magnitude of the component. Due to the highly symmetric structure, a single pair of plates is analyzed. The working principle of the electret electrostatic component is based on the phenomenon of electrostatic induction with the electret acting as the field source.

The ideal model can be derived from the charge induction and inter-electrode charge transfer theory of a parallel plate capacitor [12]. The theoretical model is based on the near-field assumption, which posits that under the condition where the distance between the plates is very small relative to the area of the plates, the electric field strength within the gap between the plates is uniformly distributed and perpendicular to the surface of the metal plate electrode. Furthermore, this model could only consider the interaction between the plates and the portion of the electret directly opposite them, because of the hypothesis that both the electret and the air are linear and uniform dielectrics, with a constant dielectric constant and a uniformly distributed internal electric field in the direction perpendicular to the upper and lower surfaces. Let the surface potential and charge of the upper side of the unipolar electret film be 0, while the lower side carries uniform unipolar surface charge. The electric field on both sides of the electret surface is discontinuous. Furthermore, the electret achieves fixed charges through high-voltage polarization; thus, its polarization effect could be neglected in the conditions of this model. Then, the induced charge on the upper surface of the metal plates could be calculated. When a unipolar electret moves from above plate 2 to above plate 1, the principle of electrostatic induction is illustrated in Figure 5 and then obtains Equation (2).

On a unipolar electret, the surface charge and electric potential on the upper surface are zero, while the charge density $\delta$ on the lower surface is fixed. As the electret moves, varying induced charges are generated in the region directly opposite the electrode plates, forming electric fields E_r and E₁ within the electret and between the plates, as well as surface potentials V₁ and V₂. As the assumption mentioned earlier, neglecting the gap between electrodes and assuming a very small separation between the electret and the electrode plate, Equation (2) describes the electrostatic induction at the region of the electret directly opposite the plates:

$$\left\{\begin{array}{l}{\epsilon }_0{\epsilon }_r{E}_r-{\epsilon }_0\epsilon E_1=\delta \hfill \\ E_{r}h-E_1{d=V}_2\hfill \\ V_2={\displaystyle \frac{Q}{C}}={\displaystyle \frac{{\delta }_{1}S}{2C}}\hfill \\ {\displaystyle \frac{1}{C}}={\displaystyle \frac{h}{{\epsilon }_0{\epsilon }_{r}S}}+{\displaystyle \frac{d}{{\epsilon }_0\epsilon S}}\hfill \\ {\delta }_1={\epsilon }_0\epsilon E_1\hfill \end{array}\right.$$

(2)

where d represents the distance between the electret and the plates, h is the thickness of the electret, ${\epsilon }_r$ and $\epsilon$ are the dielectric constants of the electret and air, respectively, S is the area of the electret directly opposite the plates, and C represents its equivalent capacitance. The induced charge density ${\delta }_1$ on plate 1 can be concluded as Equation (3):

$${\delta }_1={\displaystyle \frac{\delta }{\frac{{\epsilon }_{r}d}{\epsilon h}+1}}$$

(3)

The electret and the electrode have a sector angle of $\pi /10$. During one cycle of rotating based the hypothesis of the model, the total induced charge Q₁ on electrode 1 varies as Equation (4):

$$\begin{array}{l}{Q}_1={\delta }_{1}S\\ \\ ={\displaystyle \frac{{\omega }_{r}t{r}^2\delta }{\frac{2{\epsilon }_{r}d}{\epsilon h}-2}}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}0\le {\omega }_{r}t<{\displaystyle \frac{\pi }{10}}\\ \\ ={\displaystyle \frac{(\pi -5{\omega }_{r}t)r^2\delta }{\frac{10{\epsilon }_{r}d}{\epsilon h}-10}} {\displaystyle \frac{\pi }{10}}\le {\omega }_{r}t<{\displaystyle \frac{\pi }{5}}\end{array}$$

(4)

where S represents the area of the sector-shaped plate directly opposite the electret, and r is the radius of the sector. When the electret moves at a speed of ${\omega }_r$, the induced charge quantity varies, initially increasing and then decreasing, repeating this cyclical variation with the arrival of the next electret. It can be considered that the induced charge Q₂ on plate 2 follows a similar pattern but is $\pi /10$ phase advance.

In this model, the movement of the electret will lead to changes in the induced charge on the plates. Since there is a pathway between the plates, the induced charge can result in changes through charge transfer in the circuit, thereby generating output current. The open-circuit voltage between the plates is determined by the charge difference between them, while the output short-circuit current is determined by the amount of charge transferred between the plates [12]. Therefore, increasing the induced charge difference between the plates and its variation amplitude can enhance the output capability of the component. By using electrets with the same surface charge but opposite polarities arranged in intervals, the amplitude of the induced charge variation on plates that are close enough can be increased within one cycle, expanding the range of charge variation beyond a single polarity. When employing a unipolar electret with alternating positive and negative charges, the structural variation is illustrated in Figure 6.

The induced charge on the electrode plate is simultaneously influenced by the electret with surface charge densities of $\delta$ and $-\delta$. Continuing to analyze the right electrode plate 1, the induced charge generated by the negatively polarized electret directly opposite the area of $S^{\prime }$ is denoted as ${\delta }_1^{\prime }$. Then, Equation (4) could be modified as following Equation (5) for the optimized model, based on the same assumptions:

$$\begin{array}{l}{Q}_1={\delta }_{1}S+{\delta }_1^{\prime }{S}^{\prime }\\ \\ ={\displaystyle \frac{{\omega }_{r}t{r}^2\delta }{\frac{2{\epsilon }_{r}d}{\epsilon h}-2}}-{\displaystyle \frac{(\pi -5{\omega }_{r}t)r^2\delta }{\frac{10{\epsilon }_{r}d}{\epsilon h}-10}}\\ {=Q}_A({\omega }_{r}t)\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}[0,{\displaystyle \frac{\pi }{10}}]\\ \\ ={\displaystyle \frac{(\pi -5{\omega }_{r}t)r^2\delta }{\frac{10{\epsilon }_{r}d}{\epsilon h}-10}}-{\displaystyle \frac{(10{\omega }_{r}t-\pi )r^2\delta }{\frac{20{\epsilon }_{r}d}{\epsilon h}-20}}\\ =Q_B({\omega }_{r}t)\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}[{\displaystyle \frac{\pi }{10}},{\displaystyle \frac{\pi }{5}}]\end{array}$$

(5)

Similarly, Q₂ leads by $\pi /10$, half a cycle. If a structure with alternating positive and negative charges is not used, the number of unipolar electrets arranged at equal intervals must be less than the number of electrodes for the induced charge on the plates to vary.

The change in charge allows for current output between the two plates, where the short-circuit current I_sc and open-circuit voltage U_oc of alternating positive–negative unipolar electret structure conform to the following Equations (6) and (7) in this model:

$$\begin{array}{l}{I}_{sc}={\displaystyle \frac{d{Q}_1}{dt}}\\ ={\displaystyle \frac{{\omega }_r{r}^2\delta }{\frac{2{\epsilon }_{r}d}{\epsilon h}-2}}-{\displaystyle \frac{(-5{\omega }_r)r^2\delta }{\frac{10{\epsilon }_{r}d}{\epsilon h}-10}}\hspace{1em}\hspace{1em}\hspace{1em}[0,{\displaystyle \frac{\pi }{10}}]\\ ={\displaystyle \frac{(-5{\omega }_r)r^2\delta }{\frac{10{\epsilon }_{r}d}{\epsilon h}-10}}-{\displaystyle \frac{10{\omega }_r{r}^2\delta }{\frac{20{\epsilon }_{r}d}{\epsilon h}-20}}\hspace{1em}\hspace{1em}[{\displaystyle \frac{\pi }{10}},{\displaystyle \frac{\pi }{5}}]\end{array}$$

(6)

$$\begin{array}{l}{U}_{oc}={\displaystyle \frac{Q_1-Q_2}{2C^{\prime }}}\\ ={\displaystyle \frac{[Q_A({\omega }_{r}t)-Q_B({\omega }_{r}t+\frac{\pi }{10})]}{\frac{{\epsilon }_0\epsilon D\ln (\frac{0.7R}{r})}{\cos (\frac{\pi }{20})}}}\hspace{1em}\hspace{1em}\hspace{1em}[0,{\displaystyle \frac{\pi }{10}}]\\ ={\displaystyle \frac{[Q_B({\omega }_{r}t)-Q_A({\omega }_{r}t-\frac{\pi }{10})]}{\frac{{\epsilon }_0\epsilon D\ln (\frac{0.7R}{r})}{\cos (\frac{\pi }{20})}}}\hspace{1em}\hspace{1em}\hspace{1em}[{\displaystyle \frac{\pi }{10}},{\displaystyle \frac{\pi }{5}}]\end{array}$$

(7)

where D represents the thickness of the electrode plate, L is the length of the electrode plate, and $C^{\prime }$ is the capacitance between the plates, which becomes a constant once the dimensions and arrangement of the plates are determined. The alternating positive–negative unipolar electret structure increases the amplitude of charge variation and the charge difference between paired plates, thereby enhancing the output performance of the electret transducer component.

As the rotational speed increases, the amplitude of the short-circuit current theoretically grows linearly, while the amplitude of the open-circuit voltage remains unchanged. A finite element simulation of a steady-state electrostatic induction distribution model is constructed to calculate the output performance of the alternating positive and negative polarity electret-optimized transducer component, based on theoretical models and assumptions. Then, use the finite element simulation software COMSOL v.6.2 for modeling. Establish the boundary conditions by applying surface charge density of 0.05 mC/m² to the lower surface of the electret, while the charge and potential on the upper surface are set to zero. The surface charge distribution on the copper electrode plates is illustrated in Figure 7.

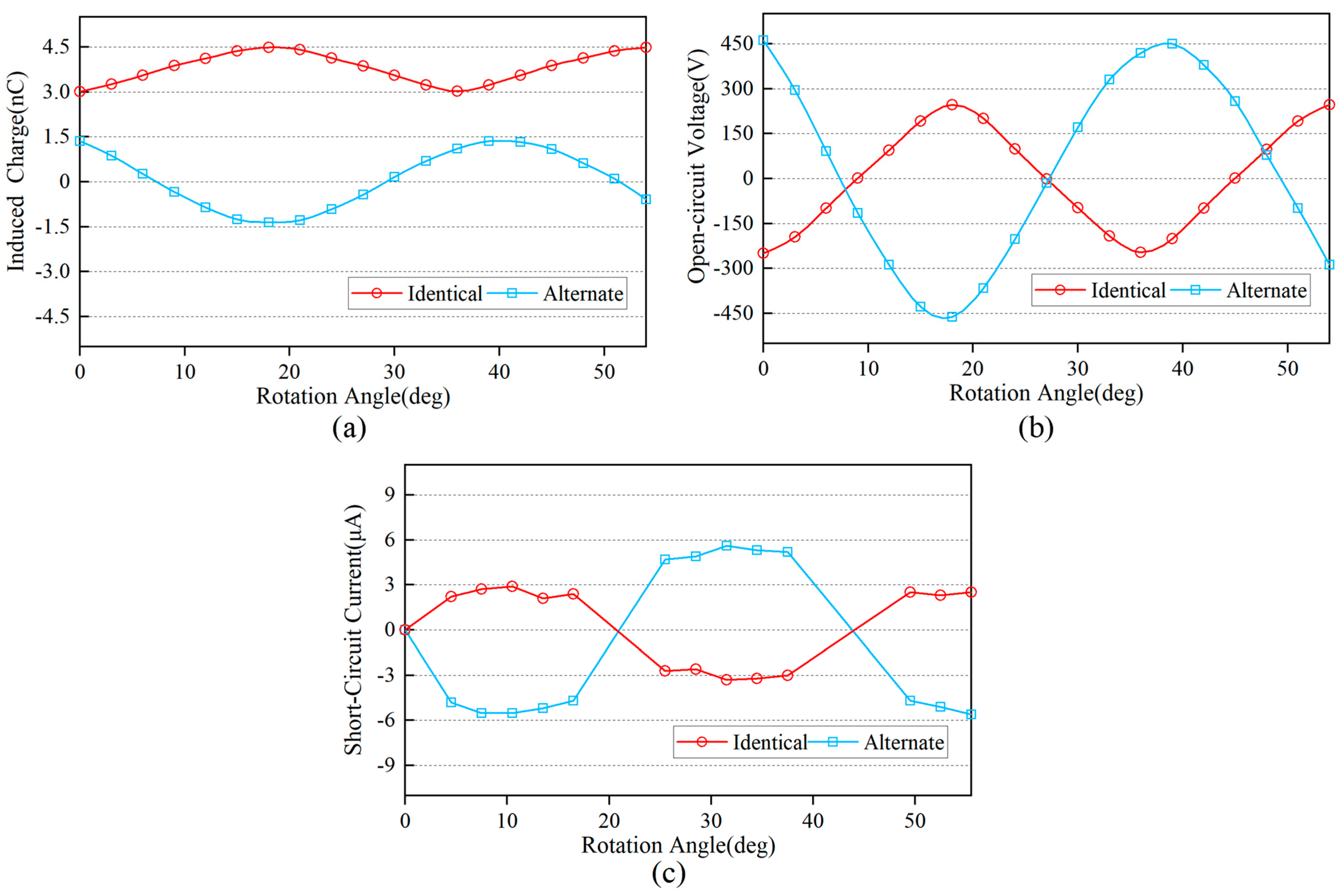
The equivalent capacitance of 2.976 pF between the paired plates is calculated via simulation. Rotating the electret layer changes the relative position between the copper electrode plates and the electret, resulting in the following variations in induced charge and open-circuit voltage for each pair of copper plates in Figure 8.

The simulation results indicate that when the distance between the electrode and the electret is sufficiently small, the induced charge on the electrode surface is dominated by the nearest electret film. Although the interleaved polarities of the electret structure lead to certain degree of reduction in the absolute charge amount on the copper electrode plates due to the partial cancelation of the opposing electric fields, this configuration can significantly enhance the variation in the induced charge on the electrode and the charge difference between paired electrode. As a result, the open-circuit voltage and short-circuit current of the component are improved. With a rotational speed set at 60 rad/s, the short-circuit current output of the component during the rotation of the electret layer is derived from Equation (6). The simulation results align closely with theoretical expectations, and electret transducer component exhibits characteristics of high open-circuit voltage, low-output current, and high dynamic equivalent resistance. And all the simulation results converge successfully, achieving the tolerance requirement of 1 × 10⁻⁶after nine iterations.

Moreover, from Equations (6) and (7), it can be inferred that with fixed size parameters and structure, both the amplitude of the current and the frequency of voltage, as well as the current variations, are brief and positively correlated with rotational speed, unaffected by complex factors. Thereby, it presents potential for inversion analysis to derive rotational speed and wind speed information from the output signals of the paired plates.

3.2. Principal and Modeling of Piezoelectric Transducer Component

The output signal of piezoelectric transducers is often difficult to apply in signal inversion monitoring due to uncertainties such as excitation frequency and damping. However, it could compensate for the limitations of electrostatic transducers, which have lower power density. The excitation frequency does not necessarily equal the vibration response frequency, and the magnetically actuated piezoelectric transducer utilizes this characteristic to achieve frequency up-conversion, which is commonly used in low-frequency situations where the excitation frequency does not easily reach the resonance frequency. As researched in [22,23], the magnetically actuated structure can be simplified to state that when the permanent magnet approaches the cantilever beam, it provides a brief magnetic excitation based on magnetic force F, causing the cantilever beam to undergo initial deformation and store maximum elastic potential energy. Once the magnet moves away, based on the principle of damped natural vibration, the excitation can be regarded as ceasing, and the cantilever beam will vibrate from the maximum amplitude, decaying exponentially at its natural frequency to stop, in the form of underdamped response, until the next magnetic excitation occurs. The motion process and output voltage have been confirmed to exhibit periodicity, while the natural frequency, which is also referred to as the first-order characteristic frequency, and the excitation frequency are the primary frequency components.

Compared to resonant systems that operate at their characteristic frequency, magnetically actuated systems operate over a much wider frequency range but with lower output. To increase the output power of the magnetically actuated piezoelectric component, in addition to the most basic way that increase the number of permanent magnets to trigger the oscillation decay process based on natural frequency more frequently, changing the structure and dimensions of the piezoelectric cantilever beam is also a method. Studies [24,25] show that replacing the rectangular cantilever beam with a variable cross-section cantilever beam structure will cause changes in the natural frequency of the piezoelectric cantilever beam, the surface area of the piezoelectric layer, and the stress or charge distribution on surface, thereby affecting the output of the piezoelectric cantilever beam. Thus, increasing the output of the magnetically actuated piezoelectric component based on the optimization method of non-uniform cross-section cantilever beams is chosen. 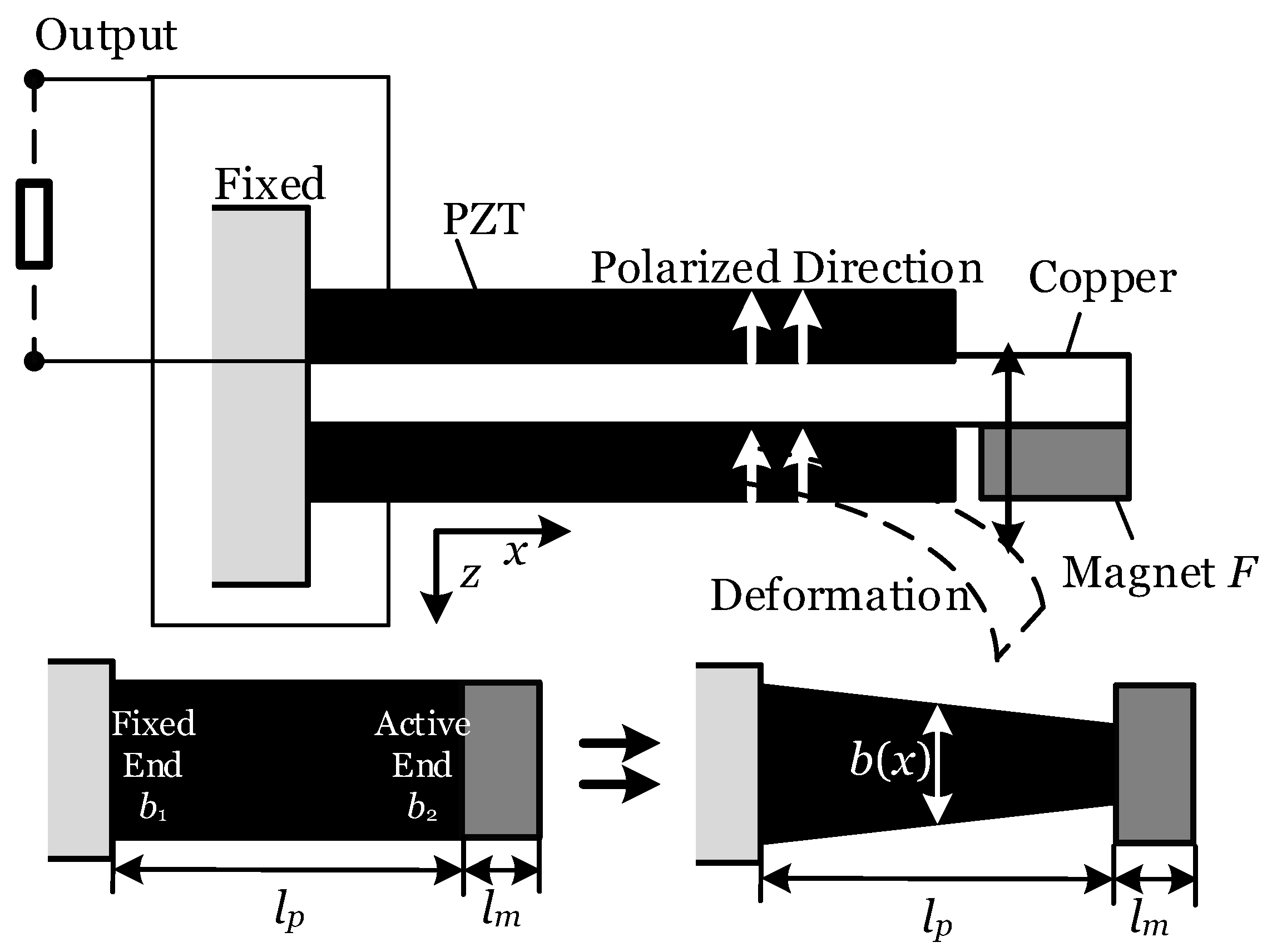The coupled structure uses four sets of piezoelectric double-layer cantilever beams in parallel, with a single component structure used for calculation and analysis shown in Figure 9.

When the polarization directions of the upper and lower piezoelectric layers are the same, the polarities are opposite during the bending deformation of the cantilever beam, and they are connected in parallel. Assuming that the piezoelectric cantilever beam model is composed of linearly elastic materials with uniform distribution, small deformations occur within the linear elastic range to avoid damaging the fragile piezoelectric layer. Under the linear elastic deformation model, stress and strain are proportional and exhibit a uniform distribution. When the rotation positions the permanent magnet directly below the active end of the piezoelectric cantilever at a certain moment, the magnetic force F between the magnets is maximized at this point, which will cause the piezoelectric cantilever to undergo the greatest linear elastic deformation. Based on the above conditions, combining with the research in [24], the strain distribution S_F(x, z) at the maximum linear elastic deformation of the length direction x can be considered as Equation (8):

$$\begin{array}{l}{S}_F={\displaystyle \frac{M(x)z}{YI(x)}}\\ ={\displaystyle \frac{F(l_p+0.5l_m-x)z}{b(x)\gamma }}\end{array}$$

(8)

where M(x) represents the bending moment, z is the coordinate in the thickness direction relative to the neutral plane, I(x) is the moment of inertia of the cross-section, Y denotes the elastic modulus, and l_p and l_m are the lengths of the piezoelectric section and the excitation section, respectively. $\gamma$ is the system modulus, which is the equivalent elastic modulus of the entire cantilever beam calculated by combining the layer thicknesses and elastic moduli of the piezoelectric layer and the copper electrode layer, and is a constant when the material and thickness are determined. b(x) is the width of the beam at position x. If the width of the fixed base is equal while the width of the movable base is relatively reduced, b(x) becomes smaller, which leads to an increase in strain at position x. Conversely, increasing the width of the fixed base results in an increase in b(x) and a decrease in strain.

The variation in b(x) not only affects the strain but also alters the area of the piezoelectric layer. The working principle of the piezoelectric cantilever beam is based on surface charge generated during deformation of the piezoelectric material. In the simplified model of piezoelectric component, the upper and lower surfaces could be regarded as capacitor plates, while the open-circuit voltage arises from the charge difference between the surfaces [12,13,24]. Deformation will alter the surface charge and also change the open-circuit voltage; the piezoelectric output of the capacitance-like simplified model can be jointly solved according to Equation (9):

$$\left\{\begin{array}{l}D(x,z)=d_{31}\tilde{Y}S(x,z)\hfill \\ C_p={\displaystyle \frac{{\epsilon }_0{\epsilon }_p{\displaystyle {\int }_0^{l_p}b(x)dx}}{z_p}}\hfill \\ Q_p={\displaystyle {\int }_0^{l_p}D(x,z)b(x)dx}\hfill \\ U_p={\displaystyle \frac{Q_p}{C_p}}\hfill \end{array}\right.$$

(9)

where D(x, z) represents the distribution of the electric displacement vector on the surface of the piezoelectric layer, d₃₁ is the piezoelectric constant of the cantilever beam structure, and $\tilde{Y}$ is the elastic modulus of the composite material, which is dependent only on the materials and layer thickness. C_p, ${\epsilon }_p$, and z_p denote the internal equivalent capacitance, dielectric constant, and thickness of the piezoelectric material, respectively. Due to the assumption of linear elastic small deformation, the strain on the upper and lower surfaces during the loading and deformation process has a negligible effect on the capacitance surface area and spacing, which could be considered constant. Q_p and U_p are the total surface charge and open-circuit voltage characterizing the output performance of the piezoelectric layer, respectively. Since the discussion is based on a linear elastic deformation model, it can be deduced from the principle of symmetry that the strains on the upper and lower surfaces of the same material section of the cantilever beam are equal in magnitude but opposite in direction, resulting in equal magnitude but opposite charges on the upper and lower surfaces of the piezoelectric layer. Organize Equations (8) and (9) to obtain the expression Equation (10) for Q_p and U_p of the model:

$$\left\{\begin{array}{l}{Q}_p={\displaystyle \frac{0.5d_{31}\tilde{Y}Fz{l}_p(l_p+l_m)}{\gamma }}\hfill \\ U_p={\displaystyle \frac{d_{31}\tilde{Y}Fz{z}_p(l_p+l_m)}{\gamma {\epsilon }_0{\epsilon }_p(b_1+b_2)}}\hfill \end{array}\right.$$

(10)

where b₁ and b₂ refer to the fixed end and the active end widths shown in Figure 9, respectively. It can be concluded that, in this model, changing either b₁ or b₂ to gain the non-uniform cross-section piezoelectric cantilever beam will alter the strain distribution and the open-circuit voltage of the component while keeping the same applied force, but it will not affect the total surface charge.

When the rotation moves the permanent magnet away from the piezoelectric cantilever beam, it can be considered that the applied force disappears, and the cantilever beam vibrates with exponentially decaying amplitude at its natural frequency ${\omega }_n$ to stop. Studies [22,23] have shown that the output voltage of the magnetically actuated structure vary with the vibrational deformation of the cantilever beam, exhibiting the same exponential oscillatory decay based on the natural frequency ${\omega }_n$, in the form of underdamped response. Therefore, the output voltage can be defined as $U_{p}X({\omega }_{n}t)$, where U_p represents amplitude, and $X({\omega }_{n}t)$ is the oscillatory function that characterizes the exponential oscillatory decay of the voltage based on the natural frequency as in Equation (11) under ideal conditions:

$$X({\omega }_{n}t)=e^{-\zeta {\omega }_{n}t}\cos ({\omega }_{n}t\sqrt{1-{\zeta }^2}+\varphi )$$

(11)

where $\varphi$ represents the initial phase, and $\zeta$ is the damping ratio. For the simplified model of linear elastic small deformation, the piezoelectric cantilever beam was expected to respond well under magnetically actuated excitation without excessive damping; this model is designed and analyzed with light damping ratio $\zeta$ of 0.045. Since it has been mentioned earlier that the internal equivalent capacitance C_p is regarded constant during the vibrational deformation process, it can be inferred that the total surface charge Q_p will also follow the same pattern as the output voltage during vibration, which can be defined as $Q_{p}X({\omega }_{n}t)$. And the output current of the piezoelectric component is derived from the change in surface charge that flows through the circuit, with no current output in the static state. During the vibration process, the output current could be represented by $d{Q}_{p}X({\omega }_{n}t)/dt$ or $C_{p}d{U}_{p}X({\omega }_{n}t)/dt$ ideally in this simplified piezoelectric model, which is as a capacitance-like structure. Therefore, increasing the natural frequency ${\omega }_n$ could increase the charge’s rate of change and then enhance the output current amplitude of the piezoelectric component within one cycle. Based on research in [24,25], a cantilever beam with a non-uniform cross-section has been approved, and it was found that increasing the width of the fixed end will enhance its bending stiffness and elevating the characteristic frequency. Conversely, reducing the width of the movable end decreases the stiffness and characteristic frequency. Thus, the method of achieving non-uniform cross-section piezoelectric cantilever beams by varying b₁ or b₂ can change the output voltage, and the output current also could be enhanced by the increase in natural frequency through this method. Based on this, the design of the piezoelectric cantilever beam’s size and structure can be optimized to improve the output voltage or output current, thereby increasing the output power of the magnetically actuated piezoelectric component.

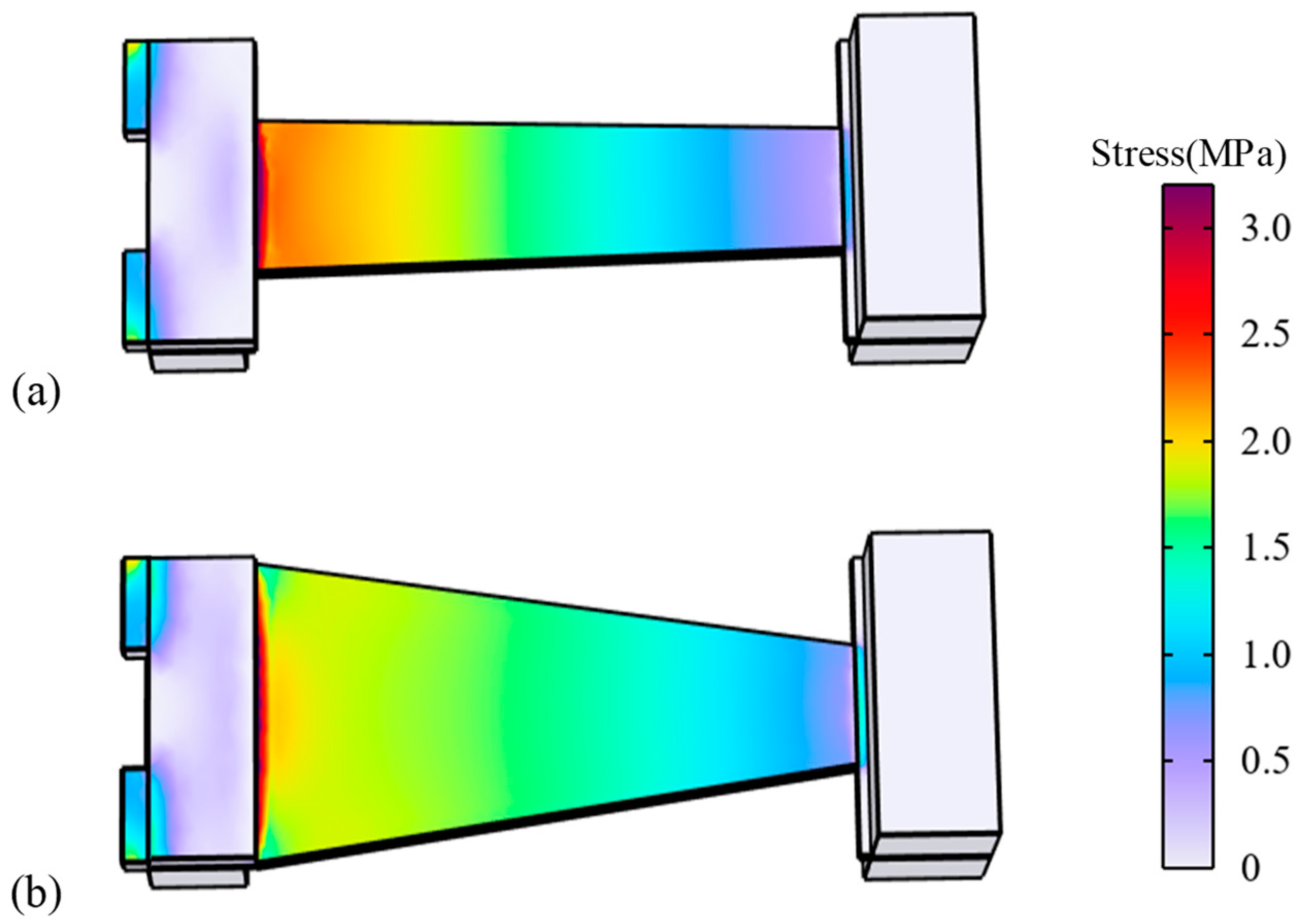
A finite element simulation of an electromechanical coupled multi-physical distributed parameter model is established to calculate the open-circuit voltage and characteristic frequency of the non-uniform cross-section model resulting from varying the widths at both ends of the cantilever beam. Using the finite element simulation software COMSOL v.6.2, set the boundary conditions with the fixed-support auxiliary base at the left end of the cantilever beam and the voltage on the inner surface of the piezoelectric sheet in parallel to be zero. The linear elastic small deformation model of the piezoelectric component and axial stress along the length direction of x in a steady state, when the tip mass at the active end on the right is subjected to the static force F of 0.4 N in the form of the volumetric load based on analysis of Equation (8), is shown in Figure 10.

From the stress distribution contour map in Figure 10, it can be observed that the extension of the fixed end reduces the level of stress under the same excitation, consistent with theoretical analysis based on Equation (8). And under the linear elastic deformation model, stress and strain are proportional, which exhibit a similar distribution pattern. The widths change $\Delta b$ of the upper and lower edges are limited to within 20 mm, with the initial condition being a rectangular cantilever beam width of 20 mm. The widths of the fixed end and the movable end are also denoted as b₁ and b₂, respectively. Let the change in size of the fixed or movable end be denoted as $\Delta b$, add or subtract $\Delta b$ from b₁, or b₂ will cause the open-circuit voltage and the natural frequency of the piezoelectric cantilever beam to change. Changing b₁ or b₂ could transform the cantilever beam from a rectangular structure to a trapezoidal structure, as shown in Figure 9, where the width of the fixed end is typically greater than that of the active end in a trapezoidal cantilever beam. This is because the fixed end experiences greater stress than the active end, and a narrower fixed end is detrimental to the structural stability. Therefore, this paper adopts the approach of b₁ + $\Delta b$ or b₂ − $\Delta b$ to form the variable cross-section trapezoidal cantilever beam model in Figure 10. Use the same piezoelectric cantilever beam simulation model in Figure 10 to calculate the open-circuit voltage under the action of the static force F and the modal analysis to calculate the natural frequency. Keep the excitation and tip mass the same, with the results shown in Figure 11.

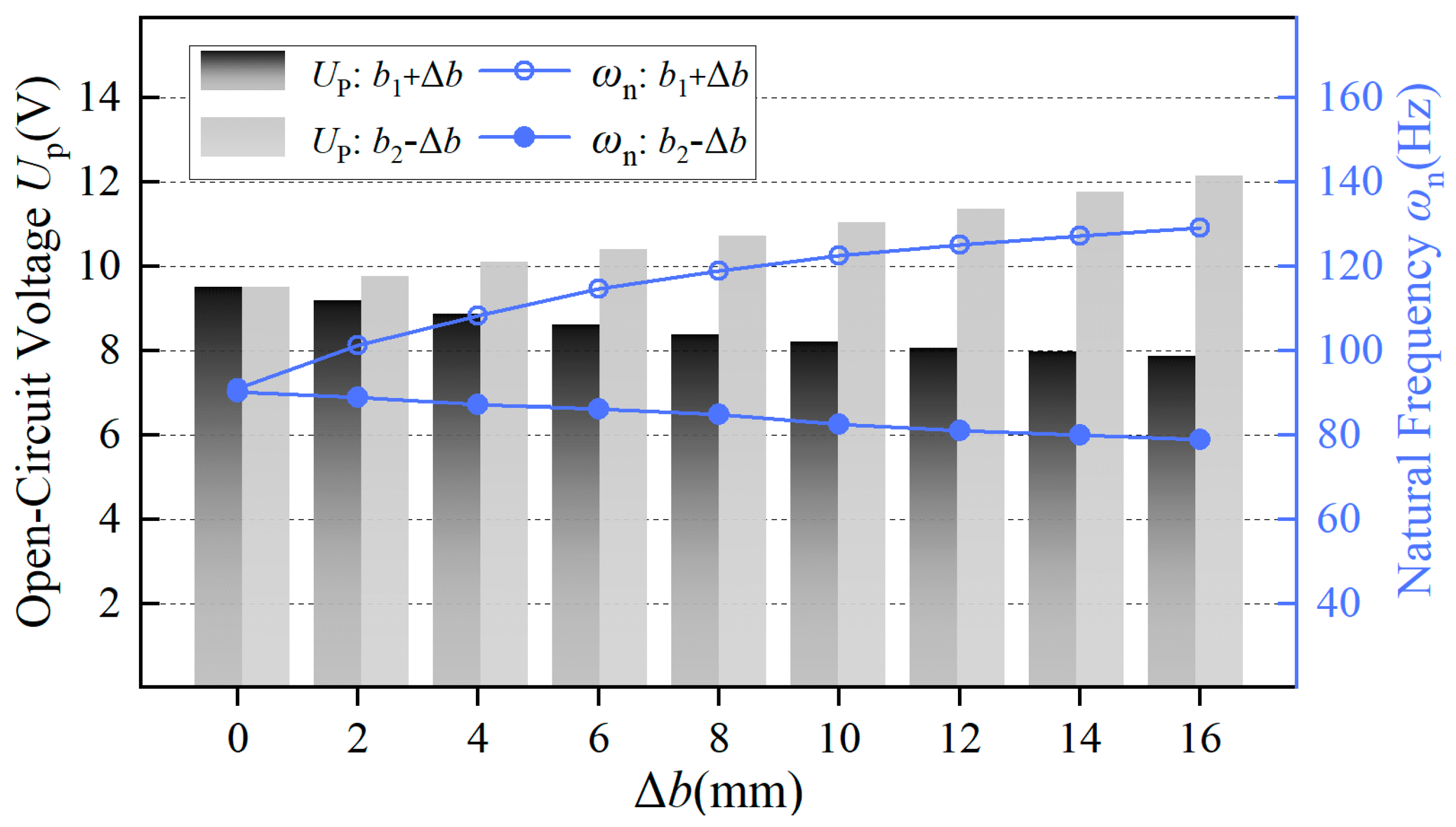
The simulation results in Figure 11 indicate that during the process of increasing the fixed end b₁, the open-circuit voltage output of the piezoelectric component gradually decreases, while the natural frequency of the piezoelectric cantilever beam structure gradually increases. Conversely, during the process of decreasing the active end b₂, the opposite characteristics are observed, which aligns with the analysis of the aforementioned theoretical model. And all the simulation results converge successfully, achieving the tolerance requirement of 1 × 10⁻⁶ after thirteen iterations.

Taking the process of increasing the fixed end in Figure 11 as an example, under the condition that the applied force F remains constant, the piezoelectric cantilever beam undergoes linear elastic small deformations. Then, according to the analysis using Equations (8)–(10), the reduction in stress and strain distribution is offset by the increase in the surface area of the piezoelectric layer, resulting in nearly unchanged total surface charge on the piezoelectric component’s surface. Meanwhile, the increased surface area of the piezoelectric layer leads to an increase in the equivalent capacitance between the upper and lower surfaces, causing a decrease in the open-circuit voltage. Consistent with the theoretical model, this does not imply that strain changes the equivalent capacitance, but rather that widening b₁ increases the equivalent capacitance. Regarding the natural frequency, the process of increasing b₁ gradually increases the structural stiffness, which in turn leads to an increase in the characteristic frequency. As mentioned earlier, increasing the natural frequency will accordingly enhance the output current. During the process of increasing the piezoelectric cantilever beam b₁, the voltage decreases, while the current correspondingly increases, allowing for the existence of suitable dimensions that can enhance the output power. It could be achieved by testing the output power through experiments; thus, the optimization of piezoelectric components is also achieved. Furthermore, the process of decreasing the active end b₂ can be explained in the same manner.

4. Experimental Validation

To validate the reliability of the theoretical research and achieve the optimized design of the device, an energy management circuit and the coupled rotating energy-harvesting structural model are created. The experimental platform is established to test the device performance at different rotational speeds. The rotary platform, based on the 5D120GU DC speed-regulating motor of Guangdong Xinxie Electric Appliance Technology Corporation (Maoming, China), achieves adjustable speeds ranging from 10 to 700 rpm, with real-time speed detection using the TM680 high-precision non-contact stroboscope tachometer of Dongguan Sanliang Precision Measuring Instruments Corporation (Dongguan, China). The energy management circuit, based on the LTC3588-1 of Linear Technology Corporation (Singapore) or high-voltage components, provides voltage step-down and regulation protection for piezoelectric or electrostatic components, along with threshold detection, to continuously output a voltage of 3.7 V to the energy storage elements. Based on the structural and dimensional design of theoretical and simulation model, the rotating energy-harvesting-testing platform is shown in Figure 12.

The experiment employed the unipolar electret with charges only on the upper sur-face. To perform the comparative experiment, the piezoelectric components can be replaced with both uniform and non-uniform cross-section cantilever beams, the electrostatic components can also be substituted with alternating polarities and only positive polarity electret. To protect the piezoelectric components, permanent magnets adhered to the white electret support utilize ferrite with an adhesion force approximately 1/8 that of strong neodymium–iron–boron magnets, rather than using the latter. The chemically inert insulated support forms a reliable and stable support for the electret, working together with the copper electrode plates to constitute the electrostatic component. And in the experimental platform, the drive power supply is used to drive a variable-speed rotating motor, replacing the original wind blades drive of the structural design. This facilitates more precise control of the rotor speed for testing the electrical output performance and optimization effects of the device. The speed range of the motor is selected based on the characteristic of the device being driven by wind power for rotation, with the testing range of 100 to 700 rpm.

Both theoretical and simulation models indicate that the frequency of change in the open-circuit voltage of the electret electrostatic component is positively correlated with the rotational speed, demonstrating the potential for inversion analysis to extract rotational speed and wind speed information from the output signals of paired electrodes. One pair of electrodes is connected to a high-resistance load for voltage division, and the output signal from the electret component is tested first and shown in Figure 13.

The experiment employed the unipolar electret with charges only on the upper surface, with arrangement of alternating-polarities electrets in this test. The output signal of the electret component, in comparison to the output of the piezoelectric component performing irregular intermittent vibrations effected by multiple interfering factor, shows a strong and brief positive correlation with rotational speed. The results suggest the potential for inverse analysis to extract information about rotational or wind speed from the output while confirming the correctness of both the theoretical and simulation models.

Subsequently, test the output power of piezoelectric components with varying bottom base widths to achieve optimization of the dimension and structural design. In alignment with the analytical methods discussed in Section 3.2, define the size parameter k as the ratio of the fixed end b₁ to the active end b₂ for different piezoelectric components. Due to the slender design of the piezoelectric cantilever beam in the theoretical model, further reducing the dimensions at the active end significantly impacts its load-bearing capacity and structural stability, making it susceptible to damage during actual operation. Therefore, the experimental model employs an approach that increases the fixed end b₁. Additionally, the effect of symmetrically distributing permanent magnets on the output is also evaluated. Optimization results of piezoelectric components at a relatively stable rotational speed of 250 rpm are illustrated in Figure 14.

The experimental results indicate that, as the fixed end b₁ increased, the magnetically actuated piezoelectric components achieved an increase in output power in the range of k from 1.2 to 1.6, with relatively maximum power output obtained around 1.4. Based on the analysis in Section 3.2, it can be concluded that increasing the fixed end b₁ enhances the structural stiffness, which in turn increases the natural frequency of the piezoelectric cantilever beam. This design effectively increases the change rate of the surface charge on the piezoelectric component, thereby enhancing the output current and improving the output power. And in Section 3.2, optimization of linear elastic piezoelectric cantilever beams has been discussed. When the fixed end of the cantilever beam is increased, the surface charge is approximately constant. Simultaneously, this adjustment increases the equivalent capacitance between the upper and lower surfaces of the piezoelectric layer. This situation results in a decrease in the output voltage of the piezoelectric component. The relationship between these factors necessitates careful consideration, as an increase in equivalent capacitance can lead to a decrease in voltage despite the improvements in current. The results in Figure 14 indicate that when the method, increasing the fixed end to enhance the natural frequency, becomes less effective after reaching a certain level of increase, the effect on the current weakens. And at this point, there is no longer a significant improvement in the power output.

Unlike the simulation analysis that focuses on effect of static force, in the dynamic process of experimental testing, increasing the number of symmetrically placed magnets can significantly reduce the trigger interval of the magnetically actuated piezoelectric cantilever beams’ oscillation decay process based on natural frequency, further improving the output power of the piezoelectric component during the rotation process. However, when the number of permanent magnets is excessive, the effect on the output power of the components tends to saturate. It could be suggested that this situation is attributed to the denser magnetic field superposition, which amplifies the magnetic force in areas where it was originally weak, affecting and hindering the vibration of the piezoelectric cantilever beam. It is more suitable to select two to eight permanent magnets and arrange them at equal intervals based on power requirement.

Thus, the device is designed by increasing the fixed-end width of the piezoelectric cantilever beam component based on k = 1.4, and four permanent magnets are used as the excitation source. When using four permanent magnets, the output power density is increased by 0.529 mW/dm² compared to a uniform cross-section piezoelectric cantilever beam at 250 rpm, and the output power increased by 11.51%, indicating the success of optimizing the piezoelectric cantilever beam through non-uniform cross-section.

The maximum power output test results of the electret–piezoelectric coupling energy-harvesting structure, based on alternating positive and negative polarities and optimized non-uniform cross-section piezoelectric cantilever beams at different rotational speeds, are shown in Figure 15.

In Figure 15, A represents the coupling structure using identical positive-polarity electrets, while B represents the coupling structure using alternating positive- and negative-polarity electrets. Due to the coupling of the magnetically actuated piezoelectric component with the electret electrostatic component, the energy-harvesting structure operates over a wide range rather than being concentrated at a specific working point. As the rotational speed increases, the output of the device gradually rises, reaching a maximum power output of 6.74 mW. The magnetically actuated piezoelectric component’s output increases with the rotational speed because the intermittent magnetic driving becomes more frequent, in line with the previous analysis. The device in this paper is designed for low-frequency excitation; if the rotational speed is too high, causing the frequency of the permanent magnet exciting the piezoelectric cantilever beam to even reach its resonance frequency, the model proposed in this paper may not be applicable. Then, compared to the identical arrangement of positively charged electrets, the alternating arrangement of positive and negative electrets increases the rate of induced charge variation and the relative charge difference, resulting in an average power output increase of 0.71 mW for components of the same volume, confirming the validity of the theoretical and simulation models in Section 3.1. Additionally, the output power density of the piezoelectric component is greater, compensating for the insufficient output power when using electrostatic components. Based on the aforementioned test results, a comparison of the device designed in this study with other rotational energy-harvesting devices is presented in

Table 1. Comparison of the device based on a non-contact electret–piezoelectric coupling structure with other rotational energy-harvesting devices.

Authors	Energy Harvesters	Output of Device	Key Features
M.Z. Bi et al. (2017) [18]	EEH of electret.	Reach 10.5 mW at 750 rpm, with 32 electrodes and 1500 V electrets.	Innovatively designed a rotational energy-harvesting structure with the same polarity electret.
M.Z. Bi et al. (2020) [19]	EEH of electret.	Reach 18.3 mW at 1000 rpm, 31% higher than that of the previous design.	Based on research [18], further optimization of the device’s electrical performance is conducted.
W.H. Zhang et al. (2023) [20]	Integrated EMEH and TEH.	The output power of DC-TEH and EMEH reach 1.78 mW and 215 mW at 180 rpm.	Proposed DC-TEH integrated with EMEH to reduce losses caused by rectification and optimize output.
Y.G. Gui et al. (2024) [21]	Integrated EMEH and TEH.	Open-circuit voltage and short-circuit current reach 3940 V and 8 mA at 120 rpm.	Designed and optimized an integrated harvester tailored to the specific requirements of designed C2H2 sensor.
Q. Wang et al. (This study)	Integrated EEH and PEH.	Reach 6.74 mW at 700 rpm, with 16 electrodes and 600 V electrets.	Designed and optimized an electret–piezoelectric coupling structure, with advantages of non-contact and facilitating integrated measurement and supply.

.

In summary, the coupling structure proposed in this study has the advantages of non-contact and facilitating integrated measurement and supply. The experimental results demonstrate the correctness of the theoretical analysis and modeling, achieving the optimized design of the coupled structure and confirming the advantages.

5. Conclusions

This paper presents a coaxial rotating non-contact coupling transducer structure based on the principles of electrostatic induction and magnetically actuated piezoelectric transduction. Although the absolute charge amount of the polar plates in the electret structure with alternating positive and negative polarities is reduced, it significantly enhances the charge variation amplitude and the charge difference between the electrodes. Consequently, the open-circuit voltage and short-circuit current of electret component are markedly increased. Additionally, the output electrical signal is less susceptible to interference, which is positively correlated with rotational speed and brief, making it more suitable than piezoelectric components for deriving rotational speed and wind speed information through inverse analysis. The magnetically actuated piezoelectric component, with an appropriately designed variable cross-section, exhibits a smaller stress distribution under load, resulting in a more stable structure. This design also changes the open-circuit voltage and natural frequency to optimize output performance and compensates for the low power density of the electrostatic components. The non-contact superposition coupling of multiple pairs of electret and piezoelectric transducers reliably enhances the absolute output of the device while providing complementary integration, broadening the operational frequency range, and optimizing performance at low rotational speeds. This design also extends the device’s lifespan. By integrating the output characteristics of each component, an energy management circuit is designed, and the device is tested. It operates reliably within a rotational speed range of 100–700 rpm, achieving a maximum overall output power of 6.74 mW. The output of the electret electrostatic component’s electrodes nearly doubled, while the output of the magnetically actuated piezoelectric component increased by up to 11.51% under certain conditions. Additionally, the signal from the electret electrostatic component exhibited a strong and brief positive correlation with rotation speed, validating the theoretical analysis. In summary, the non-contact coupled rotational energy-harvesting structure designed in this study can reduce device wear and operate over a wide range of wind speeds. The electret electrostatic component and the piezoelectric component complement each other, offering the potential for application in wind speed measurement. Additionally, by optimizing the arrangement and size, the output capability of the components is enhanced within the same space. This provides a new approach for the sustainable, reliable, and integrated design of wind-energy-harvesting devices.