Abstract
This study introduces four novel configurations of first-order and second-order multifunction inverse filters in both voltage-mode (VM) and current-mode (CM) using second-generation voltage conveyors (VCIIs). The first-order VM and CM inverse filters utilize only three passive components together with one VCII for VM and two VCIIs for CM realizations, which can provide lowpass and highpass inverse filter responses. The latter, second-order VM and CM multifunction inverse filters, can be constructed using the corresponding first-order inverse filters as their core circuits. These filters offer all the basic inverse filter functions, including lowpass, bandpass, and highpass inverse responses with all gains obtained from the same design. All the inverse filter realizations are cascadable. No component matching requirements are necessary for all filter responses. The non-ideal effects of the VCII on the performance of the proposed inverse filters are thoroughly examined. To prove the feasibility of the designs, the PSPICE program performed several simulations, utilizing model parameters of 0.18 µm CMOS technology. Some testing experiments were conducted using the commercially available IC-type AD844s for evaluating the practical performance of the designed inverse filters.
1. Introduction
In control and instrumentation, and speech applications, inverse filters are crucial circuit components used to correct distorted output signals resulting from linear or nonlinear transformations caused by signal processors or transmission systems. This filter has a frequency response that is inversely proportional to the frequency response of the system, leading to distortion. The design of inverse filters is also necessary in several communication applications, such as monitoring the relative cleanness of a signal and de-emphasizing FM systems. In control systems, it is necessary to employ inverse lowpass, highpass, and bandpass filter functions for the implementation of proportional–integral, proportional–derivative, and proportional–integral–derivative controllers. For these reasons, the authors in [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31] explicitly discuss the design and implementation of inverse filters utilizing different modern active components. The previous studies operate in various modes such as voltage mode (VM) [1,6,8,9,10,11,13,14,15,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31], current mode (CM) [2,3,4,5,7,12,14,15,17,30], and transadmittance mode [16]. In addition, the authors in [5,6,7,23,29,31] specifically developed first-order inverse filters, whereas the works referenced as [1,2,3,4,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,26,27,28,29,30] deal with second-order inverse filters.
In [1], a comprehensive approach utilizing nullors as fundamental components was introduced to derive the inverse transfer function for linear dynamic systems and the inverse transfer characteristic for nonlinear resistive circuits. An example of a Sallen–Key HP filter and the inverse of a half-wave rectifier has also been used to illustrate this approach. The previous study described in [2] provided a procedure for transforming a VM op-amp-based RC filter into a CM, four-terminal floating nullor (FTFN)-based inverse filter. The realization approach employs a network representation that utilizes nullors and RC:CR dual transformation. The work in [3] demonstrates a general method for deriving FTFN-based CM inverse filters from well-known VM filters, as well as generating a CM inverse filter from the Friend–Delyannis biquad. Since FTFN is not available commercially, one can realize it using two second-generation current conveyors (CCIIs) or two current feedback operational amplifiers (CFOAs). A number of CM inverse filter implementations using a single FTFN have been described in [4], where the simulation results reported in this study were obtained by synthesizing the FTFN using two CCIIs. Numerous additional inverse filters were given in [5,6,7,8,16,20,21,22,23,24,25]. Each configuration provides a single inverse filter function. Multifunction second-order inverse filter realizations employing more than two active components are suggested in [8,9,10,11,14,15,16,17,19,26,27,29]. Some of them also require a significant number of passive components for their realizations, i.e., at least seven passive components [17,20,21,24,25,29,30]. In [12], it is observed that the output current of the CM inverse filter is sensed through the passive components, requiring an additional buffer stage to connect to the next stage. The output voltage terminals of the second-order VM inverse filter designs in [13,14,18,19,20,21,23,24,28] do not explicitly have a low impedance level. Thus, these filters are not appropriate for cascadable connections.
This study emphasizes the use of the second-generation voltage conveyors (VCIIs) as active components in designing multifunction inverse filters. Four configurations implementing first-order and second-order inverse filters in both VM and CM are presented. The suggested first-order VM inverse filter employs only one VCII and three passive components to realize both inverse lowpass (ILP) and inverse highpass (IHP) filter functions by appropriately selecting the external impedance type. With its very low output impedance, it is suitable for cascading in VM operation. By cascading the suggested first-order VM inverse filter, the second-order VM inverse filter with all the generic inverse filter realizations, i.e., ILP, IHP, and inverse bandpass (IBP), can be obtained. The third proposed circuit features a first-order CM configuration with two VCIIs and three passive elements. On the other hand, the fourth configuration is the second-order CM type that provides ILP, IHP, and inverse allpass (IAP) filter responses within the same circuit design. Both of the proposed CM inverse filters exhibit a low-input impedance and a high-output impedance, which permits full cascadability. All of the proposed circuits possess the characteristic of orthogonal control of their pole frequency and minimum gain and do not require any criteria for component matching. The theoretical predictions are confirmed by PSPICE simulation results using TSMC 0.18 μm CMOS model parameters. Furthermore, the laboratory testing involved the utilization of commercially available IC-type AD844 CFOAs for measurement purposes. Table 1 and Table 2, respectively, provide comprehensive comparisons between previously available inverse filters and the proposed circuits in VM and CM operations. They list the advantages and disadvantages of both the previously reported works and the proposed circuits in terms of filter order, available response, cascadability, passband tunability, active and passive component count, required technology, supply voltage levels, and power dissipation.

Table 1.
Comparison of the previously available similar VM circuits and the proposed VM inverse filter.

Table 2.
Comparison of the previously available similar CM circuits and the proposed CM inverse filter.
2. Second-Generation Voltage Conveyor (VCII)
The proposed designs are based on the use of the VCII as an active element. The VCII is symbolically represented in Figure 1, which also provides the following description of its terminal relationship:
where β is the current gain between the y and x terminals, and α is the voltage gain between the x and z terminals. In an ideal case, the gain values β and α are both equal to unity. The “+” and “–” signs in Equation (1) indicate the positive VCII (VCII+) and negative VCII (VCII-), respectively. Equation (1) also reveals that the VCII has a low-input impedance y terminal, a high-output impedance x terminal, and a low-output impedance z terminal.
vy = 0, ix = ±β iy, and vz = α vx,
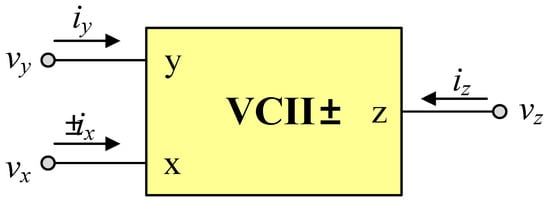
Figure 1.
Electrical symbol of the VCII.
3. Proposed Cascadable Voltage-Mode Inverse Filters
Using the VCII in Figure 1 as an active component, the implementations of the first-order and second-order VM inverse filters are demonstrated in Figure 2.
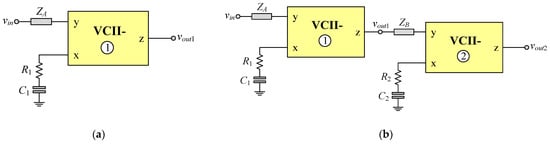
Figure 2.
Proposed VCII-based VM inverse filters. (a) 1st-order filter; (b) 2nd-order filter.
3.1. First-Order VM Inverse Filter Realization
Figure 2a depicts the realization of the first-order VM inverse filter. The circuit requires one VCII-, one resistor (R1), one capacitor (C1), and one impedance (ZA). It is worth noting that the output voltage terminal of the circuit is directly obtained from the z terminal of VCII-. This configuration offers the benefit of a cascadable terminal with a low output impedance. A straightforward circuit analysis assuming ideal VCII yields the following inverse filter transfer function:
Equation (2) clearly indicates that, by appropriately configuring the impedance ZA, the first-order ILP and IHP filter responses could be realized in a single configuration, as demonstrated in Table 3. As can also be seen from the table, the gain (G0) values of ILP and IHP filters can be tuned independently through CA and RA, respectively. An additional advantage of this realization is that no element-matching realizability conditions are necessary.

Table 3.
Selection of impedance ZA for the first-order VM inverse filter in Figure 2a.
3.2. Second-Order VM Inverse Filter Realization
Figure 2b illustrates the proposed realization of the second-order VM inverse filter, which is constructed using the cascade connection of the first-order VM inverse filter in Figure 2a. This topology still exhibits a low output impedance, making it appropriate for cascading in VM operation. The voltage transfer function of the circuit is given by
where
Similarly, the suitable impedance choices for ZA and ZB as specified in Table 4 would lead to the required second-order ILP, IHP, and IBP filter responses.

4. Proposed Cascadable Current-Mode Inverse Filters
4.1. First-Order CM Inverse Filter Realization
By slightly modifying the configuration depicted in Figure 2a, the circuit can perform a CM inverse filter as shown in Figure 3a. It consists of a primary circuit from Figure 2a and an additional VCII- #2. Due to its low input impedance and high output impedance, the scheme supports cascading inputs and outputs for CM operation. By selecting the appropriate impedance ZA, the proposed circuit in Figure 3a generates the following filter-order inverse frequency response for CM at the terminal iout1, which possesses the critical characteristics detailed in Table 5.
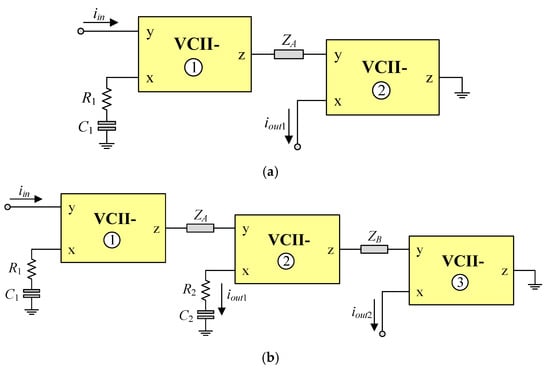
Figure 3.
Proposed VCII-based CM inverse filters. (a) 1st-order filter; (b) 2nd-order filter.

Table 5.
Selection of impedance ZA for the first-order CM inverse filter in Figure 3a.
4.2. Second-Order CM Inverse Filter Realization
The construction of the second-order CM inverse filter in Figure 3b involves cascading the first-order section of VCII- #2, R2, C2, and ZB from Figure 3a. The resulting circuit realizes the following CM transfer function at the current output terminal, iout2.
By choosing the impedances ZA and ZB as shown in Table 6, one can then realize three different second-order CM inverse filter functions.

5. Tracking Error Analysis
In non-ideal operation, current and voltage transfer errors may cause deviations from the actual values of the proposed filters. To evaluate the effect of the VCII tracking errors on the circuit performance, the gain values β and α of the k-th VCII-, where k = 1, 2, and 3, are defined as βk and αk, respectively. We also denote that βk = (1 − εi) and αk = (1 − εv), where εi (|εi| << 1) and εv (|εv| << 1) are the current and voltage tracking errors, respectively.
Consequently, we perform non-ideal analyses of the proposed circuits in Figure 2 and report their non-ideal parameters in Table 7 and Table 8. Following a similar manner, we also analyze the circuits depicted in Figure 3 for non-ideal transfer gains and present the non-ideal parameters in Table 9 and Table 10. For example, if the VCII- has gain values of β = 1.1023 and α = 0.9818 [32], and equal-value resistors and capacitors R1 = RA and C1 = CA are employed for the filter implementation, then according to Table 7, the minimum gain of the first-order VM inverse filter in Figure 2a is G0 = 1.082, which corresponds to an error of 8.2%.

Table 7.
Non-ideal parameters of the first-order VM inverse filter in Figure 2a.

Table 8.
Non-ideal parameters of the second-order VM inverse filter in Figure 2b.

Table 9.
Non-ideal parameters of the first-order CM inverse filter in Figure 3a.

Table 10.
Non-ideal parameters of the second-order CM inverse filter in Figure 3b.
From Table 7, Table 8, Table 9 and Table 10, it is obvious that the non-ideal values of ω0 and Q are not influenced by the current and voltage tracking error coefficients. The VCII tracking errors may result in slight changes in the gain values of the realized inverse filters. Nevertheless, the pre-distortion values of RA, RB, CA, or CB can compensate for this impact without affecting the ω0 value.
6. Parasitic Element Analysis
To conduct a further non-ideality analysis, it is necessary to consider the effect of the VCII parasitics on the filter characteristics. For this purpose, we use the non-ideal behavior model of the VCII, which includes a finite input resistance Ry at port y, a parasitic resistance Rx in parallel with a parasitic capacitance Cx at port x, and a low z-port resistance Rz. Figure 4 illustrates the equivalent circuit for the non-ideal VCII with its parasitic elements.
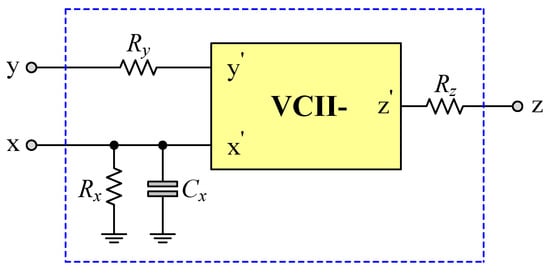
Figure 4.
Non-ideal equivalent circuit for the VCII with its parasitics.
6.1. Parasitic Effects on VM Inverse Filter Realization
A straightforward analysis of the proposed first-order VM inverse filter in Figure 2a using the VCII’s non-ideal model in Figure 4 yields the non-ideal transfer functions of the ILP and IHP filters given by the following expressions:
Typically, the value of Rx is extremely high, while the values of Ry and Cx are extremely small. As a consequence, Rx >> R1, RA >> Ry, and Cx << C1. Equations (7) and (8) demonstrate that the VCII parasitics introduce extra poles at frequencies fv1 = (1/2πR1Cx) and fv2 = (1/2πRyCA) for the ILP filter response, and at frequency fv1 in IHP. Therefore, the useful frequencies of the first-order VM ILP and IHP filters are approximated as follows:
1st-order ILP: f << min [fv1, fv2],
1st-order IHP: f << min [fv1].
For instance, if the parasitic elements of the VCII- are Ry = 38.88 Ω, Rx = 109.24 kΩ, Rz = 38.23 Ω, and Cx = 3 pF [32], and the filter components are chosen as R1 = 1 kΩ and CA = 100 pF, then the pole frequencies will be located at frequencies fv1 = 53.08 MHz and fv2 = 40.93 MHz. This implies that the first-order VM ILP and IHP filters proposed here have high frequency limitations of approximately 40.93 MHz and 53.05 MHz, respectively.
By taking into account the VCII parasitic effect on the second-order VM inverse filter realization of Figure 2b, the non-ideal transfer functions of ILP, IHP, and IBP filters are as follows:
where Cxk and Ryk are the parasitic elements Cx and Ry of the k-th VCII-. Suppose that , , , and , then the operating frequency ranges of the proposed second-order VM ILP, IHP, and IBP filters can be defined as follows:
2nd-order ILP: f << min [fv1, f″v1, f′v2, f″v2],
2nd-order IHP: f << min [f′v1, f″v1],
2nd-order IBP: f << min [f′v1, f″v1, f′v2].
These effects on the realized filter performance can be considerably minimized if the operating frequencies are chosen sufficiently lower than the parasitic pole frequencies of VCII-.
6.2. Parasitic Effects on CM Inverse Filter Realization
The non-ideal transfer functions of the proposed CM first-order inverse filter in Figure 3a are derived by accounting for the parasitic nature of the VCII-:
If and , then the frequency limitations of the proposed first-order CM ILP and IHP filters should lie in the following ranges:
1st-order ILP: f << min [fi1, fi2],
1st-order IHP: f << min [fi1].
Furthermore, we have also considered the parasitic effect on the proposed CM second-order inverse filter structure in Figure 3b. The various non-ideal expressions of ILP, IHP, and IBP filter responses are as follows:
2nd-order ILP:
2nd-order IHP:
2nd-order IBP:
which represent the additional pole frequencies expressed by , , , and .
Therefore, the frequency ranges of operation of the proposed CM second-order inverse filter in Figure 3b can be approximated from the above relations as follows:
2nd-order ILP: f << min [f′i1, f″i1, f′i2, f″i2],
2nd-order IHP: f << min [f′i1, f″i1],
2nd-order IBP: f << min [f′i1, f″i1, f′i2].
7. Simulation Verification of Filter Responses
The validity of the cascadable inverse filters proposed in Figure 2 and Figure 3 has been evaluated through a simulation conducted by PSPICE program version 16.5. In the simulation analysis, the CMOS structure of the VCII- as shown in Figure 5 has been implemented [33,34]. The ratio of width (W) to channel length (L) of the CMOS transistors employed is listed in Table 11. Supply voltages of +V = −V = 0.75 V and biasing currents of IB1 = IB2 = 25 μA are used. All the proposed inverse filter structures are tested with identical resistors and capacitors, where R1 = R2 = RA = RB = 1 kΩ, and C1 = C2 = CA = CB = 100 pF for the theoretical pole frequency of f0 = ω0/2π = 1.59 MHz.
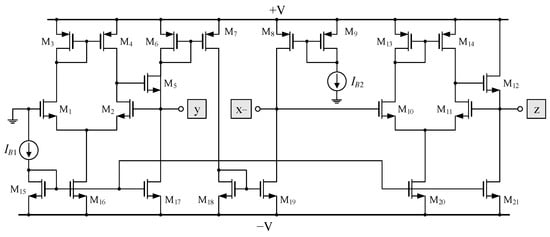
Figure 5.
CMOS implementation of VCII-.

Table 11.
W/L of the MOS transistors in Figure 5.
The simulated time and frequency responses of the VM and CM inverse filters in Figure 2 and Figure 3 compared with the theoretical responses are given in Figure 6, Figure 7, Figure 8 and Figure 9. The proposed circuits are tested at a signal frequency of 1.59 MHz with an input signal amplitude of 50 mV (peak) for VM and 50 μA (peak) for CM. The total power consumptions of the first- and second-order VM inverse filters are 0.255 mW and 0.511 mW, respectively, while the first- and second-order CM inverse filters are 0.511 mW and 0.766 mW.
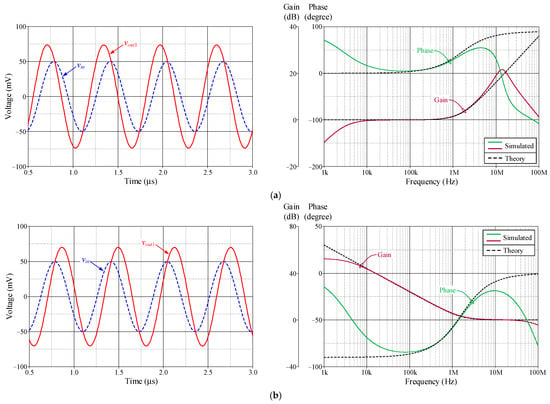
Figure 6.
Time and frequency responses of the first-order VM inverse filter in Figure 2a. (a) ILP responses; (b) IHP responses.
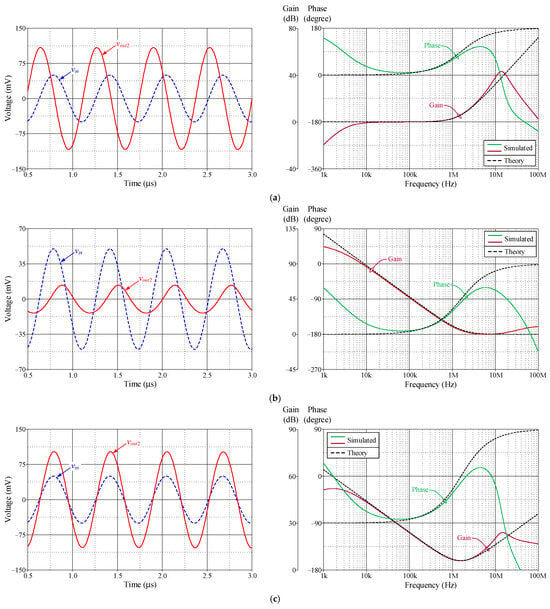
Figure 7.
Time and frequency responses of the second-order VM inverse filter in Figure 2b. (a) ILP responses; (b) IHP responses; (c) IBP responses.
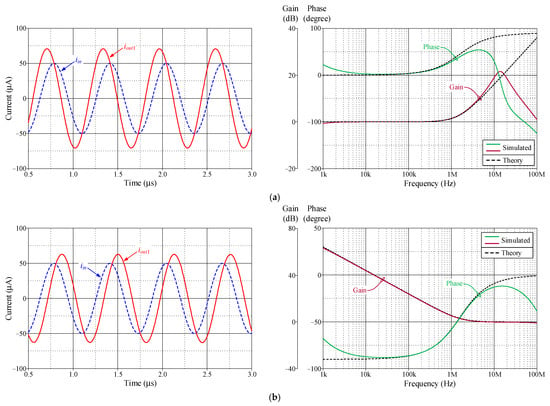
Figure 8.
Time and frequency responses of the first-order CM inverse filter in Figure 3a. (a) ILP responses; (b) IHP responses.
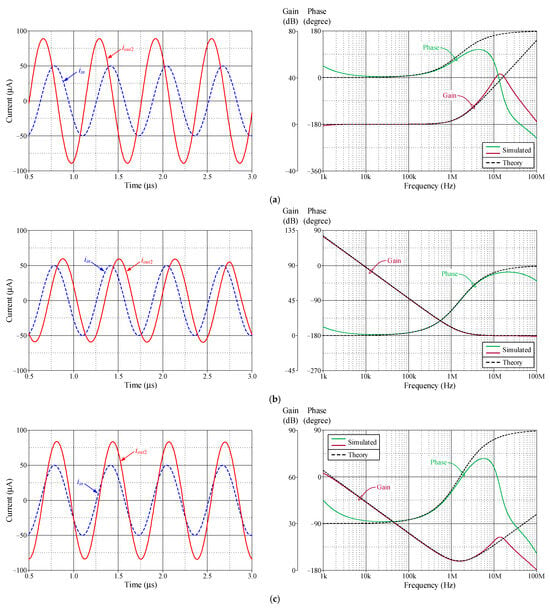
Figure 9.
Time and frequency responses of the second-order CM inverse filter in Figure 3b. (a) ILP responses; (b) IHP responses; (c) IBP responses.
The simulated cut-off frequency f0 for the first-order VM ILP and IHP responses was measured at 1.56 MHz and 1.54 MHz, respectively, and the corresponding f0 values for the second-order ILP, IHP, and IBP responses were 1.57 MHz, 1.52 MHz, and 1.55 MHz. For the CM inverse filters, the simulated f0 values of the first-order ILP and IHP responses were 1.57 MHz and 1.50 MHz, while the second-order ILP, IHP, and IBP filters provided the simulated f0 at 1.57 MHz, 1.52 MHz, and 1.56 MHz, respectively.
The f0-tuning for the IBP filter in Figure 2b was simulated with a constant value of Q. The capacitor and resistor values are C1 = C2 = CA = 100 pF, RB = 1 kΩ, and R1 = R2 = 0.5 kΩ, 2 kΩ, and 5 kΩ. With a fixed Q-value of 0.5, the corresponding values for f0 are 3.18 MHz, 795.77 MHz, and 318.31 MHz, respectively. Figure 10 illustrates the ideal and simulated gain–frequency responses, demonstrating the ability to independently adjust the f0-value of the proposed filter. The proposed VM IBP filter in Figure 2b was also simulated at different temperatures, including 0 °C, 25 °C, 50 °C, 75 °C, and 100 °C. The simulations were conducted with C1 = C2 = CA = 100 pF and R1 = R2 = RB = 1 kΩ, and the obtained results are shown in Figure 11. It is observed that the gain–frequency response of the suggested circuit is found to increase with temperature. The working transistor current reduces with increasing temperature, whilst the values of resistors and capacitors increase, leading to an increase in gain. In this instance, temperature variations influence the gain response of the proposed inverse filter, as it is dependent upon the currents in the transistor devices and the values of the resistors and capacitors. At f0 = 1.59 MHz, the deviations from its nominal value in voltage gain due to temperature variations are approximately −0.88 dBV at 0 °C and +7.10 dBV at 100 °C, which can be considered insignificant.
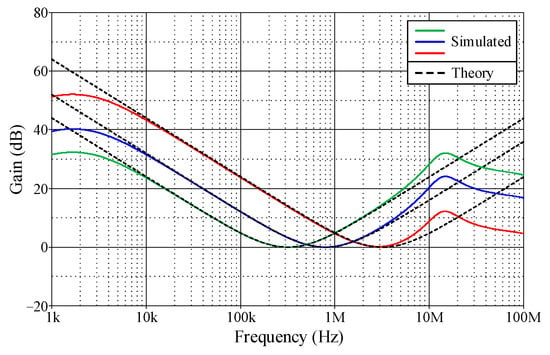
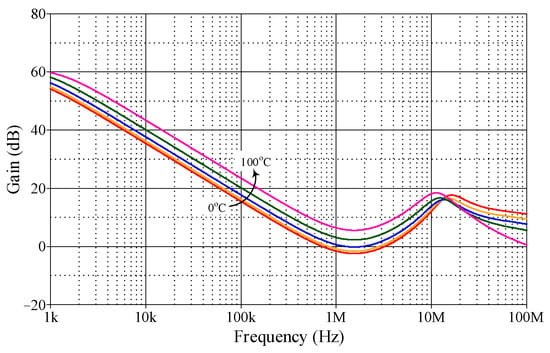
Figure 11.
Frequency responses of the IBP filter circuit in Figure 2b at different temperatures (0 °C, 25 °C, 50 °C, 75 °C, and 100 °C).
Furthermore, a Monte Carlo (MC) statistical analysis was performed on the VM IBP filter at the pole frequency of 1.59 MHz, considering nominal 5% tolerances in the values of resistors and capacitors. Figure 12 depicts the MC simulation results with a Gaussian distribution for 200 runs. The mean and standard deviation in f0 resulting from the changes in resistor and capacitor tolerances were obtained at 1.72 MHz and 47.92 kHz, respectively, even though it is not considerable.
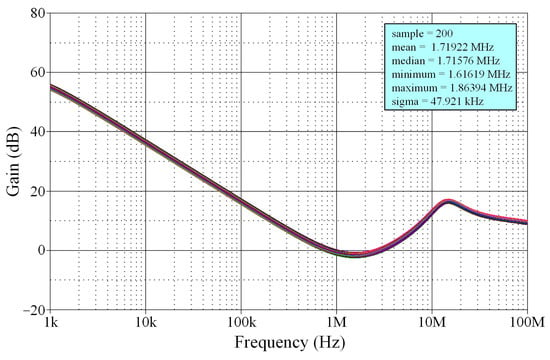
Figure 12.
Monte Carlo statistical analysis results of the VM IBP filter response.
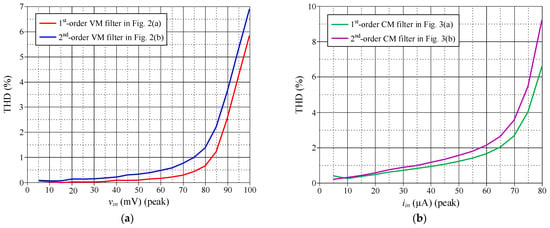
The variations in total harmonic distortion (THD) against peak sinusoidal input signal amplitudes of the proposed VM and CM inverse filters in Figure 2 and Figure 3 at 1.59 MHz operating frequency are illustrated in Figure 13a,b, respectively. The THD plots reveal that, with THD values below 1.5%, the proposed VM inverse filters can handle signals with a peak amplitude of up to 80 mV. For the proposed CM inverse filters, THD remains below 2% when the input signal amplitude is less than 55 μA peak. Furthermore, the THD can be significantly decreased by increasing the bias current of the VCII, although with an associated increase in power consumption.
8. Experimental Verification
The experimental laboratory measurement has been carried out to further validate the practicability of the proposed design. For this purpose, the practical VCII- has been realized using commercially available IC-type AD844s, as shown in Figure 14 [34]. The DC bias voltages were set to +V = −V = 5 V. The resistor and capacitor have values of R1 = 1 kΩ and C1 = CA = 1 nF, respectively, to obtain an ideal pole frequency of f0 = 159 kHz. Figure 15 shows the experimentally measured time and frequency responses for the proposed first-order VM inverse filter in Figure 2a along with the corresponding ideal responses. The input voltage was set at 100 mV peak-to-peak with a frequency of 159 kHz. The testing results thus verify the feasibility of the proposed concept. However, discrepancy between the measured responses and the theoretical predictions is mainly attributed to the tolerances of the passive components and the parasitic impedance effects of the AD844s used in hardware implementation. Note that for the AD844, the parasitic components are Rx = 50 Ω, Rz = 3 MΩ, and Rw = 15 Ω [35].
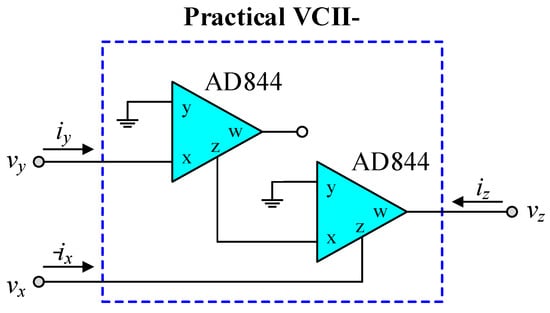
Figure 14.
Practical realization of the VCII- using commercially available IC AD844s.
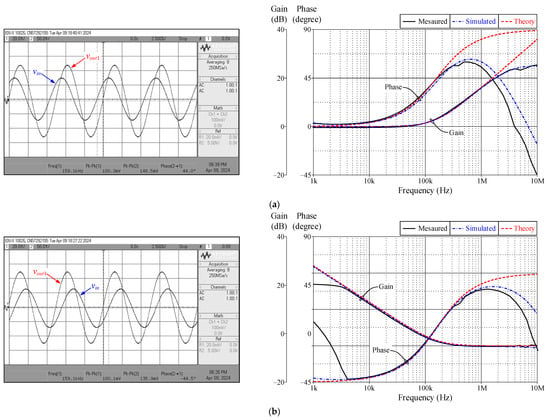
Figure 15.
Experimentally measured time and frequency responses for the first-order VM inverse filter in Figure 2a. (a) ILP responses; (b) IHP responses.
9. Conclusions
Four circuit configurations for realizing first- and second-order inverse filters using second-generation voltage conveyors (VCIIs) have been presented in this paper. Both proposed first-order inverse filters in VM and CM can realize ILP and IHP filter functions using the same circuit topology by the appropriate selection of the branch impedance. Using the same circuit concept, both of the proposed second-order VM and CM inverse filters can provide ILP, IBP, and IHP filter functions from a single design. All the suggested circuits are appropriate for cascade connections. By modifying the passive element values, it is possible to independently control the pole frequency and gain of the filters. Analyses of non-ideal performance, such as transfer errors and parasitic effects, have been examined in relation to theoretical performance. The feasibility of the circuits was confirmed by PSPICE simulations and laboratory testing measurements.
Author Contributions
Conceptualization, N.R. and W.T.; methodology, N.R. and W.T.; software, N.R. and N.L.; validation, N.R., N.L., T.P., M.F. and W.T.; formal analysis, T.P., M.F. and W.T.; investigation, N.R., T.P. and W.T.; resources, N.R. and N.L.; data curation, T.P. and M.F.; writing—original draft preparation, N.R. and N.L.; writing—review and editing, T.P., M.F. and W.T; visualization, N.R., T.P. and W.T.; supervision, T.P., M.F. and W.T; project administration, N.L.; funding acquisition, N.L. and W.T. All authors have read and agreed to the published version of the manuscript.
Funding
This work was financially supported by King Mongkut’s Institute of Technology Ladkrabang [2568-02-01-001].
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Acknowledgments
The authors appreciate the support and infrastructure provided by the Department of Instrumentation and Control Engineering, School of Engineering, King Mongkut’s Institute of Technology Ladkrabang for the completion of this work.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| VM | Voltage mode |
| CM | Current mode |
| VCII | Second-generation voltage conveyor |
| LP | Lowpass |
| HP | Highpass |
| BP | Bandpass |
| AP | Allpass |
| ILP | Inverse lowpass |
| IHP | Inverse highpass |
| IBP | Inverse bandpass |
| IBS | Inverse bandstop |
| IAP | Inverse allpass |
| PI | Proportional-integral |
| PD | Proportional-derivative |
| PID | Proportional-integral-derivative |
| TAM | Trans-admittance mode |
| R | Resistor |
| C | Capacitor |
| Z | Impedance |
| N/A | Not available |
| OA | Operational amplifier |
| FTFN | Four-terminal floating nullor |
| CCII | Second-generation current conveyor |
| CDTA | Current differencing transconductance amplifier |
| CFOA | Current feedback operational amplifier |
| MCFOA | Modified current feedback operational amplifier |
| CDBA | Current differencing buffered amplifier |
| OTA | Operational transconductance amplifier |
| OTRA | Operational transresistance amplifier |
| VDTA | Voltage differencing transconductance amplifier |
| VCVS | Voltage-controlled voltage source |
| SW | Analog switch |
| IC | Integrated circuit |
| TSMC | Taiwan Semiconductor Manufacturing Company |
| N(s) | Numerator polynomials |
| G0 | Gain |
| ω0 | Cut-off frequency |
| f0 | Pole frequency |
| Q | Quality factor |
| dB | Decibel |
| dBV | Voltage decibel |
| MC | Monte Carlo |
References
- Leuciuc, A. Using nullors for realisation of inverse transfer functions and characteristics. Electron. Lett. 1997, 33, 949–951. [Google Scholar] [CrossRef]
- Chipipop, B.; Surakampontorn, W. Realisation of current-mode FTFN-based inverse filter. Electron. Lett. 1999, 35, 690–692. [Google Scholar] [CrossRef]
- Wang, H.Y.; Lee, C.T. Using nullors for realisation of current-mode FTFN-based inverse filters. Electron. Lett. 1999, 35, 1889–1890. [Google Scholar] [CrossRef]
- Abuelma’atti, M.T. Identification of cascadable current-mode filters and inverse-filters using single FTFN. Frequenz 2000, 54, 284–289. [Google Scholar]
- Shah, N.A.; Malik, M.A. FTFN-based dual inputs current-mode allpass inverse filters. Indian J. Radio Space Phys. 2005, 34, 206–209. [Google Scholar]
- Shah, N.A.; Rather, M.F. Realization of voltage-mode CCII-based allpass filter and its inverse version. Indian J. Pure Appl. Phys. 2006, 44, 269–271. [Google Scholar]
- Shah, N.A.; Quadri, M.; Iqbal, S.Z. High output impedance current-mode allpass inverse filter using CDTA. Indian J. Pure Appl. Phys. 2008, 44, 893–896. [Google Scholar]
- Gupta, S.S.; Bhaskar, D.R.; Senani, R.; Singh, A.K. Inverse active filters employing CFOAs. Electr. Eng. 2009, 91, 23–26. [Google Scholar] [CrossRef]
- Wang, H.Y.; Chang, S.H.; Yang, T.Y.; Tsai, P.Y. A novel multifunction CFOA-based inverse filter. Circuits Syst. 2011, 2, 14–17. [Google Scholar] [CrossRef]
- Gupta, S.S.; Bhaskar, D.R.; Senani, R. New analogue inverse filters realised with current feedback op-amps. Int. J. Electron. 2011, 98, 1103–1113. [Google Scholar] [CrossRef]
- Garg, K.; Bhagat, R.; Jaint, B. A novel multifunction modified CFOA based inverse filter. In Proceedings of the 2012 IEEE 5th Indian International Conference on Power Electronics (IICPE), Delhi, India, 6–8 December 2012. [Google Scholar]
- Nasir, A.R.; Ahmad, S.N. A new current-mode multifunction inverse filter using CDBAs. Int. J. Comput. Sci. Infor. Sec. 2013, 11, 50–52. [Google Scholar]
- Pandey, R.; Pandey, N.; Negi, T.; Garg, V. CDBA based universal inverse filter. ISRN Electron. 2013, 2013, 181869. [Google Scholar] [CrossRef]
- Tsukutani, T.; Sumi, Y.; Yabuki, N. Electronically tunable inverse active filters employing OTAs and grounded capacitors. Int. J. Electron. Lett. 2014, 4, 166–176. [Google Scholar] [CrossRef]
- Patil, V.; Sharma, R.K. Novel inverse active filters employing CFOAs. Int. J. Sci. Res. Dev. 2015, 3, 359–360. [Google Scholar]
- Sharma, A.; Kumar, A.; Whig, P. On the performance of CDTA based novel analog inverse low pass filter using 0.35 μm CMOS parameter. Int. J. Sci. Tech. Manag. 2015, 4, 594–601. [Google Scholar]
- Tsukutani, T.; Kunugasa, Y.; Yabuki, N. CCII-based inverse active filters with grounded passive components. J. Electr. Eng. 2018, 6, 212–215. [Google Scholar] [CrossRef][Green Version]
- Singh, A.K.; Gupta, A.; Senani, R. OTRA-based multi-function inverse filter configuration. Advances Electr. Electron. Eng. 2017, 15, 846–856. [Google Scholar] [CrossRef]
- Kumar, P.; Pandey, N.; Paul, S.K. Realization of resistorless and electronically tunable inverse filters using VDTA. J. Circuits Syst. Comput. 2019, 28, 1950143. [Google Scholar] [CrossRef]
- Pradhan, A.; Sharma, R.K. Generation of OTRA-based inverse all pass and inverse band reject filters. Proc. Natl. Acad. Sci. India Sect. A Phys. Sci. 2020, 90, 481–491. [Google Scholar] [CrossRef]
- Bhagat, R.; Bhaskar, D.R.; Kumar, P. Inverse band reject and all pass filter structure employing CMOS CDBAs. Int. J. Eng. Res. Tech. 2019, 8, 39–44. [Google Scholar]
- Bhagat, R.; Bhaskar, D.R.; Kumar, P. Multifunction filter/inverse filter configuration employing CMOS CDBAs. Int. J. Recent Tech. Eng. 2019, 8, 8844–8853. [Google Scholar] [CrossRef]
- Kamat, D.V. New operational amplifier based inverse filters. In Proceedings of the Third International Conference Electronics Communication Aerospace Technology Coimbatore, Delhi, India, 12–14 June 2019; pp. 1177–1181. [Google Scholar]
- Banerjee, S.; Borah, S.S.; Ghosh, M.; Mondal, P. Three novel configurations of second order inverse band reject filter using a single operational transresistance amplifier. In Proceedings of the 2019 IEEE Region 10 Conference (TENCON 2019), Kerala, India, 17–20 October 2019; pp. 2173–2178. [Google Scholar]
- Borah, S.S.; Singh, A.; Ghosh, M. CMOS CDBA based 6th order inverse filter realization for low-power applications. In Proceedings of the 2020 IEEE Region 10 Conference (TENCON 2020), Osaka, Japan, 16–19 November 2020; pp. 11–16. [Google Scholar]
- Kumar, P.; Pandey, N.; Paul, S.K. Electronically tunable VDTA-based multi-function inverse filter. Iran. J. Sci. Technol.–Trans. Electr. Eng. 2021, 45, 247–257. [Google Scholar] [CrossRef]
- Raj, A.; Bhagat, R.; Kumar, P.; Bhaskar, D.R. Grounded-capacitor analog inverse active filters using CMOS OTAs. In Proceedings of the 2021 8th International Conference Signal Process Integrated Networks (SPIN), Noida, India, 26–27 August 2021; pp. 778–783. [Google Scholar]
- Paul, T.K.; Roy, S.; Pal, R.R. Realization of inverse active filters using single current differencing buffered amplifier. J. Sci. Res. 2021, 13, 85–99. [Google Scholar] [CrossRef]
- Al-Absi, M.A. Realization of inverse filters using second generation voltage conveyor (VCII). Analog Integr. Circuits Signal Process. 2021, 109, 29–32. [Google Scholar] [CrossRef]
- Al-Shahrani, S.M.; Al-Absi, M.A. Efficient inverse filters based on second-generation voltage conveyor (VCII). Arabian J. Sci. Eng. 2022, 47, 2685–2690. [Google Scholar] [CrossRef]
- Nako, J.; Psychalinos, C.; Minaei, S. Single-input multiple-output inverse filters designs with cascade capability. Int. J. Electron. Commun. (AEÜ) 2024, 175, 155061. [Google Scholar] [CrossRef]
- Safari, L.; Yuce, E.; Minae, S.; Ferri, G.; Stornelli, V. A second-generation voltage conveyor (VCII)-based simulated, grounded inductor. Int. J. Circuit Theory Appl. 2020, 48, 1180–1193. [Google Scholar] [CrossRef]
- Faseehuddin, M.; Shireen, S.; Sali, S.H.M.; Tangsrirat, W. Novel lossless positive/negative grounded capacitance multipliers using VCII. Elektron. Ir Elektrotechnika 2023, 29, 19–26. [Google Scholar] [CrossRef]
- Faseehuddin, M.; Shireen, S.; Herencsar, N.; Tangsrirat, W. Novel FDNR, FDNC and lossy inductor simulators employing second generation voltage conveyor (VCII). Int. J. Numer. Model. Electron. Netw. Devices Fields 2023, 36, e3100. [Google Scholar] [CrossRef]
- Analog Devices, AD844: 60 MHz, 2000 V/μs, Monolithic op amp with Quad Low Noise. Available online: https://www.analog.com/media/en/technical-documentation/data-sheets/AD844.pdf (accessed on 29 June 2022).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).